Application of state-of-the-art multiobjective metaheuristic algorithms in reliability-based design optimization: a comparative study

Abstract

Multiobjective reliability-based design optimization (RBDO) is a research area, which has not been investigated in the literatures comparing with single-objective RBDO. This work conducts an exhaustive study of fifteen new and popular metaheuristic multiobjective RBDO algorithms, including non-dominated sorting genetic algorithm II, differential evolution for multiobjective optimization, multiobjective evolutionary algorithm based on decomposition, multiobjective particle swarm optimization, multiobjective flower pollination algorithm, multiobjective bat algorithm, multiobjective gray wolf optimizer, multiobjective multiverse optimization, multiobjective water cycle optimizer, success history-based adaptive multiobjective differential evolution, success history-based adaptive multiobjective differential evolution with whale optimization, multiobjective salp swarm algorithm, real-code population-based incremental learning and differential evolution, unrestricted population size evolutionary multiobjective optimization algorithm, and multiobjective jellyfish search optimizer. In addition, the adaptive chaos control method is employed for the above-mentioned algorithms to estimate the probabilistic constraints effectively. This comparative analysis reveals the critical technologies and enormous challenges in the RBDO field. It also offers new insight into simultaneously dealing with the multiple conflicting design objectives and probabilistic constraints. Also, this study presents the advantage and future development trends or incurs the increased challenge of researchers to put forward an effective multiobjective RBDO algorithm that assists the complex engineering system design.

Appendices

Appendix

Multiobjective RBDO for spring

The multiobjective RBDO of spiral squeezing spring is selected as the first example, which is modified from (Kannan and Kramer 1994; Kumar et al. 2021a). The multiobjective RBDO of spring can be deemed as a real mechanical application example with integer, discrete, and continuous variables. The schematic view is shown in Fig. 

Fig. 4

Schematic view of spiral squeezing spring

4. There are two design objectives and eight constraints. The first objective is minimizing volume of the steel wire, while the second objective is minimizing the shear stress. The integer variable $x_{1}$ and the discrete variable $x_{3}$ are considered as the deterministic design variables, while the continuous variable $x_{2}$ is selected as the random variable that obeys the normal distribution with standard deviation 0.005.

$$\begin{array}{*{20}l} {{\text{find}}} \hfill & {{\mathbf{x}} = [x_{1} ,x_{2} ,x_{3} ]^{{\text{T}}} } \hfill \\ {\min } \hfill & {\left[ {f_{1} \left( {\mathbf{x}} \right),f_{2} \left( {\mathbf{x}} \right)} \right]} \hfill \\ {{\text{s}}{\text{.t}}{\text{.}}} \hfill & {P[G_{i} ({\mathbf{x}}) > 0] \ge \Phi (\beta _{i}^{t} );\;i = 1 - 8} \hfill \\ \end{array}$$

(12)

where

$$\begin{gathered} f_{1} \left( {\mathbf{x}} \right) = \frac{{\pi ^{2} x_{2} x_{3}^{2} (x_{1} + 2)}}{4}, \hfill \\ {\quad}f_{2} ({\mathbf{x}}) = \frac{{8000C_{f} x_{2} }}{{\pi x_{3}^{3} }},{\text{ }} \hfill \\ G_{1} ({\mathbf{x}}) = 189000 - \frac{{8000C_{f} x_{2} }}{{\pi x_{3}^{3} }}, \hfill \\ {\quad}G_{2} ({\mathbf{x}}) = 14 - l_{f} ,{\text{ }} \hfill \\ G_{3} ({\mathbf{x}}) = x_{3} - 0.2, \hfill \\ {\quad}G_{4} ({\mathbf{x}}) = 3 - x_{2} ,{\text{ }} \hfill \\ G_{5} ({\mathbf{x}}) = \frac{{x_{2} }}{{x_{3} }} - 3, \hfill \\ {\quad}G_{6} ({\mathbf{x}}) = 6 - \sigma _{p} , \hfill \\ G_{7} ({\mathbf{x}}) = l_{f} - \sigma _{p} - \frac{{700}}{K} - 1.05(x_{1} + 2)x_{3} , \hfill \\ {\quad}G_{8} ({\mathbf{x}}) = \frac{{700}}{K} - 1.25 \ge 0,{\text{ }} \hfill \\ C_{f} = \frac{{4{{x_{2} } \mathord{\left/ {\vphantom {{x_{2} } {x_{3} }}} \right. \kern-\nulldelimiterspace} {x_{3} }} - 1}}{{4{{x_{2} } \mathord{\left/ {\vphantom {{x_{2} } {x_{3} }}} \right. \kern-\nulldelimiterspace} {x_{3} }} - 4}} + \frac{{0.615x_{3} }}{{x_{2} }},K = \frac{{11.5 \times 10^{6} x_{3}^{4} }}{{8x_{1} x_{2}^{3} }}, \hfill \\ \sigma _{p} = \frac{{300}}{K},l_{f} = \frac{{1000}}{K} + 1.05(x_{1} + 2)x_{3} , \hfill \\ {\quad}\beta _{1}^{t} = \beta _{2}^{t} = \cdot \cdot \cdot = \beta _{8}^{t} = 3.0, \hfill \\ \end{gathered}$$

(13)

$$\begin{gathered} 1 \le x_{1} ({\text{integer}}) \le 70, \hfill \\ 0.6 \le x_{2} ({\text{continuous}}) \le 3, \hfill \\ {\kern 1pt} x_{3} ({\text{discreate}}) \in \{ 0.009,0.0095,0.0104,0.0118,0.0128,0.0132,0.014,0.015,0.0162,0.0173, \hfill \\ \quad \quad \quad \quad \quad \quad 0.018,0.020,0.023,0.025,0.028,0.032,0.035,0.041,0.047,0.054,0.063, \hfill \\ \quad \quad \quad \quad \quad \quad 0.072,0.080,0.092,0,0105,0.120,0.135,0.148,0.162,0.177,0.192,0.207, \hfill \\ \quad \quad \quad \quad \quad \quad 0.225,0.244,0.263,0.283,0.307,0.0331,{\kern 1pt} 0.362,0.394,0.4375,0.500\} , \hfill \\ x_{2} \sim N(\mu _{{x_{2} }} ,0.005). \hfill \\ \end{gathered}$$

Multiobjective RBDO for simply supported I-beam

A simply supported I-beam is used as the second examples, which is widely tested by different researches (Huang et al. 2006; Kumar et al. 2021a). The schematic diagram is plotted in Fig. 

Fig. 5

Schematic view of simply supported I-beam

5. There are two loads, i.e., P = 600 kN and Q = 50 kN. The Young’s modulus E is 2 × 10⁴ kN/cm². The length L is 200 cm. The allowable bending stress σ_b is 16 kN/cm². Two design objectives are minimizations of cross-sectional area and vertical deflection. The stress constraint is utilized. The geometric dimensions are selected as the design and random variables, which are assumed following the normal distribution with standard deviation 0.005.

$$\begin{gathered} {\text{find}}\quad {\mathbf{x}} = [x_{1} ,x_{2} ,x_{3} ,x_{4} ] \hfill \\ \min \quad \,f\left( {\mathbf{x}} \right) = \left[ {f_{1} \left( {\mathbf{x}} \right),{\kern 1pt} \,f_{2} \left( {\mathbf{x}} \right)} \right] \hfill \\ {\text{s}}{\text{.t}}{\text{.}}\quad \;\;P\left( {G({\mathbf{x}}) > 0} \right) \ge \Phi \left( {\beta _{{}}^{t} } \right) \hfill \\ {\text{where}} \hfill \\ {\kern 1pt} \quad \quad \quad f_{1} = 2x_{2} x_{4} + x_{3} (x_{1} - 2x_{4} ), \hfill \\ {\kern 1pt} \quad \quad \quad f_{2} = \frac{{PL^{3} }}{{4E\left( {x_{3} (x_{1} - 2x_{4} )^{3} + 2x_{2} x_{4} (4x_{4}^{2} + 3x_{1} (x_{1} - 2x_{4} ))} \right)}}, \hfill \\ {\kern 1pt} \quad \quad \quad G\left( {{\mathbf{x}},{\mathbf{z}}} \right) = 16 - \frac{{18000x_{1} }}{{x_{3} \left( {x_{1} - 2x_{4} } \right)^{3} + 2x_{2} x_{4} \left( {4x_{4}^{2} + 3x_{1} (x_{1} - 2x_{4} )} \right)}} \hfill \\ {\kern 1pt} \quad \quad \quad \quad \quad \quad \quad - \frac{{15000x_{2} }}{{\left( {(x_{1} - 2x_{4} )x_{3}^{3} + 2x_{4} x_{2}^{3} } \right)}}, \hfill \\ {\kern 1pt} \quad \quad \quad P = 600,L = 200,E = 20000, \hfill \\ \quad \quad \quad \beta _{{}}^{t} = 3.0,\; \hfill \\ \quad \quad \quad \;10 \le x_{1} \le 80,\;10 \le x_{2} \le 50, \hfill \\ \quad \quad \quad \;0.9 \le x_{3} \le 5,\;\;0.9 \le x_{4} \le 5, \hfill \\ \quad \quad \quad \;x_{i} \sim N(\mu _{{x_{i} }} ,0.005^{2} ). \hfill \\ \end{gathered}$$

(14)

Multiobjective RBDO for ten bar truss

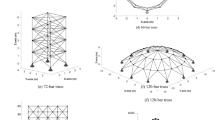
A ten bar truss is tested, which is modified from (Yi et al. 2008). The boundary condition is illustrated in Fig. 

Fig. 6

Schematic view of ten bar truss

6. The values of loads P₁ and P₂ are 10⁵ Psi. The Young’s modulus is 10⁷ Psi. Both compliance and volume are selected as the design objectives. The first ten constraints are the stresses should be less than 2.5 × 10⁴ Psi, while the eleventh constraint is the allowable vertical nodal displacement should be less than 4.5 in. The multiobjective RBDO model is as follows:

$$\begin{gathered} {\text{find}}\quad {\mathbf{x}} = [x_{1} ,x_{2} ,x_{3} ,x_{4} ,x_{5} ,x_{6} ,x_{7} ,x_{8} ,x_{9} ,x_{{10}} ] \hfill \\ \min \quad \,f\left( {\mathbf{x}} \right) = \left[ {f_{1} \left( {\mathbf{x}} \right),{\quad} f_{2} \left( {\mathbf{x}} \right)} \right] \hfill \\ {\text{s}}{\text{.t}}{\text{.}}\quad \; P\left( {G_{i} ({\mathbf{x}}) > 0} \right) \ge \Phi \left( {\beta _{i}^{t} } \right);{\quad} i = 1 - 11 \hfill \\ {\text{where}}\,\, \hfill \\ {\quad} f_{1} = {\mathbf{U}}^{T} F, \hfill \\ {\quad} f_{2} = V, \hfill \\ {\quad} G_{i} \left( {\mathbf{x}} \right) = 2.5{\quad} \times 10^{4} {\quad} {\text{ksi}} - \sigma _{i}^{{}} ,{\quad} i = 1,...,10, \hfill \\ {\quad} G_{{11}} \left( {\mathbf{x}} \right) = 4.5{\quad} {\text{in}} - y_{{\max }} , \hfill \\ \quad \beta _{1}^{t} = \beta _{2}^{t} = \cdot \cdot \cdot = \beta _{{11}}^{t} = 3.0,\; \hfill \\ \quad 0.1 \le x_{i} \le 25,{\quad} j = 1,...,10, \hfill \\ {\quad} x_{i} \sim N(\mu _{{x_{i} }} ,0.005^{2} ).\quad \hfill \\ \end{gathered}$$

(15)

Multiobjective RBDO for welded beam

As plotted in Fig. 

Fig. 7

Schematic view of a welded beam

7, the multiobjective RBDO of welded beam is performed, which is modified from the deterministic multiple-objective optimization example (Dhiman and Kumar 2018; Ray and Liew 2002). The task is to minimizing the cost and maximum deflection, while the constraints are related to the shear stress, bending stress, and buckling load. The multiobjective RBDO model is as follows:

$$\begin{gathered} {\text{find}}\quad {\mathbf{x}} = [x_{1} ,x_{2} ,x_{3} ,x_{4} ] \hfill \\ \min \quad \,f\left( {\mathbf{x}} \right) = \left[ {f_{1} \left( {\mathbf{x}} \right),{\quad} f_{2} \left( {\mathbf{x}} \right)} \right] \hfill \\ {\text{s}}{\text{.t}}{\text{.}}\quad \; P\left( {G_{i} ({\mathbf{x}}) > 0} \right) \ge \Phi \left( {\beta _{i}^{t} } \right);{\quad}i = 1 - 4 \hfill \\ {\text{where}}\,\, \hfill \\ {\quad} f_{1} = 1.10471x_{1}^{2} x_{2} + 0.04811x_{3} x_{4} (14 + x_{2} ), \hfill \\ {\quad} f_{2} = \frac{{4PL^{3} }}{{Ex_{4} x_{3}^{3} }}, \hfill \\ {\quad} G_{1} \left( {\mathbf{x}} \right) = \tau _{{\max }} - \tau ({\mathbf{x}}), \hfill \\ {\quad} G_{2} \left( {\mathbf{x}} \right) = \sigma _{{\max }} - \sigma ({\mathbf{x}}), \hfill \\ {\quad} G_{3} \left( {\mathbf{x}} \right) = x_{4} - x_{1} , \hfill \\ {\quad} G_{4} \left( {\mathbf{x}} \right) = P_{c} ({\mathbf{x}}) - P, \hfill \\ {\quad} \tau ({\mathbf{x}}) = \sqrt {(\tau ^{\prime})^{2} + \frac{{2\tau ^{\prime}\tau ^{\prime\prime}x_{2} }}{{2R}} + (\tau ^{\prime\prime})^{2} } , \hfill \\ {\quad} \tau ^{\prime} = \frac{P}{{\sqrt 2 x_{1} x_{2} }}, \hfill \\ {\quad} M = P\left( {L + \frac{{x_{2} }}{2}} \right), \hfill \\ {\quad} R = \sqrt {\frac{{x_{2}^{2} }}{4} + \left( {\frac{{x_{1} + x_{3} }}{2}} \right)^{2} } , \hfill \\ {\quad} J = 2\left( {\sqrt 2 x_{1} x_{2} \left( {\frac{{x_{2}^{2} }}{{12}} + \left( {\frac{{x_{1} + x_{3} }}{2}} \right)^{2} } \right)} \right), \hfill \\ {\quad} \sigma ({\mathbf{x}}) = \frac{{6PL}}{{x_{4} x_{3}^{2} }}, \hfill \\ {\quad} P_{c} ({\mathbf{x}}) = \frac{{4.013E\sqrt {\frac{{x_{3}^{2} x_{6}^{4} }}{{36}}} }}{{L^{2} }}\left( {1 - \frac{{x_{3} }}{{2L}}\sqrt {\frac{F}{{4G}}} } \right), \hfill \\ {\quad} P = 6000,L = 14,E = 3 \times 10^{7} , \hfill \\ {\quad} \tau _{{\max }} = 13600,\sigma _{{\max }} = 30000, \hfill \\ {\quad} \beta _{1}^{t} = \beta _{2}^{t} = \cdot \cdot \cdot = \beta _{5}^{t} = 3.0,\; \hfill \\ {\quad} 0.125 \le x_{1} \le 5,\;0.1 \le x_{2} \le 10, \hfill \\ {\quad} 0.1 \le x_{3} \le 10,\;\;0.125 \le x_{4} \le 5, \hfill \\ {\quad} x_{i} \sim N(\mu _{{x_{i} }} ,0.005^{2} ).\quad \hfill \\ \end{gathered}$$

(16)

Multiobjective RBDO for speed reducer

The fifth multiobjective RBDO example is based on the super reducer, which is a popular tested engineering optimization problem. The schematic diagram is potted in Fig. 

Fig. 8

Schematic view of speed reducer

8. There are two objectives, including minimizing the structural weight and stress. Seven uncertain variables and eleven constraints are considered. The details can been seen in studies of (Cho and Lee 2011) and (Chen et al. 2018). The multiobjective RBDO formulation is expressed as follows:

$$\begin{gathered} {\text{find}}\quad {\mathbf{x}} = [\mu _{{x_{1} }} ,\mu _{{x_{2} }} ,\mu _{{x_{3} }} ,\mu _{{x_{4} }} ,\mu _{{x_{5} }} ,\mu _{{x_{6} }} ,\mu _{{x_{7} }} ] \hfill \\ \min \quad \,f\left( {\mathbf{x}} \right) = \left[ {f_{1} \left( {\mathbf{x}} \right),{\quad} f_{2} \left( {\mathbf{x}} \right)} \right] \hfill \\ {\text{s}}{\text{.t}}{\text{.}}\quad \;P\left( {G_{i} ({\mathbf{x}}) > 0} \right) \ge \Phi \left( {\beta _{i}^{t} } \right);{\quad} i = 1 - 11 \hfill \\ {\text{where}}\,\, \hfill \\ {\quad} f_{1} = 0.7854x_{1} x_{2}^{2} \left( {\frac{{10x_{3}^{2} }}{3} + 14.933x_{3} - 43.0934} \right) \hfill \\ {\quad} - 1.508x_{1} \left( {x_{6}^{2} + x_{7}^{2} } \right) + 7.477\left( {x_{6}^{3} + x_{7}^{3} } \right) \hfill \\ {\quad} + 0.7854\left( {x_{4} x_{6}^{2} + x_{5} x_{7}^{2} } \right), \hfill \\ {\quad} f_{2} = \frac{{\sqrt {\left( {\frac{{745x_{4} }}{{x_{2} x_{3} }}} \right)^{2} + 1.67 \times 10^{7} } }}{{0.1x_{6}^{3} }}, \hfill \\ {\quad} G_{1} \left( {\mathbf{x}} \right) = \frac{1}{{27}} - \frac{1}{{x_{1} x_{2}^{2} x_{3} }}, \hfill \\ {\quad} G_{2} \left( {\mathbf{x}} \right) = \frac{1}{{397.5}} - \frac{1}{{x_{1} x_{2}^{2} x_{3}^{2} }}, \hfill \\ {\quad} G_{3} \left( {\mathbf{x}} \right) = \frac{1}{{1.93}} - \frac{{x_{4}^{3} }}{{x_{2} x_{3}^{{}} x_{6}^{4} }}, \hfill \\ {\quad} G_{4} \left( {\mathbf{x}} \right) = \frac{1}{{1.93}} - \frac{{x_{5}^{3} }}{{x_{2} x_{3}^{{}} x_{7}^{4} }}, \hfill \\ {\quad} G_{5} \left( {\mathbf{x}} \right) = 40 - x_{2} x_{3} , \hfill \\ {\quad} G_{6} \left( {\mathbf{x}} \right) = 12 - \frac{{x_{1} }}{{x_{2} }}, \hfill \\ {\quad} G_{7} \left( {\mathbf{x}} \right) = \frac{{x_{1} }}{{x_{2} }} - 5, \hfill \\ {\quad} G_{8} \left( {\mathbf{x}} \right) = - 1.9 + x_{4} - 1.5x_{6} , \hfill \\ {\quad} G_{9} \left( {\mathbf{x}} \right) = - 1.9 + x_{5} - 1.1x_{7} , \hfill \\ {\quad} G_{{10}} \left( {\mathbf{x}} \right) = - f_{2} + 1300, \hfill \\ {\quad} G_{{11}} \left( {\mathbf{x}} \right) = - \frac{{\sqrt {\left( {\frac{{745x_{5} }}{{x_{2} x_{3} }}} \right)^{2} + 1.575 \times 10^{8} } }}{{0.1x_{7}^{3} }} + 110, \hfill \\ {\quad} \beta _{1}^{t} = \beta _{2}^{t} = \cdot \cdot \cdot = \beta _{{11}}^{t} = 3.0,\; \hfill \\ \end{gathered}$$

(17)

$$\begin{gathered} \quad \quad \quad 2.6 \le x_{1} \le 3.6,\;0.7 \le x_{2} \le 0.8, \hfill \\ \quad \quad \quad x_{3} \in \{ 17,...,28\} ({\text{integer}}),7.3 \le x_{4} \le 8.3, \hfill \\ \quad \quad \quad 7.3 \le x_{5} \le 8.3,2.9 \le x_{6} \le 3.9,5 \le x_{6} \le 5.5, \hfill \\ \quad \quad \quad x_{i} \sim N(\mu _{{x_{i} }} ,0.005^{2} ). \hfill \\ \end{gathered}$$

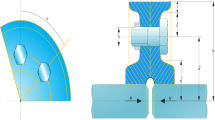
Multiobjective RBDO for disk brake

This multiobjective RBDO problem is modified from the deterministic optimization (Gong et al. 2009; Houssein et al. 2022). There are two objectives and four design variables. The design objectives include brake mass and stopping time. The design and random variables include disk radii, engaging force, and friction surface number. The multiobjective RBDO model is depicted by

$$\begin{gathered} {\text{find}}\quad {\mathbf{x}} = [x_{1} ,x_{2} ,x_{3} ,x_{4} ] \hfill \\ \min \quad \,f\left( {\mathbf{x}} \right) = \left[ {f_{1} \left( {\mathbf{x}} \right),{\quad}f_{2} \left( {\mathbf{x}} \right)} \right] \hfill \\ {\text{s}}{\text{.t}}{\text{.}}\quad \; P\left( {G_{i} ({\mathbf{x}}) > 0} \right) \ge \Phi \left( {\beta _{i}^{t} } \right);{\quad} i = 1 - 4 \hfill \\ {\text{where}}\,\, \hfill \\ {\quad} f_{1} = 4.9 \times 10^{{ - 5}} \left( {x_{2}^{2} - x_{1}^{2} } \right)\left( {x_{4} - 1} \right), \hfill \\ {\quad} f_{2} = 9.82 \times 10^{6} \left( {\frac{{x_{2}^{2} - x_{1}^{2} }}{{x_{3} x_{4} \left( {x_{2}^{3} - x_{1}^{3} } \right)}}} \right), \hfill \\ {\quad} G_{1} \left( {\mathbf{x}} \right) = (x_{2} - x_{1} ) - 20, \hfill \\ {\quad} G_{2} \left( {\mathbf{x}} \right) = 0.4 - \frac{{x_{3} }}{{3.14(x_{2}^{2} - x_{1}^{2} )}}, \hfill \\ {\quad} G_{3} \left( {\mathbf{x}} \right) = 1 - \frac{{2.22 \times 10^{{ - 3}} x_{3} (x_{2}^{3} - x_{1}^{3} )}}{{(x_{2}^{2} - x_{1}^{2} )^{2} }}, \hfill \\ {\quad}G_{4} \left( {\mathbf{x}} \right) = 2.66 \times 10^{{ - 2}} \frac{{x_{3} x_{4} (x_{2}^{3} - x_{1}^{3} )}}{{(x_{2}^{2} - x_{1}^{2} )}} - 900, \hfill \\ {\quad} \beta _{1}^{t} = \beta _{2}^{t} = \cdot \cdot \cdot = \beta _{5}^{t} = 3.0,\; \hfill \\ {\quad} 55 \le x_{1} \le 80,\;75 \le x_{2} \le 110, \hfill \\ {\quad} 1000 \le x_{3} \le 3000,\;\;11 \le x_{4} \le 20, \hfill \\ {\quad} x_{1} \sim N(\mu _{{x_{1} }} ,1^{2} ),x_{2} \sim N(\mu _{{x_{2} }} ,1^{2} ), \hfill \\ {\quad} x_{3} \sim N(\mu _{{x_{3} }} ,5^{2} ),x_{4} \sim N(\mu _{{x_{4} }} ,1^{2} ). \hfill \\ \end{gathered}$$

(18)

Multiobjective RBDO for high-dimensional example

This high-dimensional multiobjective RBDO problem is also modified from deterministic optimization problem (Cheng et al. 2021). It contains 20 random variables, and their means are considered as design variables. The multiobjective RBDO model is depicted by

$$\begin{gathered} {\text{find}}\quad {\mathbf{x}} = [x_{1} ,x_{2} ,...,x_{{20}} ] \hfill \\ \min \quad \,f\left( {\mathbf{x}} \right) = \left[ {f_{1} \left( {\mathbf{x}} \right),{\quad}f_{2} \left( {\mathbf{x}} \right)} \right] \hfill \\ {\text{s}}{\text{.t}}{\text{.}}\quad \;P\left( {G_{i} ({\mathbf{x}}) > 0} \right) \ge \Phi \left( {\beta _{i}^{t} } \right);{\quad} i = 1 - 2 \hfill \\ {\text{where}}\,\, \hfill \\ {\quad} f_{1} = x_{1} + \sum\limits_{{j \in J_{1} }} {y_{j}^{2} } , \hfill \\ {\quad} f_{2} = \left( {1 - x_{1} } \right)^{2} + \sum\limits_{{j \in J_{2} }} {y_{j}^{2} } , \hfill \\ {\quad} G_{1} \left( {\mathbf{x}} \right) = x_{2} - 0.8x_{1} \sin \left( {6\pi x_{1} + \frac{{2\pi }}{n}} \right) - sign\left( {0.5\left( {1 - x_{1} } \right) - \left( {1 - x_{1} } \right)^{2} } \right) \hfill \\ {\quad} \times \sqrt {\left| {0.5\left( {1 - x_{1} } \right) - \left( {1 - x_{1} } \right)^{2} } \right|} , \hfill \\ {\quad} G_{2} \left( {\mathbf{x}} \right) = x_{4} - 0.8x_{1} \sin \left( {6\pi x_{1} + \frac{{4\pi }}{n}} \right) - sign\left( {0.25\left( {1 - x_{1} } \right) - 0.5\left( {1 - x_{1} } \right)} \right) {\quad} \hfill \\ {\quad} \times \sqrt {\left| {0.25\left( {1 - x_{1} } \right) - 0.5\left( {1 - x_{1} } \right)} \right|} , \hfill \\ {\quad}J_{1} = \left\{ {\left. j \right|j{\text{ is odd and 2}} \le j \le 20} \right\} \hfill \\ {\quad} J_{2} = \left\{ {\left. j \right|j{\text{ is even and 2}} \le j \le 20} \right\} \hfill \\ {\quad}y_{j} = \left\{ {\begin{array}{*{20}c} {x_{j} - 0.8x_{1} \cos \left( {6\pi x_{1} + \frac{{j\pi }}{n}} \right)} & {{\text{if }}j \in J_{1} } \\ {x_{j} - 0.8x_{1} \sin \left( {6\pi x_{1} + \frac{{j\pi }}{n}} \right)} & {{\text{if }}j \in J_{2} } \\ \end{array} } \right. \hfill \\ {\quad} \beta _{1}^{t} = \beta _{2}^{t} = \cdot \cdot \cdot = \beta _{5}^{t} = 3.0,\; \hfill \\ {\quad} 0 \le x_{1} \le 1,\; - 2 \le x_{j} \le 2,j = 2,...,20 \hfill \\ {\quad} x_{j} \sim N(\mu _{{x_{j} }} ,0.01^{2} ){\quad} ,j = 1,...,20 \hfill \\ \end{gathered}$$

(19)