Efficient buckling constrained topology optimization using reduced order modeling

Abstract

We present an efficient computational approach to continuum topology optimization with linearized buckling constraints, using Reduced Order Models (ROM). A reanalysis technique is employed to generate basis vectors that subsequently are used to significantly reduce the size of the generalized eigenvalue problems. We demonstrate the efficacy of this approach by optimizing for stiffness with buckling constraints and show results for several test cases. Based on our findings, we conclude that the ROM can potentially save significant computational effort without compromising the quality of the results.

1 Introduction

Topology Optimization (TO) is a powerful computational tool for designing structural components. The archetype TO design problem is compliance minimization under a volume constraint, which favors slender designs in states of pure compression and tension. Unfortunately, these structures are inherently prone to buckle, which renders them impractical under realistic loading conditions. A common way of accommodating for stability is to constrain the critical buckling load factor (BLF) such that safety against buckling exists (Neves et al. 1995, Gao and Ma 2015, Ferrari and Sigmund 2019, Dalklint et al. 2021).

The TO problem is solved iteratively using a nested approach, wherein the implicitly enforced equilibrium equations are solved exactly in each design iteration. In practice, several hundred design iterations are required to find a minimum, and the linear system solves constitute the majority of the computational cost. One approach to reduce this cost is using Reduced Order Models (ROM), wherein the equilibrium equations are solved in a reduced space much smaller than the original high-fidelity space. The efficiency of a ROM is ultimately determined by the cost of generating the reduced space versus the loss of accuracy. One ROM approach that has been integrated into TO is to base the reduced space on previous solutions to the equilibrium equations, and update the space as new solution vectors become available (Gogu 2015, Choi et al. 2019).

An attractive ROM technique for structural optimization problems is reanalysis, in which the system matrix’s factorization is stored and reused to build a reduced space for subsequent design iterations. Kirsch (1991) introduced a particular type of reanalysis known as Combined Approximation (CA), initially intended for approximating linear static displacements. This method has been showed to be equivalent to a preconditioned conjugate gradient method for linear systems of equations (Kirsch et al. 2002), and is known for its robustness and efficiency. The scope of CA was extended to include nonlinear, dynamic and eigenvalue problems (Kirsch 2008). In the context of integrating CA into TO, Amir et al. (2009) introduced reanalysis for topology optimization, and solved compliance minimization problems. Senne et al. (2022) extended reanalysis to TO problems with geometric and material non-linearities. Bogomolny (2010) used reanalysis for vibration problems.

When buckling is included in the optimization, the computational burden increases drastically, because the BLFs are obtained from a generalized eigenvalue problem. Eigenvalue problems are notoriously expensive to solve and scale poorly with the problem size. This cost becomes prohibitive for medium to large problems, and motivates the search for efficient numerical methods.

Recently, efforts have been made to extend TO with buckling constraints to large scale problems. Dunning et al. (2016) used a Block-Jacobi CG solver with a shift-and-invert strategy based on information from previous design iterations. Ferrari and Sigmund (2020) propose a multigrid approach wherein the multigrid preconditioner from the initial equilibrium problem is reused to estimate the BLFs and to filter out nonphysical, local modes. This reduced the cost for solving the eigenvalue problems significantly, while retaining sufficient accuracy in the eigenvalues. Also worth noting is the work by Bian and Fang (2017), where an assembly free method was used to solve the large-scale eigenvalue problem, and the work by Kang et al. (2020), where the vibration modes were estimated concurrently with the progress of optimization, improving the accuracy sequentially.

To the authors knowledge, reanalysis has not been applied to buckling constrained topology optimization. In this paper, we show that ROM using CA can be effectively integrated into TO with buckling constraints.

2 Preliminaries

We consider the finite element discretized linear system

$$\begin{aligned} {\varvec{{\textsf {K}}}}_L {\varvec{{\textsf {a}}}}_o = {\varvec{{\textsf {F}}}}_o, \end{aligned}$$

(1)

in combination with appropriate boundary conditions to describe our mechanical system. In (1), ${\varvec{{\textsf {K}}}}_L\in {\mathbb {R}}^{n\times n}$ is the symmetric and positive definite linear stiffness matrix, ${\varvec{{\textsf {a}}}}_o\in {\mathbb {R}}^{n}$ is the reference displacement vector and ${\varvec{{\textsf {F}}}}_o\in {\mathbb {R}}^{n}$ is the load vector, where n is the number of degrees-of-freedom. To solve (1), we utilize the Cholesky decomposition of ${\varvec{{\textsf {K}}}}_L$ in combination with forward/backward substitutions, i.e.

$$\begin{aligned} {\varvec{{\textsf {K}}}}_L = {\varvec{{\textsf {U}}}}^T{\varvec{{\textsf {U}}}}, \end{aligned}$$

(2)

where ${\varvec{{\textsf {U}}}}\in {\mathbb {R}}^{n\times n}$ is upper triangular. After solving (1) for ${\varvec{{\textsf {a}}}}_o$ using (2), we compute the symmetric and indefinite stress stiffness matrix ${\varvec{{\textsf {K}}}}_G({\varvec{{\textsf {a}}}}_o)\in {\mathbb {R}}^{n\times n}$, which enables the generalized eigenvalue problem

$$\begin{aligned} \left( {\varvec{{\textsf {K}}}}_G({\varvec{{\textsf {a}}}}_o) + \mu _j {\varvec{{\textsf {K}}}}_L\right) \varvec{{\upphi }}_j = {\varvec{{\textsf {0}}}}, \quad j\in {\mathbb {N}}_n, \end{aligned}$$

(3)

to be solved for the eigenpairs $(\mu _j,\varvec{{\upphi }}_j)\in ({\mathbb {R}}\times {\mathbb {R}}^n)$¹. In (3), we assume $\varvec{{\upphi }}_i^T{\varvec{{\textsf {K}}}}_L\varvec{{\upphi }}_j = \delta _{ij}$ and a descending sorting of the eigenvalues. Solving the generalized eigenvalue problem in (3) for the BLFs $\lambda _j = \frac{1}{\mu _j}$, is referred to as linearized buckling analysis. The smallest BLF, i.e. largest $\mu _j$, defines the critical buckling load, ${\varvec{{\textsf {F}}}}_j=\frac{1}{\mu _j}{\varvec{{\textsf {F}}}}_o$, at which a small perturbation results in that the structure buckles in the shape of $\varvec{{\upphi }}_j$.

3 Reduced order modeling

We seek an approximation to the displacement field in (1) using a ROM,

$$\begin{aligned} {\varvec{{\textsf {a}}}}_o \approx \tilde{{\varvec{{\textsf {a}}}}}_o \equiv \sum _{i=1}^s y_i {\varvec{{\textsf {u}}}}_i = {\varvec{{\textsf {R}}}}{\varvec{{\textsf {y}}}} \end{aligned},$$

(4)

where ${\varvec{{\textsf {R}}}} = \left[ {\varvec{{\textsf {u}}}}_1, {\varvec{{\textsf {u}}}}_2, \ldots {\varvec{{\textsf {u}}}}_s\right] \in {\mathbb {R}}^{n \times s}$ contains the basis vectors and ${\varvec{{\textsf {y}}}} = [y_1, y_2, \ldots y_s]\in {\mathbb {R}}^s$ the reduced model coefficients. The coefficients ${\varvec{{\textsf {y}}}}$ are found by replacing ${\varvec{{\textsf {a}}}}_o$ in (1) with $\tilde{{\varvec{{\textsf {a}}}}}_o$ defined in (4), and projecting onto the basis ${\varvec{{\textsf {u}}}}_i$ by premultiplying with ${\varvec{{\textsf {R}}}}^T$. The success of the ROM relies on the choice of the basis vectors, that is ${\varvec{{\textsf {R}}}}$. In this work the basis vectors are generated using CA, wherein the factorization of the stiffness matrix is systematically stored and reused for subsequent design iterations. Quantities at the current design iteration and past design iterations will be distinguished using an overbar, for example $\overline{\varvec{{\textsf {K}}}}_L\overline{\varvec{{\textsf {a}}}}_o = {\varvec{{\textsf {F}}}}_o$ and ${\varvec{{\textsf {K}}}}_L{\varvec{{\textsf {a}}}}_o = {\varvec{{\textsf {F}}}}_o$. Overbar quantities are understood to belong to the same, past, design iteration and are constants with respect to the current design. Approximate quantities are distinguished from their exact counterpart by ${\tilde{\bullet }}$, for example $\tilde{{\varvec{{\textsf {a}}}}}_o \approx {\varvec{{\textsf {a}}}}_o$ denotes an approximate solution to (1).

3.1 Reanalysis of the linear equilibrium problem

Let us start by considering the approximate $\tilde{{\varvec{{\textsf {a}}}}}_o$ solution to (1) and let $\overline{{\varvec{{\textsf {K}}}}}_L$ be the stiffness matrix from a past design iteration. In the CA approach, we utilize the Cholesky factorization of $\overline{{\varvec{{\textsf {K}}}}}_L$, to compute ${\varvec{{\textsf {a}}}}_o$ i.e.

$$\begin{aligned} \left( \overline{{\varvec{{\textsf {K}}}}}_L + \Delta {\varvec{{\textsf {K}}}}_L \right) {\varvec{{\textsf {a}}}}_o = {\varvec{{\textsf {F}}}}_o, \end{aligned}$$

(5)

where $\Delta {\varvec{{\textsf {K}}}}_L \equiv {\varvec{{\textsf {K}}}}_L - \overline{{\varvec{{\textsf {K}}}}}_L$ is the stiffness change due to a design update. Applying $\overline{{\varvec{{\textsf {K}}}}}_L^{-1}$ to both sides of (5) yields

$$\begin{aligned} \left( {\varvec{{\textsf {I}}}} + \overline{{\varvec{{\textsf {K}}}}}_L^{-1}\Delta {\varvec{{\textsf {K}}}}_L \right) {\varvec{{\textsf {a}}}}_o = \overline{{\varvec{{\textsf {K}}}}}_L^{-1}{\varvec{{\textsf {F}}}}_o. \end{aligned}$$

(6)

Now, we expand the inverse of $({\varvec{{\textsf {I}}}} + \overline{{\varvec{{\textsf {K}}}}}_L^{-1}\Delta {\varvec{{\textsf {K}}}}_L )$ in a power series²

$$\begin{aligned} ({\varvec{{\textsf {I}}}} + {\varvec{{\textsf {B}}}} )^{-1} = \sum _{k=0}^\infty (-{\varvec{{\textsf {B}}}})^k, \quad \text {where} \quad {\varvec{{\textsf {B}}}}=\overline{{\varvec{{\textsf {K}}}}}_L^{-1}\Delta {\varvec{{\textsf {K}}}}_L. \end{aligned}$$

(7)

Hence, the solution to (6) is

$$\begin{aligned} {\varvec{{\textsf {a}}}}_o = \sum _{k=0}^\infty (-{\varvec{{\textsf {B}}}})^k\overline{{\varvec{{\textsf {K}}}}}_L^{-1}{\varvec{{\textsf {F}}}}_o, \end{aligned}$$

(8)

which we truncate at $k=s\ll n$, such that $\tilde{{\varvec{{\textsf {a}}}}}_o = {\varvec{{\textsf {R}}}}{\varvec{{\textsf {y}}}}$, cf. (4). The basis vectors in ${\varvec{{\textsf {R}}}}$ are obtained recursively from (8) as

$$\begin{aligned} \begin{array}{ll} \displaystyle {\varvec{{\textsf {u}}}}_1 = \overline{{\varvec{{\textsf {K}}}}}_L^{-1}{\varvec{{\textsf {F}}}}_o, &{} \\ \displaystyle {\varvec{{\textsf {u}}}}_i = -{\varvec{{\textsf {B}}}}{\varvec{{\textsf {u}}}}_{i-1}, &{} \quad i=2,...,s. \\ \end{array} \end{aligned}$$

(9)

After the basis vectors are generated, we solve the reduced $s\times s$ problem

$$\begin{aligned} {\varvec{{\textsf {R}}}}^T{\varvec{{\textsf {K}}}}_L{\varvec{{\textsf {R}}}}{\varvec{{\textsf {y}}}} = {\varvec{{\textsf {R}}}}^T{\varvec{{\textsf {F}}}}_o, \end{aligned}$$

(10)

for ${\varvec{{\textsf {y}}}}$, and insert the result into (4). In practice, the magnitudes of ${\varvec{{\textsf {u}}}}_i$ rapidly decrease due to repeated application of $\overline{{\varvec{{\textsf {K}}}}}_L^{-1}\Delta {\varvec{{\textsf {K}}}}$, resulting in a poorly conditioned system (10). To mitigate this issue we introduce normalization and ${\varvec{{\textsf {K}}}}_L$-orthogonalization of the basis vectors wherefore the final basis vectors ${\varvec{{\textsf {R}}}} = \left[ {\varvec{{\textsf {v}}}}_1, {\varvec{{\textsf {v}}}}_2, \ldots {\varvec{{\textsf {v}}}}_s\right]$ are obtained recursively as

$$\begin{aligned} \begin{array}{ll} \displaystyle {\varvec{{\textsf {u}}}}_1 = \overline{{\varvec{{\textsf {K}}}}}_L^{-1}{\varvec{{\textsf {F}}}}_o, &{} \\ \displaystyle {\varvec{{\textsf {u}}}}_i = -{\varvec{{\textsf {B}}}}{\varvec{{\textsf {t}}}}_{i-1}, &{} \quad i=2,...,s, \\ \displaystyle {\varvec{{\textsf {t}}}}_i = {\varvec{{\textsf {u}}}}_{i}({\varvec{{\textsf {u}}}}_i^T{\varvec{{\textsf {K}}}}_L{\varvec{{\textsf {u}}}}_i)^{-1/2}, &{} \quad i=1,...,s, \\ \displaystyle {\varvec{{\textsf {r}}}}_i = {\varvec{{\textsf {t}}}}_i - \sum _{j=1}^{i-1} \left( {\varvec{{\textsf {t}}}}_i^T{\varvec{{\textsf {K}}}}_L{\varvec{{\textsf {v}}}}_j\right) {\varvec{{\textsf {v}}}}_j, &{} \quad i=1,...,s, \\ \displaystyle {\varvec{{\textsf {v}}}}_i = {\varvec{{\textsf {r}}}}_i\left( {\varvec{{\textsf {r}}}}_i^T{\varvec{{\textsf {K}}}}_L{\varvec{{\textsf {r}}}}_i\right) ^{-1/2}, &{} \quad i=1,...,s. \end{array} \end{aligned}$$

(11)

Due to the orthogonalization, ${\varvec{{\textsf {R}}}}^T{\varvec{{\textsf {K}}}}_L{\varvec{{\textsf {R}}}} = {\varvec{{\textsf {I}}}}$, the reduced system in (10) boils down to ${\varvec{{\textsf {I}}}}{\varvec{{\textsf {y}}}} = {\varvec{{\textsf {y}}}} = {\varvec{{\textsf {R}}}}^T{\varvec{{\textsf {F}}}}_o$, such that the approximate solution becomes

$$\begin{aligned} \tilde{{\varvec{{\textsf {a}}}}}_o = {\varvec{{\textsf {R}}}}{\varvec{{\textsf {y}}}} = {\varvec{{\textsf {R}}}}{\varvec{{\textsf {R}}}}^T{\varvec{{\textsf {F}}}}_o. \end{aligned}$$

(12)

An alternative, numerically equivalent, approach to (12) is to use the factorization of $\overline{{\varvec{{\textsf {K}}}}}_L$ as a preconditioner in a Preconditioned Conjugate Gradients (PCG) procedure, cf. e.g. Kirsch et al. (2002) and Amir et al. (2012). However, in this work the eigenproblem (3) is solved with ROM so for consistency we use the ROM approach for the static problem (1) as well.

3.2 Reanalysis of the buckling problem

Next, we seek an approximation of each eigenpair to (3). We do this by approximating the eigenmodes, after which the eigenvalues are given by the Rayleigh quotient. The eigenmodes are approximated as

$$\begin{aligned} {\varvec{{\upphi }}}_j \approx \tilde{\varvec{{\upphi }}}_j \equiv \sum _{i=1}^s y_{ij} {\varvec{{\textsf {u}}}}_{ij} = {\varvec{{\textsf {R}}}}_j{\varvec{{\textsf {y}}}}_j \end{aligned},$$

(13)

where ${\varvec{{\textsf {R}}}}_j$ and ${\varvec{{\textsf {y}}}}_j$ are analogous to the quantities defined in (4) and $j\in {\mathbb {N}}_n$. To generate the basis vectors we utilize the additive decomposition of ${\varvec{{\textsf {K}}}}_L$ in (3), i.e.

$$\begin{aligned} \left( {\varvec{{\textsf {K}}}}_G+ \mu _j \left( \overline{{\varvec{{\textsf {K}}}}}_L+\Delta {\varvec{{\textsf {K}}}}_L\right) \right) \varvec{{\upphi }}_j={\varvec{{\textsf {0}}}}, \end{aligned}$$

(14)

where ${\varvec{{\textsf {K}}}}_G = {\varvec{{\textsf {K}}}}_G(\tilde{{\varvec{{\textsf {a}}}}}_o)$. Premultiplication of (14) by $\overline{{\varvec{{\textsf {K}}}}}_L^{-1}$ yields

$$\begin{aligned} \left( \overline{{\varvec{{\textsf {K}}}}}_L^{-1}{\varvec{{\textsf {K}}}}_G+\mu _j \left( {\varvec{{\textsf {I}}}}+{\varvec{{\textsf {B}}}}\right) \right) \varvec{{\upphi }}_j ={\varvec{{\textsf {0}}}}, \end{aligned}$$

(15)

and, using the result (7), we find from (15)

$$\begin{aligned} \varvec{{\upphi }}_j =\frac{-1}{\mu _j} \sum _{k=0}^\infty (-{\varvec{{\textsf {B}}}})^k\overline{{\varvec{{\textsf {K}}}}}_L^{-1}{\varvec{{\textsf {K}}}}_G\varvec{{\upphi }}_j, \end{aligned}$$

(16)

The basis vectors ${\varvec{{\textsf {R}}}}_j$ for mode j are obtained by truncating the infinite sum at term $k = s \ll n$, replacing $\varvec{{\upphi }}_j$ on the right-hand side with $\overline{\varvec{{\upphi }}}_j$ and ignoring the arbitrary scaling factor of $-(\mu _k)^{-1}$, i.e.

$$\begin{aligned} \begin{array}{ll} {\varvec{{\textsf {u}}}}_{1j} = \overline{{\varvec{{\textsf {K}}}}}_L^{-1}{\varvec{{\textsf {K}}}}_G\overline{\varvec{{\upphi }}}_j &{} \\ {\varvec{{\textsf {u}}}}_{ij} = -{\varvec{{\textsf {B}}}}{\varvec{{\textsf {u}}}}_{(i-1)j}, &{} \quad i=2,...,s, \\ \end{array}. \end{aligned}$$

(17)

We scale the basis vectors to ensure that their relative magnitudes do not differ significantly, analogously to the static problem. Additionally we employ orthogonalization of the basis vectors with respect to lower order modes $\tilde{\varvec{{\upphi }}}_l$ by introducing ${\varvec{{\textsf {v}}}}_{ij} = {\varvec{{\textsf {t}}}}_{ij} + \sum _{l = 1}^{j-1}\alpha _l\tilde{\varvec{{\upphi }}}_l$ and requiring $\tilde{\varvec{{\upphi }}}_l^T{\varvec{{\textsf {K}}}}_L{\varvec{{\textsf {v}}}}_{ij}=0$ for all $i\le s, l<j$. Thereby ensuring that the orthogonality condition of the eigenmodes is retained, that is $\tilde{\varvec{{\upphi }}}_l^T{\varvec{{\textsf {K}}}}_L\tilde{\varvec{{\upphi }}}_{j}=\delta _{lj}$. Due to the orthogonalization, we also avoid that the ${\tilde{\mu }}_j$ approximates the lower order $\mu _l, \; l < j$ [compare Kirsch (2008) and Bogomolny (2010)]. The old eigenmodes, $\overline{\varvec{{\upphi }}}_l$, may be chosen instead of the current approximation, allowing for independent solution of the eigenproblems. However, in this work the latter approach is taken. The basis generation can be defined recursively as

$$\begin{aligned} \begin{array}{ll} {\varvec{{\textsf {u}}}}_{1j}= \overline{{\varvec{{\textsf {K}}}}}_L^{-1}{\varvec{{\textsf {K}}}}_G\overline{\varvec{{\upphi }}}_j, &{} \\ \displaystyle {\varvec{{\textsf {u}}}}_{ij} = -{\varvec{{\textsf {B}}}}{\varvec{{\textsf {t}}}}_{(i-1)j}, &{} \quad i=2,...,s, \\ \displaystyle {\varvec{{\textsf {t}}}}_{ij} = {\varvec{{\textsf {u}}}}_{ij}\left( {\varvec{{\textsf {u}}}}_{ij}^T{\varvec{{\textsf {K}}}}_L{\varvec{{\textsf {u}}}}_{ij}\right) ^{-1/2}, &{} \quad i=1,...,s, \\ \displaystyle {\varvec{{\textsf {v}}}}_{ij} = {\varvec{{\textsf {t}}}}_{ij}-\sum _{l=1}^{j-1}\left( \tilde{\varvec{{\upphi }}}_l^T{\varvec{{\textsf {K}}}}_L{\varvec{{\textsf {t}}}}_{ij}\right) \tilde{\varvec{{\upphi }}}_l, &{} \quad i=1,...,s, \end{array} \end{aligned}$$

(18)

where $\overline{\varvec{{\upphi }}}_j$ is the jth eigenvector corresponding to the matrix $\overline{{\varvec{{\textsf {K}}}}}_L$. Now, inserting the (13) approximation into (3) and premultiplying by ${\varvec{{\textsf {R}}}}_j = \left[ {\varvec{{\textsf {v}}}}_{1j},{\varvec{{\textsf {v}}}}_{2j},\ldots {\varvec{{\textsf {v}}}}_{sj}\right]$ gives a reduced generalized eigenvalue problem

$$\begin{aligned} \left( {\varvec{{\textsf {K}}}}_G^{R_j} + {\tilde{\mu }}_j{\varvec{{\textsf {K}}}}_L^{R_j}\right) {\varvec{{\textsf {y}}}}_j = \varvec{{0}}, \end{aligned}$$

(19)

where ${\varvec{{\textsf {K}}}}_G^{R_j} = {\varvec{{\textsf {R}}}}_j^T{\varvec{{\textsf {K}}}}_G(\tilde{{\varvec{{\textsf {a}}}}}_o){\varvec{{\textsf {R}}}}_j$ and ${\varvec{{\textsf {K}}}}_L^{R_j} = {\varvec{{\textsf {R}}}}_j^T{\varvec{{\textsf {K}}}}_L{\varvec{{\textsf {R}}}}_j$. The system (19) has s solutions, and we seek the one which most accurately approximates the jth eigenpair $(\mu _j, \varvec{{\upphi }}_j)$. Since the eigenpairs are solved in order of descending magnitude and ${\varvec{{\textsf {R}}}}_j$ are ${\varvec{{\textsf {K}}}}_L$-orthogonal to $\tilde{\varvec{{\upphi }}}_l \; l < j$, we choose eigenpair with largest magnitude eigenvalue. To summarize, for each sought eigenpair, we first generate a set of basis vectors using (18), and then solve (19) for the largest magnitude $({\tilde{\mu }}_j, \tilde{\varvec{{\upphi }}}_j)$.

4 Design representation, filtration and thresholding

The goal of our topology optimization is to optimally distribute a linear elastic material in the design domain which is quantified by the piece-wise constant non-dimensional volume fraction ${\varvec{{\textsf {z}}}} \in {\mathbb {R}}^{n_\textsf {elm}}$ with $0 \le \textsf {z}_i \le 1$, where $n_\textsf {elm}$ is the number of elements. A well-posed optimization problem is obtained using restriction, via the Helmholtz PDE-filter, cf. Lazarov and Sigmund (2011). In this way, the filtered densities $\varvec{{\upnu }}$ are obtained from

$$\begin{aligned} \varvec{{\upnu }} = {\varvec{{\textsf {F}}}}_\textsf {m}^T{\varvec{{\textsf {K}}}}_{\varvec{{\upnu }}}^{-1}{\varvec{{\textsf {F}}}}_{\varvec{{\upnu }}}{\varvec{{\textsf {z}}}}, \end{aligned}$$

(20)

where ${\varvec{{\textsf {K}}}}_{\varvec{{\upnu }}}$ and ${\varvec{{\textsf {F}}}}_{\varvec{{\upnu }}}$ appear in e.g. Lazarov and Sigmund (2011); Wallin et al. (2020) and ${\varvec{{\textsf {F}}}}_{\textsf {m}}^T$ takes the nodal densities ${\varvec{{\textsf {K}}}}_{\varvec{{\upnu }}}^{-1}{\varvec{{\textsf {F}}}}_{\varvec{{\upnu }}}{\varvec{{\textsf {z}}}} \in {\mathbb {R}}^{n}$ to the averaged, element-based densities $\varvec{{\upnu }} \in {\mathbb {R}}^{n_\textsf {elm}}$ with $0 \le \upnu _i \le 1$. To limit regions wherein $\upnu _i\in (0,1)$, we use thresholding [cf. Guest et al. (2004); Wang et al. (2014)] and penalization (Bendsøe (1989)), such that

$$\begin{aligned} \begin{array}{l} \displaystyle {\varvec{{\textsf {k}}}}_L^e = \chi _L({\bar{\nu }}){\varvec{{\textsf {k}}}}_{L,o}^e \quad \text {and} \quad {\varvec{{\textsf {k}}}}_{G}^e = \chi _G({\bar{\nu }}){\varvec{{\textsf {k}}}}_{G,o}^e, \\ \displaystyle \text {where} \quad \chi _L({\bar{\nu }}) =\delta _o + {\bar{\nu }}^q(1-\delta _o), \quad \chi _G({\bar{\nu }}) ={\bar{\nu }}^q, \\ \displaystyle \text {and} \quad {\bar{\nu }} = H_{\beta ,\eta }(\nu ) = \frac{\text {tanh}(\beta \eta )+\text {tanh}(\beta (\nu -\eta ))}{\text {tanh}(\beta \eta )+\text {tanh}(\beta (1-\eta ))}. \end{array} \end{aligned}$$

(21)

In (21), $\beta$ and $\eta$ are scalars defined such that $\displaystyle \lim _{\beta \rightarrow \infty } H_{\beta ,\eta }(\nu ) = u_s(\nu -\eta )$, where $u_s$ is the unit step function. Increasing $q\in {\mathbb {R}}^+$ enforces increasing levels of penalization, and $\delta _o\in {\mathbb {R}}^+$ is the ersatz material stiffness scaling. Also, ${\varvec{{\textsf {k}}}}_L^e$ and ${\varvec{{\textsf {k}}}}_G^e$ denote element stiffness matrices of ${\varvec{{\textsf {K}}}}_L$ and ${\varvec{{\textsf {K}}}}_G$, respectively. Note that we use different density interpolations for ${\varvec{{\textsf {K}}}}_G$ and ${\varvec{{\textsf {K}}}}_L$ to limit the occurrence of spurious eigenmodes in low density regions (cf. Bendsøe MP and Sigmund (2003); Dalklint et al. (2020)).

4.1 Aggregation

In this work a lower bound constraint is enforced on the lowest magnitude BLF, that is the largest magnitude (or critical) $\mu _i$, which we denote $\mu _c$. To address the non-smoothness due to coinciding eigenvalues, we approximate $\mu _c$ using aggregation in the form of a p-norm, cf. Torii and De Faria (2017). Therefore, the constraint on the critical BLF is stated as

$$\begin{aligned} \mu _c = \underset{j\in {\mathbb {N}}}{\text {max}}\, {\mu }_j \approx {\mu }_p = \left( \sum _{i = 1}^{n_{\mu }} \mu _i^{p} \right) ^{1/p} \le \mu ^\star , \end{aligned}$$

(22)

where $\mu ^\star \in {\mathbb {R}}$ is the upper bound, $p\in {\mathbb {R}}$ and we consider $n_{\mu }\in {\mathbb {N}}_n$ BLFs.

5 Optimization formulation

The topology optimization problem we solve is

$$\begin{aligned} (\mathbb{T}\mathbb{O}) \ {\left\{ \begin{array}{ll} &{}\underset{{\varvec{{\textsf {z}}}}}{\text {min}} \ \ \displaystyle g_o = {\varvec{{\textsf {F}}}}_o^T{\varvec{{\textsf {a}}}}_o, \\ \text {s.t} &{} {\left\{ \begin{array}{ll} g_1 = \displaystyle \int _{\Omega }{\bar{\nu }}\, dV - \upxi V_{o} \le 0, \\ g_2 = \mu _p - \mu ^{\star } \le 0, \\ 0\le \textsf {z}_i\le 1, \quad i\in {\mathbb {N}}_{n_\text{elm}}, \end{array}\right. } \\ \end{array}\right. } \end{aligned}$$

(23)

which is a standard compliance minimization problem subject to a lower bound constraint on the critical buckling load factor with maximum allowed volume fraction $\upxi$. The (23) problem is solved in a nested approach wherein equilibrium equations (1) and (3) are enforced implicitly.

5.1 Sensitivity analysis

When computing the sensitivity of a non self-adjoint displacement dependent function, the implicit sensitivity of the displacements with respect to the design variables appears. In this work, we annihilate this implicit sensitivity through the adjoint method. Without going into details, the sensitivities of the BLFs are (Ferrari and Sigmund 2019)

$$\begin{aligned} \begin{array}{l} \displaystyle \frac{\partial \mu _j}{\partial \varvec{{\upnu }}} = -\varvec{{\upphi }}_j^T\left( \frac{\partial {\varvec{{\textsf {K}}}}_G }{\partial \varvec{{\upnu }}} + {\mu }_j\frac{\partial {\varvec{{\textsf {K}}}}_L}{\partial \varvec{{\upnu }}} \right) \varvec{{\upphi }}_j + {\varvec{{\textsf {a}}}}_o^T\frac{\partial {\varvec{{\textsf {K}}}}_L}{\partial \varvec{{\upnu }}}\varvec{{\Uplambda }}_j \\ \text {where} \quad \displaystyle {\varvec{{\textsf {K}}}}_L\varvec{{\Uplambda }}_j = \varvec{{\upphi }}_j^T \frac{\partial {\varvec{{\textsf {K}}}}_G}{\partial {\varvec{{\textsf {a}}}}_o}\varvec{{\upphi }}_j = {\varvec{{\textsf {b}}}}_j, \end{array} \end{aligned}$$

(24)

where it is assumed that (1) and (3) are fulfilled. An important consequence of (24) is that for each BLF we must compute an adjoint $\varvec{{\Uplambda }}_j$ which requires solving a linear system with ${\varvec{{\textsf {K}}}}_L$. The $\varvec{{\Uplambda }}_j$ can be estimated the same way ${\varvec{{\textsf {a}}}}_o$ is estimated from the ROM by generating a new set of basis vectors using (11) and solving (12), where in both cases ${\varvec{{\textsf {F}}}}_o$ is replaced by ${\varvec{{\textsf {b}}}}_j$. In this work, since we approximate ${\varvec{{\textsf {a}}}}_o$ and $\varvec{{\upphi }}_j$, we must instead use

$$\begin{aligned} \tilde{{\varvec{{\textsf {b}}}}}_j = \tilde{\varvec{{\upphi }}}_j^T\frac{\partial {\varvec{{\textsf {K}}}}_G}{\partial {\varvec{{\textsf {a}}}}_o}\tilde{\varvec{{\upphi }}}_j\bigg |_{\varvec{{a}}_o = \tilde{\varvec{{a}}}_o} \end{aligned}$$

(25)

when estimating the adjoints.

5.2 Consistent sensitivity analysis

Since the sensitivity (24) assumes that (1) and (3) are solved exactly, it is not consistent when they are solved approximately. Amir et al. (2009) and Bogomolny (2010) account for the inconsistencies by replacing $\frac{\partial \mu _j}{\partial \varvec{{\upnu }}}$ with $\frac{\partial {\tilde{\mu }}_j}{\partial \varvec{{\upnu }}}$ and introducing additional adjoint vectors corresponding to the steps in (18). This consistent sensitivity approach is computationally expensive and has shown to not offer any benefit over estimating (24) with $\tilde{{\varvec{{\textsf {a}}}}}_o$ and $({\tilde{\mu }}_j, \tilde{\varvec{{\upphi }}}_j)$. Indeed, if the approximations are accurate the sensitivities are sufficiently accurate nonetheless. In this work the latter approach will be taken, and $\varvec{{\Uplambda }}_j$ in (24) will be estimated from the ROM (12).

6 Numerical examples

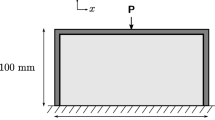
To investigate the performance of our ROM, we study the optimization problem (23) for the three geometries depicted in Figs. 1a, 3a and 5a. The design domains are discretized using $180\times 420$ quadrilateral, plane stress, bi-linear finite elements.

Fig. 1

a A uniform traction with magnitude $10^4$ is distributed over a length of W/30 on the top edge. b Stiffness optimized design. Optimized designs for compliance minimization under buckling constraints c without ROM and d with ROM

We first solve (23) without enforcing buckling constraints, that is we solve a stiffness optimization problem, which yields the critical BLF $\mu _o$. In our subsequent problems we let $\mu ^\star = \mu _o/s$ where s is the safety factor, set to 3 unless stated otherwise. The stiffness optimized designs are used as initial guesses when solving the full (23) optimization problem, see Figs. 1b, 3b and 5b.

The design updates are computed using MMA with default parameters, see Svanberg (1987). Young’s modulus and Poisson’s ratio are $2\times 10^5$ and 0.3, and the ersatz material stiffness scaling is $\delta _0 = 10^{-6}$. The material penalization is initially $q=2$, cf. (21), but is after iteration 30 incremented by 0.25 every 20 iterations until $q = 6$. Initially we set $p = 8$ in (22), but after iteration 30 p is incremented by 0.50 every 20 iterations until $p = 16$, and $n_\mu = 6$ unless stated otherwise. The filter length-scale parameter is $l_o = \frac{3}{2\sqrt{3}}$. We set the surface filter length-scale to $l_s = l_0$, everywhere except at nodes subjected to boundary conditions, where $l_s = 0$. Finally, $\beta = 6$ and $\eta = 0.5$. All parameters are dimensionless. We stop the iteration when $\left\Vert \varvec{{\upnu }}_i - \varvec{{\upnu }}_{i+1}\right\Vert _2 \le 0.01$, or if the number of iterations reaches 400.

We distinguish between two different approaches when solving for equilibrium and adjoints. In the first (reference) approach we start by computing the Choleksky factorization of ${\varvec{{\textsf {K}}}}_L$, after which we solve (1) for ${\varvec{{\textsf {a}}}}_o$, (3) for the $(\mu _j, \varvec{{\upphi }}_j)$ and (24) for the adjoint $\varvec{{\Uplambda }}_j$. The reference approach is summarized in Algorithm 1.

In the second (approximate) approach we first determine if the factorization should be updated. If so, we follow the reference approach, otherwise we solve (12) for $\tilde{{\varvec{{\textsf {a}}}}}_o$, (19) for the $({\tilde{\mu }}_j,\tilde{\varvec{{\upphi }}}_j)$, and (12) for the $\tilde{\varvec{{\Uplambda }}}_j$. A new factorization of ${\varvec{{\textsf {K}}}}_L$ is performed if 1) p or q are updated or 2) the difference between the current physical densities $\varvec{{\upnu }}_i$ and the densities in the last factorization update $\overline{\varvec{{\upnu }}}$ is too large. We choose the cosine of the angle between the designs as a measure of their similarity, that is we update the factorization if

$$\begin{aligned} \cos \theta _{\varvec{{\upnu }}_i, \overline{\varvec{{\upnu }}}} = \frac{\varvec{{\upnu }}_i^T\overline{\varvec{{\upnu }}}}{\left\Vert \varvec{{\upnu }}_i\right\Vert _2\left\Vert \overline{\varvec{{\upnu }}}\right\Vert _2} < c_\text {min} \end{aligned},$$

(26)

where we use the threshold value of $c_\text {min} = 0.9996$. The approximate approach is summarized in Algorithm 2.

6.1 Spire

The first geometry we study is shown in Fig. 1a. In Fig. 1b the stiffness maximized design is depicted. For this problem we use 8, 4 and 8 basis vectors for the linear equilibrium, eigenproblem and the adjoints, respectively. The designs obtained when constraining the critical BLF using the reference and approximate approach, shown in Fig. 1c, d, are very similar. This is also seen in Table 1 showing the value of the objective and constraints computed in a postprocessing step using the reference approach (see Algorithm 1). The constraints are satisfied for both designs, and the differences in the objective is minute. Table 1 also shows the number of matrix factorizations and triangular solves without and with ROM. We see that the number of factorizations is significantly reduced using ROM, while the difference in triangular solves is very small. Figure 2 shows the evolution of $\mu _i/\mu ^\star$ without and with ROM. We note that the evolution is similar for both approaches.

Fig. 2

Evolution of the ratio $\mu _i/\mu ^\star$ for Fig. 1c, d designs, upper bound shown in a dashed black line. a Without ROM b with ROM

Table 1 Objective values, constraint values and computational effort, without and with ROM, for Fig. 1c, d designs

To verify that our ROM performs well for cases where a good initial guess is not available, the spire problem is solved starting from a homogeneous initial guess. The same number of basis vectors as in the previous example is used. The resulting designs are very similar to each other, but are slightly different from those in Fig. 1. The post-process analysis shows that they have the same structural qualities, and the reduction in computational effort is similar to the previous example: the number of factorizations was reduced from 352 to 62, and the number of triangular solves from 31344 to 28623.

6.2 V-structure

The second geometry we study is shown in Fig. 3a. For this problem we use 8, 4 and 8 basis vectors. Again, the designs obtained without and with ROM, seen in Fig. 3c, d, are similar. The objective and constraints at the end designs are provided in Table 2. The constraints are satisfied for both approaches, and the difference in objective is, again, very small. Table 2 also shows the number of matrix factorizations and triangular solves. We note that again the number of factorizations is significantly smaller and that the number of triangular solves is slightly smaller for the approximate approach. Figure 4 shows the evolution of $\mu _i/\mu ^\star$, which is similar for the two approaches.

Fig. 3

a A uniform traction with magnitude $10^4$ is distributed over a length of W/30 on the right edge. b Stiffness optimized design. Optimized designs for compliance minimization under buckling constraints c without ROM and d with ROM

Fig. 4

Evolution of the ratio $\mu _i/\mu ^\star$ for Fig. 3c, d designs, upper bound shown in a dashed black line. a Without ROM b with ROM

Table 2 Objective values, constraint values and computational effort, without and with ROM, for Fig. 3c, d designs

6.3 Column

The last geometry we study is shown in Fig. 5a. For this problem, the number of basis vectors for the static problem, eigenproblem, and adjoint was increased from 8, 4 and 8 to 10, 6 and 10, respectively. When constraining the smallest BLF, the designs shown in Fig. 5c, d are obtained without and with ROM, respectively. For Fig. 5c design, the buckling constraint is satisfied and the p-norm approximating the smallest BLF renders undershooting. However, for Fig. 5d design, the constraint on the p-norm of the BLFs is slightly violated. Even so, due to the undershooting, the critical BLF still satisfies the upper bound constraint. The evolution of $\mu _i/\mu ^\star$ for Fig. 5c, d designs are shown in Fig. 6, and we note that, like in previous examples, the graphs are very similar.

Fig. 5

a A uniform traction with magnitude $10^4$ is distributed over a length of W/30 on the top edge. b Stiffness optimized design. Optimized designs for compliance minimization under buckling constraints c without ROM and d with ROM

Fig. 6

Evolution of the ratio $\mu _i/\mu ^\star$ for Fig. 5c, d designs, upper bound shown in a dashed black line. a Without ROM b with ROM

Additionally, Table 3 shows the number of matrix factorizations and triangular solves without and with ROM. When using ROM the number of factorizations is reduced significantly, by over $75\%$, whereas the total number of triangular solves increased by about $37\%$. While this increase is noticeably larger compared to the previous examples, it still represents a small portion of the total computational effort which is dominated by the matrix factorizations.

Table 3 Objective values, constraint values and computational effort, without and with ROM, for Fig. 5c, d designs

6.4 Mode switching

As a final example, we demonstrate that our ROM can accurately approximate the BLFs when they switch order and coincide. For this reason, we solve the spire problem with a higher safety factor of 6, starting from the compliance initial guess. We also increase the number of buckling factors to 10 to properly take into account the grouping of BLFs near the critical BLF. The number of basis vectors is increased to 10, 6 and 10, respectively.

The resulting designs, which can be found in Fig. 7, are again very similar. Table 4 shows the value of the objective and constraints, which are, in terms of stiffness and buckling resistance, almost identical. This example shows again that the ROM approach provides a significant speedup, in this case by $70\%$, and the number of triangular solves is increased only slightly. Figure 8 shows the evolution of the $\mu _i/\mu ^\star$. We can clearly see that the ROM is able to resolve both coinciding BLFs and mode switching, see for example modes 6 and 7, and modes 8, 9, 10.

Fig. 7

Optimized designs for compliance minimization under buckling constraints a without ROM and b with ROM

Fig. 8

Evolution of the ratio $\mu _i/\mu ^\star$ for Fig. 7a, b designs, upper bound shown in a dashed black line. a Without ROM b with ROM

Table 4 Objective values, constraint values and computational effort, without and with ROM, for the spire problem with higher safety factor

6.5 Residuals

Figure 9 shows the relative residuals of the eigenpairs, which we define by the quotient

$$\begin{aligned} r_j = \frac{||\left( {\varvec{{\textsf {K}}}}_G(\tilde{{\varvec{{\textsf {a}}}}}_o) + {\tilde{\mu }}_j {\varvec{{\textsf {K}}}}_L\right) \tilde{\varvec{{\upphi }}}_j||_2}{||{\varvec{{\textsf {K}}}}_L\tilde{\varvec{{\upphi }}}_j||_2}. \end{aligned}$$

Of course, when using the reference approach the residuals are determined by the tolerance of the eigenvalue solver, so residuals are only shown at design iterations where the approximate approach is used.

Fig. 9

Relative residuals of the eigenvalue problem for a the spire problem, b the V-structure problem and c the column problem. Residuals are only shown at design iterations where the approximate approach is used

The relative residuals for the column problem are, towards the end of the optimization, in the range $10^{-4}-10^{-2}$ and the residuals directly after a factorization update are higher compared to the other problems. Thus, to reduce the residuals and improve the quality of the approximation, the number of basis vectors could be increased further. For the spire problem the residuals are lower in general, but also have a larger spread which can be attributed to the spread in the BLFs themselves. For the V-structure problem, the residuals are comparatively lower, $10^{-6}-10^{-3}$, and are less scattered. Figure 9 shows that the geometry has an influence on the ROM’s efficacy. While the method works well for all considered problems, some cases require more basis vectors and/or factorizations to reach the same level of accuracy as others.

6.6 Discussion

The examples show that designs produced without and with ROM are very similar. In our implementation, we did not compute the consistent sensitivities that account for the inaccuracies of the ROM, nor did we compute the adjoints with full accuracy. Nevertheless, we still found designs very similar to those generated by the reference approach. We demonstrate that our ROM can, without modifications, be applied to problems where a good initial guess is not available. We also show that the ROM can accurately resolve both mode switching and coinciding eigenmodes.

Compared to the reference approach, the ROM approach reduced the number of factorizations significantly, and with exception to the column example, the number of triangular solves did not change significantly. Since the triangular solves only constitute a small portion of the total effort compared to the matrix factorizations, the computational effort is reduced significantly by the proposed ROM approach. When the required number of BLFs grows, the savings might decrease due to the increasing cost of approximating the adjoints.

The number of basis vectors and when to update the factorization was chosen heuristically. Even so, we were able to reduce the computational effort without fine-tuning the parameters. In some cases, the ROM was inaccurate, but adding more basis vectors improved the accuracy without significantly increasing the costs. Based on our numerical experiments, the optimal number of basis vectors depends on the problem and on the design. Ideally, the number of basis vectors and the frequency of factorization should be adaptive, such that the approximation is both efficient and sufficiently accurate.

The ROM-solver for the eigenvalue problem has several advantages over traditional eigenvalue solvers that iterate over a subspace: the number of basis vectors for each eigenpair can be chosen independently. Thus, the effort can be balanced based on how each eigenpair affects the problem—higher accuracy can be enforced for more important eigenpairs. Furthermore, the approximate solution of eigenpairs is embarrassingly parallelizable as the eigenpairs can be solved independently of each other, if the old eigenmodes are chosen in the orthogonalization step. This too should be considered in future work.

The proposed ROM requires a direct solve using the system matrix, limiting its use to problems which can be efficiently solved using direct solvers. Solving problems beyond this size requires other approaches, such as highly tailored multigrid preconditioned subspace iteration methods. For this we refer to the work by Peetz and Elbanna (2021), or the multigrid approach by Ferrari and Sigmund (2020).

7 Concluding remarks

In this paper, we have shown that a reanalysis-based ROM can be applied to topology optimization considering linearized buckling, and that it has clear potential to reduce the computational cost. Our examples indicate that the ROM works for a range of problems, and that more effort needs to be spent on developing adaptive schemes—we presume that further computational savings are possible if the number of basis vectors and the frequency of factorizations are adapted throughout the optimization process.