Integrated topology and controller optimization using the Nyquist curve

Abstract

The design of high-performance mechatronic systems is very challenging, as it requires delicate balancing of system dynamics, the controller, and their closed-loop interaction. Topology optimization provides an automated way to obtain systems with superior performance, although extension to simultaneous optimization of both topology and controller has been limited. To allow for topology optimization of mechatronic systems for closed-loop performance, stability, and disturbance rejection (i.e. modulus margin), we introduce local approximations of the Nyquist curve using circles. These circular approximations enable simple geometrical constraints on the shape of the Nyquist curve, which is used to characterize the closed-loop performance. Additionally, a computationally efficient robust formulation is proposed for topology optimization of dynamic systems. Based on approximation of eigenmodes for perturbed designs, their dynamics can be described with sufficient accuracy for optimization, while preventing the usual threefold increase of additional computational effort. The designs optimized using the integrated approach have significantly better performance (up to 350% in terms of bandwidth) than sequentially optimized systems, where eigenfrequencies are first maximized and then the controller is tuned. The proposed approach enables new directions of integrated (topology) optimization, with effective control over the Nyquist curve and efficient implementation of the robust formulation.

1 Introduction

1.1 Integrated controller-structure optimization

Many high-tech applications require positioning at both high accuracy and high speed, for which motion systems are used. These are, for instance, used in semiconductor equipment, microscopy, robotics, and medical devices (Munnig Schmidt et al. 2011; Oomen 2018). The required speed and accuracy in these positioning systems is achieved by feedback control. In the quest for more extreme performance, the design of motion systems poses a significant challenge.

The final performance and accuracy of such systems heavily depend on system dynamics, the controller, and the (closed-loop) interaction between the two (i.e. mechatronics). Various complex design problems have been effectively addressed by topology optimization in recent years, and the need exists to also apply it to the design of motion systems. Although optimization is frequently used in the design of feedback controlled systems, it is mostly applied in a sequential manner. First, the structure is designed, e.g. for maximum eigenfrequencies using topology optimization (Ma et al. 1995; Delissen et al. 2022), after which a controller is tuned for this structure that achieves system requirements, such as high bandwidth, closed-loop stability, and disturbance rejection (Munnig Schmidt et al. 2011). However, this approach usually leads to sub-optimal system performance. High eigenfrequencies are often a characteristic of good system performance, but it does not mean that higher eigenfrequencies always result in a higher bandwidth. Therefore, for superior performance of the combined system, an integrated approach is required (Fathy et al. 2001; van der Veen et al. 2015, 2017), which is also sometimes referred to as control co-design (Garcia-Sanz 2019). Through integrated (topology) optimization, the dynamic behavior of the structure and the controller can both be adapted to accommodate each other in a more optimal manner, potentially resulting in a better closed-loop performance.

A large portion of existing research on integrated controller-structure optimization is focused on state-feedback controllers in the time domain, which determine their correction signals based on the state of the structure (e.g. positions, deformations, and/or velocities). The optimal controller in this case can be calculated algebraically as the minimizer of a linear quadratic control cost function, based on $\mathcal {H}_2$ synthesis (a generalization of classic LQ/LQR/LQG theory) (Doyle et al. 1989; Anderson and Moore 1989). The result is an optimal controller balancing vibration levels and control effort over time. Most existing methods reformulate the integrated controller-structure optimization problem into a nested formulation, where an optimal controller is found algebraically during each structural design iteration (Haftka 1990; Fathy et al. 2001). The same linear quadratic cost function as the nested controller optimization can be used for the outer structural problem (Miller and Shim 1987). However, this approach is limited to truss problems with few design variables due to its significant computational effort, as the solutions are needed of an algebraic Ricatti equation and of additional Lyapunov equations for the gradients of each design variable. Alternatives in literature are based on minimizing combined strain and control energy in a steady-state setting (Ou and Kikuchi 1996a, b; Molter et al. 2013) or other (multi-)objective formulations (Zhu et al. 2002; da Silveira and Fonseca 2010). While these are computationally feasible for topology optimization, they do not directly relate to the integrated system performance. A more complete overview of different approaches is given in the review paper by Allison and Herber (2014).

1.2 Frequency domain control

In practice, state-feedback and linear quadratic optimal controllers in the time domain are rarely used for high-performance positioning systems. For positioning systems the tracking error, disturbance rejection, and noise attenuation are essential aspects to obtain high-precision. The quantification of these effects is difficult in the time domain (Doyle 1978; Zhou et al. 1996), but can be represented more easily in the frequency domain. This is one of the reasons that frequency-based proportional-integral-derivative (PID) controllers are the current industry standard (Munnig Schmidt et al. 2011).

Fig. 1

Controller and plant placed in a feedback loop, with the aim for the output y to track the reference signal r. The correction signal u generated by the controller is based on the measured error e. If tuned correctly, the closed-loop system is able to reject disturbances d

In order to clearly describe the open challenges for integrated controller-structure optimization in the frequency domain, we will first discuss some aspects of classic control theory. The influence of disturbances and noise on the controlled structure is characterized by the sensitivity function $S(j\omega )$ (Åström and Murray 2008), which is not to be confused with the design sensitivities. The sensitivity function is the transfer function between external disturbance d and output y (Fig. 1), which is dependent on the frequency $\omega$. Here, the disturbances may, for instance, be external loads on the controlled system or motions of the measurement frame. The sensitivity function is defined as

$$\begin{aligned} S(j\omega ) = \frac{1}{1 + L(j\omega )}\text {,} \end{aligned}$$

(1)

with the open-loop transfer function $L(j\omega )=H(j\omega )C(j\omega )$ of the controller and plant in series. The amplitude of the sensitivity function $\left| S(j\omega )\right|$ provides a bound on the disturbance rejection properties, of which a typical example is shown in Fig. 2a. Disturbances are attenuated by the feedback controller if $|S(j\omega )|<{0}\,\hbox {dB}$, but they are amplified if $|S(j\omega )|>{0}\,\hbox {dB}$. The controller is able to correct disturbances for frequencies below the bandwidth $\omega _\text {b}$, which ideally keeps the sensitivity function small at those frequencies and additionally ensures a small tracking error. However, the sensitivity function cannot be lowered indefinitely due to the waterbed effect: lowering the sensitivity function at certain frequencies leads to an increase at other frequencies (Munnig Schmidt et al. 2011). Therefore, peaks are to be avoided for frequencies above the bandwidth to prevent over-amplification of high-frequency noise. This is usually done by limiting the maximum value of $|S(j\omega )|$ to, for instance, ${6}\,\hbox {dB}$. Further details can be found in textbooks on control, e.g. Åström and Murray (2008); Munnig Schmidt et al. (2011).

Fig. 2

a A typical example of a sensitivity function $|S(j\omega )|$. The upper limit of ${6}\,\hbox {dB}$ is indicated in red. b The corresponding Nyquist curve of the loop gain $L(j\omega )$, with the critical $-1$ point and modulus margin indicated in red. Peaks in the sensitivity function correspond to the points of the Nyquist curve closest to the $-1$ point, as indicated by the colored dots

Examples in the literature of integrated optimization for PID control are less common than optimization based on linear quadratic control. One example is the work by Albers and Ottnad (2010), who use a PID controller optimization nested within a structural topology optimization based on strain energy minimization. Here, load cases are iteratively updated based on the control action. However, this approach will not yield optimal performance, since the structure is optimized for a minimum strain energy instead of the integrated system performance.

A truly integrated approach is proposed by van der Veen et al. (2015, 2017), who optimize feedback controlled structures for a maximum bandwidth, subject to constraints on closed-loop stability and disturbance rejection. For the disturbance rejection, constraints are used that explicitly limit the sensitivity function $|S(j\omega )|$ below a certain threshold. Since the sensitivity function is a multi-modal function (Fig. 2a), a constraint is imposed on each individual peak value. The frequencies corresponding to the peak values cannot be calculated explicitly, so a numerical search algorithm must be used to locate the peak values (see, e.g. Bruinsma and Steinbuch 1990). Even though the peaks are found numerically and as long as the constraints are not dependent on the peak frequency, it is possible to calculate correct gradient information and use them as constraints in an optimization (Giesy and Lim 1993; Venini and Pingaro 2017; Delissen et al. 2020). A drawback of the approach of van der Veen et al. (2015, 2017) is that the number of peaks changes during the optimization, depending on the controller, the structure, and their interaction. Next to that, separate constraints need to be applied to ensure closed-loop system stability. As a result, integrated optimization including control requirements, such as closed-loop stability and disturbance rejection, remains an open challenge.

For further insight into the behavior of the sensitivity function $\left| S(j\omega )\right|$, an alternative interpretation is discussed. The sensitivity function can also be interpreted using the Nyquist curve of the open-loop transfer function $L(j\omega )$, as is shown in Fig. 2b. From Eq. 1 can be deduced that the reciprocal of the sensitivity function is equal to the distance from the Nyquist curve $L(j\omega )$ to the critical point at $-1+0j$ in the complex domain (from here on called the $-1$ point). A maximum in the sensitivity function therefore corresponds to a minimum distance between the open-loop transfer function $L(j\omega )$ and the $-1$ point. This minimum distance is also commonly known as the modulus margin (Åström and Murray 2008).

Outside structural and integrated optimization, several techniques are available which focus on gradient-based tuning of controllers using the Nyquist curve, e.g. (Karimi and Galdos 2010; van Solingen et al. 2018). These apply geometric constraints on the Nyquist curve to enforce stability and disturbance rejection margins. An advantage of constraining the Nyquist curve is an enhanced flexibility in limiting both phase as well as amplitude of a transfer function, which is otherwise difficult to do. However, this approach is not suited for topology optimization, since the Nyquist curve $L(j\omega )$ is sampled using a finite number of frequencies, where each sampled point has to be constrained in the complex domain. This easily results in thousands of constraints that each require a computationally costly (dynamic) finite element analysis.

Topology optimization has not been done yet using the Nyquist curve, although it may offer several advantages. There is a straightforward geometrical interpretation of disturbance rejection using the open-loop transfer function $L(j\omega )$ as opposed to the sensitivity function $|S(j\omega )|$, which is in closed-loop. Additionally, the closed-loop stability can be directly enforced by preventing encirclements of the $-1$ point (i.e. the Nyquist stability criterion in case of a stable open-loop system). This motivates the use of the Nyquist curve in controller design.

1.3 Robust formulation

An important requirement for practical design cases is the control on minimum feature size in the design. In topology optimization, this is generally done using a density filter in combination with a robust formulation (Bendsøe and Sigmund 2003; Wang et al. 2011). Erosion and dilation operations are performed on the design in order to generate multiple perturbed designs. By optimizing the design for worst case performance, it is made robust against uniform geometric deviations. The robust formulation indirectly ensures a minimum feature size in the design, dependent on the perturbation amount and the filter radius. Additionally, it helps in obtaining a binary void-solid design without intermediate densities, possibly also reducing the appearance of local eigenmodes (Pedersen 2000). A disadvantage is that the application of this method requires the solution of additional perturbed designs, which in the present setting each require the solution of a computationally costly eigenvalue problem. Furthermore, the integrated controller-structure optimization as proposed by van der Veen et al. (2015, 2017) does not allow for aggregation of constraint values corresponding to the different perturbations. This is due to the fact that the number of peaks (and thus the number of constraints) may change due to the design perturbations, making it hard to determine which peaks to aggregate. The lack of aggregation results in the addition of many new constraints for each perturbed design, which all require the calculation of eigenmode design sensitivities. Thus, to apply the robust formulation to existing integrated optimization methods results in an unacceptable increase of computational effort by at least a factor three.

1.4 Approach and contributions

In this work, we present two main contributions towards integrated controller-structure optimization and application to more practical design cases:

• 1. Local approximation of the Nyquist curve using circles, which can be used in gradient-based optimization

• 2. An efficient robust method for dynamic topology optimization problems, that requires negligible additional computational effort

These new methods are combined, tested, and demonstrated for the integrated controller-structure topology optimization of a motion system.

Local approximation of the Nyquist curve In order to efficiently influence the shape of the Nyquist curve during optimization, local circular approximations are generated at each eigenfrequency. Using multiple circular approximations, the characteristic shape of the Nyquist curve is captured by simple geometric features. Finally, by geometric restriction of each circle in the complex domain, the global shape of the Nyquist curve can be influenced during optimization. This can be used to enforce closed-loop stability (no encirclements around the $-1$ point) and robustness (minimum distance to the $-1$ point).

This method avoids the requirement of knowing the exact frequencies at peaks in the sensitivity function, or equivalently where the Nyquist curve of $L(j\omega )$ is closest to the $-1$ point. Instead, locally approximated sections are used to describe the Nyquist curve close to the peak frequencies, which may be constrained away from the $-1$ point. Each (flexible) eigenmode in the mechanical model exhibits itself as a circle in the Nyquist curve (Fig. 2b), which together form its characteristic shape. This also prevents issues with a changing number of peaks in the sensitivity function, as the absence of a peak corresponds to a circle with a radius of zero at the corresponding eigenfrequency.

Circles in the Nyquist curve have historically been used to identify modal parameters of mechanical systems from experimental data (Kennedy and Pancu 1947; Miller 1978). Here, the reverse process is exploited by fitting a circle related to each eigenfrequency in the dynamic system, using the corresponding modal parameters. Local approximation models are actively being researched in the field of control, where they are used to, for instance, approximate the $\mathcal {H}_\infty$ norm with limited experimental data (see, e.g, Tacx and Oomen (2021)). However, to our knowledge the current approximation-based approach proposed for integrated controller-structure optimization has not been studied before.

Computationally efficient robust formulation To apply the robust formulation to topology optimization with negligible additional computational effort, we propose to approximate both the eigenfrequencies and eigenmodes of the perturbed designs. This is critical, as these are both important to the closed-loop behavior of the system. Since the eroded and dilated designs are very similar to the nominal design, it may be assumed that their dynamic behavior is also very similar. After calculation of the eigenmodes of the nominal design, approximations of eigenfrequencies and eigenmodes for the perturbed designs are constructed from linear combinations of the nominal eigenmodes. This avoids solving additional eigenvalue problems for the perturbed designs.

The eigenmodes are used to construct a reduced-order model for each perturbed design. After this, closed-loop performance is evaluated for each of the reduced-order models, using the proposed local approximation method of the Nyquist curve. The fact that the number of circles does not change during iterations allows for aggregation of the constraints. Thus, the number of constraints is equal for an optimization with or without robust formulation, which prevents calculation of additional eigenmode design sensitivities.

In this work, the contributions are applied to integrated controller and topology optimization with focus on closed-loop system stability and robustness margins on the disturbance rejection. The research is focused on mechanical linear time-invariant (LTI) and single-input single-output (SISO) systems, but many aspects can be generalized to a multi-input multi-output (MIMO) setting. A PID controller with a predefined structure is used for positioning of the mechanical system in a single motion direction. Although the controller-structure is known, its parameters are tuned during optimization. Fixed actuator and sensor locations are used in the system and modal damping is assumed. Furthermore, different problem variations are explored, such as optimization for position dependency using multiple sensor positions (i.e. single-input multiple-output (SIMO)) with the same controller and application of the proposed robust formulation.

The outline of this paper is as follows. First, in Sect. 2, the local approximation of the Nyquist curve using circles is explained and demonstrated on an analytical example. In Sect. 3, the topology optimization formulation is presented. Next, in Sect. 4, all modeling aspects are explained in detail, including the proposed efficient robust formulation for dynamic problems. In Sect. 5, the potential of the proposed methods is demonstrated using numerical examples. Finally, discussion and conclusions are given in Sects. 6 and 7, respectively.

2 Local approximation of the Nyquist curve

2.1 Circle parametrization

In this section is explained how the circular-shaped local approximations for the flexible eigenmodes in the Nyquist curve $L(j\omega )$ are constructed, based on theory from experimental modal analysis (Kennedy and Pancu 1947; Miller 1978). Given the transfer function in the Laplace domain L(s), the Nyquist curve is obtained with complex frequency $s=j\omega$, which corresponds to a line along the imaginary axis. First, the general transfer function is given by its decomposition in first-order terms as

$$\begin{aligned} L(s) = \sum _i \frac{p_i}{s - \lambda _i}\text {,} \end{aligned}$$

(2)

with participation factors $p_i\in {\mathbb {C}}$, and system poles $\lambda _i\in {\mathbb {C}}$. It is possible to obtain this decomposition from any representation of the transfer function, for instance from a state-space model as is further explained in Sect. 4.3. For frequencies $s=j\omega$ in the proximity of a system pole $\lambda _i$, the corresponding first-order term is assumed dominant, as its denominator becomes small. Therefore,

$$\begin{aligned} L(s) \approx {\tilde{L}}_i(s) = \breve{L}_i + \frac{p_i}{s - \lambda _i} \quad \text {for}\quad s \approx j\textrm{Im}\left( \lambda _i\right) \end{aligned},$$

(3)

where the local approximation ${\tilde{L}}_i(s)$ consists of a constant offset $\breve{L}_i\in {\mathbb {C}}$ and a single first-order term. The offset $\breve{L}_i$ contains the contributions of all remaining first-order terms at the frequency of interest and is calculated as

$$\begin{aligned} \breve{L}_i = L(j\textrm{Im}\left( \lambda _i\right) ) - \frac{p_i}{j\textrm{Im}\left( \lambda _i\right) - \lambda _i} = \sum _{k\ne i} \frac{p_k}{j\textrm{Im}\left( \lambda _i\right) - \lambda _k}\text {,} \end{aligned}$$

(4)

ensuring interpolation of $L(j\textrm{Im}\left( \lambda _i\right) ) = {\tilde{L}}(j\textrm{Im}\left( \lambda _i\right) )$. An illustration of a local approximation can be seen in Fig. 3.

Fig. 3

Illustration of one local circle approximation ${\tilde{L}}(j\omega )$ (in blue) fitted to the Nyquist curve $L(j\omega )$ in grey. The radius R, midpoint X, constant offset $\breve{L}$, and the interpolatory point $L(j\textrm{Im}\left( \lambda \right) )$ are indicated

From experimental modal analysis, it is known that a transfer function of the form in Eq. 3 results in a circle in the complex domain (Kennedy and Pancu 1947; Miller 1978). Its midpoint and radius are calculated, respectively, using

$$\begin{aligned} X_i = \breve{L}_i - \frac{p_i}{2\textrm{Re}\left( \lambda _i\right) }\quad \text {and}\quad R_i = \frac{\left| p_i\right| }{2\left| \textrm{Re}\left( \lambda _i\right) \right| }\text {.} \end{aligned}$$

(5)

An alternative and simplified proof of these relations, based on the theory of generalized circles (Schwerdtfeger 1979), is provided in Appendix 1. As the relations are all analytical, the derivatives can be calculated explicitly, for which the equations are given in Appendix 1. By constructing local circle approximations for each relevant system pole $\lambda _i$, the important features of the Nyquist curve of L(s) can be described using simple geometry.

Note that the radius is non-differentiable when $\left| p_i\right| = 0$ and additionally approaches infinity when $\textrm{Re}\left( \lambda _i\right) \rightarrow 0$. The former case occurs when an eigenmode is not excited by the actuator or when it has no deformation at the sensor location. The latter case will normally not occur, since the real part of a complex pole is a finite negative value for a stable system with damping. To account for non-differentiability when $\left| p_i\right| = 0$, and thus $R_i=0$, a small perturbation is added as

$$\begin{aligned} {\tilde{R}}_i = \sqrt{R_i^2 + R_\text {min}^2}\text {.} \end{aligned}$$

(6)

This ensures differentiability when $R_i=0$ by setting a (smooth) minimum radius of $R_\text {min}$.

2.2 Analytical example

Fig. 4

a A double mass spring damper system, which can be described using Eq. 7. b Bode plot of the double second-order system and c) corresponding Nyquist plot, where the approximated circles and interpolated points $H(j\textrm{Im}\left( \lambda _i\right) )$ are indicated. The parameters used are $\Omega _1={1.0}\hbox {rad/s}$, $\Omega _2={1.1}\hbox {rad/s}$, $\chi _1={0.2}{\hbox {kg}^{-1}}$ (collocated), $\chi _2={0.15}{\hbox {kg}^{-1}}$, and $\zeta _1=\zeta _2=0.01$

To demonstrate the principle of the local circle approximation, a double mass spring damper system is used, as is shown in Fig. 4a. To keep the equations simple, no controller is used for this example and circles are formed for the plant H(s) instead of the loop L(s). The transfer function H(s) for this system describes the relation between a force on either of the masses to a displacement on either. Mathematically, it is the superposition of two second-order systems (Gawronski 2004; Munnig Schmidt et al. 2011):

$$\begin{aligned} H(s) = \frac{\chi _1}{\Omega _1^2 + 2s\zeta _1\Omega _1 + s^2} + \frac{\chi _2}{\Omega _2^2 + 2s\zeta _2\Omega _2 + s^2}\text {.} \end{aligned}$$

(7)

Here, undamped eigenfrequencies are denoted $\Omega _1,\Omega _2$, relative damping factors $\zeta _1,\zeta _2$, and modal contributions $\chi _1,\chi _2$. These modal parameters can be calculated from the mass, stiffness and damping values of the double mass spring system in Fig. 4a and can be positive (e.g. collocated) or negative (e.g. non-collocated) (Gawronski 2004). This equation can be rewritten into a notation using system poles $\lambda _i$ and their conjugates $\overline{\lambda _i}$, becoming

$$\begin{aligned} H(s)= \frac{\chi _1}{(s-\lambda _1)(s-\overline{\lambda _1})} + \frac{\chi _2}{(s-\lambda _2)(s-\overline{\lambda _2})}\text {,} \end{aligned}$$

(8)

where the system poles are calculated as $\lambda _i=-\zeta _i\Omega _i + j\Omega _i\sqrt{1-\zeta _i}$ in case of an underdamped system.

The Bode plot of this system in Fig. 4b shows the frequency-dependent amplitude and phase behavior of the transfer function $H(j\omega )$. Resonances can clearly be observed, which are located at the damped eigenfrequencies $\textrm{Im}\left( \lambda _i\right)$ in the Bode plot. Alternatively, the transfer function can be represented in the complex domain by a Nyquist plot, shown in Fig. 4c. Looking at the Nyquist plot, the circular shapes can clearly be identified, with their apexes with respect to the origin coinciding with the damped eigenfrequencies $\textrm{Im}\left( \lambda \right)$. Note that the furthest point from the origin can be calculated explicitly, as opposed to the distance to the $-1$ point, which cannot be calculated.

Circles cannot be fit directly to the second-order systems, therefore the transfer function first needs to be decomposed into first-order terms. In this case, this is simply done by rewriting Eq. 8 into

$$\begin{aligned} H(s) = \frac{p_1}{s-\lambda _1} - \frac{p_1}{s-\overline{\lambda _1}} + \frac{p_2}{s-\lambda _2} - \frac{p_2}{s-\overline{\lambda _2}}\text {,} \end{aligned}$$

(9)

with corresponding participation factors

$$\begin{aligned} p_i=-\frac{j\chi _i}{2\textrm{Im}\left( \lambda _i\right) }\text {.} \end{aligned}$$

(10)

From the four first-order systems in Eq. 9, only one first-order system is assumed dominant around each of the excitation frequencies $\omega \approx \textrm{Im}\left( \lambda _i\right)$ and $\omega \approx -\textrm{Im}\left( \lambda _i\right)$. Since only positive frequencies are of interest, the two approximated circles using Eqs. 3-5 can be described with radii and midpoints being

$$\begin{aligned} \begin{aligned} R_i&= \frac{\left| \chi _i\right| }{4\zeta _i\Omega _i^2\sqrt{1-\zeta _i}}&\text {and}\, & {} X_i&= \breve{H}_i-\frac{j\chi _i}{4\zeta _i\Omega _i^2\sqrt{1-\zeta _i}} \text {,}{} & {} \end{aligned} \end{aligned}$$

(11)

with constant offsets

$$\begin{aligned} \breve{H}_i = H(j\textrm{Im}\left( \lambda _i\right) ) + \frac{j \chi _i}{2 \zeta _i \Omega _i^2 \sqrt{1-\zeta _i}}\text {.} \end{aligned}$$

(12)

Two circles are calculated and overlaid in Fig. 4c, demonstrating approximation with a close match to the original Nyquist curve. The approximation is most accurate for frequencies near the interpolation frequency $\textrm{Im}\left( \lambda _i\right)$. From Eq. 11 can be seen that increasing the damping value or eigenfrequency would decrease circle radius, and the modal contributions $\chi _i$ have a proportional effect on the radii.

Fig. 5

The Nyquist diagrams and local circle approximations for two systems showing mode interaction because of frequencies close to each other, at $\Omega _1={1.0}\,\hbox {rad/s}$ and $\Omega _2={1.01}\,\hbox {rad/s}$. The damping parameters are $\zeta _1=\zeta _2=0.01$. System input and output can be at either of the two masses. a) Interaction with both modal contributions positive ($\chi _1={0.2}{\,\hbox {kg}^{-1}}$ and $\chi _2={0.15}{\,\hbox {kg}^{-1}}$, e.g.collocated system) results in approximation smaller than the actual Nyquist curve. b) Interaction with opposed modal contributions ($\chi _1={0.3}{\,\hbox {kg}^{-1}}$ and $\chi _2={-0.15}{\,\hbox {kg}^{-1}}$, e.g. non-collocated system) results in larger circles than the Nyquist curve, as the two modes cancel each other

When eigenfrequencies are close to each other, they start interacting with each other. The mixing of modes results in non-circular shapes in the Nyquist curve. At this point the approximation in Eq. 3 is unable to fully capture the exact behavior, as the influence of other modes ($\breve{H}$) is no longer (close to) constant. Using the double second-order system, this is demonstrated in Fig. 5a for a system with positive modal contributions (e.g. in a collocated system). In this case the two second-order terms contribute in the same direction and the total response is larger than the approximations. The opposite happens when the signs of the modal contributions are opposed (e.g. in a non-collocated system), as can be seen in Fig. 5b, where the approximated circles are larger than the actual response. The two modes compensate each other and the total response becomes smaller. These examples are specifically tuned to show the effect of mode interaction, but these extreme cases may be rare to occur in an optimization setting. This will be investigated in Sect. 5 using numerical examples.

2.3 Constraining the Nyquist curve

Using the local circle approximations, the Nyquist curve can be parametrized in the complex domain using simple geometry. This is very useful for optimization problems where the Nyquist curve must geometrically be constrained in the complex domain.

Distance to a point For instance, the closest distance h from a circle to a point $\tau \in {\mathbb {C}}$ is characterized as the distance to the midpoint of the circle minus its radius

$$\begin{aligned} h(X, R) = \left| X - \tau \right| - R\text {.} \end{aligned}$$

(13)

To calculate the distance furthest away, the radius is simply added instead of subtracted

$$\begin{aligned} h(X, R) = \left| X - \tau \right| + R\text {.} \end{aligned}$$

(14)

Distance to a line The shortest distance to a line characterized by unit normal direction $n\in {\mathbb {C}}$ (with $|n|=1$) and passing through the point $\tau$ can easily be calculated as

$$\begin{aligned} h(X, R) = \textrm{Re}\left( (X-\tau )\overline{n}\right) - R\text {.} \end{aligned}$$

(15)

Distance to an area By composing distances to lines and points, also the distance from a circle to an area can be characterized. For instance, the shortest distance to a wedge-shaped area bounded by two line sections with normals $n_1, n_2\in {\mathbb {C}}$ intersecting in the point $\tau$, is defined as

$$\begin{aligned} h(X, R) = \left\{ \begin{matrix} \left| X - \tau \right| &{}\text {if} &{} \mathcal {C}_1 \\ \textrm{Re}\left( ( X - \tau )\overline{n_1}\right) &{}\text {if} &{} \mathcal {C}_2 \\ \textrm{Re}\left( (X - \tau )\overline{n_2}\right) &{}\text {if} &{} \mathcal {C}_3 \end{matrix}\right\} - R \text {,} \end{aligned}$$

(16)

where the conditions $\mathcal {C}_1$, $\mathcal {C}_2$, and $\mathcal {C}_3$ indicate which of the three sections (lines or point) is closest to the position of X. These functions are mostly smooth and differentiable, except when point X coincides with $\tau$ or at an inflection point between two segments. However, these cases will numerically rarely occur, especially when these are used in constraints that serve to keep the point X away from $\tau$.

3 Application to controller-structure optimization

3.1 Optimization formulation

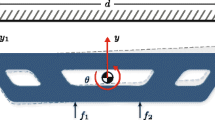
In a closed-loop controlled system, the interplay between controller and structure determines the performance that can be achieved. The feedback system consists of a PID controller C(s) and the structure H(s), which contains a rigid body mode, placed in a loop, as is shown in Fig. 1.

From an optimization point of view, there is a trade-off between performance (bandwidth) and closed-loop stability. Stability can be determined by inspecting the closed-loop poles, which must have a negative real part. Using the Nyquist stability criterion, closed-loop stability can also be interpreted with the Nyquist curve: for a stable closed-loop system, the open-loop curve $L(s=j\omega )$ must not encircle the $-1$ point (in the current case where the open-loop system is stable), which for positive $\omega$ means that $L(j\omega )$ keeps the $-1$ point to the left hand side for increasing frequencies (Munnig Schmidt et al. 2011). Here, the open-loop transfer function is calculated as the controller and plant in series $L(s)=H(s)C(s)$.

As discussed in the Introduction, the modulus margin gives information on how close a system is to instability, and it also provides a bound on the influence of disturbances on the controlled structure. It is characterized as the closest distance of the Nyquist curve $L(j\omega )$ to the $-1$ point.

To ensure a closed-loop system which is stable with a specified modulus margin, the locally approximated circles are used to constrain the trajectory of the Nyquist curve $L(j\omega )$. Constraints are defined to prevent the circle approximations, corresponding to the mechanical eigenmodes, from entering the wedge-shaped area offset by $\mu$ around the $-1$ point as indicated in Fig. 6. In this way, both stability and disturbance rejection are enforced simultaneously by the constraints.

Fig. 6

The constrained area in the Nyquist diagram indicated in red, which ensures both closed-loop stability and a modulus margin of $\mu$. The wedge-shaped area (Eq. 16) is shaded in dark red, which is offset with the modulus margin to the lighter shade of red

Multiple Nyquist curves can be constrained in an optimization, for instance, to account for position-dependent dynamics. Many high-tech positioning systems consist of motion systems stacked in series to provide positioning freedom in additional movement directions or to achieve an extended range of motion. Since contactless measurements are often used (e.g, laser interferometry or eddy current sensors), a sensor fixed on a measurement frame therefore changes position relative to the measured object. As the measurement position affects the dynamics, it becomes position-dependent (van der Veen et al. 2017). In this work, the inclusion of multiple ($N_\text {out}$) relative sensor positions is therefore also considered. This results in multiple SISO control loops, or rather SIMO, each requiring performance constraints on disturbance rejection.

For the topology optimization, a density-based formulation is used (Bendsøe and Sigmund 2003). The optimization formulation used in this work is stated as

$$\begin{aligned} \begin{aligned} \min _{\textbf{x}, \omega _\text {b}} \quad&\frac{1}{\omega _\text {b}} \text {,} \\ \quad s.t. \quad&V(\textbf{x})\le v_\text {f} V_\text {max}\text {,} \\&h_{ij}(\textbf{x}, \omega _\text {b}) \ge \mu \quad \forall \quad \left\{ \begin{matrix} i=1,\dotsc ,N \\ j=1,\dotsc ,N_\text {out} \end{matrix} \right. \text {,} \\&0\le \textbf{x}\le 1 \text {,} \end{aligned} \end{aligned}$$

(17)

where $\textbf{x}$ represents the pseudo-density variables used for topology optimization and $\omega _\text {b}$ the bandwidth, which is the tuning parameter of the PID controller. The number of flexible eigenmodes in the system is equal to N, for each of which circular approximations are constrained. The aim is to maximize the bandwidth $\omega _\text {b}$ of the closed-loop system while keeping the volume V below a volume fraction $v_\text {f}$ of the maximum volume $V_\text {max}$, and simultaneously ensuring the circle approximations remain outside of the wedge-shaped area using the distances $h_{ij}$ as defined in Eq. 16. These distances are related to the design variables through the radii $R_{ij}(\textbf{x}, \omega _\text {b})$ and midpoints $X_{ij}(\textbf{x}, \omega _\text {b})$ of the circular local approximations.

3.2 Optimization implementation and scaling

As optimizer, method of moving asymptotes (MMA) is used (Svanberg 1987). Constraint and objective scaling is critical to this method, so the original optimization formulation of Eq. 17 is reformulated as

$$\begin{aligned} \begin{aligned} \min _{\textbf{x}, x_\omega } \quad&100\frac{\omega _\text {b}^{(0)}}{\omega _\text {b}(x_\omega )}\text {,} \\ \quad s.t. \quad&10\left( \frac{V(\textbf{x})}{v_\text {f} V_\text {max}} - 1 \right) \le 0 \text {,} \\&g_{ij}(\textbf{x}, x_\omega ) \le 0\; \forall \; \left\{ \begin{matrix} i=1,\dotsc ,N \\ j=1,\dotsc ,N_\text {out} \end{matrix} \right. \text {,}\\&0\le \textbf{x}\le 1 \text {,}\\&0 \le x_\omega \le 1 \text {,} \end{aligned} \end{aligned},$$

(18)

where the objective is normalized with the bandwidth at the initial iteration $\omega _\text {b}^{(0)}$ and a normalized design variable $x_\omega$ is used to tune the controller. The constraints on the circles are scaled and normalized as

$$\begin{aligned} g_{ij} = 10\left( 1 - \frac{h_{ij}}{\mu }\right) \text {.} \end{aligned}$$

(19)

Instead of directly using the bandwidth as a variable, it is exponentially scaled between the user-defined bounds $[\omega _\text {min}, \omega _\text {max}]$ as

$$\begin{aligned} \begin{aligned} \omega _\text {b}&= \omega _{\text {min}}\left( \frac{\omega _{\text {max}}}{\omega _{\text {min}}}\right) ^{x_\omega }\text {.} \\ \end{aligned} \end{aligned}$$

(20)

This causes less sensitive behavior for parameter changes at low bandwidth, and makes all optimization variables ($\textbf{x}$ and $x_\omega$) equally bounded between 0 and 1. The objective function is thus an explicit analytical function of the design variable $x_\omega$, hence the design sensitivity analysis is straightforward.

To ensure a feasible initial controller for a given initial structure $\textbf{x}^{(0)}$ (uniform densities equal to the volume fraction $v_\text {f}$), a separate controller optimization is performed prior to the integrated controller-structure optimization. The control variable $x_\omega$ is found using the formulation of this pre-optimization, given as

$$\begin{aligned} \begin{aligned} \min _{x_\omega } \quad&100\frac{\omega _\text {min}}{\omega _\text {b}(x_\omega )} \text {,} \\ \quad s.t. \quad&g_{ij}(x_\omega ) \le 0\quad \forall \quad \left\{ \begin{matrix} i=1,\dotsc ,N \\ j=1,\dotsc ,N_\text {out} \end{matrix} \right. \text {,}\\&0 \le x_\omega \le 1 \text {,} \end{aligned} \end{aligned}$$

(21)

which has its optimum at $\omega _\text {b}^{(0)}$. This value is used as initial bandwidth for the integrated optimization given in Eq. 18.

3.3 Topology optimization parametrization

Since a density-based approach is used, the structural design variables $\textbf{x}$ are first filtered using a standard density filter, resulting in the filtered design field $\textbf{x}_\text {f}$ (Bruns and Tortorelli 2001). The Young’s modulus $E_i$ and density $\rho _i$ of each finite element i in the domain $\mathcal {E}$ are obtained from the filtered design parameters using the following material interpolation

$$\begin{aligned} \begin{aligned} E_i&= E_0 \left( x_\text {min} + (1-x_\text {min}) x_{\text {f},i}^3 \right) \quad \forall \quad i\in \mathcal {E}\text {,} \\ \rho _i&= \left\{ \begin{array}{ccc} \rho _0 x_{\text {f},i} &{} \text {for} &{} x_{\text {f},i} \ge t \\ \rho _0 \frac{x_{\text {f},i}^6}{t^5} &{}\text {for} &{}x_{\text {f},i} < t \end{array} \right. \quad \forall \quad i\in \mathcal {E}\text {.} \end{aligned} \end{aligned}$$

(22)

The small minimum design density $x_\text {min}$ prevents the stiffness matrix from becoming exactly singular when design densities are zero.

The low mass-to-stiffness ratio in Eq. 22 for low densities largely prevents the occurrence of local eigenmodes (Olhoff and Du 2005). These are unwanted eigenmodes in low density areas, with low corresponding eigenfrequencies. Local modes are further prevented using a flood fill algorithm on the design vector $\textbf{x}$, removing any material that is disconnected or very loosely connected to actuator or sensor locations. Elements that are connected to the non-design domains through densities lower than 0.2 are recursively clipped to the maximum of their neighbors. In an extreme case, the disconnection of bodies results in additional rigid body modes at frequencies close to zero. These measures prevent undesired localized modes, improving the convergence of the optimization.

Next, the stiffness and mass matrices are assembled using the material properties $\textbf{E}$ and $\pmb {\rho }$. For this, a grid of bilinear quadrilateral finite elements is used, with a full integration scheme and a plane strain condition. The assembly is performed as

$$\begin{aligned} \textbf{K}&= {{\mathbb {A}}}_{i\in \mathcal {E}} E_i \textbf{K}_0{} & {} \text {and} &&\textbf{M}&= {{\mathbb {A}}}_{i\in \mathcal {E}} \rho _i \textbf{M}_0\text {,} \end{aligned} $$

(23)

where $\textbf{K}_0$ and $\textbf{M}_0$ represent element stiffness and (lumped) mass matrix, respectively, corresponding to unit material properties, and ${{\mathbb {A}}}$ denotes the matrix assembly operation over the entire domain $\mathcal {E}$.

4 Modeling

4.1 Mechanical model

This section describes the different steps that are taken to calculate the circle radii and midpoints starting from the finite element matrices and the controller parameter. To guide the reader, a high-level visual guide of the different calculation steps is shown in Fig. 7. Furthermore, the equations to calculate gradients during each step of the optimization are given in Appendix 1.

Fig. 7

Overview of the modeling approach, starting from the controller design variable $\omega _\text {b}$ and the finite element system matrices ($\textbf{K}$ and $\textbf{M}$), which are dependent on the structural design variables ($\textbf{x}$). The flow diagram shows all steps taken in order to calculate the midpoint and radius of a circle approximation to the Nyquist curve

From the mass and stiffness matrices $\textbf{M}$ and $\textbf{K}$, a reduced-order model is first constructed using a truncated modal decomposition. This model approximates the displacement field $\textbf{u}(t)$ by superposition of a number of eigenmodes $\pmb {\phi }_i$ scaled over time with amplitudes $q_i(t)$, denoted as

$$\begin{aligned} \begin{aligned} \textbf{u}(t)&\approx \sum _{i=0}^N q_i(t) \pmb {\phi }_i = \varvec{\Phi }\textbf{q}(t) \text {,}\\ \varvec{\Phi }&= \begin{bmatrix} \pmb {\phi }_0, \pmb {\phi }_1&\dots&\pmb {\phi }_N \end{bmatrix}\text {,} \end{aligned} \end{aligned}$$

(24)

where $\varvec{\Phi }$ is the projection matrix containing all eigenmodes. The eigenfrequencies $\Omega _i$ and corresponding eigenmodes $\pmb {\phi }_i$ are obtained by solving the undamped eigenvalue problem for the lowest $N+1$ modes

$$\begin{aligned} \begin{aligned} (\textbf{K} - \Omega _i^2\textbf{M})\pmb {\phi }_i&= \textbf{0} \quad \forall \quad i=0,\dotsc ,N\text {,}\\ 0\le \Omega _0&\le \dotsc \le \Omega _N\text {,} \end{aligned} \end{aligned}$$

(25)

using mass-normalization of the eigenmodes as $\pmb {\phi }_i^T \textbf{M}\pmb {\phi }_i=1$. The lowest eigenfrequency $\Omega _0={0}\,\hbox {rad/ms}$ corresponds to the rigid body mode for the degree of freedom that is controlled by the PID controller.

The projection matrix $\varvec{\Phi }$ is used to obtain the reduced equations of motion as

$$\begin{aligned} \begin{aligned} \varvec{\Omega }^2\textbf{q}(t) + 2\zeta \varvec{\Omega }\dot{\textbf{q}}(t) + \ddot{\textbf{q}}(t) = \varvec{\Phi }^T \textbf{f} u(t) \text {,}\\ \textbf{y}(t) = \textbf{G}^T \varvec{\Phi } \textbf{q}(t)\text {,} \end{aligned} \end{aligned}$$

(26)

where $\varvec{\Omega }$ is a diagonal matrix containing the eigenfrequencies and $\zeta$ the non-dimensional damping ratio. The unit input force vector, as exerted by the actuator, is denoted as $\textbf{f}$ and the unit output displacement vectors as measured by the sensors with block-vector $\textbf{G}$, with $N_\text {out}$ columns for each sensor. The input is denoted u(t) and the outputs for all sensor positions $\textbf{y}(t)$, as indicated in Fig. 1. The transfer function of the plant becomes

$$\begin{aligned} \textbf{H}(s) = \textbf{G}^T \varvec{\Phi }\left( \varvec{\Omega }^2 + 2s\zeta \varvec{\Omega } + s^2\textbf{I} \right) ^{-1}\varvec{\Phi }^T \textbf{f}\text {,} \end{aligned}$$

(27)

which describes the behavior between the input and $N_\text {out}$ outputs of the plant in the frequency domain.

4.2 Controller

A PID controller with additional low-pass filter is used for feedback control of the rigid body mode, which is defined by the control law

$$\begin{aligned} C(s) = k\frac{s + \frac{1}{5}\omega _\text {b}}{s} \frac{3s + \omega _\text {b}}{s + 3\omega _\text {b}} \frac{5\omega _\text {b}}{s + 5\omega _\text {b}}\text {,} \end{aligned}$$

(28)

with tuning parameters gain k and bandwidth $\omega _\text {b}$. This is a PID controller based on industry standard rules-of-thumb, with integral action until $\omega _\text {b}/5$, phase lead between $\omega _\text {b}/3$ and $3\omega _\text {b}$, and first-order roll-off beyond $5\omega _\text {b}$ (Munnig Schmidt et al. 2011; van der Veen et al. 2015). The Bode plot of this controller can be seen in Fig. 8. The bandwidth is used as a design variable during the optimization and the gain is calculated using

$$\begin{aligned} k = \frac{k_0}{\left| H_m(j\omega _\text {b})\right| } = k_0 m \omega _\text {b}^2 \text {.} \end{aligned}$$

(29)

Here, m is the mass of the system and the rigid body mode response of the plant is equal to

$$\begin{aligned} H_m(s) = \frac{1}{ms^2}\text {.} \end{aligned}$$

(30)

This ensures that the open-loop gain at the bandwidth $\left| L(j\omega _\text {b})\right| = k_0$. In current work, the gain value is chosen as $k_0=1.1$, which ensures correct interaction between the controller and the rigid body mode (Munnig Schmidt et al. 2011). Note that the method is not limited to this specific control law and variations in control behavior and parametrization are possible.

Fig. 8

Bode plot of the controller $C(j\omega )$, with normalized axes. The dotted lines indicate frequencies at 1/5, 1/3, 3, and 5 times the bandwidth $\omega _\text {b}$

The control law can be rewritten into state-space form

$$\begin{aligned} \begin{aligned} \dot{\textbf{c}}(t)&= \textbf{A}_\text {c} \textbf{c}(t) + \textbf{B}_\text {c} e(t) \text {,} \\ u(t)&= \textbf{C}_\text {c} \textbf{c}(t)\text {,} \end{aligned} \end{aligned}$$

(31)

where $\textbf{A}_\text {c}{\in {\mathbb {R}}^{3\times 3}}$, $\textbf{B}_\text {c}{\in {\mathbb {R}}^{3\times 1}}$, $\textbf{C}_\text {c}{\in {\mathbb {R}}^{1\times 3}}$ represent the controller-structure in canonical form (also given in Appendix 1) (Skogestad and Postlethwaite 2001). The vector $\textbf{c}$ contains the internal state of the PID controller and is of length 3. Note that other controller-structures might require a different number of internal states.

The open-loop response is obtained by placing the controller (Eq. 31) and plant (Eq. 27) in series, connecting the output of the controller to the input of the plant. In the form of a state-space model in the time domain this becomes

$$\begin{aligned} \begin{aligned} \dot{\textbf{z}}(t)&= \textbf{A}\textbf{z}(t) + \textbf{B}e(t)\text {,} \\ \textbf{y}(t)&= \textbf{C}\textbf{z}(t)\text {,} \end{aligned} \end{aligned}$$

(32)

with system matrices (Fig. 7) and state vector

$$\begin{aligned} \begin{aligned} \textbf{A}&= \begin{bmatrix} \textbf{A}_\text {c} &{} \textbf{0} &{} \textbf{0}\\ \textbf{0} &{} \textbf{0} &{} \textbf{I} &{} \\ \varvec{\Phi }^T \textbf{f}\textbf{C}_\text {c} &{} -\varvec{\Omega }^2 &{} -2\zeta \varvec{\Omega } \end{bmatrix}\text {,}&\textbf{B}&= \begin{bmatrix} \textbf{B}_\text {c} \\ \textbf{0} \\ \textbf{0} \end{bmatrix}\text {,}\\ \textbf{C}&= \begin{bmatrix} \textbf{0}&\textbf{G}^T \varvec{\Phi }&\textbf{0} \end{bmatrix}\text {,}&\textbf{z}&= \begin{bmatrix} \textbf{c} \\ \textbf{q} \\ \dot{\textbf{q}} \end{bmatrix}\text {.} \end{aligned} \end{aligned}$$

(33)

The dimensions of these are $\textbf{A}\in {\mathbb {R}}^{M\times M}$, $\textbf{B}\in {\mathbb {R}}^{M\times N_\text {in}}$, $\textbf{C}\in {\mathbb {R}}^{N_\text {out}\times M}$, and $\textbf{z}\in {\mathbb {R}}^{M}$, where $M=2N+5$ and $N_\text {in}=1$ in the current work. Now the transfer function of the open-loop gain becomes

$$\begin{aligned} \begin{aligned} \textbf{L}(s) = \textbf{H}(s)C(s)= \textbf{C}\left( s\textbf{I} - \textbf{A}\right) ^{-1}\textbf{B}\text {,} \end{aligned} \end{aligned}$$

(34)

which can be used to calculate the open-loop responses $\textbf{L}(s)\in {\mathbb {C}}^{N_\text {out}\times N_\text {in}}$ in the frequency domain.

4.3 Modal decomposition

Before circles can be mapped to the open-loop transfer function $L(j\omega )$, the transfer function needs to be decomposed into first-order terms (Fig. 7). From the state-space model (Eq. 34), the poles can directly be obtained by an eigen-decomposition of the system matrix $\textbf{A}$ as

$$\begin{aligned} \begin{aligned} \textbf{A}\textbf{Q}&= \textbf{Q}\varvec{\Lambda }\text {,}\\ \textbf{A}&= \textbf{Q}\varvec{\Lambda }\textbf{Q}^{-1}\text {,} \end{aligned} \end{aligned}$$

(35)

where matrix $\textbf{Q}{\in {\mathbb {C}}^{M\times M}}$ contains all eigenmodes of the (right) eigenvalue problem and matrix $\varvec{\Lambda }{\in {\mathbb {C}}^{M\times M}}$ has all the complex-valued poles $\lambda _i$ on its diagonal. Substitution into the transfer function of Eq. 34 yields

$$\begin{aligned} \begin{aligned} \textbf{L}(s)&= \textbf{C}\left( s\textbf{I} - \textbf{Q}\varvec{\Lambda }\textbf{Q}^{-1}\right) ^{-1}\textbf{B} \\&= \textbf{C}\textbf{Q}\left( s\textbf{I} - \varvec{\Lambda }\right) ^{-1}\textbf{Q}^{-1}\textbf{B} \\&= \sum _i^{N_\text {s}} \frac{\textbf{P}_i}{s - \lambda _i} \text {.} \end{aligned} \end{aligned}$$

(36)

Here, the matrix $\textbf{P}_i$ denotes the participation factors of all input and output combinations for mode i. The participation factors can be calculated as

$$\begin{aligned} p_{ijk} = [\textbf{C}\textbf{Q}]_{ji} [\textbf{Q}^{-1}\textbf{B}]_{ik}{ \quad \forall \quad \begin{aligned} i&\in \left\{ 1,\dotsc ,N\right\} \\ j&\in \left\{ 1,\dotsc ,N_\text {out}\right\} \\ k&\in \left\{ 1,\dotsc ,N_\text {in}\right\} \end{aligned}} \end{aligned}$$

(37)

for a general MIMO system, where the outputs are indexed with j and the inputs with k. The current application only considers one input, so the last index is omitted. The number of first-order terms equals the number of state variables $M=2N+5$: two originating from each flexible eigenmode included in the reduced-order model, two from the rigid body mode, and three from the controller. The negative frequencies are not of interest and the poles corresponding to controller and the rigid body mode cannot be approximated by a circle. Therefore, N circles are fitted to the flexible modes and constrained in the complex domain. With this decomposition, the radii and midpoints of the circles can now be found using Eq. 5, which is the final outcome of the diagram in Fig. 7.

4.4 Efficient robust formulation

To apply the robust formulation in topology optimization, multiple perturbed designs are generated by erosion and dilation operations. This is done using the smooth Heaviside operator defined as

$$\begin{aligned} x_{\text {p},i}(\eta ) = \frac{\tanh (\beta \eta ) + \tanh (\beta (x_{\text {f}, i} - \eta ))}{\tanh (\beta \eta ) + \tanh (\beta (1 - \eta ))}\quad \forall \quad i\in \mathcal {E}\text {,} \end{aligned}$$

(38)

with the filtered design field $\textbf{x}_\text {f}$, resulting in a projected design $\textbf{x}_{\text {p}}$ (Wang et al. 2011). The parameter $\beta$ determines the edge contrast of the projection and $\eta$ the amount of dilation or erosion, where a value of $\eta =0.5$ corresponds to the nominal design. By choosing multiple different values of $\eta$, multiple perturbed designs $\textbf{x}_\text {p}(\eta _k)$ are generated.

However, straightforward analysis of each of these perturbed designs (as described in preceding sections) results in an additional computational burden, as a reduced-order model has to be created for each design. This means that for each projected design the eigenvalue problem needs to be solved (Eq. 25), which is a very computationally intensive step in the analysis.

As an alternative, we propose to approximate the eigenfrequencies and eigenmodes of the perturbed designs, using the reduction basis $\varvec{\Phi }$ with eigenmodes corresponding to the nominal design. This means that only the eigenvalue problem of the nominal design needs to be solved in each design iteration and it is assumed that the eigenmodes of the nominal model can be used to describe the behaviour of the other perturbed designs.

The eigenvalue approximation proceeds as follows: using the different perturbed designs $\textbf{x}_\text {p}(\eta _k)$, instead of the filtered design $\textbf{x}_\text {f}$, the corresponding mass $\textbf{M}_{k}$ and stiffness $\textbf{K}_{k}$ matrices are assembled using Eqs. 22 and 23. Next, the eigenvalue problem is solved (Eq. 25) using the mass and stiffness matrices corresponding to the nominal design, yielding the reduction basis $\varvec{\Phi }$. Instead of solving additional eigenvalue problems for the remaining projected designs, their system matrices are projected using the reduction basis belonging to the nominal design as

$$\begin{aligned} \tilde{\textbf{K}}_k&= \varvec{\Phi }^T \textbf{K}_{k}\varvec{\Phi }{} & {} \text {and}&&\tilde{\textbf{M}}_k&= \varvec{\Phi }^T \textbf{M}_{k}\varvec{\Phi }\text {.} \end{aligned} $$

(39)

Their dimensions correspond to the number of modes in the basis, thus $\tilde{\textbf{K}}_k,\tilde{\textbf{M}}_k \in {\mathbb {R}}^{(N+1)\times (N+1)}$. These projected matrices are then diagonalized by solving the small eigenvalue problem

$$\begin{aligned} \tilde{\textbf{K}}_k \textbf{V}_k = \tilde{\textbf{M}}_k \textbf{V}_k \varvec{\Upsilon }_k^2\text {,} \end{aligned}$$

(40)

resulting in

$$\begin{aligned} \textbf{V}_k^T \tilde{\textbf{K}}_k\textbf{V}_k&= \varvec{\Upsilon }_k^2{} & {} \text {and}&&\textbf{V}_k^T \tilde{\textbf{M}}_k\textbf{V}_k&= \textbf{I}\text {.} \end{aligned} $$

(41)

The matrix $\varvec{\Upsilon }_k{\in {\mathbb {R}}^{(N+1)\times (N+1)}}$ is a diagonal matrix containing the approximate eigenfrequencies of the perturbed design, which are in fact Ritz values. The corresponding approximate eigenmodes are linear combinations of the nominal eigenmodes, calculated as $\varvec{\Phi }\textbf{V}_k$. The system of equations for the perturbed designs now be found as

$$\begin{aligned} \begin{aligned} \varvec{\Upsilon }_k^2\textbf{q}(t) + 2\zeta \varvec{\Upsilon }_k\dot{\textbf{q}}(t) + \ddot{\textbf{q}}(t)&= \textbf{V}_k^T \varvec{\Phi }^T \textbf{f}u(t)\text {,} \\ \textbf{y}(t)&= \textbf{G}^T \varvec{\Phi }\textbf{V}_k\textbf{q}(t)\text {.} \end{aligned} \end{aligned}$$

(42)

The remainder of the analysis follows the same steps for each model as in Fig. 7, so first the controller is added to form the open-loop state-space model (Sect. 4.2). This is again decomposed into first-order systems by calculating the poles and participation factors (Sect. 4.3), after which circle approximations are formed for each eigenmode (Sect. 2.1). Finally, distances from the circles to the $-1$ point are calculated to form constraints. The effect of this approximation will be studied in Sect. 5.5.

After the calculation, each perturbed model k has different constraint values $g_{ij,k}$ for each of its circles, corresponding to mode i and sensor position j. To limit the number of constraints from the different models, they are aggregated using an induced aggregation function (Kennedy and Hicken 2015)

$$\begin{aligned} f = \frac{\sum _k{f_k \exp (b f_k)}}{\sum _k \exp (b f_k)}\text {,} \end{aligned}$$

(43)

for any constraint $f=g_{ij}$. This function approximates the worst-case constraint value (i.e the maximum) between the perturbed projections, controlled by the parameter b. For a large parameter b this expression approaches the true maximum. This particular function is chosen because $f=f_k$ in case all values $f_k$ are equal. The robust parameter $\beta$ introduced in Eq. 38 is increased during the optimization, meaning that for the initial iterations all perturbed designs are similar, and so are their constraint values. With this choice of aggregation function, the constraint values are not under- or over-estimated during the early phase of the optimization. The aggregation ensures the number of constraints does not increase when using the robust formulation, and thus no extra computational effort is required to calculate eigenmode design sensitivities (Appendix 1) (Lee 1999).

5 Results

5.1 Case and settings

The numerical case that is used to demonstrate the method is shown in Fig. 9. To ensure a position-independent system, $N_\text {out}$ different sensor positions are defined at the measurement surface. Measuring at any of these locations and using that signal for feedback control should result in a closed-loop stable system with required disturbance rejection.

Fig. 9

The case used for the optimizations, which has one rigid body mode in vertical direction. The actuator forces (green arrows) act uniformly on the non-design domain (black) to the left. The top-right non-design domain represents the surface where accuracy is required. Here, vertical displacements are measured at $N_\text {out}$ different sensor locations (blue arrows). The domain is of dimensions $300\times {100}\,\hbox {mm}$, with an in-plane thickness of ${300}\,\hbox {mm}$, and is discretized into $210\times 70$ elements

In Table 1, the settings are listed as used in the optimization, where the material properties correspond to those of aluminium. Furthermore, the maximum number of design iterations is limited to 200 to prevent excessive calculation times. For the optimization, MMA is used with default settings. A move limit of 0.05 is used on the design variables to prevent large steps and oscillations.

Table 1 Settings as used for the optimization

5.2 Sequential optimization

In order to compare performance, a reference case is presented based on a sequential optimization. First, the structure is found by maximization of eigenfrequencies, and subsequently the PID controller is optimized using the proposed method (Eq. 21). The optimization formulation used for the eigenfrequency maximization is given as

$$\begin{aligned} \begin{aligned} \min _{\textbf{x}} \quad&100 \frac{g_\Omega (\textbf{x})}{g_\Omega ^{(0)}} \text {,} \\ \quad s.t. \quad&10\left( \frac{V(\textbf{x})}{v_\text {f} V_\text {max}} - 1.0 \right) \le 0 \text {,} \\&0\le \textbf{x}\le 1 \text {,}\\ \end{aligned} \end{aligned}$$

(44)

in which $g_\Omega$ is the objective function, defined as

$$\begin{aligned} g_\Omega (\textbf{x}) = \sum _{i=0}^3\frac{1}{\Omega _i(\textbf{x})}\text {.} \end{aligned}$$

(45)

The superscripted variable $g_\Omega ^{(0)}$ denotes the value at the initial design iteration. This formulation maximizes the harmonic mean of the first three eigenfrequencies, for which further details and sensitivity analysis can be found in, e.g. Ma et al. (1995); Delissen et al. (2022).

Fig. 10

Design and Nyquist plot after maximization of eigenfrequencies and sequential maximization of bandwidth. The sensor locations are indicated with colors corresponding to the different Nyquist curves

The resulting structure after optimization of the eigenfrequencies is shown in Fig. 10 and the subsequent controller optimization is able to achieve a bandwidth of ${1.11}\,\hbox {rad/ms}$. From the Nyquist plot in Fig. 10 can be seen that the controller satisfies closed-loop stability and disturbance rejection requirements. It can also be seen that only the sensor position at the tip (position 1) is limiting the bandwidth, of which the second eigenmode is touching the margin. Therefore, optimizing for different number of sensor positions will result in an equal bandwidth, provided the sensor location at the tip is included.

5.3 Integrated optimization

Fig. 11

Resulting designs and Nyquist plots of integrated optimizations using the proposed method, for different numbers of sensor positions $N_\text {out}=1$. For the first two Nyquist plots, the local circle approximations are also shown

Fig. 12

Bode plots for the plant $H(j\omega )$ and loop gain $L(j\omega )$, comparing the sequentially optimized design with the integrated optimized design for $N_\text {out}=3$. Only the response of sensor position 1 is shown. The first eigenfrequency is indicated

Fig. 13

Comparison of the first three mode shapes for several designs. The outline of the domain in the undeformed situation is indicated

Fig. 14

Convergence history of the bandwidth for the three integrated optimizations

Using the proposed procedure, integrated optimizations are performed for different numbers of sensor positions $N_\text {out}=1, 3, 6$. The designs and corresponding Nyquist plots are shown in Fig. 11. Mechanism-like structures can clearly be identified in the designs. The Nyquist plots show that all the designs meet the requirements on closed-loop stability and modulus margin. However, not all designs contain binary zero-and-one densities that can directly be interpreted. Especially the design for one sensor position ($N_\text {out}=1$) contains large areas with intermediate densities. The design with six sensor positions also contains some areas with intermediate densities. This might be functionally interpreted as a ‘rubber band’ with a specific stiffness to tune the system dynamics.

Table 2 Performance overview of the sequential and multiple integrated optimizations

An overview of the achieved performance, as compared to the sequentially optimized design, is shown in Table 2. All the designs optimized with the integrated approach have a bandwidth about a factor 3.5 higher than the design optimized for eigenfrequencies. Moreover, the eigenfrequencies are significantly lower for the integrated optimizations, which clearly demonstrates that the system with the highest bandwidth does not necessarily need maximized eigenfrequencies.

Fig. 15

Nyquist plots showing the oscillatory behavior of integrated optimization for $N_\text {out}=1$

Fig. 16

Resulting reference designs and Nyquist plots of integrated optimizations explicitly constraining the peaks of the sensitivity function $\left| S(j\omega )\right|$, using the method of van der Veen et al. (2015, 2017), for different numbers of sensor positions

Fig. 17

Comparison of the effect of robust parameter $\eta$ on the eigenfrequencies (top) and distances from selected circles to the $-1$ point (bottom), for a robust eigenfrequency optimized design. The approximated response (Eq. 42) is compared with the exact solution (dashed lines). A value of $\beta =20$ is used and a filter radius of 5 elements

Fig. 18

Resulting designs resulting from robust integrated optimizations with different numbers of sensor positions

The integrated approach is able to achieve a high bandwidth, relatively close to the eigenfrequencies. This can be explained using the Bode diagrams in Fig. 12, in which the dynamic response of the design optimized for integrated performance with $N_\text {out}=3$ is shown. Fig. 12a shows the dynamic response of the plant. The main difference between the sequential and integrated optimized design is the fact that the integrated design generally has smaller resonance amplitudes. This allows a controller with higher bandwidth, since the eigenmode is less dominant. The effect of a controller with a higher bandwidth can be seen in the Bode plot of the open-loop system (Fig. 12b). A controller with a higher bandwidth adds more gain to the system, hence the amplitude of the integrated design is higher than that of the sequential design, particularly in the low frequency range below the bandwidth. At higher frequencies, the amplitudes of the peak frequencies are about the same height in the open-loop responses, which is a result of the disturbance rejection constraints.

The first eigenmode of the integrated design creates a resonance peak with a very small amplitude (Fig. 12a), around ${5.2}\,\hbox {rad/ms}$. This small amplitude means that the actuator is unable to ‘affect’ this mode and/or it cannot be ‘seen’ by the sensor (i.e. uncontrollable and/or unobservable). For the controller it seems as if this mode does not exist, therefore it is not limiting bandwidth. Inspecting the mode shapes of the integrated designs in Fig. 13, this effect can clearly be seen. For some modes, the actuator is virtually at a standstill, meaning that the mode is not excited by the actuator. For other modes, the location corresponding to the sensor is at a standstill, which means the sensor does not measure the mode.

Fig. 19

Nyquist plots corresponding to different robustly optimized designs. The curves are generated using the approximated reduced order models

Fig. 20

Convergence history of the bandwidth for the three robustly integrated optimizations

The convergence history of the three designs is shown in Fig. 14. Especially the design for $N_\text {out}=1$ shows significant oscillations. In the Nyquist curves of subsequent design iterations shown in Fig. 15, the circle corresponding to the first eigenfrequency flips its direction. This flipping is caused by the actuator or sensor displacement crossing zero and changing sign. Since the modes have a very small excitation amplitude (Fig. 13), the controller is able to attain a very high gain. A small variation in the design then causes a small change in the mode shape, which eventually has a large effect on the system, due to the high control gain. The designs for 3 and 6 sensor positions exhibit less oscillations and a smoother convergence. Due to the addition of multiple sensor locations, the complexity of the optimization problem is increased and involves more trade-offs, leading to designs which are less sensitive to small variations.

5.4 Comparison with explicit peak constraint

To demonstrate the added value of proposed method, also an optimization based on the method of van der Veen et al. (2015, 2017) is implemented. First, the frequencies corresponding to peaks in the sensitivity function are located numerically in each design iteration, after which they are used as constraints. Additionally, an explicit constraint ensuring closed-loop stability must be added, to prevent the Nyquist curve from encircling the $-1$ point. This is done by limiting the (smooth) maximum of all real parts of the closed-loop poles below zero, thus ensuring all poles are in the left half plane. We refer to the original publications for the full description, as our interest here is primarily in the comparison with our proposed approach.

The results of the optimization based on the method by van der Veen et al. (2017) are shown in Fig. 16. Although a structure may be recognized in the designs, the structural features look rather irregular and contain substantial amounts of intermediate densities. The design considering one actuator position faces similar convergence issues as the proposed integrated optimization (Fig. 11a), where small changes in design and mode shape cause oscillations. Next to that, the optimization for multiple sensor positions results in infeasible designs. During the design iterations, one of the Nyquist curves loops around the $-1$ point, indicating closed-loop instability (Fig. 16b, c). In this situation, two constraints are conflicting: the stability constraint requires the Nyquist curve to pass on the right side of the $-1$ point, but the peak constraint prevents this by requiring the curve to stay outside the circular margin. A change of design or bandwidth will thus violate at least one of the constraints, making it difficult to escape this situation. The proposed method does not face these issues, as stability is ensured implicitly by the geometric nature of the constraints on the Nyquist curve in combination with local circle approximations.

5.5 Robust formulation

For the application of the robust formulation to the proposed integrated optimization, the effect of the robust parameter $\eta$ is studied first. This parameter controls the amount of dilation or erosion of the design. Both the eigenfrequencies and the distances from the circle approximations to the $-1$ point change as a function of $\eta$, as is shown in Fig. 17. Here, a distinction is made between the approximate responses using the nominal eigenmodes, as explained in Sect. 4.4, and those evaluated exactly, using eigenmodes corresponding to the perturbed designs. As can be expected, the error between the exact and approximated responses deviates more as the design is perturbed further away from the nominal design at $\eta =0.5$.

Another observation that can be made in Fig. 17, is the fact that the distances to the $-1$ point are not monotonically increasing or decreasing, as is the case for compliance problems (Sigmund 2009). The lack of a monotonic behavior means that the worst-case design is not necessarily coinciding with extreme values of $\eta$. In this work, a value of $\eta =0.5\pm 0.05$ is used, for which it can be assumed that the worst-case performance is likely to be included by evaluating three designs, at $\eta =0.45$, 0.5, and 0.55. However, for larger perturbations and given the non-monotonic behavior, evaluation of the worst-case performance might require more than three designs to be analyzed.

For the robust optimization procedure, the edge contrast parameter $\beta$ is gradually increased from 1.0 to 20.0 during design iterations 50-180. Also, a filter radius of 8 elements is used to ensure a large minimum feature size.

The resulting designs of the robust integrated optimizations, using the proposed method, are shown in Fig. 18. All designs have clear boundaries between void and material, which is a characteristic property of the robust formulation. At some locations, hinges appear with intermediate densities to provide a low-stiffness connection. As for their performance, the design with one sensor position achieves a bandwidth of $\omega _\text {b}={3.5}\,\hbox {rad/ms}$, and the two other designs a bandwidth of ${1.9}\,\hbox {rad/ms}$. A design robustly optimized for maximum eigenfrequencies, with similar settings, is found to achieve a bandwidth of ${1.1}\,\hbox {rad/ms}$. This means the performance increase of robust integrated optimization is still significant.

Although the bandwidth of the design with one sensor position is very high, its disturbance rejection requirement is not met, as can be seen in Fig. 19a. This can again be explained by the dynamic response being very sensitive to (small) design variations. For the designs optimized with 3 (Fig. 19b) and 6 sensor locations, the disturbance rejection requirements are satisfied for all three design perturbations and at all sensor locations.

The convergence properties are also improved using the robust formulation, as is seen in Fig. 20. Small oscillations are still present, but significantly less than without the robust formulation (Fig. 14). A lower final bandwidth is attained for all designs, compared to the results from optimizations without the robust formulation. However, this is counterbalanced with an increased robustness against geometric perturbations and the added control on minimum feature size.

The time required for this optimization using the approximated robust formulation is 55 min. The same optimization without robust formulation requires 49 min in total. This is for a total of 200 design iterations and 3 sensor positions, on a standard corporate laptop with an Intel Core i7-6600 processor. The difference of 6 min (12% extra calculation time) is required for the Heaviside projections, approximation of perturbed eigenmodes, and analysis of the reduced-order model for the local approximations. This is significantly less than the factor 3 that would be required without the proposed method approximating the eigenmodes for the perturbed designs.

6 Discussion

In the numerical examples, no issues with severe mode interaction and ill-fitting local approximations are encountered during the optimizations, which were initially identified as potentially harmful for the optimization (Fig. 5). The current work is focused on monolithic structures made out of metal, with a low damping coefficient $\zeta$. Mode interaction might increase for applications with higher damping, which might lead to issues in convergence. More research is required into the effect of damping and mode interaction on the optimization.

In some of the designs from the numerical examples (Fig. 11), intermediate density values are present. This can make the interpretation into solid and void material difficult from a practical engineering point of view. Partly, the intermediate densities might be caused by the fact that material penalization is harder for the integrated optimization problem than, for instance, compliance minimization or eigenfrequency maximization problems. For the latter, penalization is straightforward to apply, as more mass means a lower eigenfrequency and less stiffness means a higher eigenfrequency. For the integrated optimization problem it is difficult to make this distinction, as frequencies and modes are specifically tuned with respect to the controller behavior. As can be expected, application of the robust formulation helps in reducing the amount of intermediate densities in the designs (Fig. 18). Nonetheless, the reduction of intermediate densities for complex topology optimization problems remains an important topic for research.

In the examples, a discrete number of sensor positions is used to account for position-dependent dynamics. However, position dependency occurs over a continuous line or even a surface in reality. The current implementation ensures accuracy at several locations, but it does not account for any other locations also requiring accurate positioning. Even when locations may not be sensed, their accuracy may still be important to consider in the design of a motion system.

Moreover, the inclusion of an increasing number of sensor positions leads to a growth in the number of constraints for the optimization. As eigenmode design sensitivities are required for each constraint, this directly increases computational cost. Therefore, future research should focus on methods to include many sensor locations without excessive computational cost.

The presented framework potentially allows for frequency-dependent constraints. This could be used, for instance, to incorporate more stringent limitations on high-frequency eigenmodes. Another possibility is to include the influence of time delay in the control loop, which has a frequency-dependent effect on the phase. Following the same approach based on the Nyquist curve could allow for consideration of this effect.

In reality, many systems are MIMO, for which the methods presented in the current work may also be used (e.g. sequential loop closing (Skogestad and Postlethwaite 2001)). However, for a coupled MIMO system multiple loops interact with each other, which requires further analysis of closed-loop behavior. This is done in the method of van der Veen et al. (2017), but it requires additional constraints and thus significantly more computational time. Efficient extension to MIMO systems therefore remains an open issue for future research.

7 Conclusion

A novel approach to integrated controller-structure topology optimization is proposed, with the aim of optimizing the structural design and tuning the controller parameters simultaneously for closed-loop system performance. We introduce a flexible framework enabling local approximation of the Nyquist curve using circles. These allow simple formulation of geometric constraints on the Nyquist curve in the complex domain, making them suitable for gradient-based optimization. In this manuscript, the approximating circles are used to constrain the shape of the Nyquist curve in an integrated controller-structure optimization, which enforces stability and disturbance rejection properties of the closed-loop system. The approach is general and can be extended to other control objectives or constraints that can be expressed by the Nyquist curve.

From the numerical examples, it can be seen that the proposed method is able to greatly improve closed-loop system performance. For the studied problem, the state-of-the-art method in literature (van der Veen et al. 2015) is not able to converge to feasible designs due to conflicting stability and disturbance rejection constraints. In the proposed method, this problem does not occur as stability and disturbance rejection are ensured simultaneously by geometrical restriction of the local approximations of the Nyquist curve. Using numerical examples, the integrated optimization achieves improvements up to 350% in terms of bandwidth compared to sequential optimization, while ensuring a sufficient modulus margin.

Also position-dependent dynamics is considered, by the addition of constraints on multiple SISO Nyquist curves corresponding to different sensor positions. Not only does this lead to a structure and controller that can be used at each of the sensor locations, it also improves convergence properties of the optimization. Optimizing for only one sensor position results in designs that are very sensitive to small variations in mode shape around the actuator and sensor positions, leading to severe oscillations. By optimizing for multiple sensor locations, this detrimental effect is noticeably reduced.

Furthermore, a computationally efficient robust formulation is introduced, approximating the dynamics of the eroded and dilated designs. It allows for analysis and optimization of perturbed designs without significant additional computational cost, instead of a threefold increase using the conventional approach. The validity of the approximation is demonstrated for a range of design perturbations. For larger design perturbations extra care is required, because non-monotonic behavior is observed for the modulus margins, potentially resulting in interior worst-cases for robust optimization. Using the proposed formulation, the obtained designs are more robust against geometric deviations, a length scale is imposed, and a positive effect on optimization convergence is observed. Furthermore, the approximation-based robust formulation is not limited to the current application, but may also be used for other types of topology optimization involving dynamics.

There are several gaps to bridge in order to arrive at real-world systems with ultimate performance, such as incorporation of time delay, MIMO control, ensuring accuracy over large surfaces, and further reduction of computational effort. Despite the remaining challenges, this work provides a step forward in computational design methods for next generation high-precision motion systems.

Appendices

Appendix A: Circle in the complex domain

Below, the proof of the relations in Eq. 5 is provided. It additionally proves that the single first-order mode approximation of Eq. 3 describes an exact circle in the complex domain. A generalized circle is defined by the parametric equation

$$\begin{aligned} Aw\overline{w} + \overline{\gamma }w + \gamma \overline{w} + D = 0 \text {,} \end{aligned}$$

(46)

with variable $w\in {\mathbb {C}}$, parameters $A, D\in {\mathbb {R}}$, $\gamma \in {\mathbb {C}}$, and $\overline{\bullet }$ denoting the complex conjugate. Depending on the values of the parameters, the parametric equation either describes a circle or a line (Schwerdtfeger 1979). In case of a circle, its midpoint and radius are defined by, respectively

$$\begin{aligned} w_0&= -\frac{\gamma }{A}&\text {and}{} && {} R^2 = \frac{\left| \gamma \right| ^2}{A^2} - \frac{D}{A}\text {.} \end{aligned} $$

(47)

The Nyquist curve is evaluated over a line in the direction of the imaginary axis as $s=j\omega$. This line can be described using the generalized circle equation (with $A=0$, $\gamma =1+0i$, and $D=0$) and using the complex variable s as

$$\begin{aligned} s = j\omega \Leftrightarrow s + \overline{s} = 0\text {.} \end{aligned}$$

(48)

The approximated transfer function ${\tilde{L}}_i(s)$ of Eq. 3 is a Möbius transformation (Schwerdtfeger 1979), which maps the line from the s-domain to a circle in the L(s)-domain. The parametric equation for the transformed circle can be found using the inverse mapping, with the constant offset $\breve{L}_i$ removed, as

$$\begin{aligned} w = {\tilde{L}}_i(s) - \breve{L}_i = \frac{p_i}{s-\lambda _i} \Leftrightarrow s = \frac{p_i + \lambda _i w }{w}\text {,} \end{aligned}$$

(49)

with the mapped variable $w\in {\mathbb {C}}$. Substituting this into Eq. 48 and rewriting, yields the parametric equation of the mapped curve as

$$\begin{aligned} \frac{p_i + \lambda _i w}{w} + \frac{\overline{p_i} + \overline{\lambda _i} \overline{w}}{\overline{w}} = 0\text {,} \end{aligned}$$

(50)

which can be rearranged to another generalized circle equation as

$$\begin{aligned} (\lambda _i + \overline{\lambda _i})w\overline{w} + p_i\overline{w} + \overline{p_i} w = 0\text {.} \end{aligned}$$

(51)

Using Eq. 47, the midpoint relative to the offset $\breve{L}_i$ and the radius, respectively, become

$$\begin{aligned} w_{0,i}&= - \frac{p_i}{2\textrm{Re}\left( \lambda _i\right) }{} & {} \text {and}&&R_i&= \frac{\left| p_i\right| }{2\left| \textrm{Re}\left( \lambda _i\right) \right| }\text {.} \end{aligned} $$

(52)

Again adding the constant offset $\breve{L}_i$ that was removed in Eq. 49, the midpoint of the Nyquist curve ${\tilde{L}}_i(j\omega )$ is obtained as

$$\begin{aligned} X_i = \breve{L}_i - \frac{p_i}{2\textrm{Re}\left( \lambda _i\right) }\text {.} \end{aligned}$$

(53)

Appendix B: Design sensitivities

The ingredients for the design sensitivities are given in detail in this section. The sensitivities are given for a single distance involving a circle h(X, R). In case a constraint involves multiple circles, the sensitivity can be computed by application of sum, product, quotient, or chain rule.

This appendix provides the nontrivial terms to obtain the design sensitivities of the new responses presented in this paper. The design sensitivities of the applied density filter are extensively used in topology optimization and can be found in the work of Bruns and Tortorelli (2001). Those of the material interpolation (Eq. 22) and the finite element assembly (Eq. 23) are also extensively used and are trivial to derive.

The remaining sensitivities are derived using the flow diagram in Fig. 7. Starting point are the system matrices $\textbf{K}$ and $\textbf{M}$, and the control parameters k and $\omega _\text {b}$. The sensitivities of each intermediate variable (with respect to circle distance h) are calculated using the chain rule, starting at the circle parametrization X, R and working our way backward towards $\textbf{K}$, $\textbf{M}$, k, and $\omega _\text {b}$.

1.1 Appendix B.1: Note on complex derivatives

In dealing with complex derivatives, we make use of the Wirtinger partial differential operators (Sarason 2007) defined for complex variable $z=x+jy$ as

$$\begin{aligned} \begin{aligned} \frac{\partial }{\partial z}&= \frac{1}{2}\left( \frac{\partial }{\partial x} - j\frac{\partial }{\partial y} \right) \text {,}\\ \frac{\partial }{\partial \overline{z}}&= \frac{1}{2}\left( \frac{\partial }{\partial x} + j\frac{\partial }{\partial y} \right) \text {.}\\ \end{aligned} \end{aligned}$$

(54)

With this choice of partial derivatives, the chain rule for the mapping $(z\in {\mathbb {C}}) \rightarrow (s\in {\mathbb {C}}) \rightarrow (f\in {\mathbb {R}})$ can be seen as the contribution of two independent variables z and $\overline{z}$, becomes

$$\begin{aligned} \frac{\partial f}{\partial z} = \frac{\partial f}{\partial s} \frac{\partial s}{\partial z} + \frac{\partial f}{\partial \overline{s}} \frac{\partial \overline{s}}{\partial z}\text {.} \end{aligned}$$

(55)

Following Eq. 54, the identities

$$\begin{aligned} \frac{\partial \overline{s}}{\partial \overline{z}}&= \overline{\left( \frac{\partial s}{\partial z}\right) }&\text {and}{} && {} \frac{\partial \overline{s}}{\partial z}&= \overline{\left( \frac{\partial s}{\partial \overline{z}}\right) } \end{aligned} $$

(56)

help in simplifying the chain rule. Since any final objective or constraint function used in optimization is $f(z)\in {\mathbb {R}}$, it means that

$$\begin{aligned} \frac{\partial f}{\partial \overline{z}} = \overline{\left( \frac{\partial f}{\partial z}\right) }\text {.} \end{aligned}$$

(57)

Using these identities, the chain rule can be simplified when mapping $(z\in {\mathbb {C}}) \rightarrow (r\in {\mathbb {R}})$ as

$$\begin{aligned} \frac{\partial f}{\partial z} = \frac{\partial f}{\partial r} \frac{\partial r}{\partial z} + \frac{\partial f}{\partial \overline{r}} \frac{\partial \overline{r}}{\partial z} = 2 \frac{\partial f}{\partial r} \frac{\partial r}{\partial z} \text {.} \end{aligned}$$

(58)

Conversely, the chain rule when mapping $(r\in {\mathbb {R}}) \rightarrow (s\in {\mathbb {C}})$ becomes

$$\begin{aligned} \frac{\partial f}{\partial r} = \textrm{Re}\left( \frac{\partial f}{\partial s} \frac{\partial s}{\partial r}\right) \text {.} \end{aligned}$$

(59)

Note that these definitions are not unique and other variations can be used as well. For more information on complex calculus, the reader is referred to, e.g. Sarason (2007).

1.2 Appendix B.2: Local circle approximation

Circle distance

$(X, R)\rightarrow h$, Eqs. 13-15

The sensitivity of the radius R is calculated as

$$\begin{aligned} \frac{\partial h}{\partial R}&= -1&\text {or}{} && {} \frac{\partial h}{\partial R}&= 1\text {,} \end{aligned} $$

(60)

respectively, depending on whether the distance is calculated as the smallest to or furthest from a feature.

Next, the sensitivities of the midpoint $X\in {\mathbb {C}}$ are calculated as

$$\begin{aligned} \frac{\partial h}{\partial X} = \frac{\overline{X-\tau }}{2\left| X-\tau \right| } \in {\mathbb {C}} \end{aligned}$$

(61)

for the distance to a point (Eq. 13) or as

$$\begin{aligned} \frac{\partial h}{\partial X} = \frac{\overline{n}}{2} \in {\mathbb {C}} \end{aligned}$$

(62)

for the distance to line (Eq. 15).

Circle parametrization

$(p,L_{\lambda }, \lambda _i) \rightarrow (R, X)$, Eq. 5

Partial derivatives of the participation factor $p\in {\mathbb {C}}$ can be calculated as

$$\begin{aligned} \begin{aligned} \frac{\partial X}{\partial p}&= -\frac{1}{2\textrm{Re}\left( \lambda _i\right) }\text {,}&\frac{\partial X}{\partial \overline{p}}&= 0\text {,} \\ \frac{\partial R}{\partial p}&= \frac{\overline{p}}{4\left| \textrm{Re}\left( \lambda _i\right) p\right| }\text {,}&\frac{\partial R}{\partial \overline{p}}&= \frac{p}{4\left| \textrm{Re}\left( \lambda _i\right) p\right| }\text {.} \end{aligned} \end{aligned}$$

(63)

The sensitivity $\frac{\partial h}{\partial X}$ can be calculated using the complex chain rule in Eq. 55.

Next, the variable $\breve{L}$ (Eq. 4) is directly substituted into Eq. 5. This leaves the sensitivities of the interpolation point $L_\lambda = L(j\textrm{Im}\left( \lambda _i\right) )\in {\mathbb {C}}$, which are simply

$$\begin{aligned} \begin{aligned} \frac{\partial X}{\partial L_\lambda }&= 1\text {,}&\frac{\partial X}{\partial \overline{L}_\lambda }&= 0\text {,} \\ \frac{\partial R}{\partial L_\lambda }&= 0\text {,}&\frac{\partial R}{\partial \overline{L}_\lambda }&= 0\text {.} \end{aligned} \end{aligned}$$

(64)

Finally, the partial sensitivities of the system pole $\lambda _i \in {\mathbb {C}}$ are

$$\begin{aligned} \begin{aligned} \frac{\partial X}{\partial \lambda _i}&= \frac{\partial X}{\partial \overline{\lambda _i}} = \frac{p}{4\textrm{Re}\left( \lambda _i\right) ^2}\text {,} \\ \frac{\partial R}{\partial \lambda _i}&= \frac{\partial R}{\partial \overline{\lambda _i}} = -\frac{\left| p\right| }{4\textrm{Re}\left( \lambda _i\right) \left| \textrm{Re}\left( \lambda _i\right) \right| }\text {.} \end{aligned} \end{aligned}$$

(65)

Note that $L_\lambda$ also depends on $\lambda _i$, for which a second contribution is calculated below in Eq. 70.

1.3 B.3 Open-loop response

Open-loop response

$(\textbf{A}, \textbf{B}, \textbf{C}, \lambda _i) \rightarrow \textbf{L}_\lambda$, Eq. 34

From here on, we will switch to the matrix form of the sensitivities to calculate the contributions of different inputs and outputs of the system simultaneously. The matrix $\textbf{L}(j\textrm{Im}\left( \lambda _i\right) )=\textbf{L}_\lambda \in {\mathbb {C}}^{N_\text {out}\times N_\text {in}}$ contains the various open-loop responses from different inputs to outputs.

Using the solution $\textbf{U}$ and adjoint solution $\textbf{Y}$, calculated as

$$\begin{aligned} \begin{aligned} \textbf{U}&= \left( j\textrm{Im}\left( \lambda _i\right) \textbf{I}-\textbf{A}\right) ^{-1}\textbf{B} \in {\mathbb {C}}^{M\times N_\text {in}}\text {,} \\ \textbf{Y}&= \textbf{C}\left( j\textrm{Im}\left( \lambda _i\right) \textbf{I}-\textbf{A}\right) ^{-1}\in {\mathbb {C}}^{N_\text {out}\times M}\text {,} \\ \end{aligned} \end{aligned}$$

(66)

the sensitivities can be calculated. First of the system matrix $\textbf{A}$ as

$$\begin{aligned} \frac{\partial h}{\partial \textbf{A}} = \textrm{Re}\left( \textbf{Y}^T \frac{\partial h}{\partial \textbf{L}_\lambda } \textbf{U}^T \right) \in {\mathbb {R}}^{M\times M}\text {,} \end{aligned}$$

(67)

in which the sensitivity with respect to a matrix is a matrix whose entries are $\left[ \frac{\partial h}{\partial \textbf{A}}\right] _{ij} = \frac{\partial h}{\partial A_{ij}}$. The modal decomposition basis $\textbf{Q}$ also depends on the system matrix $\textbf{A}$, so the second contribution to this sensitivity is given below in Eq. 77.

Secondly, the sensitivities of the input matrix $\textbf{B}$ and output matrix $\textbf{C}$ are

$$\begin{aligned} \frac{\partial h}{\partial \textbf{B}}&= \textrm{Re}\left( \textbf{Y}^T \frac{\partial h}{\partial \textbf{L}_\lambda } \right) \in {\mathbb {R}}^{M\times N_\text {in}}\text {,}\end{aligned}$$

(68)

$$\begin{aligned} \frac{\partial h}{\partial \textbf{C}}&= \textrm{Re}\left( \frac{\partial h}{\partial \textbf{L}_\lambda } \textbf{U}^T \right) \in {\mathbb {R}}^{N_\text {out} \times M}\text {.} \end{aligned}$$

(69)

Besides $\textbf{L}_\lambda$, the participation factors $\textbf{P}_i$ also depend on $\textbf{B}$ and $\textbf{C}$, for which the sensitivity contributions are given below in Eq. 72.

Finally, the sensitivity of the system pole $\lambda _i$ (the second contribution, next to the one given in Eq. 65) is calculated as

$$\begin{aligned} \frac{\partial h}{\partial \lambda _i} = i\textrm{Im}\left( \frac{\partial h}{\partial \textbf{L}_\lambda }:(\textbf{Y}\textbf{U})\right) \in {\mathbb {C}}\text {,} \end{aligned}$$

(70)

in which the operation $\textbf{A}:\textbf{B} = \sum _i \sum _j A_{ij} B_{ij}$ is a double contraction.

1.4 Appendix B.4: Participation factor

Participation factor

$(\textbf{Q}, \textbf{B}, \textbf{C}) \rightarrow \textbf{P}_i$, Eq. 37

To simplify the notation of sensitivities, the following notation is used here:

$$\begin{aligned} \begin{aligned} \textbf{Q}&= \begin{bmatrix}\textbf{q}_1&\cdots&\textbf{q}_M\end{bmatrix}&\text {and}{} & {} \textbf{Q}^{-1}&= \begin{bmatrix}\hat{\textbf{q}}_1^T&\cdots&\hat{\textbf{q}}^T _M \end{bmatrix}^T \text {.} \end{aligned} \end{aligned}$$

(71)

Using this notation, Eq. 37 can be rewritten as $\textbf{P}_i = \textbf{C}\textbf{q}_i\hat{\textbf{q}}_i^T \textbf{B}$.

The sensitivity contributions (the second contribution besides Eq. 68) of the input matrix $\textbf{B}$ and output matrix $\textbf{C}$ can be calculated using

$$\begin{aligned} \begin{aligned} \frac{\partial h}{\partial \textbf{B}}&= \textrm{Re}\left( \hat{\textbf{q}}_i \otimes \left( \left( \frac{\partial h}{\partial \textbf{P}_i}\right) ^T \textbf{C} \textbf{q}_i\right) \right) \in {\mathbb {R}}^{M\times N_\text {in}} \text {,} \\ \frac{\partial h}{\partial \textbf{C}}&= \textrm{Re}\left( \left( \frac{\partial h}{\partial \textbf{P}_i} \textbf{B}^T \hat{\textbf{q}}_i \right) \otimes \textbf{q}_i\right) \ \in {\mathbb {R}}^{N_\text {out} \times M}\text {.} \end{aligned} \end{aligned}$$

(72)

Here, the outer product is defined as $\textbf{A} = \textbf{u}\otimes \textbf{v} \leftrightarrow A_{ij} = u_i v_j$.

The sensitivities with respect to mode $\textbf{q}_i$ and $\hat{\textbf{q}}_i$ (which is in fact the left eigenmode) are calculated as

$$\begin{aligned} \begin{aligned} \frac{\partial h}{\partial \hat{\textbf{q}}_i}&= \textbf{B} \left( \frac{\partial h}{\partial \textbf{P}_i}\right) ^T \textbf{C}\textbf{q}_i \in {\mathbb {C}}^{M}\text {,}\\ \frac{\partial h}{\partial \textbf{q}_i}&= \textbf{C}^T \frac{\partial h}{\partial \textbf{P}_i}\textbf{B}^T \hat{\textbf{q}}_i \in {\mathbb {C}}^{M}\text {.} \end{aligned} \end{aligned}$$

(73)

Since $\textbf{q}_i$ and $\hat{\textbf{q}}_i$ are related to each other through $\textbf{Q}^{-1}$, the sensitivities with respect to the matrix $\textbf{Q}$ can now be calculated as

$$\begin{aligned} \frac{\partial h}{\partial \textbf{Q}} = -\hat{\textbf{q}}_i \otimes \left( \textbf{Q}^{-1}\frac{\partial h}{\partial \hat{\textbf{q}}_i} \right) + \begin{bmatrix} 0&\cdots&\frac{\partial h}{\partial \textbf{q}_i}&\cdots&0 \end{bmatrix} \in {\mathbb {C}}^{M\times M}\text {.} \end{aligned}$$

(74)

This is a combination of the adjoint for $\frac{\partial h}{\partial \hat{\textbf{q}}_i}$ and then adding $\frac{\partial h}{\partial \textbf{q}_i}$ in the correct column (i).

1.5 B.5 Modal decomposition

Modal decomposition

$\textbf{A} \rightarrow (\lambda _i, \textbf{Q})$, Eq. 35

Following the approach of Lee (1999), the eigenvector and eigenvalue sensitivities can be calculated using the adjoint method. Here again the matrix

$$\begin{aligned} \frac{\partial h}{\partial \textbf{Q}} = \begin{bmatrix}\frac{\partial h}{\partial \textbf{q}_1}&\frac{\partial h}{\partial \textbf{q}_2}&\dotsc&\frac{\partial h}{\partial \textbf{q}_M} \end{bmatrix} \end{aligned}$$

(75)

contains the sensitivities of the eigenmodes in its columns.

First the adjoint saddle-point problem needs to be solved for each modal pair $(\lambda _i, \textbf{q}_i)$, which is denoted

$$\begin{aligned} \begin{bmatrix} \textbf{A}^T - \lambda _i\textbf{I} &{} \;\; -\textbf{q}_i \\ -\textbf{q}_i^T &{} 0 \end{bmatrix} \begin{bmatrix} \pmb {\kappa }_i \\ \gamma _i \end{bmatrix} =\begin{bmatrix} \frac{\partial h}{\partial \textbf{q}_i} \\ \frac{\partial h}{\partial \lambda _i} \end{bmatrix}\text {.} \end{aligned}$$

(76)

This needs to be done for all eigenmodes with $\frac{\partial h}{\partial \textbf{q}_i}\ne \textbf{0}$ and/or $\frac{\partial h}{\partial \lambda _i}\ne 0$. Now the sensitivity with respect to the system matrix is calculated as

$$\begin{aligned} \frac{\partial h}{\partial \textbf{A}} = \sum _{i=1}^{M} - \textrm{Re}\left( \pmb {\kappa } \otimes \textbf{q}\right) \in {\mathbb {R}}^{M\times M}\text {.} \end{aligned}$$

(77)

This is the second contribution, besides the one given in Eq. 67. Note that these sensitivity calculations are only valid with eigenmode normalization as $\textbf{q}^T \textbf{q}=1$.

1.6 B.6 Mechanical model

Open-loop state space

$(\varvec{\Omega }, \varvec{\Phi }, \textbf{A}_\text {c}, \textbf{B}_\text {c}, \textbf{C}_\text {c})\rightarrow (\textbf{A}, \textbf{B}, \textbf{C})$, Eq. 33

The matrices $\frac{\partial h}{\partial \textbf{A}}$, $\frac{\partial h}{\partial \textbf{B}}$, and $\frac{\partial h}{\partial \textbf{C}}$ are divided into partitions such that they match the division in Eq. 33:

$$\begin{aligned} \begin{aligned} \frac{\partial h}{\partial \textbf{A}}&= \begin{bmatrix} \frac{\partial h}{\partial \textbf{A}_{11}} &{} \frac{\partial h}{\partial \textbf{A}_{12}} &{} \frac{\partial h}{\partial \textbf{A}_{13}} \\ \frac{\partial h}{\partial \textbf{A}_{21}} &{} \frac{\partial h}{\partial \textbf{A}_{22}} &{} \frac{\partial h}{\partial \textbf{A}_{23}} \\ \frac{\partial h}{\partial \textbf{A}_{31}} &{} \frac{\partial h}{\partial \textbf{A}_{32}} &{} \frac{\partial h}{\partial \textbf{A}_{33}} \\ \end{bmatrix} \text {,}&\frac{\partial h}{\partial \textbf{B}}&= \begin{bmatrix} \frac{\partial h}{\partial \textbf{B}_1} \\ \frac{\partial h}{\partial \textbf{B}_2} \\ \frac{\partial h}{\partial \textbf{B}_3} \end{bmatrix}\text {,} \\ \frac{\partial h}{\partial \textbf{C}}&= \begin{bmatrix} \frac{\partial h}{\partial \textbf{C}_1}&\frac{\partial h}{\partial \textbf{C}_2}&\frac{\partial h}{\partial \textbf{C}_3} \end{bmatrix}\text {.} \end{aligned} \end{aligned}$$

(78)

The row and column sizes in this division are equal to $(3, N+1, N+1)$. Using this division, the sensitivities with respect to the input variables can be calculated as

$$\begin{aligned} \frac{\partial h}{\partial \textbf{A}_\text {c}}&= \frac{\partial h}{\partial \textbf{A}_{11}} \in {\mathbb {R}}^{3\times 3} \text {,}\end{aligned}$$

(79)

$$\begin{aligned} \frac{\partial h}{\partial \textbf{B}_\text {c}}&= \frac{\partial h}{\partial \textbf{B}_1} \in {\mathbb {R}}^{3 \times N_\text {in}}\text {,} \end{aligned}$$

(80)

$$\begin{aligned} \frac{\partial h}{\partial \textbf{C}_\text {c}}&= \textbf{f}^T \varvec{\Phi }\frac{\partial h}{\partial \textbf{A}_{31}} \in {\mathbb {R}}^{(N+1) \times 3} \text {,}\end{aligned}$$

(81)

$$\begin{aligned} \frac{\partial h}{\partial \varvec{\Phi }}&= \textbf{f}\textbf{C}_\text {c} \left( \frac{\partial h}{\partial \textbf{A}_{31}}\right) ^T + \textbf{G}\frac{\partial h}{\partial \textbf{C}_2} \in {\mathbb {R}}^{N_\text {dof}\times (N+1)} \text {,}\end{aligned}$$

(82)

$$\begin{aligned} \frac{\partial h}{\partial \varvec{\Omega }}&= -2\varvec{\Omega }\frac{\partial h}{\partial \textbf{A}_{32}} -2\zeta \frac{\partial h}{\partial \textbf{A}_{33}} \in {\mathbb {R}}^{(N+1)\times (N+1)} \text {.} \end{aligned}$$

(83)

Modal analysis

$(\textbf{K}, \textbf{M})\rightarrow (\varvec{\Omega }, \varvec{\Phi })$, Eq. 25

The modal sensitivities are calculated again using the adjoint method of Lee (1999), but now for a generalized eigenvalue problem with symmetric system matrices ($\textbf{K}$ and $\textbf{M}$). First the adjoint saddle-point system needs to be solved for each modal pair $(\Omega _i, \pmb {\phi }_i)$, which is a time consuming step as the size of this problem is $(N_\text {dof}+1)\times (N_\text {dof}+1)$, where $N_\text {dof}$ is the number of unknowns in the finite element analysis. The adjoint problem is given as

$$\begin{aligned} \begin{bmatrix} \textbf{K} - \Omega _i^2\textbf{M} &{} \;\; -\textbf{M}\pmb {\phi }_i \\ -\pmb {\phi }_i^T \textbf{M} &{} 0 \end{bmatrix} \begin{bmatrix} \pmb {\nu }_i \\ \alpha _i \end{bmatrix} =\begin{bmatrix} \frac{\partial h}{\partial \pmb {\phi }_i} \\ \frac{1}{2\Omega _i} \frac{\partial h}{\partial \Omega _i} \end{bmatrix}\text {.} \end{aligned}$$

(84)

Using the solution pairs $(\alpha _i, \pmb {\nu }_i)$ the sensitivities with respect to the structural design variables $x_j$ can be calculated as

$$\begin{aligned} \frac{\partial h}{\partial x_j} = \sum _{i=0}^{N} -\pmb {\nu }_i^T \frac{\partial \textbf{K}}{\partial x_j} \pmb {\phi }_i + \left( \Omega _i^2 \pmb {\nu }_i + \frac{\alpha _i}{2}\pmb {\phi }_i\right) ^T \frac{\partial \textbf{M}}{\partial x_j}\pmb {\phi }_i\text {.} \end{aligned}$$

(85)

The sensitivities $\frac{\partial \textbf{K}}{\partial x_j}$ and $\frac{\partial \textbf{M}}{\partial x_j}$ include the material interpolation and density filtering.

1.7 Appendix B.7: Controller

Controller

$(k, \omega _\text {b})\rightarrow (\textbf{A}_\text {c}, \textbf{B}_\text {c}, \textbf{C}_\text {c})$, Eq. 28

To represent the control law in Eq. 28 as a state-space model, the controllable canonical form is used, which results in the following matrices

$$\begin{aligned} \begin{aligned} \textbf{A}_\text {c}&= \begin{bmatrix} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ 0 &{} -15\omega _\text {b}^2 &{} -8\omega _\text {b}\end{bmatrix} \text {,}&\textbf{B}_\text {c}&= \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}\text {,} \\ \textbf{C}_\text {c}&= \begin{bmatrix} k\omega _\text {b}^3&8k\omega _\text {b}^2&15k\omega _\text {b}\end{bmatrix}\text {.} \end{aligned} \end{aligned}$$

(86)

Now the sensitivities with respect to the control parameters can simply be calculated as

$$\begin{aligned} \frac{\partial h}{\partial \omega _\text {b}} =&-30\omega _\text {b}\frac{\partial h}{\partial A_{\text {c},32}} - 8\frac{\partial h}{\partial A_{\text {c},33}} \end{aligned}$$

(87)

$$\begin{aligned}&+ 3k\omega _\text {b}^2\frac{\partial h}{\partial C_{\text {c},1}} + 16k\omega _\text {b}\frac{\partial h}{\partial C_{\text {c},2}} + 15k\frac{\partial h}{\partial C_{\text {c},3}} \text {,}\nonumber \\ \frac{\partial h}{\partial k} =&\omega _\text {b}^3\frac{\partial h}{\partial C_{\text {c},1}} + 8\omega _\text {b}^2\frac{\partial h}{\partial C_{\text {c},2}} + 15\omega _\text {b}\frac{\partial h}{\partial C_{\text {c},3}}\text {.} \end{aligned}$$

(88)

Further sensitivity calculations (e.g. the dependency of k on $\omega _\text {b}$, Eq. 29) are straightforward.

1.8 Appendix B.8: Robust formulation

For the robust formulation, we start with the sensitivities $\frac{\partial h}{\partial \textbf{W}_k}$ (with $\textbf{W}_k=\varvec{\Phi }\textbf{V}_k$) and $\frac{\partial h}{\partial \varvec{\Upsilon }_k}$, which are equal to, respectively, $\frac{\partial h}{\partial \varvec{\Phi }}$ (Eq. 82) and $\frac{\partial h}{\partial \varvec{\Lambda }}$ (Eq. 83) that were derived earlier.

The sensitivities of the linear combination factors ($\textbf{V}_k$) used to combine the different eigenmodes are calculated as

$$\begin{aligned} \frac{\partial h}{\partial \textbf{V}_k} = \varvec{\Phi }^T \frac{\partial h}{\partial \textbf{W}_k}\text {.} \end{aligned}$$

(89)

Yet another eigenvector adjoint system is constructed for the robust modal decomposition of Eq. 41 as

$$\begin{aligned} \begin{bmatrix} \tilde{\textbf{K}} - \Upsilon _i^2\tilde{\textbf{M}} &{} \;\; -\tilde{\textbf{M}}\textbf{v}_i \\ -\textbf{v}_i^T \tilde{\textbf{M}} &{} 0 \end{bmatrix} \begin{bmatrix} \pmb {\mu }_i \\ \beta _i \end{bmatrix} =\begin{bmatrix} \frac{\partial h}{\partial \textbf{v}_i} \\ \frac{1}{2\Upsilon _i} \frac{\partial h}{\partial \Upsilon _i} \end{bmatrix}\text {.} \end{aligned}$$

(90)

Here, $\textbf{v}_i$ denotes the ith eigenvector of the system, which are normalized as $\textbf{v}_i^T \tilde{\textbf{M}}\textbf{v}_i=1$. The different eigenvectors are the columns of $\textbf{V}_k$, thus

$$\begin{aligned} \textbf{V}_k&=\begin{bmatrix}\textbf{v}_0&\cdots&\textbf{v}_{N}\end{bmatrix}&\text {and}{} && {} \frac{\partial h}{\partial \textbf{V}_k}&=\begin{bmatrix}\frac{\partial h}{\partial \textbf{v}_0}&\cdots&\frac{\partial h}{\partial \textbf{v}_{N}}\end{bmatrix}\text {.} \end{aligned} $$

(91)

Using the solution pairs $(\beta _i, \pmb {\mu }_i)$ the sensitivities with respect to the reduced-order matrices $\tilde{\textbf{K}}$ and $\tilde{\textbf{M}}$ can be calculated as

$$\begin{aligned} \frac{\partial h}{\partial \tilde{\textbf{K}}}&= \sum _{i=0}^N -\pmb {\mu }_i \otimes \textbf{v}_i \in {\mathbb {R}}^{(N+1)\times (N+1)} \text {,}\end{aligned}$$

(92)

$$\begin{aligned} \frac{\partial h}{\partial \tilde{\textbf{M}}}&= \sum _{i=0}^N \left( \Upsilon _i^2 \pmb {\mu }_i + \frac{\beta _i}{2}\textbf{v}_i\right) \otimes \textbf{v}_i \in {\mathbb {R}}^{(N+1)\times (N+1)}\text {.} \end{aligned}$$

(93)

Both the projection operation (Eq. 39) and the linear combination of eigenvectors ($\textbf{W}_k=\varvec{\Phi }\textbf{V}_k$) contribute to the sensitivities with respect to $\varvec{\Phi }$ with

$$\begin{aligned} \frac{\partial h}{\partial \varvec{\Phi }} = 2 \left( \textbf{K}\varvec{\Phi }\frac{\partial h}{\partial \tilde{\textbf{K}}} + \textbf{M}\varvec{\Phi }\frac{\partial h}{\partial \tilde{\textbf{M}}} \right) + \frac{\partial h}{\partial \textbf{W}_k}\textbf{V}_k^T \text {.} \end{aligned}$$

(94)

Now, finally the large eigenvector system is solved again (Eq. 84) and the sensitivities with respect to the design variables $x_j$ are calculated as

$$\begin{aligned}{} & {} \frac{\partial h}{\partial x_j} = \sum _{i=0}^{N} -\pmb {\nu }_i^T \frac{\partial \textbf{K}}{\partial x_j} \pmb {\phi }_i + \left( \Omega _i^2 \pmb {\nu }_i + \frac{\alpha _i}{2}\pmb {\phi }_i\right) ^T \frac{\partial \textbf{M}}{\partial x_j}\pmb {\phi }_i \nonumber \\{} & {} \quad + \frac{\partial h}{\partial \tilde{\textbf{K}}}: \left( \varvec{\Phi }^T \frac{\partial \textbf{K}}{\partial x_j} \varvec{\Phi }\right) + \frac{\partial h}{\partial \tilde{\textbf{M}}}: \left( \varvec{\Phi }^T \frac{\partial \textbf{M}}{\partial x_j} \varvec{\Phi }\right) \text {.} \end{aligned}$$

(95)