Aeroelastic shape optimization of solid foam core wings subject to large deformations

Abstract

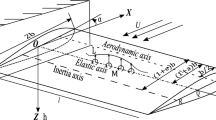
This work presents studies on static aeroelastic shape optimization of aircraft wings subject to large deformations. The physics are captured using a coupled 3D panel method and a nonlinear co-rotating beam finite element model. The wing is defined by a series of airfoils that are parameterized based on the definition of NACA 4-digit airfoils. The method assumes a solid cross section of isotropic material which is representative of foam core wings. Analytic expressions are derived for most of the cross-sectional stiffness properties, while approximations are introduced for the location of the shear center and the torsional stiffness. Optimized designs achieved using linear and nonlinear deformation models are compared and features are discussed. The objective is to minimize drag subject to constraints on geometry, tip displacement, and root bending moment. Results highlight the importance of using nonlinear models to accurately capture changes in wingspan due to large deformations, as even small differences in the wingspan can have a large effect on the induced drag. Non-planar wings with raised and drooped wingtips are also optimized, where drooped wings are found to achieve larger lift-to-drag ratios due to the increase in effective wingspan in the deformed configuration.

Appendices

Appendices

Local orientation in 3D space

The local orientation of the beam can be expressed in 3 forms: a rotation matrix which is used throughout the finite element analysis, Euler angles which describe the degrees of freedom in the finite element analysis, and quaternions which are represented as a scalar ${\bar{q}}$ and vector ${\varvec{q}}$. Quaternions are introduced because rotations in the first two forms are non-additive in 3D space (Crisfield 1997; Krenk 2009). The following procedure is adopted to calculate the current orientation, T, from an initial configuration, $\mathbf{T} _0$, having undergone the Euler rotations $\varvec{\theta }$. For more details on the theory of this procedure, readers are referred to Crisfield (1997), Chapter 16.

• 1. Convert initial configuration, $\mathbf{T} _0$, to a quaternion representation, ${\bar{q}}_0,{\varvec{q}}_0$. If $\max (\text {Tr}(\mathbf{T _0}),T_{0,11},T_{0,22},T_{0,33}) = \text {Tr}(\mathbf{T _0})$ then

  $$\begin{aligned} {\bar{q}}_0= & {} \frac{1}{2}\sqrt{1+\text {Tr}(\mathbf{T _0})} \end{aligned}$$

  (25a)
  $$\begin{aligned} q_{0,i}= & {} \frac{T_{0,kj}-T_{0,jk}}{4{\bar{q}}}\quad \text {for} \ i=1,2,3 \end{aligned}$$

  (25b)

  with i, j, k as the cyclic combination of 1,2,3. If $\max (\text {Tr}(\mathbf{T _0}),T_{0,11},T_{0,22},T_{0,33}) \ne \text {Tr}(\mathbf{T _0})$ but instead $=T_{0,ii}$

  $$\begin{aligned} q_{0,i}= & {} \sqrt{\frac{1}{2}T_{0,ii}+\frac{1}{4}(1-\text {Tr}(\mathbf{T _0}))} \end{aligned}$$

  (26a)
  $$\begin{aligned} {\bar{q}}_0= & {} \frac{T_{0,kj}-T_{0,jk}}{4q_i} \end{aligned}$$

  (26b)
  $$\begin{aligned} q_{0,l}= & {} \frac{T_{0,li}-T_{0,il}}{4q_i} \text {for} \ l=j,k \end{aligned}$$

  (26c)

  where the operation $\text {Tr}(\mathbf{T} _0)$ represents the trace of $\mathbf{T} _0$.

• 2. Convert the Euler rotations $\varvec{\theta }$ to a quaternion representation, ${\bar{q}}_r,{\varvec{q}}_r$.

  $$\begin{aligned} {\bar{q}}_r= & {} c_1 c_2 c_3 + s_1 s_2 s_3 \end{aligned}$$

  (27a)
  $$\begin{aligned} q_{r,1}= & {} s_1 c_2 c_3 - c_1 s_2 s_3 \end{aligned}$$

  (27b)
  $$\begin{aligned} q_{r,2}= & {} c_1 s_2 c_3 + s_1 c_2 s_3 \end{aligned}$$

  (27c)
  $$\begin{aligned} q_{r,3}= & {} c_1 c_2 s_3 - s_1 s_2 c_3 \end{aligned}$$

  (27d)

  where $c_i = \cos \big (\frac{\theta _i}{2}\big )$ and $s_i = \sin \big (\frac{\theta _i}{2}\big )$.

• 3. Calculate the quaternion representation of the current orientation as the quaternion sum of the initial orientation and the rotation

  $$\begin{aligned} {\bar{q}}= & {} {\bar{q}}_0{\bar{q}}_r - {\varvec{q}}_0\cdot {\varvec{q}}_r \end{aligned}$$

  (28a)
  $$\begin{aligned} {\varvec{q}}= & {} {\bar{q}}_0{\varvec{q}}_r + {\bar{q}}_r{\varvec{q}}_0 - {\varvec{q}}_0\times {\varvec{q}}_r \end{aligned}$$

  (28b)

• 4. Convert back to the rotation matrix representation

  $$\begin{aligned} \mathbf{T} = ({\bar{q}}^2 - {\varvec{q}}^\text {T}{\varvec{q}})\mathbf{I} + 2({\varvec{q}}{\varvec{q}}^\text {T}) + 2{\bar{q}}{} \mathbf{S} ({\varvec{q}}) \end{aligned}$$

  (29)

  where I is the identity matrix and $\mathbf{S} ({\varvec{q}})$ is the skew-symmetric matrix form of the cross product operation defined as

  $$\begin{aligned} \mathbf{S} ({\varvec{q}}) = \begin{pmatrix} 0 &{}\quad -q_3 &{}\quad q_2 \\ q_3 &{}\quad 0 &{}\quad -q_1 \\ -q_2 &{}\quad q_1 &{}\quad 0 \end{pmatrix} \end{aligned}$$

  (30)

Cross-sectional properties

Table 4 Comparison of cross-sectional properties calculated via BECAS and the approximations presented in the current work

This work assumes a solid isotropic cross section whose geometry is defined by the airfoil parameterization represented in Fig. 2. The parameterization is based on the equations for NACA 4-digit airfoils (Abbott and von Doenhoff 2012) which define thickness and camber distributions as

$$\begin{aligned}&\begin{aligned} {\tilde{z}}_t =&5tc\bigg (0.2969\sqrt{\frac{{\tilde{x}}}{c}}-0.1260\frac{{\tilde{x}}}{c}-0.3516\Big (\frac{{\tilde{x}}}{c}\Big )^2\\&\quad +0.2843\Big (\frac{{\tilde{x}}}{c}\Big )^3 \\&-0.1036\Big (\frac{{\tilde{x}}}{c}\Big )^4\bigg ) \end{aligned} \end{aligned}$$

(31)

$$\begin{aligned} {\tilde{z}}_m= & {} {\left\{ \begin{array}{ll} \dfrac{mc}{p^2}\Bigg (2p\dfrac{{\tilde{x}}}{c}-\bigg (\dfrac{{\tilde{x}}}{c}\bigg )^2\Bigg ), &{} \text {if} \ 0 \le \dfrac{{\tilde{x}}}{c} \le p \\ \dfrac{mc}{(1-p)^2}\Bigg (1-2p+2p\dfrac{{\tilde{x}}}{c}-\bigg (\dfrac{{\tilde{x}}}{c}\bigg )^2\Bigg ), &{} \text {if} \ p \le \dfrac{{\tilde{x}}}{c} \le 1 \end{array}\right. } \end{aligned}$$

(32)

NACA 4-digit airfoils define the thickness as normal to the camber line. The current parameterization modifies this definition such that thickness is measured normal to the chord line which ensures the derivatives are continuous (Conlan-Smith et al. 2020). The upper and lower surface of the airfoil are then be defined as

$$\begin{aligned} {\tilde{z}}_u= & {} {\tilde{z}}_m+{\tilde{z}}_t \end{aligned}$$

(33a)

$$\begin{aligned} {\tilde{z}}_l= & {} {\tilde{z}}_m-{\tilde{z}}_t \end{aligned}$$

(33b)

where the origin is at the leading edge, and subscripts u and l represent upper and lower surfaces, respectively. Now that there are analytic expressions for the airfoil, the following cross-sectional properties can be derived through evaluating the integrals provided in Johnson and Gendler (1950)

$$\begin{aligned} A= & {} \int _{0}^{c}({\tilde{z}}_u-{\tilde{z}}_l)d{\tilde{x}}=\frac{40853}{60000}tc^2 \end{aligned}$$

(34)

$$\begin{aligned} {\tilde{e}}_x= & {} \frac{1}{A}\int _{0}^{c}{\tilde{x}}({\tilde{z}}_u-{\tilde{z}}_l)d{\tilde{x}}=\frac{17072}{40853}c \end{aligned}$$

(35)

$$\begin{aligned} {\tilde{e}}_z= & {} \frac{1}{2A}\int _{0}^{c}({\tilde{z}}_u^2-{\tilde{z}}_l^2)d{\tilde{x}} \nonumber \\= & {} \frac{30000cm}{40853(p-1)^2} \big [ -0.904838096p^\frac{3}{2} + 1.80967619p^\frac{5}{2} \nonumber \\&- 0.03946666699p^6 + 0.209266666968018p^5 \nonumber \\&- 0.563566667023105p^4 - 0.18559999995126p^3 \nonumber \\&+ 0.209999999949106p^2 - 1.58539999956691p \nonumber \\&+ 1.0499285706036\big ] \end{aligned}$$

(36)

$$\begin{aligned} {\tilde{I}}_{xx}= & {} \frac{1}{3}\int _{0}^{c}({\tilde{z}}_u^3-{\tilde{z}}_l^3)d{\tilde{x}} \nonumber \\= & {} \frac{c^\frac{4}{3}}{(p-1)^4} \big [-2.056450216p^\frac{3}{2}m^2t + 8.22580086p^\frac{5}{2}m^2t \nonumber \\&- 9.62418701p^\frac{7}{2}m^2t - t(-0.1176566644t^2 - 1.310524784m^2 \nonumber \\&+ 4.066219048m^2p + 0.4706266577pt^2 - 0.7059399865t^2p^2 \nonumber \\&- 2.79677229p^\frac{9}{2}m^2 - 3.716828571p^2m^2 + 1.413257143m^2p^3 \nonumber \\&+ 0.098666667m^2p^8 - 0.11765666t^2p^4 + 0.470626658t^2p^3 \nonumber \\&+ 0.27081072p^4m^2 - 3.22688095p^5m^2 + 2.46037382p^6m^2 \nonumber \\&- 0.713157141p^7m^2)\big ] \end{aligned}$$

(37)

$$\begin{aligned} {\tilde{I}}_{xz}= & {} \frac{1}{2}\int _{0}^{c}{\tilde{x}}({\tilde{z}}_u^2-{\tilde{z}}_l^2)d{\tilde{x}} \nonumber \\= & {} -0.0123333335\frac{c^4tm}{(p-1)^2} \big [ 12.22754164p^\frac{5}{2} - 24.45508329p^\frac{7}{2} \nonumber \\&+ p^7 - 4.8907335151639p^6 + 11.698069340392p^5 \nonumber \\&+ 2.05945943106902p^4 - 3.40540535911413p^3 \nonumber \\&+ 20.856370370699p - 15.0902185805057\big ] \end{aligned}$$

(38)

$$\begin{aligned} {\tilde{I}}_{zz}= & {} \int _{0}^{c}{\tilde{x}}^2({\tilde{z}}_u-{\tilde{z}}_l)d{\tilde{x}} = \frac{32743}{210000}c^4t \end{aligned}$$

(39)

Properties notated with a tilde are defined with respect to the airfoil’s leading edge, but cross-sectional properties in (16) are defined with respect to the beam center and therefore properties in Eqs. (35)–(39) need to be corrected, e.g., using the parallel axis theorem.

Cross-sectional properties that cannot be calculated analytically include the location of the shear center and the torsional stiffness. The torsional stiffness is calculated using a technique in Kosmatka (1992) where J about the quarter chord point is approximated as $J\simeq 0.15t^3c$. A similar approximation was formed for the location of the shear center in terms of the elastic center, by stating that

$$\begin{aligned} ({\tilde{s}}_x,{\tilde{s}}_z)\simeq (k_x{\tilde{e}}_x,k_z{\tilde{e}}_z) \end{aligned}$$

(40)

where $k_x$ and $k_z$ are coefficients that are constant for all airfoils defined by the parameterization above. BECAS (Blasques 2012) was used to evaluate $k_x$ and $k_z$ for a selection of airfoils with different values of m, t, and p. Based on average values, $k_x$ and $k_z$ were found to be 0.89 and 1.45, respectively.

Table 4 compares the difference in these approximations to the values calculated via BECAS. The approximation of the shear center was shown to be accurate to within 2% and 0.7% of the chord length for ${\tilde{x}}$ and ${\tilde{z}}$ locations, receptively. The torsional stiffness approximation had a maximum relative error of 6%. It is well known that dynamic analysis, such as determining flutter speeds, can be sensitive to torsional stiffness and location of the shear center. However, we have found that static analysis is not as sensitive to these quantities. This is demonstrated in Fig. 13, which plots the relative error in lift-to-drag ratios due to these approximations of torsional stiffness and shear center location. Each wing has a rectangular planform and constant airfoil sections which are chosen based on worst case scenarios from Table 4. For large aspect ratios and higher angles of attack, the deformations will increase and with it the error, but for each case studied the relative error remains below 1%.

Fig. 13

Relative error in lift-to-drag ratio due to cross-sectional property approximations. Each point represents a rectangular wing with constant NACA 4-digit airfoil sections

Sensitivity analysis

Gradients are calculated using a discrete adjoint method, where the total derivative of an objective/constraint function $\Psi$ can be calculated as

$$\begin{aligned} \frac{d\Psi }{d\mathbf{d} } = \frac{\partial \Psi }{\partial \mathbf{d} } + \varvec{\lambda }_a^\text {T} \bigg [ \frac{\partial \mathbf{A} _\mu }{\partial \mathbf{d} }\varvec{\mu } + \frac{\partial \mathbf{A} _\sigma }{\partial \mathbf{d} }\varvec{\sigma } + \mathbf{A} _\sigma \frac{\partial \varvec{\sigma }}{\partial \mathbf{d} }\bigg ] + \varvec{\lambda }_b^\text {T} \bigg [ \frac{\partial \mathbf{p} }{\partial \mathbf{d} } - \frac{\partial \mathbf{f} }{\partial \mathbf{d} } \bigg ] \end{aligned}$$

(41)

where partial derivatives capture only the explicit dependence without solving the governing equations. The terms $\varvec{\lambda }_a$ and $\varvec{\lambda }_b$ are Langragian multipliers whose length is equal to that of $\varvec{\mu }$ and $\mathbf{u}$ , respectively, and are calculated through solving the following adjoint problem

$$\begin{aligned} \begin{bmatrix} \mathbf{A} _\mu &{} \bigg [\dfrac{\partial \mathbf{A} _\mu }{\partial \mathbf{u} }\varvec{\mu } + \dfrac{\partial \mathbf{A} _\sigma }{\partial \mathbf{u} }\varvec{\sigma } + \mathbf{A} _\sigma \dfrac{\partial \varvec{\sigma }}{\partial \mathbf{u} } \bigg ] \\ -\dfrac{\partial \mathbf{f} }{\partial \varvec{\mu }} &{} \bigg [\mathbf{K} - \dfrac{\partial \mathbf{f} }{\partial \mathbf{u} }\bigg ] \end{bmatrix}^\text {T} \begin{bmatrix} \varvec{\lambda }_a \\ \varvec{\lambda }_b \end{bmatrix} = -\begin{bmatrix} \dfrac{\partial \Psi }{\partial \varvec{\mu }} \\ \dfrac{\partial \Psi }{\partial \mathbf{u} } \end{bmatrix} \end{aligned}$$

(42)

Partial derivatives are calculated using analytic expressions, refer to Conlan-Smith et al. (2020) for further details. The viscous drag is calculated through linearly interpolating pre-calculated data points with respect to the airfoil geometry parameters. Hence, the slope of this interpolation can be used in calculating gradients. Since the interpolation is linear the gradient of the viscous drag is also first-order accurate.

Convergence behavior

An example of the typical convergence behavior for lift-to-drag ratios is shown in Fig. 14. It is difficult to choose an initial design where the lift-weight equilibrium constraint is satisfied, and as such, the initial designs are in the infeasible region of the design space. This can cause the performance to be reduced in the first few iterations as the optimizer tries to satisfy this constraint. Once in the feasible region, there is a smooth convergence behavior. Generally when viscous effects are included, there is a slight increase in the number of iterations required to meet the stopping criteria.

Fig. 14

Convergence history for designs shown in Fig. 7a and b. The y-axis plots the improvement in lift-to-drag ratio compared to the initial design