Abstract
A flexible problem-specific multiscale topology optimization is introduced to associate different areas of the design domain with diverse microstructures extracted from a dictionary of optimized unit cells. The generation of the dictionary is carried out by exploiting micro-SIMP with AnisoTropic mesh adaptivitY (microSIMPATY) algorithm, which promotes the design of free-form layouts. The proposed methodology is particularized in a proof-of-concept setting for the design of orthotic devices for the treatment of foot diseases. Different patient-specific settings drive the prototyping of customized insoles, which are numerically verified and successively validated in terms of mechanical performances and manufacturability.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Cellular materials, characterized by a porous microstructure which properly alternates solid and void, have been engineered in the last years to artificially reproduce the lightweight and the strength properties exhibited by some biological systems, such as bones, honeycombs, sponges, and wood. In parallel, the rise of innovative manufacturing techniques, such as additive processes (e.g., 3D printing), promoted the production of cellular materials in very diverse fields of application, for instance, in healthcare, aerospace, defense, construction, and automotive (Xu et al. 2018; Ivarsson et al. 2020).
The strong interest in cellular materials has favoured the proposal of a wide range of analytical, numerical, and experimental methods for an efficient design of new materials. In this context, topology optimization represents the reference mathematical methodology. Actually, this technique has been extensively adopted not only to create optimized structures (Rozvany 2012; Bendsøe and Kikuchi 1988; Bendsøe and Sigmund 2003; Sigmund and Maute 2013; Allaire et al. 2004), but also to address the design of unit cells optimized with respect to a specific goal (see, e.g., Sigmund 1994). Starting from the seminal work by Sigmund (1994), inverse and direct homogenization techniques have been massively employed to engineer and validate periodic microstructures (Andreassen and Andreasen 2014; Allaire et al. 2019).
However, it is well known that the topology optimization carried out at a monoscale (either at a macroscale or at a microscale level) may limit structural performances. Multiscale topology optimization has been proposed as a remedy to overcome such limitations (see, e.g., Rodrigues et al. 2002; Sanders et al. 2021). This strategy consists in identifying the optimal alternation of void, solid, and microstructures inside the design domain (Auricchio et al. 2020; Arabnejad Khanoki and Pasini 2012). The distribution of void, solid, and microstructures can be carried out by the user through a trial-and-error approach, or automatically driven by a topology optimization tool. A single microstructure or a multiplicity of different cells can be used to handle the transition areas between solid and void. The first option confers the same effective properties on the whole design domain, while the coexistence of several topologies at the microscale allows us to locally diversify the property of the macro domain. The layout of the employed microstructures can be selected a priori, starting from consolidated dictionaries of unit cells (Allaire et al. 2019; Vigliotti and Pasini 2013), or designed from scratch to match the requirement of interest via homogenization techniques (Coelho et al. 2008; Nakshatrala et al. 2013; Djourachkovitch et al. 2021; Ferrer et al. 2016; Ferro et al. 2020b; di Cristofaro et al. 2021).
The scenario which provides us the highest flexibility with a view to a problem-specific design is the one where the microstructures are ad hoc designed and change across the optimized macro domain. This option clearly represents the most challenging choice in terms of modeling (dedicated optimizations are employed both at the macro- and at the microscale and, possibly, follow different goal quantities, see, e.g., Gao et al. 2019), computational effort (especially, if the optimizations at the macro- and at the microscale are concurrent, see, e.g., Coelho et al. 2008; Xia and Breitkopf 2014) and manufacture (due to intrinsic limits in manufacturability, for instance, to tackle the transition among different cells, or possible defects or irregularities characterizing the optimized layouts, see, e.g., Du et al. 2018).
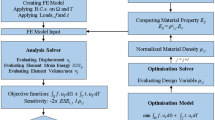
In this paper, we propose a highly flexible procedure for multiscale topology optimization characterized by a computationally affordable burden, based on a recent and already successfully validated structural design methodology, which provides some improvements in terms of manufacturability. This procedure consists of two phases. During the first one, we create a dictionary of unit cells characterized by the same or by a different topology, sharing a common mechanical objective. In the second phase, we exploit the multiscale topology optimization strategy proposed in Wang et al. (2017), combined with a suitable density material thresholding, to identify the areas of the macro domain to be associated with the different microstructures.
The computational complexity of the proposed procedure remains limited thanks to a sequential optimization of the unit cells and of the macrostructure. The independence between the macro- and the microscale allows us to increase the flexibility of the modeling, since different goal quantities can be adopted to drive the optimization of the cells and of the macro layout. The generation of the dictionary relies on the recent algorithm micro-SIMP with AnisoTropic mesh adaptivitY (microSIMPATY; Ferro et al. 2020b; di Cristofaro et al. 2021; Ferro et al. 2020c, 2019), which combines homogenization techniques together with the solid isotropic material with penalization (SIMP) method and a customized selection of the computational mesh, generalizing the SIMPATY algorithm proposed in Micheletti et al. (2019) to a microscale. SIMPATY algorithm has been successfully applied to the design of structures optimized with respect to the static compliance and to the mass of the final layout (Micheletti et al. 2019; Ferro et al. 2020a). In Ferro et al. (2020c) SIMPATY has been enriched by shape optimization to enhance the lightweight and mechanical properties of the optimized configuration, towards an out-of-the-box, free form paradigm.
In Ferro et al. (2019) the authors propose an innovative way to circumvent the computational burden typical of the SIMP approach. The idea is to resort to a proper orthogonal decomposition on SIMP snapshots to predict a rough structure, which is eventually finalized via SIMPATY, in the spirit of an offline/online paradigm (Kunisch and Volkwein 2002).
The first main novelty of this paper is the employment of microSIMPATY algorithm into a multiscale topology optimization setting. This leads us to devise a flexible problem-specific methodology to yield products that match prescribed design and mechanical requirements by alternating diverse microstructures. As a second contribution, we particularize the proposed workflow to a medical context. In particular, we focus on the design of patient-specific insoles for the treatment of foot problems (Menz et al. 2018). Indeed, among the different interventions and pain management actions, foot orthotics represent a very common conservative solution, for foot diseases such as musculoskeletal disorders, foot deformity and ulceration (Iseli et al. 2021). The reduction of plantar pressure represents a reference target to improve patient’s condition (Van Netten et al. 2018), typically ensuring the attenuation of symptoms for different pathologies (Collings et al. 2021). For this reason, several methods have been proposed to optimize the design and the production of patient-specific foot orthotics, guaranteeing a therapeutic effect (Ahmed et al. 2020) The methodology proposed in this paper provides a proof-of-concept of a new versatile design pipeline for the manufacturing of patient-specific orthoses.
The paper is organized as follows. Section 2 introduces the SIMPATY algorithm after a brief recap on the SIMP method. Section 3 is devoted to the homogenization techniques, with a particular emphasis on the inverse methodology. In Sect. 4, we exploit inverse homogenization to generate two dictionaries of new unit cells, which differ for the number of diverse microcellular topologies. The adopted multiscale topology optimization is described in Sect. 5. In Sect. 6 we establish a simplified setting with a view to the design of optimized orthotic devices. Two different patient-specific configurations are analyzed for the prototyping of customized insoles. The two scenarios are numerically verified. The most meaningful setting from a medical viewpoint is successively validated in terms of mechanical properties and 3D printing manufacturability. Finally, in the last section, some conclusions are drawn and some hints are provided on possible future developments.
2 A generic setting for structural topology optimization
Topology optimization aims at allocating the material inside the design domain in order to match a goal quantity strictly related to the application at hand, while satisfying specific physical and design constraints.
Originally, topology optimization has been settled to deal with structural problems (see, e.g., the landmark papers by Michell 1904; Rozvany 2012, 2009; Bendsøe and Kikuchi 1988). In this context, the stiffness, the stress, the vibration modes and the mass of the structure are classical examples of target quantities or constraints to the optimization, in combination with the state equation which models the physical law the structure is subject to. Successively, the crucial impact of topology optimization has been verified in several engineering fields different from structural mechanics (see, e.g., Jenkins and Maute 2016; Dapogny et al. 2017; Villanueva and Maute 2017 and the references therein). The employment of topology optimization in a wide range of different settings motivated the proposal in the literature of several mathematical and numerical methodologies.
Among the most popular approaches, we mention density-based schemes (Bendsøe and Sigmund 2003; Sigmund and Maute 2013), level-set methods (Allaire et al. 2004), topological derivative procedures (Sokolowski and Zochowski 1999; Amstutz and Andrä 2006), phase field techniques (Bourdin and Chambolle 2003), evolutionary approaches (Xie and Steven 1993), homogenization (Bendsøe and Kikuchi 1988), performance-based optimization (Liang 2005), and more recently, model reduction and machine learning tools (Alaimo et al. 2018; Watts et al. 2019; Ferro et al. 2019; Sibileau et al. 2018). The main feature distinguishing these methodologies is the modeling expedient adopted to track the solid/void alternation in the design domain. In this paper, we opt for a density-based scheme, i.e., the SIMP method.
2.1 The SIMP method
SIMP has been employed for several applications to drive topology optimization, including, for instance, fluid dynamics (Borrvall and Petersson 2003), acoustics (Yoon 2013), heat transfer (Pizzolato et al. 2017), electromagnetism (Kiziltas et al. 2004), fatigue and static failure (Jeong et al. 2015), medicine (Sun et al. 2019), aerospace engineering (Zhu et al. 2016).
SIMP introduces an auxiliary function \(\rho \in L^{\infty} (\varOmega , [0, 1])\), referred to as density or design variable, which models the distribution of the material in the design domain \(\varOmega \subset {\mathbb {R}}^{2}\), here identified with a two-dimensional setting. Function \(\rho\) is assumed to take only the extreme values, 0 and 1, where \(\rho =1\) identifies the material, whereas \(\rho = 0\) characterizes the void. In practice, \(\rho\) takes all the values in [0, 1]. This leads very often to an over-diffused material-void interface in correspondence with intermediate densities, whose physical interpretation is not straightforward. To overcome this issue, SIMP penalizes the intermediate densities by means of a suitable function of \(\rho\).
The generic formulation of the SIMP method can be formulated as
where \(\mathcal {G}(\cdot , \cdot )\) is the target functional to be optimized, the first constraint coincides with the weak form of the equation modeling the physics, the second one enforces a control on the system, with \(c_{\text {m}}\) and \(c_{\text {M}}\) the corresponding lower and upper bounds, the last two-sided inequality guarantees the well-posedness of the weak form, being \(0<\rho _{\min }< \rho _{\max } \le 1\), and where \(\mathcal {U}\) denotes a Sobolev space strictly dependent on the boundary data characterizing the physical model (Ern and Guermond 2004). We remark that the weak form includes the density function according to a law, which depends on the phenomenon under investigation. For instance, a suitable power of \(\rho\) multiplies the stiffness tensor when optimizing structures in a linear regime (Bendsøe 1995); in a fluid-dynamic setting, it is standard to consider a density-weighted inverse permeability (Borrvall and Petersson 2003); in the design of microstructures, \(\rho\) modifies the homogenization applied at the microscale (Sigmund 1994). Moreover, the system can be multi-constrained. In such a case, relation \(c_{\text {m}} \le C(u(\rho ), \rho ) \le c_{\text {M}}\) is replaced by a set of constraints (see Sect. 5).
Different algorithms are used in the literature to manage the constrained minimization in (1), such as MMA (Svanberg 1987), Interior Point OPTimizer (IPOPT; Wächter 2002), heuristic-based, genetic or machine learning routines (Chi et al. 2021).
When dealing with a structural topology optimization at the macroscale, it is common to identify the state equation in (1) with the linear elasticity problem in the small displacement regime. The bilinear form becomes
where \(\mathbf{u}:\varOmega \rightarrow \mathbb {R}^{2}\) denotes the displacement of the structure; \(\varepsilon (\mathbf{v}) = (\nabla \mathbf{v}+ \nabla \mathbf{v}^{\text {T}})/2\) is the strain tensor;
is the stress tensor penalized by a power law of the density, \(\rho ^{p}\), with \(p \ge \max \{1/(1-\nu ), 4/(1+\nu )\}\),
the Lamé coefficients, \(E_{\text {Y}}\) and \(\nu\) the Young’s modulus and the Poisson’s ratio, \(\text{ tr }(\cdot )\) the trace operator, and I the identity tensor.
Different boundary conditions may characterize the configuration of the structure. The selected boundary data define the space \({{\mathcal {U}}}\) and the right-hand side, \(F_{\rho} (\mathbf{v})\), in (1).
Problem (1) combined with the state equation (2) may be characterized by multiple local minima, due to the non-convexity of the functional \(\mathcal {G}\), so that the uniqueness of the solution is a priori not guaranteed. This is, for instance, the case of the minimum compliance benchmark problem (Bendsøe 1995; Sigmund and Petersson 1998).
We discretize the weak form in (1) by means of continuous finite elements, i.e., we look for the displacement, \(\mathbf{u}_{h}\), and the density, \(\rho _{h}\), in \(\mathcal {U}_{h} = [V_{h}^{r}]^{2} \cap \mathcal {U}\) and \(V_{h}^{s}\), respectively, with
the space of the finite elements of degree q, \({{\mathcal {T}}}_{h} = \{K\}\) a conforming triangular tessellation of the domain \(\varOmega\) and \(\mathbb {P}_{q}\) the set of polynomials of global degree q. Notice that the functions in \(V_{h}^{0}\) are discontinuous and piecewise constant on \({{\mathcal {T}}}_{h}\) (Ern and Guermond 2004).
It is well-known that SIMP method suffers from several issues related to the discretization adopted in (1). Among the main drawbacks, we list the dependence of the final layout on the grid \({{\mathcal {T}}}_{h}\), the presence of checkerboard patterns, grayscale effects (Sigmund and Petersson 1998; Bendsøe 1995), jagged boundaries and too complex topologies which make the optimized design unpractical for manufacturing.
The mesh dependence can be ascribed to the non-uniqueness of the solution. It is generally tackled by constraining or filtering the design variable.
Checkerboard effects arise when solid and void elements alternate in an uneven way. This is a standard feature for a two-field formulation, unless an ad hoc combination of the finite element spaces for the displacement, \(\mathbf{u}_{h}\), and the density, \(\rho _{h}\), is adopted (e.g., \(s=0\), \(r=2\) for quadrilateral elements Bendsøe and Sigmund 2003 and \(s=0\), \(r=1\) for triangular elements Bruggi and Verani 2011). Filtering techniques are an alternative viable remedy to get rid of checkerboard patterns, together with adapted computational meshes as detailed in the next section.
Filtering and thresholding techniques can be helpful to manage the presence of the grayscales associated with the intermediate values of \(\rho _{h}\), between 0 and 1.
Jagged material/void interfaces can be traced back to excessively coarse grids, whereas thin struts often depend on the employment of too fine meshes. As a compromise between too coarse and too fine meshes, in Micheletti et al. (2019) and Ferro et al. (2020c) the authors propose a new algorithm, presented in the next section, which enriches the SIMP method with a customized choice of the computational mesh in the framework of structural optimization.
2.2 The SIMPATY algorithm
SIMPATY algorithm has been proposed in Micheletti et al. (2019) to assist the design of lightweight and stiff structures aimed at aerospace applications. This new algorithm consists of an iterative procedure, which sequentially alternates the topology optimization in (1), tackled by the IPOPT package ( Wächter 2002), with the generation of an anisotropic adapted mesh.
SIMPATY algorithm proved to have remarkable features. As an alternative to projection methods (see, e.g., Wang et al. 2011), SIMPATY algorithm allows us to sharply detect the density across the material/void interface thus limiting filtering, i.e., the post-processing required by standard design tools. In addition, the same discrete space can be adopted both for the displacement components and the density with a consequent reduction of the computational effort. These properties identify a very cost-effective design procedure, striking a balance between accuracy and computational demands.
In this section we sketch the SIMPATY procedure as a fundamental building block for the microSIMPATY algorithm employed in Sect. 4 for the design of new dictionaries of optimized unit cells. In particular, the focus will be on mesh adaptation and on the mathematical tool we adopt to drive the generation of a problem-specific computational grid.
Standard isotropic adapted meshes allow us to improve the solution accuracy (for a certain mesh cardinality) or to contain the number of elements (for a user-defined tolerance on the numerical approximation) by optimizing the element size. These improvements can be further enhanced by resorting to anisotropic grids, which tune the size, the shape, and the orientation of the mesh triangles in order to track the directional features of the modeled phenomena, such as steep boundary and internal layers, discontinuities, sharp fronts, shocks in compressible flows, more in general areas where the problem exhibits strong gradients (Formaggia and Perotto 2001; Dompierre et al. 2002; Formaggia et al. 2002; Belhamadia et al. 2014; Porta et al. 2012; Micheletti et al. 2010; Ferro et al. 2018). The generation of anisotropic grids deserves more technicalities when compared with an isotropic context. This justifies the limited availability of anisotropic mesh adaptation modules in current simulation software.
Anisotropic mesh adaptation can be driven by heuristic or theoretically sound quantifiers. The first class exploits information prompted by the application at hand in terms of numerical solution or associated variation (e.g., gradient or Hessian). The second class is represented by the a priori and the a posteriori error estimators, which can be classified according to the controlled quantity adjusting the allocation of the elements in the adapted mesh (Ainsworth and Oden 2000).
After discretizing both the displacement and the density with affine finite elements, SIMPATY algorithm resorts to an a posteriori anisotropic recovery-based error estimator, \(\eta\), associated with the density variable. This estimator turns out to be the ideal tool to identify the steep gradients of \(\rho\) across the material/void interface, since it controls the \(H^{1}\)-seminorm of the discretization error, \(e_{\rho} = \rho - \rho _{h}\). The idea formalized by a recovery-based error estimator is very straightforward (Zienkiewicz and Zhu 1987). It consists in replacing in the definition of \(|e_{\rho} |_{H^{1}(\varOmega )}\) the exact gradient of the solution with the so-called recovered gradient, namely,
where \(P(\nabla \rho _{h})\in [V_{h}^{q}]^{2}\) is a suitable polynomial reconstruction of the exact gradient \(\nabla \rho\), for \(q\ge 0\).
Recovery-based error estimators have been exploited in several engineering contexts (see, e.g., Micheletti et al. 2010; Porta et al. 2012; Yan 2001; Mu and Jari 2013). The popularity of these estimators is justified by the good properties they have, among which we cite the independence of the specific problem and of the adopted discretization; the computational cheapness; the handy implementation; the high performance in very diverse fields of application.
Concerning the choice of the recovery operator P in (4), several proposals have been made in the literature, to target specif problem- or theoretical-driven requirements. In general, \(P(\nabla \rho _{h})\) is expected to provide a better approximation to \(\nabla \rho\) with respect to \(\nabla \rho _{h}\). Standard rules identify P with a local projection or average of the discrete gradient. Here, we adopt the area-weighted average of \(\nabla \rho _{h}\) over the patch of elements, \(\varDelta _{K}=\{ T \in {{\mathcal {T}}}_{h} \, : \, T \cap K \ne \emptyset \}\), associated with the generic element \(K \in {{\mathcal {T}}}_{h}\), being
\(|\omega |\) denoting the measure of the generic domain \(\omega \subset \mathbb {R}^{2}\), so that \(P(\nabla \rho _{h})\in [V_{h}^{0}]^{2}\). Despite the low polynomial degree, the recovered gradient in (5) proved to be a good approximation for \(\nabla \rho\) (Farrell et al. 2011; Micheletti et al. 2010; Ferro et al. 2020a, b, c; Micheletti and Perotto 2010; Micheletti et al. 2019; Porta et al. 2012), due to the large number of elements contributing to the average.
In 2010, a generalization of the recovery-based error estimators to an anisotropic setting has been proposed in Micheletti and Perotto (2010). This extension exploits the anisotropic setting proposed in Formaggia and Perotto (2001). In this paper, the generic element K of the mesh \({{\mathcal {T}}}_{h}\) is characterized by the elementwise metric \({{\mathcal {M}}}_{K} = \{\lambda _{i, K}, \mathbf{r}_{i, K}\}_{i=1,2}\), with \(\lambda _{1, K}\ge \lambda _{2, K}> 0\). In more detail, the lengths \(\lambda _{i, K}\) and the orthonormal vectors \(\mathbf{r}_{i, K}\) identify the ellipse, \(\mathcal {E}_{K}\), circumscribed to K, which coincides with the push-forward of the circle circumscribed to the reference triangle \({\hat{K}}\) via the standard affine map \(T_{K} : \hat{K} \rightarrow K\) (Ern and Guermond 2004). The scalar quantities \(\lambda _{i, K}\) measure the lengths of the semi-axes of \(\mathcal {E}_{K}\), whereas the unit vectors \(\mathbf{r}_{i, K}\) provide the corresponding directions. To quantify the deformation of the element K, it is standard to adopt the aspect ratio \(s_{K}= \lambda _{1, K}/ \lambda _{2, K}\ge 1\), with \(s_{K} = 1\) for equilateral triangles.
The anisotropic variant of the recovery-based error estimator in Zienkiewicz and Zhu (1987) relies on the correspondence, up to an area-dependent scaling factor,
between the \(H^{1}\)-seminorm of a function \(v\in H^{1}(\varDelta _{K})\) and the anisotropic counterpart proposed in Formaggia and Perotto (2001), where \(G_{\varDelta _{K}}(\cdot )\) is the symmetric positive semi-definite matrix with entries
for \(i,j=1,2\), \(\mathbf{z}=(z_{1},z_{2}) \in [L^{2}(\varOmega )]^{2}\). In (6), the first order derivatives defining the \(H^{1}\)-seminorm are projected along directions \(\mathbf{r}_{i, K}\)’s, to comply with the anisotropic characterization of the element K.
A cross-comparison between (4) and (6) yields the anisotropic error estimator
where \(\mathbf{e}^{\nabla }_{\rho} =P(\nabla \rho _{h}) - \nabla \rho _{h}\) denotes the recovered error associated with the material density.
Following Micheletti and Perotto (2006), estimator \(\eta\) is used to generate an anisotropic adapted mesh. This goal is pursued by resorting to an iterative procedure, whose generic \({\mathtt{j}}\)-th iteration consists of the following steps:
-
(i)
computation of the density function \(\rho _{h}^{\mathtt{j}}\), solution to problem (1), on the mesh \({{\mathcal {T}}}_{h}^{\mathtt{j}}\);
-
(ii)
evaluation of the a posteriori error estimator (7) for \(\rho _{h}=\rho _{h}^{\mathtt{j}}\);
-
(iii)
derivation of the piecewise constant metric \({{\mathcal {M}}}^{\mathtt{j}}\) on \({{\mathcal {T}}}_{h}^{\mathtt{j}}\);
-
(iv)
projection of the metric \({{\mathcal {M}}}^{\mathtt{j}}\) into a piecewise linear metric \({\widetilde{{{\mathcal {M}}}}}^{\mathtt{j}}\) on \({{\mathcal {T}}}_{h}^{\mathtt{j}}\);
-
(v)
generation of the adapted mesh \({{\mathcal {T}}}_{h}^{\mathtt{j+1}}\) associated with the metric \({\widetilde{{{\mathcal {M}}}}}^{\mathtt{j}}\).
We comment on steps (iii)–(v), separately, by neglecting the iteration index \({\mathtt{j}}\) to simplify the notation.
Concerning item (iii), we look for the elementwise metric \({{\mathcal {M}}}= \{{{\mathcal {M}}}_{K}^{*}\}_{K \in {{\mathcal {T}}}_{h}}\) with \({{\mathcal {M}}}_{K}^{*} = \{\lambda _{i, K}^{*}, \mathbf{r}_{i, K}^{*} \}_{i=1,2}\), the metric on K. For the derivation of \({{\mathcal {M}}}\) we enforce a certain accuracy on \(\rho _{h}\), while minimizing the mesh cardinality and equidistributing the error throughout the mesh. These critera lead to the constrained minimization problem
to be solved on each elements K, with \(\delta _{ij}\) the Kronecker symbol,
and \(\hat{G}_{\varDelta _{K}}(\mathbf{e}^{\nabla }_{\rho} )=G_{\varDelta _{K}}(\mathbf{e}^{\nabla }_{\rho} )/{|}\varDelta _{K}{|}\). Quantity \({\mathcal {J}}_{K}\) follows from the local estimator in (7), being
Notice that the area information is now confined into the term \({|}\varDelta _{K}{|}\). Due to the error equidistribution, it follows
Since minimizing the mesh cardinality is equivalent to maximize the area of the mesh elements, we derive metric \({{\mathcal {M}}}\) by solving problem (8). In Micheletti and Perotto (2006, Proposition 26), the authors supply the explicit solution to this problem, namely
with \(\{\gamma _{i,K},\mathbf{g}_{i,K}\}_{i=1,2}\) the eigen-pairs associated with matrix \(\hat{G}_{\varDelta _{K}}(\mathbf{e}^{\nabla }_{\rho} )\), with \(\gamma _{1,K} \ge \gamma _{2,K} > 0\) and \(\{\mathbf{g}_{i, K}\}_{i=1,2}\) orthonormal vectors. Directions \(\mathbf{r}_{i,K}^{*}\) provide the two directions characterizing metric \({{\mathcal {M}}}_{K}^{*}\), whereas we have only the ratio of the two lengths \(\lambda _{i, K}^{*}\). To compute \(\lambda _{1, K}^{*}\) and \(\lambda _{2, K}^{*}\) separately, we explicitly impose the error equidistribution, i.e.,
with \({\mathtt{TOL}}\) a user-defined tolerance on the density \(\rho _{h}\), \(\#{{\mathcal {T}}}_{h}\) the mesh cardinality, and where relation \({|}\varDelta _{K}{|}=\lambda _{1,K}\lambda _{2,K}{|}\varDelta _{\hat{K}}{|}\) has been exploited, with \(\varDelta _{\hat{K}} = T_{K}^{-1}(\varDelta _{K})\) the pull-back via map \(T_{K}\) of the patch \(\varDelta _{K}\).
Since \(\mathcal {J}_{K}(s_{K}^{*},\{\mathbf{r}_{i, K}^{*}\}_{i=1,2}) = 2 \, \sqrt{\gamma _{1,K} \gamma _{2,K}}\), after straightforward algebraic manipulations, we have
so that the local metric \({{\mathcal {M}}}_{K}^{*} = \{\lambda _{i, K}^{*}, \mathbf{r}_{i, K}^{*} \}_{i = 1, 2}\) and the metric \({{\mathcal {M}}}= \{{{\mathcal {M}}}_{K}^{*}\}\) are defined.
As far as item (iv) is concerned, we commute the elementwise quantities in \({{\mathcal {M}}}\) into information associated with the mesh vertices, as it is required by standard mesh generators. For this purpose, we resort to an area-weighted average across the patch of elements associated with each vertex (Micheletti et al. 2010; Farrell et al. 2011). This step identifies the new metric \({\widetilde{{{\mathcal {M}}}}}\).
Finally, metric \({\widetilde{{{\mathcal {M}}}}}\) is provided as an input to a metric-based mesh generator (see step (v)). For the numerical verification in Sect. 4, we use the software BAMG (bidimensional anisotropic mesh generator), which is the default geometric discretization tool linked to the adopted solver, FreeFEM (Hecht 2012).
3 Homogenization: direct and inverse techniques
We tackle the design of cellular materials, obtained by the periodic repetition of a unit cell, in order to match a required property at the macroscale. A standard approach is the asymptotic homogenization theory, which is, in general, adopted both in a direct and in an inverse form (Andreassen and Andreasen 2014; Sigmund 1994). The basic idea behind direct homogenization is to inherit at the macroscale the effects associated with the microscale. In this case, the microscale is the known contribution, whereas the macroscale has to be characterized. Vice versa, when dealing with inverse homogenization, we start from a desired feature at the macroscale and we look for the microscopic layout ensuring the expected macroscopic property in the homogenized scale. Some of the methodologies adopted to perform topology optimization at the macroscale have been employed to design the periodic internal structure of cellular materials (see, for instance, Sigmund 1994; Huang et al. 2011; Noël and Duysinx 2017). The high versatility of direct and inverse homogenization justifies the adoption of these techniques for diverse applications (see, e.g., Ivarsson et al. 2020; Bruggi and Corigliano 2019).
In this section, we resort to the asymptotic homogenization theory combined with the SIMP method to design new cellular materials. This leads us to solve an optimization problem which can be formalized as in (1), after a suitable redefinition of the quantities involved.
As a reference physical model, we adopt the linear elasticity framework. In particular, it is convenient to consider the componentwise stress–strain (\(\sigma {-} \varepsilon\)) relation in terms of the symmetric stiffness tensor E, given by
according to the Voigt notation (Helnwein 2001).
Direct homogenization incorporates the contribution at the microscale into the macroscale for coherence model by modifying the stiffness tensor E (Andreassen and Andreasen 2014). To this aim, it is standard to employ an asymptotic representation of the displacement field, following the two-step procedure:
-
(i)
we compute the microscopic displacement, \(\mathbf{u}^{*, ij}\), with \(ij \in I = \{11, 22, 12\}\), by solving, in the periodic function space \(\mathcal {U}_\# = [H^{1}_\circlearrowleft (Y)]^{2}\), the elliptic equation
$$\begin{aligned}&a^{ij}(\mathbf{u}^{*,ij},\mathbf{v}) := \displaystyle \dfrac{1}{{|}Y{|}}\int _{Y} \sigma (\mathbf{u}^{*,ij}) : \varepsilon (\mathbf{v}) \, {\text {d}}Y \\&\quad =\displaystyle \dfrac{1}{{|}Y{|}}\int _{Y} \sigma (\mathbf{u}^{0,ij}) : \varepsilon (\mathbf{v}) \, {\text {d}}Y =: F^{ij}(\mathbf{v}), \end{aligned}$$(12)for any \(\mathbf{v} \in \mathcal {U}_{\#}\), with Y the design unit cell, \(\mathbf{u}^{0, ij}\) a displacement imposed to Y for \(ij \in I\), and with \(H^{1}_\circlearrowleft (Y)\) the space of functions in \(H^{1}(Y)\) satisfying periodic boundary conditions on \(\partial Y\). In particular, we assign the displacements \(\mathbf{u}^{0, 11} = [x, 0]^{\text {T}}\), \(\mathbf{u}^{0, 22} = [0, y]^{\text {T}}\), \(\mathbf{u}^{0, 12} = [y, 0]^{\text {T}}\), which correspond to the linearly independent engineering strain fields, \({\varvec{\varepsilon }}^{0, 11} = [1, 0, 0]^{\text {T}}\), \({\varvec{\varepsilon }}^{0, 22} = [0, 1, 0]^{\text {T}}\), and \({\varvec{\varepsilon }}^{0, 12} = [0, 0, 1]^{\text {T}}\), respectively;
-
(ii)
the computed fields \(\mathbf{u}^{*, ij}\) and the imposed ones \(\mathbf{u}^{0, ij}\) define the components of the homogenized stiffness tensor, \(E^{\text {H}}\), according to the relation
$$\begin{aligned}&E_{ijkl}^{\text {H}}(\mathbf{u}^{*,ij}, \mathbf{u}^{*,kl})= \displaystyle \dfrac{1}{{|}Y{|}}\int _{Y} \big [\sigma (\mathbf{u}^{0,ij})-\sigma (\mathbf{u}^{*,ij})\big ] \\&\quad : \big [\varepsilon (\mathbf{u}^{0,kl})-\varepsilon (\mathbf{u}^{*,kl})\big ] \,{\text {d}}Y \end{aligned}$$(13)for \(ij, kl \in I\).
The stiffness tensor \(E^{\text {H}}\) takes into account the effect of the microscale. Thus, when dealing with a homogenized context, the linear elasticity stress–strain relation in (11) is replaced by
With reference to an inverse homogenization setting, following Sigmund (1994), we design the optimal unit cell ensuring the desired property at the macroscale by means of the SIMP method properly cast in the homogenization framework. To find the optimal distribution of material \(\rho _{\text {m}}\) (where the subscript m stands for microscale) in the unit cell, we solve problem (1) where we identify the design domain with Y, and the bilinear and linear forms with
respectively, with \(\mathbf{v} \in \mathcal {U}_{\#}\) and \(ij \in I\). The design variable \(\rho _{\text {m}}\) is selected in \(\mathcal {V}_\# = H^{1}_\circlearrowleft (Y)\) to extend the periodic conditions on \(\mathbf{u}^{*,ij}\) to the density function. This assumption simplifies the theoretical and numerical discussion below. Concerning the goal functional in (1), we choose
where ij, \(kl\in I^{\text {G}}\subseteq I\), with \(g=\# I^{\text {G}}\), \(\mathbf{u}^{*}(\rho _{\text {m}})\) is the vector in \([\mathcal {U}_{\#}]^{g}\) of components \(\mathbf{u}^{*,mn}\), with \(mn\in I^{\text {G}}\), \(E_{ijkl, \rho _{\text {m}}}^{\text {H}}=E_{ijkl, \rho _{\text {m}}}^{\text {H}}(\mathbf{u}^{*,ij}, \mathbf{u}^{*,kl};\rho _{\text {m}})\) is the tensor defined by
\(E^{\text {G}}_{ijkl}\), for \(ij, kl\in I^{\text {G}}\), denotes the goal stiffness tensor component adopted by the user to control a physical quantity of interest. Finally, the first box inequality in (1) is reduced to the one-sided constraint on the structure mass
with \(\alpha \in (0,1]\) the maximum allowed volume fraction.
To sum up, problem (1) turns into the optimization statement
with \(ij\in I^{\text {G}}\).
As in Sect. 2.2, the minimization in (19) is carried out by using IPOPT. Among the input quantities to IPOPT, the gradient, \(\nabla _{\rho _{\text {m}}} \mathcal {G}(\rho _{\text {m}})\), of the goal functional in (16) with respect to the density variable \(\rho _{\text {m}}\) requires a careful computation. To this aim, we exploit an adjoint-based Lagrangian formulation, by introducing the augmented functional
for ij, \(kl \in I^{\text {G}}\). In particular, \({\varvec{\pmb {\lambda }}}\in [\mathcal {U}_{\#}]^{g}\) is the adjoint variable used to impose the state equations, with components \({\varvec{\pmb {\lambda }}}^{mn}\).
By differentiating \(\mathcal {L}\) with respect to \(\mathbf{u}^{*, pq}\), we obtain the so-called dual problems
with \(pq \in I^{\text {G}}\); the derivative of \(\mathcal {L}\) with respect to \({\varvec{\pmb {\lambda }}}^{pq}\) yields the g state equations in (19); the gradient of the goal functional
for any \(\phi \in \mathcal {V}_{\#}\), is obtained by deriving \(\mathcal {L}\) with respect to \(\rho _{\text {m}}\). Formulas (20) and (21), together with the state equations in (19), constitute the Karush–Kuhn–Tucker (KKT) conditions (Lions 1971). These equations are discretized by employing linear finite elements for both density and displacement, thanks to the use of SIMPATY algorithm in the design of the new cells, so that \(\rho _{m,h} \in V_{\#, h}\) and \(\mathbf{u}^{*, ij}_{h} \in [V_{\#, h}]^{2}\), with \(V_{\#, h} = \mathcal {V}_{\#} \cap V_{h}^{1}\) and with \(ij \in I^{\text {G}}\).
The resulting algorithm, named microSIMPATY (Ferro et al. 2020b; di Cristofaro et al. 2021), is listed below.
The algorithm switches between an optimization phase (function \({\mathtt{optimize}}\) in line 3) and a mesh adaptation step (function \({\mathtt{adapt}}\) in line 4), based on the anisotropic adaptive strategy detailed in Sect. 2.2. In particular, three tolerances, together with a maximum number \({\mathtt{kmax}}\) of global (optimization + adaptation) iterations, constrain the optimization.
In more detail, \({\mathtt{CTOL}}\) controls the stagnation of the number of elements between two consecutive mesh adaptations; \({\mathtt{TOPT}}\) sets the accuracy for the minimization problem; \(\mathtt{TOL}\) is the user-defined accuracy characterizing the equidistribution of the error throughout the mesh elements according to (10).
MicroSIMPATY algorithm returns the optimized layout \(\tau\) identified by the distribution of \(\rho _{m, h}\) in Y, together with vector
gathering the components \(E^{\text {H}}_{ijkl, \tau }=E_{ijkl, \rho _{m,h}}^H(\mathbf{u}^{*,ij}, \mathbf{u}^{*,kl};\tau )\) of the homogenized stiffness tensor in (17) computed on \(\tau\), with ij, \(kl\in I\) (function \(\mathtt{homogenize}\) in line 9).
4 Generation of a cellular dictionaries
In this section, we provide two different strategies to generate a collection of different unit cells. We will refer to this ensemble as to a dictionary, \({{\mathcal {D}}}=\{\mathcal {W}_{1}, \ldots , \mathcal {W}_{z}\}\), consisting of z different words. The generic word \(\mathcal {W}_{s}=(\tau _{s}, \alpha _{s}, \mathbf{E}^{\text {H}}(\tau _{s}))\), with \(s=1, \ldots , z\), gathers the layout \(\tau _{s}\) generated by micro-SIMPATY algorithm, the corresponding volume fraction, \(\alpha _{s}\), and the associated homogenized stiffness tensor, \(\mathbf{E}^{\text {H}}(\tau _{s})\), defined as in (22). We consider words characterized by different volume fractions, ordered in an ascendant way, and optimized with respect to the same goal quantity \(\mathcal {G}_{\text {m}}\), even though for different values \({E}^{\text {G}}\).
We adopt a multi-objective framework, where topology optimization is contemporary driven by several goal quantities. This choice is typical of practical contexts such as the one analyzed in Sect. 6. A first instance of a multi-objective topology optimization carried out by the microSIMPATY algorithm is provided in di Cristofaro et al. (2021).
A multi-objective formulation of problem (19) implies a generalization of the definition for the goal functional \(\mathcal {G}_{\text {m}}\), here identified by the convex combination of functionals as in (16), i.e.,
for \({ij}_{t}\), \({kl}_{t}\in I^{\text {G}}\), with weights \(\beta _{t}\ge 0\) for \(t=1,\ldots , \vartheta\), such that \(\sum _{t=1}^{\vartheta} \beta _{t}=1\). The components of the goal stiffness tensor are collected in the vector \(\mathbf{E}^{\text {G}}=[E_{{ij}_{t}{kl}_{t}}]_{t=1}^{\vartheta}\) in \({\mathbb {R}}^{\vartheta}\), which replaces the scalar input \(E_{ijkl}^{\text {G}}\) to microSIMPATY algorithm.
By exploiting this optimization process, we generate two distinct dictionaries. The words of the first ensemble (referred to as single-cellular dictionary) share the same cell topology; vice versa, the second set (referred to as multi-cellular dictionary) consists of words with different topologies.
Algorithm 2 provides a unified scheme for the generation of the two dictionaries (with \(\mathtt{SvsM=}\)‘\(\mathtt{S}\)’ for the single-cellular dictionary, \(\mathtt{SvsM=}\)‘\(\mathtt{M}\)’ for the multi-cellular one). The details of the two procedures are addressed in the next sections.
4.1 Generation of a single-cellular dictionary
A single-cellular dictionary is characterized by a unique topology. We choose the reference layout, \(\tau ^{\text {R}}\), yielded by microSIMPATY algorithm for the multi-objective goal functional identified by the reference vector \(\mathbf{E}^{\text {G}} = \mathbf{E}^{{\text {G}}, {\text {R}}} \in \mathbb {R}^{\vartheta }\), and for an assigned volume fraction, \(v_{\text {f}}^{\text {R}}\), both selected by the user (lines 3–5). In particular, the words in \(\mathcal {D}\) are generated via a suitable post-processing of \(\tau ^{\text {R}}\), which essentially increases or reduces the thickness of the considered layout, according to the volume fractions in the input vector \(\mathbf{v}_{\text {f}}=[\mathbf{v}_{\text {f}}(s) ]_{s=1}^{z}\) (function \(\mathtt{offset}\) in line 7). For this purpose, we resort to a parametric design platform, which is based on the Rhino 3D CAD softwareFootnote 1 endowed with the embedded visual programming tool Grasshopper.Footnote 2
The definition of each word \(\mathcal {W}_{s}\) is completed by computing the homogenized stiffness tensor \(\mathbf{E}_{\text {H}}(\tau _{s})\) defined as in (22) (function \(\mathtt{homogenize}\) in line 8).
Finally, the words are sorted for increasing values of the volume fraction (function \(\mathtt{sort}\) in line 21 to build up the dictionary \({{\mathcal {D}}}_{\mathtt{S}}\), all the entries in \(\mathbf{v}_{\text {f}}\) being assumed distinct. We remark that the \(\tau ^{\text {R}}\) is the only topologically optimized layout in the dictionary. However, this is a standard practice in many application fields dealing with graded materials (Wang et al. 2017).
We exemplify this procedure by selecting the multi-objective goal functional
Concerning the other input parameters to Algorithm 2, we set
with \(\mathbf{v}_{\text {f}}=[0.35, 0.4:0.1:0.9]\), \(\mathcal {T}_{h}^{\mathtt{0}}\) coinciding with a structured \(50\times 50\) mesh of the unit cell \(Y=(0,10)^{2}\) (mm2), and where the flag \(\mathtt{SvsM}\) is set to ‘\(\mathtt{S}\)’ since interested in a single-cellular dictionary. The values chosen for the reference volume fraction and the homogenized stiffness tensor components are \(v_{\text {f}}^{\text {R}} = 0.5\) and \(E_{1111}^{\text {G}}=E_{1111}^{{\text {G}}, {\text {R}}}=2.50\)e−01, \(E_{2222}^{\text {G}}=E_{2222}^{{\text {G}}, {\text {R}}}=1.25\)e−01, respectively. We remark that the components both of the reference and of the homogenized stiffness tensors are scaled with respect to the corresponding full material configuration (i.e., \(\rho _{\text {m}} = 1\) in (17)), after setting \(E_{\text {Y}} = 45.00\) (N/mm2) and \(\nu = 0.49\) to characterize the base material. Finally, the penalization exponent in (15) is taken equal to 4.
The reference layout, \(\tau ^{\text {R}}\), yielded by \(\mathtt{microSIMPATY}\) algorithm, is the one in the left panel of Fig. 1. According to the colorbar, red areas (\(\rho = 1\)) identify the full material, while the blue zones (\(\rho = 0\)) represent the void. The adapted mesh is superimposed to the layout and is highlighted in cyan, in order to emphasize the anisotropic features along the structure boundaries. Figure 1 (right) shows the convergence history characterizing the optimization of the unit cell, in terms of the volume fraction and the stiffness tensor components defining the goal functional. More iterations are required by \(E_{1111, \tau ^{\text {R}}}^{\text {H}}\) and \(E_{2222, \tau ^{\text {R}}}^{\text {H}}\) to stabilize when compared with the volume fraction. The vertical lines identify the adaptation steps. We remark that each mesh adaptation introduces a slight instability in the optimization process (to be ascribed to the variables projection onto the new mesh), which is dumped within few iterations.
Reference unit cell (single-cellular dictionary): density distribution overlapped to the associated anisotropic grid (left); convergence history for the mass and the constrained stiffness components (right)
Starting from the reference design \(\tau ^{\text {R}}\) and the volume fractions in \(\mathbf{v}_{\text {f}}\), function \(\mathtt{offset}\) returns the layouts in Fig. 2. The employment of a unique optimized topology modified via offset criteria may lead to layouts that are not so handy to be manufactured. This is the case of the layouts in panels (a) and (f) which exhibit thin struts and small holes, respectively. Moreover, we have verified that volume fractions less than 0.35 yield unprintable configurations.
Optimized cells (single-cellular dictionary): density distribution overlapped to the associated anisotropic grid for the different volume fractions in \(\mathbf{v}_{\text {f}}\)
Function \(\mathtt{homogenize}\) computes the homogenized stiffness tensor characterizing \(\tau _{s}\)’s. Table 1 provides the values for the two components \(E_{1111, \tau _{s}}^{\text {H}}\) and \(E_{2222, \tau _{s}}^{\text {H}}\), for \(s = 1,\ldots , z\) (we refer to Fig. 6 for the values of the other non-null components). Notice that that the homogenized stiffness tensor components, \(E_{1111, \tau ^{\text {R}}}^{\text {H}}\), \(E_{2222, \tau ^{\text {R}}}^{\text {H}}\), exactly match the corresponding goal values (\(E_{1111}^{{\text {G}}, {\text {R}}} = 2.50\)e−1, \(E_{2222}^{{\text {G}}, {\text {R}}} = 1.25\)e−1).
4.2 Generation of a multi-cellular dictionary
A multi-cellular dictionary assembles words which are associated with different topologies. As a consequence, we run microSIMPATY algorithm z times (line 16, after selecting a multi-objective goal functional and a certain volume fraction. This leads us to pick the s-th row, for \(s=1,\ldots , z\), of the tensor \(\mathbf{E}^{\text {G}}\in {\mathbb {R}}^{z\times \vartheta }\) (line 14), collecting the goal values \(E_{{ij}_{t}{kl}_{t}}^{\text {G}}\), with \(t=1,\ldots , \vartheta\), which define the functional in (23), and the s-th component of the vector \(\mathbf{v}_{\text {f}} \in \mathbb {R}^{z}\) gathering the chosen volume fractions.
As far as the testing below, we select \(\mathbf{v}_{\text {f}}=[0.1:0.1:0.9],\) (i.e., \(z=9\)), and, for each \(s=1, \ldots , 9\), we choose the goal functional in (24) (i.e., \(\vartheta =2\)), with goal values specified in Table 2, panel 2. These targets prescribe the x-direction to be mechanically stiffer with respect to the y-direction, which turns out to be strategical with a view to the design of orthopedic devices tackled in Sect. 6. Also the selected volumes in \(\mathbf{v}_{\text {f}}\) are strictly motivated by the application of interest. Moreover, since the volume fraction constraint and the homogenized goal values may be in conflict, inappropriate target inputs might lead to an empty solution space. To overcome this issue, we selected values for the components \(E_{{1111}}^{\text {G}}\), \(E_{{2222}}^{\text {G}}\) so that the optimization turns out to be feasible.
As far as the other input parameters to dictioSIMPATY are concerned, we preserve the same values as in (25), while adopting a structured \(N_{{{\mathcal {T}}}_{h}^{0}}\times N_{{{\mathcal {T}}}_{h}^{0}}\) initial mesh, \(\mathcal {T}_{h}^{\mathtt{0}}\), the flag \(\mathtt{SvsM}\) being ‘\(\mathtt{M}\)’ since interested in a multi-cellular dictionary, \({{\mathcal {D}}}_\mathtt{M}\). Notice that, to design the nine layouts, we adopt an initial tessellation of the unit cell \(Y=(0,10)^{2}\) (mm2) characterized by a different value for \(N_{{{\mathcal {T}}}_{h}^{0}}\) (see Table 2, panel 5). The same base material as well as the same penalization law as in Sect. 4.1 are here employed.
Figure 3 collects the microSIMPATY layouts \(\tau _{s}\), for the diverse volume fractions, overlapped with the corresponding final anisotropic adapted mesh. The stretched elements of the grids allow to precisely detect the void/material interface, leading to very smooth boundaries, while regularizing the possible sharp angles of the layouts (as a clear example, see the unit cell in panel (d)). Moreover, following Ferro et al. (2020c), to improve the accuracy of the mechanical analysis, we restore an isotropic tessellation in the material portion of the cell, so that the stretched elements act only in sharply detecting the topology.
Optimized cells (multi-cellular dictionary): density distribution overlapped to the associated anisotropic grid for the different volume fractions in \(\mathbf{v}_{\text {f}}\)
The obtained configurations respond to the different design prescriptions. In more detail, except for the unit cell in panel (a) which is far from being manufacturable, the x-direction turns out to be the preferential one in terms of mass allocation, at least until the volume fraction is sufficiently far from 1. This evidence is fully in agreement with the imposed mechanical requirement which reduces the stiffness in y-direction. More quantitative information about the final adapted mesh, here denoted by \({{\mathcal {T}}}_{h}\) to simplify the notation, is provided in Table 2, panel 5, where the cardinality and the maximum aspect ratio of the grid are gathered. We observe that complex topologies require a larger number of elements, whereas the stretching of the mesh elements is strictly related to the size of the holes in the cell layout.
Concerning the homogenized stiffness tensor of the unit cells, we refer to Table 2, panel 3, for the components driving the topology optimization (and to Fig. 9 for the other components). We recognize a good matching between goal and homogenized components, as highligthed by the relative errors, \(\% E_{1111}\) and \(\% E_{2222}\), in Table 2, panel 4.
5 Multiscale topology optimization
In this section, we address the design of a macroscale geometry in terms of optimal allocation of microscopic unit cells. This process, widely employed in practice, is generally referred to as multiscale topology optimization.
In accordance with Wang et al. (2017) and Allaire et al. (2019), we detail how to employ a dictionary, \(\mathcal {D}\), of unit cells, optimized to match a goal quantity \(G_{1}\) at the homogenized scale, for the design of a structural configuration in order to satisfy a mechanical requirement, \(G_{2}\), at the macroscale.
In the literature, both pre-defined (Allaire et al. 2019; Vigliotti and Pasini 2013; Moussa et al. 2020) and ad hoc designed (Coelho et al. 2008; Nakshatrala et al. 2013; Ferro et al. 2020b; di Cristofaro et al. 2021) cells are employed as words of the dictionary \(\mathcal {D}\). We follow the second approach to exploit the dictionaries, \(\mathcal {D}_\mathtt{S}\) and \(\mathcal {D}_\mathtt{M}\), generated in the previous section.
The reference framework is still represented by problem (1) which has to be properly customized according to a multiscale formulation. In particular, we solve the problem
where \(\mathcal {G}_{\text {M}}=G_{2}\) drives the optimization at the macroscale; the bilinear form of the state equation is
with \(\mathbf{u}(\rho _{\text {M}}) \in \mathcal {U}\),
and \(\varXi ^{\text {H}}_{ijkl}(\rho _{\text {M}})\) the ijkl-th component of the multiscale homogenized stiffness tensor, at this level coinciding with a generic function of \(\rho _{\text {M}}\); \(F_{\rho _{\text {M}}}\) takes into account the work due to possible external volume or surface forces. Relation (28) combines, while generalizing, definitions (3) and (14). Indeed, it supports a completely general dependence on the multiscale design variable \(\rho _{\text {M}}\) and it contemporary takes into account the effect of the homogenization.
To explicitly define the components of the multiscale homogenized stiffness tensor, \(\varXi ^{\text {H}}\), we follow an approach similar to the one adopted in Wang et al. (2017).
First of all, we build a possible trend for the six sets of values \(\{\alpha _{s}, E^{\text {H}}_{ijkl, \tau _{s}}\}_{s = 1,\ldots , z}\) by means of a polynomial approximation \(\varPhi ^{\text {H}}_{ijkl}(\alpha )\), for ij, \(kl \in I\). In particular, the dependence of \(E^{\text {H}}_{ijkl, \tau _{s}}\) on \(\alpha _{s}\) is understood due to the implicit relation between the structure volume fraction and the layout.
As a successive step, we make matrix \(\varXi ^{\text {H}}(\rho _{\text {M}})\) computable in \(\varOmega\) to evaluate the bilinear form in (27). For this purpose, for any \(\mathbf{x}\in \varOmega\), we resort to the identification \({\alpha }=\rho _{\text {M}}(\mathbf{x})\), and we assign the value \(\varPhi ^{\text {H}}_{ijkl}({\alpha })\) to the component \(\varXi _{ijkl}^{\text {H}}(\rho _{\text {M}}(\mathbf{x}))\) (see Fig. 4 for a schematic representation of the implied correspondence between multiscale density and microscopic volume fraction).
Multiscale topology optimization: correspondence between multiscale density and microscopic volume fraction
From a computational viewpoint, consistently with the previous sections, we adopt linear finite elements to discretize both the multiscale density and the displacement, i.e., we pick \(\rho _{M,h}\in V_{h}^{1}\), \(\mathbf{u}_{h}\in [V_{h}^{1}]^{2}\cap {{\mathcal {U}}}\).
The whole multiscale topology optimization is sketched in Algorithm 3.
The algorithm combines, in a sequential way, the fitting of the data at the microscale (in line 2) with the topology optimization at the macroscale (in line 5). With a view to the optimization process, fitting functions \(\varPhi _{ijkl}^{\text {H}}\), depending on the microscopic volume fraction \(\alpha\), are identified with \(\varXi _{ijkl}^{\text {H}}\) as functions of \(\rho _{\text {M}}\). Successively, components \(\varXi _{ijkl}^{\text {H}}\), together with their derivatives, are used by the optimize routine, according to (26), since instrumental to the setting of the state equation (27) and to the gradient-based optimization procedure, respectively. The output of the procedure is the discretized multiscale design variable.
6 Design of orthopedic devices
This section is devoted to the proposal of an innovative pipeline to design patient-specific insoles for the treatment of foot diseases. The impairments led by foot problems include a higher risk of falling, lower ability to execute standard activities of daily living, and a general lower level of quality of life (López-López et al. 2018).
The investigation carried out in this section focuses on patients affected by diabetes, who suffer from foot ulcers, one of the main causes of limb amputation. Several studies highlighted how mechanical stress can be a major indicator of ulcers progression, since they often appear in the high-pressure regions of the foot (Armstrong and Lavery 1998; Ledoux et al. 2005). Due to the mechanical nature of the putative mechanism of ulcers worsening, several studies have investigated the effect of footwear design (Healy et al. 2013). In particular, the literature pointed out that wrong footwear causes over 40% of foot amputation, whereas properly designed diabetic insoles can locally reduce the mechanical stress in the areas of major pressure or in correspondence with ulcers location, thus preventing foot ulceration.
In this framework, our goal is to check whether the proposed multiscale topology optimization can be instrumental to the design of a patient-specific orthopedic device, starting from the well-established expertise gained by some of the authors in such an area (Mannisi et al. 2019). However, since the verification setting is here confined to a 2D framework, the results below have to be meant as a proof-of-concept investigation, preliminary to a 3D real design to be manufactured by a 3D printing technology.
6.1 Verification
In order to accomplish the design of the patient-specific insole, we resort to Algorithm 3, after introducing some simplifying hypotheses on the physical setting. The main simplification leads us to work on a transverse cut section of the 3D orthopedic device, thus reducing the design domain to a 2D slab in the xy Cartesian plane. Additionally, we assume that the patient-specific configuration is characterized only by three medical conditions for the sole of the foot, i.e., a healthy and an ulcerated zone, together with a possible transition region between these two areas.
With a view to the 3D printing of the optimized configuration, the 2D final layout is meant as to be extruded along the z direction.
From a mathematical viewpoint, the optimization of the insole can be cast into the generic framework in (26). In particular, the target functional \(\mathcal {G}_{\text {M}}(\mathbf{u}(\rho _{\text {M}}), \rho _{\text {M}})\) coincides with the mass of the orthotic device
The two-sided constraint in (26) is generalized to different controls to take into account that the stiffness varies according to the local clinical status of the tissue (healthy, ulcerated, or pre-ulcerated). In more detail, the three inequalities
are imposed, where
denotes the local static compliance computed on the boundary portion \(\Gamma ^{Z} \subset \Gamma _{\text{N}}\), with \(Z = H\) (healthy tissue), \(Z=U\) (ulcerated tissue) and \(Z=T\) (transition area between healthy and ulcerated tissue), scaled with respect to the corresponding compliance,
in the full-material configuration. Thus, with reference to formulation (26), it follows that
Finally, the PDE constraining the topology optimization is featured by the bilinear form in (27), the linear form
and the function space \(\mathcal {U} = H^{1}_{\varGamma _{\text {D}}}(\varOmega )\), where the boundary \(\partial \varOmega\) of the design domain is subdivided into the portions \(\varGamma _{\text {D}}\) (clamped boundary), \(\varGamma _{\text {N}}\) (traction-loaded boundary), and \(\varGamma _{\text {F}}=\partial \varOmega \setminus (\varGamma _{\text {D}} \cup \varGamma _{\text {N}})\) (traction-free boundary).
We observe that the domain \(\varOmega\), the load \(\mathbf{f}\), and the areas \(\varGamma ^{Z}\) characterize the patient-specific nature of the current modeling. Domain \(\varOmega\) strictly depends on the size of the patient’s foot; force \(\mathbf{f}\) takes into account the weight and the gait; finally, the configuration of the ulcerated zone identifies the portions \(\varGamma ^{Z}\), for \(Z = {\text {H}}, {\text {U}}, {\text {T}}.\)
Concerning the verification here performed, we select \(\varOmega = (-150, 150) \times (0, 50)\) (mm2), \(\varGamma _{\text {D}} = \{(x,y) \in \partial \varOmega : -150 \le x \le 150, y = 0\}\), \(\varGamma _{\text {N}} = \{(x,y) \in \partial \varOmega : -150 \le x \le 150, y = 50\}\), and \(\mathbf{f}\) as the profile in Fig. 5 (top) to model the pressure exerted by the heel, the pad, and the toe on the insole. The values are extracted from experimental data (Karia et al. 2016).
Patient-specific design of an orthopedic device: load distribution (top) and location of the healthy, ulcerated and pre-ulcerated areas (bottom)
We analyze two different clinical scenarios, i.e., the case of an abrupt transition between healthy and ulcerated areas (referred to as the H–U setting), and the complete configuration including the three possible status of the tissue (denoted by the H–U–T setting). The two choices essentially differ in the definition of portions \(\varGamma ^{Z}\), for \(Z = H, U, T\) (see the bottom panel in Fig. 5 for a sketch), being
with
The endpoints of the ulcerated and transition zones are derived from the intersection of the boundary portion \(\varGamma _{\text {N}}\) with two circular segment areas, in order to model the damaged and the neighboring tissue.
Concerning the adopted discretization, we use linear finite elements to approximate both the design variable, \(\rho _{\text {M}}\), and the displacement, \(\mathbf{u}\), on a \(150 \times 25\) structured computational mesh \({{\mathcal {T}}}_{h}\).
The multiscale optimization of the insole will be now driven by the dictionaries, \({{\mathcal {D}}}_\mathtt{S}\) and \({{\mathcal {D}}}_\mathtt{M}\), created in Sects. 4.1 and 4.2, respectively. In particular, the functional in (24) constraining the design of the words of the two dictionaries has been selected in order to minimize the stress component along the vertical direction on the patient’s foot. In fact, active mechanical stress transmission to the ulcers, due to standing or walking, may lead to increase the ulcer size over time. As a consequence, it turns out to be beneficial for the patient to decrease deflection at the load application regions for reducing the peaks of pressure in ulceration zones.
6.1.1 Insole optimization based on the single-cellular dictionary
To design the orthopedic device by means of a graded single topology, we resort to Algorithm 3 with the input parameters
\(\mathbf{c}_{\text {m}}\), \(\mathbf{c}_{\text {M}}\) to be properly set according to the selected H–U or H–U–T configuration, \(\rho _{M,h}^{0} = 0.95 \chi _{\varOmega }\), with \(\chi _{\varOmega }\) the characteristic function associated with domain \(\varOmega\), and where \(\mathcal {D}_{\mathtt{S}}\) is the single-cellular dictionary in Fig. 2.
As a first task, Algorithm 3 performs the fitting of the data \(\{\alpha _{s}, E^{\text {H}}_{ijkl, \tau _{s}}\}_{s = 1,\ldots , 8}\), for \(ijkl = 1111\), 2222, 1122, 1212, the components \(E^{\text {H}}_{1112,\tau _{s}}\) \(E^{\text {H}}_{2212,\tau _{s}}\) being identically null, and the full material configuration being added to the ones in Fig. 2 for \(s = 8\). To this aim, we adopt a global polynomial least-square approximation of degree n. The value \(n=5\) is the lowest degree which provides us a sufficiently reliable data approximation. In particular, Fig. 6 shows the plot of the polynomials \(\varPhi _{ijkl}^{\text{H}}(\alpha )\), where the circle markers highlight the fitted values for the homogenized tensor components. We also provide the plot of the standard SIMP (i.e., \(\alpha ^{3}\)), which exhibits a very similar trend when compared with the fitting polynomials, with a slightly more evident deviation for \(\varPhi _{1111}^{\text {H}}\). This can be justified by the promotion of the x-direction in the stiffness optimization process. Moreover, the four curves ensure tensor \(\varXi ^{\text {H}}(\rho _{\text {M}})\) to be well-defined as a function of \(\rho _{\text {M}}\). Finally, we have numerically checked that tensor \(\varXi ^{\text {H}}\) is definite positive for any \(\rho _{\text{M}}\), which implies that the bilinear form \(a_{\rho _{\text {M}}}^{\text {H}}(\cdot , \cdot )\) in (27) is coercive.
Optimized insole (single-cellular dictionary): fitting of the homogenized stiffness tensor components (solid line) and reference SIMP trend (dashed line)
The fitting in Fig. 6 becomes instrumental to function \(\mathtt{optimize}\) of Algorithm 3, since, via (28), it defines the PDE problem constraining the topology optimization in (26).
The lower and the upper bound for the two-sided constraint in (26) are set to
and
for the H–U and the H–U–T scenario, respectively corresponding to a requirement of high and low (and, if included, medium) stiffness for the insole.
The distribution of the multiscale density function \(\rho _{M,h}\) representing the output of Algorithm 3 is shown in Fig. 7 for the patient-specific H–U (top) and H–U–T (bottom) settings. The presence of the transition area between healthy and ulcerated zones induces a milder gradation of the material density in correspondence with the sick and the loaded portions of the boundary \(\varGamma _{\text {N}}\). The total mass of the two insoles is given by \(37.8\%\) and \(39.4\%\) of the full material configuration for the H–U and the H–U–T scenario, respectively.
Optimized insole (single-cellular dictionary): optimized distribution of the density \(\rho _{M, h}\) for the patient-specific H–U (top) and H–U–T (bottom) configuration
In order to grade the different unit cells across the optimized insole, we exploit again the relationship between \(\rho _{M, h}\) at the homogenized macroscale and \(\alpha\) at the microscale. In particular, we resort to a thresholding of \(\rho _{M, h}\) to identify the different subregions, \(\omega _{s}\), of the design domain associated with a specific microscopic layout, \(\tau _{s}\). The number of the subregions \(\omega _{s}\) will be, at most, equal to \(z+1\), after assuming that the full material configuration corresponds to \(s=z+1\).
According to the thresholding criterion here adopted, we define the subregions
for \(s=1,\ldots , z\), with \(\delta _{l,s}\), \(\delta _{u,s}\in {\mathbb {R}}\) properly selected by the user according to the density distribution range, and region
being \(\delta _{z+1}\in {\mathbb {R}}^+\) set by the user. We have numerically investigated the effect of thresholding in terms of mass and stiffness of the structure. The percentage variations with and without thresholding are, in general, negligible (we refer to the next section for more quantitative details).
By applying this thresholding to the configurations in Fig. 7, we obtain the four subregions \(\omega _{i}\), with \(i=1, \ldots , 4\), shown in Fig. 8, after setting \(\delta _{l,1}=0\), \(\delta _{u,1}=\delta _{l,2}=-0.025\), \(\delta _{u,2}=\delta _{l,3}=\delta _{u,4}=-0.05\), \(\delta _{u,3}=\delta _{l,4}=-0.065\). We observe that the inclusion of the pre-ulcerated portion in the insole design introduces an area of soft material just below the ulcer, and promotes the intermediate densities corresponding to the volume fractions \(\alpha =0.4\) and \(\alpha =0.5\). These results support not only the reduction of pressure below the ulcer location but confirm the need of a pressure re-distribution around the damaged areas.
Optimized insole (single-cellular dictionary): allocation of the different unit cells across the insole
6.1.2 Insole optimization based on the multi-cellular dictionary
The topology optimization of the insole is now driven by exploiting the multi-cellular dictionary \(\mathcal {D}_\mathtt{M}\) generated in Sect. 4.2. To this aim, we run Algorithm 3 with the input parameters
while selecting
for the H–U setting,
for the H–U–T configuration, and with \(\rho _{M,h}^{0}=0.95 \chi _{\varOmega }\).
The fitting of the homogenized stiffness tensor components \(E_{ijkl,\tau _{s}}^{\text {H}}\) as a function of the density \(\alpha\) is carried out, for \(s=1, \ldots , 10\) where \(s=10\) identifies the full material unit cell, by employing a polynomial of degree \(n=5\), approximating the data according to a least-squares criterion. Figure 9 gathers the polynomials \(\varPhi _{ijkl}^{\text {H}}(\alpha )\), the data to be approximated, together with the reference SIMP behaviour. A cross-comparison with Fig. 6 shows that the four curves exhibit a similar trend, except for polynomial \(\varPhi _{1111}^{\text {H}}\) which increases slower to 1 when dealing with the multi-cellular dictionary. Moreover, the SIMP curve is now very close to the functions fitting the data for all the components.
Optimized insole (multi-cellular dictionary): fitting of the homogenized stiffness tensor components (solid line) and reference SIMP trend (dashed line)
The output of Algorithm 3 coincides with the distribution of \(\rho _{M,h}\) in Fig. 10, where the optimal design of the insole is distinguished between the H–U and the H–U–T scenarios (top and bottom, respectively). The distribution of the material density is very similar with a slight difference in the total mass of the insole for the H–U and H–U–T settings, equal to \(29.8\%\) and \(32.4\%\) of the full material domain, respectively. Moreover, the ulcer is taken into account in both the H–U and H–U–T designs in contrast to Fig. 7 (top panel) where the same density characterizes the ulcerated and the healthy portions. Concerning the optimization process, we provide in Fig. 11 the convergence history characterizing the minimization of the mass and the constraints on the local static compliance \(\varUpsilon ^{\text {H}}\), \(\varUpsilon ^{\text {U}}\), and \(\varUpsilon ^{\text {T}}\). The trend is very similar for all the quantities, with an initial transient phase followed by a gradual stagnation towards the optimal values.
Optimized insole (multi-cellular dictionary): optimized distribution of the density \(\rho _{M, h}\) for the patient-specific H–U (top) and H–U–T (bottom) configuration
Optimized insole (multi-cellular dictionary): convergence history for the mass and the constrained local static compliances
With a view to the manufacturing of the optimized insoles in Fig. 10, we apply the thresholding procedure introduced in the previous section. This strategy leads us to identify three subregions, \(\omega _{2}\), \(\omega _{3}\), \(\omega _{4}\), for both the scenarios, H–U and H–U–T, after selecting \(\delta _{l,2}=0\), \(\delta _{l,3}=\delta _{l,4}=\delta _{u,s}=-0.05\) for \(s=2,3,4\). It can be checked that the thresholding leads to slight changes with respect to the mass and the stiffness of the structure. In particular, the mass is essentially invariant (32.4% to be compared with 31.6% without and with thresholding); the compliance characterizing the ulcerated portion practically remains the same, with a 0.07% increment; the compliance in the healthy area, \(\varUpsilon ^{\text {H}}\), exhibits a 2.77% reduction, while \(\varUpsilon ^{\text {T}}\) increases more significantly (10.4% with respect to the non-thresholded configuration), promoting stiffer and more flexible materials for the healthy and the pre-ulcerated tissue, respectively.
Figure 12 shows the distribution of the three regions together with the associated unit cells. When compared with the single-cellular case (see Fig. 8), we recognize that the multi-cellular dictionary involves fewer unit cells in the prototype of the insole and turns out to be less sensitive to the inclusion of the pre-ulcerated zone in the design of the orthotic device. Finally, the two panels in Fig. 12 emphasize that the presence of the transition area between the healthy and the ulcerated tissue increases the extension of region \(\omega _4\) associated with the volume fraction \(\alpha =0.4\). The transition areas favour the re-distribution of the pressure, thus avoiding undesired localization of the load. All these considerations lead us to select the setting in Fig. 12 for the validation and the comparison with standard 3D manufacturing choices.
Optimized insole (multi-cellular dictionary): allocation of the different unit cells across the insole
6.2 Validation
The optimization procedure set for the design of orthopedic devices is finally tested in practice via a mechanical validation, in the case of the patient-specific H–U–T configuration of Fig. 12. In detail, we computationally explore the macroscopic mechanical behaviour of the prototype via a finite element analysis. Then, we investigate the 3D printing manufacturability of the design, via fused deposition modelling (FDM).
6.2.1 Mechanical performance evaluation
For the finite element analysis, we refer to the 2D geometry in Fig. 13, where the insole is regarded as a porous continuum body and includes a thin layer on the top, to simulate the foot tissue (i.e., fat and skin) in contact with the orthotic device. The considered configuration coincides with the explicit representation of the microcellular material shown in Fig. 12b.
Optimized insole (mechanical validation): schematic representation for the H–U–T configuration
To evaluate the mechanical performance of the optimized insole, we assume as the reference case the standard honeycomb material. In more detail, we mechanically test three insole settings, i.e., (1) honeycomb design with constant volume fraction of 30%; (2) honeycomb design with variable volume fraction, with the same distribution as in Fig. 12b; (3) the optimized H–U–T configuration in Fig. 12b.
The foot tissue layer is assumed linearly elastic, homogeneous and isotropic, as well as the thermoplastic polyether–polyurethane elastomer (TPE) material composing the insole. In particular, Young’s modulus and Poisson’s ratio are set equal to \(E_{\text {TPE}}=45\) (MPa), \(\nu _{\text {TPE}}=0.49\), and \(E_{\text {foot}}=1\) (MPa), \(\nu _{\text {foot}}=0.4\). The loading condition applied to the top tissue layer coincides with the patient-specific load distribution in Fig. 5 (top) while the bottom boundary of the insole is constrained, as shown in Fig. 13.
The mechanical analysis for cases (1)–(3) is carried out by using the software COMSOL Multiphysics.Footnote 3
Figure 14 compares the deformation of the three designs under the imposed load, in terms of spatial distribution of the displacement magnitude. It is evident that the three insoles exhibit a different mechanical behaviour. In particular, the optimized configuration yielded by the procedure in Sect. 6.1.2 exhibits a maximum value for the displacement which is 2 and 3 times lower with respect to the one characterizing designs (1) and (2), respectively. This is confirmed by Fig. 15 (top) which shows the displacement profile along the cut line highlighted by the black dashed line in Fig. 13. It is evident that the new designed configuration localizes and attenuates the displacement in the ulcer zone, thus preventing the stress concentration in the surrounding area.
Optimized insole (mechanical validation): spatial distribution of the displacement magnitude for the insole settings (1)–(3) (top–bottom)
Optimized insole (mechanical validation): displacement magnitude (top) and von Mises stress (bottom) profiles for the insole settings (1)–(3)
In order to characterize the loading-transfer mechanism between insole and foot tissue, in Fig. 15 (bottom) we investigate the mechanical behaviour of the three designs in terms of the von Mises stress distribution along the same cut line as in Fig. 13. The optimized layout in Fig. 12b dampens the stress in the foot tissue and localizes the effect of the loading pressure. In particular, when employing the two honeycomb insoles, the pressure affects also the plantar arch zone (i.e., the region between 0.1 and 0.15 m), though this area is not loaded. This is not the case for the new proposed configuration, thus introducing an innovative and relevant advantage in the design of orthopedic insoles.
6.2.2 Manufacturing feasibility evaluation
To assess the feasibility of the orthopedic device in Fig. 12b in terms of manufacturing, we apply an axial extrusion of 0.01 (m) to the optimized insole in Fig. 13, in order to obtain a section of the 3D model. To this aim, we use the dedicated software of slicing, Simplify3D,Footnote 4 to generate a g-code for the 3D printer. The flexible TPE filament Filaflex, with a shore A equal to 82 (Filaflex 82A), has been selected to manufacture the extruded section shown in Fig. 16. This material has proved to be suitable for the 3D printing of insoles, since it has an optimal resistance to elongation and abrasion as well as a high tensile strength (Wang et al. 2020). These properties make Filaflex 82A a perfect material for the production of flexible, comfortable and resistant insoles.
Optimized insole (3D printing validation): manufacturing of the section of the orthopedic prototype in Fig. 13 with three enlarged views of the different unit cells
Different slicing parameters and profiles have been tested to obtain an optimal result in terms of reliability and quality of production. After several tests, the main printing parameters are set as: print speed 2200 mm/min, extruder temperature 235 \(^\circ\)C, cooling 60%, top/bottom/outline perimeters equal to 3, no-retraction. The model took approximately 10 h of printing.
These preliminary results confirm the feasibility of the proposed method to create innovative and patient-specific solution for foot problems. The different areas are well-defined (see the enlarged views on areas A, B and C in Fig. 16) and the process is reasonable in terms of printing time and overall quality. This proof-of-concept represents a promising starting point for the realisation of a full model of patient-specific insoles that can be used for prevention of ulceration and can lead to beneficial medical outcomes.
7 Conclusions
The multiscale topology optimization proposed in this paper provides a fully general, cost-effective tool for the design of macrostructures optimized in terms of local distribution of void, solid, and cellular materials. Among the relevant properties, we list the possibility to decouple the optimization at the macro- and at the microscale, possibly associated with different goal functionals. This feature allows us to control target quantities which are simultaneously pivotal in the design of the final product, in the spirit of a multi-objective optimization. Moreover, the non concurrent optimizations at the micro- and at the macroscale lighten the computational burden of the whole procedure. Indeed, the generation of the cell dictionary could be, a priori, confined to a preliminary phase, mimicking an offline/online paradigm.
A cross-comparison between the single-cellular and the multi-cellular dictionary optimizations leads us to an additional interesting consideration. Actually, the possibility to involve different topologies in the design of the optimized macrostructure results in the adoption of a lower number of different unit cells, i.e., in a structure simpler to be manufactured. Also, the multi-cellular dictionary admits very small volume fractions (for instance, values \(\alpha =0.2\), 0.3 excluded by \({{\mathcal {D}}}_\mathtt{S}\)). Moreover, dictionary \({{\mathcal {D}}}_\mathtt{M}\) seems to be less sensitive with respect to the analyzed patient-specific configurations. Indeed, the presence of the pre-ulcerated area in Fig. 12 essentially preserves the allocation of the unit cells when compared with the H–U scenario, just slightly increasing the extension of the zones associated with the highest density. This is in contrast to the optimized layouts in Fig. 8 associated with the single-cellular dictionary, which strongly differ in the global unit cells distribution and in the presence of a soft region just below the damaged area in the H–U–T configuration.
The validation carried out in Sect. 6.2 confirms that the developed multiscale topology optimization can lead to some benefits when compared with consolidated medical practices. In particular, the finite element analysis in Fig. 15 shows that the insole design in Fig. 12 for the H–U–T scenario reduces the stress in correspondence with the ulcerated zone and the plantar arch, when compared with standard homogeneous and heterogeneous honeycomb infills. Finally, the manufacturing analysis in Sect. 6.2.2 confirms the feasibility of the optimized prototype with respect to a 3D printing technology.
These preliminary results support the proposed multiscale topology optimization as an effective computational and manufacturing workflow for the design of custom-made insoles for specific foot pathologies.
As a first possible development, we plan to extend the methodology here presented to a 3D setting to provide a more effective solution to different foot pathologies and to comply with patient-specific clinical prescriptions.
In addition, both the optimization phases can be enriched with constraints taking into account the current limits in additive manufacturing (Moussa et al. 2020), as well as the presence of possible failures or geometric defects (Liu et al. 2017) in the final layouts.
A handy management of the transition between different cell layouts represents another crucial issue with a view to manufacturability, in particular when dealing with heterogeneous dictionaries.
Further steps towards a more comprehensive description of complex phenomena include a multi-physics optimization, where different physical problems coexist; the possibility to properly orient the unit cells according to the direction of the applied load; the inclusion of null density in the multiscale design process to concurrently modify the macroscopic topology and the cell allocation.
Notes
COMSOL Multiphysics\(\circledR\). Version 5.6, www.comsol.com, COMSOL AB, Stockholm, Sweden.
Symplify3D\(\circledR\). Version 4.0, www.simplify3d.com.
References
Ahmed S, Barwick A, Butterworth P, Nancarrow S (2020) Footwear and insole design features that reduce neuropathic plantar forefoot ulcer risk in people with diabetes: a systematic literature review. J Foot Ankle Res 13:1–13
Ainsworth M, Oden JT (2000) A posteriori error estimation in finite element analysis. Wiley, New York
Alaimo G, Auricchio F, Bianchini I, Lanzarone E (2018) Applying functional principal components to structural topology optimization. Int J Numer Methods Eng 115(2):189–208
Allaire G, Jouve F, Toader A (2004) Structural optimization using sensitivity analysis and level set-method. J Comput Phys 194:363–393
Allaire G, Geoffroy-Donders P, Pantz O (2019) Topology optimization of modulated and oriented periodic microstructures by the homogenization method. Comput Math Appl 78(7):2197–2229
Amstutz S, Andrä H (2006) A new algorithm for topology optimization using a level-set method. J Comput Phys 216(2):573–588
Andreassen E, Andreasen CS (2014) How to determine composite material properties using numerical homogenization. Comput Mater Sci 83:488–495
Arabnejad Khanoki S, Pasini D (2012) Multiscale design and multiobjective optimization of orthopedic hip implants with functionally graded cellular material. J Biomech Eng 134(3):031004
Armstrong DG, Lavery LA (1998) Diabetic foot ulcers: prevention, diagnosis and classification. Am Fam Phys 57(6):1325–1332
Auricchio F, Bonetti E, Carraturo M, Hömberg D, Reali A, Rocca E (2020) A phase-field-based graded-material topology optimization with stress constraint. Math Models Methods Appl Sci 30(8):1461–1483
Belhamadia Y, Fortin A, Bourgault Y (2014) On the performance of anisotropic mesh adaptation for scroll wave turbulence dynamics in reaction–diffusion systems. J Comput Appl Math 271:233–246
Bendsøe MP (1995) Optimization of structural topology, shape, and material. Springer, Berlin
Bendsøe MP, Kikuchi N (1988) Generating optimal topologies in structural design using a homogenization method. Comput Methods Appl Mech Eng 71(2):197–224
Bendsøe MP, Sigmund O (2003) Topology optimization: theory, methods and applications. Springer, Berlin
Borrvall T, Petersson J (2003) Topology optimization of fluids in Stokes flow. Int J Numer Methods Fluids 41(1):77–107
Bourdin B, Chambolle A (2003) Design-dependent loads in topology optimization. ESAIM Control Optim Calc Var 9:19–48
Bruggi M, Corigliano A (2019) Optimal 2D auxetic micro-structures with band gap. Meccanica 54(13):2001–2027
Bruggi M, Verani M (2011) A fully adaptive topology optimization algorithm with goal-oriented error control. Comput Struct 89(15–16):1481–1493
Chi H, Zhang Y, Tang TLE, Mirabella L, Dalloro L, Song L, Paulino GH (2021) Universal machine learning for topology optimization. Comput Methods Appl Mech Eng 375(112739):35
Coelho PG, Fernandes PR, Guedes JM, Rodrigues HC (2008) A hierarchical model for concurrent material and topology optimisation of three-dimensional structures. Struct Multidisc Optim 35(2):107–115
Collings R, Freeman J, Latour JM, Paton J (2021) Footwear and insole design features for offloading the diabetic at risk foot—a systematic review and meta-analyses. Endocrinol Diabetes Metab 4(1):e00132
Dapogny C, Faure A, Michailidis G, Allaire G, Couvelas A, Estevez R (2017) Geometric constraints for shape and topology optimization in architectural design. Comput Mech 59(6):933–965
di Cristofaro D, Galimberti C, Bianchi D, Ferrante R, Ferro N, Mannisi M, Perotto S (2021) Adaptive topology optimization for innovative 3D printed metamaterials. In: Proceedings of WCCM—ECCOMAS 2020 conference—modeling and analysis of real world and industry applications, vol 1200
Djourachkovitch T, Blal N, Hamila N, Gravouil A (2021) Multiscale topology optimization of 3d structures: a micro-architectured materials database assisted strategy. Comput Struct 255:106574
Dompierre J, Vallet MG, Bourgault Y, Fortin M (2002) Anisotropic mesh adaptation: towards user-independent, mesh-independent and solver-independent CFD. III. Unstructured meshes. Int J Numer Methods Fluids 39(8):675–702
Du Z, Zhou XY, Picelli R, Kim HA (2018) Connecting microstructures for multiscale topology optimization with connectivity index constraints. J Mech Des 140(11):111417
Ern A, Guermond JL (2004) Theory and practice of finite elements, applied mathematical sciences, vol 159. Springer, New York
Farrell PE, Micheletti S, Perotto S (2011) An anisotropic Zienkiewicz–Zhu-type error estimator for 3D applications. Int J Numer Methods Eng 85(6):671–692
Ferrer A, Oliver J, Cante JC, Lloberas-Valls O (2016) Vademecum-based approach to multi-scale topological material design. Adv Model Simul Eng Sci 3(1):23
Ferro N, Micheletti S, Perotto S (2018) Anisotropic mesh adaptation for crack propagation induced by a thermal shock in 2D. Comput Methods Appl Mech Eng 331:138–158
Ferro N, Micheletti S, Perotto S (2019) POD-assisted strategies for structural topology optimization. Comput Math Appl 77(10):2804–2820
Ferro N, Micheletti S, Perotto S (2020a) Compliance-stress constrained mass minimization for topology optimization on anisotropic meshes. SN Appl Sci 2:1196
Ferro N, Micheletti S, Perotto S (2020b) Density-based inverse homogenization with anisotropically adapted elements. In: Corsini A, Perotto S, Rozza G, van Brummelen H (eds) Numerical methods for flows, vol 132. Lecture notes in computational science and engineering. Springer, Cham, pp 211–221
Ferro N, Micheletti S, Perotto S (2020c) An optimization algorithm for automatic structural design. Comput Methods Appl Mech Eng 372:113335
Formaggia L, Perotto S (2001) New anisotropic a priori error estimates. Numer Math 89(4):641–667
Formaggia L, Micheletti S, Perotto S (2002) Anisotropic mesh adaption with application to CFD problems. In: Rammerstorfer F, Eberhardsteiner J, Mang H (eds) Proceedings of WCCM V, fifth world congress on computational mechanics, pp 1481–1493
Gao J, Luo Z, Li H, Gao L (2019) Topology optimization for multiscale design of porous composites with multi-domain microstructures. Comput Methods Appl Mech Eng 344:451–476
Healy A, Naemi R, Chockalingam N (2013) The effectiveness of footwear as an intervention to prevent or to reduce biomechanical risk factors associated with diabetic foot ulceration: a systematic review. J Diabetes Complicat 27(4):391–400
Hecht F (2012) New development in FreeFEM++. J Numer Math 20(3–4):251–265
Helnwein P (2001) Some remarks on the compressed matrix representation of symmetric second-order and fourth-order tensors. Comput Methods Appl Mech Eng 190(22–23):2753–2770
Huang X, Radman A, Xie Y (2011) Topological design of microstructures of cellular materials for maximum bulk or shear modulus. Comput Mater Sci 50(6):1861–1870
Iseli RK, Lee EK, Lewis E, Duncan G, Maier AB (2021) Foot disease and physical function in older adults: a systematic review and meta-analysis. Australas J Ageing 40(1):35–47
Ivarsson N, Wallin M, Tortorelli DA (2020) Topology optimization for designing periodic microstructures based on finite strain viscoplasticity. Struct Multidisc Optim 61(6):2501–2521
Jenkins N, Maute K (2016) An immersed boundary approach for shape and topology optimization of stationary fluid–structure interaction problems. Struct Multidisc Optim 54(5):1191–1208
Jeong SH, Choi DH, Yoon GH (2015) Fatigue and static failure considerations using a topology optimization method. Appl Math Model 39(3):1137–1162
Karia S, Parasuraman S, Khan MA, Elamvazuthi I, Debnath N, Ali SSA (2016) Plantar pressure distribution and gait stability: normal vs. high heel. In: 2016 2nd IEEE international symposium on robotics and manufacturing automation (ROMA). IEEE, pp 1–5
Kiziltas G, Kikuchi N, Volakis JL, Halloran J (2004) Topology optimization of dielectric substrates for filters and antennas using SIMP. Arch Comput Methods Eng 11(4):355–388
Kunisch K, Volkwein S (2002) Galerkin proper orthogonal decomposition methods for a general equation in fluid dynamics. SIAM J Numer Anal 40(2):492–515
Ledoux WR, Shofer JB, Smith DG, Sullivan K, Hayes SG, Assal M, Reiber GE (2005) Relationship between foot type, foot deformity, and ulcer occurrence in the high-risk diabetic foot. J Rehabil Res Dev 42(5):665
Liang Q (2005) Performance-based optimization of structures. Theory and applications. Spon Press, London
Lions JL (1971) Optimal control of systems governed by partial differential equations. Springer, New York
Liu L, Kamm P, García-Moreno F, Banhart J, Pasini D (2017) Elastic and failure response of imperfect three-dimensional metallic lattices: the role of geometric defects induced by selective laser melting. J Mech Phys Solids 107:160–184
López-López D, Becerro-de Bengoa-Vallejo R, Losa-Iglesias ME, Palomo-López P, Rodríguez-Sanz D, Brandariz-Pereira JM, Calvo-Lobo C (2018) Evaluation of foot health related quality of life in individuals with foot problems by gender: a cross-sectional comparative analysis study. BMJ Open 8(10):e023980
Mannisi M, Dell’Isola A, Andersen MS, Woodburn J (2019) Effect of lateral wedged insoles on the knee internal contact forces in medial knee osteoarthritis. Gait Posture 68:443–448
Menz HB, Auhl M, Spink MJ (2018) Foot problems as a risk factor for falls in community-dwelling older people: a systematic review and meta-analysis. Maturitas 118:7–14
Micheletti S, Perotto S (2006) Reliability and efficiency of an anisotropic Zienkiewicz–Zhu error estimator. Comput Methods Appl Mech Eng 195(9–12):799–835
Micheletti S, Perotto S (2010) Anisotropic adaptation via a Zienkiewicz–Zhu error estimator for 2D elliptic problems. In: Kreiss G, Lötstedt P, Målqvist A, Neytcheva M (eds) Numerical mathematics and advanced applications. Springer, Berlin, pp 645–653
Micheletti S, Perotto S, Farrell PE (2010) A recovery-based error estimator for anisotropic mesh adaptation in CFD. Bol Soc Esp Mat Apl SeMA 50:115–137
Micheletti S, Perotto S, Soli L (2019) Topology optimization driven by anisotropic mesh adaptation: towards a free-form design. Comput Struct 214:60–72
Michell AGM (1904) The limits of economy of material in frame-structures. Lond Edinb Dublin Philos Mag J Sci 8(47):589–597
Moussa A, Rahman S, Xu M, Tanzer M, Pasini D (2020) Topology optimization of 3D-printed structurally porous cage for acetabular reinforcement in total hip arthroplasty. J Mech Behav Biomed Mater 105:103705
Mu L, Jari R (2013) A recovery-based error estimate for nonconforming finite volume methods of interface problems. Appl Math Comput 220:63–74
Nakshatrala PB, Tortorelli DA, Nakshatrala KB (2013) Nonlinear structural design using multiscale topology optimization. Part I: static formulation. Comput Methods Appl Mech Eng 261/262:167–176
Noël L, Duysinx P (2017) Shape optimization of microstructural designs subject to local stress constraints within an XFEM-level set framework. Struct Multidisc Optim 55(6):2323–2338
Pizzolato A, Sharma A, Maute K, Sciacovelli A, Verda V (2017) Topology optimization for heat transfer enhancement in latent heat thermal energy storage. Int J Heat Mass Transf 113:875–888
Porta GM, Perotto S, Ballio F (2012) Anisotropic mesh adaptation driven by a recovery-based error estimator for shallow water flow modeling. Int J Numer Methods Fluids 70(3):269–299
Rodrigues H, Guedes J, Bendsoe M (2002) Hierarchical optimization of material and structure. Struct Multidisc Optim 24(1):1–10
Rozvany GIN (2009) A critical review of established methods of structural topology optimization. Struct Multidisc Optim 37:217–237
Rozvany GIN (2012) Structural design via optimality criteria: the Prager approach to structural optimization, mechanics of elastic and inelastic solids, vol 8. Springer, Dordrecht
Sanders ED, Pereira A, Paulino GH (2021) Optimal and continuous multilattice embedding. Sci Adv 7(16):eabf4838
Sibileau A, García-González A, Auricchio F, Morganti S, Díez P (2018) Explicit parametric solutions of lattice structures with proper generalized decomposition (PGD): applications to the design of 3D-printed architectured materials. Comput Mech 62(4):871–891
Sigmund O (1994) Materials with prescribed constitutive parameters: an inverse homogenization problem. Int J Solids Struct 31(17):2313–2329
Sigmund O, Maute K (2013) Topology optimization approaches, a comparative review. Struct Multidisc Optim 48(6):1031–1055
Sigmund O, Petersson J (1998) Numerical instabilities in topology optimization: a survey on procedures dealing with checkerboards, mesh-dependencies and local minima. Struct Optim 16(1):68–75
Sokolowski J, Zochowski A (1999) On the topological derivative in shape optimization. SIAM J Control Optim 37:1251–1272
Sun Y, Liu Y, Xu L, Lueth TC (2019) Design of a disposable compliant medical forceps using topology optimization techniques. In: 2019 IEEE international conference on robotics and biomimetics (ROBIO), pp 924–929
Svanberg K (1987) The method of moving asymptotes-a new method for structural optimization. Int J Numer Methods Eng 24(2):359–373
Van Netten JJ, Lazzarini PA, Armstrong DG, Bus SA, Fitridge R, Harding K, Kinnear E, Malone M, Menz HB, Perrin BM, Postema K, Prentice J, Schott KH, Wraight PR (2018) Diabetic Foot Australia guideline on footwear for people with diabetes. J Foot Ankle Res 11(1):1–14
Vigliotti A, Pasini D (2013) Mechanical properties of hierarchical lattices. Mech Mater 62:32–43
Villanueva CH, Maute K (2017) CutFEM topology optimization of 3D laminar incompressible flow problems. Comput Methods Appl Mech Eng 320:444–473
Wächter A (2002) An interior point algorithm for large-scale nonlinear optimization with applications in process engineering. PhD Thesis, Carnegie Mellon University
Wang F, Lazarov BS, Sigmund O (2011) On projection methods, convergence and robust formulations in topology optimization. Struct Multidisc Optim 43(6):767–784
Wang Y, Xu H, Pasini D (2017) Multiscale isogeometric topology optimization for lattice materials. Comput Methods Appl Mech Eng 316:568–585
Wang K, Lu C, Ye R, He W, Wei X, Li Y, Pan X, Zhao C, Yu X (2020) Research and development of 3D printing orthotic insoles and preliminary treatment of leg length discrepancy patients. Technol Health Care: Official J Europ Soc Eng Med 28(6):615–624
Watts S, Arrighi W, Kudo J, Tortorelli DA, White DA (2019) Simple, accurate surrogate models of the elastic response of three-dimensional open truss micro-architectures with applications to multiscale topology design. Struct Multidisc Optim 60(5):1887–1920
Xia L, Breitkopf P (2014) Concurrent topology optimization design of material and structure within FE2 nonlinear multiscale analysis framework. Comput Methods Appl Mech Eng 278:524–542
Xie Y, Steven G (1993) A simple evolutionary procedure for structural optimization. Comput Struct 49:885–896
Xu H, Farag A, Pasini D (2018) Routes to program thermal expansion in three-dimensional lattice metamaterials built from tetrahedral building blocks. J Mech Phys Solids 117:54–87
Yan N (2001) A posteriori error estimators of gradient recovery type for elliptic obstacle problems. Adv Comput Math 15(1–4):333–362
Yoon GH (2013) Acoustic topology optimization of fibrous material with Delany–Bazley empirical material formulation. J Sound Vib 332(5):1172–1187
Zhu JH, Zhang WH, Xia L (2016) Topology optimization in aircraft and aerospace structures design. Arch Comput Methods Eng 23(4):595–622
Zienkiewicz OC, Zhu JZ (1987) A simple error estimator and adaptive procedure for practical engineering analysis. Int J Numer Methods Eng 24:337–357
Acknowledgements
Nicola Ferro thanks Fondazione Fratelli Confalonieri and Istituto Nazionale di Alta Matematica (INdAM) for the awarded grants. The financial support of INdAM-GNCS Projects 2020 is gratefully acknowledged by Simona Perotto. Daniele Bianchi acknowledges the funding by the Italian Ministry of University and Research (MUR) within the PON “Ricerca e Innovazione” 2014–2020 (azione IV.6) - FSE-REACT EU.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Replication of results
All the results in the numerical assessment can be replicated in a straightforward way, starting from the algorithms and the data provided in the paper.
Additional information
Responsible Editor: Julián Andrés Norato
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ferro, N., Perotto, S., Bianchi, D. et al. Design of cellular materials for multiscale topology optimization: application to patient-specific orthopedic devices. Struct Multidisc Optim 65, 79 (2022). https://doi.org/10.1007/s00158-021-03163-z
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00158-021-03163-z