Optimal crashworthiness design of vehicle S-frame using macro-element method and evolutionary algorithm

Abstract

The paper presents the crashworthiness optimization of a thin-walled frame applied as energy-absorbing element in a car structure. Crushing parameters of S-frame are modeled using the macro-element methodology. This method is implemented in the Visual Crash Studio software that enables very fast simulation of structural behavior during the impact. The objective is to determine the optimal dimensions of the frame cross-section to achieve the maximal energy absorption. Moreover, the selection of the best angle between the frame segments is investigated. In the formulation of the optimization problem, constraints related to the progressive collapse of deformation zones, required by the macro-element modeling, have been introduced. An Evolutionary Algorithm was applied to search the best solution. A real-life example of thin-walled S-frame is investigated in numerical examples. An attempt to find the solution by solving a sequence of simpler problems with reduced number of design variables is investigated. This approach is compared to the best result obtained for the problem including all design variables at the same time. This study illustrates the potential of the optimization in early-design stages of the vehicle development process and prepares perspectives for the optimization of complex energy-absorbing systems.

1 Introduction

An extremely important aspect of the design of modern vehicles is to ensure the safety of the driver and passengers in the event of a collision. The structural elements designed to absorb crash energy in automotive engineering are mainly thin-walled beams. At the present time, CAD/CAM tools are inherently related to modeling and simulations of engineering objects. The widespread finite element method (FEM) enables the assessment of crashworthy parameters of a structure but is connected to a complicated and time-consuming process. Optimization of energy-absorbing properties of structural components modeled in this way require very high computing power. The simplified approach to strength calculation and evaluation of the crushing behavior of a vehicle’s body is proposed by the macro-element method (MEM). It may be very useful in early-design stages, when the simulation model is not highly detailed, and the structure undergoes frequent modifications. The macro-element methodology is based on a simplified modeling of the thin-walled prismatic beams to investigate the energy absorption. MEM represents a unique, kinematic approach to large deformations of the structure elements. In this methodology, the structure is discretized into beams with specific cross sections—and not into small finite elements, as in case of the FEM analysis. A smaller number of elements enables simplified calculations. This facilitates the application of modifications in a modeled structure and reduces the processing time. The main advantage of the MEM is a very fast calculation of crushing parameters. It usually takes up to several minutes on a standard PC. Consequently, the MEM approach gives the possibility of combining it with optimization procedures. This idea is developed in the present paper and applied to examples related to the vehicle development process.

The creation of the MEM is ascribed to Abramowicz et al., and the mathematical description of this methodology may be found in (Jones and Abramowicz 1984; Wierzbicki et al. 1989; Abramowicz 2003). The development of the algorithm based on macro-element method in the form of a complex software was the work of Abramowicz (Impact Design Europe 2017).

Nowadays, there is a great interest in research into improving safety issues and especially in crashworthiness optimization. Fang et al. (2017) includes a list of several hundred papers related to the optimization of crashworthy structures. It provides a comprehensive overview of the works and research classified according to the object of the study, design criteria, methods and algorithms, modeling strategies, etc. But optimization algorithms in combination with the MEM were not included in that review. This work, together with previous authors’ papers (Pyrz and Krzywobłocki 2017, 2019) completes this area. Since 2017, there has been a further increase in research dealing with the issues of optimization of crashworthy structures, for example, (Bahramian and Khalkhali 2020) related to topology optimization of square tube or (Anselma 2020) referred to the multidisciplinary optimization of the crashworthiness of hybrid electric vehicles, which are gaining in popularity in recent years. Furthermore, there is a growing interest in energy-absorbing structures made of CFRP (Li et al. 2020; Liu et al. 2020; Liu et al. 2020).

In order to determine the crashworthiness of the vehicle structure, different test scenarios may be carried out. In this paper, attention will be paid to a frontal impact case. The subject of consideration will be the subassembly that plays an essential role in the load paths transferred in this type of collision, which is the front rail. Thin-walled S-shaped structures have been widely used for this purpose to absorb energy during frontal crashes of vehicles. There is a noticeable interest in the issue of S-frame optimization. In most cases, the energy absorption is maximized, often while minimizing the peak force or weight of the structure. For this purpose, various optimization methods and procedures are used. Zhang et al. (2007) applied RSM (Response Surface Method) techniques in conjunction with DOE (Design of Experiment) in their research. The S-frame of minimal mass was searched, and peak force, structural deformation and energy absorption were the limiting constraints. Khakhali et al. (2010) carried out a multi-objective optimization of a square-shaped S-frame using the Pareto method. The criterion was simultaneous specific energy absorption maximization and peak force minimization. The multi-objective optimization of S-frame, focused on SEA (Specific Energy Absorption) maximization and peak force minimization was also undertaken by Nguyen et al. (2014) and by the Cai and Wang (2017). However, Nguyen et al. used the RSM to improve computational performance, while Cai and Wang compared three methods i.e., NSGA-II (modified non-dominated sorting genetic algorithm), MOPSO (multi-objective particle swarm optimization), and ASA (adaptive simulated annealing). Liu et al. (2014) compared the effect of the cross-section type on the absorption properties of the S-frame. In their research, they analyzed 12 different cross-sections from 3 different groups, i.e., regular and nonconvex polygon and multi-cell section. Their work also includes shape optimizations of rectangular cross-section to improve specific energy absorption of the structure using sequential response surface method (SRSM). Shape optimization of multi-cell front rail was carried out by Kohar et al. (2017). The objective was to maximize the specific energy absorption while minimizing weight. In the solution method, RSM supported with the artificial neural network and genetic algorithm were used. A recent work by Hosseini et al. (2019) describes the process of geometric optimization. The S-Frame of a universal structure was optimized for the entire vehicles’ product family. Authors sought for S-rail structure that could be used as a common underbody element in all variants of the car platform. The NSGA-II was used to solve the problem of multi-objective optimization. The mapping of geometric design variables to objective functions was achieved using a GMDH (group method of data handling) neural network type. The same method was used in the work of Khakhali et al. (2010).

Most of the S-frame optimization studies mentioned above were aided by numerical calculations carried out using the finite element method. The main disadvantage of this method is related to time-consuming calculations, especially in such complex case. Another approach to the problem may be the use of the MEM. So far, a few attempts have been made to optimize structures using this method. Pyrz and Krzywobłocki (2017) investigated the macro-element method in conjunction with evolutionary algorithms in the shape optimization problem of a prismatic beam as energy absorber. They extended their study to the optimization of the front rail dimensions (2019). Georgiou and Zeguer (2018) carried out crash analysis of the whole vehicle and individual sub-assemblies separately using this method.

The authors' recent studies (Pyrz and Krzywobłocki, 2017, 2019) have shown the efficiency of the cooperation of the macro-element method with evolutionary algorithms in dynamic problems. In addition, the advantage of this approach is the incomparably shorter time of calculating crash phenomena using MEM compared to FEM. In the presented approach, the attention is focused on a real-life structure and the search for the solution that maximizes the amount of the specific energy absorption while maintaining the assumed design constraints. The MEM-based environment of Visual Crash Studio (VCS) software was used for modeling the structure. The VCS has been coupled to the Evolutionary Algorithm, developed in C# language. The current work concerns a real-life S-frame with thin-walled cross-section with more complex geometry in comparison to the one analyzed in the previous work. In the numerical examples, three groups of variables describing the geometry of the structure are investigated for the purpose of comparative analysis. Design variables include cross-section wall thicknesses, side lengths, and the angle between front segments of the rail. Also, more complex shape requires additional constraints and restrictions to be included in the problem formulation. Thus, it was necessary to extend the optimization criteria in this case and to include limitations on the angle and bending moments.

This paper investigates an optimization strategy which consists in dividing a complex problem into simpler, independently solved subproblems with reduced number of design variables. The results of the approach are confronted with the solution obtained for all design variables taken into account at the same time. The original contribution of this paper resides in coupling the EA with the VCS software and studying the optimal cross-sectional sizing of a real-life S-frame to achieve the best energy absorption characteristics. Besides, the impact of the spatial configuration defined by the angle between s-frame’s sections has been investigated.

2 Formulation of the optimization problem

The front rail of a passenger car (Fig. 1) is the most important component to absorb energy during frontal collision and to protect the occupants of a vehicle. To increase the car safety, the absorbed energy has to be the highest possible, maintaining however, the appropriate way of deformation during the crash.

Fig. 1

Position of the front rail in a passengers’ vehicle

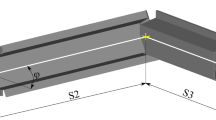
The problem under consideration concerns the optimization of dimensions of the space frame in order to achieve the maximal specific energy absorption (SEA). This criterion that represents the amount of absorbed energy per mass of the structure, is widely used in the automotive design. The VCS uses several objects to model a structure and crushing phenomena. The base objects are the nodes on which other objects are built. The super-beam is the element that includes mechanical properties of a discrete structure. In Fig. 2, the model of the front rail, composed of three super-beam segments of length S₁, S₂, and S₃ is presented. Section 1 and Sect. 3 are perpendicular to the axis of the applied load and are interconnected with Sect. 2 that forms an angle θ to Sect. 1 and Sect. 2. The cross-section is built of two hat-shaped components and the reinforcement between them (Fig. 3). The height of the cross-section is controlled by parameter L₁ and the width of the cross-section by parameter L₃ equal to L₄, together with L₅ and L₆. Moreover, the offset of the reinforcement is defined by L₂. The hat-shaped components have equal thicknesses T₁ and T₂. The thickness of the reinforcement T₃ is treated as separate variable.

Fig. 2

S-shaped thin-walled frame

Fig. 3

Dimensions of the cross-section

The design variables are the parameters that define cross-sectional dimensions (Fig. 3) and, additionally, the angle θ between segments of the frame (Fig. 2). Thus, the vector x of design variables takes in general case the form x = [L₁ L₂ L₃ L₄ L₅ L₆ T₁ T₂ T₃ θ]. In fact, the wall lengths L₁, L₂, and L₃ (equal to L₄) are independent but L₅ is associated with L₃ and, similarly, L₆ with L₃. This dependence is set to maintain the proportionality within the cross-section and to keep proper wall position. The T₁ and T₂ represent thicknesses of individual external components. T₃ is related to the internal reinforcement’s thickness. The angle θ defines spatial configuration of the front frame. This assembly is often applied in modern cars and dimensions taken in numerical examples are close to real-life components.

The main criterion concerns the highest specific energy absorption that depends generally on vehicle structure, elements’ sections and properties of material. However, several factors influence the selection of the best solution. The crashworthy structure must collapse in a predictable manner to ensure survival conditions for the vehicle occupants. This condition imposes limits on the maximum deformation force. Thus, the maximum deformation force registered P_max must not exceed the maximum reference value, denoted by P_max−ref. Another important limitation is applied to mean crushing force P_mean that has to stay below the reference value P_mean−ref. The relation between the wall lengths L and their thicknesses T can affect the crashworthy design by introducing premature global bending. Therefore, to avoid undesirable effect, the L/T ratio is limited by the lower bound (L/T)_min and the upper bound (L/T)_max, where the L/T ratio represents an average value of all cross-sectional “plate sections” as recommended by Jones (2010) or Mahmood and Paluszny (1981). The L/T ratio is the condition associated with development of a regular plastic fold. As the structural components are exposed to the load different from pure axial load, the condition in the problem formulation is not critical. Thus, the penalty coefficients, applied later in this paper, accept the L/T limit values to be exceeded a little. Finally, the solution is searched for the range of design variables limited by x_min and x_max of which components correspond to minimal and maximal values, respectively, of each design variable. The objective function is the specific energy absorption (SEA) that defines the amount of absorbed energy divided by structural mass.

The optimization problem can be presented mathematically as follows:

$${\text{maximize}}{\mkern 1mu} SEA({\mathbf{x}})$$

(1)

and satisfy the constraints

$$P_{\max } ({\mathbf{x}}) \le P_{\max - ref} ,$$

(2)

$$P_{mean} ({\mathbf{x}}) \le P_{mean - ref} ,$$

(3)

$$({L \mathord{\left/ {\vphantom {L {T)}}} \right. \kern-\nulldelimiterspace} {T)}}_{\min } \le {L \mathord{\left/ {\vphantom {L T}} \right. \kern-\nulldelimiterspace} T} \le {{(L} \mathord{\left/ {\vphantom {{(L} T}} \right. \kern-\nulldelimiterspace} T})_{\max } ,$$

(4)

$${\mathbf{x}}_{\min } \le {\mathbf{x}} \le {\mathbf{x}}_{max} .$$

(5)

The general formulation of (1–5) is not complete in the case of the macro-element methodology (Pyrz and Krzywobłocki 2019). Additional restrictions related to deformation mechanics have to be introduced into the definition of the optimization problem. The idea of super folding element has to assume a certain folding mechanism and the way of initiating folding modes. Also, the limitations must be imposed on the magnitude of the bending moments of the cross-section as the structure’s main stress component results from bending. This way the modeled space frame will be subjected to controlled deformation activating individual zones of controlled deformation. The additional conditions, on the one hand, have to limit the maximum deformation force and, on the other hand, must ensure a sufficiently high bending strength so that the collapse sequence of the real assembly progresses in proper manner.

The first of additional constraints may be formulated as follows:

$$\left| {M_{x} ({\mathbf{x}})} \right| \le M_{x - \max - ref} ,$$

(6)

$$\left| {M_{y} ({\mathbf{x}})} \right| \le M_{y - \max - ref} ,$$

(7)

where M_x and M_y refer to moments in two bending planes defined by the local coordinate system X_loc, Y_loc of the cross-section of the stringer and M_{x−max−ref} and M_{y−max−ref} are corresponding maximal values.

Furthermore, one more condition is introduced to impose the desired deformation mode:

$${\text{minimize}}\,dM = \left( {M_{x - \max - ref} - \left| {M_{x} ({\mathbf{x}})} \right|} \right)^{2} + \left( {M_{y - \max - ref} - \left| {M_{y} ({\mathbf{x}})} \right|} \right)^{2} .$$

(8)

The quantity dM defines the “distance” from the desired value of the bending moment. In the ideal case, it should vanish. The energy-absorption analysis of the space frame showed (Pyrz and Krzywobłocki 2019) that the most effective failure should occur with the highest possible value of the bending moment. Therefore, the condition (8) allows to maximize the energy absorbed in large deformations of the considered thin-walled structure. It should be underlined that three last conditions are directly connected to the macro-element methodology and specify the most advantageous crushing scenario. If they are omitted, the search for the best result would be made difficult because of inadequate folding mode and convergence problems.

3 Macro-element method in crashworthiness simulation

The macro-element method (MEM) was developed by (Wierzbicki and Abramowicz 1983; Abramowicz and Jones 1986) as an alternative to FE crashworthiness analyses for thin-walled structures. This semi-analytical approach uses the concept of super folding elements (SFE) and assumes a typical folding pattern of prismatic beams and columns under crush loading. The specific kinematics, described using trial deformation functions (Abramowicz 2004), is proposed to characterize the behavior of “deformable cells” and to analyze shape distortions of crashed prismatic beams or columns.

The SFE is applied to model energy-absorption mechanisms (in the form of the corner line of a prismatic beam). It corresponds to a single plastic wave of the crushed column as the example shown in Fig. 4.

Fig. 4

Crushed column and Super Folding Element

The mathematical apparatus of the macro-element method was implemented in the form of a computing processor inside the Visual Crash Studio (VCS) program. VCS is a software developed by the Impact Design Europe company (Impact Design Europe 2017) that enables the assessment of crashing parameters. Since the calculations are based on MEM procedures, they can be performed with much less processing effort compared to FEM solvers. The crashworthy parameters of the structural model are obtained in the VCS program in two steps. The first stage of the algorithm involves the discretization of each cross-section that belongs to the structure, on the Super Folding Elements. Thanks to this approach, SFE’s calculation data enable to determine initial absorption properties for each cross-section. In the second stage, the algorithm performs a Super Beam Element (SBE) computation, based on the cross-section results obtained in the previous step. Super Beam Elements are prismatic beams arranged in 3D space that form a model.

VCS software enables a rough discretization of the vehicle structure into prismatic beams with characteristic cross-sections (and not into a mesh composed of a large number of small elements, as is the case with the FEM). Therefore, calculations on a model built with a smaller number of elements are much faster than FEA. A short MEM calculation time results additionally from the fact that its formulation is not incremental like FEM but rather global. Model's pre-processing is also relatively shorter in MEM, especially when it is necessary to introduce changes on both 2D and 3D levels. MEM calculation of a simple structure usually takes no more than several seconds. The comparison of calculation times and the results obtained in various research scenarios was conducted by Takada and Abramowicz (2003) and Georgiou and Zeguer (2018). This works confirmed a large time gain in the calculation of the crash models by VCS processor.

Since deformation functions of macro-element method are stipulated from experimental observations, the validation was carried out on a number of cases by Abramowicz in 80 s and 90 s. More up-to-date examples include the works listed in this chapter. The recent work on this topic was carried out by Pyrz and Krzywobłocki (2019) where the verification of the S-frame calculation model was performed. The results obtained with the use of VCS were compared to the FEA of an analogous structure developed by Kim and Wierzbicki (2004). The results of both methods were very similar in comparison.

The MEM enables quick prediction of parameters that characterize energy-absorbing structures, for example, the mean crushing force, maximal force, bending torsional moments. The method is perfectly suited to early-design stages when the structure is subjected to frequent modifications.

4 Optimization procedure using evolutionary algorithm and VCS software

4.1 Evolutionary algorithm and fitness function

Evolutionary algorithm (EA) has been applied to seek the best solution. The EA procedures have been developed in C# language. The object-oriented programming facilitated data management and the development of optimization processing loops, adapted to VCS.

Evolutionary algorithm is a heuristic search method that in theory does not guarantee the global optimum, but it is able to propose very good solutions (e.g., previous works of authors Pyrz and Krzywoblocki 2017, 2019). In the problem under consideration, the potential solutions have been represented as a sequence of real-coded design variables x structures (chromosomes). The environmental adaptation and the quality of solution of an individual have been evaluated on the basis of the fitness function (defined later in this paragraph). A classical form of the algorithm has been coded. The procedure starts by building randomly the initial population. Next, individuals of the population are evaluated, which are related to computation of fitness enabling to determine better or worse solutions. Subsequently, the simulated evolution loop starts and the iterative search for the best solution begins. The individuals of the basic population are processed using specific evolutionary operators. First, chromosomes for mating are selected. The tournament selection (variant with replacement) has been used to do this. Next the crossover operator is used to create the temporary offspring population. The arithmetic crossover (Michalewicz 1996) has been applied with the probability c_p. After that, the mutation operator is applied with the probability m_p to introduce diversity into the offspring population. At the end of the iteration loop, the succession takes place and the new population is created. The succession combines the best solutions from the newly processed offspring population with the best solutions from the parent population, keeping a defined percentage contribution of each part. This enables to maintain diversity of solutions across evolved generations. The loops of simulated evolution are repeated many times to produce the best solution. A fixed number of iterations, based on the test results, have been applied in developed version of the EA.

As the evolutionary algorithms solve unconstrained optimization problems, the appropriate fitness function F has to be defined. The penalty functions have been applied to include the constraints (2–4) and (6–8), and the general definition of the fitness function takes the form:

$$\begin{gathered} F({\mathbf{x}}) = \frac{{{\text{SEA}}({\mathbf{x}})}}{{{\text{SEA}}_{ref} }} - P_{1} (P_{max} ({\mathbf{x}}),r_{1} ) - P_{2} (P_{mean} ({\mathbf{x}}),r_{2} ) + \hfill \\ - P_{3} (L/T,r_{3} ) - P_{4} (M_{x} ({\mathbf{x}}),M_{y} ({\mathbf{x}}),r_{4} ) - P_{5} (dM({\mathbf{x}}),r_{5} ). \hfill \\ \end{gathered}$$

(9)

The first term of the fitness function (9) is the objective function (1) and represents the normalized value of the specific energy absorption. The actual value of SEA(x) is divided by the reference value SEA_ref determined in the input data of the optimization procedure. Other components are penalty functions corresponding to constraints (2–4) and (6–8), respectively. The constraint (5) related to minimal and maximal values of design variables is taken into account directly in the EA procedure.

Thus, the penalty function P₁ depends on actual value of the maximal deformation force P_max and refers to the condition (2). It is expressed as follows:

$$P_{1} (P_{max} ({\mathbf{x}}),r_{1} ) = r_{1} \max \left( {0,\;\frac{{P_{\max } ({\mathbf{x}}) - P_{\max - ref} }}{{P_{\max - ref} }}} \right),$$

(10)

where r₁ is the penalty coefficient. The penalty function P₁ decreases the value of the fitness function F when the actual maximal force obtained from calculation exceeds the assumed critical reference force P_max−ref.

The component P₂ corresponds to condition (3), related to the mean crushing force. The fitness F is diminished when the calculated mean crushing force P_mean exceeds the reference value of the mean crushing force P_mean−ref. It is defined by equation

$$P_{2} (P_{mean} ({\mathbf{x}}),r_{2} ) = r_{2} \max \left( {0,\;\frac{{P_{mean} ({\mathbf{x}}) - P_{mean - ref} }}{{P_{mean - ref} }}} \right),$$

(11)

where the r₂ is the penalty coefficient.

The subsequent component P₃ refers to the limitation condition (4). It is responsible for the decrease of the fitness function value when the ratio L/T goes beyond the allowable range located between (L/T)_min and (L/T)_max. It takes the form.

$$P_{3} (L/T,r_{3} ) = r_{3} \left| {\max \left( {0,\;\frac{{{L \mathord{\left/ {\vphantom {L T}} \right. \kern-\nulldelimiterspace} T} - (L/T)_{\max } }}{{(L/T)_{\max } }}} \right) + \min \left( {0,\,\frac{{{L \mathord{\left/ {\vphantom {L T}} \right. \kern-\nulldelimiterspace} T} - (L/T)_{\min } }}{{(L/T)_{\min } }}} \right)} \right|,$$

(12)

where r₃ is the penalty coefficient.

The penalty function P₄ refers to constraints defined by (6) and (7). It has been defined as follows:

$$P_{4} (M_{x} ({\mathbf{x}}),M_{y} ({\mathbf{x}}),r_{4} ) = r_{4} \left( {\max \left( {0,\;\frac{{\left| {M_{x} ({\mathbf{x}}) - M_{x - \max - ref} } \right|}}{{M_{x - \max - ref} }}} \right) + \max \left( {0,\;\frac{{\left| {M_{y} ({\mathbf{x}}) - M_{y - \max - ref} } \right|}}{{M_{y - \max - ref} }}} \right)} \right),$$

(13)

where r₄ is the penalty coefficient. The value of P₄ grows when the actual bending moments are higher than moments reference values M_{x−max−ref} and M_{y−max−ref} and in such case decreases F function.

Final component of the fitness function, which refers to condition (8), expresses the concept of appropriate folding mode (Pyrz and Krzywobłocki 2019). The maximal bending moments have to stay as close as possible to given reference values. Thus, the last penalty function P₅ is the normalized square difference of bending moments:

$$P_{5} (dM({\mathbf{x}}),r_{5} ) = r_{5} \left( {\min \left( {\frac{{(M_{x - \max - ref} - \left| {M_{x} ({\mathbf{x}})} \right|)^{2} + (M_{y - \max - ref} - \left| {M_{y} ({\mathbf{x}})} \right|)^{2} }}{{\left( {M_{x - \max - ref} } \right)^{2} + \left( {M_{y - \max - ref} } \right)^{2} }}} \right)} \right),$$

(14)

where r₅ is the penalty coefficient.

4.2 Coupling EA to VCS software

The EA optimization procedures are connected to Visual Crash Studio environment, where crash mechanical response of potential solutions is determined. Thus, the evaluation of the fitness of an individual in the loop of EA was connected to a single run of the VCS program. A population of potential solutions contains many individuals that have to be evaluated several times, as determined by number of iterations of simulated evolution.

The communication between the optimization algorithm and the crush analysis is ensured through the interface developed in C# programming language. The object-oriented programming paradigm simplified the processing and enabled to carry out automatically hundreds of VCS models. In many procedures, the whole population was calculated at a time (and not individuals one by one). The specific data fields of the VCS software were considered as separate objects which facilitated data management and development of optimization tool. Before running VCS, input data including geometry and material information, design variables values, and other parameters had to be prepared. At the right time, the EA procedure actualized values of design variables and ran a calculation of crashworthy parameters in VCS Batch Mode. The results were gathered from VCS output files via developed interface and processed for each model individually to determine the fitness. These actions were repeated for the whole population many times in a loop of simulated evolution according to steps of the EA.

5 Numerical examples

5.1 S-frame model

The S-shaped frame (Fig. 2) is composed of several objects that define the macro-element model in the VCS environment. They include material of the structure, geometry of cross-section, positions of four nodes, and 3 Super Beam Elements. The lengths of frame segments are equal to S₁ = 400 mm, S₂ = 506.77 mm, and S₃ = 400 mm. The acute angle θ between sections is equal to 30°. The cross-section spot welds are defined as rigid object. It allows to maintain the folding mode and secure the components from internal collision. Also, the correct folding mechanism is possible if appropriate proportions of the analyzed cross-section are ensured. This is the role of the T/L requirement and additional constraints related to bending moments.

The front rail structure is subjected to quasi-static axial load according to a simple kinematic scenario. The velocity assigned to the structure’s end grows linearly in the initial simulation time of 25 ms from zero to 2.5 m/s. Subsequently, it remains constant until the end time of simulation is equal to 150 ms. Such scenario enables reducing the numerical noise and improves stability of explicit integration routine. The dynamic and inertia effects are not taken into account.

The structure is made of steel DP 350/600, and material constants are presented in Table 1. The material definition is specific for the Visual Crash Studio software. Although the material definition (isotropic in the presented case) uses the uniaxial tension test curve (true strain measure), the macro-element method calculation is based on the definition of the energy equivalent stress measure (Ambrosio 2001).

Table 1 Material parameters of space S-frame

The formulation of the optimization problem and estimation of the fitness also require definition of reference crushing parameters. Table 2 presents information about reference level of the specific energy absorption, mean crushing force, maximal force, bending moments, as well as L-to-T ratio. The reference level of the specific energy absorption corresponds to the rounded-up calculation result of the model with maximum allowable cross-sectional dimensions. The maximal crushing force, the mean crushing force, and maximal bending moments depend on vehicle specification (i.e., design space and assumed vehicle mass). The L/T ratio condition results from the assumption that the cross-section may be considered as thin walled for defined range. The limitations of cross-sectional dimensions are given in the next paragraph.

Table 2 Reference parameters for space frame design

The general crushing response of the S-Frame is represented by the force–deformation curve which is similar for all automatically generated VCS models. The force corresponding to first millimeters of deformation grows rapidly to a maximal level, after reaching that point, it drops with the progress of deformation. There is no clinch or bottoming observed. The force character is similar to the S-Frame response presented in (Pyrz and Krzywoblocki, 2019).

5.2 Optimization studies

The numerical examples are presented to illustrate the EA optimization of the front rail frame. The examples cover not only the solution of the optimization problem taking into account all design variables but also the attempts to find the best result by solving a sequence of simpler problems with reduced number of design variables. The concept of searching the solution gradually for easier problems has been inspired by intuitive approach of a designer that tries to simplify the complexity of the formulation.

The optimization procedure takes into account limitations imposed directly on the range of design variable values (5). The thicknesses T_i of the cross-section side walls will be searched within the limits from 1 to 3 mm, wall length L₁ from 65 to 160 mm, wall length L₂ from 30 to 145 mm, wall length L₃ from 40 to 80 mm, and the angle θ from 20° to 40°.

In total, four optimization cases are considered. The first three seek the best solution by solving a sequence of simpler problems. Profile thicknesses, cross-sectional dimensions, and the angle between frame segments will be searched separately. These procedures are composed of three steps. The first selects constant parameters and design variables (lengths L or thicknesses T) for the first optimization and searches the best solution. The second step takes the best values obtained in the previous step and runs the optimization for "remaining" design variables (lengths L or thicknesses T). The third step analyzes the influence of the spatial variable θ on the final result and proposes possible improvement of the solution.

Case 1 analyzes the following strategy. In the first step, only wall lengths L_i are optimization variables. Thus, the vector of unknowns in the optimization process is limited to L₁, L₂, L₃, L₄, L₅, L₆ or more precisely x = [L₁ L₂ L₃] since L₄ is equal L₃, L₅ is equal to 0.3334 L₃, and L₆ is equal to 0.39466 L₃. Wall thicknesses T_i are constants, equal to the value 2.0 mm (i.e., the average of the allowable limits), variable θ that defines the space configuration between segments S₁−S₂ and S₂−S₃ is set to the initial angle (30°). The optimization problem (9) is solved and the best wall lengths are determined. In the next step, wall lengths found before are constant and the optimization concerns the unknown thicknesses T₁, T₂, and T₃ of the cross-section side walls. The fact that T₁ is equal to T₂, enables to simplify the vector of unknowns to x = [T₁ T₃]. The optimization problem is solved again. Eventually, for the profile’s wall lengths and thicknesses of the best solution determined in previous steps, additional runs of algorithm are performed by searching for the best value of angle θ. This step is carried out by analyzing the model iteratively for the angle θ growing from 20° to 40° with increment 1°.

Case 2 is analogous but starts from constant wall lengths (maximal allowable values were taken for all walls) and the angle θ is equal to 30°. Unknowns of the first optimization are thicknesses T₁, T₂, and T₃ of the cross-section side walls. In the next step, lengths L₁, L₂, L₃ and L₄, L₅, L₆ that are associated with them are optimized. Finally, the value of angle θ that improves the solution obtained at step 2 is searched.

Case 3 is a slight modification of the previous one. The only difference is side walls lengths that at the start point were taken as average values of limit range. The first optimization starts from constant lengths L₁, L₂, L₃ equal respectively to 112.5 mm, 87.5 mm, and 60 mm. The step 2 and step 3 are performed in a similar way to Case 2.

The last Case 4 looks for a solution of the problem where all variables are treated as unknowns from the very beginning. Thus, the design variable vector includes components L₁, L₂, L₃, L₄, L₅, L₆, T₁, T₂, T₃, θ. Since T₁ is equal T₂, L₃ is equal L₄, L₄ is equal 0.3334 L₃, and L₅ is equal 0.39466 L₃, and the final vector of design variables takes the form x = [ L₁ L₂ L₃ T₁ T₃ θ].

5.3 Results

The optimization problem (9) of the S-shaped frame is solved using developed Evolutionary Algorithm. The fitness definition (9) contains the optimization criteria and constraints that are included in the form of penalty terms (10–14). After test runs and the study of magnitudes of penalty functions, the penalty coefficients have been scaled. The ratio SEA/SEA_ref has been taken as reference value r_ref, where SEA is the energy of the solution currently under consideration. In this study, the SEA_ref corresponds to the frame model with the highest possible cross-sectional lengths and thicknesses. To keep the right proportions of components in the fitness definition (9), the penalty coefficient r₁ was set to 0.4 r_ref, r₂ was equal to 0.1 r_ref, r₃ to 0.15 r_ref, r₄ to 0.1 r_ref, and finally r₅ was set to 0.3 r_ref. The obtained solutions were analyzed and evaluated by exploring results of ten independent runs of the algorithm to check the convergence and the dispersion of results. The tournament selection operation has been programmed for four randomly drawn individuals. The arithmetic crossover probability was set to c_p = 0.7 while the mutation was applied with the probability 0.005. In the succession operation, new population was composed of 60% newly created and 40% individuals from previous generation. The algorithm was set to process 40 individuals in 20 generations for all assumed calculation runs. The solutions generated for Case 1, 2, 3, and 4 will be compared and became the basis for the discussion on the effectiveness of the approach.

Before starting optimization procedures, the shaped frames corresponding to different combinations of limit values of thicknesses and profile lengths (and θ set to 30°) have been checked. The obtained SEA varied from 0.5898 to 1.4478 kJ/kg, but no solution (with one exception) fulfilled the constraints of the optimization problem. The only variant that satisfied all limitations was the frame with wall thicknesses of 1 mm and minimal allowable lengths of the profile (30, 40, and 65 mm). It was characterized by a relatively small SEA equal to 0.5898 kJ/kg, the P_mean force of 9 kN, P_max equal to 27 kN, L/T ratio of 33.724 (close to the middle of allowable range), and moments M_x and M_y distant from target values. This design can be improved.

5.3.1 Case 1: length–thickness–angle

In the first step of the Case 1, the best dimensions of wall lengths are searched. Next step intends to enhance the solution by determining the best thickness configuration of the cross-section and finally the angle θ between segments is investigated. The initial wall thicknesses were set to 2 mm for all cross-section walls, and angle θ was equal to 30°. Ten independent runs of the optimization algorithm returned the average SEA equal to 0.900 kJ/kg. The best solution corresponds to the frame of mass 9.744 kg, able to absorb the energy of 9.033 kJ which results in the specific energy absorption of 0.927 kJ/kg. The side lengths of the best solution are L₁ = 67.772 mm, L₂ = 49.364 mm, and L₃ = L₄ = 42.397 mm. Dimensions of L₅ and L₆ are equal to 16.733 mm and 14.133 mm, respectively, for dependent wall lengths. The returned crushing parameters fulfill the constraints of the problem (the maximal crushing force is equal to 64.617 kN, the mean crushing force is equal to 29.970 kN). However, the geometrical condition (4) on L/T ratio is below the defined range (equal to 18.173). The maximal bending moments M_x and M_y, in negative and positive directions, are relatively distant from the reference values. The results of ten algorithm runs for step 1 are presented in Fig. 5 in form of hollow circle markers (Table 3, 4).

Fig. 5

SEA results obtained in ten independent runs of the evolutionary algorithm

Table 3 Dimensions of the best S-frames

Table 4 Crashworthiness properties of the best solutions

In the second step, for the obtained values of L₁ to L₆ (and the initial θ), the optimization of cross-sectional thickness is carried out. New results brought improvements to crushing parameters. The average SEA of 10 algorithm runs is now equal to 0.976 kJ/kg. However, the best solution returned the maximal crushing force equal to 69.019 kN, the mean crushing force equal to 31.958 kN, and the energy absorbed 9.567 kJ, which together with the mass equal to 9.442 kg gives 1.013 kJ/kg of specific energy absorption. The results are presented in Fig. 5 in form of solid circle markers. The L/T ratio raised to 19.951 and the maximal bending moments are closer to reference values than in the previous step. Bending moments M_x and M_y (negative and positive direction) are also closer to the reference value than in step 1 (Table 5). In the third step, the best angle θ is searched for the best solution already found in two previous steps. The angle modification returns the highest value of SEA for angle θ configuration equal to 29°. The curve presenting the analysis of angle influence within defined range (from 20° to 40°) is depicted in Fig. 6. Peak value of SEA registered for Case 1 is equal to 1.027 kJ/kg.

Table 5 Maximal bending moments of the best solutions

Fig. 6

Impact of angle θ variation on SEA (for the best results obtained in Cases 1 to 4)

5.3.2 Case 2: thickness–length–angle (version 1)

Case 2 starts from the maximal allowable wall lengths and looks for the best wall thicknesses. Subsequently, basing on the obtained result, the optimization of wall lengths is carried out. Eventually, the analysis of the angle θ variable is performed. In the first step, the dimensions of the cross-section are L₁ = 160 mm and L₂ = 144 mm (as the maximum value that prevents internal collision between elements is 0.9 L₁), L₃ = L₄ = 80 mm, L₅ = 31.573 mm, and L₆ = 26.672 mm. The results returned from 10 runs of the EA optimization algorithm give the average SEA value of 0.858 kJ/kg. In this case, all first stage results violate the limit defined by reference maximal crushing force P_max-ref. The length dimensions are large, even the wall thicknesses are small (minimum L/T ratio is equal to 42.846 and maximum L/T ratio is equal to 45.398). In consequence, the maximal deformation force is also high (relatively high cross-sectional area, which for the best individual is equal to almost 1500 mm²). The best individual registered the maximal force value of 127.90 kN, and the mean crushing force equal to 46.904 kN. The energy absorbed by the structure is equal to 13.137 kJ, but in combination with 15.006 kg of structural mass, it returns SEA equal to 0.875 kJ/kg. The results are presented in Fig. 5 in form of hollow triangle markers. Maximal bending moments M_x and My, in negative and positive directions, are very high and distant from the reference values (Table 5). The wall thicknesses found in the first step are T₁ = T₂ = 1.529 mm and T₃ = 1.896 mm and become the input data for the second step, i.e., cross-sectional wall lengths optimization. The average value of SEA for the second step is 0.881 kJ/kg, which is higher than that of the first step. This time, constraints (3–8) for all runs are fulfilled. The best solution returned the maximal crushing force equal to 55.099 kN, the mean crushing force equal to 25.635 kN. The energy absorbed in the deformation process is equal to 7.582 kJ, which, together with the structural mass of 8.254 kg, results in SEA equal to 0.919 kJ/kg. The results are marked in Fig. 5 by solid triangle markers. Maximal bending moments (Table 5), in opposite to the first step, are relatively close to the reference values. The dimensions obtained in the second step optimization are L₁ = 81.735 mm, L₂ = 39.811, L₃ = L₄ = 44.500 mm, L₅ = 17.562 mm, and L₆ = 14.883 mm. The analysis of the angle θ influence (Fig. 6) shows that 30° is the best segments’ configuration obtained for the solution generated by steps 1 and 2.

5.3.3 Case 3: thickness–length–angle (version 2)

The Case 3 starts with the wall lengths equal to average values of the range defined at the beginning of this chapter and searches for the best wall thicknesses. After that, wall lengths are optimized, and the procedure ends by determining the best angle θ configuration. In the first step, 10 runs of the EA returned an average value of SEA equal to 0.818 kJ/kg. The crushing parameters registered for the best individual are the maximal crushing force of 85.580 kN, the mean crushing force equal to 32.981 kN, the energy absorbed by the structure equal to 9.312 kJ, which gives 0.839 kJ/kg considering the structural mass of 11.109 kg. The results are depicted in Fig. 5 by hollow rectangle markers. The condition (2) is not fulfilled, but the allowable limit was exceeded by less than 1%. Remaining solutions of this study are characterized by higher maximal force value. The L/T ratio is close to the middle of the accepted range. Maximal bending moments M_x and M_y are rather distant from the reference values. The resulting dimensions T₁ = T₂ = 1.524 mm and T₃ = 2.103 mm are used to look for optimal lengths in the next step. In the second step, ten runs of the algorithm returned an average SEA of 0.879 kJ/kg. The best individual is distinguished by 55.641 kN of maximal crushing force, 24.883 kN of mean crushing force, 7.382 kJ of energy absorbed, and 0.934 kJ/kg of SEA which results indirectly from the structural mass of 7.905 kg. The solid rectangles represent the SEA values as shown in Fig. 5. The L/T ratio equal to 22.727 is situated within the limits, close to the lower bound. Maximal bending moments are closer to reference values than solution obtained in the step 1 (Table 5). The cross-sectional variables of the best solution have dimensions L₁ = 71.862 mm L₂ = 30.134 mm, L₃ = L₄ = 45.549 mm, L₅ = 17.977 mm, and L₆ = 15.183 mm. The analysis of the angle θ influence is very similar to Case 2 (Fig. 6) and 30° is the best space configuration.

5.3.4 Case 4: all variables simultaneously

In the Case 4, the entire structure and all design variables were considered. The average SEA value from 10 independent runs of the EA was equal to 0.997 kJ/kg (three times, the best SEA was exceeded 1 kJ/kg). The best solution corresponds to SEA of 1.052 kJ/kg, maximal crushing force equal to 66.431 kN, mean crushing force equal to 31.294 kN, the absorbed energy of 9.293 kJ and the mass of 8.836 kg. The profile dimensions are: T₁ = T₂ = 1.786 mm, T₃ = 2.27 mm, L₁ = 67.145 mm, L₂ = L₃ = 40.564 mm, L₅ = 16.009 mm, L₆ = 13.522 mm. The angle θ between frame segments was equal to 24.825° i.e., less than the initial value of 30°. The results are presented in Fig. 5 using the cross markers. Additional calculations have been carried out to investigate how the angle θ influences the best result. For the obtained cross-sectional dimensions 21 models with the angle changing from 20° to 40° were analyzed. The calculation revealed that the angle equal to 24.825° corresponds to the maximum of the SEA for given cross-sectional configuration, and any change of θ returns lower SEA values (Fig. 6).

5.3.5 Comparison and discussion

In this part, the results of analyzed approaches are compared. The corresponding crashworthiness properties of the modeled frame are given in Table 4, including intermediary results at steps 1, 2, and 3, denoted by S1, S2, and S3.

Figure 5 presents example of SEA results obtained in ten independent runs of the EA optimization procedure. The dimensions of the best S-frames obtained in all cases, and steps are summarized in Table 3.

Several examples provide sufficient information to indicate the most effective way of finding the best solution. There are three cases that consists of 3-step optimization procedure and Case 4 where all design parameters are searched at one time.

The value of SEA is the main criterion that characterizes the solution; however, conditions (2–3) and (5) must be fulfilled to accept final design. The general observation suggests that multi-step optimization returns lower SEA in the first step and higher values in the second step for particular case and algorithm run (Fig. 5). The third step, where the space angle configuration is tested, generally does not improve solutions obtained in step 1 and step 2. Fig. 6 shows the study of impact of angle θ carried out for the best results of each studied case.

The difference between the best solutions obtained in all cases is visible. Case 1 (that started from average thickness and searched for cross-sectional lengths) returned relatively high values of the SEA from the initial optimization step. The second step improved the solution, what can be noticed in Table 4 presenting the crushing parameters. The only drawback is the violation of geometrical condition (4) by less than 1%.

Case 2 (that starts from maximal wall lengths and searches for thicknesses) returns significantly lower SEA in the first step, than it was in Case 1. Even though result parameters are in transitional step, they violate fixed boundaries. Successfully, the second stage returned much better crushing parameters. The change of wall lengths allowed to fulfill conditions imposed to P_max, P_mean, and L/T ratio. Moreover, the maximal bending moments are closer to the reference values (Table 5).

The Case 3 (starting from average wall lengths and searching for thicknesses) returned the lowest value of the SEA in the first optimization step. All conditions except (2) were fulfilled. However, the maximal force in the transitional step 1 was violated by less than 1%. The second step improved the best solution by reducing the P_max and increased SEA, which gave better result than Case 2. The bending moments are relatively close to the reference values.

Case 4 contrasts with the multi-step optimization procedure. Four runs returned solutions with the SEA value much higher than the best solutions in Cases 1 to 3. The best solution is characterized by higher SEA value than solutions returned in remaining calculation. The P_max and P_mean are relatively high level, but within the allowed range, which is a desired feature from the energy absorption point of view. Similarly, to the Case 1, the L/T ratio condition is slightly below the assumed limit. The best solution has been obtained for the angle smaller than the default configuration.

5.4 Discussion

The calculation examples (Case 1–Case 4) presenting various strategies for the search of the best solution indicate similarities and differences within the results. The intuitive step-by-step optimization procedure was performed in Case 1 to Case 3, being aware that variables are interrelated, and the change of one variable influences the others. These optimization schemes return worse solutions in the first step, but the second step improved the design. In the third step, where the s-shaped frame angle configuration was tested, the confirmation of the input angle value was obtained (Fig. 6).

The best solution has been obtained in Case 4. It corresponds to smaller angle θ than in other studies. This configuration has not been detected in “step by step” procedures and probably is not possible to find it that way. The interdependence between design variables is strong, and the problem is highly nonlinear. In multi-step strategies, a possible enhancement of the design is the result of previous choices and assumptions. Thus, the choice of initial values influences future decisions. Even the order of solving subproblems matters. However, the decomposition of the optimization problem enables to propose a solution much better than the initial one. The number of calculations is decidedly smaller than in the case of “full” problem; thus, the preparation time is shorter. This aspect is important in designing process. But one has to accept that the result may be worse.

The dimensions obtained in Case 1 to Case 4 have common characteristics for thickness relation. The T₃ variable is always larger than T₁. Additionally, for Case 1, Case 3, and Case 4, the value of variable L₁ is close to 70 mm in contrast to Case 2, where L₁ is over 80 mm. There are no similarities observed across the best solutions for the reinforcement offset dimension L₂. The lowest value is equal to 30.134 mm (Case 3) and the highest 49.364 mm (Case 1). The dimension L₃, also linearly related L₅ and L₆ defining cross-sectional width, return relatively close results between cases. The evaluation conducted basing on the obtained results shows that the Case 1 returned the best solution among three studied subproblem approaches. However, the solution of Case 4 considers the nonlinearity of the problem. The results indicate sensitive interaction between variables change and crushing parameters obtained from simulations. The different (not significantly) geometrical configuration can return similar results. The comparison of cross-sectional geometry of the best solutions obtained in the research is presented in Fig. 7 (dash line represents the maximal dimensions of the cross-sectional design space).

Fig. 7

Comparison of the best profiles (Case 1 and Case 4) with design space

6 Conclusion

The optimization of thin-walled front rail of a car used to absorb the energy of collision was investigated. This study illustrates the potential of the optimization in early-design stages of the vehicle development process. Crushing parameters of the structure were modeled using the macro-element methodology that enables very fast simulation of the impact parameters. An individual S-Frame is calculated by VCS in just above 1 s on a PC.

The dimensions of the frame cross-section and geometry were searched so as to achieve the maximal energy absorption. As the real-life example of thin-walled S-frame was investigated in numerical examples, the Evolutionary Algorithm was introduced to solve complex optimization problem. However, combining the fitness formulation and application of constraints was not an easy task. The preliminary tests were necessary to adjust the algorithm to the specific S-frame model application. The obtained solutions were compared specifying the results of a different approach. One is decomposing the same problem into subproblems (including various starting points) and solving them step by step. Each step involved optimization of one type of variable only, similar to a designer approach searching to simplify the complex problem. Other is the optimization process, which involved full problem definition, where all variables are searched at the same algorithm run. The second "full" approach provided better solutions than the first. It is obvious because of the nonlinearity of the problem and a strong interdependence between design variables. In addition, the preparation of the optimization algorithm to run was conducted once, and the calculation time was finally shorter. However, step-by-step, or subproblem optimization in some variants may produce also valuable results, depending on the search strategy. In the case of analyzed S-frame the maximal difference of SEA, i.e., difference between two most distant solutions (case 2 and case 4) was within 12.64%, and the difference between two best solutions of Case 1 and Case 4 was only 2.38% (despite the difference in θ value). The results of subproblem optimization depend on the input data and succession of procedures. Consequently, it is more difficult to find promising configurations as in the case of full problem solution. It is visible that initial decisions determine the progress of enhancing the solution on each calculation step and the final calculation outcome. However, the study shows that using different starting points could help to improve the results. That fact encourages us to look from the engineering point of view as well. As the optimization procedures involve simplified modeling, where complex technical issues of part manufacturing and assembly are not considered, it is worth reflecting on more options. There is a possibility that the solution neighbor to the best one can provide the geometrical specification that fits more to actual requirements without significant loss of the SEA.

The optimization of a complex S-frame structure using EA was possible thanks to use of the macro-element simulations. A properly defined optimization task can be solved successfully in a reasonable time. For example, a single run of EA takes about 30 min on a PC, and that time the VCS is invoked about 1000 times. The optimization procedures and the calculation output presented in the numerical examples illustrate a successful approach for automated searching for the best design using the macro-element method. It can help enhance the structural design at the initial development stage before the detailed and time-consuming FEA is conducted. The definition of simplified modeling based on a real-life fragment of the vehicle structure shows the advantage of fast calculation routines applied into optimization procedures. However, the key to success is to correctly determine the conditions that influence the modeled phenomena and to set the limitations which keep the model valid within the design space. Also, the correct problem formulation and the way of including constraints have to be studied carefully.