New blending constraints and a stack-recovery strategy for the multi-scale design of composite laminates

Abstract

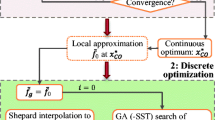
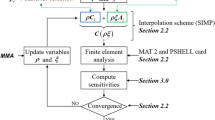
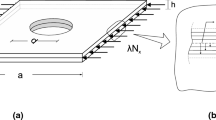
This work presents a new strategy for dealing with blending requirements in the composite structures design. Firstly, new analytical expressions of blending constraints, in the polar parameters space, are derived. Secondly, a dedicated numerical strategy for the recovery of blended stacking sequences is presented. The proposed approach is implemented in the framework of the multi-scale two-level optimisation strategy (MS2LOS) for composite laminates design. The theoretical aspects of this work are supported by the application of the proposed methodology to a numerical benchmark taken from the literature. The results obtained by means of the MS2LOS based on the polar formalism outperform those reported in the literature.

Appendices

Appendix 1. A note on the square of the sum of n terms

Consider the square of the sum of terms $a_{1}, a_{2}, \dots ,a_{n}$, $n\in \mathbb {N}$. Hence, it easy to see that

$$ \begin{array}{@{}rcl@{}} \left( {\sum}_{k=1}^{n} a_{k} \right)^{2} &=& \sum\limits_{k=1}^{n} {a_{k}^{2}} + 2\sum\limits_{k=1}^{n-1}a_{k}\sum\limits_{j=k+1}^{n} a_{j} \\&=& \sum\limits_{k=1}^{n} {a_{k}^{2}} + 2\sum\limits_{k=1}^{n-1}\sum\limits_{j=k+1}^{n} a_{k} a_{j}, \end{array} $$

(A1.1)

where the distributivity property of sum and product operators has been used.

The number of the double-product terms is equal to

$$ \begin{array}{@{}rcl@{}} \sum\limits_{k=1}^{n-1}\sum\limits_{j=k+1}^{n} 1 =\sum\limits_{k=1}^{n-1} \left( n- k\right) = n\sum\limits_{k=1}^{n-1} - \sum\limits_{k=1}^{n-1}k = n(n-1)\\ - \frac{n(n-1)}{2} = \frac{n(n-1)}{2}.\\ \end{array} $$

(A1.2)

If a n-term sequence {a_k} has indices k progressively taking values in an arbitrary, but ordered, set of n natural numbers, say $\mathcal {A}$, the square of the sum of the sequence elements can be written as

$$ \left( {\sum}_{k\in\mathcal{A}} a_{k} \right)^{2} = \sum\limits_{k\in\mathcal{A}}{a_{k}^{2}} + 2 \underset{j>k}{\underset{k,j\in \mathcal{A}}{\sum}} a_{k}a_{j}. $$

(A1.3)

Of course, the result of (A1.2) still holds.

Appendix 2. Study of B ^∗ = O for blending constraints

Uncoupling condition on laminates is B^∗ = O, which can be stated as follows:

$$ \sum\limits_{k=1}^{N} b_{k} \mathrm{e}^{\mathrm{i}\beta\theta_{k}} = 0, \beta=2,4. $$

(A2.1)

Considering (6) and (9), (A2.1) may be expressed as:

$$ \frac{N(N+1)}{2} \rho_{0K} \mathrm{e}^{\mathrm{i}4{\varPhi}_{1}^{A^{*}}} = \sum\limits_{k=1}^{N} k \mathrm{e}^{\mathrm{i}4\theta_{k}}, $$

(A2.2)

$$ \frac{N(N+1)}{2} \rho_{1} \mathrm{e}^{\mathrm{i}2{\varPhi}_{1}^{A^{*}}} = \sum\limits_{k=1}^{N} k \mathrm{e}^{\mathrm{i}2\theta_{k}}. $$

(A2.3)

As already done in Section 5, consider two laminates denoted with labels p and q, such that, without loss of generality, N_p > N_q. Writing (A2.2) and (A2.3) for the two laminates, subtracting member-by-member, taking the square of both members, one obtains:

$$ \begin{array}{ll} \left[{\Delta}_{pq} \left( \frac{N(N+1)}{2}\rho_{0K} c_{4}\right)\right]^{2} + \left[ {\Delta}_{pq} \left( \frac{N(N+1)}{2}\rho_{0K} s_{4}\right) \right]^{2} \\=\left( \sum\limits_{k\in \mathcal{N}} k\cos 4\theta_{k} + \sum\limits_{k=1}^{N_{q}} \left[\mathcal{B}(k) - k \right]\cos 4\theta_{k} \right)^{2} \\ + \left( \sum\limits_{k\in \mathcal{N}} k\sin 4\theta_{k} + \sum\limits_{k=1}^{N_{q}} \left[\mathcal{B}(k) - k \right]\sin 4\theta_{k} \right)^{2}, \end{array} $$

(A2.4)

and

$$ \begin{array}{ll} \left[{\Delta}_{pq} \left( \frac{N(N+1)}{2}\rho_{1} c_{2}\right)\right]^{2} + \left[ {\Delta}_{pq} \left( \frac{N(N+1)}{2}\rho_{1} s_{2}\right) \right]^{2} \\=\left( \sum\limits_{k\in \mathcal{N}} k\cos 2\theta_{k} + \sum\limits_{k=1}^{N_{q}} \left[\mathcal{B}(k) - k \right]\cos 2\theta_{k} \right)^{2} \\ + \left( \sum\limits_{k\in \mathcal{N}} k\sin 2\theta_{k} + \sum\limits_{k=1}^{N_{q}} \left[\mathcal{B}(k) - k \right]\sin 2\theta_{k} \right)^{2}. \end{array} $$

(A2.5)

Consider, for the sake of simplicity, the right-hand side of (A2.4) (similar considerations hold for (A2.5). It can be expressed as:

$$ \begin{array}{@{}rcl@{}} \left( \sum\limits_{k\in \mathcal{N}} k\cos 4\theta_{k} \right)^{2} &+& \left( \sum\limits_{k=1}^{N_{q}} \left[\mathcal{B}(k) - k \right]\cos 4\theta_{k} \right)^{2} \\&+& 2 \left( \sum\limits_{k\in \mathcal{N}} k\cos 4\theta_{k}\right)\left( \sum\limits_{k=1}^{N_{q}} \left[\mathcal{B}(k) - k \right]\cos 4\theta_{k} \right)\\ &+& \left( \sum\limits_{k\in \mathcal{N}} k\sin 4\theta_{k} \right)^{2} + \left( \sum\limits_{k=1}^{N_{q}} \left[\mathcal{B}(k) - k \right]\sin 4\theta_{k} \right)^{2} \\&+& 2 \left( \sum\limits_{k\in \mathcal{N}} k\sin 4\theta_{k}\right)\left( \sum\limits_{k=1}^{N_{q}} \left[\mathcal{B}(k) - k \right]\sin 4\theta_{k} \right),\\ &=:& c_{1} + c_{2} + c_{3} + c_{4} + c_{5} + c_{6}. \end{array} $$

(A2.6)

Considering Appendix 1 and the elementary trigonometric identity $\cos \limits \alpha \cos \limits \beta + \sin \limits \alpha \sin \limits \beta = \cos \limits (\alpha - \beta )$, the sum c₁ + c₄ gives:

$$ \sum\limits_{k\in \mathcal{N}} k^{2} + 2 \underset{j>k}{\underset{k,j\in \mathcal{N}}{\sum}} kj \cos 4(\theta_{j} - \theta_{k}). $$

(A2.7)

In a complete similar manner, the sum c₂ + c₅ simplifies to

$$ \sum\limits_{k=1}^{N_{q}} \left[\mathcal{B}(k) - k \right]^{2} + 2 \sum\limits_{k=1}^{N_{q}-1} \sum\limits_{j=k+1}^{N_{q}} \left[\mathcal{B}(k) - k \right]\!\left[\mathcal{B}(j) - j \right]\cos 4(\theta_{k} - \theta_{j}). $$

(A2.8)

The sum c₃ + c₆ can be rewritten as (using the distributivity property of sum and product operators and the aforementioned trigonometric identity)

$$ \begin{array}{ll} &2\sum\limits_{k=1}^{N_{q}} \sum\limits_{j\in \mathcal{N}} \left[\mathcal{B}(k) - k \right] j\cos 4\theta_{j} \cos 4\theta_{k} \\&+ 2 \sum\limits_{k=1}^{N_{q}} \sum\limits_{j\in \mathcal{N}} \left[\mathcal{B}(k) - k \right] j\sin 4\theta_{j}\sin 4\theta_{k} \\ =&2\sum\limits_{k=1}^{N_{q}} \sum\limits_{j\in \mathcal{N}} \left[\mathcal{B}(k) - k \right] j \left( \cos 4\theta_{j} \cos 4\theta_{k} + \sin 4\theta_{j} \sin 4\theta_{k}\right) \\ =&2\sum\limits_{k=1}^{N_{q}} \sum\limits_{j\in \mathcal{N}} \left[\mathcal{B}(k) - k \right] j \cos 4(\theta_{j} - \theta_{k}) . \end{array} $$

(A2.9)

Assembling (A2.7), (A2.8) and (A2.9), (A2.6) simplifies to:

$$ \begin{array}{ll} &\sum\limits_{k\in \mathcal{N}} k^{2} + 2 \underset{j>k}{\underset{k,j\in \mathcal{N}}{\sum}} kj \cos(4(\theta_{j} - \theta_{k})) + \sum\limits_{k=1}^{N_{q}} \left[\mathcal{B}(k) - k \right]^{2}\\ &+ 2 \sum\limits_{k=1}^{N_{q}-1} \sum\limits_{j=k+1}^{N_{q}} \left[\mathcal{B}(k) - k \right]\left[\mathcal{B}(j) - j \right]\cos 4(\theta_{k} - \theta_{j})\\ &+ 2\sum\limits_{k=1}^{N_{q}}\sum\limits_{j\in \mathcal{N}} j\left[\mathcal{B}(k) - k \right] \cos 4(\theta_{k} - \theta_{j}). \end{array} $$

(A2.10)

It is simple to see that

$$ \begin{array}{ll} &\text{Equation (A2.10)} \leq \sum\limits_{k\in \mathcal{N}} k^{2} + 2 \underset{j>k}{\underset{k,j\in \mathcal{N}}{\sum\limits}} kj \\&+ \sum\limits_{k=1}^{N_{q}} \left[\mathcal{B}(k) - k \right]^{2} \\&+ 2 \sum\limits_{k=1}^{N_{q}-1} \sum\limits_{j=k+1}^{N_{q}} \left[\mathcal{B}(k) - k \right]\left[\mathcal{B}(j) - j \right]\\&+ 2\sum\limits_{k=1}^{N_{q}}\sum\limits_{j\in \mathcal{N}} j\left[\mathcal{B}(k) - k \right], \end{array} $$

(A2.11)

since terms of the form $\left ({\mathcal{B}}(\cdot ) - \cdot \right )$ are always non-negative, because of property (b) of Def. 2.2.

Consider the particular case for which ${\mathcal{B}}(k)=k$; it follows that $\mathcal {N}=\{i \ | \ N_{q}+1\leq i\leq N_{p}\}$. Equation (A2.11) simplifies to:

$$ \begin{array}{@{}rcl@{}} &&\sum\limits_{k=N_{q}+1}^{N_{p}} k^{2} + 2 \sum\limits_{i=N_{q}+1}^{N_{p}-1}\sum\limits_{j=i+1}^{N_{p}} ij \\&&= \frac{1}{4}[ {N_{p}^{4}} + {N_{q}^{4}} + 2\left( {N_{p}^{3}} + {N_{q}^{3}}\right) + {N_{p}^{2}} + {N_{q}^{2}}\\ &&- 2N_{p}N_{q}\left( N_{p}N_{q} + N_{p} + N_{q} + 1\right) ] =: C_{B}. \end{array} $$

(A2.12)

The final blending constraints, for the considered particular case, read:

$$ \begin{array}{@{}rcl@{}} g_{\text{blend}-0}^{\mathrm{C_{B}}} &:=& \left[{\Delta}_{pq} \left( \frac{N(N+1)}{2}\rho_{0K} c_{4}\right)\right]^{2} \\&&+ \left[ {\Delta}_{pq} \left( \frac{N(N+1)}{2}\rho_{0K} s_{4}\right) \right]^{2} - C_{B}, \\ g_{\text{blend}-1}^{\mathrm{C_{B}}} &:=& \left[{\Delta}_{pq} \left( \frac{N(N+1)}{2}\rho_{1} c_{2}\right)\right]^{2} \\&&+ \left[ {\Delta}_{pq} \left( \frac{N(N+1)}{2}\rho_{1} s_{2}\right) \right]^{2} - C_{B},\\ g_{\text{blend}-i}^{\mathrm{C_{B}}} \leq 0, \ i&=&0,1. \end{array} $$

(A2.13)

Figure 10 shows, for the reference laminate of Section 5, that condition of (20) is stricter than the one expressed by (A2.13). Even though C_B is not the sharpest upper bound of (A2.11), the fact that the condition B^∗ = O does not introduce further constraints on PPs can be inferred. In fact, if there exists another estimate C > C_B (for which (A2.13) would read $g_{\text {blend}-i}^{C} \leq 0$, i = 0, 1, with a clear meaning of notation), the feasible domain can only be larger than the (green) one in Fig. 10.

Fig. 10

Comparison between blending constraints

The result may be due to the fact that increasing separately the “angle terms”, as done in (A2.11), and the “arrangement terms”, as done in (A2.12), is too rude. Indeed, a coupling between the aforementioned terms exists, which makes finding a good estimate of (A2.10) a cumbersome, probably impossible, task.