Limited Range Extrapolation with Quantitative Bounds and Applications

Abstract

In recent years, sharp or quantitative weighted inequalities have attracted considerable attention on account of the $A_2$ conjecture solved by Hytönen. Advances have greatly improved conceptual understanding of classical objects such as Calderón–Zygmund operators. However, plenty of operators do not fit into the class of Calderón–Zygmund operators and fail to be bounded on all $L^p(w)$ spaces for $p \in (1, \infty )$ and $w \in A_p$. In this paper we develop Rubio de Francia extrapolation with quantitative bounds to investigate quantitative weighted inequalities for operators beyond the (multilinear) Calderón–Zygmund theory. We mainly establish a quantitative multilinear limited range extrapolation in terms of exponents $p_i \in (\mathfrak {p}_i^-, \mathfrak {p}_i^+)$ and weights $w_i^{p_i} \in A_{p_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/p_i)'}$, $i=1, \ldots , m$, which refines a result of Cruz-Uribe and Martell. We also present an extrapolation from multilinear operators to the corresponding commutators. Additionally, our result is quantitative and allows us to extend special quantitative estimates in the Banach space setting to the quasi-Banach space setting. Our proof is based on an off-diagonal extrapolation result with quantitative bounds. Finally, we present various applications to illustrate the utility of extrapolation by concentrating on quantitative weighted estimates for some typical multilinear operators such as bilinear Bochner–Riesz means, bilinear rough singular integrals, and multilinear Fourier multipliers. In the linear case, based on the Littlewood–Paley theory, we include weighted jump and variational inequalities for rough singular integrals.

1 Introduction

1.1 Motivation and Main Results

The main goal of this paper is to establish multivariable Rubio de Francia extrapolation with quantitative bounds in order to investigate quantitative weighted inequalities for multilinear operators beyond the multilinear Calderón–Zygmund theory. We focus on the limited range extrapolation with exponents $p_i \in (\mathfrak {p}_i^-, \mathfrak {p}_i^+)$ and weights $w_i^{p_i} \in A_{p_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/p_i)'}$, $i=1, \ldots , m$, which is quite different from [76] for $\textbf{w}=(w_1, \ldots , w_m) \in A_{\textbf{p}}$ (or general weights $A_{\textbf{p}, \textbf{r}}$). The main reason why we study it is that plenty of operators are beyond the Calderón–Zygmund theory so that they may not be bounded on all $L^p(w)$ spaces for $p \in (1, \infty )$ and $w \in A_p$. This is the case for operators with the strong singularity, such as Bochner–Riesz means [6], rough singular integrals [89], Riesz transforms and square functions associated with second-order elliptic operators [3], operators associated with the Kato conjecture [4], and singular “non-integral” operators [9]. As well as the classes $A_p$ are natural for the Calderón–Zygmund operators and characterize the weighted boundedness of Hardy–Littlewood maximal operators, the classes $A_{\textbf{p}}$ are also the natural ones for multilinear Calderón–Zygmund operators and the multilinear Hardy–Littlewood maximal operators (cf. Theorem 2.10). In the multilinear setting, there are also many operators so that weighted inequalities holds for limited ranges. For multilinear Fourier multipliers, it is interesting that different forms of Sobolev regularity appear to determine whether product of scalar weights or multiple weights $A_{\textbf{p}}$ could be used. Fujita and Tomita [43, 44] proved that whenever the symbol satisfies a product type Sobolev regularity, the weighted boundedness of multilinear Fourier multipliers holds for $\textbf{w} \in A_{p_1/r_1} \times \cdots \times A_{p_m/r_m}$ but does not hold for $\textbf{w} \in A_{(p_1/r_1, \ldots , p_m/r_m)}$, while the latter is valid under the classical Sobolev regularity. Other examples include strongly singular bilinear Calderón–Zygmund operators [7, Corollary 3.2], bilinear differential operators associated with fractional Leibniz rules [34, Theorem 1.1], bilinear pseudo-differential operators with symbols in the Hörmander classes [75, Remark 3.4], and so on.

The main contributions of this article are the following.

• Our first main result, Theorem 1.1, improves [30, Theorem 1.3] to an extrapolation with the quantitative weighted bounds, which in turn covers the multivariable extrapolation in [40, Theorem 6.1] and [47, Theorem 1.1] by taking $\mathfrak {p}_i^-=1$ and $\mathfrak {p}_i^+=\infty$, $i=1, \ldots , m$.

• Our second main result, Theorem 1.2, establishes an extrapolation for commutators, which extends [8, Theorem 4.3] from the Banach range to the quasi-Banach range.

• We prove a limited range, off-diagonal extrapolation theorem with sharp weighted bounds (cf. Theorem 4.8), whose proof is distinct from and much simpler than that in [30, Theorem 1.8] because it only needs to define a Rubio de Francia iteration algorithm each time we consider the case $q<q_0$ or $q>q_0$. Thus, we not only refine [30, Theorem 1.8] to Theorem 4.8 with sharp bounds, but also remove the restriction $\frac{1}{q_0} - \frac{1}{p_0} + \frac{1}{\mathfrak {p}_+} \ge 0$.

• Although our weights class is a special case of the class $A_{\textbf{p}, \textbf{r}}$, Theorem 1.1 is independent of [76, Theorem 2.2], that is, one does not imply another one.

• When the exponents are greater than one, we can obtain quantitative $A_p$ and off-diagonal extrapolation (cf. Theorems 4.1 and 4.5) by showing a “product-type embedding” theorem (cf. Theorems 4.2 and 4.6), respectively, which is quite different from the embedding technique used in [18, Proposition 3.18] to get extrapolation on general weighted Banach function spaces.

• Based on $A_p$ extrapolation and interpolation, we present an extrapolation from weak type inequalities to strong type estimates (cf. Theorem 4.4). This allows us to obtain quantitative weighted strong estimates from weak (1, 1) type.

• This is the first time to use extrapolation to establish quantitative weighted norm inequalities for plenty of operators beyond the Calderón–Zygmund theory (cf. Sect. 5). The strong singularity of those operators leads the weights class to be $A_{p_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/p_i)'}$, $i=1, \ldots , m$, instead of the more general class $A_{\textbf{p}, \textbf{r}}$. It is totally novel to obtain quantitative estimates for those operators, although we do not show the sharpness, which goes beyond the scope of this article and will be our further topic.

In order to state our main results we need some notation. More definitions and notation are given in Sect. 2. Given $1 \le \mathfrak {p}_- < \mathfrak {p}_+ \le \infty$ and $p \in [\mathfrak {p}_-, \mathfrak {p}_+]$ with $p \ne \infty$, considering Lemma 2.6, for any $w^p \in A_{p/\mathfrak {p}_-} \cap RH_{(\mathfrak {p}_+/p)'}$, we define

$$\begin{aligned} {[}w^p]_{A_{p/\mathfrak {p}_-} \cap RH_{(\mathfrak {p}_+/p)'}} := {\left\{ \begin{array}{ll} {[}w^{p(\mathfrak {p}_+/p)'}]_{A_{\tau _p}}, &{} p < \mathfrak {p}_+,\\ \max \{[w^p]_{A_{p/\mathfrak {p}_-}}, [w^p]_{RH_{(\mathfrak {p}_+/p)'}}\}, &{} p =\mathfrak {p}_+, \end{array}\right. } \end{aligned}$$

(1.1)

where $\tau _p:= \big (\frac{\mathfrak {p}_+}{p}\big )' \big (\frac{p}{\mathfrak {p}_-} -1\big ) +1$. Throughout this paper, given $p_i, q_i \in [\mathfrak {p}_i^-, \mathfrak {p}_i^+]$, we always denote

$$\begin{aligned} \gamma _i(p_i, q_i) := {\left\{ \begin{array}{ll} \max \big \{1, \frac{\tau _{q_i} - 1}{\tau _{p_i} -1} \big \}, &{} q_i<\mathfrak {p}_i^+,\\ \frac{q_i}{\tau _{p_i} -1} \big (\frac{1}{\mathfrak {p}_i^-} - \frac{1}{\mathfrak {p}_i^+} \big ), &{} q_i = \mathfrak {p}_i^+. \end{array}\right. } \end{aligned}$$

Let $\mathcal {F}$ denote a family of $(m+1)$-tuples $(f, f_1, \ldots , f_m)$ of non-negative measurable functions. We would like to present an abstract methodology for extrapolation. We will see that extrapolation enables us to obtain vector-valued inequalities and weak-type estimates from extrapolation results immediately. In the current paper, we mainly apply this methodology to obtain quantitative weighted norm inequalities for plenty of operators.

Our first main result is formulated as follows.

Theorem 1.1

Given $m \ge 1$, let $\mathcal {F}$ be a family of extrapolation (m+1)-tuples. Let $1 \le \mathfrak {p}_i^- < \mathfrak {p}_i^+ \le \infty$ for each $i=1, \ldots , m$. Assume that for each $i=1, \ldots , m$, there exists an exponent $q_i \in (0, \infty )$ with $q_i \in [\mathfrak {p}_i^-, \mathfrak {p}_i^+]$ such that for all weights $v_i^{q_i} \in A_{q_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/q_i)'}$, $i=1, \ldots , m$,

$$\begin{aligned} \Vert f\Vert _{L^q(v^q)} \le \prod _{i=1}^m \Phi _i \big ([v_i^{q_i}]_{A_{q_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/q_i)'}}\big ) \Vert f_i\Vert _{L^{q_i}(v_i^{q_i})}, \quad (f, f_1, \ldots , f_m) \in \mathcal {F}, \nonumber \\ \end{aligned}$$

(1.2)

where $\frac{1}{q} = \sum _{i=1}^m \frac{1}{q_i}$, $v= \prod _{i=1}^m v_i$, and $\Phi _i: [1, \infty ) \rightarrow [1, \infty )$ is an increasing function. Then for all exponents $p_i \in (\mathfrak {p}_i^{-}, \mathfrak {p}_i^{+})$ and all weights $w_i^{p_i} \in A_{p_i/\mathfrak {p}_i^{-}} \cap RH_{(\mathfrak {p}_i^{+}/p_i)'}$, $i=1, \ldots , m$,

$$\begin{aligned}{} & {} \Vert f\Vert _{L^p(w^p)} \nonumber \\{} & {} \quad \le \prod _{i=1}^m \mathfrak {C}_i \, \Phi _i \Big (C_i \, [w_i^{p_i}]_{A_{p_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/p_i)'}}^{\gamma _i(p_i, q_i)}\Big ) \Vert f_i\Vert _{L^{p_i}(w_i^{p_i})}, \quad (f, f_1, \ldots , f_m) \in \mathcal {F},\nonumber \\ \end{aligned}$$

(1.3)

where $\frac{1}{p} = \sum _{i=1}^m \frac{1}{p_i}$, $w=\prod _{i=1}^m w_i$, $\mathfrak {C}_i:= 2^{\max \{\frac{\tau _{p_i}}{p_i}, \frac{\tau '_{p_i}}{q_i}\}}$, and $C_i$ depends only on n, $p_i$, $q_i$, $\mathfrak {p}_i^-$, and $\mathfrak {p}_i^+$.

Moreover, for the same family of exponents and weights, and for all exponents $r_i \in (\mathfrak {p}_i^-, \mathfrak {p}_i^+)$,

$$\begin{aligned} \bigg \Vert \Big (\sum _k |f^k|^r \Big )^{\frac{1}{r}}\bigg \Vert _{L^p(w^p)} \le \prod _{i=1}^m \mathfrak {C}'_i \, \Phi _i \Big (C'_i \, {[}w_i^{p_i}]_{A_{p_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/p_i)'}}^{\gamma _i(p_i, r_i) \gamma _i(r_i, q_i)}\Big ) \bigg \Vert \Big (\sum _k |f^k_i|^{r_i} \Big )^{\frac{1}{r_i}}\bigg \Vert _{L^{p_i}(w_i^{p_i})},\nonumber \\ \end{aligned}$$

(1.4)

for all $\{(f^k, f^k_1, \cdots , f^k_m)\}_k \subset \mathcal {F}$, where $\frac{1}{r}{=}\sum _{i{=}1}^m \frac{1}{r_i}$, $\mathfrak {C}'_i{:=} 2^{\max \{\frac{\tau _{p_i}}{p_i}, \frac{\tau '_{p_i}}{r_i}\} + \max \{\frac{\tau _{r_i}}{r_i}, \frac{\tau '_{r_i}}{q_i}\}}$, and the constant $C'_i$ depends only on n, $p_i$, $q_i$, $r_i$, $\mathfrak {p}_i^-$, and $\mathfrak {p}_i^+$.

As a result of Theorem 1.1 we can extend weighted estimates only valid in the Banach range to the quasi-Banach range. For example, weighted norm inequalities for the commutators of multilinear operators T with ${\text {BMO}}$ functions, more singular than operators T, were just proved in the case $p \ge 1$ [8] since one used the trick of so-called Cauchy integral and Minkowski’s inequality. We will use Theorem 1.1 to deal with this problem and obtain a quantitative extrapolation from operators to the corresponding commutators with full ranges (cf. Theorem 1.2). Concerning the proof of Theorem 1.1, we borrow the ideas from [30, 40], which essentially reduce the multilinear problem to a linear extrapolation (cf. Theorem 4.8) by acting on one function at a time. In the linear case, the core of the proof is to obtain the quantitative bounds, which is due to the sharp weighted estimate (1.9) and sharp reverse Hölder’s inequality in Lemma 2.3.

In order to present an extrapolation theorem for commutators, let us introduce relevant notation and some definitions. Given a function $b \in L^1_{{\text {loc}}}(\mathbb {R}^n)$, we say that $b \in {\text {BMO}}$ if

where the supremum is taken over the collection of all cubes $Q \subset \mathbb {R}^n$. Here and elsewhere, we write .

Let T be an operator from $X_1 \times \cdots \times X_m$ into Y, where $X_1, \ldots , X_m$ are some normed spaces and and Y is a quasi-normed space. Given $\textbf{f}:= (f_1, \ldots ,f_m) \in X_1 \times \cdots \times X_m$, ${\textbf {b}}=(b_1, \ldots , b_m)$ of measurable functions, and $k \in \mathbb {N}$, we define, whenever it makes sense, the k-th order commutator of T in the i-th entry of T as

$$\begin{aligned} {[}T, {\textbf {b}}]_{k e_i} (\textbf{f})(x) := T(f_1,\ldots , (b_i(x)-b_i)^k f_i, \ldots , f_m)(x), \quad 1 \le i \le m, \end{aligned}$$

where $e_i$ is the basis of $\mathbb {R}^n$ with the i-th component being 1 and other components being 0. Then, for a multi-index $\alpha = (\alpha _1, \ldots , \alpha _m) \in \mathbb {N}^m$, we define

$$\begin{aligned} {[}T, {\textbf {b}}]_{\alpha }:= [\cdots [[T, {\textbf {b}}]_{\alpha _1 e_1}, {\textbf {b}}]_{\alpha _2 e_2} \cdots , {\textbf {b}}]_{\alpha _m e_m}. \end{aligned}$$

In particular, if T is an m-linear operator with a kernel representation of the form

$$\begin{aligned} T(\textbf{f})(x):= \int _{\mathbb {R}^{nm}} K(x, \textbf{y}) f_1(y_1) \cdots f_m(y_m) \, d\textbf{y}, \end{aligned}$$

then one can write $[T, {\textbf {b}}]_{\alpha }$ as

$$\begin{aligned} {[}T, {\textbf {b}}]_{\alpha }(\textbf{f})(x):= \int _{\mathbb {R}^{nm}} \prod _{i=1}^m (b_i(x)-b_i(y_i))^{\alpha _i} K(x, \textbf{y}) f_1(y_1) \cdots f_m(y_m) \, d\textbf{y}. \end{aligned}$$

Our second main result is the following.

Theorem 1.2

Let T be an m-linear operator and let $1 \le \mathfrak {p}_i^{-}<\mathfrak {p}_i^{+} \le \infty$, $i=1, \ldots , m$, be such that $\frac{1}{\mathfrak {p}_+}:= \sum _{i=1}^m \frac{1}{\mathfrak {p}_i^+}<1$. Assume that for each $i=1, \ldots , m$, there exists an exponent $q_i \in (0, \infty )$ with $q_i \in {[}\mathfrak {p}_i^{-}, \mathfrak {p}_i^{+}]$ such that for all weights $v_i^{q_i} \in A_{q_i/\mathfrak {p}_i^{-}} \cap RH_{(\mathfrak {p}_i^{+}/q_i)'}$, $i=1, \ldots , m$, we have

$$\begin{aligned} \Vert T(\textbf{f})\Vert _{L^q(v^q)} \le \prod _{i=1}^m \Phi _i \Big ([v_i^{q_i}]_{A_{q_i/\mathfrak {p}_i^{-}} \cap RH_{(\mathfrak {p}_i^{+}/q_i)'}}\Big ) \Vert f_i\Vert _{L^{q_i}(v_i^{q_i})}, \end{aligned}$$

(1.5)

where $\textbf{f}=(f_1, \ldots , f_m)$, $\frac{1}{q} = \sum _{i=1}^m \frac{1}{q_i}$, $v= \prod _{i=1}^m v_i$, and $\Phi _i: [1, \infty ) \rightarrow [1, \infty )$ is an increasing function. Then for all exponents $p_i \in (\mathfrak {p}_i^{-}, \mathfrak {p}_i^{+})$, all weights $w_i^{p_i} \in A_{p_i/\mathfrak {p}_i^{-}} \cap RH_{(\mathfrak {p}_i^{+}/p_i)'}$, for all functions ${\textbf {b}}=(b_1,\ldots , b_m) \in {\text {BMO}}^m$, and for each multi-index $\alpha \in \mathbb {N}^m$,

$$\begin{aligned}{} & {} \Vert [T, {\textbf {b}}]_{\alpha }(\textbf{f})\Vert _{L^p(w^p)} \nonumber \\{} & {} \quad \le C_0 \prod _{i=1}^m {\widetilde{\Phi }}_i \Big (C'_i \, [w_i^{p_i}]_{A_{p_i/\mathfrak {p}_i^{-}} \cap RH_{(\mathfrak {p}_i^{+}/p_i)'}}^{\gamma _i(p_i, s_i)}\Big ) \Vert b_i\Vert _{{\text {BMO}}}^{\alpha _i} \Vert f_i\Vert _{L^{p_i}(w_i^{p_i})}, \end{aligned}$$

(1.6)

whenever $s_i \in (\mathfrak {p}_i^-, \mathfrak {p}_i^+)$, $i=1, \ldots , m$, satisfy $\frac{1}{s}:= \sum _{i=1}^m \frac{1}{s_i} \le 1$, where $\frac{1}{p} = \sum _{i=1}^m \frac{1}{p_i}$, $w=\prod _{i=1}^m w_i$, ${\widetilde{\Phi }}_i(t):= t^{\alpha _i \max \{1, \frac{1}{\tau _{s_i}-1}\}} \Phi _i(C_i \, t^{\gamma _i(s_i, q_i)})$, $C_i$ depends only on n, $s_i$, $q_i$, $\mathfrak {p}_i^-$, and $\mathfrak {p}_i^+$, $C'_i$ depends only on n, $p_i$, $s_i$, $\mathfrak {p}_i^-$, and $\mathfrak {p}_i^+$, and $C_0$ depends only on $\alpha$, n, $p_i$, $q_i$, $s_i$, $\mathfrak {p}_i^-$, and $\mathfrak {p}_i^+$.

Moreover, for the same family of exponents $\textbf{p}$, weights $\textbf{w}$, functions ${\textbf {b}}$, multi-index $\alpha$, and for all exponents $r_i \in (\mathfrak {p}_i^-, \mathfrak {p}_i^+)$,

$$\begin{aligned} \bigg \Vert \Big (\sum _k | [T, {\textbf {b}}]_{\alpha }(\textbf{f}^k)|^r \Big )^{\frac{1}{r}} \bigg \Vert _{L^p(w^p)}&\le C \prod _{i=1}^m {\widetilde{\Phi }}_{i} \Big (C''_i \, [w_i^{p_{i}}]_{A_{p_i/\mathfrak {p}_i^{-}} \cap RH_{(\mathfrak {p}_{i}^{+}/p_{i})'}}^{\gamma _i(p_{i}, r_{i}) \gamma _i(r_{i}, s_{i})}\Big ) \nonumber \\&\quad \times \Vert b_{i}\Vert _{{\text {BMO}}}^{\alpha _i} \bigg \Vert \Big (\sum _k |f^k_{i}|^{r_i} \Big )^{\frac{1}{r_{i}}}\bigg \Vert _{L^{p_{i}}(w_{i}^{p_{i}})}, \end{aligned}$$

(1.7)

where $\textbf{f}^k=(f_1^k, \ldots , f_m^k)$, $\frac{1}{r} = \sum _{i=1}^m \frac{1}{r_i}$, C depends only on $\alpha$, n, $p_i$, $q_i$, $r_i$, $s_i$, $\mathfrak {p}_i^-$, and $\mathfrak {p}_i^+$, and $C''_i$ depends only on n, $p_i$, $r_i$, $s_i$, $\mathfrak {p}_i^-$, and $\mathfrak {p}_i^+$.

Remark 1.3

Let us see the existence of $s_i \in (\mathfrak {p}_i^-, \mathfrak {p}_i^+)$, $i=1, \ldots , m$, satisfying $\frac{1}{s}:= \sum _{i=1}^m \frac{1}{s_i} \le 1$. Indeed, by means of Theorem 1.1, the estimate (1.5) can be improved to all exponents $s_i \in (\mathfrak {p}_i^-, \mathfrak {p}_i^+)$, $i=1, \ldots , m$. Given $s_i \in (\mathfrak {p}_i^-, \mathfrak {p}_i^+)$, $i=1, \ldots , m$, there holds

$$\begin{aligned} \frac{1}{s} = \sum _{i=1}^m \frac{1}{s_i} = \sum _{i=1}^m \bigg (\frac{1}{s_i} - \frac{1}{\mathfrak {p}_i^+} \bigg ) + \sum _{i=1}^m \frac{1}{\mathfrak {p}_i^+} \rightarrow \frac{1}{\mathfrak {p}_+} < 1, \quad \text { if } s_i \rightarrow \mathfrak {p}_i^+, \, i=1, \ldots , m. \end{aligned}$$

This means that whenever $\mathfrak {p}_+>1$, one can always choose $s_i$ (for example, sufficiently close to $\mathfrak {p}_i^+$) such that $\frac{1}{s} \le 1$.

To illustrate the existence, we present a special case:

$$\begin{aligned} \frac{1}{\mathfrak {p}_-} - \frac{1}{\mathfrak {p}_+} < \mathfrak {p}_i^+ \bigg (\frac{1}{\mathfrak {p}_i^-} - \frac{1}{\mathfrak {p}_i^+}\bigg ), \quad i=1, \ldots , m, \end{aligned}$$

where $\frac{1}{\mathfrak {p}_{\pm }}:= \sum _{i=1}^m \frac{1}{\mathfrak {p}_i^{\pm }}$. In this scenario, picking

$$\begin{aligned} s_i:= \mathfrak {p}_i^- \bigg [1 + \bigg (\frac{1}{\mathfrak {p}_-} - \frac{1}{\mathfrak {p}_+}\bigg )\bigg ], \quad i=1, \ldots , m, \end{aligned}$$

we easily verify that $s_i \in (\mathfrak {p}_i^-, \mathfrak {p}_i^+)$ and

$$\begin{aligned} \frac{1}{s} = \sum _{i=1}^m \frac{1}{s_i} =\frac{1}{\mathfrak {p}_-} \bigg [\frac{1}{\mathfrak {p}_-} + \bigg ( 1- \frac{1}{\mathfrak {p}_+}\bigg )\bigg ]^{-1} <1, \end{aligned}$$

provided $\mathfrak {p}_+>1$.

Remark 1.4

Let T be an m-linear operator. If the hypotheses (1.2) and (1.5) are assumed for T and all exponents $q_i \in (\mathfrak {p}_i^-, \mathfrak {p}_i^+)$, then we will get better estimates. This means the following extrapolation: Assume that for all exponents $p_i \in (\mathfrak {p}_i^{-}, \mathfrak {p}_i^{+})$ and all weights $w_i^{p_i} \in A_{p_i/\mathfrak {p}_i^{-}} \cap RH_{(\mathfrak {p}_i^{+}/p_i)'}$, $i=1, \ldots , m$,

$$\begin{aligned} \Vert T(\textbf{f})\Vert _{L^p(w^p)} \le \prod _{i=1}^m \Phi _i \Big ([w_i^{p_i}]_{A_{p_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/p_i)'}}\Big ) \Vert f_i\Vert _{L^{p_i}(w_i^{p_i})}, \end{aligned}$$

where $\frac{1}{p} = \sum _{i=1}^m \frac{1}{p_i}$ and $w=\prod _{i=1}^m w_i$. Then for all exponents $p_i, r_i \in (\mathfrak {p}_i^{-}, \mathfrak {p}_i^{+})$ and all weights $w_i^{p_i} \in A_{p_i/\mathfrak {p}_i^{-}} \cap RH_{(\mathfrak {p}_i^{+}/p_i)'}$, $i=1, \ldots , m$, we have

$$\begin{aligned}{} & {} \bigg \Vert \Big (\sum _k |T(\textbf{f}^k)|^r \Big )^{\frac{1}{r}}\bigg \Vert _{L^p(w^p)} \\{} & {} \quad \le C_0 \prod _{i=1}^m \Phi _i \Big (C_i \, [w_i^{p_i}]_{A_{p_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/p_i)'}}^{\gamma _i(p_i, r_i)}\Big ) \bigg \Vert \Big (\sum _k |f^k_i|^{r_i} \Big )^{\frac{1}{r_i}}\bigg \Vert _{L^{p_i}(w_i^{p_i})}, \end{aligned}$$

where $\textbf{f}^k=(f_1^k, \ldots , f_m^k)$, $\frac{1}{r} = \sum _{i=1}^m \frac{1}{r_i}$, $C_0$ and $C_i$ depend only on n, $p_i$, $r_i$, $\mathfrak {p}_i^-$, and $\mathfrak {p}_i^+$.

Moreover, for the same family of exponents $\textbf{p}$ and weights $\textbf{w}$, for all functions ${\textbf {b}}=(b_1,\ldots , b_m) \in {\text {BMO}}^m$, and for each multi-index $\alpha \in \mathbb {N}^m$, we have

$$\begin{aligned} \Vert [T, {\textbf {b}}]_{\alpha }(\textbf{f})\Vert _{L^p(w^p)} \le C'_0 \prod _{i=1}^m {\widetilde{\Phi }}_i \Big (C'_i \, [w_i^{p_i}]_{A_{p_i/\mathfrak {p}_i^{-}} \cap RH_{(\mathfrak {p}_i^{+}/p_i)'}}^{\gamma _i(p_i, s_i)}\Big ) \Vert b_i\Vert _{{\text {BMO}}}^{\alpha _i} \Vert f_i\Vert _{L^{p_i}(w_i^{p_i})}, \end{aligned}$$

and

$$\begin{aligned} \bigg \Vert \Big (\sum _k | [T, {\textbf {b}}]_{\alpha }(\textbf{f}^k)|^r \Big )^{\frac{1}{r}} \bigg \Vert _{L^p(w^p)}&\le C''_0 \prod _{i=1}^m {\widetilde{\Phi }}_i \Big (C''_i \, [w_i^{p_i}]_{A_{p_i/\mathfrak {p}_i^{-}} \cap RH_{(\mathfrak {p}_i^{+}/p_i)'}}^{\gamma _i(p_i, r_i) \gamma _i(r_i, s_i)}\Big ) \\&\qquad \times \Vert b_i\Vert _{{\text {BMO}}}^{\alpha _i} \bigg \Vert \Big (\sum _k |f^k_i|^{r_i} \Big )^{\frac{1}{r_i}}\bigg \Vert _{L^{p_i}(w_i^{p_i})}, \end{aligned}$$

whenever $\frac{1}{s}:= \sum _{i=1}^m \frac{1}{s_i} \le 1$ with $s_i \in (\mathfrak {p}_i^-, \mathfrak {p}_i^+)$, where ${\widetilde{\Phi }}_i(t):= t^{\alpha _i \max \{1, \frac{1}{\tau _{s_i}-1}\}} \Phi _i(C_i \, t)$, $C'_0$ depends only on $\alpha$, n, $p_i$, $s_i$, $\mathfrak {p}_i^-$, and $\mathfrak {p}_i^+$, $C'_i$ depends only on n, $p_i$, $s_i$, $\mathfrak {p}_i^-$, and $\mathfrak {p}_i^+$, and $C''_0$ depends only on $\alpha$, n, $p_i$, $r_i$, $s_i$, $\mathfrak {p}_i^-$, and $\mathfrak {p}_i^+$, and $C''_i$ depends only on n, $p_i$, $r_i$, $s_i$, $\mathfrak {p}_i^-$, and $\mathfrak {p}_i^+$. The proof is the same as that of Theorems 1.1 and 1.2. Details are left to the reader.

1.2 Historical Background

In the last two decades, it has been of great interest to obtain sharp weighted norm inequalities for operators T, which concerns estimates of the form

$$\begin{aligned} \Vert T\Vert _{L^p(w) \rightarrow L^p(w)} \le C_{n, p, T} \, {[}w]_{A_p}^{\alpha _p(T)}, \quad \forall p \in (1, \infty ), \, w \in A_p, \end{aligned}$$

(1.8)

where the positive constant $C_{n, p, T}$ depends only on n, p, and T, and the exponent $\alpha _p(T)$ is optimal such that (1.8) holds. This kind of estimates gives the exact rate of growth of the weights norm. The first result was given by Buckley [10] for the Hardy–Littlewood maximal operator M that

$$\begin{aligned} \Vert M\Vert _{L^p(w) \rightarrow L^p(w)} \le C_{n, p} \, {[}w]_{A_p}^{\frac{1}{p-1}},\quad \forall p \in (1, \infty ), \, w \in A_p, \end{aligned}$$

(1.9)

and the exponent $\frac{1}{p-1}$ is the best possible. The problem (1.8) for singular integrals gained new momentum from certain important applications to PDE. In the borderline case, a long-standing regularity problem for the solution of Beltrami equation on the plane was conjectured by Astala, Iwaniec, and Saksman [1], and first settled by Petermichl and Volberg [83] based on the sharp weighted estimate for the Ahlfors-Beurling operator B with $\alpha _2(B)=1$. Then a question arose whether (1.8) with $\alpha _2(T)=1$ holds for the general Calderón–Zygmund operators T, which is known as the $A_2$ conjecture. Focusing on the critical case $p=2$ results from a quantitative version of Rubio de Francia extrapolation due to Dragičević et al. [38].

Since then, many remarkable publications came to enrich the literature in this area. Petermichl [80] applied the method of Bellman function to obtain (1.8) for Hilbert transform H by showing $\alpha _2(H)=1$. The same estimate holds for Riesz transforms $R_j$ on $\mathbb {R}^n$, see [81]. Later on, Lacey, Petermichl, and Reguera [62] investigated Haar shift operators $S_{\tau }$ with parameter $\tau$ in order to present a unified approach to obtain the sharp weighted estimates for B, H, and $R_j$, by proving $\alpha _2(S_{\tau })=1$ and noting that such three kinds of operators can be obtained by appropriate averaging of Haar shifts, see [39, 79, 82]. By means of local mean oscillation and extrapolation with sharp constants [38], Lerner [64] established the sharp estimates (1.8) for Littlewood–Paley operators S with $\alpha _p(S)=\max \{\frac{1}{2}, \frac{1}{p-1}\}$, and Cruz-Uribe et al. [33] gave an alternative and simpler proof of (1.8) for B, H, and $R_j$. In 2012, Hytönen [51] fully solved the $A_2$ conjecture by showing a resulting representation of an arbitrary Calderón–Zygmund operator as an average of dyadic shifts over random dyadic systems. Significantly, it opened the study of dyadic analysis in the fields including the multilinear theory, the multiparameter theory, and the non-homogeneous theory. In particular, in terms of sharp weighted estimates, it promoted the development of sparse domination for varieties of operators. To sum up, there are three kinds of sparse domination: identities with suitable averaging, pointwise dominations, and bilinear forms. The specific type depends on the singularity of operators. For example, the Calderón–Zygmund operator [51] and Riesz potential [17] can be recovered from dyadic operators by averaging over dyadic grids. The pointwise sparse dominations hold for the Calderón–Zygmund operators [65] and the corresponding commutators [69], the multilinear Calderón–Zygmund operators [37], the multilinear pseudo-differential operators [20], and the multilinear Littlewood–Paley operators with minimal regularity [21]. Additionally, the sparse domination with a bilinear form goes to singular non-integral operators [9], Bochner–Riesz multipliers [6, 60], rough operators [27], and oscillatory integrals [63].

As aforementioned, one of the most useful and powerful tools in the weighted theory is the celebrated Rubio de Francia extrapolation theorem [84], which states that if a given operator T is bounded on $L^{p_0}(w_0)$ for some $p_0 \in [1, \infty )$ and for all $w_0 \in A_{p_0}$, then T is bounded on $L^p(w)$ for all $p \in (1, \infty )$ and for all $w \in A_p$. Indeed, extrapolation theorems allow us to reduce the general weighted $L^p$ estimates for certain operators to a suitable case $p=p_0$, for example, see [20] for the Coifman-Fefferman’s inequality for $p_0 = 1$, [33, 51] for the Calderón–Zygmund operators for $p_0 = 2$, [33, 64] for square functions for $p_0=3$, and [61] for fractional integral operators for $p_0 \in (1, n/\alpha )$ with $0<\alpha <n$. Even more, the technique of extrapolation can refine some weighted estimates, see [31] for the Sawyer conjecture, [66, 67] for the weak Muckenhoupt–Wheeden conjecture, and [20, 77] for the local exponential decay estimates. Another interesting point is that by means of extrapolation, the vector-valued inequalities immediately follows from the corresponding scalar-valued estimates.

Over the years, Rubio de Francia’s result has been extended and complemented in different manners, see [32] and the references therein. Using the boundedness of the Hardy–Littlewood maximal operator instead of the Muckenhoupt weights, Cruz-Uribe and Wang [35] presented extrapolation in variable Lebesgue spaces, which was improved to generalized Orlicz spaces [29] and general Banach function spaces [18]. It is worth mentioning that the latter was stated in measure spaces and for general Muckenhoupt bases. This leads lots of applications, such as the well-posedness of the Dirichlet problem in the upper half-space whenever the boundary data belongs to different function spaces, the weighted boundedness of layer potential operators on domains, and the local Tb theorem for square functions in non-homogeneous spaces. Recently, a longstanding problem about extrapolation for multilinear Muckenhoupt classes of weights was solved by Li, Martell, and Ombrosi [71] by introducing some new multilinear Muckenhoupt classes $A_{\textbf{p}, \textbf{r}}$ (cf. Definition 2.7), which contains the multivariable nature and is a generalization of the classes $A_{\textbf{p}}$ introduced in [68] (cf. (2.31) below). Shortly afterwards, it was improved to the case with infinite exponents in [72] and with a quantitative bound in [76]. On the other hand, Hytönen and Lappas [53, 54] established a “compact version” of Rubio de Francia’s extrapolation theorem, which allows one to extrapolate the compactness of an operator from just one space to the full range of weighted spaces, provided that the operator is bounded. This result has been extended to the multilinear setting [19] by means of weighted interpolation for multilinear compact operators and weighted Fréchet–Kolmogorov characterization of compactness in the non-Banach case.

1.3 Structure of the Paper

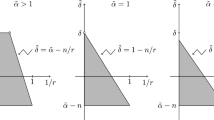
In Sect. 2, we present some preliminaries and auxiliary results including the embedding and factorization of Muckenhoupt weights. Section 3 includes quantitative weighted estimates for various operators. Section 4 is devoted to showing Theorems 1.1 and 1.2 by means of a limited range off-diagonal extrapolation and extrapolation for commutators with Banach ranges. We also establish “product-type embedding” theorems to deduce quantitative $A_p$ and off-diagonal extrapolation. In Sect. 5, we include many applications of Theorems 1.1 and 1.2. First, we give quantitative weighted norm inequalities for the bilinear Bochner–Riesz means of order $\delta$ and commutators, where we utilize the $A_{p_1} \times A_{p_2}$ weights when $\delta \ge n-1/2$, and the $A_{p_1/\mathfrak {p}_1^-} \cap RH_{(\mathfrak {p}_1^+/p_1)'} \times A_{p_2/\mathfrak {p}_2^-} \cap RH_{(\mathfrak {p}_2^+/p_2)'}$ weights when $0<\delta <n-1/2$. The same weights conditions are used for the bilinear rough singular integrals for $\Omega \in L^{\infty }(\mathbb {S}^{n-1})$ and $L^q(\mathbb {S}^{n-1})$ with $q \in (1, \infty )$, respectively. Additionally, under the minimal Sobolev regularity, we obtain the quantitative weighted bounds for the m-linear Fourier multipliers, the corresponding higher order commutators, and vector-valued inequalities, which only hold for product of scalar weights as mentioned before. Beyond that, after presenting quantitative weighted Littlewood–Paley theory, we establish weighted jump and variational inequalities for rough operators with $\Omega \in L^q(\mathbb {S}^{n-1})$ with $q \in (1, \infty )$. The proof also needs quantitative weighted estimates for rough singular integrals $T_{\Omega }$ and rough maximal operators $M_{\Omega }$, see Sect. 3. They contain many applications to Harmonic Analysis since variation inequalities not only immediately yield the pointwise convergence of the family of operators without using the Banach principle, but also can be used to measure the speed of convergence. Finally, we end up Sect. 5 with Riesz transforms associated to Schrödinger operators.

2 Preliminaries and Auxiliary Results

A measurable function w on $\mathbb {R}^n$ is called a weight if $0<w(x)<\infty$ for a.e. $x \in \mathbb {R}^n$. For $p \in (1, \infty )$, we define the Muckenhoupt class $A_p$ as the collection of all weights w on $\mathbb {R}^n$ satisfying

where the supremum is taken over all cubes $Q \subset \mathbb {R}^n$. As for the case $p=1$, we say that $w\in A_1$ if

Then, we define $A_{\infty }:=\bigcup _{p\ge 1}A_p$ and $[w]_{A_{\infty }}=\inf _{p>1} [w]_{A_p}$.

Given $1 \le p \le \infty$ and $0<q \le \infty$, we say that $w \in A_{p,q}$ if it satisfies

where one has to replace the first term by $\mathop {\mathrm {ess\,sup}}\limits _Q w$ when $q=\infty$ and the second term by $\mathop {\mathrm {ess\,sup}}\limits _Q w^{-1}$ when $p=1$. One can easily check that $w \in A_{p, q}$ if and only if $w^q \in A_{1+q/p'}$ if and only if $w^{-p'} \in A_{1+p'/q}$ with

$$\begin{aligned} {[}w]_ {A_{p, q}} =[w^q]_{A_{1+q/p'}}^{\frac{1}{q}} =[w^{-p'}]_{A_{1+p'/q}}^{\frac{1}{p'}}, \quad \text {when }\, 1<p \le \infty , \, 0<q<\infty . \end{aligned}$$

If $p=1$ and $0<q<\infty$, then $w \in A_{p, q}$ if and only if $w^q \in A_1$ with $[w]_{A_{p, q}} = [w^q]_{A_1}^{\frac{1}{q}}$. If $1<p \le \infty$ and $q=\infty$, $w \in A_{p, q}$ if and only if $w^{-p'} \in A_1$ with $[w]_{A_{p, q}}=[w^{-p'}]_{A_1}^{\frac{1}{p'}}$.

For $s\in (1,\infty ]$, the reverse Hölder class $RH_s$ is the collection of all weights w such that

When $s=\infty$, is understood as $(\mathop {\mathrm {ess\,sup}}\limits _{Q}w)$. Define $RH_1:= \bigcup \limits _{1<s \le \infty } RH_s$. Then we see that $RH_1=A_{\infty }$ (cf. [45, Theorem 7.3.3]).

2.1 Muchenhoupt Weights

The Hardy–Littlewood maximal operator M is defined by

where the supremum is taken over all cubes $Q \subset \mathbb {R}^n$ containing x. We begin with the following estimate concerning the growth of $C_{n, p}$ in (1.9) with respect to n and p.

Lemma 2.1

For any $p \in (1, \infty )$ and $w \in A_p$,

$$\begin{aligned} \Vert M\Vert _{L^p(w) \rightarrow L^p(w)} \le 2^n \cdot 3^{n\left( \frac{p}{p-1}+\frac{6}{p}\right) } \, [w]_{A_p}^{\frac{1}{p-1}}. \end{aligned}$$

(2.1)

Proof

We follow the proof of [45, Theorem 7.1.9] to track the precise constants. Given a weight w, the centered weighted Hardy-Littlewood maximal operator $M_w^c$ is defined by

$$\begin{aligned} M_w^c f(x):= \sup _{Q \ni x} \frac{1}{w(Q)} \int _Q |f(y)| \, dw(y), \end{aligned}$$

where the supremum is taken over all cubes $Q \subset \mathbb {R}^n$ centered at x. Let $M^c$ denote $M_w^c$ when $w \equiv 1$. It was proved in [45, p.509] that

$$\begin{aligned} \Vert M_w^c\Vert _{L^1(w) \rightarrow L^{1, \infty }(w)} \le 24^n \quad \text { and }\quad \Vert M_w^c\Vert _{L^{\infty }(w) \rightarrow L^{\infty }(w)} \le 1, \end{aligned}$$

(2.2)

which together with interpolation theorem gives that for any weight w,

$$\begin{aligned} \Vert M_w^c\Vert _{L^p(w) \rightarrow L^p(w)} \le 24^{\frac{n}{p}}, \quad \forall p \in (1, \infty ). \end{aligned}$$

(2.3)

To proceed, we fix $w \in A_p$ with $p \in (1, \infty )$, and set $\sigma :=w^{-\frac{1}{p-1}}$. As shown in [45, p. 508] that

$$\begin{aligned} Mf(x) \le 2^n M^c f(x) \le 2^n \cdot 3^{\frac{np}{p-1}} {[}w]_{A_p}^{\frac{1}{p-1}} M_w^c\big (M_{\sigma }^c(f \sigma ^{-1})^{p-1} w^{-1} \big )(x)^{\frac{1}{p-1}}. \end{aligned}$$

which along with (2.3) in turn implies

$$\begin{aligned} \Vert M\Vert _{L^p(w) \rightarrow L^p(w)}&\le 2^n \cdot 3^{\frac{np}{p-1}} {[}w]_{A_p}^{\frac{1}{p-1}} \Vert M_w^c\Vert _{L^{p'}(w) \rightarrow L^{p'}(w)}^{\frac{1}{p-1}} \Vert M_{\sigma }^c\Vert _{L^p(\sigma ) \rightarrow L^p(\sigma )} \\&\le 2^n \cdot 3^{\frac{np}{p-1}} \cdot 24^{\frac{n}{p'(p-1)} + \frac{n}{p}} [w]_{A_p}^{\frac{1}{p-1}} < 2^n \cdot 3^{n(\frac{p}{p-1}+\frac{6}{p})} [w]_{A_p}^{\frac{1}{p-1}}. \end{aligned}$$

The proof is complete. $\square$

Based on the weighted boundedness of Hardy–Littlewood maximal operator above, one can establish Rubio de Francia extrapolation theorem below, whose proof was contained in [32].

Theorem 2.2

For any $p \in (1, \infty )$ and $w \in A_p$, there exists an operator $\mathcal {R}: L^p(w) \rightarrow L^p(w)$ such that for every non-negative function $h \in L^p(w)$,

• (a) $h \le \mathcal {R} h$;

• (b) $\Vert \mathcal {R} h\Vert _{L^p(w)} \le 2 \Vert h\Vert _{L^p(w)}$;

• (c) $\mathcal {R}h \in A_1$ with $[\mathcal {R} h]_{A_1} \le 2 \Vert M\Vert _{L^p(w) \rightarrow L^p(w)}$.

Let us recall the sharp reverse Hölder’s inequality.

Lemma 2.3

Let $p \in (1, \infty )$ and $w \in A_p$. Then there holds

(2.4)

for every cube Q, where

$$\begin{aligned} \gamma _w= {\left\{ \begin{array}{ll} \frac{1}{2^{n+1}[w]_{A_1}}, &{} p=1, \\ \frac{1}{2^{n+1+2p}[w]_{A_p}}, &{}p \in (1, \infty ), \\ \frac{1}{2^{n+11}[w]_{A_{\infty }}}, &{}p=\infty . \end{array}\right. } \end{aligned}$$

(2.5)

In particular, for any measurable subset $E \subset Q$,

$$\begin{aligned} w(E)/w(Q) \le 2 (|E|/|Q|)^{\frac{\gamma _w}{1+\gamma _w}}. \end{aligned}$$

(2.6)

Proof

The estimate (2.4) was proved in [26, 55, 66]. Let us prove (2.6). If we set $r:=1+\gamma _w$, then (2.4) implies that for any measurable subset $E \subset Q$,

This shows (2.6). $\square$

Lemma 2.4

For any $q \in (1, \infty )$ and $v \in A_q$, there exist $\gamma \in (0, 2^{-n-3})$ and $q_0 \in (1, q)$ such that

$$\begin{aligned} \begin{aligned} q_0&= \frac{q}{1+\varepsilon }, \quad \frac{(q-1)\gamma }{q(1+\gamma )'}< \varepsilon < \frac{q-1}{(1+\gamma )'}, \quad (1+\gamma )' \simeq {[}v]_{A_q}^{\max \{1, \frac{1}{q-1}\}},\\&\quad [v^{1+\gamma }]_{A_q} \le 2^{q(1+\gamma )} [v]_{A_q}^{1+\gamma }, \quad \text { and }\quad [v]_{A_{q_0}} \le 2^q [v]_{A_q}. \end{aligned} \end{aligned}$$

(2.7)

Proof

Let $q \in (1, \infty )$ and $v \in A_q$. Then, $v^{1-q'} \in A_{q'}$, and by Lemma 2.3,

(2.8)

and

(2.9)

for any cube $Q \subset \mathbb {R}^n$, where

$$\begin{aligned} \gamma _1 := \frac{1}{2^{n+1+2q}[v]_{A_q}} \quad \text { and }\quad \gamma _2 := \frac{1}{2^{n+1+2q}[v^{1-q'}]_{A_{q'}}}. \end{aligned}$$

(2.10)

Setting

$$\begin{aligned} \gamma := \min \{\gamma _1, \gamma _2\} < 2^{-n-3} \quad \text {and}\quad q_0 := \frac{q}{1+\varepsilon } = \frac{q+\gamma }{1+\gamma } \in (1, q), \end{aligned}$$

(2.11)

we see that

$$\begin{aligned} \frac{(q-1)\gamma }{q(1+\gamma )'}<\varepsilon = \frac{(q-1) \gamma }{q+\gamma } < \frac{(q-1)\gamma }{1+\gamma } = \frac{q-1}{(1+\gamma )'}, \end{aligned}$$

and use Jensen’s inequality and (2.8)–(2.10) to obtain

$$\begin{aligned} (1+\gamma )' \simeq \max \{[v]_{A_q}, [v^{1-q'}]_{A_{q'}}\} = {[}v]_{A_q}^{\max \{1, \frac{1}{q-1}\}}, \end{aligned}$$

and

which immediately implies (2.7). $\square$

Lemma 2.5

The following properties hold:

• (a) Let $1 \le p \le p_0 < \infty$. Then for any $u \in A_p$ and $v \in A_1$,

  $$\begin{aligned} uv^{p-p_0} \in A_{p_0} \quad \text {with}\quad [u v^{p-p_0}]_{A_{p_0}} \le [u]_{A_p} [v]_{A_1}^{p_0-p}. \end{aligned}$$

• (b) Let $1 \le q_0, q_1<\infty$. Then for any $w_0 \in A_{q_0}$, $w_1 \in A_{q_1}$, and $\theta \in [0, 1]$,

  $$\begin{aligned} {[}w]_{A_q} \le [w_0]_{A_{q_0}}^{(1-\theta ) \frac{q}{q_0}} {[}w_1]_{A_{q_1}}^{\theta \frac{q}{q_1}}, \end{aligned}$$

  where $\frac{1}{q} = \frac{1-\theta }{q_0} + \frac{\theta }{q_1}$ and $w^{\frac{1}{q}} = w_0^{\frac{1-\theta }{q_0}} w_1^{\frac{\theta }{q_1}}$. In particular, for any $1 \le p_0< p<\infty$, $u \in A_p$, and $v \in A_1$,

  $$\begin{aligned} u^{\frac{p_0-1}{p-1}} v^{\frac{p-p_0}{p-1}} \in A_{p_0} \quad \text { with }\quad \big [u^{\frac{p_0-1}{p-1}} v^{\frac{p-p_0}{p-1}} \big ]_{A_{p_0}} \le [u]_{A_p}^{\frac{p_0-1}{p-1}} {[}v]_{A_1}^{\frac{p-p_0}{p-1}}. \end{aligned}$$

Proof

We begin with showing part (a). Let $u \in A_p$ and $v \in A_1$. For each cube Q,

(2.12)

Set $r=\frac{p'-1}{p'_0-1} = \frac{p_0-1}{p-1} \ge 1$. Then $r'=\frac{p_0-1}{p_0-p}$, and by Hölder’s inequality,

(2.13)

Then it follows from (2.12) and (2.13) that $[u v^{p-p_0}]_{A_{p_0}} \le [u]_{A_p} [v]_{A_1}^{p_0-p}$.

Next, let us prove part (b). Note that $\frac{1}{q} = \frac{1-\theta }{q_0} + \frac{\theta }{q_1}$, and then

$$\begin{aligned} \frac{1-\theta }{\frac{q_0}{q_0-1}} + \frac{\theta }{\frac{q_1}{q_1-1}} =(1-\theta ) \bigg (1-\frac{1}{q_0}\bigg ) + \theta \bigg (1-\frac{1}{q_1}\bigg ) =1-\frac{1-\theta }{q_0} - \frac{\theta }{q_1} =\frac{q-1}{q}. \end{aligned}$$

Thus, Hölder’s inequality gives

(2.14)

and

(2.15)

By definition, (2.14), and (2.15), we immediately obtain $[w]_{A_q} \le [w_0]_{A_{q_0}}^{(1-\theta ) \frac{q}{q_0}} [w_1]_{A_{q_1}}^{\theta \frac{q}{q_1}}$. To conclude the proof, it suffices to pick

$$\begin{aligned} w_0:= u, w_1:= v, q_0:= p, q_1:= 1, q:= p_0, \quad w:= u^{\frac{p_0-1}{p-1}} v^{\frac{p-p_0}{p-1}}, \theta := \frac{p-p_0}{p_0(p-1)}, \end{aligned}$$

and note that $w_0^{\frac{1-\theta }{q_0}} w_1^{\frac{\theta }{q_1}} =u^{\frac{p_0-1}{p_0(p-1)}} v^{\frac{p-p_0}{p_0(p-1)}} =w^{\frac{1}{p_0}} =w^{\frac{1}{q}}$, and

$$\begin{aligned} \frac{1-\theta }{q_0} + \frac{\theta }{q_1}&=\frac{p_0-1}{p_0(p-1)} + \frac{p-p_0}{p_0(p-1)} =\frac{1}{p_0} = \frac{1}{q}. \end{aligned}$$

The proof is complete. $\square$

We sum up some of the properties of these classes in the following result.

Lemma 2.6

The following statements hold:

• (a) For any $w_1, w_2 \in A_1$, $w:=w_1^{1/s} w_{2}^{1-p} \in A_p \cap RH_s$ for all $1 \le p < \infty$ and $1<s \le \infty$. Moreover,

  $$\begin{aligned} \max \{[w]_{A_p}, [w]_{RH_s} \} \le [w_1]_{A_1}^{\frac{1}{s}} {[}w_2]_{A_1}^{p-1}. \end{aligned}$$

  (2.16)

• (b) Given $1 \le p < \infty$ and $1 \le s < \infty$, $w \in A_p \cap RH_s$ if and only if $w^s \in A_{\tau }$. Moreover,

  $$\begin{aligned} {[}w^s]_{A_{\tau }} \le [w]_{A_p}^s [w]_{RH_s}^s \quad \text {and}\quad \max \big \{[w]_{A_p}^s, [w]_{RH_s}^s \big \} \le [w^s]_{A_{\tau }}, \end{aligned}$$

  (2.17)

  where $\tau =s(p-1)+1$.

• (c) Let $1 \le \mathfrak {p}_- < \mathfrak {p}_+ \le \infty$ and $p \in (\mathfrak {p}_-, \mathfrak {p}_+)$. Then $w^p \in A_{p/\mathfrak {p}_-} \cap RH_{(\mathfrak {p}_+/p)'}$ if and only if $w^{-p'} \in A_{p'/\mathfrak {p}'_+} \cap RH_{(\mathfrak {p}'_-/p')'}$ with

  $$\begin{aligned} {[}w^{p(\mathfrak {p}_+/p)'}]_{A_{\tau _p}} = {[}w^{-p'(\mathfrak {p}'_-/p')'}]_{A_{\tau '_p}}^{\tau _p -1}, \end{aligned}$$

  (2.18)

  where $\tau _p= \big (\frac{\mathfrak {p}_+}{p}\big )' \big (\frac{p}{\mathfrak {p}_-} -1\big ) +1$.

• (d) Given $1 \le \mathfrak {p}_- < \mathfrak {p}_+ \le \infty$, $p \in (\mathfrak {p}_-, \mathfrak {p}_+)$, and $w^p \in A_{p/\mathfrak {p}_-} \cap RH_{(\mathfrak {p}_+/p)'}$, there exists ${\widetilde{\mathfrak {p}}}_- \in (\mathfrak {p}_-, p)$ such that $w^p \in A_{p/{\widetilde{\mathfrak {p}}}_-} \cap RH_{(\mathfrak {p}_+/p)'}$ with

  $$\begin{aligned} {[}w^{p(\mathfrak {p}_+/p)'}]_{A_{{\widetilde{\tau }}_p}} \le 2^{\tau _p} {[}w^{p(\mathfrak {p}_+/p)'}]_{A_{\tau _p}} \quad \text { and }\quad \frac{\frac{1}{{\widetilde{\mathfrak {p}}}_-}}{\frac{1}{{\widetilde{\mathfrak {p}}}_-} - \frac{1}{p}} < (1+2^{-n-3}) \frac{\frac{1}{\mathfrak {p}_-}}{\frac{1}{\mathfrak {p}_-} - \frac{1}{p}}, \end{aligned}$$

  (2.19)

  where $\tau _p= \big (\frac{\mathfrak {p}_+}{p}\big )' \big (\frac{p}{\mathfrak {p}_-} -1\big ) +1$ and ${\widetilde{\tau }}_p = \big (\frac{\mathfrak {p}_+}{p}\big )' \big (\frac{p}{{\widetilde{\mathfrak {p}}}_-} -1\big ) +1$.

Proof

Parts (a)–(c) are essentially contained in [3, 56]. We present a detailed proof to track the weight norms. To show (a), we fix $1 \le p < \infty$, $1<s \le \infty$, and let $w_1, w_2 \in A_1$. By Jensen’s inequality,

(2.20)

and

(2.21)

when $p=1$, the inequality (2.21) is replaced by

$$\begin{aligned} \mathop {\mathrm {ess\,sup}}\limits _Q w^{-1} = \big (\mathop {\mathrm {ess\,sup}}\limits _Q w_1^{-1} \big )^{\frac{1}{s}}. \end{aligned}$$

(2.22)

Then it follows from (2.20)–(2.22) that

$$\begin{aligned} {[}w]_{A_p} \le [w_1]_{A_1}^{\frac{1}{s}} [w_2]_{A_1}^{p-1}. \end{aligned}$$

Moreover, by definition and Jensen’s inequality, we have

when $s=\infty$, the above still holds since is replaced by $\mathop {\mathrm {ess\,sup}}\limits _Q w$. This means

$$\begin{aligned} {[}w]_{RH_s} \le [w_1]_{A_1}^{\frac{1}{s}} [w_2]_{A_1}^{p-1}. \end{aligned}$$

Let us next show (b). Assume first that $w \in A_p \cap RH_s$. Note that for any cube Q,

(2.23)

This implies

and hence,

$$\begin{aligned} {[}w^s]_{A_{\tau }} \le [w]_{A_p}^s [w]_{RH_s}^s . \end{aligned}$$

(2.24)

On the other hand, assuming $w^s \in A_{\tau }$, we deduce by Jensen’s inequality and (2.23),

(2.25)

and

(2.26)

which follows from

Then, (2.25) and (2.26) imply

$$\begin{aligned} {[}w]_{A_p} \le [w^s]_{A_{\tau }}^{\frac{1}{s}} \quad \text { and }\quad {[}w]_{RH_s} \le [w^s]_{A_{\tau }}^{\frac{1}{s}}. \end{aligned}$$

(2.27)

Hence, (b) follows from (2.24) and (2.27).

We turn to the proof of (c). One can check that

$$\begin{aligned} \bigg (\frac{\mathfrak {p}_+}{p}\bigg )' (\tau '_p - 1) = \bigg (\frac{\mathfrak {p}'_-}{p'} \bigg )'(p' -1) \quad \text { and }\quad \tau '_p = \bigg (\frac{\mathfrak {p}'_-}{p'} \bigg )' \bigg (\frac{p'}{\mathfrak {p}'_+} - 1 \bigg ) +1 . \end{aligned}$$

(2.28)

Then it follows that

$$\begin{aligned} -p'(\mathfrak {p}'_-/p')' (1-(\tau '_p)') = p(p'-1) (\mathfrak {p}'_-/p')' (\tau _p - 1) = p(\mathfrak {p}_+/p)', \end{aligned}$$

and for any cube Q,

which implies

$$\begin{aligned} {[}w^{p(\mathfrak {p}_+/p)'}]_{A_{\tau _p}} = {[}w^{-p(\mathfrak {p}'_-/p')'}]_{A_{\tau '_p}}^{\tau _p -1}. \end{aligned}$$

Finally, let us demonstrate (d). By part (b), there holds $v:= w^{p(\mathfrak {p}_+/p)'} \in A_{\tau _p}$, which along with (2.7) and (2.11) applied to exponents $q=\tau _p$ and $q_0={\widetilde{\tau }}_p$, to arrive at the first estimate in (2.19) and

$$\begin{aligned} {\widetilde{\mathfrak {p}}}_- = \frac{p}{1+\frac{\tau _p - 1}{(\mathfrak {p}_+/p)' (1+\gamma )}} = \frac{1}{\frac{1}{p} + \frac{1}{1+\gamma }(\frac{1}{\mathfrak {p}_-} - \frac{1}{p})} \in (\mathfrak {p}_-, p). \end{aligned}$$

Moreover,

$$\begin{aligned} \frac{\frac{1}{{\widetilde{\mathfrak {p}}}_-}}{\frac{1}{{\widetilde{\mathfrak {p}}}_-} - \frac{1}{p}} = (1+\gamma ) \frac{\mathfrak {p}_-}{{\widetilde{\mathfrak {p}}}_-} \frac{\frac{1}{\mathfrak {p}_-}}{\frac{1}{\mathfrak {p}_-} - \frac{1}{p}} < (1+2^{-n-3}) \frac{\frac{1}{\mathfrak {p}_-}}{\frac{1}{\mathfrak {p}_-} - \frac{1}{p}}, \end{aligned}$$

This proves the second estimate in (2.19) and completes the proof. $\square$

2.2 Multilinear Muckenhoupt Weights

The multilinear maximal operator is defined by

(2.29)

where the supremum is taken over all cubes Q containing x.

We are going to present the definition of the multilinear Muckenhoupt classes $A_{\textbf{p}, \textbf{r}}$ introduced in [71, 72]. Given $\textbf{p}=(p_1, \ldots , p_m)$ with $1 \le p_1, \ldots , p_m \le \infty$ and $\textbf{r}=(r_1, \ldots , r_{m+1})$ with $1 \le r_1, \ldots , r_{m+1} < \infty$, we say that $\textbf{r} \preceq \textbf{p}$ whenever

$$\begin{aligned} r_i \le p_i,\, i=1, \ldots , m, \text { and } r'_{m+1} \ge p, \text { where } \frac{1}{p}:=\frac{1}{p_1}+\dots +\frac{1}{p_m}. \end{aligned}$$

Analogously, we say that $\textbf{r} \prec \textbf{p}$ if $r_i<p_i$ for each $i=1, \ldots , m$, and $r'_{m+1}>p$.

Definition 2.7

Let $\textbf{p}=(p_1,\ldots ,p_m)$ with $1\le p_1, \ldots , p_m \le \infty$ and let $\textbf{r}=(r_1, \ldots , r_{m+1})$ with $1 \le r_1, \ldots , r_{m+1} < \infty$ such that $\textbf{r} \preceq \textbf{p}$. Suppose that $\textbf{w}=(w_1,\ldots ,w_m)$ and each $w_i$ is a weight on $\mathbb {R}^n$. We say that $\textbf{w} \in A_{\textbf{p}, \textbf{r}}$ if

(2.30)

where $\frac{1}{p} = \sum _{i=1}^m \frac{1}{p_i}$, $w=\prod _{i=1}^m w_i$, and the supremum is taken over all cubes $Q \subset \mathbb {R}^n$. When $p=r'_{m+1}$, the term corresponding to w needs to be replaced by $\mathop {\mathrm {ess\,sup}}\limits _Q w$ and, analogously, when $p_i=r_i$, the term corresponding to $w_i$ should be $\mathop {\mathrm {ess\,sup}}\limits _Q w_i^{-1}$. Also, if $p_i = \infty$, the term corresponding to $w_i$ becomes . If $p=\infty$, one will necessarily have $r_{m+1} = 1$ and $p_1= \cdots = p_m=\infty$, hence the term corresponding to w must be $\mathop {\mathrm {ess\,sup}}\limits _Q w$ while the terms corresponding to $w_i$ become . When $r_{m+1} = 1$ and $p<\infty$ the term corresponding to w needs to be replaced by .

Denote $A_{\textbf{p}}:= A_{\textbf{p}, (1, \ldots , 1)}$ in Definition 2.7, that is,

(2.31)

where $\frac{1}{p} = \sum _{i=1}^m \frac{1}{p_i}$ and $w=\prod _{i=1}^m w_i$. We would like to observe that our definition of the classes $A_{\textbf{p}}$ and $A_{\textbf{p}, \textbf{r}}$ is slightly different to that in [68] and [71]. Essentially, they are the same since picking $w_i=v_i^{p_i}$ for every $i=1, \ldots , m$ in (2.30) and (2.31), we see that $\textbf{v}=(v_1, \ldots , v_m)$ belongs to $A_{\textbf{p}, \textbf{r}}$ in [71] and to $A_{\textbf{p}}$ in [68], respectively.

Lemma 2.8

Let $1 \le \mathfrak {p}_i^{-}<\mathfrak {p}_i^{+} \le \infty$, $i=1, \ldots , m$. Assume that $p_i \in [\mathfrak {p}_i^-, \mathfrak {p}_i^+]$ and $w_i^{p_i} \in A_{p_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/p_i)'}$, $i=1, \ldots , m$. Then $\textbf{w}=(w_1, \ldots , w_m) \in A_{\textbf{q}, \textbf{r}}$ with

$$\begin{aligned} {[}\textbf{w}]_{A_{\textbf{q}, \textbf{r}}} \le \prod _{i=1}^m {[}w_i^{p_i(\mathfrak {p}_i^+/p_i)'}]_{A_{\tau _{p_i}}}^{\frac{1}{p_i} - \frac{1}{\mathfrak {p}_i^+}}, \end{aligned}$$

for any $\textbf{q}=(q_1, \ldots , q_m)$ with $1 \le q_1, \ldots , q_m < \infty$ and $\textbf{r} = (r_1, \ldots , r_{m+1})$ with $1 \le r_1, \ldots , r_{m+1} < \infty$ such that $\textbf{r} \preceq \textbf{q}$, and

$$\begin{aligned} \frac{1}{q} - \frac{1}{r'_{m+1}} = \sum _{i=1}^m \bigg (\frac{1}{p_i} - \frac{1}{\mathfrak {p}_i^+}\bigg ), \qquad \frac{1}{r_i} - \frac{1}{q_i} = \frac{1}{\mathfrak {p}_i^-} - \frac{1}{p_i}, \quad i=1, \ldots , m. \end{aligned}$$

(2.32)

Proof

By Lemma 2.6 part (b), one has

$$\begin{aligned} {\Big [}w_i^{p_i(\mathfrak {p}_i^+/p_i)'}\Big ]_{A_{\tau _{p_i}}} \le \Big ([w_i^{p_i}]_{A_{p_i/\mathfrak {p}_i^-}} [w_i^{p_i}]_{RH_{(\mathfrak {p}_i^+/p_i)'}} \Big )^{p_i(\mathfrak {p}_i^+/p_i)'}, \end{aligned}$$

where $\tau _{p_i}:= \big (\frac{\mathfrak {p}_i^+}{p_i} \big )' \big (\frac{p_i}{\mathfrak {p}_i^-} -1 \big ) +1$, $i=1, \ldots , m$. Set

$$\begin{aligned} \frac{1}{t_i} := \frac{1}{p_i} - \frac{1}{\mathfrak {p}_i^+} \quad \text { and }\quad \frac{1}{s_i} := 1- \bigg (\frac{1}{\mathfrak {p}_i^-} - \frac{1}{p_i} \bigg ), \quad i=1, \ldots , m. \end{aligned}$$

(2.33)

Then it is easy to check that

$$\begin{aligned} t_i = p_i(\mathfrak {p}_i^+/p_i)' \quad \text { and }\quad s'_i = t_i (\tau '_{p_i} -1), \quad i=1, \ldots , m, \end{aligned}$$

(2.34)

which gives

(2.35)

On the other hand, let $\textbf{q}=(q_1, \ldots , q_m)$ with $1 \le q_1, \ldots , q_m < \infty$ and $\textbf{r}=(r_1, \ldots , r_{m+1})$ with $1\le r_1, \ldots , r_{m+1}<\infty$ such that $\textbf{r} \preceq \textbf{q}$ and (2.32) holds. It follows from (2.32) and (2.33) that

$$\begin{aligned} \frac{1}{q}-\frac{1}{r'_{m+1}} = \frac{1}{t_1}+\cdots +\frac{1}{t_m} \quad \text { and }\quad \frac{1}{r_i} - \frac{1}{q_i} = \frac{1}{s'_i}, \quad i=1, \ldots , m. \end{aligned}$$

(2.36)

Thus, writing $w=\prod _{i=1}^m w_i$, we use (2.36) and Hölder’s inequality to obtain

(2.37)

As a consequence, collecting (2.33), (2.34), (2.35), and (2.37), we conclude that

$$\begin{aligned} {[}\textbf{w}]_{A_{\textbf{q}, \textbf{r}}} \le \prod _{i=1}^m [w_i]_{A_{s_i, t_i}} = \prod _{i=1}^m [w_i^{t_i}]_{A_{\tau _{p_i}}}^{\frac{1}{t_i}} = \prod _{i=1}^m {[}w_i^{p_i(\mathfrak {p}_i^+/p_i)'}]_{A_{\tau _{p_i}}}^{\frac{1}{p_i} - \frac{1}{\mathfrak {p}_i^+}}. \end{aligned}$$

This completes the proof. $\square$

Lemma 2.9

Let $1 \le \mathfrak {p}_i^{-}<\mathfrak {p}_i^{+} \le \infty$, $i=1, \ldots , m$. Assume that $p_i \in [\mathfrak {p}_i^-, \mathfrak {p}_i^+]$ and $w_i^{p_i} \in A_{p_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/p_i)'}$, $i=1, \ldots , m$. Write $w=\prod _{i=1}^m w_i$. Then $w^p \in A_{p/\mathfrak {p}_-} \cap RH_{(\mathfrak {p}_+/p)'}$ with

$$\begin{aligned}{}[{w}^{p(\mathfrak {p}_+/p)'}]_{A_{\tau _p}} \le \prod _{i=1}^m \left[ {w}_i^{p_i(\mathfrak {p}_i^+/p_i)'}\right] _{A_{\tau _{p_i}}}^{\frac{\frac{1}{p_i} - \frac{1}{\mathfrak {p}_i^+}}{\frac{1}{p} - \frac{1}{\mathfrak {p}_+}}}, \end{aligned}$$

(2.38)

where $\frac{1}{p}= \frac{1}{p_1} + \cdots + \frac{1}{p_m}$ and $\frac{1}{\mathfrak {p}_{\pm }} = \frac{1}{\mathfrak {p}_1^{\pm }} + \cdots + \frac{1}{\mathfrak {p}_m^{\pm }}$. In particular, if we take

$$\begin{aligned} w_{m+1} := w^{-1}, \quad p_{m+1} := p', \quad \mathfrak {p}_{m+1}^- := \mathfrak {p}'_+, \quad \text { and }\quad \mathfrak {p}_{m+1}^+ := \mathfrak {p}'_-, \end{aligned}$$

(2.39)

then it follows

$$\begin{aligned} {\Big [}w_{m+1}^{p_{m+1}(\mathfrak {p}_{m+1}^+/p_{m+1})'}\Big ]_{A_{\tau _{p_{m+1}}}} \le \prod _{i=1}^m {\Big [}w_i^{p_i(\mathfrak {p}_i^+/p_i)'}\Big ]_{A_{\tau _{p_i}}}^{\frac{\frac{1}{p_i} - \frac{1}{\mathfrak {p}_i^+}}{\frac{1}{\mathfrak {p}_-} - \frac{1}{p}}}. \end{aligned}$$

(2.40)

Proof

Set

$$\begin{aligned} \frac{1}{r}&:= \frac{1}{p} - \frac{1}{\mathfrak {p}_+} = \sum _{i=1}^m \Big (\frac{1}{p_i} -\frac{1}{\mathfrak {p}_i^+} \Big ) =: \sum _{i=1}^m \frac{1}{r_i}, \end{aligned}$$

(2.41)

$$\begin{aligned} \frac{1}{s}&:= \frac{1}{\mathfrak {p}_-} - \frac{1}{p} = \sum _{i=1}^m \Big (\frac{1}{\mathfrak {p}_i^-} - \frac{1}{p_i} \Big ) =: \sum _{i=1}^m \frac{1}{s_i}. \end{aligned}$$

(2.42)

Observe that

$$\begin{aligned} p_i(\mathfrak {p}_i^+/p_i)' = \frac{1}{\frac{1}{p_i} - \frac{1}{\mathfrak {p}_i^+}} \quad \text { and }\quad \frac{p_i(\mathfrak {p}_i^+/p_i)'}{\tau _{p_i}-1} = \frac{1}{\frac{1}{\mathfrak {p}_i^-} - \frac{1}{p_i}}, \quad i=1, \ldots , m. \nonumber \\ \end{aligned}$$

(2.43)

With (2.41)–(2.43) in hand, we use Hölder’s inequality to obtain

(2.44)

Analogously, we have

(2.45)

Then gathering (2.44) and (2.45), we arrive at

which immediately gives (2.38).

To proceed, we note that by (2.28) and (2.39),

$$\begin{aligned} \tau _{p_{m+1}} = \bigg (\frac{\mathfrak {p}_{m+1}^+}{p_{m+1}} \bigg )' \bigg (\frac{p_{m+1}}{\mathfrak {p}_{m+1}^-} -1 \bigg ) +1 = \bigg (\frac{\mathfrak {p}'_-}{p'} \bigg )' \bigg (\frac{p'}{\mathfrak {p}'_+} -1 \bigg ) +1 = \tau '_p, \end{aligned}$$

which along with Lemma 2.6 part (c) and (2.38) yields

$$\begin{aligned}&{\Big [}w_{m+1}^{p_{m+1}(\mathfrak {p}_{m+1}^+/p_{m+1})'}\Big ]_{A_{\tau _{p_{m+1}}}} = {[}w^{-p' (\mathfrak {p}'_-/p')'}]_{A_{\tau '_p}} = [w^{p (\mathfrak {p}_+/p)'}]_{A_{\tau _p}}^{\frac{1}{\tau _p-1}} \\&\le \prod _{i=1}^m {\Big [}w_i^{p_i(\mathfrak {p}_i^+/p_i)'}\Big ]_{A_{\tau _{p_i}}}^{\frac{\frac{1}{p_i} - \frac{1}{\mathfrak {p}_i^+}}{\frac{1}{\mathfrak {p}_-} - \frac{1}{p}}}. \end{aligned}$$

This shows (2.40). $\square$

2.3 Multilinear Calderón–Zygmund Operators

Given $\delta >0$, we say that a function $K: \mathbb {R}^{n(m+1)} {\setminus } \{x=y_1=\cdots =y_m\} \rightarrow \mathbb {C}$ is a $\delta$-Calderón–Zygmund kernel, if there exists a constant $A>0$ such that

$$\begin{aligned} |K(x,\textbf{y})|&\le \frac{A}{\big (\sum _{j=1}^{m}|x-y_j|\big )^{mn}},\\ |K(x,\textbf{y}) - K(x',\textbf{y})|&\le \frac{A \, |x-x'|^{\delta }}{\big (\sum _{j=1}^{m}|x-y_j|\big )^{mn+\delta }}, \end{aligned}$$

whenever $|x-x'| \le \frac{1}{2} \max \limits _{1\le j \le m}|x-y_j|$, and for each $i=1,\ldots ,m$,

$$\begin{aligned} |K(x,\textbf{y}) - K(x,y_1,\ldots ,y'_i,\ldots ,y_m)|&\le \frac{A \, |y_i-y'_i|^{\delta }}{\big (\sum _{j=1}^{m}|x-y_j|\big )^{mn+\delta }}, \end{aligned}$$

whenever $|y_i-y_i'| \le \frac{1}{2} \max \limits _{1\le j \le m}|x-y_j|$.

An m-linear operator $T: \mathcal {S}(\mathbb {R}^n) \times \cdots \times \mathcal {S}(\mathbb {R}^n) \rightarrow \mathcal {S}'(\mathbb {R}^n)$ is called a $\delta$-Calderón–Zygmund operator if there exists a $\delta$-Calderón–Zygmund kernel K such that

$$\begin{aligned} T(\textbf{f})(x) =\int _{(\mathbb {R}^n)^m} K(x, \textbf{y}) f_1(y_1)\cdots f_m(y_m) d\textbf{y}, \end{aligned}$$

whenever $x \not \in \bigcap _{i=1}^m {\text {supp}}(f_i)$ and $\textbf{f}=(f_1,\ldots ,f_m) \in \mathscr {C}_c^{\infty }(\mathbb {R}^n) \times \cdots \times \mathscr {C}_c^{\infty }(\mathbb {R}^n)$, and T can be boundedly extended from $L^{q_1}(\mathbb {R}^n) \times \cdots \times L^{q_m}(\mathbb {R}^n)$ to $L^q(\mathbb {R}^n)$ for some $\frac{1}{q}=\frac{1}{q_1}+\cdots +\frac{1}{q_m}$ with $1<q_1,\ldots ,q_m<\infty$.

Given a symbol $\sigma$, the m-linear Fourier multiplier $T_{\sigma }$ is defined by

$$\begin{aligned} T_{\sigma }(\textbf{f})(x) := \int _{(\mathbb {R}^n)^m} \sigma (\mathbf {\xi }) e^{2\pi i x \cdot (\xi _1+\cdots +\xi _m)} {\widehat{f}}_1(\xi _1) \cdots {\widehat{f}}_m(\xi _m) d\mathbf {\xi }, \end{aligned}$$

for all $f_i \in \mathcal {S}(\mathbb {R}^n)$, $i=1,\ldots ,m$. The operator $T_{\sigma }$ is called an m-linear Coifman–Meyer multiplier, if the symbol $\sigma \in \mathscr {C}^s(\mathbb {R}^{nm} \setminus \{0\})$ satisfies

$$\begin{aligned} \big |\partial _{\mathbf {\xi }}^{\alpha } \sigma (\mathbf {\xi }) \big |&\le C_{\alpha } (|\mathbf {\xi }|)^{- |\alpha |}, \quad \forall \mathbf {\xi } \in \mathbb {R}^{nm} \setminus \{0\}, \end{aligned}$$

for each multi-indix $\alpha =(\alpha _1,\ldots ,\alpha _m)$ with $|\alpha |=\sum _{i=1}^m|\alpha _i| \le mn+1$.

It was shown in [48, Proposition 6] that Coifman–Meyer multipliers are examples of multilinear Calderón–Zygmund operators.

Below, the sharp weighted inequality for multilinear Calderón–Zygmund operators was given in [73, Theorem 1.4] with $p \ge 1$ and extended to the case $p<1$ in [76, Corollary 4.4].

Theorem 2.10

Let T be an m-linear Calderón–Zygmund operator. Then for all $1< p_1, \ldots p_m < \infty$ and $\textbf{w} \in A_{\textbf{p}}$,

$$\begin{aligned} \Vert T\Vert _{L^{p_1}(w_1^{p_1}) \times \cdots \times L^{p_m}(w_m^{p_m}) \rightarrow L^p(w^p)} \lesssim [\textbf{w}]_{A_{\textbf{p}}}^{\max \{p, p'_1, \ldots , p'_m\}}, \end{aligned}$$

where $w=\prod _{i=1}^m w_i$ and $\frac{1}{p}=\sum _{i=1}^m \frac{1}{p_i}$.

Theorem 2.11

[8, Theorem 4.3] Let T be an m-linear operator. Fix $\theta _i >0$ and $r_i \in (1, \infty )$, $i=1, \ldots , m$. Let $\frac{1}{p}=\sum _{i=1}^m \frac{1}{p_i} \le 1$ with $1<p_1, \ldots , p_m<\infty$. Assume that there exist increasing functions $\Psi _i: [1, \infty ) \rightarrow [0, \infty )$ such that for all $v_i^{\theta _i} \in A_{r_i}$, $i=1, \ldots , m$,

$$\begin{aligned} \Vert T(\textbf{f})\Vert _{L^p(v^p)} \le \prod _{i=1}^m \Psi _i([v_i^{\theta _i}]_{A_{r_i}}) \Vert f_i\Vert _{L^{p_i}(v_i^{p_i})}, \end{aligned}$$

(2.46)

where $v=\prod _{i=1}^m v_i$. Then, for all weights $w_i^{\eta _i \theta _i} \in A_{s_i}$ with some $\eta _i \in (1, \infty )$, for all ${\textbf {b}}= (b_1, \ldots , b_m) \in {\text {BMO}}^m$, and for each multi-index $\alpha \in \mathbb {N}^m$,

$$\begin{aligned} \Vert [T, {\textbf {b}}]_{\alpha }(\textbf{f})\Vert _{L^p(w^p)} \le \alpha ! \prod _{i=1}^m \delta _i^{-\alpha _i} \Psi _i \big (4^{\delta _i \theta _i} [w_i^{\eta _i \theta _i}]_{A_{r_i}}^{\frac{1}{\eta _i}} \big ) \Vert b_i\Vert _{{\text {BMO}}}^{\alpha _i} \Vert f_i\Vert _{L^{p_i}(w_i^{p_i})}, \end{aligned}$$

(2.47)

where $w=\prod _{i=1}^m w_i$, and $\delta _i = \min \{1, r_i-1\}/(\eta '_i \theta _i)$, $i=1, \ldots , m$.

Let us record Marcinkiewicz–Zygmund inequalities contained in [22, Proposition 5.3].

Lemma 2.12

Let $0< p, q_1, \ldots , q_m< r < 2$ or $r=2$ and $0<p, q_1, \ldots , q_m <\infty$. Let $\mu _1, \ldots , \mu _m$ and $\nu$ be arbitrary $\sigma$-finite measures on $\mathbb {R}^n$. Let T be an m-linear operator. Then, there exists a constant $C>0$ such that the following estimates hold:

• (i) If T is bounded from $L^{q_1}(\mu _1) \times \cdots \times L^{q_m}(\mu _m)$ to $L^p(\nu )$, then

  $$\begin{aligned} \bigg \Vert \bigg (\sum _{k_1, \ldots , k_m} |T(f^1_{k_1}, \ldots , f^m_{k_m})|^r \bigg )^{\frac{1}{r}}\bigg \Vert _{L^p(\nu )} \le C \Vert T\Vert \prod _{i=1}^m \bigg \Vert \bigg (\sum _{k_i} |f^i_{k_i}|^r \bigg )^{\frac{1}{r}}\bigg \Vert _{L^{q_i}(\mu _i)}, \end{aligned}$$

  where $\Vert T\Vert := \Vert T\Vert _{L^{q_1}(\mu _1) \times \cdots \times L^{q_m}(\mu _m) \rightarrow L^p(\nu )}$.

• (ii) If T is bounded from $L^{q_1}(\mu _1) \times \cdots \times L^{q_m}(\mu _m)$ to $L^{p, \infty }(\nu )$, then

  $$\begin{aligned} \bigg \Vert \bigg (\sum _{k_1, \ldots , k_m} |T(f^{1}_{k_1}, \ldots , f^m_{k_m})|^r \bigg )^{\frac{1}{r}}\bigg \Vert _{L^{p, \infty }(\nu )} \le C \Vert T\Vert _{\textrm{weak}} \prod _{i=1}^m \bigg \Vert \bigg (\sum _{k_i} |f^i_{k_i}|^r \bigg )^{\frac{1}{r}}\bigg \Vert _{L^{q_i}(\mu _i)}, \end{aligned}$$

  where $\Vert T\Vert _\textrm{weak}:= \Vert T\Vert _{L^{q_1}(\mu _1) \times \cdots \times L^{q_m}(\mu _m) \rightarrow L^{p, \infty }(\nu )}$.

3 Quantitative Weighted Estimates

The goal of this section is to establish quantitative weighted estimates for (rough) maximal operators and singular integrals. We begin with the following interpolation result with change of measures due to Stein and Weiss [87], which plays an important role in dealing with weighted estimates.

Theorem 3.1

[87] Let $p_0, p_1 \in [1, \infty ]$, and let $w_0$ and $w_1$ be weights. If the sublinear operator T satisfies

$$\begin{aligned} \Vert Tf\Vert _{L^{p_i}(w_i)} \le K_i \Vert f\Vert _{L^{p_i}(w_i)}, \quad i=0, 1, \end{aligned}$$

then for any $\theta \in (0, 1)$,

$$\begin{aligned} \Vert Tf\Vert _{L^p(w)} \le K \Vert f\Vert _{L^p(w)} \quad \text {with}\quad K \le K_0^{1-\theta } K_1^{\theta }, \end{aligned}$$

where $\frac{1}{p}=\frac{1-\theta }{p_0} + \frac{\theta }{p_1}$ and $w^{\frac{1}{p}}=w_0^{\frac{1-\theta }{p_0}} w_1^{\frac{\theta }{p_1}}$.

The sharp maximal function$M^{\#}$ is defined by

The following Fefferman-Stein inequality was shown in [16, Remark 1.9].

Lemma 3.2

For every $p \in (0, \infty )$ and $w \in A_{\infty }$,

$$\begin{aligned} \Vert Mf\Vert _{L^p(w)}&\le C_{n, p} \, [w]_{A_{\infty }} \Vert M^{\#}f\Vert _{L^p(w)}, \end{aligned}$$

whenever $Mf \in L^p(w)$ or $f \in L^{\infty }_c(\mathbb {R}^n)$.

We present a sharp weighted vector-valued Fefferman-Stein inequality.

Lemma 3.3

For any $1< p, r < \infty$ and $w \in A_p$,

$$\begin{aligned} \bigg \Vert \Big (\sum _k |M f_k|^r \Big )^{\frac{1}{r}}\Big \Vert _{L^p(w)} \lesssim {[}w]_{A_p}^{\max \{\frac{1}{r}, \frac{1}{p-1}\}} \bigg \Vert \Big (\sum _k |f_k|^r \Big )^{\frac{1}{r}}\bigg \Vert _{L^p(w)}. \end{aligned}$$

Moreover, the exponent $\max \{\frac{1}{r}, \frac{1}{p-1}\}$ is the best possible.

Proof

This inequality was given in [33, Theorem 1.12]. We here present a different proof. Let $r \in (1, \infty )$. It was proved in [23, Theorem 1.11] that there exist $3^n$ dyadic lattices $\mathcal {D}_j$ and sparse families $\mathcal {S}_j \subset \mathcal {D}_j$ such that

$$\begin{aligned} \Big (\sum _k |M f_k(x)|^r \Big )^{\frac{1}{r}} \le C_{n, r} \sum _{j=1}^{3^n} \mathcal {A}_{\mathcal {S}_j}^r \bigg (\Big (\sum _k |f_k|^r \Big )^{\frac{1}{r}}\bigg )(x), \quad \text {a.e. } x \in \mathbb {R}^n, \end{aligned}$$

(3.1)

where

$$\begin{aligned} \mathcal {A}_{\mathcal {S}}^r f(x) := \bigg (\sum _{Q \in \mathcal {S}} \langle |f| \rangle _Q^r {\textbf {1}}_Q(x) \bigg )^{\frac{1}{r}}. \end{aligned}$$

(3.2)

It follows from [13, Theorem2.1] that for all $p \in (1, \infty )$ and $w \in A_p$,

$$\begin{aligned} \Vert \mathcal {A}_{\mathcal {S}}^{\gamma } f\Vert _{L^p(w)} \le C_{n, p, \gamma } {[}w]_{A_p}^{\max \{\frac{1}{\gamma }, \frac{1}{p-1}\}} \Vert f\Vert _{L^p(w)}, \quad \gamma >0. \end{aligned}$$

(3.3)

Thus, (3.1) and (3.3) imply the desired estimate. $\square$

Lemma 3.4

Let $\mathscr {B}_1$ and $\mathscr {B}_2$ be Banach spaces, and let $\mathscr {L}(\mathscr {B}_1, \mathscr {B}_2)$ be the Banach space defined by all bounded linear operators from $\mathscr {B}_1$ to $\mathscr {B}_2$ with the operator norm $\Vert \cdot \Vert _{\mathscr {L}(\mathscr {B}_1, \mathscr {B}_2)}$. Let T be a linear operator mapping $\mathscr {B}_1$-valued functions into $\mathscr {B}_2$-valued functions satisfying

• (i) T is bounded from $L^2(\mathbb {R}^n, \mathscr {B}_1)$ into $L^2(\mathbb {R}^n, \mathscr {B}_2)$.

• (ii) There exists a kernel function $K(x) \in \mathscr {L}(\mathscr {B}_1, \mathscr {B}_2)$ such that

  $$\begin{aligned} \Vert K(x-y) - K(x)\Vert _{\mathscr {L}(\mathscr {B}_1, \mathscr {B}_2)} \le C_K |y| |x|^{-n-1}, \quad 2|y| < |x|, \end{aligned}$$

  and for every $f \in L^2(\mathbb {R}^n, \mathscr {B}_1)$ with compact support,

  $$\begin{aligned} Tf(x) = \int _{\mathbb {R}^n} K(x-y) f(y) \, dy, \qquad \text {a.e. } x \not \in {\text {supp}}(f), \end{aligned}$$

Then for every $p \in (1, \infty )$ and $w \in A_p$,

$$\begin{aligned} \Vert Tf\Vert _{L^p(w, \mathscr {B}_2)} \lesssim [w]_{A_p}^{\frac{7}{2}\max \{1, \frac{1}{p-1}\}} \Vert f\Vert _{L^p(w, \mathscr {B}_1)}. \end{aligned}$$

Proof

It was shown in [85, p. 41–42] that

$$\begin{aligned}&\Vert Tf\Vert _{L^{1, \infty }(\mathbb {R}^n, \mathscr {B}_2)} \lesssim C_T \, \Vert f\Vert _{L^1(\mathbb {R}^n, \mathscr {B}_1)}, \end{aligned}$$

(3.4)

$$\begin{aligned}&M^{\#}(\Vert Tf\Vert _{\mathscr {B}_2})(x) \lesssim C_T \, M_r(\Vert f\Vert _{\mathscr {B}_1})(x), \quad 2 \le r<\infty , \, x \in \mathbb {R}^n, \end{aligned}$$

(3.5)

where $C_T:= \Vert T\Vert _{L^2(\mathbb {R}^n, \mathscr {B}_1) \rightarrow L^2(\mathbb {R}^n, \mathscr {B}_2)} + C_K$. Then interpolating between the assumption (i) and (3.5) yields that for any $1<r_0<r<2$,

$$\begin{aligned} \Vert Tf\Vert _{L^{r_0}(\mathbb {R}^n, \mathscr {B}_2)}&\lesssim C_T \, (r_0-1)^{-\frac{1}{r_0}} \Vert f\Vert _{L^{r_0}(\mathbb {R}^n, \mathscr {B}_1)}, \end{aligned}$$

(3.6)

where the implicit constant is independent of $r_0$. As argued in the proof of (3.5), the inequality (3.6) implies for any $1<r_0<r<2$,

$$\begin{aligned} M^{\#}(\Vert Tf\Vert _{\mathscr {B}_2})(x)&\lesssim C_T \, (r_0-1)^{-\frac{1}{r_0}} M_r(\Vert f\Vert _{\mathscr {B}_1})(x), \quad x \in \mathbb {R}^n, \end{aligned}$$

(3.7)

Now let $p \in (1, \infty )$ and $w \in A_p$. Then, by Lemma 2.4, there exists $\gamma \in (0, 2^{-n-3})$ and $q_0 \in (1, p)$ such that $q_0 = \frac{p}{1+\varepsilon }$, $\frac{p-1}{p(1+\gamma )'}<\varepsilon <\frac{p-1}{(1+\gamma )'}$, $(1+\gamma )' \simeq [w]_{A_p}^{\max \{1, \frac{1}{p-1}\}}$, and $[w]_{A_{q_0}} \le 2^p [w]_{A_p}$. Set $r:=p/q_0=1+\varepsilon$. If $r \ge 2$, it follows from Lemma 3.2 and (3.5) that

$$\begin{aligned} \Vert T f\Vert _{L^p(w, \mathscr {B}_2)}&\le \Vert M(\Vert T f\Vert _{\mathscr {B}_2})\Vert _{L^p(w)} \lesssim [w]_{A_p} \Vert M^{\#}(\Vert Tf\Vert _{\mathscr {B}_2})\Vert _{L^p(w)}\\&\lesssim [w]_{A_p} \Vert M_r(\Vert f\Vert _{\mathscr {B}_1})\Vert _{L^p(w)} \lesssim {[}w]_{A_p} [w]_{A_{q_0}}^{\frac{1}{r(q_0-1)}} \Vert f\Vert _{L^p(w, \mathscr {B}_1)}\\&\lesssim [w]_{A_p}^{1+ \frac{1}{p-r}} \Vert f\Vert _{L^2(w, \mathscr {B}_1)} \le [w]_{A_p}^{\frac{5}{2} \max \{1, \frac{1}{p-1}\}} \Vert f\Vert _{L^p(w, \mathscr {B}_1)}, \end{aligned}$$

since

$$\begin{aligned} p-r=p-1-\varepsilon>p-1-\frac{p-1}{(1+\gamma )'} =\frac{p-1}{1+\gamma }>\frac{p-1}{1+2^{-n-3}} >\frac{p-1}{3/2}. \end{aligned}$$

If $1<r<2$, we choose $r_0=1+\frac{p-1}{p(1+\gamma )'}$ and invoke Lemma 3.2 and (3.7) to obtain that

$$\begin{aligned} \Vert T f\Vert _{L^p(w, \mathscr {B}_2)}&\lesssim \frac{1}{r_0-1} [w]_{A_p} \Vert M_r(\Vert f\Vert _{\mathscr {B}_1})\Vert _{L^p(w)}\\&\lesssim \frac{p(1+\gamma )'}{p-1} [w]_{A_p}^{1 + \frac{1}{p-r}} \Vert f\Vert _{L^p(w, \mathscr {B}_1)}\\&\lesssim [w]_{A_p}^{\frac{7}{2} \max \{1, \frac{1}{p-1}\}} \Vert f\Vert _{L^p(w, \mathscr {B}_1)}. \end{aligned}$$

This completes the proof. $\square$

Lemma 3.5

Let $\varphi \in \mathcal {S}(\mathbb {R}^n)$ be such that $\int _{\mathbb {R}^n} \varphi \, dx=0$ and ${\text {supp}}({\widehat{\varphi }}) \subset \{\xi \in \mathbb {R}^n: c_1 \le |\xi | \le c_2\}$ for some $0<c_1<c_2 < \infty$. Set $\varphi _k(x):= 2^{kn} \varphi (2^k x)$ for any $k \in \mathbb {Z}$. Then for every $p \in (1, \infty )$ and $w \in A_p$,

$$\begin{aligned}&\bigg \Vert \Big (\sum _{k \in \mathbb {Z}} |\varphi _k * f|^2\Big )^{\frac{1}{2}}\bigg \Vert _{L^p(w)} \lesssim [w]_{A_p}^{\max \{\frac{1}{2}, \frac{1}{p-1}\}} \Vert f\Vert _{L^p(w)}, \end{aligned}$$

(3.8)

$$\begin{aligned}&\bigg \Vert \sum _{k \in \mathbb {Z}} \varphi _k * f_k \bigg \Vert _{L^p(w)} \lesssim [w]_{A_p}^{\frac{7}{2} \max \{1, \frac{1}{p-1}\}} \bigg \Vert \Big (\sum _{k \in \mathbb {Z}} |f_k|^2\Big )^{\frac{1}{2}}\bigg \Vert _{L^p(w)}, \end{aligned}$$

(3.9)

$$\begin{aligned}&\bigg \Vert \Big (\sum _{k \in \mathbb {Z}} |\varphi _k * f_k|^2\Big )^{\frac{1}{2}} \bigg \Vert _{L^p(w)} \lesssim [w]_{A_p}^{\max \{\frac{1}{2}, \frac{1}{p-1}\}} \bigg \Vert \Big (\sum _{k \in \mathbb {Z}} |f_k|^2\Big )^{\frac{1}{2}}\bigg \Vert _{L^p(w)}. \end{aligned}$$

(3.10)

If we assume in addition that $\sum _{k \in \mathbb {Z}} |{\widehat{\varphi }}(2^{-k} \xi )|^2 = C_{\varphi }>0$ for all $\xi \ne 0$, then

$$\begin{aligned} \Vert f\Vert _{L^p(w)} \lesssim [w]_{A_p}^{\max \{1, \frac{1}{2(p-1)}\}} \bigg \Vert \Big (\sum _{k \in \mathbb {Z}} |\varphi _k * f|^2\Big )^{\frac{1}{2}}\bigg \Vert _{L^p(w)}. \end{aligned}$$

(3.11)

Proof

Since $\varphi \in \mathcal {S}(\mathbb {R}^n)$, one can check that there exists $C'_{\varphi }>0$ such that for any $\beta \in (0, 1]$ and any $y \in \mathbb {R}^n$, $|\varphi (x)| \le C'_{\varphi } (1+|x|)^{-n-\beta }$ and

$$\begin{aligned} |\varphi (x-y) - \varphi (x)|&\le C'_{\varphi } \bigg [\frac{|y|^{\beta }}{(1+|x|)^{n+1+\beta }} + \frac{|y|^{\beta }}{(1+|x-y|)^{n+1+\beta }}\bigg ]. \end{aligned}$$

Recalling that $\int _{\mathbb {R}^n} \varphi \, dx=0$, we see that $\varphi /C'_{\varphi } \in \mathcal {C}_{\beta , 1}$, which is defined in [90, Definition 6.2]. Then by [90, Theorem 6.3],

$$\begin{aligned} S_{\varphi } f(x) := \Big (\sum _{k \in \mathbb {Z}} |\varphi _k * f(x)|^2\Big )^{\frac{1}{2}} \le {\widetilde{\sigma }}_{\beta , 1} f(x) \lesssim \sigma _{\beta }f(x) \lesssim G_{\beta } f(x), \quad x \in \mathbb {R}^n, \end{aligned}$$

(3.12)

where the implicit constant is independent of f and x. Thus, (3.8) follows from (3.12) and the sharp weighted estimate for $G_{\beta }$ in [64, Theorem 1.1].

To show (3.9), we will use vector-valued singular integrals. By the support of ${\widehat{\varphi }}$, there exist $j_0, j_1 \in \mathbb {N}$ such that ${\text {supp}}({\widehat{\varphi }}_{j+k}) \cap {\text {supp}}({\widehat{\varphi }}_j) = \emptyset$ whenever $k \le -j_0-1$ or $k \ge j_1+1$. This and Plancherel’s identity give

$$\begin{aligned} \int _{\mathbb {R}^n}&\Big |\sum _{k \in \mathbb {Z}} \varphi _k*f_k(x) \Big |^2 dx =\int _{\mathbb {R}^n} \Big |\sum _{k \in \mathbb {Z}} {\widehat{\varphi }}_k(\xi ) {\widehat{f}}_k(\xi ) \Big |^2 d\xi \\&=\sum _{k, j \in \mathbb {Z}} \int _{\mathbb {R}^n} {\widehat{\varphi }}_k(2^{-k}\xi ) {\widehat{f}}_k(\xi ) {\widehat{\varphi }}_j(2^{-j}\xi ) \overline{{\widehat{f}}_k(\xi )} d\xi \\&=\sum _{j \in \mathbb {Z}} \sum _{k=j-j_0}^{j+j_1} \int _{\mathbb {R}^n} {\widehat{\varphi }}_k(2^{-k}\xi ) {\widehat{f}}_k(\xi ) {\widehat{\varphi }}_j(2^{-j}\xi ) \overline{{\widehat{f}}_k(\xi )} d\xi \\&=\sum _{j \in \mathbb {Z}} \sum _{k=-j_0}^{j_1} \int _{\mathbb {R}^n} {\widehat{\varphi }}_{j+k}(2^{-j-k}\xi ) {\widehat{\varphi }}_j(2^{-j}\xi ) {\widehat{f}}_{j+k}(\xi ) \overline{{\widehat{f}}_k(\xi )} d\xi \\&\lesssim \sum _{k=-j_0}^{j_1} \int _{\mathbb {R}^n} \sum _{j \in \mathbb {Z}} |{\widehat{f}}_{j+k}(\xi )| |{\widehat{f}}_k(\xi )| d\xi \\&\lesssim \sum _{k=-j_0}^{j_1} \bigg (\int _{\mathbb {R}^n} \sum _{j \in \mathbb {Z}} |{\widehat{f}}_{j+k}(\xi )|^2 d\xi \bigg )^{\frac{1}{2}} \bigg (\int _{\mathbb {R}^n} \sum _{j \in \mathbb {Z}} |{\widehat{f}}_j(\xi )|^2 d\xi \bigg )^{\frac{1}{2}}\\&\lesssim \Vert \{f_k\}_{k \in \mathbb {Z}}\Vert _{L^2(\mathbb {R}^n, \ell ^2)}^2. \end{aligned}$$

This means that the operator T defined by $T(\{f_k\}_{k \in \mathbb {Z}}):= \sum _{k \in \mathbb {Z}} \varphi _k*f_k$, is a bounded linear operator from $L^2(\mathbb {R}^n, \ell ^2)$ to $L^2(\mathbb {R}^n)$, with the kernel $K(x)=\{\varphi _k(x)\}_{k \in \mathbb {Z}}$ satisfying $\Vert \nabla K(x)\Vert _{\mathscr {L}(\ell ^2, \mathbb {C})} \lesssim |x|^{-n-1}$ for all $x \ne 0$. Hence, Lemma 3.4 implies (3.9).

Note that the inequality (3.10) is a consequence of Lemma 3.3 and that $|\varphi _k * f_k| \lesssim Mf_k$ uniformly in $k \in \mathbb {Z}$.

Finally, to get (3.11), we use Parseval’s identity and $\sum _{k \in \mathbb {Z}} |{\widehat{\varphi }}_k(\xi )|^2=\sum _{k \in \mathbb {Z}} |{\widehat{\varphi }}(2^{-k} \xi )|^2 = C_{\varphi }$ to get that for any $f, g \in L^2(\mathbb {R}^n)$,

$$\begin{aligned} \int _{\mathbb {R}^n} \sum _{k \in \mathbb {Z}} \varphi _k*f(x) \, \varphi _k*g(x) \, dx =C_{\varphi } \int _{\mathbb {R}^n} f(x) g(x) \, dx. \end{aligned}$$

Then it follows that for $g \in \mathcal {S}(\mathbb {R}^n)$ with $\Vert g\Vert _{L^{p'}(w^{1-p'})}=1$,

$$\begin{aligned} \bigg |\int _{\mathbb {R}^n} f(x) g(x) \, dx\bigg |&\lesssim \bigg |\int _{\mathbb {R}^n} \sum _{k \in \mathbb {Z}} \varphi _k*f(x) \, \varphi _k*g(x) \, dx\bigg |\\&\le \int _{\mathbb {R}^n} S_{\varphi }f(x) S_{\varphi } g(x) \, dx \le \Vert S_{\varphi }f\Vert _{L^p(w)} \Vert S_{\varphi } g\Vert _{L^{p'}(w^{1-p'})}\\&\lesssim [w^{1-p'}]_{A_{p'}}^{\max \{\frac{1}{2}, \frac{1}{p'-1}\}} \Vert S_{\varphi }f\Vert _{L^p(w)} {=}[w]_{A_p}^{\max \{1, \frac{1}{2(p{-}1)}\}} \Vert S_{\varphi }f\Vert _{L^p(w)}, \end{aligned}$$

where we have used (3.8) in the last inequality. This gives at once (3.11). $\square$

Lemma 3.6

Given $\varepsilon >0$ and a pairwise disjoint family of cubes $\{Q_j\}$, we set

$$\begin{aligned} \Omega := \bigcup _j Q_j \quad \text { and }\quad \mathfrak {M}_{\varepsilon }(x) := \sum _j \frac{\ell (Q_j)^{n+\varepsilon }}{|x-x_{Q_j}|^{n+\varepsilon } + \ell (Q_j)^{n+\varepsilon }}, \quad x \in \mathbb {R}^n. \end{aligned}$$

(3.13)

Then $\Vert \mathfrak {M}_{\varepsilon }\Vert _{L^2(w)} \lesssim [w]_{A_2} w(\Omega )^{\frac{1}{2}}$ for any $w \in A_2$.

Proof

Note that

$$\begin{aligned} \mathfrak {M}_{\varepsilon }(x) \lesssim \sum _j \bigg [\frac{1}{(|x-x_{Q_j}|/\ell (Q_j))^n +1} \bigg ]^{n+\varepsilon } \lesssim \sum _j M{\textbf {1}}_{Q_j}(x)^{\frac{n+\varepsilon }{n}}, \end{aligned}$$

which together with Lemma 3.3 gives that for any $w \in A_2$,

$$\begin{aligned}&\bigg (\int _{\mathbb {R}^n} \mathfrak {M}_{\varepsilon }(x)^2\, w(x) \, dx \bigg )^{\frac{n}{2(n+\varepsilon )}} \lesssim \bigg (\int _{\mathbb {R}^n} \Big (\sum _j M{\textbf {1}}_{Q_j}(x)^{\frac{n+\varepsilon }{n}} \Big )^{\frac{n}{n+\varepsilon } \cdot \frac{2(n+\varepsilon )}{n}} w(x) \, dx \bigg )^{\frac{n}{2(n+\varepsilon )}}\\&\quad \lesssim [w]_{A_{\frac{2(n+\varepsilon )}{n}}}^{\max \{\frac{n}{n+\varepsilon }, \frac{1}{\frac{2(n+\varepsilon )}{n}-1}\}} \bigg (\int _{\mathbb {R}^n} \Big (\sum _j {\textbf {1}}_{Q_j}(x) \Big )^{2} w(x) \, dx \bigg )^{\frac{n}{2(n+\varepsilon )}} \le [w]_{A_2}^{\frac{n}{n+\varepsilon }} w(\Omega )^{\frac{n}{2(n+\varepsilon )}}, \end{aligned}$$

where we have use the disjointness of $\{Q_j\}$. This implies the desired estimate. $\square$

Given $\Omega \in L^1(\mathbb {S}^{n-1})$, the rough maximal operator $M_{\Omega }$ and singular integral $T_{\Omega }$ are defined by

(3.14)

and

$$\begin{aligned} T_{\Omega } f(x)&:= \text {p. v. } \int _{\mathbb {R}^n} \frac{\Omega (y')}{|y|^n}f(x-y) \, dy. \end{aligned}$$

(3.15)

Theorem 3.7

Let $q \in (1, \infty )$ and $\Omega \in L^q(\mathbb {S}^{n-1})$ be such that $\int _{\mathbb {S}^{n-1}} \Omega \, d\sigma =0$. Then for all $p \in (q', \infty )$ and for all $w \in A_{p/q'}$,

$$\begin{aligned} \Vert M_{\Omega }f\Vert _{L^p(w)}&\lesssim [w]_{A_{p/q'}}^{\frac{1}{p-q'}} \Vert f\Vert _{L^p(w)}, \end{aligned}$$

(3.16)

$$\begin{aligned} \Vert T_{\Omega }f\Vert _{L^p(w)}&\lesssim [w]_{A_{p/q'}}^{\max \{1, \frac{1}{p/q'-1}\} + \max \{1, \frac{1}{p-q'}\}} \Vert f\Vert _{L^p(w)}. \end{aligned}$$

(3.17)

Moreover, the vector-valued inequality holds for $q>2$:

$$\begin{aligned} \bigg \Vert \Big (\sum _j |M_{\Omega }f_j|^2\Big )^{\frac{1}{2}}\bigg \Vert _{L^p(w)}&\lesssim [w]_{A_{p/q'}}^{\frac{1}{p-q'}} \bigg \Vert \Big (\sum _j |f_j|^2\Big )^{\frac{1}{2}}\bigg \Vert _{L^p(w)}. \end{aligned}$$

(3.18)

Proof

By definition and Hölder’s inequality, one has

$$\begin{aligned} M_{\Omega }f(x) \le \Vert \Omega \Vert _{L^q(\mathbb {S}^{n-1})} \, M_{q'}f(x), \quad x \in \mathbb {R}^n, \end{aligned}$$

which together with (2.1) immediately gives (3.16). Then (3.18) is a consequence of (3.16), Theorem 1.1, and Remark 1.4.

To treat (3.17), we choose a radial nonnegative function $\varphi \in \mathscr {C}_c^{\infty }(\mathbb {R}^n)$ such that ${\text {supp}}\varphi \subset \{|x|< 1/4\}$ and $\int _{\mathbb {R}^n} \varphi \, dx =1$. Set $\varphi _j(x):= 2^{-nj} \varphi (2^{-j} x)$ and $\nu _j(x):= \frac{\Omega (x')}{|x|^n} {\textbf {1}}_{\{2^j \le |x|<2^{j+1}\}}(x)$ for each $j \in \mathbb {Z}$. Define

$$\begin{aligned} T_j f:= K_j * f \quad \text { and }\quad K_j:= \sum _{k \in \mathbb {Z}} \nu _k * \varphi _{k-j}, \quad j \in \mathbb {Z}. \end{aligned}$$

Then,

$$\begin{aligned} T_{\Omega } = T_1 + \sum _{j=1}^{\infty } (T_{j+1} - T_j). \end{aligned}$$

(3.19)

It was proved in [89, p. 396] that for some $\delta _0>0$,

$$\begin{aligned} \Vert T_j f\Vert _{L^2(\mathbb {R}^n)} \lesssim \Vert f\Vert _{L^2(\mathbb {R}^n)}, \quad j \ge 1, \end{aligned}$$

(3.20)

$$\begin{aligned} \Vert (T_{j+1} - T_j) f\Vert _{L^2(\mathbb {R}^n)} \lesssim 2^{-\delta _0 j} \Vert f\Vert _{L^2(\mathbb {R}^n)}, \quad j \ge 1, \end{aligned}$$

(3.21)

where the implicit constants are independent of j.

On the other hand, it follows from [89, Lemma 2] that

$$\begin{aligned} K_j \text { satisfies the} L^q \text {-H}\ddot{\textrm{o}}\text {rmander condition}, \end{aligned}$$

(3.22)

which together with [89, Theorem 2] gives

$$\begin{aligned}&T_j \text { is bounded from} L^1(\mathbb {R}^n) \text { to} L^{1, \infty }(\mathbb {R}^n), \end{aligned}$$

(3.23)

$$\begin{aligned}&T_j \text { is bounded on } L^p(\mathbb {R}^n), \quad 1<p<\infty . \end{aligned}$$

(3.24)

In particular, (3.24) implies

$$\begin{aligned} T_j \hbox { is bounded from} L^{q'}(\mathbb {R}^n) \hbox {to} L^{q', \infty }(\mathbb {R}^n), \quad 1<q<\infty , \end{aligned}$$

(3.25)

and the interpolation theorem, (3.21), and (3.24) yield that for some $\delta >0$,

$$\begin{aligned} \Vert (T_{j+1} - T_j) f\Vert _{L^p(\mathbb {R}^n)} \lesssim 2^{-\delta j} \Vert f\Vert _{L^p(\mathbb {R}^n)}, \quad j \ge 1, \, 1<p<\infty . \end{aligned}$$

(3.26)

Hence, by (3.22), (3.25), and [70, Theorem 1.2], we obtain that for any $f \in L^{\infty }_c(\mathbb {R}^n)$ there exists a sparse family $\mathcal {S}_j$ such that

$$\begin{aligned} T_j f(x) \lesssim \sum _{Q \in \mathcal {S}_j} \langle |f|^{q'} \rangle _Q^{\frac{1}{q'}} {\textbf {1}}_Q(x) =\mathcal {A}_{\mathcal {S}_j}^{\frac{1}{q'}} (|f|^{q'})(x)^{\frac{1}{q'}}, \quad \text {a.e. } x \in \mathbb {R}^n, \end{aligned}$$

(3.27)

where the dyadic operator $\mathcal {A}_{\mathcal {S}}^{\gamma }$ is defined in (3.2) and the implicit constant is independent of j. Accordingly, we use (3.3), (3.27), and a density argument to arrive at

$$\begin{aligned} \Vert T_j f\Vert _{L^p(v)} \lesssim [v]_{A_{p/q'}}^{\max \{1, \frac{1}{p-q'}\}} \Vert f\Vert _{L^p(v)}, \quad \forall p \in (q', \infty ), \, v \in A_{p/q'}. \end{aligned}$$

(3.28)

Now fix $p \in (q', \infty )$ and $w \in A_{p/q'}$. By Lemma 2.4, there exists $\gamma \in (0, 1)$ such that

$$\begin{aligned} (1+\gamma )' = c_n [w]_{A_{p/q'}}^{\max \{1, \frac{1}{p/q'-1}\}} =: c_n B_0, \quad \text {and}\quad [w^{1+\gamma }]_{A_{p/q'}} \lesssim [w]_{A_{p/q'}}^{1+\gamma }, \end{aligned}$$

which along with (3.28) implies

$$\begin{aligned} \Vert (T_{j+1} -T_j)f\Vert _{L^p(w^{1+\gamma })} \lesssim [w]_{A_{p/q'}}^{(1+\gamma )\max \{1, \frac{1}{p-q'}\}} \Vert f\Vert _{L^p(w^{1+\gamma })}. \end{aligned}$$

(3.29)

In light of Theorem 3.1 with $w_0 \equiv 1$, $w_1=w^{1+\gamma }$, and $\theta =\frac{1}{1+\gamma }$, interpolating between (3.26) and (3.29) gives

$$\begin{aligned} \Vert (T_{j+1} -T_j) f\Vert _{L^p(w)} \lesssim 2^{-(1-\theta )\delta j} [w]_{A_{p/q'}}^{\max \{1, \frac{1}{p-q'}\}} \Vert f\Vert _{L^p(w)}, \quad j \ge 1. \end{aligned}$$

(3.30)

Note that $1-\theta = \frac{1}{(1+\gamma )'}$ and $e^{-t} < 2t^{-2}$ for any $t >0$. As a consequence, (3.19), (3.28), and (3.30) imply

$$\begin{aligned} \Vert T_{\Omega } f\Vert _{L^p(w)}&\lesssim \sum _{j=0}^{\infty } 2^{-\frac{c'_n j}{B_0}} [w]_{A_{p/q'}}^{\max \{1, \frac{1}{p-q'}\}} \Vert f\Vert _{L^p(w)}\\&= \bigg (\sum _{j \le B_0} + \sum _{j> B_0} \bigg ) 2^{-\frac{c'_n j}{B_0}} [w]_{A_{p/q'}}^{\max \{1, \frac{1}{p-q'}\}} \Vert f\Vert _{L^p(w)}\\&\lesssim \bigg (B_0 + \sum _{j > B_0} j^{-2}B_0^2 \bigg ) [w]_{A_{p/q'}}^{\max \{1, \frac{1}{p-q'}\}} \Vert f\Vert _{L^p(w)}\\&\lesssim B_0 \, [w]_{A_{p/q'}}^{\max \{1, \frac{1}{p-q'}\}} \Vert f\Vert _{L^p(w)}\\&= [w]_{A_{p/q'}}^{\max \{1, \frac{1}{p/q'-1}\} + \max \{1, \frac{1}{p-q'}\}} \Vert f\Vert _{L^p(w)}. \end{aligned}$$

This completes the proof. $\square$

Theorem 3.8

Let $q \in (1, \infty )$ and $\Omega \in L^q(\mathbb {S}^{n-1})$. Then for all $p \in (1, q)$ and for all $w^{1-p'} \in A_{p'/q'}$,

$$\begin{aligned} \Vert M_{\Omega }f\Vert _{L^p(w)} \lesssim [w^{1-p'}]_{A_{p'/q'}}^{\max \{1, \frac{1}{p'/q'-1}\} + \max \{1, \frac{1}{p'-q'}\}} \Vert f\Vert _{L^p(w)}. \end{aligned}$$

(3.31)

Proof

Fix $p \in (1, q)$ and $w^{1-p'} \in A_{p'/q'}$. For $j \in \mathbb {Z}$, set $\nu _{\Omega , j}(x):= \frac{\Omega (x')}{|x|^n} {\textbf {1}}_{\{2^j \le |x|<2^{j+1}\}}(x)$. Define

$$\begin{aligned} {\textbf {S}}_{\Omega }f(x) := \bigg (\sum _{j \in \mathbb {Z}} |{\textbf {T}}_{\Omega , j} f(x)|^2 \bigg )^{\frac{1}{2}}, \quad \text {where}\quad {\textbf {T}}_{\Omega , j} f := \nu _{\Omega , j}*f. \end{aligned}$$

If we set for any $x' \in \mathbb {S}^{n-1}$, there there holds

$$\begin{aligned} \Omega _0 \in L^q(\mathbb {S}^{n-1}), \quad \int _{\mathbb {S}^{n-1}} \Omega _0 \, d\sigma =0, \quad \text {and}\quad M_{\Omega } f \lesssim Mf + {\textbf {S}}_{\Omega _0}(|f|). \end{aligned}$$

(3.32)

Since $w^{1-p'} \in A_{p'/q'} \subset A_{p'}$, we see that $w \in A_p$ and by (2.1),

$$\begin{aligned} \Vert Mf\Vert _{L^p(w)} \lesssim [w]_{A_p}^{\frac{1}{p-1}} \Vert f\Vert _{L^p(w)} = [w^{1-p'}]_{A_{p'}} \Vert f\Vert _{L^p(w)} \le [w^{1-p'}]_{A_{p'/q'}} \Vert f\Vert _{L^p(w)}. \end{aligned}$$

(3.33)

In order to estimate ${\textbf {S}}_{\Omega _0}$, we define a linear operator

$$\begin{aligned} {\textbf {T}}_{\Omega _0}^{\varepsilon }:= \sum _{m \in \mathbb {Z}} \varepsilon _m {\textbf {T}}_{\Omega _0, m}, \quad \text { where } \, \varepsilon := \{\varepsilon _m = \pm 1\}. \end{aligned}$$

Writing

$$\begin{aligned} k:= \sum _{m \in \mathbb {Z}} \varepsilon _m \nu _{\Omega _0, m} \quad \text { and }\quad k^{(m)}:= \nu _{\Omega _0, m}, \quad m\in \mathbb {Z}, \end{aligned}$$

one can verify that [89, Lemmas 1 and 2] hold for k and $k^{(m)}$, with bounds independent of $\varepsilon$. This means that ${\textbf {T}}_{\Omega _0}^{\varepsilon }$ behaves as $T_{\Omega }$ in Theorem 3.7. Then by (3.17),

$$\begin{aligned} \sup _{\varepsilon } \Vert {\textbf {T}}_{\Omega _0}^{\varepsilon } f\Vert _{L^s(v)}&\lesssim [v]_{A_{s/q'}}^{\max \{1, \frac{1}{s/q'-1}\} + \max \{1, \frac{1}{s-q'}\}} \Vert f\Vert _{L^s(v)}. \end{aligned}$$

(3.34)

for any $s \in (q', \infty )$ and $v \in A_{s/q'}$. By duality, (3.34) implies

$$\begin{aligned} \sup _{\varepsilon } \Vert {\textbf {T}}_{\Omega _0}^{\varepsilon } f\Vert _{L^p(w)}&\lesssim [w^{1-p'}]_{A_{p'/q'}}^{\max \{1, \frac{1}{p'/q'-1}\} + \max \{1, \frac{1}{p'-q'}\}} \Vert f\Vert _{L^p(w)}. \end{aligned}$$

(3.35)

We would like to use (3.35) to bound ${\textbf {S}}_{\Omega _0}$. Let $\{r_m(\cdot )\}_{m \in \mathbb {N}}$ be the system of Rademacher functions in [0, 1). By Khintchine’s inequality (cf. [45, p. 586]) and (3.35) applied to $\varepsilon (t):= \{r_m(t)\}_{m \in \mathbb {Z}}$, we have

$$\begin{aligned}&\Vert {\textbf {S}}_{\Omega _0} f\Vert _{L^p(w)} \simeq \bigg \Vert \bigg (\int _0^1 \Big |\sum _{m \in \mathbb {Z}} r_m(t) {\textbf {T}}_{\Omega _0, m} f\Big |^p dt \bigg )^{\frac{1}{p}}\bigg \Vert _{L^p(w)} \nonumber \\&\quad = \bigg (\int _0^1 \Vert {\textbf {T}}_{\Omega _0}^{\varepsilon (t)} f\Vert _{L^p(w)}^p dt \bigg )^{\frac{1}{p}} \lesssim [w^{1-p'}]_{A_{p'/q'}}^{\max \{1, \frac{1}{p'/q'-1}\} + \max \{1, \frac{1}{p'-q'}\}} \Vert f\Vert _{L^p(w)}. \end{aligned}$$

(3.36)

Therefore, (3.31) follows from (3.32), (3.33), and (3.36). $\square$

Lemma 3.9

Let $\psi \in \mathscr {C}_c^{\infty }(\mathbb {R}^n)$ be a radial function such that $0 \le \psi \le 1$, ${\text {supp}}\psi \subset \{1/2 \le |\xi | \le 2\}$ and $\sum _{l \in \mathbb {Z}} \psi (2^{-l}\xi )^2 =1$ for $|\xi | \ne 0$. Define the multiplier $\Delta _l$ by $\widehat{\Delta _l f}(\xi ) = \psi (2^{-l}\xi ) {\widehat{f}}(\xi )$. For $j \in \mathbb {Z}$, set $\nu _j(x):= \frac{\Omega (x')}{|x|^n} {\textbf {1}}_{\{2^j\le |x|<2^{j+1}\}}(x)$, where $\Omega$ is the same as in Theorem 3.7. Then for all $p \in (q', \infty )$ and $w \in A_{p/q'}$,

$$\begin{aligned} \sup _{s \in \mathbb {Z}} \bigg \Vert \Big (\sum _{k \in \mathbb {Z}} |\nu _{k+s} *\Delta _{l-k}^2 f|^2\Big )^{\frac{1}{2}}\bigg \Vert _{L^p(w)} \lesssim [w]_{A_{p/q'}}^{\frac{5}{2} \max \{1, \frac{1}{p/q'-1}, \frac{2}{p-1}\}} \Vert f\Vert _{L^p(w)}. \end{aligned}$$

(3.37)

Proof

Let $p \in (q', \infty )$ and $w \in A_{p/q'}$. Observe that

$$\begin{aligned} \sup _{s \in \mathbb {Z}} \sup _{k \in \mathbb {Z}} |\nu _{k+s} *f_k| \le M_{\Omega }\Big (\sup _{k \in \mathbb {Z}} |f_k| \Big ). \end{aligned}$$

(3.38)

This and (3.16) yield

$$\begin{aligned} \sup _{s \in \mathbb {Z}} \Big \Vert \sup _{k \in \mathbb {Z}} |\nu _{k+s} *f_k| \Big \Vert _{L^p(w)} \lesssim [w]_{A_{p/q'}}^{\frac{1}{p-q'}} \Big \Vert \sup _{k \in \mathbb {Z}} |f_k| \Big \Vert _{L^p(w)}. \end{aligned}$$

(3.39)

In light of Theorem 3.8, (3.38) implies that for any $r \in (1, q)$ and $v^{1-r'} \in A_{r'/q'}$,

$$\begin{aligned} \sup _{s \in \mathbb {Z}} \Big \Vert \sup _{k \in \mathbb {Z}} |\nu _{k+s} *f_k| \Big \Vert _{L^r(v)} \lesssim [v^{1-r'}]_{A_{r'/q'}}^{\max \{1, \frac{1}{r'/q'-1}\} + \max \{1, \frac{1}{r'-q'}\}} \Big \Vert \sup _{k \in \mathbb {Z}} |f_k| \Big \Vert _{L^r(v)}, \end{aligned}$$

which together with duality gives

$$\begin{aligned} \sup _{s \in \mathbb {Z}} \bigg \Vert \sum _{k \in \mathbb {Z}} |\nu _{k+s} *f_k| \bigg \Vert _{L^p(w)} \lesssim [w]_{A_{p/q'}}^{\max \{1, \frac{1}{p/q'-1}\} + \max \{1, \frac{1}{p-q'}\}} \bigg \Vert \sum _{k \in \mathbb {Z}} |f_k| \bigg \Vert _{L^p(w)}. \end{aligned}$$

(3.40)

Then, interpolating between (3.39) and (3.40), we obtain

$$\begin{aligned} \sup _{s \in \mathbb {Z}} \bigg \Vert \Big (\sum _{k \in \mathbb {Z}} |\nu _{k+s} *f_k|^2 \Big )^{\frac{1}{2}} \bigg \Vert _{L^p(w)} \lesssim [w]_{A_{p/q'}}^{\frac{1}{2} \max \{1, \frac{1}{p/q'-1}\} + \max \{1, \frac{1}{p-q'}\}} \bigg \Vert \Big (\sum _{k \in \mathbb {Z}} |f_k|^2 \Big )^{\frac{1}{2}}\bigg \Vert _{L^p(w)}. \end{aligned}$$

Combining (3.10) with (3.8) and that $[w]_{A_p} \le [w]_{A_{p/q'}}$, this immediately implies (3.37). $\square$

4 Proof of Main Theorems

In this section, we will prove Theorems 1.1 and 1.2. The first step is to show Theorem 1.1, which will follow from Theorem 4.8, a limited rang, off-diagonal extrapolation with quantitative weights norms. Before proving the latter, we present some other quantitative extrapolation.

4.1 $A_p$ Extrapolation

We begin with the $A_p$ extrapolation with quantitative bounds.

Theorem 4.1

Let $\mathcal {F}$ be a family of extrapolation pairs. Assume that there exist exponents $p_0 \in [1, \infty ]$ such that for all weights $v^{p_0} \in A_{p_0}$,

$$\begin{aligned} \Vert f v\Vert _{L^{p_0}} \le \Phi ([v^{p_0}]_{A_{p_0}}) \Vert g v\Vert _{L^{p_0}}, \quad (f, g) \in \mathcal {F}, \end{aligned}$$

(4.1)

where $\Phi : [1, \infty ) \rightarrow [1, \infty )$ is an increasing function. Then for all exponents $p \in (1, \infty )$ and all weights $w^p \in A_p$,

$$\begin{aligned} \Vert f w\Vert _{L^p} \le 2 \Phi \Big (C_p \, [w^p]_{A_p}^{\max \{1, \frac{p_0 - 1}{p -1}\}}\Big ) \Vert g w\Vert _{L^p}, \quad (f, g) \in \mathcal {F}, \end{aligned}$$

(4.2)

where $C_p=3^{n(p'+8)(p_0-p)}$ if $p<p_0$, and $C_p=3^{n(p+8)}$ if $p>p_0$.

Theorem 4.1 was shown in [38, 40] without the explicit constant $C_p$. We restudy it by presenting a stronger result as follows.

Theorem 4.2

Let $q \in [1, \infty ]$ and $p \in (1, \infty )$. Then for any $w^p \in A_p$, $f \in L^p(w^p)$, and $g \in L^{p'}(w^{-p'})$, there exists $v^q \in A_q$ with $[v^q]_{A_q} \le C_p \, [w^p]_{A_p}^{\max \{1, \frac{q-1}{p-1}\}}$ such that

$$\begin{aligned} \Vert fv\Vert _{L^q} \Vert gv^{-1}\Vert _{L^{q'}} \le 2 \Vert fw\Vert _{L^p} \Vert gw^{-1}\Vert _{L^{p'}}, \end{aligned}$$

(4.3)

where $C_p=3^{n(p'+8)(q-p)}$ if $p<q$, and $C_p=3^{n(p+8)}$ if $p>q$.

Proof

Let $p \in (1, \infty )$, $w^p \in A_p$, $f \in L^p(w^p)$, and $g \in L^{p'}(w^{-p'})$. We may assume that f and g are nonnegative and non-trivial. Let us first consider the case $p<q$. By $w^p \in A_p$ and Theorem 2.2, there exists an operator $\mathcal {R}: L^p(w^p) \rightarrow L^p(w^p)$ such that

$$\begin{aligned} f \le \mathcal {R} f, \quad \Vert \mathcal {R} f\Vert _{L^p(w^p)} \le 2 \Vert f\Vert _{L^p(w^p)}, \quad \text { and }\quad [\mathcal {R} f]_{A_1} \le 2 \Vert M\Vert _{L^p(w^p)}. \end{aligned}$$

(4.4)

Define

$$\begin{aligned} v := w^{\frac{p}{q}} (\mathcal {R} f)^{-1+\frac{p}{q}}. \end{aligned}$$

(4.5)

Then by Lemma 2.5, the last estimate in (4.4), and (2.1),

$$\begin{aligned}{}[v^q]_{A_q} = [w^p (\mathcal {R} f)^{p-q}]_{A_q} \le [w^p]_{A_p} [\mathcal {R} f]_{A_1}^{q-p} \le 3^{n(p' + 8) (q-p)} [w^p]_{A_p}^{\frac{q-1}{p-1}}. \end{aligned}$$

(4.6)

On the other hand, it follows from the first two estimate in (4.4) that

$$\begin{aligned} \Vert fv\Vert _{L^q} =\Vert f (\mathcal {R} f)^{-1+\frac{p}{q}} w^{\frac{p}{q}}\Vert _{L^q} \le \Vert (\mathcal {R} f \cdot w)^{\frac{p}{q}}\Vert _{L^q} =\Vert \mathcal {R} f \cdot w\Vert _{L^p}^{\frac{p}{q}} \le (2 \Vert fw\Vert _{L^p})^{\frac{p}{q}}. \end{aligned}$$

(4.7)

In view of $p<q$, we set $\frac{1}{r}:= \frac{1}{p} - \frac{1}{q}$. Then, $\frac{1}{q'}=\frac{1}{p'} + \frac{1}{r}$, and by Hölder’s inequality,

$$\begin{aligned} \Vert gv^{-1}\Vert _{L^{q'}} =\Vert (g w^{-1}) (wv^{-1})\Vert _{L^{q'}} \le \Vert gw^{-1}\Vert _{L^{p'}} \Vert wv^{-1}\Vert _{L^r}. \end{aligned}$$

(4.8)

Observe that

$$\begin{aligned} \Vert wv^{-1}\Vert _{L^r} =\Vert (\mathcal {R}f \cdot w)^{p(\frac{1}{p}-\frac{1}{q})}\Vert _{L^r} =\Vert \mathcal {R}f \cdot w\Vert _{L^p}^{1 - \frac{p}{q}} \le (2 \Vert fw\Vert _{L^p})^{1 - \frac{p}{q}}, \end{aligned}$$

(4.9)

where the second estimate estimate in (4.4) was used in the last step. Now collecting (4.7)–(4.9), we obtain

$$\begin{aligned} \Vert fv\Vert _{L^q} \Vert gv^{-1}\Vert _{L^{q'}} \le 2 \Vert fw\Vert _{L^p} \Vert gw^{-1}\Vert _{L^{p'}}. \end{aligned}$$

This and (4.6) show (4.3) in the case $p<q$.

Let us deal with the case $q<p$, which is equivalent to $p'<q'$. Also, $w^p \in A_p$ is equivalent to $w^{-p'} \in A_{p'}$. Note that $g \in L^{p'}(w^{-p'})$ and $f \in L^p(w^p)$. Invoking (4.3) for $p'$, $q'$, g, f, $w^{-1}$ in place of p, q, f, g, and w, respectively, one can find a weight $u^{q'} \in A_{q'}$ with

$$\begin{aligned}{}[u^{-q'}]_{A_{q'}} \le 3^{n(p+8)(q'-p')} [w^{-p'}]_{A_{p'}}^{\frac{q'-1}{p'-1}} \end{aligned}$$

(4.10)

such that

$$\begin{aligned} \Vert gu\Vert _{L^{q'}} \Vert f u^{-1}\Vert _{L^q} \le 2 \Vert gw^{-1}\Vert _{L^{p'}} \Vert fw\Vert _{L^p}. \end{aligned}$$

(4.11)

Picking $v=u^{-1}$ and using (4.10), we see that

$$\begin{aligned}{}[v^q]_{A_q} = [u^{-q}]_{A_q} = [u^{-q'}]_{A_{q'}}^{\frac{1}{q'-1}}&\le 3^{n(p+8) \frac{q'-p'}{q'-1}} [w^{-p'}]_{A_{p'}}^{\frac{1}{p'-1}} < 3^{n(p+8)} [w^p]_{A_p}, \end{aligned}$$

and (4.11) can be rewritten as

$$\begin{aligned} \Vert f v\Vert _{L^q} \Vert gv^{-1}\Vert _{L^{q'}} \le 2 \Vert fw\Vert _{L^p} \Vert gw^{-1}\Vert _{L^{p'}}. \end{aligned}$$

This shows (4.3) in the case $q<p$. $\square$

Proof of Theorem 4.1

Let $p \in (1, \infty )$ and $w^p \in A_p$. By duality,

$$\begin{aligned} \Vert fw\Vert _{L^p} = \sup _{\begin{array}{c} 0 \le h \in L^{p'}(w^{-p'}) \\ \Vert hw^{-1}\Vert _{L^{p'}} = 1 \end{array}} |\langle f, h \rangle |. \end{aligned}$$

(4.12)

Fix a nonnegative function $h \in L^{p'}(w^{-p'})$ with $\Vert hw^{-1}\Vert _{L^{p'}} = 1$. In view of Theorem 4.2, one can find a weight $v^{p_0} \in A_{p_0}$ such that

$$\begin{aligned}{}[v^{p_0}]_{A_{p_0}}&\le C_p \, [w^p]_{A_p}^{\max \{1, \frac{p_0 - 1}{p -1}\}}, \end{aligned}$$

(4.13)

$$\begin{aligned} \Vert gv\Vert _{L^{p_0}} \Vert h v^{-1}\Vert _{L^{p'_0}}&\le 2 \Vert gw\Vert _{L^p} \Vert hw^{-1}\Vert _{L^{p'}}, \end{aligned}$$

(4.14)

where $C_p=3^{n(p'+8)(p_0-p)}$ if $p<p_0$, and $C_p=3^{n(p+8)}$ if $p>p_0$. Hence, by (4.1), (4.13), and (4.14),

$$\begin{aligned} |\langle f, h \rangle | \le \Vert fv\Vert _{L^{p_0}} \Vert hv^{-1}\Vert _{L^{p'_0}}&\le \Phi ([v^{p_0}]_{A_{p_0}}) \Vert gv\Vert _{L^{p_0}} \Vert hv^{-1}\Vert _{L^{p'_0}}\\&\le 2 \Phi (C_p [w^p]_{A_p}^{\max \{1, \frac{p_0 - 1}{p -1}\}}) \Vert gw\Vert _{L^p} \Vert hw^{-1}\Vert _{L^{p'}}, \end{aligned}$$

which along with (4.12) yields at once (4.2) as desired. $\square$

Next, we would like to use Theorem 4.1 to get additional results.

Theorem 4.3

Let $\mathcal {F}$ be a family of extrapolation pairs. Assume that there exist exponents $p_0 \in (0, \infty )$ and $q_0 \in [1, \infty )$ such that for all weights $v \in A_{q_0}$,

$$\begin{aligned} \Vert f\Vert _{L^{p_0}(v)} \le \Phi ([v]_{A_{q_0}}) \Vert g\Vert _{L^{p_0}(v)}, \quad (f, g) \in \mathcal {F}, \end{aligned}$$

(4.15)

where $\Phi : [1, \infty ) \rightarrow [1, \infty )$ is an increasing function. Then for all exponents $p \in (1, \infty )$ and all weights $w \in A_p$,

$$\begin{aligned} \Vert f\Vert _{L^{pp_0/q_0}(w)} \le 2^{\frac{q_0}{p_0}} \Phi \Big (C_p \, [w]_{A_p}^{\max \{1, \frac{q_0 - 1}{p -1}\}}\Big ) \Vert g\Vert _{L^{pp_0/q_0}(w)}, \quad (f, g) \in \mathcal {F}, \end{aligned}$$

(4.16)

where $C_p=3^{n(p'+8)(q_0-p)}$ if $p<q_0$, and $C_p=3^{n(p+8)}$ if $p>q_0$.

Proof

Set

$$\begin{aligned} {\widetilde{\mathcal {F}}}:= \big \{(F, G)= \big (f^{\frac{p_0}{q_0}}, g^{\frac{p_0}{q_0}}\big ): (f, g) \in \mathcal {F}\big \}. \end{aligned}$$

Note that (4.15) implies that for all weights $v \in A_{q_0}$,

$$\begin{aligned} \Vert F\Vert _{L^{q_0}(v)} = \Vert f\Vert _{L^{p_0}(v)}^{\frac{p_0}{q_0}} \le \Phi ([v]_{A_{q_0}})^{\frac{p_0}{q_0}} \Vert g\Vert _{L^{p_0}(v)}^{\frac{p_0}{q_0}} =\Phi ([v]_{A_{q_0}})^{\frac{p_0}{q_0}} \Vert G\Vert _{L^{q_0}(v)}, \nonumber \\ \end{aligned}$$

(4.17)

for all $(F, G) \in {\widetilde{\mathcal {F}}}$. Then it follows from (4.17) and Theorem 4.1 with $p_0$ replaced by $q_0$ that for all exponent $p \in (1, \infty )$ and for all weights $w \in A_p$,

$$\begin{aligned} \Vert F\Vert _{L^p(w)} \le 2 \Phi \Big (C_p \, [w]_{A_p}^{\max \{1, \frac{q_0 - 1}{p -1}\}}\Big )^{\frac{p_0}{q_0}} \Vert G\Vert _{L^{q_0}(w)}, \quad (F, G) \in {\widetilde{\mathcal {F}}}, \end{aligned}$$

which can be rewritten as

$$\begin{aligned} \Vert f\Vert _{L^{pp_0/q_0}(w)} \le 2^{\frac{q_0}{p_0}} \Phi \Big (C_p \, [w]_{A_p}^{\max \{1, \frac{q_0 - 1}{p -1}\}}\Big ) \Vert g\Vert _{L^{pp_0/q_0}(w)}, \quad (f, g) \in \mathcal {F}, \end{aligned}$$

where $C_p=3^{n(p'+8)(q_0-p)}$ if $p<q_0$, and $C_p=3^{n(p+8)}$ if $p>q_0$. This shows (4.16). $\square$

Theorem 4.4

Let T be a sublinear operator. Assume that there exists $p_0 \in [1, \infty )$ such that for all $v \in A_{p_0}$,

$$\begin{aligned} \Vert Tf\Vert _{L^{p_0, \infty }(v)} \le \Phi ([v]_{A_{p_0}}) \Vert f\Vert _{L^{p_0}(v)}, \end{aligned}$$

(4.18)

where $\Phi : [1, \infty ) \rightarrow [1, \infty )$ is an increasing function. Then for all $p \in (1, \infty )$ and for all $w \in A_p$,

$$\begin{aligned} \Vert Tf\Vert _{L^{p, \infty }(w)}&\le 2 \Phi \Big (C_p \, [w^p]_{A_p}^{\max \{1, \frac{p_0 - 1}{p -1}\}}\Big ) \Vert f\Vert _{L^p(w)}, \end{aligned}$$

(4.19)

$$\begin{aligned} \Vert Tf\Vert _{L^p(w)}&\le 2 \Phi \Big (C_p \, [w^p]_{A_p}^{\max \{1, \frac{3(p_0 - 1)}{p -1}\}}\Big ) \Vert f\Vert _{L^p(w)}. \end{aligned}$$

(4.20)

Proof

Given an arbitrary number $\lambda >0$, we denote

$$\begin{aligned} \mathcal {F}_{\lambda } :=\{(F_{\lambda }, G) := (\lambda {\textbf {1}}_{\{x \in \mathbb {R}^n: |Tf(x)| > \lambda \}}, f): f \}. \end{aligned}$$

The hypothesis (4.18) implies that for all weights $v \in A_{p_0}$,

$$\begin{aligned} \Vert F_{\lambda }\Vert _{L^{p_0}(v)}&= \lambda \, v(\{x \in \mathbb {R}^n: |Tf(x)| > \lambda \})^{\frac{1}{p_0}} \le \Vert Tf\Vert _{L^{p_0, \infty }(v)} \nonumber \\&\le \Phi ([v]_{A_{p_0}}) \Vert f\Vert _{L^{p_0}(v)} = \Phi ([v]_{A_{p_0}}) \Vert G\Vert _{L^{p_0}(v)}, \end{aligned}$$

(4.21)

for all $(F_{\lambda }, G) \in \mathcal {F}_{\lambda }$. Thus, (4.21) means that (4.1) is satisfies for the family $\mathcal {F}_{\lambda }$. Then Theorem 4.1 yields that for all exponents $p \in (1, \infty )$ and all weights $w \in A_p$,

$$\begin{aligned} \lambda \,&w(\{x \in \mathbb {R}^n: |Tf(x)| > \lambda \})^{\frac{1}{p}} = \Vert F_{\lambda }\Vert _{L^p(w)} \\&\le 2 \Phi \Big (C_p \, [w^p]_{A_p}^{\max \{1, \frac{p_0 - 1}{p -1}\}}\Big ) \Vert G\Vert _{L^p(w)} = 2 \Phi \Big (C_p \, [w^p]_{A_p}^{\max \{1, \frac{p_0 - 1}{p -1}\}}\Big ) \Vert f\Vert _{L^p(w)}, \end{aligned}$$

where $C_p=3^{n(p'+8)(p_0-p)}$ if $p<p_0$, and $C_p=3^{n(p+8)}$ if $p>p_0$, which along with the arbitrariness of $\lambda$ implies (4.19).

To prove (4.20), we fix $q \in (1, \infty )$ and $w \in A_q$. By Lemma 2.4, there exist $\gamma \in (0, 1)$ and $q_0 \in (1, q)$ so that

$$\begin{aligned} q_0 = \frac{q}{1+\varepsilon }, \quad 0<\varepsilon <\frac{q-1}{(1+\gamma )'}, \quad (1+\gamma )' \simeq [v]_{A_q}^{\max \{1, \frac{1}{q-1}\}}, \quad [w]_{A_{q_0}} \le 2^q [w]_{A_q}. \end{aligned}$$

(4.22)

We may assume that $\varepsilon <\frac{1}{2}$ since in this case (4.22) still holds. Choose $q_1:= \frac{q}{1-\varepsilon } \in (q, 2q)$ such that $\frac{1}{q}=\frac{1-\theta }{q_0} + \frac{\theta }{q_1}$ with $\theta =\frac{1}{2}$. Then,

$$\begin{aligned} w \in A_q \subset A_{q_1} \quad \text { with }\quad [w]_{A_{q_1}} \le [w]_{A_q}. \end{aligned}$$

(4.23)

Then it follows from (4.22), (4.23), and (4.19) (with the exact constant $C_p$, see the proof above) that

$$\begin{aligned} \Vert Tf\Vert _{L^{q_0, \infty }(w)}&\le 2 \Phi \Big (C_{q_0} \, [w]_{A_{q_0}}^{\max \{1, \frac{p_0 - 1}{q_0 -1}\}}\Big ) \Vert f\Vert _{L^{q_0}(w)}, \end{aligned}$$

(4.24)

$$\begin{aligned} \Vert Tf\Vert _{L^{q_1, \infty }(w)}&\le 2 \Phi \Big (C_{q_1} \, [w]_{A_{q_1}}^{\max \{1, \frac{p_0 - 1}{q_1 -1}\}}\Big ) \Vert f\Vert _{L^{q_1}(w)}, \end{aligned}$$

(4.25)

where

$$\begin{aligned} C_{q_i}= {\left\{ \begin{array}{ll} 3^{n(q'_i+8)(p_0-q_i)}, &{} \text { if } q_i<p_0, \\ 3^{n(q_i+8)}, &{}\text { if } q_i>p_0, \end{array}\right. } \qquad i=0, 1. \end{aligned}$$

Additionally, by the choice of $q_0$ and $q_1$, and that $\varepsilon <(q-1)/2$, we have

$$\begin{aligned}&q_0-1=\frac{q}{1+\varepsilon } -1> \frac{q-1}{2(1+\varepsilon )} >\frac{q-1}{3}, \quad q'_0 = \frac{q}{q-1-\varepsilon } < 2q', \end{aligned}$$

(4.26)

$$\begin{aligned}&C_{q_i} \le C'_q, \quad \text {and}\quad [w]_{A_{q_i}}^{\max \{1, \frac{p_0 - 1}{q_i -1}\}} \le [w]_{A_q}^{\max \{1, \frac{3(p_0 - 1)}{q -1}\}}, \quad i=0, 1, \end{aligned}$$

(4.27)

where $C'_q$ depends only on n, $p_0$, and q. Thus, invoking (4.27), we interpolate between (4.24) and (4.25) to conclude

$$\begin{aligned} \Vert Tf\Vert _{L^q(w)}&\le 2 \Phi \Big (C'_q \, [w^p]_{A_p}^{\max \{1, \frac{3(p_0 - 1)}{q -1}\}}\Big ) \Vert f\Vert _{L^q(w)}. \end{aligned}$$

This completes the proof. $\square$

4.2 Off-Diagonal Extrapolation

We next present a quantitative off-diagonal extrapolation below, which improves Theorem 4.1 to the limited range case.

Theorem 4.5

Let $\mathcal {F}$ be a family of extrapolation pairs and $1 \le \mathfrak {p}_- < \mathfrak {p}_+ \le \infty$. Assume that there exist exponents $p_0 \in [\mathfrak {p}_-, \mathfrak {p}_+]$ and $q_0 \in (1, \infty )$ such that for all weights $v^{p_0} \in A_{p_0/\mathfrak {p}_-} \cap RH_{(\mathfrak {p}_+/p_0)'}$,

$$\begin{aligned} \Vert f v\Vert _{L^{q_0}} \le \Phi \big ([v^{p_0(\mathfrak {p}_+/p_0)'}]_{A_{\tau _{p_0}}}\big ) \Vert g v\Vert _{L^{p_0}}, \quad (f, g) \in \mathcal {F}, \end{aligned}$$

(4.28)

where $\Phi : [1, \infty ) \rightarrow [1, \infty )$ is an increasing function. Then for all exponents $p \in (\mathfrak {p}_-, \mathfrak {p}_+)$ and $q \in (1, \infty )$ satisfying $\frac{1}{p} - \frac{1}{q} = \frac{1}{p_0} - \frac{1}{q_0}$, and all weights $w^p \in A_{p/\mathfrak {p}_-} \cap RH_{(\mathfrak {p}_+/p)'}$,

$$\begin{aligned} \Vert f w\Vert _{L^q} \le 2^{\max \{\frac{\tau _{p_0}}{p_0}, \frac{\tau _p}{p}\}} \Phi \Big (C_{p, q} \, [w^{p(\mathfrak {p}_+/p)'}]_{A_{\tau _p}}^{\max \{1, \frac{\tau _{p_0} - 1}{\tau _p -1}\}}\Big ) \Vert g w\Vert _{L^p}, \quad (f, g) \in \mathcal {F}.\nonumber \\ \end{aligned}$$

(4.29)

To show Theorem 4.5, we present a more general result below.

Theorem 4.6

Let $\beta \in (0, \infty )$, $p_0, q_0 \in [1, \infty )$, $p, q \in (1, \infty )$, and let $r_0, r \in (\frac{1}{\beta }, \infty )$ be such that $\frac{1}{q} - \frac{1}{q_0} = \frac{1}{r} - \frac{1}{r_0} = \frac{1}{p} - \frac{1}{p_0}$. Then for all weights $w^r \in A_{r \beta }$ and for all functions $f \in L^p(w^p)$ and $g \in L^{q'}(w^{-q'})$, there exists a weight $v^{r_0} \in A_{r_0 \beta }$ such that

$$\begin{aligned}{}[v^{r_0}]_{A_{r_0 \beta }}&\lesssim [w^r]_{A_{r \beta }}^{\max \{1, \frac{r_0 \beta -1}{r \beta -1}\}}, \end{aligned}$$

(4.30)

$$\begin{aligned} \Vert fv\Vert _{L^{p_0}} \Vert g v^{-1}\Vert _{L^{q'_0}}&\le 2^{\max \{\frac{r \beta }{p}, \frac{(r \beta )'}{q'}\}} \Vert fw\Vert _{L^p} \Vert gw^{-1}\Vert _{L^{q'}}. \end{aligned}$$

(4.31)

Proof

Fix $w^r \in A_{r \beta }$, $f \in L^p(w^p)$, and $g \in L^{q'}(w^{-q'})$. We first consider the case $q<q_0$ (equivalently, $p<p_0$ and $r<r_0$). Pick

$$\begin{aligned} h := f^{\frac{p}{r \beta }} w^{\frac{p-r}{r \beta }} \quad \text { so that }\quad \Vert h\Vert _{L^{r\beta }(w^r)} = \Vert fw\Vert _{L^p}^{\frac{p}{r \beta }}. \end{aligned}$$

(4.32)

By $w^r \in A_{r \beta }$ and Theorem 2.2, there exists an operator $\mathcal {R}: L^{r \beta }(w^r) \rightarrow L^{r \beta }(w^r)$ such that

$$\begin{aligned} h \le \mathcal {R} h, \quad \Vert \mathcal {R} h\Vert _{L^{r \beta }(w^r)} \le 2 \Vert h\Vert _{L^{r \beta }(w^r)}, \quad \text { and }\quad [\mathcal {R} h]_{A_1} \le 2 \Vert M\Vert _{L^{r \beta }(w^r)}. \end{aligned}$$

(4.33)

Define

$$\begin{aligned} v := w^{\frac{r}{r_0}} (\mathcal {R} h)^{\frac{(r-r_0)\beta }{r_0}}. \end{aligned}$$

(4.34)

Then by Lemma 2.5 part (a), the last inequality in (4.33), and (2.1),

$$\begin{aligned}{}[v^{r_0}]_{A_{r_0 \beta }} =[w^r (\mathcal {R} h)^{r\beta - r_0 \beta }]_{A_{r_0 \beta }} \le [w^r]_{A_{r \beta }} [\mathcal {R}h]_{A_1}^{r_0 \beta - r \beta } \lesssim [w^r]_{A_{r \beta }}^{\frac{r_0 \beta -1}{r \beta -1}}. \end{aligned}$$

(4.35)

It follows from (4.32), (4.33), and (4.34) that

$$\begin{aligned} \Vert fv\Vert _{L^{p_0}}&= \Big \Vert \big (h^{\frac{r \beta }{p}} w^{\frac{r}{p}-1+\frac{r}{p_0}} \big ) (\mathcal {R} h)^{\frac{(r-r_0) \beta }{r_0}} \Big \Vert _{L^{p_0}} \le \Big \Vert \big [(\mathcal {R} h)^{r \beta } w^r \big ]^{\frac{1}{p} - \frac{1}{r} + \frac{1}{r_0}} \Big \Vert _{L^{p_0}} \nonumber \\&=\Vert \mathcal {R}h\Vert _{L^{r\beta }(w^r)}^{\frac{r \beta }{p_0}} \le (2 \Vert h\Vert _{L^{r\beta }(w^r)})^{\frac{r \beta }{p_0}} = \big (2 \Vert fw\Vert _{L^p}^{\frac{p}{r \beta }} \big )^{\frac{r \beta }{p_0}} = 2^{\frac{r \beta }{p_0}} \Vert fw\Vert _{L^p}^{\frac{p}{p_0}}. \end{aligned}$$

(4.36)

To proceed, we set $\frac{1}{t}:= \frac{1}{q} - \frac{1}{q_0}$, equivalently $\frac{1}{q'_0} = \frac{1}{q'} + \frac{1}{t}$. By Hölder’s inequality,

$$\begin{aligned} \Vert gv^{-1}\Vert _{L^{q'_0}} \le \Vert gw^{-1}\Vert _{L^{q'}} \Vert wv^{-1}\Vert _{L^t}, \end{aligned}$$

(4.37)

and by (4.32)–(4.34),

$$\begin{aligned} \Vert wv^{-1}\Vert _{L^t}&=\Big \Vert (\mathcal {R} h)^{\beta (1-\frac{r}{r_0})} w^{1-\frac{r}{r_0}} \Big \Vert _{L^t} =\Vert \mathcal {R}h\Vert _{L^{r\beta }(w^r)}^{r\beta (\frac{1}{r} - \frac{1}{r_0})} \le \big (2 \Vert h\Vert _{L^{r\beta }(w^r)} \big )^{r\beta (\frac{1}{r} - \frac{1}{r_0})} \nonumber \\&= \big (2 \Vert fw\Vert _{L^p}^{\frac{p}{r \beta }} \big )^{r\beta (\frac{1}{r} - \frac{1}{r_0})} = 2^{r\beta (\frac{1}{r} - \frac{1}{r_0})} \Vert fw\Vert _{L^p}^{p(\frac{1}{r} - \frac{1}{r_0})}. \end{aligned}$$

(4.38)

Now collecting (4.36), (4.37), and (4.38), we deduce that

$$\begin{aligned} \Vert fv\Vert _{L^{p_0}} \Vert gv^{-1}\Vert _{L^{q'_0}} \le 2^{\frac{r \beta }{p}}\Vert fw\Vert _{L^p} \Vert gw^{-1}\Vert _{L^{q'}}, \end{aligned}$$

(4.39)

provided $\frac{1}{q} - \frac{1}{q_0} = \frac{1}{r} - \frac{1}{r_0} = \frac{1}{p} - \frac{1}{p_0}$. This shows the case $q<q_0$.

Next let us deal with the case $q>q_0$ (equivalently, $p>p_0$ and $r>r_0$). Set

$$\begin{aligned} s := \frac{r}{r \beta -1} \quad \text { and }\quad s_0 := \frac{r_0}{r_0 \beta -1}. \end{aligned}$$

(4.40)

Recall that $w^r \in A_{r \beta }$. Then we see that

$$\begin{aligned} w^{-s} \in A_{s \beta }, \quad q'<q'_0, \quad \text { and }\quad \frac{1}{s} - \frac{1}{s_0} = \frac{1}{r_0} - \frac{1}{r} = \frac{1}{p'} - \frac{1}{p'_0} = \frac{1}{q'} - \frac{1}{q'_0}.\nonumber \\ \end{aligned}$$

(4.41)

Hence, the conclusion in the preceding case applied to the tuple $(q', p', s, q'_0, p'_0, s_0, g, f, w^{-1})$ in place of $(p, q, r, p_0, q_0, r_0, f, g, w)$ gives that there exists a weight $u^{s_0} \in A_{s_0 \beta }$ so that

$$\begin{aligned}{}[u^{s_0}]_{A_{s_0 \beta }}&\lesssim [w^{-s}]_{A_{s \beta }}^{\frac{s_0 \beta -1}{s \beta -1}}, \end{aligned}$$

(4.42)

$$\begin{aligned} \Vert gu\Vert _{L^{q'_0}} fu^{-1}\Vert _{L^{p_0}}&\le 2^{\frac{s\beta }{q'}} \Vert gw^{-1}\Vert _{L^{q'}} \Vert fw\Vert _{L^p}. \end{aligned}$$

(4.43)

Note that by (4.40),

$$\begin{aligned} (r \beta -1) (s \beta -1) =1 \quad \text { and }\quad (r_0 \beta -1) (s_0 \beta -1) =1. \end{aligned}$$

(4.44)

Pick $v:= u^{-1}$. Then by (4.41), (4.42), and (4.44),

$$\begin{aligned}{}[v^{r_0}]_{A_{r_0 \beta }}&=[u^{-r_0}]_{A_{r_0 \beta }} =[u^{\frac{r_0}{r_0 \beta -1}}]_{A_{(r_0 \beta )'}}^{r_0 \beta -1} =[u^{s_0}]_{A_{s_0 \beta }}^{r_0 \beta -1} \\&\lesssim [w^{-s}]_{A_{s \beta }}^{\frac{1}{s \beta -1}} =[w^{-\frac{r}{r \beta -1}}]_{A_{(r \beta )'}}^{r \beta -1} =[w^r]_{A_{r \beta }}, \end{aligned}$$

and (4.43) can be rewritten as

$$\begin{aligned} \Vert fv\Vert _{L^{p_0}} \Vert gv^{-1}\Vert _{L^{q'_0}} \le 2^{\frac{(r \beta )'}{q'}} \Vert fw\Vert _{L^p} \Vert gw^{-1}\Vert _{L^{q'}}. \end{aligned}$$

In the case $q=q_0$, taking $v:=w$, the conclusion is trivial. This completes the proof. $\square$

The following conclusion is a particular case of Theorem 4.6.

Theorem 4.7

Let $1 \le \mathfrak {p}_- < \mathfrak {p}_+ \le \infty$, $p_0 \in [\mathfrak {p}_-, \mathfrak {p}_+]$, $p \in (\mathfrak {p}_-, \mathfrak {p}_+)$, and let $q_0, q \in (1, \infty )$ be such that $\frac{1}{q} - \frac{1}{q_0} = \frac{1}{p} - \frac{1}{p_0}$. Then for all weights $w^p \in A_{p/\mathfrak {p}_-} \cap RH_{(\mathfrak {p}_+/p)'}$ and for all functions $f \in L^p(w^p)$ and $g \in L^{q'}(w^{-q'})$, there exists a weight $v^{p_0} \in A_{p_0/\mathfrak {p}_-} \cap RH_{(\mathfrak {p}_+/p_0)'}$ such that

$$\begin{aligned}{}[v^{p_0(\mathfrak {p}_+/p_0)'}]_{A_{\tau _{p_0}}}&\lesssim [w^{p(\mathfrak {p}_+/p)'}]_{A_{\tau _p}}^{\max \{1, \frac{\tau _{p_0} - 1}{\tau _p -1}\}}, \end{aligned}$$

(4.45)

$$\begin{aligned} \Vert fv\Vert _{L^{p_0}} \Vert g v^{-1}\Vert _{L^{q'_0}}&\le 2^{\max \{\frac{\tau _p}{p}, \frac{\tau '_p}{q'}\}} \Vert fw\Vert _{L^p} \Vert gw^{-1}\Vert _{L^{q'}}. \end{aligned}$$

(4.46)

Proof

Denote

$$\begin{aligned} r := p(\mathfrak {p}_+/p)', \quad r_0 := p_0(\mathfrak {p}_+/p_0)', \quad \text { and }\quad \beta := \frac{1}{\mathfrak {p}_-} - \frac{1}{\mathfrak {p}_+}. \end{aligned}$$

(4.47)

Then one can check that

$$\begin{aligned} r \beta = \tau _p, \quad r_0 \beta = \tau _{p_0}, \quad \text { and }\quad \frac{1}{r} - \frac{1}{r_0} =\frac{1}{p} - \frac{1}{p_0} =\frac{1}{q} - \frac{1}{q_0}. \end{aligned}$$

(4.48)

Let $w^p \in A_{p/\mathfrak {p}_-} \cap RH_{(\mathfrak {p}_+/p)'}$, $f \in L^p(w^p)$, and $g \in L^{q'}(w^{-q'})$. Then it follows from Lemma 2.6 part (b) and (4.48) that $w^r \in A_{r \beta }$, which together with Theorem 4.6 implies that there exists a weight $v^{r_0} \in A_{r_0 \beta }$ such that

$$\begin{aligned}{}[v^{r_0}]_{A_{r_0 \beta }}&\lesssim [w^r]_{A_{r \beta }}^{\max \{1, \frac{r_0 \beta -1}{r \beta -1}\}}, \end{aligned}$$

(4.49)

$$\begin{aligned} \Vert fv\Vert _{L^{p_0}} \Vert g v^{-1}\Vert _{L^{q'_0}}&\le 2^{\max \{\frac{r \beta }{p}, \frac{(r \beta )'}{q'}\}} \Vert fw\Vert _{L^p} \Vert gw^{-1}\Vert _{L^{q'}}. \end{aligned}$$

(4.50)

In view of (4.47), (4.48), and Lemma 2.6 part (b), we conclude from (4.49) and (4.50) that $v^{p_0} \in A_{p_0/\mathfrak {p}_-} \cap RH_{(\mathfrak {p}_+/p_0)'}$ so that (4.45) and (4.46) hold. $\square$

Let us see how we deduce Theorem 4.5 from Theorem 4.7.

Proof of Theorem 4.5

By duality,

$$\begin{aligned} \Vert fw\Vert _{L^q} = \sup _{\begin{array}{c} 0 \le h \in L^{q'}(w^{-q'}) \\ \Vert hw^{-1}\Vert _{L^{q'}} = 1 \end{array}} |\langle f, h \rangle |. \end{aligned}$$

(4.51)

Fix a nonnegative function $h \in L^{q'}(w^{-q'})$ with $\Vert hw^{-1}\Vert _{L^{q'}} = 1$. By Theorem 4.7, there exists a weight $v^{p_0} \in A_{p_0/\mathfrak {p}_-} \cap RH_{(\mathfrak {p}_+/p_0)'}$ such that

$$\begin{aligned}{}[v^{p_0(\mathfrak {p}_+/p_0)'}]_{A_{\tau _{p_0}}}&\lesssim [w^{p(\mathfrak {p}_+/p)'}]_{A_{\tau _p}}^{\max \{1, \frac{\tau _{p_0} - 1}{\tau _p -1}\}}, \end{aligned}$$

(4.52)

$$\begin{aligned} \Vert gv\Vert _{L^{p_0}} \Vert h v^{-1}\Vert _{L^{q'_0}}&\le 2^{\max \{\frac{\tau _p}{p}, \frac{\tau '_p}{q'}\}} \Vert gw\Vert _{L^p} \Vert hw^{-1}\Vert _{L^{q'}}. \end{aligned}$$

(4.53)

Then, in view of (4.52), we use (4.28) and (4.53) to obtain

$$\begin{aligned} |\langle f, h \rangle |&\le \Vert fv\Vert _{L^{q_0}} \Vert hv^{-1}\Vert _{L^{q'_0}} \le \Phi ([v^{p_0(\mathfrak {p}_+/p_0)'}]_{A_{\tau _{p_0}}}) \Vert gv\Vert _{L^{q_0}} \Vert hv^{-1}\Vert _{L^{q'_0}} \\&\le 2^{\max \{\frac{\tau _p}{p}, \frac{\tau '_p}{q'}\}} \Phi \left( C \left[ w^{p(\mathfrak {p}_+/p)'}\right] _{A_{\tau _p}}^{\max \{1, \frac{\tau _{p_0} - 1}{\tau _p -1}\}}\right) \Vert gw\Vert _{L^p} \Vert hw^{-1}\Vert _{L^{q'}}. \end{aligned}$$

This along with (4.51) gives at once (4.29) as desired. $\square$

4.3 Multilinear Extrapolation

If we use Theorem 4.5 to show Theorem 1.1, it requires all the exponents are Banach. Thus, we have to improve Theorem 4.5 to the non-Banach ranges as follows. But in this case, we cannot establish a “product-type embedding” as Theorem 4.7.

Theorem 4.8

Let $\mathcal {F}$ be a family of extrapolation pairs and $1 \le \mathfrak {p}_- < \mathfrak {p}_+ \le \infty$. Assume that there exist exponents $p_0, q_0 \in (0, \infty )$ such that $p_0 \in [\mathfrak {p}_-, \mathfrak {p}_+]$ and for all weights $v^{p_0} \in A_{p_0/\mathfrak {p}_-} \cap RH_{(\mathfrak {p}_+/p_0)'}$,

$$\begin{aligned} \Vert f v\Vert _{L^{q_0}} \le \Phi \big ([v^{p_0}]_{A_{p_0/\mathfrak {p}_-} \cap RH_{(\mathfrak {p}_+/p_0)'}}\big ) \Vert g v\Vert _{L^{p_0}}, \quad (f, g) \in \mathcal {F}, \end{aligned}$$

(4.54)

where $\Phi : [1, \infty ) \rightarrow [1, \infty )$ is an increasing function. Then for all exponents $p \in (\mathfrak {p}_-, \mathfrak {p}_+)$ and $q \in (0, \infty )$ satisfying $\frac{1}{p} - \frac{1}{q} = \frac{1}{p_0} - \frac{1}{q_0}$, and all weights $w^p \in A_{p/\mathfrak {p}_-} \cap RH_{(\mathfrak {p}_+/p)'}$,

$$\begin{aligned} \Vert f w\Vert _{L^q} \le 2^{\max \{\frac{\tau _p}{p}, \frac{\tau '_p}{p_0}\}} \Phi \big (C_0 \, [w^p]_{A_{p/\mathfrak {p}_-} \cap RH_{(\mathfrak {p}_+/p)'}}^{\gamma (p, \, p_0)} \big ) \Vert g w\Vert _{L^p}, \quad (f, g) \in \mathcal {F}, \nonumber \\ \end{aligned}$$

(4.55)

where the constant $C_0$ depends only on n, p, $p_0$, $\mathfrak {p}_-$, and $\mathfrak {p}_+$, and

$$\begin{aligned} \gamma (p, p_0):= {\left\{ \begin{array}{ll} \max \big \{1, \frac{\tau _{p_0} - 1}{\tau _p -1} \big \}, &{} p_0<\mathfrak {p}_+, \\ \frac{p_0}{\tau _p -1} \big (\frac{1}{\mathfrak {p}_-} - \frac{1}{\mathfrak {p}_+}\big ), &{} p_0 = \mathfrak {p}_+. \end{array}\right. } \end{aligned}$$

Proof

Fix $p \in (\mathfrak {p}_-, \mathfrak {p}_+)$ and $q \in (0, \infty )$ satisfying $\frac{1}{p} - \frac{1}{q} = \frac{1}{p_0} - \frac{1}{q_0}$, and let $w^p \in A_{p/\mathfrak {p}_-} \cap RH_{(\mathfrak {p}_+/p)'}$. Fix $(f, g) \in \mathcal {F}$. Without loss of generality we may assume that $0< \Vert gw\Vert _{L^p} < \infty$. Indeed, if $\Vert gw\Vert _{L^p} = \infty$ there is nothing to prove, and if $\Vert gw\Vert _{L^p} = 0$, then $g=0$ a.e. and by (4.54) we see that $f=0$ a.e., which trivially implies (4.55). We split the proof into two cases.

Case I: $q<q_0$. Recall that $\tau _t = \big (\frac{\mathfrak {p}_{+}}{t} \big )' \big (\frac{t}{\mathfrak {p}_-}-1)+1$ for any $t \in [\mathfrak {p}_{-}, \mathfrak {p}_+]$. Obviously, $\tau _t$ is an increasing function in t. Lemma 2.6 part (b) gives

$$\begin{aligned} w^{p(\mathfrak {p}_+/p)'} \in A _{\tau _p}. \end{aligned}$$

(4.56)

Set

$$\begin{aligned} h := g^{\frac{p}{\tau _{p}}}w^{\frac{p}{\tau _{p}}[1-(\mathfrak {p}_+/p)']} \quad \text { so that }\quad \Vert h\Vert _{L^{\tau _p}(w^{p(\mathfrak {p}_+/p)'})} =\Vert gw\Vert _{L^p}^{\frac{p}{\tau _p}} < \infty , \end{aligned}$$

(4.57)

which along with (4.56) and Theorem 2.2 implies that there exists an operator $\mathcal {R}: L^{\tau _p}(w^{p(\mathfrak {p}_+/p)'}) \rightarrow L^{\tau _p}(w^{p(\mathfrak {p}_+/p)'})$ such that

$$\begin{aligned} h \le \mathcal {R} h, \quad \Vert \mathcal {R}h\Vert _{L^{\tau _p}(w^{p(\mathfrak {p}_+/p)'})} \le 2 \Vert h\Vert _{L^{\tau _p}(w^{p(\mathfrak {p}_+/p)'})}, \, \text { and }\, [\mathcal {R}h]_{A_1} \le 2\Vert M\Vert _{L^{\tau _p}(w^{p(\mathfrak {p}_+/p)'})}. \end{aligned}$$

(4.58)

Then (4.57) and the second estimate in (4.58) yield

$$\begin{aligned} \Vert \mathcal {R}h\Vert _{L^{\tau _p}(w^{p(\mathfrak {p}_+/p)'})} \le 2 \Vert gw\Vert _{L^p}^{\frac{p}{\tau _p}}. \end{aligned}$$

(4.59)

Assume first that $p_0<\mathfrak {p}_+$. Pick

$$\begin{aligned} v := w^{\frac{p(\mathfrak {p}_+/p)'}{p_0(\mathfrak {p}_+/p_0)'}}(\mathcal {R}h)^{\frac{\tau _p - \tau _{p_0}}{p_0(\mathfrak {p}_+/p_0)'}}. \end{aligned}$$

(4.60)

Considering $p<p_0$, (4.56), and the last estimate in (4.58), we use Lemma 2.5 and (2.1) to get $v^{p_0(\mathfrak {p}_+/p_0)'} \in A _{\tau _{p_0}}$ with

$$\begin{aligned}{}[v^{p_0(\mathfrak {p}_+/p_0)'}]_{A_{\tau _{p_0}}} \le [w^{p(\mathfrak {p}_+/p)'}]_{A_{\tau _p}} [\mathcal {R}h]_{A_1}^{\tau _{p_0} - \tau _p} \le C_1 [w^{p(\mathfrak {p}_+/p)'}]_{A_{\tau _p}}^{\frac{\tau _{p_0} - 1}{\tau _p -1}}, \end{aligned}$$

(4.61)

where the constant $C_1$ depends only on n, p, $p_0$, $\mathfrak {p}_-$, and $\mathfrak {p}_+$, which together with Lemma 2.6 part (b) implies

$$\begin{aligned} v^{p_0} \in A_{p_0/\mathfrak {p}_-} \cap RH_{(\mathfrak {p}_+/p_0)'}. \end{aligned}$$

(4.62)

On the other hand, note that

$$\begin{aligned}&\frac{1}{p(\mathfrak {p}_+/p)'} - \frac{1}{p_0(\mathfrak {p}_+/p_0)'} = \frac{1}{p} - \frac{1}{p_0} = \frac{1}{q} - \frac{1}{q_0} , \end{aligned}$$

(4.63)

$$\begin{aligned}&\frac{\tau _p}{p(\mathfrak {p}_+/p)'} = \frac{1}{\mathfrak {p}_-} - \frac{1}{\mathfrak {p}_+} = \frac{\tau _{p_0}}{p_0(\mathfrak {p}_+/p_0)'}, \end{aligned}$$

(4.64)

provided

$$\begin{aligned} \tau _p = \bigg (\frac{\mathfrak {p}_{+}}{p}\bigg )' \bigg (\frac{p}{\mathfrak {p}_{-}}-1 \bigg ) + 1 =\frac{\frac{1}{\mathfrak {p}_{-}}-\frac{1}{p}}{\frac{1}{p}-\frac{1}{\mathfrak {p}_{+}}}+1 =\frac{\frac{1}{\mathfrak {p}_{-}}-\frac{1}{\mathfrak {p}_{+}}}{\frac{1}{p}-\frac{1}{\mathfrak {p}_{+}}}, \end{aligned}$$

(4.65)

which also implies

$$\begin{aligned} \frac{\tau _p}{p} + \frac{\tau _p - \tau _{p_0}}{p_0(\mathfrak {p}_+/p_0)'}&=\tau _p \bigg [\frac{1}{p} + \frac{1-\tau _{p_0}/\tau _p}{p_0(\mathfrak {p}_+/p_0)'} \bigg ] \nonumber \\&= \tau _p \bigg [\frac{1}{p} + \bigg (\frac{1}{p_0}-\frac{1}{\mathfrak {p}_+}\bigg )\bigg (1-\frac{\frac{1}{p}-\frac{1}{\mathfrak {p}_+}}{\frac{1}{p_0}-\frac{1}{\mathfrak {p}_+}}\bigg )\bigg ] = \frac{\tau _p}{p_0}. \end{aligned}$$

(4.66)

By (4.57), the first estimate in (4.58), (4.63), and (4.66),

$$\begin{aligned}&\Vert gv\Vert _{L^{p_0}} = \bigg \Vert h^{\frac{\tau _p}{p}} w^{(\mathfrak {p}_+/p)'-1+\frac{p(\mathfrak {p}_+/p)'}{p_0(\mathfrak {p}_+/p_0)'}} (\mathcal {R}h)^{\frac{\tau _p - \tau _{p_0}}{p_0(\mathfrak {p}_+/p_0)'}} \bigg \Vert _{L^{p_0}} \nonumber \\&\le \bigg \Vert (\mathcal {R}h)^{\frac{\tau _p}{p} + \frac{\tau _p - \tau _{p_0}}{p_0(\mathfrak {p}_+/p_0)'}} w^{p(\mathfrak {p}_+/p)' \left[ \frac{1}{p} - \left( \frac{1}{p(\mathfrak {p}_+/p)'} - \frac{1}{p_0(\mathfrak {p}_+/p_0)'}\right) \right] } \bigg \Vert _{L^{p_0}} =\Vert \mathcal {R}h\Vert _{L^{\tau _p}(w^{p(\mathfrak {p}_+/p)'})}^{\frac{\tau _p}{p_0}}. \end{aligned}$$

(4.67)

To proceed, we denote $\frac{1}{r}:= \frac{1}{q} - \frac{1}{q_0}>0$. Then in light of (4.60), (4.63), and (4.64), it follows from Hölder’s inequality that

$$\begin{aligned} \Vert fw\Vert _{L^q}&= \bigg \Vert \Big [f \, w^{\frac{p(\mathfrak {p}_+/p)'}{p_0(\mathfrak {p}_+/p_0)'}} (\mathcal {R}h)^{\frac{\tau _p - \tau _{p_0}}{p_0(\mathfrak {p}_+/p_0)'}} \Big ] \Big [(\mathcal {R} h)^{\frac{\tau _p}{p(\mathfrak {p}_+/p)'}} w \Big ]^{\Big (1-\frac{p(\mathfrak {p}_+/p)'}{p_0(\mathfrak {p}_+/p_0)'}\Big )} \bigg \Vert _{L^q} \\&\le \Vert fv\Vert _{L^{q_0}} \Big \Vert \big [(\mathcal {R} h)^{\frac{\tau _p}{p(\mathfrak {p}_+/p)'}} w \big ]^{1-\frac{p(\mathfrak {p}_+/p)'}{p_0(\mathfrak {p}_+/p_0)'}} \Big \Vert _{L^r} \\&= \Vert fv\Vert _{L^{q_0}} \Big \Vert \big [(\mathcal {R} h)^{\tau _p} w^{p(\mathfrak {p}_+/p)'} \big ]^{\frac{1}{q} - \frac{1}{q_0}} \Big \Vert _{L^r} \\&= \Vert fv\Vert _{L^{q_0}} \Vert \mathcal {R} h\Vert _{L^{\tau _p}(w^{p(\mathfrak {p}_+/p)'})}^{\tau _p(\frac{1}{q} - \frac{1}{q_0})}. \end{aligned}$$

Furthermore, invoking (4.61), (4.62), and (4.54), we arrive at

$$\begin{aligned} \Vert fw\Vert _{L^q}&\le \Phi \big ([v^{p_0(\mathfrak {p}_+/p_0)'}]_{A_{\tau _{p_0}}}\big ) \Vert g v\Vert _{L^{p_0}} \Vert \mathcal {R} h\Vert _{L^{\tau _p}(w^{p(\mathfrak {p}_+/p)'})}^{\tau _p(\frac{1}{q} - \frac{1}{q_0})} \nonumber \\&\le \Phi \big ([v^{p_0(\mathfrak {p}_+/p_0)'}]_{A_{\tau _{p_0}}}\big ) \Vert \mathcal {R} h\Vert _{L^{\tau _p}(w^{p(\mathfrak {p}_+/p)'})}^{\tau _p(\frac{1}{p_0} + \frac{1}{q} - \frac{1}{q_0})} \nonumber \\&\le 2^{\frac{\tau _p}{p}} \Phi \Big (C_1 [w^{p(\mathfrak {p}_+/p)'}]_{A_{\tau _p}}^{\frac{\tau _{p_0} - 1}{\tau _p -1}}\Big ) \Vert gw\Vert _{L^p}, \end{aligned}$$

(4.68)

where we have used (4.67), (4.59), and that $\frac{1}{p} - \frac{1}{q} = \frac{1}{p_0} - \frac{1}{q_0}$.

Let us next treat the case $p_0=\mathfrak {p}_+$. Choose $v:= (\mathcal {R}h)^{\frac{1}{\mathfrak {p}_+} - \frac{1}{\mathfrak {p}_-}}$. Then it follows from Lemma 2.6 part (a) that

$$\begin{aligned} v^{p_0} = (\mathcal {R}h)^{1-\frac{p_0}{\mathfrak {p}_-}} \in A_{p_0/\mathfrak {p}_-} \cap RH_{\infty } = A_{p_0/\mathfrak {p}_-} \cap RH_{(\mathfrak {p}_+/p_0)'} \end{aligned}$$

(4.69)

with

$$\begin{aligned} \max \big \{[v^{p_0}]_{A_{p_0/\mathfrak {p}_-}}, [v^{p_0}]_{RH_{\infty }} \big \} \le [\mathcal {R}h]_{A_1}^{\frac{p_0}{\mathfrak {p}_-} - 1} \lesssim [w^{p(\mathfrak {p}_+/p)'}]_{A_{\tau _p}}^{\frac{p_0}{\tau _p-1}(\frac{1}{\mathfrak {p}_-} - \frac{1}{\mathfrak {p}_+})}, \end{aligned}$$

(4.70)

where we have used the last estimate in (4.58) and (2.1). In the current scenario,

$$\begin{aligned}&\frac{\tau _p}{p} + \frac{1}{\mathfrak {p}_+} - \frac{1}{\mathfrak {p}_-} =\tau _p \bigg [\frac{1}{p} - \bigg (\frac{1}{p} - \frac{1}{\mathfrak {p}_+}\bigg ) \bigg ] =\frac{\tau _p}{\mathfrak {p}_+} =\frac{\tau _p}{p_0}, \end{aligned}$$

(4.71)

$$\begin{aligned}&p_0[(\mathfrak {p}_+/p)' -1] =\frac{p_0p}{\mathfrak {p}_+-p} =\frac{\mathfrak {p}_+ p}{\mathfrak {p}_+ - p} =p(\mathfrak {p}_+/p)', \end{aligned}$$

(4.72)

$$\begin{aligned}&\frac{1}{r} := \frac{1}{q} - \frac{1}{q_0} = \frac{1}{p} - \frac{1}{p_0} = \frac{1}{p} - \frac{1}{\mathfrak {p}_+} =\frac{1}{p(\mathfrak {p}_+/p)'}, \end{aligned}$$

(4.73)

$$\begin{aligned}&\text {and}\quad r \bigg (\frac{1}{\mathfrak {p}_-} -\frac{1}{\mathfrak {p}_+} \bigg ) =\frac{\frac{1}{\mathfrak {p}_-} -\frac{1}{\mathfrak {p}_+}}{\frac{1}{p} -\frac{1}{\mathfrak {p}_+}} =\tau _p. \end{aligned}$$

(4.74)

In view of (4.57), (4.71), and (4.72), there holds

$$\begin{aligned} \Vert gv\Vert _{L^{p_0}} = \Big \Vert h^{\frac{\tau _p}{p}} w^{(\mathfrak {p}_+/p)'-1} (\mathcal {R} h)^{\frac{1}{\mathfrak {p}_+} - \frac{1}{\mathfrak {p}_-}}\Big \Vert _{L^{p_0}} \le \Vert \mathcal {R} h\Vert _{L^{\tau _p}(w^{p(\mathfrak {p}_+/p)'})}^{\frac{\tau _p}{p_0}}. \end{aligned}$$

(4.75)

Hence, invoking (4.69)–(4.75), Hölder’s inequality, and (4.54), we deduce

$$\begin{aligned} \Vert fw\Vert _{L^q}&= \Big \Vert \Big [f \, (\mathcal {R}h)^{\frac{1}{\mathfrak {p}_+} - \frac{1}{\mathfrak {p}_-}} \Big ] \Big [(\mathcal {R}h)^{\frac{1}{\mathfrak {p}_-} - \frac{1}{\mathfrak {p}_+}} w \Big ] \Big \Vert _{L^q}\\&\le \Vert fv\Vert _{L^{q_0}} \big \Vert (\mathcal {R}h)^{\frac{1}{\mathfrak {p}_-} - \frac{1}{\mathfrak {p}_+}} w\big \Vert _{L^r}\\&= \Vert fv\Vert _{L^{q_0}} \Vert \mathcal {R} h\Vert _{L^{\tau _p}(w^{p(\mathfrak {p}_+/p)'})}^{\tau _p(\frac{1}{p} - \frac{1}{p_0})}\\&\le \Phi \big (\max \{[v^{p_0}]_{A_{p_0/{\mathfrak {p}_-}}},\, [v^{p_0}]_{RH_{(\mathfrak {p}_+/p_0)'}}\}\big ) \Vert g v\Vert _{L^{p_0}} \Vert \mathcal {R} h\Vert _{L^{\tau _p}(w^{p(\mathfrak {p}_+/p)'})}^{\tau _p(\frac{1}{p} - \frac{1}{p_0})} \\&\le \Phi \big (\max \{[v^{p_0}]_{A_{p_0/{\mathfrak {p}_-}}},\, [v^{p_0}]_{RH_{(\mathfrak {p}_+/p_0)'}}\}\big ) \Vert \mathcal {R} h\Vert _{L^{\tau _p}(w^{p(\mathfrak {p}_+/p)'})}^{\frac{\tau _p}{p}} \\&\le 2^{\frac{\tau _p}{p}} \Phi \Big (C_1 [w^{p(\mathfrak {p}_+/p)'}]_{A_{\tau _p}}^{\frac{p_0}{\tau _p-1}(\frac{1}{\mathfrak {p}_-} - \frac{1}{\mathfrak {p}_+})}\Big ) \Vert gw\Vert _{L^p}, \end{aligned}$$

where (4.59) was used in the last step.

Case II: $q_0<q$. By Lemma 2.6 parts (b) and (c),

$$\begin{aligned} w^{-s} \in A_{\tau '_p} \quad \text { with }\quad [w^{-s}]_{A_{\tau '_p}} = [w^{p(\mathfrak {p}_+/p)'}]_{A_{\tau _p}}^{\frac{1}{\tau _p-1}}, \end{aligned}$$

(4.76)

where $s=p'(\mathfrak {p}'_-/p')'=\frac{1}{\frac{1}{\mathfrak {p}_-} - \frac{1}{p}}$. This and Theorem 2.2 yield that there exists an operator $\mathcal {R}: L^{\tau '_p}(w^{-s}) \rightarrow L^{\tau '_p}(w^{-s})$ such that for any nonnegative function ${\widetilde{h}} \in L^{\tau '_p}(w^{-s})$,

$$\begin{aligned} {\widetilde{h}} \le \mathcal {R} {\widetilde{h}}, \quad \Vert \mathcal {R} {\widetilde{h}}\Vert _{L^{\tau '_p}(w^{-s})} \le 2 \Vert {\widetilde{h}}\Vert _{L^{\tau '_p}(w^{-s})}, \, \text { and }\, [\mathcal {R} {\widetilde{h}}]_{A_1} \le 2 \Vert M\Vert _{L^{\tau '_p}(w^{-s})}. \end{aligned}$$

(4.77)

Write $\frac{1}{r}:= \frac{1}{q_0} - \frac{1}{q} = \frac{1}{p_0} - \frac{1}{p}>0$, equivalently, $\frac{q}{q-q_0}=\frac{r}{q_0}$. By duality there exists a nonnegative function $h \in L^{\frac{q}{q-q_0}}(w^q)$ with $\Vert h\Vert _{L^{\frac{q}{q-q_0}}(w^q)} \le 1$ such that

$$\begin{aligned} \Vert fw\Vert _{L^q}^{q_0} =\Vert f^{q_0}\Vert _{L^{\frac{q}{q_0}}(w^q)} = \int _{\mathbb {R}^n} f^{q_0} h \, w^q \, dx. \end{aligned}$$

(4.78)

Setting $H:= \mathcal {R} \Big (h^{\frac{r}{\tau '_p q_0}} w^{\frac{s+q}{\tau '_p}} \Big )^{\frac{\tau '_p q_0}{r}} w^{-\frac{(s+q)q_0}{r}}$, we utilize (4.77) to obtain that $h \le H$, and by (2.1) and (4.76),

$$\begin{aligned} \big [H^{\frac{r}{\tau '_p q_0}} w^{\frac{s+q}{\tau '_p}} \big ]_{A_1} = \Big [\mathcal {R} \Big (h^{\frac{r}{\tau '_p q_0}} w^{\frac{s+q}{\tau '_p}} \Big )\Big ]_{A_1} \lesssim [w^{-s}]_{A_{\tau '_p}}^{\frac{1}{\tau '_p -1}} =[w^{p(\mathfrak {p}_+/p)'}]_{A_{\tau _p}}, \end{aligned}$$

(4.79)

provided that

$$\begin{aligned} \Vert h^{\frac{r}{\tau '_p q_0}} w^{\frac{s+q}{\tau '_p}}\Vert _{L^{\tau '_p}(w^{-s})} = \Vert h\Vert _{L^{\frac{r}{q_0}}(w^q)}^{\frac{r}{\tau '_p q_0}} = \Vert h\Vert _{L^{\frac{q}{q-q_0}}(w^q)}^{\frac{r}{\tau '_p q_0}} \le 1, \end{aligned}$$

which also gives

$$\begin{aligned} \Vert H\Vert _{L^{\frac{r}{q_0}}(w^q)} = \Big \Vert \mathcal {R} \Big (h^{\frac{r}{\tau '_p q_0}} w^{\frac{s+q}{\tau '_p}} \Big ) \Big \Vert _{L^{\tau '_p}(w^{-s})}^{\frac{\tau '_p q_0}{r}} \le 2^{\frac{\tau '_p q_0}{r}} \Big \Vert h^{\frac{r}{\tau '_p q_0}} w^{\frac{s+q}{\tau '_p}} \Big \Vert _{L^{\tau '_p}(w^{-s})}^{\frac{\tau '_p q_0}{r}} \le 2^{\frac{\tau '_p q_0}{r}}. \end{aligned}$$

(4.80)

Now picking $v:= w^{\frac{q}{q_0}} \, H^{\frac{1}{q_0}}$, we see that by (4.80)

$$\begin{aligned} \Vert vw^{-1}\Vert _{L^r} = \Vert H\Vert _{L^{\frac{r}{q_0}}(w^q)}^{\frac{1}{q_0}} \le 2^{\frac{\tau '_p}{r}} \le 2^{\frac{\tau '_p}{p_0}}. \end{aligned}$$

(4.81)

To proceed, we observe that $p_0< p <\mathfrak {p}_+$ and use (4.65) to deduce that

$$\begin{aligned}&\tau '_p \, p_0(\mathfrak {p}_+/p_0)'/r =\frac{\tau _p}{\tau _p -1} \frac{\frac{1}{p_0} - \frac{1}{p}}{\frac{1}{p_0} - \frac{1}{\mathfrak {p}_+}} =\frac{\tau _p}{\tau _p -1} \bigg (1- \frac{\tau _{p_0}}{\tau _p} \bigg ) =\frac{\tau _p - \tau _{p_0}}{\tau _p -1}, \end{aligned}$$

(4.82)

$$\begin{aligned}&\frac{\tau _p -1}{p(\mathfrak {p}_+/p)'} =\frac{1}{\mathfrak {p}_-} - \frac{1}{p} =\frac{1}{s}, \quad \text { and }\quad \frac{\tau _{p_0} -1}{p_0(\mathfrak {p}_+/p_0)'} =\frac{1}{\mathfrak {p}_-} - \frac{1}{p_0} =: \frac{1}{s_0}, \end{aligned}$$

(4.83)

which in turn implies

$$\begin{aligned} \frac{q}{q_0} - \frac{q}{r} - \frac{s}{r} =1-\frac{s}{r} =s \bigg (\frac{1}{s} - \frac{1}{r}\bigg ) =s \bigg (\frac{1}{\mathfrak {p}_-} - \frac{1}{p_0}\bigg ) =\frac{s}{s_0} =\frac{p(\mathfrak {p}_+/p)'}{p_0(\mathfrak {p}_+/p_0)'} \frac{\tau _{p_0} -1}{\tau _p -1}. \end{aligned}$$

(4.84)

Hence, it follows from (4.82) and (4.84) that

$$\begin{aligned} v^{p_0(\mathfrak {p}_+/p_0)'}&=w^{(\frac{q}{q_0} - \frac{s}{r} - \frac{q}{r})p_0(\mathfrak {p}_+/p_0)'} \, \big (H^{\frac{r}{\tau '_p q_0}} w^{\frac{s+q}{\tau '_p}} \big )^{\tau '_p p_0(\mathfrak {p}_+/p_0)'/r} \\&=\big (w^{p(\mathfrak {p}_+/p)'}\big )^{\frac{\tau _{p_0} -1}{\tau _p -1}} \big (H^{\frac{r}{\tau '_p q_0}} w^{\frac{s+q}{\tau '_p}} \big )^{\frac{\tau _p - \tau _{p_0}}{\tau _p -1}}, \end{aligned}$$

which along with (4.56), (4.79), and Lemma 2.5 part (b), yields

$$\begin{aligned}{}[v^{p_0(\mathfrak {p}_+/p_0)'}]_{A_{\tau _{p_0}}} \le \big [w^{p(\mathfrak {p}_+/p)'}\big ]_{A_{\tau _p}}^{\frac{\tau _{p_0} -1}{\tau _p -1}} \big [H^{\frac{r}{\tau '_p q_0}} w^{\frac{s+q}{\tau '_p}} \big ]_{A_1}^{\frac{\tau _p - \tau _{p_0}}{\tau _p -1}} \le C_2 \big [w^{p(\mathfrak {p}_+/p)'}\big ]_{A_{\tau _p}}, \end{aligned}$$

(4.85)

where the constant $C_2$ depends only on n, p, $p_0$, $\mathfrak {p}_-$, and $\mathfrak {p}_+$. By Lemma 2.6 part (b), this means that

$$\begin{aligned} v^{p_0} \in A_{p_0/\mathfrak {p}_-} \cap RH_{(\mathfrak {p}_+/p_0)'}. \end{aligned}$$

(4.86)

With (4.78) and (4.86) in hand, the hypothesis (4.54) implies

$$\begin{aligned} \Vert fw\Vert _{L^q}&\le \bigg (\int _{\mathbb {R}^n} f^{q_0} H \, w^q \, dx \bigg )^{\frac{1}{q_0}} = \Vert f v\Vert _{L^{q_0}} \le \Phi \big ([v^{p_0(\mathfrak {p}_+/p_0)'}]_{A_{\tau _{p_0}}}\big ) \Vert g v\Vert _{L^{p_0}} \nonumber \\&\le \Phi \big ([v^{p_0(\mathfrak {p}_+/p_0)'}]_{A_{\tau _{p_0}}}\big ) \Vert g w\Vert _{L^p} \Vert vw^{-1}\Vert _{L^r} \le 2^{\frac{\tau '_p}{p_0}} \Phi \big (C_2 [w^{p(\mathfrak {p}_+/p)'}]_{A_{\tau _p}}\big ) \Vert g w\Vert _{L^p}, \end{aligned}$$

(4.87)

where (4.81) and (4.85) were used in the last inequality. As a consequence, (4.55) follows at once from (4.68) and (4.87). $\square$

Proof of Theorem 1.1

Fix $v_i^{q_i} \in A_{q_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/q_i)'}$, $i=2, \ldots , m$. Set

$$\begin{aligned} \mathcal {F}_1 := \bigg \{(F, G) := \bigg (\frac{f \prod _{i=2}^m v_i}{\prod _{i=2}^m \Vert f_i v_i\Vert _{L^{q_i}}}, f_1 \bigg ) : (f, f_1, \ldots , f_m) \in \mathcal {F}\bigg \}. \end{aligned}$$

By hypothesis (1.2), we see that for every $v_1^{q_1} \in A_{q_1/\mathfrak {p}_1^-} \cap RH_{(\mathfrak {p}_1^+/q_1)'}$

$$\begin{aligned}&\Vert F v_1\Vert _{L^q} = \frac{\Vert f v\Vert _{L^q}}{\prod _{i=2}^m \Vert f_i v_i\Vert _{L^{q_i}}} \le \prod _{i=1}^m \Phi _i \big ([v_i^{q_i}]_{A_{q_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/q_i)'}}\big ) \Vert f_1 v_1\Vert _{L^{q_1}} \\&\quad = \prod _{i=1}^m \Phi _i \big ([v_i^{q_i}]_{A_{q_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/q_i)'}}\big ) \Vert G v_1\Vert _{L^{q_1}}, \quad (F, G) \in \mathcal {F}_1, \end{aligned}$$

where $\frac{1}{q} = \sum _{i=1}^m \frac{1}{q_i}$ and $v=\prod _{i=1}^m v_i$. This verifies the hypothesis (4.54) for the family $\mathcal {F}_1$. Then Theorem 4.8 implies that for every $p_1 \in (\mathfrak {p}_1^-, \mathfrak {p}_1^+)$ and every $w_1^{p_1} \in A_{p_1/\mathfrak {p}_1^-} \cap RH_{(\mathfrak {p}_1^+/p_1)'}$,

$$\begin{aligned} \frac{\Vert fw_1 \prod _{i=2}^m v_i\Vert _{L^{s_1}}}{\prod _{i=2}^m \Vert f_i v_i\Vert _{L^{q_i}}}&= \Vert Fw_1\Vert _{L^{s_1}} \le \mathfrak {N}_1 \prod _{i=2}^m \Phi _i \big ([v_i^{q_i}]_{A_{q_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/q_i)'}}\big ) \Vert G w_1\Vert _{L^{p_1}} \nonumber \\&= \mathfrak {N}_1 \prod _{i=2}^m \Phi _i \big ([v_i^{q_i}]_{A_{q_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/q_i)'}}\big ) \Vert f_1 w_1\Vert _{L^{p_1}}, \quad (F, G) \in \mathcal {F}_1, \end{aligned}$$

(4.88)

where $\frac{1}{s_1} - \frac{1}{p_1} = \frac{1}{q} - \frac{1}{q_1}$,

$$\begin{aligned}&\mathfrak {N}_1 := 2^{\max \{\frac{\tau _{p_1}}{p_1}, \frac{\tau '_{p_1}}{q_1}\}} \Phi _1 \Big (C_1 \, [w_1^{p_1}]_{A_{p_1/\mathfrak {p}_1^-} \cap RH_{(\mathfrak {p}_1^+/p_1)'}}^{\gamma _1(p_1, q_1)}\Big ), \end{aligned}$$

(4.89)

$$\begin{aligned}&\gamma _1(p_1, q_1) := {\left\{ \begin{array}{ll} \max \big \{1, \frac{\tau _{q_1} - 1}{\tau _{p_1} -1} \big \}, &{} q_1<\mathfrak {p}_1^+,\\ \frac{q_1}{\tau _{p_1} -1} \big (\frac{1}{\mathfrak {p}_1^-} - \frac{1}{\mathfrak {p}_1^+} \big ), &{} q_1 = \mathfrak {p}_1^+. \end{array}\right. } \end{aligned}$$

(4.90)

Considering (4.88), we have

$$\begin{aligned} \bigg \Vert fw_1\prod _{i=2}^m v_i \bigg \Vert _{L^{s_1}} \le \mathfrak {N}_1 \Vert f_1 w_1\Vert _{L^{p_1}} \prod _{i=2}^m \Phi _i \big ([v_i^{q_i}]_{A_{q_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/q_i)'}}\big ) \Vert f_i v_i\Vert _{L^{q_i}}, \end{aligned}$$

(4.91)

for all $(f, f_1, \ldots , f_m) \in \mathcal {F}$, for all $p_1 \in (\mathfrak {p}_1^-, \mathfrak {p}_1^+)$, for all $w_1^{p_1} \in A_{p_1/\mathfrak {p}_1^-} \cap RH_{(\mathfrak {p}_1^+/p_1)'}$, and for all $v_i^{q_i} \in A_{q_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/q_i)'}$, $i=2, \ldots , m$.

Now fix $p_1 \in (\mathfrak {p}_1^-, \mathfrak {p}_1^+)$, $w_1^{p_1} \in A_{p_1/\mathfrak {p}_1^-} \cap RH_{(\mathfrak {p}_1^+/p_1)'}$, and $v_i^{q_i} \in A_{q_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/q_i)'}$, $i=3, \ldots , m$. Set

$$\begin{aligned} \mathcal {F}_2 := \bigg \{(F, G) := \bigg (\frac{f w_1 \prod _{i=3}^m v_i}{\Vert f_1 w_1\Vert _{L^{p_1}} \prod _{i=3}^m \Vert f_i v_i\Vert _{L^{q_i}}}, f_2 \bigg ): (f, f_1, \ldots , f_m) \in \mathcal {F}\bigg \}. \end{aligned}$$

It follows from (4.91) that for every $v_2^{q_2} \in A_{q_2/\mathfrak {p}_2^-} \cap RH_{(\mathfrak {p}_2^+/q_2)'}$,

$$\begin{aligned} \Vert Fv_2\Vert _{L^{s_1}}&=\frac{\Vert fw_1 \prod _{i=2}^m v_i\Vert _{L^{s_1}}}{\Vert f_1w_1\Vert _{L^{p_1}} \prod _{i=3} \Vert f_i v_i\Vert _{L^{q_i}}} \\&\le \mathfrak {N}_1 \prod _{i=2}^m \Phi _i \big ([v_i^{q_i}]_{A_{q_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/q_i)'}}\big ) \Vert f_2 v_2\Vert _{L^{q_2}} \\&= \mathfrak {N}_1 \prod _{i=2}^m \Phi _i \big ([v_i^{q_i}]_{A_{q_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/q_i)'}}\big ) \Vert G v_2\Vert _{L^{q_2}}, \quad (F, G) \in \mathcal {F}_2. \end{aligned}$$

Invoking Theorem 4.8 applied to $\mathcal {F}_2$, we have that for every $p_2 \in (\mathfrak {p}_2^-, \mathfrak {p}_2^+)$ and every $w_2^{p_2} \in A_{p_2/\mathfrak {p}_2^-} \cap RH_{(\mathfrak {p}_2^+/p_2)'}$,

$$\begin{aligned}&\frac{\Vert fw_1w_2 \prod _{i=3}^m v_i\Vert _{L^{s_2}}}{\Vert f_1w_1\Vert _{L^{p_1}} \prod _{i=3} \Vert f_i v_i\Vert _{L^{q_i}}} =\Vert Fw_2\Vert _{L^{s_2}} \nonumber \\&\quad \le \mathfrak {N}_1 \mathfrak {N}_2 \prod _{i=3}^m \Phi _i \big ([v_i^{q_i}]_{A_{q_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/q_i)'}}\big ) \Vert G w_2\Vert _{L^{p_2}} \nonumber \\&\quad = \mathfrak {N}_1 \mathfrak {N}_2 \prod _{i=3}^m \Phi _i \big ([v_i^{q_i}]_{A_{q_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/q_i)'}}\big ) \Vert f_2 w_2\Vert _{L^{p_2}}, \quad (F, G) \in \mathcal {F}_2, \end{aligned}$$

(4.92)

where $\frac{1}{s_2} - \frac{1}{p_2} = \frac{1}{s_1} - \frac{1}{q_2}$,

$$\begin{aligned}&\mathfrak {N}_2 := 2^{\max \{\frac{\tau _{p_2}}{p_2}, \frac{\tau '_{p_2}}{q_2}\}} \Phi _2 \Big (C_2 \, [w_2^{p_2}]_{A_{p_2/\mathfrak {p}_2^-} \cap RH_{(\mathfrak {p}_2^+/p_2)'}}^{\gamma _2(p_2, q_2)}\Big ), \end{aligned}$$

(4.93)

$$\begin{aligned}&\gamma _2(p_2, q_2) := {\left\{ \begin{array}{ll} \max \big \{1, \frac{\tau _{q_2} - 1}{\tau _{p_2} -1} \big \}, &{} q_2<\mathfrak {p}_2^+,\\ \frac{q_2}{\tau _{p_2} -1} \big (\frac{1}{\mathfrak {p}_2^-} - \frac{1}{\mathfrak {p}_2^+} \big ), &{} q_2 = \mathfrak {p}_2^+. \end{array}\right. } \end{aligned}$$

(4.94)

It follows from (4.92) that for every $p_i \in (\mathfrak {p}_i^-, \mathfrak {p}_i^+)$, for every $w_i^{p_i} \in A_{p_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/p_i)'}$, $i=1, 2$, and for every $v_j^{q_j} \in A_{q_j/\mathfrak {p}_j^-} \cap RH_{(\mathfrak {p}_j^+/q_j)'}$, $j=3, \ldots , m$,

$$\begin{aligned} \bigg \Vert fw_1w_2 \prod _{j=3}^m v_j \bigg \Vert _{L^{s_2}} \le \prod _{i=1}^2 \mathfrak {N}_i \Vert f_i w_i\Vert _{L^{p_i}} \prod _{j=3}^m \Phi _j \big ([v_j^{q_j}]_{A_{q_j/\mathfrak {p}_j^-} \cap RH_{(\mathfrak {p}_j^+/q_j)'}}\big ) \Vert f_j w_j\Vert _{L^{q_j}}, \end{aligned}$$

for all $(f, f_1, \ldots , f_m) \in \mathcal {F}$.

Inductively, one can show that for each $k \in \{1, \ldots , m\}$, for every $p_i \in (\mathfrak {p}_i^-, \mathfrak {p}_i^+)$, for every $w_i^{p_i} \in A_{p_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/p_i)'}$, $i \in \{1, \ldots , k\}$, and for every $v_j^{q_j} \in A_{q_j/\mathfrak {p}_j^-} \cap RH_{(\mathfrak {p}_j^+/q_j)'}$, $j=\{k+1, \ldots , m\}$,

$$\begin{aligned} \bigg \Vert f \prod _{i=1}^k w_i \prod _{j=k+1}^m v_j \bigg \Vert _{L^{s_k}} \le \prod _{i=1}^k \mathfrak {N}_i \Vert f_i w_i\Vert _{L^{p_i}} \prod _{j=k+1}^m \Phi _j \big ([v_j^{q_j}]_{A_{q_j/\mathfrak {p}_j^-} \cap RH_{(\mathfrak {p}_j^+/q_j)'}}\big ) \Vert f_j v_j\Vert _{L^{q_j}}, \end{aligned}$$

(4.95)

for all $(f, f_1, \ldots , f_m) \in \mathcal {F}$, where $s_0:= q$,

$$\begin{aligned}&\frac{1}{s_k} - \frac{1}{p_k} = \frac{1}{s_{k-1}} - \frac{1}{q_k}, \end{aligned}$$

(4.96)

$$\begin{aligned}&\mathfrak {N}_k := 2^{\max \{\frac{\tau _{p_k}}{p_k}, \frac{\tau '_{p_k}}{q_k}\}} \Phi _k \Big (C_k \, [w_k^{p_k}]_{A_{p_k/\mathfrak {p}_k^-} \cap RH_{(\mathfrak {p}_k^+/p_k)'}}^{\gamma _k(p_k, q_k)}\Big ), \end{aligned}$$

(4.97)

$$\begin{aligned}&\gamma _k(p_k, q_k) := {\left\{ \begin{array}{ll} \max \big \{1, \frac{\tau _{q_k} - 1}{\tau _{p_k} -1} \big \}, &{} q_k<\mathfrak {p}_k^+,\\ \frac{q_k}{\tau _{p_k} -1} \big (\frac{1}{\mathfrak {p}_k^-} - \frac{1}{\mathfrak {p}_k^+} \big ), &{} q_k = \mathfrak {p}_k^+. \end{array}\right. } \end{aligned}$$

(4.98)

To conclude the proof, we take $\frac{1}{s_m} = \frac{1}{p}:= \sum _{i=1}^m \frac{1}{p_i}$, and then (4.96) is satisfied. The inequality (4.95) immediately gives (1.3) as desired.

It remains to show the vector-valued inequality (1.4). Fix $r_i \in (\mathfrak {p}_i^-, \mathfrak {p}_i^+)$, $i=1, \ldots , m$, and set $\frac{1}{r} = \sum _{i=1}^m \frac{1}{r_i}$. Given $N \in \mathbb {N}$, we define

$$\begin{aligned} \mathcal {F}_{\textbf{r}}^N&:= \Big \{(F, F_1, \ldots , F_m) := \bigg (\Big (\sum _{|k|< N} |f^k|^r \Big )^{\frac{1}{r}}, \Big (\sum _{|k|< N} |f^k_1|^{r_1} \Big )^{\frac{1}{r_1}}, \ldots ,\\&\qquad \Big (\sum _{|k| < N} |f^k_m|^{r_m} \Big )^{\frac{1}{r_m}} \bigg ): \{(f^k, f^k_1, \cdots , f^k_m)\}_k \subset \mathcal {F}\bigg \}. \end{aligned}$$

By (1.3), for all $(F, F_1, \ldots , F_m) \in \mathcal {F}_{\textbf{r}}^N$, and for all weights $v_i^{r_i} \in A_{r_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/r_i)'}$, $i=1, \ldots , m$,

$$\begin{aligned} \Vert F\Vert _{L^r(v^r)}&= \bigg \Vert \Big (\sum _{|k|< N} |f^k|^r \Big )^{\frac{1}{r}} \bigg \Vert _{L^r(v^r)} = \bigg (\sum _{|k|<N} \Vert f^k\Vert _{L^r(v^r)}^r \bigg )^{\frac{1}{r}} \nonumber \\&\le \bigg (\sum _{|k|<N} \prod _{i=1}^m \mathfrak {C}_{i, 1} \Phi _i \Big (C_i [v_i^{r_i}]_{A_{r_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/r_i)'}}^{\gamma _i(r_i, q_i)} \Big )^r \Vert f^k_i\Vert _{L^{r_i}(v_i^{r_i})}^r \bigg )^{\frac{1}{r}} \nonumber \\&\le \prod _{i=1}^m \mathfrak {C}_{i, 1} \Phi _i \Big (C_i [v_i^{r_i}]_{A_{r_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/r_i)'}}^{\gamma _i(r_i, q_i)}\Big ) \bigg (\sum _{|k|<N} \Vert f^k_i\Vert _{L^{r_i}(v_i^{r_i})}^{r_i} \bigg )^{\frac{1}{r_i}} \nonumber \\&= \prod _{i=1}^m \mathfrak {C}_{i, 1} \Phi _i \Big (C_i [v_i^{r_i}]_{A_{r_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/r_i)'}}^{\gamma _i(r_i, q_i)}\Big ) \Vert F_i\Vert _{L^{r_i}(v_i^{r_i})}, \end{aligned}$$

(4.99)

where $\mathfrak {C}_{i, 1}:= 2^{\max \{\frac{\tau _{r_i}}{r_i}, \frac{\tau '_{r_i}}{q_i}\}}$. This corresponds to (1.2) for the family $\mathcal {F}_{\textbf{r}}^N$ and the exponent $\textbf{r}=(r_1, \ldots , r_m)$. Then the estimate (1.3) applied to $\mathcal {F}_{\textbf{r}}^N$ gives that for all exponents $p_i \in (\mathfrak {p}_i^{-}, \mathfrak {p}_i^{+})$ and all weights $w_i^{p_i} \in A_{p_i/\mathfrak {p}_i^{-}} \cap RH_{(\mathfrak {p}_i^{+}/p_i)'}$, $i=1, \ldots , m$,

$$\begin{aligned} \Vert F\Vert _{L^p(w^p)} \le \prod _{i=1}^m \mathfrak {C}_{i, 1} \mathfrak {C}_{i, 2} \, \Phi _i \Big (C'_i \, [w_i^{p_i}]_{A_{p_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/p_i)'}}^{\gamma _i(p_i, r_i) \gamma _i(r_i, q_i)}\Big ) \Vert F_i\Vert _{L^{p_i}(w_i^{p_i})}, \end{aligned}$$

(4.100)

for all $(F, F_1, \ldots , F_m) \in \mathcal {F}_{\textbf{r}}^N$, where $\mathfrak {C}_{i, 2}:= 2^{\max \{\frac{\tau _{p_i}}{p_i}, \frac{\tau '_{p_i}}{r_i}\}}$. The estimate (4.100) in turn implies

$$\begin{aligned} \bigg \Vert \Big (\sum _{|k|<N} |f^k|^r \Big )^{\frac{1}{r}}\bigg \Vert _{L^p(w^p)} \le \prod _{i=1}^m \mathfrak {C}'_i \, \Phi _i \Big (C'_i \, [w_i^{p_i}]_{A_{p_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/p_i)'}}^{\gamma _i(p_i, r_i) \gamma _i(r_i, q_i)}\Big ) \bigg \Vert \Big (\sum _k |f^k_i|^{r_i} \Big )^{\frac{1}{r_i}}\bigg \Vert _{L^{p_i}(w_i^{p_i})}, \end{aligned}$$

(4.101)

for all $\{(f^k, f^k_1, \cdots , f^k_m)\}_k \subset \mathcal {F}$, where $\mathfrak {C}'_i:= 2^{\max \{\frac{\tau _{p_i}}{p_i}, \frac{\tau '_{p_i}}{r_i}\} + \max \{\frac{\tau _{r_i}}{r_i}, \frac{\tau '_{r_i}}{q_i}\}}$, and the constant $C'_i$ depends only on n, $p_i$, $q_i$, $r_i$, $\mathfrak {p}_i^-$, and $\mathfrak {p}_i^+$. Letting $N \rightarrow \infty$, we conclude (1.4) as desired. $\square$

Proof of Theorem 1.2

Let $s_i \in (\mathfrak {p}_i^-, \mathfrak {p}_i^+)$, $i=1, \ldots , m$, be such that $\frac{1}{s}:= \sum _{i=1}^m \frac{1}{s_i} \le 1$. It follows from (1.5) and Theorem 1.1 that for all $v_i^{s_i} \in A_{s_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/s_i)'}$, $i=1, \ldots , m$,

$$\begin{aligned} \Vert T(\textbf{f})\Vert _{L^s(v^s)} \le C_0 \prod _{i=1}^m \Phi _i \Big (C_i \, [v_i^{s_i}]_{A_{s_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/s_i)'}}^{\gamma _i(s_i, q_i)}\Big ) \Vert f_i\Vert _{L^{s_i}(v_i^{s_i})}, \end{aligned}$$

(4.102)

where both $C_0$ and $C_i$ depend only on n, $s_i$, $q_i$, $\mathfrak {p}_i^-$, and $\mathfrak {p}_i^+$.

Fix ${\textbf {b}}= (b_1, \ldots , b_m) \in {\text {BMO}}^m$ and multi-index $\alpha \in \mathbb {N}^m$. Given $v_i^{s_i} \in A_{s_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/s_i)'}$, $i=1, \ldots , m$, in light of Lemma 2.6 part (b), we see that

$$\begin{aligned} v_i^{s_i(\mathfrak {p}_i^+/s_i)'} \in A_{\tau _{s_i}}, \end{aligned}$$

(4.103)

which together with Lemma 2.4 yields that there exists $\eta _i \in (1, 2)$ such that

$$\begin{aligned} \eta _i' \simeq \Big [v_i^{s_i(\mathfrak {p}_i^+/s_i)'}\Big ]_{A_{\tau _{s_i}}}^{\max \{1, \frac{1}{\tau _{s_i}-1}\}}, \quad \text {and}\quad \Big [v_i^{\eta _i s_i(\mathfrak {p}_i^+/s_i)'}\Big ]_{A_{\tau _{s_i}}}^{\frac{1}{\eta _i}} \le 2^{\tau _{s_i}} \Big [v_i^{s_i(\mathfrak {p}_i^+/s_i)'}\Big ]_{A_{\tau _{s_i}}}. \end{aligned}$$

(4.104)

Then in view of (4.102)–(4.104), Theorem 2.11 applied to $p:=s \ge 1$, $p_i:=s_i$, $r_i:= \tau _{s_i}$, and $\theta _i:=s_i(\mathfrak {p}_i^+/s_i)$, gives that for all $v_i^{s_i} \in A_{s_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/s_i)'}$, $i=1, \ldots , m$,

$$\begin{aligned}&\Vert [T, {\textbf {b}}]_{\alpha }(\textbf{f})\Vert _{L^s(v^s)} \le C_0 \prod _{i=1}^m (\eta '_i)^{\alpha _i} \Phi _i \Big (C_i \, \Big [v_i^{\eta _i s_i(\mathfrak {p}_i^+/s_i)'}\Big ]_{A_{\tau _{s_i}}}^{\frac{1}{\eta _i} \gamma _i(s_i, q_i)}\Big ) \Vert b_i\Vert _{{\text {BMO}}}^{\alpha _i} \Vert f_i\Vert _{L^{s_i}(v_i^{s_i})} \nonumber \\&\quad \le C_0 \prod _{i=1}^m [v_i^{s_i(\mathfrak {p}_i^+/s_i)'}]_{A_{\tau _{s_i}}}^{\alpha _i \max \{1, \frac{1}{\tau _{s_i}-1}\}} \Phi _i \Big (C_i \, \Big [v_i^{s_i(\mathfrak {p}_i^+/s_i)'}\Big ]_{A_{\tau _{s_i}}}^{\gamma _i(s_i, q_i)}\Big ) \Vert b_i\Vert _{{\text {BMO}}}^{\alpha _i} \Vert f_i\Vert _{L^{s_i}(v_i^{s_i})}, \end{aligned}$$

(4.105)

where $C_i$ depends only on n, $s_i$, $q_i$, $\mathfrak {p}_i^-$, and $\mathfrak {p}_i^+$, and $C_0$ depends only on the same parameters and additionally on $\alpha$.

Observe that for each $i=1, \ldots , m$,

$$\begin{aligned} {\widetilde{\Phi }}_i(t) := t^{\alpha _i \max \{1, \frac{1}{\tau _{s_i}-1}\}} \Phi _i(C_i \, t^{\gamma _i(s_i, q_i)}) \text { is an increasing function}. \end{aligned}$$

(4.106)

Now with (4.105) and (4.106) in hand, we use Theorem 1.1 applied to $s_i$ and $C_0^{\frac{1}{m}} {\widetilde{\Phi }}_i$ in place of $q_i$ and $\Phi _i$ to deduce that for all exponents $p_i, r_i \in (\mathfrak {p}_i^{-}, \mathfrak {p}_i^{+})$ and for all weights $w_i^{p_i} \in A_{p_i/\mathfrak {p}_i^{-}} \cap RH_{(\mathfrak {p}_i^{+}/p_i)'}$, $i=1, \ldots , m$,

$$\begin{aligned} \Vert [T, {\textbf {b}}]_{\alpha }(\textbf{f})\Vert _{L^p(w^p)} \le C_0 \prod _{i=1}^m {\widetilde{\Phi }}_i \big (C'_i \, [w_i^{p_i(\mathfrak {p}_i^+/p_i)'}]_{A_{\tau _{p_i}}}^{\gamma _i(p_i, s_i)}\big ) \Vert b_i\Vert _{{\text {BMO}}}^{\alpha _i} \Vert f_i\Vert _{L^{p_i}(w_i^{p_i})}, \end{aligned}$$

where $C_0$ depends only on $\alpha$, n, $p_i$, $q_i$, $s_i$, $\mathfrak {p}_i^-$, and $\mathfrak {p}_i^+$, $C'_i$ depends only on n, $p_i$, $s_i$, $\mathfrak {p}_i^-$, and $\mathfrak {p}_i^+$, and

$$\begin{aligned} \bigg \Vert \Big (\sum _k | [T, {\textbf {b}}]_{\alpha }(\textbf{f}^k)|^r \Big )^{\frac{1}{r}} \bigg \Vert _{L^p(w^p)}&\le C \prod _{i=1}^m {\widetilde{\Phi }}_i \Big (C''_i \, [w_i^{p_i}]_{A_{p_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/p_i)'}}^{\gamma _i(p_i, r_i) \gamma _i(r_i, s_i)}\Big )\\&\qquad \times \Vert b_i\Vert _{{\text {BMO}}}^{\alpha _i} \bigg \Vert \Big (\sum _k |f^k_i|^{r_i} \Big )^{\frac{1}{r_i}}\bigg \Vert _{L^{p_i}(w_i^{p_i})}, \end{aligned}$$

where $\frac{1}{r} = \sum _{i=1}^m \frac{1}{r_i}$, C depends only on $\alpha$, n, $p_i$, $q_i$, $r_i$, $s_i$, $\mathfrak {p}_i^-$, and $\mathfrak {p}_i^+$, and $C''_i$ depends only on n, $p_i$, $r_i$, $s_i$, $\mathfrak {p}_i^-$, and $\mathfrak {p}_i^+$. This completes the proof of Theorem 1.2. $\square$

5 Applications

This section is dedicated to using extrapolation to prove quantitative weighted inequalities for a variety of operators. This also shows that extrapolation theorems are useful and powerful.

5.1 Bilinear Bochner–Riesz Means

Given $\delta \in \mathbb {R}$, the bilinear Bochner–Riesz means of order $\delta$ is defined by

$$\begin{aligned} \mathcal {B}^{\delta }(f_1, f_2)(x) := \int _{\mathbb {R}^{2n}} (1-|\xi _1|^2-|\xi _2|^2)^{\delta }_{+} \, \widehat{f_1}(\xi _1) \, \widehat{f_2}(\xi _2) e^{2\pi i x \cdot (\xi _1 + \xi _2)} d\xi _1 d\xi _2. \end{aligned}$$

Theorem 5.1

Let $n \ge 2$ and $\delta \ge n-1/2$. Then for all $p_i \in (1, \infty )$, for all $w_i^{p_i} \in A_{p_i}$, for all ${\textbf {b}}=(b_1, b_2) \in {\text {BMO}}^2$, and for each multi-index $\alpha \in \mathbb {N}^2$,

$$\begin{aligned} \Vert \mathcal {B}^{\delta }(f_1, f_2)\Vert _{L^p(w^p)}&\lesssim \prod _{i=1}^2 [w_i^{p_i}]_{A_{p_i}}^{\beta _i(\delta )} \Vert f_i\Vert _{L^{p_i}(w_i^{p_i})}, \end{aligned}$$

(5.1)

$$\begin{aligned} \Vert [\mathcal {B}^{\delta }, {\textbf {b}}]_{\alpha }(f_1, f_2)\Vert _{L^p(w^p)}&\lesssim \prod _{i=1}^2 [w_i^{p_i}]_{A_{p_i}}^{\eta _i(\delta )} \Vert b_i\Vert _{{\text {BMO}}}^{\alpha _i} \Vert f_i\Vert _{L^{p_i}(w_i^{p_i})}, \end{aligned}$$

(5.2)

whenever $\frac{1}{s}:= \frac{1}{s_1} + \frac{1}{s_2} \le 1$ with $s_1, s_2 \in (1, \infty )$, where $w=w_1 w_2$, $\frac{1}{p}=\frac{1}{p_1}+\frac{1}{p_2}$,

$$\begin{aligned} \beta _i(\delta ) = {\left\{ \begin{array}{ll} \frac{1}{p_i-1}, &{} \delta >n-1/2,\\ \max \{1, \frac{1}{p_i-1}\}, &{} \delta =n-1/2, \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} \eta _i(\delta ) = {\left\{ \begin{array}{ll} (\alpha _i+\frac{1}{p_i-1}) \max \{1, \frac{1}{s_i-1}, \frac{1}{p_i-1}, \frac{s_i-1}{p_i-1}\}, &{} \delta >n-1/2,\\ (\alpha _i+1)\max \{1, \frac{1}{s_i-1}, \frac{1}{p_i-1}, \frac{s_i-1}{p_i-1}\}, &{} \delta =n-1/2. \end{array}\right. } \end{aligned}$$

Proof

Let us first consider the case $\delta >n-1/2$. In this case, it was shown in [58, Lemma 3.1] that

$$\begin{aligned} |\mathcal {B}^{\delta }(f_1, f_2)(x)| \lesssim Mf_1(x) Mf_2(x), \qquad x \in \mathbb {R}^n, \end{aligned}$$

(5.3)

where the implicit constant is independent of x, $f_1$, and $f_2$. Combining (5.3) with (2.1) and Hölder’s inequality, we obtain that for all $p_i \in (1, \infty )$ and for all $w_i^{p_i} \in A_{p_i}$,

$$\begin{aligned} \Vert \mathcal {B}^{\delta }(f_1, f_2)\Vert _{L^p(w^p)}&\lesssim \prod _{i=1}^2 [w_i^{p_i}]_{A_{p_i}}^{\frac{1}{p_i-1}} \Vert f_i\Vert _{L^{p_i}(w_i^{p_i})}, \end{aligned}$$

(5.4)

where $w=w_1 w_2$ and $\frac{1}{p}=\frac{1}{p_1}+\frac{1}{p_2}$. Then it follows from (5.4), Theorem 1.2, and Remark 1.4 that for all ${\textbf {b}}=(b_1, b_2) \in {\text {BMO}}^2$ and for each multi-index $\alpha \in \mathbb {N}^2$,

$$\begin{aligned} \Vert [\mathcal {B}^{\delta }, {\textbf {b}}]_{\alpha }(f_1, f_2)\Vert _{L^p(w^p)} \lesssim \prod _{i=1}^2 [w_i^{p_i}]_{A_{p_i}}^{(\alpha _i+\frac{1}{p_i-1}) \max \{1, \frac{1}{s_i-1}, \frac{1}{p_i-1}, \frac{s_i-1}{p_i-1}\}} \Vert b_i\Vert _{{\text {BMO}}}^{\alpha _i} \Vert f_i\Vert _{L^{p_i}(w_i^{p_i})}, \end{aligned}$$

whenever $s_1, s_2 \in (1, \infty )$ satisfy $\frac{1}{s}:= \frac{1}{s_1} + \frac{1}{s_2} \le 1$.

Next, we turn to the case $\delta =n-1/2$. Given $\varepsilon _1 \in (0, \frac{1}{2})$, and $\varepsilon _2>0$, we write

$$\begin{aligned} \delta (\theta ) := (1+\varepsilon _1)(1-\theta ) + \theta (n-1/2 + \varepsilon _2),\quad \theta \in (0, 1). \end{aligned}$$

(5.5)

We first claim that for any $u_1, u_2 \in A_2$,

$$\begin{aligned} \Vert \mathcal {B}^{\delta (\theta )}(f_1, f_2)\Vert _{L^1(u^{\theta })} \le \phi _1(\varepsilon _1)^{1-\theta } \phi _2(\varepsilon _2)^{\theta } \prod _{i=1}^2 [u_i]_{A_2}^{\theta } \Vert f_i\Vert _{L^2(u_i^{\theta })}, \quad \forall \theta \in (0, 1), \end{aligned}$$

(5.6)

where $u=u_1 u_2$ and the constant $\phi _1, \phi _2$ are non-negative function and $\phi _2$ is increasing. Indeed, (5.6) can be obtained by following the proof of [58, Theorem 1.8]. We here only mention the difference:

$$\begin{aligned} \sup _{t \in \mathbb {R}} |\psi (it)|&\le \phi _1(\varepsilon _1) \Vert h\Vert _{L^{\infty }(\mathbb {R}^n)} \prod _{i=1}^2 \Vert f_i\Vert _{L^2(\mathbb {R}^n)},\\ \sup _{t \in \mathbb {R}} |\psi (1+it)|&\le \phi _2(\varepsilon _2) \Vert h\Vert _{L^{\infty }(\mathbb {R}^n)} \prod _{i=1}^2 [u_i]_{A_2} \Vert f_i\Vert _{L^2(\mathbb {R}^n)}, \end{aligned}$$

provided the sharp estimate for the Hardy–Littlewood maximal operator in (2.1).

Now let $v_1^2, v_2^2 \in A_2$, $v:=v_1 v_2$, and by Lemma 2.4, there exists $\gamma \in (0, 2^{-n-3})$ such that

$$\begin{aligned}{}[v_i^{2(1+\gamma )}]_{A_2} \le 2^{2(1+\gamma )} [v_i^2]_{A_2}^{1+\gamma }. \end{aligned}$$

(5.7)

Then, (5.6) applied to $u_i=v_i^{2(1+\gamma )}$, $i=1, 2$, gives the for any $\theta \in (0, 1)$,

$$\begin{aligned} \Vert \mathcal {B}^{\delta (\theta )}(f_1, f_2)\Vert _{L^1(v^{2(1+\gamma )\theta })} \le \phi _1(\varepsilon _1)^{1-\theta } \phi _2(\varepsilon _2)^{\theta } \prod _{i=1}^2 [v_i^{2(1+\gamma )}]_{A_2}^{\theta } \Vert f_i\Vert _{L^2(v_i^{2(1+\gamma )\theta })} \nonumber \\ \le \phi _1(\varepsilon _1)^{1-\theta } \phi _2(\varepsilon _2)^{\theta } 2^{4(1+\gamma ) \theta } \prod _{i=1}^2 [v_i^2]_{A_2}^{(1+\gamma )\theta } \Vert f_i\Vert _{L^2(v_i^{2(1+\gamma )\theta })}, \end{aligned}$$

(5.8)

where (5.7) was used in the last step. Picking $\theta =(1+\gamma )^{-1}$, $\varepsilon _1=1/4$, and $\varepsilon _2=(n-7/4) \gamma$, we utilize (5.5) and (5.8) to deduce that $\delta (\theta )=n-1/2$ and

$$\begin{aligned} \Vert \mathcal {B}^{n-1/2}(f_1, f_2)\Vert _{L^1(v^2)} \lesssim \prod _{i=1}^2 [v_i^2]_{A_2} \Vert f_i\Vert _{L^2(v_i^2)}, \end{aligned}$$

(5.9)

where we had used that $\phi _1(\varepsilon _1)^{1-\theta } \phi _2(\varepsilon _2)^{\theta } \le \max \{1, \phi _1(1/4), \phi _2(n)\}$, and the implicit constant depends only on n.

Having proved (5.9) and invoking Theorems 1.1 and 1.2 applied to $\mathfrak {p}_i^-=1$, $\mathfrak {p}_i^+=\infty$, $q_i=2$, and $\Phi _i(t)=t$, we conclude (5.1) and (5.2). $\square$

The next result considers the case $\delta <n-\frac{1}{2}$, which can be viewed as a complement of Theorem 5.1.

Theorem 5.2

Let $n \ge 2$, $0<\delta <n-\frac{1}{2}$, and $0<\delta _1,\delta _2\le \frac{n}{2}$ be such that $\delta _1+\delta _2<\delta$. Set $\mathfrak {p}_1^-:= \frac{2n}{n+2\delta _1}$, $\mathfrak {p}_2^-:= \frac{2n}{n+2\delta _2}$, and $\mathfrak {p}_1^+ = \mathfrak {p}_2^+:=2$. Then for all $w_i^2 \in A_{2/\mathfrak {p}_i^-}\cap RH_{(\mathfrak {p}_i^+/2)'}$, $i=1, 2$,

$$\begin{aligned} \Vert \mathcal {B}^{\delta }(f_1, f_2)\Vert _{L^1(w)}&\lesssim \prod _{i=1}^2 [w_i^2]_{A_{2/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/2)'}} \Vert f_i\Vert _{L^2(w_i^2)}. \end{aligned}$$

(5.10)

Moreover, for all $p_i \in (\mathfrak {p}_i^-, \mathfrak {p}_i^+)$ and for all $w_i^{p_i} \in A_{p_i/\mathfrak {p}_i^-}\cap RH_{(\mathfrak {p}_i^+/p_i)'}$, $i=1, 2$,

$$\begin{aligned} \Vert \mathcal {B}^{\delta }(f_1, f_2)\Vert _{L^p(w^p)}&\lesssim \prod _{i=1}^2 [w_i^{p_i}]_{A_{p_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/p_i)'}}^{\gamma _i(p_i, 2)} \Vert f_i\Vert _{L^{p_i}(w_i^{p_i})}, \end{aligned}$$

(5.11)

where $w=w_1 w_2$ and $\frac{1}{p}=\frac{1}{p_1}+\frac{1}{p_2}$.

Proof

We modify the proof of [74, Theorem 2] into the current setting. First, choose a nonnegative function $\varphi \in \mathscr {C}_c^{\infty }(0,\,\infty )$ satisfying ${\text {supp}}\varphi \subset (\frac{1}{2},\,2)$ and $\sum _{j \in \mathbb {Z}} \varphi (2^j s)=1$ for any $s>0$. For each $j \ge 0$, we define the bilinear operator

$$\begin{aligned} T_j(f_1, f_2):= \int _{0}^{\infty }\int _{0}^{\infty }\varphi _j^\delta (\lambda _1,\lambda _2) R_{\lambda _1}f_1 \, R_{\lambda _2}f_2 \,\lambda _1^{n-1}\lambda _2^{n-1} \, d\lambda _1 \, d\lambda _2, \end{aligned}$$

where

$$\begin{aligned} \varphi _j^\delta (s_1, s_2)&:= (1-s_1^2-s_2^2)_+^\delta \, \varphi (2^j(1-s_1^2-s_2^2)),\\ R_{\lambda }f(x)&:= \int _{\mathbb {S}^{n-1}}{{\widehat{f}}}(\lambda \omega ) e^{2\pi ix\cdot \lambda \omega } \, d\sigma (\omega ),\ \ \lambda >0. \end{aligned}$$

Here $d\sigma$ is the surface measure on $\mathbb {S}^{n-1}$. Then one has

$$\begin{aligned} \mathcal {B}^\delta =\sum _{j=0}^{\infty }T_j. \end{aligned}$$

(5.12)

Given $j\ge 0$, let $B_j=\{x\in \mathbb {R}^n: |x| < 2^{j(1+\gamma )}\}$ with $\gamma >0$ chosen later, and split the kernel function $K_j$ of $T_j$ into four parts:

$$\begin{aligned}&K_j^1(y_1, y_2) := K_j(y_1, y_2) {\textbf {1}}_{B_j}(y_1) {\textbf {1}}_{B_j}(y_2),\ \ \ K_j^2(y_1, y_2) := K_j(y_1, y_2) {\textbf {1}}_{B_j}(y_1) {\textbf {1}}_{B_j^c}(y_2),\\&K_j^3(y_1, y_2) := K_j(y_1, y_2) {\textbf {1}}_{B_j^c}(y_1) {\textbf {1}}_{B_j}(y_2),\ \ \ K_j^4(y_1, y_2) := K_j(y_1, y_2) {\textbf {1}}_{B_j^c}(y_1) {\textbf {1}}_{B_j^c}(y_2). \end{aligned}$$

Letting $T_j^\ell$ denote the bilinear operator with kernel $K_j^\ell$, $\ell =1,2,3,4$, we see that

$$\begin{aligned} T_j = T_j^1 + T_j^2 + T_j^3 + T_j^4. \end{aligned}$$

(5.13)

Note that a straightforward calculation gives

$$\begin{aligned} |K_j(x_1,x_2)| \lesssim 2^{-j\delta }2^{-j}(1+2^{-j}|x_1|)^{-N}(1+2^{-j}|x_2|)^{-N}, \quad \forall N>0, \nonumber \\ \end{aligned}$$

(5.14)

and

(5.15)

In view of Theorem 1.1, it suffices to prove (5.10). Now let $q_1=q_2=2$, $v_1^2 \in A_{q_1/\mathfrak {p}_1^-} \cap RH_{(\mathfrak {p}_1^+/q_1)'} = A_{1+\frac{2\delta _1}{n}} \cap RH_{\infty }$, and $v_2^2 \in A_{q_2/\mathfrak {p}_2^-} \cap RH_{(\mathfrak {p}_2^+/q_2)'} = A_{1+\frac{2\delta _2}{n}} \cap RH_{\infty }$. Considering (5.12)–(5.13), we are reduced to showing that there exists $\varepsilon >0$ such that

$$\begin{aligned} \Vert T_j^{\ell }(f_1, f_2)\Vert _{L^1(v)} \lesssim 2^{-\varepsilon j} \prod _{i=1}^2 [v_i^2]_{A_{2/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/2)'}} \Vert f_i\Vert _{L^2(v_1^2)}, \quad j \ge 0, \, \ell =1, 2, 3, 4.\nonumber \\ \end{aligned}$$

(5.16)

To control $T_j^4$, note that $v_1^2 \in A_{1 + \frac{2\delta _1}{n}} \subset A_2$ and $v_2^2 \in A_{1+\frac{2\delta _2}{n}} \subset A_2$ since $\max \{n+2\delta _1, n+2\delta _2\} \le 2n$. Using (5.14), Cauchy–Schwarz inequality, (5.15), (2.1), and (1.1), we have

$$\begin{aligned} \Vert T_j^4(f_1, f_2)\Vert _{L^1(v)}&\lesssim \int _{\mathbb {R}^n} \int _{B_j^c} \int _{B_j^c} \frac{|f_1(x-y_1)|}{(1+2^{-j}|y_1|)^N} \frac{|f_2(x-y_2)|}{(1+2^{-j}|y_2|)^N} dy_1 dy_2\,v(x)dx \nonumber \\&\le \biggl (\int _{\mathbb {R}^n}\biggl (\int _{B_j^c} \frac{|f_1(x-y_1)|}{(1+2^{-j}|y_1|)^N} dy_1\biggr )^2v_1^2(x)dx \biggr )^{\frac{1}{2}} \nonumber \\&\quad \times \biggl (\int _{\mathbb {R}^n}\biggl (\int _{B_j^c} \frac{|f_2(x-y_2)|}{(1+2^{-j}|y_2|)^N} dy_2\biggr )^2v_2^2(x)dx \biggr )^{\frac{1}{2}} \nonumber \\&\lesssim 2^{-j[N\gamma - (1+\gamma )n]} \Vert Mf_1\Vert _{L^2(v_1^2)} \Vert Mf_2\Vert _{L^2(v_2^2)} \nonumber \\&\lesssim 2^{-\varepsilon j} [v_1^2]_{A_2} [v_2^2]_{A_2} \Vert f_1\Vert _{L^2(v_1^2)} \Vert f_2\Vert _{L^2(v_2^2)} \nonumber \\&\le 2^{-\varepsilon j} \prod _{i=1}^2 [v_i^2]_{A_{2/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/2)'}} \Vert f_i\Vert _{L^2(v_i^2)}, \end{aligned}$$

(5.17)

where in the second-to-last inequality we have picked $N>0$ large enough so that $N\gamma >(1+\gamma )n$, and then taken $0<\varepsilon <N\gamma -(1+\gamma )n$. Similarly,

$$\begin{aligned} \Vert T_j^3(f_1, f_2)\Vert _{L^1(v)}&\lesssim \biggl (\int _{\mathbb {R}^n}\biggl (\int _{|y_1| \ge 2^{j(1+\gamma )}} \frac{|f_1(x-y_1)|}{(1+2^{-j}|y_1|)^N} dy_1\biggr )^2 v_1^2(x) dx\biggr )^{\frac{1}{2}} \nonumber \\&\quad \times \biggl (\int _{\mathbb {R}^n}\biggl (\int _{|y_2| < 2^{j(1+\gamma )}} \frac{|f_2(x-y_2)|}{(1+2^{-j} |y_2|)^N}dy_2 \biggr )^2v_2^2(x)dx\biggr )^{\frac{1}{2}} \nonumber \\&\lesssim 2^{-j[N\gamma -(1+\gamma )n]} 2^{j(1+\gamma )n} \Vert Mf_1\Vert _{L^2(v_1^2)} \Vert Mf_2\Vert _{L^2(v_2^2)} \nonumber \\&\lesssim 2^{-j[N\gamma -2(1+\gamma )n]} [v_1^2]_{A_2} [v_2^2]_{A_2} \Vert f_1\Vert _{L^2(v_1^2)} \Vert f_2\Vert _{L^2(v_2^2)} \nonumber \\&\le 2^{-\varepsilon j} \prod _{i=1}^2 [v_i^2]_{A_{2/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/2)'}} \Vert f_i\Vert _{L^2(v_i^2)}, \end{aligned}$$

(5.18)

where we have chosen $N>0$ sufficiently large so that $N\gamma - 2(1+\gamma )n > \varepsilon$. Symmetrically to $T_j^3(f_1, f_2)$, there holds

$$\begin{aligned} \Vert T_j^2(f_1, f_2)\Vert _{L^1(v)} \lesssim 2^{-\varepsilon j} \prod _{i=1}^2 [v_i^2]_{A_{2/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/2)'}} \Vert f_i\Vert _{L^2(v_i^2)}. \end{aligned}$$

Finally, to prove (5.16) for $T_j^1$, we proceed as follows. For fixed $y\in \mathbb {R}^n$, set $B_j(y, r)=\{x\in \mathbb {R}^n: |x-y|\le 2^{j(1+\gamma )} r\}$ with $r>0$, and split $f_1$ and $f_2$ into three parts, respectively:

$$\begin{aligned} f_1 = f_{1, 1} + f_{1, 2} + f_{1, 3}, \quad \text {and}\quad f_2 = f_{2, 1} + f_{2, 2} + f_{2, 3}, \end{aligned}$$

where

$$\begin{aligned}&f_{1, 1} := f_1 {\textbf {1}}_{B_j(y,\frac{3}{4})},\quad f_{1, 2} := f_1 {\textbf {1}}_{B_j(y,\frac{5}{4})\setminus B_j(y,\frac{3}{4})}, \quad f_{1, 3} := f_1 {\textbf {1}}_{B_j(y,\frac{5}{4})^c},\\&f_{2, 1} := f_2 {\textbf {1}}_{B_j(y,\frac{3}{4})}, \quad f_{2, 2} := f_2 {\textbf {1}}_{B_j(y,\frac{5}{4})\setminus B_j(y,\frac{3}{4})}, \quad f_{2, 3} := f_2 {\textbf {1}}_{B_j(y,\frac{5}{4})^c}. \end{aligned}$$

We should mention that each $f_{1, i}$ and $f_{2, i}$, $i=1, 2, 3$, depend on the variable y. Let $x\in B_j(y, \frac{1}{4})$. Since $f_{1,3}$ is supported on $\mathbb {R}^n\setminus B_j(y,\frac{5}{4})$, it follows from $f_{1, 3}(x-y_1) \ne 0$ that $|x-y_1-y| \ge \frac{5}{4} 2^{j(1+\gamma )}$, and so $|y_1| \ge 2^{j(1+\gamma )}$. Noting that the kernel $K_j^1$ is supported on $B_j\times B_j$, we get $T_j^1(f_{1, 3}, f_2)=0$. Similarly, $T_j^1(f_1, f_{2, 3})=0$. Hence, for any $x\in B_j(y, \frac{1}{4})$,

$$\begin{aligned} T_j^1(f_1, f_2)(x)&= T_j^1(f_{1, 1}, f_{2, 1})(x) + T_j^1(f_{1, 1}, f_{2, 2})(x) \nonumber \\&\qquad + T_j^1(f_{1, 2}, f_{2, 1})(x) + T_j^1(f_{1, 2}, f_{2, 2})(x). \end{aligned}$$

(5.19)

Since $f_{1, 2}$ and $f_{2, 2}$ are supported on $B_j(y,\frac{5}{4})\setminus B_j(y,\frac{3}{4})$, it follows from $f_{1, 2}(x-y_1) f_{2, 2}(x-y_2) \ne 0$ that $|y_1| \ge 2^{j(1+\gamma )-1}$ and $|y_2| \ge 2^{j(1+\gamma ) - 1}$. Then, repeating the proof of (5.17) yields

$$\begin{aligned} \Vert T_j^1(f_{1, 2}, f_{2, 2})v\Vert _{L^1(B_j(y,\frac{1}{4}))} \le 2^{-\varepsilon j} \prod _{i=1}^2 [v_i^2]_{A_{2/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/2)'}} \Vert f_{i, 2}\Vert _{L^2(v_i^2)}. \end{aligned}$$

(5.20)

Since $f_{1, 1}$ is supported on $B_j(y,\frac{3}{4})$, it follows from $f_{1, 1}(x-y_1) f_{2, 2}(x-y_2)\ne 0$ that $|y_1| \le 2^{j(1+\gamma )}$ and $|y_2| \ge 2^{j(1+\gamma )-1}$. Thus, we calculate much as in (5.18) to get

$$\begin{aligned} \Vert T_j^1(f_{1,1}, f_{2,2})v\Vert _{L^1(B_j(y,\frac{1}{4}))} \le 2^{-\varepsilon j} \prod _{i=1}^2 [v_i^2]_{A_{2/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/2)'}} \Vert f_{i, i}\Vert _{L^2(v_i^2)}. \nonumber \\ \end{aligned}$$

(5.21)

Symmetrically,

$$\begin{aligned} \Vert T_j^1(f_{1, 2}, f_{2,1})v\Vert _{L^1(B_j(y,\frac{1}{4}))} \le 2^{-\varepsilon j} \prod _{i=1}^2 [v_i^2]_{A_{2/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/2)'}} \Vert f_{i, 3-i}\Vert _{L^2(v_i^2)}.\nonumber \\ \end{aligned}$$

(5.22)

It remains to consider $T_j^1(f_{1,1}, f_{2,1})$. Given $\mathfrak {m}\in L^\infty (\mathbb {R})$, set $T_{\mathfrak {m}} h:= \int _0^1 \mathfrak {m}(\lambda ) \, R_\lambda h \, \lambda ^{n-1} \, d\lambda$. Then [74, Lemma 3.1] states that

$$\begin{aligned} \Vert T_{\mathfrak {m}} h\Vert _{L^2(\mathbb {R}^n)} \lesssim \Vert \mathfrak {m}\Vert _{L^\infty (\mathbb {R}^n)} \Vert h\Vert _{L^p(\mathbb {R}^n)}, \quad 1\le p\le 2. \end{aligned}$$

(5.23)

Let $r=1+2\delta _2/n$. Then $v_2^2 \in A_r \cap RH_{\infty }$. Using (5.23) and Hölder’s inequality, we have that for $h \in L^2(v_2^2)$ with ${\text {supp}}h \subset B_j(y,\frac{3}{4})$,

(5.24)

where the definition (1.1) was used in the last inequality. Similarly,

$$\begin{aligned} \Vert (T_{\mathfrak {m}} h) v_1\Vert _{L^2(B_j(y,\frac{1}{4}))} \lesssim 2^{j(1+\gamma )\delta _1} \Vert \mathfrak {m}\Vert _{L^\infty (\mathbb {R}^n)} [v_1^2]_{A_{q_1/\mathfrak {p}_2^-} \cap RH_{(\mathfrak {p}_+/q_1)'}} \Vert h v_1\Vert _{L^2(B_j(y,\frac{3}{4}))}. \end{aligned}$$

(5.25)

Observe that

$$\begin{aligned} T_j^1 (f_{1,1}, f_{2,1})(x) = T_j (f_{1,1}, f_{2,1})(x), \quad x \in B_j(y, 1/4). \end{aligned}$$

(5.26)

As argued in [74, (3.7)], we utilize (5.24)–(5.26) to get that for any fixed $0<\kappa <\delta$,

$$\begin{aligned} \Vert&T_j^1(f_{1,1}, f_{2,1})v\Vert _{L^1(B_j(y,\frac{1}{4}))} \nonumber \\&\lesssim 2^{-j(\delta -\kappa ) + j(1+\gamma )(\delta _1+\delta _2)} \prod _{i=1}^2 [v_i^2]_{A_{2/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/2)'}} \Vert f_{i, 1}\Vert _{L^2(v_i^2)} \nonumber \\&\lesssim 2^{-\varepsilon j} \prod _{i=1}^2 [v_i^2]_{A_{2/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/2)'}} \Vert f_{i, 1}\Vert _{L^2(v_i^2)}, \end{aligned}$$

(5.27)

provided choosing $\kappa , \gamma , \varepsilon$ small enough so that $\delta -\kappa -(1+\gamma )(\delta _1+\delta _2)>\varepsilon$. Summing (5.19)–(5.22) and (5.27) yields

$$\begin{aligned} \Vert T_j^1(f_1, f_2)v\Vert _{L^1(B_j(y,\frac{1}{4}))} \lesssim 2^{-\varepsilon j} \prod _{i=1}^2 [v_i^2]_{A_{2/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/2)'}} \Vert f_i {\textbf {1}}_{B_j(y,\frac{5}{4})}\Vert _{L^2(v_i^2)}. \end{aligned}$$

(5.28)

Now, integrating the both sides of (5.28) with respect to y, using Cauchy–Schwarz inequality, and interchanging the order of integration, we conclude

$$\begin{aligned} \Vert T_j^1(f_1, f_2)\Vert _{L^1(v)} \lesssim 2^{-\varepsilon j} \prod _{i=1}^2 [v_i^2]_{A_{2/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/2)'}} \Vert f_i\Vert _{L^2(v_i^2)}. \end{aligned}$$

This shows (5.16) for $T_j^1$ and completes the whole proof. $\square$

5.2 Bilinear Rough Singular Integrals

Given $\Omega \in L^q(\mathbb {S}^{2n-1})$ with $1 \le q \le \infty$ and $\int _{\mathbb {S}^{2n-1}} \Omega \, d\sigma =0$, we define the rough bilinear singular integral operator $T_{\Omega }$ by

$$\begin{aligned} T_{\Omega }(f, g)(x)=\text {p.v.} \int _{\mathbb {R}^{2n}} K_{\Omega }(x-y, x-z) f(y) g(z) dy dz, \end{aligned}$$

where the rough kernel $K_{\Omega }$ is given by $K_{\Omega }(y, z) = \frac{\Omega ((y, z)/|(y, z)|)}{|(y, z)|^{2n}}$.

A typical example of the rough bilinear operators is the Calderón commutator defined in [14] as

$$\begin{aligned} \mathcal {C}_a (f)(x) := \text {p.v.} \int _{\mathbb {R}} \frac{A(x)-A(y)}{|x-y|^2} f(y) dy, \end{aligned}$$

where a is the derivative of A. C. Calderón [15] established the boundedness of $\mathcal {C}_a$ in the full range of exponents $1<p_1, p_2< \infty$. It was shown in [14] that the Calderón commutator can be written as

$$\begin{aligned} \mathcal {C}_a(f)(x):= \text {p.v.} \int _{\mathbb {R}\times \mathbb {R}} K(x-y, x-z) f(y) a(z) \, dydz, \end{aligned}$$

where the kernel is given by

$$\begin{aligned} K(y, z)=\frac{e(z)-e(z-y)}{y^2}=\frac{\Omega ((y, z)/|(y,z)|)}{|(y, z)|^2}, \end{aligned}$$

where $e(t)=1$ if $t>0$ and $e(t)=0$ if $t<0$. Observe that K(y, z) is odd and homogeneous of degree $-2$ whose restriction on $\mathbb {S}^1$ is $\Omega (y,z)$. It is also easy to check that $\Omega$ is odd and bounded, and hence Theorems 5.3–5.4 below can be applied to $\mathcal {C}_a$.

Theorem 5.3

Let $\Omega \in L^{\infty }(\mathbb {S}^{2n-1})$ and $\int _{\mathbb {S}^{2n-1}} \Omega \, d\sigma =0$. Then for all $p_i \in (1, \infty )$, for all $w_i^{p_i} \in A_{p_i}$, for all ${\textbf {b}}=(b_1, b_2) \in {\text {BMO}}^2$, and for each multi-index $\alpha \in \mathbb {N}^2$,

$$\begin{aligned} \Vert T_{\Omega }(f_1, f_2)\Vert _{L^p(w^p)}&\lesssim \prod _{i=1}^2 [w_i^{p_i}]_{A_{p_i}}^{\frac{3}{2} \max \{1, \frac{1}{p_i-1}\}} \Vert f_i\Vert _{L^{p_i}(w_i^{p_i})}, \end{aligned}$$

(5.29)

$$\begin{aligned} \Vert [T_{\Omega }, {\textbf {b}}]_{\alpha }(f_1, f_2)\Vert _{L^p(w^p)}&\lesssim \prod _{i=1}^2 [w_i^{p_i}]_{A_{p_i}}^{(\alpha _i+\frac{3}{2})\max \{1, \frac{1}{s_i-1}, \frac{1}{p_i-1}, \frac{s_i-1}{p_i-1}\}} \Vert b_i\Vert _{{\text {BMO}}}^{\alpha _i} \Vert f_i\Vert _{L^{p_i}(w_i^{p_i})}, \end{aligned}$$

(5.30)

whenever $\frac{1}{s}:= \frac{1}{s_1} + \frac{1}{s_2} \le 1$ with $s_1, s_2 \in (1, \infty )$, where $w=w_1 w_2$ and $\frac{1}{p}=\frac{1}{p_1}+\frac{1}{p_2}$.

Proof

Picking $r_1=r_2=r_3=1$ and $p_1=p_2=q_1=q_2=2$, we see that (2.32) holds and $p_i \in (1, \infty )$, $i=1, 2$. Then Lemma 2.8 gives that

$$\begin{aligned}{}[\textbf{w}]_{A_{(2, 2)}} \le [w_1^2]_{A_2}^{\frac{1}{2}} [w_2^2]_{A_2}^{\frac{1}{2}}. \end{aligned}$$

(5.31)

On the other hand, it was proved in [24] that for every $\textbf{w}=(w_1, w_2) \in A_{(2, 2)}$,

$$\begin{aligned} \Vert T_{\Omega }\Vert _{L^2(w_1^2) \times L^2(w_2^2) \rightarrow L^1(w)} \lesssim \Vert \Omega \Vert _{L^{\infty }} [\textbf{w}]_{A_{(2, 2)}}^3 \lesssim \Vert \Omega \Vert _{L^{\infty }} [w_1^2]_{A_2}^{\frac{3}{2}} [w_2^2]_{A_2}^{\frac{3}{2}}, \end{aligned}$$

(5.32)

where (5.31) was used in the last step. Thus, (5.29) and (5.30) follow at once from (5.32) and Theorems 1.1 and 1.2 applied to $\mathfrak {p}_i^-=1$, $\mathfrak {p}_i^+=\infty$, $q_i=2$, $\Phi _i(t)=t^{\frac{3}{2}}$. $\square$

Theorem 5.4

Let $\Omega \in L^q(\mathbb {S}^{2n-1})$ with $q>\frac{4}{3}$ and $\int _{\mathbb {S}^{2n-1}} \Omega \, d\sigma =0$. Let $\pi _q< \mathfrak {p}_i^- < \mathfrak {p}_i^+ \le \infty$, $i=1, 2$, be such that $\frac{1}{\pi '_q}< \frac{1}{\mathfrak {p}_+}:= \frac{1}{\mathfrak {p}_i^+} + \frac{1}{\mathfrak {p}_2^+} <1$, where $\pi _q:= \max \big \{\frac{24n+3q-4}{8n+3q-4}, \frac{24n+q}{8n+q}\big \}$. Then for all $p_i \in (\mathfrak {p}_i^-, \mathfrak {p}_i^+)$, for all $w_i^{p_i} \in A_{p_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/p_i)'}$, for all ${\textbf {b}}=(b_1, b_2) \in {\text {BMO}}^2$, and for each multi-index $\alpha \in \mathbb {N}^2$,

$$\begin{aligned}&\Vert T_{\Omega }(f_1, f_2)\Vert _{L^p(w^p)} \lesssim \prod _{i=1}^2 [w_i^{p_i(\mathfrak {p}_i^+/p_i)'}]_{A_{\tau _{p_i}}}^{\theta (\frac{1}{p_i} - \frac{1}{\mathfrak {p}_i^+})} \Vert f_i\Vert _{L^{p_i}(w_i^{p_i})}, \end{aligned}$$

(5.33)

$$\begin{aligned}&\Vert [T_{\Omega }, {\textbf {b}}]_{\alpha } (f_1, f_2)\Vert _{L^p(w^p)} \lesssim \prod _{i=1}^2 \Psi _i \big ([w_i^{p_i(\mathfrak {p}_i^+/p_i)'}]_{A_{\tau _{p_i}}}^{\gamma _i(p_i, s_i)}\big ) \Vert b_i\Vert _{{\text {BMO}}}^{\alpha _i} \Vert f_i\Vert _{L^{p_i}(w_i^{p_i})}, \end{aligned}$$

(5.34)

whenever $\frac{1}{s}:= \frac{1}{s_1} + \frac{1}{s_2} \le 1$ with $s_i \in (\mathfrak {p}_i^-, \mathfrak {p}_i^+)$, where $w=w_1 w_2$, $\frac{1}{p} = \frac{1}{p_1} + \frac{1}{p_2}$, $\frac{1}{r} = \frac{1}{r_1} + \frac{1}{r_2}$,

$$\begin{aligned} \theta = \max _{i=1, 2} \bigg \{\frac{\frac{1}{\mathfrak {p}_i^-}}{\frac{1}{\mathfrak {p}_i^-} - \frac{1}{p_i}}, \frac{1-\frac{1}{\mathfrak {p}_+}}{\frac{1}{p} - \frac{1}{\mathfrak {p}_+}}\bigg \}, \quad \text { and }\quad \Psi _i(t) := t^{\alpha _i \max \{1, \frac{1}{\tau _{s_i}-1}\} + \theta (\frac{1}{p_i} - \frac{1}{\mathfrak {p}_i^+})}. \end{aligned}$$

Proof

By assumption, $p_0:= \min \{\mathfrak {p}_1^-, \mathfrak {p}_2^-, \mathfrak {p}'_+\} > \pi _q$, which together with [49, Theorem 1.1] gives

$$\begin{aligned} |\langle T_{\Omega }(f_1, f_2), f_3 \rangle | \lesssim \sup _{\mathcal {S}: \text { sparse}} \Lambda _{\mathcal {S}, (p_0, p_0, p_0)}(f_1, f_2, f_3) \le \sup _{\mathcal {S}: \text { sparse}} \Lambda _{\mathcal {S}, (\mathfrak {p}_1^-, \mathfrak {p}_2^-, \mathfrak {p}'_+)}(f_1, f_2, f_3),\nonumber \\ \end{aligned}$$

(5.35)

for all $f_1, f_2, f_3 \in \mathscr {C}_c^{\infty }(\mathbb {R}^n)$. This and Theorem 5.6 below imply (5.33) and (5.34) as desired. $\square$

Remark 5.5

In Theorem 5.3, the exponent $\mathfrak {p}_i^- > \pi _q$ can be relaxed to $\mathfrak {p}_i^- \ge \pi _q$, at the cost of a larger exponent appearing in (5.33) and (5.34). Indeed, to get the first inequality in (5.35), it requires that $p_0$ is strictly greater than $\pi _q$. When $\mathfrak {p}_i^- = \pi _q$ and $w_i^{p_i} \in A_{p_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/p_i)'}$, Lemma 2.4 implies that there exists $\mathfrak {p}_i^-< {\widetilde{\mathfrak {p}}}_i^- < p_i$ such that $w_i^{p_i} \in A_{p_i/{\widetilde{\mathfrak {p}}}_i^-} \cap RH_{(\mathfrak {p}_i^+/p_i)'}$, $i=1, 2$. Then $p_0:= \min \{{\widetilde{\mathfrak {p}}}_1^-, {\widetilde{\mathfrak {p}}}_2^-, \mathfrak {p}'_+\} > \pi _q$. Combining this with Lemma 2.4 and the result in the case $\mathfrak {p}_i^- > \pi _q$, we can formulate similar estimates as in Theorem 5.3. Details are left to the reader.

Recall that a family $\mathcal {S}$ of cubes is called sparse if for every cube $Q \in \mathcal {S}$, there exists $E_Q \subset Q$ such that $|E_Q | \ge \eta |Q|$ for some $0<\eta <1$ and the collection $\{E_Q\}_{Q \in \mathcal {S}}$ is pairwise disjoint.

Given a sparse family $\mathcal {S}$ and $\mathbf {\mathfrak {s}}=(\mathfrak {s}_1, \ldots , \mathfrak {s}_{m+1})$ with $\mathfrak {s}_i \ge 1$, $i=1, \dots , m+1$, we define the $(m+1)$-sparse form

We are interested in those operators T that dominated by certain sparse form

$$\begin{aligned} |\langle T(f_1, \ldots , f_m), f_{m+1}\rangle | \le C(\mathbf {\mathfrak {s}}) \sup _{\mathcal {S}: \text { sparse}} \Lambda _{\mathcal {S}, \mathbf {\mathfrak {s}}}(f_1, \ldots , f_{m+1}), \end{aligned}$$

(5.36)

for all $f_1, \ldots , f_{m+1} \in \mathscr {C}_c^{\infty }(\mathbb {R}^n)$.

Theorem 5.6

Let $1 \le \mathfrak {p}_i^- < \mathfrak {p}_i^+ \le \infty$, $i=1, \dots , m$. Assume that the operator T satisfies (5.36) for the exponents $\mathbf {\mathfrak {s}} = (\mathfrak {p}_1^-, \ldots , \mathfrak {p}_m^-, \mathfrak {p}'_+)$, where $\frac{1}{\mathfrak {p}_+}:= \sum _{i=1}^m \frac{1}{\mathfrak {p}_i^+} < 1$. Then for all exponents $p_i, r_i \in (\mathfrak {p}_i^{-}, \mathfrak {p}_i^{+})$ and for all weights $w_i^{p_i} \in A_{p_i/\mathfrak {p}_i^{-}} \cap RH_{(\mathfrak {p}_i^{+}/p_i)'}$,

$$\begin{aligned} \Vert T(\textbf{f})\Vert _{L^p(w^p)}&\lesssim \prod _{i=1}^m [w_i^{p_i(\mathfrak {p}_i^+/p_i)'}]_{A_{\tau _{p_i}}}^{\theta (\frac{1}{p_i} - \frac{1}{\mathfrak {p}_i^+})} \Vert f_i\Vert _{L^{p_i}(w_i^{p_i})}, \end{aligned}$$

(5.37)

$$\begin{aligned} \bigg \Vert \Big (\sum _j |T(\textbf{f}^j)|^r \Big )^{\frac{1}{r}}\bigg \Vert _{L^p(w^p)}&\lesssim \prod _{i=1}^m [w_i^{p_i(\mathfrak {p}_i^+/p_i)'}]_{A_{\tau _{p_i}}}^{\theta (\frac{1}{p_i} - \frac{1}{\mathfrak {p}_i^+}) \gamma _i(p_i, r_i)} \bigg \Vert \Big (\sum _j |f_i^j|^{r_i}\Big )^{\frac{1}{r_i}}\bigg \Vert _{L^{p_i}(w_i^{p_i})}, \end{aligned}$$

(5.38)

where

$$\begin{aligned} w=\prod _{i=1}^m w_i, \quad \frac{1}{p} = \sum _{i=1}^m \frac{1}{p_i}, \quad \frac{1}{r} = \sum _{i=1}^m \frac{1}{r_i}, \quad \text { and }\quad \theta = \max _{1\le i \le m} \bigg \{\frac{\frac{1}{\mathfrak {p}_i^-}}{\frac{1}{\mathfrak {p}_i^-} - \frac{1}{p_i}}, \frac{1-\frac{1}{\mathfrak {p}_+}}{\frac{1}{p} - \frac{1}{\mathfrak {p}_+}}\bigg \}. \end{aligned}$$

If in addition T is an m-linear linear operator, then for the same exponents and weights as above, for all ${\textbf {b}}=(b_1, \ldots , b_m) \in {\text {BMO}}^m$, and for each multi-index $\alpha$, we have

$$\begin{aligned} \Vert [T, {\textbf {b}}]_{\alpha } (\textbf{f})\Vert _{L^p(w^p)} \lesssim \prod _{i=1}^m \Psi _i \big ([w_i^{p_i(\mathfrak {p}_i^+/p_i)'}]_{A_{\tau _{p_i}}}^{\gamma _i(p_i, s_i)}\big ) \Vert b_i\Vert _{{\text {BMO}}}^{\alpha _i} \Vert f_i\Vert _{L^{p_i}(w_i^{p_i})}, \end{aligned}$$

(5.39)

and

$$\begin{aligned} \bigg \Vert \Big (\sum _{j}\big |[T, {\textbf {b}}]_{\alpha }(\textbf{f}^j)\big |^r \Big )^{\frac{1}{r}}\bigg \Vert _{L^p(w^p)}&\lesssim \prod _{i=1}^m \Psi _i \big ([w_i^{p_i(\mathfrak {p}_i^+/p_i)'}]_{A_{\tau _{p_i}}}^{\gamma _i(p_i, r_i) \gamma _i(r_i, s_i)}\big ) \nonumber \\&\qquad \times \Vert b_i\Vert _{{\text {BMO}}}^{\alpha _i} \bigg \Vert \Big (\sum _{j} \big |f_i^j\big |^{r_i}\Big )^{\frac{1}{r_i}}\bigg \Vert _{L^{p_i}(w_i^{p_i})}, \end{aligned}$$

(5.40)

whenever $\frac{1}{s}:= \sum _{i=1}^m \frac{1}{s_i} \le 1$ with $s_i \in (\mathfrak {p}_i^-, \mathfrak {p}_i^+)$, where $\Psi _i(t):= t^{\alpha _i \max \{1, \frac{1}{\tau _{s_i}-1}\} + \theta (\frac{1}{p_i} - \frac{1}{\mathfrak {p}_i^+})}$.

Proof

Let $p_i \in (\mathfrak {p}_i^{-}, \mathfrak {p}_i^{+})$ and $w_i^{p_i} \in A_{p_i/\mathfrak {p}_i^{-}} \cap RH_{(\mathfrak {p}_i^{+}/p_i)'}$, $i=1, \ldots , m$. By density, we may assume that $f_1, \ldots , f_m \in \mathscr {C}_c^{\infty }(\mathbb {R}^n)$ in this sequel. By Lemma 2.8, one has $\textbf{w} \in A_{\textbf{p}, \textbf{r}}$ with

$$\begin{aligned}{}[\textbf{w}]_{A_{\textbf{p}, \mathbf {\mathfrak {s}}}} \le \prod _{i=1}^m [w_i^{p_i(\mathfrak {p}_i^+/p_i)'}]_{A_{\tau _{p_i}}}^{\frac{1}{p_i} - \frac{1}{\mathfrak {p}_i^+}}. \end{aligned}$$

(5.41)

Then it follows from (5.41) and [76, Corollary 4.2] that

$$\begin{aligned} \Vert T(f_1, \ldots , f_m)\Vert _{L^p(w^p)} \lesssim [\textbf{w}]_{A_{\textbf{p}, \mathbf {\mathfrak {s}}}}^{\theta } \prod _{i=1}^m \Vert f_i\Vert _{L^{p_i}(w_i^{p_i})}, \end{aligned}$$

(5.42)

Thus, (5.37) is a consequence of (5.41) and (5.42). With Theorem 1.1 and Remark 1.4 in hand, the estimate (5.37) in turn gives (5.38). Additionally, (5.39) and (5.40) follow from (5.37), Theorem 1.2, and Remark 1.4. The proof is complete. $\square$

We close the subsection with the following remark, which shows Theorems 1.1–1.2 and Theorem 5.6 contain a lot of applications. Details are left to the interested reader.

Remark 5.7

Now let us present some examples in terms of the hypothesis in Theorem 5.6.

• In [9], Bernicot et al. established a bilinear sparse domination $\Lambda _{\mathcal {S}, p_0, q'_0}$ for singular non-integral operators under certain assumptions. This verifies the hypothesis (5.36) for $r_1=p_0$ and $r_2=q'_0$. Note also that our extrapolation theorems above can be extended to spaces of homogeneous type since the corresponding sharp estimate for the Hardy–Littlewood operator (2.1) was established in [52, Proposition 7.13].

• For Bochner–Riesz means $\mathcal {B}^{\alpha }$ in $\mathbb {R}^2$, the authors [6] proved a similar spare bilinear form to (5.36) with $r_1=6/5$ and $r_2=2$ whenever $\alpha >1/6$. Much as before, one can not only recover [6, Theorem 1.2], but also obtain quantitative weighted estimates and vector-valued inequalities.

• Bui et. al [12] studied the Schrödinger operator $L=\Delta +V$ on $\mathbb {R}^n$ with $n \ge 3$, where $V \in RH_q$ and $q \in (n/2, n)$. Letting $p_0=\big (\frac{1}{q}-\frac{1}{n}\big )^{-1}$ and K(x, y) be the kernel of the Riesz transform $L^{-1/2}\nabla$, we see that K satisfies the Bui-Duong’s condition (cf. [12, Theorem 5.6]). The latter implies $L^r$-Hörmander condition (cf. [70, Proposition 3.2]). Then, combining the $L^p$ bounds for $\nabla L^{-1/2}$ with $p \in (1, p_0]$ (cf. [86]) and the pointwise sparse domination in [70], we use a duality argument to conclude that there exists a sparse family $\mathcal {S}$ such that $|\langle \nabla L^{-1/2}f, g \rangle | \lesssim \Lambda _{\mathcal {S}, 1, p_0}(f, g)$. That is, the hypothesis (5.36) is satisfied for the Riesz transform $\nabla L^{-1/2}$.

• For the m-linear Calderón–Zygmund operators and the corresponding maximal truncation, pointwise sparse dominations were obtained in [28, 37], which immediately implies (5.36) with $\textbf{r}=(1, \ldots , 1)$. Then one can improve Corollaries 8.2 and 8.3 in [47] to the quantitative weighted estimates.

• Let $1 \le r < \infty$ and $\mathfrak {g}$ be the square function with the kernel $K_t$ satisfies the m-linear $L^r$-Hörmander condition defined in [21]. Under the assumption that $\mathfrak {g}$ is bounded from $L^r(\mathbb {R}^n) \times \cdots \times L^r(\mathbb {R}^n)$ to $L^{r/m, \infty }(\mathbb {R}^n)$, Cao and Yabuta [21] obtained a pointwise control of $\mathfrak {g}$ by $\Lambda _{\mathcal {S}, \textbf{r}}$, where $\textbf{r}=(r, \ldots , r, 1)$. Then, the square function $\mathfrak {g}$ verifies (5.36).

• The operators satisfying (5.36) also include the discrete cubic Hilbert transform [36] and oscillatory integrals [63].

5.3 Multilinear Fourier Multipliers

Given $s, m \in \mathbb {N}$, a function $\sigma \in \mathscr {C}^s(\mathbb {R}^{nm} {\setminus } \{0\})$ is said to belong to $\mathcal {M}^s(\mathbb {R}^{nm})$ if

$$\begin{aligned} \big |\partial _{\xi _1}^{\alpha _1} \cdots \partial _{\xi _m}^{\alpha _m} \sigma (\mathbf {\xi }) \big |&\le C_{\alpha } (|\xi _1|+\cdots +|\xi _m|)^{-\sum _{i=1}^m |\alpha _i|}, \quad \forall \mathbf {\xi } \in \mathbb {R}^{nm} \setminus \{0\}, \end{aligned}$$

for each multi-index $\alpha =(\alpha _1, \ldots , \alpha _m)$ with $\sum _{i=1}^m |\alpha _i| \le s$.

Given $s \in \mathbb {R}$, the (usual) Sobolev space $W^s(\mathbb {R}^{nm})$ is defined by the norm

$$\begin{aligned} \Vert f\Vert _{W^s(\mathbb {R}^{nm})} :=\bigg (\int _{\mathbb {R}^{nm}} (1+|\mathbf {\xi }|^2)^{s}|{\widehat{f}}(\mathbf {\xi })|^2 d\mathbf {\xi }\bigg )^{\frac{1}{2}}, \end{aligned}$$

where ${\widehat{f}}$ is the Fourier transform in all the variables. For $\textbf{s}=(s_1,\ldots ,s_m) \in \mathbb {R}^m$, the Sobolev space of product type $W^{\textbf{s}}(\mathbb {R}^{nm})$ consists of all $f \in \mathcal {S}'(\mathbb {R}^{nm})$ such that

$$\begin{aligned} \Vert f\Vert _{W^{\textbf{s}}(\mathbb {R}^{nm})} :=\bigg (\int _{\mathbb {R}^{nm}} (1+|\xi _1|^2)^{s_1} \cdots (1+|\xi _m|^2)^{s_m} |{\widehat{f}}(\mathbf {\xi })|^2 d\mathbf {\xi }\bigg )^{\frac{1}{2}} < \infty . \end{aligned}$$

Given a function $\sigma$ on $\mathbb {R}^{nN}$, we set

$$\begin{aligned} \sigma _j(\mathbf {\xi }) :=\Psi (\mathbf {\xi }) \sigma (2^j \mathbf {\xi }), \quad j \in \mathbb {Z}, \end{aligned}$$

(5.43)

where $\Psi \in \mathcal {S}(\mathbb {R}^{nm})$ satisfy ${\text {supp}}\Psi \subset \{1/2 \le |\mathbf {\xi }| \le 2 \}$, and $\sum _{k \in \mathbb {Z}} \Psi (2^{-k}\mathbf {\xi }) =1$ for all $\mathbf {\xi } \in \mathbb {R}^{nm} {\setminus }\{0\}$. Denote

$$\begin{aligned} \mathcal {W}^s(\mathbb {R}^{nm})&:= \big \{\sigma \in L^{\infty }(\mathbb {R}^{nm}): \sup _{j \in \mathbb {Z}} \Vert \sigma _j\Vert _{W^s(\mathbb {R}^{nm})}<\infty \big \},\\ \mathcal {W}^{\textbf{s}}(\mathbb {R}^{nm})&:= \big \{\sigma \in L^{\infty }(\mathbb {R}^{nm}): \sup _{j \in \mathbb {Z}} \Vert \sigma _j\Vert _{W^{\textbf{s}}(\mathbb {R}^{nm})}<\infty \big \}. \end{aligned}$$

Then one has

$$\begin{aligned} \mathcal {M}^{s}(\mathbb {R}^{nm}) \subsetneq \mathcal {W}^{s}(\mathbb {R}^{nm}) \subsetneq \mathcal {W}^{(\frac{s}{m},\ldots ,\frac{s}{m})}(\mathbb {R}^{nm}). \end{aligned}$$

For a bounded function $\sigma$ on $\mathbb {R}^{nm}$, the m-linear Fourier multiplier $T_{\sigma }$ is defined by

$$\begin{aligned} T_{\sigma }&(\textbf{f})(x) := \int _{\mathbb {R}^{nm}} e^{2\pi ix \cdot (\xi _1+\dots +\xi _m)} \sigma (\mathbf {\xi }) {\widehat{f}}_1(\xi _1) \cdots {\widehat{f}}_m(\xi _m) \, d\mathbf {\xi }, \end{aligned}$$

for all $f_1,\ldots f_m \in \mathcal {S}(\mathbb {R}^n)$.

Be means of extrapolation theorems, we improve Theorems 1.2 (i) and 6.2 in [43] to the weighted estimates with quantitative bounds. We can also establish the corresponding weighted estimates for the higher order commutators and vector-valued inequalities as follows.

Theorem 5.8

Let $m \ge 2$, $n/2 < s_i \le n$, $i=1, \ldots , m$. Assume that $\sigma \in \mathcal {W}^{\textbf{s}}(\mathbb {R}^{nm})$. Then for every $p_i>n/s_i$, for every $w_i^{p_i} \in A_{p_i s_i/n}$, $i=1, \ldots , m$, for all ${\textbf {b}}=(b_1,\ldots , b_m) \in {\text {BMO}}^m$, and for each multi-index $\alpha \in \mathbb {N}^m$,

$$\begin{aligned} \Vert T_{\sigma }(\textbf{f})\Vert _{L^p(w^p)}&\lesssim \prod _{i=1}^m [w_i^{p_i}]_{A_{p_i s_i/n}}^{\frac{3}{2} \gamma _i(p_i, 2m)} \Vert f_i\Vert _{L^{p_i}(w_i^{p_i})}, \end{aligned}$$

(5.44)

$$\begin{aligned} \Vert [T_{\sigma }, {\textbf {b}}]_{\alpha }(\textbf{f})\Vert _{L^p(w^p)}&\lesssim \prod _{i=1}^m [w_i^{p_i}]_{A_{p_is_i/n}}^{(\alpha _i + \frac{3}{2}) \gamma _i(p_i, 2m)} \Vert b_i\Vert _{{\text {BMO}}}^{\alpha _i} \Vert f_i\Vert _{L^{p_i}(w_i^{p_i})}, \end{aligned}$$

(5.45)

where $\frac{1}{p} = \sum _{i=1}^m \frac{1}{p_i}$ and $w=\prod _{i=1}^m w_i$.

Moreover, for any $r \in (n/s_i, 2]$, $i=1, \ldots ,m$,

$$\begin{aligned} \bigg \Vert \bigg (\sum _{k_1, \ldots , k_m} |T_{\sigma }(f^1_{k_1}, \ldots , f^m_{k_m})|^r \bigg )^{\frac{1}{r}}\bigg \Vert _{L^p(w^p)}&\lesssim \prod _{i=1}^m [w_i^{p_i}]_{A_{p_i s_i/n}}^{\beta _i(r)} \bigg \Vert \bigg (\sum _{k_i} |f^i_{k_i}|^r \bigg )^{\frac{1}{r}}\bigg \Vert _{L^{p_i}(w_i^{p_i})},\\ \bigg \Vert \bigg (\sum _{k_1, \ldots , k_m} |[T_{\sigma }, {\textbf {b}}]_{\alpha }(f^1_{k_1}, \ldots , f^m_{k_m})|^r \bigg )^{\frac{1}{r}}\bigg \Vert _{L^p(w^p)}&\lesssim \prod _{i=1}^m [w_i^{p_i}]_{A_{p_i s_i/n}}^{\eta _i(r)} \Vert b_i\Vert _{{\text {BMO}}}^{\alpha _i} \bigg \Vert \bigg (\sum _{k_i} |f^i_{k_i}|^r \bigg )^{\frac{1}{r}}\bigg \Vert _{L^{p_i}(w_i^{p_i})}, \end{aligned}$$

where

$$\begin{aligned} \beta _i(r):= {\left\{ \begin{array}{ll} \frac{3}{2} \gamma _i(p_i, 2m), &{} r=2,\\ \frac{3}{2} \gamma _i(p_i, q_i) \gamma _i(q_i, 2m), &{} r \ne 2, \end{array}\right. } \qquad \eta _i(r):= {\left\{ \begin{array}{ll} (\alpha _i + \frac{3}{2}) \gamma _i(p_i, 2m), &{} r=2,\\ (\alpha _i + \frac{3}{2}) \gamma _i(p_i, q_i) \gamma _i(q_i, 2m), &{} r \ne 2, \end{array}\right. } \end{aligned}$$

provided $q_i \in (n/s_i, r)$, $i=1, \ldots , m$.

Proof

We borrow some ideas from [43], but now we can give a proof without using the weighted Hardy space argument. Let $\mathfrak {p}_i^-:= n/s_i$ and $\mathfrak {p}_i^+:= \infty$ for each $i=1, \ldots , m$. Let $q=2$ and $q_i=2m$ for $1\le i \le m$. Then, $q_i \in (\mathfrak {p}_i^-, \mathfrak {p}_i^+)$. Checking the proof of [43, Theorem 6.2], we can obtain that for any weight $v_i^{q_i} \in A_{q_is_i/n}=A_{q_i/\mathfrak {p}_i^-} \cap RH_{(\mathfrak {p}_i^+/q_i)'}$, $i=1, \ldots , m$,

$$\begin{aligned} \Vert T_{\sigma }(\textbf{f})\Vert _{L^q(v^q)} \lesssim \prod _{i=1}^m [v_i^{q_i}]_{A_{q_is_i/n}}^{\frac{3}{2}} \Vert f_i\Vert _{L^{q_i}(v_i^{q_i})}. \end{aligned}$$

(5.46)

Thus, (5.44) follows from (5.46) and Theorem 1.1 applied to $\Phi _i(t) = t^{3/2}$.

Note that in the current scenario, $\gamma _i(q_i, q_i)=1$, $\tau _{q_i}=2ms_i/n$, and hence,

$$\begin{aligned} {\widetilde{\Phi }}_i(t):= t^{\alpha _i \max \{1, \frac{1}{\tau _{q_i}-1}\}} \Phi _i(C_i \, t^{\gamma _i(q_i, q_i)}) = C_i^{\frac{3}{2}} \, t^{\frac{3}{2} + \alpha _i \max \{1, \frac{1}{2Ns_i/n-1}\}} = C_i^{\frac{3}{2}} \, t^{\frac{3}{2} + \alpha _i}. \end{aligned}$$

Then in view of (5.46), Theorem 1.2 applied to $s_i=q_i=2m$ implies (5.45).

On the other hand, Lemma 2.12 and (5.44) give that for every $q_i>n/s_i$, for every $w_i^{q_i} \in A_{q_i s_i/n}$, $i=1, \ldots , m$,

$$\begin{aligned} \bigg \Vert \bigg (\sum _{k_1, \ldots , k_m} |T_{\sigma }(f^1_{k_1}, \ldots , f^m_{k_m})|^r \bigg )^{\frac{1}{r}}\bigg \Vert _{L^q(v^q)} \lesssim \prod _{i=1}^m [v_i^{q_i}]_{A_{q_i s_i/n}}^{\frac{3}{2} \gamma _i(q_i, 2m)} \bigg \Vert \bigg (\sum _{k_i} |f^i_{k_i}|^r \bigg )^{\frac{1}{r}}\bigg \Vert _{L^{q_i}(v_i^{q_i})}, \end{aligned}$$

provided $r=2$ or $r \in (n/s_i, 2)$ and $q_i \in (n/s_i, r)$, where $\frac{1}{q}=\sum _{i=1}^m \frac{1}{q_i}$ and $v=\prod _{i=1}^m v_i$. Therefore, the vector-valued inequalities above follow from Theorem 1.1 applied to $\Phi _i(t) = t^{\frac{3}{2} \gamma _i(q_i, 2\,m)}$. $\square$

Theorem 5.9

Let $1 \le r \le 2$ and $s_1, s_2>1/r$. Let $\sigma$ be a bounded function on $\mathbb {R}^2$ satisfying

$$\begin{aligned} \sup _{j \in \mathbb {Z}} \big \Vert (I-\Delta _{\xi _1})^{\frac{s_1}{2}} (I-\Delta _{\xi _2})^{\frac{s_2}{2}} \sigma _j\big \Vert _{L^r(\mathbb {R}^2)} < \infty , \end{aligned}$$

where $\sigma _j$ is given in (5.43) with $n=1$. Assume that $1 \le \mathfrak {p}_1^{-}, \mathfrak {p}_2^{-}<\infty$ and $\max \limits _{1 \le i \le 2}\frac{1}{s_i} < \min \limits _{1 \le i \le 2} \mathfrak {p}_i^{-}$. Then for all exponents $p_i \in (\mathfrak {p}_i^{-}, \infty )$ and all weights $w_i^{p_i} \in A_{p_i/\mathfrak {p}_i^-}$, $i=1, 2$,

$$\begin{aligned} \Vert T_{\sigma }(\textbf{f})\Vert _{L^p(w^p)} \lesssim \prod _{i=1}^2 [w_i^{p_i}]_{A_{p_i/\mathfrak {p}_i^-}}^{\frac{15}{p_i} + 2 \max \{\frac{1}{2}, \frac{1}{p_i-\mathfrak {p}_i^-}\}} \Vert f_i\Vert _{L^{p_i}(w_i^{p_i})}, \end{aligned}$$

where $\frac{1}{p} = \frac{1}{p_1} + \frac{1}{p_2} \ge 1$ and $w=w_1 w_2$.

Proof

We will use the same notation as [46]. By the same argument as [46, p. 970], we are deduced to showing the boundedness of $T_{\sigma _1}$ and $T_{\sigma _2}$, which satisfy

$$\begin{aligned} |\Delta _j^{\theta }(T_{\sigma _1}(f_1, f_2))|&\lesssim M(|f_1|^{\rho })^{\frac{1}{\rho }} M\big (|\Delta _j^{\eta } f_2|^{\rho }\big )^{\frac{1}{\rho }}, \end{aligned}$$

(5.47)

$$\begin{aligned} T_{\sigma _2}(f_1, f_2)&=\sum _{j \in \mathbb {Z}} T_{\sigma _2}(f_1, \Delta _j^{\theta } f_2), \end{aligned}$$

(5.48)

$$\begin{aligned} T_{\sigma _2}(f_1, \Delta _j^{\theta } f_2)&\lesssim M\big (|\Delta _j^{\zeta } f_1|^{\rho }\big )^{\frac{1}{\rho }} M\big (|\Delta _j^{\theta } f_2|^{\rho }\big )^{\frac{1}{\rho }}. \end{aligned}$$

(5.49)

Here, $\rho \in (1, 2)$ satisfies $\max \limits _{i=1, 2}\frac{1}{s_i}< \rho < \min \{\mathfrak {p}_1^{-}, \mathfrak {p}_2^{-}, r\}$ if $r>1$, and $\rho =1$ if $r=1$. The multiplier $\Delta _j^{\theta }$ is defined by $\widehat{\Delta _j^{\theta } f}={\widehat{\theta }}(2^{-j}\cdot ) {\widehat{f}}$, for each $j \in \mathbb {Z}$, where $\theta \in \mathcal {S}(\mathbb {R})$ satisfies ${\text {supp}}({\widehat{\theta }}) \subset \{ \xi \in \mathbb {R}: 1/c_0 \le |\xi | \le c_0 \}$, for some $c_0>1$, and $\sum _{j \in \mathbb {Z}} {\widehat{\theta }}(2^{-j}\xi )=C_{\theta }$ for all $\xi \in \mathbb {R}\setminus \{0\}$. Considering the same property of $\Delta _j^{\theta }$ and $\Delta _j^{\zeta }$, we will suppress $\theta$ and $\zeta$ in this sequel.

Let $w_i^{p_i} \in A_{p_i/\mathfrak {p}_i^-}$, $i=1, 2$. By the choice of $\rho$, we have

$$\begin{aligned} w_i^{p_i} \in A_{p_i/\rho } \subset A_{p_i} \quad \text { with }\quad [w_i^{p_i}]_{A_{p_i}} \le [w_i^{p_i}]_{A_{p_i/\rho }} \le [w_i^{p_i}]_{A_{p_i/\mathfrak {p}_i^-}}, \quad i=1, 2. \end{aligned}$$

(5.50)

Let us control $T_{\sigma _1}$ and $T_{\sigma _2}$. Invoking (5.48)–(5.50), (2.1), and Lemma 3.3, we use Hölder’s inequality to conclude that

$$\begin{aligned} \Vert T_{\sigma _2} (f_1, f_2)\Vert _{L^p(w^p)}&\lesssim \bigg \Vert \sum _{j \in \mathbb {Z}} M\big (|\Delta _j f_1|^{\rho }\big )^{\frac{1}{\rho }} M\big (|\Delta _j f_2|^{\rho }\big )^{\frac{1}{\rho }} \bigg \Vert _{L^p(w^p)}\\&\le \prod _{i=1}^2 \bigg \Vert \Big (\sum _{j \in \mathbb {Z}} M\big (|\Delta _j f_i|^{\rho }\big )^{\frac{2}{\rho }} \Big )^{\frac{1}{2}} \bigg \Vert _{L^{p_i}(w_i^{p_i})}\\&\lesssim \prod _{i=1}^2 [w_i^{p_i}]_{A_{p_i/\rho }}^{\max \{\frac{1}{2}, \frac{1}{p_i-\rho }\}} \bigg \Vert \Big (\sum _{j \in \mathbb {Z}} |\Delta _j f_i|^2 \Big )^{\frac{1}{2}} \bigg \Vert _{L^{p_i}(w_i^{p_i})}\\&\lesssim \prod _{i=1}^2 [w_i^{p_i}]_{A_{p_i/\rho }}^{\max \{\frac{1}{2}, \frac{1}{p_i-\rho }\}} [w_i^{p_i}]_{A_{p_i}}^{\max \{\frac{1}{2}, \frac{1}{p_i-1}\}} \Vert f_i\Vert _{L^{p_i}(w_i^{p_i})}\\&\lesssim \prod _{i=1}^2 [w_i^{p_i}]_{A_{p_i/\mathfrak {p}_i^-}}^{2 \max \{\frac{1}{2}, \frac{1}{p_i-\mathfrak {p}_i^-}\}} \Vert f_i\Vert _{L^{p_i}(w_i^{p_i})}, \end{aligned}$$

where the inequality (3.8) was used in the second-to-last step. To estimate $T_{\sigma _1}$, we note that by Lemma 2.9,

$$\begin{aligned}{}[w^p]_{A_2} \le [w^p]_{A_{p/\mathfrak {p}_-}} \le \prod _{i=1}^2 [w_i^{p_i}]_{A_{p_i/\mathfrak {p}_i^-}}^{\frac{p}{p_i}}, \end{aligned}$$

(5.51)

since $\frac{1}{\mathfrak {p}_-}:= \frac{1}{\mathfrak {p}_1^-} + \frac{1}{\mathfrak {p}_2^-} \le 2$ and $p \le 1 \le 2\mathfrak {p}_-$. Therefore, in view of Lemma 5.10 applied to $r=2$ and $v=w^p$, (5.51), and (5.47), we proceed as above to obtain

$$\begin{aligned}&\Vert T_{\sigma _1}(f_1, f_2)\Vert _{L^p(w^p)} \lesssim [w^p]_{A_2}^{\frac{15}{p}} \bigg \Vert \bigg (\sum _{j \in \mathbb {Z}}|\Delta _j (T_{\sigma _1}(f_1, f_2))|^2 \bigg )^{\frac{1}{2}}\bigg \Vert _{L^p(w^p)}\\&\quad \lesssim \prod _{i=1}^2 [w_i^{p_i}]_{A_{p_i/\mathfrak {p}_i^-}}^{\frac{15}{p_i}} \bigg \Vert M(|f_1|^{\rho })^{\frac{1}{\rho }} \bigg (\sum _{j \in \mathbb {Z}}M\big (|\Delta _j f_2|^{\rho } \big )^{\frac{2}{\rho }}\bigg )^{\frac{1}{2}} \bigg \Vert _{L^p(w^p)}\\&\quad \lesssim \prod _{i=1}^2 [w_i^{p_i}]_{A_{p_i/\mathfrak {p}_i^-}}^{\frac{15}{p_i}} \big \Vert M(|f_1|^{\rho })^{\frac{1}{\rho }} \big \Vert _{L^{p_1}(w_1^{p_1})} \bigg \Vert \bigg (\sum _{j \in \mathbb {Z}}M\big (|\Delta _j f_2|^{\rho } \big )^{\frac{2}{\rho }}\bigg )^{\frac{1}{2}} \bigg \Vert _{L^{p_2}(w_2^{p_2})}\\&\quad \lesssim [w_1^{p_1}]_{A_{p_1/\rho }}^{\frac{15}{p_1}+\frac{1}{p_1-\rho }} [w_2^{p_2}]_{A_{p_2/\rho }}^{\frac{15}{p_2}+\max \{\frac{1}{2}, \frac{1}{p_2-\rho }\}} \Vert f_1\Vert _{L^{p_1}(w_1^{p_1})} \bigg \Vert \bigg (\sum _{j \in \mathbb {Z}} |\Delta _j f_2|^2 \bigg )^{\frac{1}{2}} \bigg \Vert _{L^{p_2}(w_2^{p_2})} \\&\quad \lesssim \prod _{i=1}^{m} [w_i^{p_i}]_{A_{p_i/\mathfrak {p}_i^-}}^{\frac{15}{p_i} + 2 \max \{\frac{1}{2}, \frac{1}{p_i-\mathfrak {p}_i^-}\}} \Vert f_i\Vert _{L^{p_i}(w_i^{p_i})}. \end{aligned}$$

This completes the proof. $\square$

In this subsection, we always choose $\phi \in \mathcal {S}(\mathbb {R}^n)$ with $\int _{\mathbb {R}^n} \phi \, dx=1$, and set $\phi _t(x):= t^{-n} \phi (x/t)$ for any $x \in \mathbb {R}^n$ and $t>0$. And let $\psi ,\,\Phi \in \mathcal {S}(\mathbb {R}^n)$ satisfy $0 \le {\widehat{\psi }}(\xi )\le {\textbf {1}}_{\{1/2 \le |\xi | \le 2\}}$, ${\widehat{\psi }}(\xi ) \ge 0$ for $1/2 \le |\xi | \le 2$, $\sum _{j \in \mathbb {Z}} {\widehat{\psi }}(2^j\xi )=1$ for $|\xi |\ne 0$, and ${\textbf {1}}_{\{1/2 \le |\xi | \le 2\}} \le {\widehat{\Phi }}(\xi ) \le {\textbf {1}}_{\{1/3 \le |\xi | \le 3\}}$. Denote $\psi _j(x)=2^{-jn}\psi (x/2^j)$ and $\Phi _j(x)=2^{-jn}\Phi (x/2^j)$ for each $j \in \mathbb {Z}$.

Lemma 5.10

For all $0<p \le 1 \le r \le 2$ and for all $v \in A_r$,

$$\begin{aligned} \Vert f\Vert _{L^p(v)} \le \bigg \Vert \sup _{t>0} |\phi _t*f| \bigg \Vert _{L^p(v)} \lesssim [v]_{A_2}^{\frac{11+2r'}{p}} \bigg \Vert \bigg (\sum _{j \in \mathbb {Z}} |\Delta _j f|^2 \bigg )^{\frac{1}{2}} \bigg \Vert _{L^p(v)}. \end{aligned}$$

Proof

It suffices to show the second inequality since $|f(x)| \le \sup _{t>0} |\phi _t*f(x)|$ for all $x \in \mathbb {R}^n$. By Lemma 5.11–5.12 below and estimates in [11, p. 588], we have

$$\begin{aligned} \Vert f\Vert _{H^p(v)}&= \Big \Vert \sum _j \Phi _j *\psi _j *f\Big \Vert _{H^p(v)} \lesssim [v]_{A_2}^{\frac{9}{p}+\frac{2r'}{p}} \Big \Vert \sup _{t>0} \Big (\sum _j |\phi _t*\psi _j *f|^2\Big )^{\frac{1}{2}} \Big \Vert _{L^p(v)}\\&\le [v]_{A_2}^{\frac{9}{p}+\frac{2r'}{p}} \Big \Vert \Big (\sum _j \sup _{t>0} |\phi _t*\psi _j *f|^2\Big )^{\frac{1}{2}} \Big \Vert _{L^p(v)} \lesssim [v]_{A_2}^{\frac{9}{p}+\frac{2r'}{p}} \Big \Vert \Big (\sum _j |\psi _{j \lambda }^{*}f|^2 \Big )^{\frac{1}{2}}\Big \Vert _{L^{p}(v)}\\&\lesssim [v]_{A_2}^{\frac{9}{p}+\frac{2r'}{p}} \bigg \Vert \Big [\sum _j M(|\psi _j *f|^s)(x)^{\frac{2}{s}}\Big ]^{\frac{s}{2}} \bigg \Vert _{L^{p/s}(v)}^{\frac{1}{s}}\\&\lesssim [v]_{A_2}^{\frac{9}{p}+\frac{2r'}{p}} [v]_{A_{p/s}}^{\max \{\frac{1}{2}, \frac{1}{p-s}\}} \bigg \Vert \Big [\sum _j |\psi _j *f(x)|^2 \Big ]^{\frac{1}{2}} \bigg \Vert _{L^p(v)} \end{aligned}$$

where we used Lemma 3.3 and that $\lambda >\max \{\frac{nr}{p}, \frac{n}{2}\} = \frac{nr}{p}$, so $s:= \frac{n}{\lambda }<\frac{p}{r}$ and $[v]_{A_{p/s}} \le [w]_r$. If we take $\frac{n}{\lambda }=\frac{p(1-\varepsilon )}{r}$ for some $\varepsilon \in (0, 1)$, then $p-s=p-\frac{n}{\lambda } = p(1-\frac{1-\varepsilon }{r}) \ge p(1-(1 - \varepsilon ) ) = p \varepsilon$. This means $\max \{\frac{1}{2}, \frac{1}{p-s}\} < \frac{1}{p\varepsilon }$. Consequently, taking $\varepsilon =1/2$, we get the desired estimate. $\square$

We use the maximal operators $N, N^+, N^*$ defined in [11]. Moreover, given a sequence ${\textbf {f}}=\{f_j\}$, a function u on $\mathbb {R}^{n+1}_+$, and $\alpha , \kappa >0$, we define

$$\begin{aligned} N_{\kappa }^{**} {\textbf {f}}(x)&:= \sup _{y \in \mathbb {R}^n, t>0} \bigg (\sum _j |\phi _t*f_j(x)|^q \bigg )^{\frac{1}{q}} \bigg (\frac{t}{t+|x-y|}\bigg )^{\kappa },\\ {\widetilde{N}}_{\alpha } u(x)&:= \sup _{|x-y|<\alpha t} |u(y, t)|, \quad {\widetilde{N}}_{\kappa }^{**} u(x) := \sup _{y \in \mathbb {R}^n, t>0} |u(y, t)| \bigg (\frac{t}{t+|x-y|}\bigg )^{\kappa }. \end{aligned}$$

Lemma 5.11

For any $p \in (0, \infty )$, $r \in (1, \infty )$, and $w \in A_r$,

$$\begin{aligned} \Vert {\widetilde{N}}^{**}_{\kappa } u\Vert _{L^p(w)}&\lesssim [w]_{A_r}^{\frac{r'}{p}} \Vert {\widetilde{N}}_1 u\Vert _{L^p(w)}, \end{aligned}$$

(5.52)

$$\begin{aligned} \Vert N^* {\textbf {f}}\Vert _{L^p(w)}&\lesssim [w]_{A_r}^{\frac{r'}{p}} \Vert N {\textbf {f}}\Vert _{L^p(w)}, \end{aligned}$$

(5.53)

$$\begin{aligned} \Vert N {\textbf {f}}\Vert _{L^p(w)}&\lesssim [w]_{A_r}^{\frac{r'}{p}} \Vert N^+ {\textbf {f}}\Vert _{L^p(w)}. \end{aligned}$$

(5.54)

Proof

The inequality (5.52) follows from the following

$$\begin{aligned} {\widetilde{N}}^{**}_{\kappa } u \lesssim \sup _{m \in \mathbb {N}} 2^{-mn} {\widetilde{N}}_{2^m} u \quad \text { and }\quad w(\{{\widetilde{N}}_{\beta }u>\eta \}) \lesssim (1+\beta /\alpha )^{nr} [w]_{A_r}^{r'} w(\{{\widetilde{N}}_{\alpha }u>\eta \}), \end{aligned}$$

for all $\eta >0$, where the first estimate is trivial and the second one is contained in [50]. The inequality (5.53) is a consequence of (5.52) and the pointwise estimate $N^*{\textbf {f}} \lesssim {\widetilde{N}}^{**}_{\kappa } {\textbf {f}}$.

To show (5.54), we trace the proof of $\Vert N {\textbf {f}}\Vert _{L^p(w)} \lesssim \Vert N^+ {\textbf {f}}\Vert _{L^p(w)}$ in [11]. Firstly, by (5.52) we have

$$\begin{aligned} \Vert N^{**}_\lambda f\Vert _{L^p(w)} \lesssim [w]_{A_r}^{\frac{r'}{p}} \Vert N {\textbf {f}}\Vert _{L^p(w)}. \end{aligned}$$

Setting ${\widetilde{N}}_\mu u_i(x):= \sup _{t>0, |x-y|<\mu t} \big (\sum _{j\in \mathbb {Z}}|\phi _t^{(i)}*f_j(y)|^q \big )^{\frac{1}{q}}$, where $\phi ^{(i)}=\frac{\partial \phi }{\partial x_i}$ and $\mu >1$, we use (5.53) to get

$$\begin{aligned} \Vert {\widetilde{N}}_\mu u_i\Vert _{L^p(w)} \lesssim [w]_{A_r}^{\frac{r'}{p}} \Vert N {\textbf {f}}\Vert _{L^p(w)}. \end{aligned}$$

(5.55)

Since $r>1$ and $w\in A_r$, Lemma 2.4 gives that $r>\inf \{\rho >0: w\in A_\rho \}$. So, for $s\in (0,1]$ with $p/s = r> \inf \{\rho >0: w\in A_\rho \}$, and $\delta >0$ satisfying $\Gamma _\delta (y)\subset \Gamma _\mu (x)$ for all $(y,t) \in \Gamma _1(x)$, we get

$$\begin{aligned} N{{{\textbf {f}}}}(x)^s\le (1+1/\delta )^n M((N^+ {\varvec{f}})^s)(x) + \delta ^s\sum _{i=1}^{n} {\widetilde{N}}_\mu u_i(x)^s. \end{aligned}$$

Hence, taking $L^{p/s}(w)$-norm of both sides of the above, and using (5.55), we see that

$$\begin{aligned} \Vert N {\textbf {f}}\Vert ^s_{L^p(w)} \le C_1 (1+1/\delta )^n[w]_{A_{p/s}}^{\frac{1}{p/s-1}} \Vert N^+ {\textbf {f}}\Vert ^s_{L^p(w)} + C_2 \delta ^s\Vert N {\textbf {f}}\Vert _{L^p(w)}. \end{aligned}$$

Choosing $\delta$ so small that $C_2 \delta ^s<1/2$, we obtain

$$\begin{aligned} \Vert N {\textbf {f}}\Vert _{L^p(w)} \lesssim [w]_{A_{p/s}}^{\frac{1}{p-s}} \Vert N^+ {\textbf {f}}\Vert _{L^p(w)} =[w]_{A_{r}}^{\frac{r'}{p}} \Vert N^+ {\textbf {f}}\Vert _{L^p(w)}. \end{aligned}$$

This completes the proof of (5.54). $\square$

Lemma 5.12

Then for any $p \in (0, 1]$ and $w \in A_2$,

$$\begin{aligned} \bigg \Vert \sup _{0<t<\infty } \Big |\phi _t *\Big (\sum _j \Phi _j *f_j \Big ) \Big |\bigg \Vert _{L^p(w)} \lesssim [w]_{A_2}^{\frac{9}{p}} \Vert N^*{\textbf {f}}\Vert _{L^p(w)}. \end{aligned}$$

Proof

Fix $w \in A_2$ and $\lambda >0$. It suffices to show

$$\begin{aligned} \mathcal {J}_{\lambda }&:= w \Big (\Big \{x \in \mathbb {R}^n: \sup \limits _{t>0} \Big |\phi _t * \Big (\sum _j \Phi _j *f_j \Big )(x) \Big | > \lambda \Big \} \Big ) \nonumber \\&\lesssim [w]_{A_2}^9 \bigg \{\lambda ^{-2} \int _{\mathbb {R}^n\backslash \Omega _{\lambda }}\sum _j |f_{j}(x)|^2 w(x) \, dx + w(\Omega _{\lambda }) \bigg \}, \end{aligned}$$

(5.56)

where the implicit constant is independent of $\lambda$, and $\Omega _{\lambda }:= \{N^* {\textbf {f}}>\lambda \}$ (cf. [85, p. 190]).

It follows from Whitney decomposition that one can find a pairwise disjoint family of cubes $\{Q_j\}$ such that $\Omega _{\lambda } = \bigcup _k Q_k$ and ${\text {dist}}(\mathbb {R}^n\backslash \Omega _{\lambda }, Q_k) \simeq \ell (Q_k)$. Then we choose a sequence of nonnegative functions $\{\varphi _k\}_k$ such that ${\textbf {1}}_{\Omega _{\lambda }} = \sum _k \varphi _k$, with the following properties

$$\begin{aligned} {\text {supp}}(\varphi _k) \subset \frac{6}{5} Q_k, \quad a_k:= \int _{\mathbb {R}^n} \varphi _k\, dx \simeq |Q_k|, \quad \Vert \partial ^{\alpha }\varphi _k \Vert _{L^{\infty }(\mathbb {R}^n)} \lesssim \ell (Q_k)^{-|\alpha |}. \end{aligned}$$

Setting

$$\begin{aligned} {\widetilde{f}}_j(x):= f_j(x) {\textbf {1}}_{\mathbb {R}^n\backslash \Omega _{\lambda }} + \sum _k b_{k, j} \, \varphi _k \quad \text { and }\quad b_{k, j}:= \frac{1}{a_k} \int _{\mathbb {R}^n} f_j(x) \varphi _k(x) \, dx, \end{aligned}$$

we see that for all $x \in \mathbb {R}^n$,

$$\begin{aligned} \sum _j |{\widetilde{f}}_j(x)|^2 \lesssim \sum _j |f_j(x)|^2 {\textbf {1}}_{\mathbb {R}^n\setminus \Omega _{\lambda }} + \sum _j |b_{k, j}(x)|^2 \lesssim \lambda ^2 + N^* {\textbf {f}}(x_j) \lesssim \lambda ^2, \end{aligned}$$

where $x_j \in C_0 Q_j \cap (\mathbb {R}^n{\setminus } \Omega _{\lambda }) \ne \emptyset$ for all j and for some $C_0>0$, which follows from the construction of Whitney decomposition of $\Omega$.

Writing

$$\begin{aligned} \mathcal {J}'_{\lambda }&:= w \Big (\Big \{x \in \mathbb {R}^n\setminus \Omega _{\lambda }: \sup \limits _{t>0} \Big |\phi _t * \Big (\sum _j \Phi _j *(f_j - {\widetilde{f}}_j) \Big )(x) \Big | > \lambda \Big \} \Big ), \end{aligned}$$

and observing that

$$\begin{aligned} \sup \limits _{t>0} \Big |\phi _t * \Big (\sum _j \Phi _j *(f_j - {\widetilde{f}}_j) \Big )(x) \Big | \lesssim \lambda \, \mathfrak {M}_1(x), \quad x \in \mathbb {R}^n\backslash \Omega _{\lambda }, \end{aligned}$$

where $\mathfrak {M}_1(x)$ is defined in (3.13), we invoke Lemma 3.6 to deduce

$$\begin{aligned} \mathcal {J}'_{\lambda } \lesssim \Vert \mathfrak {M}_1\Vert _{L^2(w)}^2 \lesssim [w]_{A_2}^2 w(\Omega _{\lambda }). \end{aligned}$$

(5.57)

By Chebyshev’s inequality and (2.1),

$$\begin{aligned} \mathcal {J}''_{\lambda }&:= w \Big (\Big \{x \in \mathbb {R}^n: \sup \limits _{t>0} \Big |\phi _t * \Big (\sum _j \Phi _j *{\widetilde{f}}_j \Big )(x) \Big |> \lambda \Big \} \Big ) \nonumber \\&\le \lambda ^{-2} \bigg \Vert \sup \limits _{t>0} \Big |\phi _t * \Big (\sum _j \Phi _j *{\widetilde{f}}_j \Big ) \Big | \bigg \Vert _{L^2(w)}^2 \lesssim \lambda ^{-2} \bigg \Vert M\Big (\sum _j \Phi _j *{\widetilde{f}}_j \Big ) \bigg \Vert _{L^2(w)}^2 \nonumber \\&\lesssim \lambda ^{-2} [w]_{A_2}^2 \bigg \Vert \sum _j \Phi _j *{\widetilde{f}}_j \bigg \Vert _{L^2(w)}^2 = \lambda ^{-2} [w]_{A_2}^2 \int _{\mathbb {R}^n} \Big |\sum _j \Phi _j *{\widetilde{f}}_j(x) \Big |^2 w(x) \, dx. \end{aligned}$$

(5.58)

To control the last term, we let T be the singular integral with $\mathscr {L}(\ell ^2(\mathbb {Z}),{\mathbb {C}})$-valued kernel $\Phi =\{\Phi _j\}_{j \in \mathbb {Z}}$ defined by $T({\textbf {g}}):= \sum _{j\in \mathbb {Z}} \Phi _j*g_j$ for good $\ell ^2$-valued functions ${\textbf {g}}=\{g_j\}_{j \in \mathbb {Z}}$. One can check that T is bounded from $L^2(\mathbb {R}^n,\ell ^2)$ to $L^2(\mathbb {R}^n, \ell ^2)$, $\Vert \Phi \Vert _{\mathscr {L}(\ell ^2(\mathbb {Z}),{\mathbb {C}})}\lesssim |x|^{-n}$, and $\Vert \nabla \Phi \Vert _{{\mathscr {L}}(\ell ^2(\mathbb {Z}),{\mathbb {C}})}\lesssim |x|^{-n-1}$ (cf. [88, p. 165]). Hence, this, Lemma 3.4, and (5.58) yield

$$\begin{aligned} \mathcal {J}''_{\lambda }&\lesssim \lambda ^{-2} [w]_{A_2}^9 \int _{\mathbb {R}^n} \sum _j |\widetilde{f_j}(x)|^2 w(x)dx \nonumber \\&\le \lambda ^{-2} [w]_{A_2}^9 \int _{\mathbb {R}^n\backslash \Omega _{\lambda }} \sum _j |f_j(x)| ^2 w(x) dx + [w]_{A_2}^9 w(\Omega _{\lambda }). \end{aligned}$$

(5.59)

As a consequence, (5.56) immediately follows from (5.57) and (5.59). $\square$

5.4 Weighted Jump Inequalities for Rough Operators

Let $\mathcal {F}:= \{F_t(x)\}_{t>0}$ be a family of Lebesgue measurable functions defined on $\mathbb {R}^n$. Given $\lambda >0$, we introduce the $\lambda$-jump function $N_\lambda ({\mathcal {F}})$ of ${\mathcal {F}}$, its value at x is the supremum over all N such that there exist $s_1<t_1\le s_2<t_2\le \dotsc \le s_N<t_N$ with

$$\begin{aligned} |F_{t_k}(x)-F_{s_k}(x)|>\lambda , \quad \forall k=1, \ldots , N. \end{aligned}$$

Given $\rho >0$, the value of the strong $\rho$-variation function $\mathcal {V}_\rho ({\mathcal {F}})$ at x is defined by

$$\begin{aligned} \mathcal {V}_\rho ({\mathcal {F}})(x):= \sup _{\{t_k\}_{k \ge 0}} \bigg ( |F_{t_0}(x)|^{\rho } + \sum _{k \ge 1} |F_{t_k}(x)-F_{t_{k-1}}(x)|^{\rho } \bigg )^{\frac{1}{\rho }}, \end{aligned}$$

where the supremum runs over all increasing sequences $\{t_k\}_{k \ge 0}$.

Given $\Omega \in L^1(\mathbb {S}^{n-1})$ and $\varepsilon >0$, the truncated singular integral operator $T_{\varepsilon }$ is defined by

$$\begin{aligned} T_{\Omega , \varepsilon } f(x):= \int _{|y| \ge \varepsilon }\frac{\Omega (y')}{|y|^n}f(x-y)dy. \end{aligned}$$

The principal value singular integral and its maximal version are defined by

$$\begin{aligned} T_{\Omega } f(x):= \lim _{\varepsilon \rightarrow 0^+} T_{\Omega , \varepsilon } f(x) \quad \text { and }\quad T_{\Omega , \#} f(x):= \sup _{\varepsilon >0} |T_{\Omega , \varepsilon } f(x)|, \quad x \in \mathbb {R}^n. \end{aligned}$$

In this sequel, we write $\mathcal {T}:= \{T_{\Omega , \varepsilon }\}_{\varepsilon >0}$.

Theorem 5.13

Let $\rho >2$ and $\Omega \in L^q(\mathbb {S}^{n-1})$ with $q \in (1, \infty )$ be such that $\int _{\mathbb {S}^{n-1}} \Omega \, d\sigma =0$. Then for all $p \in (q', \infty )$ and for all $w \in A_{p/q'}$,

$$\begin{aligned} \Vert \mathbb {T}f\Vert _{L^p(w)} \lesssim [w]_{A_{p/q'}}^{7\max \{1, \frac{2}{p/q'-1}\}} \Vert f\Vert _{L^p(w)}, \end{aligned}$$

(5.60)

where $\mathbb {T} \in \big \{\sup \limits _{\lambda >0} \lambda \sqrt{N_{\lambda } \circ \mathcal {T}}, \mathcal {V}_{\rho } \circ \mathcal {T}, T_{\Omega , \#}\big \}$.

It suffices to show (5.60) for $\mathbb {T}=\sup \limits _{\lambda >0} \lambda \sqrt{N_{\lambda } \circ \mathcal {T}}$, which immediately implies (5.60) for $\mathbb {T} \in \{\mathcal {V}_{\rho } \circ \mathcal {T}, T_{\Omega , \#}\}$ since the following pointwise domination holds

$$\begin{aligned} T_{\Omega , \#} f(x) \le \mathcal {V}_{\rho }(\mathcal {T} f)(x) \le \sup _{\lambda >0} \lambda \sqrt{N_\lambda (\mathcal {T} f)(x)}, \qquad x \in \mathbb {R}^n, \end{aligned}$$

provided that $\ell ^{2,\infty }(\mathbb {N})$ embeds into $\ell ^\rho (\mathbb {N})$ for all $\rho >2$.

Let us turn to the proof of (5.60) for $\mathbb {T}=\sup \limits _{\lambda >0} \lambda \sqrt{N_{\lambda } \circ \mathcal {T}}$. It was proved in [57, Lemma 1.3] that

$$\begin{aligned} \lambda \sqrt{N_\lambda (\mathcal Tf)(x)} \lesssim S_2(\mathcal Tf)(x)+\lambda \sqrt{N_{\lambda /3}(\{T_{\Omega , 2^k}f\})(x)}, \quad x \in \mathbb {R}^n, \end{aligned}$$

where

$$\begin{aligned} S_2(\mathcal Tf)(x)&:= \bigg (\sum _{j\in {\mathbb {Z}}} V_{2, j}(\mathcal Tf)(x)^2\bigg )^{\frac{1}{2}},\\ V_{2,j}(\mathcal Tf)(x)&:= \left( \sup _{\begin{array}{c} t_1<\cdots <t_N \\ {[}t_l,t_{l+1}]\subset [2^j,2^{j+1}] \end{array}} \sum _{l=1}^{N-1}|T_{\Omega , t_{l+1}}f(x)-T_{\Omega , t_l}f(x)|^2\right) ^{\frac{1}{2}}. \end{aligned}$$

Thus, we are reduced to proving

$$\begin{aligned} \Big \Vert \sup _{\lambda >0}\lambda \sqrt{N_\lambda (\{T_{\Omega , 2^k}f\})} \Big \Vert _{L^p(w)}&\lesssim {[}w]_{A_{p/q'}}^{7\max \{1, \frac{2}{p/q'-1}\}} \Vert f\Vert _{L^p(w)}, \end{aligned}$$

(5.61)

$$\begin{aligned} \Vert S_2(\mathcal Tf)\Vert _{L^p(w)}&\lesssim {[}w]_{A_{p/q'}}^{4\max \{1, \frac{2}{p/q'-1}\}} \Vert f\Vert _{L^p(w)}. \end{aligned}$$

(5.62)

5.4.1 Dyadic Jump Estimates

We are going to show (5.61) in this subsection. Let $\phi \in \mathcal {S}(\mathbb {R}^n)$ be a radial function such that ${\widehat{\phi }}(\xi )=1$ for $|\xi | \le 2$ and ${\widehat{\phi }}(\xi )=0$ for $|\xi |>4$. Define ${\widehat{\phi }}_k(\xi ) = {\widehat{\phi }}(2^k\xi )$ for each $k \in \mathbb {Z}$. For each $j \in \mathbb {Z}$, set $\nu _j(x):= \frac{\Omega (x)}{|x|^n} {\textbf {1}}_{\{2^j\le |x|<2^{j+1}\}}(x)$. Then for any $k \in \mathbb {Z}$,

$$\begin{aligned} T_{\Omega , 2^k} f(x)&= \int _{|x-y| \ge 2^k} \frac{\Omega (x-y)}{|x-y|^n}f(y) \, dy =\sum _{j \ge k} \nu _j *f(x)\\&=\phi _k *T_{\Omega } f + \sum _{s \ge 0}(\delta _0 - \phi _k) *\nu _{k+s} *f - \phi _k *\sum _{s<0} \nu _{k+s}*f\\&=: T^1_k f + T^2_k f - T_k^3 f, \end{aligned}$$

where $\delta _0$ is the Dirac measure at 0. Let ${\mathscr {T}}^if$ denote the family $\{T^i_{k}f\}_{k \in \mathbb {Z}}$, $i=1, 2, 3$. Hence, to get (5.61) it suffices to prove the following:

$$\begin{aligned} \Big \Vert \sup _{\lambda >0}\lambda \sqrt{N_{\lambda }({\mathscr {T}}^if)} \Big \Vert _{L^p(w)} \lesssim [w]_{A_{p/q'}}^{7\max \{1, \frac{2}{p/q'-1}\}} \Vert f\Vert _{L^p(w)}, \quad i=1,2,3. \end{aligned}$$

(5.63)

We begin with showing (5.63) for $i=1$. Define

$$\begin{aligned} \mathbb {D}_j f:= \mathbb {E}_j f - \mathbb {E}_{j-1} f, \quad \mathscr {E}f:=\{\mathbb {E}_j f\}_{j \in \mathbb {Z}}, \quad \text { where }\quad \mathbb {E}_j f:= \sum _{Q \in \mathcal {D}_j} \langle f \rangle _Q {\textbf {1}}_Q, \end{aligned}$$

where $\mathcal {D}_j$ is the family of dyadic cubes with sidelength $2^j$.

Lemma 5.14

For any $p \in (1, \infty )$ and $w \in A_p$,

$$\begin{aligned} \Vert \mathbb {T}f\Vert _{L^p(w)} \lesssim [w]_{A_p}^{\max \{1, \frac{1}{p-1}\}} \Vert f\Vert _{L^p(w)}, \end{aligned}$$

(5.64)

where $\mathbb {T}f \in \big \{\big (\sum _{j \in \mathbb {Z}} |\mathbb {D}_j f|^2 \big )^{\frac{1}{2}},\, \sup _{\lambda >0} \lambda \sqrt{N_{\lambda }(\mathscr {E}f)}\big \}$.

Proof

For $p=2$, the estimate (5.64) for dyadic operators is contained in [62], which established a sharp weighted inequality for the Haar shift operators. The general case is a consequence of the case $p=2$ and Theorem 4.1. Then (5.64) for jump operators follows at once from (5.64) for $\mathbb {T}f =\big (\sum _{j \in \mathbb {Z}} |\mathbb {D}_j f|^2 \big )^{\frac{1}{2}}$ and the proof of [59, Proposition 4.1]. $\square$

Define the square function as follows:

$$\begin{aligned} \mathfrak {S} f:= \bigg (\sum _{k \in \mathbb {Z}} |\phi _k*f - \mathbb {E}_k f|^2 \bigg )^{\frac{1}{2}}. \end{aligned}$$

(5.65)

Lemma 5.15

For any $w \in A_1$,

$$\begin{aligned} \Vert \mathfrak {S}\Vert _{L^2(w) \rightarrow L^2(w)} \lesssim [w]_{A_1}^2 \quad \text { and }\quad \Vert \mathfrak {S}\Vert _{L^1(w) \rightarrow L^{1, \infty }(w)} \lesssim [w]_{A_1}^5, \end{aligned}$$

(5.66)

where the implicit constant is independent of $[w]_{A_1}$.

Proof

We claim that for all $k, j \in \mathbb {Z}$,

$$\begin{aligned} \Vert \mathcal {I}_{k, j}\Vert _{L^2(w)} := \Vert \phi _{k+j}*\mathbb {D}_j f - \mathbb {E}_{k+j} \mathbb {D}_j f\Vert _{L^2(w)} \lesssim 2^{-\theta |k|} [w]_{A_1} \Vert \mathbb {D}_j f\Vert _{L^2(w)}, \end{aligned}$$

(5.67)

for some $\theta >0$, where the implicit constant and $\theta$ are independent of k and j. To show (5.67), we first note that by [57, p. 6722], for any $k \ge 0$,

$$\begin{aligned} \mathbb {E}_{k+j} \mathbb {D}_j f=0 \quad \text { and }\quad |\phi _{k+j} *\mathbb {D}_j f| \lesssim 2^{-k} M(\mathbb {D}_j f), \end{aligned}$$

which along with (2.1) gives

$$\begin{aligned} \Vert \mathcal {I}_{k, j}\Vert _{L^2(w)} \lesssim 2^{-k} \Vert M(\mathbb {D}_j f)\Vert _{L^2(w)} \lesssim 2^{-k} [w]_{A_2} \Vert \mathbb {D}_j f\Vert _{L^2(w)} \le 2^{-k} [w]_{A_1} \Vert \mathbb {D}_j f\Vert _{L^2(w)}. \end{aligned}$$

To control the case $k<0$, we use the argument in [25, p. 2461–2463] and that

$$\begin{aligned} w(\lambda Q) \le \lambda ^n [w]_{A_1} w(Q), \quad \text { for any cube } Q, \end{aligned}$$

to see $\mathcal {I}_{k, j}(x) = \sum _{d \ge 0} I_d(x)$, where for some $\delta >0$,

$$\begin{aligned} \Vert I_d\Vert _{L^2(w)}&\lesssim 2^{-\delta |k|n/4} [w]_{A_1}^{\frac{1}{2}} \Vert \mathbb {D}_j f\Vert _{L^2(w)}, \quad d \le |k|/2,\\ \Vert I_d\Vert _{L^2(w)}&\lesssim 2^{-d} [w]_{A_1}^{\frac{1}{2}} \Vert \mathbb {D}_j f\Vert _{L^2(w)}, \quad d \ge |k|/2, \end{aligned}$$

Then summing these estimates up, we obtain (5.67) as desired.

Having shown (5.67), we use $f(x) = \sum _{j \in \mathbb {Z}} \mathbb {D}_j f(x)$, a.e. $x \in \mathbb {R}^n$, to deduce that

$$\begin{aligned} \Vert \mathfrak {S}f\Vert _{L^2(w)}&= \bigg \Vert \bigg (\sum _{k \in \mathbb {Z}} \Big | \sum _{j \in \mathbb {Z}} \big (\phi _k* \mathbb {D}_j f - \mathbb {E}_k \mathbb {D}_j f \big ) \Big |^2 \bigg )^{\frac{1}{2}}\bigg \Vert _{L^2(w)}\\&\le \bigg (\sum _{k \in \mathbb {Z}} \Big (\sum _{j \in \mathbb {Z}} \Vert \phi _k* \mathbb {D}_j f - \mathbb {E}_k \mathbb {D}_j f\Vert _{L^2(w)} \Big )^2 \bigg )^{\frac{1}{2}}\\&\lesssim [w]_{A_1} \bigg (\sum _{k \in \mathbb {Z}} \Big (\sum _{j \in \mathbb {Z}} 2^{-\theta |k-j|} \Vert \mathbb {D}_j f\Vert _{L^2(w)} \Big )^2 \bigg )^{\frac{1}{2}}\\&\lesssim [w]_{A_1} \bigg [\sum _{k \in \mathbb {Z}} \Big (\sum _{j \in \mathbb {Z}} 2^{- \theta |k-j|} \Big ) \Big (\sum _{j \in \mathbb {Z}} 2^{- \theta |k-j|} \Vert \mathbb {D}_j f\Vert _{L^2(w)}^2 \Big ) \bigg ]^{\frac{1}{2}}\\&\lesssim [w]_{A_1} \bigg [\sum _{j \in \mathbb {Z}} \Big (\sum _{k \in \mathbb {Z}} 2^{- \theta |k-j|} \Big ) \Vert \mathbb {D}_j f\Vert _{L^2(w)}^2 \bigg ]^{\frac{1}{2}}\\&\simeq [w]_{A_1} \bigg \Vert \Big (\sum _{j \in \mathbb {Z}} |\mathbb {D}_j f|^2 \Big )^{\frac{1}{2}} \bigg \Vert _{L^2(w)} \lesssim [w]_{A_1}^2 \Vert f\Vert _{L^2(w)}, \end{aligned}$$

where we have used Minkowski’s inequality, (5.67), Cauchy–Schwarz inequality, and (5.64). This shows the first estimate in (5.66). Then, using the first inequality in (5.66) and Calderón–Zygmund decomposition as in [25, p. 2458–2460], we obtain the second estimate in (5.66). The proof is complete. $\square$

Lemma 5.16

Let $\mathscr {U}$ be a family of operators given by $\mathscr {U}f:=\{\phi _k * f\}_{k \in \mathbb {Z}}$. Then for all $p \in (1, \infty )$ and for all $w \in A_p$,

$$\begin{aligned} \Big \Vert \sup _{\lambda >0} \lambda \sqrt{N_{\lambda }(\mathscr {U}f)} \Big \Vert _{L^p(w)}&\lesssim [w]_{A_p}^{\max \{5, \frac{1}{p-1}\}} \Vert f\Vert _{L^p(w)}. \end{aligned}$$

Proof

Since $N_{\lambda }$ is subadditive,

$$\begin{aligned} N_{\lambda }(\mathscr {U}f) \le N_{\lambda }(\mathscr {D}f) + N_{\lambda }(\mathscr {E}f), \end{aligned}$$

(5.68)

where $\mathscr {D}f:=\{\phi _k * f - \mathbb {E}_k f\}_{k \in \mathbb {Z}}$ and $\mathscr {E}f:=\{\mathbb {E}_k f\}_{k \in \mathbb {Z}}$. Recall the square function in (5.65) and observe that $\sup _{\lambda >0} \lambda \sqrt{N_{\lambda }(\mathscr {D}f)} \le \mathfrak {S} f$, which together with (5.66) and Theorem 4.4 applied to $p_0=1$ implies

$$\begin{aligned} \Big \Vert \sup _{\lambda >0} \lambda \sqrt{N_{\lambda }(\mathscr {D}f)} \Big \Vert _{L^p(w)} \lesssim [w]_{A_p}^5 \Vert f\Vert _{L^p(w)}. \end{aligned}$$

In view of (5.64) and (5.68), this gives at once the desired estimate. $\square$

Now using Lemma 5.16 and (3.17), we obtain

$$\begin{aligned}&\Big \Vert \sup _{\lambda>0} \lambda \sqrt{N_{\lambda }(\mathscr {T}^1 f)} \Big \Vert _{L^p(w)} = \Big \Vert \sup _{\lambda >0} \lambda \sqrt{N_{\lambda }(\{\phi _k*(T_{\Omega }f)\}}) \Big \Vert _{L^p(w)}\\&\quad \lesssim [w]_{A_p}^{\max \{5, \frac{1}{p-1}\}} \Vert T_{\Omega }f\Vert _{L^p(w)} \lesssim [w]_{A_{p/q'}}^{7 \max \{1, \frac{1}{p/q'-1}\}} \Vert f\Vert _{L^p(w)}, \end{aligned}$$

which shows (5.63) for $i=1$.

For the term with $\mathscr {T}^2$, it was shown in [25, p. 2453] that

$$\begin{aligned} \sup _{\lambda >0} \lambda \sqrt{N_\lambda ({\mathscr {T}}^{2}f)} \le \sum _{s \ge 0} \Big (\sum _{k\in \mathbb {Z}} \big |(\delta _0 - \phi _k) *\nu _{k+s} *f\big |^2\Big )^{\frac{1}{2}} =: \sum _{s \ge 0} G_s f, \end{aligned}$$

(5.69)

where

$$\begin{aligned} G_s f \le \sum _{l \in \mathbb {Z}}\bigg (\sum _{k\in \mathbb {Z}} |(\delta _0-\phi _k) *\nu _{s+k} *\Delta _{l-k}^2 f|^2\bigg )^{\frac{1}{2}} =: \sum _{l\in \mathbb {Z}} G_s^l f, \end{aligned}$$

with

$$\begin{aligned} \Vert G_s^l f\Vert _{L^2(\mathbb {R}^n)} \lesssim 2^{ -\gamma _0 s} \min \{2^l, 2^{-\gamma _0 l}\}\Vert f\Vert _{L^2(\mathbb {R}^n)}. \end{aligned}$$

(5.70)

It follows from Lemmas 3.5 and 3.9 that for any $v \in A_{p/q'}$,

$$\begin{aligned} \Vert G_s^l f\Vert _{L^p(v)}&\lesssim [v]_{A_p}^{\frac{1}{2} \max \{1, \frac{2}{p-1}\}} \bigg \Vert \Big (\sum _{k \in \mathbb {Z}} |\nu _{s+k} *\Delta _{l-k}^2 f|^2\Big )^{\frac{1}{2}}\bigg \Vert _{L^p(v)} \nonumber \\&\lesssim [v]_{A_p}^{\frac{1}{2} \max \{1, \frac{2}{p-1}\} + \frac{5}{2}\max \{1, \frac{2}{p/q'-1}\}} \Vert f\Vert _{L^p(v)} \lesssim [v]_{A_p}^{3\max \{1, \frac{2}{p/q'-1}\}} \Vert f\Vert _{L^p(v)}. \end{aligned}$$

(5.71)

Then interpolating between (5.70) and (5.71) with $v \equiv 1$ gives

$$\begin{aligned} \Vert G_s^l f\Vert _{L^p(\mathbb {R}^n)} \lesssim 2^{ -\alpha s} 2^{-\beta |l|} \Vert f\Vert _{L^p(\mathbb {R}^n)}, \quad \text {for some } \alpha , \beta >0. \end{aligned}$$

(5.72)

On the other hand, for $w \in A_{p/q'}$, by Lemma 2.4, there exists $\gamma =\gamma _w \in (0, 1)$ such that

$$\begin{aligned} (1+\gamma )' = c_n [w]_{A_{p/q'}}^{\max \{1, \frac{1}{p/q'-1}\}} =: c_n B_0, \quad \text {and}\quad [w^{1+\gamma }]_{A_p} \le [w^{1+\gamma }]_{A_{p/q'}} \lesssim [w]_{A_{p/q'}}^{1+\gamma }, \end{aligned}$$

which along with (5.71) implies

$$\begin{aligned} \Vert G_s^l f\Vert _{L^p(w^{1+\gamma })} \lesssim [w]_{A_{p/q'}}^{3(1+\gamma )\max \{1, \frac{2}{p/q'-1}\}} \Vert f\Vert _{L^p(w^{1+\gamma })}. \end{aligned}$$

(5.73)

Considering Theorem 3.1 with $w_0 \equiv 1$, $w_1=w^{1+\gamma }$, and $\theta =\frac{1}{1+\gamma }$, we interpolate between (5.72) and (5.73) to arrive at

$$\begin{aligned} \Vert G_s^l f\Vert _{L^p(w)} \lesssim 2^{ -\alpha s(1-\theta )} 2^{-\beta |l| (1-\theta )} [w]_{A_{p/q'}}^{3\max \{1, \frac{2}{p/q'-1}\}} \Vert f\Vert _{L^p(w)}. \end{aligned}$$

(5.74)

Note that $e^{-t}<2t^{-2}$ for any $t>0$, and

$$\begin{aligned} \sum _{s \ge 0} 2^{-\alpha s(1-\theta )} =\sum _{0 \le s \le B_0} 2^{-\frac{\alpha s}{c_n B_0}} + \sum _{s> B_0} 2^{-\frac{\alpha s}{c_n B_0}} \lesssim B_0 + \sum _{s>B_0} s^{-2} B_0^2 \lesssim B_0. \end{aligned}$$

(5.75)

Similarly,

$$\begin{aligned} \sum _{l \in \mathbb {Z}} 2^{-\beta |l| (1-\theta )} \lesssim B_0. \end{aligned}$$

(5.76)

Hence, (5.69) and (5.74)–(5.76) imply

$$\begin{aligned} \Big \Vert \sup _{\lambda >0} \lambda \sqrt{N_{\lambda }(\mathscr {T}^2 f)} \Big \Vert _{L^p(w)} \lesssim [w]_{A_{p/q'}}^{4 \max \{1, \frac{2}{p/q'-1}\}} \Vert f\Vert _{L^p(w)}. \end{aligned}$$

This shows (5.63) for $i=2$.

To control the term with $\mathscr {T}^3$, we note that by [25, p. 2456],

$$\begin{aligned} \sup _{\lambda >0} \lambda \sqrt{N_\lambda ({\mathscr {T}}^3f)} \le \sum _{s<0} \Big (\sum _{k\in \mathbb {Z}}\big | \phi _k*\nu _{k+s} *f\big |^2 \Big )^{\frac{1}{2}} =: \sum _{s<0}H_{s}f, \end{aligned}$$

where

$$\begin{aligned} \Vert H_s f\Vert _{L^p(w)} \le \sum _{l \in \mathbb {Z}} \bigg \Vert \Big (\sum _{k\in \mathbb {Z}} |\phi _k *\nu _{k+s} *\Delta _{l-k}^2 f|^2 \Big )^{\frac{1}{2}}\bigg \Vert _{L^p(w)} =: \sum _{l \in \mathbb {Z}} \Vert H_s^l f\Vert _{L^p(w)}, \end{aligned}$$

with

$$\begin{aligned} \Vert H_s^l f\Vert _{L^2(\mathbb {R}^n)} \lesssim 2^s \min \{2^l, 2^{-\gamma l}\} \Vert f\Vert _{L^2(\mathbb {R}^n)}. \end{aligned}$$

Analogously to (5.74), one has

$$\begin{aligned} \Vert H_s^l f\Vert _{L^p(w)} \lesssim 2^{ -\alpha s(1-\theta )} 2^{-\beta |l| (1-\theta )} [w]_{A_{p/q'}}^{3\max \{1, \frac{2}{p/q'-1}\}} \Vert f\Vert _{L^p(w)}, \end{aligned}$$

and eventually,

$$\begin{aligned} \Big \Vert \sup _{\lambda >0} \lambda \sqrt{N_{\lambda }(\mathscr {T}^3 f)} \Big \Vert _{L^p(w)} \lesssim [w]_{A_{p/q'}}^{4 \max \{1, \frac{2}{p/q'-1}\}} \Vert f\Vert _{L^p(w)}. \end{aligned}$$

This shows (5.63) for $i=3$.

5.4.2 Short Variation Estimates

We will prove (5.62) in this subsection. As did in [25],

$$\begin{aligned}&S_2(\mathcal {T} f) (x) \le \sum _{k \in \mathbb {Z}} S_{2, k}(\mathcal {T} f) (x), \end{aligned}$$

(5.77)

$$\begin{aligned}&\Vert S_{2, k}(\mathcal {T} f)\Vert _{L^p(\mathbb {R}^n)} \lesssim 2^{-\delta |k|} \Vert f\Vert _{L^p(\mathbb {R}^n)}, \quad \forall k \in \mathbb {Z}, \end{aligned}$$

(5.78)

$$\begin{aligned}&S_{2, k}(\mathcal {T} f) (x) \lesssim \bigg (\sum _{j \in \mathbb {Z}} |M_{\Omega }(\Delta _{k-j}^2 f)(x)| \bigg )^{\frac{1}{2}}, \quad \forall k \in \mathbb {Z}, \end{aligned}$$

(5.79)

and for $q<2$,

$$\begin{aligned} \big \Vert S_{2,k}(\mathcal {T}f)\big \Vert _{L^p(w)} \le \Vert I_{1, k}f\Vert _{L^p(w)}^{\frac{1}{2}} \Vert I_{2,k}f\Vert _{L^p(w)}^{\frac{1}{2}}, \end{aligned}$$

(5.80)

where

$$\begin{aligned} \Vert I_{1,k} f\Vert _{L^p(w)}&\le \bigg (\int _1^2 \bigg \Vert \Big (\sum _{j \in \mathbb {Z}} |\nu _{j, t} * \Delta _{k-j}^2 f|^2 \Big )^{\frac{1}{2}}\bigg \Vert _{L^p(w)}^2 \frac{dt}{t} \bigg )^{\frac{1}{2}},\\ \Vert I_{2, k} f\Vert _{L^p(w)}&\lesssim \bigg (\int _{\mathbb {R}^n} M_{\Omega ^{2-q}}(g w)(x) \sum _{j \in \mathbb {Z}} |\Delta _{k-j}^2 f(x)|^2 \, dx \bigg )^{\frac{1}{2}}, \end{aligned}$$

where $\nu _{j, t}(x):= \frac{\Omega (x)}{|x|^n} {\textbf {1}}_{\{2^j t \le |x| \le 2^{j+1}\}}(x)$.

We claim that

$$\begin{aligned} \big \Vert S_{2,k}(\mathcal {T}f)\big \Vert _{L^p(w)} \lesssim [w]_{A_{p/q'}}^{3 \max \{1, \frac{2}{p/q'-1}\}} \Vert f\Vert _{L^p(w)}. \end{aligned}$$

(5.81)

Once (5.81) is obtained, we use (5.77), (5.78), and Stein-Weiss’s interpolation Theorem 3.1 as before to get

$$\begin{aligned} \big \Vert S_2(\mathcal {T}f)\big \Vert _{L^p(w)} \lesssim [w]_{A_{p/q'}}^{4 \max \{1, \frac{2}{p/q'-1}\}} \Vert f\Vert _{L^p(w)}, \end{aligned}$$

which shows (5.62) as desired.

It remains to demonstrate (5.81). If $q>2$, we invoke (5.79), (3.18), (3.10), and (3.8) to deduce

$$\begin{aligned} \big \Vert S_{2,k}(\mathcal {T}f)\big \Vert _{L^p(w)}&\lesssim [w]_{A_{p/q'}}^{\frac{1}{p-q'}} \bigg \Vert \Big (\sum _{j \in \mathbb {Z}} |\Delta _{k-j}^2 f|^2 \Big )^{\frac{1}{2}}\bigg \Vert _{L^p(w)}\\&\lesssim [w]_{A_{p/q'}}^{\frac{1}{p-q'}+\frac{1}{2}\max \{1, \frac{2}{p-1}\}} \bigg \Vert \Big (\sum _{j \in \mathbb {Z}} |\Delta _{k-j} f|^2 \Big )^{\frac{1}{2}}\bigg \Vert _{L^p(w)}\\&\lesssim [w]_{A_{p/q'}}^{\frac{1}{p-q'}+\max \{1, \frac{2}{p-1}\}} \Vert f\Vert _{L^p(w)} \lesssim [w]_{A_{p/q'}}^{\frac{3}{2}\max \{1, \frac{2}{p-q'}\}} \Vert f\Vert _{L^p(w)}. \end{aligned}$$

To treat the case $q<2$ (trivially, $p>2$), we observe that much as (3.37),

$$\begin{aligned} \Vert I_{1, k} f\Vert _{L^p(w)} \lesssim [w]_{A_{p/q'}}^{\frac{7}{2}\max \{1, \frac{2}{p/q'-1}\}} \Vert f\Vert _{L^p(w)}, \end{aligned}$$

(5.82)

and

$$\begin{aligned} \Omega ^{2-q} \in L^{\frac{q}{2-q}}(\mathbb {S}^{n-1}), \quad \big (w^{1-(p/2)'}\big )^{1-p/2} = w \in A_{p/q'} = A_{(p/2)/(\frac{q}{2-q})'}. \end{aligned}$$

The latter, along with by Hölder’s inequality, Theorem 3.8 applied to $(p/2)'$ and $\frac{q}{2-q}$ instead of p and q, (3.10), and (3.8), gives

$$\begin{aligned} \Vert I_{2, k} f\Vert _{L^p(w)}&\lesssim \big \Vert M_{\Omega ^{2-q}}(g w)\Vert _{L^{(p/2)'}(w^{1-(p/2)'})}^{\frac{1}{2}} \bigg \Vert \Big (\sum _{j \in \mathbb {Z}} |\Delta _{k-j}^2 f|^2\Big )^{\frac{1}{2}}\bigg \Vert _{L^p(w)} \nonumber \\&\lesssim [w]_{A_{p/q'}}^{\max \{1, \frac{1}{p/q'-1}\} + \frac{1}{2}\max \{1, \frac{2}{p-1}\}} \bigg \Vert \Big (\sum _{j \in \mathbb {Z}} |\Delta _{k-j} f|^2 \Big )^{\frac{1}{2}}\bigg \Vert _{L^p(w)} \nonumber \\&\lesssim [w]_{A_{p/q'}}^{\max \{1, \frac{1}{p/q'-1}\} + \max \{1, \frac{2}{p-1}\}} \Vert f\Vert _{L^p(w)} \lesssim [w]_{A_{p/q'}}^{2 \max \{1, \frac{2}{p/q'-1}\}} \Vert f\Vert _{L^p(w)}. \end{aligned}$$

(5.83)

Therefore, in the case $q<2$, (5.81) follows from (5.80), (5.82), and (5.83). $\square$

5.5 Riesz Transforms Associated to Schrödinger Operators

Consider a real vector potential $\textbf{a}=(a_1,\ldots , a_n)$ and an electric potential V. Assume that

$$\begin{aligned} 0 \le V \in L^1_{{\text {loc}}}(\mathbb {R}^n) \quad \text {and}\quad a_k \in L^2_{{\text {loc}}}(\mathbb {R}^n), \quad \, k=1, \ldots , n. \end{aligned}$$

(5.84)

Denote

$$\begin{aligned} L_0=V^{1/2} \quad \text {and} \quad L_k=\partial _k - i a_k, \quad k=1, \ldots , n. \end{aligned}$$

We define the form Q by

$$\begin{aligned} Q(f, g)=\sum _{k=1}^n \int L_k f(x) \overline{L_k g(x)} \, dx + \int _{\mathbb {R}^n} Vf(x) \overline{g(x)} \, dx \end{aligned}$$

with domain

$$\begin{aligned} \mathcal {D}(Q) := \{f \in L^2(\mathbb {R}^n): L_k f \in L^2(\mathbb {R}^n), \, k=0, 1, \ldots , n \}. \end{aligned}$$

Let us denote by A the self-adjoint operator associated with Q. Then A is given by the expression

$$\begin{aligned} A f = \sum _{k=1}^n L_k^{*} L_k f + V f, \end{aligned}$$

and the domain of A is given by

$$\begin{aligned} \mathcal {D}(A) =\Big \{f \in \mathcal {D}(Q), \exists g \in L^2(\mathbb {R}^n) \text{ such } \text{ that } Q(f, \varphi )=\int _{\mathbb {R}^n} g {\overline{\varphi }} \, dx, \forall \varphi \in \mathcal {D}(Q) \Big \}. \end{aligned}$$

Formally, we write

$$\begin{aligned} A = - (\nabla -i \textbf{a}) \cdot (\nabla - i \textbf{a})+V. \end{aligned}$$

For convenience, denote

$$\begin{aligned} \mathcal {R}_k:= L_k A^{-1/2},\quad k = 0, 1, \ldots , n. \end{aligned}$$

Duong et al. [41, 42] consecutively established the $L^p$ boundedness of Riesz transform $\mathcal {R}_k$ and its commutator $[\mathcal {R}_k, b]$, $k=0, 1, \ldots , n$. More specifically, under the assumption (5.84), we have for any $1<p<2$

$$\begin{aligned} \mathcal {R}_k, [\mathcal {R}_k, b]: L^p(\mathbb {R}^n) \rightarrow L^p(\mathbb {R}^n),\quad k=0, 1, \ldots , n, \end{aligned}$$

(5.85)

provided by $b \in {\text {BMO}}$.

We would like to establish weighted version of (5.85) as follows.

Theorem 5.17

Assume that $\textbf{a}$ and V satisfy (5.84). Let $b \in {\text {BMO}}$. Then for every $p \in (1, 2)$, for every weight $w^p \in A_p \cap RH_{(2/p)'}$, and for every $k=0, 1, \ldots , n$, both $\mathcal {R}_k$ and $[\mathcal {R}_k, b]$ are bounded on $L^p(w^p)$.

A particular case is the operator $\mathscr {L}_V = -\Delta +V$, where $V \in L^1_{{\text {loc}}}(\mathbb {R}^n)$ is a non-negative function. The $L^2(\mathbb {R}^n)$ boundedness of $\mathcal {R}_V:= \nabla \mathscr {L}_V^{-1/2}$ was given in [78, Theorem 8.1], while it was proved in [41] that $\mathcal {R}_V$ is bounded from $H_L^1(\mathbb {R}^n)$ to $L^1(\mathbb {R}^n)$. Then the interpolation implies

$$\begin{aligned} \mathcal {R}_V \text { is bounded on } L^p(\mathbb {R}^n), \quad \forall p \in (1, 2]. \end{aligned}$$

(5.86)

However, (5.86) fails for general potentials $V \in L^1_{{\text {loc}}}(\mathbb {R}^n)$ when $p>2$, see [86]. Now Theorem 5.17 immediately implies the following weighted inequalities.

Theorem 5.18

Let $\mathscr {L}_V=-\Delta +V$ with $0 \le V \in L^1_{{\text {loc}}}(\mathbb {R}^n)$, and set $\mathcal {R}_V:= \nabla \mathscr {L}_V^{-1/2}$. Then for any $p \in (1, 2)$, for any $w^p \in A_p \cap RH_{(2/p)'}$, and for any $b \in {\text {BMO}}$, both $\mathcal {R}_V$ and $[\mathcal {R}_V, b]$ are bounded on $L^p(w^p)$.

The rest of this subsection is devoted to showing Theorem 5.17. For this purpose, we present two useful lemmas below.

Lemma 5.19

[3] Fix $1<q \le \infty$, $a \ge 1$ and $w \in RH_{s'}$, $1 \le s<\infty$. Assume that F, G, $H_1$ and $H_2$ are non-negative measurable functions on $\mathbb {R}^n$ such that for each ball B there exist non-negative functions $G_B$ and $H_B$ with $F(x) \le G_B(x) + H_B(x)$ for a.e. $x \in B$ and for all $x, {\bar{x}} \in B$,

(5.87)

Then for all $p \in (0, q/s)$,

$$\begin{aligned} \Vert M F\Vert _{L^p(w)} \le C \, \big (\Vert G\Vert _{L^{p}(w)}+\Vert H_1\Vert _{L^p(w)}+\Vert H_2\Vert _{L^p(w)}\big ), \end{aligned}$$

(5.88)

where the constant C depends only on n, a, p, q, and $[w]_{RH_{s'}}$.

To proceed, we introduce some notation. Given a ball B we set $C_j(B):= 4B$ for $j=1$ and $C_j(B):= 2^{j+1}B {\setminus } 2^jB$ for $j \ge 2$, and

Lemma 5.20

Let $1\le q \le 2$ and B be a given ball and $f \in L^q(\mathbb {R}^n)$ with ${\text {supp}}(f) \subseteq B$. Let $\mathcal {A}_{r_B}=I-(I-e^{-r_B^2 A})^m$ with a given integer $m \ge 1$. Then for all $j \ge 1$ and $k=0, 1, \ldots , n$,

(5.89)

and

(5.90)

where the implicit constants are independent of B, f, j and k.

Proof

We begin with showing (5.89). It follows from (3.1) and (3.2) in [42] that the kernel $p_t(x,y)$ of $e^{-tA}$ satisfies

$$\begin{aligned} |p_t(x, y)|&\le (4 \pi t)^{-\frac{n}{2}} \exp \bigg (-\frac{|x-y|^{2}}{4 t}\bigg ), \quad \forall t>0 \text { and a.e.}\ x,y \in \mathbb {R}^n,\\ |\partial _t^k p_t(x, y)|&\le C_k t^{-(n/2+k)} \exp \bigg (-\frac{|x-y|^{2}}{c_k t}\bigg ), \quad \forall t>0 \text { and a.e. } x, y \in \mathbb {R}^n. \end{aligned}$$

Thus for all $x \in C_j(B)$ and $j \ge 2$, we have $|x-y| \simeq 2^j r_B$ for any $y \in B$ and

(5.91)

The above inequality also holds for $j=1$. The desired estimate (5.89) immediately follows from (5.91) and the expansion

$$\begin{aligned} \mathcal {A}_{r_B}=I - (I-e^{-r^2_B A})^m =\sum _{k=1}^m (-1)^{k+1} C_m^k e^{-k r_B^2 A}. \end{aligned}$$

Now we turn to the proof of (5.90). Recalling that

$$\begin{aligned} A^{-1/2} = \frac{1}{\sqrt{\pi }} \int _{0}^{\infty }e^{-tA} \frac{dt}{\sqrt{t}}, \end{aligned}$$

one has

$$\begin{aligned} \mathcal {R}_k(I-\mathcal {A}_{r_B}) f =\int _{0}^{\infty } g_{r_B}(t) L_k e^{-tA}f \, dt, \end{aligned}$$

where $g_{r}(t) = \sum _{\ell =0}^m (-1)^{\ell } C_m^{\ell } \frac{{\textbf {1}}_{\{t>\ell r^{2}\}}}{\sqrt{t-\ell r^{2}}}$. Now we claim that

$$\begin{aligned} \int _{0}^{\infty } |g_r(t)| e^{-\frac{4^j r^{2}}{c t}} \bigg (\frac{r}{t^{1/2}}\bigg )^{n-1} \frac{dt}{\sqrt{t}} \le C_m \, 2^{-nj}. \end{aligned}$$

(5.92)

Moreover, it was proved in [42, Proposition 3.1] that for any $j \ge 2$, there exist positive constants $c_1$ and $c_2$ such that

which along with (5.92) gives

It remains to demonstrate (5.92). We will use the elementary estimates for $g_r(t)$:

$$\begin{aligned} |g_r(t)|&\le \frac{C_m}{\sqrt{t-\ell r^2}}, \quad \ell r^2 < t \le (\ell +1)r^2, \ell =0,1,\ldots ,m, \end{aligned}$$

(5.93)

$$\begin{aligned} |g_r(t)|&\le C_m r^{2m} t^{-m-\frac{1}{2}}, \quad t>(m+1)r^2. \end{aligned}$$

(5.94)

The first one is easy. The second one is an application of Taylor’s formula, see [2, Sec. 3]. Denote $\alpha =4^j/c$. Then the inequality (5.94) gives that

$$\begin{aligned}&\int _{(m+1)r^2}^{\infty } |g_r(t)| e^{-\frac{4^j r^{2}}{c t}} \bigg (\frac{r}{t^{1/2}}\bigg )^{n-1} \frac{dt}{\sqrt{t}} \le C_m \int _{(m+1)r^2}^{\infty } \bigg (\frac{r}{t^{1/2}}\bigg )^{2m+n-1} e^{-\frac{4^j r^{2}}{c t}} \frac{dt}{t} \nonumber \\&\quad =C_m \alpha ^{-(m+\frac{n}{2}+\frac{1}{2})} \int _{0}^{\frac{\alpha }{m+1}} s^{m+\frac{n}{2}-\frac{3}{2}} e^{-s} ds \le C_m 2^{-j(2m+n-1)} \Gamma \Big (m+\frac{n}{2}+\frac{1}{2} \Big ). \end{aligned}$$

(5.95)

Write $\phi (s)=s^{-\frac{n}{2}} e^{-\frac{\alpha }{s}}$, $s>0$. It is easy to see that $\phi '(s)=s^{-\frac{n}{2}-2}e^{-\frac{\alpha }{s}}(\alpha -\frac{n}{2}s)$ and

$$\begin{aligned} \phi (s) \le \phi (2\alpha /n) =(2\alpha /n)^{-\frac{n}{2}} e^{-\frac{n}{2}} \le C_n 2^{-nj}, \quad \forall s>0. \end{aligned}$$

(5.96)

Thus, by (5.93), changing variables and (5.96), we have for any $0 \le \ell \le m$,

$$\begin{aligned} \mathcal {I}_{\ell }&:= \int _{\ell r^2}^{(\ell +1)r^2} |g_r(t)| e^{-\frac{4^j r^{2}}{c t}} \bigg (\frac{r}{t^{1/2}}\bigg )^{n-1} \frac{dt}{\sqrt{t}} \nonumber \\&\le C_m \int _{\ell r^2}^{(\ell +1)r^2} \frac{e^{-\frac{4^j r^{2}}{c t}}}{\sqrt{t-\ell r^2}} \bigg (\frac{r}{t^{1/2}}\bigg )^{n-1} \frac{dt}{\sqrt{t}} \nonumber \\&=C_m \int _{\ell }^{\ell +1} \frac{s^{-\frac{n}{2}} e^{-\frac{\alpha }{s}}}{\sqrt{s-\ell }} ds =C_m \int _{\ell }^{\ell +1} \frac{\phi (s)}{\sqrt{s-\ell }} ds \nonumber \\&=2C_m \phi (\ell +1) - 2 C_m \int _{\ell }^{\ell +1} (s-\ell )^{\frac{1}{2}} \phi '(s) ds \nonumber \\&\le C_m 2^{-nj} + C_m 4^j \int _{0}^{\infty } s^{-\frac{n}{2}-2} e^{-\frac{\alpha }{s}} ds \nonumber \\&= C_m 2^{-nj} + C_m 4^j \alpha ^{-\frac{n}{2}-1} \int _{0}^{\infty } t^{\frac{n}{2}} e^{-t} dt \nonumber \\&= C_m 2^{-nj} + C_m c^{\frac{n}{2}+1} 2^{-nj} \Gamma \Big (\frac{n}{2}+1 \Big ) \le C_m 2^{-nj}, \end{aligned}$$

(5.97)

where the constant $C_m$ depending only on m and n varies from line to line. Accordingly, the inequality (5.92) follows from (5.95) and (5.97). This completes the proof. $\square$

Proof of Theorem 5.17

Let $p \in (1, 2)$ and $w^p \in A_p \cap RH_{(2/p)'}$.We follow the ideas in [5]. Choose $p_0$ and $q_0$ such that $1<p_0<p<q_0<2$ and $w^p \in A_{p/p_0} \cap RH_{(q_0/p)'}$. This together with Lemma 2.6 part (c) gives that $w^{-p'} \in A_r \cap RH_{s'}$, where $r=p'/q'_0$, $s=p'_0/p'$, and $\tau _p=\big (\frac{q_0}{p}\big )' \big (\frac{p}{p_0}-1\big )+1$. Note that $w^{-p'} \in \cap RH_{s'}$ implies $w^{-p'} \in RH_{s'_0}$ for some $s_0 \in (1, s)$.

Fix $f \in L_c^{\infty }$ and a ball B with the radius $r_B$. Write

$$\begin{aligned} F := |\mathcal {R}_k^* f|^{q'_0}\quad \text {and}\quad \mathcal {A}_{r_B} := I-(I-e^{-r_B^2 A})^m, \end{aligned}$$

where $m \in \mathbb {N}$ is large enough. Observe that

$$\begin{aligned} F&\le 2^{q'_0-1} \big |(I-\mathcal {A}_{r_B}^*) \mathcal {R}^*_k f\big |^{q'_0} + 2^{q'_0-1} \big |\mathcal {A}_{r_B}^* \mathcal {R}^*_k f\big |^{q'_0} =: G_B + H_B. \end{aligned}$$

We first control $G_B$. By duality, there exists $g \in L^{q_0}(B, dx/|B|)$ with norm 1 such that for all $x \in B$,

(5.98)

where we have used (5.90). To estimate $H_B$, we set $q:=p'_0/q'_0$ and observe that by duality there exists $h \in L^{p_0}(B, dx/|B|)$ with norm 1 such that for all $x \in B$,

(5.99)

where (5.89) was used in the last step.

Consequently, (5.98) and (5.99) verify the hypotheses (5.87) with $G(x) = M (|f|^{q'_0})(x)$ and $H_1=H_2 \equiv 0$. Observe that $r=p'/q'_0=q/s<q/s_0$. Then, invoking (5.88) applied to r, $s_0$, and $w^{-p'}$ in place of p, s, and w, respectively, we obtain

$$\begin{aligned} \Vert \mathcal {R}_k^{*} f \Vert _{L^{p'}(w^{-p'})}^{q'_0}&=\Vert F\Vert _{L^r(w^{-p'})} \le \Vert M F\Vert _{L^r(w^{-p'})} \lesssim \Vert M(|f|^{q'_0})\Vert _{L^r(w^{-p'})} \lesssim \Vert f\Vert _{L^{p'}(w^{-p'})}^{q'_0}, \end{aligned}$$

which together with duality yields the $L^p(w^p)$-boundedness of $\mathcal {R}_k$. This along with Theorem 1.2 implies the $L^p(w^p)$-boundedness of $[\mathcal {R}_k, b]$. $\square$