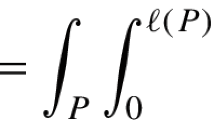Abstract
We investigate the quantitative weighted estimates for a large class of the multilinear Littlewood–Paley square operators. Our kernels satisfy the minimal regularity assumption, called \(L^r\)-Hörmander condition. We respectively establish the pointwise sparse domination for the multilinear square functions and their iterated commutators. Based on them, we obtain the strong type quantitative bounds and endpoint estimates. We recover lots of known weighted inequalities for Littlewood–Paley operators. Significantly, the approach is dyadic, quite elementary and simpler than that presented previously.
Similar content being viewed by others
References
Benea, C., Bernicot, F., Luque, T.: Sparse bilinear forms for Bochner-Riesz multipliers and applications. Trans. Lond. Math. Soc. 4(1), 110–128 (2017)
Bernicot, F., Frey, D., Petermichl, S.: Sharp weighted norm estimates beyond Calderón-Zygmund theory. Anal. PDE 9(5), 1079–1113 (2016)
Buckley, S.: Estimates for operator norms on weighted spaces and reverse Jensen inequalities. Trans. Am. Math. Soc. 340(1), 253–272 (1993)
Bui, T.A., Duong, X.T.: Weighted norm inequalities for multilinear operators and applications to multilinear Fourier multipliers. Bull. Sci. Math. 137(1), 63–75 (2013)
Bui, T.A., Hormozi, M.: Weighted bounds for multilinear square functions. Potential Anal. 46, 135–148 (2017)
Chen, S., Wu, H., Xue, Q.: A note on multilinear Muckenhoupt classes for multiple weights. Stud. Math. 223, 1–18 (2014)
Chen, X., Xue, Q., Yabuta, K.: On multilinear Littlewood-Paley operators. Nonlinear Anal. 115, 25–40 (2015)
Chung, D., Pereyra, M.C., Pérez, C.: Sharp bounds for general commutators on weighted Lebesgue spaces. Trans. Am. Math. Soc. 364, 1163–1177 (2012)
Cladek, L., Ou, Y.: Sparse domination of Hilbert transforms along curves. arXiv:1704.07810
Conde-Alonso, J., Rey, G.: A pointwise estimate for positive dyadic shifts and some applications. Math. Ann. 365, 1111–1135 (2016)
Conde-Alonso, J., Culiuc, A., Di Plinio, F., Ou, Y.: A sparse domination principle for rough singular integrals. Anal. PDE 10, 1255–1284 (2017)
Culiuc, A., Di Plinio, F., Ou, Y.: Domination of multilinear singular integrals by positive sparse forms. arXiv:1603.05317
Damián, W., Hormozi, M., Li, K.: New bounds for bilinear Calderón-Zygmund operators and applications. Rev. Mat. Iberoam (to appear)
Fefferman, C., Stein, E.M.: \(H^p\) spaces of several variables. Acta Math. 129, 137–193 (1972)
Grafakos, L.: Classical and Modern Fourier Analysis. Prentice Hall, New Jersey (2004)
Grafakos, L., Torres, R.H.: Multilinear Calderón-Zygmund theory. Adv. Math. 165, 124–164 (2002)
Grafakos, L., Liu, L., Pérez, C., Torres, R.H.: The multilinear strong maximal function. J. Geom. Anal. 21, 118–149 (2011)
Hänninen, T.S.: Remark on dyadic pointwise domination and median oscillation decomposition. arXiv:1502.05942v1
He, S., Xue, Q., Mei, T., Yabuta, K.: Existence and boundedness of multilinear Littlewood-Paley operators on Campanato spaces. J. Math. Anal. Appl. 432, 86–102 (2015)
Holmes, I., Lacey, M.T., Wick, B.D.: Commutators in the two-weight setting. Math. Ann. 367, 51–80 (2017)
Hormozi, M., Li, K.: \(A_p\)-\(A_{\infty }\) estimates for general multilinear sparse operators. arXiv:1508.06105v3
Hu, G., Li, D.: A Cotlar type inequality for the multilinear singular integral operators and its applications. J. Math. Anal. Appl. 290, 639–653 (2004)
Hytönen, T.: The sharp weighted bound for general Calderón-Zygmund operators. Ann. Math. 175(3), 1473–1506 (2012)
Hytönen, T.: The \(A_2\) Theorem: Remarks and Complements. Contemporary Mathematics, vol. 612, pp. 91–106. American Mathematical Society, Providence (2014)
Hytönen, T.P., Lacey, M.T., Pérez, C.: Sharp weighted bounds for the \(q\)-variation of singular integrals. Bull. Lond. Math. Soc. 45, 529–540 (2013)
Hytönen, T., Pérez, C.: Sharp weighted bounds involving \(A_\infty \). Anal. PDE. 6, 777–818 (2013)
Hytönen, T., Roncal, L., Tapiola, O.: Quantitative weighted estimates for rough homogeneous singular integrals. Israel J. Math. 218, 133–164 (2017)
Lacey, M.: An elementary proof of the \(A_2\) bound. Israel J. Math. 217, 181–195 (2017)
Lacey, M., Spencer, S.: Sparse bounds for oscillatory and random singular integrals. N. Y. J. Math. 23, 119–131 (2017)
Lerner, A.: Sharp weighted norm inequalities for Littlewood-Paley operators and singular integrals. Adv. Math. 226, 3912–3926 (2011)
Lerner, A.: A simple proof of the \(A_2\) conjecture. Int. Math. Res. Not. 14, 3159–3170 (2013)
Lerner, A.: On sharp aperture-weighted estimates for square functions. J. Four. Anal. Appl. 20, 784–800 (2014)
Lerner, A.: On pointwise estimates involving sparse operators. N. Y. J. Math. 22, 341–349 (2016)
Lerner, A., Nazarov, F.: Intuitive dyadic calculus: the basics. arXiv:1508.05639
Lerner, A.K., Ombrosi, S., Pérez, C., Torres, R.H., Trujillo-González, R.: New maximal functions and multiple weights for the multilinear Calderón-Zygmund theory. Adv. Math. 220, 1222–1264 (2009)
Lerner, A.K., Ombrosi, S., Rivera-Ríos, I.P.: On pointwise and weighted estimates for commutators of Calderón-Zygmund operators. Adv. Math. 319, 153–181 (2017)
Li, K.: Sparse domination theorem for multilinear singular integral operators with \(L^r\)-Hörmander condition. Michigan Math. J. (to appear)
Li, K., Sun, W.: Weak and strong type weighted estimates for multilinear Calderón-Zygmund operators. Adv. Math. 254, 736–771 (2014)
Li, K., Moen, K., Sun, W.: The sharp weighted bound for multilinear maximal functions and Calderón-Zygmund operators. J. Four. Anal. Appl. 20, 751–765 (2014)
Lorente, M., Riveros, M.S., de la Torre, A.: Weighted estimates for singular integral operators satisfying Hörmander’s conditions of Young type. J. Fourier Anal. Appl. 11, 497–509 (2015)
Martell, J., Pérez, C., Trujillo-González, R.: Lack of natural weighted estimates for some singular integral operators. Trans. Am. Math. Soc. 357, 385–396 (2005)
O’Neil, R.: Fractional integration in Orlicz spaces. Trans. Am. Math. Soc. 115, 300–328 (1965)
Pérez, C., Rivera-Ríos, I.P.: Borderline weighted estimates for commutators of singular integrals. Israel J. Math. 217, 435–475 (2017)
Pérez, C., Pradolini, G., Torres, R.H., Trujillo-González, R.: End-point estimates for iterated commutators of multilinear singular integrals. Bull. Lond. Math. Soc. 46, 26–42 (2014)
Shi, S., Xue, Q., Yabuta, K.: On the boundedness of multilinear Littlewood-Paley \(g_{\lambda }^*\) function. J. Math. Pures Appl. 101, 394–413 (2014)
Si, Z., Xue, Q., Yabuta, K.: On the bilinear square Fourier multiplier operators and related multilinear square functions. Sci. China Math. 60, 1477–1502 (2017)
Stein, E.M.: Singular integrals and Differentiability Properties of Functions. Princeton Mathematical Series, vol. 30. Princeton University Press, Princeton, NJ (1970)
Xue, Q., Yan, J.: On multilinear square function and its applications to multilinear Littlewood-Paley operators with non-convolution type kernels. J. Math. Anal. Appl. 422, 1342–1362 (2015)
Xue, Q., Peng, X., Yabuta, K.: On the theory of multilinear Littlewood-Paley \(g\)-function. J. Math. Soc. Jpn. 67, 535–559 (2015)
Yabuta, K.: On the kernel of pseudo-differential operators. Bull. Fac. Sci. Ibaraki Univ. A 18, 13–18 (1986)
Zorin-Kranich, P.: Intrinsic square functions with arbitrary aperture. arXiv:1605.02936
Acknowledgements
The authors would like to thank the referee for valuable suggestions which have improved the quality of this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Loukas Grafakos.
Appendix
Appendix
In this section, we will present some observations about \(L^p (\log L)^a\) functions, which will help us to comprehend the inverse of \(L^p (\log L)^a\) functions. Those can not be found in any other references.
Henceforth, given a Young function A, we mean that \(A^{-1}(x) = \inf \{y \in \mathbb {R}: A(y) > x\}\) for \(x \in [0,\infty ]\), where \(\inf \emptyset = \infty \).
Proposition 7.1
Let \(-\infty<a<\infty \). Let \(\Phi (x) = x(1 + \log ^+ x)^a\). Then \(\Phi ^{-1}(x)\approx x(1 + \log ^+ x)^{-a}\) on \([0,\infty ]\) if \(a\ge -1\), and on \([0,1]\cup [e^{-a-1},\infty ]\) if \(a<-1\).
Proof
Let \(\Psi (x)= x(1 + \log ^+ x)^{-a}\).
-
(i)
The case \(a=0\). In this case tivially \(\Phi ^{-1}(t)=\Psi (t)\).
-
(ii)
The case \(a>0\). For \(0\le t\le 1\) we have
$$\begin{aligned} \Phi (\Psi (t))=t, \end{aligned}$$which means that
$$\begin{aligned} \Phi ^{-1}(t)=\Psi (t)\ \text { for }0\le t\le 1. \end{aligned}$$For \(t>1\), there holds
$$\begin{aligned} \Phi (\Psi (t))&=t(1+\log ^+ t)^{-a}\bigl (1+\log ^+(t(1+\log ^+ t)^{-a})\bigr )^a \\&<t(1+\log ^+ t)^{-a}\bigl (1+\log ^+t\bigr )^a=t, \end{aligned}$$which combined with the increasingness of \(\Phi (t)\) yields that
$$\begin{aligned} \Phi ^{-1}(t)\ge \Psi (t)\ \text { for } 1<t<\infty . \end{aligned}$$Next, let \(A\ge \max \{2^a,(2a)^a\}\). Then
$$\begin{aligned} \Phi (A\Psi (t)) =At(1+\log ^+ t)^{-a}\bigl (1+\log ^+(At(1+\log ^+ t)^{-a})\bigr )^a. \end{aligned}$$(7.1)In the case \(0<a\le \frac{1}{2}\), we see that
$$\begin{aligned} (1+\log ^+ t)^{a}\le (1+\log ^+ t)^{1/2}\le \sqrt{t}. \end{aligned}$$This and (7.1) yield that
$$\begin{aligned} \Phi (A\Psi (t))&>At(1+\log ^+ t)^{-a}\bigl (1+\log ^+\sqrt{t})\bigr )^a \\&\ge \frac{A}{2^a}t(1+\log ^+ t)^{-a}\bigl (1+\log ^+ t)\bigr )^a =\frac{A}{2^a} t>t. \end{aligned}$$Hence, we deduce that
$$\begin{aligned} \Phi ^{-1}(t)\le A\Psi (t)\ \text { for }1< t<\infty . \end{aligned}$$(7.2)In the case \(a>\frac{1}{2}\), let
$$\begin{aligned} f(t)=A^{\frac{1}{a}}t^{\frac{1}{2a}}-1-\log t. \end{aligned}$$Then \(f(1)=A^{\frac{1}{a}}-1>0\), and noting \(A\ge (2a)^a\), we get
$$\begin{aligned} f'(t)=\frac{A^{\frac{1}{a}}}{2a}t^{\frac{1}{2a}-1}-\frac{1}{t} =\frac{A^{\frac{1}{a}}}{2at}\Bigl (t^{\frac{1}{2a}}-\frac{2a}{A^{\frac{1}{a}}} \Bigr )>0\ \text { for }t>1. \end{aligned}$$Hence we have
$$\begin{aligned} A\sqrt{t}> (1+\log ^+t)^a\ \text { for }t>1, \end{aligned}$$and so combinig (7.1) we get
$$\begin{aligned} \Phi (A\Psi (t))>At(1+\log ^+ t)^{-a}\bigl (1+\log ^+\sqrt{t})\bigr )^a. \end{aligned}$$So, as in the case \(0<a\le \frac{1}{2}\), we have (7.2). For \(t=\infty \) we have trivially \(\Phi ^{-1}(\infty )=\Psi (\infty )=\infty \). All together we obtain
$$\begin{aligned} \Psi (t)\le \Phi ^{-1}(t)\le A\Psi (t) \ \text { for }0\le t\le \infty . \end{aligned}$$ -
(iii)
The case \(a<0\).
On [0, 1], \(\Phi (t)=1\), and so the conclusion is clear. On \((1,\infty )\) we have
$$\begin{aligned} \Phi (\Psi (t))&=t\frac{(1+\log ^+ t)^{-a}}{\bigl (1+\log ^+(t(1+\log ^+ t)^{-a})\bigr )^{-a}} \\&<t(1+\log ^+ t)^{-a}\bigl (1+\log ^+t\bigr )^a=t. \end{aligned}$$Since \(\Phi (t)\) is increasing on \([e^{-a-1},\infty ]\), we see that
$$\begin{aligned} \Phi ^{-1}(t)\ge \Psi (t) \ \text { on } [e^{-a-1},\infty ). \end{aligned}$$(7.3)For \(A\ge (-2a)^{-a}\)
$$\begin{aligned} \Phi (A\Psi (t))=At\frac{(1+\log ^+ t)^{-a}}{\bigl (1+\log ^+(At(1+\log ^+ t)^{-a})\bigr )^{-a}}. \end{aligned}$$(7.4)In (ii), we showed that if \(A\ge (-2a)^{-a}\)
$$\begin{aligned} A\sqrt{t}> (1+\log ^+t)^{-a}\ \text { for }t>1. \end{aligned}$$This combined with (7.4) gives
$$\begin{aligned} \Phi (A\Psi (t))=At\frac{(1+\log ^+ t)^{-a}}{\bigl (1+\log ^+(A^2t^{3/2})\bigr )^{-a}} \le \frac{A}{\bigl (\frac{3}{2}(1+2\log A)\bigr )^{-a}}\,t. \end{aligned}$$So, if \(A\ge (-3a)^{-a}\), we have \(\frac{A}{\bigl (\frac{3}{2}(1+2\log A)\bigr )^{-a}}\ge 1\), and
$$\begin{aligned} \Phi (A\Psi (t))\ge t\ \text { for }t>1. \end{aligned}$$Thus, since \(\Phi (t)\) is increasing on \([e^{-a-1},\infty ]\), we get
$$\begin{aligned} \Phi ^{-1}(t)\le A\Psi (t) \ \text { for }t\ge e^{-a-1}, \end{aligned}$$(7.5)if \(A\ge \max \{(-2a)^{-a},\,(-3a)^{-a}\}\). By (7.3) and (7.5), we obtain
$$\begin{aligned} \Psi (t)\le \Phi ^{-1}(t)\le A\Psi (t) \ \text { for }t\ge e^{-a-1}. \end{aligned}$$This completes the proof of Proposition 7.1. \(\square \)
Remark 7.2
Let \(\Phi (t)=t(1+\log ^+ t)^a\) and \(a\in \mathbb R\). If \(a\ge 0\), \(\Phi (t)\) is increasing and convex on \([0,\infty ]\).
If \(-1\le a<0\), \(\Phi (t)\) is increasing on \([0,\infty ]\). If \(a<-1\), then \(\Phi (t)\) is increasing on \([0,1]\cup [e^{-a-1},\infty ]\), and is decreasing on \([1,e^{-a-1}]\). Moreover, for \(a<0\), \(\Phi ''(t)=0\) on (0, 1), \(>0\) on \((1,e^{-a})\) and \(<0\) on \((e^{-a},\infty )\).
Proposition 7.3
Let \(-\infty<a<\infty \) and \(p>0\). Let \(\Phi _p(x) = x^p(1 + \log ^+ x)^a\) and \(\tilde{\Phi }_p(x) = x^p(1 + \log ^+ x^p)^a\). Then there exist \(A_1, A_2\ge 1\) such that
and
Proof
If \(x\in [0,1]\) or \(a=0\), \(\Phi _p(x)=\tilde{\Phi }_p(x)=x\), and so we have only to treat the case \(x>1\) and \(a\ne 0\). We consider the following four cases: \(p\ge 1\) and \(a>0\), \(p\ge 1\) and \(a<0\), \(0<p<1\) and \(a>0\), and \(0<p<1\) and \(a<0\).
Case 1\(p\ge 1\)and\(a>0\). Clearly \(\Phi _p(x)\le \tilde{\Phi }_p(x)\). And
Case 2\(p\ge 1\)and\(a<0\). Clearly \(\Phi _p(x)\ge \tilde{\Phi }_p(x)\). And
There exists \(A_0>0\) such that
In this case \(pA_0\ge 1\). Hence, letting \(A_1=(pA_0)^{-a/p}>1\) we have
Case 3\(0<p<1\)and\(a>0\). It is easy to see that \(\Phi _p(x)\ge \tilde{\Phi }_p(x)\). And
Case 4\(0<p<1\)and\(a<0\). There holds
And for \(A>1\)
There exists \(A_4>1\) such that
In this case \(A_4/p\ge 1\). Hence, letting \(A_2=(A_4/p)^{-a/p}>1\) we have
Lemma 7.4
Let \(a_1\ge 0\) and let \(\Phi _1\), \(\Phi _2\) be nonnegative, increasing and continuous functions on \([a_1,\infty )\). If for some \(A_1\ge 1\)
then it holds
Proof
From (7.6) we get for \(t\ge \Phi _1(a_1)\)
which implies that
Proposition 7.5
Let \(-\infty<a<\infty \) and \(p>1\). Let \(\Phi _p(x) = x^p(1 + \log ^+ x)^a\). Then \(\Phi _p^{-1}(x)\approx x^{1/p}(1 + \log ^+ x)^{-a/p}\) on \([0,\infty ]\) if \(a\ge -1\), and on \([0,1]\cup [-ae^{-a-1},\infty ]\) if \(a<-1\).
Proof
One can easily check that \(\Phi _p(t)\) is increasing on \([0,\infty )\) if \(a\ge -p\), and is increasing on \([0,1]\cup [e^{-a/p -1},\,\infty )\). Let \(\tilde{\Phi }_p(t)=t^p(1 + \log ^+ t^p)^a\). We know that \(\tilde{\Phi }_p(t)\) is increasing on \([0,\infty )\) if \(a\ge -1\), and is increasing on \([0,1]\cup [e^{-(a+1)/p},\,\infty )\). Hence, if \(a\ge 1\), by Proposition 7.3 and Lemma 7.4 we see that \(\Phi _p^{-1}(t)\approx \tilde{\Phi }_p^{-1}(t)\) on \([0, \infty )\).
Here we see easily that \(\tilde{\Phi }_p^{-1}=(\Phi ^{-1}(t))^{1/p}\), where \(\Phi (t)=t(1 + \log ^+ t)^a\). Hence by Proposition 7.1 we obtain
In the case \(a<-1\), on [0, 1] it is trivial. Next, we observe that \(e^{-a/p -1}<e^{-(a+1)/p}\) and \(\Phi _p(e^{-a/p -1})=-\frac{a}{p} e^{-\frac{a}{p} -1}<-ae^{-(a+1)} =\tilde{\Phi }_p(e^{-(a+1)/p})\). By the proof of Proposition 7.3, we know that \(\tilde{\Phi }_p(t)\le \Phi _p(t)\le \tilde{\Phi }_p(At)\)\((0\le t<\infty )\), for some \(A>1\). So, by Lemma 7.4 we see that \(\Phi _p^{-1}(t)\approx \tilde{\Phi }_p^{-1}(t)\) on \([-ae^{-(a+1)},\,\infty )\).
Remark 7.6
In genera, the following does not hold: Let \(a_1\ge 0\) and let \(\Phi _1\), \(\Phi _2\) be nonnegative, increasing and continuous functions on \([a_1,\infty )\).
Then, from \(\Phi _1(t)\approx \Phi _2(t)\) it follows \(\Phi _1^{-1}(t)\approx \Phi _2^{-1}(t)\). In fact, let \(\Phi _1(t)=\log (1+t)\) and \(\Phi _2(t)=\log (1+t)^2\). Then \(\Phi _1(t)\approx \Phi _2(t)\), but \(\Phi _1^{-1}(t)=e^t -1\) and \(\Phi _2^{-1}(t)=e^{t/2} -1\). And there exists no \(C>0\) such that \(\Phi _1^{-1}(t)\le C\Phi _2^{-1}(t)\).
However, if we suppose the convexty in addition, then we get a good result.
Lemma 7.7
Let \(\Phi _1\), \(\Phi _2\) be nonnegative, increasing and convex functions on [0, B]. If for some \(A_1, A_2\ge 1\)
then it holds
Proof
Since \(\Phi _2(0)=0\) and \(\Phi _2\) is convex on [0, B], we have
and hence \(A_2\Phi _2(t)\le \Phi _2(A_2t)\), \(0\le t<\infty \). Thus we get
Similarly we have
Rights and permissions
About this article
Cite this article
Cao, M., Yabuta, K. The Multilinear Littlewood–Paley Operators with Minimal Regularity Conditions. J Fourier Anal Appl 25, 1203–1247 (2019). https://doi.org/10.1007/s00041-018-9613-7
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00041-018-9613-7