Haar Frame Characterizations of Besov–Sobolev Spaces and Optimal Embeddings into Their Dyadic Counterparts

Abstract

We study the behavior of Haar coefficients in Besov and Triebel–Lizorkin spaces on ${\mathbb R}$, for a parameter range in which the Haar system is not an unconditional basis. First, we obtain a range of parameters, extending up to smoothness $s<1$, in which the spaces $F^s_{p,q}$ and $B^s_{p,q}$ are characterized in terms of doubly oversampled Haar coefficients (Haar frames). Secondly, in the case that $1/p<s<1$ and $f\in B^s_{p,q}$, we actually prove that the usual Haar coefficient norm, $\Vert \{2^j\langle f, h_{j,\mu }\rangle \}_{j,\mu }\Vert _{b^s_{p,q}}$ remains equivalent to $\Vert f\Vert _{B^s_{p,q}}$, i.e., the classical Besov space is a closed subset of its dyadic counterpart. At the endpoint case $s=1$ and $q=\infty$, we show that such an expression gives an equivalent norm for the Sobolev space $W^{1}_p({\mathbb R})$, $1<p<\infty$, which is related to a classical result by Bočkarev. Finally, in several endpoint cases we give optimal inclusions between $B^s_{p,q}$, $F^s_{p,q}$, and their dyadic counterparts.

1 Introduction and Statement of Main Results

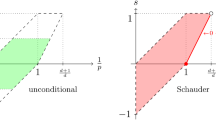
In this paper we investigate the validity of norm characterizations for elements f in Besov and Triebel–Lizorkin spaces, $B^s_{p,q}({\mathbb R})$ and $F^s_{p,q}({\mathbb R})$, in terms of expressions involving their Haar coefficients or suitable variations thereof. The novelty in the current paper is that we obtain results for a range of the parameters (s, p, q) in which the Haar system is not an unconditional basis of the above spaces (see Figs. 1 and 2); this complements earlier work of the authors [11,12,13,14, 23] where a complete description was given for the parameter range in which the unconditional or Schauder basis property holds in each such space.

We denote the (inhomogeneous) Haar system in ${\mathbb R}$ by

$$\begin{aligned} {\mathscr {H}}=\big \{h_{j,\mu }{\,\,\,:\,\,\,}j\ge -1, \,\mu \in {\mathbb Z}\big \}, \end{aligned}$$

(1.1)

where we let $h(x)= {\mathbb {1}}_{[0,\frac{1}{2})}(x)-{\mathbb {1}}_{[\frac{1}{2}, 1)}(x)$ and

$$\begin{aligned} h_{j,\mu } (x):= h(2^jx-\mu ),\quad \text{ if } \mu \in {\mathbb Z}, j=0,1,2,\dots \end{aligned}$$

(1.2)

Note that $h_{j,\mu }$ is supported in the closure of the dyadic interval

$$\begin{aligned} I_{j,\mu }=\big [2^{-j}\mu , 2^{-j}(\mu +1)\big ). \end{aligned}$$

In the case $j=-1$, we just let

$$\begin{aligned} h_{-1,\mu }:={\mathbb {1}}_{I_{-1,\mu }}={\mathbb {1}}_{[\mu ,\mu +1)},\quad \mu \in {\mathbb Z}. \end{aligned}$$

Let $F^s_{p,q}({\mathbb R})$ and $B^s_{p,q}({\mathbb R})$ denote the usual Triebel–Lizorkin and Besov spaces [27]. It has been shown in [23, 24, 30] that ${\mathscr {H}}$ is an unconditional basis of $F^s_{p,q}({\mathbb {R}})$ if and only if s belongs to the range

$$\begin{aligned} \max \Big \{1/p-1,1/q-1\Big \}< s < \min \Big \{1/p,1/q, 1\Big \}; \end{aligned}$$

(1.3)

moreover, in the range (1.3), $F^s_{p,q}$ is characterized by the property

$$\begin{aligned} \Big \Vert \Big (\sum _{j=-1}^\infty 2^{jsq}\Big [\sum _{\mu \in {\mathbb {Z}}} 2^j |\langle f,h_{j,\mu }\rangle | {\mathbb {1}}_{I_{j,\mu }} \Big ]^q\Big )^{1/q}\Big \Vert _p<\infty , \end{aligned}$$

(1.4)

and this expression defines an equivalent quasinorm in $F^s_{p,q}$.

Fig. 1

Parameter domain for ${\mathscr {H}}$ to be an unconditional basis (left figure) or a Schauder basis (right figure) in $F^s_{p,q}({\mathbb R})$

It was also shown in [12] that ${\mathscr {H}}$ is a Schauder basis of $F^s_{p,q}({\mathbb R})$ (with respect to natural enumerations) in the larger range

$$\begin{aligned} 1/p-1< s< \min \Big \{1/p, 1\Big \},\quad \text{ for } \text{ all } 0<q<\infty . \end{aligned}$$

(1.5)

At the endpoints, the Schauder basis property holds for $F^s_{p,q}$ if and only if

$$\begin{aligned} s=1/p-1{\quad \hbox {and}\quad }1/2<p\le 1 \end{aligned}$$

(1.6)

also for all $0<q<\infty$; see [13]. These regions are depicted in Fig. 1.

For the spaces $B^s_{p,q}({\mathbb R})$ there is no such distinction, and ${\mathscr {H}}$ is an unconditional basis under (1.5) (and also a Schauder basis under (1.6), if $p=q$); see [14]. Moreover, in the range (1.5), $B^s_{p,q}$ is characterized by the property

$$\begin{aligned} \Big (\sum _{j=-1}^\infty 2^{j(s-\frac{1}{p})q}\Big (\sum _{\mu \in {\mathbb {Z}}} |2^j \langle f,h_{j,\mu }\rangle |^p \Big )^{q/p} \Big )^{1/q}<\infty , \end{aligned}$$

(1.7)

and this expression in an equivalent quasinorm in $B^s_{p,q}$.

1.1 The Oversampled Haar Systems: Haar Frames

A main feature of this paper is to show that the above characterizations in terms of Haar coefficients can be extended to the larger regions depicted in Fig. 2, provided that we doubly oversample with Haar type coefficients obtained by a shift.

More concretely, we now define

$$\begin{aligned} \widetilde{h}_{j,\nu } (x):= h(2^jx-\tfrac{\nu }{2}) \quad \text{ if } j=0,1,2,\dots \text{ and } \nu \in {\mathbb Z}. \end{aligned}$$

(1.8)

Observe that for even $\nu =2\mu$ we recover the original Haar functions, $\widetilde{h}_{j, 2\mu }=h_{j,\mu }$ supported in $I_{j,\mu }$, but for odd $\nu$ we obtain a shifted Haar function

$$\begin{aligned} \widetilde{h}_{j,2\mu +1}=h_{j,\mu } (\cdot - 2^{-j-1}), \end{aligned}$$

which is supported in the interval $[2^{-j}(\mu +1/2), 2^{-j}(\mu +3/2))=I_{j,\mu }+2^{-j-1}$. As before, for $j=-1$ we just let

$$\begin{aligned} \widetilde{h}_{-1,\nu }:=h_{-1,\nu }={\mathbb {1}}_{[\nu , \nu +1)}. \end{aligned}$$

Then the extended Haar system is defined by

$$\begin{aligned} {\mathscr {H}^{\textrm{ext}}}= \Big \{\widetilde{h}_{j,\nu }{\,\,\,:\,\,\,}j\ge -1,\,\nu \in {\mathbb Z}\Big \}. \end{aligned}$$

(1.9)

In what follows we will need to work with appropriate spaces of distributions on which the (generalized) Haar coefficients are well defined. Given a bounded interval $I\subset {\mathbb R}$, consider the linear functional (distribution)

$$\begin{aligned} \lambda _I(f)=\int _I f(x)dx, \end{aligned}$$

(1.10)

which applied to $f\in L_1^{\text { loc}}$ satisfies the trivial inequality

$$\begin{aligned} |\lambda _I(f)| \le \int _{I}|f(x)|dx. \end{aligned}$$

(1.11)

Below, we shall also deal with distributions f, associated with certain negative smoothness parameters, which may not belong to $L_1^{\text { loc}}$. To handle these we choose as a reference space the set of distributions

$$\begin{aligned} \mathscr {B}:= B^{-1}_{\infty ,1}({\mathbb {R}}). \end{aligned}$$

(1.12)

By standard embeddings, see e.g. [27, 2.7.1], we have

$$\begin{aligned} B^s_{p,q}({\mathbb R})\hookrightarrow \mathscr {B},\quad \hbox {if }s>\frac{1}{p}-1,\hbox { or } s=\frac{1}{p}-1\hbox { and }0<q\le 1, \end{aligned}$$

(1.13)

and

$$\begin{aligned} F^s_{p,q}({\mathbb R})\hookrightarrow \mathscr {B},\quad \hbox {if }s>\frac{1}{p}-1,\hbox { or } s=\frac{1}{p}-1\hbox { and }0<p\le 1. \end{aligned}$$

(1.14)

In particular, all the spaces that are used in Theorems 1.2–1.10 are embedded into $\mathscr {B}$.

Proposition 1.1

  For a bounded interval $I\subset {\mathbb R}$ consider the distribution $\lambda _I$ in (1.10). Then

(i) $\lambda _I$ extends to a bounded linear functional on $\mathscr {B}$, with operator norm $O(1+|I|)$.

(ii) For every $h\in {\mathscr {H}^{\textrm{ext}}}$ the linear functional $f\mapsto \langle f,h\rangle$ is bounded on $\mathscr {B}$ with uniformly bounded operator norm.

(iii) If $f\in \mathscr {B}$ and $\langle f,h\rangle =0$, for all $h\in {\mathscr {H}}$, then $f=0$.

Remark

Clearly, using (1.11) one can also replace in (i) the space $\mathscr {B}$ with $\mathscr {B}+L_1^{\text { loc}}$. We note that $L_1$ is not embedded into $\mathscr {B}$, see Remark 11.4.

In the rest of the paper, when $f\in \mathscr {B}$, we use the following notation, combining the standard Haar coefficients with the coefficients obtained from the shifted Haar functions:

$$\begin{aligned} {\mathfrak {c}}_{j,\mu }(f) =2^j |\langle f,\widetilde{h}_{j,2\mu }\rangle | + 2^j|\langle f,\widetilde{h}_{j,2\mu +1}\rangle |\, , \end{aligned}$$

(1.15)

when $j=0,1,\dots$, and

$$\begin{aligned} {\mathfrak {c}}_{-1,\mu }(f) =\langle f,h_{-1,\mu }\rangle =\langle f,{\mathbb {1}}_{[\mu ,\mu +1)}\rangle . \end{aligned}$$

Our first main result provides a characterization where in (1.4) the Haar coefficients $2^j\langle f,h_{j,\mu }\rangle$ are replaced with the ${\mathfrak {c}}_{j,\mu }(f)$. This covers as well the quasi-Banach range of parameters; see Fig. 2.

Theorem 1.2

Let $1/2<p<\infty$, $1/2 < q \le \infty$ and

$$\begin{aligned} \max \{1/p-1,1/q-1\}< s < 1\,. \end{aligned}$$

(1.16)

Then $F^s_{p,q}({\mathbb {R}})$ is the collection of all $f\in \mathscr {B}$ such that

$$\begin{aligned} \Big \Vert \Big (\sum \limits _{j=-1}^{\infty } 2^{jsq}\Big |\sum \limits _{\mu \in {\mathbb {Z}}} {\mathfrak {c}}_{j,\mu }(f) {\mathbb {1}}_{I_{j,\mu }}\Big |^q \Big )^{1/q}\Big \Vert _p < \infty . \end{aligned}$$

(1.17)

Moreover, the latter quantity represents an equivalent quasi-norm in $F^s_{p,q}({\mathbb {R}})$.

Using terminology introduced by Gröchenig [16], one may say that ${\mathscr {H}^{\textrm{ext}}}$ is a (quasi-)Banach frame¹ for $F^s_{p,q}({\mathbb {R}})$. In signal processing language, this can be interpreted by saying that one may stably recover f from the sampled information $\{\langle f,h\rangle : h\in {\mathscr {H}^{\textrm{ext}}}\}$.

We remark that the condition $s>\frac{1}{q}-1$ in (1.16) is necessary, in view of the examples in [23]; see Remark 4.3. The analogous characterization for Besov spaces is valid in a larger range:

Theorem 1.3

Let $1/2<p\le \infty$, $0 < q \le \infty$ and

$$\begin{aligned} 1/p-1< s < 1. \end{aligned}$$

Then $B^s_{p,q}({\mathbb {R}})$ is the collection of all functions $f\in \mathscr {B}$ such that

$$\begin{aligned} \Big (\sum \limits _{j=-1}^{\infty } 2^{j(s-1/p)q}\Big (\sum \limits _{\mu \in {\mathbb {Z}}}| {\mathfrak {c}}_{j,\mu }(f) |^p\Big )^{q/p}\Big )^{1/q} < \infty . \end{aligned}$$

Moreover, the latter quantity represents an equivalent quasi-norm in ${B^s_{p,q}({\mathbb R})}$.

Fig. 2

Parameter domain for ${\mathscr {H}}^\textrm{ext}$ to be a characterizing frame for $F^s_{p,q}({\mathbb R})$ (left figure, Theorem 1.2) and $B^s_{p,q}({\mathbb R})$ (right figure, Theorem 1.3)

Figure 2 shows the regions of parameters where ${\mathscr {H}^{\textrm{ext}}}$ is a characterizing frame for each of the spaces $F^s_{p,q}({\mathbb {R}})$ and $B^s_{p,q}({\mathbb {R}})$.

We remark that a related result, in the special case of the Hölder spaces $C^{\alpha }=B^{\alpha }_{\infty ,\infty }({\mathbb R})$, ${\alpha }\in (0,1)$, and using a 1/3-shifted Haar frame, has been recently obtained by Jaffard and Krim; see [17, Theorem 1]. As pointed out by A. Cohen in [17, Remark 5], related characterizations of Besov spaces $B^s_{p,q}[0,1]$, up to smoothness $s<1$, appeared in the spline community in the 70 s (see e.g. [9, §12.2]), in that case in terms of classes of best linear approximation by piecewise constant functions with equally spaced (or sufficiently mixed) knots. In particular, compare the statements of Theorems 1.3 and 1.4, with [9, Theorem 12.2.4] parts (iv) and (ii), respectively; see also Remark 4.10.

1.2 Characterization of $W^{1}_{p}({\mathbb {R}})$ Via Haar Frames

We now let $s=1$, and consider in the Banach range $1\le p\le \infty$ the Sobolev space $W^{1}_{p} ({\mathbb {R}})$, endowed with the usual norm

$$\begin{aligned} \Vert f\Vert _{W^{1}_{p}({\mathbb {R}})}=\Vert f\Vert _p+\Vert f'\Vert _p. \end{aligned}$$

We also let $BV({\mathbb {R}})$ be the subspace of $L_1({\mathbb {R}})$ for which the distributional derivative belongs to the space ${\mathcal {M}}$ of bounded Borel measures (with the norm given by the total variation of the measure) and define

$$\begin{aligned} \Vert f\Vert _{BV({\mathbb {R}})}=\Vert f\Vert _1+\Vert f'\Vert _{{\mathcal {M}}}. \end{aligned}$$

Note that by our definition $BV\subset L_1$ which deviates from the definition in some other places in the literature. We have the following result, that provides characterizations in terms of the oversampled Haar system ${\mathscr {H}}^{\textrm{ext}}$.

Theorem 1.4

For all $f\in \mathscr {B}$ the following hold.

(i) If $1<p\le \infty$ then

$$\begin{aligned} \Vert f\Vert _{W^1_p} \approx \sup \limits _{j\ge -1} 2^{j(1-1/p)}\Big (\sum \limits _{\mu \in {\mathbb {Z}}} |{\mathfrak {c}}_{j,\mu } (f)|^p\Big )^{1/p}. \end{aligned}$$

(ii) In the case $p=1$ we have instead

$$\begin{aligned} \Vert f\Vert _{BV} \approx \sup \limits _{j\ge -1} \sum \limits _{\mu \in {\mathbb {Z}}} |{\mathfrak {c}}_{j,\mu } (f)|. \end{aligned}$$

Clearly part (ii) implies the inequality

$$\begin{aligned} \sup \limits _{j\ge -1} \sum \limits _{\mu \in {\mathbb {Z}}} |{\mathfrak {c}}_{j,\mu } (f)|\lesssim \Vert f\Vert _{W^1_1}\end{aligned}$$

(1.18)

for all $f\in {\mathcal {B}}$. However the converse of this inequality fails as one checks by testing it with $f={\mathbb {1}}_{[0,1]} \in BV\setminus W^1_1$; we have $\sup _j\sum _{\mu } |{\mathfrak {c}}_{j,\mu } ({\mathbb {1}}_{[0,1]})| <\infty$.

The fact that the Sobolev $W^1_p({\mathbb R})$ norm can be expressed in terms of a discrete norm of $b^1_{p,\infty }$ type may seem surprising at first, but actually results of this sort can be found in the literature since the 60 s, see [1]. The theorem is also reminiscent of characterizations via the uniform bounds for difference quotients $h^{-1}(f(\cdot +h)-f)$, see [26, Prop V.3] and more recently [4, 5].

1.3 Dyadic Besov Spaces

In this section we present stronger results involving the standard Haar system ${\mathscr {H}}$, and suitable dyadic variants $B^{s,\textrm{dyad}}_{p,q}$ of the Besov spaces.

We first recall the definition of the sequence spaces $b^s_{p,q}$ and $f^s_{p,q}$; see [10]. If $s\in {\mathbb {R}}$ and $0<p, q\le \infty$, we define, for $\beta = \{\beta _{j,\mu }\}_{j\ge {-1}, \mu \in {\mathbb {Z}}}$,

$$\begin{aligned} \Vert \beta \Vert _{b^s_{p,q}} := \Big (\sum \limits _{j=-1}^\infty \Big [2^{j(s-1/p)}\Big (\sum \limits _{\mu \in {\mathbb {Z}}} |\beta _{j,\mu }|^p\Big )^{\frac{1}{p}} \Big ]^q\Big )^{\frac{1}{q}}, \end{aligned}$$

(1.19)

and if $p<\infty$ we let

$$\begin{aligned} \Vert \beta \Vert _{f^s_{p,q}} := \Big \Vert \Big (\sum \limits _{j=-1}^\infty \Big |2^{js}\sum \limits _{\mu \in {\mathbb {Z}}} \beta _{j,\mu } {\mathbb {1}}_{I_{j,\mu }}(\cdot )\Big |^q\Big )^{1/q}\Big \Vert _p\,. \end{aligned}$$

(1.20)

These expressions have the obvious interpretations if $\max \{p,q\}=\infty$.

We additionally define for every $f\in \mathscr {B}$ the quantity

$$\begin{aligned} \Vert f\Vert _{B^{s,\textrm{dyad}}_{p,q}}:=\Big \Vert \big \{2^j\langle f,h_{j,\mu }\rangle \big \}_{j,\mu }\Big \Vert _{b^s_{p,q}} \end{aligned}$$

and the vector spaces

$$\begin{aligned} B^{s,\textrm{dyad}}_{p,q}({\mathbb {R}}) = \Big \{f\in \mathscr {B}{\,\,\,:\,\,\,}\Vert f\Vert _{B^{s,\textrm{dyad}}_{p,q} }<\infty \Big \}. \end{aligned}$$

Observe that ${\text {span}}{\mathscr {H}}\subset B^{s,\textrm{dyad}}_{p,q}$, so the spaces are not null. Also, the quantity $\Vert f\Vert _{B^{s,\textrm{dyad}}_{p,q}}$ is a quasi-norm (not just a semi-norm), by Proposition 1.1. Since $2^j|\langle f,h_{j,\mu }\rangle |\le {\mathfrak {c}}_{j,\mu }(f)$ we note the following immediate consequence of Theorem 1.4.

Corollary 1.5

If $1\le p \le \infty$ then

$$\begin{aligned} W^1_p\hookrightarrow B^{1,{\textrm{dyad}}}_{p,\infty } . \end{aligned}$$

(1.21)

To avoid pathological cases, below we shall typically consider the range

$$\begin{aligned} \frac{1}{p}-1<s < 1, \end{aligned}$$

(1.22)

and some end-point cases of these. We remark that when $s>1$ (or $s=1$ and $0<q<\infty$), the spaces $B^{1,{\textrm{dyad}}}_{p,q}$ contain no nontrivial $C^1$ functions (see Proposition 11.1), while for $s<1/p-1$ the spaces are not complete (see Proposition 11.2). Recall also that in the range $1/p-1<s<\min \{1/p,1\}$ we have $B^s_{p,q}=B^{s,{\textrm{dyad}}}_{p,q}$, cf. (1.7).

Assume now that (1.22) holds. By Theorem 1.3 we have $B^s_{p,q}\hookrightarrow B^{s,\textrm{dyad}}_{p,q}$, and the inclusion is proper provided that

$$\begin{aligned} 1/p<s<1,\quad \text { or }\, s=1/p{\quad \hbox {and}\quad }\,q<\infty \end{aligned}$$

(1.23)

(since in that range Haar functions do not belong to $B^s_{p,q}$). Our goal is to prove converse inequalities of the form

$$\begin{aligned} \Vert f\Vert _{B^s_{p,q}}\, \lesssim \, \Vert f\Vert _{B^{s,\textrm{dyad}}_{p,q}} ,\quad provided \,\hbox { that }\, f\in B^s_{p,q}({\mathbb R}). \end{aligned}$$

(1.24)

Such inequalities will imply that $\Vert \cdot \Vert _{B^{s,\textrm{dyad}}_{p,q}}$ is an equivalent norm in $B^s_{p,q}$, a result which may seem surprising outside the usual unconditionality region. Our first result in this direction is the following.

Theorem 1.6

Let $1< p \le \infty$, $0<q\le \infty$, and $1/p<s<1$. Then (1.24) holds. In particular, $B^s_{p,q}$ is a proper closed subspace of $B^{s,\textrm{dyad}}_{p,q}$, and we have

$$\begin{aligned} \Vert f\Vert _{B^s_{p,q}} \approx \Vert f\Vert _{B^{s,\textrm{dyad}}_{p,q}}, \text { for all } f \in B^s_{p,q}({\mathbb {R}}). \end{aligned}$$

(1.25)

There are also some precedent results of this nature in the literature. When $p=q=\infty$, a norm equivalence as in (1.25) (for continuous functions in the interval [0,1]) was proved by Golubov [15, Corollary 6]; see also [19, Corollary 3.2], [20, Theorem 7.c.3] and references therein.

1.4 Inclusions for the Limiting Case $s=1$

In what follows the notation ${\mathfrak {X}}_1\hookrightarrow {\mathfrak {X}}_2$ will indicate a continuous embedding of the space ${\mathfrak {X}}_1$ in the space ${\mathfrak {X}}_2$. As already remarked above we may focus on the cases $s<1$ or $s=1$, $q=\infty$, cf. Proposition 11.1.

We now state inclusions into the spaces ${B^{s,\textrm{dyad}}_{p,q}}$, in the case that $s=1$ and $q=\infty$. Note that in one of the inclusions we use the smaller space

$$\begin{aligned} F^{1,\textrm{dyad}}_{p,\infty }:=\Big \{f\in \mathscr {B}{\,\,\,:\,\,\,}\big \{2^j\langle {f,h_{j,\mu }}\rangle \big \}_{\begin{array}{c} j\ge -1\\ \mu \in {\mathbb {Z}} \end{array}}\in f^1_{p,\infty }\Big \}. \end{aligned}$$

Theorem 1.7

Let $1/2\le p\le \infty$. Then the following hold.

(i) If $1/2\le p < \infty$ then

$$\begin{aligned} B^1_{p,q}&\hookrightarrow B^{1,{\textrm{dyad}}}_{p,\infty } \,\iff \, q\le \min \{p,2\}\,, \end{aligned}$$

(1.26)

$$\begin{aligned} F^1_{p,q}&\hookrightarrow B^{1,{\textrm{dyad}}}_{p,\infty } \,\iff \, q\le 2\, . \end{aligned}$$

(1.27)

For $p=\infty$ we have

$$\begin{aligned} B^1_{\infty ,q} \hookrightarrow B^{1,{\textrm{dyad}}}_{\infty ,\infty } \,\iff \, q\le 1\,. \end{aligned}$$

(1.28)

(ii) For $1/2<p<\infty$

$$\begin{aligned} F^1_{p,2} \hookrightarrow F^{1,{\textrm{dyad}}}_{p,\infty } . \end{aligned}$$

(1.29)

The next result gives a converse inequality to the embedding (1.21), which in particular implies that

$$\begin{aligned} \Vert f\Vert _{B^{1,\textrm{dyad}}_{p,\infty }} = \sup \limits _{j\ge -1} 2^{j(1-1/p)} \Big (\sum \limits _{\mu \in {\mathbb {Z}}} |2^j{\langle {f},{h_{j,\mu }}\rangle }|^p\Big )^{1/p} \end{aligned}$$

is an equivalent norm in $W^1_p({\mathbb R})$. Earlier bounds of this type, for absolutely continuous functions in the interval [0, 1], can be found in the work of Bočkarev, see [1, Theorem 7], [2, Theorem I.3.4], or [20, Corollary 7.b.2] and references therein. Below we establish, by different methods, the following result, which is complementary to Theorem 1.4.

Theorem 1.8

Let $1< p\le \infty$. Then

$$\begin{aligned} \Vert f\Vert _{W^1_p}\,\lesssim \,\Vert f\Vert _{B^{1,\textrm{dyad}}_{p,\infty }}, \quad \hbox {provided} \quad f\in W^1_p({\mathbb R}). \end{aligned}$$

(1.30)

In particular, $W^{1}_{p}({\mathbb R})$ is a proper closed subspace of $B_{p,\infty }^{1,\textrm{dyad}}$, and it holds

$$\begin{aligned} \Vert f\Vert _{W^{1}_{p}}\approx \Vert f\Vert _{B^{1,\textrm{dyad}}_{p,\infty }}\approx \Vert f\Vert _{F^{1,\textrm{dyad}}_{p,\infty }},\quad \text {for } f\in W^{1}_p ({\mathbb {R}}), \quad 1<p<\infty . \end{aligned}$$

(1.31)

Remark

The inequality in (1.30) (and hence, the first equivalence in (1.31)) is also true when $p=1$, due to the result of Bočkarev [1]. The proof we give here, however, is only valid for $p>1$.

1.5 Inclusions for the Limiting Case $s=1/p-1$

We state inclusions into the spaces ${B^{s,\textrm{dyad}}_{p,q}}$, in the case that $s=1/p-1$ and $q=\infty$.

Theorem 1.9

(i) For $0<p, u\le \infty$ the embedding $B^{1/p-1}_{p,u}\hookrightarrow B^{1/p-1, {\textrm{dyad}}}_{p,q}$ can only hold when $q=\infty$.

(ii) If $p\ge 1/2$ then

$$\begin{aligned} B^{1/p-1}_{p,q} \hookrightarrow B^{1/p-1,\textrm{dyad}}_{p,\infty } \,\iff \, q\le \min \{1,p\} \end{aligned}$$

(1.32)

(iii) If $1/2<p\le 1$ then

$$\begin{aligned} F^{1/p-1}_{p,\infty } \hookrightarrow B^{1/p-1,\textrm{dyad}}_{p,\infty }. \end{aligned}$$

(1.33)

Remark

When $p=1$, we also have the straightforward inequality

$$\begin{aligned} \sup _{j\ge -1} \sum _{\mu \in {\mathbb {Z}}} |\langle f,h_{j,\mu }\rangle | \lesssim \Vert f\Vert _1,\quad f\in L^1, \end{aligned}$$

which leads to the inclusion $L_1\cap \mathscr {B}\subset B^{0, \textrm{dyad}}_{1,\infty }$.

1.6 The Case $s=1/p$

When $1<p<\infty$, the standard Haar characterization of Besov spaces implies that

$$\begin{aligned} B^s_{p,q}(\mathbb {R})= B^{s,\textrm{dyad}}_{p,q}(\mathbb {R})\,, \quad \frac{1}{p}-1<s<\frac{1}{p}. \end{aligned}$$

On the other hand, Theorem 1.6 implies the norm equivalence

$$\begin{aligned} \Vert f\Vert _{B^s_{p,q}} \approx \Vert f\Vert _{B^{s,\textrm{dyad}}_{p,q}} , \quad f \in B^s_{p,q}, \quad \frac{1}{p}<s<1. \end{aligned}$$

These two results might suggest that the norm equivalence could hold also at the dividing line $s=1/p$. Here we show that this is not the case, at least when $q=\infty$.

Theorem 1.10

Let $1\le p<\infty$. Then

(i) there exists a sequence $\{f_N\}_{N=1}^\infty$ of functions in $B^{1/p}_{p,\infty }$ such that

$$\begin{aligned} \Vert f_N\Vert _{B^{1/p,{\textrm{dyad}}}_{p,\infty }} =1\text { and } \Vert f_N\Vert _{B^{1/p}_{p,\infty } }\gtrsim N, \end{aligned}$$

(ii) $B^{1/p,{\textrm{dyad}}}_{p,\infty } \setminus B^{1/p}_{p,\infty } \ne \emptyset$.

Remarks

(i) The previous result shows that, if $1<p<\infty$, then Theorem 1.6 cannot hold at the dividing line $s=1/p$ (at least if $q=\infty$). Namely, the embedding of $B^{1/p}_{p,\infty }$ into $B^{1/p,\textrm{dyad}}_{p,\infty }$, which is established by Theorem 1.3, is proper, that is, $B^{1/p}_{p,\infty }\,\subsetneq B^{1/p, \textrm{dyad} }_{p,\infty }$, and moreover, on the smaller space $B^{1/p}_{p,\infty }$, the norms are not equivalent, i.e.,

$$\begin{aligned} \sup \big \{ \Vert f\Vert _{B^{1/p}_{p,\infty }} \,: \, f\in B^{1/p}_{p,\infty }\text { and } \Vert f\Vert _{B^{1/p,\textrm{dyad}}_{p,\infty }}=1 \big \} =\infty \,. \end{aligned}$$

(1.34)

Both statements are an immediate consequence of Theorem 1.10.

(ii) Observe that $BV({\mathbb {R}}) \hookrightarrow B^1_{1,\infty }({\mathbb {R}})$ and that for $p=1$ we have the embedding $BV({\mathbb {R}})\hookrightarrow B^{1,{\textrm{dyad}}}_{1,\infty }$ as a consequence of Theorem 1.4. Theorem 1.10 shows that this embedding is also proper, i.e. $B^{1,{\textrm{dyad}}}_{1,\infty } \setminus BV({\mathbb {R}}) \ne \emptyset$.

1.7 Further Directions

We mention a few problems left open in this paper.

1.7.1 Besov-Type Spaces

Concerning (1.34) in Theorem 1.10, we do not know whether the inequality

$$\begin{aligned} \Vert f\Vert _{B^{1/p}_{p,\infty }}\,\le \,C\,\Vert f\Vert _{B^{1/p, \text {dyad} }_{p,\infty }} \end{aligned}$$

(1.35)

could be true for $1<p<\infty$ when restricted to $f\in {\mathcal {S}}({\mathbb {R}})$. It is also open to determine whether such inequality could hold if the $B^{1/p}_{p,\infty }$ norm is replaced by $B^{1/p}_{p,q}$ with $q<\infty$.

1.7.2 $F^s_{p,q}$ Versus $F^{s,{\textrm{dyad}}}_{p,q}$

It would be interesting to establish an optimal analogue of Theorem 1.6 for Triebel–Lizorkin spaces.

1.7.3 Wavelet Frames

The sharp results on the failure of unconditional convergence of Haar expansions in [23] (described above) have been extended by R. Srivastava [25] to classes of spline wavelets with more restrictive smoothness assumptions. It is then natural to investigate extensions of our results on Haar frames to suitable classes of oversampled systems of spline wavelets.

1.7.4 Higher Dimensions

In this paper we have found it appropriate to present our results for function spaces in ${\mathbb R}$ (rather than ${\mathbb R}^d$). It seems likely that many arguments in the paper could be adapted, with only standard modifications, to the higher dimensional context (such as those in §4 or §6). On the other hand, the arguments in which the 1-dimensional setting is more present (such as the bootstrapping in §7) may require more elaborate changes. We do not pursue these questions here.

1.8 Structure of the Paper

In §2 we compile notation and known results about maximal operators in function spaces. We also review some properties about the Chui-Wang wavelet basis, that will be used later in our proofs.

In §3 we clarify the role of the space $\mathscr {B}$ and prove Proposition 1.1.

In §4 we consider the characterization of function spaces via Haar frames, giving the proofs of Theorems 1.2 and 1.3 (as a combination of four Propositions 4.1, 4.4, 4.5 and 4.9).

In §5 we establish Haar frame characterizations of Sobolev and bounded variation spaces and give a proof of Theorem 1.4.

In §6 we prove the sufficiency of the conditions for the embeddings into $B^{1,{\textrm{dyad}}}_{p,\infty }$ or $F^{1,{\textrm{dyad}}}_{p,\infty }$ in Theorem 1.7, and the sufficiency for the conditions of embedding into $B^{1/p-1,{\textrm{dyad}}}_{p,\infty }$ in Theorem 1.9.

In §7 we prove Theorems 1.6 and 1.8.

In §8 we prove necessary conditions for the embeddings into $B^{1,{\textrm{dyad}}}_{p,\infty }$. Specifically, in Theorem 1.7 the necessary conditions $q\le p$ in (1.26), $q\le 2$ in (1.27), (1.26), and $q\le 1$ in (1.28) correspond to Lemmas 8.1, 8.2, and 8.3, respectively.

In §9 we obtain necessary conditions in part (ii) of Theorem 1.9 for the embeddings into $B^{1/p-1,{\textrm{dyad}}}_{p,\infty }$.

In §10 we prove Theorem 1.10.

In §11 we give a simple proof for the fact that $C^1$ functions in $B^{1,{\textrm{dyad}}}_{p,q}$, with $q<\infty$, are constant (Proposition 11.1); moreover show that $B^{s,{\textrm{dyad}}}_{p,q}$ is not complete when $s<1/p-1$ (Proposition 11.2) and finally prove part (i) of Theorem 1.9 (see Proposition 11.3).

2 Preliminaries on Function Spaces and Wavelet Bases

2.1 Definition of Spaces

Let $s\in {\mathbb R}$ and $0<p, q\le \infty$ be given. We shall use both definitions and characterizations of $B^s_{p,q}$ and $F^s_{p,q}$ in terms of dyadic frequency decompositions and in terms of sequences of compactly supported kernels with cancellation (see e.g. [28, 2.5.3, 2.4.6] or [29, §1.3,1.4] where the terminology local means is used).

Consider two functions $\beta _0, \beta \in {\mathcal {S}}({\mathbb R})$ such that $|\widehat{\beta }_0(\xi )|>0$ when $|\xi |\le 1$ and $|\widehat{\beta }(\xi )|>0$ when $1/4\le |\xi |\le 1$. Assume further that $\beta (\cdot )$ has vanishing moments up to a sufficiently large order $M\in {\mathbb {N}}$, that is,

$$\begin{aligned} \int _{{\mathbb {R}}} \beta (x)\,x^{m}\,dx = 0\quad \hbox {when}\quad m < M\,. \end{aligned}$$

(2.1)

The precise value of M is not relevant, but for the properties used in the paper it will suffice with

$$\begin{aligned} M >1/p+|s|+2 . \end{aligned}$$

(2.2)

We let $\beta _k(x):=2^{k}\beta (2^kx)$, $k\ge 1$, and define for $k\in {\mathbb N}_0$ the convolution operators

$$\begin{aligned} L_kf:=\beta _k*f, \end{aligned}$$

acting on distributions $f\in {\mathcal {S}}'({\mathbb R})$.

The Besov space $B^s_{p,q}({\mathbb {R}})$ is the set of all distributions $f\in {\mathcal {S}}'({\mathbb {R}})$ such that

$$\begin{aligned} \Vert f\Vert _{B^s_{p,q}} := \Big (\sum _{k=0}^\infty \Big (2^{ks}\Vert L_k f\Vert _p\Big )^q\Big )^{1/q} <\infty . \end{aligned}$$

(2.3)

If $p<\infty$, the Triebel–Lizorkin space $F^s_{p,q}({\mathbb {R}})$ is the set of all $f\in {\mathcal {S}}'({\mathbb {R}})$ such that

$$\begin{aligned} \Vert f\Vert _{F^s_{p,q}} := \Big \Vert \Big (\sum _{k=0}^\infty 2^{ksq}|L_k f(x)|^q\Big )^{1/q}\Big \Vert _p<\infty . \end{aligned}$$

(2.4)

Different choices of $\beta _0,\beta$ give rise to the same spaces and equivalent quasi-norms; see e.g. [29, Theorem 1.7]. From now on we will assume that

$$\begin{aligned} {\text { supp }}\beta _0\subset (-1/2,1/2){\quad \hbox {and}\quad }{\text { supp }}\beta \subset (-1/2,1/2). \end{aligned}$$

We shall often use the following decomposition of distributions in ${\mathcal {S}}'({\mathbb R})$. Let $\eta _0\in C^\infty _0({\mathbb {R}})$ be supported on $\{|\xi |<3/4\}$ and such that $\eta _0(\xi )=1$ when $|\xi |\le 1/2$. Define the convolution operators $\Lambda _0$, and $\Lambda _k$ for $k\ge 1$, by

$$\begin{aligned} \widehat{\Lambda _0 f}(\xi )&=\frac{\eta _0(\xi )}{\widehat{\beta }_0(\xi )}\widehat{f}(\xi ) \\ \widehat{\Lambda _k f}(\xi )&=\frac{\eta _0(2^{-k}\xi ) -\eta _0(2^{-k+1}\xi )}{\widehat{\beta }(2^{-k}\xi )}\widehat{f}(\xi ), \quad k\ge 1. \end{aligned}$$

Then, for all $f\in {\mathcal {S}}'({\mathbb R})$ we have

$$\begin{aligned} f=\sum _{k=0}^\infty L_k \Lambda _k f \end{aligned}$$

(2.5)

with convergence in ${\mathcal {S}}'({\mathbb R})$. Also, it holds

$$\begin{aligned} \Big (\sum _{k=0}^\infty \Big (2^{ks}\Vert \Lambda _k f\Vert _p\Big )^q\Big )^{1/q}\lesssim \Vert f\Vert _{B^s_{p,q}}, \end{aligned}$$

and likewise for the F-norms.

2.2 Maximal Functions

We follow Triebel [27, 28]. Given $f\in L_1^\textrm{loc}({\mathbb R})$, consider the Hardy-Littlewood maximal function, defined by

$$\begin{aligned} Mf(x) := \sup \limits _{x \in I} \frac{1}{|I|}\int _I |f(x)|\,dx\,, \end{aligned}$$

(2.6)

where the $\sup$ is taken over all intervals I that contain x. A classical result of Fefferman and Stein asserts that, if $1<p<\infty$ and $1<q\le \infty$ then

$$\begin{aligned} \Big \Vert \Big (\sum \limits _{j} |Mf_j|^q\Big )^{1/q}\Big \Vert _p \lesssim \Big \Vert \Big (\sum \limits _{j} |f_j|^q\Big )^{1/q}\Big \Vert _p\,. \end{aligned}$$

(2.7)

for all sequences of measurable functions $\{f_j\}$ with finite right hand side.

Let us further define the Peetre maximal functions [21]. Given $j\in {\mathbb {N}}$ and $A>0$ we let

$$\begin{aligned} {\mathfrak {M}}^{**}_{j,A} f(x)= \sup _{h\in {\mathbb {R}}} \frac{|f(x+h)|}{(1+2^j|h|)^A}. \end{aligned}$$

Let ${\mathcal {E}}_j$ be the set of distributions $f\in {\mathcal {S}}'({\mathbb {R}})$ such that ${\text { supp }}\widehat{f}$ is supported in an interval of diameter $\le 2^{j+2}$. Then for all $f\in {\mathcal {E}}_j$ it holds

$$\begin{aligned} {\mathfrak {M}}^{**}_{j,A} f(x) \lesssim _{s, A}\,\big [M(|f|^s)(x)\big ]^{1/s}, \end{aligned}$$

(2.8)

provided that $s\ge 1/A$; see [21] or [27, Theorem 1.3.1]. In particular, if $0<p\le \infty$ and $A>1/p$ then

$$\begin{aligned} \Vert {\mathfrak {M}}^{**}_{j,A} f\Vert _p \le C_{p,A} \Vert f\Vert _p, \quad f\in {\mathcal {E}}_j. \end{aligned}$$

(2.9)

Also, from (2.7) and (2.8), if $0<p<\infty$, $0<q\le \infty$ and $A>\max \{ 1/p, 1/q\}$, then

$$\begin{aligned} \Big \Vert \Big (\sum _{j} |{\mathfrak {M}}^{**}_{j,A} f_j|^q\Big )^{1/q} \Big \Vert _p \le C_{p,q,A} \Big \Vert \Big (\sum _{j} | f_j|^q\Big )^{1/q} \Big \Vert _p \end{aligned}$$

(2.10)

for all sequences of functions $(f_j)$ such that $f_j\in {\mathcal {E}}_j$.

Below we shall also use the (smaller) maximal functions

$$\begin{aligned} {\mathfrak {M}}_jf(x)=\sup _{|h|\le 2^{-j}}|f(x+h)|{\quad \hbox {and}\quad }{\mathfrak {M}}^*_jf(x)=\sup _{|h|\le 2^{-j+2}}|f(x+h)|. \end{aligned}$$

(2.11)

Note that for all $A>0$ it holds

$$\begin{aligned} {\mathfrak {M}}_jf(x)\le {\mathfrak {M}}^*_jf(x)\lesssim {\mathfrak {M}}^{**}_{j,A}f(x), \end{aligned}$$

so in particular, for all $0<p\le \infty$ we have

$$\begin{aligned} \big \Vert {\mathfrak {M}}^*_jf\Vert _p\lesssim \Vert f\Vert _p,\quad f\in {\mathcal {E}}_j. \end{aligned}$$

(2.12)

We shall also make use of the following elementary inequality: if $0<p\le \infty$ then

$$\begin{aligned} \Vert {\mathfrak {M}}^*_j f\Vert _p\lesssim 2^{\ell /p}\,\Vert {\mathfrak {M}}_{j+\ell }f\Vert _p,\quad \ell \ge 0. \end{aligned}$$

(2.13)

To prove this assertion, if we let $x_\nu =\nu 2^{-(j+\ell )}$, then we have

$$\begin{aligned} {\mathfrak {M}}^*_jf(x)\le \sup _{|\nu |\le 2^{\ell +2}}|{\mathfrak {M}}_{j+\ell }f(x+x_\nu )|\le \Big (\sum _{|\nu |\le 2^{\ell +2}}|{\mathfrak {M}}_{j+\ell }f(x+x_\nu )|^p\Big )^\frac{1}{p}. \end{aligned}$$

Then, taking $L_p$ quasi-norms one easily obtains (2.13).

2.3 Chui–Wang Wavelets

The proofs of  Theorems 1.2 and 1.3 will require a characterization in terms of a wavelet basis generated by the Chui-Wang polygon and its dual.

Define the m-fold convolution ${\mathcal {N}}_m$ of characteristic functions of [0, 1), i.e. ${\mathcal {N}}_1={\mathbb {1}}_{[0,1)}$, and, for $m\ge 2$, ${\mathcal {N}}_m={\mathcal {N}}_{m-1} *{\mathbb {1}}_{[0,1)}$. In particular we get for $m=2$ the hat function

$$\begin{aligned} {\mathcal {N}}_2(x)= {\left\{ \begin{array}{ll} x, &{}\quad x\in [0,1], \\ 2-x, &{}\quad x\in [1,2], \\ 0, &{}\quad x\in {\mathbb {R}}\setminus [0,2]. \end{array}\right. }\end{aligned}$$

(2.14)

Let

$$\begin{aligned} {\mathcal {N}}_{2;j,\nu }(x):={\mathcal {N}}_2(2^{j}x-\nu ),\quad j\ge 0, \,\nu \in {\mathbb Z}, \end{aligned}$$

which is a hat function adapted to ${\text { supp }}{\mathcal {N}}_{2;j,\nu }=[2^{-j}\nu , 2^{-j}(\nu +2)]$.

The next elementary observation will be crucial in what follows.

Lemma 2.1

If f is locally absolutely continuous in ${\mathbb R}$, then for all $j\ge 1$ and $\nu \in {\mathbb Z}$ it holds

$$\begin{aligned} {\langle {f'},{{\mathcal {N}}_{2;j,\nu }}\rangle } \,=\,-2^j\,{\langle {f},{\tilde{h}_{j-1,\nu }}\rangle }, \end{aligned}$$

(2.15)

while for $j=0$ it holds

$$\begin{aligned} {\langle {f'},{{\mathcal {N}}_{2;0,\nu }}\rangle }=-{\langle {f},{h_{-1,\nu }}\rangle }+{\langle {f},{h_{-1,\nu +1}}\rangle },\quad \nu \in {\mathbb Z}. \end{aligned}$$

Proof

Integrating by parts one has

$$\begin{aligned} {\langle {f'},{{\mathcal {N}}_{2;j,\nu }}\rangle } \,=\,-{\langle {f},{({\mathcal {N}}_{2;j,\nu })'}\rangle }. \end{aligned}$$

Now, a simple computation gives

$$\begin{aligned} ({\mathcal {N}}_{2;j,\nu })'= & {} 2^j{\mathbb {1}}_{(2^{-j}\nu , 2^{-j}(\nu +1))}-2^j{\mathbb {1}}_{(2^{-j}(\nu +1), 2^{-j}(\nu +2))}\\= & {} 2^j{\mathbb {1}}_{I_{j,\nu }}-2^j{\mathbb {1}}_{I_{j,\nu +1}} \,=\,2^j\,\tilde{h}_{j-1,\nu }, \end{aligned}$$

where the last equality follows from the definition of the shifted Haar system in (1.8) (if $j\ge 1$). Combining the two expressions one obtains (2.15). The case $j=0$ is similar. $\square$

The Chui-Wang polygon [7, Theorem 1], [6, 6.2.5, 6.2.6] is the compactly supported wavelet given by

$$\begin{aligned} \begin{aligned} \psi (x)&= \frac{1}{2}\sum \limits _{\ell = 0}^2(-1)^{\ell }{\mathcal {N}}_4(\ell +1)\mathcal {N}_{4}^{\,''}(2x-\ell )\,,\\&= \frac{1}{2}\sum \limits _{\ell = 0}^2(-1)^{\ell }\mathcal {N}_4(\ell +1)\sum \limits _{j=0}^2(-1)^j\left( {\begin{array}{c}2\\ j\end{array}}\right) \mathcal {N}_2(2x-j-\ell )\\&= \sum \limits _{k\in {\mathbb {Z}}} b_k\cdot \mathcal {N}_2(2x-k) \end{aligned} \end{aligned}$$

(2.16)

where $(b_k)$ is a finite sequence supported in $\{0,\ldots ,4\}$. The wavelet $\psi$ is compactly supported and has two vanishing moments, i.e., $\int \psi (x) dx = \int x\psi (x)dx = 0$. For $j\in {\mathbb {N}}_0$ and $\mu \in {\mathbb {Z}}$ let

$$\begin{aligned} \psi _{j,\mu } (x)=\psi (2^j x-\mu ), \end{aligned}$$

while for $j=-1$ we let

$$\begin{aligned} \psi _{-1,\mu }(x)={\mathcal {N}}_{2;0,\mu }(x)={\mathcal {N}}_2(x-\mu ). \end{aligned}$$

Then we have the orthogonality relations with respect to different scales

$$\begin{aligned} \langle \psi _{j,\mu }, \psi _{j',\mu '} \rangle = 0\quad ,\quad j \ne j'. \end{aligned}$$

Fig. 3

The Chui-Wang wavelet $\Psi _2$ of order 2 and its dual $\Psi _2^*$

In contrast to that it only forms a Riesz basis within one and the same scale with respect to different translations. The dual basis can be computed precisely [8] and does not provide compact support. However, the coefficients $a_k$ in

$$\begin{aligned} \psi ^*(x) = \sum \limits _{k\in {\mathbb {Z}}} a_k\psi (x-k) \end{aligned}$$

(2.17)

are exponentially decaying; see the paper [8] for explicit formulas for $a_k$, and Fig. 3 below for a graphical representation. Observe from (2.17) that also $\psi ^*$ has two vanishing moments.

Using this construction, Derevianko and Ullrich provided the following characterization for the $F^s_{p,q}$ and $B^s_{p,q}$ spaces; see [8, Theorem 5.1].

Theorem 2.2

[8] Let $0<p\le \infty$, $0<q\le \infty$.

(i) If $p<\infty$ and

$$\begin{aligned} \max \{1/p,1/q\}-2< r < 1+\min \{1/p,1/q, 1\}\end{aligned}$$

(2.18)

then we have for all $f \in B^{-2}_{\infty ,1}({\mathbb {R}})$

$$\begin{aligned} \Vert f\Vert _{F^r_{p,q}}\approx \Big \Vert \Big (\sum \limits _{j=-1}^{\infty } 2^{jrq}\Big |\sum \limits _{\mu \in {\mathbb {Z}}} 2^j\langle f,\psi _{j,\mu }\rangle {\mathbb {1}}_{I_{j,\mu }}\Big |^q \Big )^{1/q}\Big \Vert _p. \end{aligned}$$

(2.19)

(ii) If

$$\begin{aligned} 1/p-2<r<\max \{1+1/p,2\} \end{aligned}$$

(2.20)

then we have for all $f\in B^{-2}_{\infty ,1}({\mathbb {R}})$

$$\begin{aligned} \Vert f\Vert _{B^r_{p,q}} \approx \Big (\sum \limits _{j=-1}^{\infty } 2^{j(r-1/p) q}\Big [\sum \limits _{\mu \in {\mathbb {Z}}} |2^j\langle f,\psi _{j,\mu }\rangle |^p\Big ]^{q/p} \Big )^{1/q} \,. \end{aligned}$$

(2.21)

Remark 2.3

Concerning part (i), we remark that the result stated in [8, Theorem 5.1], requires the additional restriction $r<1$, which comes from a similar restriction in [8, Proposition 5.4]. This restriction, however, can be lifted and replaced by $r<1+\max \{1/p,1/q\}$, using a complex interpolation argument which involves part (ii) (case $p=q$), as we discuss in Step 3 of Proposition 4.5 below.

3 Haar Functions as Linear Functionals on $\mathscr {B}$: Proof of Proposition 1.1

3.1 Proof of (i) and (ii)

Since every $h\in {\mathscr {H}}$ is a difference of two characteristic functions of intervals of length $\le 1$ part (ii) is an immediate consequence of part (i). It suffices to analyze $\lambda _I$ on $\mathscr {B}$, for each bounded interval I. Let $f\in \mathscr {B}=B^{-1}_{\infty ,1}({\mathbb R})$. Using the decomposition in (2.5) we can write $f=\sum _{k=0}^\infty L_k f_k$ where the Fourier transform $\widehat{f}_k$ is supported in $\{\xi :|\xi |\le 2^k\}$ and the $f_k$ satisfy

$$\begin{aligned} \sum _{k\ge 0} 2^{-k} \Vert f_k\Vert _\infty \lesssim \Vert f\Vert _{\mathscr {B}}; \end{aligned}$$

(3.1)

here, $L_k f=\beta _k*f$ where $\beta _0,\beta$ are even functions in $C^\infty _c(-1/2,1/2)$, and $\beta _k=2^{k}\beta (2^{k}\cdot )$, for $k\ge 1$. Also, $\int \beta (x)dx=0$.

We let $\lambda _I(f):=\sum _{k=0}^\infty {\langle {f_k},{L_k{\mathbb {1}}_I}\rangle }$, which we sometimes denote by ${\langle {f},{{\mathbb {1}}_I}\rangle }$. Note that

$$\begin{aligned} \Vert L_0{\mathbb {1}}_I\Vert _1\lesssim |I|.\end{aligned}$$

(3.2)

By (3.1) one needs to show that $\Vert L_k {\mathbb {1}}_I \Vert _1\lesssim 2^{-k}$ for $k\ge 1$; one actually gets the better estimate

$$\begin{aligned} \Vert L_k {\mathbb {1}}_I \Vert _1\lesssim \min \{ |I|, 2^{-k}\}, \quad k\ge 1. \end{aligned}$$

(3.3)

Hence $|\lambda _I(f)|\lesssim \max \{|I|,1\} \sum _{k\ge 0} 2^{-k} \Vert f_k\Vert _\infty$ and we deduce that $\lambda _I$ extends to a bounded linear functional on $\mathscr {B}$, with $\Vert \lambda _I\Vert _{\mathscr {B}^*}\lesssim \max \{1,|I|\}$.

It remains to verify (3.3). Fix I, with center $y_I$, and assume first that $2^{-k}>|I|$. Then the function $L_k {\mathbb {1}}_I=\beta _k*{\mathbb {1}}_I$ is supported in an interval centered at $y_I$ with length $O(2^{-k})$ and satisfies $|\beta _k *{\mathbb {1}}_I(x)|\le \Vert \beta _k\Vert _\infty \,\Vert {\mathbb {1}}_I\Vert _1 \lesssim 2^{k} |I|.$ Thus we obtain $\Vert \beta _k *{\mathbb {1}}_I\Vert _1\lesssim |I|$ which is in (3.3) in this case.

Now assume $2^{-k}\le |I|$. Let $y_+$ and $y_-$ be the endpoints of I. Let ${\mathcal {U}}_k$ be the union of the two closed intervals of length $2^{-k+2}$ centered at $y_+$ and $y_-$. Then $\beta _k*{\mathbb {1}}_I$ is supported in ${\mathcal {U}}_k$, which has size $|{\mathcal {U}}_k|=O(2^{-k})$. This assertion, combined with $\Vert \beta _k *{\mathbb {1}}_I \Vert _\infty \le \Vert \beta _k\Vert _1\,=O(1)$, also implies (3.3) in this case.

3.2 Proof of (iii)

For the argument below we shall use the dyadic averaging operators, defined for $N\ge 0$ by

$$\begin{aligned} {\mathbb {E}}_N f(x):=\sum _{\mu \in {\mathbb {Z}}} \,2^{N} \,\langle f, {\mathbb {1}}_{I_{N,\mu }}\rangle \,{\mathbb {1}}_{I_{N,\mu }}(x). \end{aligned}$$

(3.4)

In view of (i), these operators can be defined acting on distributions $f\in \mathscr {B}$ such that $\mathbb {E}_N:\mathscr {B}\rightarrow L_\infty$ has operator norm $O(2^N)$.

Let now $f\in \mathscr {B}$ such that $\langle f,h\rangle =0$, for all $h\in {\mathscr {H}}$. Since each ${\mathbb {1}}_{I_{N,\mu }}$ belongs to ${\text{ span }}{\,\mathscr {H}}$, this implies that ${\mathbb E}_Nf=0$, for all $N\ge 0$. We then must show that $f=0$, which is a direct consequence of part (b) in the following lemma.

Lemma 3.1

(a) The operators ${\mathbb E}_N$ satisfy the uniform bound

$$\begin{aligned} \sup _{N\ge 0}\big \Vert {\mathbb E}_N\Vert _{\mathscr {B}\rightarrow B^{-1}_{\infty ,\infty }}<\infty . \end{aligned}$$

(b) If $f\in \mathscr {B}$  then $\,\Vert {\mathbb E}_Nf -f \Vert _{B^{-1}_{\infty ,\infty }}\rightarrow 0$ as $N\rightarrow \infty$.

Proof

Part (a) is implicit in [14]. Indeed, it follows by combining the estimates stated in the four propositions in [14, §4], for the cases $s=-1$ and $p=\infty$.

We now show part (b). Let $f\in \mathscr {B}$ and write $f=\sum _{k=0}^\infty L_k f_k$ as at the beginning of §3.1. The above series converges in ${\mathcal {S}}'$ and also in the $\mathscr {B}$-norm. Then, given ${\varepsilon }>0$ one can find $g=\sum _{k=0}^JL_kf_k$ such that

$$\begin{aligned} \Vert f-g\Vert _\mathscr {B}<{\varepsilon }. \end{aligned}$$

Observe that g is bounded, since

$$\begin{aligned} \Vert g\Vert _\infty \le \sum _{k=0}^J\Vert L_kf_k\Vert _\infty \lesssim \sum _{k=0}^J \Vert f_k\Vert _\infty \lesssim 2^J\Vert f\Vert _\mathscr {B}. \end{aligned}$$

A similar reasoning shows that $\Vert g'\Vert _\infty <\infty$, so in particular g is uniformly continuous. Thus there exists an integer $N_0\in {\mathbb N}$ such that

$$\begin{aligned} \Vert g-{\mathbb E}_Ng\Vert _\infty <{\varepsilon }, \text { for all }\,N\ge N_0. \end{aligned}$$

Combining these assertions, and using the trivial embeddings

$$\begin{aligned} L_\infty \hookrightarrow \mathscr {B}\hookrightarrow B^{-1}_{\infty ,\infty }, \end{aligned}$$

we obtain, for all $N\ge N_0$,

$$\begin{aligned} \Vert f-{\mathbb E}_Nf\Vert _{B^{-1}_{\infty ,\infty }}\le & {} \Vert f-g\Vert _{\mathscr {B}} +\Vert g-{\mathbb E}_Ng\Vert _\infty + \Vert {\mathbb E}_N(g-f)\Vert _{B^{-1}_{\infty ,\infty }}\\\lesssim & {} 2{\varepsilon }+ C\,\Vert g-f\Vert _\mathscr {B}\lesssim {\varepsilon }, \end{aligned}$$

where in the second inequality we have used part (a).

Remark 3.2

As H. Triebel pointed out to us, it is possible to give a different proof of Proposition 1.1 based on duality identities as in [27, Remark 2, p.180]. To do so, one can regard ${\langle {f},{{\mathbb {1}}_I}\rangle }$ as a duality pairing using the facts ${\mathbb {1}}_I\in B^1_{1,\infty }=(\mathring{B}^{-1}_{\infty ,1})^*$, and $f\in \mathring{B}^{-1}_{\infty ,1}$ whenever $f\in \mathscr {B}$ with compact support.

4 Characterizations by Haar Frames: Proofs of Theorems 1.2 and 1.3

The proofs of Theorems 1.2 and 1.3 will follow from the four Propositions 4.1, 4.4, 4.5 and 4.9 stated below.

The first proposition is a strengthening of [30, Proposition 2.8]. It gives one of the inclusions asserted in Theorems 1.2 and 1.3. The region of indices is the same as in Fig. 2. We set ${\mathfrak {c}}(f)=\{{\mathfrak {c}}_{j,\mu }(f)\}_{j\ge -1, \mu \in {\mathbb {Z}}}$ with ${\mathfrak {c}}_{j,\mu }(f)$ as in (1.15).

Proposition 4.1

Let $0< p, q \le \infty$ and $s\in {\mathbb R}$.

(i) If $p<\infty$ and $\max \{1/p-1,1/q-1\}< s < 1\,$, then for all $f\in F^s_{p,q}$

$$\begin{aligned} \Vert {\mathfrak {c}}(f)\Vert _{f^s_{p,q}} \lesssim \Vert f\Vert _{F^s_{p,q}}\,. \end{aligned}$$

(4.1)

(ii) If $1/p-1<s<1$, then for all $f\in B^s_{p,q}$

$$\begin{aligned} \Vert {\mathfrak {c}}(f)\Vert _{b^s_{p,q}} \lesssim \Vert f\Vert _{B^s_{p,q}}. \end{aligned}$$

Proof

To avoid dealing separately with $\widetilde{h}_{j,\nu }$ with $\nu$ even or odd, we prove a slightly more general result. For a fixed ${\delta }\in [0,1]$ and for $j\ge 0$ and $\mu \in {\mathbb Z}$, consider the shifted Haar function

$$\begin{aligned} h^{{\delta }}_{j,\mu }(x):=h_{j,\mu }(x-{\delta }2^{-j})=h\big (2^jx-(\mu +{\delta })\big ), \end{aligned}$$

whose support is the interval $I_{j,\mu }+{\delta }2^{-j}$. When $j=-1$, we just let $h^{{\delta }}_{-1,\mu }=h_{-1,\mu }={\mathbb {1}}_{[\mu ,\mu +1)}$. Part (i) will then be a consequence of the following estimate

$$\begin{aligned} \Big \Vert \Big (\sum \limits _{j=-1}^{\infty } 2^{jsq}\Big |\sum \limits _{\mu \in {\mathbb {Z}}} 2^j\langle f, h^{{\delta }}_{j,\mu }\rangle \, {\mathbb {1}}_{I_{j,\mu }}\Big |^q \Big )^{1/q}\Big \Vert _p \lesssim \Vert f\Vert _{F^s_{p,q}}\,, \end{aligned}$$

(4.2)

where the constants are independent of ${\delta }\in [0,1]$. Indeed, (4.1) follows from (4.2) applied to ${\delta }=0$ and ${\delta }=1/2$.

We now prove (4.2) for a fixed ${\delta }\in [0,1]$. In the proof below we denote by ${\Delta }_{j,\mu }$ the set of discontinuity points of $h^{{\delta }}_{j,\mu }$, that is

$$\begin{aligned} {\Delta }_{j,\mu }=\big \{(\mu +{\delta }+i)2^{-j}{\,\,\,:\,\,\,}i=0,\tfrac{1}{2},1\big \}. \end{aligned}$$

Lemma 4.2

Let $g\in L_1^{\textrm{loc}}({\mathbb R})$, $k\in {\mathbb N}_0$ and $j\ge -1$. Then

a) If $k\ge j$ then

$$\begin{aligned} \big |2^j{\langle {g},{L_kh^{{\delta }}_{j,\mu }}\rangle } \big |\lesssim 2^{-(k-j)}\,\sum _{z\in {\Delta }_{j,\mu }}{\mathfrak {M}}_k(g)(z); \end{aligned}$$

(4.3)

moreover, for every $A>0$,

$$\begin{aligned} \begin{aligned} \big |2^j{\langle {g},{L_kh^{{\delta }}_{j,\mu }}\rangle }\big |\,{\mathbb {1}}_{I_{j,\mu }}(x)\,&\lesssim \, 2^{-(k-j)}\,{\mathfrak {M}}^*_{j}(g)(x)\\&\lesssim \, 2^{-(k-j)}\,2^{(k-j)A}\,{\mathfrak {M}}^{**}_{k,A}(g)(x). \end{aligned} \end{aligned}$$

(4.4)

b) If $j>k$ then, for every $A>0$,

$$\begin{aligned} \begin{aligned} \big |2^j{\langle {g},{L_kh^{{\delta }}_{j,\mu }}\rangle }\big |\,{\mathbb {1}}_{I_{j,\mu }}(x)&\lesssim \, 2^{-(j-k)}\,{\mathfrak {M}}_{k}(g)(x)\\&\lesssim \, 2^{-(j-k)}\,{\mathfrak {M}}^{**}_{k,A}(g)(x). \end{aligned} \end{aligned}$$

(4.5)

Proof

a) If $k\ge j$ then the function $L_kh^{{\delta }}_{j,\mu }=\beta _k*h^{{\delta }}_{j,\mu }$ is supported in ${\Delta }_{j,\mu }+O(2^{-k})$ and has size

$$\begin{aligned} \Vert \beta _k*h^{{\delta }}_{j,\mu }\Vert _\infty \le \Vert \beta _k\Vert _1=O(1). \end{aligned}$$

This immediately gives (4.3). Now, if $z\in {\Delta }_{j,\mu }$ and $x\in I_{j,\mu }$ we have

$$\begin{aligned} {\mathfrak {M}}_kg(z) = \sup _{|h|\le 2^{-k}}|g(z+h)|\le & {} \sup _{|u|\le 2^{-j+2}}|g(x+u)|= {\mathfrak {M}}^*_j(g)(x)\\\lesssim & {} 2^{(k-j)A}\,{\mathfrak {M}}^{**}_{k,A}(g)(x), \end{aligned}$$

which together with (4.3) proves (4.4).

b) If $k<j$ and $x\in I_{j,\mu }$, then the function $L_kh^{{\delta }}_{j,\mu }=\beta _k*h^{{\delta }}_{j,\mu }$ is supported in $x+O(2^{-k})$, and we can bound its size by

$$\begin{aligned} |L_kh^{{\delta }}_{j,\mu }(u)|\lesssim 2^{2(k-j)}. \end{aligned}$$

(4.6)

This last assertion follows from the property $\int h^{{\delta }}_{j,\mu }=0$, by writing

$$\begin{aligned} |L_kh^{{\delta }}_{j,\mu }(u)|= & {} \Big |\int \big (\beta _k(u-y)-\beta _k(u-x)\Big )\,h^{{\delta }}_{j,\mu }(y)\,dy\Big |\\= & {} \Big |\int \int _0^1 \beta '_k\big (u-(1-t)x-ty\big )\,dt\,(x-y)\,h^{{\delta }}_{j,\mu }(y)\,dy\Big |\\\lesssim & {} 2^{2k-2j}, \end{aligned}$$

using in the last step that $|x-y|\le 2^{-j+1}$ when $x\in I_{j,\mu }$ and $y\in {\text { supp }}h^{{\delta }}_{j,\mu }$. Combining the above support and size estimates, one easily obtains (4.5). $\square$

We continue the proof of Proposition 4.1.i. Let $f\in F^s_{p,q}$, and write it as $f=\sum _{k=0}L_kf_k$ with $f_k=\Lambda _kf$ as in (2.5). Note that, since $F^s_{p,q}\subset \mathscr {B}$, we have

$$\begin{aligned} {\langle {f},{h^{{\delta }}_{j,\mu }}\rangle }= \sum _{k=0}^\infty {\langle {f_k},{L_kh^{{\delta }}_{j,\mu }}\rangle }. \end{aligned}$$

Now, the estimates in Lemma 4.2, suitably applied to each $f_k$, can be grouped into

$$\begin{aligned} \sum _{\mu }\big |2^j{\langle {f},{h^{{\delta }}_{j,\mu }}\rangle }\big |\,{\mathbb {1}}_{I_{j,\mu }}(x)\lesssim&{} \sum _{k\ge 0} 2^{-|k-j|} 2^{A\,(k-j)_+}\,{\mathfrak {M}}^{**}_{k,A}(f_k)(x)\nonumber \\ {\tiny (\ell =k-j)}\;\lesssim&{} \sum \limits _{\ell \in {\mathbb {Z}}} a(\ell ,A)\,{\mathfrak {M}}^{**}_{j+\ell ,A} [f_{j+\ell }] (x)\, =:G_j(x), \end{aligned}$$

(4.7)

where we set $f_m\equiv 0$ for $m<0$ and

$$\begin{aligned} a(\ell ,A) = \left\{ \begin{array}{rcl} 2^{\ell }&{}:&{} \ell <0,\\ 2^{(A-1)\ell }&{}:&{} \ell \ge 0. \end{array}\right. \end{aligned}$$

(4.8)

At this point one takes $L_p(\ell _q)$ quasi-norms of the above expressions. Letting $u:=\min \{p,q,1\}$, and using the u-triangle inequality we obtain

$$\begin{aligned} \begin{aligned}&\Big \Vert \Big (\sum \limits _{j \ge -1}\Big |2^{js}G_j\Big |^q\Big )^{1/q}\Big \Vert _p\\ {}&\quad \lesssim \Big (\sum \limits _{\ell \in {\mathbb {Z}}} \Big [a(\ell ,A)2^{-s\ell }\,\Big \Vert \Big ( \sum \limits _{j\in {\mathbb Z}}|2^{(j+\ell )s}{\mathfrak {M}}^{**}_{j+\ell ,A}[f_{j+\ell }]|^q\Big )^{1/q}\Big \Vert _p\Big ]^u\Big )^{1/u}\\ {}&\quad \lesssim \Vert f\Vert _{F^s_{p,q}}\,\Big (\sum \limits _{\ell \in {\mathbb Z}}\big (a(\ell ,A)2^{-s\ell }\big )^u\Big )^{1/u}\,\lesssim \Vert f\Vert _{F^s_{p,q}}, \end{aligned} \end{aligned}$$

(4.9)

where in the last line we use Peetre’s maximal inequality (2.10) and $A>\max \{1/p,1/q\}$, and in the last step we additionally need that $A-1< s < 1$. This can always be achieved for an appropriate choice of A because of our assumption $\max \{\frac{1}{p},\frac{1}{q}\}-1<s<1.$

As before, part (ii) in Proposition 4.1 will be a consequence of the more general estimate

$$\begin{aligned} \Big (\sum \limits _{j=-1}^{\infty } 2^{j(s-1/p)q}\Big (\sum \limits _{\mu \in {\mathbb {Z}}}| 2^j{\langle {f},{h^{{\delta }}_{j,\mu }}\rangle }|^p\Big )^{q/p}\Big )^{1/q} \lesssim \, \Vert f\Vert _{B^s_{p,q}}, \end{aligned}$$

(4.10)

for ${\delta }\in [0,1]$. Notice that

$$\begin{aligned} B_j:=2^{-j/p}\Big (\sum _{\mu }\big |2^j{\langle {f},{h^{{\delta }}_{j,\mu }}\rangle }\big |^p\Big )^\frac{1}{p}=\Big \Vert \sum _\mu \big |2^j{\langle {f},{h^{{\delta }}_{j,\mu }}\rangle }\big |\,{\mathbb {1}}_{I_{j,\mu }}\Big \Vert _{p}. \end{aligned}$$

(4.11)

We shall argue a bit differently to refine the pointwise estimate in (4.7). Observe from Lemma 4.2 that we can also write

$$\begin{aligned} \Big \Vert \sum _\mu \big |2^j{\langle {f_k},L_k{h^{{\delta }}_{j,\mu }}\rangle }\big |\,{\mathbb {1}}_{I_{j,\mu }}\Big \Vert _{p}\lesssim&{} 2^{-|k-j|}\big \Vert {\mathfrak {M}}^*_{\min \{j,k\}}(f_k)\big \Vert _p\\ {\tiny \text {by }\;(2.13)}\;\lesssim&{} 2^{-|k-j|}\,2^{\frac{(k-j)_+}{p}}\,\big \Vert {\mathfrak {M}}_{k}(f_k)\big \Vert _p \\=&{} a(k-j, \tfrac{1}{p})\,\big \Vert {\mathfrak {M}}_{k}(f_k)\big \Vert _p, \end{aligned}$$

using in the last step the definition of $a(\ell ,A)$ in (4.8). So, letting as before $u:=\min \{p,q,1\}$, and using the u-triangle inequality we obtain

(4.12)

Observe that this time we apply the simpler estimate $\Vert {\mathfrak {M}}_{k}[f_{k}]\Vert _{p}\lesssim \Vert f_k\Vert _p$, see (2.12), while the very last step requires $1/p-1< s < 1$. $\square$

Remark 4.3

In view of the examples in [23], the condition $s>1/q-1$ is necessary in Proposition 4.1.i, even for the validity of the weaker inequality

$$\begin{aligned} \Vert f\Vert _{F^{s, \textrm{dyad}}_{p,q}}:= \Big \Vert \Big (\sum \limits _{j=-1}^{\infty } 2^{jsq}\Big |\sum \limits _{\mu \in {\mathbb {Z}}} 2^j\langle f,{h}_{j,\nu }\rangle {\mathbb {1}}_{I_{j,\mu }}\Big |^q \Big )^{1/q}\Big \Vert _p \lesssim \Vert f\Vert _{F^s_{p,q}}. \end{aligned}$$

(4.13)

Indeed, arguing as in [23, §6], for each $N\ge 2$ one constructs a (smooth) function $f=f_N\in F^{1/q-1}_{p,q}({\mathbb R})$ and a finite set,²$E=E_N\subset {\mathscr {H}}$ such that if $0<q\le p<\infty$ then

$$\begin{aligned} \Vert f\Vert _{F^{1/q-1}_{p,q}({\mathbb R})}\lesssim N^{1/q} {\quad \hbox {and}\quad }\Vert P_{E}(f)\Vert _{F^{1/q-1}_{p,q}({\mathbb R})} \ge N^{1+\frac{1}{q}}, \end{aligned}$$

(4.14)

where $P_E(f)$ denotes the projection onto ${\text {span}}\{h\}_{h\in E}$. Now observe that

$$\begin{aligned} \Vert f\Vert _{F^{s, \textrm{dyad}}_{p,q}}\ge \Vert P_E(f)\Vert _{F^{s, \textrm{dyad}}_{p,q}} \gtrsim \Vert P_E(f)\Vert _{F^{s}_{p,q}}, \end{aligned}$$

using in the last step the inequality in (4.20) (which holds for $s=1/q-1$). Thus, we conclude from (4.14) that

$$\begin{aligned} {\Vert f\Vert _{F^{1/q-1, \textrm{dyad}}_{p,q}}}\gtrsim N\,{\Vert f\Vert _{F^{1/q-1}_{p,q}}}. \end{aligned}$$

We turn to the converse inequalities in Theorems 1.2 and 1.3, which will be proved in Proposition 4.9. Before doing so we shall need some results concerning the inclusions $F^{s, \textrm{dyad}}_{p,q}\hookrightarrow F^s_{p,q}$ (and likewise for B-spaces) for the usual Haar system. Results of this nature can be found in [30, Proposition 2.6], but we give here direct proofs which are valid in a larger range of indices. These may have an independent interest.

The first result is obtained by duality from Proposition 4.1, but the range of indices is restricted to $1<p,q<\infty$. Recall the definitions of the sequence spaces $b^s_{p,q}$, $f^s_{p,q}$ in (1.19) and (1.20).

Proposition 4.4

Let $1<p,q<\infty$. (i) If $-1<s < \min \{1/p,1/q\}$ and $\beta =\{\beta _{j,\mu }\} \in f^s_{p,q}$ then

$$\begin{aligned} f:=\sum \limits _{j=-1}^\infty \sum \limits _{\mu \in {\mathbb {Z}}} \beta _{j,\mu }h_{j,\mu } \end{aligned}$$

(4.15)

converges in $F^s_{p,q}({\mathbb {R}})$ and

$$\begin{aligned} \Vert f\Vert _{F^s_{p,q}} \lesssim \Vert \beta \Vert _{f^s_{p,q}} \end{aligned}$$

(4.16)

(ii) If $-1<s<1/p$ and $\beta =\{\beta _{j,\mu }\} \in b^s_{p,q}$ then (4.15) converges in $B^s_{p,q}({\mathbb {R}})$ and

$$\begin{aligned} \Vert f\Vert _{B^s_{p,q}} \lesssim \Vert \beta \Vert _{b^s_{p,q}}. \end{aligned}$$

(4.17)

Proof

Consider the following duality pairing for sequences

$$\begin{aligned} \begin{aligned} \big \langle \alpha ,\beta \big \rangle&:= \sum \limits _{j}2^{-j}\sum \limits _{\mu } \alpha _{j,\mu }\,\beta _{j,\mu }\\&= \sum \limits _{j} \int _{-\infty }^{\infty }\Big (\sum \limits _{\mu }\alpha _{j,\mu } {\mathbb {1}}_{I_{j,\mu }}(x)\Big )\Big ( \sum \limits _{\mu '}\beta _{j,\mu '}{\mathbb {1}}_{j,\mu '}(x)\Big )\,dx \le \Vert \alpha \Vert _{f^s_{p,q}} \Vert \beta \Vert _{f^{-s}_{p',q'}}. \end{aligned} \end{aligned}$$

We define the so-called analysis (or sampling) operator ${\mathscr {A}}$ by

$$\begin{aligned} \begin{aligned}&{\mathscr {A}}: \, F^s_{p,q}({\mathbb {R}}) \longrightarrow f^s_{p,q}\\&\quad \quad f\longmapsto {\mathscr {A}}f(j,\mu ) = 2^j\langle f,h_{j,\mu }\rangle . \end{aligned} \end{aligned}$$

(4.18)

Its dual operator ${\mathscr {A}}'$ (the synthesis operator) is given by

$$\begin{aligned} \begin{aligned}&{\mathscr {A}}'\beta (x) = \sum \limits _{j,\mu } \beta _{j,\mu } h_{j,\mu }(x) . \end{aligned}\end{aligned}$$

(4.19)

Indeed, if $f\in F^s_{p,q}$ and $\beta = \{\beta _{j,\mu } \}$ is a finite sequence, then

$$\begin{aligned} \begin{aligned} \langle {\mathscr {A}}f, \beta \rangle&= \sum \limits _{j} 2^{-j} \sum \limits _{\mu } 2^j\langle f,h_{j,\mu }\rangle \cdot \beta _{j,\mu } \\&= \int f(x) \sum \limits _{j}\sum \limits _{\mu } \beta _{j,\mu }h_{j,\mu }(x)\,dx= \int f(x)\,{\mathscr {A}}'\beta (x)\,dx. \end{aligned} \end{aligned}$$

By Proposition 4.1, the operator ${\mathscr {A}}: F^s_{p,q}({\mathbb {R}})\rightarrow f^s_{p,q}$ is bounded when $\max \{1/p-1,1/q-1\}<s<1$. Hence, if we assume that $1\le p,q<\infty$, then ${\mathscr {A}}'$ will be bounded from $f^{-s}_{p',q'}$ to $F^{-s}_{p',q'}({\mathbb {R}})$, where

$$\begin{aligned} -1<-s<\min \{1/p',1/q'\}. \end{aligned}$$

In other words, if $-1<s<\min \{1/p,1/q\}$ and $1<p,q\le \infty$ then

$$\begin{aligned} \Big \Vert \sum \limits _{j,\mu } \beta _{j,\mu }h_{j,\mu }\Big \Vert _{F^s_{p,q}} \lesssim \Vert \beta \Vert _{f^s_{p,q}}. \end{aligned}$$

The proof of part (ii) is completely analogous. $\square$

In the following proposition we extend the previous estimate to the quasi-Banach range of parameters. The proof, which is now more involved, uses a non-trivial interpolation argument from [30, Proposition 2.6]. The range of indices we obtain is larger than in [30]; see Fig. 4.

Fig. 4

Parameter domain for the validity of Proposition 4.5, for $F^s_{p,q}({\mathbb R})$ (left figure) and $B^s_{p,q}({\mathbb R})$ (right figure)

Proposition 4.5

Let $0<p, q\le \infty$.

(i) If $p<\infty$ and $\max \{1/p,1/q,1\}-2<s<\min \{1/p,1/q\}$, then for every $\beta \in f^s_{p,q}$ the series in (4.15) converges to a distribution f in $F^s_{p,q}({\mathbb {R}})$, and it holds

$$\begin{aligned} \Vert f\Vert _{F^s_{p,q}} \lesssim \Vert \beta \Vert _{f^s_{p,q} }. \end{aligned}$$

(4.20)

Moreover if $q<\infty$ the series in (4.15) converges unconditionally in $F^s_{p,q}$, and otherwise in $F^{s-\varepsilon }_{p,\infty }({\mathbb {R}})$, for all $\varepsilon >0$.

(ii) If $\max \{1/p,1\}-2<s<1/p$, then for every $\beta \in b^s_{p,q}$ the series in (4.15) converges to a distribution f in $B^s_{p,q}({\mathbb {R}})$, and it holds

$$\begin{aligned} \Vert f\Vert _{B^s_{p,q}}\lesssim \Vert \beta \Vert _{b^s_{p,q}}. \end{aligned}$$

(4.21)

Moreover, if $q <\infty$ the series in (4.15) converges unconditionally in the norm of $B^s_{p,q}$, and otherwise in the quasi-norm of $B^{s-\varepsilon }_{p,\infty }({\mathbb {R}})$, for all $\varepsilon >0$.

Proof

It suffices to prove the results when $f=\sum _{j\ge -1}\sum _{\mu \in {\mathbb {Z}}} \beta _{j,\mu }h_{j,\mu }$, with $(\beta _{j,\mu })$ a finite sequence of scalars. The other assertions will then follow by completeness of the spaces.

Step 1 Let $L_k$, $k\ge 0$, be the local convolution operators from Sect. 2.1. If $j\ge -1$ is fixed, then we have

$$\begin{aligned} \Big |L_k \Big (\sum \limits _{\mu \in {\mathbb {Z}}}\beta _{j,\mu }h_{j,\mu }\Big )(x)\Big | \le \sum \limits _{\mu \in {\mathbb {Z}}} |\beta _{j,\mu }|\cdot |(L_k h_{j,\mu })(x)|\,=:\,G_{j,k}(x). \end{aligned}$$

(4.22)

Arguing as in Lemma 4.2, one sees that, in the case $\ell =j-k>0$, then

$$\begin{aligned} {\text { supp }}L_k h_{j,\mu }\subset \mu 2^{-j}+O(2^{-k}){\quad \hbox {and}\quad }\big |(L_k h_{j,\mu })(x)\big | \lesssim 2^{-2\ell }, \end{aligned}$$

(4.23)

while in the case $\ell =j-k \le 0$ we have

$$\begin{aligned} {\text { supp }}L_k h_{j,\mu }\subset \mu 2^{-j}+O(2^{-j}){\quad \hbox {and}\quad }\big |(L_k h_{j,\mu })(x)\big | \lesssim 1. \end{aligned}$$

(4.24)

The following lemma is a variation of a result by Kyriazis; see [18, Lem. 7.1]. For $r>0$ we denote

$$\begin{aligned} M_r(g)(x)=\big [M(|g|^r)(x)\big ]^{1/r}, \end{aligned}$$

where M is the usual Hardy-Littlewood maximal operator.

Lemma 4.6

Let $0<r\le 1$. Then, it holds

$$\begin{aligned} G_{j,k}(x)\,\lesssim \, a(j-k)\, M_r\Big (\sum _\mu |\beta _{j,\mu }|\,{\mathbb {1}}_{I_{j,\mu }}\Big )(x). \end{aligned}$$

(4.25)

where $a(\ell )=2^{-2\ell }2^{{\ell }/r}$ if $\ell >0$, and $a(\ell )=1$ if $\ell \le 0$.

Proof

Assume that $\ell =j-k>0$. If $x\in I_{j,\nu }$, for some fixed $\nu \in {\mathbb Z}$, then the size and support estimates in (4.23) give

$$\begin{aligned} G_{j,k}(x)^r\lesssim \,\sum _{\mu :|\mu -\nu |\le 2^{j-k}}|\beta _{j,\mu }|^r\,2^{-2\ell r}. \end{aligned}$$

On the other hand, if $x\in I_{j,\nu }$,

$$\begin{aligned} M\Big (\sum _\mu |\beta _{j,\mu }|^r\,{\mathbb {1}}_{I_{j,\mu }}\Big )(x)\gtrsim & {} 2^k\int _{|y-2^{-j}\nu |\le 2\cdot 2^{-k}} \Big (\sum _\mu |\beta _{j,\mu }|^r\,{\mathbb {1}}_{I_{j,\mu }}\Big )(y)\,dy\\\ge & {} 2^{k-j}\,\sum _{\mu :|\mu -\nu |\le 2^{j-k}}|\beta _{j,\mu }|^r. \end{aligned}$$

These two estimates clearly give (4.25) in the case $\ell >0$. The case $\ell \le 0$ is proved similarly using (4.24). $\square$

We continue with the proof of Proposition 4.5.i. Below we shall agree that $\beta _{m, \mu }=0$ and $G_{m,k}\equiv 0$ whenever $m<-1$. Then letting $u = \min \{p,q,1\}$, we can apply the u-triangle inequality and the above results to obtain

$$\begin{aligned} \Vert f\Vert _{F^s_{p,q}}= & {} \Big \Vert \Big (\sum _{k\ge 0}|2^{ks}L_kf|^q\Big )^{1/q}\Big \Vert _p\, \le \, \Big \Vert \Big (\sum _{k\ge 0}(2^{ks}\sum _{\ell \in {\mathbb Z}}G_{k+\ell ,k})^q\Big )^{1/q}\Big \Vert _p\\\lesssim & {} \Big [\sum \limits _{\ell \in {\mathbb Z}}\Big (a(\ell )\,2^{-\ell s}\Big )^u \Big \Vert \Big (\sum \limits _{k\ge 0 }\Big [2^{(k+\ell )s}\,M_r\Big (\sum \limits _{\mu \in {\mathbb {Z}}}|\beta _{k+\ell ,\mu }|{\mathbb {1}}_{I_{k+\ell ,\mu }}\Big ) \Big ]^{q}\Big )^{\frac{1}{q}}\Big \Vert ^u_p\Big ]^{\frac{1}{u}}\\\lesssim & {} \Big \Vert \Big (\sum \limits _{m\in {\mathbb Z}} \Big (2^{ms}\sum \limits _{\mu \in {\mathbb {Z}}} |\beta _{m,\mu }|{\mathbb {1}}_{I_{m,\mu }}\Big )^q \Big )^{\frac{1}{q}}\Big \Vert _p, \end{aligned}$$

where the last line is justified by the Fefferman-Stein inequality (2.7), provided $r<\min \{p,q,1\}$, and the finite summation in $\ell \in {\mathbb Z}$ holds whenever $1/r-2<s<0$ . Such an r can always be chosen under the assumption

$$\begin{aligned} \max \{1/p,1/q,1\}-2<s<0 \end{aligned}$$

(which in particular implies $p,q>1/2$). We shall see in Step 3 below how to enlarge this range to cover as well the cases $s\ge 0$.

Step 2 We now prove (4.21). The same notation as above gives

$$\begin{aligned} \Vert f\Vert _{B^s_{p,q}} = \Big (\sum _{k\ge 0}\big (2^{ks}\Vert L_kf\Vert _p\big )^q\Big )^{1/q} \le \Big (\sum _{k\ge 0}(2^{ks}\big \Vert \sum _{\ell \in {\mathbb Z}}G_{k+\ell ,k}\big \Vert _p)^q\Big )^{1/q}. \end{aligned}$$

At this point we distinguish two cases, $\ell > 0$ and $\ell \le 0$. In the first case we use literally the same arguments as above; since for the $\ell _q(L_p)$ quasi-norm we just use the scalar Hardy-Littlewood maximal inequality we only need to impose $r<\min \{1,p\}$, together with $s>1/r-2$. Such an r can always be chosen under the assumption

$$\begin{aligned} \max \{1/p,1\}-2<s. \end{aligned}$$

To control the sum over $\ell \le 0$ we must replace the crude bound in (4.24) by the sharper estimate

$$\begin{aligned} {\text { supp }}L_k h_{j,\mu }\subset {\Delta }_{j,k}+O(2^{-k}){\quad \hbox {and}\quad }\big |(L_k h_{j,\mu })(x)\big | \lesssim 1, \end{aligned}$$

(4.26)

where ${\Delta }_{j,\mu }$ are the discontinuity points of $h_{j,\mu }$; see the proof of Lemma 4.2.a. So, if $\ell =j-k\le 0$ we have

$$\begin{aligned} \big \Vert G_{k+\ell ,k}\big \Vert _p\lesssim 2^{-k/p}\Big (\sum \limits _{\mu \in {\mathbb {Z}}} |\beta _{k+\ell ,\mu }|^p\Big )^{1/p}. \end{aligned}$$

Using as before the u-triangle inequality, this yields

$$\begin{aligned} \begin{aligned} \Big (\sum _{k\ge 0}&\Big (2^{ks}\big \Vert \sum _{\ell \le 0}G_{k+\ell ,k}\big \Vert _p\Big )^q\Big )^{1/q}\\&\lesssim \, \Big [\sum _{\ell \le 0}2^{u(\frac{1}{p}-s)\ell }\Big (\sum _{k\ge 0}\Big \{ 2^{(k+\ell )(s-\frac{1}{p})} \Big (\sum \limits _{\mu \in {\mathbb {Z}}} |\beta _{k+\ell ,\mu }|^p\Big )^{1/p}\Big \}^q\Big )^{\frac{u}{q}}\Big ]^\frac{1}{u} \\&\lesssim \, \Big (\sum _{\ell \le 0}2^{u(\frac{1}{p}-s)\ell }\Big )^\frac{1}{u}\,\Big (\sum _{m\in {\mathbb Z}}\Big \{2^{m(s-\frac{1}{p})} \Big (\sum \limits _{\mu \in {\mathbb {Z}}} |\beta _{m,\mu }|^p\Big )^{1/p}\Big \}^q\Big )^{\frac{1}{q}}, \end{aligned} \end{aligned}$$

where the sum in $\ell \le 0$ is a finite constant due to the assumption $s<1/p$. This completes the proof of part (ii) in Proposition 4.5.

Step 3 In the Triebel–Lizorkin case, the direct argument in Step 1 only allows for $s<0$ (and $p,q>1/2$), which is the desired region only when $q=\infty$ or $p\rightarrow \infty$. By Step 2, the range of parameters can be extended to $s<1/p$ when $p=q$. Then, a complex interpolation argument in the three indices (s, 1/p, 1/q), as proposed by Triebel in [30, Prop. 2.6], gives the validity of the result for all $\max \{1/p,1/q,1\}-2<s < \min \{1/p,1/q\}$; see Fig. 5. $\square$

Fig. 5

Parameter domain for F-spaces in Steps 1 and 2 (left figure), and after the interpolation argument in Step 3 (right figure) of the proof of Proposition 4.5

Remark 4.7

We remark that the decomposition of a distribution $f\in {\mathcal {S}}'$ as an infinite series

$$\begin{aligned} f=\sum _{j\ge -1}\sum _{\mu \in {\mathbb {Z}}} \beta _{j,\mu }h_{j,\mu } \end{aligned}$$

(4.27)

may not necessarily be unique. For instance, the Dirac delta satisfies

$$\begin{aligned} {\delta }={\mathbb {1}}_{[0,1)}+\sum _{j=0}^\infty 2^j h_{j,0}={\mathbb {1}}_{[-1,0)}-\sum _{j=0}^\infty 2^j h_{j,-1} \quad \hbox {in }S'({\mathbb R}). \end{aligned}$$

In this example, the coefficient sequences belong to $b^s_{p,q}$ if $s<\frac{1}{p}-1$ (or $s=\frac{1}{p}-1$ and $q=\infty$), and the same happens for the property ${\delta }\in B^s_{p,q}({\mathbb R})$. For such cases of non-uniqueness, Proposition 4.5 should be interpreted as

$$\begin{aligned} \Vert f\Vert _{B^s_{p,q}}\lesssim \inf \Big \{\Vert (\beta _{j,\mu })\Vert _{b^s_{p,q}}{\,\,\,:\,\,\,}(4.27) \hbox { holds }\Big \}, \end{aligned}$$

and likewise for the $F^s_{p,q}$-quasinorms.

The next result shows that uniqueness holds when $s>1/p-1$.

Corollary 4.8

Let $0<p,q\le \infty$ and $s\in {\mathbb R}$.

(i) If $p<\infty$ and $\max \{1/p-1,1/q-2\}< s < \min \{1/p,1/q\}$ then for all $f \in \mathscr {B}$ it holds

$$\begin{aligned} \Vert f\Vert _{F^s_{p,q}} \lesssim \Big \Vert \Big (\sum \limits _{j=-1}^{\infty }\Big |2^{js}\sum \limits _{\mu \in {\mathbb {Z}}} 2^j\langle f, h_{j,\mu }\rangle {\mathbb {1}}_{I_{j,\mu }}\Big |^q\Big )^{1/q}\Big \Vert _p. \end{aligned}$$

(4.28)

(ii) If $~1/p-1< s < 1/p$ then for all $f \in \mathscr {B}$ it holds

$$\begin{aligned} \Vert f\Vert _{B^s_{p,q}} \lesssim \Big (\sum \limits _{j=-1}^{\infty } 2^{j(s-1/p)q} \Big (\sum \limits _{\mu \in {\mathbb {Z}}}|2^j\langle f,h_{j,\mu }\rangle |^p\Big )^{q/p}\Big )^{1/q}. \end{aligned}$$

(4.29)

Proof

Let $f\in \mathscr {B}$ be such that the right hand side of (4.28) is finite. By Proposition 4.5 this implies the convergence of the series

$$\begin{aligned} g:=\sum \limits _{j=-1}^{\infty } \sum \limits _{\mu \in {\mathbb {Z}}} 2^j\langle f,h_{j,\mu } \rangle h_{j,\mu }, \end{aligned}$$

to some distribution $g\in F^s_{p,q}\hookrightarrow \mathscr {B}$. Due to the range of parameters, and the convergence in $F^{s-\varepsilon }_{p,q}({\mathbb {R}})$ for $\varepsilon$ small enough, we also have convergence in $\mathscr {B}$. We deduce that $\langle g, h\rangle = \langle f,h\rangle$ for all $h \in {\mathscr {H}}$, and therefore, by Proposition 1.1, that $f=g$. Finally, Proposition 4.5 gives (4.28). The proof for (4.29) works analogously. $\square$

We finally turn to the remaining implications in Theorems 1.2 and 1.3, which are also valid in a larger range.

Proposition 4.9

Let $0<p, q\le \infty$ and $s\in {\mathbb R}$ be such that

$$\begin{aligned} \frac{1}{p}-1<s<1+\frac{1}{p}. \end{aligned}$$

(i) If $p<\infty$ and additionally $1/q-2<s<2+1/q$, then for all $f\in \mathscr {B}$

$$\begin{aligned} \Vert f\Vert _{F^s_{p,q}} \lesssim \Vert {\mathfrak {c}}(f)\Vert _{f^s_{p,q}} \end{aligned}$$

(4.30)

(ii) For all $f\in \mathscr {B}$ it holds

$$\begin{aligned} \Vert f\Vert _{B^s_{p,q}}\lesssim \Vert {\mathfrak {c}}(f)\Vert _{b^s_{p,q}} \end{aligned}$$

(4.31)

Proof

Note that, for all $f\in {\mathcal {S}}'({\mathbb {R}})$, it holds

$$\begin{aligned} \Vert f\Vert _{F^s_{p,q}} \approx \Vert f\Vert _{F^{s-1}_{p,q}} + \Vert f'\Vert _{F^{s-1}_{p,q}}, \end{aligned}$$

(4.32)

see e.g. [27, 2.3.8] . We shall bound each of the summands in (4.32) by the right hand side of (4.30).

Clearly $\Vert f\Vert _{F^{s-1}_{p,q}} \lesssim \Vert f\Vert _{B^{r}_{p,p}}$ for any $s-1 < r$. We distinguish two cases. In case $s>1/p$ we choose $r:=1/p-\varepsilon$, for a sufficiently small $\varepsilon >0$ so that

$$\begin{aligned} 1/p-1<r<1/p {\quad \hbox {and}\quad }s-1< r < s; \end{aligned}$$

(4.33)

this is possible by the assumption $s<1+1/p$. In case $s \le 1/p$ we put $r:= s-\varepsilon$, for some $\varepsilon >0$ so that (4.33) also holds (this time using the assumption $s>1/p-1$). Hence, from the embeddings $B^r_{pp}\hookrightarrow F^{s-1}_{pq}$ and $f^s_{pq}\hookrightarrow b^r_{pp}$, together with Corollary 4.8.ii, we obtain

$$\begin{aligned} \Vert f\Vert _{F^{s-1}_{p,q}}\lesssim \Vert f\Vert _{B^{r}_{p,p}}\lesssim \Vert \{2^j\langle f,h_{j,\mu }\rangle \}_{j,\mu }\Vert _{b^r_{pp}}\lesssim \Vert \{{\mathfrak {c}}_{j,\mu } (f)\}_{j,\mu }\Vert _{f^s_{pq}}. \end{aligned}$$

(4.34)

We now take care of the second term in (4.32). Here we quote the analog of Corollary 4.8.i for the Chui-Wang system $\{\psi _{j,\mu }\}$, which can be obtained from [8, Proposition 5.4] and Remark 2.3 above. Letting $r=s-1$, this gives

$$\begin{aligned} \Vert f'\Vert _{F^r_{p,q}} \lesssim \Big \Vert \Big (\sum \limits _{j\ge -1} 2^{jrq}\Big |\sum \limits _{\mu \in {\mathbb {Z}}} 2^j\langle f',\psi _{j,\mu }\rangle {\mathbb {1}}_{I_{j,\mu }}(x)\Big |^q \Big )^{1/q}\Big \Vert _p, \end{aligned}$$

(4.35)

provided

$$\begin{aligned} \max \{1/p-1,1/q-2\}-1< r < 1+\min \{1/p,1/q\}, \end{aligned}$$

which holds when $1/p-1<s<1/p+1$ and $1/q-2<s<2+1/q$.

Now, recall that

$$\begin{aligned} \psi _{j,\mu }(x)=\sum _{k\in {\mathbb Z}}b_k {\mathcal {N}}_2(2^{j+1}x-(2\mu +k)\big ), \end{aligned}$$

(4.36)

for a sequence of coefficients $b_k$ supported in $\{0,\ldots ,4\}$; see (2.16). In addition, we know from Lemma 2.1 that

$$\begin{aligned} \langle f',{\mathcal {N}}_2(2^{j+1}\cdot -\nu ) \rangle =-2^{j+1}\langle f, {\widetilde{h}}_{j,\nu } \rangle , \quad j\ge 0,\,\nu \in {\mathbb Z}\end{aligned}$$

(4.37)

(and a similar expression for $j=-1$). So, combining (4.36) and (4.37), we obtain an estimate for $|2^j{\langle {f'},{\psi _{j,\mu }}\rangle }|$ in terms of the coefficients ${\mathfrak {c}}_{j,\mu +\ell }(f)$, $\ell \in \{0,1,2\}$, which inserted into (4.35) gives

$$\begin{aligned} \Vert f'\Vert _{F^r_{p,q}}\lesssim & {} \sum _{\ell =0}^2 \Big \Vert \Big (\sum \limits _{j\ge -1} 2^{jrq}\Big |\sum \limits _{\mu \in {\mathbb {Z}}} {\mathfrak {c}}_{j,\mu +\ell }(f){\mathbb {1}}_{I_{j,\mu }}(x)\Big |^q \Big )^{1/q}\Big \Vert _p\,\\\lesssim & {} \Vert ({\mathfrak {c}}_{j,\mu } (f))_{j,\mu }\Vert _{f^s_{pq}}, \end{aligned}$$

using in the last step a maximal function estimate as in Lemma 4.6. This, together with (4.34) concludes the proof of part (i).

The result for $B^s_{p,q}$ in part (ii) goes similarly, using instead Corollary 4.8.ii, and the corresponding version for the Chui-Wang system $\{\psi _{j,\mu }\}$ which can be obtained from [8, Proposition 5.3]. $\square$

Remark 4.10

As pointed out by one of the referees, in the specific case of Besov spaces $B^s_{p,q}({\mathbb R})$ with $1/p\le s<1$ (and $1<p\le \infty$), one could give a more direct proof of the inequality

$$\begin{aligned} \Vert f\Vert _{B^s_{p,q}}\lesssim \Vert {\mathfrak {c}}(f)\Vert _{b^s_{p,q}},\quad f\in L^1_\textrm{loc}({\mathbb R}), \end{aligned}$$

by estimating the modulus of continuity $\omega (f,2^{-j})_{L^p({\mathbb R})}$ in terms of the errors of best linear approximation by piecewise constants over the collections of intervals $\{I_{j,\mu }\}_{\mu \in {\mathbb Z}}$ and $\{I_{j,\mu }+2^{-j-1}\}_{\mu \in {\mathbb Z}}$. When $s>1$ (or $s=1$ and $q<\infty$) this argument also shows that

$$\begin{aligned} \Vert {\mathfrak {c}}(f)\Vert _{b^s_{p,q}}<\infty \implies \omega (f,2^{-j})_{L^p({\mathbb R})}=o(2^{-j}), \end{aligned}$$

which in turn implies that f is constant (see e.g. [9, Ch 2, Prop 7.1]). This type of reasoning is reminiscent of some works that appeared in the spline community in the 70 s, see e.g. [22, Theorem 3] or the references quoted in [9, §12.2].

We are finally ready to give the

Proof of Theorems 1.2 and 1.3

Just combine Propositions 4.1 and 4.9. Note that the smallest range of parameters corresponds to that in Proposition 4.1. $\square$

5 $W^1_p$ and BV: Proof of Theorem 1.4

The proof has three steps. We use the classical norm definition for $W^1_p({\mathbb {R}})$, when $1\le p\le \infty$, namely

$$\begin{aligned} \Vert f\Vert _{W^1_p}:= \Vert f\Vert _p + \Vert f'\Vert _p. \end{aligned}$$

5.1 Step 1

We show that, for $1\le p\le \infty$, it holds

$$\begin{aligned} \sup \limits _{j\ge -1} 2^{j(1-1/p)}\Big (\sum \limits _{\nu \in {\mathbb {Z}}} |2^j\langle f,{\widetilde{h}}_{j,\nu }\rangle |^p\Big )^{1/p}\lesssim \Vert f\Vert _{W^1_p}, \quad f\in W^1_p({\mathbb R}), \end{aligned}$$

(5.1)

moreover

$$\begin{aligned} \sup \limits _{j\ge -1} \sum \limits _{\nu \in {\mathbb {Z}}} |2^j\langle f,{\widetilde{h}}_{j,\nu }\rangle |\lesssim \Vert f\Vert _{BV}, \quad f\in BV({\mathbb R}), \end{aligned}$$

(5.2)

In view of Lemma 2.1, for every $j\ge 0$ we have

$$\begin{aligned} \big |2^{j+1}\langle f,{\widetilde{h}}_{j,\nu } \rangle \big | \le \int |f'(x){\mathcal {N}}_{2;j+1,\nu }(x)|\,dx \lesssim 2^{-j/p'}\Big [\int _{{\tilde{I}}_{j,\nu }}|f'|^p\,dx\Big ]^{1/p},\qquad \end{aligned}$$

(5.3)

where ${\tilde{I}}_{j,\nu }={\text { supp }}{\mathcal {N}}_{2;j+1,\nu }=[\nu /2^{j+1},(\nu +2)/2^{j+1}]$. Hence,

$$\begin{aligned} \sup \limits _{j\ge 0} 2^{j(1-1/p)}\Big (\sum \limits _{\nu \in {\mathbb {Z}}} |2^j\langle f,{\widetilde{h}}_{j,\nu }\rangle |^p\Big )^{1/p} \lesssim \Vert f'\Vert _p. \end{aligned}$$

Likewise, if $j = -1$ we simply have

$$\begin{aligned} |\langle f, {\widetilde{h}}_{-1,\nu }\rangle | = \Big |\int _{{I}_{0,\nu }}f(x)dx\Big | \le \Big (\int _{{I}_{0,\nu }}|f(x)|^p dx\Big )^{1/p} \end{aligned}$$

and hence

$$\begin{aligned} \Big (\sum \limits _{\nu \in {\mathbb {Z}}} |\langle f, {\widetilde{h}}_{-1,\nu }\rangle |^p\Big )^{1/p} \lesssim \Vert f\Vert _p. \end{aligned}$$

We have thus established (5.1). To handle (5.2) we work with an approximation of the identity, $\{\Phi _\ell \}$ where $\Phi _\ell =2^\ell \Phi (2^\ell \cdot )$ with $\Phi \in C^\infty _c$ and $\int \Phi =1$. Let $f\in BV$ (which implies $f\in L_\infty$). Then $\Phi _\ell *f\in W^1_1$ with $\Vert \Phi _\ell *f\Vert _{W^1_1} \lesssim \Vert f\Vert _{BV}$ and $\Phi _\ell *f(x)\rightarrow f(x)$ almost everywhere. By dominated convergence $\langle \Phi _\ell *f,{{\widetilde{h}}}_{j,\nu }\rangle \rightarrow \langle f,\widetilde{h}_{j,\nu }\rangle$ and by a further application of Fatou’s lemma and (5.1)

$$\begin{aligned} \sum \limits _{\nu \in {\mathbb {Z}}} |2^j\langle f,{\widetilde{h}}_{j,\nu }\rangle | \le \liminf _{\ell \rightarrow \infty } \sum \limits _{\nu \in {\mathbb {Z}}} |2^j\langle f*\Phi _\ell ,{\widetilde{h}}_{j,\nu }\rangle | \lesssim \liminf _{\ell \rightarrow \infty } \Vert \Phi _\ell *f\Vert _{W^1_1} \lesssim \Vert f\Vert _{BV}, \end{aligned}$$

where the implicit constants are independent of j. This yields (5.2).

Step 2. We show that, for $1\le p\le \infty$, we have

$$\begin{aligned} \Vert f\Vert _p \,\lesssim \, \sup \limits _{j\ge -1} 2^{j(1-1/p)}\Big (\sum \limits _{\nu \in {\mathbb {Z}}} |2^j\langle f,{\widetilde{h}}_{j,\nu }\rangle |^p\Big )^{1/p}\,=:\,A(p)=A. \end{aligned}$$

Recall from Lemma 3.1.b that ${\mathbb E}_Nf\rightarrow f$ in ${\mathcal {S}}'$. Assuming (as we may) that $f\in \mathscr {B}$ has finite right hand side it suffices to show that ${\mathbb {E}}_N f$ converges in $L_p$ and $\sup _{N\ge 0}\big \Vert {\mathbb E}_Nf\big \Vert _p\lesssim A.$ To see this, one expands

$$\begin{aligned}{\mathbb E}_Nf={\mathbb E}_0f+\sum _{0\le j<N}\sum _{\mu \in {\mathbb Z}} 2^j {\langle {f},{h_{j,\mu }}\rangle }h_{j,\mu },\end{aligned}$$

and notes that

$$\begin{aligned} \big \Vert \sum _{\mu \in {\mathbb Z}} 2^j {\langle {f},{h_{j,\mu }}\rangle }h_{j,\mu }\big \Vert _{p}=2^{-j/p}\Big (\sum _{\mu \in {\mathbb Z}} |2^j {\langle {f},{h_{j,\mu }}\rangle }|^p\Big )^\frac{1}{p} \le 2^{-j}\,A, \end{aligned}$$

hence $\Vert {\mathbb {E}}_{N_1}f-{\mathbb {E}}_{N_2} f\Vert _p\lesssim 2^{-N_1}\, A$, for all $N_2> N_1$, and thus

$$\begin{aligned}\Vert f\Vert _p\le \sup _N\Vert {\mathbb {E}}_N f\Vert _p\le A.\end{aligned}$$

Step 3.

We finally show, for $1< p\le \infty$, that

$$\begin{aligned} \Vert f'\Vert _p \,\lesssim \, \sup \limits _{j\ge -1} 2^{j(1-1/p)}\Big (\sum \limits _{\nu \in {\mathbb {Z}}} |2^j\langle f,{\widetilde{h}}_{j,\nu }\rangle |^p\Big )^{1/p}\,=:\,A, \end{aligned}$$

and when $p=1$ then $f'$ is a finite Borel measure and $\Vert f'\Vert _{{\mathcal {M}}}\lesssim A.$ Consider the multiresolution analysis in $L_2({\mathbb R})$ generated by the subspaces

$$\begin{aligned} V_N = {\overline{\text {span}}}\,\Big \{{\mathcal {N}}_{N,\mu }:={\mathcal {N}}_2(2^{N+1}\cdot -\mu )~:~\mu \in {\mathbb {Z}}\Big \}\quad ,\quad N=-1,0,1,2,... \end{aligned}$$

That is, $V_N$ consists of continuous piecewise linear functions with nodes in $2^{-N-1}{\mathbb Z}$. Let ${\mathcal {N}}^*(\cdot )$ be the (polygonal) function which generates the dual Riesz basis to $\{{\mathcal {N}}_{N,\mu }~:~\mu \in {\mathbb {Z}}\}$; see e.g. [7, §3]. Then, the operator

$$\begin{aligned} h\in L_2\longmapsto P_N(h):=\sum _{\mu \in {\mathbb Z}}2^N\langle {h,{\mathcal {N}}^{*}_{N,\mu }}\rangle {\mathcal {N}}_{N,\mu } \end{aligned}$$

is the orthogonal projection onto $V_N$. Let

$$\begin{aligned} g_N(x):= \sum \limits _{\mu \in {\mathbb {Z}}} 2^N\langle f', {\mathcal {N}}_{N,\mu } \rangle {\mathcal {N}}^{*}_{N,\mu }(x). \end{aligned}$$

Using Lemma 2.1,³ we have the uniform bound

$$\begin{aligned}{} & {} 2^{-\frac{N}{p}}\Big (\sum \limits _{\mu \in {\mathbb {Z}}} |2^N\langle f', {\mathcal {N}}_{N,\mu }\rangle |^p\Big )^\frac{1}{p}\\{} & {} \quad \lesssim 2^{N(1-\frac{1}{p})}\Big (\sum \limits _{\mu \in {\mathbb {Z}}} |2^N\langle f, {\widetilde{h}}_{N,\mu }\rangle |^p\Big )^\frac{1}{p}\,\le A<\infty . \end{aligned}$$

So, the exponential decay of ${\mathcal {N}}^{*}(\cdot )$ guarantees that the series defining $g_N(x)$ converges, and moreover

$$\begin{aligned} \begin{aligned} \Vert g_N\Vert _p&\lesssim 2^{-N/p}\Big (\sum \limits _{\mu \in {\mathbb {Z}}} |2^N\langle f', {\mathcal {N}}_{N,\mu }\rangle |^p\Big )^{1/p}\,\le A. \end{aligned} \end{aligned}$$

(5.4)

Then, if $p>1$ there exists $g\in L_p$ which is the weak $^*$-limit of a subsequence of $\{g_N\}$. Now, if $j,\nu$ are fixed, for all $N\ge j$ we have

$$\begin{aligned} {\langle {g_N},{\psi _{j,\nu }}\rangle }=\Bigl \langle {f',\sum _{\mu \in {\mathbb Z}}2^N\langle {\psi _{j,\nu },{\mathcal {N}}^{*}_{N,\mu }}\rangle {\mathcal {N}}_{N,\mu }}\Bigr \rangle ={\langle {f'},{\psi _{j,\nu }}\rangle }, \end{aligned}$$

(5.5)

because $P_N(\psi _{j,\nu })=\psi _{j,\nu }$. Thus, taking limits as $N\rightarrow \infty$ in (5.5) we obtain

$$\begin{aligned} \langle {g,\psi _{j,\,\nu }}\rangle =\langle {f',\psi _{j,\,\nu }}\rangle ,\quad \hbox {for all } j,\nu . \end{aligned}$$

This implies that $g=f'\in L_p$ and $\Vert f'\Vert _p\lesssim A$.

When $p=1$ the weak* sequential-compactness argument only provides that $\Vert g\Vert _{\mathcal {M}}\lesssim A$ and then $\Vert f'\Vert _{\mathcal {M}}\lesssim A$. $\square$

6 Embeddings into $B^{s,{\textrm{dyad}}}_{p,\infty }$: The Cases $s=1$ and $s=1/p-1$

In this section we prove the sufficiency of the conditions for the embeddings into $B^{1,{\textrm{dyad}}}_{p,\infty }$ or $F^{1,{\textrm{dyad}}}_{p,\infty }$ in Theorem 1.7 and the sufficiency for the conditions of embedding into $B^{1/p-1,{\textrm{dyad}}}_{p,\infty }$ in Theorem 1.9.

Lemma 6.1

Let $1/2\le p\le \infty$, $\frac{1}{p}-1\le s\le 1$. Then $B^s_{p,\min \{p,1\}} \hookrightarrow B^{s,{\textrm{dyad}}}_{p,\infty }$ is a continuous embedding.

Proof

Using the notation in the proof of part (ii) of Proposition 4.1 we can write

$$\begin{aligned} \Vert f\Vert _{B^{s,\textrm{dyad}}_{p,\infty }}=\sup _{j\ge -1} 2^{js}\,B_j \end{aligned}$$

where $B_j$ is defined as in (4.11) with $\delta =0$. Letting $u=\min \{p,1\}$, we obtain for each j, arguing as in relation (4.12)

$$\begin{aligned} 2^{js}\,B_j\lesssim & {} \Big (\sum \limits _{\ell \in {\mathbb Z}}\Big [a(\ell ,\tfrac{1}{p})\,2^{js}\,\big \Vert {\mathfrak {M}}_{j+\ell }(f_{j+\ell })\big \Vert _p\Big ]^u\Big )^{1/u}\\\lesssim & {} \Big (\sup _{\ell \in {\mathbb Z}}\, a(\ell ,\tfrac{1}{p})2^{-\ell s}\Big ) \,\Vert f\Vert _{B^s_{p,u}}, \end{aligned}$$

where $a(\ell , 1/p)=2^{(1/p-1)\ell }$ for $\ell >0$ and $a(\ell ,1/p)=2^\ell$ for $\ell <0$. Since $\sup _{\ell \in {\mathbb Z}}\, a(\ell ,1/p)2^{-s\ell } < \infty$ whenever $1/p-1\le s \le 1$, we obtain the desired inequality $\Vert f\Vert _{B^{s,\textrm{dyad}}_{p,\infty }} \lesssim \Vert f\Vert _{B^s_{p,\min \{p,1\}}}$. $\square$

Proposition 6.2

Let $1/2<p<\infty$. Then $F^1_{p,2} \hookrightarrow F^{1,{\textrm{dyad}}}_{p,\infty }$ is a continuous embedding.

Proof

Let $f\in F^1_{p,2}$. we must show that

$$\begin{aligned} \Vert f\Vert _{F^{1,\textrm{dyad}}_{p,\infty }}=\big \Vert \sup _{j\ge -1} 2^j\sum _{\nu \in {\mathbb Z}}|2^j\langle f,h_{j,\nu }\rangle | \,{\mathbb {1}}_{I_{j,\nu }}\big \Vert _p \lesssim \Vert f\Vert _{F^1_{p,2}}. \end{aligned}$$

With the notation from Sect. 2.1, we write $f=\sum _{k\ge 0}L_kf_k$, and for each $j\ge -1$ we split $f=\Pi _jf +\Pi _j^\perp f$ where

$$\begin{aligned} \Pi _jf:=\sum _{k=0}^jL_kf_k,{\quad \hbox {and}\quad }\Pi _j^\perp f:=\sum _{k>j}L_kf_k. \end{aligned}$$

If $j=-1$, we understand that $\Pi _{-1}f=0$ and $\Pi ^\perp _{-1}f=f$. We shall first bound

$$\begin{aligned} A_0:=\big \Vert \sup _{j\ge 0} 2^j\sum _{\nu \in {\mathbb Z}}|2^j\langle \Pi _jf,h_{j,\nu }\rangle | \,{\mathbb {1}}_{I_{j,\nu }}\big \Vert _p. \end{aligned}$$

The same argument in the proof of [13, Lemma 3.3] gives

$$\begin{aligned} |2^j\langle \Pi _jf,h_{j,\nu }\rangle |\lesssim {\mathfrak {M}}^{**}_{j,A}\big (2^{-j}(\Pi _jf)'\big )(x), \quad x\in I_{j,\nu }. \end{aligned}$$

Thus,

$$\begin{aligned} 2^j\sum _{\nu \in {\mathbb Z}}|2^j\langle \Pi _jf,h_{j,\nu }\rangle |\,{\mathbb {1}}_{I_{j,\nu }}(x)\lesssim {\mathfrak {M}}^{**}_{j,A}\big ((\Pi _jf)'\big )(x), \quad x\in {\mathbb R}, \end{aligned}$$

and taking a supremum over all $j\ge 0$, and then $L_p$-norms, we obtain

$$\begin{aligned} A_0\,\lesssim \, \big \Vert \sup _{j\ge 0} {\mathfrak {M}}^{**}_{j,A}\big ((\Pi _jf)'\big )\big \Vert _p\, \lesssim \big \Vert \sup _{j\ge 0} |(\Pi _jf)'|\big \Vert _p, \end{aligned}$$

(6.1)

using (2.10) in the last step with $A>1/p$. Now, the maximal function characterization of the $h^p=F^0_{p,2}$ norms yields

$$\begin{aligned} \big \Vert \sup _{j \ge 0} |(\Pi _jf)'|\big \Vert _p = \big \Vert \sup _{j\ge 0} |\Pi _j(f')|\big \Vert _p \lesssim \Vert f'\Vert _{F^0_{p,2}} \,\lesssim \,\Vert f\Vert _{F^1_{p,2}}. \end{aligned}$$

(6.2)

To estimate the remaining part involving $\Pi _j^\perp f$, we may quote the standard proof in Proposition 4.1⁴ above, which gives

$$\begin{aligned} A_1:=\big \Vert \sup \limits _{j\ge -1} 2^j\sum _{\nu \in {\mathbb Z}}|2^j\langle \Pi _j^\perp f,h_{j,\nu }\rangle |\,{\mathbb {1}}_{I_{j,\nu }}(x)\big \Vert _p \lesssim \Vert f\Vert _{F^1_{p,\infty }}, \end{aligned}$$

(6.3)

provided that $s>\max \{1/p,1/q\}-1$, with $s=1$ and $q=\infty$. So, we obtain

$$\begin{aligned} A_1\,\lesssim \, \Vert f\Vert _{F^1_{p,\infty }}\lesssim \Vert f\Vert _{F^1_{p,2}}, \end{aligned}$$

under the assumption that $p>1/2$. Finally, (6.1), (6.2), (6.3) yield the desired estimate $\Vert f\Vert _{F^{1,\textrm{dyad}}_{p,\infty }} \lesssim \Vert f\Vert _{F^1_{p,2}}$. $\square$

Corollary 6.3

Let $1/2\le p<\infty$ and $q\le \min \{p,2\}$. Then $B^1_{p,q}\hookrightarrow B^{1,{\textrm{dyad}}}_{p,\infty }$ is a continuous embedding.

Proof

For $q\le p\le 1$ this follows from Lemma 6.1. For $1/2<p<\infty$ it follows from Proposition 6.2 together with the inequality

$$\begin{aligned} \Vert f\Vert _{B^{1,{\textrm{dyad}}}_{p,\infty }} \lesssim \Vert f\Vert _{F^{1,{\textrm{dyad}}}_{p,\infty } } \end{aligned}$$

(6.4)

and the inequality

$$\begin{aligned}\Vert f\Vert _{F^1_{p,2}} \lesssim \Vert f\Vert _{B^1_{p,\min \{p,2\}}};\end{aligned}$$

the latter being a consequence of Minkowski’s inequalities.

Inequality (6.4) in turn follows by definition from the sequence space inequality $\Vert \beta \Vert _{b^s_{p,\infty } }\le \Vert \beta \Vert _{f^s_{p,\infty } }$ (in the case $s=1$), i.e. from the elementary inequality

$$\begin{aligned}{} & {} \sup _j \Big (\sum _{\mu \in {\mathbb {Z}}} \int _{I_{j,\mu }} | 2^{js} \beta _{j,\mu } {\mathbb {1}}_{I_{j,\mu }}(x) |^p dx\Big )^{1/p}\nonumber \\{} & {} \quad \le \Big (\int \Big [ \sup _j 2^{js} \Big |\sum _{\mu \in {\mathbb {Z}}} \beta _{j,\mu } {\mathbb {1}}_{I_{j,\mu }}(x) \Big |\Big ]^p dx\Big )^{1/p}. \end{aligned}$$

(6.5)

$\square$

We now consider the other limiting case, where $s=1/p-1$.

Proposition 6.4

Let $1/2<p\le 1$ and $0<q\le \infty$. Then $F^{\frac{1}{p}-1}_{p,q} \hookrightarrow B^{\frac{1}{p}-1,{\textrm{dyad}}}_{p,\infty }$ is a continuous embedding.

Proof

Since $F^{\frac{1}{p}-1}_{p,q} \hookrightarrow F^{\frac{1}{p}-1}_{p,\infty }$ it suffices to prove this for $q=\infty$.

Let $f\in F^{1/p-1}_{p,\infty }$, which as before we shall split as

$$\begin{aligned} f=\Pi _jf+ \Pi _j^\perp f. \end{aligned}$$

This time, the standard proof in Proposition 4.1 (that is, the part of the proof involving the indices $\ell =k-j\le 0$) gives

$$\begin{aligned} \Big \Vert \Big (\sum \limits _{j\ge 0} 2^{jsq}\sum _{\nu \in {\mathbb Z}}|2^j\langle \Pi _j f,h_{j,\nu }\rangle |^q\,{\mathbb {1}}_{I_{j,\nu }}\Big )^{1/q}\Big \Vert _{L_p({\mathbb {R}})} \lesssim \Vert f\Vert _{F^s_{p,q}} \end{aligned}$$

provided that $s<1$. So in particular, letting $s=1/p-1$ and $q=\infty$ we obtain (after trivial embeddings)

$$\begin{aligned} \sup _{j\ge 0} 2^{j(1/p-1)} \Big \Vert \sum _{\nu \in {\mathbb Z}}2^j\langle \Pi _j f,h_{j,\nu }\rangle \,{\mathbb {1}}_{I_{j,\nu }}\Big \Vert _{L_p({\mathbb {R}})} \lesssim \Vert f\Vert _{F^{\frac{1}{p}-1}_{p,\infty }}, \end{aligned}$$

(6.6)

whenever $p>1/2$.

So, it remains to establish a similar estimate with $\Pi _j^{\perp }f$ instead of $\Pi _j f$. We borrow some notation from [13]. Let ${\mathcal {D}}_j$ denote the dyadic intervals of length $2^{-j}$. If $I\in {\mathcal {D}}_j$ is fixed and $k\ge j$ we let

• (a) ${\mathcal {D}}_k(\partial I)=\big \{J\in {\mathcal {D}}_k{\,\,\,:\,\,\,}{\bar{J}}\cap \partial I\not =\emptyset \big \}$

• (b) $\omega (J)=\{x\in J{\,\,\,:\,\,\,}\textrm{dist}(x,\partial I)\ge 2^{-k-1}\}$, when $J\in {\mathcal {D}}_k(\partial I)$.

We will use the maximal function ${\mathfrak {M}}^*_kg$ (cf. (2.11)) and note that, as in [13, (42)], when $J\in {\mathcal {D}}_{k}(\partial I)$, $k>j$, it holds

(6.7)

Now, let $I=I_{j,\nu }\in {\mathcal {D}}_j$ be fixed, and let $I^\pm$ be its dyadic sons. For each $k>j$, the function $L_k(h_{j,\nu })$ has support contained in the union of the intervals J belonging to ${\mathcal {D}}_k(\partial I^\pm )$, and $|L_k(h_{j,\nu })|\lesssim 1$. Thus, since we are assuming $p\le 1$, we have

$$\begin{aligned} \big |\langle 2^j h_{j,\nu },\Pi ^\perp _jf\rangle \big |^p\le & {} \sum _{k>j}\big |\langle L_k(2^jh_{j,\nu }),f_k \rangle \big |^p\\\lesssim & {} \sum _{k>j}2^{-(k-j)p}\sum _{J\in {\mathcal {D}}_k(\partial I^\pm )}\Vert f_k\Vert _{L_\infty (J)}^p \end{aligned}$$

which, by (6.7), is bounded by

where $I^*$ is the 2-fold dilation of the interval I. Summing up in all intervals $I=I_{j,\nu }\in {\mathcal {D}}_j$ we obtain

$$\begin{aligned} \sum _{\nu \in {\mathbb Z}}\big |\langle 2^j h_{j,\nu },\Pi ^\perp _jf\rangle \big |^p\lesssim 2^{jp}\, \int _{\mathbb R}\sup _{k>j}\big |2^{(\frac{1}{p}-1)k}\,{\mathfrak {M}}^*_kf_k\big |^p. \end{aligned}$$

This implies

$$\begin{aligned} \sup _j 2^{-j}\Big (\sum _{\nu \in {\mathbb Z}}\big |\langle 2^j h_{j,\nu },\Pi ^\perp _jf\rangle \big |^p\Big )^{1/p}\lesssim \Big (\int _{\mathbb R}\sup _{k>j}\big |2^{(\frac{1}{p}-1)k}\,{\mathfrak {M}}^*_kf_k\big |^p\Big )^{1/p}. \end{aligned}$$

(6.8)

Now, ${\mathfrak {M}}^*_kg\lesssim {\mathfrak {M}}_{k,A}^{**}g$ for any $A>0$, so choosing $A>1/p$ and using (2.10) we have

$$\begin{aligned} \big \Vert \sup _{k\ge 0}2^{(\frac{1}{p}-1)k}\,{\mathfrak {M}}^*_kf_k\big \Vert _p\lesssim \big \Vert \sup _{k\ge 0}2^{(\frac{1}{p}-1)k}\,|f_k|\big \Vert _p \lesssim \Vert f\Vert _{F^{\frac{1}{p}-1}_{p,\infty }}. \end{aligned}$$

(6.9)

Finally, the inequality

$$\begin{aligned}\Vert f\Vert _{B^{ \frac{1}{p}-1,{\textrm{dyad}}}_{p,\infty } }\lesssim \Vert f\Vert _{F^{\frac{1}{p}-1}_{p,\infty }} \end{aligned}$$

follows by combining (6.6), (6.8) and (6.9). $\square$

We now consider the remaining endpoint case where the two limiting cases coincide, that is, we have both $s=1$ and $s=1/p-1$, and thus $p=1/2$ (the corresponding Besov embedding is already covered in Lemma 6.1).

Proposition 6.5

For $p=1/2$ we have the continuous embedding

$$\begin{aligned}F^1_{ 1/2,2} \hookrightarrow B^{1,{\textrm{dyad}}}_{ 1/2,\infty }.\end{aligned}$$

Proof

We examine the proof of Propositions 6.4 and 6.2 and note that (6.8) and (6.9) remain valid for $p=1/2$, that is

$$\begin{aligned} \sup _{j \ge -1} 2^{-j}\Big (\sum _{\nu \in {\mathbb Z}}\big |\langle 2^j h_{j,\nu },\Pi ^\perp _jf\rangle \big |^\frac{1}{2} \Big )^{2}\lesssim \Vert f\Vert _{F^{1}_{ 1/2,\infty }}. \end{aligned}$$

Similarly, the arguments in (6.1) and (6.2) do not require a restriction on p, so we also have

$$\begin{aligned} \big \Vert \sup _{j\ge 0}2^j\sum \limits _{\nu \in {\mathbb {Z}}}|2^j\langle \Pi _j f,h_{j,\nu }\rangle | h_{j,\nu }\big \Vert _{1/2} \lesssim \Vert f\Vert _{F^1_{ 1/2,2}}. \end{aligned}$$

Now the proposition follows from the trivial embeddings $F^1_{1/2,2} \hookrightarrow F^1_{1/2,\infty }$ and $f^1_{1/2,\infty }\hookrightarrow b^1_{1/2,\infty }$ (cf. (6.5)). $\square$

7 Norm Equivalences on Suitable Subspaces: The Proofs of Theorems 1.6 and 1.8

7.1 A Bootstrapping Lemma

Consider a sequence ${\mathfrak {a}}=\{a_{j,\mu }\}$ indexed by $j\in {\mathbb {N}}\cup \{0\}$ and $\mu \in {\mathbb {Z}}$. As in (1.19) let $b^s _{p,q}$ be the set of all ${\mathfrak {a}}$ for which

$$\begin{aligned} \Vert {\mathfrak {a}}\Vert _{b^s _{p,q} }= \Big (\sum _{j=0}^\infty 2^{j(s -\frac{1}{p}) q}\Big [\sum _{\mu \in {\mathbb {Z}}}|a_{j,\mu }|^p\Big ]^{\frac{q}{p}}\Big )^{1/q}<\infty . \end{aligned}$$

(7.1)

We split each sequence as ${\mathfrak {a}}={{\mathfrak {a}}^{\textrm{even}}}+{{\mathfrak {a}}^{\textrm{odd}}}$, where

$$\begin{aligned} {\mathfrak {a}}^{\textrm{even}}_{j,\mu } = {\left\{ \begin{array}{ll} a_{j,\mu } &{} \text { if } \mu \text { is even } \\ 0&{}\text { if }\mu \text { is odd,} \end{array}\right. } {\quad \hbox {and}\quad }{\mathfrak {a}}^{\textrm{odd}}_{j,\mu }= {\left\{ \begin{array}{ll}0 &{} \text { if }\mu \text { is even } \\ a_{j,\mu }&{}\text { if }\mu \text { is odd.} \end{array}\right. } \end{aligned}$$

Then

$$\begin{aligned}\big \Vert {{\mathfrak {a}}^{\textrm{even}}}\big \Vert _{b^s _{p,q} }&= \Big (\sum _{j=0}^\infty 2^{j(s -\frac{1}{p}) q}\Big [\sum _{\nu \in {\mathbb {Z}}}|a_{j,2\nu }|^p\Big ]^{\frac{q}{p}}\Big )^{1/q} \\ \big \Vert {{\mathfrak {a}}^{\textrm{odd}}}\big \Vert _{b^s _{p,q} }&= \Big (\sum _{j=0}^\infty 2^{j(s -\frac{1}{p}) q}\Big [\sum _{\nu \in {\mathbb {Z}}}|a_{j,2\nu +1}|^p\Big ]^{\frac{q}{p}}\Big )^{1/q} \end{aligned}$$

The key result is the following lemma, which, under suitable conditions, allows us to control $\Vert {\mathfrak {a}}\Vert _{b^s _{p,q}}$ in terms of $\Vert {{\mathfrak {a}}^{\textrm{even}}}\Vert _{b^{s }_{p,q}}$. The general hypothesis in (7.3) will be linked later to a refinement condition which will appear in (7.6).

Lemma 7.1

Let $0<p, q\le \infty$, $s \in {\mathbb {R}}$ and $\vec \lambda =(\lambda _0,\lambda _1,\lambda _2)\in {\mathbb {C}}^3$ such that

$$\begin{aligned} |\lambda _1|<2^{s -\frac{1}{p}}. \end{aligned}$$

(7.2)

Then, there exists $C=C(p,q,s,\vec \lambda )>0$ such that for every sequence ${\mathfrak {a}}\in b^s _{p,q}$ satisfying the condition

$$\begin{aligned} |a_{j,2\nu +1}|\le \sum _{\ell =0}^2 |\lambda _\ell | \,|a_{j+1, 4\nu +2+\ell }|, \text { for all } j\ge 0,\, \nu \in {\mathbb {Z}}. \end{aligned}$$

(7.3)

we have

$$\begin{aligned} \big \Vert {\mathfrak {a}}\big \Vert _{b^s _{p,q}}\le \, C\, \big \Vert {{\mathfrak {a}}^{\textrm{even}}}\big \Vert _{b^s _{p,q}}. \end{aligned}$$

(7.4)

Proof

Let $\rho =\min \{1,p,q\}$, and for simplicity write $\sigma =s -1/p$. Condition (7.3) together with the $\rho$-triangle inequality gives

$$\begin{aligned}\big \Vert {{\mathfrak {a}}^{\textrm{odd}}}\big \Vert _{b^s _{p,q}}^\rho&\le \sum _{\ell =0,1,2}|\lambda _\ell |^\rho \Big (\sum _{j=0}^\infty 2^{j\sigma q } \Big [\sum _{\nu \in {\mathbb {Z}}} |a_{j+1, 4\nu +2+\ell } |^p\Big ]^{q/p} \Big )^{\rho /q} \\&= (|\lambda _1| 2^{-\sigma })^\rho \Big (\sum _{j=0}^\infty 2^{ (j+1)\sigma q } \Big [\sum _{\nu \in {\mathbb {Z}}} |a_{j+1, 4\nu +3} |^p\Big ]^{q/p} \Big )^{\rho /q} \\ {}&\quad + \sum _{\ell =0,2} (|\lambda _\ell | 2^{-\sigma })^{\rho } \Big (\sum _{j=0}^\infty 2^{ (j+1) \sigma q } \Big [\sum _{\nu \in {\mathbb {Z}}} |a_{j+1, 4\nu +2+\ell } |^p\Big ]^{q/p} \Big )^{\rho /q}. \end{aligned}$$

Using the assumptions $|\lambda _1|< 2^\sigma$ and ${\mathfrak {a}}\in b^s _{p,q}$, the previous display implies

$$\begin{aligned} \Big (1- \frac{|\lambda _1|^\rho }{2^{\sigma \rho } }\Big )\, \big \Vert {{\mathfrak {a}}^{\textrm{odd}}}\big \Vert _{b^s _{p,q}}^\rho \le (|\lambda _0|^\rho +|\lambda _2|^\rho ) 2^{-\sigma \rho } \Vert {{\mathfrak {a}}^{\textrm{even}}}\Vert _{b^s _{p,q}}^\rho . \end{aligned}$$

This gives

$$\begin{aligned} \Vert {\mathfrak {a}}\Vert _{b^s _{p,q} }&\le \Big ( \Vert {{\mathfrak {a}}^{\textrm{odd}}}\Vert _{b^s _{p,q}} ^\rho +\Vert {{\mathfrak {a}}^{\textrm{even}}}\Vert _{b^s _{p,q}}^\rho \Big )^{1/\rho } \\&\le \Big (\frac{|\lambda _0|^\rho +|\lambda _2|^\rho }{2^{\sigma \rho }- |\lambda _1|^\rho }+1\Big )^{1/\rho } \Vert {{\mathfrak {a}}^{\textrm{even}}}\Vert _{b^s _{p,q}}, \end{aligned}$$

which finishes the proof. $\square$

7.2 Proof of Theorem 1.6

We must show (1.24), that is

$$\begin{aligned} \Vert f\Vert _{B^s_{p,q}} \lesssim \Vert f\Vert _{B^{s,\textrm{dyad}}_{p,q}}, \quad \hbox {provided }f\in B^s_{p,q}, \end{aligned}$$

(7.5)

which, as we shall see, holds actually in the larger range

$$\begin{aligned} \frac{1}{p}<s<1+\frac{1}{p}.\end{aligned}$$

By part (ii) of Proposition 4.9, we know that

$$\begin{aligned} \Vert f\Vert _{B^s_{p,q}} \lesssim \big \Vert \{{\mathfrak {c}}_{j,\mu }(f)\}_{ {j\ge 0, \mu \in {\mathbb Z}}}\big \Vert _{b^s_{p,q}} \,+\,\big \Vert \big \{{\langle {f},{h_{-1,\mu }}\rangle }\big \}_{\mu \in {\mathbb Z}}\big \Vert _{\ell _p}=A+B. \end{aligned}$$

Clearly, B is bounded by the right hand side of (7.5), so we focus on A. Define a sequence ${\mathfrak {a}}={\mathfrak {a}}(f)=\{a_{j,\nu }\}$ by

$$\begin{aligned} a_{j,\nu }=2^j|{\langle {f},{\tilde{h}_{j,\nu }}\rangle }|, \quad j\in {\mathbb N}_0, \,\nu \in {\mathbb Z}. \end{aligned}$$

Observe from the definition of the coefficients ${\mathfrak {c}}_{j,\mu }(f)$ in (1.15) that

$$\begin{aligned} A\,\lesssim \, \Vert {\mathfrak {a}}\Vert _{b^s_{p,q}}. \end{aligned}$$

Note also from (1.8) that $a_{j, 2\mu }=2^j|{\langle {f},{h_{j,\mu }}\rangle }|$, so in particular

$$\begin{aligned} \Vert {{\mathfrak {a}}^{\textrm{even}}}\Vert _{b^s _{p,q}}=\big \Vert \big \{ 2^j{\langle {f},{h_{j,\mu }}\rangle }\} _{j\ge 0,\mu \in {\mathbb Z}}\big \Vert _{b^s_{p,q}}\le \Vert f\Vert _{B^{s,\textrm{dyad}}_{p,q}}. \end{aligned}$$

Therefore, we have reduced matters to prove that

$$\begin{aligned} \big \Vert {\mathfrak {a}}\big \Vert _{b^s _{p,q}}\lesssim \, \big \Vert {{\mathfrak {a}}^{\textrm{even}}}\big \Vert _{b^s _{p,q}}. \end{aligned}$$

We shall do so using Lemma 7.1, so we need to verify the hypothesis (7.3), for suitable scalars $(\lambda _0,\lambda _1,\lambda _2)$. This will follow from an elementary property of the spline functions

$$\begin{aligned} {\mathcal {N}}_{j,\mu }(x):={\mathcal {N}}_{2;j,\mu }(x)={\mathcal {N}}_2(2^jx-\mu ), \end{aligned}$$

defined in §2.3. Recall that these are piecewise linear functions supported in the intervals $[2^{-j}\mu , 2^{-j}(\mu +2)]$. It is then straightforward to verify that

$$\begin{aligned} {\mathcal {N}}_{j,\mu }(x)=\tfrac{1}{2}\,{\mathcal {N}}_{j+1, 2\mu }(x)+\,{\mathcal {N}}_{j+1, 2\mu +1}(x)+\tfrac{1}{2}\,{\mathcal {N}}_{j+1, 2\mu +2}(x); \end{aligned}$$

(7.6)

see Fig. 6. We refer to (7.6) as the refinement identity.

Fig. 6

Refinement equation for ${\mathcal {N}}_{j,\nu }(x)$; see (7.6)

Now, if $\mu =2\nu +1$ is an odd integer, then the integration by parts formula and the refinement identity give

$$\begin{aligned} a_{j,\mu }=&{} 2^j\,|\langle {f, \tilde{h}_{j,\mu }}\rangle |=\frac{1}{2}\,|\langle { f',{\mathcal {N}}_{j+1,\mu }}\rangle |\\ {\tiny \text {by }\; (7.6)\;}\le&{} \frac{1}{4}\,|\langle { f',{\mathcal {N}}_{j+2,2\mu }}\rangle |+ \frac{1}{2}\,|\langle { f',{\mathcal {N}}_{j+2,2\mu +1}}\rangle |+\frac{1}{4}\,|\langle { f',{\mathcal {N}}_{j+2,2\mu +2}}\rangle |\\ {\tiny \text {by }\; (2.15)\;}=&{} \frac{1}{2}\,a_{j+1,2\mu }+ \,a_{j+1,2\mu +1}+\frac{1}{2}\,a_{j+1,2\mu +2}, \end{aligned}$$

which implies (7.3) with $(\lambda _0,\lambda _1,\lambda _2)=(1/2, 1, 1/2)$. So we can apply Lemma 7.1, under the assumption

$$\begin{aligned} |\lambda _1|=1<2^{s-\frac{1}{p}}, \end{aligned}$$

which holds precisely when $s>\frac{1}{p}$. This completes the proof. $\square$

7.3 Proof of Theorem 1.8

We first show that, if $1<p\le \infty$ and $f\in W^{1}_p({\mathbb {R}})$, then

$$\begin{aligned} \Vert f\Vert _{W^{1}_p} \approx \sup \limits _{j \ge -1} 2^{j(1-1/p)}\Big (\sum \limits _{\mu \in {\mathbb {Z}}}|2^j\langle f,h_{j,\mu }\rangle |^p\Big )^{1/p}. \end{aligned}$$

In view of Theorem 1.4, this reduces to prove

$$\begin{aligned} \begin{aligned} A&:= \sup \limits _{j\ge -1} 2^{j(1-1/p)}\Big (\sum \limits _{\mu \in {\mathbb {Z}}} |{\mathfrak {c}}_{j,\mu }(f)|^p\Big )^{1/p} \\&\lesssim \,\sup \limits _{j\ge -1} 2^{j(1-1/p)}\Big (\sum \limits _{\mu \in {\mathbb {Z}}} |2^j\langle f,h_{j,\mu }\rangle |^p\Big )^{1/p}, \end{aligned} \end{aligned}$$

(7.7)

whenever A is finite. The argument is completely analogous to that for proving Theorem 1.6 , this time using the spaces $b^1_{p,\infty }$. Note, that this argument only needs that $1=s>1/p$.

Finally, the assertion in (1.31), for $f\in W^1_p$, follows now easily from

$$\begin{aligned} \Vert f\Vert _{W^1_p}\lesssim \Vert f\Vert _{B^{1,\textrm{dyad}}_{p,\infty }}\lesssim \Vert f\Vert _{F^{1,\textrm{dyad}}_{p,\infty }}\lesssim \Vert f\Vert _{F^1_{p,2}}\equiv \Vert f\Vert _{W^1_p}, \end{aligned}$$

where the third inequality was shown in part (ii) of Theorem 1.7 and for the last three steps we assume $p<\infty$. $\square$

8 Necessary Condition for the Embeddings for $s=1$

We prove the necessary conditions in Theorem 1.7 for various embeddings into $B^{1,{\textrm{dyad}}}_{p,\infty }$.

Lemma 8.1

Suppose $1/2\le p<\infty$. Then

$$\begin{aligned} B^1_{p,q} \hookrightarrow B_{p,\infty }^{1,{\textrm{dyad}}} \implies q\le p \end{aligned}$$

(8.1)

Proof

We shall work with an example that has been used in [14, §6.2] to prove lower bounds for the norms of ${\mathbb E}_N$ on $B^1_{p,q}$. Let $u\in C^\infty _c$ be supported in (1/8, 7/8) so that $u(x)=1$ on [1/4, 3/4]. For $N\gg 1$ and $N/4\le j\le N/2$ define

$$\begin{aligned}g_{N,j}(x)= u\big (N(x-\tfrac{2j}{N})\big ) e^{2\pi i 2^j x} \end{aligned}$$

and let $f_N(x) =\sum _{N/4\le j\le N/2} 2^{-j} g_{N,j}(x)$. Then by [14, Lemma 29] (Lemma 6.3 in arxiv:1901:09117) we have $\Vert f_N\Vert _{B^1_{p,q} }\lesssim N^{-(1/p-1/q)}$ for $p\le q$. We show that $\Vert f_N\Vert _{B^{1,{\textrm{dyad}}}_{p,\infty }} \gtrsim 1$ for large N, which will imply that $B^1_{p,q}$ is not continuously embedded into $B^{1,{\textrm{dyad}}}_{p,\infty }$ when $q>p$.

To see this we prove lower bounds for many of the Haar coefficients of $f_N$ at Haar frequency $2^N$. Let $J^{N,j}=(\frac{2j}{N}+\frac{1}{4N}, \frac{2j}{N}+\frac{3}{4N})$; we observe that for fixed N the intervals $J^{N,j}$ are disjoint and that $f_N(x)=e^{ 2^j 2\pi i x}$ for $x\in J^{N,j}$. We get by a Taylor expansion

$$\begin{aligned} \langle f_N,h_{N,\mu }\rangle&=2^{-2N-2} f_N'\big (2^{-N}(\mu +\tfrac{1}{2})\big ) + R_{N,\mu } \end{aligned}$$

(8.2)

with $|R_{N,\mu }|\le 2^{-3N} \sup _{I_{j,\mu }} |f_N''|$. Let ${\mathcal {Z}}^{N,j}$ be the set of all integers $\mu$ such that $2^{-N}\mu$ and $2^{-N}(\mu +1)$ belong to $J^{N,j}$; then for $\mu \in {\mathcal {Z}}^{N,j}$

$$\begin{aligned}|\langle f_N,h_{j,\mu }\rangle |=|\langle 2^{-j} g_{N,j},h_{j,\mu }\rangle |= 2\pi \,2^{-2N-2}+ O(2^{j-3N})\end{aligned}$$

and hence

$$\begin{aligned}\Vert f_N\Vert _{B^{1,{\text {dyad}}}_{p,\infty }} \ge 2^{N(1-1/p)} \Big ( \sum _{\frac{N}{4}<j<\frac{N}{2}} \sum _{\mu \in {\mathcal {Z}}^{N,j}} \big |2^N\langle f_N,h_{j,\mu }\rangle \big |^p\Big )^{1/p}. \end{aligned}$$

Since $\#({\mathcal {Z}}^{N,j}) \approx 2^N N^{-1}$ for large N and $N/4<j<N/2$ we obtain $\Vert f_N\Vert _{B^{1,{\textrm{dyad}}}_{p,\infty }} \gtrsim 1$. $\square$

Lemma 8.2

Suppose $1/2\le p<\infty$. Then

$$\begin{aligned}{} & {} F^1_{p,q} \hookrightarrow B_{p,\infty }^{1,{\textrm{dyad}}} \implies q\le 2, \end{aligned}$$

(8.3)

$$\begin{aligned}{} & {} B^1_{p,q} \hookrightarrow B_{p,\infty }^{1,{\textrm{dyad}}} \implies q\le 2. \end{aligned}$$

(8.4)

Proof

We consider the same example that was used in [13, §7.2.1]. Namely, let $\psi \in C^\infty _c(0,1)$ with $\psi \equiv 1$ in [1/4, 3/4], and for each large $N\gg 1$, let

$$\begin{aligned} {\mathfrak {Z}}_N=\{j\in {\mathbb N}{\,\,\,:\,\,\,}N/4< j<N/2\} \end{aligned}$$

(8.5)

and

$$\begin{aligned} f_t(x):=\sum _{j\in {\mathfrak {Z}}_N}\frac{r_j(t)}{2^j}e^{2\pi i 2^jx}\,\psi (x),\quad t\in [0,1], \end{aligned}$$

(8.6)

where $r_j(t)$, $t\in [0,1]$, are the usual Rademacher functions. Using Lemma 7.3 from [13] one can verify that

$$\begin{aligned} \sup _{t\in [0,1]} \Vert f_t\Vert _{F^1_{p,q}} \lesssim N^{1/q}; \end{aligned}$$

(8.7)

a similar argument also gives

$$\begin{aligned} \sup _{t\in [0,1]} \Vert f_t\Vert _{B^1_{p,q}} \lesssim N^{1/q}. \end{aligned}$$

(8.8)

Let $\psi _j(x)=2^{-j}e^{2\pi i 2^jx}\psi (x)$, for $j\in {\mathfrak {Z}}_N$, and let ${\mathcal {Z}}_N$ be the set of all $\mu \in {\mathbb Z}$ such that $I_{N,\mu }\subset (1/4,3/4)$. Using the Taylor expansion as in (8.2) one sees that

$$\begin{aligned} |\langle {\psi _j, 2^Nh_{N,\mu }}\rangle |=2\pi 2^{-N-2}+O(2^{j-2N}),\quad \mu \in {\mathcal {Z}}_N. \end{aligned}$$

(8.9)

Now observe that

$$\begin{aligned} \Vert f_t\Vert _{B^{1,\textrm{dyad}}_{p,\infty }}\ge 2^{N(1-1/p)}\,\Big (\sum _{\mu \in {\mathcal {Z}}_N}|{\langle {f_t},{2^Nh_{N,\mu }}\rangle }|^p\Big )^\frac{1}{p}. \end{aligned}$$

(8.10)

So, raising to the p-th power and taking the expectation in the t variable, we obtain from Khintchine’s inequality

$$\begin{aligned} \Big (\int _0^1\Vert f_t\Vert _{B^{1,\textrm{dyad}}_{p,\infty }}^pdt\Big )^\frac{1}{p}\ge & {} 2^{N(1-\frac{1}{p})}\,\Big (\sum _{\mu \in {\mathcal {Z}}_N}\int _0^1 \big |\sum _{j\in {\mathfrak {Z}}_N}r_j(t){\langle {\psi _j},{2^Nh_{N,\mu }}\rangle }\big |^pdt\Big )^\frac{1}{p}\\\gtrsim & {} 2^{N(1-\frac{1}{p})}\,\Big (\sum _{\mu \in {\mathcal {Z}}_N} \Big [ \sum _{j\in {\mathfrak {Z}}_N}\big |{\langle {\psi _j},{2^Nh_{N,\mu }}\rangle }\big |^2\Big ]^\frac{p}{2}\Big )^\frac{1}{p}. \end{aligned}$$

An application of (8.9), together with the cardinalities of ${\mathfrak {Z}}_N$ and ${\mathcal {Z}}_N$, then gives

$$\begin{aligned} \Big (\int _0^1 \Vert f_t\Vert _{B^{1,\textrm{dyad}}_{p,\infty }}^p dt \Big )^\frac{1}{p}\,\gtrsim \, \sqrt{N}. \end{aligned}$$

This together with (8.7), (8.8) implies that the inclusions $B^1_{p,q}\hookrightarrow B^{1,\textrm{dyad}}_{p,\infty }$ and $F^1_{p,q}\hookrightarrow B^{1,\textrm{dyad}}_{p,\infty }$ can only hold if $q\le 2$. $\square$

Lemma 8.3

For $p=\infty$ we have

$$\begin{aligned} B^1_{\infty ,q} \hookrightarrow B_{\infty ,\infty }^{1,{\textrm{dyad}}} \implies q\le 1. \end{aligned}$$

(8.11)

Proof

We assume that $B^1_{\infty ,q} \hookrightarrow B_{\infty ,\infty }^{1,{\textrm{dyad}}}$, and we shall prove that necessarily $q\le 1$. Let ${\mathcal {Z}}_N$ be as in (8.5) and consider the function

$$\begin{aligned} f(x):=\sum _{j\in {\mathfrak {Z}}_N}2^{-j}e^{2\pi i 2^jx}\,\psi (x), \end{aligned}$$

which is defined as in (8.6), but with all the $r_j(t)$ set equal to 1. This time we shall assume that $\psi \in C^\infty _c(-1/2,1/2)$ with $\psi =1$ in $(-1/4,1/4)$. As in (8.8) we have

$$\begin{aligned} \Vert f\Vert _{B^1_{p,q}} \lesssim N^{1/q}. \end{aligned}$$

(8.12)

On the other hand, note that

$$\begin{aligned} \Vert f\Vert _{B^{1,\textrm{dyad}}_{\infty ,\infty }}\ge 2^{N}\,|{\langle {f},{2^Nh_{N,0}}\rangle }|. \end{aligned}$$

(8.13)

Arguing as in (8.2) we see that

$$\begin{aligned} {\langle {f},{2^Nh_{N,0}}\rangle }= & {} \sum _{j\in {\mathfrak {Z}}_N}{\langle {\psi _j},{2^Nh_{N,0}}\rangle }=\sum _{j\in {\mathfrak {Z}}_N}\big [2^{-j}2^{-N-2}\psi _j'(0) +O(2^{j-2N})\big ]\\= & {} 2\pi i 2^{-N-2}\,\mathrm{Card\,}({\mathfrak {Z}}_N)\, +O(2^{-3N/2}), \end{aligned}$$

which inserted into (8.13) gives

$$\begin{aligned} \Vert f\Vert _{B^{1,\textrm{dyad}}_{\infty ,\infty }}\gtrsim \,N. \end{aligned}$$

(8.14)

The lemma is proved after combining (8.12), (8.14) and letting $N\rightarrow \infty$. $\square$

9 Necessary Condition for Embedding into $B^{1/p-1,{\textrm{dyad}}}_{p,\infty }$

Proposition 9.1

Let $0<p,q\le \infty$. Then

$$\begin{aligned} B^{1/p-1}_{p,q}\hookrightarrow B^{1/p-1,\textrm{dyad}}_{p,\infty } \,\implies \, q\le \min \{1,p\}. \end{aligned}$$

Proof

We first assume $1<p\le \infty$. Suppose the embedding $B^{s}_{p,q}\hookrightarrow B^{s,{\textrm{dyad}}}_{p,\infty }$ holds, with $s=1/p-1$. By definition of the latter space we have the inequality

$$\begin{aligned} |\langle f,h_{j,\mu } \rangle | \lesssim 2^{j(\frac{1}{p}-1-s)} \Vert f\Vert _{B^{s,{\textrm{dyad}}}_{p,\infty }}, \end{aligned}$$

(9.1)

so the assumed embedding would then imply that $h_{j,\mu }$ defines a bounded linear functional on $B^{-1+1/p}_{p,q}$ (or in the subspace $\mathring{B}^{-1+1/p}_{p,q}$ defined by the closure of ${\mathcal {S}}$ in the $B^{-1+1/p}_{p,q}$ norm, in case that p or q are $\infty$). By the duality identities of Besov spaces, see [27, §2.11], this means that $h_{j,\mu } \in B^{1/p'}_{p',q'}$ which cannot be the case if $q'<\infty$, i.e. if $1<q\le \infty$.

Let $p\le 1$. We use an example from [14, §10.1]. We let $\eta _l(x)=2^l \eta (2^l x)$ where $\eta \in C^\infty _c({\mathbb {R}})$ is an odd function supported in $(-1/2,1/2)$ such that $\int _0^{1/2} \eta (s) ds=1$ and such that $\int _0^{1/2}\eta (s)s^n ds=0$ for $n=1,2,\dots , M$, for a sufficiently large integer M. Let

$$\begin{aligned}f_N(x)=\sum _{m=1}^\infty a_m \eta _{N+m} (x-2^{-N+5}m).\end{aligned}$$

By [14, (85)] we have

$$\begin{aligned}\Vert f_N\Vert _{B_{p,q}^{1/p-1}} \lesssim \Big (\sum _{m=1}^\infty |a_m|^q\Big )^{1/q}.\end{aligned}$$

On the other hand a calculation shows $\langle f_N,h_{N, 2^5m}\rangle =a_m$ and thus

$$\begin{aligned}\Vert f_N\Vert _{B^{1/p-1,{\textrm{dyad}}}_{p,\infty } } \ge \Big (\sum _\mu |\langle f_N,h_{N,\mu }\rangle |^p\Big )^{1/p} \gtrsim \Big (\sum _{m=1}^\infty |a_m|^p\Big )^{1/p} \end{aligned}$$

which forces $q\le p$. $\square$

10 $B^{1/p}_{p,q}$ and $B^{1/p,{\textrm{dyad}}}_{p,q}$: The proof of Theorem 1.10

10.1 Proof of Part (i) of Theorem 1.10

Let

$$\begin{aligned} f_N=\sum _{j=0}^{N-1}h_{j,0}, \quad \hbox { for}\ N=1,2,\ldots \end{aligned}$$

(10.1)

Observe that

$$\begin{aligned} \Vert f_N\Vert _{B^{s, \textrm{dyad}}_{p,\infty }}=\sup _{j\ge 0}2^{j(s-\frac{1}{p})}\big [\sum _{\mu \in {\mathbb {Z}}}|2^j \langle f_N,h_{j,\mu }\rangle |^p\big ]^{1/p}=1, \quad \hbox {if }s=1/p. \end{aligned}$$

(10.2)

On the other hand, using the characterization with differences of order 2 for the $B^s_{p,q}$-norm (since $s\in (0,1]$), see [27, Theorem 2.5.12], we have

$$\begin{aligned} \Vert f_N\Vert _{B^{1/p}_{p,\infty }}\gtrsim & {} 2^{N/p}\,\big \Vert {\Delta }^2_{2^{-N}}(f_N)\big \Vert _p\nonumber \\\ge & {} 2^{N/p}\,\Big [\int _{-2^{1-N}}^{-2^{-N}}\Big |\sum _{0\le j<N}{\Delta }^2_{2^{-N}}h_{j,0}(x) \Big |^p\,dx\Big ]^\frac{1}{p}. \end{aligned}$$

(10.3)

Now a simple computation shows that, if ${\delta }\in (0, 2^{-j-1}]$, then

$$\begin{aligned} h_{j,0}(\cdot +{\delta })-h_{j,0}(\cdot ) = {\mathbb {1}}_{[-{\delta },0)}-2{\mathbb {1}}_{[2^{-j-1}-{\delta },2^{-j-1})}+{\mathbb {1}}_{[2^{-j}-{\delta },2^{-j})} \end{aligned}$$

and therefore,

$$\begin{aligned} {\Delta }_{\delta }^2h_{j,0}(x)=1, \quad x\in [-2{\delta },-{\delta }). \end{aligned}$$

Setting $\delta =2^{-N}$ and inserting this expression into (10.3) we get

$$\begin{aligned} \Vert f_N\Vert _{B^{1/p}_{p,\infty }}\gtrsim 2^{N/p}\,\big \Vert {\Delta }^2_{2^{-N}}f_N\big \Vert _p\ge N, \end{aligned}$$

(10.4)

and hence part (i) of Theorem 1.10 follows. $\square$

10.2 Proof of Part (ii) of Theorem 1.10

Consider this time the function

$$\begin{aligned} f=\sum _{j=0}^\infty h_{j,0}, \end{aligned}$$

and as before $f_N=\sum _{j=0}^{N-1}h_{j,0}$, i.e. $f=\lim _{N\rightarrow \infty } f_N$ with convergence in $L_p$. Indeed

$$\begin{aligned} \Vert f-f_N\Vert _p\le \sum _{j\ge N}\big \Vert h_{j,0}\Vert _p=\sum _{j\ge N}2^{-j/p}\,\approx \,2^{-N/p}. \end{aligned}$$

(10.5)

As in (10.2), it is again easy to verify that

$$\begin{aligned} \Vert f\Vert _{B^{1/p, \text {dyad} }_{p,\infty }}=1. \end{aligned}$$

(10.6)

We claim that $f\notin B^{1/p}_{p,\infty }$. Indeed, for large N we have

$$\begin{aligned} \Vert f\Vert _{B^{1/p}_{p,\infty }}\gtrsim & {} 2^{N/p}\,\big \Vert {\Delta }^2_{2^{-N}}(f-f_N)+{\Delta }^2_{2^{-N}}f_N\big \Vert _p\nonumber \\\ge & {} 2^{N/p}\big ( \big \Vert {\Delta }^2_{2^{-N}}f_N\big \Vert _p-4\Vert f-f_N\Vert _p\big ). \end{aligned}$$

(10.7)

Inserting the bounds (10.4) and (10.5) into (10.7) gives

$$\begin{aligned} \Vert f\Vert _{B^{1/p}_{p,\infty }}\,\gtrsim \,2^{N/p}\,\big \Vert {\Delta }^2_{2^{-N}}(f_N)\big \Vert _p-O(1)\,\gtrsim \, N, \end{aligned}$$

which letting $N\nearrow \infty$ proves the assertion. $\square$

11 Some Pathologies of the Spaces $B^{s,{\textrm{dyad}}}_{p,q}$

We include in this section some pathologies of the spaces ${B^{s,\textrm{dyad}}_{p,q}}$ when $s>1$, or $s=1$, $q<\infty$, or $s<1/p-1$, which were mentioned in the introduction.

11.1 Failure of Embedding into $B^{s,{\textrm{dyad}}}_{p,q}$ for $s>1$ or $s=1$, $q<\infty$

The following proposition is a simple result on the theme of Brezis’ paper [3] on how to recognize constant functions.

Proposition 11.1

Let $0<p,q\le \infty$ and assume that either (i) $s>1$, or (ii) $s=1$ and $q<\infty$.

Then every $f\in C^1({\mathbb {R}}) \cap B_{p,q}^{s,{\textrm{dyad}}}({\mathbb {R}})$ is a constant function.

Remark

Bočkarev’s results [1, Theorem 3] indicate that less restrictive assumptions can be made but we will not pursue the problem of optimal hypotheses here.

Proof

We argue as in the proof of Lemma 8.1, now using Taylor’s formula in the form

$$\begin{aligned} \sup _{b\in K}\sup _{|b-y|\le \varepsilon } | f(y)- f(b) - f'(b) (y-b) | = o(\varepsilon ) \end{aligned}$$

for any compact K. Take $b\equiv b_{j,\mu }= 2^{-j} (\mu +\frac{1}{2})$ to see that

$$\begin{aligned} \langle f,h_{j,\mu } \rangle = f'(2^{-j}(\mu +\tfrac{1}{2})) 2^{-2j-2} +o(2^{-2j})\end{aligned}$$

(11.1)

with uniformity in the remainder as $b_{j,\mu }$ ranges over a compact set.

Now assume that $f\in C^1$ and that $f'$ is not identically zero. Then there is a dyadic interval $J=[\nu 2^{-\ell }, (\nu +1) 2^{-\ell } )$ and $c>0$ such that for $j\ge j_0>\ell$

$$\begin{aligned} |\langle f,h_{j,\mu } \rangle | \ge c2^{-2j}, \quad \hbox { if}\ I_{j,\mu }\subset J.\end{aligned}$$

Hence

$$\begin{aligned} \Vert f\Vert _{{B^{s,\textrm{dyad}}_{p,q}}}\ge & {} \Big (\sum _{j=j_0}^\infty \Big [2^{j(s-\frac{1}{p})}\Big (\sum _{\mu : I_{j,\mu }\subset J} |2^j\langle {f,h_{j,\mu }}\rangle |^p\Big )^\frac{1}{p} \Big ]^q\Big )^\frac{1}{q}\\\ge & {} \Big (\sum _{j=j_0}^\infty \Big [2^{j(s-{1/p})} 2^{(j-\ell )/p} c2^{-j}\Big ]^q\Big )^\frac{1}{q} \ge c_\ell \Big (\sum _{j=j_0}^\infty 2^{j(s-1)q}\Big )^{1/q} \end{aligned}$$

with $c_\ell >0$. Hence $\Vert f\Vert _{B^{s,{\textrm{dyad}}}_{p,q}}=\infty$ when $s>1$ or when $s=1$ and $q<\infty$.

We conclude that for this range we have $f'\equiv 0$ for every $f\in C^1\cap B^{s,{\textrm{dyad}}}_{p,q}$ and Proposition 11.1 follows. $\square$

11.2 The Dyadic Besov-Spaces for $s<1/p-1$: Failure of Completeness

Proposition 11.2

Let $0<p,q\le \infty$. If $s<1/p-1$ then the spaces ${B^{s,\textrm{dyad}}_{p,q}}({\mathbb R})$ are not complete.

Proof

Consider the functions

$$\begin{aligned} f_N={\mathbb {1}}_{[0,1)}+\sum _{j=0}^{N-1}2^jh_{j,0}=2^N{\mathbb {1}}_{[0,2^{-N})}, \quad N=1,2,\ldots \end{aligned}$$

(11.2)

It is easily seen that, under the assumption $s<1/p-1$, then

$$\begin{aligned} \Vert f_{M}-f_N\Vert _{{B^{s,\textrm{dyad}}_{p,q}}}=\Big (\sum _{N\le j<M} [2^{j(s+1-\frac{1}{p})}]^q\Big )^\frac{1}{q}\rightarrow 0, \end{aligned}$$

when $M>N\rightarrow \infty$. So, $\{f_N\}_{N\ge 1}$ is a Cauchy sequence in ${B^{s,\textrm{dyad}}_{p,q}}$. However, the distributional limit of $f_N$ is the Dirac measure ${\delta }$, which does not belong to the space $\mathscr {B}$. $\square$

11.3 Failure of an Embedding for $s=1/p-1$

A small variation of the last example shows also part (i) of Theorem 1.9 and at the same time the optimality of the condition $s>1/p-1$ in part (ii) of Proposition 4.1 when $q<\infty$.

Proposition 11.3

Let $0<p, u\le \infty$. Then

$$\begin{aligned} B^{1/p-1}_{p,u}\not \hookrightarrow B^{1/p-1, \textrm{dyad}}_{p,q}, \quad 0<q<\infty . \end{aligned}$$

Proof

Consider $f_N$ as in (11.2), and let $g_N=f_N-f_N(-\cdot )$ be its odd extension. Then, it was shown in [14, Proposition 52] (Proposition 13.3 in arxiv:1901.09117) that

$$\begin{aligned} \Vert g_N\Vert _{B^{1/p-1}_{p,u}}\lesssim 1, \end{aligned}$$

for all $0<p,u\le \infty$. However, it is easily seen that

$$\begin{aligned} \Vert g_N\Vert _{B^{1/p-1, \textrm{dyad}}_{p,q}}\ge \Vert f_N\Vert _{B^{1/p-1, {\textrm{dyad}}}_{p,q}}\ge N^{1/q}. \end{aligned}$$

$\square$

Remark 11.4

Note that the above proof also shows that $L_1$ is not continuously embedded into $\mathscr {B}=B^{-1}_{\infty ,1}$. Indeed, the functions $f_N=2^N{\mathbb {1}}_{[0,2^{-N})}$ in (11.2) satisfy $\Vert f_N\Vert _1=1$ and $\Vert f_N\Vert _{\mathscr {B}}\gtrsim N$.