Skip to main content
SpringerLink
Log in

Dynamical analysis of an age-structured SEIR model with relapse

  • Published:
Zeitschrift für angewandte Mathematik und Physik Aims and scope Submit manuscript

Abstract

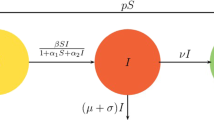
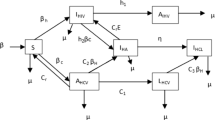
Mathematical models play a crucial role in controlling and preventing the spread of diseases. Based on the communication characteristics of diseases, it is necessary to take into account some essential epidemiological factors such as the time delay that takes an individual to progress from being latent to become infectious, the infectious age which refers to the duration since the initial infection and the occurrence of reinfection after a period of improvement known as relapse, etc. Moreover, age-structured models serve as a powerful tool that allows us to incorporate age variables into the modeling process to better understand the effect of these factors on the transmission mechanism of diseases. In this paper, motivated by the above fact, we reformulate an SEIR model with relapse and age structure in both latent and infected classes. Then, we investigate the asymptotic behavior of the model by using the stability theory of differential equations. For this purpose, we introduce the basic reproduction number \(\mathcal {R}_0\) of the model and show that this threshold parameter completely governs the stability of each equilibrium of the model. Our approach to show global attractivity is based on the fluctuation lemma and Lyapunov functionals method with some results on the persistence theory. The conclusion is that the system has a disease-free equilibrium which is globally asymptotically stable if \(\mathcal {R}_0<1\), while it has only a unique positive endemic equilibrium which is globally asymptotically stable whenever \(\mathcal {R}_0>1\). Our results imply that early diagnosis of latent infection with decrease in both transmission and relapse rates may lead to control and restrict the spread of disease. The theoretical results are illustrated with numerical simulations, which indicate that the age variable is an essential factor affecting the spread of the epidemic.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Castillo-Chávez, C., Song, B.: Dynamical models of tuberculosis and their applications. Math. Biosci. Eng. 1(2), 361–40 (2004)

    Article  MathSciNet  Google Scholar 

  2. Capasso, V.: Mathematical structures of epidemic systems. Berlin Heidelberg: Springer-Verlag (1993). https://doi.org/10.1007/978-3-540-70514-7

  3. Diekmann, O., Heesterbeek, J.A., Metz, J.A.: On the definition and the computation of the basic reproduction ratio \(\cal{R} _0\) in models for infectious diseases in heterogeneous populations. J. Math. Biol. 28, 365–382 (1990)

    Article  MathSciNet  Google Scholar 

  4. Kermack, W.O., McKendrick, A.G.: A contribution to the mathematical theory of epidemics. Proc. Royal Soc. London A 115(772), 700–721 (1927)

    Google Scholar 

  5. Xu, R., Ma, Z.: Global stability of a SIR epidemic model with nonlinear incidence rate and time delay. Nonlinear Anal. Real World Appl. 10(5), 3175–3189 (2009)

    Article  MathSciNet  Google Scholar 

  6. Zaman, G., Han Kang, Y., Jung, I.H.: Stability analysis and optimal vaccination of an SIR epidemic model. Biosystems 93(3), 240–249 (2008)

    Article  Google Scholar 

  7. Yuan, X., Wang, F., Xue, Y., Liu, M.: Global stability of an SIR model with differential infectivity on complex networks. Phys. A 499, 443–456 (2018)

    Article  MathSciNet  Google Scholar 

  8. Hu, Z., Teng, Z., Zhang, L.: Stability and bifurcation analysis in a discrete SIR epidemic model. Math. Comput. Simul. 97, 80–93 (2014)

    Article  MathSciNet  Google Scholar 

  9. Tahir, H., Khan, A., Din, A., Khan, A., Zaman, G.: Optimal control strategy for an age-structured SIR endemic model. Discret. Contin. Dynamic. Syst.-S 14(7), 2535–2555 (2021)

    Article  MathSciNet  Google Scholar 

  10. Brookmeyer, R.: Incubation period of infectious diseases. In Wiley StatsRef: Statistics Reference (2015). https://doi.org/10.1002/9781118445112.stat05241.pub2

  11. Wang, L., Xu, R.: Global stability of an SEIR epidemic model with vaccination. Int. J. Biomath. 09(06), 1650082 (2016)

    Article  MathSciNet  Google Scholar 

  12. McCluskey, C.C.: Global stability for an SEIR epidemiological model with varying infectivity and infinite delay. Math. Biosci. Eng. 6(3), 603–610 (2009)

    Article  MathSciNet  Google Scholar 

  13. Xue, C.: Study on the global stability for a generalized SEIR epidemic model. Comput. Intell. Neurosci. (2022). https://doi.org/10.1155/2022/8215214

    Article  Google Scholar 

  14. Wang, J., Shu, H.: Global analysis on a class of multi-group SEIR model with latency and relapse. Math. Biosci. Eng. 13(1), 209–225 (2016)

    Article  MathSciNet  Google Scholar 

  15. Bernoussi, A.: Stability analysis of an SIR epidemic model with homestead-isolation on the susceptible and infectious, immunity, relapse and general incidence rate. Int. J. Biomath. 16(05), 2250102 (2023)

    Article  MathSciNet  Google Scholar 

  16. Pradeep, B.G.S.A., Ma, W., Wang, W.: Stability and Hopf bifurcation analysis of an SEIR model with nonlinear incidence rate and relapse. J. Stat. Manag. Syst. 20(3), 483–497 (2017)

    Google Scholar 

  17. Tudor, D.: A deterministic model for herpes infections in human and animal populations. SIAM Rev. 32(1), 136–139 (1990)

    Article  MathSciNet  Google Scholar 

  18. Wang, J., Pang, J., Liu, X.: Modelling diseases with relapse and nonlinear incidence of infection: a multi-group epidemic model. J. Biol. Dyn. 8(1), 99–116 (2014)

    Article  MathSciNet  Google Scholar 

  19. Guo, Z.K., Xiang, H., Huo, H.F.: Analysis of an age-structured tuberculosis model with treatment and relapse. J. Math. Biol. (2021). https://doi.org/10.1007/s00285-021-01595-1

    Article  MathSciNet  Google Scholar 

  20. Liu, L., Ren, X., Jin, Z.: Threshold dynamical analysis on a class of age-structured tuberculosis model with immigration of population. Adv. Difference Equ. (2017). https://doi.org/10.1186/s13662-017-1295-y

    Article  MathSciNet  Google Scholar 

  21. Huang, G., Liu, X., Takeuchi, Y.: Lyapunov functions and global stability for age-structured HIV infection model. SIAM J. Appl. Math. 72(1), 25–38 (2012)

    Article  MathSciNet  Google Scholar 

  22. Xu, J., Geng, Y., Zhou, Y.: Global dynamics for an age-structured HIV virus infection model with cellular infection and antiretroviral therapy. Appl. Math. Comput., Elsevier 305(C), 62–83 (2017)

    Article  MathSciNet  Google Scholar 

  23. Shi, L., Wang, L., Zhu, L., Din, A., Qi, X., WuL, P.: Dynamics of an infection-age HIV diffusive model with latent infected cell and Beddington–DeAngelis infection incidence. Eur. Phy. J. Plus (2022). https://doi.org/10.1140/epjp/s13360-022-02428-w

    Article  Google Scholar 

  24. Zou, L., Ruan, S., Zhang, W.: An age-structured model for the transmission dynamics of hepatitis B. SIAM J. Appl. Math. 70(8), 3121–3139 (2010)

    Article  MathSciNet  Google Scholar 

  25. Thieme, H.R., Castillo-Chávez, C.: How may infection-age-dependent infectivity affectthe dynamics of HIV/AIDS? SIAM J. Appl. Math. 53(5), 1447–1479 (1993)

    Article  MathSciNet  Google Scholar 

  26. Webb, G.F.: Theory of Nonlinear Age-Dependent Population Dynamics. Marcel Dekker, New York (1985)

    Google Scholar 

  27. Magal, P., McCluskey, C.C., Webb, G.: Lyapunov functional and global asymptotic stability for an infection-age model. Appl. Anal. 89(7), 1109–1140 (2010)

    Article  MathSciNet  Google Scholar 

  28. McCluskey, C.C.: Delay versus age-of-infection-global stability. Appl. Math. Comput. 217(7), 3046–3049 (2010)

    MathSciNet  Google Scholar 

  29. Melnik, V.A., Korobeinikov, A.: Lyapunov functions and global stability for SIR and SEIR models withage-dependent susceptibility. Math. Biosci. Eng. 10(2), 369–378 (2013)

    Article  MathSciNet  Google Scholar 

  30. Liu, W.M., Levin, S.A., Iwasa, Y.: Influence of nonlinear incidence rates upon the behaviour of SIRS epidemiological models. J. Math. Biol. 23, 187–204 (1986)

    Article  MathSciNet  Google Scholar 

  31. Henshaw, S., McCluskey, C.C.: Global stability of a vaccination model with immigration. Electron. J. Differ. Equ. 2015(92), 1–10 (2015)

    MathSciNet  Google Scholar 

  32. Yang, Y., Li, J., Zhou, Y.: Global stability of two tuberculosis models with treatment and self-cure. Rocky Mt. J. Math. 42(4), 1367–1386 (2012)

    Article  MathSciNet  Google Scholar 

  33. McCluskey, C.C.: Global stability for an SEI epidemiological model with continuous age-structure in the exposed and infectious classes. Math. Biosci. Eng. 9(4), 819–841 (2012)

    Article  MathSciNet  Google Scholar 

  34. Yang, Y., Li, J., Ma, Z., Liu, L.: Global stability of two models with incomplete treatment for tuberculosis. Chaos, Solitons & Fractals 43(1), 79–85 (2010)

    Article  MathSciNet  Google Scholar 

  35. Hu, R., Liu, L., Ren, X., Liu, X.: Global stability of an information-related epidemic model with age-dependent latency and relapse. Ecol. Complex. 36, 30–47 (2018)

    Article  Google Scholar 

  36. Xu, R.: Global dynamics of an epidemiological model with age of infection and disease relapse. J. Biol. Dyn. 12(1), 118–145 (2018)

    Article  MathSciNet  Google Scholar 

  37. Din, A., Li, Y.: Controlling heroin addiction via age-structured modeling. Adv. Difference Equ. (2020). https://doi.org/10.1186/s13662-020-02983-5

    Article  MathSciNet  Google Scholar 

  38. Iannelli, M.: Mathematical Theory of Age-Structured Population Dynamics, In : Applied Mathematics Monographs. Vol. 7, comitato Nazionale per le Scienze Matematiche, Consiglio Nazionale delle Ricerche (C.N.R.), Giardini, Pisa (1995)

  39. Magal, P.: Compact attractors for time-periodic age-structured population models. Electron. J. Differ. Equ. 65, 1–35 (2001)

    MathSciNet  Google Scholar 

  40. Hale, J.K.: Asymptotic Behavior of Dissipative Systems. American Mathematical Society, Providence (1988)

    Google Scholar 

  41. Yosida, K.: Functional Analysis, 2nd edn. Springer, Berlin, Heidelberg (1968)

    Book  Google Scholar 

  42. Smith, H. L., Thieme, H. R.: Dynamical Systems and Population Persistence, American Mathematical Society, Providence, 118 (2011)

  43. Hirsch, W.M., Hanisch, H., Gabriel, P.: Differential equation models of some parasitic infections: Methods for the study of asymptotic behavior. Commun. Pure Appl. Math. 38(6), 733–753 (1985)

    Article  MathSciNet  Google Scholar 

  44. Hale, J.K.: Dynamical systems and stability. J. Math. Anal. Appl. 26(1), 39–59 (1969)

    Article  MathSciNet  Google Scholar 

  45. Walker, J.A.: Dynamical Systems and Evolution Equations: Theory and Applications. Plenum Press, New York (1980)

    Book  Google Scholar 

  46. Goh, B.S.: Global stability in many species systems. Am. Nat. 111(977), 135–142 (1977)

    Article  Google Scholar 

  47. Foss, A.M., Vickerman, P.T., Chalabi, Z., Mayaud, P., Alary, M., Watts, C.H.: Dynamic modelling of herpes simplex virus type-2 (HSV-2) transmission: issue in structure uncertainty. Bull. Math. Biol. 71(3), 720–749 (2009)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

I would like to thank the anonymous referees for their comments which contributed to improve this paper.

Author information

Authors and Affiliations

  1. Department of Mathematics and Computer Systems, Laboratory of Mathematics, and Informatic Systems (LAMIS), University of Tebessa, Tebessa, 12000, Algeria

    Abderrazak NABTi

Authors
  1. Abderrazak NABTi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Abderrazak NABTi.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

NABTi, A. Dynamical analysis of an age-structured SEIR model with relapse. Z. Angew. Math. Phys. 75, 84 (2024). https://doi.org/10.1007/s00033-024-02227-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00033-024-02227-6

Keywords

Mathematics Subject Classification

Search

Navigation