Skip to main content
SpringerLink
Log in

Defect detection using Cauchy data on a part of outer boundary of an elastic body

  • Published:
Zeitschrift für angewandte Mathematik und Physik Aims and scope Submit manuscript

Abstract

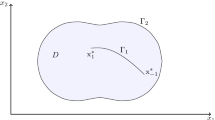
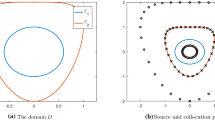
An inverse elastostatic problem is considered. It is assumed that as a result of static test one type of boundary data (Dirichlet or Neumann) is measured on the whole external boundary of an elastic body and both types of boundary data are measured only on a part of the external boundary. A method for defect (inclusion, cavity or a crack) detection and localization by means of the measured data is developed. The idea of the method is to construct a set of subdomains, continuously depending on a parameter. The set must have the following properties. The subdomains increase with increasing parameter, eventually reaching the entire domain occupied by the body. As the parameter tends to the minimal value, the subdomains tend to the part of the boundary on which the Cauchy data are specified. A functional that depends on a subdomain of the set is constructed. The value of the functional is equal zero if intersection of the subdomain with the defect is empty. The value of the functional is not zero if the subdomain contains the defect inside. Thus, we obtain a criterion for the defect detection. The proposed approach enables also to evaluate approximately the position of the defect. In case when the shape of the defect is a convex polygon, the developed method enables to determine its vertices. Numerical examples are considered that illustrate the effectiveness of the proposed method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. Karageorghis, A., Lesnic, D., Marin, L.: The method of fundamental solutions for the detection of rigid inclusions and cavities in plane linear elastic bodies. Comput. Struct. 106, 176–188 (2012)

    Article  Google Scholar 

  2. Karageorghis, A., Lesnic, D., Marin, L.: A moving pseudo-boundary method of fundamental solutions for void detection. Numer. Methods Partial Differ. Equ. 29(3), 935–960 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  3. Karageorghis, A., Lesnic, D., Marin, L.: The method of fundamental solutions for three-dimensional inverse geometric elasticity problems. Comput. Struct. 166, 51–59 (2016)

    Article  Google Scholar 

  4. Ammari, H., Kang, H., Nakamura, G., Tanuma, K.: Complete asymptotic expansions of solutions of the system of elastostatics in the presence of an inclusion of small diameter and detection of an inclusion. J. Elast. Phys. Sci. Solids 67(2), 97–129 (2002)

    MathSciNet  MATH  Google Scholar 

  5. Kang, H., Kim, E., Lee, J.-Y.: Identification of elastic inclusions and elastic moment tensors by boundary measurements. Inverse Prob. 19(3), 703–724 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  6. Ammari,H., Kang, H.: Reconstruction of small inhomogeneities from boundary measurements. Lecture Notes in Mathematics 1846 (2004)

  7. Ammari, H., Kang, H.: Polarization and moment tensors: with applications to inverse problems and effective medium theory. Appl. Math. Sci. 162 (2007)

  8. Ikehata, M.: Enclosing a polygonal cavity in a two-dimensional bounded domain from Cauchy data. Inverse Prob. 15(5), 1231–1241 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  9. Ikehata, M.: A regularized extraction formula in the enclosure method. Inverse Prob. 18(2), 435–440 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  10. Ikehata, M., Ohe, T.: A numerical method for finding the convex hull of polygonal cavities using the enclosure method. Inverse Prob. 18(1), 111–124 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  11. Andrieux, S., Ben Abda, A.: Identification of planar cracks by complete overdetermined data: inversion formulae. Inverse Probl. 12(5), 553–563 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  12. Andrieux, S., Ben Abda, A., Bui, H.D.: Reciprocity principle and crack identification. Inverse Probl. 15(1), 59–65 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  13. Bannour, T., Ben Abda, A., Jaoua, M.: A semi-explicit algorithm for the reconstruction of 3D planar cracks. Inverse Probl. 13(4), 899–917 (1997)

    Article  MATH  Google Scholar 

  14. Goldstein, R.V., Shifrin, E.I., Shushpannikov, P.S.: Application of invariant integrals to the problems of defect identification. Int. J. Fract. 147(1), 45–54 (2007)

    Article  MATH  Google Scholar 

  15. Shifrin, E.I.: Ellipsoidal defect identification in an elastic body from the results of a uniaxial tension (compression) test. Mech. Solids 45(3), 417–426 (2010)

    Article  Google Scholar 

  16. Shifrin, E.I., Shushpannikov, P.S.: Identification of a spheroidal defect in an elastic solid using a reciprocity gap functional. Inverse Prob. 26(5), 055001 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  17. Shifrin, E.I., Shushpannikov, P.S.: Identification of an ellipsoidal defect in an elastic solid using boundary measurements. Int. J. Solids Struct. 48(7–8), 1154–1163 (2011)

    Article  MATH  Google Scholar 

  18. Shifrin, E.I., Shushpannikov, P.S.: Reconstruction of an ellipsoidal defect in anisotropic elastic solid, using results of one static test. Inverse Probl. Sci. Eng. 21(5), 781–800 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  19. Shifrin, E.I., Shushpannikov, P.S.: Identification of small well-separated defects in an isotropic elastic body using boundary measurements. Int. J. Solids Struct. 50(22–23), 3707–3716 (2013)

    Article  Google Scholar 

  20. Shifrin, E.I., Shushpannikov, P.S.: Identification of finitely many small defects in an anisotropic linearly elastic body from a single static test. Mech. Solids 50(4), 421–431 (2015)

    Article  Google Scholar 

  21. Shifrin, E.I., Kaptsov, A.V.: Identification of multiple cracks in 2D elasticity by means of the reciprocity principle and cluster analysis. Inverse Prob. 34(1), 015009 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  22. Colton, D., Kirsch, A.: A simple method for solving inverse scattering problems in the resonance region. Inverse Prob. 12(4), 383–393 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  23. Colton, D., Piana, M., Potthast, R.: A simple method using Morozov’s discrepancy principle for solving inverse scattering problems. Inverse Prob. 13(6), 1477–1493 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  24. Arens, T.: Linear sampling methods for 2D inverse elastic wave scattering. Inverse Prob. 17(5), 1445–1464 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  25. Cakoni, F., Colton, D.: The linear sampling method for cracks. Inverse Prob. 19(2), 279–295 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  26. Dehghan Manshadi, S.H., Khaji, N., Rahimian, M.: Cavity/inclusion detection in plane linear elastic bodies using linear sampling method. J. Nondestruct. Evaluat. 33(1), 93–103 (2014)

    Google Scholar 

  27. Kirsch, A.: Characterization of the shape of a scattering obstacle using the spectral data of the far field operator. Inverse Prob. 14(6), 1489–1512 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  28. Hähner, P.: An inverse problem in electrostatics. Inverse Prob. 15(4), 961–975 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  29. Grinberg, N.I.: Obstacle visualization via the factorization method for the mixed boundary value problem. Inverse Prob. 18(6), 1687–1704 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  30. Kirsch, A.: The factorization method for a class of inverse elliptic problems. Math. Nachr. 278(3), 258–277 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  31. Shifrin, E.I.: Factorization method in the geometric inverse problem of static elasticity. Mech. Solids 51(5), 562–570 (2016)

    Article  Google Scholar 

  32. Bonnet, M., Constantinescu, A.: Inverse problems in elasticity. Inverse Prob. 21(2), R1–R50 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  33. Potthast, R.: A survey on sampling and probe methods for inverse problems. Inverse Prob. 22(2), R1–R47 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  34. Kohn, R.V., Vogelius, M.: Relaxation of a variational method for impedance computed tomography. Commun. Pure Appl. Math. 40(6), 745–777 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  35. Ben Ameur, H., Burger, M., Hackl, B.: Level set methods for geometric inverse problems in linear elasticity. Inverse Probl. 20(3), 673–696 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  36. Ben Ameur, H., Burger, M., Hackl, B.: Cavity identification in linear elasticity and thermoelasticity. Math. Methods Appl. Sci. 30(6), 625–647 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  37. Engelhardt, M., Schanz, M., Stavroulakis, G.E., Antes, H.: Defect identification in 3-D elastostatics using a genetic algorithm. Optim. Eng. 7(1), 63–79 (2006)

    Article  MATH  Google Scholar 

  38. Amstutz, S., Horchani, I., Masmoudi, M.: Crack detection by the topological gradient method. Control. Cybern. 34, 81–101 (2005)

    MathSciNet  MATH  Google Scholar 

  39. Ammari, H., Garapon, P., Jouve, F., Kang, H., Lim, M., Yu, S.: A new optimal control approach for the reconstruction of extended inclusions. SIAM J. Control. Optim. 51(2), 1372–1394 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  40. Hassine, M., Kallel, I.: One-iteration reconstruction algorithm for geometric inverse problems. Appl. Math. E-Notes 18, 43–50 (2018)

    MathSciNet  MATH  Google Scholar 

  41. Kovtunenko, V.A., Kunisch, K.: High precision identification of an object: optimality-conditions-based concept of imaging. SIAM J. Control. Optim. 52(1), 773–796 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  42. Cakoni, F., Kovtunenko, V.A.: Topological optimality condition for the identification of the center of an inhomogeneity. Inverse Prob. 34(3), 035009 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  43. Ferrier, R., Kadri, M., Gosselet, P.: Crack identification with incomplete boundary data in linear elasticity by the reciprocity gap method. Comput. Mech. 67(6), 1559–1579 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  44. Kozlov, V.A., Maz’ya, V.G., Fomin, A.V.: An iterative method for solving the Cauchy problem for elliptic equations. USSR Comput. Math. Math. Phys. 31(1), 45–52 (1991)

    MathSciNet  MATH  Google Scholar 

  45. Cimetiere, A., Delvare, F., Jaoua, M., Pons, F.: Solution of the Cauchy problem using iterated Tikhonov regularization. Inverse Prob. 17(3), 553–570 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  46. Baranger, T.N., Andrieux, S.: An optimization approach for the Cauchy problem in linear elasticity. Struct. Multidiscip. Optim. 35(2), 141–152 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  47. Bilotta, A., Turco, E.: A numerical study on the solution of the Cauchy problem in elasticity. Int. J. Solids Struct. 46(25–26), 4451–4477 (2009)

    Article  MATH  Google Scholar 

  48. Liu, C.-S., Atluri, S.N.: Numerical solution of the Laplacian Cauchy problem by using a better postconditioning collocation Trefftz method. Eng. Anal. Bound. Elem. 37(1), 74–83 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  49. Delvare, F., Cimetière, A.: Unique discrete harmonic continuation and data completion problems using the fading regularization method. Numer. Algorithms 75(3), 731–751 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  50. Kasparova, E.A., Shifrin, E.I.: Solution for the geometric elastostatic inverse problem by means of not completely overdetermined boundary data. Mech. Solids 55(8), 1298–1307 (2020)

    Article  MATH  Google Scholar 

  51. Muskhelishvili, N.I.: Some basic problems of the mathematical theory of elasticity. Noordhoof (1977)

  52. Ang, D.D., Trong, D.D., Yamamoto, M.: Unique continuation and identification of boundary of an elastic body. J. Inverse Ill-posed Probl. 3, 417–428 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  53. Washizu, K.: Variational Methods in Elasticity and Plasticity. Pergamon Press, Oxford (1982)

    MATH  Google Scholar 

  54. Bogy, D.B., Wang, K.S.: Stress singularities at interface corners in bonded dissimilar isotropic elastic materials. Int. J. Solids Struct. 7(8), 993–1005 (1971)

    Article  MATH  Google Scholar 

  55. Tikhonov, A.N., Arsenin, V.Y.: Solutions of Ill-Posed Problems. Wiley, New York (1977)

    MATH  Google Scholar 

Download references

Acknowledgements

The support of Russian Ministry of Science and Higher Education (Project Reg. No AAAA-A20- 120011690132-4) and RFBR (Project No 19-01-00100) is gratefully acknowledged.

Author information

Authors and Affiliations

  1. Ishlinsky Institute for Problems in Mechanics of the Russian Academy of Sciences (IPMech RAS), Pr. Vernadskogo 101-1, Moscow, Russia, 119526

    Efim I. Shifrin & Elena A. Kasparova

Authors
  1. Efim I. Shifrin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Elena A. Kasparova
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Efim I. Shifrin.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shifrin, E.I., Kasparova, E.A. Defect detection using Cauchy data on a part of outer boundary of an elastic body. Z. Angew. Math. Phys. 73, 134 (2022). https://doi.org/10.1007/s00033-022-01765-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00033-022-01765-1

Keywords

Mathematics Subject Classification

Search

Navigation