Skip to main content
SpringerLink
Log in

Boundary Integrals for Data Reconstruction on an Elastostatic Crack

  • Original Paper
  • Published:
International Journal of Applied and Computational Mathematics Aims and scope Submit manuscript

Abstract

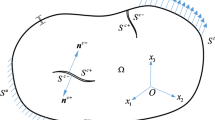
The elastostatic Cauchy problem of fracture mechanics is studied in a two-dimensional bounded domain containing a crack. Given Cauchy data on the boundary of the domain, the displacement and normal stress (traction) are reconstructed on the crack. The reconstruction is done by reducing the original problem, via the elastostatic potential, to a system of integral equations to be solved for densities over the boundary of the domain and the crack. Discretization is carried out by the Nyström method using quadrature formulas adjusted for singularities manifesting at the endpoints of the crack. Tikhonov regularization is applied for the stable solution of the discretized system. The results of numerical experiments for different input data and parameters are given showing that relevant physical quantities on the crack can be stably reconstructed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Data Availability Statement

In the numerical simulations of the submitted work, synthetic data is used. Formulas to generate the data are stated within the work itself.

References

  1. Alessandrini, G., Rondi, L., Rosset, E., Vessella, S.: The stability for the Cauchy problem for elliptic equations. Inverse Prob. 25, 123004 (2009)

    Article  MathSciNet  Google Scholar 

  2. Andrieux, S., Ben Abda, A., Bui, H.D.: Reciprocity principle and crack identification. Inverse Prob. 15, 59 (1999)

    Article  MathSciNet  Google Scholar 

  3. Andrieux, S., Baranger, T.N.: Emerging crack front identification from tangential surface displacements. Comptes Rendus Mécanique 340, 565–574 (2012)

    Article  Google Scholar 

  4. Andrieux, S., Baranger, T.N.: Three-dimensional recovery of stress intensity factors and energy release rates from surface full-field displacements. Int. J. Solids Struct. 50, 1523–1537 (2013)

    Article  Google Scholar 

  5. Bonnet, M., Constantinescu, A.: Inverse problems in elasticity. Inverse Prob. 21, R1–R50 (2005)

    Article  MathSciNet  Google Scholar 

  6. Broek, D.: Elementary Engineering Fracture Mechanics. Springer-Verlag, Berlin (2012)

    MATH  Google Scholar 

  7. Cakoni, F., Kress, R.: Integral equations for inverse problems in corrosion detection from partial Cauchy data. Inverse Problems Imaging 1, 229–245 (2007)

    Article  MathSciNet  Google Scholar 

  8. Carpinteri, A., Paggi, M.: Asymptotic analysis in linear elasticity: From the pioneering studies by Wieghardt and Irwin until today. Eng. Fract. Mech. 76, 1771–1784 (2009)

    Article  Google Scholar 

  9. Chapko, R., Johansson, B.T.: An alternating potential-based approach for a Cauchy problem for the Laplace equation in a planar domain with a cut. Comput. Methods Appl. Math. 8, 315–335 (2008)

    Article  MathSciNet  Google Scholar 

  10. Chapko, R., Johansson, B.T.: Boundary-integral approach for the numerical solution of the Cauchy problem for the Laplace equation. Ukr. Math. J. 68, 1665–1682 (2016)

    MathSciNet  Google Scholar 

  11. Chapko, R., Johansson, B.T., Shtoyko, M.: A double-layer potential approach for planar Cauchy problems for the Laplace equation, submitted to Visnyk of the Lviv University

  12. Chapko, R., Johansson, B.T., Shkolyk, M.: On a boundary integral equation method for elastostatic Cauchy problems in annular planar domains. J. Numer. Appl. Math. 126, 16–32 (2017)

    Google Scholar 

  13. Chapko, R., Johansson, B.T., Sobeyko, O.: On the numerical solution of a Cauchy problem in an elastostatic half-plane with a bounded inclusion. CMES Comput. Model. Eng. Sci. 62, 57–75 (2010)

    MathSciNet  MATH  Google Scholar 

  14. Chapko, R., Kress, R., Moench, L.: On the numerical solution of a hypersingular integral equation for elastic scattering from a planar crack. IMA J. Numer. Anal. 29, 601–619 (2000)

    Article  MathSciNet  Google Scholar 

  15. Chapko, R., Johansson, B.T., Vavrychuk, V.: A projected iterative method based on integral equations for inverse heat conduction in domains with a cut. Inverse Prob. 29, 065003 (2013)

    Article  MathSciNet  Google Scholar 

  16. Costabel, M., Dauge, M.: Crack singularities for general elliptic systems. Math. Nachr. 235, 29–49 (2002)

    Article  MathSciNet  Google Scholar 

  17. Eldén, L.: Algorithms for regularization of ill-conditioned least-squares problems. BIT 17, 134–145 (1977)

    Article  MathSciNet  Google Scholar 

  18. Faverjon, B., Puig, B., Baranger, T.N.: Identification of boundary conditions by solving Cauchy problem in linear elasticity with material uncertainties. Comput. Math. Appl. 73, 494–504 (2017)

    Article  MathSciNet  Google Scholar 

  19. Hansen, P.C.: The L-curve and its use in the numerical treatment of inverse problems, Ed. P. Johnston, in Computational Inverse Problems in Electrocardiology, WIT Press, Southampton, 119–142 (2001)

  20. Helsing, J., Jonsson, A.: A seventh-order accurate and stable algorithm for the computation of stress inside cracked rectangular domains. Internat. J. Multiscale Comput. Engrg. 2, 47–68 (2004)

    Google Scholar 

  21. Hsiao, G.C., Stephan, E.P., Wendland, W.L.: On the Dirichlet problem in elasticity for a domain exterior to an arc. J. Comput. Appl. Math. 34, 1–19 (1991)

    Article  MathSciNet  Google Scholar 

  22. Ikehata, M., Itou, H.: Reconstruction of a linear crack in an isotropic elastic body from a single set of measured data. Inverse Prob. 23, 589–607 (2007)

    Article  MathSciNet  Google Scholar 

  23. Isakov, V.: Inverse Problems for Partial Differential Equations, 3rd edn. Springer-Verlag, Cham (2017)

    Book  Google Scholar 

  24. Ferrier, R., Kadri, M., Gosselet, P.: Crack identification with incomplete boundary data in linear elasticity by the reciprocity gap method. Comput. Mech. 6, (2021). https://doi.org/10.1007/s00466-021-02006-4

  25. Kress, R.: Linear Integral Equation, 3rd edn. Springer-Verlag, New York (2014)

    Book  Google Scholar 

  26. Kubo, S.: Inverse problems related to the mechanics and fracture of solids and structures. JSME Int. J. 31, 157–166 (1988)

    Google Scholar 

  27. Kupradze, V.D.: Potential Methods in the Theory of Elasticity, Jerusalem: Israel Program for Scientific Translations, (1965)

  28. Marin, L., Hào, D.N., Lesnic, D.: Conjugate gradient-boundary element method for the Cauchy problem in elasticity. Quart. J. Mech. Appl. Math. 55, 227–247 (2002)

    Article  MathSciNet  Google Scholar 

  29. Marin, L., Karageorghis, A., Lesnic, D.: Regularized MFS solution of inverse boundary value problems in three-dimensional steady-state linear thermoelasticity. Int. J. Solids Struct. 91, 127–142 (2016)

    Article  Google Scholar 

  30. Zehnder, A.T.: Fracture Mechanics. Springer-Verlag, London (2012)

    Book  Google Scholar 

  31. Zhang, A., Gu, Y., Hua, Q., Chen, W., Zhang, C.: A regularized singular boundary method for inverse Cauchy problem in three-dimensional elastostatics. Adv. Appl. Math. Mech. 10, 1459–1477 (2018)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors are grateful for valuable suggestions and careful reading by the anonymous referees.

Funding

There is no funding to report for this work.

Author information

Authors and Affiliations

  1. Faculty of Applied Mathematics and Informatics, Ivan Franko National University of Lviv, Lviv, 79000, Ukraine

    Roman Chapko & Mariia Vlasiuk

  2. Mathematics, ITN, Campus Norrköping, Linköping University, 601 74, Norrköping, Sweden

    B. Tomas Johansson

Authors
  1. Roman Chapko
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. B. Tomas Johansson
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mariia Vlasiuk
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

The workload has been evenly distributed, with each author having a substantial contribution.

Corresponding author

Correspondence to Roman Chapko.

Ethics declarations

Conflict of interest

No conflict of interest to declare.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chapko, R., Johansson, B.T. & Vlasiuk, M. Boundary Integrals for Data Reconstruction on an Elastostatic Crack. Int. J. Appl. Comput. Math 8, 40 (2022). https://doi.org/10.1007/s40819-021-01232-x

Download citation

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40819-021-01232-x

Keywords

Search

Navigation