Skip to main content
SpringerLink
Log in

N-soliton solutions and asymptotic analysis for a Kadomtsev–Petviashvili–Schrödinger system for water waves

  • Published:
Zeitschrift für angewandte Mathematik und Physik Aims and scope Submit manuscript

Abstract

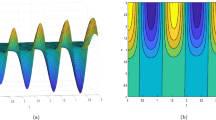
Under investigation in this paper is a Kadomtsev–Petviashvili–Schrödinger system, which describes the long waves in shallow water. Integrability study has been made through the Painlevé test. Via the Hirota method, the bilinear form and N-soliton solutions are obtained with an auxiliary variable. Collision of two solitons is found to be elastic by means of the asymptotic analysis. From the graphical descriptions of the two- and three-soliton solutions, it is found that both the bright and dark solitons collide with one another without any change in the physical quantities except for some small phase shifts during the process of each collision.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Osborne A.R.: The inverse scattering transform: tools for the nonlinear fourier analysis and filtering of ocean surface waves. Chaos Solitons Fractals 5, 2623–2637 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  2. Das G.C., Sarma J.: Response to comment on a new mathematical approach for finding the solitary waves in dusty plasma. Phys. Plasmas 6, 4394–4397 (1999)

    Article  MathSciNet  Google Scholar 

  3. Hong H.S., Lee H.J.: Korteweg-de Vries equation of ion acoustic surface waves. Phys. Plasmas 6, 3422–3424 (1999)

    Article  Google Scholar 

  4. Selwyn G.S., Heidenreich J.E., Haller K.L.: Particle trapping phenomena in radio frequency plasmas. Appl. Phys. Lett. 57, 1876–1878 (1990)

    Article  Google Scholar 

  5. Abbasbandy S., Zakaria F.S.: Soliton solutions for the fifth-order KdV equation with the homotopy analysis method. Nonlinear Dyn. 51, 83–87 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  6. Bridges T.J., Derks G., Gottwald G.: Stability and instability of solitary waves of the fifth-order KdV equation: a numerical framework. Phys. D 172, 190–216 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  7. Kaya D.: An explicit and numerical solutions of some fifth-order KdV equation by decomposition method. Appl. Math. Comput. 144, 353–363 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  8. Sun Z.Y., Gao Y.T., Liu Y., Yu X.: Soliton management for a variable-coefficient modified Korteweg-de Vries equation. Phys. Rev. E 84, 026606 (2011)

    Article  Google Scholar 

  9. Sun Z.Y., Gao Y.T., Yu X., Liu Y.: Dynamics of bound vector solitons induced by stochastic perturbations: soliton breakup and soliton switching. Phys. Lett. A 377, 3283–3290 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  10. Barnett M.P., Capitani J.F., Gathen J., Gerhard J.: Symbolic calculation in chemistry: selected examples. Int. J. Quantum Chem. 100, 80–104 (2004)

    Article  Google Scholar 

  11. Wazwaz A.M.: Exact solutions with solitons and periodic structures for the Zakharov–Kuznetsov (ZK) equation and its modified form. Commun. Nonlinear Sci. Numer. Simul. 10, 597–606 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  12. Teramond G.F., Brodsky S.J.: Light-front holography: a first approximation to QCD. Phys. Rev. Lett. 102, 081601–081604 (2009)

    Article  Google Scholar 

  13. Schrödinger E.: An undulatory theory of the mechanics of atoms and molecules. Phys. Rev. 28, 1049–1070 (1926)

    Article  MATH  Google Scholar 

  14. Schrödinger E.: Der stetige Übergang von der Mikro-zur Makromechanik. Naturwissenschaften 14, 664–666 (1926)

    Article  MATH  Google Scholar 

  15. Griffiths D.J.: Introduction to Quantum Mechanics. 2nd edn. Pearson Education, Boston (2004)

    Google Scholar 

  16. Shanker R.: Principles of Quantum Mechanics. 2nd edn. Plenum Press, New York (1994)

    Book  Google Scholar 

  17. Ablowitz M.J., Villarroel J.: Solutions to the time dependent Schrödinger and the Kadomtsev–Petviashvili equations. Phys. Rev. Lett. 78, 570–573 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  18. Ablowitz M.J., Chakravarty S., Trubatch A.D., Villarroel J.: A novel class of solutions of the non-stationary Schrödinger and the Kadomtsev–Petviashvili I equations. Phys. Lett. A 267, 132–146 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  19. Villarroel J., Ablowitz M.J.: On the discrete spectrum of the nonstationary Schrödinger equation and multipole lumps of the Kadomtsev–Petviashvili I equation. Commun. Math. Phys. 207, 1–42 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  20. Zhou X.: Inverse scattering transform for the time dependent Schrödinger equation with applications to the KPI aquation. Commun. Math. Phys. 128, 551–564 (1990)

    Article  MATH  Google Scholar 

  21. Bekir A.: Painlevé test for some (2+1)-dimensional nonlinear equations. Chaos Solitons Fractals 32, 449–445 (2007)

  22. Rida S.Z., Khalfallah M.: New periodic wave and soliton solutions for a Kadomtsev–Petviashvili (KP) like equation coupled to a Schrödinger equation. Commun. Nonlinear Sci. Numer. Simul. 15, 2818–2827 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  23. Elboree M.K.: New soliton solutions for a Kadomtsev–Petviashvili (KP) like equation coupled to a Schrödinger equation. Appl. Math. Comput. 218, 5966–5973 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  24. Kücükarslan S.: Homotopy perturbation method for coupled Schrödinger–KdV equation. Nonlinear Anal. 10, 2264–2271 (2009)

    Article  MATH  Google Scholar 

  25. Estévez P.G.: A nonisospectral problem in (2+1) dimensions derived from KP. Inverse Probl. 17, 1043–1052 (2001)

    Article  MATH  Google Scholar 

  26. Matveev V.B., Salle M.A.: Darboux Transformations and Solitons. Springer, Berlin (1991)

    Book  MATH  Google Scholar 

  27. Gao Y.T., Tian B.: On the non-planar dust-ion-acoustic waves in cosmic dusty plasmas with transverse perturbations. Europhys. Lett. 77, 15001–15006 (2007)

    Article  Google Scholar 

  28. Hirota R.: The Direct Method in Soliton Theory. Cambridge University Press, Cambridge (2004)

    Book  MATH  Google Scholar 

  29. Freeman N.C., Nimmo J.J.: Soliton solutions of the Korteweg-de Vries and Kadomtsev–Petviashvili equations: the Wronskian technique. Phys. Lett. A 95, 1–13 (1983)

    Article  MathSciNet  Google Scholar 

  30. Matveev V.B.: Generalized Wronskian formula for solutions of the KdV equations: first applications. Phys. Lett. A 166, 205–208 (1992)

    Article  MathSciNet  Google Scholar 

  31. Sun Z.Y., Gao Y.T., Yu X., Liu Y.: Amplification of nonautonomous solitons in the Bose–Einstein condensates and nonlinear optics. Europhys. Lett. 93, 40004 (2011)

    Article  Google Scholar 

  32. Gao Y.T., Tian B.: (3+1)-dimensional generalized Johnson model for cosmic dust-ion-acoustic nebulons with symbolic computation. Phys. Plasmas Lett. 13, 120703–120706 (2006)

    Article  Google Scholar 

  33. Feng Y.J., Gao Y.T., Sun Z.Y., Zuo D.W., Shen Y.J., Sun Y.H., Xue L., Yu X.: Anti-dark solitons for a variable-coefficient higher-order nonlinear Schrodinger equation in an inhomogeneous optical fiber. Phys. Scr. 90, 045201 (2015)

    Article  Google Scholar 

  34. Tian B., Gao Y.T.: Symbolic computation on cylindrical-modified dust-ion-acoustic nebulons in dusty plasmas. Phys. Lett. A 362, 283–288 (2007)

    Article  MATH  Google Scholar 

  35. Zuo D.W., Gao Y.T., Xue L., Feng Y.J., Sun Y.H.: Rogue waves for the generalized nonlinear Schrodinger–Maxwell–Bloch system in optical-fiber communication. Appl. Math. Lett. 40, 78–83 (2015)

    Article  MathSciNet  Google Scholar 

  36. Zuo D.W., Gao Y.T., Xue L., Sun Y.H., Feng Y.J.: Rogue-wave interaction for the Heisenberg ferromagnetism system. Phys. Scr. 90, 035201 (2015)

    Article  Google Scholar 

  37. Estévez P.G., Gordoa P.R.: Darboux transformations via Painlevé analysis. Inverse Probl. 13, 939–957 (1997)

    Article  MATH  Google Scholar 

  38. Weiss J., Tabor M., Carnevale G.: The Painlevé property for partial differential equations. J. Math. Phys. 24, 522–526 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  39. Weiss J.: The sine-Gordon equation: complete and partial integrability. J. Math. Phys. 25, 2226–2235 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  40. Fordy A.P., Pickering A.: Analysing negative resonances in the Painlevé test. Phys. Lett. A 160, 347–354 (1991)

    Article  MathSciNet  Google Scholar 

  41. Conte R., Fordy A.P., Pickering A.: A perturbative Painlevé approach to nonlinear differential equations. Phys. D 69, 33–38 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  42. Hereman W., Zhuang W.: Symbolic software for soliton theory. Acta Appl. Math. 39, 361–378 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  43. Zhang H.Q., Tian B., Lü X., Li H., Meng X.H.: Soliton interaction in the coupled mixed derivative nonlinear Schrödinger equations. Phys. Lett. A 373, 4315–4321 (2009)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. State Key Laboratory of Information Photonics and Optical Communications, and School of Science, Beijing University of Posts and Telecommunications, Beijing, 100876, China

    Yu-Feng Wang, Bo Tian, Li-Cai Liu, Min Li & Bo Qin

Authors
  1. Yu-Feng Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Bo Tian
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Li-Cai Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Min Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Bo Qin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Bo Tian.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, YF., Tian, B., Liu, LC. et al. N-soliton solutions and asymptotic analysis for a Kadomtsev–Petviashvili–Schrödinger system for water waves. Z. Angew. Math. Phys. 66, 2543–2553 (2015). https://doi.org/10.1007/s00033-015-0538-6

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00033-015-0538-6

Mathematics Subject Classification

Keywords

Search

Navigation