Existence and uniqueness result for a fluid–structure–interaction evolution problem in an unbounded 2D channel

Abstract

In an unbounded 2D channel, we consider the vertical displacement of a rectangular obstacle in a regime of small flux for the incoming flow field, modelling the interaction between the cross-section of the deck of a suspension bridge and the wind. We prove an existence and uniqueness result for a fluid–structure-interaction evolution problem set in this channel, where at infinity the velocity field of the fluid has a Poiseuille flow profile. We introduce a suitable definition of weak solutions and we make use of a penalty method. In order to prevent the obstacle from going excessively far from the equilibrium position and colliding with the boundary of the channel, we introduce a strong force in the differential equation governing the motion of the rigid body and we find a unique global-in-time solution.

1 Introduction and main result

Suspension bridges may experience several types of instability phenomena, which affect more or less critically each component of the structure. Among all components, the deck is the most sensitive part. When analyzing the dynamic response of the bridge to the wind from the engineering point of view, we observe that the bridge may suffer from a variety of problems: one degree and two degrees of freedom instability, buffeting and vortex shedding. Two degrees of freedom instability, also known as flutter instability, occurs when the vertical and the torsional motion of the deck synchronize so that aerodynamic forces introduce energy into the system. However, this only occurs after reaching a critical value of the incoming wind velocity (see [9, 14, 28]). Thus, the vertical and torsional displacements are decoupled in a regime of small oscillations.

We set up our model precisely under the hypothesis of a small flux for the incoming flow field. We consider the interaction between an obstacle and a fluid in a 2D unbounded channel, where the flow is of Poiseuille type at infinity; we analyze a fluid–structure problem by allowing the obstacle to move in a vertical translation. In a regime of strong incoming flux, it would be necessary to consider the full coupled vertical-torsional motion.

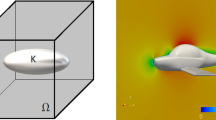
We follow the two-dimensional fluid–structure-interaction evolution problem introduced in [4]. We label as $B=[-d,d]\times [-\delta ,\delta ]$ a rectangular rigid body representing the 2D cross-section of the deck of a suspension bridge; we denote by $m>0$ the mass of the body. Without loss of generality, we can assume d to be equal to 1, by using the length of the body as reference length scale. Such body is free to move vertically inside an infinitely long 2D channel $A={\mathbb {R}}\times (-L,L)$, driven by the action of both a smooth elastic restoring force and the fluid flow: see Fig. 1. The upper and lower boundaries of such channel are denoted by $\Gamma ={\mathbb {R}}\times \{-L,L\}$ and h indicates the position of the center of the rigid body from the middle line $x_2=0$. Thus,

$$\begin{aligned} B_h=B+h{\hat{e}}_2 \quad \forall \, |h|<L-\delta \end{aligned}$$

tracks the position of the body after the vertical translation. Notice that, when $|h|=L-\delta$, the obstacle collides with $\Gamma$. Due to the motion of the rigid body, the domain occupied by the fluid $\Omega _h$ depends itself on h, which explains the subscript, and it is given by:

$$\begin{aligned} \Omega _h={\mathbb {R}}\times (-L,L){\setminus } B_h=A{\setminus } B_h. \end{aligned}$$

(1.1)

Fig. 1

The channel with the vertically moving obstacle B

At infinity, the velocity field reproduces a Poiseuille flow profile, which we label as q. Before giving the formulation of the problem, we point out that, by a little abuse of notation, we will make use of the following Cartesian product

$$\begin{aligned} \Omega _{h(t)}\times (0,T) \end{aligned}$$

to indicate the non-cylindrical space-time domain given by $\{(x,t): 0<t<T, x\in \Omega _{h(t)}\}$. The fluid–structure-interaction evolution problem is then:

$$\begin{aligned} \begin{aligned}&u_t=\mu \,\Delta u-(u\cdot \nabla )u-\nabla p,\quad \text {div}\, u=0\qquad (x,t)\in \Omega _{h(t)}\times (0,T),\\&u=0 \qquad (x,t)\in \Gamma \times (0,T),\qquad u={h'}(t)\,{\hat{e}}_2 \qquad (x,t)\in \partial B_{h(t)}\times (0,T),\\&\quad \lim _{|x_1|\rightarrow \infty }u(x_1,x_2)=q:=\lambda (L^2-x_2^2)\,{\hat{e}}_1,\\&m\,{h''(t)} +f(h(t))=-{\hat{e}}_2\cdot \int _{\partial B_{h(t)}} {\mathcal {T}}(u,p){\hat{n}}\qquad t\in (0,T), \end{aligned} \end{aligned}$$

(1.2)

to which we associate the initial conditions $u(x,0)=u_0$, $h(0)=h_0$, ${h'}(0)=k_0$. Here $u:\Omega _{h(t)}\times (0,T)\rightarrow {\mathbb {R}}^2$ and $p:\Omega _{h(t)}\times (0,T)\rightarrow {\mathbb {R}}$ are respectively the unknown velocity vector field and the unknown scalar pressure field, while ${\hat{n}}$ denotes the outward normal to $\partial \Omega _h$, thus directed in the interior of $\partial B_h$. The constant $\lambda$ in q measures the magnitude of the Poiseuille flow, which is prescribed, thus $\lambda$ is given. The motion of the body is governed by the ODE in (1.2): f(h) is an elastic smooth restoring force, which we suppose to be $f\in C^1(-L+\delta ,L-\delta )$, and ${\mathcal {T}}(u,p)=-p{\mathbf {I}}+2\mu D(u)$ is the fluid Cauchy stress tensor, with ${\mathbf {I}}$ the $2\times 2$-identity matrix and

$$\begin{aligned} D(u)=\frac{1}{2}(\nabla u+\nabla u^T), \end{aligned}$$

thus the right hand side of the ODE corresponds to the fluid lift. We also assume that f(h) satisfies some further conditions, given later in (1.4), which translate the assumption of f being a strong force, preventing the obstacle from colliding with the boundary of the channel $\Gamma$. From the physical view point indeed, f resumes the action of three kind of forces acting on the deck of a suspension bridge, as also explained in [4, Introduction]: the upward restoring force due to the elastic action of both the hangers and the sustaining cables, the weight of the deck acting downwards and the elastic resistance to deformations of the whole deck, preventing the obstacle to go too far from its equilibrium horizontal position (see also [14]). Our model indeed loses its physical meaning in case of collisions; on the other hand, collisions would be purely virtual in the physical framework at consideration, because we can not expect the bridge to be subjected to very large deformations. This justifies the limit in the assumption in (1.4); we emphasize that, in this context, we are not interested in choosing the optimal hypothesis on f ensuring the absence of collisions. As in [26], we suppose that the initial velocity $u_0$ admits the following representation

$$\begin{aligned} u_0(x)={\bar{u}}_0(x)+\zeta (x_1)\,\lambda (L^2-x_2^2){\hat{e}}_1, \quad \text {with} \quad {\bar{u}}_0(x)\in L^2(\Omega _h),\quad \text {div}\, u_0(x)=0,\nonumber \\ \end{aligned}$$

(1.3)

where $\zeta (x_1)$ is a smooth cutoff function such that $\zeta (\tau )=0$, if $|\tau |<2$, $\zeta (\tau )=1$ if $|\tau |>3$.

In [4], the authors prove that for the stationary version of (1.2) the equilibrium position of the obstacle is perfectly symmetric under smallness assumption on the imposed flow rate magnitude of the Poiseuille flow; actually, they are able to prove their result with an assumption on f weaker than (1.4). The main purpose of our work is to prove the existence and the uniqueness of a weak solution for the fluid–structure-interaction evolution problem (1.2). In the literature several definitions of weak solutions have been adopted, as well as several techniques to find such solutions (see, e.g., [6, 8] for the 3D case, [23, 27] for the 2D case). In order to prove existence we adopt a penalty method devised in a paper by Fujita and Sauer, see [10]; this technique was later exploited by Conca, San Martin and Tucsnak in [6] in order to prove existence of solutions for a boundary problem modelling the motion of a rigid ball in a viscous fluid occupying a bounded domain. Among the several aforementioned techniques, we choose to apply the method by [6], because it enables to work with a non-global weak formulation, in the sense that the terms concerning the fluid sub-problem and those concerning the rigid body sub-problem of (1.2), although coupled, remain distinguished. On the other hand, both the method introduced in [8, 23, 27] would require working with global quantities and a global weak formulation, in the sense that the integrals would be defined on the whole domain A; in this context, the approach by [6] is more convenient because of the presence of the strong force f in the ordinary differential equation governing the motion of the obstacle, which makes it non-trivial to define a global weak form for the original coupled frame. The main difference with the problem considered in [6] lies in the fact that the domain occupied by both the rigid body and the fluid in (1.2) is an unbounded channel where a non-zero velocity field is imposed at infinity; this requires building a solenoidal extension of the Poiseuille flow. Moreover, besides the less affecting difference of a rectangular shaped obstacle, the introduction of the strong force f in the ordinary differential equation governing the motion of the obstacle in (1.2) allows to obtain solutions with a global character in time, as well as uniqueness of such solutions: indeed, this force prevents the obstacle from colliding with the boundary of the channel.

Collisions are a delicate issue in the context of fluid–structure-interaction problems, especially because different phenomena occur in the context of strong or weak solutions. For strong solutions, in some particular 2D cases, collisions are excluded (see [21, 22, 30]). However, this no-collision result appears physically unrealistic both at the macroscopic and microscopic scales, as pointed out in [19, 20] where it is suggested that the flaw lies in the modelling. If we move to the realm of weak solutions, it is not known in general whether collisions do occur in finite time or not, although, in some particular cases, where the contact surfaces are regular enough, they might be excluded, see [30, Theorem 3.1]. However weak solutions exist globally even if collisions occur in finite time, because they are characterized by vanishing relative velocity; this result holds under regularity hypothesis on the boundary of the body and on the fluid domain, see [27, 30]. In [31] the author was able to construct at least two weak solutions admitting collision in finite time and, in order to guarantee uniqueness of weak solutions, one then needs to exclude collisions as pointed out in [16]. In particular, while uniqueness of strong solutions is a known fact both in two and three-dimensions, and both for no-slip case and the slip case (see [1, 7, 18, 32]), in [16] the authors proved for the first time a result of uniqueness for weak solutions for a two-dimensional fluid-rigid body system and in [5] the author proved it for the slip case. Here, we adopt a different strategy in order to explore existence and uniqueness of weak solutions, we make use of the strong force f, as it is done in [4].

Our main result states the existence and uniqueness of weak solutions to problem (1.2).

Theorem 1.1

Let $\Omega _h$ be as in (1.1). Assume that $f(h)\in C^1(-L+\delta , L-\delta )$ satisfies the following assumption

$$\begin{aligned}&\exists \, r>0 \quad \text {s.t.}\quad f'(h)>0\,\forall \,h\in (-L+\delta ,L-\delta ),\nonumber \\&\lim _{|h|\rightarrow L-\delta }{|f(h)|}\,\frac{1}{\exp \frac{1}{{{(L-\delta -|h|)^{4+r}}}}}=+\infty . \end{aligned}$$

(1.4)

Moreover, let $|h_0|<L-\delta$ and $u_0$ satisfying (1.3) be such that $u_0\cdot {\hat{n}}= k_0{\hat{e}}_2\cdot {\hat{n}}$ on $\partial B_{h_0}$. Then, problem (1.2) admits a unique weak solution (u, h), defined in a suitable sense, for any $T<\infty$. Moreover the energy of (u, h) is bounded.

Theorem 1.1 deserves some comments. First, we emphasize that, since (1.2) is a fluid–structure-interaction problem, one needs to give a suitable definition of weak solutions which takes into account the presence of the moving obstacle. Because of such difficulty, we adopt a definition of weak solutions which is a compromise between the one given in [13] and the one in [6]; weak solutions are defined in Definition 2.3 after transforming problem (1.2) into an equivalent problem, as we shall see in Sect. 2. Finally, the global-in-time property of solutions is ensured because of the energy estimate associated to problem (1.2), which guarantees that no collision occurs between the obstacle and the boundary of the channel. Such energy estimate will be made explicit in Theorem 2.6 for the equivalent problem. In particular, as in the case of the Navier–Stokes equations in a 2D domain with cylindrical outlets to infinity, we merely obtain an inequality, differently from what one usually obtains in a bounded 2D domain: see [26].

The rest of the paper is devoted to proving Theorem 1.1 and it is organized as follows. In Sect. 2 we present some notations and preliminary results which are essential to apply the penalty method and are useful throughout the paper. Then we reformulate problem (1.2) in a reference frame attached to the obstacle; this produces the equivalent problem, (2.7)–(2.8). At the end of Sect. 2, Theorem 2.6 states the existence and uniqueness of solutions for the equivalent problem (2.7)–(2.8). Thus, Theorem 1.1 is proven once we develop the proof of such statement, which is addressed in the subsequent sections. In Sect. 3, we introduce an auxiliary problem, at the core of the penalty method, for which we prove existence of solutions with the Faedo–Galerkin procedure. In Sect. 4, after some additional results, we conclude the proof of the existence part of Theorem 2.6 and, consequently, the existence part of the main result of the work, Theorem 1.1. Section 5 is devoted to proving uniqueness of solutions to problem (2.7)–(2.8), which concludes the proof of Theorem 2.6 and thus also of Theorem 1.1. The main difficulty of proving uniqueness is that we cannot simply take the difference between two weak solutions of problem (2.7)–(2.8) because, since the fluid domain has moving boundaries, those solutions are not defined on the same domain, thus we will adopt a suitable change of variables to solve such issue, following the work in [16]. As we already mentioned, if we moved to the regime of strong incoming flux, we would have to consider an obstacle characterized by a fully-coupled vertical-torsional motion. As a step towards this direction, it appears interesting to look at the second model introduced in [4] where the obstacle is immersed in the same channel but it is only free to rotate around a fixed pin. In particular, in Sect. 6 we make some remarks about this second fluid–structure-interaction evolution problem: we highlight how this is a significantly different problem with respect to the case of vertical translation both from the physical and mathematical point of view.

2 Preliminaries: an equivalent formulation

Problem (1.2) is set in a 2D unbounded channel with a prescribed non-zero velocity field at infinity. We begin by capturing the flow at large $|x_1|$: we construct a suitable extension of the Poiseuille velocity profile at infinity by using similar arguments to the classical procedure by Ladyzhenskaya [25] (see also [2]). Let $b_3$ be the following function, defined over $(-L,L)$,

$$\begin{aligned} b_3(x_2)=\lambda \, L^3\bigg [\frac{x_2}{L}-\frac{1}{3}\bigg (\frac{x_2}{L}\bigg )^3\,\bigg ]. \end{aligned}$$

(2.1)

Observe that

$$\begin{aligned} b'_3(x_2)=\lambda (L^2-x_2^2). \end{aligned}$$

We consider a partition of the channel A as

$$\begin{aligned} \displaystyle A= & {} \bigcup _{i=0}^{2} A_{i}, \quad A_{0}= A\cap \{-3\le x_1\le 3\}, \quad A_{1}=A\cap \{x_1<-3\},\nonumber \\ A_{2}= & {} A\cap \{x_1>3\}. \end{aligned}$$

(2.2)

We define $\zeta _1$ to be a smooth cutoff function acting in the horizontal direction such that

$$\begin{aligned} \zeta _1(x)=\zeta _1(x_1)= {\left\{ \begin{array}{ll} 1 &{}\quad \text{ if }\,\,|x_1|<2 \\ 0 &{}\quad \text{ if }\,\,|x_1|>3 \end{array}\right. }, \qquad \zeta _1\in C^\infty ({\mathbb {R}}\times [-L,L]). \end{aligned}$$

Then, let $\varepsilon _0>0$. We take $\zeta _2$ to be a twice continously differentiable cutoff function acting in the vertical direction

$$\begin{aligned} \zeta _2(x)=\zeta _2(x_2)= {\left\{ \begin{array}{ll} 1 &{}\quad \text{ if }\,\,|x_2|<L-\varepsilon _0/2 \\ 0 &{}\quad \text{ if }\,\,|x_2|>L-\varepsilon _0/4 \end{array}\right. },\qquad \zeta _2\in C^2({\mathbb {R}}\times [-L,L]), \end{aligned}$$

obeying the inequalities

$$\begin{aligned} |\zeta _2(x_2)|\le C, \qquad \bigg |\frac{\partial \zeta _2(x_2)}{\partial x_2}\bigg |\le \frac{C}{\varepsilon _0},\qquad \bigg |\frac{\partial ^2 \zeta _2(x_2)}{\partial x_2^2}\bigg |\le \frac{C}{\varepsilon ^2_0}, \end{aligned}$$

with some constants $C>0$. Then we take

$$\begin{aligned} \zeta (x)=\zeta (x_1,x_2)=1- \zeta _1(x_1)\,\zeta _2(x_2) \qquad \forall \, x\in A. \end{aligned}$$

(2.3)

The above construction enables us to state:

Lemma 2.1

Let $A ={\mathbb {R}}\times (-L,L)$, q as in (1.2) and let $\varepsilon _0>0$ small be arbitrarily fixed. Let

$$\begin{aligned} s(x)=\left( \frac{\partial }{\partial x_2} \big (b_3(x)\zeta (x)\big ),-\frac{\partial }{\partial x_1} \big (b_3(x)\zeta (x)\big )\right) , \end{aligned}$$

where $b_3(x)$ is as in (2.1), and $\zeta (x)$ as in (2.3). Then the vector field s(x) is such that

$$\begin{aligned} \nabla \cdot s=0 \quad \text {in}\,\,A, \qquad s=q\quad \text {in}\,\ A_1\cup A_2, \end{aligned}$$

with $A_{i}, i=1,2$ defined in (2.2). Moreover $s \in W^ {1,\infty }(A)\cap H^2_{loc}(A)$, and $\mathrm {supp}(s)=A{\setminus } \{|x_1|<2\wedge |x_2|<L-\varepsilon _0\}$, and, for every $\varepsilon _0>0$, there hold the estimates

$$\begin{aligned} \Vert \nabla s\Vert _{L^\infty (A)}\le \frac{c_1}{\varepsilon _0^2}, \qquad \Vert \nabla s\Vert _{L^2(A_{0})}\le \frac{c_2}{\varepsilon _0^2}, \end{aligned}$$

(2.4)

where $c_1,c_2>0$ depend on L and $\lambda$.

As a first step of the penalty method implemented in [6], we change problem (1.2) into an equivalent problem by considering a frame attached to the rigid body, whose origin coincides with its center of mass. Thus we set

$$\begin{aligned} y=x-h(t)\,{\hat{e}}_2, \end{aligned}$$

and we denote

$$\begin{aligned} \begin{aligned}&v(y,t)=u(y+h(t)\,{\hat{e}}_2,t),\;\, {\mathfrak {p}}(y,t)=p(y+h(t)\,{\hat{e}}_2,t),\\&{\mathcal {T}}(v,{\mathfrak {p}})=-{\mathfrak {p}} {\mathbf {I}}+\mu [\nabla v+(\nabla {v})^T] \\&{\tilde{\Omega }}(t)=\Omega _{h(t)}-h(t){\hat{e}}_2, \;\, A_{h(t)}=A-h(t){\hat{e}}_2, \;\, {\tilde{\Gamma }}(t)=\Gamma -h(t){\hat{e}}_2,\\&B=B_{h(t)}-h(t){\hat{e}}_2. \end{aligned} \end{aligned}$$

(2.5)

The domain of the fluid in the new reference frame ${\tilde{\Omega }}$ shall also be partitioned

$$\begin{aligned}&\displaystyle {\tilde{\Omega }}(t)= \bigcup _{i=0}^{2} {\tilde{\Omega }}_{i}(t), \quad {\tilde{\Omega }}_{0}(t)= {\tilde{\Omega }}(t)\cap \{-3\le y_1\le 3\}, \nonumber \\&{\tilde{\Omega }}_{1}(t)={\tilde{\Omega }}(t)\cap \{y_1<-3\},\qquad {\tilde{\Omega }}_{2}(t)={\tilde{\Omega }}(t)\cap \{y_1>3\}. \end{aligned}$$

(2.6)

We emphasize that the obstacle is now fixed, while the domain occupied by both the fluid and the rigid body, $A_{h(t)}=B\cup \partial B\cup {\tilde{\Omega }}(t)$, changes with time. Then, we notice that

$$\begin{aligned} \nabla _y v=\nabla _x u, \quad \text {div}_y\, v=\text {div}_x\, u,\quad \Delta _y v=\Delta _x u, \quad v_t=u_t+ (h'{\hat{e}}_2\cdot \nabla _y) v . \end{aligned}$$

Thus, we obtain the following problem (see also [12]):

$$\begin{aligned} \begin{aligned}&v_t=\mu \,\Delta v-(v\cdot \nabla )\,v-\nabla {\mathfrak {p}}+(h'(t){\hat{e}}_2\cdot \nabla )\,v,\quad \text {div}\, v=0\quad (y,t)\in {\tilde{\Omega }}(t)\times (0,T)\\&v=0 \quad (y,t)\in {\tilde{\Gamma }}(t)\times (0,T),\quad v=h'(t){\hat{e}}_2 \quad (y,t)\in \partial B \times (0,T),\\&\lim _{|y_1|\rightarrow \infty }v(y)={\tilde{q}}(y):=\lambda (L^2-(y_2+h(t))^2)\,{\hat{e}}_1 \\&v(y,0)=v_0(y)\quad y\in {\tilde{\Omega }}(0) \end{aligned} \end{aligned}$$

(2.7)

where $v_0(y)=u_0(y+h_0{\hat{e}}_2)$ with $u_0$ as in (1.3). Notice that all derivatives appearing in this problem are now taken with respect to the new variable $y=(y_1,y_2)$. The Poiseuille flow at infinity is obtained by transporting q as in (1.2) to the new reference frame:

$$\begin{aligned} {\tilde{q}}(y)=q(y+h(t){\hat{e}}_2). \end{aligned}$$

The motion of the rectangular body is governed by:

$$\begin{aligned} m\,{h''(t)} +f(h(t))=-{\hat{e}}_2\cdot \int _{\partial B}{\mathcal {T}}(v,{\mathfrak {p}}){\hat{n}}\qquad t\in (0,T). \end{aligned}$$

(2.8)

The original problem (1.2) is equivalent to (2.7)–(2.8), because we simply adopted a change in the system of coordinates. Thus Theorem 1.1 is proven if we prove existence of solutions to (2.7)–(2.8). We look for solutions to the problem (2.7)–(2.8) of the form

$$\begin{aligned} v={\hat{v}}+a, \end{aligned}$$

where a is the solenoidal extension of the Poiseuille flow in the new reference frame, strongly depending on h and on the choice of $\varepsilon _0$ in Lemma 2.1:

$$\begin{aligned} a(y)=a_{h(t)}(y;\varepsilon _0)=s(y+h(t)\,{\hat{e}}_2). \end{aligned}$$

(2.9)

The function a enjoys the same properties of s stated in Lemma 2.1 once we substituted q and A with their counterparts in the new reference frame, ${\tilde{q}}$ and $A_h$, and we partitioned ${A}_h$ similarly to what we did in (2.2). Assume that

$$\begin{aligned} h_0\in [-L+\delta +{\hat{\varepsilon }}, L-\delta -{\hat{\varepsilon }}] \end{aligned}$$

where ${\hat{\varepsilon }}>0$ small is arbitrarily fixed. Then, the function ${\hat{v}}$ solves the following problem:

$$\begin{aligned} \begin{aligned}&{\hat{v}}_t-\mu \,\Delta {\hat{v}}+({\hat{v}}\cdot \nabla )\,{\hat{v}}+\nabla {\mathfrak {p}}-(h'(t){\hat{e}}_2\cdot \nabla )\,{\hat{v}} \\&-(h'(t){\hat{e}}_2\cdot \nabla )\,a+({\hat{v}}\cdot \nabla )\,a+(a\cdot \nabla )\,{\hat{v}}={\hat{g}}\\&(y,t)\in {\tilde{\Omega }}(t)\times (0,T),\\&\text {div}\, {\hat{v}}=0\;\,(y,t)\in \tilde{ \Omega }(t)\times (0,T),\\&{\hat{v}}=0 \;\, (y,t)\in {\tilde{\Gamma }}(t)\times (0,T),\;\, {\hat{v}} =h'(t){\hat{e}}_2 \;\, (y,t)\in \partial B\times (0,T),\;\, \lim _{|y_1|\rightarrow \infty }{\hat{v}}=0, \\&{\hat{v}}(y,0)={\hat{v}}_0(y)=v_0-a_{h_0}(y;{\hat{\varepsilon }})\;\, y\in {\tilde{\Omega }}(0), \end{aligned} \end{aligned}$$

(2.10)

where

$$\begin{aligned} {\hat{g}}:=\mu \,\Delta a -(a\cdot \nabla )\,a. \end{aligned}$$

(2.11)

Notice that ${\hat{v}}\rightarrow 0$ as $|y_1|\rightarrow \infty$ and ${\hat{v}}_0\in L^2({\tilde{\Omega }}(0))$ is such that ${\hat{v}}_0\cdot {\hat{n}}=k_0{\hat{e}}_2\cdot {\hat{n}}$ on $\partial B$. We also point out that supp$({\hat{g}})\in A_h{\setminus }\{|y_1|<2\wedge |y_2|<L-\varepsilon _0-h\}$. The vertical translation of the obstacle h responds to

$$\begin{aligned} m\, {h''(t)} +f(h(t))=-{\hat{e}}_2\cdot \int _{\partial B} {\mathcal {T}}({\hat{v}}+a,{\mathfrak {p}}){\hat{n}}\qquad t\in (0,T), \end{aligned}$$

(2.12)

with initial conditions $h(0)=h_0$, ${h'}(0)=k_0$.

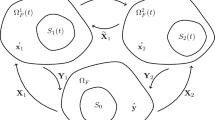
As already mentioned, in order to prove our main result we make use of a procedure which is similar to the one adopted in [6]: problem (2.10)–(2.12) is set in a region with moving boundaries, ${\tilde{\Omega }}(t)$, which makes it impossible to apply the Faedo–Galerkin approximation with the standard functional spaces of hydrodynamic evolutionary problems. The idea exploited in [6] is that of a penalty method and it was first elaborated in the paper by Fujita and Sauer (see [10]). The crucial idea of the method implies introducing an auxiliary fixed, infinite domain ${\tilde{A}}$ given by:

$$\begin{aligned} {\tilde{A}}=A-A=\{x-y\,|\,x\in A,y\in A\}, \end{aligned}$$

(2.13)

such that ${\tilde{\Omega }}(t)\subset A_{h(t)}\subset {\tilde{A}}$ (see Fig. 2 for the new configuration). Notice that the vertical translation of ${\tilde{\Omega }}(t)$ inside ${\tilde{A}}$ is confined: dist ($\partial {\tilde{A}}, {\tilde{\Gamma }}(t))\ge \delta$. This is an obvious consequence of impenetrability of bodies but we will later prove that this inequality actually holds strictly, thus the obstacle never collides with the boundary of the channel. Inside the auxiliary fixed domain ${\tilde{A}}$, we can naturally extend the velocity field at infinity ${\tilde{q}}(y)$ outside $A_{h(t)}$ for every h(t) through its definition in (2.7), see Fig. 2.

We report three facts, that we will later use. First, an estimate for the $L^2$-norm of the gradient of ${\tilde{q}}$ in each one-dimensional section of the domain ${\tilde{A}}$:

$$\begin{aligned} \Vert \nabla {\tilde{q}}\Vert _{L^2(-2L+\delta ,\,2L-\delta )}\le \lambda \, {\tilde{\xi }}\quad \text {with}\,\,\, {\tilde{\xi }}=\sqrt{\frac{8}{3}\,(2L-\delta )\,(7L^2-10\,L\,\delta +4\,\delta ^2)}.\nonumber \\ \end{aligned}$$

(2.14)

Then, we give the following partition of ${\tilde{A}}$:

$$\begin{aligned} \displaystyle {{\tilde{A}}}= & {} \bigcup _{i=0}^{2} {{\tilde{A}}}_{i}, \quad {{\tilde{A}}}_{0}= \tilde{{A}}\cap \{-3\le y_1\le 3\},\ \quad \tilde{{A}}_{1}={{\tilde{A}}}\cap \{y_1<-3\},\nonumber \\ \tilde{{A}}_{2}= & {} \tilde{{A}}\cap \{y_1>3\}. \end{aligned}$$

(2.15)

Finally, we comment on some properties which can be derived from the assumptions of f in (2.12) being a strong force, given in (1.4). In particular, from (1.4) it follows that $f(h)h>0$ for all $h\ne 0$ and there exists $\rho$ such that $f'(h)>\rho >0$ for all h. Hence, if we call

$$\begin{aligned} F(h)=\int _0^h f(s)ds \end{aligned}$$

(2.16)

we obtain

$$\begin{aligned} f(h)h\ge F(h)\ge \frac{\rho }{2}h^2. \end{aligned}$$

(2.17)

The last condition (1.4) may be interpreted in the spirit of [17]. In [17], the author considers systems of the general type $x''+\nabla V(x)=0$, with $x\in {\mathbb {R}}^n$, where the potential V(x) associated to a conservative dynamical system, such as a n-body system, is assumed to be $C^2$ everywhere except at a closed non empty set S at which it has infinitely deep wells, i.e. $V(x)\rightarrow -\infty$ as $x\rightarrow S$; then, the system is said to satisfy the strong force condition if and only if there exists a neighborhood N of S and $U\in C^2$ such that $U(x)\rightarrow -\infty$ as $x\rightarrow S$ and $-V(x)\ge |\nabla U(x)|^2$ for all $x\in N{\setminus } S$. In a n-body system the singularities correspond to collisions of the masses and the strong force condition allows to avoid them (see also [3]). In our case, in the terminology of [17], f plays the role of $V'$ and the ODE in (2.12) satisfies the strong force assumption, with the singularity exhibited at $|h|=L-\delta$.

Fig. 2

The channel, after the change of variables, moves in the fixed red region ${\tilde{A}}$

Now, we seek a rigorous definition of weak solutions to (2.7)–(2.8). We introduce some classical functional spaces from mathematical fluid dynamics (see [33] for instance):

$$\begin{aligned}&{\mathcal {V}}({\tilde{A}})=\{v\in {\mathcal {D}}({\tilde{A}})\,|\, \text {div}\,v=0\},\\&H({\tilde{A}})=\text {closure of } {\mathcal {V}} \text { w.r.t. the norm } {\Vert \cdot \Vert }_{L^2({\tilde{A}})},\\&V({\tilde{A}})=\text {closure of } {\mathcal {V}}\text { w.r.t. the norm } {\Vert \nabla \cdot \Vert }_{L^2({\tilde{A}})}. \end{aligned}$$

We emphasize that since ${\tilde{A}}$ is bounded in the vertical direction, there holds the Poincaré inequality, which makes $H_0^1({\tilde{A}})$ an Hilbert space with respect to the scalar product $(u,v)_{H_0^1({\tilde{A}})}=(\nabla u,\nabla v)_{L^2({\tilde{A}})}$. The presence of the obstacle B requires introducing some further spaces:

$$\begin{aligned}&{\mathcal {W}}({\tilde{A}})=\{(v,l)\in {\mathcal {V}}({\tilde{A}})\times {\mathbb {R}}\,|\, v|_{B}=l\,{\hat{e}}_2\},\\&{\mathbb {H}}({\tilde{A}})=\text {closure of } {\mathcal {W}}\text { in } L^2({\tilde{A}})\times {\mathbb {R}},\;\; {\mathbb {V}}({\tilde{A}})=\text {closure of } {\mathcal {W}}\text { in } H^1_0({\tilde{A}})\times {\mathbb {R}} \end{aligned}$$

to which we associate the scalar products

$$\begin{aligned} \langle (v_1,l_1),(v_2,l_2)\rangle _{ {\mathbb {H}}({\tilde{A}})}= & {} \int _{{\tilde{A}}{\setminus } B} v_1\cdot v_2\,dy+ml_1l_2,\\ \langle (v_1,l_1),(v_2,l_2)\rangle _{ {\mathbb {V}}({\tilde{A}})}= & {} 2\int _{{\tilde{A}}{\setminus } B} D (v_1)\cdot D( v_2)\,dy+ml_1l_2. \end{aligned}$$

Finally, the weak formulation of problem (2.7)–(2.8) will exploit the following spaces, which may be defined for any given function h(t). In particular, for every t

$$\begin{aligned} {\mathcal {W}}_{h(t)}= & {} \{(v,l)\in {\mathcal {W}}({\tilde{A}})\,|\, \text {supp}\, v\in A_{h(t)} \},\nonumber \\ {\mathbb {H}}_{h(t)}= & {} \text {closure of } {\mathcal {W}}_{h(t)}\text { in } L^2({\tilde{A}})\times {\mathbb {R}},\; {\mathbb {V}}_{h(t)}=\text {closure of } {\mathcal {W}}_{h(t)}\text { in } H^1_0({\tilde{A}})\times {\mathbb {R}}.\nonumber \\ \end{aligned}$$

(2.18)

Then, we introduce the standard trilinear form:

$$\begin{aligned} \psi (u,v,w)=\int _{{\tilde{\Omega }}} (u\cdot \nabla )\, v \cdot w. \end{aligned}$$

(2.19)

We are ready to state and prove the following proposition. Let us denote by $\langle \cdot ,\cdot \rangle$ the duality pairing between V and ${V}'$.

Proposition 2.2

Let the couple (v, h) be a classical solution to (2.7)–(2.8) such that $|h(t)|\le L-\delta -\varepsilon _0$ for all $t\in [0,T]$ for some $\varepsilon _0>0$. Then, building the extension $a=a_h(y;\varepsilon _0)$ in (2.9) choosing the same $\varepsilon _0$, the function ${\hat{v}}=v-a$ satisfies

$$\begin{aligned} \begin{aligned}&-\int _0^T\{({\hat{v}},\phi _t)_{L^2({\tilde{\Omega }}(t))}+\!m\,h'l'-f(h)\,l\}\! +\!2\mu \int _0^T(D({\hat{v}}),D( \phi ))_{L^2({\tilde{\Omega }}(t))}\\&\quad +\int _0^T\{\psi ({\hat{v}},{\hat{v}},\phi )+\psi ({\hat{v}},a,\phi )+\psi (a,{\hat{v}},\phi )\\&\quad -\psi (h'{\hat{e}}_2,a,\phi )-\psi (h'{\hat{e}}_2,{\hat{v}},\phi )\}=\int _0^T\langle {\hat{g}},\phi \rangle +m\,k_0\,l(0)+({\hat{v}}_0,\phi (0))_{L^2({\tilde{\Omega }}(0))} \end{aligned} \end{aligned}$$

(2.20)

for every $(\phi ,l)\in C^1([0,T];{\mathbb {V}}_{h(t)}) \,\,\text {such that}\,\, \phi (\cdot ,T)=l(T)=0$, with ${\hat{g}}:=\mu \,\Delta a -(a\cdot \nabla )\,a$.

Proof

Consider the problem satisfied by $({\hat{v}},h)$, (2.10)–(2.12). In order to obtain (2.20), we choose a test couple $(\phi ,l)\in C^1([0,T], {\mathbb {V}}_{h(t)})$ such that $\phi (\cdot , T)=l(T)=0$. We multiply the first equation in (2.10) by $\phi$ and integrate by parts on ${\tilde{Q}}_T={\tilde{\Omega }}(t)\times [0,T]$. All terms may be treated in a standard manner (see, e.g., [11]). Though, a particular attention must be devoted to the diffusive and pressure terms. Indeed, we temporally move the term $\mu \Delta a$ appearing in ${\hat{g}}$ in (2.10) on the left-hand side and we get:

$$\begin{aligned} \int _0^T(-\mu \Delta {\hat{v}}-\mu \Delta a + \nabla {\mathfrak {p}},\phi )_{L^2({\tilde{\Omega }}(t))}&=\int _0^T(\text {div}{\mathcal {T}}({\hat{v}}+a,{\mathfrak {p}}),\phi )_{L^2({\tilde{\Omega }}(t))}\\&=-\int _0^T\int _{\partial B}({\mathcal {T}}{\hat{n}})\cdot \phi +\int _0^T\int _{{\tilde{\Omega }}(t)} {\mathcal {T}}:\nabla \phi \\&=-\int _0^T{\hat{e}}_2\cdot \int _{\partial B}({\mathcal {T}}({\hat{v}}+a,{\mathfrak {p}}){\hat{n}})\,l\\&\quad +\int _0^T\int _{{\tilde{\Omega }}(t)} {\mathcal {T}}({\hat{v}}+a,{\mathfrak {p}}):\nabla \phi \\ {}&=\int _0^T(m\,h''+f(h))\,l\\&\quad +2\mu \int _0^T{(D( {\hat{v}}),D (\phi ))_{L^2({\tilde{\Omega }}(t))}}\\&\quad +2\mu \int _0^T{(D(a),D(\phi ))_{L^2({\tilde{\Omega }}(t))}}\\&=\!-\!\!\int _0^T\!\!\!\!\!m\, h'l' \!\!+\!\!\int _0^T\!\!\!\! \!\!f(h)l\!\\&\quad +\!2\mu \!\! \int _0^T\!\!\!\!\!\!{(D({\hat{v}}),D( \phi ))_{L^2({\tilde{\Omega }}(t))}}\!\\&\quad +\!2\mu \!\!\int _0^T\!\!\!\!\!\!{(D(a),D(\phi ))_{L^2({\tilde{\Omega }}(t))}}\!\!-\!m\,k_0l(0). \end{aligned}$$

Thus, given $\psi$ in (2.19) and

$$\begin{aligned} \langle {\hat{g}},\phi \rangle =2\mu (D(a),D(\phi ))_{L^2({\tilde{\Omega }}(t))}-\psi (a,a,\phi ). \end{aligned}$$

we obtain the weak formulation (2.20). $\square$

These tools enable us to define weak solutions of (2.7)–(2.8). This definition is a compromise between the definition given in [6, Definition 1] and the one given in [13, Definition 3.1], although the extension in [13] is constructed so as to isolate the obstacle.

Definition 2.3

A couple (v, h) is called a weak solution of (2.7)–(2.8) with initial data ${v}_0,h_0,k_0$ if, given ${\hat{v}}=v-a$, where $a=a_h$ is the extension in (2.9) depending on some $\varepsilon _0=\varepsilon _0(v_0,h_0,k_0,T)>0$, it satisfies the following requirements:

$$\begin{aligned}&h\in W^{1,\infty }(0,T;{\mathbb {R}})\cap C^0([0,T];[-L+\delta +\varepsilon _0, L-\delta -\varepsilon _0]), \end{aligned}$$

(2.21)

$$\begin{aligned}&({\hat{v}},h')\in L^2(0,T;{\mathbb {V}}_{h(t)})\cap L^\infty (0,T;{\mathbb {H}}_{h(t)}) , \nonumber \\&({\hat{v}},h)\,\text {satisfies (2.30) for every } (\phi ,l)\in C^1([0,T];{\mathbb {V}}_{h(t)}) \nonumber \\&\quad \text {such that}\,\, \phi (\cdot ,T)=l(T)=0. \end{aligned}$$

(2.22)

Remark 2.4

The requirement $h\in C^0([0,T];[-L+\delta +\varepsilon _0, L-\delta -\varepsilon _0])$ ensures that no collision occurs between the obstacle and the boundary of the channel as there exists a separation strip of size $\varepsilon _0>0$ for all $t\in [0,T]$. This makes the definition of weak solution consistent, since it also allows to build the solenoidal extension $a=a_h$ in (2.9) precisely by choosing such $\varepsilon _0>0$. As already mentioned, we will prove that this requirement is satisfied by making use of the strong force assumption satisfied by f, given in (1.4). On the other hand, it is worth mentioning that, one could prove the no-collisions result without adding the strong force assumption, at least in the case of an obstacle purely translating in the vertical direction, because the contact surfaces are of the class $C^\infty$ (see [20, 30]). However, as soon as one allows the obstacle to rotate, this result does not hold anymore because the contact surfaces are merely Lipschitz continuous.

Finally, we provide an estimate on the norm of ${\hat{g}}$, defined as in (2.11), on the auxiliary domain ${\tilde{A}}$, which we will exploit later.

Lemma 2.5

Let ${\hat{g}}$ be defined as in (2.11), a(y) as in (2.9) for some $\varepsilon _0>0$ and ${\tilde{A}}_0$ as in (2.15). Then ${\hat{g}}\in V'({\tilde{A}})$, the dual space of $V({\tilde{A}})$, and

$$\begin{aligned} \Vert {\hat{g}}\Vert _{V'({\tilde{A}})}\le \mu \Vert \nabla a\Vert _{L^2({\tilde{A}}_0)}+\Vert a\Vert ^2_{L^4({\tilde{A}}_0)}. \end{aligned}$$

Proof

Multiply ${\hat{g}}$ by $\varphi \in V({\tilde{A}})$ and integrate by parts over ${\tilde{A}}$. Since $\varphi =0$ on $\partial {\tilde{A}}$, we obtain

$$\begin{aligned} \int _{{\tilde{A}}}{\hat{g}}\,\cdot \varphi \,dy=\mu (\nabla a,\nabla \varphi )_{L^2({\tilde{A}})}-\psi (a,a,\varphi ). \end{aligned}$$

(2.23)

We proceed similarly to [15, Lemma 4.1] and we exploit the partition (2.15) together with the properties of a once we naturally extended this function to the whole fixed domain ${\tilde{A}}$ through its definition (2.9). In particular $a={\tilde{q}}$ in ${\tilde{A}}_1\cup {\tilde{A}}_2$. Thus we divide the first term in (2.23):

$$\begin{aligned} (\nabla {a},\nabla \varphi )_{L^2({\tilde{A}})}=\int _{{\tilde{A}}_0}\nabla {a}:\nabla \varphi \,dy+\int _{{\tilde{A}}_1}\nabla {a}:\nabla \varphi \,dy +\int _{{\tilde{A}}_2}\nabla {a}:\nabla \varphi \,dy \end{aligned}$$

and we remark that

$$\begin{aligned} \int _{{\tilde{A}}_1}\nabla {\tilde{q}}: \nabla \varphi \,dy=\int _{{\tilde{A}}_1}\Delta {\tilde{q}}\cdot \varphi \,dy=-2\lambda \int _{-\infty }^{-3}\bigg [\int _{-2L+\delta }^{2L-\delta }\varphi \cdot {\hat{n}}\,dy_2\bigg ]dy_1=0 \end{aligned}$$

as $\varphi$ carries no flux being divergence-free on ${\tilde{A}}$. For the same reason, also the integral over ${\tilde{A}}_2$ vanishes and we obtain, by applying the Hölder inequality,

$$\begin{aligned} \big |\mu \,(\nabla {a},\nabla \varphi )_{L^2({\tilde{A}})}\big |\le \mu \left| \int _{{\tilde{A}}_0}\nabla {a}:\nabla \varphi \, dx\right| \le \mu \Vert \nabla {a}\Vert _{L^2({\tilde{A}}_0)}\Vert \nabla \varphi \Vert _{L^2({\tilde{A}}_0)}. \end{aligned}$$

Since $a={\tilde{q}}$ in ${\tilde{A}}_1\cup {\tilde{A}}_2$ and since $({\tilde{q}}\cdot \nabla ){\tilde{q}} \equiv 0$, we have that, again by the Hölder inequality and the property of the trilinear form (see [33, Chapter 2, Lemma 1.3]),

$$\begin{aligned} \big |\psi \,(a,a,\varphi )\big |=\big |\psi \,(a,\varphi ,a)\big |=\left| \int _{{\tilde{A}}_0}(a\cdot \nabla )\varphi \cdot a\, dx\right| \le \Vert a\Vert ^2_{L^4({\tilde{A}}_0)} \Vert \nabla \varphi \Vert _{L^2({\tilde{A}}_0)} . \end{aligned}$$

Thus we obtain

$$\begin{aligned} \bigg |\int _{{\tilde{A}}}{\hat{g}}\,\cdot \varphi \,dy\bigg |= & {} |\mu (\nabla a,\nabla \varphi )_{L^2({\tilde{A}})}-\psi (a,a,\varphi )|\\\le & {} \bigg (\mu \Vert \nabla a\Vert _{L^2({\tilde{A}}_0)}+\Vert a\Vert ^2_{L^4({\tilde{A}}_0)}\bigg )\Vert \nabla \varphi \Vert _{L^2({\tilde{A}})}\qquad \forall \,\varphi \in V({\tilde{A}}), \end{aligned}$$

from which the thesis of the lemma follows. $\square$

The following theorem states existence and uniqueness of weak solutions to problem (2.7)–(2.8).

Theorem 2.6

Let ${\tilde{\Omega }}$ be as in (2.5). Let $f\in C^1(-L+\delta ,L-\delta )$ satisfy conditions (1.4). Let $h_0\in [-L+\delta +{\hat{\varepsilon }}, L-\delta -{\hat{\varepsilon }}],$ for some ${\hat{\varepsilon }}>0$ small arbitrarily fixed, and $({v}_0-a_{h_0}(y,{\hat{\varepsilon }}),k_0)\in {\mathbb {H}}_{h_0}$, where $a_h$ is as in (2.9). Then, problem (2.7)–(2.8) admits a unique weak solution (v, h), defined as in Definition 2.3, for any $T<\infty$. Moreover, let F be defined as in (2.16) and let $\varepsilon _0=\varepsilon _0(v_0,h_0,k_0,T)>0$ be such that $|h(t)|\le L-\delta -\varepsilon _0$ for all $t\in [0,T]$. Then, given ${\hat{v}}=v-a$, where $a=a_h(y,{\varepsilon _0})$, the pair $({\hat{v}},h')$ is almost everywhere equal to a function continuous from [0, T] into ${\mathbb {H}}_{h(t)}$, and $({\hat{v}},h)$ satisfies the following energy estimate:

$$\begin{aligned} \begin{aligned}&\Vert {\hat{v}}(t)\Vert ^2_{L^2({\tilde{\Omega }}(t))}+m\Vert h'(t)\Vert ^2_{L^\infty (0,T;{\mathbb {R}})}+2\,F(h(t))+4\,\mu \,\int _0^t{\Vert D({\hat{v}}(s))\Vert }^2_{L^2({\tilde{\Omega }}(s))}\,ds \\&\quad \le \Vert {\hat{v}}_{0}\Vert ^2_{L^2({\tilde{A}}{\setminus } B)}+\!m|k_{0}|^2+2F(h_0) +\frac{4}{\mu }\!\int _0^T\!\!\!\!{\Vert {{\hat{g}}(s)} \Vert }^2_{{V}'({\tilde{A}}{\setminus } B)}ds\\&\qquad + \frac{4}{\mu } \!\frac{(4 L-2\delta )^2}{\pi ^2}\!\cdot \!\max \bigg ( {\left\| \nabla a \right\| }^2_{L^\infty ({\tilde{A}}{\setminus } B)}, \frac{1}{m} ( {\left\| \nabla a \right\| }^2_{L^2({\tilde{A}}_0)}+\lambda ^2{\tilde{\xi }}^2)\bigg )\\&\qquad \cdot \int _0^T \!\! \alpha (s)\,\exp \bigg [ \frac{4}{\mu } \!\frac{(4 L-2\delta )^2}{\pi ^2}\cdot {\max }\bigg ( {\left\| \nabla a \right\| }^2_{L^\infty ({\tilde{A}}{\setminus } B)}, \frac{1}{m} ( {\left\| \nabla a \right\| }^2_{L^2({\tilde{A}}_0)}+\lambda ^2{\tilde{\xi }}^2)\bigg )s\bigg ]ds, \end{aligned} \end{aligned}$$

(2.24)

where $\alpha (s)$ is defined as

$$\begin{aligned} \alpha (s)=\Vert {\hat{v}}_{0}\Vert ^2_{L^2({\tilde{A}}{\setminus } B)}+m|k_{0}|^2+2\,F(h_0)+\frac{4}{\mu }\,\int _0^s{\Vert {{\hat{g}}}(\tau ) \Vert }^2_{{V}'({\tilde{A}}{\setminus } B)}\,d\tau . \end{aligned}$$

(2.25)

We observe that one may expect the energy inequality in Theorem 2.6 to be an equality as for the case of the Navier–Stokes equations in a bounded 2D domain, but so far it is not known whether we should expect an equality also in the case of a 2D domain with cylindrical outlets to infinity (see [26]). Since the original problem (1.2) is equivalent to problem (2.7)–(2.8), the proof of Theorem 1.1 is completed if we prove Theorem 2.6. We emphasize that Theorem 2.6 has a stronger statement than Theorem 1.1, because it guarantees the continuity of the (unique) solution in a suitable sense. The proof of the existence part is developed in Sects. 3 and 4 and, as previously mentioned, it takes advantage of a penalty method. Uniqueness is proven in Sect. 5: there, we will consider two weak solutions of problem (2.7)–(2.8), $(v_1,h_1)$ and $({v}_2,{h}_2)$, in the sense of Definition 2.3. Given the extensions of the Poiseuille flow $a_1=a_{h_1}$ and ${a}_2=a_{{h}_2}$ defined as in (2.9), one can put ${\hat{v}}_1=v_1-a_1$ and $\hat{{v}}_2={v}_2-{a}_2$ and do the computations on $({\hat{v}}_1,h_1)$ and $(\hat{{v}}_2,{h}_2)$. As we already pointed out in the Introduction, we are not allowed to take the difference between the equation in weak form satisfied by the two solutions, (2.20), because ${\hat{v}}_1$ and $\hat{{v}}_2$ are not defined on the same domain: the definition of the functional spaces, (2.18), depends on $h_1$, ${h}_2$, and the weak formulation (2.20) is set on two different domains, ${\tilde{\Omega }}^1(t)$ and $\tilde{{\Omega }}^2(t)$. To solve such issue, we follow the procedure devised in [16]; here, the authors build a map $\psi _t$ projecting $\tilde{{\Omega }}^2(t)$ on ${\tilde{\Omega }}^1(t)$, which allows to define a change of variables, so that they can introduce a solenoidal velocity vector field $\mathfrak {\hat{{v}}}_2$, the pullback of $\hat{{v}}_2$ by such map, on ${\tilde{\Omega }}^1(t)$. As a consequence, one can define

$$\begin{aligned} w:={\hat{v}}_1-\mathfrak {\hat{{v}}}_2, \qquad {\hat{h}}:=h_1-{h}_2. \end{aligned}$$

(2.26)

Then, one proceeds standardly, obtaining the equation satisfied by $(w,{\hat{h}})$, providing some proper estimates, and finally one can conclude by applying a Grönwall’s inequality.

3 A penalized problem

After changing problem (1.2) into the equivalent problem (2.10)–(2.12), the second step of the penalty method exactly implies penalizing (2.20), which is the weak formulation of problem (2.10)–(2.12). We denote by $E_h$ the complementary domain of $A_h$ in ${\tilde{A}}$, $E_h={\tilde{A}}{\setminus } A_h$ and we introduce its characteristic function $\chi _{E_h}$. We emphasize that the functions belonging to ${\mathcal {W}}({\tilde{A}})$ differ from those belonging to ${\mathcal {W}}_{h}$ precisely because their support might be also in $E_{h}$. The penalty method eliminates the difficulty induced by the time dependent domain by allowing to solve the problem in the fixed domain ${\tilde{A}}$, so that classical methods can be applied, by introducing a penalization term which takes care of the remainder in $E_h$.

We extend ${\hat{v}}_0$ by zero outside $A_{h(0)}$, while a(y) is naturally extended outside $A_{h(t)}$ to the whole fixed domain ${\tilde{A}}$ through its definition (2.9) for every $t\in [0,T]$ and we solve the following problem:

Let $n\ge 1$ be fixed. Find

$$\begin{aligned}&h\in W^{1,\infty }(0,T;{\mathbb {R}}) \cap C^0([0,T];[-L+\delta +\varepsilon _0, L-\delta -\varepsilon _0])\\&\quad ({\hat{v}},h')\in L^2(0,T;{\mathbb {V}}({\tilde{A}}))\cap L^\infty (0,T;{\mathbb {H}}({\tilde{A}})), \end{aligned}$$

for some $\varepsilon _0=\varepsilon _0({\hat{v}}_0,h_0,k_0,T)>0$, satisfying

$$\begin{aligned} \begin{aligned}&-\!\!\!\int _0^T\!\!\!\!\{({\hat{v}},\phi _t)_{L^2({\tilde{A}}{\setminus } B)}\!\!+\!m\,h'l'\!-\!f(h)\,l\}+2\mu \!\! \int _0^T\!\!(D({\hat{v}}),D(\phi ))_{L^2({\tilde{A}}{\setminus } B)}\!\!\\&\quad +\!\!\int _0^T\!\!\{\psi ({\hat{v}},{\hat{v}},\phi )+\psi ({\hat{v}},a,\phi )+\psi (a,{\hat{v}},\phi )\!-\!\psi (h'{\hat{e}}_2,a,\phi )\\&\quad -\psi (h'{\hat{e}}_2,{\hat{v}},\phi )\}+ n\int _0^T(\chi _{E_h}{\hat{v}},\phi )_{L^2({\tilde{A}})}\\&\quad =\int _0^T\langle {\hat{g}},\phi \rangle +m\,k_0l(0)+({\hat{v}}_0,\phi (0))_{L^2({\tilde{A}}{\setminus } B)}, \\&\forall \, (\phi ,l)\in C^1([0,T],{\mathbb {V}}({\tilde{A}})) \,\,\text {such that}\,\, \phi (\cdot ,T)=l(T)=0. \end{aligned} \end{aligned}$$

(3.1)

We remark that the trilinear forms in (3.1) are defined as in (2.19), where the integral is now on ${\tilde{A}}{\setminus } B$, but with a little abuse of notation we still use $\psi$ as a label function. The existence of a solution to the penalized problem is proven in the following proposition:

Proposition 3.1

Let ${\tilde{A}}$ be a fixed domain defined by (2.13), partitioned as in (2.15). Let $f\in C^1(-L+\delta ,L-\delta )$ satisfy conditions (1.4). Assume that $h_0\in [-L+\delta +{\hat{\varepsilon }}, L-\delta -{\hat{\varepsilon }}]$ for some ${\hat{\varepsilon }}>0$ small arbitrarily fixed, and $({\hat{v}}_0,k_0)\in {\mathbb {H}}({\tilde{A}})$. Then, there exists at least one solution $({\hat{v}},h)$ to problem (3.1) such that $|h(t)|\le L-\delta -\varepsilon _0$ for some $\varepsilon _0=\varepsilon _0({\hat{v}}_0,h_0,k_0,T)>0$. This solution is global in time and, moreover, $({\hat{v}},h')$ is almost everywhere equal to a function continuous from [0, T] into ${\mathbb {H}}({\tilde{A}})$; furthermore, given F(h) as in (2.16), it satisfies the energy estimate:

$$\begin{aligned} \begin{aligned}&\Vert {\hat{v}}(t)\Vert ^2_{L^2({\tilde{A}}{\setminus } B)}+\!m\Vert h'(t)\Vert ^2_{L^\infty (0,T;{\mathbb {R}})}+2\,F(h(t)) +4\mu \!\int _0^t{\Vert D( {\hat{v}}(s))\Vert }^2_{L^2({\tilde{A}}{\setminus } B)}\,ds\\&\qquad + 2\,n\int _0^t\int _{{E_{h}}}|{\hat{v}}(s)|^2\,ds \\&\quad \le \Vert {\hat{v}}_{0}\Vert ^2_{L^2({\tilde{A}}{\setminus } B)}+\!m|k_0|^2+2F(h_0)+\frac{4}{\mu }\!\!\int _0^T\!\!{\Vert {{\hat{g}}(s)} \Vert }^2_{{V}'({\tilde{A}}{\setminus } B)}ds\\&\qquad + \frac{4}{\mu } \!\frac{(4 L-2\delta )^2}{\pi ^2}\!\cdot \!{\max }\bigg ( {\left\| \nabla a \right\| }^2_{L^\infty ({\tilde{A}}{\setminus } B)}, \frac{1}{m} ( {\left\| \nabla a \right\| }^2_{L^2({\tilde{A}}_0)}+\lambda ^2{\tilde{\xi }}^2)\bigg )\\&\qquad \cdot \int _0^T \!\! \alpha (s)\,\exp \bigg [ \frac{4}{\mu } \!\frac{(4 L-2\delta )^2}{\pi ^2}\cdot {\max }\bigg ( {\left\| \nabla a \right\| }^2_{L^\infty ({\tilde{A}}{\setminus } B)}, \frac{1}{m} ( {\left\| \nabla a \right\| }^2_{L^2({\tilde{A}}_0)}+\lambda ^2{\tilde{\xi }}^2)\bigg )s\bigg ]ds \end{aligned} \end{aligned}$$

(3.2)

with

$$\begin{aligned} \alpha (s)=\Vert {\hat{v}}_{0}\Vert ^2_{L^2({\tilde{A}}{\setminus } B)}+m|k_0|^2+2\,F(h_0)+\frac{4}{\mu }\,\int _0^s{\Vert {{\hat{g}}(\tau )} \Vert }^2_{{V}'({\tilde{A}}{\setminus } B)}\,d\tau . \end{aligned}$$

Proof

Since the domain ${\tilde{A}}$ is fixed, we can apply the Faedo–Galerkin procedure. The space ${\mathbb {V}}({\tilde{A}})$ is a separable Hilbert space, hence we can choose a sequence given by a countable set of couples $\{(w_i,1)\}_{i=1}^\infty$ beloging to $\mathcal {W}(\tilde{A})$ to be a basis in ${\mathbb {V}}({\tilde{A}})$, orthonormal in ${\mathbb {H}}({\tilde{A}})$. For each $N\ge 1$ we construct an approximate solution

$$\begin{aligned} {{\hat{v}}_N \atopwithdelims ()H_N} = \sum _{i=1}^N c_{iN}(t) {w_i \atopwithdelims ()1}, \end{aligned}$$

where the coefficients $c_{iN}$ are determined by the following first-order integro-ordinary differential system

$$\begin{aligned}&\sum _{i=1}^N\!(w_i,w_j)_{L^2({\tilde{A}}{\setminus } B)}c'_{iN}(t)\!+\!m\sum _{i=1}^N c'_{iN}(t)\!+\!f(h_N(t)) \nonumber \\&\quad + 2\mu \sum _{i=1}^N(D(w_i),D(w_j))_{L^2({\tilde{A}}{\setminus } B)}c_{iN}(t) +\!\sum _{i,l=1}^k\!\!\psi (w_i,w_l,w_j)\, c_{iN}(t)c_{lN}(t)\nonumber \\&\quad +\sum _{i=1}^N\psi (w_i,a,w_j)\,c_{iN}(t)+\sum _{l=1}^N\psi (a,w_l,w_j)\,c_{lN}(t) -\sum _{i=1}^N\psi ({\hat{e}}_2,a,w_j)\,c_{iN}(t)\nonumber \\&\quad -\sum _{i,l=1}^k\psi ({\hat{e}}_2,w_l,w_j)\, c_{iN}(t)c_{lN}(t) \nonumber \\&\quad + \sum _{i=1}^N n(\chi _{E_{h_N}}w_i,w_j)_{L^2({\tilde{A}})}c_{iN}(t) = \langle {\hat{g}},w_j\rangle \qquad j=1,\ldots ,N \end{aligned}$$

(3.3)

$$\begin{aligned}&h_N(t)=h_0+\sum _{i=1}^N\int _0^t c_{iN}(s)ds,\\&c_{iN}(0)=\text {the } i{th} \text { component of }{\hat{v}}_{0,N}, \quad H_N(0)=k_{0,N}. \end{aligned}$$

The initial conditions are given by the orthogonal projections in ${\mathbb {H}}({\tilde{A}})$ of $({\hat{v}}_0, k_0)$ onto the space spanned by $\{(w_i,1)\}_{i=1}^N$, which we call $({\hat{v}}_{0,N},k_{0,N})$. This system has a solution defined on some interval $[0,t_N]$, provided that there exists $\varepsilon _0>0$ such that

$$\begin{aligned} |h_N(t)|\le L-\delta -\varepsilon _0\qquad \forall \, t\in [0,t_N]. \end{aligned}$$

(3.4)

In this way, we are allowed to build the function a as in (2.9), by choosing the same $\varepsilon _0$. We shall see that this condition is indeed always guaranteed for any $t\in [0,T]$ with $T<\infty$, because of the presence of f in (2.8). We will prove this claim at the end of the proof of this proposition.

Our aim is finding an apriori estimate for the approximate solution $({\hat{v}}_N,H_N)$. To this end, we multiply (3.3) by $c_{jN}(t)$ and add the equations for $j=1,\ldots ,N$:

$$\begin{aligned} \begin{aligned}&({\hat{v}}'_N,{\hat{v}}_N)_{L^2({\tilde{A}}{\setminus } B)}\!+\!mH_N'H_N+f(h_N)H_N\! +\!2\mu \,{\Vert D({\hat{v}}_N)\Vert }^2_{L^2({\tilde{A}}{\setminus } B)}+\psi ({\hat{v}}_N,a,{\hat{v}}_N)\!\\&\quad -\!\psi (H_N{\hat{e}}_2,a,{\hat{v}}_N) + n\Vert {\hat{v}}_N\Vert ^2_{L^2({E_{H_N}})} =\langle {\hat{g}},{\hat{v}}_N\rangle \quad j=1,\ldots ,N \end{aligned} \end{aligned}$$

which we rewrite as

$$\begin{aligned}&\frac{1}{2} \frac{d}{dt}\bigg (\Vert {\hat{v}}_N\Vert ^2_{L^2({\tilde{A}}{\setminus } B)}+m|H_N|^2+2\,F(h_N)\bigg )\! \nonumber \\&\qquad +2\mu \,{\Vert D({\hat{v}}_N)\Vert }^2_{L^2({\tilde{A}}{\setminus } B)}+ n\Vert {\hat{v}}_N\Vert ^2_{L^2({E_{H_N}})}\nonumber \\&\quad =\langle {\hat{g}},{\hat{v}}_N\rangle -\psi ({\hat{v}}_N,a,{\hat{v}}_N)+\psi (H_N{\hat{e}}_2,a,{\hat{v}}_N), \end{aligned}$$

(3.5)

where F is defined in (2.16). Our aim is finding an a priori estimate for the approximate solution $({\hat{v}}_N, H_N)$. To this end, we start by estimating the right-hand side of (3.5). The first trilinear form may be bounded exploiting the Hölder inequality and the Young inequality

$$\begin{aligned} \begin{aligned} \psi ({\hat{v}}_N,a,{\hat{v}}_N)&\le {\left\| \nabla a \right\| }_{L^\infty ({\tilde{A}}{\setminus } B)} {\left\| {\hat{v}}_N\right\| }^2_{L^2({\tilde{A}}{\setminus } B)} \\&\le \frac{ (4L-2\delta )}{\pi } {\left\| \nabla a \right\| }_{L^\infty ({\tilde{A}}{\setminus } B)} {\left\| {\hat{v}}_N\right\| }_{L^2({\tilde{A}}{\setminus } B)}{\left\| \nabla {\hat{v}}_N\right\| }_{L^2({\tilde{A}}{\setminus } B)}\\ {}&\le \frac{2}{\mu }\frac{ (4L-2\delta )^2}{\pi ^2} {\left\| \nabla a \right\| }^2_{L^\infty ({\tilde{A}}{\setminus } B)} {\left\| {\hat{v}}_N\right\| }^2_{L^2({\tilde{A}}{\setminus } B)}+\frac{\mu }{8}{\left\| \nabla {\hat{v}}_N\right\| }^2_{L^2({\tilde{A}}{\setminus } B)} , \end{aligned} \end{aligned}$$

where we used the fact that the Poincaré constant in the domain ${\tilde{A}}$ is $\pi ^2/(4L-2\delta )^2$. For what concerns the second trilinear form, we exploit again the definition of a, as we did when proving Lemma 2.5. Since a(y) is equal to 0 on the obstacle B, we write

$$\begin{aligned} \psi (H_N{\hat{e}}_2,a,{\hat{v}}_N)= & {} \int _{{\tilde{A}}{\setminus } B}(H_N{\hat{e}}_2\cdot \nabla )a\cdot {\hat{v}}_N =\int _{{\tilde{A}}}(H_N{\hat{e}}_2\cdot \nabla )a\cdot {\hat{v}}_N\\= & {} \int _{-\infty }^{+\infty }\bigg (\int _{-2L+\delta }^{2L-\delta } (H_N{\hat{e}}_2\cdot \nabla )a\cdot {\hat{v}}_N\,dy_2\bigg )\,dy_1. \end{aligned}$$

Then

$$\begin{aligned} \begin{aligned} \psi (H_N{\hat{e}}_2,a,{\hat{v}}_N)&\le \bigg |\int _{-\infty }^{-3}\bigg (\int _{-2L+\delta }^{2L-\delta } (H_N{\hat{e}}_2\cdot \nabla ){\tilde{q}}\cdot {\hat{v}}_N\,dy_2\bigg )\,dy_1\\&\quad +\int _{-3}^{+3}\bigg (\int _{-2L+\delta }^{2L-\delta } (H_N{\hat{e}}_2\cdot \nabla )a\cdot {\hat{v}}_N\,dy_2\bigg )\,dy_1\\ {}&\quad +\int ^{\infty }_{+3}\bigg (\int _{-2L+\delta }^{2L-\delta } (H_N{\hat{e}}_2\cdot \nabla ){\tilde{q}}\cdot {\hat{v}}_N\,dy_2\bigg )\,dy_1\bigg |. \end{aligned} \end{aligned}$$

(3.6)

Consider the partition (2.15). The first term is treated as follows, by using (2.14):

$$\begin{aligned} \begin{aligned}&\bigg |\int _{-\infty }^{-3}\bigg (\int _{-2L+\delta }^{2L-\delta } (H_N{\hat{e}}_2\cdot \nabla ){\tilde{q}}\cdot {\hat{v}}_N\,dy_2\bigg )\,dy_1\bigg |\\&\quad \le |H_N|\int _{-\infty }^{-3}\bigg ( \Vert \nabla {\tilde{q}}\Vert _{L^2(-2L+\delta ,2L-\delta )}\Vert {\hat{v}}_N\Vert _{L^2(-2L+\delta ,2L-\delta )}\bigg )\,dy_1\\ {}&\quad \le |H_N|\lambda \,{\tilde{\xi }}\int _{-\infty }^{-3} \Vert {\hat{v}}_N\Vert _{L^2(-2L+\delta ,2L-\delta )}\,dy_1\\ {}&\quad \le |H_N|\lambda \,{\tilde{\xi }} \,\Vert {\hat{v}}_N\Vert _{L^2({\tilde{A}}_1)}\le \frac{4 L-2\delta }{\pi }|H_N|\lambda \,{\tilde{\xi }}\,\Vert \nabla {\hat{v}}_N\Vert _{L^2({\tilde{A}}_1)}. \end{aligned} \end{aligned}$$

The third integral in (3.6) can be treated analogously, so that we obtain:

$$\begin{aligned} \begin{aligned} \bigg |\int _{+3}^{-\infty }\bigg (\int _{-2L+\delta }^{2L-\delta } (H_N{\hat{e}}_2\cdot \nabla ){\tilde{q}}\cdot {\hat{v}}_N\,dy_2\bigg )\,dy_1\bigg | \le \frac{4 L-2\delta }{\pi }|H_N|\lambda \,{\tilde{\xi }}\,\Vert \nabla {\hat{v}}_N\Vert _{L^2({\tilde{A}}_2)}. \end{aligned} \end{aligned}$$

For what concerns the term in the region ${\tilde{A}}_0=[-3,3]\times [-2L+\delta ,2L-\delta ]$:

$$\begin{aligned}&\int _{-3}^{+3}\bigg (\int _{-2L+\delta }^{2L-\delta } (H_N{\hat{e}}_2\cdot \nabla )a\cdot {\hat{v}}_N\,dy_2\bigg )\,dy_1 \\&\quad \le \frac{4 L-2\delta }{\pi }|H_N|\Vert \nabla a\Vert _{L^2({\tilde{A}}_0)}\Vert \nabla {\hat{v}}_N\Vert _{L^2({\tilde{A}}{\setminus } B)}. \end{aligned}$$

Thus, we finally obtain that:

$$\begin{aligned} \begin{aligned} \psi (H_N{\hat{e}}_2,a,{\hat{v}}_N)&\le \frac{4 L-2\delta }{\pi } {|H_N |} {\left\| \nabla a \right\| }_{L^2({\tilde{A}}_0)} {\left\| \nabla {\hat{v}}_N\right\| }_{L^2({\tilde{A}}{\setminus } B)}\\&\quad +\frac{4 L-2\delta }{\pi }|H_N|\lambda \,{\tilde{\xi }} \,\Vert \nabla {\hat{v}}_N\Vert _{L^2({\tilde{A}}{\setminus } B)}\\ {}&\le \frac{2}{\mu } \frac{(4 L-2\delta )^2}{\pi ^2} {|H_N |^2}( {\left\| \nabla a \right\| }^2_{L^2({\tilde{A}}_0)}+\lambda ^2{\tilde{\xi }}^2) + \frac{\mu }{4}{\left\| \nabla {\hat{v}}_N\right\| }^2_{L^2({\tilde{A}}{\setminus } B)} \end{aligned} \end{aligned}$$

where we used the Young inequality and the fact that $\Vert \nabla {\hat{v}}_N\Vert ^2_{L^2({\tilde{A}}_1)}+\Vert \nabla {\hat{v}}_N\Vert ^2_{L^2({\tilde{A}}_2)}\le {\left\| \nabla {\hat{v}}_N\right\| }^2_{L^2({\tilde{A}}{\setminus } B)}$. Then, we apply again the Young inequality, after the Schwarz inequality, to provide a bound for the first term on the right-hand side in (3.5):

$$\begin{aligned} | \langle {\hat{g}},{\hat{v}}_N \rangle |\le \Vert {\hat{g}}\Vert _{{V}'({\tilde{A}}{\setminus } B)} {\left\| \nabla {\hat{v}}_N\right\| }_{L^2({\tilde{A}}{\setminus } B)}\!\le \!\frac{2}{\mu }{\Vert {\hat{g}} \Vert }^2_{V'({\tilde{A}}{\setminus } B)}+\frac{\mu }{8} \,{\left\| \nabla {\hat{v}}_N\right\| }^2_{L^2({\tilde{A}}{\setminus } B)}, \end{aligned}$$

since Lemma 2.5 guarantees that ${\hat{g}}\in V'({\tilde{A}}{\setminus } B)$. Thus, by reordering Eq. (3.5), once we have plugged these estimates and used the following fact

$$\begin{aligned} \int _{{\tilde{A}}{\setminus } B}|\nabla {\hat{v}}_N|^2\,dy\le \int _{{\tilde{A}}}|\nabla {\hat{v}}_N|^2\,dy=2\int _{{\tilde{A}}}|D({\hat{v}}_N)|^2\,dy=2\int _{{\tilde{A}}{\setminus } B}|D({\hat{v}}_N)|^2\,dy, \end{aligned}$$

since ${\hat{v}}_N$ is a divergence free vector field vanishing on $\partial {\tilde{A}}$, we obtain

$$\begin{aligned} \begin{aligned}&\frac{d}{dt}\!\bigg (\!\Vert {\hat{v}}_N\Vert ^2_{L^2({\tilde{A}}{\setminus } B)}\!+m|H_N|^2+2F(h_N)\!\!\bigg )\!+\mu {\Vert \nabla {\hat{v}}_N\Vert }^2_{L^2({\tilde{A}}{\setminus } B)}\!+ 2n\Vert {\hat{v}}_N\Vert ^2_{L^2({E_{H_N}})}\\ {}&\quad \le \frac{4}{\mu }{\Vert {{\hat{g}}} \Vert }^2_{{V}'({\tilde{A}}{\setminus } B)}+ \frac{4}{\mu }\frac{ (4L-2\delta )^2}{\pi ^2} {\left\| \nabla a \right\| }^2_{L^\infty ({\tilde{A}}{\setminus } B)} {\left\| {\hat{v}}_N\right\| }^2_{L^2({\tilde{A}}{\setminus } B)}\\&\qquad + \frac{4}{\mu } \frac{(4 L-2\delta )^2}{\pi ^2} {|H_N |^2}( {\left\| \nabla a \right\| }^2_{L^2({\tilde{A}}_0)}+\lambda ^2{\tilde{\xi }}^2). \end{aligned} \end{aligned}$$

(3.7)

From (3.7), by integrating between 0 and t, we deduce that

$$\begin{aligned}&\Vert {\hat{v}}_N(t)\Vert ^2_{L^2({\tilde{A}}{\setminus } B)}\!+\!m|H_N(t)|^2\!+\!2F(h_N(t)) +2\mu \!\!\int _0^t\!\!\!{\Vert \nabla {\hat{v}}_N(s)\Vert }^2_{L^2({\tilde{A}}{\setminus } B)}\,ds\\&\quad + 2n\!\!\int _0^t\!\!\!\int _{{E_{H_N}}}\!\!|{\hat{v}}_N(s)|^2\,ds \\&\quad \le \!\Vert {\hat{v}}_{0,N}\Vert ^2_{L^2({\tilde{A}}{\setminus } B)}\!+\!m|k_{0,N}|^2\!+\!2F(h_0)+\frac{4}{\mu }\!\!\int _0^t\!\!{\Vert {{\hat{g}}(s)} \Vert }^2_{{V}'({\tilde{A}}{\setminus } B)}ds\!\\&\qquad +\! \frac{4}{\mu }\frac{ (4L-2\delta )^2}{\pi ^2} {\left\| \nabla a \right\| }^2_{L^\infty ({\tilde{A}}{\setminus } B)}\!\!\int _0^t \!\!{\left\| {\hat{v}}_N(s)\right\| }^2_{L^2({\tilde{A}}{\setminus } B)}ds\\ {}&\qquad +\frac{4}{\mu } \frac{(4 L-2\delta )^2}{\pi ^2} ( {\left\| \nabla a \right\| }^2_{L^2({\tilde{A}}_0)}+\lambda ^2{\tilde{\xi }}^2)\!\!\int _0^t\!\!{|H_N(s) |^2}ds \\ {}&\quad \le \Vert {\hat{v}}_{0}\Vert ^2_{L^2({\tilde{A}}{\setminus } B)}+\!m|k_0|^2+2\,F(h_0)+\frac{4}{\mu }\!\!\int _0^t\!\!{\Vert {{\hat{g}}(s)} \Vert }^2_{{V}'({\tilde{A}}{\setminus } B)}ds\!\\&\qquad +\! \frac{4}{\mu }\frac{ (4L-2\delta )^2}{\pi ^2} {\left\| \nabla a \right\| }^2_{L^\infty ({\tilde{A}}{\setminus } B)}\!\!\int _0^t \!\!{\left\| {\hat{v}}_N(s)\right\| }^2_{L^2({\tilde{A}}{\setminus } B)}ds\\&\qquad + \frac{4}{\mu } \!\frac{(4 L-2\delta )^2}{m\pi ^2} ( {\left\| \nabla a \right\| }^2_{L^2({\tilde{A}}_0)}+\lambda ^2{\tilde{\xi }}^2)\!\!\int _0^t\!\!m{|H_N(s) |^2}ds\\ {}&\quad \le \Vert {\hat{v}}_{0}\Vert ^2_{L^2({\tilde{A}}{\setminus } B)}\!+\!m|k_0|^2\!+\!2F(h_0)\!+\!\frac{4}{\mu }\!\int _0^t\!{\Vert {{\hat{g}}(s)} \Vert }^2_{{V}'({\tilde{A}}{\setminus } B)}ds\\&\qquad + \frac{4}{\mu } \!\frac{(4 L-2\delta )^2}{\pi ^2}\!\cdot \!{\max }\bigg ( {\left\| \nabla a \right\| }^2_{L^\infty ({\tilde{A}}{\setminus } B)}, \frac{1}{m} ( {\left\| \nabla a \right\| }^2_{L^2({\tilde{A}}_0)}+\lambda ^2{\tilde{\xi }}^2)\bigg )\\ {}&\qquad \cdot \int _0^t \!\!\bigg ({\left\| {\hat{v}}_N(s)\right\| }^2_{L^2({\tilde{A}}{\setminus } B)}+m{|H_N(s) |^2}\bigg )ds. \end{aligned}$$

Since $F(h_N)\ge 0$ by (2.17), invoking Grönwall’s lemma, we obtain for any instant $t\in [0,T]$:

$$\begin{aligned}&\Vert {\hat{v}}_N(t)\Vert ^2_{L^2({\tilde{A}}{\setminus } B)}+ m |H_N(t)|^2\\&\quad \le \alpha (t)\,\exp \bigg [ \frac{4}{\mu } \!\frac{(4 L-2\delta )^2}{\pi ^2}\cdot {\max }\bigg ( {\left\| \nabla a \right\| }^2_{L^\infty ({\tilde{A}}{\setminus } B)}, \frac{1}{m} ( {\left\| \nabla a \right\| }^2_{L^2({\tilde{A}}_0)}+\lambda ^2{\tilde{\xi }}^2)\bigg )t\bigg ], \end{aligned}$$

with

$$\begin{aligned} \alpha (t)=\Vert {\hat{v}}_{0}\Vert ^2_{L^2({\tilde{A}}{\setminus } B)}+m|k_0|^2+2\,F(h_0)+\frac{4}{\mu }\,\int _0^t{\Vert {{\hat{g}}(s)} \Vert }^2_{{V}'({\tilde{A}}{\setminus } B)}\,ds. \end{aligned}$$

Thus, we finally get

$$\begin{aligned} \begin{aligned}&\Vert {\hat{v}}_N(t)\Vert ^2_{L^2({\tilde{A}}{\setminus } B)}\!+\!m|H_N(t)|^2\!+\!2\,F(h_N(t))\!\\&\qquad +\!2\,\mu \,\int _0^t{\Vert \nabla {\hat{v}}_N(s)\Vert }^2_{L^2({\tilde{A}}{\setminus } B)}\,ds\!+\! 2\,n\int _0^t\int _{{E_{H_N}}}|{\hat{v}}_N(s)|^2\,ds\\&\quad \le \Vert {\hat{v}}_{0}\Vert ^2_{L^2({\tilde{A}}{\setminus } B)}+\!m|k_0|^2+2F(h_0)+\frac{4}{\mu }\!\!\int _0^t\!\!{\Vert {{\hat{g}}(s)} \Vert }^2_{{V}'({\tilde{A}}{\setminus } B)}ds\\&\qquad + \frac{4}{\mu } \!\frac{(4 L-2\delta )^2}{\pi ^2}\!\cdot \!{\max }\bigg ( {\left\| \nabla a \right\| }^2_{L^\infty ({\tilde{A}}{\setminus } B)}, \frac{1}{m} ( {\left\| \nabla a \right\| }^2_{L^2({\tilde{A}}_0)}+\lambda ^2{\tilde{\xi }}^2)\bigg )\\&\qquad \cdot \int _0^t \!\! \alpha (s)\,\exp \bigg [ \frac{4}{\mu } \!\frac{(4 L-2\delta )^2}{\pi ^2}\cdot {\max }\bigg ( {\left\| \nabla a \right\| }^2_{L^\infty ({\tilde{A}}{\setminus } B)}, \frac{1}{m} ( {\left\| \nabla a \right\| }^2_{L^2({\tilde{A}}_0)}+\lambda ^2{\tilde{\xi }}^2)\bigg )s\bigg ]ds\\&\quad \le \Vert {\hat{v}}_{0}\Vert ^2_{L^2({\tilde{A}}{\setminus } B)}+\!m|k_0|^2+2F(h_0)\!+\!\frac{4}{\mu }\!\!\int _0^T\!{\Vert {{\hat{g}}(s)} \Vert }^2_{{V}'({\tilde{A}}{\setminus } B)}ds\\&\qquad + \frac{4}{\mu } \!\frac{(4 L-2\delta )^2}{\pi ^2}\!\cdot \!{\max }\bigg ( {\left\| \nabla a \right\| }^2_{L^\infty ({\tilde{A}}{\setminus } B)}, \frac{1}{m} ( {\left\| \nabla a \right\| }^2_{L^2({\tilde{A}}_0)}+\lambda ^2{\tilde{\xi }}^2)\bigg )\\&\qquad \cdot \int _0^T \!\! \alpha (s)\,\exp \bigg [ \frac{4}{\mu } \!\frac{(4 L-2\delta )^2}{\pi ^2}\cdot {\max }\bigg ( {\left\| \nabla a \right\| }^2_{L^\infty ({\tilde{A}}{\setminus } B)}, \frac{1}{m} ( {\left\| \nabla a \right\| }^2_{L^2({\tilde{A}}_0)}+\lambda ^2{\tilde{\xi }}^2)\bigg )s\bigg ]ds \end{aligned}\nonumber \\ \end{aligned}$$

(3.8)

for all $t\in [0,T]$, where the right hand-side is bounded if $T<\infty$. In particular, the solution exists globally in time provided that condition (3.4) holds, which we still need to prove; such condition in the original inertial reference system translates the condition of absence of collisions occurring between the rectangular obstacle and the boundary of the channel.

Estimate (3.8) implies the existence of a couple $({\hat{v}},h')\in L^\infty (0,T;{\mathbb {H}}({\tilde{A}}))\cap L^2(0,T;{\mathbb {V}}({\tilde{A}}))$ and of a subsequence, which we denote by $({\hat{v}}_N,h_N')$, such that, as $N\rightarrow \infty$:

$$\begin{aligned} \begin{aligned}&({\hat{v}}_N,h'_N)\rightharpoonup ({\hat{v}},h') \;\, \text {in}\,L^2(0,T;{\mathbb {V}}({\tilde{A}})),\; ({\hat{v}}_N,h'_N)\overset{*}{\rightharpoonup }({\hat{v}},h')\; \text {in}\,L^\infty (0,T;{\mathbb {H}}({\tilde{A}})),\\&\quad h_N\rightarrow h \; \text {in}\,C^0([0,T];{\mathbb {R}}), \end{aligned}\nonumber \\ \end{aligned}$$

(3.9)

the latter holding because of the compact embedding of $W^{1,\infty }(0,T;{\mathbb {R}})$ into $C^0([0,T];{\mathbb {R}})$. Moreover, through classical methods (see [6, Section 3] and [33, Chapter 3, Section 3]), in view of (3.8) together with the fact that $f(h_N)$ can be thought to be a bounded function as long as the rigid obstacle does not touch the boundary of the channel, one can prove a further convergence property (up to the extraction of a subsequence):

$$\begin{aligned} (\hat{v}_N,h'_N)\rightarrow (\hat{v},h') \qquad \text {in}\,L^2(0,T;\mathbb {H}(\mathcal {O}))\qquad \text {for any compact set} \mathcal {O}\subset \tilde{A}. \end{aligned}$$

By [6, Lemma 1] we also have that

(3.10)

The convergence results in (3.9) together with (3.10), where we choose as $\mathcal {O}$ the support of $w_j$, us to pass to the limit in the system satisfied by $({\hat{v}}_N,h'_N)$, which is

$$\begin{aligned}&({\hat{v}}_N',w_j)_{L^2({\tilde{A}}{\setminus } B)}+mh_N'+f(h'_N)+2\mu \,(D({\hat{v}}_N),D( w_j))_{L^2({\tilde{A}}{\setminus } B)}\\&\quad +\,\psi ({\hat{v}}_N,{\hat{v}}_N,w_j)\, +\psi ({\hat{v}}_N,a,w_j)+\psi (a,{\hat{v}}_N,w_j)\\&\quad -\,\psi (h'_N{\hat{e}}_2,a,w_j)-\psi (h'_N{\hat{e}}_2,{\hat{v}}_N,w_j)+ n(\chi _{E_{h_N}}{\hat{v}}_N,w_j)_{L^2({\tilde{A}})} = \langle {\hat{g}},w_j\rangle \\&\quad j=1,\ldots ,N \\&{\hat{v}}_N(0)={\hat{v}}_{0,N},\quad h'_N(0)=k_{0,N}, \end{aligned}$$

and to obtain that (${\hat{v}},h)$ in (3.9) satisfies (3.1), as well as ${\hat{v}}(0)={\hat{v}}_0$ in the distributional sense, by exploiting classical arguments (see for instance [33, Chapter 3, Section 3]). To prove that $({\hat{v}},h')$ is almost everywhere equal to a function continuous from [0, T] into ${\mathbb {H}}({\tilde{A}})$, one can easily proceed as in [33, Chapter 3, Theorem 3.1] to obtain that $({\hat{v}}',h'')\in L^2(0,T;{\mathbb {V}}'({\tilde{A}}))$ and then apply [33, Chapter 3, Lemma 1.2], by exploiting the fact that $\{{\mathbb {V}}({\tilde{A}}), {\mathbb {H}}({\tilde{A}}),{\mathbb {V}}'({\tilde{A}})\}$ is an Hilbert triplet. Moreover, the function ${\hat{v}}$ obeys the energy inequality (3.2), which is a natural consequence of the convergence results that we have just proved.

The proof of Proposition 3.1 is complete once we prove the following lemma, which, combined with the last convergence result in (3.9), allows to conclude on the global-in-time character of the solution.

Lemma 3.2

For all $T<\infty$, there exists $\varepsilon _0=\varepsilon _0({\hat{v}}_0,h_0,k_0,T)>0$ such that

$$\begin{aligned} |h_N(t)|\le L-\delta -\varepsilon _0 \qquad \forall \, t\in [0,T]. \end{aligned}$$

Proof

By contradiction, let us suppose that there exists $T<\infty$ such that $h_N({\bar{t}})=L-\delta$ for some ${\bar{t}}\in [0,T]$. The same procedure can be applied if $h_N=-L+\delta$. Since $h_N\in C^0([0,T];{\mathbb {R}})$, for any $\eta >0$ small there exist ${\varepsilon }_1>\varepsilon _2>0$ such that

$$\begin{aligned} h_N(t)\in [L-\delta -2\eta , L-\delta -\eta ], \qquad \forall \, t\in ({\bar{t}}-{\varepsilon _1},{\bar{t}}-\varepsilon _2). \end{aligned}$$

Taking into account the conditions satisfied by f reported in (1.4), one can take $\eta$ small enough so that there exists a constant ${\bar{C}}>0$ such that

$$\begin{aligned} F(h_N)> & {} \int _{L-\delta -2\eta }^{L-\delta -\eta }f(s)ds >\int _{L-\delta -2\eta }^{L-\delta -\eta }{{\bar{C}}}\exp \frac{1}{(L-\delta -s)^{4+r}}\,ds\nonumber \\= & {} \int _\eta ^{2\eta }{\bar{C}}\exp \frac{1}{\tau ^{4+r}}\,d\tau \ge {\bar{C}}\eta \,\exp \frac{1}{(2\eta )^{4+r}}. \end{aligned}$$

(3.11)

The solenoidal extension a in (2.9) is now built taking $\varepsilon _0=\eta$, thus

$$\begin{aligned} a(y)=a_{h_N}(y;\eta ). \end{aligned}$$

From the energy estimate (3.8) (which is uniform with respect to N), (3.11) and the estimates (2.4), we obtain that there exist a positive constant $C_0$, depending on the initial data $h_0,k_0,{\hat{v}}_0$, and two positive constants $C_1,C_2$ depending on the geometrical and physical parameters, i.e. $m,\lambda ,L,\delta , \mu$, such that

$$\begin{aligned} \begin{aligned}&2\,{\bar{C}}\eta \,\exp \frac{1}{(2\eta )^{4+r}}<C_0+\frac{C_1}{\eta ^4}T+ \frac{C_2}{\eta ^4}\int _0^T \left( C_0+\frac{C_1}{\eta ^4}s\right) \,\exp \left( \frac{C_2}{\eta ^4}s\right) ds. \end{aligned}\nonumber \\ \end{aligned}$$

(3.12)

Integrating by parts the right-hand side of (3.12), we obtain that

$$\begin{aligned} 2\,{\bar{C}}\eta \,\exp \frac{1}{(2\eta )^{4+r}}<\frac{C_1}{C_2}+C_0\exp \frac{C_2T}{\eta ^4}-\frac{C_1}{C_2}\exp \frac{C_2T}{\eta ^4}+\frac{C_1}{\eta ^4}+\frac{C_1}{\eta ^4}T\exp \frac{C_2T}{\eta ^4}. \end{aligned}$$

This immediately yields a contradiction, since $r>0$. From the above argument, for all $T<\infty$ it must be that $|h_N(t)|<L-\delta$ when $t\in [0,T]$. Since $h_N\in C^0([0,T];{\mathbb {R}})$ and [0, T] is compact, the thesis of the lemma follows. $\square$

4 Proof of the main result: existence

We already mentioned how proving Theorem 1.1 is equivalent to proving Theorem 2.6. The idea of the proof of the first part of Theorem 2.6 is exploiting the result of existence for the penalized problem, given in Proposition 3.1. Indeed, the next step of the penalty method implies passing to the limit in (3.1) with respect to n. Again, we will follow the procedure by [6], highlighting the differences when it is necessary. Let us label the weak solution to (3.1) making the dependence on n explicit as $({\hat{v}}_n,h_n)$; of course $E_h$ also depends on n, thus it may be relabelled as $E_{h_n}$ This solution satisfies the energy estimate (3.2), where we should also make explicit the dependence on n. Let us state and prove two consequences of this fact.

The first consequence is natural: there exists a subsequence, which we denote again by $({\hat{v}}_n,h'_n)$ such that

$$\begin{aligned}&({\hat{v}}_n,h'_n)\rightharpoonup ({\hat{v}},h') \qquad \text {in}\,L^2(0,T;{\mathbb {V}}({\tilde{A}})),\qquad ({\hat{v}}_n,h'_n)\overset{*}{\rightharpoonup }({\hat{v}},h')\nonumber \\&\quad \text {in}\,L^\infty (0,T;{\mathbb {H}}({\tilde{A}})), \qquad h_n\rightarrow h \qquad \text {in}\,C^0([0,T];{\mathbb {R}}), \end{aligned}$$

(4.1)

where the latter is due to the compact embedding of $W^{1,\infty }(0,T;{\mathbb {R}})$ onto $C^0([0,T];{\mathbb {R}})$.

The second consequence is proven in the following lemma.

Lemma 4.1

For any $K\subset {\tilde{A}}$ compact set, the sequence ${\hat{v}}_n$ satisfies

$$\begin{aligned} \lim _{n\rightarrow \infty } \int _0^T\int _{{E_{h}\cap K}}|{\hat{v}}_n|^2\,dy\,ds= 0. \end{aligned}$$

(4.2)

Proof

From (3.2), we obtain that

$$\begin{aligned} \lim _{n\rightarrow \infty } \int _0^T\int _{{E_{h_n}}}|{\hat{v}}_n|^2\,dy\,ds=0. \end{aligned}$$

(4.3)

Following [6], we write

$$\begin{aligned} \int _0^T\int _{{E_{h}\cap K}}|{\hat{v}}_n|^2\,dy\,ds\le \int _0^T\int _{{E_{h_n}\cap K}}|{\hat{v}}_n|^2\,dy\,ds+ \int _0^T\int _{\{{E_{h}{\setminus } E_{h_n}}\}\cap K}|{\hat{v}}_n|^2\,dy\,ds.\nonumber \\ \end{aligned}$$

(4.4)

Then, we use the Hölder inequality:

$$\begin{aligned}&\int _0^T\int _{\{{E_{h}{\setminus } E_{h_n}}\}\cap K}|{\hat{v}}_n|^2\,dy\,ds\nonumber \\&\quad = \int _0^T\int _{{\tilde{A}}}\chi _{{\{{E_{h}{\setminus } E_{h_n}\}\cap K}}}|{\hat{v}}_n|^2\,dy\,ds\nonumber \\&\quad \le \int _0^T\Vert \chi _{{\{{E_{h}{\setminus } E_{h_n}\}\cap K}}}\Vert _{L^2({\tilde{A}})}\Vert {\hat{v}}_n\Vert ^2_{L^4({\tilde{A}})}\rightarrow 0 \quad \text {as}\,\, n\rightarrow \infty , \end{aligned}$$

(4.5)

where we exploit the result provided in [6, Lemma 1] to infer that $\chi _{{\{{E_{h}{\setminus } E_{h_n}\}\cap K}}}\rightarrow 0$ in $L^p({\tilde{A}}\times [0,T])$ strongly $\forall \, p\in [1,\infty )$ and that $u\in L^4({\tilde{A}}\times [0,T])$ as it is proven in [33, Lemma 3.3]. If we combine (4.3), (4.5), (4.4), we obtain the sought result (4.2). $\square$

Now, we introduce, for any $\eta >0$, given ${\mathcal {O}}_{h(t)}$ any bounded set such that ${\bar{B}}\subset {\mathcal {O}}_{h(t)}\subset A_{h(t)}$,

$$\begin{aligned} Q_{{\mathcal {O}}_{h(t)}}= & {} \{(y,t)\in {\tilde{A}}\times [0,T] \,|\, y\in {\mathcal {O}}_{h(t)}\},\nonumber \\ \Sigma _{{h(t)},{{\mathcal {O}}_{h(t)}}}= & {} \{(y,t)\in {\tilde{A}}\times [0,T] \,|\, y\in \partial {\mathcal {O}}_{h(t)}\},\nonumber \\ Q_{i,\eta ,{{\mathcal {O}}}_{h(t)}}= & {} \{(y,t)\in {\tilde{A}}\times [0,T] \,|\, y\in {\mathcal {O}}_{h(t)},\,d(y,\partial {\mathcal {O}}_{h(t)})<\eta \}, \end{aligned}$$

(4.6)

that is $Q_{i,\eta }$ contains the couple (y, t) such that y belongs to the interior boundary strip of ${\mathcal {O}}_{h}$. The sets in (4.6) depend on the choice of ${\mathcal {O}}_h$, but from now on we will omit the subscript ${{\mathcal {O}}_h}$ not to make the notation heavy. In order to develop the proof of Theorem 2.6, we need to first prove an auxiliary result, i.e. that ${\hat{v}}_n$ is relatively compact in $L^2(Q)$, which implies the existence of a subsequence, still labelled as ${\hat{v}}_n$, satisfying the following strong convergence result

$$\begin{aligned} {\hat{v}}_n\rightarrow {\hat{v}}\qquad \text {in } L^2(Q). \end{aligned}$$

(4.7)

The procedure implemented in [6] in order to prove such convergence result implies exploiting an Aubin–Lions type lemma: more precisely, one wants to apply [10, Lemma 4.6]. However, first we need to build the structure to apply such lemma. Thus, we introduce an open bounded set $D\subset R^2$ with Lipschitz boundary such that ${\bar{B}}\subset D$, and the function spaces

$$\begin{aligned} \begin{aligned}&M(D)=\{(v,l)\in L^2({\bar{D}})\times {\mathbb {R}}\,|\,\text {div}\, v=0, v|_B=l\,{\hat{e}}_2\},\\&Z(D)=\{(v,l)\in H(D)\times {\mathbb {R}}\,|\, v|_B=l\,{\hat{e}}_2\}\subset M(D), \end{aligned} \end{aligned}$$

where H(D) can be characterized as follows since D is a Lipschitz open bounded set (see [33, Theorem 1.4])

$$\begin{aligned} H(D)=\{v\in L^2(D)\,|\,\text {div}\,v=0\,,\,\gamma _\nu u=0\,\text {on}\,\partial D\}. \end{aligned}$$

We associate to both Z(D) and M(D) the following scalar product:

$$\begin{aligned} ((v_1,v_2))=\int _{D{\setminus } B}v_1\cdot v_2 \,dy+l_1l_2, \end{aligned}$$

which makes both of them Hilbert spaces. Then, we define the projector P(D),

$$\begin{aligned} P(D): M(D)\rightarrow Z(D). \end{aligned}$$

We will now prove two technical lemmas, starting by a useful property of such projector.

Lemma 4.2

There exists a positive constant C such that

$$\begin{aligned} \Vert v-P(D)v\Vert _{L^2(D)}\le C\Vert v\Vert _{L^2(\partial D)}\qquad \forall \, v\in M(D)\cap H^1(D). \end{aligned}$$

Proof

We follow step by step the proof of [6, Lemma 4]. We emphasize that even if D is merely a Lipschitz domain this does not compromise the validity of the proof. $\square$

Then we prove the second technical lemma needed to guarantee (4.7).

Lemma 4.3

Let D be defined as above. Then we choose $0<\alpha<\beta <T$, so that $D\times (\alpha ,\beta )\subseteq Q$; let $U_n$ be the restriction of ${\hat{v}}_n$ to $D\times (\alpha ,\beta )$. Then $P(D)U_n$ is strongly convergent in $L^2(D\times (\alpha ,\beta ))$.

Proof

We introduce an auxiliary function space:

$$\begin{aligned} F(D)=\{(v,l)\in H^1_0({D})\times {\mathbb {R}}\,|\,\text {div}\, v=0, v|_B=l\,{\hat{e}}_2\}. \end{aligned}$$

Any element in F(D) can be extended by 0 in ${\tilde{A}}{\setminus } B$, so we can consider $F(D)\subseteq {\mathbb {V}}({\tilde{A}})$. We pick as a test function $\phi$ in (3.1) $\phi =a(t)\varphi$, with $\varphi \in F(D)$ and $a(t)\in {\mathcal {D}}(\alpha ,\beta )$ to obtain

$$\begin{aligned} \begin{aligned}&\frac{d}{dt}\{(U_n,\varphi )_{L^2(D{\setminus } B)}\!\!+m\,h_n'\,l\}\!+\!f(h_n)\,l={}_{F(D)'}{\langle g_n,\varphi \rangle }{}_{F(D)}\qquad \forall \,\varphi \in F(D)\\ {}&\frac{d}{dt}((U_n,\varphi ))={}_{F(D)'}\langle g_n,\varphi \rangle {}_{F(D)}-f(h_n)\,l\qquad \forall \,\varphi \in F(D) \end{aligned} \end{aligned}$$

(4.8)

where

$$\begin{aligned} {}_{F(D)'}\langle g_n,\varphi \rangle {}_{F(D)}\!= & {} \!-2\mu (D(U_n),D(\varphi ))_{L^2(D)}\!-\!\psi (U_n,U_n,\varphi )\!-\!\psi (U_n,a,\varphi )\\&-\psi (a,U_n,\varphi )+\psi (h'_n{\hat{e}}_2,a,\varphi )+\psi (h'_n{\hat{e}}_2,U_n,\varphi ) \!-\! \langle {\hat{g}},\varphi \rangle , \end{aligned}$$

provided that n is large enough. Since $F(D)\subseteq Z(D)$, we may rewrite (4.8) as

$$\begin{aligned} \frac{d}{dt}((P(D)U_n,\varphi ))= {}_{F(D)'}\langle g_n,\varphi \rangle {}_{F(D)}-\!f(h_n)\,l\qquad \forall \,\varphi \,\in F(D). \end{aligned}$$

(4.9)

From (4.9), we have that

$$\begin{aligned} |\frac{d}{dt}((P(D)U_n,\varphi ))|= |{}_{F(D)'}\langle g_n,\varphi \rangle {}_{F(D)}|+|f(h_n)\,l|\qquad \forall \,\varphi \,\in F(D).\nonumber \\ \end{aligned}$$

(4.10)

Then, we can prove that the right-hand side of (4.10) can be bounded. Indeed, by exploiting classical estimates (see [33, Chapter 3, Section 3.3]), Lemma 2.5, the energy estimate (2.24), we obtain that

$$\begin{aligned} |{}_{F(D)'}\langle g_n,\varphi \rangle {}_{F(D)}|\le M_1\Vert \nabla \varphi \Vert _{L^2(D)},\quad \forall \, n\ge 1, \end{aligned}$$

(4.11)

where $M_1$ is a constant depending on $T,\mu ,\lambda$, the geometry of the problem and the initial conditions. Also

$$\begin{aligned} |f(h_n)\,l|\le M_2|l|,\quad \forall \, n\ge 1, \end{aligned}$$

(4.12)

because $f(h_n)$ can be thought to be a bounded function as long as the rigid obstacle does not touch the boundary of the channel, which has been proven. Bounds (4.11) and (4.12) imply that

$$\begin{aligned} \left\| \frac{d}{dt}P(D)U_n\right\| _{L^2(0,T;\,\,[F(D)]')}\le M_1+M_2,\quad \forall \, n\ge 1. \end{aligned}$$

This inequality, together with the fact that $U_n$ is a bounded set in $L^2(0,T;Z(D)\cap H^1(D))$ because of the energy estimate (3.2), and the compact inclusions $Z(D)\cap H^1(D)\subset Z(D)\subset [F(D)]'$, allow to apply [10, Lemma 4.6] so as to obtain that $P(D)U_n$ forms a compact set in $L^2(D\times (\alpha ,\beta ))$. $\square$

Finally, one can give the following lemma:

Lemma 4.4

The sequence ${\hat{v}}_n$ is relatively compact in $L^2(Q)$, thus there holds (4.7).

Proof

In order to prove this lemma, one can follow precisely the procedure given in [6, Theorem 3], once we declare the following notations: given $s\in {\mathbb {N}}$, define $\alpha _0,\alpha _1,\ldots ,\alpha _s$, real numbers, and the sets $\Omega _1,\Omega _2,\ldots ,\Omega _s$ such that

$$\begin{aligned}&0=\alpha _0<\alpha _1<\cdots <\alpha _s=T \\&{\bar{\Omega }}_i\times ]\alpha _{i-1},\alpha _i[\,\subset Q, \qquad Q{\setminus } ( \Omega _i\times ]\alpha _{i-1},\alpha _i[)\,\subset Q_{i,\eta }. \end{aligned}$$

Then we denote

$$\begin{aligned} I_\eta =\bigcup _{i=1}^s {\Omega }_i\times ]\alpha _{i-1},\alpha _i[, \qquad Q_\eta =Q{\setminus } I_\eta . \end{aligned}$$

With the help of such definitions, we follow step by step the proof of [6, Theorem 3], which is divided in two parts. The first part uses Lemma 4.3, while the second part aims at exploiting the classical compactness result by Kolmogorov, [24, Chapter 3, Section 11.3, Theorem 3]. $\square$

We can now proceed to the proof of Theorem 2.6. The objective is proving that the limit $({\hat{v}},h)$ in (4.1) is a solution to the original problem, thus it satisfies (2.21)–(2.22)–(2.20).

We start by proving that (2.20) is satisfied. In other words, we pass to the limit in (3.1). Take $(\phi ,l)\in C^1([0,T];{\mathcal {W}}_{h(t)})$. Since there holds the last convergence result in (4.1), there exists $n_0\in {\mathbb {N}}$ such that

$$\begin{aligned} (\phi ,l)\in C^1([0,T];{\mathcal {W}}_{h_n(t)})\qquad \forall n\ge n_0, \end{aligned}$$

and the penalty term in (3.1) vanishes for all $n\ge n_0$, by applying Lemma 4.1, where K is the compact support of $\phi$. The convergence results (4.1), (4.7) (where as ${\mathcal {O}}_h$ defining Q in (4.6) we take the compact support of $\phi$) together with the density of ${\mathcal {W}}_{h(t)}$ in ${\mathbb {V}}_{h(t)}$ prove that $({\hat{v}},h)$ also satisfies (2.20) for $T<\infty$.

The results of convergence (4.1) prove that $({\hat{v}},h)\in L^2(0,T;{\mathbb {V}}({\tilde{A}}))\cap L^\infty (0,T;{\mathbb {H}}({{\tilde{A}}}))$. By contradiction, let us suppose that supp(${\hat{v}}$) invades $E_h$. Then, we can find $K\subset {\tilde{A}}$ such that supp(${\hat{v}})\subset K$. However, from (4.7) and Lemma 4.1, we get a contradiction; thus in particular we obtain that $({\hat{v}},h)$ satisfies (2.21)–(2.22). Moreover, with analogous considerations as those that we did when proving Proposition 3.1, we obtain the continuity property of $({\hat{v}},h)$ expressed in the statement of Theorem 2.6. Finally, the energy estimate (2.24) simply follows from taking the limit as $n\rightarrow \infty$ in (3.2); that explains the expression for $\alpha (s)$ in (2.25). As a consequence of (3.2), we also obtain the global character in time of the solution and the existence of some $\varepsilon _0>0$ such that $|h(t)|\le L-\delta -\varepsilon _0$ for all $t\in [0,T]$, by proceeding precisely as in Lemma 3.2.

5 Proof of the main result: uniqueness

We begin by stating the following regularity property on a solution given by Theorem 2.6.

Lemma 5.1

Let (v, h) be a weak solution to problem (2.7)–(2.8) in the sense of Definition 2.3. Then, given ${\hat{v}}=v-a$, where $a=a_h$ is the extension defined as in (2.9), there holds

$$\begin{aligned} t\,{\hat{v}}\in L^2(0,T;{\mathbb {V}}_{h(t)}),\qquad t\,\partial _t{\hat{v}}\in L^2(0,T;{\mathbb {V}}'_{h({t})}). \end{aligned}$$

(5.1)

Moreover, one can estimate the trilinear form as follows, for any $w\in H^1_0({\tilde{\Omega }}(t))$:

$$\begin{aligned} \begin{aligned} |\,\psi (w, {\hat{{v}}},w)|\le 2^{1/2}\Vert w\Vert _{L^2({\tilde{\Omega }}(t))}\Vert \nabla w\Vert _{L^2({\tilde{\Omega }}(t))}\Vert \nabla {\hat{v}}\Vert _{L^2({\tilde{\Omega }}(t))}. \end{aligned} \end{aligned}$$

(5.2)

Proof

The result in (5.1) follows immediately from the properties of any weak solutions to problem (2.7)–(2.8) (see Theorem 2.6) (see also [16, Lemma 6]). For what concerns (5.2), we can exploit the Hölder inequality together with the classical interpolation argument [33, Chapter 3, Lemma 3.3]:

$$\begin{aligned} |\,\psi (w, {\hat{{v}}},w)|\le & {} \Vert w\Vert ^2_{L^4({\tilde{\Omega }}(t))}\Vert \nabla {\hat{v}}\Vert _{L^2({\tilde{\Omega }}(t))} \\\le & {} 2^{1/2}\Vert w\Vert _{L^2({\tilde{\Omega }}(t))}\Vert \nabla w\Vert _{L^2({\tilde{\Omega }}(t))}\Vert \nabla {\hat{v}}\Vert _{L^2({\tilde{\Omega }}(t)).} \end{aligned}$$

$\square$

Let us consider two weak solutions of the equivalent problem (2.7)–(2.8), $(v_1,h_1)$ and $(v_2,h_2)$, in the sense of Definition 2.3, with the same initial conditions, where $v_1$ is defined on the fluid domain ${\tilde{\Omega }}^1(t)$ while $v_2$ is defined on ${\tilde{\Omega }}^2(t)$. Let $\varepsilon _0>0$ be such that $\min _{t\in [0,T]}(\text {dist}(B,\partial {\tilde{\Omega }}^i))\ge \varepsilon _0$ for $i=1,2$; the existence of such $\varepsilon _0$ comes from Theorem 2.6. Finally, let $\zeta (y_1,y_2)$ be a smooth cutoff function equal to 0 in a $\varepsilon _0/4$ neighbourhood of $\partial B$ and to 1 for any (t, y) such that dist($y,\partial B)\ge \varepsilon _0/2$. Then, for each of the two solutions, we define a solenoidal velocity vector field $V_i:[0,T]\times {\tilde{\Omega }}^i\rightarrow {\mathbb {R}}^2$ as

$$\begin{aligned} V_i(t,y):=\{-y_1h'_i\partial _{y_2}\zeta ,\zeta h_i'+y_1h'_i\partial _{y_1}\zeta \}. \end{aligned}$$

(5.3)

Notice that

$$\begin{aligned} V_i(t,y)={\left\{ \begin{array}{ll}0 &{}\quad \text {if dist}(y,\partial B)\ge \varepsilon _0/2\\ -h'_i{\hat{e}}_2&{}\quad \text {if dist}(y,\partial B)\le \varepsilon _0/4. \end{array}\right. } \end{aligned}$$

We introduce a further domain ${\tilde{\Omega }}^0$, which serves as reference configuration, corresponding to the initial condition $(v_0,h_0)$. Then, we build the deformation mappings of such domain respectively into ${\tilde{\Omega }}^1$ and ${\tilde{\Omega }}^2$, $X_i:[0,T]\times {\tilde{\Omega }}^0\rightarrow {\tilde{\Omega }}^i(t)$, $i=1,2$ as the flow associated to (5.3):

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial }{\partial t}X_i(t,y)=V_i(t,X_i(t,y))\\ X_i(0,y)=y. \end{array}\right. } \end{aligned}$$

Notice that, since $\nabla \cdot V_i=0$, $X_i$ is volume preserving. More precisely, taking $y=(y_1, y_2)\in {\tilde{\Omega }}^0$,

$$\begin{aligned} X_i(t,y_1,y_2)={\left\{ \begin{array}{ll}(y_1,y_2+h_0-h_i(t)) &{}\quad \text {if dist}(y,\partial B)\ge \varepsilon _0/2\\ (y_1,y_2)&{}\quad \text {if dist}(y,\partial B)\le \varepsilon _0/4. \end{array}\right. } \end{aligned}$$

The mapping $X_i$ is a smooth function of $V_i$. In particular, for some $C>0$

$$\begin{aligned} \Vert {\partial _t}^j X_i(t,y)\Vert _{C^k(\bar{{\tilde{\Omega }}}_i)}\le C |h^{(j)}_i|\qquad \forall \,j=0,1,\qquad \forall \, k\in {\mathbb {N}}. \end{aligned}$$

(5.4)

For each $t\in [0,T]$ we define the volume preserving diffeomorphisms

$$\begin{aligned} \begin{aligned} \psi _t: {\tilde{\Omega }}^2(t)&\longrightarrow {\tilde{\Omega }}^1(t) \\ y&\longmapsto \psi _t(y)=X_1(t,X_2^{-1}(t,y))\\ \varphi _t=\psi _t^{-1}: {\tilde{\Omega }}^1(t)&\longrightarrow {\tilde{\Omega }}^2(t) \\ y&\longmapsto \varphi _t(y)=X_2(t,X_1^{-1}(t,y)). \end{aligned} \end{aligned}$$

(5.5)

Thus for any $y=(y_1,y_2)$ such that dist$(y,\partial B)\ge \varepsilon _0/2$

$$\begin{aligned} \begin{aligned}&\psi _t(y_1,y_2)=(y_1,y_2+h_2(t)-h_1(t)), \qquad \varphi _t(y_1,y_2)=(y_1,y_2+h_1(t)-h_2(t)). \end{aligned} \end{aligned}$$

Given the extensions of the Poiseuille flow associated to each of the two solutions, $a_1=a_{h_1}$ and $a_2=a_{h_2}$, defined as in (2.9), we put ${\hat{v}}_1=v_1-a_1$ and ${\hat{v}}_2=v_2-a_2$. For any given $y=(y_1,y_2)\in {\tilde{\Omega }}^1(t)$, we introduce the function

$$\begin{aligned} \begin{aligned} \mathfrak {\hat{{v}}}_2=\nabla \psi _t(y)\cdot {\hat{v}}_2(t,\varphi _t(y)), \end{aligned} \end{aligned}$$

the pullback of ${\hat{v}}_2$ by map $\varphi _t$ in (5.5). Since $a_2=0$ near the obstacle B, because of (2.9) and the properties of s as in Lemma 2.1, we obtain that the pullback of $a_2$ corresponds to

$$\begin{aligned} \mathfrak {{{a}}}_2=\nabla \psi _t(y)\cdot {a}_2(\varphi _t(y))={a}_2(y_1,y_2+h_1-h_2)=s(y_1,y_2+h_1-h_2+h_2)=a_1, \end{aligned}$$

which implies that the solenoidal extension $a_1$ and ${\mathfrak {a}}_2$ are equal after the change of variables. Thus, from now on, $a_1={\mathfrak {a}}_2=a$. We remark that $\mathfrak {\hat{{v}}}_2$ mantains the property of being solenoidal since $\varphi _t$ is volume preserving.

The weak formulation satisfied by $({\hat{v}}_1,h_1)$ can be obtained from (2.20), after rewriting the equation by integrating by parts the two first terms. For a.e. $t\in [0,T]$, there holds, for every $(\phi (t),l(t))\in {\mathbb {V}}_{h_1} \,\,\text {such that}\,\, \phi (\cdot ,T)=l(T)=0$,

$$\begin{aligned} \begin{aligned}&\langle \partial _t {\hat{{v}}}_1(t),\phi (t)\rangle +m\,h_1''(t)\,l(t)+f(h_1(t))\,l(t)\\&\quad +2\mu (D({\hat{{v}}}_1(t)),D(\phi (t)))_{L^2({\tilde{\Omega }}^1(t))}+\psi ( {\hat{{v}}}_1(t), {\hat{{v}}}_1(t),\phi (t))+\psi ( {\hat{{v}}}_1(t),a,\phi (t)) \\&\quad +\psi (a,{\hat{{v}}}_1(t),\phi (t))-\psi (h'_1(t){\hat{e}}_2, {\hat{{v}}}_1(t),\phi )-\psi (h'_1(t){\hat{e}}_2,a,\phi (t))=\langle {\hat{g}},\phi (t)\rangle . \end{aligned} \end{aligned}$$

We refer to [16, Section 3.2] for the explicit computation of the partial derivatives of ${\hat{v}}_2$ in terms of those of $\mathfrak {{\hat{v}}}_2$, so as to obtain that the equation satisfied by ${\mathfrak {v}}_2$ reads as

$$\begin{aligned} \begin{aligned}&\langle \partial _t \mathfrak {\hat{{v}}}_2,\phi \rangle +m\,h_2''\,l+f(h_2)\,l+2\mu \,(D (\mathfrak {\hat{{v}}}_2),D(\phi ))_{L^2({\tilde{\Omega }}^1(t))}\\&\quad +\psi ( \mathfrak {\hat{{v}}}_2, \mathfrak {\hat{{v}}}_2,\phi )+\psi ( \mathfrak {\hat{{v}}}_2,a,\phi )+ \psi (a,\mathfrak {\hat{{v}}}_2,\phi )\\&\quad -\psi (h'_2{\hat{e}}_2, \mathfrak {\hat{{v}}}_2,\phi )-\psi (h'_2{\hat{e}}_2,a,\phi )=\langle {\hat{g}},\phi \rangle -\langle {\mathfrak {f}},\phi \rangle , \end{aligned} \end{aligned}$$

for every $(\phi (t),l(t))\in {\mathbb {V}}_{h_1} \,\,\text {such that}\,\, \phi (\cdot ,T)=l(T)=0$, where, using Einstein’s summation convention and omitting the index t in $\psi _t$ and $\varphi _t$,

$$\begin{aligned} \begin{aligned} {\mathfrak {f}}^i=&+(\partial _k\varphi ^i-\delta _{ik})\partial _t\mathfrak {\hat{{v}}}_2^k+\partial _k\varphi ^i\partial _l \mathfrak {\hat{{v}}}_2^k(\partial _t\psi ^l)+(\partial _k\partial _t\varphi ^i)\mathfrak {\hat{{v}}}_2^k\\&+(\partial ^2_{kl}\varphi ^i)(\partial _t\psi ^l)\mathfrak {\hat{{v}}}_2^k+\mathfrak {\hat{{v}}}_2^l\partial _l\mathfrak {\hat{{v}}}_2^k(\partial _k\varphi ^i-\delta _{ik}) +(\partial ^2_{lk}\varphi ^i)\mathfrak {\hat{{v}}}_2^l\mathfrak {\hat{{v}}}_2^k\\&-\partial _j\psi ^m(\partial _{mk}^2\varphi ^i)\partial _l\mathfrak {\hat{{v}}}_2^k\partial _j\psi ^l-(\partial _k\varphi ^i\partial _j\psi ^m\partial _j\psi ^l\\&-\delta _{ik}\delta _{jm}\delta _{jl})\partial _{ml}^2\mathfrak {\hat{{v}}}_2^k-\partial _k\varphi ^i\partial _l\mathfrak {\hat{{v}}}_2^k(\partial ^2_{jj}\psi ^l)\\&-\partial _j\psi ^m(\partial ^3_{mlk}\varphi ^i)\partial _j\psi ^l\mathfrak {\hat{{v}}}_2^k -(\partial ^2_{lk}\varphi ^i)\partial ^2_{jj}\psi ^l\mathfrak {\hat{{v}}}_2^k-(\partial ^2_{lk}\varphi ^i)\partial _j\psi ^l\partial _j\psi ^m\partial _m\mathfrak {\hat{{v}}}_2^k. \end{aligned} \end{aligned}$$

Now, let $(w,{\hat{h}})$ be defined as in (2.26). Then, taking the difference of the weak formulations satisfied by ${\hat{v}}_1$ and ${\mathfrak {v}}_2$, one has

$$\begin{aligned} \begin{aligned}&\langle \partial _t w,\phi \rangle +m\,{\hat{h}}''\,l+[f(h_1)-f(h_2)]\,l+2\mu (D(w),D(\phi ))_{L^2({\tilde{\Omega }}^1(t))}\\&\quad +\psi ({\hat{v}}_1, w,\phi )+\psi (w, \mathfrak {\hat{{v}}}_2,\phi )+\psi ( w,a,\phi ) \\ {}&\quad +\psi (a,w,\phi )-\psi (h'_1{\hat{e}}_2, w,\phi )-\psi ({\hat{h}}'{\hat{e}}_2,\mathfrak {\hat{{v}}}_2,\phi )-\psi ({\hat{h}}'{\hat{e}}_2,a,\phi )=\langle {\mathfrak {f}},\phi \rangle . \end{aligned} \end{aligned}$$

Then we take $(\phi ,l)=(w,h')$ and we obtain

$$\begin{aligned} \begin{aligned}&\langle \partial _t w,w\rangle +\!m\,{\hat{h}}''\,{\hat{h}}'+[f(h_1)-f(h_2)]\,{\hat{h}}'+2\mu \Vert D(w)\Vert ^2_{L^2({\tilde{\Omega }}^1(t))}\\&\quad =\langle {\mathfrak {f}},w\rangle -\psi (w, \mathfrak {\hat{{v}}}_2,w)-\psi ( w,a,w)+\psi ({\hat{h}}'{\hat{e}}_2,a,w). \end{aligned} \end{aligned}$$

Thus, using [33, Chapter 3, Lemma 1.2] and the fact that $(w',{\hat{h}}'')\in L^2(0,T;{\mathbb {V}}'_{{h_1}})$ from the properties of weak solutions to problem (2.7)–(2.8), there holds

$$\begin{aligned}&\frac{d}{dt}\bigg \{\Vert w\Vert ^2_{L^2({\tilde{\Omega }}^1)}+m\,|{\hat{h}}'|^2+2\int _{h_2}^{h_1}\!\!f(s)\,ds\bigg \}+4\,\mu \Vert D(w)\Vert ^2_{L^2({\tilde{\Omega }}^1)}\nonumber \\&\quad =2\langle {\mathfrak {f}},\phi \rangle -2\,\psi (w, \mathfrak {\hat{{v}}}_2,w)-2\,\psi ( w,a,w)+2\,\psi ({\hat{h}}'{\hat{e}}_2,a,w). \end{aligned}$$

(5.6)

Now, we estimate the right hand side of the above inequality, starting from the trilinear forms. For what concerns the second term, we exploit Lemma 5.1 and the Young inequality:

$$\begin{aligned} \begin{aligned} |2\,\psi (w, \mathfrak {\hat{{v}}}_2,w)|&\le 2\Vert w\Vert ^2_{L^4({\tilde{\Omega }}^1(t))}\Vert \nabla \hat{{\mathfrak {v}}}_2\Vert _{L^2({\tilde{\Omega }}^1(t))}\\&\le 2^{3/2}\Vert w\Vert _{L^2({\tilde{\Omega }}^1(t))}\Vert \nabla w\Vert _{L^2({\tilde{\Omega }}^1(t))}\Vert \nabla {\mathfrak {v}}_2\Vert _{L^2({\tilde{\Omega }}^1(t))}\\ {}&\le \frac{10}{\mu } \Vert w\Vert ^2_{L^2({\tilde{\Omega }}^1(t))}\Vert \nabla \hat{ {\mathfrak {v}}}_2\Vert ^2_{L^2({\tilde{\Omega }}^1(t))}+\frac{\mu }{5}\Vert \nabla w\Vert ^2_{L^2({\tilde{\Omega }}^1(t))} \end{aligned} \end{aligned}$$

The third term can be estimated analogously to what we did in the proof of Proposition 3.1, through the Hölder inequality, the Poincaré inequality in the domain ${\tilde{\Omega }}^1(t)$ and the Young inequality:

$$\begin{aligned} |2\,\psi ( w,a,w)|\le & {} \frac{ 4L}{\pi } {\left\| \nabla a \right\| }_{L^\infty ({\tilde{\Omega }}^1(t))} {\left\| \nabla w\right\| }_{L^2({\tilde{\Omega }}^1(t))}{\left\| w\right\| }_{L^2({\tilde{\Omega }}^1(t))}\\\le & {} \frac{5}{4\mu } \frac{ 16L^2}{\pi ^2} {\left\| \nabla a \right\| }^2_{L^\infty ({\tilde{\Omega }}^1(t))}{\left\| w\right\| }^2_{L^2({\tilde{\Omega }}^1(t))}+\frac{\mu }{5} {\left\| \nabla w\right\| }^2_{L^2({\tilde{\Omega }}^1(t))}. \end{aligned}$$

Then, we consider the domain ${\tilde{\Omega }}^1(t)$ to be partitioned as in (2.6) and we recall that the function a enjoys the same properties of s stated in Lemma 2.1 once we substituted q and $A_h$ with ${\tilde{q}}$ as in (2.7) (where, instead of h, we consider $h_1$) and $A_{h_1}$. The last term on the right hand side of (5.6) is bounded following the reasoning developed in the proof of Proposition 3.1 for the terms in (3.6). Given

$$\begin{aligned} \Vert \nabla {\tilde{q}}\Vert _{L^2(-L,\,L)}=\lambda \,\xi \qquad \text {with } \xi =\sqrt{\frac{8L^3}{3}}, \end{aligned}$$

one can write

$$\begin{aligned} |2\,\psi ({\hat{h}}'{\hat{e}}_2,a,w)|\le \frac{5}{2\mu } \frac{4 L^2}{\pi ^2} {|{\hat{h}}' |^2}( {\left\| \nabla a \right\| }^2_{L^2({\tilde{\Omega }}^1_{0}(t))}+\lambda ^2{\xi }^2)+ \frac{2\mu }{5}{\left\| \nabla w \right\| }^2_{L^2({\tilde{\Omega }}^1(t))} \end{aligned}$$

In order to estimate the first term on the right-hand side of Eq. (5.6), following [16], we divide ${\mathfrak {f}}$ into pieces

$$\begin{aligned} {\mathfrak {f}}={\mathfrak {f}}_1+{\mathfrak {f}}_2+{\mathfrak {f}}_3+{\mathfrak {f}}_4+{\mathfrak {f}}_5 \end{aligned}$$

with

$$\begin{aligned} \begin{aligned} {\mathfrak {f}}_1:=\,&(\partial _k\partial _t\varphi ^i)\mathfrak {\hat{{v}}}_2^k+(\partial ^2_{kl}\varphi ^i)(\partial _t\psi ^l)\mathfrak {\hat{{v}}}_2^k\\&-\sum _j \bigg [\partial _j\psi ^m(\partial ^3_{mlk}\varphi ^i)\partial _j\psi ^l\mathfrak {\hat{{v}}}_2^k+(\partial ^2_{lk}\varphi ^i)\partial ^2_{jj}\psi ^l\mathfrak {\hat{{v}}}_2^k\bigg ], \\ {\mathfrak {f}}_2 := \,&\partial _k\varphi ^i\partial _l \mathfrak {\hat{{v}}}_2^k(\partial _t\psi ^l)-\sum _j\bigg [\partial _j\psi ^m(\partial _{mk}^2\varphi ^i)\partial _l\mathfrak {\hat{{v}}}_2^k\partial _j\psi ^l+\partial _k\varphi ^i\partial _l\mathfrak {\hat{{v}}}_2^k(\partial ^2_{jj}\psi ^l)\\&+(\partial ^2_{lk}\varphi ^i)\partial _j\psi ^l\partial _j\psi ^m\partial _m\mathfrak {\hat{{v}}}_2^k\bigg ], \\ {\mathfrak {f}}_3:=&\,(\partial ^2_{lk}\varphi ^i)\mathfrak {\hat{{v}}}_2^l\mathfrak {\hat{{v}}}_2^k,\quad {\mathfrak {f}}_4:=\mathfrak {\hat{{v}}}_2^l\partial _l\mathfrak {\hat{{v}}}_2^k(\partial _k\varphi ^i-\delta _{ik}),\\ {\mathfrak {f}}_5:=&\,(\partial _k\varphi ^i-\delta _{ik})\partial _t\mathfrak {\hat{{v}}}_2^k-\sum _j(\partial _k\varphi ^i\partial _j\psi ^m\partial _j\psi ^l-\delta _{ik}\delta _{jm}\delta _{jl})\partial _{ml}^2\mathfrak {\hat{{v}}}_2^k. \end{aligned} \end{aligned}$$

We have the following estimates, where we use (5.4).

• Concerning the first three terms:

  $$\begin{aligned} \bigg |\int _0^t\int _{{\tilde{\Omega }}^1(s)}{\mathfrak {f}}_1\cdot w\,dy\,ds\bigg |&\le C\Vert \mathfrak {\hat{{v}}}_2\Vert _{L^\infty (0,T;L^2({\tilde{\Omega }}^1))}\\&\quad \int _0^t\bigg (\max _{[0,s]}\Vert w(\cdot ,s)\Vert _{L^2({\tilde{\Omega }}^1(s))}\max _{[0,s]}|({\hat{h}}(s),{\hat{h}}'(s))|\bigg )\,ds\\&\le C \Vert \mathfrak {\hat{{v}}}_2\Vert _{L^\infty (0,T;L^2({\tilde{\Omega }}^1))}\\&\quad \int _0^t\bigg (\max _{[0,s]}\Vert w(\cdot ,s)\Vert ^2_{L^2({\tilde{\Omega }}^1(s))}+\max _{[0,s]}|({\hat{h}}(s),{\hat{h}}'(s))|^2\bigg )\,ds,\\ \bigg |\int _0^t\int _{{\tilde{\Omega }}^1(s)}{\mathfrak {f}}_2\cdot w\,dy\,ds\bigg |&\le C \int _0^t\Vert \nabla \mathfrak {\hat{{v}}}_2(\cdot ,s)\Vert _{L^2({\tilde{\Omega }}^1(s))}\\&\quad \bigg (\max _{[0,s]}\Vert w(\cdot ,s)\Vert _{L^2({\tilde{\Omega }}^1(s))}\max _{[0,s]}|({\hat{h}}(s),{\hat{h}}'(s))|\bigg )\,ds \\ {}&\le C \int _0^t\Vert \nabla \mathfrak {\hat{{v}}}_2(\cdot ,s)\Vert _{L^2({\tilde{\Omega }}^1(s))}\\&\quad \bigg (\max _{[0,s]}\Vert w(\cdot ,s)\Vert ^2_{L^2({\tilde{\Omega }}^1(s))}+\max _{[0,s]}|({\hat{h}}(s),{\hat{h}}'(s))|^2\bigg )\,ds,\\ \bigg |\int _0^t\int _{{\tilde{\Omega }}^1(s)}{\mathfrak {f}}_3\cdot w\,dy\,ds\bigg |&\le C\int _0^t\Vert \mathfrak {\hat{{v}}}_2(\cdot ,s)\Vert ^2_{L^4({\tilde{\Omega }}^1(a))}\Vert w(\cdot ,s)\Vert _{L^2({\tilde{\Omega }}^1(s))}\max _{[0,s]}|{\hat{h}}(s)|\,ds\\&\le C \Vert \mathfrak {\hat{{v}}}_2\Vert _{L^\infty (0,T;L^2({\tilde{\Omega }}^1))}\\&\quad \int _0^t \Vert \nabla \mathfrak {\hat{{v}}}_2(\cdot ,s)\Vert _{L^2({\tilde{\Omega }}^1(s))}\max _{[0,s]}\Vert w(\cdot ,s)\Vert _{L^2({\tilde{\Omega }}^1)}\max _{[0,s]}|{\hat{h}}(s)|\,ds \\ {}&\le C \Vert \mathfrak {\hat{{v}}}_2\Vert _{L^\infty (0,T;L^2({\tilde{\Omega }}^1))} \int _0^t \Vert \nabla \mathfrak {\hat{{v}}}_2(\cdot ,s)\Vert _{L^2({\tilde{\Omega }}^1(s))}\\&\quad \bigg (\max _{[0,s]}\Vert w(\cdot ,s)\Vert ^2_{L^2({\tilde{\Omega }}^1(s))}+\max _{[0,s]}|{\hat{h}}(s)|^2\bigg )\,ds \\ {}&\le C \Vert \mathfrak {\hat{{v}}}_2\Vert _{L^\infty (0,T;L^2({\tilde{\Omega }}^1))} \int _0^t \Vert \nabla \mathfrak {\hat{{v}}}_2(\cdot ,s)\Vert _{L^2({\tilde{\Omega }}^1(s))}\\&\quad \bigg (\max _{[0,s]}\Vert w(\cdot ,s)\Vert ^2_{L^2({\tilde{\Omega }}^1(s))}+\max _{[0,s]}|{\hat{h}}(s),{\hat{h}}'(s)|^2\bigg )\,ds. \end{aligned}$$

• For the fourth and fifth terms, we introduce

  $$\begin{aligned}&b_1(t):=\Vert \nabla \mathfrak {\hat{{v}}}_2(\cdot ,t)\Vert ^2_{L^2({\tilde{\Omega }}^1(t))}\Vert t\,\nabla \mathfrak {\hat{{v}}}_2(\cdot ,t)\Vert ^2_{L^2({\tilde{\Omega }}^1(t))},\\&b_2(t):=\Vert t\,\partial _t\mathfrak {\hat{{v}}}_2(\cdot ,t)\Vert ^2_{H^{-1}({\tilde{\Omega }}^1(t))}+\Vert t\,\Delta \mathfrak {\hat{{v}}}_2(\cdot ,t)\Vert ^2_{H^{-1}({\tilde{\Omega }}^1(t))}, \end{aligned}$$

  which belong to $L^1(0,T)$ thanks to Lemma 5.1, and we have

  $$\begin{aligned} \bigg |\int _0^t\int _{{\tilde{\Omega }}^1(s)}{\mathfrak {f}}_4\cdot w\,dy\,ds\bigg |&\le C\,\int _0^t\Vert \mathfrak {\hat{{v}}}_2(\cdot ,s)\Vert _{L^4({\tilde{\Omega }}^1(s))} \Vert t\,\nabla \mathfrak {\hat{{v}}}_2(\cdot ,s)\Vert _{L^2({\tilde{\Omega }}^1(s))}\\&\quad \left\| \frac{1}{t}(\partial _k\varphi ^i-\delta _{ik})\right\| _{L^\infty ({\tilde{\Omega }}^1(s))}\Vert w(\cdot ,s)\Vert _{L^4({\tilde{\Omega }}^1(s))}\,ds\\&\le C\,\int _0^t\Vert \mathfrak {\hat{{v}}}_2(\cdot ,s)\Vert _{L^4({\tilde{\Omega }}^1(s))} \Vert t\,\nabla \mathfrak {\hat{{v}}}_2(\cdot ,s)\Vert _{L^2({\tilde{\Omega }}^1(s))}\\&\quad \max _{[0,s]}|{\hat{h}}'(s)|\Vert w(\cdot ,s)\Vert _{L^4({\tilde{\Omega }}^1(s))}\,ds\\&\le C\,\int _0^t\Vert \nabla \mathfrak {\hat{{v}}}_2(\cdot ,s)\Vert _{L^2({\tilde{\Omega }}^1(s))} \Vert t\,\nabla \mathfrak {\hat{{v}}}_2(\cdot ,s)\Vert _{L^2({\tilde{\Omega }}^1(s))}\\&\quad \max _{[0,s]}|{\hat{h}}'(s)|\Vert \nabla w(\cdot ,s)\Vert _{L^2({\tilde{\Omega }}^1(s))}\,ds\\&\le \frac{\mu }{5}\int _0^t\Vert \nabla w(\cdot ,s)\Vert ^2_{L^2({\tilde{\Omega }}^1(s))}\,ds\\&\quad +C\frac{5}{4\mu }\int _0^tb_1(s)\max _{[0,s]}|{\hat{h}}'(s)|^2\,ds \\&\le \frac{\mu }{5}\int _0^t\Vert \nabla w(\cdot ,s)\Vert ^2_{L^2({\tilde{\Omega }}^1(s))}\,ds+C\frac{5}{4\mu }\int _0^tb_1(s)\\&\quad \max _{[0,s]}|{\hat{h}}(s),{\hat{h}}'(s)|^2\,ds, \end{aligned}$$

  where we use the Hölder inequality, the Young inequality, [33, Lemma 3.3] and the Poincaré inequality.

  $$\begin{aligned}&\bigg |\int _0^t\int _{{\tilde{\Omega }}^1(s)}{\mathfrak {f}}_5\cdot w\,dy\,ds\bigg | \\&\quad \le C\,\int _0^t \Vert t\,\partial _t\mathfrak {\hat{{v}}}_2(\cdot ,s)\Vert _{H^{-1}({\tilde{\Omega }}^1(s))}\\&\quad \quad \left\| \frac{1}{t}(\partial _k\varphi ^i-\delta _{ik})\right\| _{L^\infty ({\tilde{\Omega }}^1(s))}\Vert \nabla w(\cdot ,s)\Vert _{L^2({\tilde{\Omega }}^1(s))}\,ds\\&\quad \quad +C\,\int _0^t \Vert t\,\Delta \mathfrak {\hat{{v}}}_2(\cdot ,s)\Vert _{H^{-1}({\tilde{\Omega }}^1(s))}\Vert \frac{1}{t}(\partial _k\varphi ^i-\delta _{ik})\Vert _{L^\infty ({\tilde{\Omega }}^1(s))}\Vert \nabla w(\cdot ,s)\Vert _{L^2({\tilde{\Omega }}^1(s))}\,ds \\&\quad \le C\,\int _0^t \Vert t\,\partial _t\mathfrak {\hat{{v}}}_2(\cdot ,s)\Vert _{H^{-1}({\tilde{\Omega }}^1(s))}\max _{[0,s]}|{\hat{h}}'(s)|\Vert \nabla w(\cdot ,s)\Vert _{L^2({\tilde{\Omega }}^1(s))}\,ds\\&\quad \quad +C\,\int _0^t \Vert t\,\Delta \mathfrak {\hat{{v}}}_2(\cdot ,s)\Vert _{H^{-1}({\tilde{\Omega }}^1(s))}\max _{[0,s]}|{\hat{h}}'(s)|\Vert \nabla w(\cdot ,s)\Vert _{L^2({\tilde{\Omega }}^1(s))}\,ds \\&\quad \le \int _0^t\bigg (C \frac{5}{4\mu }\Vert t\,\partial _t\mathfrak {\hat{{v}}}_2(\cdot ,s)\Vert ^2_{H^{-1}({\tilde{\Omega }}^1(s))}\max _{[0,s]}|{\hat{h}}'(s)|^2+\frac{\mu }{5}\Vert \nabla w(\cdot ,s)\Vert ^2_{L^2({\tilde{\Omega }}^1(s))}\bigg )\,ds\\&\quad \quad +\int _0^t\bigg ( C\frac{5}{4\mu }\Vert t\,\Delta \mathfrak {\hat{{v}}}_2(\cdot ,s)\Vert ^2_{H^{-1}({\tilde{\Omega }}^1(s))}\max _{[0,s]}|{\hat{h}}'(s)|^2+\frac{\mu }{5}\Vert \nabla w(\cdot ,s)\Vert ^2_{L^2({\tilde{\Omega }}^1(s))}\bigg )\,ds\\&\quad \le \frac{2\mu }{5}\,\int _0^t\Vert \nabla w(\cdot ,s)\Vert ^2_{L^2({\tilde{\Omega }}^1(s))}\,ds+C\,\frac{5}{4\mu }\int _0^tb_2(s)\max _{[0,s]}|{\hat{h}}(s),{\hat{h}}'(s)|^2\,ds. \end{aligned}$$

If we set

$$\begin{aligned} A(t):= & {} \Vert \mathfrak {\hat{{v}}}_2\Vert _{L^\infty (0,T;L^2({\tilde{\Omega }}^1(t)))}+\Vert \nabla \mathfrak {\hat{{v}}}_2(\cdot ,t)\Vert _{L^2({\tilde{\Omega }}^1(t))}\\&+\, \Vert \mathfrak {\hat{{v}}}_2\Vert _{L^\infty (0,T;L^2({\tilde{\Omega }}^1(t)))} \Vert \nabla \mathfrak {\hat{{v}}}_2(\cdot ,t)\Vert _{L^2({\tilde{\Omega }}^1(t))}\in L^2(0,T)\subset L^1(0,T), \\ B(t):= & {} \Vert \mathfrak {\hat{{v}}}_2\Vert _{L^\infty (0,T;L^2({\tilde{\Omega }}^1(t)))}+\Vert \nabla \mathfrak {\hat{{v}}}_2(\cdot ,t)\Vert _{L^2({\tilde{\Omega }}^1(t))}\\&+ \Vert \mathfrak {\hat{{v}}}_2\Vert _{L^\infty (0,T;L^2({\tilde{\Omega }}^1(t)))}\Vert \nabla \mathfrak {\hat{{v}}}_2(\cdot ,t)\Vert _{L^2({\tilde{\Omega }}^1(t))}+\frac{5}{4\mu }(b_1(t)+b_2(t))\in L^1(0,T), \end{aligned}$$

we obtain

$$\begin{aligned} \begin{aligned}&\bigg |\int _0^t\int _{{\tilde{\Omega }}^1(s)}{\mathfrak {f}}\cdot w\,dy\,ds\bigg |\\&\quad \le \, C \int _0^t\bigg (A(s)\max _{[0,s]}\Vert w(\cdot ,s)\Vert ^2_{L^2({\tilde{\Omega }}^1(s))}+B(s)\max _{[0,s]}|({\hat{h}}(s),{\hat{h}}'(s))|^2\bigg )\,ds\\&\qquad + \frac{3\mu }{5}\int _0^t\Vert \nabla w(\cdot ,s)\Vert ^2_{L^2({\tilde{\Omega }}^1(s))}\,ds. \end{aligned} \end{aligned}$$

Then, given A(t) and B(t) as above, we define

$$\begin{aligned}&{\bar{A}}(t):=A(t)+\frac{10}{\mu }\Vert \nabla \mathfrak {\hat{{v}}}_2(\cdot ,t)\Vert ^2_{L^2({\tilde{\Omega }}^1(t))}+\frac{5}{4\mu }\frac{16 L^2}{\pi ^2}\Vert \nabla a\Vert ^2_{L^\infty ({\tilde{\Omega }}^1(t))},\\&{\bar{B}}(t):=B(t)+\frac{5}{2\mu }\frac{4L^2}{\pi ^2}(\Vert \nabla a\Vert ^2_{L^2({\tilde{\Omega }}^1_{0}(t))}+\lambda ^2\xi ^2). \end{aligned}$$

We reorder (5.6) once we plugged the above estimates, considering the above definitions and using that

$$\begin{aligned} \int _{{\tilde{\Omega }}^1}|\nabla w|^2\,dy\le \int _{A_{h_1}}|\nabla w|^2\,dy=2\int _{A_{h_1}}|D(w)|^2\,dy=2\int _{{\tilde{\Omega }}^1}|D(w)|^2\,dy, \end{aligned}$$

since w is a divergence free vector field vanishing on $\partial A_{h_1}$. Thus, integrating between 0 and t we obtain, since $w(0)=0={\hat{h}}'(0)$,

$$\begin{aligned}&\Vert w(t)\Vert ^2_{L^2({\tilde{\Omega }}^1(t))}+m|{\hat{h}}'(t)|^2+2\int _{h_2(t)}^{h_1(t)}\!\!f(s)\,ds\nonumber \\&\quad \le \, C\int _0^t\bigg ({\bar{A}}(s)\max _{[0,s]}\Vert w(\cdot ,s)\Vert ^2_{L^2({\tilde{\Omega }}^1(s))}\nonumber \\&\quad +{\bar{B}}(s)\max _{[0,s]}|({\hat{h}}(s),{\hat{h}}'(s))|^2\bigg )\,ds. \end{aligned}$$

(5.7)

Then we set

$$\begin{aligned} {\mathcal {D}}(t)={\bar{A}}(t)+{\bar{B}}(t) \end{aligned}$$

and from (5.7), we infer

$$\begin{aligned}&\Vert w(t)\Vert ^2_{L^2({\tilde{\Omega }}^1(t))}+m|{\hat{h}}'(t)|^2 \\&\quad \le \int _0^t C\,{\mathcal {D}}(s)\bigg (\max _{[0,s]}\Vert w(\cdot ,s)\Vert ^2_{L^2({\tilde{\Omega }}^1(s))}+\max _{[0,s]}|({\hat{h}}(s),{\hat{h}}'(s))|^2\bigg )\,ds. \end{aligned}$$

As in [16], we notice that

$$\begin{aligned} \frac{d}{dt}|{\hat{h}}|^2\le C(|{\hat{h}}'|^2+|{\hat{h}}|^2). \end{aligned}$$

(5.8)

Using ${\mathcal {D}}(t)\in L^1$ and Grönwall’s lemma, we conclude that

$$\begin{aligned} \Vert w(t)\Vert ^2_{L^2({\tilde{\Omega }}^1(t))}+m|{\hat{h}}'(t)|^2=0, \end{aligned}$$

which, if one uses (5.8), implies finishing the proof.

6 Some remarks on torsional movements

If we aim at developing the analysis of the interaction between wind and suspension bridges in the hypothesis of strong incoming flux, we need to consider also the torsional movement of the deck. Hence, we refer to the second model introduced in [4]. This section is devoted to discussing some remarks about such a problem. In particular, we will briefly present the problem and illustrate the mathematical differences that the diverse physical behaviour of the obstacle entails: we focus on the reasons why we do not expect the proof used in the case of translation to work also in this case, because the same technique will generate an infinite energy term.

Fig. 3

The channel with the rotating obstacle B

In this case, as already mentioned, the obstacle B is free to rotate around a fixed pin placed at its center of mass; this imposes a constraint on the dimensions of the channel and of the obstacle $L^2>\delta ^2+d^2$, because we assume that the obstacle may a priori reach a vertical position. We denote by ${\mathcal {J}}$ the inertia of the body and by $\theta$ the angle of rotation with respect to the horizontal. The position of the body is tracked by

$$\begin{aligned} B_{\theta }=\begin{pmatrix} \cos {\theta } &{}\quad -\sin {\theta } \\ \sin {\theta } &{}\quad \cos {\theta } \end{pmatrix} B= R\,B\qquad \forall \,|\theta |<\frac{\pi }{2}, \end{aligned}$$

(6.1)

thus the fluid domain depends on $\theta$ and it is given by $\Omega _\theta ={\mathbb {R}}\times (-L,L){\setminus } B_\theta = A{\setminus } B_\theta$: see Fig. 3. Let us denote again as $\Gamma$ the union of the upper and lower boundaries of the channel, $\Gamma ={\mathbb {R}}\times \{-L,L\}$. The fluid–structure-interaction evolution problem that we analyze is:

$$\begin{aligned} \begin{aligned}&u_t=\mu \,\Delta u-(u\cdot \nabla )u-\nabla p,\quad \text {div}\, u=0\quad (x,t)\in \Omega _{\theta (t)}\times (0,T)\\ {}&u=0 \quad (x,t)\in \Gamma \times (0,T),\qquad u={\theta '(t)} x^{\perp } \quad (x,t)\in \partial B_{\theta (t)} \times (0,T),\\&\quad \lim _{|x_1|\rightarrow \infty }u(x_1,x_2)=q:=\lambda (L^2-x_2^2)\,{\hat{e}}_1\\ {}&{\mathcal {J}}{\theta ''(t)} +g(\theta (t))=-\int _{\partial B_{\theta (t)}} x^{\perp } \cdot {\mathcal {T}}(u,p){\widehat{n}} \quad t\in (0,T), \end{aligned} \end{aligned}$$

(6.2)

to which we associate the initial conditions $u(x,0)=u_0$, $\theta (0)=\theta _0$, ${\theta '}(0)=\theta _1$. The rectangular rigid body B is free to rotate driven by the action of both an elastic angular restoring force $g(\theta )$ and the torque imposed by the fluid stress. The force g plays the role which was played by f in the case of pure translation, thus it resumes the action of the same three forces acting on the deck of a suspension bridge (see Introduction): in this case the action of the hangers and cables is symmetric, which makes g an odd function, and it is not as strong as the action of resistance to deformations of the whole deck. In particular, we assume that $g(\theta )\in C^1(-\frac{\pi }{2},\frac{\pi }{2})$ satisfies the following conditions

$$\begin{aligned} g\, \text {odd},\quad g'(\theta )>0\,\,\,\forall \,\theta \in \left( -\frac{\pi }{2},\frac{\pi }{2}\right) ,\quad \lim _{\theta \rightarrow \pi /2}g(\theta )=+\infty . \end{aligned}$$

(6.3)

We emphasize that the third hypothesis in (6.3) is needed in order to prevent the obstacle to reach a vertical position; if we imagine the obstacle to representing the cross section of the deck of a bridge, this assumption seems physically reasonable. We point out that (6.3) compared to (1.4) is not a strong force assumption, but it is weaker, as collisions are already ruled out by the geometric configuration.

The difference in the physics, and consequently in the mathematics of this problem with respect to the case of an obstacle vertically translating is revealed when we introduce the change of variables allowing to write the equations of motion in a frame attached to B, whose coordinates are labelled as $(y_1,y_2)$:

$$\begin{aligned} R\, y=x, \end{aligned}$$

(6.4)

where R is defined as in (6.1). The fluid–structure-interaction evolution problem in the new rotating reference frame is obtained consequently, similarly to what is done in [12, 29]. We just highlight that the Poiseuille flow at infinity after the change of variables (6.4) assumes the following expression, for each value of $\theta$:

$$\begin{aligned} {\tilde{q}}(y)=\bigg (\cos [{\theta }\,\lambda \big (L^2-(y_1\sin {\theta }+y_2\cos {\theta })^2\big )], -\sin [{\theta }\,\lambda \big (L^2-(y_1\sin {\theta }+y_2\cos {\theta })^2\big )]\bigg ).\nonumber \\ \end{aligned}$$

(6.5)

The auxiliary fixed domain that we labelled ${\tilde{A}}$ in Sect. 2 is given by:

$$\begin{aligned} {\tilde{A}}=A-A=\{x-y\,|\,x\in A,y\in A\}, \end{aligned}$$

and it corresponds to ${\mathbb {R}}^2$; indeed, the channel is unbounded and a priori it may cover the whole plane when rotating. Here lies the essential difference in the physical framework of this problem with respect to the previous one; in the case of an obstacle purely vertically translating, the movement of the channel was still confined to a region bounded in one direction. Figure 4 represents the new configuration. The auxiliary domain ${\tilde{A}}$ corresponding to the whole plane ${\mathbb {R}}^2$ also reveals the difference in the mathematical framework. Indeed, the velocity field at infinity ${\tilde{q}}$ defined in (6.5) in the new reference frame is supposed to be extended outside the rotating channel, which we label $A_{\theta (t)}$, to the whole ${\mathbb {R}}^2$ if one wants to apply the penalty method, as we did in Sect. 2. Thus, the Poiseuille flow would be extended to be a parabolic branch diverging to infinity: see Fig. 4, where we represented such extension only for the horizontal position not to burden the picture. This implies that the solenoidal extension now captures a flow to which it is associated an infinite energy, thus compromising the possibility to prove existence of a weak solution to the penalized problem and, consequently, also to the original problem, through the penalty method. On the other hand, as already mentioned in the Introduction, besides the penalty method, different methods have been conceived to find existence of solutions (see [8, 23, 27]), which would allow handling rotation without falling into the aforementioned difficulties. However, they require building global quantities and a global weak formulation, where the integrals must be defined on the whole domain A; as we are not dealing with a simple Newton law in (6.2) due to the presence of $g(\theta )$, such methods are not of trivial application.

Fig. 4

The channel, after the change of variables, moves in the whole plane ${\mathbb {R}}^2$. Three possible positions of the channel are represented. The Poiseuille flow at the outlets of the channel extends to the whole plane