Abstract
We study three graph complexes related to the higher genus Grothendieck–Teichmüller Lie algebra and diffeomorphism groups of manifolds. We show how the cohomology of these graph complexes is related, and we compute the cohomology as the genus g tends to \(\infty \). As a byproduct, we find that the Malcev completion of the genus g mapping class group relative to the symplectic group is Koszul in the stable limit, partially answering a question of Hain.
Similar content being viewed by others
1 Introduction
Let m be a fixed positive integer. In this paper we study three related graph complexes that arise in connection to the diffeomorphism groups of the manifolds
More precisely, we consider graph complexes \(\textsf{GC}_{(g)}\), \(\textsf{GC}_{(g),1}\) and  as follows.
as follows.
-
Elements of
 are \({\mathbb {Q}}\)-linear series of isomorphism classes of connected graphs whose vertices are decorated by zero or more elements of the reduced homology \({{\bar{H}}}_\bullet (W_{g,1})\). We require that each vertex has valence at least 3, with the valence of a vertex being defined as the number of incident half-edges plus the number of decorations. As the superscript indicates, the graphs may have tadpoles, that is edges connecting a vertex to itself.
are \({\mathbb {Q}}\)-linear series of isomorphism classes of connected graphs whose vertices are decorated by zero or more elements of the reduced homology \({{\bar{H}}}_\bullet (W_{g,1})\). We require that each vertex has valence at least 3, with the valence of a vertex being defined as the number of incident half-edges plus the number of decorations. As the superscript indicates, the graphs may have tadpoles, that is edges connecting a vertex to itself. 
The differential on these complexes has two terms, \(\delta =\delta _{split}+\delta _{glue}\). The piece \(\delta _{split}\) is defined by summing over vertices, and splitting the vertex,
 (1)
(1)Here one sums over all ways of distributing the decorations and incident half-edges between two newly created vertices, that produce at least trivalent graphs. The piece \(\delta _{glue}\Gamma \) is defined on a graph \(\Gamma \) by summing over all pairs \((\alpha ,\beta )\) of \({{\bar{H}}}_\bullet (W_{g,1})\)-decorations in the graph \(\Gamma \), replacing the pair of decorations by an edge, and multiplying the graph with the numeric prefactor \(\langle \alpha ,\beta \rangle \), using the canonical pairing \(\langle -,-\rangle : {{\bar{H}}}_\bullet (W_{g,1})\times {{\bar{H}}}_\bullet (W_{g,1}) \rightarrow {\mathbb {Q}}\).
-
The complex

is the quotient obtained by setting all graphs with tadpoles to zero.
-
The complex \(\textsf{GC}_{(g)}\) is defined similarly to \(\textsf{GC}_{(g),1}\), except for three differences. First, one decorates vertices by \({{\bar{H}}}_\bullet (W_{g})\) instead of \({{\bar{H}}}_\bullet (W_{g,1})\). Second, the piece of the differential \(\delta _{glue}\) uses the pairing
$$\begin{aligned} \langle -,-\rangle : H_\bullet (W_{g})\times H_\bullet (W_{g}) \rightarrow {\mathbb {Q}}\end{aligned}$$(2)instead.
Third, there is an additional piece of the differential \(\delta _Z\) that glues a new vertex to a decoration with the top class \(\omega \in H_{2m}(W_{g})\). The new vertex is then decorated by the canonical diagonal element \(\Delta _1\in H_m(W_{g})\otimes H_m(W_{g})\).

We refer to Sect. 3 below for more precise definitions, including signs, prefactors and degrees. We note that these complexes depend on the chosen integer m, although this dependence is kept implicit in the notation. All three of the complexes above are in fact dg Lie algebras, with the Lie brackets defined similarly to \(\delta _{glue}\) above, just operating on a pair of decorations on two distinct graphs.
One has natural maps between the above complexes for various g that fit into a commutative diagram of dg Lie algebras

Furthermore, one has a natural action of the symplectic or orthogonal group
on all three dg Lie algebras considered. Moreover, \(\textsf{GC}_{(g)}\) may naturally be extended by a nilpotent, negatively graded Lie algebra \(\mathfrak {osp}^{nil}_g\) of endomorphisms of \(H_\bullet (W_g)\) that respect the pairing (2), and we will define below an extended dg Lie algebra
All the graph complexes above carry a natural grading by weight, with the weight of a graph with e edges, v vertices and total (homological) decoration degree Dm defined to be the number
This positive integer valued quantity is preserved by the differentials and Lie brackets. In particular our graph complexes split into a direct product of finite dimensional subcomplexes according to weight. We shall denote the graded piece of the complexes or cohomology of given weight W by the prefix \({{\,\textrm{gr}\,}}^W (\cdots )\).
The purpose of this paper is two-fold. First, we describe the relation between the three dg Lie algebras above, with the following result.
Theorem 1
-
(i)
The projection
 defined by setting graphs with tadpoles to zero induces an isomorphism
defined by setting graphs with tadpoles to zero induces an isomorphism  (3)
(3)for all \(W\ge 2\) and \(g\ge 0\).
-
(ii)
For \(g\ge 2\) one has a short exact sequence of graded Lie algebras
$$\begin{aligned} 0 \rightarrow \pi ^{\mathbb {Q}}S T W_{g} \rightarrow H(\textsf{GC}_{(g),1}) \rightarrow H(\textsf{GC}^{\text {ex}}_{(g)}) \rightarrow 0. \end{aligned}$$with \(\pi ^{\mathbb {Q}}S T W_{g}\) being the rational homotopy groups of the unit sphere bundle of the tangent bundle to \(W_{g}\).
We note that the weight 1 part of the cohomology of all our graph complexes may be explicitly computed for all genera g, see Sect. 4.1 below.
The second main topic of this paper is the study of the cohomology of our three dg Lie algebras above for large g. To this end we have the following vanishing result.
Theorem 2
-
(i)
For all \(g\ge 0\), \(W\ge 1\) and \(k<(1-m)W\) we have that
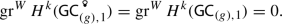
-
(ii)
(partially contained in [15, Theorem 82]) For all \(g\ge 2\), \(W\ge 1\) and \(k<(1-m)W\)
$$\begin{aligned} {{\,\textrm{gr}\,}}^W H^{k}(\textsf{GC}^{\text {ex}}_{(g)}) = 0. \end{aligned}$$ -
(iii)
For all \(W\ge 1\), \(g\ge W+2\) and \(k>(1-m)W\) we have that

In other words, for \(g\ge W+2\), the cohomology of the weight W part of all three graph complexes becomes concentrated in degree \(-(m-1)W\). From this, one also obtains that all three dg Lie algebras become formal in the limit \(g\rightarrow \infty \).
A similar result can be obtained for the Chevalley-Eilenberg cohomology \(H_{CE}(-)\) of all three dg Lie algebras. More precisely, we define the Chevalley-Eilenberg complex of any of the three Lie algebras above (say \({\mathfrak {g}}\) collectively) as the cobar construction of the graded dual
Then \(C_{CE}({\mathfrak {g}})\) is a differential graded commutative algebra. It is equipped with an additional grading by weight, inherited from \({\mathfrak {g}}\). We denote by \({{\,\textrm{gr}\,}}^W H_{CE}(-)\) the weight W piece of the Chevalley-Eilenberg cohomology.
Theorem 3
For any \(g\ge 3W\) and \(k\ne m W\) we have that

In other words, for large g the cohomology of the weight W piece becomes concentrated in cohomological degree mW. It follows from Theorem 3 in particular that in the limit \(g\rightarrow \infty \) the Chevalley-Eilenberg complex becomes formal as a differential graded commutative algebra. Furthermore, it follows from Theorems 2 and 3 together that as \(g\rightarrow \infty \) the cohomology and Chevalley-Eilenberg cohomology of our dg Lie algebras form Koszul pairs. We refer to Sects. 7 and 8 below for more precise formulations of these statements as well as refined degree bounds.
The final question is then to compute the non-vanishing cohomologies for high genera. For this introduction we shall restrict ourselves to the case \(m=1\) and the complex \(\textsf{GC}^{\text {ex}}_{(g)}\) for brevity. Analogous results for the other cases can be found in Sect. 8 below. We shall give an explicit presentation of the stable cohomology of the Lie algebra. The answer is closely related to Hain’s presentation of the Malcev completion of the Torelli group [18, 19].
Note that for \(m=1\) the cohomology of \(\textsf{GC}^{\text {ex}}_{(g)}\) becomes concentrated in degree 0 as \(g\rightarrow \infty \), and furthermore \(\textrm{OSp}_g=\textrm{Sp}(2g)\). Fix a system of fundamental weights \(\lambda _1,\dots ,\lambda _g\) of \(\textrm{Sp}(2g)\). Denote by \(V(\lambda )\) the irreducible \(\textrm{Sp}(2g)\)-representation of highest weight \(\lambda \). In particular \(V(\lambda _1)\cong H^1(W_g)\cong H^1(W_{g,1})\). We note that one has the following decomposition into irreducible \(\textrm{Sp}(2g)\)-representations, for \(g\ge 3\).
The projection to \(V(\lambda _1)\) is obtained by the contraction of two of the three factors \(V(\lambda _1)\) with the given bilinear form. We may easily identify
by identifying \(\wedge ^3 V(\lambda _1)\) with the space of graphs with one vertex and three decorations.

We may furthermore decompose, for \(g\ge 6\),
Let \(R_{(g)}\) be the \(\textrm{Sp}(2g)\)-invariant complement of \(V(2\lambda _2)\) in \(\wedge ^2 V(\lambda _3)\). Denote by
the Lie algebra generated by \(V(\lambda _3)\) with the quadratic relations \(R_{(g)}\subset \wedge ^2 V(\lambda _3)\). We equip \({\mathfrak {t}}_{(g)}\) with a grading by assigning the generators degree 1.
Theorem 4
The inclusion \(V(\lambda _3)\cong {{\,\textrm{gr}\,}}^1\,H^0(\textsf{GC}^{\text {ex}}_{(g)})\subset H^0(\textsf{GC}^{\text {ex}}_{(g)})\) extends to a Lie algebra homomorphism
This Lie algebra homomorphism induces an isomorphism on the graded components
as soon as \(g\ge 3W\ge 6\).
To study the Chevalley-Eilenberg cohomology let us next define a graded commutative algebra \(A_{(g)}\) as the Koszul dual commutative algebra of the Lie algebra \({\mathfrak {t}}_{(g)}\). Concretely, one has a presentation
where \(V(\lambda _3)\cong V(\lambda _3)^*\) is identified with the dual space of the space of generators of \({\mathfrak {t}}_{(g)}\) and \((R_{(g)})^\perp \cong V(2\lambda _2)\) is the annihilator of \(R_{(g)}\) in \(S^2( V(\lambda _3)[-1])\cong \wedge ^2 V(\lambda _3)^*[-2]\). Note also that \(A_{(g)}\) inherits an additional grading by weight.
Theorem 5
One has a zigzag of morphism of dg commutative algebras
that induces an isomorphism in cohomology
as soon as \(g\ge 3W\ge 6\).
The Lie and commutative algebras above appear in various contexts and places in the literature. For example, in [15] it is shown that in the case \(m=1\) one has that \(\mathfrak {sp}_g < imes H^0(\textsf{GC}^{\text {ex}}_{(g)})\) is identified with a genus-g-version of the Grothendieck–Teichmüller Lie algebra. The Chevalley-Eilenberg cohomology of  appears as the cohomology of the space \(X_1(g)\) of [22, section 4.3] (for large g), that captures the major part of the cohomology of the Torelli subgroup of the boundary preserving framed diffeomorphism group of \(W_{g,1}\). Finally the Lie algebra \({\mathfrak {t}}_{(g)}\) (in our notation) can be identified with a relative Malcev completion \({\mathfrak {u}}_g\) (in Hain’s notation) of the mapping class group (for \(g\ge 6\)) as computed by Hain in [19, Theorem 7.7]. One may then reformulate a less precise version our results above as follows.
appears as the cohomology of the space \(X_1(g)\) of [22, section 4.3] (for large g), that captures the major part of the cohomology of the Torelli subgroup of the boundary preserving framed diffeomorphism group of \(W_{g,1}\). Finally the Lie algebra \({\mathfrak {t}}_{(g)}\) (in our notation) can be identified with a relative Malcev completion \({\mathfrak {u}}_g\) (in Hain’s notation) of the mapping class group (for \(g\ge 6\)) as computed by Hain in [19, Theorem 7.7]. One may then reformulate a less precise version our results above as follows.
Corollary 6
The Malcev completion \({\mathfrak {u}}_g\cong {\mathfrak {t}}_{(g)}\) of the genus g mapping class group relative to the symplectic group as computed by R. Hain in [19, Theorem 7.7] is Koszul in the limit \(g\rightarrow \infty \).
This means more precisely that the Koszulness condition for \({\mathfrak {t}}_{(g)}\) is satisfied in a range of weights that tends to \(\infty \) as \(g\rightarrow \infty \).
2 Notation and preliminaries
2.1 Notation
Unless otherwise stated all vector spaces are taken over the rationals \({\mathbb {Q}}\). We abbreviate the term differential graded by dg. We always use cohomological conventions, that is, differentials have degree \(+1\), and we use \({\mathbb {Z}}\)-gradings unless otherwise stated. For V a graded vector space we denote by V[k] the same graded vector space with degrees shifted downwards by k units. For example, if V is concentrated in degree 0, then V[k] is concentrated in degree \(-k\). To condense the notation we denote the cohomology of a manifold M by \(H(M):=H^\bullet (M)\), i.e., we omit the \(\bullet \), while we keep the notation \(H_\bullet (M)\) for the homology. The latter will however be less frequently needed.
Almost all objects we consider will be graded objects in dg vector spaces or similar categories. That is, these objects come with two gradings, the cohomological grading and an additional (“weight") grading. Concretely, we will consider two incarnations of the additional grading, namely a graded dg vector space V may be written either as a direct sum
or as a direct product
of dg sub-vector spaces \({{\,\textrm{gr}\,}}^k V \subset V\). We will call the second type of grading complete gradings. For example, the dual vector space \(V^*\) of a dg vector space with additional grading \(V=\bigoplus _k {{\,\textrm{gr}\,}}^k V\) has a complete grading
Often it is hence helpful to consider instead the graded dual dg vector space
If V is equipped with further algebraic structure, for example a dg Lie or dg commutative algebra structure, then we will say that the additional grading is compatible with that algebraic structure if the defining algebraic operations (say the Lie bracket or commutative product) restrict to morphisms of dg vector spaces
We shall consider several forms of truncations of dg objects with additional grading. For \(\alpha \) an integer, we denote by
the bigraded vector space whose part of additional degree k is concentrated in cohomological degree \(\alpha k\) and agrees with the cohomology of \({{\,\textrm{gr}\,}}^k V\) there. We define for a dg vector space the truncation
Here \(V^j\) refers to the part of V of cohomological degree j. Furthermore, for a dg vector space V with additional grading and \(\alpha \) an integer we set
We note that if V carries further algebraic structure (say a dg Lie or dg commutative algebra structure), compatible with the additional grading, then \({{\,\mathrm{\textrm{tr}}\,}}^{[\alpha ]}V\) and \(H^{[\alpha ]}(V)\) inherit that structure. Furthermore, one always has a zigzag of dg vector spaces with additional grading
given by the natural inclusion and projection. This zigzag also preserves the given algebraic structure on V if present.
Finally, we will use (co)chain homotopies for computing cohomology groups. More specifically we shall use the following convenient result.
Lemma 7
Let (V, d) be a dg vector space. Let \(h:V\rightarrow V\) be a linear map of degree \(-1\) such that \(A:= d h+h d\) is diagonalizable. Then \(\ker A\subset V\) is a dg subvector space and the inclusion is a quasi-isomorphism.
Proof
Diagonalizability of A means that V decomposes into eigenspaces \(V_\lambda \) of A,
Since \(dA=Ad\) this is in fact an isomorphism of dg vector spaces, i.e., \(dV_\lambda \subset V_\lambda \). It follows that the inclusion \(V_0=\ker A\rightarrow V\) induces an injective map on cohomology.
Define the linear map \(A'\) such that for \(v\in V_\lambda \),
Then \(dA'=A'd\) and \(\pi _0= id - A'A\) is the projector onto \(V_0\). Let \(h'=A'h\), then
Hence any cocycle \(v\in V\) is cohomologous to a cocycle in \(V_0\), namely
Hence the map on cohomology induced by the inclusion \(V_0\rightarrow V\) is also surjective. \(\quad \square \)
2.2 Representation theory of the symmetric and orthogonal groups
We use the notation
to either denote the symplectic group, or the orthogonal group associated to the non-degenerate bilinear form of signature (g, g). We understand \(\textrm{OSp}_g\) as an algebraic group over \({\mathbb {Q}}\), and we denote by \(\textrm{OSp}_g({{\mathbb {K}}})\) the \({{\mathbb {K}}}\)-points for a field \({{\mathbb {K}}}\supset {\mathbb {Q}}\). We shall recall some standard facts on the representation theory of these groups. We refer to [21, section 2] for a beautiful overview that is perfectly suited for the present paper.
Every finite dimensional representation of \(\textrm{OSp}_g\) decomposes into irreducible representations (cf. [27, Proposition 22.41]). Let \(V_g:= {\mathbb {Q}}^{2g}\) be equipped with the standard symplectic form for m odd or the standard non-degenerate symmetric form of signature (g, g) for m even. Slightly abusively, we also denote by \(V_g\) the defining representation of \(\textrm{OSp}_g\). Every finite dimensional irreducible representation of \(\textrm{OSp}_g\) is contained in a tensor product \(V_g^{\otimes n}\) for some n (see [27, Theorem 4.14]). We will say that a finite dimensional representation V of \(\textrm{OSp}_g\) is of order n if it is a subquotient of the representation \(V_g^{\otimes n}\otimes U\), for U some finite dimensional vector space, considered as a trivial representation. Equivalently, this means that in the decomposition of V into irreducibles only those irreducibles appearing in \(V_g^{\otimes n}\) are present. We say an algebraic representation V of \(\textrm{OSp}_g\) is of order \(\le n\) if it is a direct sum of representations of order \(0,1,2,\dots , n\).
Lemma 8
Let V be a representation of \(\textrm{OSp}_g\) of order n. Then \(V=0\) iff the space of invariants
vanishes.
Proof
We need to check that for V non-zero the invariant space above is non-zero.
We may pick a surjective map of representations \(\pi : V_g^{\otimes n}\otimes U\rightarrow V\). This is a non-zero element in
using that \(V_g\) is self-dual due to the presence of the non-degenerate pairing. But the presence of a the non-zero element \(\pi \) implies that the first factor in the tensor product on the right-hand side is not zero. \(\square \)
Note that we allow the zero vector space to be a (necessarily trivial) representation by convention. We will use the above Lemma in the following form.
Lemma 9
Let
be a dg vector space with a compatible action of \(\textrm{OSp}_g\). Suppose that the degree k-subspace \(C^k\) is a finite dimensional representation of order \(\le n\) (in the sense above). Then \(H^k(C)=0\) iff
for any \(M\le n\).
Proof
By the assumption \(H^k(C)\) is of order \(\le n\), and hence by the previous Lemma we need to check that
Using Schur’s Lemma one can see that taking invariants of a complex of completely reducible representations commutes with taking cohomology. Hence
and we are done. \(\square \)
Let us also remark that \(\textrm{OSp}_g({\mathbb {Q}})\subset \textrm{OSp}_g({{\mathbb {C}}})\) is Zariski dense (this can be seen from [10, Corollary 18.3]). Hence the complexification of the space of invariants of a (rational) representation V can be identified with the invariants of the complexification, so that one has isomorphisms

One may use this observation to almost always work with complex representations of the complex semisimple Lie group \(\textrm{OSp}_g({{\mathbb {C}}})\) if desired, forgoing the need to use results from algebraic group theory.
Second, we shall need the classical invariant theory for the groups \(\textrm{OSp}_g\). We directly state a version with the appropriate degree shifts appearing in our application. To this end let \(\Delta _1\in (V_g[-m]\otimes V_g[-m])^{S_2}\) be the symmetric element that is dual to the given canonical bilinear form on \(V_g\). Next consider the action of the symmetric group \(S_{2N}\) on the tensor product \(V_g[-m]^{\otimes 2N}\) by permuting factors. The action on the element \(\Delta _1^{\otimes N}\) then gives a map
This map factorizes over the cosets \(S_{2N}/(S_2\wr S_N)\) (with \(\wr \) denoting the wreath product). Furthermore, the image is obviously \(\textrm{OSp}_g\)-invariant, since so is \(\Delta _1\).
Theorem 10
(A version of the First and Second Fundamental Theorems of Classical Invariant Theory) The map
is surjective for all g, N, and an isomorphism for \(g\ge N\).
The statement can be found in the present form as [21, Theorem 2.6]. The statement for \(\textrm{Sp}(2g,{\mathbb {Q}})\) is also [24, Theorems 9.5.9, 9.5.11], going back to [31]. One also finds the analogous statement for O(2g) in [24, Theorems 9.5.2, 9.5.5], from which the statement for O(g, g) may be obtained via complexification.
2.3 Bar and cobar construction and Koszul duality for Lie and commutative algebras
The bar and cobar construction form a pair of adjoint functors between the category of augmented algebras over a Koszul operad \({\mathcal {P}}\), and the category of conilpotent coaugmented dg coalgebras over the Koszul dual cooperad, see [25, chapter 11]. We shall only need the case where \({\mathcal {P}}\) is either the operad \(\textsf{Lie}\) governing Lie algebras or the operad \(\textsf{Com}\) governing (non-unital, or equivalently augmented unital) commutative algebras, with the Koszul dual cooperads those governing cocommutative or Lie coalgebras. In this case we have adjoint pairs
between the category of dg Lie algebras (resp. augmented dg commutative algebras) on the left-hand side and the category of conilpotent coaugmented dg cocommutative coalgebras (resp. conilpotent dg Lie coalgebras) on the right-hand side. Concretely, one has that for a dg Lie algebra \({\mathfrak {g}}\)
is the free cocommutative coalgebra cogenerated by \({\mathfrak {g}}[1]\), with the Chevalley-Eilenberg differential. Similarly, for a coaugmented dg cocommutative coalgebra C one has that
is the free Lie algebra generated by the degree shifted coaugmentation coideal \({{\bar{C}}}\), equipped with the Harrison differential. The other two cases are obtained by swapping the role of \(\textsf{Com}\) and \(\textsf{Lie}\). If no confusion can arise we will often omit the subscript of the bar/cobar functors and just write \(\texttt{B}A\) which shall mean \(\texttt{B}_{\textsf{Lie}} A\) if A is a dg Lie algebra and \(\texttt{B}_\textsf{Com}A\) if A is an augmented dg commutative algebra.
It is known that the adjunction units and counits \(\texttt{B}^c\texttt{B}A\rightarrow A\) and \(C\rightarrow \texttt{B}\texttt{B}^c C\) are quasi-isomorphisms, see [34, Proposition 2.5 and Theorem 2.6]. Furthermore, the functor \(\texttt{B}\) sends quasi-isomorphisms to quasi-isomorphisms [25, Proposition 11.2.7]. The functor \(\texttt{B}^c\) does not preserve quasi-isomorphisms in general. However, it does preserve quasi-isomorphisms in most "good cases". For example if, as in all relevant cases for us, the quasi-isomorphism preserves an additional grading, and domain and codomain are degree-wise finite-dimensional, then \(\texttt{B}^c X\cong (\texttt{B}X^c)^c\), so that one can use that \(\texttt{B}\) preserves quasi-isomorphisms.
Next we consider a (non-differential) graded Lie algebra \({\mathfrak {g}}\) defined by a homogeneous quadratic presentation
with the generating graded vector space V, the space of relations
and \(\langle R\rangle \) the ideal generated by R. Such a graded Lie algebra automatically has an additional grading by the number of generators, i.e., we declare any k-ary bracket of generators to live in additional degree k. This grading is then inherited by the bar construction \(\texttt{B}{\mathfrak {g}}\).
For simplicity, and since this is true in all our cases, we assume that the generators V are concentrated in the single cohomological degree \(\alpha \). Then \({{\,\textrm{gr}\,}}^W {\mathfrak {g}}\) is concentrated in degree \(\alpha W\). Furthermore \({{\,\textrm{gr}\,}}^W\texttt{B}{\mathfrak {g}}\) is concentrated in cohomological degrees
In particular, one has a map of dg cocommutative coalgebras
using the notation of Sect. 2.1. The graded cocommutative coalgebra \(C=H^{[\alpha -1]}(\texttt{B}{\mathfrak {g}})\) is called the Koszul dual of \({\mathfrak {g}}\). Looking at the definition of the bar construction, C also has a homogeneous quadratic presentation, with the space of cogenerators V[1], and the space of quadratic corelations given by the annihilator \(R^\perp \) of R. We also consider the graded dual dg commutative algebra \(C^c\), and call it the Koszul dual dg commutative algebra of \({\mathfrak {g}}\). It then has the quadratic presentation
The same reasoning applies also if we invert the roles of the commutative and Lie operads.
We will usually consider only finite dimensional spaces of generators V. In this case the relation of being the Koszul dual is clearly reflexive, that is, the Koszul dual of \(C^c\) above is again \({\mathfrak {g}}\).
Definition 11
Let \({\mathfrak {g}}={\mathbb {F}}_\textsf{Lie}(V)/\langle R \rangle \) be a graded Lie algebra with space of generators V concentrated in cohomological degree \(\alpha \) and the homogeneous quadratic space of relations R. Then we say that \({\mathfrak {g}}\) is Koszul if the canonical map from the Koszul dual cocommutative coalgebra
is a quasi-isomorphism.
Likewise, a commutative algebra \(A={\mathbb {F}}_\textsf{Com}(V)/\langle R \rangle \) given by a homogeneous quadratic presentation with V concentrated in cohomological degree \(\alpha \) is Koszul if the canonical morphism of dg Lie coalgebras
from the Koszul dual graded Lie coalgebra \({\mathfrak {c}}\) is a quasi-isomorphism.
Note that, trivially, if \({\mathfrak {g}}\) is Koszul then \(\texttt{B}{\mathfrak {g}}\) is formal as a dg cocommutative coalgebra.
Lemma 12
Let \({\mathfrak {g}}={\mathbb {F}}_\textsf{Lie}(V)/\langle R \rangle \) be a quadratically presented Lie algebra as above, with V finite dimensional, and \(A={\mathbb {F}}_{\textsf{Com}}(V^*[-1])/\langle R^\perp \rangle \) the Koszul dual graded commutative algebra. Then the following are equivalent:
-
\({\mathfrak {g}}\) is Koszul.
-
A is Koszul.
Proof
We only show one direction, the other follows by symmetry. Koszulness of \({\mathfrak {g}}\) means that
is a quasi-isomorphism. Taking graded duals \((-)^c\) on both sides and using the finite dimensionality of V this is equivalent to
being a quasi-isomorphism. Taking the bar construction, and using that the bar construction preserves quasi-isomorphisms, we find that
is a quasi-isomorphism. But hence so is the composition
so that A is Koszul. \(\square \)
In the case that A is the Koszul dual of \({\mathfrak {g}}\) and either (and hence both of) \({\mathfrak {g}}\) and A are Koszul, we will call \(({\mathfrak {g}},A)\) a Koszul pair.
We will encounter Koszul objects in the following form, except for the additional complication that quasi-isomorphisms only hold in a range of additional degrees. (See also Proposition 41 below.)
Proposition 13
Suppose that \({\mathfrak {g}}\) is a dg Lie algebra with an additional positive grading with the property that there is an \(\alpha \) such that \({{\,\textrm{gr}\,}}^W H({\mathfrak {g}})\) is concentrated in cohomological degree \(\alpha W\) for any W. Then \({\mathfrak {g}}\) is formal.
Suppose in addition that the cohomology \({{\,\textrm{gr}\,}}^W H(\texttt{B}{\mathfrak {g}})\) of the graded pieces of the bar construction is concentrated in degree \((\alpha -1)W\) for any W, and that the \({{\,\textrm{gr}\,}}^W {\mathfrak {g}}\) are finite dimensional. Then \(H({\mathfrak {g}})\) is Koszul with Koszul dual graded commutative algebra \(A:=H(\texttt{B}{\mathfrak {g}})^c\). Furthermore, A and \(H({\mathfrak {g}})\) have quadratic presentations of the form
Proof
For the first statement note that under the assumptions the zigzag
realizes the formality.
For the second statement, we can show in exactly the same way that \((\texttt{B}{\mathfrak {g}})^c\) is formal as a dg commutative algebra. Hence we find that
is connected by a zig-zag of quasi-isomorphisms to the cobar construction of \(\texttt{B}^c A^c\), and all arrows preserve the additional grading. By assumption \({{\,\textrm{gr}\,}}^W A^c\) is concentrated in degree \((\alpha -1)W\), and by the assumption that the additional grading is positive (i.e., \(W\ge 1\)) one has that \({{\,\textrm{gr}\,}}^W\texttt{B}^c A^c\) is concentrated in cohomological degrees \((\alpha -1)W,\dots ,\alpha W\). But \({{\,\textrm{gr}\,}}^W H({\mathfrak {g}})\) is concentrated in degree \(\alpha W\) and hence must be identified with the top piece of the cohomology of \({{\,\textrm{gr}\,}}^W\texttt{B}^c A^c\). But this top piece is (by the definition of the cobar construction) the graded Lie algebra generated by \({{\,\textrm{gr}\,}}^1 {{\bar{A}}}^c[-1]\cong {{\,\textrm{gr}\,}}^1\,H({\mathfrak {g}})\), with relations being the image of \({{\,\textrm{gr}\,}}^2 {{\bar{A}}}^c\) under the coproduct
We may proceed in the same manner for A and see that A is connected to \(\texttt{B}^cH({\mathfrak {g}})^c\) by a zigzag of quasi-isomorphisms preserving the additional gradings
and that A also has a quadratic presentation as indicated. This also shows that A is generated by \({{\,\textrm{gr}\,}}^1 A\), so that in particular the map (6) is injective. (...and likewise the analogous map realizing \({{\,\textrm{gr}\,}}^2 H({\mathfrak {g}})^c\) as the space of generators for the presentation of A.)
Finally, Koszulness of \(H({\mathfrak {g}})\) means that \({{\,\textrm{gr}\,}}^W H(\texttt{B}H({\mathfrak {g}}))\) is concentrated in degree \((\alpha -1)W\), and that follows from the fact that \(\texttt{B}H({\mathfrak {g}})\) is quasi-isomorphic to \(A^c\) as seen above, and the assumption on A. \(\square \)
Remark 1
The material in this section is standard, and can be found in the literature in some form. A general account of Koszul duality for algebras over operads can be found in [5, 17, 26], and for the special case of Koszul duality of commutative and Lie algebras we also refer to [7].
More classically, one considers Koszul duality for associative algebras instead of commutative and Lie algebras. Concretely, one may just replace \(\textsf{Com}\) and \(\textsf{Lie}\) above by the associative operad \(\textsf{Assoc}\) to recover the standard notion of Koszulness of associative algebras. Furthermore, if a commutative algebra A with a homogenous quadratic presentation (and say degree-wise finite dimensional) is Koszul in our sense then it is Koszul as an associative algebra. To see this, note that the associative cobar construction and the commutative cobar construction are related by the universal enveloping algebra construction U, i.e., \(\texttt{B}_{\textsf{Assoc}}^c A^c = U(\texttt{B}_{\textsf{Com}}^c A^c)\). Furthermore, \(U(-)\) preserves quasi-isomorphisms and the grading. (Since on the level of complexes U is just the symmetric product by the Poincaré-Birkhoff-Witt Theorem.) Hence \({{\,\textrm{gr}\,}}^W H(\texttt{B}_{\textsf{Assoc}}^c A^c)\) is concentrated in degree \((1-\alpha )W\) iff so is \({{\,\textrm{gr}\,}}^W H(\texttt{B}_{\textsf{Com}}^c A^c)\).
2.4 Remarks on the cobar construction, and Lie algebra actions
For later use we shall note that a dg Lie (co)algebra is completely determined by its (co)bar construction. Concretely, let \({\mathfrak {c}}\) be a dg Lie coalgebra with differential \(d_{\mathfrak {c}}\) and cobracket \(\Delta :{\mathfrak {c}}\rightarrow \Lambda ^2 {\mathfrak {c}}\). The cobar construction \(\texttt{B}^c{\mathfrak {c}}=S({\mathfrak {c}}[-1])\) is a free graded commutative algebra. For \(x\in {\mathfrak {c}}\) let \({\textbf{s}}x\in {\mathfrak {c}}[-1]\) denote the same element in \({\mathfrak {c}}[-1]\), and let
be the natural isomorphism between the exterior square of \({\mathfrak {g}}\) and the symmetric square of \({\mathfrak {g}}[-1]\). Then the differential d on \(\texttt{B}^c{\mathfrak {c}}\) may be defined as the unique graded commutative algebra derivation such that for \(x\in {\mathfrak {c}}\)
The identity \(d^2=0\) is then equivalent to the co-Jacobi identity for the Lie cobracket and the identites
Conversely, suppose we are given some derivation D of degree \(+1\) on the free graded commutative algebra \(S({\mathfrak {c}}[-1])\) such that \(D^2=0\). Suppose furthermore that the image of a generator under D has only linear and quadratic terms. Then, the linear term uniquely defines a differential \(d_D\) on \({\mathfrak {c}}\), and the quadratic term defines a cobracket \(\Delta _D\), such that \((S({\mathfrak {c}}[-1]),D)\) is the cobar construction of \(({\mathfrak {c}},d_D,\Delta _D)\) as above. The identity \(D^2=0\) ensures that \(\Delta _D\) satisfies the co-Jacobi identity and the compatitibilty relations (7) hold. In practice, this trick will later allow us to define a dg Lie coalgebra structure by defining only one operation D and verifying only one identity \(D^2=0\), instead of three.
Next, we will use that the dual Lie algebra \({\mathfrak {c}}^*\) acts on the bar construction, and can in particular be used to twist the differential. We shall however provide an elementary description of this twisting procedure, on the commutative algebra \(\texttt{B}^c{\mathfrak {c}}=S({\mathfrak {c}}[-1])\). To this end, let \(\xi \in ({\mathfrak {c}}[-1])^*\) and split the differential d on the cobar construction \(\texttt{B}^c{\mathfrak {c}}\) into its linear and quadratic part, \(d=d_1+d_2\). Extend \(\xi \) to a derivation of \(S({\mathfrak {c}}[-1])\), which we denote by the same letter. Then we define the action of \(\xi \) on \(S({\mathfrak {c}}[-1])\) to the derivation given by the commutator
Lemma 14
For \(\xi ,\nu \in ({\mathfrak {c}}[-1])^*\) one has that
In particular, if \(\xi \) is of degree 0, then one has
Proof
The equation \(d^2=0\) implies \(d_1^2=[d_1,d_2]=d_2^2=0\), from which all equations follow by elementary formula manipulation. \(\square \)
In particular, if \(\xi \) satisfies the Maurer-Cartan equation
then \((d+L_\xi )^2=0\), and one calls \(d+L_\xi \) the twisted differential.
3 Graph complexes
In this section we shall introduce the various graph complexes we consider. All of these complexes, or at least close variants thereof, have appeared in the literature before [11, 15, 20]. However, since the conventions differ, and since some results are scattered, we shall present here a relatively detailed construction, including several standard computations for graph complexes.
We note that the signs and prefactors in graph complexes are to a large extent conventional, and might differ from definitions elsewhere, even though the resulting complexes are isomorphic. Outside of this section, signs and prefactors will not be important for any argument, beyond the fact that there is a consistent choice, rendering the graph complexes well-defined.
3.1 Definitions of the fundamental graph complex \(\textsf{fG}_{V,2m}\)
We say that a (directed) graph with n vertices and k edges is an ordered set of k pairs (i, j) of numbers \(i,j\in \{1,\dots ,n\}\). We say that these k elements are the edges of the graph, with the edge (i, j) pointing from vertex i to vertex j. At this point we allow arbitrary sets of edges, in particular tadpoles (or short cycles), that is edges of the form (i, i), and we do not ask that the graph is connected. We denote the set of such graphs with n vertices and k edges by \( gra _{n,k}\). This set carries an action of the group \(S_n\times (S_2 \wr S_k)\), with \(S_n\) acting by renumbering vertices, \(S_k\) by reordering edges and the \(S_2\) by changing the directions of the edges, i.e., by flipping the two members of the pairs.
Let furthermore V be any finite dimensional graded vector space and m an integer. We then define a graded vector space of coinvariants
Here the group \(S_n\) acts diagonally on the vector space \({\mathbb {Q}} gra _{n,k}\) generated by the set \( gra _{n,k}\) and the n symmetric product factors S(V), and \(S_k\) acts diagonally on \({\mathbb {Q}} gra _{n,k}\) and by permuting the factors \({\mathbb {Q}}[1-2m]\), with appropriate Koszul signs. We may interpret elements of \(\textsf{fG}_{V,2m}\) as linear combinations of isomorphism classes of graphs, each of whose vertices j is decorated by one element \(p_j\in S(V)\). It is furthermore natural and advantageous to think of each factor V in the symmetric product as contributing one decoration. In particular, if a vertex is decorated by the unit \(1\in S(V)\) then we intepret this is no decoration (in V). Generally, if vertex j is decorated by \(p_j=\alpha _1\cdots \alpha _r\in S^r(V)\), then we think of this vertex as carrying r decorations in V. In pictures, we also use this combinatorial interpretation, that is:

We say that the valence of a vertex in a graph is the number of incident half-edges, plus the number of decorations in V. For example, a vertex with 3 incident half-edges and decoration in \(S^2(V)\) has valence 5. Note also that we include the empty graph as the single element of \( gra _{0,0}\) by convention.
We define on \(\textsf{fG}_{V,2m}\) a differential \(d_c'\) as follows. Let \(\Gamma \in \textsf{fG}_{V,2m}\) be a graph with an ordered list of k edges and with n vertices. Mind that elements of \(\textsf{fG}_{V,2m}\) are in fact equivalence classes of linear combinations of graphs with additional tensor factors, and “... a graph \(\Gamma \in \textsf{fG}_{V,2m}\)" shall mean that we take a representative of an equivalence class with only one term. We then set
with the graph \(\Gamma /(j)\) obtained by contracting the j-th edge. Specifically, if the j-th edge is \(e_j=(u,v)\) between vertices u and v the graph \(\Gamma /(j)\) is defined as follows:
-
1.
If \(u=v\) the edge is a tadpole and we define \(\Gamma /(j)=0\). Otherwise we may assume without loss of generality that \(u<v\), due to having taken \(S_2\)-coinvariants.
-
2.
Then remove the edge \(e_j\) and replace all occurrences of “v” by u in the list of edges, i.e., merge vertices u and v. We renumber the vertices again by \(1,2,\dots ,n-1\) and order the edges, preserving the original order.
-
3.
Finally we alter the decorations by multiplying the decorations corresponding to u and v in S(V). That is, we apply the natural map
$$\begin{aligned}{} & {} S(V)^{\otimes n}\rightarrow S(V)^{\otimes n-1} \\{} & {} A_1\otimes \cdots \otimes A_u\otimes \cdots \otimes A_v \otimes \cdots \otimes A_n \mapsto (-1)^{|A_v|(|A_{u+1}|+\cdots + |A_{v-1}|)}\\{} & {} A_1\otimes \cdots \otimes A_uA_v\otimes \cdots \otimes {{\hat{A}}}_v \otimes \cdots \otimes A_n \end{aligned}$$on the decorations.
It is an elementary exercise to check that for \(1\le i<j\le n\) we have
From this we easily compute that
Next we assume that we have an element (the “diagonal") of degree 2m
with 1 a symbol that we shall interpret as the unit in S(V).Footnote 1
We then define a second differential \(d_{cut}\) such that
where the sum is again over edges and \(\textrm{cut}(\Gamma ,j)\) is defined as follows:
-
(1)
We again assume that the j-th edge is (u, v) with \(u\le v\). Then we remove the edge (u, v) from the graph, preserving the relative ordering of the other edges.
-
(2)
Furthemore, we multiply \(\Delta \) from the left into the decorations \(S(V)^{\otimes n}\), at positions u and v of the tensor product. To make this precise, including the signs, let us write \(\Delta =\sum _\alpha \Delta _\alpha ' \otimes \Delta _\alpha ''\in S(V)\otimes S(V)\). Then if the decorations on \(\Gamma \) are \(A_1\otimes \cdots \otimes A_n\in S(V)^{\otimes n}\), then the decorations on \(\textrm{cut}(\Gamma ,j)\) are defined to be
$$\begin{aligned}{} & {} \sum _\alpha (-1)^{ (|A_1|+\cdots +|A_{u-1}|)|\Delta _\alpha '| + (|A_1|+\cdots +|A_{v-1}|)|\Delta _\alpha ''| }\\{} & {} \quad A_1\otimes \cdots \otimes \Delta _\alpha 'A_u \otimes \cdots \otimes \Delta _\alpha ''A_v \otimes \cdots \otimes A_n\in S(V)^{\otimes n}, \end{aligned}$$taking into account the appropriate Koszul signs.
One then checks that for \(1\le i<j\le n\)
Analogously to (9) one then computes that \(d_{cut}^2=0\), and furthermore
Hence also \((-d_c'+d_{cut})^2=0\).
3.2 Algebra structure, and twist of the differential
We also note that \(\textsf{fG}_{V,2m}\) is naturally a graded commutative algebra, with the product given by disjoint union of graphs. Since the differentials act by derivations, we have that \((\textsf{fG}_{V,2m},-d_c'+d_{cut})\) is a dg commutative algebra. Furthermore, since every graph decomposes uniquely into connected components,
is the free graded commutative algebra generated by the subspace \({\textsf{G}}_{V,2m}\subset \textsf{fG}_{V,2m}\) spanned by the non-empty connected graphs. Since our differential \(-d_c'+d_{cut}\) changes the number of connected components by zero or one, it defines a dg Lie coalgebra structure on \({\textsf{G}}_{V,2m}[1]\), see Sect. 2.4. Concretely, let us split
into a part \(d_{cut}'\) that leaves the number of connected components invariant and one part \(d_{cut}''\) that increases that number by one. Then, \(-d_c'+d_{cut}'\) determines the internal differential on the Lie coalgebra \({\textsf{G}}_{V,2m}\), and \(d_{cut}''\) the cobracket.
We now specialize further to the situation at hand and let \(V={{\bar{H}}}^\bullet (W_{g})\), and \(\Delta \in S^2(H^\bullet (W_{g}))\) be the canonical diagonal element. More precisely, an orientation on \(W_g\) defines a canonical map
that we extend to a map \(\epsilon :H(W_g)\rightarrow {\mathbb {Q}}\) of degree \(-2m\). Then \(\Delta =\sum _\alpha \Delta _i'\otimes \Delta _i''\) is uniquely determined by the property that for any homogeneous \(\alpha ,\beta \in H(W_g)\)
To be concrete we may fix basis elements
such that \(\epsilon (\omega )=1\) and \(a_ib_j=\delta _{ij}\omega \). Then
We note that \(\epsilon \) also defines a map
by precomposition with the cup product, that we denote by the same letter.
We need a final piece to the differential, which we obtain by twisting as in Sect. 2.4. To this end define two derivations
such that for a connected graph \(\Gamma \in {\textsf{G}}_{{{\bar{H}}}(W_g),2\,m}\) we have

In particular, \(\lambda \) and \(\mu \) are zero on all connected graphs with more than one vertex. The degree of \(\lambda \) is zero, that of \(\mu \) is \(+1\).
Then we define the operation \(d_{mul}\) (the third and final part of the differential) as
We furthermore consider the degree 1 derivation
on \(\textsf{fG}_{V,2m}\). We would like to make d into a differential, but unfortunately, by Lemma 14 we have that
The defect X can be evaluated as follows:
Lemma 15
The derivation X as above is equal to \((2+(-1)^m 2g)\mu \).
Proof
Since X and \(\mu \) are derivations it is sufficient to show that \(X(\Gamma ) =(2+(-1)^m 2g)\mu (\Gamma )\) for each connected graph \(\Gamma \in {\textsf{G}}_{{{\bar{H}}}(W_g),2m}\). Since \(\lambda \) maps connected graphs to scalars we have
Suppose first that  is the graph with one undecorated (i.e., decorated by 1) vertex and one tadpole edge. Then \(d_c'\Gamma =d_{cut}''\Gamma =0\) and
is the graph with one undecorated (i.e., decorated by 1) vertex and one tadpole edge. Then \(d_c'\Gamma =d_{cut}''\Gamma =0\) and
We hence only need to check that for all other connected graphs \(X(\Gamma ) =0\). Since \(\lambda \) is zero on graphs with more than one vertex or with an edge, and since \(d_c'\) (resp. \(d_{mul}\)) decrease the number of vertices by one and edges by one (respectively vertices by zero and edges by one), \(X(\Gamma ) =0\) if \(\Gamma \) has more than two vertices, or two vertices and more than one edge, or one vertex and no edge. If \(\Gamma \) has exactly one edge and one vertex with a decoration of positive degree, then \(X(\Gamma ) =0\) by degree reasons already. That leaves only the case of \(\Gamma \) of the form

with \(A,B\in S({{\bar{H}}}(W_g))\). We then have

and hence
On the other hand

And hence
Hence the Lemma is shown. \(\square \)
To go further, it is helpful to consider the combinatorial form of \(d_{mul}=[\lambda ,d_{cut}'']\) and the defect \([\mu , d_{cut}'']\). In each case \(d_{cut}''\) cuts a connected graph into two connected components, and then \(\lambda \) (or \(\mu \)) picks up one of them. In the case of \(\lambda \) this connected component must be an isolated vertex to produce a non-zero result.

We also note that the expression \(\sum _i \epsilon (\Delta _i'A)\Delta _i''\) equals the image of A under the cup product map \(S({{\bar{H}}}(W_g))\rightarrow H(W_g)\), as follows from the defining relation of the diagonal (10)
Hence \(d_{mul}\) acts via the formula
with the sum being over vertices with a single attached edge, which is the \(j_v\)-th in the ordering, and \(mul(\Gamma ,v)\) is obtained by the following procedure:
-
Replace the decorations of v in \({{\bar{H}}}(W_g)\) by their cup product in \({{\bar{H}}}(W_g)\).
-
Contract the edge adjacent to v as in the definition of \(d_c'\).
Note that by degree reasons we obtain a nonzero contribution only if v has at most two decorations. We shall furthermore split
with \(d_{mul}'\) containing the contributions for which v has 0 or 1 decorations, and \(d_{mul}''\) those for which v has two decorations. Note that the term \(d_{mul}'\) is identical to some summands of the contraction differential \(d_c'\), while \(d_{mul}''\) creates at least one \(\omega \)-decoration.
Similarly, the operation \(d^2= (2-(-1)^m2g)[\mu , d_{cut}'']\) acts on a graph \(\Gamma \) by summing over all tadpoles with a single adjacent edge, and replacing the tadpole by an \(\omega \)-decoration, multiplied by \(2+(-1)^m 2g\). Pictorially:

We may then obtain from \(\textsf{fG}_{V,2m}\) a complex on which \(d^2=0\) in one of three ways.
-
We define the quotient

by dividing by the ideal formed by graphs that contain an \(\omega \)-decoration, or a vertex of valence \(\le 2\). On this quotient \(d^2=0\) since \(d^2\) creates one \(\omega \)-decoration.
-
We define the subcomplex

that furthermore contains no tadpoles.
-
We define the subquotient of \(\textsf{fG}_{V,2m}\)
$$\begin{aligned} \textsf{fG}_{(g)} \end{aligned}$$by taking the subcomplex containing no tadpoles, and quotienting by the graphs that contain at least one vertex of valence \(\le 2\).
Lemma 16
The above subquotients of \((\textsf{fG}_{V,2m},d)\) are well-defined and in particular the differential squares to zero on these subquotients.
Proof
We first claim that I as in the definition is closed under d, that is, \(dI\subset I\). (It is clear that I is an ideal.) First we note that the differential d cannot remove a decoration by \(\omega \) on a graph in \(\textsf{fG}_{V,2m}\). We then have to check that the differential d cannot remove vertices of valence \(\le 2\). Since d acts “locally” on only two vertices, it is clear that for a graph \(\Gamma \) with three or more vertices of valence \(\le 2\), \(d\Gamma \) contains no graphs that have no vertices of valence \(\le 2\). Furthermore, if \(\Gamma \) contains exactly two vertices of valence \(\le 2\) then in the worst case the differential can contract an edge between them, and hence still produce a vertex of valence \(\le 2\). So we are left with the case that \(\Gamma \) contains a unique vertex v of valence \(\le 2\), and we need to consider the parts of d affecting v. The piece \(d_{cut}\) cannot increase the valence of vertices anyway. But the terms of the piece \(d_c'\) that would remove a single vertex v of valence \(\le 2\) are cancelled by the contribution \(d_{mul}'\) since \(d_c'\) and \(d_{mul}\) enter the differential with opposite signs. Hence we conclude that \(dI\subset I\) as desired. Furthermore, since \(d^2\) creates an \(\omega \)-decoration, we have that \(d^2\Gamma \subset I\) for all \(\Gamma \in \textsf{fG}_{V,2m}\), and hence  is a well defined dg vector space.
is a well defined dg vector space.
Next, the differential can clearly not create tadpoles: The only piece that potentially could is the contraction part \(d_c'\) acting on an edge of a double edge. But graphs with multiple edges have odd symmetries by permuting these edges, and hence are zero. Hence no tadpoles can be created by the differential and  is indeed a subcomplex.
is indeed a subcomplex.
For \(\textsf{fG}_{(g)}\) one notes that if a graph \(\Gamma \) has no tadpole, then \(d^2\Gamma =0\). So the subspace of \(\textsf{fG}_{V,2m}\) spanned by graphs without tadpoles is a complex. One then shows in the same way as above that the quotient by the subspace spanned by graphs with vertices of valence \(\le 2\) is well-defined, to see that \(\textsf{fG}_{(g)}\) is a well-defined dg vector space. \(\square \)
For later use we shall also define
thus removing the pieces from \(d_c'\) that are cancelled by \(d_{mul}'\).
Suppose that \(\Gamma \) is a graph in one of the three graph complexes \(\textsf{fG}_{(g),1}\),  or \(\textsf{fG}_{(g)}\) above, with e edges, v vertices and a total decoration degree mD. (In other words, \(\Gamma \) has D decorations if we count the top class \(\omega \) as two decorations.) Then the cohomological degree of \(\Gamma \) is
or \(\textsf{fG}_{(g)}\) above, with e edges, v vertices and a total decoration degree mD. (In other words, \(\Gamma \) has D decorations if we count the top class \(\omega \) as two decorations.) Then the cohomological degree of \(\Gamma \) is
We furthermore define the weight of \(\Gamma \) as
The weight is preserved by the differential, and hence the graph complexes split into a direct sum of pieces of fixed weight.
All three graph complexes are equipped with a commutative product by taking disjoint union of graphs. This product is compatible with the differential and the weight grading, since the weight is additive. Furthermore, any graph splits uniquely as a union of connected graphs. It follows that our three graph complexes above are quasi-free as (non-unital) graded commutative algebras, so that we can write

Here we denoted by \({\textsf{G}}_{(g),1}[-1]\subset \textsf{fG}_{(g),1}\) the subcomplex spanned by connected graphs, and similarly for the other complexes. Since the differential is compatible with the commutative algebra structure (i.e., a derivation) in each case, it endows the degree shifted connected parts \({\textsf{G}}_{(g),1}\),  and \({\textsf{G}}_{(g)}\) with dg Lie coalgebra structures as in Sect. 2.4.
and \({\textsf{G}}_{(g)}\) with dg Lie coalgebra structures as in Sect. 2.4.
3.3 Dual graph complexes
The dual spaces of graph complexes can themselves be understood as graph complexes as well. For example, from (8) one sees that
This graded vector space is similar to \(\textsf{fG}_{V^*,2m}\), but note that the cohomological degrees are inverted and direct products replace direct sums. We shall hence think of elements \((\textsf{fG}_{V,2m})^*\) as formal series of graphs with decorations in \(V^*\). The adjoint of the differential on \(\textsf{fG}_{V,2m}\) yields a differential on \((\textsf{fG}_{V,2m})^*\). This dual differential also has a pretty combinatorial description, see also the discussion in the introduction. To derive this description it is convenient to fix a basis \(B=\{e_1,\dots ,e_N\}\) of V. Then elements of \(\textsf{fG}_{V,2m}\) can be understood as linear combinations of graphs with decorations in the set B. The graphs come with an ordering of the set of edges and decorations, and we identify two such orderings up to sign. We furthermore identify isomorphic graphs up to sign, an isomorphism being a bijection on the sets of vertices, half-edges and decorations, preserving all incidence relations. A basis of \(\textsf{fG}_{V,2m}\) is then given by chosing one B-decorated graph in each isomorphism class, with some ordering of edges and decorations.
Dually, generators of \(\textsf{fG}_{V,2m}^*\) can be seen as graphs with decorations in the dual basis \(B^*=\{e_1^*,\dots ,e_N^*\}\), also with an ordering of the sets of edges and decorations. More precisely, let \(\Gamma ^*\) be such a \(B^*\)-decorated graph. Then we associate to it the linear map \(\textsf{fG}_{V,2m}\rightarrow {\mathbb {Q}}\) that sends a basis element (B-decorated graph) \(\Gamma \in \textsf{fG}_{V,2m}\) to the rational number
Here the sum is over all bijective maps of graphs \(\Gamma ^*\rightarrow \Gamma \), i.e., all bijections of the sets of vertices, half-edges and decorations preserving the incidence relations, that send each decoration \(e_j^*\) to \(e_j\). We shall call such bijections isomorphisms, slightly abusing the term. The sign \({{\,\textrm{sgn}\,}}(f)\) is the sign of the permutation that relates the given ordering of edges and decorations on \(\Gamma \) with the one pushed forward from \(\Gamma ^*\) via f. Formulated differently, \(\Gamma ^*(\Gamma )\) is zero if the graphs are not isomorphic, and otherwise \(is \pm the\) order of the automorphism group of \(\Gamma \).
Next, one can derive the combinatorial form of the dual differential. For v a vertex of \(\Gamma ^*\) let \(\textrm{Splits}(\Gamma ,v)\) the set of partitions of the sets of half-edges and decorations incident at v into two disjoint subsets. For \(S\in \textrm{Splits}(\Gamma ,v)\) such a partition let \(\textrm{split}(\Gamma ^*,v,S)\) be the graph formed by replacing vertex v by two vertices v and \(v+1\), connected by one new edge, and reconneting the previous half-edges and decorations at v to v and \(v+1\) according to the partition S. The newly added edge becomes the first in the ordering of edges. Then we define
and
with the sum running over all vertices v of \(\Gamma \).
Lemma 17
The operation \(\delta _{split}'\) is the dual of the edge contraction differential \(d_c'\), that is, for \(\Gamma ,\Gamma ^*\) as above we have
Proof
Inserting the definitions:
with the sum over j running over the indices of edges of \(\Gamma \). Similarly,
Let \((v, S\in \textrm{Splits}(\Gamma ^*,v), g: \textrm{split}(\Gamma ^*, v, S) \xrightarrow {\sim } \Gamma )\) be a tuple occurring in the summation in (15). To it we associate a tuple \((j, f: \Gamma ^* \xrightarrow {\sim } \Gamma /(j))\) occurring in the summation in (14) by taking for j the (index of the) image under g of the edge produced by the splitting, and for f the isomorphism naturally induced by g. This association is 2:1, in that from the tuple (j, f) the tuple (v, S, g) may be uniquely recovered, up to the ordering of the two subsets of the partition S. Furthermore, we have that \({{\,\textrm{sgn}\,}}(g)=(-1)^{j+1}{{\,\textrm{sgn}\,}}(f)\), since the permutations on edges and odd decorations induced by f and g are the same, except that g sends the edge created by splitting from the first to the j-th position, introducing the sign \((-1)^{j+1}\). \(\square \)
In this paper, we shall mostly be interested in the smaller dual graph complexes (cf. (12))

All three of these carry dg Lie algebra structures, since they are duals of dg Lie coalgebras. We denote the differential by
with \(\delta _Z:=0\) for \(\textsf{GC}_{(g),1}\) and  .
.
As explained above the dual graph complexes above may also be thought of as generated by graphs but in this case decorated by elements of \(({{\bar{H}}}(W_g))^*\cong {{\bar{H}}}_\bullet (W_g)\) in place of \({{\bar{H}}}(W_g):= {{\bar{H}}}^\bullet (W_g)\). The different pieces of the differential then have combinatorial interpretations as explained in the introduction. The verification that the given combinatorial formulas indeed yield the dual operators is similar to the argument for the base case, Lemma 17, and is left to the reader.
Let us also record that the cohomological degree of a graph \(\Gamma \) in \(\textsf{GC}_{(g),1}\),  or \(\textsf{GC}_{(g)}\) with v vertices, e edges and total (homological) degree of dcorations mD is computed by the formula
or \(\textsf{GC}_{(g)}\) with v vertices, e edges and total (homological) degree of dcorations mD is computed by the formula
3.4 Action of the orthogonal or symplectic group
All graph complexes considered carry a natural action of the orthogonal or symplectic group \(\textrm{OSp}_g\) of linear endomorphisms of \(V_g:= H^m(W_{g,1})= H^m(W_{g})\) that preserve the natural pairing on \(V_g\). The action is by transforming the decorations in \({{\bar{H}}}(W_{g,1})\) on vertices of graphs. Accordingly, one has an action of the Lie algebra of \(\textrm{OSp}_g\), that we denote by \(\mathfrak {osp}_g^0\).
In the case of the graph complexes \(\textsf{fG}_{(g)}\), \({\textsf{G}}_{(g)}\) and \(\textsf{GC}_{(g)}\) the action of \(\mathfrak {osp}_g^0\) may be enlarged to an action of a graded Lie algebra
of graded endomorphisms of \(H(W_g):=H^\bullet (W_g)\) that preserve the pairing and kill the unit element \(1\in H^0(W_g)\). To be specific, any element \(\mathfrak {osp}_g^{nil}\) is an endomorphism
defined for \(c\in H^m(W_g)\) such that
Here \(\omega \) is again the cohomology class represented by the unit volume form on \(W_g\). The endomorphisms \(\phi _c\) preserve the Poincaré-duality pairing in the sense that
for any homogeneous \(x,y\in H(W_g)\). As an \(\textrm{OSp}_g\)- (and \(\mathfrak {osp}_g\)-)representation \(\mathfrak {osp}_g^{nil}\) is equivalent to the 2g-dimensional defining representation, concentrated in cohomological degree \(-m\). Furthermore, by degree reasons \(\mathfrak {osp}_g^{nil}\subset \mathfrak {osp}_g\) is an abelian Lie subalgebra, i.e, the commutators \([\phi _c,\phi _d]=0\) vanish.
We let \(\mathfrak {osp}_g^{nil}\) act on \(\textsf{fG}_{{{\bar{H}}}(W_g),2m}\) as follows. First note that we may write \(S({{\bar{H}}}(W_g))\) as a quotient
of \(S(H(W_g))\) by the ideal generated by difference between the unit in the symmetric algebra and the unit in \(H^0(W_g)\). Since the action of \(\mathfrak {osp}_g^{nil}\) on \(H(W_g)\) sends the unit element in \(H(W_g)\) to zero, it descends to this quotient. Hence \(\mathfrak {osp}_g^{nil}\) also acts on the graded vector space \(\textsf{fG}_{{{\bar{H}}}(W_g),2m}\) by transforming the decoration in \(S({{\bar{H}}}(W_g))\) on each vertex. Note that this action can generally reduce the number of decorations in \({{\bar{H}}}(W_g)\).
The action of \(\mathfrak {osp}_g^{nil}\) on \(\textsf{fG}_{{{\bar{H}}}(W_g),2m}\) clearly descends to an action on (the graded vector space) \(\textsf{fG}_{(g)}\), since the action cannot create tadpoles in graphs, nor can it increase the valence of vertices.
The action intertwines with the differentials \(d_c'\) and \(d_{cut}\) (and in fact \(d_{cut}'\), \(d_{cut}''\) separately) on \(\textsf{fG}_{{{\bar{H}}}(W_g),2m}\), since \(\mathfrak {osp}_g^{nil}\) preserves the diagonal element \(\Delta \) by construction. Writing \(\phi _c\cdot \) for the action of \(\phi _c\in \mathfrak {osp}_g^{nil}\) we hence have
However, \(\phi _c\cdot \) does a priori not commute with the operation \(d_{mul}\). Instead we have
Here the derivation \([\phi _c \cdot ,\lambda ]\) corresponds to an element \(Y_c\in \textsf{GC}_{{{\bar{H}}}(W_g),2m}\) of degree \(1-m\), which is obtained by restricting \([\phi _c \cdot ,\lambda ]\) to connected graphs. I. e., on connected graphs \(\Gamma \in \textsf{fG}_{{{\bar{H}}}(W_g),2\,m}\) we have \([\phi _c \cdot ,\lambda ](\Gamma )=-\lambda (\phi _c\cdot \Gamma )=:Y_c(\Gamma )\). If we think of elements of \(\textsf{GC}_{{{\bar{H}}}(W_g),2m}\) as \({{\bar{H}}}_\bullet (W_g)\)-decorated graphs as explained in the previous subsection, we have more concretely

with \(\Delta _1^*\in H_m(W_g)\otimes H_m(W_g)\) the diagonal element Poincaré dual to \(\Delta _1\) as in (11) and \(c^*=\langle c,-\rangle \in (H^m(W_g))^*\cong H_m(W_g)\) the Poincaré dual element to c.
By duality we have an action of \(\mathfrak {osp}_g^{nil}\) on the dual space \(\textsf{fG}_{(g)}^*\), and also on \(\textsf{GC}_{(g)}\). As discussed, action does not commute with the differential. Instead the commutator with the differential \(\delta \) is the Lie bracket with the element \(Y_c\), i.e.,
Mind that the \([-,-]\) on the left-hand side denotes the commutator of operators, whereas the \([-,-]\) is the Lie bracket on \(\textsf{GC}_{(g)}\). We now extend the dg Lie algebra \(\textsf{GC}_{(g)}\) to the dg Lie algebra \(\textsf{GC}^{\text {ex}}_{(g)}\), defined as a graded vector space as
We endow \(\textsf{GC}^{\text {ex}}_{(g)}\) with a graded Lie algebra structure by extending the Lie bracket on \(\textsf{GC}_{(g)}\) to a Lie bracket on \(\textsf{GC}^{\text {ex}}_{(g)}\) such that for \(\phi _c\in \mathfrak {osp}_{g}^{nil}\) and \(\Gamma \in \textsf{GC}_{(g)}\) \( [\phi _c,\Gamma ] \) is obtained by acting with \(\phi _c\) on the decorations as discussed before. We extend the differential such that
This ensures that \(\textsf{GC}^{\text {ex}}_{(g)}\) is a dg Lie algebra, despite the action of \(\mathfrak {osp}_{g}^{nil}\) on \(\textsf{GC}_{(g)}\) not respecting the differential, because for \(\Gamma \in \textsf{GC}_{(g)}\),
We may also extend the weight grading on \(\textsf{GC}^{\text {ex}}_{(g)}\) by declaring the elements of \(\mathfrak {osp}_g^{nil}\) to have weight 1. Note that this is necessary so that the differential and Lie bracket still preserve the weight.
For notational convenience we will define for \(\alpha \in H_m(W_g)\)
using the identification of \(H_m(W_g)\) and \(H^m(W_g)\) by Poincaré duality.
Finally, we also introduce the following notation: We denote the graded dual Lie coalgebra by
As a graded vector space this is \({\textsf{G}}_{(g)}\oplus \mathfrak {osp}_g^{nil,c}\). Furthermore, we consider the version with disconnected graphs \(\textsf{fG}^{\text {ex}}_{(g)}\) defined as the cobar construction (Chevalley-Eilenberg complex)
This complex also has a graphical interpretation, see Sect. 7.1 below.
3.5 Auxiliary graph complexes \(\textsf{SG}_{(g)}\) and \(\textsf{SGC}_{(g)}\)
In [11] Campos and the third author define graphical dg cocommutative coalgebra models for framed configuration spaces of n points on surfaces (i.e., for \(W_g\) if \(m=1\) in our notation). As auxiliary objects in some proofs below, we will need to use closely analogous graph complexes defined for general m, but only \(n=1\), which we denote by \(\textsf{SG}_{(g)}\) and \(\textsf{SGC}_{(g)}\).
The graph complex \(\textsf{SG}_{(g)}\) is a variant of the complex \({\textsf{G}}_{(g)}\) of connected graphs defined above. Elements of \(\textsf{SG}_{(g)}\) are linear combinations of connected graphs with exactly one distinguished vertex, which we call "external", and the other vertices "internal". All vertices carry decorations in \({{\bar{H}}}(W_g)\) as for \({\textsf{G}}_{(g)}\). The internal vertices must be at least trivalent and cannot carry tadpole edges. The external vertex may have any valence, and is allowed to support a tadpole edge. Here are some examples, with the white vertex the external vertex and \(\alpha _j\in {{\bar{H}}}(W_g)\).

The cohomological degree of a graph \(\Gamma \) with v internal vertices, e edges and degree of decorations Dm is
As for \({\textsf{G}}_{(g)}\), one fixes an ordering of the edges and odd decorations and identifies two such orderings up to sign.
The differential \(d=d_c+d_{cut}'+d_{mul}''\) from \({\textsf{G}}_{(g)}\) also readily adapts to \(\textsf{SG}_{(g)}\). The pieces \(d_{cut}'+d_{mul}''\) remain well defined by the same combinatorial formulas as before. For the edge contraction differential \(d_c\) one just has to clarify that if the edge connects the external with some internal vertex, then the new vertex created in the contration remains external:

Furthermore, the dg vector space \(\textsf{SG}_{(g)}\) is a quasi-free dg commutative algebra, with the commutative product defined by gluing together graphs at the external vertex:

The dgca \(\textsf{SG}_{(g)}\) is a model for the unit sphere bundle \(STW_g\) of \(W_g\). To see this, consider the much smaller model for the unit sphere bundle
with \(\vartheta \) of degree \(2m-1\) and differential \(d\vartheta = (2 + (-1)^m 2\,g) \omega \in H^{2\,m}(W_g)\).
We then a define map of dgcas
as follows:
-
Any graph \(\Gamma \in \textsf{SG}_{(g)}\) that has an internal vertex is sent to zero.
-
The general graph \(\Gamma \in \textsf{SG}_{(g)}\) without internal vertices is of the form
 (18)
(18)that is, it consists of the external vertex, possibly carrying one tadpole, and decorations \(\alpha _1,\dots ,\alpha _k\in {{\bar{H}}}(W_g)\). In case there is no tadpole, the graph is sent to the cup product \(\alpha _1\cdots \alpha _k\in H(W_g)\). If there is a tadpole, the graph is similarly sent to \(\vartheta \alpha _1\cdots \alpha _k\in \vartheta H(W_g)\).
Lemma 18
The map (17) defined above is a map of dg commutative algebras.
Proof
The map (17) clearly intertwines the commutative products. Let us check that it intertwines the differentials. Let \(\Gamma \in \textsf{SG}_{(g)}\) be a graph. Note that the differential reduces the number of edges by exactly one. Hence, if \(\Gamma \) has more than two edges, then trivially \(dF(\Gamma )=F(d\Gamma )=0\). If \(\Gamma \) has no edge, then again \(dF(\Gamma )=F(d\Gamma )=0\) since \(d\Gamma =0\) and the image of graphs with no edges contains no \(\vartheta \) and is hence closed in \(C^\bullet (STW_g)\). Next suppose that \(\Gamma \) has exactly one edge, forming a tadpole, see the right-hand graph in (18). If the number k of other decorations is positive, then by degree reasons \(dF(\Gamma )=F(d\Gamma )=0\), so we can assume \(k=0\). Then we have

Hence
with the products being cup products in \(H(W_g)\). Finally suppose that \(\Gamma \) has one edge and one internal vertex,

Then \(F(\Gamma )=0\), while

with the two terms being produced by the edge contraction part \(d_c\) and the part \(d_{mul}''\) of the differential, and we understand that the cup product in \({{\bar{H}}}(W_g)\) is taken for the term in brackets. But then \(F(d\Gamma )=0\) as required.
Finally suppose that \(\Gamma \) has exactly two edges. By compatibility of F with the products we can furthermore assume that \(\Gamma \) cannot be written as a product. This means that \(\Gamma \) is internally connected in the sense that deleting the external vertex leaves the graph connected. Furthermore, graphs with multiple edges are zero by symmetry. These constraints leave only the following case to be considered:

However, since this graph has two internal vertices and the differential can remove at most one, we again have \(dF(\Gamma )=F(d\Gamma )=0\). \(\square \)
Lemma 19
The map (17) is a quasi-isomorphism.
Proof
We filter \(\textsf{SG}_{(g)}\) by the total degree of the decorations in \({{\bar{H}}}(W_g)\). The pieces \(d_c\) and \(d_{mul}''\) of the differential leave this degree the same, while \(d_{cut}'\) increases it by 2m. Hence the associated graded complex is identified with \((\textsf{SG}_{(g)},d_c+d_{mul}'')\). In particular, the differential cannot create or remove the tadpole and hence this complex splits into a direct sum of complexes
with \(\textsf{SG}_{(g)}'\) (resp. \(\textsf{SG}_{(g)}''\)) spanned by the graphs without (resp. with) a tadpole at the external vertex, and furthermore \((\textsf{SG}_{(g)}',d_c+d_{mul}'')\cong (\textsf{SG}_{(g)}''[2m-1],d_c+d_{mul}'')\). We claim that \((\textsf{SG}_{(g)}',d_c+d_{mul}'')\cong H(W_g)\). To this end we write

with \(U_{1}\subset \textsf{SG}_{(g)}'\) the subspace spanned by graphs in which the external vertex has valence \(\le 1\) and \(U_{1}\subset \textsf{SG}_{(g)}'\) spanned by graphs in which the external vertex has valence \(\ge 2\). (Mind that decorations in \({{\bar{H}}}(W_g)\) count towards valence.) The arrows indicate the pieces of the differential. In particular, the map \(f:U_1\rightarrow U_2\) is the part of \(d_c\) that contracts the unique edge at the external vertex if present,

This map f is clearly surjective. In this situation it is elementary to check that the complex \((\textsf{SG}_{(g)}',d_c+d_{mul}'')\) is quasi-isomorphic to \(\ker f\), see [30, Lemma 2.1]. The kernel of f is spanned by graphs with no edge and at most one decoration in \({{\bar{H}}}(W_g)\) at the external vertex. But those are identified with \(H(W_g)\), so the claim is shown.
It follows that the \(E^1\)-page of our spectral sequence is isomorphic to \(C^\bullet (STW_g)\). We may endow \(C^\bullet (STW_g)\) with a similar filtration by the degree in \(H(W_g)\). Then the \(E^1\) page agrees with \(C^\bullet (STW_g)\) trivially. Furthermore, the map \(F\) respects the filtrations and induces an isomorphism on the \(E^1\)-pages. Hence \(F\) is a quasi-isomorphism by standard spectral sequence comparison results. \(\square \)
Recall that the piece \(d_{cut}''\) of the cutting differential that creates an additional connected component gives rise to the Lie cobracket on the dg Lie coalgebra \({\textsf{G}}_{(g)}\). In the same manner, we may define an operation \(d_{cut}''\) on \(\textsf{SG}_{(g)}\) that then gives rise to a Lie coaction of \({\textsf{G}}_{(g)}\) on \(\textsf{SG}_{(g)}\).
For later use we shall prefer to work with the dual complex
that we may again interpret as a graph complex, see Sect. 3.3 above. By Lemma 19 we then have that
Furthermore, \(\textsf{SGC}_{(g)}\) carries an action of the dg Lie algebra \(\textsf{GC}_{(\textrm{g})}\).
Finally, let us also mention the following versions corresponding to \(STW_{g,1}\) and \(W_{g,1}\). Namely, we can consider the dg subcoalgebra \(\textsf{SGC}_{(g),1} \subset \textsf{SGC}_{(g)}\) consisting of graphs that do not contain any decorations with the top homology class \(\omega \). In this case, the action above induces an action of \(\textsf{GC}_{(g),1}\). The same proof as above shows that \(\textsf{SGC}_{(g),1}\) is a model for \(STW_{g,1}\). Finally taking the quotient  , where \(\textsf{SGC}_{(g),1}^{\ge 1}\) is the subcomplex of graphs having a tadpole at the external vertex gives a model for \(W_{g,1}\) with an induced action of \(\textsf{GC}_{(g),1}\). In particular, there is a quasi-isomorphism of dg algebra
, where \(\textsf{SGC}_{(g),1}^{\ge 1}\) is the subcomplex of graphs having a tadpole at the external vertex gives a model for \(W_{g,1}\) with an induced action of \(\textsf{GC}_{(g),1}\). In particular, there is a quasi-isomorphism of dg algebra

4 Proof of part (i) of Theorem 1
As defined above  , with
, with  being the (closed) subspace spanned by graphs with at least one tadpole. We will check that
being the (closed) subspace spanned by graphs with at least one tadpole. We will check that  is 2g-dimensional, concentrated in degree \(2-m\), spanned by graphs of the form
is 2g-dimensional, concentrated in degree \(2-m\), spanned by graphs of the form

with \(\alpha \in H^m(W_{g,1})\). The graphs \(\Gamma _\alpha \) have weight 1, hence  is zero in weights \(\ge 2\), and part (i) of Theorem 1 follows.
is zero in weights \(\ge 2\), and part (i) of Theorem 1 follows.
To compute  we proceed analogously to the proof of [35, Proposition 3.4], but we shall streamline the proof a bit. First we filter
we proceed analogously to the proof of [35, Proposition 3.4], but we shall streamline the proof a bit. First we filter  by the number of loops, i.e., we define the bounded above, descending complete filtration
by the number of loops, i.e., we define the bounded above, descending complete filtration

with  spanned by graphs with first Betti number at least p. The (complete) associated graded complex may be identified with
spanned by graphs with first Betti number at least p. The (complete) associated graded complex may be identified with  . We claim that
. We claim that  is 2g-dimensional, concentrated in degree \(2-m\), and spanned by the classes of the graphs \(\Gamma _\alpha \) above. If we assume this claim the proof concludes, since the spectral sequence must converge at this point by degree reasons.
is 2g-dimensional, concentrated in degree \(2-m\), and spanned by the classes of the graphs \(\Gamma _\alpha \) above. If we assume this claim the proof concludes, since the spectral sequence must converge at this point by degree reasons.
To show the claim, let us call a long tadpole a tadpole at a trivalent vertex without decorations

and the edge adjacent to the tadpole the long tadpole edge. We filter  again by the number of edges that are not long tadpole edges. The associated graded complex may then be identified with
again by the number of edges that are not long tadpole edges. The associated graded complex may then be identified with  , with \(\delta _{split}'\) the piece of the differential that creates one long tadpole edge,
, with \(\delta _{split}'\) the piece of the differential that creates one long tadpole edge,

This differential has an obvious homotopy

where the sum is over all long tadpole edges, and \(\Gamma /e\) is obtained by contracting the edge. One easily computes that
with \(N(\Gamma )\) the number of tadpoles in the graph \(\Gamma \) that are either long tadpoles, or attached to a vertex of valency \(\ge 4\) (including the two tadpole half-edges). But since there must be at least one tadpole in the graph by definition of  , we see that \(N(\Gamma )>0\) for all graphs except for those of the form \(\Gamma _\alpha \). Invoking Lemma 7 we thus finish the computation of
, we see that \(N(\Gamma )>0\) for all graphs except for those of the form \(\Gamma _\alpha \). Invoking Lemma 7 we thus finish the computation of  , and hence the proof that (3) is an isomorphism for \(W\ge 2\).
, and hence the proof that (3) is an isomorphism for \(W\ge 2\).
4.1 Comparison in weight 1
Note that part (i) of Theorem 1 excludes weights \(\le 1\). Also note that our graph complexes are concentrated in positive weight: Due to the trivalence condition (and since decorations contribute to the valence) we have the inequality
Rearranging, one obtains
Hence the only nontrivial weight not covered by Theorem 1 is weight \(W=1\). In this section we shall fill this gap and compute the weight 1 parts of our three dg Lie algebras.
First consider \({{\,\textrm{gr}\,}}^1\textsf{GC}_{(g),1}\). This complex is spanned by graphs with a single vertex and three decorations

living in cohomological degree \(1-m\). The differential is zero, and hence the cohomology is trivially identified with
Next consider  . This complex is spanned by the graphs \(\Gamma _{\alpha \beta \gamma }\) of (21), and in addition the graphs \(\Gamma _\alpha \) of (20). The differential acts as
. This complex is spanned by the graphs \(\Gamma _{\alpha \beta \gamma }\) of (21), and in addition the graphs \(\Gamma _\alpha \) of (20). The differential acts as
with \(\langle -,-\rangle \) the canonical pairing on \({{\bar{H}}}^m(W_{g,1})\). Note that the graphs \(\Gamma _\alpha \) span a 2g-dimensional subspace equivalent to the defining (2g-dimensional) representation of \(\textrm{OSp}_g\). Since this representation is irreducible, we know by Schur’s Lemma that \(\delta \) must be either surjective or zero. If \(g\ge 2\) one easily checks that \(\delta \) is not zero, and hence surjective. For \(g=0\) one has that trivially \({{\,\textrm{gr}\,}}^1\textsf{GC}_{(g),1}=0\). For \(g=1\) and m odd one has \(S^3 {{\bar{H}}}_\bullet (W_{(g),1})=0\), and hence \(\delta \) is zero trivially. For \(g=1\) and m even one again checks easily that \(\delta \) is not zero and hence surjective.
Finally we turn to \({{\,\textrm{gr}\,}}^1\textsf{GC}^{\text {ex}}_{(g)}\). This complex is spanned by the graphs \(\Gamma _{\alpha \beta \gamma }\) for \(\alpha ,\beta ,\gamma \in H_m(W_g)\), and the elements \(\phi _{\alpha } \in \mathfrak {osp}_g^{nil}\). The differential is defined such that
with \(\Delta _1^*=\sum _{i,j} g_{ij} c_i\otimes c_j\in H_m(W_g)\otimes H_m(W_g)\) a representation of the diagonal element in some basis \(\{c_i\}\) of the homology. The space \(\mathfrak {osp}_g^{nil}\) is equivalent to the defining \(\textrm{OSp}_g\)-representation, and hence the differential is either zero or injective by Schur’s Lemma. If \(g\ge 2\) the differential is non-zero as one checks on an element, and hence injective. For \(g=0\) we have \({{\,\textrm{gr}\,}}^1\textsf{GC}^{\text {ex}}_{(g)}=0\) trivially. For \(g=1\) and m odd all \(\Gamma _{\alpha \beta \gamma }\) are zero and hence the differential is zero. For \(g=1\) and m even the differential is again injective as one checks by explicit computation.
Overall we have the following table of cohomologies for m odd, as \(\textrm{Sp}(2g)\)-representations
\(g=0\) | \(g=1\) | \(g=2\) | \(g\ge 3\) | |
|---|---|---|---|---|
| 0 | \(V(\lambda _1)[m-2]\) | 0 | \(V(\lambda _3)[m-1]\) |
\({{\,\textrm{gr}\,}}^1H(\textsf{GC}_{(g),1})\) | 0 | 0 | \(V(\lambda _1)[m-1]\) | \((V(\lambda _1)\oplus V(\lambda _3))[m-1]\) |
\({{\,\textrm{gr}\,}}^1H(\textsf{GC}^{\text {ex}}_{(g)})\) | 0 | \(V(\lambda _1)[m]\) | 0 | \(V(\lambda _3)[m-1]\) |
Here \(V(\lambda )\) denotes a representation of highest weight \(\lambda \), and \(\lambda _1, \lambda _2,\dots \) is a system of fundamental weights.
For m even we similarly have the following table.
\(g=0\) | \(g\ge 1\) | |
|---|---|---|
| 0 | \(V(3\lambda _1)[m-1]\) |
\({{\,\textrm{gr}\,}}^1H(\textsf{GC}_{(g),1})\) | 0 | \((V(\lambda _1) \oplus V(3\lambda _1))[m-1]\) |
\({{\,\textrm{gr}\,}}^1H(\textsf{GC}^{\text {ex}}_{(g)})\) | 0 | \(V(3\lambda _1)[m-1]\) |
Here one shall remark that providing highest weights only describes a representation of \( SO (g,g)\) a priori, but the representations here extend to O(g, g). Concretely, \(V(\lambda _1)\cong V_g\) shall be the defining 2g-dimensional representation of O(g, g) and \(V(3\lambda _1)\) the kernel of the canonical map
defined by contraction with the pairing.
In all cases the canonical maps  send the summands \(V(\lambda _3)\) (resp. \(V(3\lambda _1)\)) isomorphically onto themselves, as the corresponding cohomology classes are always represented by graphs of the form \(\Gamma _{\alpha \beta \gamma }\) that exist in all complexes.
send the summands \(V(\lambda _3)\) (resp. \(V(3\lambda _1)\)) isomorphically onto themselves, as the corresponding cohomology classes are always represented by graphs of the form \(\Gamma _{\alpha \beta \gamma }\) that exist in all complexes.
5 Comparing \(\textsf{GC}_{(g),1}\) and \(\textsf{GC}_{(g)}\), and the proof of part (ii) of Theorem 1
In this section we will need a natural action of \(\textsf{GC}^{\text {ex}}_{(g)}\) on \(\textsf{SGC}_{(g)}\), defined in a similar manner to the Lie algebra structure on \(\textsf{GC}^{\text {ex}}_{(g)}\). More precisely, recall that \(\textsf{SGC}_{(g)}\) has an action of \(\textsf{GC}_{(\textrm{g})}\) (by dualizing the coaction of \({\textsf{G}}_{(g)}\) on \(\textsf{SG}_{(g)}\) defined by the operation \(d_{cut}''\)). The action of \(\mathfrak {osp}_g^{nil}\) is on decorations (including decorations on the external vertex) in the same manner as for \(\textsf{GC}^{\text {ex}}_{(g)}\).
Recall that \(\textsf{SG}_{(g)}\) is a quasi-free dg commutative algebra on generators given by graphs which remain connected after deletion of the external vertex. Dually, \(\textsf{SGC}_{(g)}\) is cofree as a coalgebra. We denote the space of cogenerators by \(\textsf{ICG}_{(\textrm{g})}[1]\), i.e. \(\textsf{SGC}_{(g)}= S^c (\textsf{ICG}_{(\textrm{g})}[1])\). In other words, \(\textsf{ICG}_{(\textrm{g})}\) is an \(L_\infty \)-algebra whose cobar construction is \(\textsf{SGC}_{(g)}\). Graphs in \(\textsf{ICG}_{(\textrm{g})}\) also satisfy the connectivity property above and are referred to as “internally connected”. The cohomological degree of a graph with v internal vertices, e edges and (non-positive) degree of decorations Dm is
The action of \(\textsf{GC}^{\text {ex}}_{(g)}\) on \(\textsf{SGC}_{(g)}\) is compatible with the coalgebra structure on \(\textsf{SGC}_{(g)}\) and thus we obtain a morphism of dg Lie algebras
where \(\textrm{Der}(\textsf{SGC}_{(g)})\) is the dg Lie algebra of coalgebra coderivations of \(\textsf{SGC}_{(g)}\).
The coalgebra \(\textsf{SGC}_{(g)}\) is coaugmented by the inclusion of the “empty” graph consisting of the external vertex and no further vertices, edges or decorations. However this coaugmentation is not preserved by the action of \(\textsf{GC}^{\text {ex}}_{(g)}\) (since the action of a graph with \(\omega \)-decorated vertices on the “empty” graph is generally non-zero). We thus get a non-trivial chain map induced by the action on the coaugmentation
The map can be described as follows:
-
Elements \(\Gamma \in \textsf{GC}_{(g)}\) act on the “empty” graph with one external vertex and no internal vertices or edges. Namely, we sum over all ways of connecting an \(\omega \)-decoration to the external vertex.
-
If \(\phi _{c_i}\in \mathfrak {osp}_g^{nil}\) is an element that sends \(1\in H_0(W_g)\) to \(c_i \in H_m(W_g)\) then we map it to the graph with one external vertex and decoration \(c_i\).
From this description it follows that the dg Lie subalgebra \(\textsf{GC}_{(g),1} \subset \textsf{GC}_{(\textrm{g})}\) preserves the coaugmentation (i.e. gluing any graph of \(\textsf{GC}_{(g),1}\) to the "empty" graph gives 0), since none of the vertices carry \(\omega \)-decorations.
Proposition 20
The sequence
where the first map is the inclusion, is a fiber/cofiber sequence, i.e. the composition of the two maps is zero and the corresponding total complex is acyclic.
Proof
The two maps compose to zero by the description of the map f as gluing \(\omega \)-decorations to the external vertex and \(\textsf{GC}_{(g),1}\) not having any \(\omega \)-decorations. Thus we obtain a chain map
which we will show is a quasi-isomorphism. Denote by \(\textsf{ICG}_{(\textrm{g})}^\bullet \subset \textsf{ICG}_{(\textrm{g})}\) the subcomplex consisting of diagrams having at least one internal vertex, and by \(\textsf{ICG}_{(\textrm{g})}^0\) the subspace spanned by diagrams with no internal vertices. The latter does not define a subcomplex. By the description of the map f given above, we have \(f(\textsf{GC}_{(\textrm{g})})\subset \textsf{ICG}_{(\textrm{g})}^\bullet [1]\), while \(f(\mathfrak {osp}^{nil}_g)\subset \textsf{ICG}_{(\textrm{g})}^0[1]\). Next, we equip \(\textsf{GC}_{(g),1}\) with the complete descending filtration given by
and similarly the mapping cone with the complete descending filtration
where by an internal edge we mean an edge connecting two internal vertices. On the level of the associated graded complexes we have, on the one hand, \(({{\,\textrm{gr}\,}}\textsf{GC}_{(g),1},0)\), whereas \({{\,\textrm{gr}\,}}\textrm{cone}(f[-1])\) splits into the direct sum of subcomplexes
Let us first show that the first subcomplex is acyclic. As a vector space  . The associated graded differential sends
. The associated graded differential sends

Recall that \(\mathfrak {osp}_g^{nil}\) has a basis \(\{ \phi _{c_i} \}\), i.e. is isomorphic to \(H_m(W_g)\) and we have defined the map f such that it is the inclusion  ,
,

Thus \({{\,\textrm{gr}\,}}(\mathfrak {osp}^{nil}_g \oplus \textsf{ICG}_{(\textrm{g})}^0)\) is identified with the cone of the identity on \(H_m(W_g) \oplus H_{2m}(W_g)\) and hence contractible.
For the summand \( {{\,\textrm{gr}\,}}(\textsf{GC}_{(\textrm{g})}\oplus \textsf{ICG}_{(\textrm{g})}^\bullet )\) we notice that the only remaining differential is given by replacing \(\omega \)-decorations with an edge connected to the external vertex.

Here we think of graphs in \(\textsf{GC}_{(\textrm{g})}\) as having an external vertex but not being connected to it. This differential has an obvious homotopy
given by replacing edges connected to the external vertex by an \(\omega \)-decoration at the respective internal vertex. It satisfies
where \(N(\Gamma )\) is the number of \(\omega \)-decorations plus the number of edges incident at the external vertex. Using Lemma 7 we obtain that the inclusion of the diagrams with \(N(\Gamma ) = 0\) is a quasi-isomorphism. But \(N(\Gamma ) = 0\) means exactly graphs with no \(\omega \)-decorations and no edges connected to the external vertex, i.e. diagrams in \({{\,\textrm{gr}\,}}\textsf{GC}_{(g),1}\subset {{\,\textrm{gr}\,}}(\textsf{GC}_{(\textrm{g})}\oplus \textsf{ICG}_{(\textrm{g})}^\bullet )\). Thus
is a quasi-isomorphism, and so is
\(\square \)
We obtain a long exact sequence on cohomology groups
By the equivalence of quasi-cofree dg cocommutative coalgebras and \(L_\infty \)-algebras we obtain that \(\textsf{ICG}_{(\textrm{g})}\) is an \(L_\infty \)-algebra (see for instance [25, Proposition 10.1.20]). More concretely, the k-ary bracket \([\Gamma _1, \dots , \Gamma _k]\) is obtained by applying the differential to \(\Gamma _1 \vee \dots \vee \Gamma _k\) and keeping the internally connected component, where \(\Gamma _1 \vee \dots \vee \Gamma _k\) is the union of the graphs \(\Gamma _1,\dots , \Gamma _k\) glued together at their external vertex. The 1-ary bracket defines a differential on \(\textsf{ICG}_{(\textrm{g})}\) such that the 2-ary bracket induces a Lie bracket on \(H(\textsf{ICG}_{(\textrm{g})})\).
Lemma 21
The image of
lies in the center of the graded Lie algebra \(H(\textsf{ICG}_{(\textrm{g})})\).
The proof will follow from the following more general lemma. Let \(S^c({\mathfrak {h}}[1])\) be a quasi-cofree dg coalgebra (i.e. the bar construction of an \(L_\infty \)-algebra).
Lemma 22
Let \(F :S^c({\mathfrak {h}}[1]) \rightarrow S^c({\mathfrak {h}}[1])\) be a coderivation of the coalgebra structure commuting with the differential. Then F(1) lies in the center of \(H({\mathfrak {h}})\).
Since \(\Delta (1) = 1 \otimes 1\) and F is a coderivation we obtain that F(1) is primitive, hence \(F(1) \subset {\mathfrak {h}}[1]\). Let \(\pi :S^c({\mathfrak {h}}[1]) \rightarrow {\mathfrak {h}}[1]\) be the projection onto cogenerators. The coderivation F is completely determined by its composition with the projection onto cogenerators \(\phi = \pi \circ F :S^c({\mathfrak {h}}[1]) \rightarrow {\mathfrak {h}}[1]\) and we have \(F(1) = \phi (1)\) and \(F(x) = \phi (x) + \phi (1) \vee x\) for all \(x \in {\mathfrak {h}}\) (with the same proof as [25, Proposition 1.2.9]). Since F commutes with the differential we obtain that
Suppose now that \(x \in {\mathfrak {h}}\) such that \(dx = 0\) (in \({\mathfrak {h}}\) and hence also in \(S^c({\mathfrak {h}}[1])\)) and thus the left-hand side is 0. Projecting the right-hand side onto cogenerators we obtain
since the projection onto cogenerators of  is the definition of the 2-ary bracket (up to a conventional sign). Thus we have obtained that \(\phi (1) = F(1)\) lies in the center of \(H({\mathfrak {h}})\).
is the definition of the 2-ary bracket (up to a conventional sign). Thus we have obtained that \(\phi (1) = F(1)\) lies in the center of \(H({\mathfrak {h}})\).
Proof of Lemma 21
The action of \(\textsf{GC}^{\text {ex}}_{(g)}\) on \(\textsf{SGC}_{(g)}\) is in particular compatible with the differential. Thus any \(\gamma \in H^\bullet (\textsf{GC}^{\text {ex}}_{(g)})\) defines a coderivation of \(\textsf{SGC}_{(g)}\) that commutes with the differential. The statement is then a direct application of Lemma 22. \(\square \)
Let us also note the following general fact about the situation above
Lemma 23
Let \({\mathfrak {g}}\) be a dg Lie algebra acting on the bar construction \(\texttt{B}({\mathfrak {h}})\) of an \(L_\infty \)-algebra \({\mathfrak {h}}\) by coalgebra-coderivations preserving the coaugmentation. Such an action is determined by its composition with the projection onto the cogenerators and thus given by linear maps
for \(k \ge 1\). Then the map \(\phi _1\) induces an action of \(H({\mathfrak {g}})\) on \(H({\mathfrak {h}})\) by Lie algebra derivations
Proof
By functoriality (with respect to coaugmentation preserving maps) of the bar construction we obtain a dg-action
which descend to
Finally, bar-cobar adjunction gives us the identification \(H(\texttt{B}^c \texttt{B}({\mathfrak {h}})) = H({\mathfrak {h}})\). \(\square \)
The lemma can be applied to the following situation. Recall that \(\textsf{GC}_{(g),1}\) acts on the quasi-free coalgebra  by coaugmentation-preserving coalgebra coderivations. Let us denote by \(\textsf{ICG}_{(g),1}[1]\) the \(L_\infty \)-algebra of cogenerators. Thus by the above lemma we obtain an action
by coaugmentation-preserving coalgebra coderivations. Let us denote by \(\textsf{ICG}_{(g),1}[1]\) the \(L_\infty \)-algebra of cogenerators. Thus by the above lemma we obtain an action
We will see shortly that \(\textsf{ICG}_{(g),1}\) is Quillen model for \(W_{g,1}\) and hence a free Lie algebra.
5.1 Rational homotopy Lie algebra of \(W_{g}\)
We define the graded Lie algebra \({\mathfrak {w}}_g\) to be the Koszul dual Lie algebra to the graded commutative algebra \(H^\bullet (W_g)\). Concretely, \({\mathfrak {w}}_g\) has the following presentation. It is generated as a graded Lie algebra by symbols \(c_1,\dots , c_{2g}\) of degree \(1-m\), corresponding to a basis of \(H_m(W_g)\). Let us denote the matrix of the non-degenerate pairing with respect to the given basis by \(g_{ij}\). Then
It is clear that \({\mathfrak {w}}_g\) is the quadratic dual to the quadratic commutative algebra \(H^\bullet (W_g)\). To see that it is the Koszul dual it suffices to show that either \(H^\bullet (W_g)\) or \(U({\mathfrak {w}}_g)\) is a Koszul algebra. Note that \(U({\mathfrak {w}}_g)\) is a quadratic algebra with generators \(c_i\) and the single relation
and it is Koszul by [25, Theorem 4.1.1] since in particular there are no critical monomials on which to test the confluence condition,Footnote 2 We also set
and note that it is the Koszul dual Lie algebra to \(H^\bullet (W_{g,1})\).
Moreover, consider a central extension of the graded Lie algebra \({\mathfrak {w}}_g\) with central element c of degree \(2-2m\).
This is a Quillen model for the sphere bundle \(STW_g\). One has a map of graded Lie algebras
by setting \(c=0\). Both Lie algebras above carry an additional grading, assigning the generators \(c_i\) degree \(+1\) and the generator c degree \(+2\). We denote by \(\hat{{\mathfrak {w}}}_g^{fr}\), \(\hat{{\mathfrak {w}}}_g\) and \(\hat{{\mathfrak {w}}}_{g,1}\) the respective completions. (They only differ from \({\mathfrak {w}}_g^{fr}\), \({\mathfrak {w}}_g\) and \({\mathfrak {w}}_{g,1}\) in the case \(m=1\), in fact.)
We shall need the following result, which can be deduced from [4, Proposition A’] (see also [15, Lemma 74] for a different proof).
Proposition 24
([4, Proposition A’], see also [8, Proposition 5.10]) For \(g\ge 2\) the center of \({\mathfrak {w}}_g\) is trivial, and the center of \({\mathfrak {w}}_g^{fr}\) is one-dimensional, spanned by c.
There is a morphism of \(L_\infty \)-algebras
which is given as follows.
-
If a graph \(\Gamma \in \textsf{ICG}_{(\textrm{g})}\) contains either a loop, a \(\ge 4\)-valent vertex or an \(\omega \)-decoration, then \(\phi _{(g)}(\Gamma ) = 0\).
-
If \(\Gamma \in \textsf{ICG}_{(\textrm{g})}\) is a trivalent tree with no \(\omega \)-decorations, it can be interpreted as a Lie tree and determines an element in the free Lie algebra \(L_\Gamma \in \textrm{FreeLie}(c_1, \dots , c_{2\,g}) \rightarrow \hat{{\mathfrak {w}}}_g^{fr}\). In that case \(\phi _{(g)}(\Gamma ) = [L_\Gamma ] \in \hat{{\mathfrak {w}}}_g^{fr}\).
The same description also gives a morphism of \(L_\infty \)-algebras
Lemma 25
The morphisms \(\phi _{(g)}:\textsf{ICG}_{(\textrm{g})}\rightarrow \hat{{\mathfrak {w}}}_g^{fr}\) and \(\phi _{(g),1} :\textsf{ICG}_{(g),1} \rightarrow \hat{{\mathfrak {w}}}_{(g),1}\) are quasi-isomorphisms.
Proof
In both cases, by bar-cobar duality it suffices to show that the induced morphisms on the respective bar complexes
and

are quasi-isomorphisms.
Equivalently, we will show that the following compositions are quasi-isomorphisms

where \(C_\bullet (STW_{g}) \rightarrow \textsf{SGC}_{(g)}\) and  are the dual maps to the quasi-isomorphisms (17) and (19). The map \(\psi _{(g),1}\) is exhibiting \(\hat{{\mathfrak {w}}}_{(g),1}\) as Koszul dual of \(C_\bullet (W_{(g),1})\) and is hence a quasi-isomorphism. We will now treat the case \(\psi _{(g)}\).
are the dual maps to the quasi-isomorphisms (17) and (19). The map \(\psi _{(g),1}\) is exhibiting \(\hat{{\mathfrak {w}}}_{(g),1}\) as Koszul dual of \(C_\bullet (W_{(g),1})\) and is hence a quasi-isomorphism. We will now treat the case \(\psi _{(g)}\).
Since all the maps are maps of coalgebra, \(\textsf{SGC}_{(g)}\) and \(B(\hat{{\mathfrak {w}}}_g^{fr})\) are freely cogenerated by \(\textsf{ICG}_{(\textrm{g})}\) and \(\hat{{\mathfrak {w}}}_g^{fr}\), respectively, and the second map is induced by a map on cogenerators, we obtain that \(\psi \) is determined by its projection
which we can see as an element \(g \in C^\bullet (STW_{g}) \otimes \hat{{\mathfrak {w}}}_g^{fr}\). Tracing through the definitions of the maps we obtain that
where \(c^i \otimes c_i\) is the identity in \(H^m(W_g) \otimes H_m(W_g)\) (i.e. \(c^i\) is a dual basis to \(c_i\)). From this description we see that the diagram

commutes, where the upper horizontal arrow is the canonical map exhibiting \(\hat{{\mathfrak {w}}}_g\) as the Koszul dual of \(H_\bullet (W_g)\) and hence a quasi-isomorphism. It remains to show that \(\psi _{(g)}\) is a quasi-isomorphism on the vertical kernels. Let us for simplicity again dualize and take vertical cokernels

The cokernels are \(H^\bullet (W_{g})\)- and \(\texttt{B}(\hat{{\mathfrak {w}}}_g)^*\)-modules, respectively. Moreover, they are both freely generated by \(\vartheta \) on the left hand side and a class dual to c on the right hand side. But these classes are sent to each other under \(\psi _{(g)}^*\). Thus we also obtain a quasi-isomorphism on the cokernels and hence \(\psi _{(g)}^*\) and \(\psi _{(g)}\) are quasi-isomorphisms. \(\square \)
Proposition 26
For \(g \ge 2\), we have \(H(f)=0\). In particular, the long exact sequence (22) splits into
For \(g = 1\), the sequence splits into
Proof
Let us first treat the case \(g \ge 2\). By Lemma 21 and Proposition 24 it suffices to show that the connecting homomorphism \(q:\hat{{\mathfrak {w}}}_g^{fr}\rightarrow H(\textsf{GC}_{(g),1})\) from the sequence (22) is injective on the center \(Z(\hat{{\mathfrak {w}}}_g^{fr})={{\mathbb {K}}}c\). The central element c has the following representative in \(H(\textsf{ICG}_{(\textrm{g})})\)

where \(\Delta _1 \in H_m(W_g)^{\otimes 2}\) is the diagonal element. The connecting homomorphism q maps this element to

In order to prove injectivity, we will show that the image of (25) under the action 23 given by Lemma 23 is non-zero. That is, using Lemma 25 we obtain a natural action
Concretely this is obtained by projecting onto the trivalent tree part before performing the gluing operation onto any Lie tree. The element (25) above is sent to the inner derivation determined by the element
and is hence non-zero in \(H(\textsf{GC}_{(g),1})\). Note that the last statement also holds for \(g=1\), namely the image of the central element c is always non-zero in \(H(\textsf{GC}_{(g),1})\). Let us now consider the case \(g=1\). In this case, \(\hat{{\mathfrak {w}}}_1^{fr}\) is finite-dimensional and given by
For m odd, \(\mathfrak {osp}^{nil}_1\) is two-dimensional, both generators are closed in \(\textsf{GC}^{\text {ex}}_{(1)}\) and their images in \(\hat{{\mathfrak {w}}}_1^{fr}\) are precisely \({{\mathbb {K}}}c_1 \oplus {{\mathbb {K}}}c_2\). For m even, H(f) maps the closed graphs

to \([c_1,c_1]\) and \([c_2,c_2]\), respectively, while the connecting homomorphism \(\hat{{\mathfrak {w}}}_1^{fr} \rightarrow H(\textsf{GC}_{(1),1})\) sends \(c_1\) and \(c_2\) to

respectively. From this we get the following description of the images of \(c_1\) and \(c_2\) (and c) under the map \(\nu :\hat{{\mathfrak {w}}}_1^{fr} \rightarrow H(\textsf{GC}_{(1),1}) \rightarrow \textrm{Der}(\textrm{FreeLie}({\bar{H}}(W_{1,1})))\). Namely,
Note that these three derivations have different bidegrees if we give \(\hat{{\mathfrak {w}}}_{(1),1}\) the bigrading where \(c_1\) has bidegree (1, 0) and \(c_2\) has bidegree (0, 1). Thus they are linearly independent and we get that \({{\mathbb {K}}}c \oplus {{\mathbb {K}}}c_1 \oplus {{\mathbb {K}}}c_2\) maps injectively into \(H(\textsf{GC}_{(1),1})\). \(\square \)
The connecting homomorphism \(q :\hat{{\mathfrak {w}}}_g^{fr} \rightarrow H(\textsf{GC}_{(g),1})\) from the sequence (22) sends generators \(c_j\) of \(\hat{{\mathfrak {w}}}_g^{fr}\) to

with \(\Delta _1\in H_m(W_{(g),1})^{\otimes 2}\) being the diagonal element. This completely determines it by the following.
Proposition 27
The connecting homomorphism \(q :\hat{{\mathfrak {w}}}_g^{fr} \rightarrow H(\textsf{GC}_{(g),1})\) is a homomorphism of Lie algebras.
Proof
The statement is equivalent to showing that the identification of the cocone of \(\textsf{GC}_{(g),1}\rightarrow \textsf{GC}^{\text {ex}}_{(g)}\) with \(\hat{{\mathfrak {w}}}_g^{fr}\) given in Proposition 26 can be made into a quasi-isomorphism of dg Lie algebras. Notice that cocones of dg Lie algebras are again dg Lie algebras and the natural projection (which is the connecting homomorphism from above) is a map of dg Lie algebras. We have the following commuting diagram of dg Lie algebras

where \(\textrm{Der}_+ (\textsf{SGC}_{(g)}))\) are derivations preserving the coaugmentation and the morphisms going from the second to third row are as in [16, Theorem 1]. It induces quasi-isomorphims of dg Lie algebras between the horizontal cocones. To see this, we take the cone of the morphism of the first row and the cokernel of the two other, to obtain the sequence of quasi-isomorphisms of dg vector spaces
The cocone of the last row may be identified via the adjoint action with \(\texttt{B}^c (\textsf{SGC}_{(g)})\). By Lemma 25, \(\texttt{B}^c(\textsf{SGC}_{(g)})\) is quasi-isomorphic to \(\hat{{\mathfrak {w}}}_{g}^{fr}\) as dg Lie algebras. \(\square \)
In particular, this concludes the proof of part (ii) of Theorem 1. We end this section with the following remark indicating a possible technical application of Proposition 26. It is not used in the rest of the paper and can safely be skipped.
Remark 2
We briefly sketch how the \(g=1\) case of Proposition 26 allows to deduce the conjecture stated in the introduction of [2] and in [32] from the results of [15]. Details thereof will appear elsewhere.
The conjecture asks about a genus one version of Alekseev and Torossian’s theorem [3] which states that there is a Lie algebra homomorphism
where \(\mathfrak {{grt}}_1\) is Drinfeld’s Grothendieck–Teichmüller Lie algebra and \(\mathfrak {krv}\) is the Kashiwara-Vergne Lie algebra (appearing as the symmetry group of the Kashiwara-Vergne problem in Lie theory).
The genus one version asks whether the natural formula proposed in [1, 2, 32] (see [28] for partial results) indeed defines a map
where \(\mathfrak {{grt}}_{ell}\) and \(\mathfrak {krv}_{ell}\) are genus one analogues of the above defined in [13] and [2, 32], respectively. Enriquez [13] shows that \(\mathfrak {{grt}}_{ell} = \mathfrak {{grt}}_1 < imes {\mathfrak {r}}^{ell}\) and [2, 32] show that the natural formula works for the \(\mathfrak {{grt}}_1\)-part. Thus it remains to show that the proposed formula defines a map
The strategy to prove this is to imitate the proof for the genus zero case in [33] that goes through Kontsevich’s graph complex \(\textsf{GC}\). In detail, [35, Theorem 1.1] computes \(\mathfrak {{grt}}_1 = H^0(\textsf{GC})\), whereas [33] show that the one-loop approximation of the latter is identified with \(\mathfrak {krv}\).
In the genus one case, [15, Corollary 3] gives a calculation of  and shows that it can be identified with the Lie algebra \({\mathfrak {r}}^{ell}\). The arguments of [33] can be adjusted to show the \(\le 1\)-loop part of \(\textsf{GC}_{(1),1}\) coincides with \(\mathfrak {krv}_{ell}\) as defined in [1, 2, 32], i.e.
and shows that it can be identified with the Lie algebra \({\mathfrak {r}}^{ell}\). The arguments of [33] can be adjusted to show the \(\le 1\)-loop part of \(\textsf{GC}_{(1),1}\) coincides with \(\mathfrak {krv}_{ell}\) as defined in [1, 2, 32], i.e.
where \(\textsf{GC}^{\le 1}_{(1),1}\) is the quotient of \(\textsf{GC}_{(1),1}\) by graphs of loop order \(>1\). Proposition 26 together with Theorem part (i) of 2 tell us that  and \(H^0(\textsf{GC}_{(1),1})\) agree up to finitely many classes. Treating those classes by hand one constructs a map
and \(H^0(\textsf{GC}_{(1),1})\) agree up to finitely many classes. Treating those classes by hand one constructs a map
Going through all those identifications in detail one checks that this map coincides with the one proposed in [1, 2, 32].
6 Degree bounds and proof of Theorem 2
6.1 Degree bounds on the "ordinary" graph complex
We shall make use of degree bounds on the hairy graph cohomology that are shown in [12, Theorem 1.6]. The hairy graph complexes are defined similarly to the graph complexes considered in this paper, but they are not the same. More precisely, analogously to the definitions in Sect. 3 above, we may consider a complex \(\textsf{HGC}_{0,2}^{[h]}\) of (isomorphism classes of) connected at least trivalent graphs with h hairs labeled \(1,\dots ,h\) and no tadpoles at vertices. The cohomological degree of such a graph \(\Gamma \in \textsf{HGC}_{0,2}^{[h]}\) is
Here we count the hairs as edges, but without a vertex at the end of the hair. For example, the graph

has three vertices, 6 edges and cohomological degree 0. The differential \(\delta =\delta _{split}\) is again given by splitting vertices. The graph complex \(\textsf{HGC}_{0,2}^{[h]}\) appears at various places in the literature, in particular in the embedding calculus, and it also computes (up to degree shifts) the top weight cohomology of the moduli spaces of curves. The following degree bound is known.
Proposition 28
(Chan-Galatius-Payne, [12, Theorem 1.6]) The cohomology of \(\textsf{HGC}_{0,2}^{[h]}\) is concentrated in cohomological degrees \(\ge -1\).
Proof
To account for different degree conventions, let us briefly recall the argument of [12]. There the authors show that the part of the graph cohomology with k internal (i.e., non-hair) edges, h hairs and of loop order g computes the weight 0 part of the compactly supported cohomology \(H^k_c({{\mathcal {M}}}_{g,h})\) of the moduli space of curves. But \({{\mathcal {M}}}_{g,h}\) has real dimension \(6g-6+2h\), and by a computation of Harer it has vcd \(4\,g-4 +h +\delta _{0,g}-\delta _{0,h}\). Hence we need to have \(k\ge 2\,g-2 +h-\delta _{0,g}+\delta _{0,h}\). Converting back to the degree d in our graph complex we find
\(\square \)
In fact, one sees from the proof that the bound is saturated for tree graphs only.
Remark 3
The statement of Proposition 28 can alternatively be deduced from the proof of [36, Lemmas 1.2, 1.4]. More precisely, in [36] only the part of \(\textsf{HGC}_{0,2}^{[h]}\) that is symmetric or antisymmetric under the interchange of labels \(1,\dots ,h\) is considered. However, the argument in that paper does not use the symmetrization, and goes through for the non-symmetrized complex as well. Furthermore, in [36] graphs are allowed to have tadpoles, but this does not alter the result, as can be seen by the arguments of Sect. 4 above.
6.2 Lower bound and proof of part (i) of Theorem 2
In view of part (i) of Theorem 1, that we have already proven and the weight 1 computation in Sect. 4.1, it suffices to show part (i) of Theorem 2 for \(\textsf{GC}_{(g),1}\).
Filter \(\textsf{GC}_{(g),1}\) by loop order, as in Sect. 4 above. Considering the associated spectral sequence, it then suffices to show that \(H(\textsf{GC}_{(g),1},\delta _{split})\) is concentrated in the degree range stated in part (i) of Theorem 2.
Consider first the case \(m=1\), and pick some basis \(c_1,\dots ,c_{2g}\) of \(H_1(W_{g,1})\). Then \((\textsf{GC}_{(g),1},\delta _{split})\) splits into a direct product of subcomplexes according to the number of decorations \(c_1,\dots ,c_{2g}\) in graphs. Concretely, fix some multi-index \({\underline{n}}=(n_1,\dots ,n_{2g})\) and denote the respective subcomplex by \(\textsf{GC}_{(g),1}^{{\underline{n}}}\subset \textsf{GC}_{(g),1}\). (It is spanned by graphs with \(n_1\) decorations \(c_1\), \(n_2\) decorations \(c_2\) etc.) This subcomplex is then identified with a summand of the complex \(\textsf{HGC}_{0,2}^{[|n|]}\), concretely
with the symmetric groups acting by permuting hair labels. The additional degree shift in (29) reflects the shift by \(+1\) in the definitions (16) and (28) of the degrees on \(\textsf{GC}_{(g),1}\) and \(\textsf{HGC}_{0,2}^{[|{\underline{n}}|]}\) respectively. Invoking Proposition 28 this then shows that \(H(\textsf{GC}_{(g),1}^{{\underline{n}}},\delta _{split})\) is concentrated in non-negative degrees. Hence the same holds for \(H(\textsf{GC}_{(g),1})\), finishing the proof for the case \(m=1\). Note that the complexes \({{\,\textrm{gr}\,}}^W\textsf{GC}_{(g),1}\) are isomorphic for any odd m, up to overall degree shifts. Concretely, changing m by \(+2\) reduces the degree of a given graph by 2W. Hence the vanishing statement of 2 (i) follows for odd m.
For even m one has to mind that the decorations by \(H_m(W_{g,1})\) are now even objects. However, the same proof as above goes through, except that one has to antisymmetrize, instead of symmetrize over hair labels in (29).
In fact, in either case one sees from the proof of Proposition 28 that the degree bound is saturated (only) by trees, and in fact only trivalent such trees.
6.3 Proof of part (ii) of Theorem 2
By part (ii) of Theorem 1 we know that for \(g\ge 2\) we have that \(H(\textsf{GC}^{\text {ex}}_{(g)})\) is a summand (as a graded vector space) of \(H(\textsf{GC}_{(g),1})\), in a way preserving the weight grading. Hence part (ii) of Theorem 2 follows immediately from part (i).
6.4 Graph complex with two-colored edges: recollection from [9]
Let \(\Gamma \) be a graph with vertex set \(\{1,\dots ,N\}\) and k (ordered) edges. Consider the complex
with C a two-dimensional acyclic complex,
we interpret the natural basis elements of \(C^{\otimes k}\) as assignments of “colors"Footnote 3 to edges of \(\Gamma \), say the \({\mathbb {Q}}[1]\) corresponding to a solid edge, and \({\mathbb {Q}}\) to a dashed edge. Hence \(C^{\otimes k}\) has a natural basis that can be identified with colorings of the edges of \(\Gamma \) such as the following.

The differential acts by summing over edges, and replacing a solid edge by a dashed one. It is clear that the complex \(C^{\otimes k}\) is acyclic if \(k\ge 1\), i.e., if \(\Gamma \) has at least one edge.
Let \(I_{disc}\subset C^{\otimes k}\) be the subcomplex spanned by all colored graphs for which the subgraph comprised of the vertices and the solid edges is not connected. We define
to be the quotient complex obtained by setting to zero all such solid-disconnected graphs. We note that, obviously, \(C_\Gamma \) is bounded and concentrated in cohomological degrees \(-k,\dots , 1-N\).
Lemma 29
(Lemma 8.8 of [9]) The cohomology of \(C_\Gamma \) is concentrated in the top degree \(1-N\).
The cohomology is hence given by linear combinations of solid trees, modulo the differential of solid one-loop graphs.
Proof
We proceed by induction on the number N of vertices and the number k of edges. The base cases (either \(N=1\) or \(k=0\)) are trivial. Suppose we know the statement for all graphs with \(<N\) vertices or with N vertices and \(<k\) edges.
Pick some edge (i, j). We may assume \(i\ne j\) for clarity, for otherwise \(C_\Gamma \) is obviously acyclic. We have a splitting of graded vector spaces

where \(V_0\subset C_\Gamma \) is spanned by graphs in which the edge (i, j) is solid, and \(V_1\) spanned by graphs where it is dashed. The arrows indicate the pieces of the differential. We hence interpret \(C_\Gamma \) accordingly as a (quite trivial) two-column double complex, with \(V_0\) constituting the first column and \(V_1\) the second. We take the associated column-wise spectral sequence, which converges to the cohomology by finite dimensionality of our complexes. The first page is given by the column-wise cohomology, i.e.,
But the complex \(V_0\) is isomorphic to \(C_{\Gamma /(i,j)}\), with \(\Gamma /(i,j)\) the graph obtained by contracting the edge (i, j). Similarly \(V_1\) is isomorphic to \(C_{\Gamma \setminus (i,j)}\), with \(\Gamma \setminus (i,j)\) obtained by removing edge (i, j) from \(\Gamma \). Invoking the induction hypothesis we are hence done. \(\square \)
6.5 Upper bound and proof of part (iii) of Theorem 2
We next want to show the vanishing statement Theorem 2 (iii), thus finishing the proof of Theorem 2. By using Theorem 1 it is sufficient to show the statement for  , and for the other two complexes it then follows. More precisely, By Theorem 1 (i) we know that
, and for the other two complexes it then follows. More precisely, By Theorem 1 (i) we know that  for weights \(W\ge 2\). But the weight one-part \({{\,\textrm{gr}\,}}^1\textsf{GC}_{(g),1}\) is concentrated in degree \(1-m\). Similarly, by Theorem 1 (ii) we have that \({{\,\textrm{gr}\,}}^W H(\textsf{GC}^{\text {ex}}_{(g)})\) is a summand of \({{\,\textrm{gr}\,}}^W H(\textsf{GC}_{(g),1})\) as long as \(g\ge 2\), and by assumption we have \(g\ge W+2\ge 3\).
for weights \(W\ge 2\). But the weight one-part \({{\,\textrm{gr}\,}}^1\textsf{GC}_{(g),1}\) is concentrated in degree \(1-m\). Similarly, by Theorem 1 (ii) we have that \({{\,\textrm{gr}\,}}^W H(\textsf{GC}^{\text {ex}}_{(g)})\) is a summand of \({{\,\textrm{gr}\,}}^W H(\textsf{GC}_{(g),1})\) as long as \(g\ge 2\), and by assumption we have \(g\ge W+2\ge 3\).
Hence we need to show part (iii) of Theorem 2 only for  . In fact, we will equivalently show the dual vanishing statement for the graded dual complex
. In fact, we will equivalently show the dual vanishing statement for the graded dual complex  . Concretely we need to show that
. Concretely we need to show that

for \(k<(m-1)W\) and \(g\ge W+2\). Let us filter  by the total number of vertices by setting
by the total number of vertices by setting  to be the subspace spanned by graphs with \(\le p\) vertices. By finite dimensionality of the complex the associated spectral sequence converges to the cohomology. The differential on the associated graded is just the part \(d_{cut}\) of the full differential. Hence it suffices to show that
to be the subspace spanned by graphs with \(\le p\) vertices. By finite dimensionality of the complex the associated spectral sequence converges to the cohomology. The differential on the associated graded is just the part \(d_{cut}\) of the full differential. Hence it suffices to show that

To go further, we would like to apply Lemma 9. To this end we check:
Lemma 30
Let mD be the total degree of decorations appearing in a graph \(\Gamma \) in \({{\,\textrm{gr}\,}}^W {\textsf{G}}_{(g),1}\),  or \({{\,\textrm{gr}\,}}^W {\textsf{G}}_{(g)}\). Then
or \({{\,\textrm{gr}\,}}^W {\textsf{G}}_{(g)}\). Then
The bound is saturated for tree graphs.
Proof
For a graph with e edges, v vertices and decorations of degree mD the weight is by definition \(W=2(e-v)+D\), and hence \(D=W-2(e-v)\). Since for a connected graph \(e-v\ge -1\), with equality precisely for tree graphs, the result follows. \(\square \)
We hence find that the \(\textrm{OSp}_g\)-representation  is of order \(\le W+2\), in the notation of Sect. 2.2, as is clear from the definition, see in particular (8).
is of order \(\le W+2\), in the notation of Sect. 2.2, as is clear from the definition, see in particular (8).
But by Lemma 9 it then suffices to check that

for all \(M=0,1,\dots , W+2\) and \(k<(m-1)W\). Suppose next that \(g\ge W+2\). Then we may apply classical invariant theory in the form of Theorem 10. This then identifies

with a complex of graphs with no decorations, but two types of edges, say solid and dashed, and M external dashed legs. Here is an example graph for \(M=3\) and \(W=6\):

Each dashed edge represents a copy of the diagonal as in Theorem 10. The differential \(d_{cut}\) acts by replacing a solid edge by a dashed edge, as long as this leaves the solid subgraph connected.

Note that the differential \(d_{cut}\) does not alter the core graph, by which we mean the graph obtained by forgetting the color (solid or dashed) of edges. Hence  splits as a direct sum of subcomplexes according to core graphs \(\Gamma \), each of which has the form
splits as a direct sum of subcomplexes according to core graphs \(\Gamma \), each of which has the form
with \(\Gamma '\) obtained from \(\Gamma \) by removing the legs, \(C_{\Gamma '}\) the two-colored (solid-dashed) complex from the previous subsection, \(\textrm{Aut}(\Gamma )\) the (finite) automorphism group of the core graph \(\Gamma \) and \(K(\Gamma )\) some one-dimensional representation of \(\textrm{Aut}(\Gamma )\) taking care of signs and degrees. But by Lemma 29 we know that \(H(C_{\Gamma '})\) is represented by two-colored graphs whose solid subgraph is a spanning tree. The same is hence true for any direct summand of \(C_{\Gamma '}\), and in particular for (34). But a graph in  of weight W with e edges has cohomological degree
of weight W with e edges has cohomological degree
For tree graphs one has furthermore that \(D=W+2\), and also \(e\le D-3=W-1\) from the condition that all vertices need to be at least trivalent. It follows that
thus finishing the proof of part (iii) of Theorem 2. \(\square \)
7 The Chevalley Eilenberg complex, and proof of Theorem 3
7.1 Definition, and graphical interpretation
We define the Chevalley-Eilenberg complexes of the three dg Lie algebras considered in this paper as the cobar constructions of the respective graded dual Lie coalgebras

In particular, the Chevalley-Eilenberg complexes thus defined are dg commutative algebras, and graphically the commutative product is given by the disjoint union of graphs. They furthermore inherit the weight grading from the Lie algebras. The summands \({{\,\textrm{gr}\,}}^W C_{CE}(\cdots )\) of fixed weight are furthermore finite dimensional dg vector spaces since the weight on the Lie algebras is positive.
In fact, by the very definition of the Lie bracket of our graphical dg Lie algebras, we can identify the Chevalley-Eilenberg complexes with the respective complexes of (possibly) non-connected graphs from Sect. 3,

Here we should remark that the interpretation of \(\textsf{fG}^{\text {ex}}_{(g)}\) as a complex of graphs requires us to also provide a suitable graphical interpretation of the factors \(\mathfrak {osp}^{nil,c}_g\cong {\mathbb {Q}}^{2g}[-m]\). In \(\textsf{fG}^{\text {ex}}_{(g)}\) we shall represent such a factor by a special (crossed) univalent vertex with a decoration in \(H^m(W_g)\):

Here the special vertex formally carries degree \(+1\) in the Chevalley-Eilenberg complex, so that the cohomological degree of a graph \(\Gamma \) with v (“normal") vertices, c crossed vertices, e edges and total decoration degree mD is
This formula applies to all three Chevalley-Eilenberg complexes, with \(c=0\) in the cases \(\textsf{fG}_{(g),1}\) and  .
.
We shall also give the combinatorial interpretation of the differential. The differential on the Chevalley-Eilenberg complex consists of two pieces, induced from the internal differential of the Lie coalgebra, and the Lie cobracket. These terms neatly unite in the Chevalley complex to give a total differential of the form \(d=d_{c} + d_{cut} + d_{mul}''+ d_{\times }\), with the three pieces as follows. The piece \(d_c\) sums over all edges, contracting the edge. The piece \(d_{cut}\) sums over all edges, replacing the edge by a pair of decorations. The piece \(d_{mul}''\) is only present in the third of our three Chevalley-Eilenberg complexes (i.e., \(C_{CE}(\textsf{GC}^{\text {ex}}_{(g)})\)) and acts by multiplying two decorations and contracting an adjacent edge as in Sect. 3. The piece \(d_{\times }\) is also only present in \(C_{CE}(\textsf{GC}^{\text {ex}}_{(g)})\), and acts by creating a crossed vertex. There are two kinds of terms, the first coming from the Lie cobracket:

The second type of term comes from the piece of the differential \({\textsf{G}}_{(g)}\rightarrow \mathfrak {osp}_{g}^{nil, c}\), and this only acts on isolated vertices with exactly three decorations in \(H^m(W_g)\),

Let us also introduce a second grading, the grading by E-number, on our complexes. On \(C_{CE}(\textsf{GC}_{(g),1})\) and  the E-number of some graph (in the graphical interpretation of the Chevalley-Eilenberg complex) is simply the number of edges. For \(C_{CE}(\textsf{GC}^{\text {ex}}_{(g)})\) we define the E-number as the number of edges minus the number of special vertices “\(\times \)”. In any case, note that the cohomological degree is then expressed through the weight W and E-number E as
the E-number of some graph (in the graphical interpretation of the Chevalley-Eilenberg complex) is simply the number of edges. For \(C_{CE}(\textsf{GC}^{\text {ex}}_{(g)})\) we define the E-number as the number of edges minus the number of special vertices “\(\times \)”. In any case, note that the cohomological degree is then expressed through the weight W and E-number E as
In particular note that the differential is homogeneous of degree \(-1\) with respect to the E-number, and hence the cohomology inherits a grading by E-number. In fact, one can think of the E number as an m-independent shifted version of the homological degree, that will be convenient to use below. Note that Theorem 3 states that for g large enough the cohomology of our Chevalley-Eilenberg complexes becomes concentrated in E-number 0.
7.2 Proof of Theorem 3 in the first two cases
Let us turn to the proof Theorem 3 for the cases \(C_{CE}(\textsf{GC}_{(g),1})\) and  . We will show the following refined version.
. We will show the following refined version.
Proposition 31
We have that

if either of the following conditions is satisfied:
-
(i)
\(k>mW\).
-
(ii)
\(k<mW\) and \(g\ge 2k - (2\,m-3)W+1\).
In particular if \(g\ge 3W\) and \(k\ne mW\), then one of the two conditions above is always satisfied.
We first note that the E-number in \(C_{CE}(\textsf{GC}_{(g),1})\) and  is just the number e of edges in the graph, and hence non-negative. It follows that, trivially,
is just the number e of edges in the graph, and hence non-negative. It follows that, trivially,

if \(k>mW\), and hence the first statement of Proposition 31 follows as well.
For the second statement we will need invariant theory and the following Lemma.
Lemma 32
The maximal number of decorations of a non-trivial graph  (resp. \(\Gamma \in C_{CE}(\textsf{GC}_{(g),1})\)) of weight W and E-number (i.e., number of edges) e is
(resp. \(\Gamma \in C_{CE}(\textsf{GC}_{(g),1})\)) of weight W and E-number (i.e., number of edges) e is
In particular the maximum number of decorations in any graph of weight W is 3W. The bound is saturated by a graph with no edges, and all vertices carrying three decorations.
Proof
Let v be the number of vertices in a graph \(\Gamma \) and D the number of decorations. We have that \(W=2(e-v)+D\) and, by the trivalence condition, \(3v\le 2v+D\). Eliminating v from this system of inequalities yields \(D\le 3W-2e\). \(\square \)
We return to the proof of statement (ii) of Proposition 31. In fact, we shall focus on the case of  , with the statements for \(\textsf{GC}_{(g),1}\) being shown analogously.
, with the statements for \(\textsf{GC}_{(g),1}\) being shown analogously.
From Lemma 32 we see in particular that the representation  of \(\textrm{OSp}_g\) is of order \(\le 3W\), and specifically the part of E-number e is a representation of order \(\le 3W-2e\) in the sense of Sect. 2.2. Equivalently, using that the cohomological degree is \(k=mW-e\), the degree k-part
of \(\textrm{OSp}_g\) is of order \(\le 3W\), and specifically the part of E-number e is a representation of order \(\le 3W-2e\) in the sense of Sect. 2.2. Equivalently, using that the cohomological degree is \(k=mW-e\), the degree k-part  is of order \(\le 3W-2(mW-k)=2k-(2\,m-3)W\).
is of order \(\le 3W-2(mW-k)=2k-(2\,m-3)W\).
Let us define the complex of invariants

To show the part (ii) of Proposition 31, it suffices by Lemma 9 to check that
for each \(k<mW\) and \(M\le 3W-2e=2k-(2\,m-3)W\), provided \(g\ge 3W-2e+1\). Also note that one has natural maps of complexes
Furthermore, it follows from Theorem 10 and Lemma 32 that these maps are isomorphisms on the degree k part
if \(2g\ge M+3W-2e=M+2k-(2m-3)W\). We shall denote the stable limit by
Similarly to the proof in Sect. 6.5 the complex \(J_{\infty ,M,W}\) is identified with a complex of graphs with two kinds of edges, say “solid” and “dashed”, but without decorations, such that each dashed edge represents a copy of the diagonal element \(\Delta _1\) to be inserted at its endpoints. There are precisely M external dashed legs. See (32) for a picture. Note however that in contrast to Sect. 6.5 above the solid subgraph does now not need to be connected.
The differential is \(d=d_c + d_{cut}\) with \(d_c\) contracting an edge and \(d_{cut}\) replacing it by a dashed one as in (33).
Lemma 33
The cohomology of \(J_{\infty ,M,W}\) is concentrated in degree \(k=mW\).
Proof
Using again a spectral sequence on the filtration by the number of vertices, it suffices to show that the cohomology of \((J_{\infty ,M,W}, d_{cut})\) is concentrated in degree mW. However, note that in contrast to the proof in Sect. 6.5 there is no connectivity requirement on the resulting graphs in the present case. We may hence introduce a homotopy
where the sum is over all dashed edges e between two vertices (i.e., not external legs) and \(\text {undash}_e(\Gamma )\) is the graph obtained by replacing the dashed edge e by a normal one, which becomes the first in the ordering of edges to fix the sign. One then verifies that
with \(N(\Gamma )\) the number of edges (dashed or normal alike) between two vertices of \(\Gamma \). Invoking Lemma 7 this implies in particular that the cohomology is concentrated in E-number zero, or equivalently in cohomological degree \(k=mW\). \(\square \)
We return to the proof of Proposition 31. We know (from Theorem 10) that the map
is an isomorphism for \(2g\ge M + 2k - (2m-3)W\). It follows that the induced map
is an isomorphism for \(2g\ge M + 2k+2 - (2m-3)W\). In particular, if \(g\ge 2k - (2m-3)W+1\) then
for each \(k<mW\) and \(M\le 2k-(2\,m-3)W\). This shows Proposition 31 for the case  .
.
Note that the argument is agnostic of whether or not the graphs have tadpoles, and so the same proof goes through for the case \(C_{CE}(\textsf{GC}_{(g),1})\). \(\square \)
7.3 Proof of Theorem 3 for \(\textsf{GC}^{\text {ex}}_{(g)}\)
We shall proceed analogously to the previous subsection, with some additional complications. For simplicity, we shall also restrict to showing Theorem 3 and not the refined genus bounds as in Proposition 31 in this case.
Lemma 34
Let \(\Gamma \in {{\,\textrm{gr}\,}}^W C_{CE}(\textsf{GC}^{\text {ex}}_{(g)})\) be a graph of weight W with total degree of decorations mD. Then \(D\le 3W\). If \(\Gamma \) has E-number E then \(D\le 3W-2E\).
The bound \(D\le 3W\) is again saturated by a graph with no edges, and all vertices carrying three decorations.
Proof
Let v be the number of (non-crossed) vertices in a graph \(\Gamma \), c the number of crossed vertices, e the number of edges and D the number of decorations. To be concrete, a factor in \(\mathfrak {osp}_g^{(nil)}\) counts as zero non-crossed vertices, one crossed vertex, zero edges, and one decoration. Then the weight of \(\Gamma \) is \(W=2(e-v)+D\). By the trivalence condition we have \(3v+c\le 2v+D\). Eliminating v from this system of inequalities yields \(D\le 3W-2e-2c=3W-2E-4c\), and this is \(\le 3W\) and \(\le 3W-2E\) since \(e,c\ge 0\). \(\square \)
As before, to show Theorem 3 it suffices to show that
has cohomology concentrated in E-number 0, for all \(M\le 3W\). Furthermore, for \(2g\ge 3W+M\) we can again invoke Theorem 10 to compute \(K_{g,M,W}\) explicitly. Again \(K_{g,M,W}\) may be interpreted as a complex of graphs with two kinds of edges, solid and dashed, with the dashed edges corresponding to copies of the "reduced" diagonal element
or graphically

In the following we always quietly assume that \(2g\ge 3W+M\), so that we are in the “stable” situation.Footnote 4 On \(K_{g,M,W}\) the differential is then \(d=d_{c}+d_{cut}+d_{mul}''+d_\times \) with the pieces acting as follows
-
\(d_c\) sums over (solid) edges contracting them as before.
-
\(d_{cut}\) sums over solid edges, replacing them by a diagonal \(\Delta =\omega \otimes 1 +1\otimes \omega + \Delta _1\) (with \(\omega \) being again the top cohomology class). If the cutting procedure produces a vertex v of valence less than three (and hence necessarily of valence two), then the graph is set to zero.
-
\(d_{mul}''\) removes a vertex with precisely 2 incident dashed half-edges and one solid half-edge, by contracting the solid edge, adding one \(\omega \)-decoration, and fusing the two dashed half-edges. If the dashed half-edges form a tadpole then they are instead removed and the graph is multiplied by \((-1)^m 2g\).

-
The piece \(d_\times \) comes from the \(\mathfrak {osp}_g^{nil,c}\)-coaction on \({\textsf{G}}_{(g)}\) and the part of the differential \({\textsf{G}}_{(g)}\rightarrow \mathfrak {osp}_{g}^{nil, c}\). The former piece replaces an \(\omega \)-decoration by a dashed edge towards a crossed vertex. Furthermore, it replaces a dashed edge between internal vertices by a crossed vertex and one dashed edge, attached to either side. Pictorially
 (35)
(35) (36)
(36)Similarly, \(d_\times \) acts on dashed edges that are not between two internal vertices in the same manner, and one drops the respective graphs if they are not in the complex. More explicitly, the complete list of cases is as follows, with an empty endpoint of the edge denoting an external leg.
 (37)
(37) (38)
(38) (39)
(39)All the above terms, coming from the Lie cobracket, introduce a new crossed vertex but do not alter the number of vertices otherwise. The terms stemming from the differential read:

Here open dashed edges can be connected to internal vertices, or be external legs.
To go further define the subspace \({{\tilde{K}}}_{g,M,W}\subset K_{g,M,W}\) to be spanned by graphs that contain one of the following features:
-
A crossed vertex.
-
An \(\omega \)-decoration.
-
A connected component that is of the form

that is, the connected component contains a single vertex with a dashed tadpole and a dashed external leg. We will temporarily call such connected components islands in the following.
We will temporarily call the features above the forbidden features.
Lemma 35
The subspace \({{\tilde{K}}}_{g,M,W}\subset K_{g,M,W}\) is closed under the differential.
Proof
One just goes through the list of pieces of the differential and checks that no piece can remove one of the forbidden features above without introducing another. In other words the number of forbidden features is left the same or increased by the differential. \(\square \)
Lemma 36
The projection to the quotient
is a quasi-isomorphism.
Proof
We introduce a descending filtration on \(K_{g,M,W}\) by the number of forbidden features. Concretely, let \({\mathcal {F}}^pK_{g,M,W}\) be spanned by graphs with \(\ge p\) forbidden features. In particular \({\mathcal {F}}^1K_{g,M,W}={{\tilde{K}}}_{g,M,W}\). It then suffices to check that the associated graded pieces \({{\,\textrm{gr}\,}}^p K_{g,M,W}\) (with respect to the filtration by the number of forbidden features) are acyclic for \(p\ge 1\). Considering the above description of the differential, the pieces contributing to the associated graded are \(d_{cut}\), \(d_c\), and the pieces (35) and (37) of \(d_\times \). Let us denote these latter pieces of \(d_\times \) by \(d_\times '\). We hence have to show that the complex \(({{\tilde{K}}}_{g,M,W},d_c+d_{cut}+d_\times ')\) is acyclic. By taking a further associated graded with respect to the increasing filtration by the number of solid edges it in fact suffices that \(({{\tilde{K}}}_{g,M,W},d_\times ')\) is acyclic.
But this can be achieved by introducing the homotopy
with the sum running over all crossed vertices x, and \(G_x(\Gamma )\) being defined by replacing the vertex x according to the following rule:
-
If x is connected to an internal vertex, remove x and place a decoration \(\omega \) at the internal vertex.
-
If x is connected to an external leg, remove x, glue in an island instead, and multiply the graph by \(\frac{1}{2+(-1)^m 2g}\). Note that since \(W\ge 1\) and \(g\ge 3W\) we automatically have \(2+(-1)^m 2g\ne 0\).
One then checks by explicit computation that
with \(N(\Gamma )\) being the number of forbidden features. Since by construction \(N(\Gamma )>0\) for any graph \(\Gamma \in {{\tilde{K}}}^L\) we are done, using Lemma 7. \(\square \)
Note that the remaining pieces of the differential on \(K_{g,M,W}/{{\tilde{K}}}_{g,M,W}\) are \(d_c+d_{cut}\), since the \(d_\times \)-terms produce a crossed vertex, and \(d_{mul}''\) creates an \(\omega \)-decoration. We may now proceed similarly to the previous subsection to compute the cohomology of \(K_{g,M,W}/{{\tilde{K}}}_{g,M,W}\). We define a filtration on \(K_{g,M,W}/{{\tilde{K}}}_{g,M,W}\) by defining \({\mathcal {F}}^p K_{g,M,W}/{{\tilde{K}}}_{g,M,W}\) to be spanned by graphs with \(\le p\) edges (solid or dashed). The associated graded is identified with \((K_{g,M,W}/{{\tilde{K}}}_{g,M,W},d_{cut})\). As in the previous subsection this differential has a homotopy and we conclude that the inclusion \({\mathcal {F}}^0 K_{g,M,W}/{{\tilde{K}}}_{g,M,W}\rightarrow K_{g,M,W}/{{\tilde{K}}}_{g,M,W}\) is a quasi-isomorphism. Since \({\mathcal {F}}^0 K_{g,M,W}/{{\tilde{K}}}_{g,M,W}\) is concentrated in E-number zero (since it is spanned by graphs with no solid edges and no crossed vertices), we find that the spectral sequence abuts by degree reasons. Overall we have shown that \(H(K_{g,M,W})\) is concentrated in E-number zero, thus showing the remaining piece of Theorem 3. \(\square \)
7.4 Formality and presentation
Let C temporarily denote any of the three Chevalley-Eilenberg complexes above. Denote by \({{\,\mathrm{\textrm{tr}}\,}}^{[m]} (C)\) the truncation as defined in (5). Note that \({{\,\mathrm{\textrm{tr}}\,}}^{[m]} (C)\) consists of the elements of C of positive E-number, and the closed elements of E-number zero. Using the notation \(H^{[m]}(C)\) (see (4)) for the part of the cohomology of C of E-number zero we have a zig-zag of dg commutative algebras
Theorem 3 then implies that this zigzag of dg commutative algebra morphisms induces an isomorphism on the pieces of the cohomology of weight \(W\le \frac{g}{3}\). In particular C is formal up to weight g/3. Furthermore note that since the E-number for the cases of \(C=C_{CE}(\textsf{GC}_{(g),1})\) and  is nonnegative, we have that \({{\,\mathrm{\textrm{tr}}\,}}^{[m]} (C)=C\) in these cases. Together we find the following Corollary of Theorem 3.
is nonnegative, we have that \({{\,\mathrm{\textrm{tr}}\,}}^{[m]} (C)=C\) in these cases. Together we find the following Corollary of Theorem 3.
Corollary 37
The morphisms of dg commutative algebras

induce isomorphisms on the weight W-pieces of the cohomology for \(g\ge 3W\).
In particular, the \(E=0\)-parts

of the cohomology are given by graphs without edges, modulo the differential of graphs with exactly one edge. Note also that any graph without edges is just a union of single vertices carrying at least three decorations. A graph with a single edge in addition either has a pair of vertices connected by that edge, or the edge forms a tadpole. In particular, one has the following presentations
-
 is generated as a graded commutative algebra by the graded vector space \(S^{\ge 3} (H^m(W_{g,1})[-m])\). We denote the generator corresponding to a monomial \(a_1\cdots a_k\in S^{\ge 3} (H^m(W_{g,1})[-m])\) by \(c(a_1\cdots a_k)\). Then the relations read, for \((e_i)\) a basis of \(H^m(W_{g,1})\) and \((e_i^*)\) the Poincaré dual basis, $$\begin{aligned} c(a_1\cdots a_k) = \sum _{i=1}^{2g}&c(a_1\cdots a_l e_i) c(e_i^* a_{l+1}\cdots a_k) \quad \text {for }l=2,\dots k-2 \end{aligned}$$(41)$$\begin{aligned}&\sum _{i=1}^{2g} c(a_1\cdots a_ke_ie_i^*) = 0. \end{aligned}$$(42)
is generated as a graded commutative algebra by the graded vector space \(S^{\ge 3} (H^m(W_{g,1})[-m])\). We denote the generator corresponding to a monomial \(a_1\cdots a_k\in S^{\ge 3} (H^m(W_{g,1})[-m])\) by \(c(a_1\cdots a_k)\). Then the relations read, for \((e_i)\) a basis of \(H^m(W_{g,1})\) and \((e_i^*)\) the Poincaré dual basis, $$\begin{aligned} c(a_1\cdots a_k) = \sum _{i=1}^{2g}&c(a_1\cdots a_l e_i) c(e_i^* a_{l+1}\cdots a_k) \quad \text {for }l=2,\dots k-2 \end{aligned}$$(41)$$\begin{aligned}&\sum _{i=1}^{2g} c(a_1\cdots a_ke_ie_i^*) = 0. \end{aligned}$$(42) -
\({{\tilde{A}}}_{(g),1}\) is also generated as a graded commutative algebra by the graded vector space \(S^{\ge 3} (H^m(W_{g,1})[-m])\), but only with the relation (41), but not (42).
7.5 Stabilization and degrees
We note that one has the following lower degree bounds on the complexes above.
Corollary 38
-
(i)
The maximum E-number of a graph \(\Gamma \) of weight W in \(C_{CE}(\textsf{GC}_{(g),1})\) or
 or \(C_{CE}(\textsf{GC}^{\text {ex}}_{(g)})\) is \(\frac{3}{2} W\).
or \(C_{CE}(\textsf{GC}^{\text {ex}}_{(g)})\) is \(\frac{3}{2} W\). -
(ii)
The minimal cohomological degree of a graph \(\Gamma \) of weight W in \(C_{CE}(\textsf{GC}_{(g),1})\) or
 or \(C_{CE}(\textsf{GC}^{\text {ex}}_{(g)}\) is \((m-\frac{3}{2})W\).
or \(C_{CE}(\textsf{GC}^{\text {ex}}_{(g)}\) is \((m-\frac{3}{2})W\).
Proof
Let D be the number of decorations and E the E-number of \(\Gamma \). Then by Lemmas 32 and 34 we have the inequality \(D\le 3W-2E\). Hence \(2E\le 3W-D\le 3W\) since \(D\ge 0\). This shows the first statement. The second follows from the formula for the cohomological degree k, \(k=mW-E\). \(\square \)
Using this result we see that for \(m\ge 2\) and each fixed k only finitely many weights W contribute to the degree k piece of our Chevalley-Eilenberg complexes. Hence the degree k cohomology also stabilizes (in the sense discussed) for \(g\rightarrow \infty \). Here we just state for reference the corresponding stabilization result in degree that is an immediate reformulation of Proposition 31.
Corollary 39
Suppose that \(m\ge 2\). Then the maps

are isomorphisms as soon as \(g\ge 2k\).
Proof
One just notes that \((2m-3)W\ge W\ge 1\) in the statement of Proposition 31. \(\quad \square \)
7.6 Invariant part
Setting \(M=0\) in the proofs of Sects. 7.2 and 7.3 we see that we have in particular computed the cohomology of the \(\textrm{OSp}_g\)-invariant piece of the Chevalley-Eilenberg complex.
Proposition 40
-
(1)
For \(2g\ge 2k-(2m-3W) +2\) or \(k>mW\) we have that
 .
. -
(2)
Let \(\kappa _j\) represent the graph

Then the map
$$\begin{aligned} {{\,\textrm{gr}\,}}^W{\mathbb {Q}}[\kappa _1,\kappa _2,\dots ]\rightarrow {{\,\textrm{gr}\,}}^W H_{CE}(\textsf{GC}_{(g),1})^{\textrm{OSp}_g} \end{aligned}$$is an isomorphism in degree k if \(2g\ge 2k-(2m-3W) +2\) or \(k>mW\).
-
(3)
Similarly, the map
$$\begin{aligned} {{\,\textrm{gr}\,}}^W{\mathbb {Q}}[\kappa _1,\kappa _2,\dots ]\rightarrow {{\,\textrm{gr}\,}}^W H_{CE}(\textsf{GC}^{\text {ex}}_{(g)})^{\textrm{OSp}_g} \end{aligned}$$is an isomorphism for \(2g\ge 3W\).
Proof
One follows again the proofs of Sects. 7.2 and 7.3, but with M in these proofs set to zero. The condition on g (for the cohomology to agree with the stable one) in Sect. 7.2 then becomes \(2g\ge M+2k-(2m-3W) +2=2k-(2m-3W) +2\). For the less refined argument of Sect. 7.3 it becomes \(2\,g\ge 3W\).
Hence it suffices to consider the stable cohomology for \(M=0\). Revisiting the proofs above this is computed to be 0 for  , and (freely) spanned by classes without any edges (i.e., unions of the \(\kappa _j\)’s) for the other two cases. \(\square \)
, and (freely) spanned by classes without any edges (i.e., unions of the \(\kappa _j\)’s) for the other two cases. \(\square \)
8 Koszulness and quadratic presentations of the cohomology
We have shown so far that for large enough g the cohomology of the weight W part of our dg Lie algebras \(\textsf{GC}_{(g),1}\),  and \(\textsf{GC}^{\text {ex}}_{(g)}\) becomes concentrated in the single degree \((1-m)W\). We have also shown that the cohomology of the Chevalley-Eilenberg complex becomes concentrated in degree mW. In this section we shall derive quadratic presentations of the cohomology in those degrees, and show that both cohomologies (i.e., the cohomology of the Lie algebra, and that of its Chevalley-Eilenberg complex) are Koszul dual (in a range, for g large).
and \(\textsf{GC}^{\text {ex}}_{(g)}\) becomes concentrated in the single degree \((1-m)W\). We have also shown that the cohomology of the Chevalley-Eilenberg complex becomes concentrated in degree mW. In this section we shall derive quadratic presentations of the cohomology in those degrees, and show that both cohomologies (i.e., the cohomology of the Lie algebra, and that of its Chevalley-Eilenberg complex) are Koszul dual (in a range, for g large).
8.1 A version of Proposition 13
We first formulate a slightly technical version of Proposition 13 that is appropriate for our setting.
Proposition 41
Let \(W_0\ge 2\) and \(\alpha \) be integers. Suppose that \({\mathfrak {g}}\) is a dg Lie algebra with an additional positive (“weight") grading, satisfying the following properties.
-
Each graded piece \({{\,\textrm{gr}\,}}^W{\mathfrak {g}}\) is finite dimensional.
-
\({{\,\textrm{gr}\,}}^W H({\mathfrak {g}})\) is concentrated in cohomological degree \(\alpha W\) for any \(W\le W_0\).
-
The cohomology of the weight W piece of the cobar construction \({{\,\textrm{gr}\,}}^W \texttt{B}^c {\mathfrak {g}}^c\) is concentrated in cohomological degree \((1-\alpha )W\) for any \(W\le W_0\).
Then the following hold:
-
(i)
\({\mathfrak {g}}\) is formal up to weight \(W_0\) in the sense that the zigzag of morphisms of dg Lie algebras
$$\begin{aligned} {\mathfrak {g}}\leftarrow {{\,\mathrm{\textrm{tr}}\,}}^{[\alpha ]}{\mathfrak {g}}\rightarrow H^{[\alpha ]}({\mathfrak {g}}) \end{aligned}$$(see (5), (4) for the notation) induces a zigzag of quasi-isomorphisms of complexes on the part of weight W for any \(W\le W_0\).
-
(ii)
Similarly, the dg commutative algebra \(\texttt{B}^c {\mathfrak {g}}^c\) is formal up to weight \(W_0\) in the sense that the zigzag of morphisms of dg commutative algebras
$$\begin{aligned} \texttt{B}^c {\mathfrak {g}}^c \leftarrow {{\,\mathrm{\textrm{tr}}\,}}^{[1-\alpha ]} \texttt{B}^c {\mathfrak {g}}^c \rightarrow H^{[1-\alpha ]}(\texttt{B}^c {\mathfrak {g}}^c) \end{aligned}$$induces quasi-isomorphisms on the part of weight \(W\le W_0\).
-
(iii)
Let \(V:={{\,\textrm{gr}\,}}^1 H({\mathfrak {g}})\cong {{\,\textrm{gr}\,}}^1 H(\texttt{B}{\mathfrak {g}})[-1]\), \(R:= {{\,\textrm{gr}\,}}^2\,H(\texttt{B}{\mathfrak {g}})\) and \(S:={{\,\textrm{gr}\,}}^2\,H({\mathfrak {g}}^c)\). Then the maps
$$\begin{aligned} R&\rightarrow \wedge ^2V&S\rightarrow S^2(V[-1]^*) \end{aligned}$$(43)given by the (reduced) coproduct and the cobracket are injections. We denote the images by R and S as well, abusing notation. Furthermore, S is (up to degree shift) the annihilator of R if we identify \((\wedge ^2V)^*\cong S^2(V[-1]^*)[2]\).
-
(iv)
The graded Lie algebra \({\mathfrak {t}}\) and graded commutative algebra A defined via the quadratic presentations
$$\begin{aligned} {\mathfrak {t}}&= \textrm{FreeLie}(V)/R&A= S(V^*[-1]) / S. \end{aligned}$$are quadratic duals of each other.
-
(v)
The maps of graded Lie, respectively graded commutative algebras
$$\begin{aligned} {\mathfrak {t}}&\rightarrow H({\mathfrak {g}}) \quad A\rightarrow H(\texttt{B}^c {\mathfrak {g}}^c) \end{aligned}$$(44)defined by the obvious inclusion of generators are well-defined, respect the weight grading and induce isomorphisms on the parts of weight W for each \(W\le W_0\).
-
(vi)
The pair \({\mathfrak {t}}\) and A are Koszul up to weight \(W_0\) in the sense that the cohomology of \({{\,\textrm{gr}\,}}^W\texttt{B}{\mathfrak {t}}\) (respectively \({{\,\textrm{gr}\,}}^W\texttt{B}A\)) is concentrated in cohomological degree \((\alpha -1) W\) (respectively \(-\alpha W\)) for \(W\le W_0\).
Proof
Items (i) and (ii) are immediate by the assumptions on the cohomology in weights \(W\le W_0\).
By (i) and (ii) we then know that the following zigzags of dg Lie or dg commutative algebras
are quasi-isomorphisms up to weight \(W_0\). By assumption the cohomology of the weight W part of the left-hand sides is concentrated in degree \(\alpha W\) (resp. \((1-\alpha )W\)) for \(W\le W_0\).
Proof of (iii): Since \(W_0\ge 2\) by assumption this means in particular that \({{\,\textrm{gr}\,}}^2\texttt{B}^c(H^{[\alpha ]} ({\mathfrak {g}})^c)\) is concentrated in degree \(2-2\alpha \). But the complex \({{\,\textrm{gr}\,}}^2\texttt{B}^c(H^{[\alpha ]} ({\mathfrak {g}})^c)\) has the form
with the differential given by the cobracket, the left-hand term living in degree \(1-2\alpha \), and the right-hand term living in degree \(2-2\alpha \). Since the cohomology is concentrated in degree \(2-2\alpha \) the differential must be injective. Similarly, one checks that the coproduct map of (43) is injective. Furthermore, the cohomology of (47) is \(R^*\), and is identified with the dual of the cokernel of the differential, that is the annihilator of the image S. Hence the final statement of (iii) of the proposition follows.
(iv) is immediate from (iii).
(v) It is clear that the maps preserve the weight grading. To check that the maps are well-defined we just have to check that the relations R (resp. S) are sent to zero, and this can be checked in the part of weight 2. But the weight 2 part of \(H(\texttt{B}^c{\mathfrak {g}}^c )\) is the cohomology of (47), and hence the image of S is zero essentially by definition. Similarly, the weight 2 part of \(H({\mathfrak {g}})\) is the cohomology of \({{\,\textrm{gr}\,}}^2\texttt{B}^c H(\texttt{B}{\mathfrak {g}})\) and again R is identified with the image of the differential, and hence zero in cohomology.
Next, consider the cobar construction \(\texttt{B}^c (H^{[1-\alpha ]}(\texttt{B}^c {\mathfrak {g}}^c)^c)\). In weight W its piece of top cohomological degree is identified with \({{\,\textrm{gr}\,}}^W\textrm{FreeLie}(V)\), in degree \(\alpha W\). The piece of top-minus-1-degree has precisely one factor of R. The top degree cohomology is hence identified with \({{\,\textrm{gr}\,}}^W {\mathfrak {t}}\), so that
Since we know that the zigzag (45) of dg Lie algebra morphisms induces a zigzag of isomorphisms in weight \(\le W_0\)-cohomology, we obtain that \({{\,\textrm{gr}\,}}^W{\mathfrak {t}}\cong {{\,\textrm{gr}\,}}^W H({\mathfrak {g}})\) for \(W\le W_0\). This isomorphism is the identity \(V\cong V\) in weight 1 and the Lie brackets are respected, at least up to weight \(W_0\). Hence it agrees with the fist map of (44), which hence also is an isomorphism in weights \(\le W_0\). One argues similarly for the second map of (44), which agrees with the top degree cohomology map induced by (46) in weights \(\le W_0\), and is hence an isomorphism in these weights.
For (vi) note that by (v) \(\texttt{B}{\mathfrak {g}}\) and \(\texttt{B}{\mathfrak {t}}\) are quasi-isomorphic in weights \(\le W_0\). But the statement follows directly from the assumption on the cohomology of \(\texttt{B}{\mathfrak {g}}\). Similarly, \(\texttt{B}A\) is quasi-isomorphic to \(\texttt{B}H(\texttt{B}^c {\mathfrak {g}})=\texttt{B}H^{[1-\alpha ]}(\texttt{B}^c {\mathfrak {g}})\) in weights \(\le W_0\) by (v). Hence, since (45) consists of quasi-isomorphisms in weights \(\le W_0\), the remaining statement of (vi) follows by the assumption on \(H({\mathfrak {g}})\). \(\square \)
8.2 Main results
Suppose that \(g\ge 6\). We can apply the general construction of the previous subsection to the case of \({\mathfrak {g}}\) being either of \(\textsf{GC}_{(g),1}\),  or \(\textsf{GC}^{\text {ex}}_{(g)}\). In each case it is shown in Theorem 2 that the cohomology of \({{\,\textrm{gr}\,}}^W{\mathfrak {g}}\) is concentrated in cohomological degree \(\alpha W\) with \(\alpha =(1-m)\), in the range \(W\le W_0=g/3\ge 2\) (since \(3W\ge W+2\)). Furthermore, we know by Theorem 3 that in the same W-range the cohomology of \({{\,\textrm{gr}\,}}^W\texttt{B}^c {\mathfrak {g}}^c\) is concentrated in degree \((1-\alpha )W=mW\). Hence Proposition 41 is applicable and we find that \(H({\mathfrak {g}})\) and \(H_{CE}({\mathfrak {g}})\) form a Koszul pair, in the given weight range. The spaces of generators are then
or \(\textsf{GC}^{\text {ex}}_{(g)}\). In each case it is shown in Theorem 2 that the cohomology of \({{\,\textrm{gr}\,}}^W{\mathfrak {g}}\) is concentrated in cohomological degree \(\alpha W\) with \(\alpha =(1-m)\), in the range \(W\le W_0=g/3\ge 2\) (since \(3W\ge W+2\)). Furthermore, we know by Theorem 3 that in the same W-range the cohomology of \({{\,\textrm{gr}\,}}^W\texttt{B}^c {\mathfrak {g}}^c\) is concentrated in degree \((1-\alpha )W=mW\). Hence Proposition 41 is applicable and we find that \(H({\mathfrak {g}})\) and \(H_{CE}({\mathfrak {g}})\) form a Koszul pair, in the given weight range. The spaces of generators are then

The spaces of relations can be identified with

We hence find the following result, extending Theorem 4.
Theorem 42
The morphisms of graded Lie algebras

and the morphisms of graded commutative algebras

defined on generators by the obvious inclusion induce isomorphisms on the parts of weight W as long as \(g\ge 3W\ge 6\). Furthermore, the pairs \(({\mathfrak {t}}_{(g),1}, A_{(g),1})\) and  and \(({\mathfrak {t}}_{(g)}, A_{(g)})\) are Koszul in the same range of weights, in the sense of Proposition 41. \(\square \)
and \(({\mathfrak {t}}_{(g)}, A_{(g)})\) are Koszul in the same range of weights, in the sense of Proposition 41. \(\square \)
8.3 Computation of generators and relations
It remains to compute explicitly the spaces of generators and relations appearing in Theorem 42. Concretely, in this section we will compute their decomposition into irreducible representations of \(\textrm{OSp}_g\). We assume again that \(g\ge 6\). There will be 6 cases to be considered, namely each of the three dg Lie algebras we study, either for odd or even m. However, to find the spaces of generators we may re-use the computation of the weight-1-cohomology of Sect. 4.1.
As before, let \(\lambda _1,\dots ,\lambda _g\) be the usual system of fundamental weights. We shall use the notation \(V(\lambda )\) to denote an irreducible representation of \(\textrm{OSp}_g\) of highest weight \(\lambda \). Note that when m is even \(\textrm{OSp}(g)=O(g,g)\) is not connected, and the irreducible representation is not uniquely determined by the highest weight. However, one may construct irreducible representations of O(g, g) associated to Young diagrams by using Weyl’s construction, see e.g. [14, 19.5] or [31, 11.6.5]. We shall eventually only need the irreducible representations of O(g, g) of the form \(V(j \lambda _1 + k \lambda _2)\), which we define as the irreducible representation associated to a Young diagram with k columns of length 2 and j columns of length 1.
The decompositions of several tensor products of representations stated below without proof have been computed using the SageMath computer algebra software.
Case  : The complex
: The complex  has the form
has the form
with \(V_g\cong H_m(W_{g,1})\) and the (surjective) differential obtained by contraction with the canonical bilinear form. Graphically this corresponds to the differential

The cohomology is easily computed, see Sect. 4.1, and in the notation of that section we find that the space of generators of our graded Lie algebra  is, as \(\textrm{OSp}_g\)-representation,
is, as \(\textrm{OSp}_g\)-representation,

Next we turn to the relations. We first compute the cohomology of the complex  . There are four types of graphs contributing, and the complex is schematically depicted as
. There are four types of graphs contributing, and the complex is schematically depicted as

The right-hand column forms an acyclic subcomplex and can be omitted—cf. also the proof of part (i) of Theorem 1 in Sect. 4. The left-hand column is, up to degree shifts, given by the cocommutative coproduct
that is an injective map. We record the decompositions
for odd m and
for even m. Hence we find that, as \(\textrm{OSp}_g\)-representations

We compare this to the exterior square of the generators, which are up to degree shifts obtained by the decompositions (for \(g\ge 6\))
We hence find that the spaces of relations are, as \(\textrm{OSp}_{g}\)-representations

Case \(\textsf{GC}_{(g),1}\): One proceeds anologously, except that one omits all graphs with tadpoles. We suppose that \(g\ge 6\) for simplicity. Concretely, the space of generators is
By Theorem 1 we have that  , so we can re-use the computations from above for that space. The exterior square of the generators decomposes as
, so we can re-use the computations from above for that space. The exterior square of the generators decomposes as
Hence we find that the space of generators is, as \(\textrm{OSp}_g\)-representation

Case \(\textsf{GC}_{(g)}^{{\text {ex}}}\): The generating space
can again be copied from Sect. 4.1. We have

Next we consider the complex \({{\,\textrm{gr}\,}}^2 \textsf{GC}_{(g)}^{{\text {ex}}}={{\,\textrm{gr}\,}}^2 \textsf{GC}_{(g)}\). Graphically, it has the following terms

The right-hand column is the complex computing \({{\,\textrm{gr}\,}}^2\,H(\textsf{GC}_{(g),1})\), so we ca re-use the computation from above. The graphs in the upper left have two decorations in \(H_m(W_g)\) and one (\(\omega \)) in \(H_{2m}(W_g)\). Representation-wise, this contributes
The upper horizontal arrow replaces \(\omega \) by an edge towards a new vertex decorated by the reduce diagonal \(\Delta _1\). One checks by a small computation that this map induces an injection, and so (using (48)) we find that
and the formula is valid for both even and odd m. Using (49) for the exterior square of the generators we determine that the relations are
8.4 Proofs of statements of the introduction
We finally turn to the remaining statements of the introduction. First, Theorem 4 is one case of Theorem 42, if combined with the explicit computation of the relations in this subsection. Next, the zigzag of Theorem 5 can be taken to be taken to be
This induces isomorphisms on the cohomology in weight W cohomology if \(g\ge 3W\ge 6\) by Theorem 42, so that Theorem 5 is shown. Finally, Corollary 6 is just a less precise rewording of statement (vi) of Proposition 41 applied to \({\mathfrak {g}}=\textsf{GC}^{\text {ex}}_{(g)}\) in the case \(m=1\).
Notes
Specifically, the inclusion we use is
$$\begin{aligned} S^2(V\oplus {\mathbb {Q}}1 ){} & {} \cong \left( (V\oplus {\mathbb {Q}}1)\otimes (V\oplus {\mathbb {Q}}1)\right) ^{S_2} \subset (V\oplus {\mathbb {Q}}1)\otimes (V\oplus {\mathbb {Q}}1) \\ {}{} & {} = (V\otimes V) \oplus (V\otimes {\mathbb {Q}}) \oplus ({\mathbb {Q}}\otimes V) \oplus ({\mathbb {Q}}\otimes {\mathbb {Q}}) \subset S(V) \otimes S(V). \end{aligned}$$Or rather dash-patterns, for compatibility with grayscale printing.
Note that we do not have a meaningful comparison map between the complexes \(\textsf{GC}^{\text {ex}}_{(g)}\) and \(\textsf{GC}^{\text {ex}}_{(g+1)}\). Hence we cannot take a limit \(g\rightarrow \infty \) at this point as in the previous section.
References
Alekseev, A., Kawazumi, N., Kuno, Y., Naef, F.: Higher genus Kashiwara–Vergne problems and the Goldman–Turaev Lie bialgebra. C. R. Math. Acad. Sci. Paris 355(2), 123–127 (2017)
Alekseev, A., Kawazumi, N., Kuno, Y., Naef, F.: The Goldman–Turaev Lie bialgebra and the Kashiwara–Vergne problem in higher genera (2018). Preprint arXiv:1804.09566
Alekseev, A., Torossian, C.: The Kashiwara–Vergne conjecture and Drinfeld’s associators. Ann. of Math. (2) 175(2), 415–463 (2012)
Asada, M., Kaneko, M.: On the automorphism group of some pro-\(l\) fundamental groups. Galois representations and arithmetic algebraic geometry (Kyoto, 1985/Tokyo, 1986). Adv. Stud. Pure Math. 12, 137–159, North-Holland, Amsterdam (1987)
Berglund, A.: Koszul spaces. Trans. Am. Math. Soc. 366(9), 4551–4569 (2014)
Berglund, A., Börjeson, K.: Free loop space homology of highly connected manifolds. Forum Math. 29(1), 201–228 (2017)
Berglund, A., Madsen, I.: Homological stability of diffeomorphism groups. Pure Appl. Math. Q. 9(1), 1–48 (2013)
Berglund, A., Madsen, I.: Rational homotopy theory of automorphisms of manifolds. Acta Math. 224(1), 67–185 (2020)
Bökstedt, M., Minuz, E.: Graph cohomologies and rational homotopy type of configuration spaces (2019). Preprint. arXiv:1904.01452
Borel, A.: Linear Algebraic Groups. Graduate Texts in Mathematics, vol. 126, 2nd edn. Springer, New York (1991). (xii+288 pp. ISBN: 0-387-97370-2)
Campos, R., Willwacher, T.: A model for configuration spaces of points. Preprint arXiv:1604.02043
Chan, M., Galatius, S., Payne, S.: Topology of moduli spaces of tropical curves with marked points (2019). arxiv:1903.07187
Enriquez, B.: Elliptic associators. Selecta Math. (N.S.) 20(2), 491–584 (2014)
Fulton, W., Harris, J.: Representation Theory. A First course. Graduate Texts in Mathematics, Readings in Mathematics, vol. 129. Springer, New York (1991). (xvi+551 pp. ISBN: 0-387-97527-6; 0-387-97495-4)
Felder, M.: Graph complexes and higher genus Grothendieck–Teichmüller Lie algebras (2021). Preprint. arXiv:2105.02056
Gatsinzi, J.-B.: The homotopy Lie algebra of classifying spaces. J. Pure Appl. Algebra 120(3), 281–289 (1987)
Ginzburg, V., Kapranov, M.: Koszul duality for operads. Duke Math. J. 76(1), 203–272 (1994)
Hain, R.: Infinitesimal presentations of the Torelli groups. J. Am. Math. Soc. 10(3), 597–651 (1997)
Hain, R.: Genus 3 mapping class groups are not Kähler. J. Topol. 8(1), 213–246 (2015)
Idrissi, N.: The Lambrechts–Stanley model of configuration spaces. Invent. Math. 216(1), 1–68 (2019)
Kupers, A., Randal-Williams, O.: On the cohomology of Torelli groups (2019). Preprint arXiv:1901.01862
Kupers, A., Randal-Williams, O.: On diffeomorphisms of even-dimensional discs (2020). Preprint arXiv:2007.13884
Kupers, A., Randal-Williams, O.: On the Torelli Lie algebra (2021). Preprint arXiv:2106.16010
Loday, J.-L.: Cyclic Homology. Appendix E by María O. Ronco. Grundlehren der Mathematischen Wissenschaften, vol. 301. Springer, Berlin (1992). (xviii+454 pp. ISBN: 3-540-53339-7)
Loday, J.-L., Vallette, B.: Algebraic operads. Grundlehren Math. Wiss., vol. 346. Springer, Heidelberg (2012)
Millès, J.: The Koszul complex is the cotangent complex. Int. Math. Res. Not. IMRN 3, 607–650 (2012)
Milne, J.S.: Algebraic Groups. The Theory of Group Schemes of Finite Type Over a Field. Cambridge Studies in Advanced Mathematics, vol. 170. Cambridge University Press, Cambridge (2017). (xvi+644 pp. ISBN: 978-1-107-16748-3)
Naef, F., Qin, Y.: The Elliptic Kashiwara–Vergne Lie algebra in low weights. J. Lie Theory 31(2), 583–598 (2021)
Neisendorfer, J.: The rational homotopy groups of complete intersections. Illinois J. Math. 23(2), 175–182 (1979)
Payne, S., Willwacher, T.: Weight two compactly supported cohomology of moduli spaces of curves. Preprint. arXiv:2110.05711
Procesi, C.: The invariant theory of \(n\times n\) matrices. Adv. Math. 19(3), 306–381 (1976)
Raphael, E., Schneps, L.: On linearised and elliptic versions of the Kashiwara–Vergne Lie algebra (2017). Preprint arXiv:1706.08299
Ševera, P., Willwacher, T.: Equivalence of formalities of the little discs operad. Duke Math. J. 160(1), 175–206 (2011)
Vallette, B.: Homotopy theory of homotopy algebras. Ann. Inst. Fourier (Grenoble) 70(2), 683–738 (2020)
Willwacher, T.: Kontsevich’s graph complex and the Grothendieck-Teichmüller Lie algebra. Invent. Math. 200(3), 671–760 (2015)
Willwacher, T.: On truncated mapping spaces of \(E_n\) operads. arXiv:1911.00709
Acknowledgements
We thank Alexander Berglund, Alexander Kupers and Oscar Randal-Williams for helpful discussions. We shall also note that results partially overlapping ours have independently been obtained by Kupers and Randal-Williams [23]. We moreover thank the referee for carefully reading the manuscript and for his extensive comments which improved the paper substantially.
Funding
Open access funding provided by Swiss Federal Institute of Technology Zurich
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
M.F. and T.W. have been supported by the ERC starting Grant 678156 GRAPHCPX, and the NCCR SwissMAP, funded by the Swiss National Science Foundation. F.N. has been supported by the Marie Sklodowska-Curie Grant 896370.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Felder, M., Naef, F. & Willwacher, T. Stable cohomology of graph complexes. Sel. Math. New Ser. 29, 23 (2023). https://doi.org/10.1007/s00029-023-00830-5
Accepted:
Published:
DOI: https://doi.org/10.1007/s00029-023-00830-5


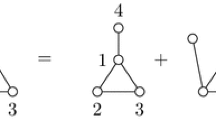

 are
are 



 defined by setting graphs with tadpoles to zero induces an isomorphism
defined by setting graphs with tadpoles to zero induces an isomorphism 
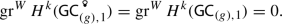














 is generated as a graded commutative algebra by the graded vector space
is generated as a graded commutative algebra by the graded vector space  or
or  or
or  .
.