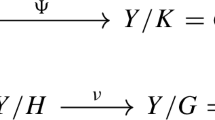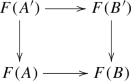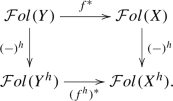Algebraic foliations and derived geometry: the Riemann–Hilbert correspondence

Abstract

This is the first in a series of papers about foliations in derived geometry. After introducing derived foliations on arbitrary derived stacks, we concentrate on quasi-smooth and rigid derived foliations on smooth complex algebraic varieties and on their associated formal and analytic versions. Their truncations are classical singular foliations defined in terms of differential ideals in the algebra of forms. We prove that a quasi-smooth rigid derived foliation on a smooth complex variety X is formally integrable at any point, and, if we suppose that its singular locus has codimension $\ge 2$, its analytification is a locally integrable singular foliation on the associated complex manifold $X^h$. We then introduce the derived category of perfect crystals on a quasi-smooth rigid derived foliation on X, and prove a Riemann-Hilbert correspondence for them when X is proper. We discuss several examples and applications.

1 Introduction

This is the first of a series of works on foliations (mainly algebraic and holomorphic) and derived geometry. In this paper we present a notion of a derived foliation on algebraic or holomorphic varieties, that we think is interesting for the study of foliations with singularities. The point of view adopted here is not completely new and goes back to previous works by Tony Pantev and the authors on existence of potentials for shifted symplectic structures (see e.g. [15]). In a nutshell, a derived foliation ${\mathcal {F}}$ on a scheme X consists of a perfect complex ${\mathbb {L}}_{{\mathcal {F}}}$ on X together with a map $a : {\mathcal {O}}_X \longrightarrow {\mathbb {L}}_{{\mathcal {F}}}$ that satisfies formal properties of being a de Rham differential (i.e. is a derivation squaring to zero). One major difficulty is to define the precise higher coherences for such a structure, encoding the fact that $a^2$ does not really identically vanish but is only homotopic to zero in a homotopy coherent way. This is achieved by defining derived foliation as graded mixed commutative differential graded algebras (graded mixed cdga’s, for short) satisfying some extra properties (see Definition 1.2.1).

In this work we quickly restrict to the case of quasi-smooth derived foliations ${\mathcal {F}}$, which consists of restricting ${\mathbb {L}}_{{\mathcal {F}}}$ to be just a two terms complex of vector bundles. Among derived foliations, these quasi-smooth derived foliations are the closest to classical foliations in the usual sense, and we think they form the most important class of derived foliations. A quasi-smooth derived foliation ${\mathcal {F}}$ on a smooth variety X can be truncated into a usual algebraic singular foliation $\tau _0({\mathcal {F}})$ on X (e.g. in the sense of [1, 2]). More precisely, the kernel of the morphism $\Omega _X^1 \longrightarrow H^0({\mathbb {L}}_{\mathcal {F}})$, induced by a, defines a differential ideal inside differential forms and thus a singular foliation $\tau _0({\mathcal {F}})$ on X. We remark however that arbitrary singular foliations are not derived foliations: they can be represented by graded mixed algebras, but these do not satisfy our conditions (except if the foliation has no singularities). Notice also that being the truncation of a derived foliation is a non-trivial condition, even locally in the analytic topology. Therefore, derived foliations are not really generalizations of singular foliations, and these two class of objects do not live in the same categories. Rather, it is more useful to keep in mind the intuition that derived foliations are additional structures on their truncated singular foliations making them better behaved objects.

The first two main results of this work are the following integrability theorems. Note that for a derived quasi-smooth foliation being integrable, i.e. being induced by a morphism between smooth varieties, implies that its truncated singular foliation is also integrable (by the same morphism). However, the converse is in general wrong.

Theorem 0.0.1

(Proposition 2.3.2 and Corollary 2.3.4) Let X be a smooth variety and ${\mathcal {F}}$ be a quasi-smooth derived foliation on X. Assume that ${\mathcal {F}}$ is rigid (i.e. the induced map $H^0(a): \Omega _X^1 \rightarrow H^0({\mathbb {L}}_{{\mathcal {F}}})$ is surjective). Then

• (1) The derived foliation ${\mathcal {F}}$ is formally integrable around each point $x \in X$.

• (2) If we further assume that ${\mathcal {F}}$ has no singularities outside a closed subset of codimension at least 2, then ${\mathcal {F}}$ is analytically integrable, locally in the analytic topology on X. As a consequence the truncated singular foliation $\tau _0({\mathcal {F}})$ is analytically integrable, locally in the analytic topology on X.

Part (1) of the above theorem is a consequence (Corollary 1.5.4) of a more general result concerning the local structure of quasi-smooth derived foliations (see Proposition 1.5.1), while part (2) is a consequence of (1) and of a theorem of Malgrange ([12]). We remark here that a consequence of the above result is that a singular foliation which is not formally integrable locally at all points can not be the truncation of a derived quasi-smooth foliation.

The second main result of this work is a Riemann–Hilbert correspondence for derived quasi-smooth foliations. We first introduce the notion of a crystal along a derived foliation ${\mathcal {F}}$, which morally consists of a vector bundle together with a partial connection along the leaves of ${\mathcal {F}}$. Once again, there are homotopical coherences to be taken into account, and crystals are rather defined as certain graded mixed dg-modules over the graded mixed dg-algebra defining the derived foliation. On the other hand, a derived foliation ${\mathcal {F}}$ defines a sheaf ${\mathcal {O}}_{{\mathcal {F}}^h}$, in the analytic topology, of locally constant functions along ${\mathcal {F}}$. This is a sheaf of commutative dg-algebras, which is in general not concentrated in degree zero, and whose higher cohomology sheaves reflect the singularities of ${\mathcal {F}}$. The Riemann–Hilbert correspondence can then be stated as follows (see Corollary 4.2.2):

Theorem 0.0.2

Let ${\mathcal {F}}$ be a quasi-smooth and rigid foliation on a smooth and proper algebraic variety X. Assume that ${\mathcal {F}}$ is non-singular outside of a closed subset of codimension at least 2. There is an equivalence of categories

$$\begin{aligned} \textsf {Vect} ({\mathcal {F}}) \simeq \textsf {Vect} ({\mathcal {O}}_{{\mathcal {F}}^h}) \end{aligned}$$

between on the l.h.s. the category of crystals along ${\mathcal {F}}$, and on the r.h.s. the category of sheaves of ${\mathcal {O}}_{{\mathcal {F}}^h}$-dg-modules which are locally free of finite rank.

The above theorem is a consequence of two results proved in the text: a more general statement (valid without the rigidity or codimension assumptions) which relates perfect complexes of crystals with a nilpotent condition (we call such crystals h-nilpotent) and perfect complexes of ${\mathcal {O}}_{{\mathcal {F}}^h}$-dg-modules (see Theorem 4.2.1), and the fact that a vector bundle crystal (i.e. an object in $\textsf {Vect} ({\mathcal {F}})$) is h-nilpotent once ${\mathcal {F}}$ satisfies the hypotheses of Theorem 0.0.2 (see Theorem 3.2.3). We also prove that the above theorem is compatible with cohomologies, giving rise to an isomorphism between algebraic de Rham cohomology along the leaves of a crystal and the analytic cohomology of the corresponding sheaf of ${\mathcal {O}}_{{\mathcal {F}}^h}$-module. Note that Theorem 0.0.2 recovers for instance Deligne’s relative Riemann–Hilbert correspondence (see [7]) and extends it to the case of a possibly non-smooth morphism (see Sect. 4.3.1 for details). It is also possible to recover from Theorem 4.2.1 Kato-Nakayama’s logarithmic Riemann–Hilbert correspondence (see Sect. 4.3.3).

Plan of the paper. The present work is organized in four parts. In the first section we present the notion of derived foliations. We present several examples and show a formal structure theorem for quasi-smooth and rigid derived foliations. We also discuss the notion of leaves in the setting. The second section is devoted to the analytic aspects of derived foliation. We construct the analytification functor and discuss local integrability, in the analytic topology, of derived foliations. The third section contains the definition of crystals along a derived foliations, their analytifications, as well as the notion of h-nilpotent crystals. Finally, the last section contains the statement and proof of the Riemann–Hilbert correspondence. We also have included some examples and applications.

Related works. In [3], the authors borrow their definition of derived foliation from [15], and study Lagrangian derived foliations in relation with the problem of realizing the moduli space of sheaves on a Calab-Yau fourfold as the derived critical locus of a (shifted) potential. In [1], J. Ayoub have systematically studied underived singular foliation on schemes; his theory lives algebraic geometry rather than in derived geometry, and his purposes are somehow different, being related to differential Galois theory.

Conventions and notations. Everything, like vector spaces, commutative dg-algebras (often shortened as cdga’s), algebraic varieties etc., is defined over the field ${\mathbb {C}}$ of complex numbers. The $\infty$-category of complexes (of ${\mathbb {C}}$-vector spaces) is denoted by ${{\mathbf {d}}}{{\mathbf {g}}}$, and the $\infty$-category of topological spaces by Top.

By convention $\mathbf {dAff}$ is the $\infty$-category of derived affine schemes locally of finite presentation over ${\mathbb {C}}$. Derived Artin stacks are, by definition, locally of finite presentation. For a derived stack F we denote by QCoh(F) its $\infty$-category of quasi-coherent complexes. In the same manner $\textsf {Perf} (F) \subset QCoh(F)$ denotes the full sub-$\infty$-category of perfect complexes on F.

All the various functors, Sym, $\otimes$, $\wedge$, $f_*$, $f^*$, etc. will be suitably derived when necessary. We will occasionally need underived functors for which we will use specific notations $Sym^u$, $\otimes ^u$, $f_*^u$, etc., if necessary.

A vector bundle on X will be a locally free ${\mathcal {O}}_X$-Module of finite rank.

2 Derived algebraic foliations

In this section, after some reminders on mixed graded structures, we define derived foliations on arbitrary derived stacks, give several classes of examples of derived foliations, study derived foliations on formal completions, and finally establish the local structure of quasi-smooth rigid derived foliations. We also discuss the notion of formal, algebraic and analytic leaves of derived foliations in general.

2.1 Reminders on graded mixed objects

We remind from [6] (see also the digest [18]) the $\infty$-category of graded mixed complexes (over ${\mathbb {C}}$). Its objects are ${\mathbb {Z}}$-graded objects $E=\oplus _{n\in {\mathbb {Z}}} E(n)$, inside the category of cochain complexes together with extra differentials $\epsilon _n : E(n) \longrightarrow E(n+1)[-1]$. These extra differentials combine into a morphism of graded complexes $\epsilon : E \longrightarrow E((1))[-1]$ (where E((1)) is the graded complex obtained from E by shifting the weight-grading by $+1$), satisfying $\epsilon ^2=0$. The datum of $\epsilon$ is called a graded mixed structure on the graded complex E. The complex E(n) is itself called the weight n part of E.

Morphisms of graded mixed complexes are defined in an obvious manner, and among them, the quasi-isomorphisms are the morphisms inducing quasi-isomorphisms on all the weight-graded pieces individually. By inverting quasi-isomorphisms, graded mixed complexes constitute an $\infty$-category denoted by $\epsilon -{{\mathbf {d}}}{{\mathbf {g}}}^{gr}$. Alternatively, the $\infty$-category $\epsilon -{{\mathbf {d}}}{{\mathbf {g}}}^{gr}$ can be defined as the $\infty$-category of quasi-coherent complexes $\textsf {QCoh} (B{\mathcal {H}})$, over the classifying stack $B{\mathcal {H}}$ for the group stack $B{\mathbb {G}}_a \rtimes {\mathbb {G}}_m$ (see [6, Rmk. 1.1.1] and [17, Prop. 1.1]).

The $\infty$-category $\epsilon -{{\mathbf {d}}}{{\mathbf {g}}}^{gr}$ comes equipped with a canonical symmetric monoidal structure $\otimes$. It is defined on objects by the usual tensor product of ${\mathbb {Z}}$-graded complexes (taken over the base field ${\mathbb {C}}$), with the mixed structure defined by the usual formula $\epsilon \otimes 1 + 1\otimes \epsilon$ (see [6, §1.1]). When viewed as $\textsf {QCoh} (B{\mathcal {H}})$, this is the usual symmetric monoidal structure on quasi-coherent complexes on stacks.

Commutative algebras in $\epsilon -{{\mathbf {d}}}{{\mathbf {g}}}^{gr}$ form themselves an $\infty$-category $\epsilon -\mathbf {cdga}^{gr}$, whose objects are called graded mixed cdga’s. Its objects can be described as ${\mathbb {Z}}$-graded cdga’s $A=\oplus _n A(n)$, endowed with a graded mixed structure $\epsilon$ which is compatible with the multiplication in A (i.e. is a graded biderivation). The fundamental example of such a graded mixed cdga is given by the de Rham algebra. For a cdga A we can consider its dg-module $\Omega _A^1$ of dg-derivations as well as its symmetric cdga $Sym^u_A(\Omega ^1_A[1])$. The usual de Rham differential induces a graded mixed structure on $Sym^u_A(\Omega _A^1[1])$ making it into a graded mixed cdga for which the induced morphism $\epsilon : A \longrightarrow \Omega _A^1$ is the usual universal derivation. Applied to a cofibrant model $A'$ of A we get a graded mixed cdga ${{\mathbf {D}}}{{\mathbf {R}}}(A):=Sym^u_{A'}(\Omega _{A'}^1[1])$ which is functorial, in the sense of $\infty$-categories, in A. This defines an $\infty$-functor

$$\begin{aligned} {{\mathbf {D}}}{{\mathbf {R}}}: \mathbf {cdga}\longrightarrow \epsilon -\mathbf {cdga}^{gr}\end{aligned}$$

which can be checked to be the left adjoint to the forgetful $\infty$-functor sending a graded mixed cdga A to its weight 0 part A(0).

We remind the existence of the realization $\infty$-functor

$$\begin{aligned} |-| : \epsilon -{{\mathbf {d}}}{{\mathbf {g}}}^{gr}\longrightarrow {{\mathbf {d}}}{{\mathbf {g}}}\end{aligned}$$

given by ${\mathbb {R}}{\underline{Hom}}({\mathbb {C}},-)$, where the derived hom is taken as graded mixed complexes, and ${\mathbb {C}}$ is equipped with the trivial graded mixed complexes purely concentrated in weight and cohomological degree 0. The object ${\mathbb {C}}$ being the unit of the symmetric monoidal structure on $\epsilon -{{\mathbf {d}}}{{\mathbf {g}}}^{gr}$, the $\infty$-functor $|-|$ possesses a natural lax monoidal structure and thus sends graded mixed cdga’s to cdga’s. It can be explicitly described as follows. For a graded mixed complex E we from the product

$$\begin{aligned} |E|:=\prod _{p\ge 0}E(p)[-2p] \end{aligned}$$

and endow |E| with the total differential $d+\epsilon$, where d is the cohomological differential of E and $\epsilon$ is the graded mixed structure. When E is a graded mixed cdga the formula above for |E| can also be used to describe the multiplicative structure, which is induced by the natural maps $E(n)[-2n]\otimes E(m)[-2m] \longrightarrow E(n+m)[-2n-2m]$.

Remark 1.1.1

The following simple observations will be useful in the rest of the paper.

• For $A \in \mathbf {cdga}$, the underlying graded cdga of ${{\mathbf {D}}}{{\mathbf {R}}}(A)$, obtained by forgetting the mixed structure, is naturally equivalent to $Sym_A({\mathbb {L}}_A[1])$, where ${\mathbb {L}}_A$ is the cotangent complex of A.

• As a consequence of the comment above, when A is a smooth algebra, the graded mixed cdga ${{\mathbf {D}}}{{\mathbf {R}}}(A)$ is canonically equivalent to the usual de Rham algebra $Sym_A(\Omega _A^1[1])$ endowed with its usual de Rham differential as graded mixed structure.

The notions of graded mixed complexes, graded mixed cdga’s and de Rham algebras ${{\mathbf {D}}}{{\mathbf {R}}}$ as defined above, all make sense internally to a (nice enough) base symmetric monoidal ${\mathbb {C}}$-linear $\infty$-category (see [6, Section 1.3.2], as well as [18, Rmk 1.5 and Section 2.1]). These internal notions and constructions can be understood simply as follows. Graded mixed cgda’s and modules make sense over any derived stack F, as quasi-coherent sheaves of ${\mathcal {O}}_F$-linear graded mixed cdga’s and modules. Equivalently the $\infty$-category of graded mixed modules over a derived F can be defined as $\textsf {QCoh} (F\times B{\mathcal {H}})$, where, as above, ${\mathcal {H}}$ is the group stack $B{\mathbb {G}}_a \rtimes {\mathbb {G}}_m$. Graded mixed cdga’s are then naturally defined as commutative ring objects inside the symmetric monoidal $\infty$-category $\textsf {QCoh} (F\times B{\mathcal {H}})$.

Any commutative ring A in $\textsf {QCoh} (F)$ will be called an ${\mathcal {O}}_F$-cdga. Any such ${\mathcal {O}}_F$-cdga possesses an internal de Rham complex, which is a graded mixed cdga over F. We denote this object by ${{\mathbf {D}}}{{\mathbf {R}}}^{int}(A)$. Moreover, we can apply the direct image functor along $F\times B{\mathcal {H}} \longrightarrow F$ to get a lax monoidal $\infty$-functor $\textsf {QCoh} (F\times B{\mathcal {H}}) \longrightarrow \textsf {QCoh} (F).$ This lax monoidal $\infty$-functor is called the realization $\infty$-functor and is denoted by

$$\begin{aligned} |-| : \textsf {QCoh} (F\times B{\mathcal {H}}) \longrightarrow \textsf {QCoh} (F). \end{aligned}$$

When A is a cdga over F, we have a graded mixed cdga ${{\mathbf {D}}}{{\mathbf {R}}}^{int}(A)$ over F, and by applying $|-|$ we get a cdga denoted by ${{\mathbf {D}}}{{\mathbf {R}}}(A):=|{{\mathbf {D}}}{{\mathbf {R}}}^{int}(A)|$, and called the de Rham cohomology of A over F. There is also a relative version, for a morphism $A \longrightarrow B$ of cdga’s over F, which is $|{{\mathbf {D}}}{{\mathbf {R}}}^{int}(B/A)|$, another cdga. The explicit formula giving the realization recalled earlier is also valid in this internal setting. Indeed, for an object $E \in \textsf {QCoh} (F\times B{\mathcal {H}})$, its realization |E| is the object in $\textsf {QCoh} (F)$ given by

$$\begin{aligned} |E|=\prod _{p\ge 0}E(p)[-2p] \end{aligned}$$

endowed with the total differential, sum of the cohomological differential and the de Rham differential.

This discussion applies in particular to $F=B{\mathcal {H}}$ itself. We have to note here that $\textsf {QCoh} (B{\mathcal {H}} \times B{\mathcal {H}})$ consists of doubly graded mixed complexes, i.e. complexes endowed with two extra gradings and two associated graded mixed structures compatible with each others. By our convention the realization

$$\begin{aligned} |-| : \textsf {QCoh} (B{\mathcal {H}} \times B{\mathcal {H}}) \longrightarrow \textsf {QCoh} (B{\mathcal {H}}) \end{aligned}$$

consists of realizing the first graded mixed structure. For example, if one starts with an algebra A in $\textsf {QCoh} (B{\mathcal {H}})$ (i.e. a graded mixed cdga), then $|{{\mathbf {D}}}{{\mathbf {R}}}^{int}(A)|$ is another graded mixed cdga. It is obtained by considering ${{\mathbf {D}}}{{\mathbf {R}}}^{int}(A) \in \textsf {QCoh} (B{\mathcal {H}} \times B{\mathcal {H}})$ and realizing it with respect to the internal mixed structure, that is the one induced from the graded mixed structure on A as opposed to the one given by the de Rham differential. Using the correct convention here is essential for the rest of the paper.

If we have a morphism of graded mixed cdga’s $A \longrightarrow B$, the above construction produces an internal graded mixed cdga ${{\mathbf {D}}}{{\mathbf {R}}}^{int}(B/A)$ inside graded mixed complexes. Its realization is thus a graded mixed cdga ${{\mathbf {D}}}{{\mathbf {R}}}(B/A)$ called the internal de Rham cohomology of B relative to A.

With these notations, we have the following lemma recovering a class of graded mixed cdga’s A from their ${{\mathbf {D}}}{{\mathbf {R}}}^{int}(A(0)/A)$. We will use this lemma very often in the rest of the text.

Lemma 1.1.2

Let A be a graded mixed cdga and assume that the canonical morphism

$$\begin{aligned} Sym_{A(0)}(A(1)) \longrightarrow A \end{aligned}$$

is a quasi-isomorphism of graded cdga’s. Then, the canonical morphism of graded mixed cdga’s

$$\begin{aligned} A \longrightarrow |{{\mathbf {D}}}{{\mathbf {R}}}^{int}(A(0)/A)| \end{aligned}$$

is a quasi-isomorphism.

Proof

Let $B=A(0)$ and $E=A(1)$. The internal cotangent complex of B relative to $Sym_B(E)$ is identified with E[1]. The internal de Rham algebra ${{\mathbf {D}}}{{\mathbf {R}}}(B/A)$ is then equivalent to $Sym_B(E[2])$. We are interested in realizing the internal graded mixed structure coming from the one of A. As E is pure of weight 1, the induced graded mixed structure on E is trivial. The same is true for $Sym^p(E[2])$, and we thus conclude that the internal graded mixed structure on $Sym_B(E[2])$ is trivial. Since we are realizing internally, we have to realize each graded piece individually. But the realization of a graded mixed complex M which is pure of weight p is simply $M[-2p]$. Therefore, the realization of the internal de Rham algebra is tautologically given by

$$\begin{aligned} |{{\mathbf {D}}}{{\mathbf {R}}}^{int}(B/A)|\simeq \oplus _{p\ge 0}|Sym^p(E[2])| = \oplus _{p\ge 0}Sym^p(E). \end{aligned}$$

$\square$

2.2 Derived algebraic foliations as graded mixed cdga’s

In this section we present a very general notion of derived foliations over general derived stacks. Though later in this paper, we will only be dealing with derived foliations over smooth varieties, we have decided to give a general definition for further record and applications.

Definition 1.2.1

An affine derived foliation is a graded mixed cdga A satisfying the following extra conditions.

• (1) (Connectivity) The underlying cdga A(0) is cohomologically concentrated in non-positive degrees and is finitely presented over ${\mathbb {C}}$.

• (2) (Perfectness) The A(0)-dg-module $A(1)[-1]$ is perfect and connective.

• (3) (Quasi-freeness) The natural morphism of graded cdga’s

  $$\begin{aligned} Sym_{A(0)}(A(1)) \longrightarrow A \end{aligned}$$

  is a quasi-isomorphism of graded cdga’s.

For a derived foliation A as above, the derived affine scheme $X=Spec\, A(0)$ is called the underlying derived scheme of the foliation, and we will say that the foliation is given over X. The perfect complex on X determined by $A(1)[-1]$ is called the cotangent complex of the foliation.

Example 1.2.2

Let $X=Spec \, R$ be a smooth affine ${\mathbb {C}}$-scheme, TX its tangent bundle, and $V\subseteq TX$ a sub-bundle whose local sections are closed under the Lie bracket canonically defined on local vector fields (i.e. on local sections of TX/X). It is well known that if ${\mathcal {V}}^{\vee }$ denotes the R-module of local sections of the dual vector bundle $V^{\vee }$, then the Lie bracket on local sections of V induces a differential on $A:=Sym_R({\mathcal {V}}^{\vee }[1])$. This gives A the structure of a derived foliation over X. Therefore, an algebraic foliation in the usual sense can be seen as a derived foliation.

More general examples of derived foliations will be given later in this Section.

Affine derived foliations form an $\infty$-category as follows. Consider the $\infty$-category $(\epsilon -\mathbf {cdga}^{gr})^{op}$, opposite to the $\infty$-category of graded mixed cdga’s. The $\infty$-category of affine derived foliations is defined to be the full sub-$\infty$-category of $(\epsilon -\mathbf {cdga}^{gr})^{op}$ consisting of the graded mixed cdga’s satisfying the conditions of Definition 1.2.1. This $\infty$-category will be denoted by $\mathbf {dAff}^{\mathcal {F}}$.

We have a canonical $\infty$-functor

$$\begin{aligned} \mathbf {dAff}^{\mathcal {F}}\longrightarrow \mathbf {dAff}\end{aligned}$$

sending an affine derived foliation A to the derived affine scheme $Spec\, (A(0))$.

Proposition 1.2.3

The above $\infty$-functor is fibered in the sense of [23, §2.3]. Moreover, the corresponding $\infty$-functor

$$\begin{aligned} {\mathcal {F}}ol: \mathbf {dAff}^{op} \longrightarrow \mathbf {Cat}_{\infty }\end{aligned}$$

is a stack for the étale topology.

Proof

By construction, the $\infty$-category ${\mathcal {F}}ol(Spec\, A)$ is equivalent to the opposite $\infty$-category of graded mixed cdga’s C satisfying the conditions of Definition 1.2.1 and equipped with a cdga quasi-isomorphism $C(0)\simeq A$. The $\infty$-category has two distinguished objects, the final and initial objects. The final object is A itself, considered as a graded mixed cdga’s purely in weight 0 with zero graded mixed structure. On the other hand, the initial object is ${{\mathbf {D}}}{{\mathbf {R}}}(A)$.

Let now $f: X=Spec\, A \longrightarrow Y=Spec\, B$ be a morphism of derived affine schemes corresponding to a morphism of cdga’s $B \longrightarrow A$. The pull-back $\infty$-functor

$$\begin{aligned} f^* : {\mathcal {F}}ol(Y) \longrightarrow {\mathcal {F}}ol(X) \end{aligned}$$

can be understood as follows. Let ${\mathcal {F}} \in {\mathcal {F}}ol(Y)$ be an object corresponding to a graded mixed cdga C satisfying the conditions of Definition 1.2.1 and equipped with a quasi-isomorphism $C(0) \simeq B$. Associated to ${\mathcal {F}}$ is a natural diagram of graded mixed cdgas

The pull-back foliation $f^*({\mathcal {F}}) \in {\mathcal {F}}ol(X)$ is then given by the graded mixed cdga $C\otimes _{{{\mathbf {D}}}{{\mathbf {R}}}(B)}{{\mathbf {D}}}{{\mathbf {R}}}(A)$. This indeed satisfies the conditions of Definition 1.2.1 since it is equivalent, as a graded cdga, to $Sym_{A}(E)$, where E is the following push-out in B-dg-modules

where A(1) is viewed as a B-dg-module via the map $B \rightarrow A$. This proves the first statement in the proposition, and moreover provides an explicit description of pull-back $\infty$-functors. This description in turns easily implies that the $\infty$-functor ${\mathcal {F}}ol$ is a stack for the étale topology, as this reduces to the fact that quasi-coherent modules is a stack for the étale topology. $\square$

The above proposition can be used, by Kan extension along $\mathbf {dAff}^{op} \rightarrow \mathbf {dSt}^{op}$, in order to define derived foliations over any base derived stack.

Definition 1.2.4

Let $X \in \mathbf {dSt}$. The $\infty$-category

$$\begin{aligned} {\mathcal {F}}ol(X):= \lim _{Spec\, A \rightarrow F}{\mathcal {F}}ol(Spec\,A) \end{aligned}$$

is called the $\infty$-category of derived foliations over X.

We note here that when X is a derived DM-stack, then ${\mathcal {F}}ol(X)$ can be described as the limit $\lim _{U}{\mathcal {F}}ol(U)$, where U runs over all derived affine schemes étale over X. By the explicit description of pull-backs given in the proof of Proposition 1.2.3, we see that an object in this limit can be simply represented by a sheaf of graded mixed cdga’s ${\mathcal {A}}$ over the small étale site $X_{\acute{\mathrm{e}}\text {t}}$ of X, together with an equivalence ${\mathcal {A}}(0)\simeq {\mathcal {O}}_X$, and satisfying the following two conditions.

• The sheaf of ${\mathcal {O}}_X$-dg-modules ${\mathcal {A}}(1)[-1]$ is perfect and connective.

• The natural morphism of sheaves of graded cdgas

  $$\begin{aligned} Sym_{{\mathcal {O}}_X}({\mathcal {A}}(1)) \longrightarrow {\mathcal {A}}\end{aligned}$$

  is a quasi-isomorphism.

This simple description in terms of sheaves of cdga’s is not valid anymore for derived foliation over more general derived stacks, such as derived Artin stacks for instance. We will quickly restrict ourselves to derived foliations over smooth.

We introduce the following notations.

Definition 1.2.5

Let X be a derived DM-stack and ${\mathcal {F}}\in {\mathcal {F}}ol(X)$ be a derived foliation over X.

• The sheaf of graded mixed cdga’s ${\mathcal {A}}$ over X corresponding to ${\mathcal {F}}$ is called the de Rham algebra along ${\mathcal {F}}$. It is denoted by ${{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})$.

• The perfect complex ${{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})(1)[-1]$ over X is called the cotangent complex of ${\mathcal {F}}$ and is denoted by ${\mathbb {L}}_{{\mathcal {F}}}$. We thus have a quasi-isomorphism of quasi-coherent sheaves of graded cdga’s over X

  $$\begin{aligned} {{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})\simeq Sym_{{\mathcal {O}}_X}({\mathbb {L}}_{\mathcal {F}}[1]). \end{aligned}$$

Before giving some examples of derived foliations, we fix the following terminology.

Definition 1.2.6

Let X be a derived DM-stack, ${\mathcal {F}}\in {\mathcal {F}}ol(X)$ be a derived foliation over X and ${\mathbb {L}}_{\mathcal {F}}\in \textsf {QCoh} (X)$ is cotangent complex.

• We say that the foliation ${\mathcal {F}}$ is smooth if ${\mathbb {L}}_{\mathcal {F}}$ is quasi-isomorphic to a vector bundle on X sitting in degree 0.

• We say that the foliation ${\mathcal {F}}$ is quasi-smooth if ${\mathbb {L}}_{\mathcal {F}}$ is quasi-isomorphic to perfect complex of amplitude contained in cohomological degrees $[-1,0]$.

• We say that the foliation ${\mathcal {F}}$ is rigid if the induced morphism of coherent sheaves

  $$\begin{aligned} H^0({\mathbb {L}}_X) \longrightarrow H^0({\mathbb {L}}_{\mathcal {F}}) \end{aligned}$$

  is surjective.

Remark 1.2.7

Definition 1.2.4 above can be extended to more general settings. To start with, we may allow X being any derived Artin stack, and we may furthermore drop the connectivity assumption on ${\mathbb {L}}_F$ in order to define non-connective derived foliations. These are useful for instance in the setting of shifted symplectic and Poisson structures (see e.g. [3, 15]), but will not be considered in the present work.

To finish this section, we describe a more geometric interpretation of derived foliations in terms of derived loop spaces and their natural circle action. This point of view will not be used further in the present paper, but has the advantage of being useful in some contexts, and comes handy. Moreover, using the graded circle of [13] instead of the formal circle, makes it possible to extend the notions of derived foliations outside of the characteristic zero context.

We consider the formal additive group $\widehat{{\mathbb {G}}}_a$, as well as its classifying stack ${\widehat{S}}^1:=B\widehat{{\mathbb {G}}}_a \in \mathbf {dSt}$. The group ${\mathbb {G}}_m$ acts on the formal group $\widehat{{\mathbb {G}}}_a$ and thus on the formal circle ${\widehat{S}}^1$. The stack ${\widehat{S}}^1$ is itself a group stack and thus acts on itself by translation. These two actions combine into an action of the group stack ${\mathcal {H}}:={\widehat{S}}^1\rtimes {\mathbb {G}}_m$. As explained in [17, Prop. 1.3] the symmetric monoidal $\infty$-category $\textsf {QCoh} (B{\mathcal {H}})$ is naturally equivalent to the symmetric monoidal $\infty$-category of graded mixed complexes.

For a derived DM-stack $X \in \mathbf {dSt}$, its formal derived loop stack is defined by

$$\begin{aligned} {\mathcal {L}}^fX :=\mathbf {Map}({\widehat{S}}^1,X). \end{aligned}$$

It comes equipped with a canonical action of ${\mathcal {H}}$. By the equivalence recalled above, between $\textsf {QCoh} (B{\mathcal {H}})$ and graded mixed complexes, we see that a derived foliation over X is the exact same thing as a a derived stack ${\mathcal {F}}$ over ${\mathcal {L}}^fX$, together with an ${\mathcal {H}}$-action on ${\mathcal {F}}$ covering the canonical action on ${\mathcal {L}}^fX$ and such that ${\mathcal {F}}$ is relatively affine over X and of the form $Spec_{{\mathcal {O}}_X}({\mathbb {L}}_{{\mathcal {F}}}[1])$ (compatibly with the grading where ${\mathbb {L}}_{{\mathcal {F}}}$ is of weight one) for ${\mathbb {L}}_{\mathcal {F}}$ a connective perfect complex over X. As a result, ${\mathcal {F}}ol(X)$ can be realized as a full sub-$\infty$-category of $(\mathbf {dSt}/{\mathbb {L}}^fX)^{\mathcal {H}}$, of ${\mathcal {H}}$-equivariant derived stacks over ${\mathbb {L}}^fX$.

The above interpretation of derived foliations makes pull-back of foliations more natural. For a morphism of derived DM-stacks $f : X \longrightarrow Y$, there is an induced ${\mathcal {H}}$-equivariant morphism ${\mathcal {L}}^fX \longrightarrow {\mathcal {L}}^fY$. For a derived foliation ${\mathcal {F}}\in {\mathcal {F}}ol(Y)$, realized as an ${\mathcal {H}}$-equivariant derived stack ${\mathcal {F}}\longrightarrow Y$, the pull-back $f^*({\mathcal {F}})$ simply is realized by the pull-back of derived stacks

$$\begin{aligned} f^*({\mathcal {F}})\simeq {\mathcal {F}}\times _{{\mathcal {L}}^fY}{\mathcal {L}}^fX, \end{aligned}$$

equipped with its natural projection down to ${\mathcal {L}}^fX$.

Remark 1.2.8

In [8], D. Gaitsgory and N. Rozenblyum define a notion of formal moduli problem under X. It is beyond the scope of this paper to make a precise comparison between derived foliations and this notion of formal moduli problems. However, we thank the referee for the following suggestion. For a nice enough stack X, it is reasonable to expect that relative de Rham cohomology yields a conservative (possibly fully-faithful) functor going from formal moduli problems $X\rightarrow Y$ under X, with perfect and co-connective relative tangent complex, to derived foliations on X.

2.3 Examples

We finish this Section by giving some classes of examples of derived foliations.

2.3.1 Lie algebroids

Let us now assume that X is a smooth DM stack. Its tangent sheaf ${\mathbb {T}}_X$ is a sheaf of Lie-algebras on the small étale site $X_{et}$ where the Lie bracket is the usual bracket of vector fields. Recall from [14] that a Lie algebroid on X consists of a vector bundle T on X, together two additional structures:

• (1) a ${\mathbb {C}}$-linear Lie bracket $[-,-]$ on T.

• (2) an ${\mathcal {O}}_X$-linear morphism $a : T \longrightarrow {\mathbb {T}}_X$.

These data are required to satisfy the following compatibility relation: for any local sections s, t of T, and any function f on X

$$\begin{aligned}{}[s,ft]=f[s,t]+a(s)(f)t. \end{aligned}$$

We can associate to a Lie algebroid on X a natural derived foliation on X as follows. We consider the graded ${\mathcal {O}}_X$-cdga $Sym_{{\mathcal {O}}_X}(T^*[1])$, where $T^*$ is the ${\mathcal {O}}_X$-linear dual to T. The bracket on T induces a ${\mathbb {C}}$-linear differential $d : T^* \longrightarrow T^* \wedge _{{\mathcal {O}}_X}T^*$, which endows $Sym_{{\mathcal {O}}_X}(T^*[1])$ with the structure of graded mixed cdga. This is an object in ${\mathcal {F}}ol(X)$. The cotangent complex of this derived foliation is $T^*$ by construction, and this the above derived foliation is obviously smooth. However, it is rigid only when $a : T \longrightarrow {\mathbb {T}}_X$ identifies T with a subbundle of ${\mathbb {T}}_X$.

It is easy to show that this construction produces a fully faithful $\infty$-functor

$$\begin{aligned} \mathsf {LieAlgbd}/X \longrightarrow {\mathcal {F}}ol(X) \end{aligned}$$

where $\mathsf {LieAlgbd}/X$ is the category of Lie algebroids over X. The essential image of this $\infty$-functor can be shown to coincide with the full $\infty$-subcategory consisting of smooth derived foliations over X (Definition 1.2.6). To be more precise, for any vector bundle V on X, the classifying space of graded mixed structures on the sheaf of graded cgda $Sym_{{\mathcal {O}}_X}(V[1])$ turns out to be discrete and in bijection with Lie algebroid structures on $V^*$. In particular, we get that the $\infty$-category of smooth derived foliations over $Spec\, {\mathbb {C}}$ is equivalent to the usual category of finite dimensional complex Lie algebras.

There is also a relation between derived foliations and dg-Lie algebroids as considered in [5, 14]. To a dg-Lie algebroid T over an affine variety $X=Spec\, A$, we can associate its Chevalley-Eilenberg cochain complex $C^*(T):=Sym_{A}(T^*[1])$, considered as a graded mixed cdga using the Lie bracket as mixed structure. Though this will not be relevant in this paper, we think that this construction produces a fully faithful $\infty$-functor from the full $\infty$-subcategory consisting of dg-Lie algebroids that are perfect over A and of amplitude in $[0,\infty )$, to derived foliations over X.

2.3.2 Initial and final foliations

The $\infty$-category ${\mathcal {F}}ol(X)$ possesses two important distinguished objects, namely the initial and final objects. The initial object is called the punctual derived foliation, or the trivial derived foliation, and is denoted by ${\mathbf {0}}_X \in {\mathcal {F}}ol(X)$. The corresponding graded mixed cdga ${{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})$ is ${\mathcal {O}}_X$ endowed with the trivial graded mixed structure (concentrated in weight and cohomological degree 0). When X is smooth, $0_X$ can also be represented by the 0 Lie algebroids on X and intuitively corresponds to the foliation on X whose leaves are the points of X.

The final object in ${\mathcal {F}}ol(X)$ is called the tautological derived foliation, or the de Rham derived foliation. It corresponds to the graded mixed cdga ${{\mathbf {D}}}{{\mathbf {R}}}(X)$ which is the derived de Rham algebra of X. when X is smooth, it can also be represented by the tautological Lie algebroid ${\mathbb {T}}_X$ itself, and intuitively is the foliation for which X is its only leaf.

2.3.3 Algebraically integrable derived foliations

Suppose that we are given a morphism of derived DM-stacks $f : X \longrightarrow Y$ that is locally of finite presentation. The relative de Rham algebra of X over Y defines a sheaf of graded mixed cdga ${{\mathbf {D}}}{{\mathbf {R}}}(X/Y)$ on the small étale site of X, which is a derived foliation over X. Its underlying sheaf of graded cdga’s simply is $Sym_{{\mathcal {O}}_X}({\mathbb {L}}_{X/Y}[1])$, where ${\mathbb {L}}_{X/Y}$ is the relative cotangent complex of X over Y. This is called the derived foliation induced by the morphism f. We will use the notation

$$\begin{aligned} {\mathcal {F}}_f := {{\mathbf {D}}}{{\mathbf {R}}}(X/Y) \in {\mathcal {F}}ol(X) \end{aligned}$$

for this foliation. Note that ${\mathcal {F}}_f$ can also be understood as the pull-back $f^*({\mathbf {0}}_Y)$, where ${\mathbf {0}}_Y$ is the punctual foliation described above.

We set the following definition, and use the expression d-integrable to avoid confusions with the usual notions of integrability of singular underived foliations that we will meet later on (see Sect. 1.3.4).

Definition 1.3.1

Let X be a derived DM stack. A derived foliation F on X (locally) equivalent to one of the form ${\mathcal {F}}_f=f^*({\mathbf {0}}_Y)$, for a (locally defined) morphism $f:X\rightarrow Y$ locally of finite presentation between derived DM stacks, will be called algebraically (locally) d-integrable.

The reason for this name is that the derived foliation ${\mathcal {F}}_f$ corresponds intuitively to the foliation on X whose leaves on are the derived fibers of the map f. See also Remark 1.3.4. It is obvious to see that ${\mathcal {F}}_f$ is quasi-smooth (resp. smooth) if and only if f is quasi-smooth (resp. smooth). Also, ${\mathcal {F}}_f$ is automatically rigid.

2.3.4 Pfaffian systems as quasi-smooth and rigid derived foliations

Let X be a smooth algebraic variety. Assume that we are given differential forms $w_i \in \Gamma (X,\Omega _X^1)$, for $i=1,\dots ,n$, such that the graded ideal $(w_1,\dots ,w_k) \subset \Gamma (X,Sym_{{\mathcal {O}}_X}(\Omega _X^1[1]))$ is stable by the de Rham differential. We chose differential forms $w_{ij}\in \Gamma (X,\Omega ^1_X)$ such that for all i we have

$$\begin{aligned} d(w_i)=\sum _j w_{ij}\wedge w_j. \end{aligned}$$

We assume furthermore that the $k\times k$ matrix of forms $W=(w_{ij})_{ij}$ satisfy the following integrability condition

$$\begin{aligned} d(W) + W\wedge W = 0. \end{aligned}$$

Out of these data $w_i$ and W as above, we construct a sheaf of graded mixed cdga’s on X by considering $Sym_{{\mathcal {O}}_X}({\mathbb {L}}[1])$ where ${\mathbb {L}}$ is the two terms perfect complex

The graded mixed structure on $Sym_{{\mathcal {O}}_X}({\mathbb {L}}[1])$ is itself determined by a morphism of complexes of sheaves of ${\mathbb {C}}$-vector spaces

$$\begin{aligned} {\mathbb {L}}\longrightarrow \wedge ^2_{{\mathcal {O}}_X}{\mathbb {L}}\end{aligned}$$

compatible with the de Rham differential on $\Omega _X^1$. Such a morphism is obtained for instance by specifying a morphism ${\mathcal {O}}_X^k \longrightarrow {\mathcal {O}}_X^k \otimes _{{\mathcal {O}}_X} \Omega _X^1$ which is a flat connection on the vector bundle ${\mathcal {O}}_X^k$. Therefore, the matrix W defines such a graded mixed structure, and therefore a derived foliation on X.

The derived foliations defined above depends not only on the $w_i$’s, but also on the choice of the matrix W. It is clear that such derived foliations are quasi-smooth and rigid. We call such derived foliations Pfaffian derived foliations for obvious reasons. Derived foliations which are algebraically d-integrable are always locally, for the Zariski topology, equivalent to Pfaffian derived foliations.

2.3.5 Pull-backs of smooth and rigid foliations

Let $f : X \longrightarrow Y$ be a morphism of smooth algebraic varieties and ${\mathcal {F}}\in {\mathcal {F}}ol(Y)$. We have seen that there is a pull-back $f^*({\mathcal {F}}) \in {\mathcal {F}}ol(X)$. It is easy to see that when ${\mathcal {F}}$ is smooth, then $f^*({\mathcal {F}})$ is always quasi-smooth. If ${\mathcal {F}}$ is moreover rigid, then so is $f^*({\mathcal {F}})$. We will see later that, at least if one admits Y to be a formal scheme, all rigid and quasi-smooth derived foliations are locally of this form (see Proposition 1.5.1). This follows from an important property of pull-backs, namely the existence of a homotopy push-out of cotangent complexes

The intuition behind this is that the leaves of $f^*({\mathcal {F}})$ are obtained by derived pull-back along f of the leaves of ${\mathcal {F}}$. The defect of transversality of f with respect to the leaves of ${\mathcal {F}}$ implies that the leaves of $f^*({\mathcal {F}})$ can be singular, but are always quasi-smooth.

2.3.6 Derived foliations, truncations and singular algebraic foliations

Our derived foliations bear an important relation with the singular foliations classically considered in the algebraic and holomorphic contexts. There are several possible definitions of singular foliations in the literature. In [2, Definition 1.11] they are defined as full coherent differential ideals of the sheaf of differential 1-forms. For our purposes, the property of being full will be irrelevant, and will simply define a singular foliation (on a smooth variety X) as a coherent subsheaf $D \subset \Omega _X^1$ satisfying the condition

$$\begin{aligned} d(D) \subset D\wedge \Omega _X^1 \subset \Omega _X^2, \end{aligned}$$

where $d : \Omega _X^1 \longrightarrow \Omega _X^2$ is the de Rham differential. This is equivalent to [1, Definition 6.1.1].

Let now ${\mathcal {F}}\in {\mathcal {F}}ol(X)$ be a derived foliation on a smooth variety X. We consider the anchor map $a : \Omega _X^1 \longrightarrow {\mathbb {L}}_{{\mathcal {F}}}$ and its induced morphism $\Omega _X^1 \longrightarrow H^0({\mathbb {L}}_{{\mathcal {F}}}).$ We let $D \subset \Omega _X^1$ be the kernel of the above map, which is a coherent subsheaf of $\Omega _X^1$. As a comes from a morphism ${{\mathbf {D}}}{{\mathbf {R}}}(X) \longrightarrow Sym_{{\mathcal {O}}_X}({\mathbb {L}}_{{\mathcal {F}}}[1])$ of graded mixed cdga’s over X, it follows that the ideal in $\Omega _X^*$ generated by D is in fact a differential ideal ($d(D) \subset D\wedge \Omega _X^1$), i.e. D is an underived singular foliation on X.

Definition 1.3.2

The kernel D of $H^0(a):\Omega _X^1 \longrightarrow H^0({\mathbb {L}}_{{\mathcal {F}}})$ is a singular foliation on X called the truncation of ${\mathcal {F}}$, and denoted by $\tau _{0}({\mathcal {F}})$.

This produces an $\infty$-functor $\tau _{0}$ from ${\mathcal {F}}ol(X)$ to the category of singular foliations on X. However, we will see later that not all singular foliation arise this way, and the existence of a derived enhancement of a singular foliation is a sublte question related to local integrability. This question will be studied in details for quasi-smooth and rigid derived foliation (see Corollary 2.3.3).

Conversely, let $D \subset \Omega _X^1$ be a singular foliation on X. We can construct a graded algebra

$$\begin{aligned} {{\mathbf {D}}}{{\mathbf {R}}}(D):=\bigoplus _{p} \left( \Omega _X^p/<D>\right) [p], \end{aligned}$$

which is the (underived) quotient of the algebra of differential forms $\Omega _X^*$ by the graded ideal generated by D. As D is a differential ideal, the de Rham differential induces a graded mixed structure on ${{\mathbf {D}}}{{\mathbf {R}}}(D)$ in such a way that the canonical morphism

$$\begin{aligned} {{\mathbf {D}}}{{\mathbf {R}}}(X) \longrightarrow {{\mathbf {D}}}{{\mathbf {R}}}(D) \end{aligned}$$

becomes a morphism of graded mixed cdga’s. Note that however, ${{\mathbf {D}}}{{\mathbf {R}}}(D)$ does not satisfy the condition of definition 1.2.1, as $Sym(\Omega ^1_X/D[1])$ involves derived wedge powers of the coherent sheaf $\Omega ^1_X/D[1]$, and might differ from $(\Omega ^p/<D>)[p]$. Therefore, ${{\mathbf {D}}}{{\mathbf {R}}}(D)$ does not define a derived foliation in our sense. To be more precise, the underlying graded algebra ${{\mathbf {D}}}{{\mathbf {R}}}(D)$ is of the form $Sym_{{\mathcal {O}}_{X}}^u(\Omega ^1_X/D[1])$, where $Sym^u$ is the underived symmetric algebra functor. The construction $D \mapsto {{\mathbf {D}}}{{\mathbf {R}}}(D)$ is easily seen to be an equivalence of categories, from singular foliations on X to graded mixed algebras of the form $Sym_{{\mathcal {O}}_{X}}^u(M[1])$ such that $\Omega _X^1 \longrightarrow M$ is a coherent quotient. This however does not define a functor from singular foliations to derived foliations.

Finally, the truncation $\infty$-functor $\tau _0$ enjoys a certain universal property described as follows. The derived foliation ${\mathcal {F}}$ has a realization $|{{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})|$, and in the same way, the truncation $\tau _0({\mathcal {F}})$ has an underived de Rham complex $(\Omega _X^*/<D>)$ where the differential is the de Rham differential. There is an induced canonical morphism

$$\begin{aligned} |{{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})| \longrightarrow (\Omega _X^*/<D>). \end{aligned}$$

This morphism is far from being an isomorphism in general, although it is an isomorphism in low degrees under appropriate conditions (see Proposition 3.1.5).

Note that there is a notion of pullback of singular foliation along an map $f:X\rightarrow Y$, with X and Y smooth. For simplicity we state it in the algebraic case, but the analytic and formal versions are alike. If $D\subset \Omega ^1_Y$ is an algebraic singular foliation on Y, then it’s pullback is, by definition, the subsheaf image of the composite map $f^*(D) \rightarrow f^*(\Omega ^1_Y) \rightarrow \Omega ^1_X$. Using this notion we give the following definition.

Definition 1.3.3

An algebraic (resp. formal, resp. analytic) singular foliation on a smooth algebraic variety (resp. formallly smooth formal scheme, resp. smooth analytic space) X is locally integrable if locally in the Zariski topology (resp. locally formally, resp. locally in the analytic topology) at each point of X there exists a morphism $f : X \rightarrow Y$ such that D equals is the pull-back by f of the punctual foliation on Y. Equivalently, D is the image of $f^*(\Omega _Y^1) \rightarrow \Omega _X^1$.

Clearly, if a derived foliation ${\mathcal {F}}$ is d-integrable in the sense of Sect. 1.3.1, then its truncation $\tau _0({\mathcal {F}})$ is integrable in the sense above.

Remark 1.3.4

In the literature, a (locally) integrable singular foliation is also sometimes called (locally) completely integrable. We note here that the notion of integrability of Definition 1.3.3 only coincides with the notion of [12, §3] if one further assume that f is generically smooth on X (this is condition b) at p. 73 of loc.cit). Therefore, to distinguish between the two, we will refer to Malgrange’s stronger notion as local strong integrability.

2.4 Foliations over formal completions

Let X be a smooth affine variety and $Y \subset X$ be a closed subvariety. For simplicity we assume that the ideal of Y in X is generated by a regular sequence $(f_1,\dots ,f_k)$. We denote by ${\widehat{{\mathcal {O}}}}_Y$ the ring of functions on the formal completion of X along Y.

Recall that we have a module $\widehat{\Omega _Y^1}$ of differential forms on the formal completion of X along Y, defined as the formal completion of $\Omega _X^1$ along (the ideal defining) Y. This is a locally free ${\widehat{{\mathcal {O}}}}_Y$-module of rank the dimension of X. Moreover, it comes equipped with a canonical derivation $d : \widehat{{\mathcal {O}}_Y} \longrightarrow \widehat{\Omega _Y^1}$ which extends to a full structure of graded mixed cdga ${\widehat{{{\mathbf {D}}}{{\mathbf {R}}}}}(Y)$ on the graded cdga $Sym_{{\widehat{{\mathcal {O}}}}_Y}(\widehat{\Omega _Y^1}[1]).$ We can then consider the $\infty$-category of graded mixed cdga’s A endowed with a morphism

$$\begin{aligned} u : {\widehat{{{\mathbf {D}}}{{\mathbf {R}}}}}(Y) \longrightarrow A \end{aligned}$$

and satisfying the following conditions.

• The morphism u induces an isomorphism ${\widehat{{\mathcal {O}}}}_Y \longrightarrow A(0)$.

• The ${\widehat{{\mathcal {O}}}}_Y$-dg-module $A(1)[-1]$ is perfect and connective.

• The natural morphism of graded cdga’s

  $$\begin{aligned} Sym_{{\widehat{{\mathcal {O}}}}_Y}(A(1)) \longrightarrow A \end{aligned}$$

  is a quasi-isomorphism.

Let us denote by ${\widehat{{\mathcal {F}}ol}}({\widehat{Y}})$ the opposite $\infty$-category of the above $\infty$-category of graded mixed cdga’s under ${\widehat{{{\mathbf {D}}}{{\mathbf {R}}}}}(Y)$. We call its objects formal derived foliations on the formal scheme ${\widehat{Y}}$. On the other hand, we may identify the formal scheme ${\widehat{Y}}$ with its associated (derived) stack, and therefore we may consider its $\infty$-category of foliations ${\mathcal {F}}ol({\widehat{Y}})$, according to Definition 1.2.4.

Proposition 1.4.1

There exists a natural equivalence of $\infty$-categories

$$\begin{aligned} {\widehat{{\mathcal {F}}ol}}({\widehat{Y}})\simeq {\mathcal {F}}ol({\widehat{Y}}). \end{aligned}$$

Proof

The formal completion of X along Y, denoted by ${\widehat{Y}}$, is equivalent, as an object of $\mathbf {dSt}$, to a colimit

$$\begin{aligned} {\widehat{Y}}:=colim_n Y_n \end{aligned}$$

where $Y_n \subset X$ is the closed sub-scheme defined by the equations $(f_1^n,\dots ,f_k^n)$, where $(f_1,\dots ,f_k)$ is the regular sequence generating the ideal of Y in X. We thus have ${\mathcal {F}}ol({\widehat{Y}})\simeq lim_n {\mathcal {F}}ol(Y_n)$. Now, the right hand side is directly related to ${\widehat{{\mathcal {F}}ol}}({\widehat{Y}})$ by the limit $\infty$-functor

$$\begin{aligned} lim : lim_n {\mathcal {F}}ol(Y_n) \longrightarrow {\widehat{{\mathcal {F}}ol}}({\widehat{Y}}). \end{aligned}$$

Note that this is well defined as $lim_n{{\mathbf {D}}}{{\mathbf {R}}}(Y_n)\simeq {\widehat{{{\mathbf {D}}}{{\mathbf {R}}}}}(Y)$, because $\Omega ^1_{{\widehat{Y}}} \simeq lim_n {\mathbb {L}}_{Y_n}$. The inverse functor is defined by sending a graded mixed cgda A under ${\widehat{{{\mathbf {D}}}{{\mathbf {R}}}}}(Y)$ to its families of restriction

$$\begin{aligned} \{A\otimes _{{\widehat{{{\mathbf {D}}}{{\mathbf {R}}}}}(Y)}{{\mathbf {D}}}{{\mathbf {R}}}(Y_n)\}_n \in lim_n {\mathcal {F}}ol(Y_n). \end{aligned}$$

The fact that these two $\infty$-functors are inverse to each others is an immediate consequence of the fact that the natural $\infty$-functor

$$\begin{aligned} \mathsf {Perf}({\widehat{Y}}) \longrightarrow lim_n \mathsf {Perf}(Y_n) \end{aligned}$$

is an equivalence. $\square$

The following is the formal version of Definition 1.3.1.

Definition 1.4.2

Let ${\widehat{Y}}$ (respectively, $\widehat{Y')}$) be the formal completion of a smooth affine scheme Y (resp. $Y'$) along an ideal generated by a regular sequence. We say that a foliation ${\mathcal {F}}$ on ${\widehat{Y}}$ is formally (locally) d-integrable if there exists a (locally defined) morphism of formal schemes $f:{\widehat{Y}} \rightarrow \widehat{Y'}$ such that ${\mathcal {F}}$ is (formally locally) equivalent to the pullback $f^*({\mathbf {0}}_{\widehat{Y'}})$ of the final foliation ${\mathbf {0}}_{\widehat{Y'}}$ on $\widehat{Y'}$ via f.

If X is a smooth variety, $x\in X$, and ${\widehat{X}}_x$ denotes the formal completion of X at x, then an algebraic foliation ${\mathcal {F}}\in {\mathcal {F}}ol(X)$ is said to be formally d-integrable at x if its restriction ${\widehat{{\mathcal {F}}}}$ to ${\widehat{X}}_x$ (which is a formal foliation on ${\widehat{X}}_x$) is formally d-integrable according to the previous definition.

Note that, in the above definition, the underlying graded cdga’s of $f^*({\mathbf {0}}_{\widehat{Y'}})$ is $Sym_{{\mathcal {O}}_X}({\widehat{{\mathbb {L}}}}_{{\widehat{Y}}/\widehat{Y'}}[1])$, where ${\widehat{{\mathbb {L}}}}_{{\widehat{Y}}/\widehat{Y'}}$ is the cotangent complex of $f:{\widehat{Y}} \rightarrow \widehat{Y'}$.

2.5 Formal structure of rigid quasi-smooth derived foliations

In the proposition below we let $\widehat{{\mathbb {A}}}^n$ be the formal completion of ${\mathbb {A}}^n$ at 0.

Proposition 1.5.1

Let X be smooth variety and ${\mathcal {F}}\in {\mathcal {F}}ol(X)$ be a rigid and quasi-smooth derived foliation on X. Then, Zariski locally on X, there exists $n\ge 0$ and a smooth and rigid derived foliation ${\mathcal {F}}'$ on the formal scheme $X\times \widehat{{\mathbb {A}}}^n$, such that ${\mathcal {F}}$ is the pull-back of ${\mathcal {F}}'$ by the zero section $X \longrightarrow X \times \widehat{{\mathbb {A}}}^n$.

Proof

We will freely use the material and notations about internal De Rham complexes and their realizations, recalled in Sect. 1.1. First of all, the statement being Zariski local, we may assume that $X=Spec\, A$ is a smooth affine variety. We consider ${\mathcal {F}}\in {\mathcal {F}}ol(X)$, a rigid and quasi-smooth derived foliation, which corresponds to a graded mixed cdga ${{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})$ with an identification ${{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})(0)\simeq A$ and satisfying the conditions of Definitions 1.2.1 and 1.2.6. There is a natural morphism $\Omega _A^1 \longrightarrow {\mathbb {L}}_{\mathcal {F}},$ whose cone, by the rigidity and quasi-smooth hypothesis, must be of the form $N^*[1]$, for a vector bundle $N^*$ over X. By localizing further on X we may suppose $N^*$ isomorphic to ${\mathcal {O}}_X^n$ for some $n\ge 0$. We consider the push-out of graded mixed cdga’s

$$\begin{aligned} {{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}) \longrightarrow {{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})\otimes _{{{\mathbf {D}}}{{\mathbf {R}}}(X)}A. \end{aligned}$$

On the underlying graded cdga’s, this morphism looks like

$$\begin{aligned} Sym_A({\mathbb {L}}_{{\mathcal {F}}}[1]) \longrightarrow Sym_A(N^*[2]) \end{aligned}$$

and is induced by applying the Sym construction to the boundary map ${\mathbb {L}}_{\mathcal {F}}\rightarrow N^*[1]$. Moreover, as $N^*$ is a vector bundle (and X is affine) we see that the graded mixed structure on the graded mixed cdga $Sym_A(N^*[2])$ must be trivial.

We now consider the induced morphism on the internal relative de Rham algebra

$$\begin{aligned} {{\mathbf {D}}}{{\mathbf {R}}}^{int}(Sym_A(N^*[2])/{{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})) \longrightarrow {{\mathbf {D}}}{{\mathbf {R}}}^{int}(A/{{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})). \end{aligned}$$

We can then consider their internal realization, and the induced morphism on the internal de Rham cohomology

$$\begin{aligned} |{{\mathbf {D}}}{{\mathbf {R}}}^{int}(Sym_A(N^*[2])/{{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}))| \longrightarrow |{{\mathbf {D}}}{{\mathbf {R}}}^{int}(A/{{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}))|. \end{aligned}$$

This is a new morphism of graded mixed cdga’s and thanks to Lemma 4.1.2, the right hand side is canonically equivalent to ${{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})$, so we get a morphism

$$\begin{aligned} |{{\mathbf {D}}}{{\mathbf {R}}}^{int}(Sym_A(N^*[2])/{{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}))| \longrightarrow {{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}). \end{aligned}$$

The left hand side is a graded mixed cdga, say B, whose degree zero part is $|Sym_A(N^*[2])|\simeq {\widehat{Sym}}_A(N^*)\simeq {\mathcal {O}}(X\times \widehat{{\mathbb {A}}}^n)$. Moreover, by construction, it is not hard to see that B is free, as a graded cdga, over the B(0)-module $\Omega _A^1\otimes _A B(0)$. Therefore, Proposition 1.4.1 tells us that B corresponds to a smooth foliation ${\mathcal {F}}'$ on $X\times \widehat{{\mathbb {A}}}^n$.

The morphism of graded mixed cdga’s $B \longrightarrow {{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})$ induces a morphism $e^*({\mathcal {F}}') \longrightarrow {\mathcal {F}}$ in ${\mathcal {F}}ol(X)$, where $e : X \longrightarrow X \times \widehat{{\mathbb {A}}}^n$ is the zero section. This morphism is furthermore an equivalence by observing the induced morphism on cotangent complexes. In particular, $e^*({\mathcal {F}}')$ is rigid, and this automatically implies that ${\mathcal {F}}'$ is rigid as a foliation on $X\times \widehat{{\mathbb {A}}}^n$. $\square$

Remark 1.5.2

Proposition 1.5.1 has the following conceptual refinement. First of all, the same proof shows that there exists a globally defined pair $({\mathfrak {X}}' , {\mathcal {F}}')$ consisting of a formally smooth formal scheme ${\mathfrak {X}}'$ and a smooth rigid foliation ${\mathcal {F}}'$ on ${\mathfrak {X}}'$, together with a map $f:X \rightarrow {\mathfrak {X}}'$ such that $f_{red}$ is an isomorphism and there exists an equivalence ${\mathcal {F}} \simeq f^*({\mathcal {F}}')$. This is achieved by defining

$$\begin{aligned} {\mathfrak {X}}':= \mathrm {Spf}(|{{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})\otimes _{{{\mathbf {D}}}{{\mathbf {R}}}(X)}A|), \end{aligned}$$

and ${\mathcal {F}}'$ as the derived foliation on ${\mathfrak {X}}'$ defined by the graded mixed cdga on X

$$\begin{aligned} |{{\mathbf {D}}}{{\mathbf {R}}}^{int}(({{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})\otimes _{{{\mathbf {D}}}{{\mathbf {R}}}(X)}A)/{{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}))|. \end{aligned}$$

Note that if ${\mathcal {N}}^*$ is the vector bundle on X such that ${\mathcal {N}}^*[1]$ is the cofiber of the canonical map $\Omega _{X}^1 \longrightarrow {\mathbb {L}}_{\mathcal {F}}$, the underlying graded cdga ${{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})\otimes _{{{\mathbf {D}}}{{\mathbf {R}}}(X)}A$ is $Sym_{{\mathcal {O}}_X}(N^*[2])$. However, when X is not affine the mixed structure on $Sym_{{\mathcal {O}}_X}(N^*[2])$ can possibly be non-trivial. We note here that this mixed structure captures the difference between the formal scheme ${\mathfrak {X}}'$ and the formal completion $\widehat{{\mathcal {N}}}$ of the normal bundle of ${\mathfrak {X}}$ in ${\mathfrak {X}}'$. Finally, Proposition 1.5.1 boils down to the fact that, Zariski locally on X, ${\mathfrak {X}}'$ can be chosen of the form $X\times \widehat{{\mathbb {A}}}^n$ (and this is simply due that ${\mathcal {N}}^*$ is locally free of finite rank), and that, under this identification, f becomes identified with the zero section map $X \rightarrow X\times \widehat{{\mathbb {A}}}^n$.

Remark 1.5.3

Without the rigidity assumption, but still for quasi-smooth derived foliations, Proposition 1.5.1 remains true if one replaces the formal scheme $X\times \widehat{{\mathbb {A}}}^n$ by a formally smooth formal Artin stack containing X as its reduced part.

When restricting to the formal completion at a point $x \in X$, Proposition 1.5.1 has the following important consequence.

Corollary 1.5.4

Let ${\mathcal {F}}\in {\mathcal {F}}ol(X)$ be a derived quasi-smooth and rigid derived foliation over a smooth algebraic variety X. Let $x \in X$ and ${\widehat{X}}_x=Spf({\widehat{{\mathcal {O}}}}_{X,x})$ be the formal completion of X at x, and ${\widehat{{\mathcal {F}}}} \in {\mathcal {F}}ol({\widehat{X}}_x)$ the restriction of ${\mathcal {F}}$. Then, there exists $m\ge 0$, a morphism $f : {\widehat{X}}_x \longrightarrow \widehat{{\mathbb {A}}}^m$ and an isomorphism

$$\begin{aligned} f^*({\mathbf {0}}_{\widehat{{\mathbb {A}}}^m}) \simeq {\widehat{{\mathcal {F}}}}. \end{aligned}$$

In other words, ${\mathcal {F}}$ is formally d-integrable at each point (Definition 1.4.2).

Proof

Indeed, by Proposition 1.5.1, ${\mathcal {F}}$ is, locally at x, the pull-back of a smooth and rigid derived foliation ${\mathcal {F}}'$ on $X \times \widehat{{\mathbb {A}}}^n$. Thus, ${\widehat{{\mathcal {F}}}}$ becomes isomorphic to the pull-back of a smooth and rigid derived foliation ${\widehat{{\mathcal {F}}}}'$ on ${\widehat{X}}_x \times \widehat{{\mathbb {A}}}^n$. By the formal version of Frobenius theorem (see for instance [4, Thm. 2]), we know that ${\widehat{{\mathcal {F}}}}'$ is formally integrable and thus d-integrable as it is a smooth derived foliation. This implies that ${\widehat{{\mathcal {F}}}}$ is d-integrable. $\square$

Remark 1.5.5

The above corollary is also true for non-quasi-smooth derived foliation, but $\widehat{{\mathbb {A}}}^m$ must be replaced by a more general, eventually not formally smooth, derived formal schemes. It shows in particular that not all singular foliation is the truncation of a quasi-smooth and rigid derived foliation, not even at the formal level. Indeed, formal integrability is not always satisfied for singular foliations.

2.6 Leaves of a derived foliation

Given a derived foliation ${\mathcal {F}}$ on a smooth variety X, and a point $x\in X$, it is possible to define the notion of leaf of ${\mathcal {F}}$ passing through x, at least at the formal level. For this, we start by recalling the notion of formal moduli problems in the sense of [11] (see also [22] for an overview).

We let $\mathbf {dgart}^*$ be the $\infty$-category of commutative, Artinian, connective, local and augmented dg-algebras. Recall that these are cdga’s A, together with an augmentation $A \longrightarrow {\mathbb {C}}$, and such that the following conditions are satisfied:

• The ring $H^0(A)$ is local and artinian.

• The vector space $H^*(A)$ is finite dimensional over ${\mathbb {C}}$.

By definition, a formal moduli problem is an $\infty$-functors

$$\begin{aligned} F : \mathbf {dgart}^* \longrightarrow \mathbf {Top} \end{aligned}$$

satisfying the following two conditions:

• The space $F({\mathbb {C}})$ is contractible.

• For any cartesian square in $\mathbf {dgart}^*$

  

  such that the map $H^0(A) \longrightarrow H^0(B)$ is surjective, the induced commutative diagram of spaces

  

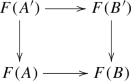
  is cartesian in $\mathbf {Top}$.

Graded mixed cdga’s can be used to define formal moduli problems as follows (see also [6] for more about the relations between formal geometry and graded mixed cdga’s). To start with, there is an $\infty$-functor

$$\begin{aligned} {{\mathbf {D}}}{{\mathbf {R}}}({\mathbb {C}}/-) : \mathbf {dgart}^* \longrightarrow \epsilon -{{\mathbf {d}}}{{\mathbf {g}}}^{gr}\end{aligned}$$

sending an augmented cdga $A \rightarrow {\mathbb {C}}$ to ${{\mathbf {D}}}{{\mathbf {R}}}({\mathbb {C}}/A)$, the de Rham algebra of ${\mathbb {C}}$ relative to A, through the augmentation. This $\infty$-functor is easily seen to be fully faithful, the artinian cdga A being recovered as the realization $|{{\mathbf {D}}}{{\mathbf {R}}}({\mathbb {C}}/A)|$. According to the classification of formal moduli problems by dg-Lie algebras, this $\infty$-functor can also be described as follows. An object $A \in \mathbf {dgart}^*$ gives rise to a tangent dg-lie algebra $\ell _A:={\mathbb {T}}_{{\mathbb {C}}/A}$, the dg-lie algebra of derived A-linear derivations on ${\mathbb {C}}$. The graded mixed cdga ${{\mathbf {D}}}{{\mathbf {R}}}({\mathbb {C}}/A)$ is then canonically equivalent to $C^*(\ell _A)$, the Chevalley complex of the dg-Lie algebra $\ell _A$, considered as a graded mixed cdga (see [22] for details).

For a given graded mixed cdga B we thus define its formal spectrum $\textsf {Spf} \, B : \mathbf {dgart}^* \longrightarrow \mathbf {Top}$ by

$$\begin{aligned} (\textsf {Spf} \, B)(A):=\mathrm {Map}_{\epsilon -{{\mathbf {d}}}{{\mathbf {g}}}^{gr}}(B,{{\mathbf {D}}}{{\mathbf {R}}}({\mathbb {C}}/A)). \end{aligned}$$

The $\infty$-functor $\textsf {Spf} \, B$ is then a formal moduli problem, called the formal spectrum of B.

Let now ${\mathcal {F}}$ be a derived foliation on the smooth variety X, and $x\in X$. Taking an affine chart around x we can consider X to be affine, say $X=Spec\, A$. We start by considering the augmentation induced by the point x

$$\begin{aligned} {{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}) \longrightarrow A \longrightarrow {\mathbb {C}}. \end{aligned}$$

This is a morphism of graded mixed cdga’s and we can form the corresponding push-out ${{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}_x):=A \otimes _{{{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})}{\mathbb {C}}.$ This is a new graded mixed cdga which corresponds to a derived foliation over $Spec\, {\mathbb {C}}$, and whose cotangent complex is ${\mathbb {L}}_{{\mathcal {F}},x}[1]$, the shift of the fiber at x of the cotangent complex of ${\mathcal {F}}$. The formal spectrum of ${{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}_x)$ defines a formal moduli problem

$$\begin{aligned} {\widehat{{\mathcal {F}}}}_x := \textsf {Spf} \, ({{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}_x)) : \mathbf {dgart}^* \longrightarrow \mathbf {Top}. \end{aligned}$$

Definition 1.6.1

The formal moduli problem ${\widehat{{\mathcal {F}}}}_x$ defined above is called the formal leaf of ${\mathcal {F}}$ passing through x.

Note that the tangent dg-Lie algebra of the formal leaf ${\widehat{{\mathcal {F}}}}_x$ is given by ${\mathbb {T}}_{{\mathcal {F}},x}[-1]$, the fiber at x of the tangent complex of the derived foliation ${\mathcal {F}}$. In particular, amplitude considerations tell us that ${\widehat{{\mathcal {F}}}}_x$ is always representable by a derived formal scheme (see [11]).

When applied to the tautological foliation, ${{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})={{\mathbf {D}}}{{\mathbf {R}}}(X)$, we get that ${{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}_x)=Sym_{{\mathbb {C}}}(\Omega ^1_{X,x}[1])$ with the trivial mixed structure. In this case we see that $\textsf {Spf} \, ({{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}_x))$ is canonically isomorphic to ${\widehat{X}}_x$, the formal completion of X at x. Moreover, using the canonical map ${{\mathbf {D}}}{{\mathbf {R}}}(X) \longrightarrow {{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})$, the formal moduli ${\widehat{{\mathcal {F}}}}_x$ comes equipped with a canonical morphism

$$\begin{aligned} {\widehat{{\mathcal {F}}}}_x \longrightarrow {\widehat{X}}_x \end{aligned}$$

to the formal completion of X at the point x. When ${\mathcal {F}}$ is rigid this morphism is a closed embedding of derived formal schemes, and thus ${\widehat{{\mathcal {F}}}}_x$ sits inside ${\widehat{X}}_x$ as a closed formal derived subscheme.

The morphism induced by ${\widehat{{\mathcal {F}}}}_x \longrightarrow {\widehat{X}}_x$ at the level of rings of functions, can be described as follows. The commutative dg-algebra of functions on ${\widehat{F}}_x$ is $|{{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}_x)|$, the realization of ${{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}_x)$. The natural morphism ${{\mathbf {D}}}{{\mathbf {R}}}(X) \longrightarrow {{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}_x)$ induces a canonical morphism of cdga’s

$$\begin{aligned} {\mathcal {O}}({\widehat{X}}_x)\simeq |Sym_{{\mathbb {C}}}(\Omega ^1_{X,x}[1])| \longrightarrow |{{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}_x)|=:{\mathcal {O}}({\widehat{{\mathcal {F}}}}_x), \end{aligned}$$

which is the induced morphism obtained by restriction of functions along the embedding ${\widehat{{\mathcal {F}}}}_x \subset {\widehat{X}}_x$.

Note that one can define analytic and algebraic leaves as well, but of course, contrary to the formal case, their existence is not guaranteed. We give below the definition in the algebraic setting, the case of analytic leaves being completely similar.

We define an algebraic leaf of ${\mathcal {F}}$ on X to be a derived scheme L together with a pointwise injective morphism of derived schemes $j : L \longrightarrow X$ such that the following condition is satisfied: for all point $x \in L$, there exists an equivalence of formal derived schemes ${\widehat{L}}_x \simeq {\widehat{F}}_x$, that makes the diagram below commutative

When ${\mathcal {F}}$ is globally integrable by a morphism $f : X \longrightarrow Y$, then clearly the inclusions of derived fibers $f^{-1}(y) \longrightarrow X$ are leaves in the sense above. As we will see later (Corollary 2.3.4), under an appropriate codimension 2 condition, rigid and quasi-smooth derived foliations always admit analytic leaves locally. i.e. their formal leaves are in fact “convergent”.

3 The analytic theory

The general notion of derived foliations has a complex analytic analogue. We will not need the most general definition, that would require some advanced tools of derived analytic geometry (see e.g. [16]), and we will restrict ourselves to derived foliations over smooth complex analytic spaces, for which the basic definitions can be given more directly.

3.1 Analytic derived foliations

Let X be a smooth complex analytic space. It has a sheaf of holomorphic 1-forms $\Omega _X^1$, and a de Rham algebra ${{\mathbf {D}}}{{\mathbf {R}}}(X):=Sym_{{\mathcal {O}}_X}(\Omega _X^1[1])$. This is a sheaf of graded cdga’s over X, which is equipped with a canonical graded mixed structure given by the holomorphic de Rham differential.

Definition 2.1.1

A holomorphic or analytic derived foliation over X consists of a sheaf A of graded mixed cdga’s over X, together with a morphism of sheaves of graded mixed cdga’s

$$\begin{aligned} {{\mathbf {D}}}{{\mathbf {R}}}(X) \longrightarrow A \end{aligned}$$

satisfying the following conditions:

• (1) The induced morphism ${\mathcal {O}}_X \longrightarrow A(0)$ is a quasi-isomorphism.

• (2) The complex of ${\mathcal {O}}_X$-modules $A(1)[-1]$ is perfect and connective.

• (3) The natural morphism $Sym_{{\mathcal {O}}_X}(A(1)) \longrightarrow A$ is a quasi-isomorphism of sheaves of graded cdga’s.

The analytic derived foliations over a complex manifold X form an $\infty$-category, denoted by ${\mathcal {F}}ol(X)$. It is a full sub-$\infty$-category of the $\infty$-category of sheaves of graded mixed ${{\mathbf {D}}}{{\mathbf {R}}}(X)$-algebras over X. For any morphism $f : X \longrightarrow Y$ of complex manifolds, we have a pull-back $\infty$-functor

$$\begin{aligned} f^* : {\mathcal {F}}ol(Y) \longrightarrow {\mathcal {F}}ol(X). \end{aligned}$$

It is defined as in the algebraic case. There is a natural morphism $f^{-1}({{\mathbf {D}}}{{\mathbf {R}}}(Y)) \longrightarrow {{\mathbf {D}}}{{\mathbf {R}}}(X)$ of sheaves of graded mixed cgda’s on Y. For ${\mathcal {F}}\in {\mathcal {F}}ol(Y)$, corresponding to a sheaf of graded mixed cdga ${{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})$, we define $f^*({\mathcal {F}}) \in {\mathcal {F}}ol(X)$ as the derived foliation associated to the sheaf of graded mixed cdga’s given by the base change

$$\begin{aligned} {{\mathbf {D}}}{{\mathbf {R}}}(f^*({\mathcal {F}})):={{\mathbf {D}}}{{\mathbf {R}}}(X) \otimes _{f^{-1}({{\mathbf {D}}}{{\mathbf {R}}}(Y))}f^{-1}({{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})). \end{aligned}$$

As in Definition 1.2.6, we have the notions of smooth, quasi-smooth, and rigid derived foliations over a complex manifold. As in Definition 1.3.2, we have a notion of truncation of an analytic derived foliation on a complex manifold; this truncation is an analytic singular foliation on the same complex space.

The following is the analytic version of Definition 1.3.1.

Definition 2.1.2

An analytic derived foliation ${\mathcal {F}}$ on a complex manifold X is (locally) d-integrable if there exists a (locally defined) analytic map $F:X\rightarrow Y$ of complex manifolds and a (local in the analytic topology) equivalence ${\mathcal {F}}\simeq f^*({\mathbf {0}}_{Y})$, where ${\mathbf {0}}_Y$ is the final derived analytic foliation on Y.

3.2 Analytification

Let X be a smooth algebraic variety and $X^h$ be the corresponding complex analytic space. We are going to construct an analytification $\infty$-functor

$$\begin{aligned} (-)^h : {\mathcal {F}}ol(X) \longrightarrow {\mathcal {F}}ol(X^h). \end{aligned}$$

We have a morphism of ringed spaces

$$\begin{aligned} u : (X^h,{\mathcal {O}}_X^h) \longrightarrow (X,{\mathcal {O}}_X). \end{aligned}$$

This morphism induces a canonical isomorphism $u^*(\Omega _X^1) \simeq \Omega _{X^h}^1$ of vector bundles on $X^h$. This extends to a natural isomorphisms $u^*(\Omega _X^*)\simeq \Omega _{X^h}^*$, which is compatible with the de Rham differential in the sense that the composed morphism

$$\begin{aligned} u^{-1}({{\mathbf {D}}}{{\mathbf {R}}}(X)) \longrightarrow u^*({{\mathbf {D}}}{{\mathbf {R}}}(X)) \simeq {{\mathbf {D}}}{{\mathbf {R}}}(X^h) \end{aligned}$$

is not only a morphism of graded cdga’s but of graded mixed cdga’s.

For an algebraic derived foliation ${\mathcal {F}}\in {\mathcal {F}}ol(X)$, corresponding to a morphism of sheaf of graded mixed cdga’s ${{\mathbf {D}}}{{\mathbf {R}}}(X) \longrightarrow {{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})$, we consider

$$\begin{aligned} {{\mathbf {D}}}{{\mathbf {R}}}(X^h) \longrightarrow u^{-1}({{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})) \otimes _{{{\mathbf {D}}}{{\mathbf {R}}}(X)}{{\mathbf {D}}}{{\mathbf {R}}}(X^h). \end{aligned}$$

This defines a derived foliation ${\mathcal {F}}^h \in {\mathcal {F}}ol(X^h)$. Obviously, the construction ${\mathcal {F}}\mapsto {\mathcal {F}}^h$ is functorial and defines an $\infty$-functor

$$\begin{aligned} (-)^h : {\mathcal {F}}ol(X) \longrightarrow {\mathcal {F}}ol(X^h). \end{aligned}$$

Definition 2.2.1

The analytification $\infty$-functor for derived foliations is the $\infty$-functor

$$\begin{aligned} (-)^h : {\mathcal {F}}ol(X) \longrightarrow {\mathcal {F}}ol(X^h) \end{aligned}$$

defined above.

The analytification $\infty$-functor shares the following straightforward properties.

• (Functoriality) Let $f : X \longrightarrow Y$ be a morphism of smooth algebraic varieties and $f^h : X^h \longrightarrow Y^h$ the corresponding morphism of complex spaces. Then, we have a naturally commutative diagram of $\infty$-functors

  

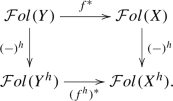
• A derived foliation ${\mathcal {F}}\in {\mathcal {F}}ol(X)$ is smooth (resp. quasi-smooth, resp. rigid) if and only if ${\mathcal {F}}^h$ is smooth (resp. quasi-smooth, resp. rigid).

• For any smooth variety X, the analytification $\infty$-functor $(-)^h : {\mathcal {F}}ol(X) \longrightarrow {\mathcal {F}}ol(X^h)$ is conservative.

• Exactly as done in 1.3.6 for the algebraic case, there is a truncation $\infty$-functor $\tau _0: {\mathcal {F}}ol(Y) \rightarrow \mathsf {SingFol}(Y)$ from analytic derived foliations to analytic singular foliations over a complex manifold Y. Moreover, it is easy to check that, if X is a smooth algebraic variety, the following diagram commutes

  

When X is smooth and proper GAGA implies furthermore the following statement.

Proposition 2.2.2

For a smooth and proper algebraic variety X the analytification $\infty$-functor

$$\begin{aligned} (-)^h : {\mathcal {F}}ol(X) \longrightarrow {\mathcal {F}}ol(X^h) \end{aligned}$$

is an equivalence.

Proof

We let $\Omega _X^*[*]:=Sym_{{\mathcal {O}}_X}(\Omega _X^1[1])$ be the sheaf of cdga’s on X. Its analytification is $\Omega _{X^h}^*[*]=Sym_{{\mathcal {O}}_{X^h}}(\Omega _{X^h}^1[1])$. The analytification functor produces an dg-functor between dg-categories of dg-modules

$$\begin{aligned} \Omega _X^*[*]-Mod \longrightarrow \Omega _{X^h}^*[*]-Mod. \end{aligned}$$

We restrict this $\infty$-functor to the full sub-dg-categories of perfect dg-modules, i.e. sheaves of dg-modules which locally are obtained by finite limits and colimits of $\Omega _X^*[*]$ (resp. $\Omega _{X^h}^*[*]$), and pass to ind-completion to get

$$\begin{aligned} \mathsf {IndPerf}(\Omega _X^*[*]) \longrightarrow \mathsf {IndPerf}(\Omega _{X^h}^*[*]). \end{aligned}$$

By GAGA this is an equivalence. We recall here that for any graded mixed cdga A, the dg-category of dg-modules $A-Mod\simeq \mathsf {IndPerf}(A)$ has a canonical action of the group stack ${\mathcal {H}}=B{\mathbb {G}}_a \rtimes {\mathbb {G}}_m$. The ${\mathbb {G}}_m$-action is induced by the grading on A, while the action of $B{\mathbb {G}}_a$ by the mixed structure. The dg-category of fixed points by ${\mathcal {H}}$ is moreover equivalent to the dg-category of graded mixed A-dg-modules (see [17]). By sheafification, this implies that the group ${\mathcal {H}}$ acts on both dg-categories $\mathsf {IndPerf}(\Omega _X^*[*])$ and $\mathsf {IndPerf}(\Omega _{X^h}^*[*])$ and the analytification dg-functor becomes an ${\mathcal {H}}$-equivariant dg-equivalence

$$\begin{aligned} \mathsf {IndPerf}(\Omega _X^*[*]) \simeq \mathsf {IndPerf}(\Omega _{X^h}^*[*]). \end{aligned}$$

We apply the fixed points construction (see [17] for details) and get this way a new equivalence of $\infty$-categories

$$\begin{aligned} \mathsf {IndPerf}(\Omega _X^*[*])^{h{\mathcal {H}}} \simeq \mathsf {IndPerf}(\Omega _{X^h}^*[*])^{h{\mathcal {H}}}. \end{aligned}$$

The analytification functor being compatible with tensor products, the above $\infty$-functor has a natural symmetric monoidal structure and thus induces an $\infty$-equivalence on the level of $\infty$-categories of commutative algebras. The proposition follows by the observation that ${\mathcal {F}}ol(X)$ (resp. ${\mathcal {F}}ol(X^h)$) is a full sub-$\infty$-category of the $\infty$-category of commutative algebras in $\mathsf {IndPerf}(\Omega _X^*[*])^{h{\mathcal {H}}}$ (resp. in $\mathsf {IndPerf}(\Omega _{X^h}^*[*])^{h{\mathcal {H}}}$) and that these sub-$\infty$-categories match by the above equivalence. $\square$

3.3 Analytic integrability

We have seen that quasi-smooth and rigid derived foliations are always formally d-integrable, a property which distinguishes them from the underived singular foliations. We now study analytic d-integrability (Definition 2.1.2) of quasi-smooth and rigid derived foliations, locally in the analytic topology. We think it is not true that analytic d-integrability always holds for quasi-smooth and rigid derived foliations, but we will see below (Proposition 2.3.2 and Corollary 2.3.4) that they are always locally integrable under a rather common codimension $\ge 2$ condition.

Let ${\mathcal {F}}\in {\mathcal {F}}ol(X)$ be a quasi-smooth and rigid derived foliation on a smooth algebraic variety X and ${\mathcal {F}}^h \in {\mathcal {F}}ol(X^h)$ its analytification. We consider the truncation $\tau _0({\mathcal {F}})$ (Definition 1.3.2), which is an algebraic singular foliation on X, and its analytification $\tau _0({\mathcal {F}}^h)$, which is an analytic singular foliation on $X^h$.

The cotangent complex ${\mathbb {L}}_{{\mathcal {F}}^h}$ is perfect complex of amplitude $[-1,0]$ on $X^h$.

Definition 2.3.1

With the above notations and assumptions on ${\mathcal {F}}$, the smooth locus of ${\mathcal {F}}$ is the Zariski open subset in X of points where ${\mathbb {L}}_F$ is quasi-isomorphic to a vector bundle sitting in degree 0. Its closed complement $Sing({\mathcal {F}}) \subset X$ is called the singular locus of ${\mathcal {F}}$.

Equivalently, since ${\mathcal {F}}$ is supposed to be quasi-smooth and rigid, $Sing({\mathcal {F}})$ is the support of the coherent sheaf $H^1({\mathbb {T}}_{\mathcal {F}})$, where ${\mathbb {T}}_{\mathcal {F}}:={\mathbb {L}}_{{\mathcal {F}}}^{\vee }$ denotes the tangent complex of ${\mathcal {F}}$. Note that, in particular, the smooth locus of such an ${\mathcal {F}}$ might be empty.

The following result entails local analytic integrability of the truncation of any quasi-smooth and rigid derived foliation as soon as we impose smoothness outside a codimension $\ge 2$ subset. More precisely, we have the following result.

Proposition 2.3.2

Let X be a smooth irreducible algebraic variety and ${\mathcal {F}}\in {\mathcal {F}}ol(X)$ be a quasi-smooth rigid derived foliation. We assume that the singular locus $Sing({\mathcal {F}}) \subset X$ is at least of codimension 2. Then, the truncated analytic singular foliation $\tau _0({\mathcal {F}}^h)$ on $X^h$ is locally strongly integrable in the analytic topology.

Proof

This is in fact an easy consequence of our Corollary 1.5.4, which ensures that the foliation ${\mathcal {F}}$ in the statement of Proposition 2.3.2 is formally d-integrable at each point. This implies that its truncation $\tau _0({\mathcal {F}}^h)$ is a singular foliation on $X^h$ which is formally integrable at each point. At this point, we would like to apply [12, Thm. 3.1] that proves that a formally strongly integrable singular foliation is analytically strongly integrable if its singular locus has codimension $\ge 2$ (for the notion of formally or analytically strongly integrable singular foliation, see Remark 1.3.4) to deduce that $\tau _0({\mathcal {F}}^h)$ is, a fortiori, analytically integrable locally around each point of X. But in order to do this, we need to show that $\tau _0({\mathcal {F}}^h)$ is not only formally integrable but also formally strongly integrable (at each point). Now, by hypothesis, the smooth locus of ${\mathcal {F}}$ is a non-empty Zariski open in X, hence dense, since X is irreducible, so our ${\mathcal {F}}$ is a quasi-smooth rigid derived foliation which is actually smooth on an open Zariski dense subset of X. Now, for a quasi-smooth (rigid) derived foliation ${\mathcal {F}}$ on X which is smooth on a dense open Zariski subset of X, formal d-integrability of ${\mathcal {F}}$ at $x\in X$ implies formal strong integrability at x for its truncation $\tau _0({\mathcal {F}})$ (since, for $f: X\rightarrow Y$ locally defined at x, the fact that the pullback derived foliation $f^*({\mathbf {0}}_Y)$ is generically smooth entails generic smoothness for the map f itself¹). Thus we are in a position to apply [12, Thm. 3.1], and deduce local analytic (strong) integrability around any x for the analytification $\tau _0({\mathcal {F}}^h)$. $\square$

An important consequence of Proposition 2.3.2 is the following statement, establishing a precise relation between underived singular foliations and quasi-smooth rigid derived foliations.

Corollary 2.3.3

Let X be a smooth irreducible algebraic variety and D an underived singular foliation on X whose singular locus $Sing({\mathcal {F}}) \subset X$ is of codimension at least 2. Then D is locally, for the analytic topology, the truncation of a quasi-smooth and rigid derived foliation if and only if it is formally strongly integrable at each point.

To finish this section we mention the following stronger version of Proposition 2.3.2, though it will not be used in the rest of the paper.

Corollary 2.3.4

Let X be a smooth irreducible algebraic variety and ${\mathcal {F}}\in {\mathcal {F}}ol(X)$ be a quasi-smooth rigid derived foliation. We assume that the singular locus $Sing({\mathcal {F}}) \subset X$ is at least of codimension 2. Then ${\mathcal {F}}^h$ is, locally on $X^h$, a d-integrable derived foliation.

Proof

By Proposition 2.3.2, it is enough to show that, under the codimension 2 hypothesis in the statement, an analytic rigid quasi-smooth derived foliation is d-integrable if its truncation is strongly integrable.

We thus let Y be a complex smooth manifold and ${\mathcal {G}}$ a rigid and quasi-smooth derived analytic foliation on Y. We assume that $Sing({\mathcal {G}})$, the locus in Y where $\mathbb {{\mathbb {L}}}_{\mathcal {G}}$ is not a vector bundle (sitting in degree 0), is of codimension at least 2. Suppose that the truncation $\tau _0({\mathcal {G}})$ is strongly integrable by a morphism $f : Y \longrightarrow S$ (see Sect.1.3.4). The morphism f is therefore automatically generically smooth on Y. We fix an isomorphism between $\tau _0({\mathcal {G}})$ and the singular foliation induced by f.

If ${{\mathbf {D}}}{{\mathbf {R}}}(Y) \longrightarrow {{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {G}})$ is the natural morphism of graded mixed cdga’s over Y, we first want to construct a factorization

We remind that we have a push-out square of graded mixed cdga’s on Y

This implies that a choice of the factorization as above is equivalent to a choice of a factorization of the natural morphism $f^{-1}({{\mathbf {D}}}{{\mathbf {R}}}(S)) \longrightarrow {{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {G}})$ as

By the universal property of the de Rham graded mixed cdga ${{\mathbf {D}}}{{\mathbf {R}}}(S)$, choosing such a factorization is equivalent to promote the natural morphism of graded cdga’s $f^{-1}({\mathcal {O}}_S) \longrightarrow {{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {G}})$ to a morphism of graded mixed cdga’s, where the mixed structure on the left hand side is trivial.

We consider the sheaf of algebras $H^0(|{{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {G}})|)$. Its comes equipped with a canonical morphism of sheaves of cdga’s $H^0(|{{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {G}})|) \longrightarrow |{{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {G}})|$. Moreover, by adjunction, there is a natural morphism of graded mixed cdga’s

$$\begin{aligned} |{{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {G}})| \longrightarrow {{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {G}}) \end{aligned}$$

where the graded mixed structure on the left hand side is the trivial one. We thus obtain this way a morphism of graded mixed cgda’s

$$\begin{aligned} u : H^0(|{{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {G}})|) \longrightarrow {{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {G}}). \end{aligned}$$

Now we invoke Proposition 3.1.5, which shows that $H^0(|{{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {G}})|)$ is also isomorphic to the kernel of the morphism ${\mathcal {O}}_X \longrightarrow \Omega ^1_Y/D$, where D is the differential ideal defining the singular foliation $\tau _0({\mathcal {G}})$. In particular, the natural morphism $f^{-1}({\mathcal {O}}_S) \longrightarrow {\mathcal {O}}_Y$ factors through this kernel, and thus produces a morphism of sheaves of algebras $f^{-1}({\mathcal {O}}_S) \longrightarrow H^0(|{{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {G}})|)$. By composition with the morphism u above, we get the required morphism of graded mixed cdga’s $v : f^{-1}({\mathcal {O}}_S) \longrightarrow {{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {G}})$. As explained before this defines a natural morphism

$$\begin{aligned} {\bar{v}}: {{\mathbf {D}}}{{\mathbf {R}}}(Y/S) \longrightarrow {{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {G}}). \end{aligned}$$

To finish the proof of the corollary, we need to show that ${\bar{v}}$ is, in fact, an equivalence of derived foliations. For this, it is enough to show that it induces an equivalence on the corresponding cotangent complexes

$$\begin{aligned} {\mathbb {L}}_{Y/S} \longrightarrow {\mathbb {L}}_{{\mathcal {G}}}. \end{aligned}$$

Note that $f : Y \longrightarrow S$ being generically smooth on Y, the natural projections

$$\begin{aligned} {\mathbb {L}}_{Y/S} \longrightarrow \Omega _{Y/S}^1 \qquad {\mathbb {L}}_{\mathcal {G}}\longrightarrow \Omega _Y^1/D \end{aligned}$$

are quasi-isomorphisms. Finally, by construction, the induced morphism ${\mathbb {L}}_{Y/S} \longrightarrow {\mathbb {L}}_{{\mathcal {G}}}$ is the isomorphism $\Omega ^1_{Y/S} \simeq \Omega _Y^1/D$ coming from the fact that f integrates the singular $\tau _0({\mathcal {G}})$. $\square$

4 Derived categories of algebraic foliations

In this section we define and study the derived category of crystals over a derived foliation, both in the algebraic and in the analytic setting. In this paper we will consider only perfect crystals on smooth varieties. The study of more general derived categories of derived foliations will appear elsewhere.

4.1 Crystals along a derived foliation

We let ${\mathcal {F}}\in {\mathcal {F}}ol(X)$ be a derived foliation on a smooth algebraic variety X and ${{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})$ the corresponding graded mixed cdga. We consider ${{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})-\epsilon -{{\mathbf {d}}}{{\mathbf {g}}}^{gr}$ the $\infty$-category of graded mixed ${{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})$-dg-modules.

Definition 3.1.1

With the notations above, a perfect crystal over ${\mathcal {F}}$ is a graded mixed ${{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})$-dg-module E satisfying the following two conditions.

• The dg-module E(0) is perfect over ${\mathcal {O}}_X\simeq {{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})(0)$.

• The natural morphism

  $$\begin{aligned} E(0)\otimes _{{\mathcal {O}}_X}{{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}) \longrightarrow E \end{aligned}$$

  is a quasi-isomorphism of graded ${{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})$-dg-modules.

For a perfect crystal E over ${\mathcal {F}}$, the perfect complex E(0) on X, will be referred to as the underlying perfect complex of E. A perfect crystal E over ${\mathcal {F}}$ will be simply called a vector bundle over ${\mathcal {F}}$ if its underlying perfect complex is quasi-isomorphic to a vector bundle on X sitting in degree 0. The $\infty$-category of perfect crystals over ${\mathcal {F}}$ is the full sub-$\infty$-category $\textsf {Perf} ({\mathcal {F}})$ of ${{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})-\epsilon -{{\mathbf {d}}}{{\mathbf {g}}}^{gr}$ consisting of perfect crystals. The full sub-$\infty$-category of $\textsf {Perf} ({\mathcal {F}})$ consisting of vector bundles over ${\mathcal {F}}$ will be denoted by $\textsf {Vect} ({\mathcal {F}})$.

Since we will only be considering perfect crystals we will often omit the adjective perfect when speaking about objects in $\textsf {Perf} ({\mathcal {F}})$.

The $\infty$-category $\textsf {Perf} ({\mathcal {F}})$ is obviously functorial in ${\mathcal {F}}$ in the following sense. Let $f : X \longrightarrow Y$ be a morphism of smooth algebraic varieties. Let ${\mathcal {F}}' \in {\mathcal {F}}ol(Y)$ and ${\mathcal {F}}\in {\mathcal {F}}ol(X)$ be derived foliations, and $u : {\mathcal {F}}\longrightarrow f^*({\mathcal {F}}')$ a morphism in ${\mathcal {F}}ol(X)$. Then, there is a base change $\infty$-functor

$$\begin{aligned} \textsf {Perf} ({\mathcal {F}}') \longrightarrow \textsf {Perf} ({\mathcal {F}}). \end{aligned}$$

On affine derived foliation this base change functor is simply induced by the usual base change ${{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}) \otimes _{{{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}')}(-)$ on graded mixed dg-modules.

Before proceeding to de Rham cohomology of crystals, let us give two specific examples of crystals, relating this notion to more standard notions of ${\mathcal {D}}$-modules and more generally of representations of Lie algebroids.

Crystals and ${\mathcal {D}}$-modules. Let E be a quasi-coherent complex of ${\mathcal {D}}$-modules on a smooth algebraic variety X. We can represent E as a pair consisting of a quasi-coherent E(0) complex on X together with a flat connection $\nabla : E(0) \longrightarrow E(0)\otimes _{{\mathcal {O}}_X}\Omega ^1_X.$ The de Rham complex of this connection produces a graded mixed structure on ${{\mathbf {D}}}{{\mathbf {R}}}(E)=E(0) \otimes _{{\mathcal {O}}_X} {{\mathbf {D}}}{{\mathbf {R}}}(X)$, making it into a graded mixed ${{\mathbf {D}}}{{\mathbf {R}}}(X)$-module. This construction defines an equivalence between the $\infty$-category of quasi-coherent ${\mathcal {D}}$-modules on X and the $\infty$-category of graded mixed ${{\mathbf {D}}}{{\mathbf {R}}}(X)$-dg-modules which are graded-free (see [17, Prop. 2.5]). Restricting to perfect complexes we see that perfect crystals over the final derived foliation on X form an $\infty$-category naturally equivalent to the $\infty$-category of ${\mathcal {D}}$-modules which are perfect over X.

Crystals over smooth derived foliations. Let now ${\mathcal {F}}$ be a smooth derived foliation over a smooth algebraic variety X. We have seen already (§ 1.3.1) that ${\mathcal {F}}$ corresponds to a Lie algebroid $a : T \longrightarrow {\mathbb {T}}_X$. A representation of this Lie algebroid is, by definition, a pair consisting of a vector bundle V together with a morphism $\nabla : V \longrightarrow V\otimes _{{\mathcal {O}}_X}T^*$ satisfying the obvious Leibniz rule, and $\nabla ^2=0$. Such a representation has a de Rham complex ${{\mathbf {D}}}{{\mathbf {R}}}(V):=V\otimes _{{\mathcal {O}}_X}{{\mathbf {D}}}{{\mathbf {R}}}(X)$, on which $\nabla$ defines a graded mixed structure. This construction produces an $\infty$-functor from the category of representations of the Lie algebroid T to the $\infty$-category $\textsf {Perf} ({\mathcal {F}})$. It is easy to show that this $\infty$-functor is fully faithful, and that its essential image is $\textsf {Vect} ({\mathcal {F}})$.

The derived categories of crystals over derived foliations can be used in order to define de Rham cohomology of derived foliations with coefficients in a crystal. This de Rham cohomology is usually referred to as foliated or leafwise cohomology in the setting of classical foliations or Lie algebroids.

Let ${\mathcal {F}}$ be a derived foliation over a smooth algebraic variety X. The $\infty$-category $\textsf {Perf} ({\mathcal {F}})$ can be identified with a dg-category (or, equivalently, has the structure of a ${\mathbb {C}}$-linear $\infty$-category), and we will simply denote by $Hom(E,E')$ the complex of ${\mathbb {C}}$-vectors spaces of Hom’s from E to $E'$ in this dg-category structure. Notice that the projection ${{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}) \rightarrow {\mathcal {O}}_X$ on the weight 0 part, defines a structure of a graded mixed ${{\mathbf {D}}}{{\mathbf {R}}}(X)$-module on ${\mathcal {O}}_X$ (concentrated in weight 0 and degree 0). For an arbitrary perfect crystal E over ${\mathcal {F}}$, we consider the complex of morphisms $Hom({\mathcal {O}}_X,E)$, from ${\mathcal {O}}_X$ to E. We denote this complex of ${\mathbb {C}}$-vector spaces by

$$\begin{aligned} {\mathbb {H}}_{DR}({\mathcal {F}};E):=Hom({\mathcal {O}}_X,E) \end{aligned}$$

and call it de Rham cohomology of ${\mathcal {F}}$ with coefficients in E. Note that the dg-category $\textsf {Perf} ({\mathcal {F}})$ is also endowed with a natural closed symmetric monoidal structure (equivalently, has a structure of ${\mathbb {C}}$-linear closed symmetric monoidal $\infty$-category) induced by tensor products of ${\mathcal {O}}_X$-modules.

Remark 3.1.2

Though we will not need this in this paper, we mention that the symmetric monoidal structure on $\textsf {Perf} ({\mathcal {F}})$ implies existence natural multiplicative structure morphisms

$$\begin{aligned} {\mathbb {H}}_{DR}({\mathcal {F}};E) \otimes _{{\mathbb {C}}} {\mathbb {H}}_{DR}({\mathcal {F}};E') \longrightarrow {\mathbb {H}}_{DR}({\mathcal {F}},E\otimes _{{\mathcal {O}}_X}E'). \end{aligned}$$

In particular, ${\mathbb {H}}_{DR}({\mathcal {F}}; {\mathcal {O}}_X)$ is a commutative dg-algebra, and ${\mathbb {H}}_{DR}({\mathcal {F}};E)$ is a dg-module over ${\mathbb {H}}_{DR}({\mathcal {F}};{\mathcal {O}}_X)$, for any $E\in \textsf {Perf} ({\mathcal {F}})$.

The complex ${\mathbb {H}}_{DR}({\mathcal {F}},E)$ can also be described as the hypercohomology of X with coefficients in an explicit complex of sheaves. We consider E as a sheaf of graded mixed ${{\mathbf {D}}}{{\mathbf {R}}}(X)$-modules. We can apply the realization $\infty$-functor $|-| : \epsilon -{{\mathbf {d}}}{{\mathbf {g}}}^{gr}\longrightarrow {{\mathbf {d}}}{{\mathbf {g}}}$, and thus get a complex of sheaves |E| of ${\mathbb {C}}$-vector spaces on X. We then have a natural quasi-isomorphism

$$\begin{aligned} {\mathbb {H}}_{DR}({\mathcal {F}},E) \simeq {\mathbb {H}}(X,|E|). \end{aligned}$$

Note that |E| is explicitly given by the complex of sheaves $\prod _{i\ge 0}E(i)[-2i]$ endowed with its total differential (sum of the cohomological differential and the mixed structure). As E(i) is naturaly equivalent to $E(0)\otimes _{{\mathcal {O}}_X}\wedge ^i {\mathbb {L}}_{\mathcal {F}}[i]$, ${\mathbb {H}}_{DR}({\mathcal {F}},E)$ may be considered as a version of the (derived) de Rham complex of E along the foliation ${\mathcal {F}}$.

Proposition 1.5.1 has the following extension, stating that perfect cyrstals on quasi-smooth and rigid derived foliations are always, locally, pull-backs of perfect crystals on a smooth and rigid foliation on a formal scheme.

Proposition 3.1.3

Let ${\mathcal {F}}\in {\mathcal {F}}ol(X)$ be a rigid and quasi-smooth derived foliation on a smooth algebraic variety X, and $E \in \textsf {Perf} ({\mathcal {F}})$ be a perfect crystal on ${\mathcal {F}}$. Then, Zariski locally on X, there exists a smooth and rigid foliation ${\widehat{{\mathcal {F}}}}$ on $X\times \widehat{{\mathbb {A}}}^n$, and a perfect crystal ${\widehat{E}} \in \textsf {Perf} ({\widehat{{\mathcal {F}}}})$, such that

$$\begin{aligned} e^*({\widehat{E}})\simeq E \end{aligned}$$

where $e : X \hookrightarrow X\times \widehat{{\mathbb {A}}}^n$ is the zero section.

Proof

The proof is almost the same, verbatim, as that of Proposition 1.5.1. The only changes consist in considering pairs of a graded mixed cdga’s A together with a graded mixed A-module M, all along the argument. We leave these details to the reader. $\square$

Let $D\subset \Omega ^1_X$ be a (underived) singular foliation on X. A coherent sheaf with flat connection along D is defined to be a coherent sheaf E on X together with a ${\mathbb {C}}$-linear map

$$\begin{aligned} \nabla : E \longrightarrow E\otimes ^u_{{\mathcal {O}}_X}(\Omega _X^1/D) \end{aligned}$$

satisfying the usual Leibniz rule, and being flat (that is $\nabla ^2=0$ in the obvious sense). In terms of underived graded mixed algebras, coherent sheaves with flat connection along D are exactly graded mixed ${{\mathbf {D}}}{{\mathbf {R}}}(D)$-modules E such that E(0) is coherent and E is free on E(0). If we denote by $\textsf {Coh} (D)$ the category of the coherent sheaves with flat connection along D, then, there is a truncation $\infty$-functor

$$\begin{aligned} \tau _0: \textsf {Vect} ({\mathcal {F}}) \longrightarrow \textsf {Coh} (\tau _{0}({\mathcal {F}})) \end{aligned}$$

which sends a crystal E to E(0) endowed with the induced map

$$\begin{aligned} E(0) \longrightarrow E(1) \longrightarrow H^0(E(1))\simeq E(0)\otimes ^u_{{\mathcal {O}}_X} (\Omega _X^1/D). \end{aligned}$$

Exactly as crystals on a derived foliation have de Rham cohomology, coherent sheaves with flat connections along a singular foliation D have naive de Rham complexes. For such an object $(E, \nabla )\in \textsf {Coh} (D)$, we form its de Rham complex modulo D

The hypercohomology of this complex on X will be denoted by

$$\begin{aligned} {\mathbb {H}}_{DR,naive}(D,E). \end{aligned}$$

If one starts with a derived foliation ${\mathcal {F}}$ on X, and $E \in \textsf {Vect} (E)$, then the truncation functor induces a canonical projection

$$\begin{aligned} {\mathbb {H}}_{DR}({\mathcal {F}},E) \longrightarrow {\mathbb {H}}_{DR,naive}(\tau _0({\mathcal {F}}),\tau _{0}(E)), \end{aligned}$$

which is functorial in an obvious manner. Without further assumptions on ${\mathcal {F}}$, this morphism is not injective nor surjective in cohomology. However, we have the following result, showing that the closer ${\mathcal {F}}$ is to be smooth, the closer this morphism is to an equivalence.

Remark 3.1.4

If D is an analytic singular foliation on a complex manifold Y, the definitions of $\textsf {Coh} (D)$, ${\mathbb {H}}_{DR,naive}(D,E)$, for $E \in \textsf {Coh} (D)$, and of the map ${\mathbb {H}}_{DR}({\mathcal {G}},{\mathcal {E}}) \longrightarrow {\mathbb {H}}_{DR,naive}(\tau _0({\mathcal {G}}),\tau _{0}({\mathcal {E}})),$ for ${\mathcal {G}}$ an analytic derived foliation on Y and ${\mathcal {E}}\in \textsf {Perf} ({\mathcal {G}})$, all make sense and are completely analogous to the algebraic case treated above. And, obviously, the usual analytification functor for sheaves, induces a functor $\textsf {Coh} (F) \rightarrow \textsf {Coh} (F^{h})$, for an algebraic singular foliation F on a smooth algebraic variety X, where $F^{an}$ is the analytification of F, which is an analytic singular foliation on $X^{h}$.

Proposition 3.1.5

Let ${\mathcal {F}}$ be a quasi-smooth, rigid and derived foliation over a smooth algebraic variety X and $E\in \textsf {Vect} ({\mathcal {F}})$. Assume that ${\mathbb {L}}_{{\mathcal {F}}}$ is quasi-isomorphic to a vector bundle on a Zariski open in X whose complement is of codimension at least $d\ge 1$. Then, the morphism

$$\begin{aligned} {\mathbb {H}}^i_{DR}({\mathcal {F}},E) \longrightarrow {\mathbb {H}}^i_{DR,naive}(\tau _0({\mathcal {F}}),\tau _0(E))) \end{aligned}$$

is an isomorphism for $i<d-1$ and is surjective for $i=d-1$.

Proof

We start by the following well known lemma.

Lemma 3.1.6

Let be a complex of vector bundles on X with W sitting in degree 0, and assume that s is a monomorphism which is a sub-bundle on a Zariski open $(X-S)$ with S of codimension $\ge d$. Then, for all $p\ge 0$, the perfect complex $\wedge ^p({\mathbb {L}})[p]$ is cohomologically concentrated in degrees $[\inf (d-2p,-p),-p]$.

Proof of the lemma

The complex computing $E:=\wedge ^p({\mathbb {L}})$ is the perfect complex whose term in degree $-i$ is given by $Sym^{p-i}(V)\otimes \wedge ^i(W)$. It is of amplitude contained in $[-p,0]$. By assumption its higher cohomology sheaves $H^i$ for $i< 0$ are all coherent sheaves with supports of dimension less than $(\dim X - d)$. Its dual $E^*$ is a perfect complex of amplitude [0, p] with all its higher cohomology sheaves being coherent with supports of dimension less than $(\dim X - d)$. Therefore, we get the following vanishing for ext-sheaves

$$\begin{aligned} {\mathcal {E}}xt^{i}(H^i(E^*),{\mathcal {O}}_X)=0 \; \forall \; i < d. \end{aligned}$$

This implies that the cohomology sheaves of the perfect complex $E\simeq (E^*)^*$ are concentrated in $[\inf (d-p,0),0]$ as required. $\square$

We now consider the morphism of complexes of sheaves on X

$$\begin{aligned} |E| \longrightarrow {\mathbb {H}}^i_{DR,naive}(\tau _0({\mathcal {F}}),\tau _0(E))). \end{aligned}$$

The fiber of this map is the realization of the graded mixed complex K whose weight p piece is

$$\begin{aligned} K(p)=\tau _{\le -1}(\wedge ^p({\mathbb {L}}_{\mathcal {F}}) \otimes E)[p], \end{aligned}$$

the fiber of the natural morphism

$$\begin{aligned} (\wedge ^p({\mathbb {L}}_{\mathcal {F}}) \otimes E)[p] \longrightarrow (\Omega ^p_X/<D>\otimes E)[p]. \end{aligned}$$

By the previous lemma, each K(p) sits in cohomological degrees $[\inf (d-2p,-p),\infty )$, and thus $K(p)[-2p]$ sits in cohomological degrees $[\inf (d,p),\infty )$. Note also that $K(p)\simeq 0$ if $p\le d$. Therefore, its realization, given by the complex $\prod _{p> d}K(p)[-2p]$ with the appropriate differential, lies in degrees $[d,\infty )$. This concludes the proof of the proposition. $\square$

4.2 Analytification and h-nilpotent crystals

The analytification $\infty$-functor for derived foliation (see Sect. 2.2) has the following variant for crystals. Let ${\mathcal {F}}$ be a derived foliation on smooth algebraic variety X, and ${\mathcal {F}}^h$ the corresponding analytic derived foliation on $X^h$. We define $\textsf {Perf} ({\mathcal {F}}^h)$ as the $\infty$-category of sheaves of graded mixed ${{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}^h)$-modules E on $X^h$ satisfying the following two conditions.

• The dg-module E(0) is perfect over ${\mathcal {O}}_{X^h}\simeq {{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}^h)(0)$.

• The natural morphism

  $$\begin{aligned} E(0)\otimes _{{\mathcal {O}}_{X^h}}{{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}^h) \longrightarrow E \end{aligned}$$

  is a quasi-isomorphism of graded ${{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}^h)$-dg-modules.

It is easy to check that the usual analytification $\infty$-functor for sheaves induces an $\infty$-functor

$$\begin{aligned} (-)^h : \textsf {Perf} ({\mathcal {F}}) \longrightarrow \textsf {Perf} ({\mathcal {F}}^h). \end{aligned}$$

Before introducing h-nilpotent crystals, we note that the following GAGA result for perfect crystals.

Proposition 3.2.1

Let X be a smooth and proper algebraic variety, and ${\mathcal {F}}$ be a derived foliation on X. Then, the analytification $\infty$-functor

$$\begin{aligned} \textsf {Perf} ({\mathcal {F}}) \longrightarrow \textsf {Perf} ({\mathcal {F}}^h) \end{aligned}$$

is an equivalence of $\infty$-categories.

Proof

Similar to the proof of Proposition 2.2.2 and left to the reader. $\square$

We now introduce the h-nilpotent crystals.

Definition 3.2.2

Let X be a smooth algebraic variety, ${\mathcal {F}}$ a derived foliation on X, and $E \in \textsf {Perf} ({\mathcal {F}})$ be a perfect crystal over ${\mathcal {F}}$. We say that E is h-nilpotent if, locally on $X^h$, the sheaf of of graded mixed ${{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}^h)$-dg-modules corresponding to $E^h$, belongs to the thick triangulated subcategory generated by the trivial crystal ${{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}^h)$ (considered as a graded mixed dg-module over itself).

The adjective nilpotent in Definition 3.2.2 is justified by the following observation. Let $X=Spec\, {\mathbb {C}}$ and ${\mathcal {F}}$ be given by a finite dimensional Lie algebra $\mathfrak {g}$. A crystal on ${\mathcal {F}}$ is nothing else than a complex of linear representations E of $\mathfrak {g}$ with finite dimensional cohomologies. Such an object is a h-nilpotent crystal if and only if furthermore the induced representation of $\mathfrak {g}$ on $H^i(E)$ is nilpotent for all i. This shows, in particular, that nilpotency for crystals is a non-trivial condition. However, we will now show that it always holds for an important class of examples.

Theorem 3.2.3

Let ${\mathcal {F}}\in {\mathcal {F}}ol(X)$ be a quasi-smooth and rigid derived foliation on a smooth algebraic variety X. If $Sing({\mathcal {F}}) \subset X$ is of codimension at least 2, then any $E \in \textsf {Vect} ({\mathcal {F}})$ is h-nilpotent.

Proof

This theorem will be in fact a consequence of Proposition 2.3.2. Let $E \in \textsf {Vect} ({\mathcal {F}})$, and S(E) the free graded mixed ${{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})$-algebra generated by E, i.e. $S(E)=Sym(E)$, where Sym is computed inside the symmetric monoidal $\infty$-category $\textsf {Perf} ({\mathcal {F}})$. The graded mixed cdga S(E) defines a derived foliation ${\mathcal {F}}_E$ over V, where $\pi : V \longrightarrow X$ is the total space of the vector bundle $E(0)^*$ on X, dual of E(0). As a graded algebra, we have

$$\begin{aligned} S(E)\simeq Sym_{{\mathcal {O}}_X}(E(0))\otimes _{{\mathcal {O}}_X}Sym_{{\mathcal {O}}_X}({\mathbb {L}}_{\mathcal {F}}[1]), \end{aligned}$$

so that, in particular, the cotangent complex of ${\mathcal {F}}_E$ is $\pi ^*({\mathbb {L}}_{\mathcal {F}})$, hence ${\mathcal {F}}_E$ is a quasi-smooth derived foliation on V.

Now, the natural morphism $\Omega ^1_{V} \longrightarrow \pi ^*({\mathbb {L}}_{\mathcal {F}})$ is given by the derivation $Sym_{{\mathcal {O}}_X}(E(0)) \longrightarrow Sym_{{\mathcal {O}}_X}(E(0)) \otimes _{{\mathcal {O}}_X}{\mathbb {L}}_F$, itself induced by the derivation $\Omega _X^1 \rightarrow {\mathbb {L}}_{\mathcal {F}}$ and by multiplicativity from the crystal structure

$$\begin{aligned} E(0) \longrightarrow E(0) \otimes _{{\mathcal {O}}_X}{\mathbb {L}}_F \end{aligned}$$

of E. In particular, the induced morphism of coherent sheaves $\Omega ^1_{V} \longrightarrow \pi ^*({\mathbb {L}}_{\mathcal {F}})\simeq {\mathbb {L}}_{{\mathcal {F}}_E}$ is surjective on $H^0$ because the composite

$$\begin{aligned} \pi ^*(\Omega _X^1) \longrightarrow \Omega ^1_{V} \longrightarrow \pi ^*({\mathbb {L}}_{\mathcal {F}}) \end{aligned}$$

is the pull-back by $\pi$ of $\Omega _X^1 \rightarrow {\mathbb {L}}_F$ (which is surjective on $H^0$ by the rigidity assumption on ${\mathcal {F}}$). I.e. the derived foliation ${\mathcal {F}}_E$ on V is also rigid.

The derived foliation ${\mathcal {F}}_E$ on V thus satisfies both the conditions of Proposition 2.3.2, so that its truncation $\tau _0({\mathcal {F}}^h_E)$ can be integrated locally on $V^h$. Let $f_1,\dots ,f_k$ be holomorphic functions, defined locally around a point $x\in X^h \subset V^h$, that integrate $\tau _0({\mathcal {F}}^h_E)$. We fix a local trivialization of $\pi ^h:V^h \rightarrow X^h$ around x, as $X^h \times V_x$, where $V_x$ is the fiber of V at x, so that local parameters at x on $V^h$ are given by $(z_1,\dots ,z_n,t_1,\dots ,t_r)$, where $z_i$ are local parameters on $X^h$ and $t_j\in V_x$ form a vector space basis. Let us consider the Taylor series expansions of the functions $f_i$ as

$$\begin{aligned} f_i=\sum _{\nu =(\nu _1,\dots ,\nu _r)} a_{i,\nu }t^\nu , \end{aligned}$$

where $a_{i,\nu }$ are functions around x on $X^h$.

By construction, the homogenous part of degree p of each function $f_i$ are sections of the bundle $Sym^{p}(V^*)^h$. Moreover, the fact that the $f_i$ integrate the foliation $\tau _0({\mathcal {F}}_E)$ implies that these sections are in fact flat sections, i.e. they are local sections of the sheaf $H^0_{DR,naive}(Sym^p(E)^h)$. We consider new functions at $x \in V^h$ by taking the weight one pieces

$$\begin{aligned} g_{i}:=\sum _{j} a_{i,(j)}t_j, \end{aligned}$$

wherer $(j):=(0,\dots ,1,\dots ,0)$ and $1\le j\le r$. Each function $g_i$ can be, and will be, considered as a germ of holomorphic section at x of the vector bundle E(0), the dual of V. These germs are flat, and thus they collectively define an analytic germ morphisms of crystals at x

$$\begin{aligned} \phi : {\mathcal {O}}_{X^h}^k \longrightarrow E^h. \end{aligned}$$

The above morphism $\phi$ is clearly an isomorphism ouside of the closed subset $Sing({\mathcal {F}}) \subset X$, so $\phi$ is in particular an injective morphism of sheaves. As $Sing({\mathcal {F}})$ is of codimension $\ge 2$,by Hartogs theorem, we deduce that $\phi$ is in fact an isomorphism at x.

This finishes the proof that E is h-nilpotent as required. $\square$

5 The Riemann–Hilbert correspondence

5.1 The sheaf of flat functions

Let ${\mathcal {F}}\in {\mathcal {F}}ol(X)$ be a derived foliation over a smooth algebraic variety X, and ${\mathcal {F}}^h \in {\mathcal {F}}ol(X^h)$ its analytification. The realization $|{{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}^h)|$ of ${{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}^h)$ (see Sect. 1.1) defines a sheaf of commutative dg-algebras on $X^h$.

Definition 4.1.1

With the notations above, the sheaf of cdga’s $|{{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}^h)|$ on $X^h$ is called the sheaf of locally constant functions along ${\mathcal {F}}$. It is denoted by ${\mathcal {O}}_{{\mathcal {F}}^h}$.

5.1.1 The smooth case

In the case of smooth derived foliations the sheaf ${\mathcal {O}}_{{\mathcal {F}}^h}$ is easy to understand. As a start, let us assume that ${\mathcal {F}}$ is furthermore rigid, so that it defines an actual classical holomorphic regular foliation on $X^h$. The sheaf of cdga’s ${\mathcal {O}}_{{\mathcal {F}}^h}$ is then concentred in degree zero and is isomorphic to the subsheaf of ${\mathcal {O}}_{X^h}$ of holomorphic functions which are locally constant along the leaves. This explains the name we gave to ${\mathcal {O}}_{{\mathcal {F}}^h}$ in general. Locally on $X^h$, the foliation is induced by a smooth holomorphic map $f : X^h \longrightarrow {\mathbb {C}}^n$ and the sheaf ${\mathcal {O}}_{{\mathcal {F}}^h}$ is simply given by $f^{-1}({\mathcal {O}}_{{\mathbb {C}}^n}^h)$.

When ${\mathcal {F}}$ is smooth but not necessarily rigid, it corresponds to a Lie algebroid $T \longrightarrow {\mathbb {T}}_X$ on X (see Sect. 1.3.1). Its analytification is thus a holomorphic Lie algebroid $T^h \longrightarrow {\mathbb {T}}_X^h$ on $X^h$. This Lie algebroid possesses a Chevalley-Eilenberg cohomology complex $C^*(T^h)$, which is a sheaf of ${\mathbb {C}}$-linear cdga’s on $X^h$. It is explicitely given by $Sym_{{\mathcal {O}}_{X^h}}((T^*)^h[-1])$ endowed with the standard Chevalley-Eilenberg differential. Then, the sheaf of cdga’s ${\mathcal {O}}_{{\mathcal {F}}^h}$ is quasi-isomprhic to $C^*(T^h)$. Therefore, for an arbitrary non-rigid smooth derived foliation ${\mathcal {F}}$, ${\mathcal {O}}_{{\mathcal {F}}^h}$ is cohomologically bounded, but not necessarily concentrated in degree 0 anymore. For instance, if the Lie algebroid T is abelian then ${\mathcal {O}}_{{\mathcal {F}}^h}$ is $Sym_{{\mathcal {O}}_{X^h}}((T^*)^h[-1])$ with trivial differential.

5.1.2 Local structure

The local structure of the sheaf ${\mathcal {O}}_{{\mathcal {F}}^h}$ can be understood using Proposition 1.5.1 as follows. Let $x\in X$ and let $A={\mathcal {O}}_{X,x}^h$ be the ring of germs of holomorphic functions on X at x. By Proposition 1.5.1 we know that there exist a smooth and rigid foliation ${\mathcal {F}}'$ on $B=A[[t_1,\dots ,t_n]]$, i.e. k linearly independent commuting derivations $\nu _1,\dots ,\nu _k$ on $A[[t_1,\dots ,t_n]]$ which are holomorphic along X and formal in the variables $t_i$’s. More explicitly, the derivations $\nu _i$ are given by expressions of the form

$$\begin{aligned} \sum _{i} a_i.\frac{\partial }{\partial x_i} + \sum _j b_j.\frac{\partial }{\partial t_j} \end{aligned}$$

where $a_i$ and $b_j$ are elements of B and the $x_i$’s are local coordinates of X at x. The derivations $\nu _i$ define a de Rham complex

This complex is a model for the stalk of ${\mathcal {O}}_{{\mathcal {F}}^h}$ at the point x.

We can say more when the derived foliation ${\mathcal {F}}$ is moreover locally d-integrable (Definition 2.1.2). Assume that we are given $f : X \longrightarrow Y$ a holomorphic map between complex manifolds. As we are interested in a local description we can assume that X and Y are Stein manifolds, and will allow ourselves to restrict to open subsets in necessary. We assume that ${\mathcal {F}}:=f^*({\mathbf {0}}_Y)$ is the induced analytic derived foliation on X. By construction, the sheaf of cdga ${\mathcal {O}}_{{\mathcal {F}}}$ is the sheaf on X, for the analytic topology, of relative derived de Rham cohomology: it associates to an open $U \subset X$ the cdga ${\mathcal {O}}_{{\mathcal {F}}}(U):=|{{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})|=|{{\mathbf {D}}}{{\mathbf {R}}}(U/Y)|$. This sheaf can explicitly be computed as follows. We let be a factorization of f as a closed immersion followed by a smooth morphism (where j is the graph of f). The sheaf of rings ${\widehat{{\mathcal {O}}}}_{X}$ of formal functions on Z along X, has a natural structure of a ${\mathcal {D}}_Z$-module on Z. Therefore, we can consider the relative de Rham complex of ${\widehat{{\mathcal {O}}}}_X$ over Y, and obtain a sheaf $|{{\mathbf {D}}}{{\mathbf {R}}}({\widehat{{\mathcal {O}}}}_X/Y)|$ of cdga’s on Z. This sheaf is set-theoretically supported on X, and thus can be considered as a sheaf of cdga’s over X.

Lemma 4.1.2

There exists an equivalence of sheaves of cdga’s on X

$$\begin{aligned} |{{\mathbf {D}}}{{\mathbf {R}}}({\widehat{{\mathcal {O}}}}_X/Y)| \simeq {\mathcal {O}}_{{\mathcal {F}}}. \end{aligned}$$

Proof

The cotangent complex of ${\mathcal {F}}$ sits in the following exact triangle of perfect complexes on X

where $N^*=f^*(\Omega _Y^1)$. We thus have a push-out of graded mixed cdga’s over X

As X is Stein, we see that the graded mixed structure on $Sym_{{\mathcal {O}}_X}(N^*[2])$ is automatically trivial. We consider the internal de Rham algebra ${{\mathbf {D}}}{{\mathbf {R}}}^{int}(B/{{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}))$. This is a cdga endowed with two extra gradings, and two commuting graded mixed structures. As such, it has a total realization defined by

$$\begin{aligned} ||{{\mathbf {D}}}{{\mathbf {R}}}^{int}(B/{{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}))||:={\mathbb {R}}\underline{{\mathcal {H}}om}({\mathcal {O}}_X,{{\mathbf {D}}}{{\mathbf {R}}}^{int}(B/{{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}))) \end{aligned}$$

where ${\mathcal {O}}_X$ is considered as a trivial double graded mixed complex of sheaves. This total realization can be obtained by successive realizations of the two graded mixed structures, and thus in two different manners depending on the orders in which these realizations are taken. If we realize the first graded mixed structure, the one defined by the graded mixed structure on ${{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})$, we get $|{{\mathbf {D}}}{{\mathbf {R}}}({\widehat{{\mathcal {O}}}}_X/Y)|$. Realizing the second one, gives back ${{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})$. We thus obtain this way the desired equivalence after taking the second realization. $\square$

A consequence of the above lemma is the following explicit description of the stalks of ${\mathcal {O}}_{{\mathcal {F}}}$ at a given point $x \in X$. Let $(x_1,\dots ,x_k)$ and $(y_1,\dots ,y_n)$ be local coordinates of X at x and Y at $y=f(x)$. The ring of germs of functions on $X\times Y$ at (x, y) can then be identified with ${\mathbb {C}}\{x_*,y_*\}$, the ring of germs of holomorphic functions at $0 \in {\mathbb {C}}^{k+n}$, and the graph of f defines an ideal $I \subset {\mathbb {C}}^{k+n}$. We thus have the relative de Rham complex of ${\mathbb {C}}\{x_*,y_*\}$ over ${\mathbb {C}}\{y_*\}$, and its completion along I

The differential in this complex is induced by the derivative relative to Y, sending a function f to $\sum _{j\le k}\frac{\partial f}{\partial x_j}. dx_j$. The above complex is naturaly quasi-isomorphic to the stalk of ${\mathcal {O}}_{\mathcal {F}}$ at x.

5.1.3 Flat functions and singularities

In general, the complex of sheaves of flat functions ${\mathcal {O}}_{{\mathcal {F}}}$ is not cohomologically concentrated in degree 0, as we will show in some specific examples below. Its non-zero cohomology sheaves contain subtle informations about the singularities of ${\mathcal {F}}$, that can be sometimes expressed in terms of vanishing cohomology.

Let us have a look at the specific case of codimension one quasi-smooth derived foliations, and the local structure of the sheaf ${\mathcal {O}}_{{\mathcal {F}}^h}$. Assume that locally, in the analytic topology, such a derived foliation is induced by a holomorphic map

$$\begin{aligned} f : X \longrightarrow {\mathbb {C}}. \end{aligned}$$

The derived foliation on X is then $f^*(0)$, the pull-back of the trivial foliation on ${\mathbb {C}}$. If the map f is constant, say 0, then it is easy to see that ${\mathcal {O}}_{{\mathcal {F}}^h})$ is the constant sheaf on X with stalks ${\mathbb {C}}[[x]]$ the formal functions on ${\mathbb {C}}$ at 0. Indeed, in this case the cotangent complex of f splits as $\Omega _X^1\oplus {\mathcal {O}}_X[1]$, and the graded mixed cdga ${{\mathbf {D}}}{{\mathbf {R}}}(X/{\mathbb {C}})$ is ${{\mathbf {D}}}{{\mathbf {R}}}(X)[u]$ where u is a free variable in degree 2. The realization of this graded mixed cdga is $|{{\mathbf {D}}}{{\mathbf {R}}}(X)|[[x]]$ the formal power series in the absolute de Rham complex of X. As a sheaf on X this is quasi-isomorphic to ${\mathbb {C}}[[x]]$. This situation generalizes easily to the case of an arbitrary holomorphic map $f : X \longrightarrow {\mathbb {C}}^n$ having constant rank (left to the reader).

Let us now assume that $f : X \longrightarrow {\mathbb {C}}$ is not constant. The graded mixed cdga corresponding to ${\mathcal {F}}=f^*(0)$ is the relative de Rham algebra ${{\mathbf {D}}}{{\mathbf {R}}}(X/{\mathbb {C}})$. The cotangent complex of f is now represented by the complex

given by the differential of f. As graded cdga, ${{\mathbf {D}}}{{\mathbf {R}}}(X/{\mathbb {C}})$ is then ${{\mathbf {D}}}{{\mathbf {R}}}(X)[u]$, with u in degree 2, and where the cohomological differential sends u to df. The graded mixed structure on ${{\mathbf {D}}}{{\mathbf {R}}}(X)[u]$, at least locally on X, is simply given by the derivation ${\mathcal {O}}_X \longrightarrow \Omega _X^1 \longrightarrow {\mathbb {L}}_f$ where the second map is the canonical map. According to this, the realization of ${{\mathbf {D}}}{{\mathbf {R}}}(X/{\mathbb {C}})$ is a version of the formal twisted de Rham complex of [19]. To be more precise, we consider the sheaf of graded algebras on X

$$\begin{aligned} {\widehat{Sym}}_{{\mathcal {O}}_X}({\mathcal {O}}_X \oplus \Omega _X^1[-1])\simeq \prod _{p\ge 0}\Omega _X^{*\le p}, \end{aligned}$$

where $\Omega _X^*$ stands for $Sym_{{\mathcal {O}}_X}(\Omega _X^1[-1])$. We consider the differential $t.d_{DR}+\wedge df$, where $t.d_{DR}$ means the de Rham differential going from the p-component to the $(p+1)$-component. This complex is naturally quasi-isomorphic to the realization of ${{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}})={{\mathbf {D}}}{{\mathbf {R}}}(X/{\mathbb {C}})$ and thus is a model for the sheaf ${\mathcal {O}}_{{\mathcal {F}}^h}$.

Assume that f has an isolated singularity at $x \in X$, and let us restrict X so that x is the only critical point of f. Then, lemma 3.1.6 implies that for any p the complexes of sheaves

are cohomologically concentrated in degree p and thus quasi-isomorphic to the a p-shift of the sheaf ${\mathcal {H}}_p(f):=\Omega _X^p/df\wedge \Omega _X^{p-1}$. The fiber of the truncation map

$$\begin{aligned} |{{\mathbf {D}}}{{\mathbf {R}}}(X/{\mathbb {C}})| \longrightarrow (\Omega _X^*/df,d_{DR}), \end{aligned}$$

where $(\Omega _X^*/df,d_{DR})$ is the naive relative de Rham complex, is thus the realization of the graded mixed complex whose component of weight p are zero if $p\le Dim X$ and ${\mathcal {H}}_{Dim X}[2p-Dim X]$ if $p>n$. Therefore, this realization is quasi-isomorphic to $\prod _{p>Dim X}{\mathcal {H}}_{dim X}(f)[-dim X]$. As obviously $H^{Dim X}(\Omega _X^*/df,d_{DR}))\simeq 0$, we deduce that we have

$$\begin{aligned} H^p({\mathcal {O}}_{{\mathcal {F}}^h}) \simeq H^p(\Omega _X^*/df,d_{DR}) \end{aligned}$$

for $p<Dim X-1$, and we have a long exact sequence

In particular, we see that the top cohomology sheaf of ${\mathcal {O}}_{{\mathcal {F}}^h}$ is supported at x and contains and infinite number of copies of J(f), the Jacobian ring of f at x.

In the general situation, it is surely possible to relate the cohomology sheaves of ${\mathcal {O}}_{{\mathcal {F}}^h}$ to some twisted de Rham complex as described in [19], and thus to vanishing cohomology. Note also that the complex ${\mathcal {O}}_{{\mathcal {F}}^h}$ appears in a disguised form, under the name Koszul-de Rham algebra, in [20], where it is explicitely related to the naive relative de Rham complex and the singularities of the map f.

5.2 The Riemann–Hilbert correspondence

Let X be a smooth algebraic variety and ${\mathcal {F}}\in {\mathcal {F}}ol(X)$ be a derived quasi-smooth foliation on X. We first construct the Riemann–Hilbert $\infty$-functor for ${\mathcal {F}}$

$$\begin{aligned} RH : \textsf {Perf} ({\mathcal {F}}) \longrightarrow {\mathcal {O}}_{{\mathcal {F}}^h}-{{\mathbf {d}}}{{\mathbf {g}}}. \end{aligned}$$

It is defined as the composite

where ${\mathbb {R}}\underline{{\mathcal {H}}om}({\mathcal {O}}_{X^h},-)$ sends a crystal E over ${\mathcal {F}}^h$ to the complex ${\mathbb {R}}\underline{{\mathcal {H}}om}({\mathcal {O}}_{X^h},E)$ of sheaves of ${\mathbb {C}}$-vector spaces, endowed with its natural module structure over

$$\begin{aligned} {\mathbb {R}}\underline{{\mathcal {H}}om}({\mathcal {O}}_{X^h},{\mathcal {O}}_{X^h})\simeq |{{\mathbf {D}}}{{\mathbf {R}}}({\mathcal {F}}^h)|={\mathcal {O}}_{{\mathcal {F}}^h}. \end{aligned}$$

We let $\textsf {Perf} ^{nil}({\mathcal {F}})$ be the full sub-$\infty$-category of $\textsf {Perf} ({\mathcal {F}})$ consisting of h-nilpotent crystals in the sense of Definition 3.2.2. By definition of nilpotency for crystals, the $\infty$-functor RH defined above restricts to

$$\begin{aligned} RH : \textsf {Perf} ^{nil}({\mathcal {F}}) \longrightarrow \textsf {Perf} ({\mathcal {O}}_{{\mathcal {F}}^h}), \end{aligned}$$

where $\textsf {Perf} ({\mathcal {O}}_{{\mathcal {F}}^h})$ is the $\infty$-category of sheaves of perfect ${\mathcal {O}}_{{\mathcal {F}}^h}$-dg-modules on $X^h$.

Theorem 4.2.1

Let ${\mathcal {F}}\in {\mathcal {F}}ol(X)$ be a quasi-smooth derived foliation on a smooth algebraic variety X. If X is proper, then the $\infty$-functor

$$\begin{aligned} RH : \textsf {Perf} ^{nil}({\mathcal {F}}) \longrightarrow \textsf {Perf} ({\mathcal {O}}_{{\mathcal {F}}^h}) \end{aligned}$$

is an equivalence.

Proof

By GAGA (see Proposition 3.2.1) we know that the analytification $\infty$-functor induces an equivalence $\textsf {Perf} ^{nil}({\mathcal {F}}) \simeq \textsf {Perf} ^{nil}({\mathcal {F}}^h)$. Now, both $\infty$-categories $\textsf {Perf} ^{nil}({\mathcal {F}}^h)$ and $\textsf {Perf} ({\mathcal {O}}_{{\mathcal {F}}^h})$ are global sections of natural stacks of triangulated $\infty$-categories on $X^h$. Let us denote these stacks by ${\underline{\textsf {Perf} }}^{nil}({\mathcal {F}}^h)$ and ${\underline{\textsf {Perf} }}({\mathcal {O}}_{{\mathcal {F}}^h})$. Moreover, the RH $\infty$-functor is itself obtained by taking global sections of a morphism of stacks ${\underline{RH}} : {\underline{\textsf {Perf} }}^{nil}({\mathcal {F}}^h) \longrightarrow {\underline{\textsf {Perf} }}({\mathcal {O}}_{{\mathcal {F}}^h})$. By definition of nilpotency, ${\mathcal {O}}_{X^h}$ locally generates (in the sense of triangulated $\infty$-categories) ${\underline{\textsf {Perf} }}^{nil}({\mathcal {F}}^h)$, while ${\mathcal {O}}_{{\mathcal {F}}^h}$ locally generates $\textsf {Perf} ({\mathcal {O}}_{{\mathcal {F}}^h})$, and by definition $RH({\mathcal {O}}_{X^h})\simeq {\mathcal {O}}_{{\mathcal {F}}^h}$. We then conclude that ${\underline{RH}}$ is locally fully faithful and locally essentially surjective. It is therefore a local equivalence of stacks, and thus a global equivalence, i.e. RH is an equivalence. $\square$

Combining Theorem 4.2.1 with Theorem 3.2.3, we get our main result. For ${\mathcal {F}}\in {\mathcal {F}}ol(X)$ be a quasi-smooth and rigid derived foliation on a smooth and proper algebraic variety X, we denote by $\textsf {Perf} ^{v}({\mathcal {F}}) \subset \textsf {Perf} ({\mathcal {F}})$ the full triangulated sub-$\infty$-category generated by objects in $\textsf {Vect} ({\mathcal {F}})$.

Corollary 4.2.2

Let ${\mathcal {F}}\in {\mathcal {F}}ol(X)$ be a quasi-smooth and rigid derived foliation on a smooth and proper algebraic variety X. If the singular locus $Sing({\mathcal {F}})$ has codimension $\ge 2$, then the Riemann–Hilbert correspondence

$$\begin{aligned} RH : \textsf {Perf} ^{v}({\mathcal {F}}) \longrightarrow \textsf {Perf} ^v({\mathcal {O}}_{{\mathcal {F}}^h}) \end{aligned}$$

is an equivalence of $\infty$-categories.

5.3 Examples

5.3.1 Smooth and rigid foliations

Let X be a smooth and proper algebraic variety and ${\mathcal {F}}$ be smooth and rigid derived foliations on X. We represent ${\mathcal {F}}$ by a differential ideal $D \subset \Omega _X^1$ which is furthermore a subbundle. The category $\textsf {Vect} ({\mathcal {F}})$, of vector bundle crystals along ${\mathcal {F}}$ is equivalent to the category of vector bundles V on X endowed with a partial flat connection

$$\begin{aligned} \nabla : V \longrightarrow V\otimes \Omega _X^1/D \end{aligned}$$

satisfying the standard properties. As already observed (see 4.1.1), the sheaf ${\mathcal {O}}_{{\mathcal {F}}^h}$ is then a genuine sheaf of commutative algebras: it is the subsheaf of ${\mathcal {O}}_{X^h}$, of holomorphic functions on X, which are locally constant along the leaves, i.e. local functions f on X such that $df \in D \subset \Omega _X^1$. Locally on $X^h$, the foliation is given by a smooth holomorphic map $X \longrightarrow {\mathbb {C}}^p$, and the sheaf ${\mathcal {O}}_{{\mathcal {F}}^h}$ can then be described as $f^{-1}({\mathcal {O}}_{{\mathbb {C}}^p})$, the sheafy inverse image of the sheaf of holomorphic functions on ${\mathbb {C}}^p$.

The Riemann–Hilbert correspondence of Theorem 4.2.1 and Corollary 4.2.2 implies the existence of an equivalence of categories

$$\begin{aligned} \textsf {Vect} ({\mathcal {F}}) \simeq \textsf {Vect} ({\mathcal {O}}_{{\mathcal {F}}^h}) \end{aligned}$$

where $\textsf {Vect} ({\mathcal {O}}_{{\mathcal {F}}^h})$ is the category of sheaves of ${\mathcal {O}}_{{\mathcal {F}}^h}$-modules on $X^h$ which are locally free of finite rank. When ${\mathcal {F}}$ is furthermore induced by a smooth and proper morphism $f : X \longrightarrow Y$, i.e. $f^*({\mathbf {0}}_Y)\simeq {\mathcal {F}}$, this equivalence is essentially the relative Riemann–Hilbert correspondence of [7]. The extension from vector bundles to perfect complexes essentially states that this equivalence is also compatible with cohomology, and also induces a quasi-isomorphism

$$\begin{aligned} {\mathbb {H}}_{DR}({\mathcal {F}};V) \simeq {\mathbb {H}}_{B}(X^h,RH(V)), \end{aligned}$$

between the algebraic de Rham cohomology of V over X to the (Betti) cohomology of $X^h$ with coefficients in the sheaf of ${\mathcal {O}}_{{\mathcal {F}}^h}$-modules RH(V).

5.3.2 Lie algebroids

Let X be a smooth and proper algebraic variety and ${\mathcal {F}}$ be smooth derived foliation on X. We have seen that such a derived foliation corresponds to a classical Lie algebroid with anchor map $a : T \longrightarrow {\mathbb {T}}_X$ (see § 1.3.1). The category $\textsf {Vect} ({\mathcal {F}})$ can then be described as representations of T in vector bundles, i.e. vector bundles V together with a connection along ${\mathcal {F}}$

$$\begin{aligned} \nabla : V \longrightarrow V\otimes T^* \end{aligned}$$

satisfying the Leibniz and flatness $\nabla ^2=0$. In this case, the sheaf ${\mathcal {O}}_{{\mathcal {F}}^h}$ is the sheaf of cdga’s on $X^h$

where d is the rank of V. This is a sheaf of cdga’s not concentrated in degree 0 in general. If the anchor map a turns out to be a subbundle on a Zariski open $U \subset X$, then the higher cohomology sheaves have supports on $X-U$.

We denote by ${\mathcal {K}}$ the kernel of the anchor map $a : T \longrightarrow {\mathbb {T}}_X$, considered as a sheaf on the big étale site of X. As such it is representable by a Lie algebra scheme $K \longrightarrow X$, whose fiber $K_x$ at a point $x \in X$ is the kernel of the map $a_x : T_x \longrightarrow {\mathbb {T}}_{X,x}$, which is a ${\mathbb {C}}$-linear Lie algebra. For an object $V \in \textsf {Vect} ({\mathcal {F}})$, and a point $x\in X$, the Lie algebra $K_x$ acts naturally on the fiber $V_x$. If V is h-nilpotent in the sense of Definition 3.2.2, then for all points $x \in X$ the $K_x$-module $V_x$ is a nilpotent representation of the Lie algebra $K_x$.

The Riemann–Hilbert correspondence of Theorem 4.2.1 induces an equivalence of categories

$$\begin{aligned} \textsf {Vect} ^{nil}({{\mathcal {F}}}) \simeq \textsf {Vect} ({\mathcal {O}}_{{\mathcal {F}}^h}). \end{aligned}$$

The extension to perfect complexes again essentially states that this equivalence is also compatible with the natural cohomologies on both sides, i.e. algebraic de Rham cohomology and Betti cohomology.

5.3.3 Log vector fields

Let X be a smooth and proper algebraic variety and $D \subset X$ be a divisor with simple normal crossings. We let ${\mathbb {T}}_X(log(D)) \subset {\mathbb {T}}_X$ be the subsheaf of vector fields that stabilize D, i.e. derivations preserving the ideal defining D. This defines a Lie algebroid on X, and thus a smooth derived foliation ${\mathcal {F}}$, to which we can apply our Riemann–Hilbert correspondence (Theorem 4.2.1 and Corollary 4.2.2). Let us unravel the two sides of the Riemann–Hilbert correspondence in this case. Note first that $\textsf {Vect} ({\mathcal {F}})$ consists of pairs consisting of a vector bunlde on X together with a logarithmic flat connections along D

$$\begin{aligned} \nabla : V \longrightarrow V\otimes \Omega ^1_X(log(D)). \end{aligned}$$

The structure sheaf ${\mathcal {O}}_{{\mathcal {F}}^h}$ is then the sheaf of cdga’s on $X^h$ given by the logarithmic de Rham complex

By Grothendieck’s log-de Rham theorem, this is a resolution of the sheaf of cdga’s $j_*({\mathbb {C}})$, where $j : (X-D) \longrightarrow X$ and ${\mathbb {C}}$ is the constant sheaf (with stalks ${\mathbb {C}}$) on $(X-D)$. Note that $j_*({\mathbb {C}})$ is not concentrated in degree 0, as its fiber at a point $x\in D$ is the cohomology algebra of an m-dimensional torus $H^*((S^1)^m,{\mathbb {C}})$, if the local equation of D at m is of the form $x_1.\dots .x_m=0$ (for $(x_1, \cdots , x_{d})$ a system of local parameters at x in X, and $m\le d$).

The Lie algebroid ${\mathbb {T}}_X(log(D))$ has isotropy along D. For a point $x \in D$, in a neigborhood of which D has equation $x_1.\dots .x_m=0$, the kernel of the anchor map $a: {\mathbb {T}}_X(log(D))\rightarrow {\mathbb {T}}_X$ at x is an abelian Lie algebra of dimension m. Generators of this Lie algebra are given by the local vector fields $x_i.\frac{\partial }{\partial x_i}$ for $1\le i\le m$, which are local sections of ${\mathbb {T}}_X(log(D))$ that, once evaluated at x, provide a basis for the Lie algebra $Ker(a_x)$. As we have already remarked, if $V \in \textsf {Vect} ({\mathcal {F}})$ is h-nilpotent, then the actions of the Lie algebras $Ker(a_x)$ on $V_x$ must be nilpotent. In our case, these actions are given by the residues of the connection $\nabla$ along the components of D, and thus when V is h-nilpotent these residues must be nilpotent too. The converse is true: $V\in \textsf {Vect} ({\mathcal {F}})$ is h-nilpotent if and only if it has nilpotent residues. This follows from the local analytic structure of flat connections with logarithmic poles along D, and the fact that they correspond to local systems on $X-D$ with unipotent local monodromies around D (see e.g. [7]). The Riemann–Hilbert correspondence of Theorem 4.2.1 then becomes the following equivalence of categories

$$\begin{aligned} RH : \textsf {Vect} ^{nil}({\mathcal {F}}) \simeq \textsf {Vect} (j_*({\mathbb {C}})), \end{aligned}$$

where $\textsf {Vect} ^{nil}({\mathcal {F}})$ can be identified with vector bundles on X endowed with flat connections with logarithmic poles along D. Its extension to perfect complexes

$$\begin{aligned} RH : \textsf {Perf} ^{nil}({\mathcal {F}}) \simeq \textsf {Perf} (j_*({\mathbb {C}})) \end{aligned}$$

implies that the previous equivalence $RH : \textsf {Vect} ^{nil}({\mathcal {F}}) \simeq \textsf {Vect} (j_*({\mathbb {C}}))$ is also compatible with cohomology theories on both sides. Note here that $j_*({\mathbb {C}})$ can also be described as $\pi _*({\mathbb {C}}_{X^h})$, where $\pi : X^{log} \longrightarrow X^h$ is the logarithmic homotopy type of the pair (X, D) in the sense of [10], and that ${\mathbb {C}}$ generates, in the sense of triangulated categories, the categrory of unipotent local systems. Therefore, perfect ${\mathcal {O}}_{{\mathcal {F}}^h}$-dg-modules can also be understood as perfect complexes of ${\mathbb {C}}$-modules on $X^{log}$ which are relatively unipotent over $X^h$, i.e. those which become unipotent along the fibers of $\pi$. These statements have a straightforward generalization to the case where (X, D) is replaced by a more general log-structure on X. The equivalences above recovers the logarithmic Riemann–Hilbert correspondence of [10, Thm. 0.5].

5.3.4 The RH correspondence along a non-smooth morphism

Let $f : X \longrightarrow Y$ be a morphism between smooth and proper algebraic varieties, and ${\mathcal {F}}=f^*(0_Y)\in {\mathcal {F}}ol(X)$ be the derived foliation induced by f (recall that $f^*$ denotes here the pull-back functor on foliations, and $0_Y$ is the final foliation on Y). We associate to f the morphism between de Rham shapes (first introduced in [21]) $f_{DR}: X_{DR} \longrightarrow Y_{DR}$, where for a scheme Z the functor $Z_{DR}$ sends an algebra A to $Z(A_{red})$. The relative de Rham shape is defined

$$\begin{aligned} (X/Y)_{DR}:=X_{DR}\times _{Y_{DR}}Y. \end{aligned}$$

Quasi-coherent sheaves on $(X/Y)_{DR}$ are by definition relative crystals on X over Y. Note that these are also the quasi-coherent sheaves on the relative infinitesimal site $(X/Y)_{\text {inf}}$ of X over Y (see [9]). This site has objects commutative diagrams of the form

where $S_{red} \longrightarrow X$ is a Zariski open. The topology is itself defined in the natural way. It comes equipped with a structure sheaf ${\mathcal {O}}_{X/Y,\text {inf}}$ sending a diagram as above to ${\mathcal {O}}(S)$. It is then possible to prove that there exists a natural equivalence of $\infty$-categories

$$\begin{aligned} \textsf {Perf} ({\mathcal {F}}) \simeq \textsf {Perf} ({\mathcal {O}}_{X/Y,\text {inf}}). \end{aligned}$$

Therefore, perfect crystals along the foliation ${\mathcal {F}}$ are nothing else than perfect complexes on the relative infinitesimal site of X over Y.

In this situation, the sheaf ${\mathcal {O}}_{{\mathcal {F}}^h}$ on $X^h$ is the relative analytic derived de Rham complex of $X^h$ over $Y^h$. As explained earlier, it has a projection onto the naive de Rham complex $(\Omega _{X^h/Y^h}^*[-*],dR)$, which is the de Rham complex of relative holomorphic differential forms

It is important to remark that the projection

$$\begin{aligned} {\mathcal {O}}_{{\mathcal {F}}^h} \longrightarrow (\Omega _{X^h/Y^h}^*[-*],dR) \end{aligned}$$

is far from being an equivalence in general. For example, if $f: X \rightarrow Y$ is a closed immersion the right hand side is just the sheaf ${\mathcal {O}}_{X^h}$ whereas the left hand side is ${\widehat{{\mathcal {O}}}}_{X^h}$, the structure sheaf of the formal completion of X inside Y. Proposition 3.1.5 implies that this morphism is an isomorphism on cohomology groups in degree less than d if the map f is smooth outside of codimension $(d+1)$ closed subset.

Let us assume now that $f : X \longrightarrow Y$ is flat with reduced fibers and of strictly positive relative dimension. By generic smoothness f is smooth on $X-S$ where S is a closed subset of codimension $d>1$. By Proposition 3.1.5 we have that

$$\begin{aligned} H^0({\mathcal {O}}_{{\mathcal {F}}^h}) \simeq H^0((\Omega _{X^h/Y^h}^*[-*],dR)). \end{aligned}$$

The right hand side is the subsheaf of functions on $X^h$ which are locally constant along the fibers of f, i.e. those which are pull-backs of functions on $Y^h$. In other words, we have an isomorphism of sheaves of rings

$$\begin{aligned} H^0({\mathcal {O}}_{{\mathcal {F}}^h}) \simeq f^{-1}({\mathcal {O}}_{Y^h}). \end{aligned}$$

Therefore, ${\mathcal {O}}_{{\mathcal {F}}^h}$ has a canonical structure of a sheaf of $f^{-1}({\mathcal {O}}_{Y^h})$-cdga’s. Therefore, for any point $y \in Y$, we can consider the following sheaf of cdga’s on $X^h$

$$\begin{aligned} {\mathcal {O}}_{{\mathcal {F}}^h} \otimes _{f^{-1}({\mathcal {O}}_{Y^h})}{\mathbb {C}}_y, \end{aligned}$$

where the map $f^{-1}({\mathcal {O}}_{Y^h}) \longrightarrow {\mathbb {C}}_y={\mathbb {C}}$ is given by evaluation at y. The resulting sheaf is the derived analytic de Rham cohomology of the fiber $f^{-1}(y)$, and thus it is the constant sheaf ${\mathbb {C}}$ on that fiber. We deduce that

$$\begin{aligned} {\mathcal {O}}_{{\mathcal {F}}^h} \otimes _{f^{-1}({\mathcal {O}}_{Y^h})}{\mathbb {C}}_y \simeq (i_y)_*({\mathbb {C}}) \end{aligned}$$

where $i_y : f^{-1}(y) \hookrightarrow X$ is the inclusion of the fiber at y.

The previous discussion prompts the following interpretation. For any $E \in \textsf {Vect} ({\mathcal {O}}_{{\mathcal {F}}^h})$, we define its base changes $E_y := E \otimes _{f^{-1}({\mathcal {O}}_{Y^h})}{\mathbb {C}}_y$ which are genuine local systems on $f^{-1}(y)$. Therefore, the notion of perfect complexes of ${\mathcal {O}}_{{\mathcal {F}}^h}$-dg-modules should be understood as a notion of analytic families of perfect complexes of local systems along the fibers. With this interpretation, the Riemann–Hilbert correspondence

$$\begin{aligned} RH : \textsf {Perf} ({\mathcal {F}}) \simeq \textsf {Perf} ({\mathcal {O}}_{{\mathcal {F}}^h}) \end{aligned}$$

of Theorem 4.2.1 should be actually understood as an equivalence between algebraic families of crystals along the fibers of f, and analytic families of perfect local systems along the fibers.