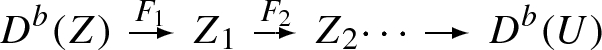Abstract
In this paper we introduce new categorical notions and give many examples. In an earlier paper we proved that the Bridgeland stability space on the derived category of representations of K(l), the l-Kronecker quiver, is biholomorphic to \({{\mathbb {C}}} \times {\mathcal {H}}\) for \(l\ge 3\). In the present paper we define a new notion of norm, which distinguishes \(\{D^b(K(l)) \}_{l\ge 2}\). More precisely, to a triangulated category \({\mathcal {T}}\) which has property of a phase gap we attach a non-negative real number \(\left\| {\mathcal {T}}\right\| ^{\varepsilon }\). Natural assumptions on a SOD \({\mathcal {T}} =\langle {\mathcal {T}}_1,{\mathcal {T}}_2\rangle \) imply \(\left\| \langle {\mathcal {T}}_1,{\mathcal {T}}_2\rangle \right\| ^{\varepsilon }\le {\mathrm{min}}\{\left\| {\mathcal {T}}_1 \right\| ^{\varepsilon },\left\| {\mathcal {T}}_2\right\| ^{\varepsilon } \}\). Using the norm we define a topology on the set of equivalence classes of proper triangulated categories with a phase gap, such that the set of discrete derived categories is a discrete subset, whereas the rationality of a smooth surface S ensures that \([D^b(point)] \in \mathrm{Cl}([D^b(S)])\). Categories in a neighborhood of \(D^b(K(l))\) have the property that \(D^b(K(l))\) is embedded in each of them. We view such embeddings as non-commutative curves in the ambient category and introduce categorical invariants based on counting them. Examples show that the idea of non-commutative curve-counting opens directions to new categorical structures and connections to number theory and classical geometry. We give a definition, which specializes to the non-commutative curve-counting invariants. In an example arising on the A side we specialize our definition to non-commutative Calabi–Yau curve-counting, where the entities we count are a Calabi–Yau modification of \(D^b(K(l))\). In the end we speculate that one might consider a holomorphic family of categories, introduced by Kontsevich, as a non-commutative extension with the norm, introduced here, playing a role similar to the classical notion of degree of an extension in Galois theory.
We’re sorry, something doesn't seem to be working properly.
Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.
Avoid common mistakes on your manuscript.
1 Introduction
Motivated by M. Douglas’s work in string theory T. Bridgeland defined in [10] a map:

For a triangulated category \({\mathcal {T}}\) the associated complex manifold \(\mathrm {Stab}({\mathcal {T}})\) is referred to as the space of stability conditions (or the stability space or the moduli space of stability conditions) on \({\mathcal {T}}\).
The map (1) behaves well with respect to orthogonal decompositions (Definition 5.1). Due to lack of a reference in the literature we show this in Sect. 5. In particular, there is a a bijection
which is biholomorphism, when the categories are with finite rank Grothendieck groups (Proposition 5.2). Our previous paper [19, Theorem 1.1 ] contains examples of semi-orthogonal decomposition, SOD, \({\mathcal {T}}=\langle {\mathcal {T}}_1, {\mathcal {T}}_2 \rangle \) where \({\mathrm{rank}}(K_0({\mathcal {T}}))=2 \) and \(\mathrm {Stab}({\mathcal {T}})\) is not biholomorphic to \(\mathrm {Stab}({\mathcal {T}}_1)\times \mathrm {Stab}({\mathcal {T}}_2)\).
The behavior of the map (1) with respect to general SOD has been studied in [16]. This is a difficult problem and no formula relating \(\mathrm {Stab}(\langle {\mathcal {T}}_1,{\mathcal {T}}_2 \rangle )\) and \(\mathrm {Stab}({\mathcal {T}}_1)\), \(\mathrm {Stab}({\mathcal {T}}_2)\) is obtained.
In this paper using Bridgeland stability conditions we define (Definition 4.11) for any \(0<\varepsilon <1\) a function (the domain is explained below and it does not depend on \(\varepsilon \)):

and prove (Theorem 6.1) that if \({\mathcal {T}} =\left\langle {\mathcal {T}}_1,{\mathcal {T}}_2\right\rangle \) is a semi-orthogonal decomposition in which \({\mathcal {T}}\) is proper,Footnote 1 \({\mathrm{rank}}(K_0({\mathcal {T}}))<\infty \), \({\mathcal {T}}_1\) and \({\mathcal {T}}_2\) have phase gaps, then \({\mathcal {T}}\) has phase gap as well and
For the proof of this inequality we employ the method for gluing of stability conditions in [16], crucial role has also [11, Lemma 4.5] which ensures certain finiteness property of a stability condition with a phase gap.
The function (3) depends on \(\varepsilon \in (0,1)\), however the three subsets of its domain determined by the three conditions on the first row in the following table do not depend on \(\varepsilon \) (Lemma 4.16):
Categories with: | \(\left\| \cdot \right\| _{\varepsilon }=0\) | \(0<\left\| \cdot \right\| _{\varepsilon }<\pi (1-\varepsilon )\) | \(\left\| \cdot \right\| _{\varepsilon }=\pi (1-\varepsilon )\) |
|---|---|---|---|
examples: | for any acyclic quiver Q \(D^b(Q)\) is here iff Q is Dynkin or affine, any discrete derived category is here | \(D^b(K(l_1))\oplus \dots \oplus D^b(K(l_N))\) where \(N\in {\mathbb {Z}}_{\ge 1}, l_i\ge 3\) for some i | \(D^b({\mathbb {P}}^1 \times {\mathbb {P}}^1), D^b({\mathbb {P}}^n) n \ge 2, D^b({\mathbb {F}}_m) m\ge 0\), many wild quivers as in Prop. 8.5 (a) |
Further examples can be obtained by using (4) and the property that for a proper \({\mathcal {T}} \) with \({\mathrm{rank}}(K_0({\mathcal {T}}))<\infty \) and decomposition \({\mathcal {T}} ={\mathcal {T}}_1 \oplus {\mathcal {T}}_2 \) with \(\left\| {\mathcal {T}}_1\right\| _\varepsilon = 0\) holds \( \left\| {\mathcal {T}}_1 \oplus {\mathcal {T}}_2\right\| _\varepsilon = \left\| {\mathcal {T}}_2\right\| _\varepsilon \) (Corollary 5.6). In particular by blowing up the varieties in last column one obtains other elements in this column (see Corollary 6.4).
In Sect. 11 using (3) we introduce a topology on the class of proper triangulated categories with a phase gap up to equivalence. The function \( \left\| \cdot \right\| ^{\varepsilon }=\pi (1-\varepsilon )-\left\| \cdot \right\| _\varepsilon \) is upper semi-continuous for this topology. The class of discrete derived categories modulo equivalence is a discrete subset w.r. to it (see Sect. 10). For a proper \({\mathcal {T}}\) with \({\mathrm{rank}}(K_0({\mathcal {T}}))\ge 3\) we show in Proposition 11.9 that the following condition:Footnote 2
implies \([D^b(point)]\in {\mathrm{Cl}}\left( [{\mathcal {T}}] \right) \). In Proposition 8.5 we verify (5) in \(D^b(X)\) for any smooth complete rational surface X and for some higher dimensional smooth varieties. A conjecture stated by Orlov says that a surface over an algebraically closed field admits a full exceptional collection only if it is rational (see e.g. [41, p. 5]). If this conjecture holds, then the presented results would imply that for any smooth projective surface S with a full exceptional collection holds (5) and hence \([D^b(point)] \in \mathrm{Cl}([D^b(S)])\). The condition (5) fails for \(D^b(K(n))\), and Conjecture 1.3 would imply that it fails for the quivers depicted there. Related questions are:
Question 1.1
Let X denote a smooth projective variety X, different from \({\mathbb {P}}^1\), with a full exceptional collection. Is there X, s. t. \([D^b(point)] \not \in \mathrm{Cl}([D^b(X)])\) ? Is there X and a natural number \(N\in {\mathbb {N}}\) s. t. for any full exceptional collection \((E_0,\dots , E_n)\) in \(D^b(X)\) and any \(0\le i<j\le n\) we have \(\hom ^{min}(E_i,E_j)\le N\) ?
A positive answer of some of the questions in 1.1 with \(\dim (X)=2\) would be a counterexample of Orlov conjecture.
Another class of categorical invariants introduced in this paper is motivated by the following question (many of these invariants behave in a certain sense monotone with respect to SOD):
For the topology from Sect. 11 any category (except \(D^b(A_1)\)) in table 1 is in a neighborhood of \(N{\mathbb {P}}^l\) for some l ( following Kontsevich–Rosenberg [32] we denote sometimes \(D^b(K(l+1))\) by \(N{\mathbb {P}}^l\)). More precisely, there is a SOD \(\langle N{\mathbb {P}}^l, {\mathcal {A}} \rangle \) for some l and some \({\mathcal {A}}\). Recalling that Gromow-Witten invariants count pseudo-holomorphic curves, we view such embeddings of \(N{\mathbb {P}}^l\) into \({\mathcal {T}}\) as analogous to a “pseudo-holomorphic curve” in the category \({\mathcal {T}}\) and ask a question: can we count such entities in a given \({\mathcal {T}}\), how many are they ?
In Sect. 12 and in [20] we show that the answer is positive. The idea is: for two triangulated catogories \( {\mathcal {A}} \), \({\mathcal {T}}\), a subgroup \(\Gamma {\subset } {\mathrm{Aut}}({\mathcal {T}})\), and a choice of some additional restrictions P of fully faithful functors we define the set of equivalence classes of fully faithful functors from \({\mathcal {A}}\) to \({\mathcal {T}}\) satisfying P with two functors \(F, F'\) being equivalent iff \(F\circ \alpha \cong \beta \circ F'\) for some \(\alpha \in {\mathrm{Aut}}(N{\mathbb {P}}^l)\), \(\beta \in \Gamma \). This set is denoted by \(C_{{\mathcal {A}}, P}^{\Gamma }({\mathcal {T}})\) (see Definition 12.5). We prefer to choose some \({\mathcal {A}}\), which is non-trivial but well studied.
The studies in this paper naturally impose \(N{\mathbb {P}}^l\) as our first choice - we consider also \(N {\mathbb {P}}^{-1}\), which is a category generated by an orthogonal exceptional pair. We refer to \( N{\mathbb {P}}^l\) as a non-commutative curve and by rescaling \(\left\| \cdot \right\| _{\frac{1}{2}}\) (see Sect. 12.1) we define an invariant:

to which we refer to as “non-commutative genus”. In particular, \(N{\mathbb {P}}^l\) is a non-commutative curve of genus l for \(l\ge 0\). Although \(N{\mathbb {P}}^{-1}\) has homological dimension 0 we refer to it as a non-commutative curve of genus \(-1\) (see Remark 12.2 for further motivation).
Using the inequality in (6) we have derived vanishing theorem for \(C^{\Gamma }_{N{\mathbb {P}}^l,P}({\mathcal {T}})\) for certaion choice of P (see Remark 12.6). Choosing \({\mathcal {A}} = N{\mathbb {P}}^l\), assuming that \({\mathcal {T}}\) is \({\mathbb {K}}\)-linear and choosing the additional restriction P of the functors to be \({\mathbb {K}}\)-linear, we write just \(C_{l}^\Gamma ({\mathcal {T}})\) instead of \(C_{N{\mathbb {P}}^l, P}^\Gamma ({\mathcal {T}})\) and refer to this set as to the set of non-commutative curves of genus l in \({\mathcal {T}}\) modulo the subgroup \(\Gamma \). Furthermore, by fixing a stability condition \(\sigma \in \mathrm {Stab}({\mathcal {T}})\) we strengthen the restriction P depending on \(\sigma \) to define the set of \(\sigma \)-semistable, resp. \(\sigma \)-stable non-commutative curves in \({\mathcal {T}}\) and denote it by \(C_{l,\sigma }^{\Gamma }({\mathcal {T}})\), resp. \(C_{l,\sigma \sigma }^{\Gamma }({\mathcal {T}})\) (Definition 12.12). The definitions of the counting invariants introduced here are carefully explained in a subsequent work [20].
From this vanishing criterion (174), Remark 12.7 and after determining \(\dim _{nc}(D^b(Q))\) for affine and Dynkin Q (see Remark 12.1) follow these vanishings:
It is interesting to find further examples of wild quivers Q with \(\dim _{nc}(D^b(Q))<\infty \), we propose potential examples, see Conjecture 1.3, analogous vanishings for \(C_l(D^b(Q))\) for big enough l would follow by the vanishing criterion (174).
It is easy to prove that \(\left| C_l^{\{{\text {Id}}\}}(N{\mathbb {P}}^k)\right| =\delta _{l,k}\) for \(l,k\ge -1\). For \(l\ge 1\) we describe the zones in \(\mathrm {Stab}(N{\mathbb {P}}^l)\), where \(\left| C_{l,\sigma }^{\{{\text {Id}}\}}(N{\mathbb {P}}^l)\right| \) is zero and one respectively, in particular one sees the walls, where a wall-crossing takes place (see part 1.3 of the introduction below and Proposition 12.13).
The numbers \(\left| C_l^{\Gamma }({\mathcal {T}})\right| \) are computed for two affine quivers in [20, Section 6], and estimated for \(D^b({\mathbb {P}}^2)\) in [20, Section 8]. In Sect. 12.3 here we present the results of these computations. In particular, part of Proposition 12.10 is that \(C_l^{\mathrm {Aut}_{{\mathbb {C}}}(D^b({\mathbb {P}}^2))}\left( D^b({\mathbb {P}}^2))\right) \) is finite for all l and non-empty iff \(l=3 m -1\) for some Markov number m, where \({\mathbb {P}}^2\) is the complex projective plane and \(\mathrm {Aut}_{{\mathbb {C}}}(D^b({\mathbb {P}}^2))\) is the group of \({\mathbb {C}}\)-linear auto-equivalences of \({\mathbb {P}}^2\). Furthermore, Corollary 12.11 is that the Markov’s conjecture in number theory and a conjecture by Tyurin ([36, p. 100] or [25, Section 7.2.3 ]) are true iff for each Markov number \(m\ne 1, m\ne 2\) we have \(\left| C_{3 m -1}^{\mathrm {Aut}_{\mathbb {C}}(D^b({\mathbb {P}}^2))}(D^b({\mathbb {P}}^2))\right| =2\). Via the latter Corollary in future works we plan to approach Markov’s conjecture using homological mirror symmetry and applying A side techniques for computing the non-commutative curve-counting invariants.
In Sect. 12.4 we explain an example, where \(\left| C_{1,\sigma }^{\{{\text {Id}}\}}({\mathcal {T}})\right| \) takes all possible values in \(\left\{ 0,1,2=\left| C_{1}^{\{{\text {Id}}\}}({\mathcal {T}})\right| \right\} \) as \(\sigma \) varies in \(\mathrm {Stab}({\mathcal {T}})\) (the proof is in the master thesis [6]).
Section 12.5 contains a conjectural example of finite sets \(C_{{\mathcal {A}}, P}^{\Gamma }({\mathcal {T}})\) of different origin (the proof is postponed for future work as well). Here \({\mathcal {T}}\) is the so called Fukaya category of an elliptic curve, \({\mathrm{Fuk}}(E)\). In this case we set \({\mathcal {A}}\) to be a a Calabi–Yau modification of \(D^b(K(l))\), denoted by CY(l). The question about the cardinalities of \(C_{CY(l),{\mathbb {C}}}^{\Gamma }\left( {\mathrm{Fuk}}(S)\right) \) for higher genus curves should be related to counting geodesics on S.
Finally (Sect. 13), relating our norm to the notion of holomorphic family of categories introduced by Kontsevich we suggest a framework in which sequences of holomorphic families of categories are viewed as sequences of extensions of non-commutative manifolds.
This paper is the beginning of a longer pursuit motivated by the invariants introduced here. In [20] we extend our studies of \(C_{{\mathcal {A}}, P}^{\Gamma }({\mathcal {T}})\) beyond counting: besides numbers we extract from \(C_{{\mathcal {A}}, P}^{\Gamma }({\mathcal {T}})\) categorical versions of classical geometric structures which open new perspectives in non-commutative geometry.
1.1. We give here more details on the definition of \(\left\| {\mathcal {T}}\right\| _{\varepsilon }\) and on the examples.
By definition each stability condition \(\sigma \in \mathrm {Stab}({\mathcal {T}})\) determines a set of non-zero objects in \({\mathcal {T}}\) (called semi-stable objects) labeled by real numbers (called phases of the semistable objects). The semi-stable objects correspond to the so called “BPS” branes in string theory. The set of semi-stable objects will be denoted by \(\sigma ^{ss}\), and \(\phi _\sigma (X)\in {\mathbb {R}}\) denotes the phase of a semi-stable X. For any \(\sigma \in \mathrm {Stab}({\mathcal {T}})\) we denote by \(P_\sigma ^{{\mathcal {T}}}\) the subset of the unit circle \(\{\exp ({\mathrm {i}}\pi \phi _\sigma (X)):X\in \sigma ^{ss}\} {\subset } {\mathbb {S}}^1\). A categorical analogue of the density of the set of slopes of closed geodesics on a Riemann surface was proposed in [18]. In [18, section 3] the focus falls on constructing stability conditions for which the set \(P_\sigma \) is dense in a non-trivial arc of the circle. The result is the following characterization of the map (1), when restricted to categories of the form \(D^b(Rep_{{\mathbb {K}}}(Q))\) (Q denotes an acyclic quiver):

In [21, Proposition 3.29] are constructed stability conditions \(\sigma \in \mathrm {Stab}(D^b(Q))\) with two limit points of \(P_\sigma \) for any affine quiver Q (by \(D^b(Q)\) we mean \(D^b(Rep_k(Q))\)).
Stability conditions on wild quivers whose set of phases are dense in an arc were constructed in [18], however for them the set of phases is still not dense in the entire \({\mathbb {S}}^1\), i.e. \(P_\sigma \) does misses a non-trivial arc, in which case we say for short that \(P_\sigma \) has a gap. In particular all the categories in table (9) are examples of what we call in this paper a triangulated category with phase gap, this is a triangulated category \({\mathcal {T}}\) for which there exists a fullFootnote 3 \(\sigma \in \mathrm {Stab}({\mathcal {T}})\) whose set of phases \(P_\sigma ^{{\mathcal {T}}}\) has a gap. Stability conditions whose set of phases is not dense in \({\mathbb {S}}^1\) and their relation to so called algebraic stability conditions have been studied in [37]. In particular the results in [37] imply that when \({\mathrm{rank}}K_0({\mathcal {T}})<\infty \), then \({\mathcal {T}}\) has a phase gap iff there exists a bounded t-structure in \({\mathcal {T}}\) whose heart is of finite length and has finitely many simple objects (Lemma 4.7). Whence the domain of the invariant (3) contains also the CY3 categories discussed in [12].
By definition \(\left\| {{\mathcal {T}}}\right\| _\varepsilon \) is the supremum ofFootnote 4 \(\mathrm {vol}\left( \overline{P_\sigma } \right) /2\) as \(\sigma \) varies in the subset \(\mathrm {Stab}_\varepsilon ({\mathcal {T}}) {\subset } \mathrm {Stab}({\mathcal {T}})\) of those stability conditions \(\sigma \) for which \(P_\sigma \) misses at least one closed \(\varepsilon \)-arc (see Definitions 38, 4.3).
From the definition and table (9) it follows that for any acyclic quiver Q the norm \(\left\| D^b(Q)\right\| _{\varepsilon }\) vanishes iff Q is Dynkin or affine. Thus, using [19, table (4)] we obtain the table

and [19, Conjecture 1.2] can be reformulated as follows:
Conjecture 1.2
Let \(0<\varepsilon <1\) and let Q be any acyclic quiver. The stability space \(\mathrm {Stab}(D^b(Q))\) is affine (of the form \({\mathbb {C}}^n\)) iff \(\left\| D^b(Q)\right\| _{\varepsilon }=0\).
In table (9) we see that the map (1) has the same value (up to biholomorphism) on all the categories \(\{ D^b(K(l)) \}_{l\ge 3}\). In this paper we compute \(\left\| D^b(K(l))\right\| _\varepsilon \) for any l and \(0<\varepsilon <1\) and show:
Some criteria ensuring that \(\left\| {\mathcal {T}}\right\| _{\varepsilon }=\pi (1-\varepsilon )\) explained below imply that for many of the wild quivers Q we have \(\left\| D^b(Q)\right\| _{\varepsilon }=\pi (1-\varepsilon )\) (see Proposition 8.5 (a)) and also \(\left\| D^b(X)\right\| _{\varepsilon } = \pi (1-\varepsilon )\) where X is \({\mathbb {P}}^n\), \(n\ge 2\), \({\mathbb {P}}^1\times {\mathbb {P}}^1\), \({\mathbb {F}}_a\), \(a\ge 0\) or a smooth algebraic variety obtained from these by a sequence of blow ups in finitely many points (see Proposition 8.5e, f), for \(n=1\) we have \(\left\| D^b({\mathbb {P}}^1)\right\| _{\varepsilon }=0\). Actually, the condition \(\left\| {\mathcal {T}}\right\| _{\varepsilon }< \pi (1-\varepsilon )\) imposes restrictions on the full exceptional collections in \({\mathcal {T}}\) (see Corollary 8.4).
The criteria for \(\left\| {\mathcal {T}}\right\| _{\varepsilon }=\pi (1-\varepsilon )\) obtained here do not apply to category of the form \({\mathcal {T}} \cong D^b(K(l_1))\oplus D^b(K(l_2))\oplus \dots \oplus D^b(K(l_N))\) and we do prove that \(\left\| {\mathcal {T}}\right\| _\varepsilon <\pi (1-\varepsilon )\) in this case.
We expect that the criterion in Corollary 8.3 does not apply to all wild quivers, and we do know that its corollary, Corollary 8.5 (a), cannot be applied to all of them, for example, to the following:

We conjecture, that:
Conjecture 1.3
For \(i=1,2,3\) we have \(0<\left\| D^b(S_i)\right\| _{\varepsilon }<\pi (1-\varepsilon ) \), which is equivalent to \(\dim _{nc}(D^b(S_i))<\infty \) (see (6)). Furthermore we conjecture that \(C_{l}^{\{{\text {Id}}\}}({\mathcal {T}})\) is finite for all \(l\ge 1\).
1.2. It follows a brief discussion on the computations of \(\left\| {\mathcal {T}}\right\| _\varepsilon \). In Sect. 7 we denote \({\mathcal {T}}_l = D^b(K(l))\) and compute \(\left\| {{\mathcal {T}}}_l\right\| _\varepsilon \). To that end we start in Sect. 7.1 by recalling the construction and some properties of the helix of exceptional objects \(\{s_i\}_{i\in {\mathbb {Z}}}\) in \({\mathcal {T}}_l\) (infinite in both directions sequence of exceptional objects and any two consecutive form a full exceptional pair). In Sect. 7.2 we determine explicitly the set of phases \(P_\sigma ^l\) for each \(\sigma \in \mathrm {Stab}({\mathcal {T}}_l)\) and each \(l\ge 2\) (Proposition 7.4). It turns out that for \(l\ge 3\) a stability condition has \(\mathrm {vol}\left( \overline{P_\sigma ^l}\right) \ne 0\) and satisfies \(\sigma \in \mathrm {Stab}_{\varepsilon }({\mathcal {T}}_l)\) iff there exists \(j\in {\mathbb {Z}}\) such that \(s_j, s_{j+1} \in \sigma ^{ss}\) and \(\varepsilon< \phi _\sigma ( s_{j+1})- \phi _\sigma (s_{j})<1\), the set \(P_\sigma ^l\) for such a \(\sigma \) is the set of fractions \(\{n/m: (n,m) \in \Delta _+(K(l))\}\) appropriately embedded in the circle via a function depending on the stability condition. In Lemma 7.3 we shed light on the structure of the set \(\{n/m: (n,m) \in \Delta _+(K(l))\}\) (see formulas 80, 81) and use it in the proof of Proposition 7.4.
We start Sect. 7.3 by deriving a formula expressing the non-vanishing numbers \(\mathrm {vol}\left( \overline{P_\sigma ^l} \right) /2\) as a smooth function depending on \(\frac{\left| Z(s_{j+1})\right| }{ \left| Z(s_j)\right| }\) and \(\phi _{\sigma }(s_{j+1})-\phi _\sigma (s_j)\) for any \(j\in {\mathbb {Z}}\) (see Proposition 7.6). After computing partial derivatives of this function we find that the supremum of \(\mathrm {vol}\left( \overline{P_\sigma ^l} \right) /2\) as \(\sigma \) varies in \(\mathrm {Stab}_\varepsilon ({\mathcal {T}}_l)\) is equal to \(\mathrm {vol}\left( \overline{P_\sigma ^l} \right) /2\) where \(\sigma \) has \(s_j, s_{j+1} \in \sigma ^{ss}\), \(\frac{\left| Z(s_{j+1})\right| }{ \left| Z(s_j)\right| }=1\) and \(\phi _{\sigma }(s_{j+1})-\phi _\sigma (s_j)=\varepsilon \). The precise formula for \(\left\| {\mathcal {T}}_l\right\| _{\varepsilon }\) is in Proposition 7.7 and it produces (11), (12). In particular it follows that
Section 8 contains examples of \({\mathcal {T}}\) with \(\left\| {\mathcal {T}}\right\| _{\varepsilon }=\pi (1-\varepsilon )\) (Proposition 8.5). This section is based on (13) and the observation (Proposition 8.1) that for any exceptional pair \((E_1,E_2)\) in a proper \({\mathcal {T}}\) holds \( \left\| \left\langle E_1,E_2\right\rangle \right\| _{\varepsilon }\ge \left\| {\mathcal {T}}_l\right\| _{\varepsilon }\) where \(l=\hom ^{min}(E_1,E_2)\). It follows that the condition \(\left\| {\mathcal {T}}\right\| _{\varepsilon }< \pi (1-\varepsilon )\) imposes restrictions on \(\hom ^{min}(E_i,E_j)\) in a full exceptional collection \((E_0,\dots ,E_n)\) (see Corollary 8.4).
Section 9 is devoted to the proof that \( \left\| D^b(K(l_1))\oplus \dots \oplus D^b(K(l_N))\right\| _\varepsilon <\pi (1-\varepsilon )\) for any \(N\in {\mathbb {Z}}_{\ge 1}\) and any \(0<\varepsilon <1\). Using the results for the sets \(P_\sigma ^{l}\) from Sects. 7.2, 7.3 we show here that, whenever \(P_\sigma ^l\) is contained in \(C \cup - C\) for an open arc \(C{\subset }{\mathbb {S}}^1\) with length less than \(\pi \), then for some closed arc \(p_\sigma ^l{\subset } C \cap \overline{P_\sigma ^l}\) the set \(\overline{P_\sigma ^l}{\setminus } (p_\sigma ^l\cup -p_\sigma ^l)\) is at most countable, and furthermore, provided that the length of C is fixed, we show that when some of the end points of \(p_\sigma ^l\) is very close to some of the end points of C, then \(p_\sigma ^l\) itself has very small length (Corollary 9.3). Due to the fact, proven in Sect. 5, that for any orthogonal decomposition \({\mathcal {T}}={\mathcal {T}}_1\oplus \dots \oplus {\mathcal {T}}_n \) and any \(\sigma \in \mathrm {Stab}({\mathcal {T}})\) holds \(P_\sigma ^{{\mathcal {T}}}=\bigcup _{i=1}^n P_{\sigma _i}^{{\mathcal {T}}_i}\), where \((\sigma _1, \dots , \sigma _n)\) is the value of the map (2) at \(\sigma \) (see Proposition 5.2 and Corollary 5.5), the proof of the desired inequality reduces to proving that the measure of union of arcs \(\cup _{i=1}^n p_\sigma ^{l_i}{\subset } C\) of the type explained above, cannot become arbitrary close to the length of C. Having proved this for one arc (in Sect. 7.3) we perform induction and the tool for the induction step is the already discussed Corollary 9.3.
In Sect. 10 we discuss the class of discrete derived categories and show that \(\left\| {\mathcal {T}}\right\| _\varepsilon =0\) for any such category. These categories were introduced by Vossieck [42], they were classified in [4] and thoroughly studied in [14], whereas the topology of the stability spaces on them were studied in [13, 37], in particular it was shown that these spaces are all contractible. This class contains the categories \(\{D^b(Q): Q \ \hbox {is Dynkin}\}\), and the discrete derived categories not contained in this list are of the form \(D^b(\Lambda (r,n,m))\) for \(n\ge r \ge 1\) and \(m\ge 0\), where \(\Lambda (r,n,m)\) is the path algebra of the quiver with relations shown on [37, Section 4.3, Figure 1]. Actually, we show that if \({\mathcal {T}}\) is a category with phase gap, s.t. every heart of a bounded t-structure has finitely many indecomposable objects up to isomorphism, then \(\left\| {\mathcal {T}}\right\| _\varepsilon = 0\).
1.3. Using the helix \(\{s_j\}_{j\in {\mathbb {Z}}}\) in \(D^b(K(l+1))\cong N{\mathbb {P}}^l\) we can explain what we mean by a \(\sigma \)-semistable non-commutative curve (see Definition 12.12 for precise statement). Let \(\mathrm {Stab}({\mathcal {T}})\ne \emptyset \) and \(\sigma \in \mathrm {Stab}({\mathcal {T}})\). Recall that a non-commutative curve of genus l in \({\mathcal {T}}\) is equivalence class of fully faithful exact \({\mathbb {K}}\)-linear functors from \(N{\mathbb {P}}^l\) to \({\mathcal {T}}\) (equivalence is re-parametrization in the domain), we will say that the curve is \(\sigma \)-semistable, resp. \(\sigma \)-stable, if for infinitely many, resp. for all, \(j\in {\mathbb {Z}}\) the object \(F(s_j)\in {\mathcal {T}}\) is \(\sigma \)-semistable object (it does not matter which functor F we take as a representative). We denote the set of \(\sigma \)-semistable, resp. \(\sigma \)-stable, non-commutative curves of genus l, and modulo subgroup \(\Gamma {\subset } {\mathrm{Aut}}(N{\mathbb {P}}^l)\), by \(C_{l,\sigma }^{\Gamma }({\mathcal {T}})\), resp. \(C_{l,\sigma \sigma }^{\Gamma }({\mathcal {T}})\). Our basic example is \(C_{l,\sigma \sigma }^{\{{\text {Id}}\}}(N{\mathbb {P}}^l)\), \(l\ge 1\). First note that from Remark 12.3 it follows that \(C_j^{\{{\text {Id}}\}}(N{\mathbb {P}}^j)=\delta _{i,j}\) for \(i,j\ge 0\). In Propositions 12.13, 7.2 is shown that for any \(l\ge 1\) and any \(\sigma \in \mathrm {Stab}(N{\mathbb {P}}^l)\) we have one of the following possibilities
-
only two consecutive elements in the helix, of the form \(s_j, s_{j+1}\), are semi-stable and \(\phi _\sigma (s_{j+1})>\phi _\sigma (s_j)+1\), in particular \(C_{l,\sigma }^{\{{\text {Id}}\}}(N{\mathbb {P}}^l)=0\)
-
all elements \(\{s_j\}_{j\in {\mathbb {Z}}}\) are semistable and \(\phi _\sigma (s_{j+1})=\phi _\sigma (s_j)+1\) for some \(j\in {\mathbb {Z}}\), hence \(C_{l,\sigma \sigma }^{\{{\text {Id}}\}}(N{\mathbb {P}}^l)=1\)
-
all elements \(\{s_j\}_{j\in {\mathbb {Z}}}\) are semistable and \(\phi _\sigma (s_j)<\phi _\sigma (s_{j+1})<\phi _\sigma (s_j)+1\) for all \(j\in {\mathbb {Z}}\), hence \(C_{l,\sigma }^{\{{\text {Id}}\}}(N{\mathbb {P}}^l)=1\)
2 Notations
In this paper the letters \({{\mathcal {T}}}\) and \({\mathcal {A}}\) denote a triangulated category and an abelian category, respectively, and \({\mathbb {K}}\) denotes an algebraically closed field. The shift functor in \({{\mathcal {T}}}\) is designated by [1]. We write \(\mathrm {Hom}^i(X,Y)\) for \(\mathrm {Hom}(X,Y[i])\) and, if \({\mathcal {T}}\) is \({\mathbb {K}}\)-linear, we write \(\hom ^i(X,Y)\) for \(\dim _{{\mathbb {K}}}(\mathrm {Hom}(X,Y[i]))\), where \(X,Y\in {\mathcal {T}}\). For \(X,Y\in {\mathcal {A}}\), writing \(\mathrm {Hom}^i(X,Y)\), we consider X, Y as elements in \({\mathcal {T}}=D^b({\mathcal {A}})\), i.e. \(\mathrm {Hom}^i(X,Y)={{\mathrm{Ext}}}^i(X,Y)\).
A \({\mathbb {K}}\)-linear triangulated category \({\mathcal {T}}\) is called proper if \(\sum _{i\in {\mathbb {Z}}} \hom ^i(X,Y)<+\infty \) for any two objects X, Y in \({\mathcal {T}}\). For \(X,Y\in {\mathcal {T}}\) in a proper \({\mathcal {T}}\), we denote:
We write \(\langle S \rangle {\subset } {\mathcal {T}}\) for the triangulated subcategory of \({\mathcal {T}}\) generated by S, when \(S {\subset } Ob({\mathcal {T}})\).
An exceptional object in a \({\mathbb {K}}\)-linear \({\mathcal {T}}\) is an object \(E\in {\mathcal {T}}\) satisfying \(\mathrm {Hom}^i(E,E)=0\) for \(i\ne 0\) and \(\mathrm {Hom}(E,E)=k \).
An exceptional collection is a sequence \({\mathcal {E}} = (E_0,E_1,\dots ,E_n){\subset } {\mathcal {T}}_{exc}\) satisfying \(\hom ^*(E_i,E_j)=0\) for \(i>j\). If in addition we have \(\langle {\mathcal {E}} \rangle = {\mathcal {T}}\), then \({\mathcal {E}}\) will be called a full exceptional collection.
If an exceptional collection \({\mathcal {E}} = (E_0,E_1,\dots ,E_n){\subset } {\mathcal {T}}_{exc}\) satisfies \(\hom ^k(E_i,E_j)=0\) for any i, j and for \(k\ne 0\), then it is said to be strong exceptional collection.
An abelian category \({\mathcal {A}}\) is said to be hereditary, if \({\mathrm{Ext}}^i(X,Y)=0\) for any \(X,Y \in {\mathcal {A}}\) and \(i\ge 2\), it is said to be of finite length, if it is Artinian and Noterian.
By Q we denote an acyclic quiver and by \(D^b(Rep_{{\mathbb {K}}}(Q))\), or just \(D^b(Q)\), - the derived category of the category of representations of Q.
For an integer \(l\ge 1\) the l-Kronecker quiver (the quiver with two vertices and l parallel arrows) will be denoted by K(l).
For a complex number \(z=(a+{\mathrm {i}}b)\), \(a,b\in {\mathbb {R}}\) we denote \(\mathfrak {I}(z)=b\), \(\mathfrak {R}(z)=a\), and by \({\mathcal {H}}\) we denote the upper half plane, i.e. \({\mathcal {H}}=\{ z\in {\mathbb {C}}: \mathfrak {I}(z)>0 \}\), whereas \({\mathbb {H}}={\mathcal {H}} \cup \{ z\in {\mathbb {C}}: \mathfrak {I}(z)=0, \mathfrak {R}(z)<0 \}\). The number of elements of a finite set X we denote by |X| or by \(\#(X)\).
3 On Bridgeland stability conditions
We use freely the axioms and notations on stability conditions introduced by Bridgeland in [10] and some additional notations used in [22, Subsection 3.2]. In particular, the underlying set of the manifold \(\mathrm {Stab}({\mathcal {T}})\) is the set of locally finite stability conditions on \({\mathcal {T}}\) and for \(\sigma = (Z, {{\mathcal {P}}}) \in \mathrm {Stab}({\mathcal {T}})\) we denote by \(\sigma ^{ss}\) the set of \(\sigma \)-semistable objects, i.e.
Also for a heart \({\mathcal {A}}\) of bounded t-structure in \({\mathcal {T}}\) we denote by \({\mathbb {H}}^{{\mathcal {A}}}{\subset } \mathrm {Stab}({\mathcal {T}})\) the subset of the stability conditions \((Z, {\mathcal {P}})\in \mathrm {Stab}({\mathcal {T}})\) for which \({\mathcal {P}}(0,1]={\mathcal {A}}\) (see [21, Definition 2.28]).
Recall that one of Bridgeland’s axioms [10] is: for any nonzero \(X \in Ob({{\mathcal {T}}})\) there exists a diagram of distinguished triangles called Harder–Narasimhan filtration:

where \(\{ A_i \in {{\mathcal {P}}}(t_i) \}_{i=1}^n \), \(t_1> t_2> \dots > t_n \) and \(A_i\) is non-zero object for any \(i=1,\dots ,n\) (the non-vanishing condition makes the factors \(\{ A_i \in {{\mathcal {P}}}(t_i) \}_{i=1}^n\) unique up to isomorphism). Following [10] we denote \(\phi _\sigma ^-(X):=t_n\), \(\phi _\sigma ^+(X):=t_1\), and the phase of a semistable object \(A \in {{\mathcal {P}}}(t){\setminus } \{0\}\) is denoted by \(\phi _{\sigma }(A):=t\). The positive integer: \( m_{\sigma }(X)=\sum _{i=1}^n \left| Z(A_i)\right| \) is called the mass of X w.r. to \(\sigma \)([10, p.332]). We will use also the following axioms [10]:
Finally we note that:
which follows easily from the arguments for the proof of [21, Lemma 2.25].
3.1 Actions on \(\mathrm {Stab}({\mathcal {T}})\)
3.1.1 The universal covering group of \(GL^+(2,{\mathbb {R}})\).
The universal covering group \(\widetilde{GL}^+(2,{\mathbb {R}})\) of \(GL^+(2,{\mathbb {R}})\) can be constructed as follows (we point the steps without proving them). First step is to show that the following set with the specified bellow operations and metric is a topological group:
Second step is to show that the following is a covering map:

The subset \(U_\varepsilon =\{G\in GL^+(2,{\mathbb {R}}) ; \sup _{t\in {\mathbb {R}}}\{\left| G(\exp ({\mathrm {i}}\pi t))-\exp ({\mathrm {i}}\pi t)\right| \}<\sin (\pi \varepsilon ) \}\)Footnote 5 is evenly covered by a family of open subsets \(\{(G,\psi ); G \in U_\varepsilon \ \ \sup _{t\in {\mathbb {R}}} \left| \psi (t)-t-2 k\right| <\varepsilon \}\) indexed by \(k\in {\mathbb {Z}}\) for small enough \(\varepsilon \). In particular one obtains a structure or a Lie Group on \(\widetilde{GL}^+(2,{\mathbb {R}})\) such that \(\pi \) is a morphism of Lie groups.
Finally, one can show that \( \widetilde{GL}^+(2,{\mathbb {R}}) \) is simply connected by recalling that \(\pi _1(GL^+(2,{\mathbb {R}}))\cong {\mathbb {Z}}\) is generated by \({\mathbb {S}}^1= SO(2){\subset } GL^+(2,{\mathbb {R}}) \) and then by finding the lifts of this path in \(\widetilde{GL}^+(2,{\mathbb {R}})\).
Remark 3.1
For any \(0<\varepsilon <1\), \(0<\varepsilon ' <1\) there exists unique \(g_{\varepsilon ,\varepsilon '}=(G,\psi )\in \widetilde{\mathrm{GL}}^+(2,{\mathbb {R}})\) such that \(G^{-1}(1)=1\) and \(G^{-1}(\exp ({\mathrm {i}}\pi \varepsilon ))=\exp ({\mathrm {i}}\pi \varepsilon ')\) and \(\psi (0)=0 , \psi (1)=1, \psi (\varepsilon ')=\varepsilon \), in particular :
Furthermore, \((g_{\varepsilon , \varepsilon '})^{-1}=g_{\varepsilon ', \varepsilon }\).
The right action of \(\widetilde{GL}^+(2,{\mathbb {R}})\) on \(\mathrm {Stab}({\mathcal {T}})\) is defined by (recall [10]):
Using the formula (24) determining the topology on \(\widetilde{GL}^+(2,{\mathbb {R}})\) and the basis of the topology in \(\mathrm {Stab}({\mathcal {T}})\) explained on [10, p. 335] one can show that the function in (27) is continuous.
We recall also (see [10, Theorem 1.2]) that the projection  , \(proj(Z, {\mathcal {P}})=Z\) restricts to a local biholomorphism between each connected component of \(\mathrm {Stab}({\mathcal {T}})\) and a corresponding vector subspace of \(\mathrm {Hom}(K_0({\mathcal {T}}),{\mathbb {C}})\) with a well defined linear topology (when \(\mathrm rank(K_0({\mathcal {T}}))<+\infty \) this is the ordinary linear topology). Note also that the results in [10] imply that \(\mathrm {Stab}({\mathcal {T}})\) is locally path connected (follows from the results in [10, Section 6] and [10, Theorem 7.1]), therefore the components and the path components of \(\mathrm {Stab}({\mathcal {T}})\) coincide and they are open subsets in \(\mathrm {Stab}({\mathcal {T}})\).
, \(proj(Z, {\mathcal {P}})=Z\) restricts to a local biholomorphism between each connected component of \(\mathrm {Stab}({\mathcal {T}})\) and a corresponding vector subspace of \(\mathrm {Hom}(K_0({\mathcal {T}}),{\mathbb {C}})\) with a well defined linear topology (when \(\mathrm rank(K_0({\mathcal {T}}))<+\infty \) this is the ordinary linear topology). Note also that the results in [10] imply that \(\mathrm {Stab}({\mathcal {T}})\) is locally path connected (follows from the results in [10, Section 6] and [10, Theorem 7.1]), therefore the components and the path components of \(\mathrm {Stab}({\mathcal {T}})\) coincide and they are open subsets in \(\mathrm {Stab}({\mathcal {T}})\).
Finally, assume for simplicity that \({\mathrm{rank}}(K_0({\mathcal {T}}))<+\infty \). Due to continuity of (27) it follows that for each connected component \(\Sigma \) of \(\mathrm {Stab}({\mathcal {T}})\) the action (27) restricts to a continuous action \(\Sigma \times \widetilde{GL}^+(2,{\mathbb {R}}) \rightarrow \Sigma \) and it is easy to show that there is a commutative diagram:

where \(V(\Sigma ){\subset } \mathrm {Hom}(K_0({\mathcal {T}}),{\mathbb {C}})\) is the corresponding to \(\Sigma \) vector subspace, such that the vertical arrows are local diffeomorphisms (the right arrow is local biholomorphism), and the lower horizontal arrow is an action of the form \((A,G) \mapsto A\circ G^{-1}\) on \(V(\Sigma )\). Now it follows that the upper horizontal arrow is smooth, and therefore (27) is smooth as well.
3.1.2 The action of \(\pmb {{\mathbb {C}}}\)
There is a Lie group homomorphism \({\mathbb {C}}\rightarrow \widetilde{GL}^+(2,{\mathbb {R}})\) given by \(\lambda \mapsto \left( {\mathrm{e}}^{-\lambda }, {\text {Id}}_{\mathbb {R}} - \frac{\mathfrak {I}(\lambda )}{\pi }\right) \). And composing the action (27) with this homomorphism results in the action (29) below. This action is free [34, Definition 2.3, Proposition 4.1]. It is easy to show that for any \(X\in {\mathcal {T}}\), \(\sigma \in \mathrm {Stab}({\mathcal {T}})\), \(z\in {\mathbb {C}}\) hold the properties in (30), (31) below, and the HN filtrations of X w.r. to \(\sigma \) and to \(z\star \sigma \) are the same:

4 Triangulated categories with phase gaps and their norms
4.1 Full stability conditions
We start this section by recalling what is meant when saying that a stability condition is full.
Full stability condition on K3 surface is defined in [10, Definition 4.2]. Analogous definition can be given for any triangulated category \({\mathcal {T}}\) and locally finite stability condition whose central charge factors through a given group homomorphism \(ch: K_0({\mathcal {T}}) \rightarrow {\mathbb {Z}}^n \).
When \(K_0({\mathcal {T}})\) has finite rank, we choose always the trivial homomorphism \(K_0({\mathcal {T}})\rightarrow K_0({\mathcal {T}})\). Now the projection  , \(proj(Z, {\mathcal {P}})=Z\) restricts to a local biholomorphism between each connected component of \(\mathrm {Stab}({\mathcal {T}})\) and a corresponding vector subspace of \(\mathrm {Hom}(K_0({\mathcal {T}}),{\mathbb {C}})\) (see [10, Theorem 1.2]). A stability condition \(\sigma \in \mathrm {Stab}({\mathcal {T}})\) in this case is a full stability condition, if the vector subspace of \(\mathrm {Hom}(K_0({\mathcal {T}}),{\mathbb {C}})\) corresponding to the connected component \(\Sigma \) containing \(\sigma \) is the entire \(\mathrm {Hom}(K_0({\mathcal {T}}),{\mathbb {C}})\), which is equivalent to the equality \(\dim _{\mathbb {C}}(\Sigma ) = {\mathrm{rank}} (K_0({\mathcal {T}}))\).
, \(proj(Z, {\mathcal {P}})=Z\) restricts to a local biholomorphism between each connected component of \(\mathrm {Stab}({\mathcal {T}})\) and a corresponding vector subspace of \(\mathrm {Hom}(K_0({\mathcal {T}}),{\mathbb {C}})\) (see [10, Theorem 1.2]). A stability condition \(\sigma \in \mathrm {Stab}({\mathcal {T}})\) in this case is a full stability condition, if the vector subspace of \(\mathrm {Hom}(K_0({\mathcal {T}}),{\mathbb {C}})\) corresponding to the connected component \(\Sigma \) containing \(\sigma \) is the entire \(\mathrm {Hom}(K_0({\mathcal {T}}),{\mathbb {C}})\), which is equivalent to the equality \(\dim _{\mathbb {C}}(\Sigma ) = {\mathrm{rank}} (K_0({\mathcal {T}}))\).
As we will see later all stability conditions on K(l) are full, for all \(l\ge 1\) (see table (10)). It is reasonable to hope that, whenever \(\mathrm {Stab}({\mathcal {T}}) \ne \emptyset \), there are always full stability conditions on \({\mathcal {T}}\) and, to the best of our knowledge, there are no counterexamples of this statement so far.
4.2 The \(\varepsilon \)-norm of a triangulated category
Recall that for \(\sigma = (Z, {\mathcal {P}}) \in \mathrm {Stab}({\mathcal {T}})\) we denote (see [18, Section 3]):
Here we will use also the notation:
The sets \( P_\sigma ^{{\mathcal {T}}}\) and \(\widetilde{P}_\sigma ^{{\mathcal {T}}}\) satisfy \(P_\sigma ^{{\mathcal {T}}}=- P_\sigma ^{{\mathcal {T}}}\), \(\widetilde{P}_\sigma ^{{\mathcal {T}}}+1=\widetilde{P}_\sigma ^{{\mathcal {T}}}\). In particular the closures \(\overline{ P_\sigma ^{{\mathcal {T}}}}\), \(\overline{\widetilde{P}_\sigma ^{{\mathcal {T}}}}\) satisfy:
where \(\mu \) is the Lebesgue measure in \({\mathbb {R}}\) and \(\mathrm {vol}\) is the corresponding measure in \({\mathbb {S}}^1\) with \(\mathrm {vol}({\mathbb {S}}^1)=2 \pi \). Due to (27), (30), for any \(z\in {\mathbb {C}}\), any \(g=(G,\psi )\in \widetilde{GL}^+(2,{\mathbb {R}})\), and any \(\sigma \in \mathrm {Stab}({\mathcal {T}})\) we have:
Definition 4.1
Let \(0<\varepsilon <1\). Any subset of \({\mathbb {S}}^1\) of the form \(\exp ({\mathrm {i}}\pi [a,a+\varepsilon ])\), where \(a\in {\mathbb {R}}\) will be referred to as a closed\(\varepsilon \) -arc in \(\mathbb S^1\).
Remark 4.2
The action of \({\mathrm{Aut}}({\mathcal {T}})\) on \(\mathrm {Stab}({\mathcal {T}})\) was recalled in the end of the previous section. Following this definition one defines straightforwardly a biholomorphism \([F]:\mathrm {Stab}({\mathcal {T}}_1)\rightarrow \mathrm {Stab}({\mathcal {T}}_2)\) for any equivalence F between triangulated categories \({\mathcal {T}}_1\) and \({\mathcal {T}}_2\) satisfying \(P_{[F](\sigma )}^{{\mathcal {T}}_2}=P_{\sigma }^{{\mathcal {T}}_1}\) for each \(\sigma \in \mathrm {Stab}({\mathcal {T}}_1)\).
In Definition 4.11 we will use the following subset of the set of stability conditions:
Definition 4.3
For any \(0<\varepsilon <1\) and any triangulated category \({\mathcal {T}}\) we denote:
It is obvious that (recall also 35):
The next simple observation is:
Lemma 4.4
Let \(g_{\varepsilon , \varepsilon '}\in \widetilde{GL}^{+}(2,{\mathbb {R}})\) be as in Remark 3.1. For any \(0<\varepsilon <1\), \(0<\varepsilon ' <1\) holds:
Proof
Using (35), (26), and the fact that \(\psi \) is diffeomorphism we compute
Now the lemma follows from the very Definition 4.3 and the property \(g_{\varepsilon ,\varepsilon '}^{-1}=g_{\varepsilon ',\varepsilon }\). \(\square \)
Corollary 4.5
Let \({\mathcal {T}}\) be any triangulated category. The following are equivalent:
-
(a)
\(\mathrm {Stab}_{\varepsilon }({\mathcal {T}}) \ne \emptyset \) for some \(\varepsilon \in (0,1)\)
-
(b)
\(\mathrm {Stab}_{\varepsilon }({\mathcal {T}}) \ne \emptyset \) for each \(\varepsilon \in (0,1)\)
-
(c)
\(P^{{\mathcal {T}}}_{\sigma } \) is not dense in \({\mathbb {S}}^1\) for some full \(\sigma \in \mathrm {Stab}({\mathcal {T}})\).
Proof
- (a) \(\Rightarrow \) (b).:
- (b) \(\Rightarrow \) (c).:
-
It is obvious from the definitions that for any \(0<\varepsilon <1\) and any \(\sigma \in \mathrm {Stab}_{\varepsilon }({\mathcal {T}}) \) the set \(P_\sigma ^{{\mathcal {T}}}\) is not dense in \({\mathbb {S}}^1\).
- (c) \(\Rightarrow \) (a).:
-
If \(P_{\sigma }^{{\mathcal {T}}}\) is not dense, then \({{\mathbb {S}}}^1{\setminus } P_{\sigma }^{{\mathcal {T}}}\) contains an open arc, but then it contains a closed arc as well and then \(\sigma \in \mathrm {Stab}_{\varepsilon }({\mathcal {T}}) \) for some \(\varepsilon \in (0,1)\).
\(\square \)
Definition 4.6
A triangulated category \({\mathcal {T}}\) will be called a category with phase gap if \(P^{{\mathcal {T}}}_{\sigma } \) is not dense in \({\mathbb {S}}^1\) for some full \(\sigma \in \mathrm {Stab}({\mathcal {T}})\) (by Corollary 4.5 then \(\mathrm {Stab}_{\varepsilon }({\mathcal {T}})\) is not empty for any \(0<\varepsilon <1\)).
Lemma 4.7
If \(K_0({\mathcal {T}})\) has finite rank, then \({\mathcal {T}}\) has a phase gap iff there exists a bounded t-structure in \({\mathcal {T}}\) whose heart is of finite length and has finitely many simple objects.
Proof
Let \({\mathcal {A}}\) be such a heart and let \(s_1, s_2, \dots , s_n\) be the simple objects in \({\mathcal {A}}\). Under the given assumptions \(K_0({\mathcal {T}})\cong K_0({\mathcal {A}})\cong {\mathbb {Z}}^n\). [10, Proposition 2.4, Proposition 5.3] imply that for any sequence of vectors \(z_1, z_2, \dots , z_n\) in \({\mathbb {H}}\) there exists unique stability condition \(\sigma = (Z, {\mathcal {P}}) \) with \({\mathcal {P}}(0,1]={\mathcal {A}}\) and \(Z(s_i)=z_i\), \(i=1,\dots , n\). For this \(\sigma \) we have \(Z({\mathcal {P}}(0,1]{\setminus }\{0\})=\left\{ \sum _{i=1}^n a_i z_i: (a_1,a_2,\dots , a_n)\in {\mathbb {N}}^n{\setminus }\{0\}\right\} \) and therefore \(Z(\sigma ^{ss}){\subset } \pm \left\{ \sum _{i=1}^n a_i z_i: (a_1,a_2,\dots , a_n)\in {\mathbb {N}}^n{\setminus }\{0\}\right\} \), now from [16, Lemma 1.1] it follows that \(\sigma \) is locally finite. Recall that we denote by \({\mathbb {H}}^{{\mathcal {A}}}{\subset } \mathrm {Stab}({\mathcal {T}})\) the subset of the stability conditions \((Z, {\mathcal {P}})\in \mathrm {Stab}({\mathcal {T}})\) for which \({\mathcal {P}}(0,1]={\mathcal {A}}\) (see after 15). So far we constructed \(\sigma \in {\mathbb {H}}^{{\mathcal {A}}}\) determined uniquely by any sequence \(z_1, z_2, \dots , z_n\) in \({\mathbb {H}}\). Varying the vector \((z_1,z_2,\dots ,z_n)\in {\mathbb {H}}^n\) we obtain a biholomorphism between \({\mathbb {H}}^n\) and the subset \({\mathbb {H}}^{{\mathcal {A}}}{\subset }\mathrm {Stab}({\mathcal {T}})\). In particular the stability conditions in \({\mathbb {H}}^{{\mathcal {A}}}\) are full. Since for \(\sigma \in {\mathbb {H}}^{{\mathcal {A}}}\) corresponding to a sequence \(z_1, z_2, \dots , z_n\) in \({\mathbb {H}}\) holds \(Z(\sigma ^{ss}){\subset } \pm \left\{ \sum _{i=1}^n a_i z_i: (a_1,a_2,\dots , a_n)\in {\mathbb {N}}^n{\setminus }\{0\}\right\} \), it follows that \(Z(\sigma ^{ss}){\subset } \pm \{x \exp ({\mathrm {i}}\pi a)+y \exp ({\mathrm {i}}\pi (a+1-\varepsilon ): x,y\in (0,+\infty ) \}\) for some \(a\in {\mathbb {R}}\) and some \(0<\varepsilon <1\), therefore by (17) \({{\mathbb {S}}}^1{\setminus } P_\sigma ^{{\mathcal {T}}}\) contains a closed \(\varepsilon \) arc, hence \(\sigma \in \mathrm {Stab}_\varepsilon ({\mathcal {T}})\), and hence \({\mathcal {T}}\) has a phase gap (recall Definitions 4.3, 4.6).
Conversely, let \(\sigma '=(Z, {\mathcal {P}})\in \mathrm {Stab}_\varepsilon ({\mathcal {T}})\). By definition \(\sigma '\) is a full stability condition. Due to (36), we can choose \(\lambda \in {\mathbb {C}}\), so that the stability condition \(\sigma = \lambda \star \sigma '\) satisfies \({\mathcal {P}}_{\sigma }(t)=\{0\}\) for \(t\in [0,\varepsilon ]\) and \({\mathcal {P}}_{\sigma }(0,1]= {\mathcal {P}}_{\sigma }(\varepsilon /2,1]\). From [11, Lemma 4.5] it follows that \({\mathcal {P}}_{\sigma }(0,1]= {\mathcal {P}}_{\sigma }(\varepsilon /2,1]\) is a finite length quasi-abelian category (here the property of \(\sigma \) being full is used), and since \(\sigma \) is a stability condition, \({\mathcal {P}}_{\sigma }(0,1]\) is a heart of a bounded t-structure. Therefore \({\mathcal {P}}_{\sigma }(0,1]\) is a finite length abelian category whose simple objects are a basis of \(K_0({\mathcal {T}})\), in particular the simple objects are finitely many. \(\square \)
Remark 4.8
The elements \(\sigma \in \mathrm {Stab}({\mathcal {T}})\) for which \({\mathcal {P}}(0,1]\) is of finite length and with finitely many simple objects are called algebraic stability conditions and have been discussed extensively in [37].
Remark 4.9
In [12] they define a quiver with potential starting with a triangulation of a compact closed surface with marked points. The full subcategory of the derived category of the complete Ginzburg algebra of this quiver consisting of modules with finite-dimensional cohomology is a CY3 category. Due to (i), (ii) in [12, Subsection 7.1] and Lemma 4.7 CY3 categories obtained by this procedure have phase gaps.
Remark 4.10
Let \({\mathcal {T}}\) be proper and with a full exceptional collection. [22, Remark 3.20] and Corollary 4.5 imply that \(\mathrm {Stab}_\varepsilon ({\mathcal {T}}) \ne \emptyset \) for any \(0<\varepsilon <1\), i.e. \({\mathcal {T}}\) is a category with a phase gap.
The main definition of this section is:
Definition 4.11
Let \({\mathcal {T}}\) be a triangulated category with phase gap. Let \(0<\varepsilon <1\). We define:
Remark 4.12
For a category \({\mathcal {T}}\) which carries a full stability condition, but has no phase gap (i.e. \(P_{\sigma }^{{\mathcal {T}}}\) is dense in \(\mathbb S^1\) for all full stability conditions \(\sigma \)) it seems reasonable to define \(\left\| {\mathcal {T}}\right\| _{\varepsilon }= \pi (1-\varepsilon )\), but we will restrict our attention to categories with phase gaps in the rest.
In remarks 4.13, 4.14 \(\varepsilon \) and \({\mathcal {T}}\) are as in Definition 4.11.
Remark 4.13
Using (34), (35), (36) one shows that (\(\mu \) is the Lebesgue measure of \({\mathbb {R}}\)):
Remark 4.14
We have always \( 0\le \left\| {\mathcal {T}}\right\| _{\varepsilon }\le \pi (1-\varepsilon ) \).
Remark 4.15
Using Remark 4.2 we see that if \({\mathcal {T}}_1\), \({\mathcal {T}}_2\) are equivalent triangulated categories with finite rank Grothendieck groups, then for any \(0<\varepsilon <1\) holds \(\left\| {{\mathcal {T}}}_{1}\right\| _\varepsilon =\left\| {{\mathcal {T}}}_{2}\right\| _\varepsilon \).
Lemma 4.16
Let \(\varepsilon \), \(\varepsilon '\) be any two numbers in (0, 1).
-
(a)
There exist \(0<m<M\) such that \(m \left\| {\mathcal {T}}\right\| _{\varepsilon }\le \left\| {\mathcal {T}}\right\| _{\varepsilon '}\le M \left\| {\mathcal {T}}\right\| _{\varepsilon }\) for any category with a phase gap \({\mathcal {T}}\). In particular, for any category with a phase gap \({\mathcal {T}}\) we have: \(\left\| {\mathcal {T}}\right\| _{\varepsilon }=0 \iff \left\| {\mathcal {T}}\right\| _{\varepsilon '}=0\).
-
(b)
For any category with a phase gap \({\mathcal {T}}\) we have \(\left\| {\mathcal {T}}\right\| _{\varepsilon }=\pi (1-\varepsilon )\iff \left\| {\mathcal {T}}\right\| _{\varepsilon '}=\pi (1-\varepsilon ')\).
Proof
We will use the element \(g_{\varepsilon ,\varepsilon '}=(G,\psi )\in \widetilde{GL}^+(2,{\mathbb {R}})\) from Remark 3.1. In particular the function \(\psi \in C^{\infty }({\mathbb {R}})\) restricts to a diffeomorphsim \(\psi _{\vert }:[\varepsilon ',1]\rightarrow [\varepsilon ,1]\). Let us denote the inverse function by \(\kappa \), then we choose \(m, M\in {\mathbb {R}}\) as follows:
With the help of [39, formula (15) on page 156], we see that for any Lebesgue measurable subset \(A{\subset } [\varepsilon ,1]\) holds (for a subset \(E{\subset } [\varepsilon ',1]\) or \(E{\subset } [\varepsilon ,1]\) we denote by \(\chi _E\) the function equal to 1 at the points of E and 0 elsewhere):
which by (40) implies:
Using Remark 4.13, Lemma 4.4, and the second equality in (35) we get:
Now (a) follows from (41), (42), (43).
(b) Let \(\left\| {\mathcal {T}}\right\| _{\varepsilon }=\pi (1-\varepsilon )\) and \(\delta >0\). We will prove that (43) equals \((1-\varepsilon ')\) by finding \(\sigma \in \mathrm {Stab}_{[0,\varepsilon ]}({\mathcal {T}})\) such that \(\mu \left( \kappa \left( [\varepsilon ,1]\cap \overline{\widetilde{P}_{\sigma }} \right) \right) >1-\varepsilon '-\delta \). Since \( 1-\varepsilon ' = \mu ([\varepsilon ',1]) = \mu \left( \kappa \left( [\varepsilon ,1]\cap \overline{\widetilde{P}_{\sigma }} \right) \right) + \mu \left( \kappa \left( [\varepsilon ,1]{\setminus } \overline{\widetilde{P}_{\sigma }} \right) \right) \), we need to find \(\sigma \in \mathrm {Stab}_{[0,\varepsilon ]}({\mathcal {T}})\) such that:
Since \(\left\| {\mathcal {T}}\right\| _{\varepsilon }=\pi (1-\varepsilon )\), (42) ensures that there is \(\sigma \in \mathrm {Stab}_{[0,\varepsilon ]}({\mathcal {T}})\) such that \(\mu \left( [\varepsilon ,1]\cap \overline{\widetilde{P}_\sigma }\right) > 1-\varepsilon - \frac{\delta }{M}\), which due to the equality \(\mu \left( [\varepsilon ,1]\cap \overline{\widetilde{P}_\sigma }\right) +\mu \left( [\varepsilon ,1]{\setminus } \overline{\widetilde{P}_\sigma }\right) = 1-\varepsilon \) is the same as \( \mu \left( [\varepsilon ,1]{\setminus } \overline{\widetilde{P}_\sigma }\right) < \frac{\delta }{M} . \) We combine (41) and the latter inequality to deduce the desired (44): \(\mu \left( \kappa \left( [\varepsilon ,1]{\setminus } \overline{\widetilde{P}_{\sigma }} \right) \right) \le M \mu \left( [\varepsilon ,1]{\setminus } \overline{\widetilde{P}_\sigma }\right) <\delta .\) \(\square \)
[18, Corollary 3.28] (see [21, Corollary 3.25] for any algebraically closed field \({\mathbb {K}}\)) amounts to the following criteria for non-vanishing of \(\left\| {\mathcal {T}}\right\| _{\varepsilon }\)
Proposition 4.17
Let \((E_0,E_1,\dots ,E_n)\) be a full exceptional collection in a \({\mathbb {K}}\)-linear proper triangulated category \({\mathcal {D}}\). If for some i the pair \((E_i,E_{i+1})\) satisfies \(\hom ^1(E_i,E_{i+1})\ge 3\) and \(\hom ^{\le 0}(E_i,E_{i+1})=0\), then \(\left\| {\mathcal {D}}\right\| _{\varepsilon } >0\).
Corollary 4.18
Let \(\varepsilon \in (0,1)\). Then:
-
(a)
If Q is an acyclic quiver, which is neither Dynkin nor affine, then \(\left\| D^b(Q)\right\| _{\varepsilon }>0\).
-
(b)
\(\left\| D^b(coh(X))\right\| _{\varepsilon }>0\), where X is a smooth projective variety over \({\mathbb {C}}\), such that \(D^b(coh(X))\) is generated by a strong exceptional collection of three elements
Proof
-
(a)
Follows from the previous proposition, [18, Proposition 3.34], and the fact that each exceptional collection in \(D^b(Q)\) can be extended to a full exceptional collection (see [17]).
- (b)
\(\square \)
In Sect. 8 we will refine Proposition 4.17, which will help us to prove that \(\left\| D^b(coh(X)\right\| _{\varepsilon }=\pi (1-\varepsilon )\) if X is \({\mathbb {P}}^1 \times {\mathbb {P}}^1\), \({\mathbb {P}}^n\) with \(n\ge 2\) or some of these blown up in finite number of points.
Proposition 4.19
Let \(\varepsilon \in (0,1)\). For acyclic quiver Q we have \(\left\| D^b(Q)\right\| _{\varepsilon } = 0\) iff Q is affine or Dynkin. In particular \(\left\| D^b(coh({\mathbb {P}}^1))\right\| _{\varepsilon }=0\).
Proof
If Q is affine or Dynkin, then from the first and the second raws of table (9) we see that \(\mathrm {vol}\left( \overline{P_\sigma }\right) =0\) for any \(\sigma \in \mathrm {Stab}(D^b(Q))\), therefore \(\left\| D^b(Q)\right\| _{\varepsilon } = 0\), and in Corollary 4.18 we showed that \(\left\| D^b(Q)\right\| _{\varepsilon } > 0\) for the rest quivers. \(\square \)
5 Stability conditions on orthogonal decompositions
First we recall the definition of a semi-orthogonal, resp. orthogonal, decomposition of a triangulated category:
Definition 5.1
If \({\mathcal {T}}\) is a triangulated category, \({\mathcal {T}}_1\), \({\mathcal {T}}_2\), \(\dots \), \({\mathcal {T}}_n\) are triangulated subcategories in it satisfying the equalities \({\mathcal {T}} = \langle {\mathcal {T}}_1, {\mathcal {T}}_2,\dots {\mathcal {T}}_n \rangle \) and \(\mathrm {Hom}({\mathcal {T}}_j, {\mathcal {T}}_i)=0\) for \(j>i\), then we say that \({\mathcal {T}} = \langle {\mathcal {T}}_1, {\mathcal {T}}_2,\dots {\mathcal {T}}_n \rangle \) is a semi-orthogonal decomposition. If in addition holds \(\mathrm {Hom}({\mathcal {T}}_i,{\mathcal {T}}_j)=0\) for \(i<j\), then we say that \({\mathcal {T}} = \langle {\mathcal {T}}_1, {\mathcal {T}}_2,\dots {\mathcal {T}}_n \rangle \) is an orthogonal decomposition, in which case we will write sometimes \({\mathcal {T}}={\mathcal {T}}_1 \oplus {\mathcal {T}}_2\oplus \dots \oplus {\mathcal {T}}_n\). Obviously, if \({\mathcal {T}} = \langle {\mathcal {T}}_1, {\mathcal {T}}_2,\dots {\mathcal {T}}_n \rangle \) is an orthogonal decomposition, then \({\mathcal {T}} = \langle {\mathcal {T}}_{s(1)}, {\mathcal {T}}_{s(2)},\dots {\mathcal {T}}_{s(n)} \rangle \) is an orthogonal decomposition for any permutation \(s:\{ 1,\dots ,n \} \rightarrow \{ 1,\dots ,n \}\).
Proposition 5.2
Let \({\mathcal {T}} = \langle {\mathcal {T}}_1, {\mathcal {T}}_2, \dots , {\mathcal {T}}_n \rangle \) be any orthogonal decomposition. Let  , \(1\le i,j \le n\) be the natural biproduct diagram. Then:
, \(1\le i,j \le n\) be the natural biproduct diagram. Then:
-
(a)
The following map is a bijection:
$$\begin{aligned}&\mathrm {Stab}({\mathcal {T}}) \rightarrow \mathrm {Stab}({\mathcal {T}}_1)\times \mathrm {Stab}({\mathcal {T}}_2) \times \cdots \times \mathrm {Stab}({\mathcal {T}}_n) \end{aligned}$$(45)$$\begin{aligned}&(Z,\{ {\mathcal {P}}(t) \}_{t \in {\mathbb {R}}}) \mapsto \left( (Z\circ pr_1,\{ {\mathcal {P}}(t)\cap {\mathcal {T}}_1 \}_{t \in {\mathbb {R}}}),\right. \nonumber \\&\quad \left. \dots , (Z\circ pr_n,\{ {\mathcal {P}}(t)\cap {\mathcal {T}}_n \}_{t \in {\mathbb {R}}}) \right) . \end{aligned}$$(46) -
(b)
For any \((Z,\{ {\mathcal {P}}(t) \}_{t \in {\mathbb {R}}})\in \mathrm {Stab}({\mathcal {T}})\) and any \(t\in {\mathbb {R}}\) the subcategory \({\mathcal {P}}(t)\) is non-trivial iff for some j \({\mathcal {P}}(t)\cap {\mathcal {T}}_j\) is non-trivial.
-
(c)
If \({\mathrm{rank}}(K_0({\mathcal {T}}_i))<+\infty \) for all \(i=1,2,\dots ,n\), then the map defined above is biholomorphism.
-
(d)
For each \(\sigma \in \mathrm {Stab}({\mathcal {T}})\) holds \(P_\sigma ^{{\mathcal {T}}}=\cup _{i=1}^n P_{\sigma _i}^{{\mathcal {T}}_i} \), where \((\sigma _1,\dots ,\sigma _n)\) is the value of (45) at \(\sigma \).
Proof
We will give all details for the proof of (a), (b), (c) in the case \(n=2\). The general case follows easily by induction. (d) follows from the very definition (32) and (a), (b).
It is well known that for each \(X\in {\mathcal {T}}\) there exists unique up to isomorphism triangle \(E_2 \rightarrow X \rightarrow E_1 \rightarrow E_2[1]\) with \(E_i\in {\mathcal {T}}_i\), \(i=1,2\). By \(\mathrm {Hom}({\mathcal {T}}_1, {\mathcal {T}}_2)=0\) it follows that each of these triangles is actually part of a direct product diagram and \(pr_i([X])=[E_i]\) for \(i=1,2\).
Now let \(X\in {\mathcal {T}}_1\) and \(U\rightarrow X \rightarrow B \rightarrow U[1]\) be a triangle in \({\mathcal {T}}\). Using \(\mathrm {Hom}({\mathcal {T}}_2, {\mathcal {T}}_1)=\mathrm {Hom}({\mathcal {T}}_1, {\mathcal {T}}_2)=0\) and decomposing U into direct summands \(U_1 \oplus U_2\) with \(U_i\in {\mathcal {T}}_i\) one easily concludes that the triangle \(U\rightarrow X \rightarrow B \rightarrow U[1]\) is isomorphic to a triangle of the form \(U_1 \oplus U_2 \rightarrow X \rightarrow B'\oplus U_2[1] \rightarrow U_1[1] \oplus U_2 [1]\). If we apply these arguments to the last triangle in (16) and using that \(\hom (E_{n-1}, A_n[i])=0\) for \(i\le 0\), we immediately obtain \(E_{n-1}, A_n \in {\mathcal {T}}_1\) and then by induction it follows that the entire HN filtration of X lies in \({\mathcal {T}}_1\), in particular \(A_i \in {\mathcal {P}}(t_i) \cap {\mathcal {T}}_1\) for \(i=1,2,\dots ,n\), furthermore we have \(Z_1 ([X]) =Z (pr_1([X])) \) for each \(X \in {\mathcal {P}}(t) \cap {\mathcal {T}}_1\) and now it is obvious that \( (Z\circ pr_1,\{ {\mathcal {P}}(t)\cap {\mathcal {T}}_1 \}_{t \in {\mathbb {R}}})=(Z_1, {\mathcal {P}}_1)\) is a stability condition on \({\mathcal {T}}_1\).
The same arguments as in the previous paragraph apply to the case \(X \in {\mathcal {T}}_2\) and show that \(\left( Z\circ pr_2,\{ {\mathcal {P}}(t)\cap {\mathcal {T}}_2 \}_{t \in {\mathbb {R}}}\right) =(Z_2, {\mathcal {P}}_2)\) is a stability condition on \({\mathcal {T}}_2\). We will show that \(\sigma _i\) are locally finite for \(i=1,2\).
Indeed, since \(\sigma \) is locally finite stability condition on \({\mathcal {T}}\), then there exists \(\frac{1}{2}> \varepsilon >0\) such that \({\mathcal {P}}(t-\varepsilon ,t+\varepsilon )\) is quasi-abelian category of finite length for each \(t\in {\mathbb {R}}\). One easily shows that \({\mathcal {P}}_i(t-\varepsilon ,t+\varepsilon )={\mathcal {T}}_i \cap {\mathcal {P}}(t-\varepsilon ,t+\varepsilon )\) for each t. From [10, Lemma 4.3] we know that a sequence \(A\rightarrow B \rightarrow C\) in \({\mathcal {P}}_i(t-\varepsilon ,t+\varepsilon )\) is a strict short exact sequence iff it is part of a triangle \(A\rightarrow B \rightarrow C \rightarrow A[1]\) in \({\mathcal {T}}_i\). Since for A, B, C in \({\mathcal {T}}_i\) \(A\rightarrow B \rightarrow C \rightarrow A[1]\) is triangle in \({\mathcal {T}}_i\) iff it is a triangle in \({\mathcal {T}}\), we deduce that for \(A, B, C \in {\mathcal {P}}_i(t-\varepsilon ,t+\varepsilon )\) \(A\rightarrow B \rightarrow C \) is a strict exact sequence in \({\mathcal {P}}_i(t-\varepsilon ,t+\varepsilon )\) iff it is a strict exact sequence in \({\mathcal {P}}(t-\varepsilon ,t+\varepsilon )\), and now from the fact that \({\mathcal {P}}(t-\varepsilon ,t+\varepsilon )\) is of finite length it follows that \({\mathcal {P}}_i(t-\varepsilon ,t+\varepsilon )\) is of finite length and \(\sigma _i \in \mathrm {Stab}({\mathcal {T}}_i)\) for \(i=1,2\).
So far we showed that the map is well defined. Since for any interval \(I{\subset } {\mathbb {R}}\) the subcategory \({\mathcal {P}}(I)\) is thick (see e.g. [21, Lemma 2.20.]), it follows that \({\mathcal {P}}(t)={\mathcal {P}}_1(t)\oplus {\mathcal {P}}_2(t)\) for each \(t \in {\mathbb {R}}\) and hence follows the injectivity of the map. Furthermore, using the terminology of [16, Definition before Proposition 2.2] we see that \(\sigma \) is glued from \(\sigma _1\) and \(\sigma _2\). From the given arguments it follows also that for \(X\in {\mathcal {T}}_i\) the HN filtrations w.r. to \(\sigma \) and w.r. to \(\sigma _i\) coincide, in particular:
on the other hand any \(X\in {\mathcal {T}}\) can be represented uniquely (up to isomorphism) as a biproduct \(X\cong X_1\oplus X_2 \) with \(X_i\in {\mathcal {T}}_i\) for \(i=1,2\) and (19) imply
Conversely, if \((\sigma _1,\sigma _2) \in \mathrm {Stab}({\mathcal {T}}_1)\times \mathrm {Stab}({\mathcal {T}}_2)\), then [16, Proposition 3.5] ensures existence of a locally finite stability condition \(\sigma \in \mathrm {Stab}({\mathcal {T}})\) glued from \(\sigma _1\), \(\sigma _2\) and using [16, (3) in Proposition 2.2]) one easily shows that our map sends the glued \(\sigma \) to the pair \((\sigma _1,\sigma _2)\), hence the surjectivity of the map follows.
Now we will show that if \({\mathrm{rank}}(K_0({\mathcal {T}}_i))<+\infty \) for \(i=1,2\), then the map defined above is biholomorphism. First we show that it is continuous.
[10, Proposition 8.1.] says that for any triangulated category \({\mathcal {T}}\) assigning to any two \(\sigma _1,\sigma _2 \in \mathrm {Stab}({\mathcal {T}})\) the following:
defines a generalized metric whose topology coincides with the topology of \(\mathrm {Stab}({\mathcal {T}})\).
We denote by d, \(d_1\), \(d_2\) the generalized metrics on \(\mathrm {Stab}({\mathcal {T}})\), \(\mathrm {Stab}({\mathcal {T}}_1)\), \(\mathrm {Stab}({\mathcal {T}}_2)\). For any \(\sigma , \sigma '\in \mathrm {Stab}({\mathcal {T}})\) let \((\sigma _1,\sigma _2)\) and \((\sigma '_1,\sigma '_2)\) be the pairs assigned via the bijection. To show that the map is homeomorphism we will show that :
The first (50) follows easily from (47). The second requires a bit more computations, which we will present partly. Take any \(X\in {\mathcal {T}}\) and decompose it \(X \cong X_1 \oplus X_2\), \(X_i\in {\mathcal {T}}_i\), then from (48) we see that
where we used, besides the definition of the generalized metrics (49), the following lemma:
Lemma 5.3
For any positive real numbers \(x_1,x_2,y_1,y_2\) holds the inequality:
Proof
We can assume that \(\frac{x_1+x_2}{y_1+y_2}\ge 1\) (otherwise take \(\frac{y_1+y_2}{x_1+x_2}\)). Now we consider three cases:
If \(\frac{x_1}{y_1}\ge 1\) and \(\frac{x_2}{y_2}\ge 1\), then the desired inequality becomes \( \log \frac{x_1+x_2}{y_1+y_2}\le \log \frac{x_1}{y_1}+\log \frac{x_2}{y_2}\) which after exponentiating is equivalent to
the latter inequality follows from \(x_1\ge y_1\), \(x_2\ge y_2\).
If \(\frac{x_1}{y_1}\le 1\) and \(\frac{x_2}{y_2}\ge 1\), then the desired inequality becomes \( \log \frac{x_1+x_2}{y_1+y_2}\le \log \frac{y_1}{x_1}+\log \frac{x_2}{y_2} \) which after exponentiating is equivalent to
the latter inequality follows from \(y_1\ge x_1\), \(x_2\ge y_2\).
If \(\frac{x_1}{y_1}\le 1\) and \(\frac{x_2}{y_2}\le 1\), then the desired inequality becomes \( \log \frac{x_1+x_2}{y_1+y_2}\le \log \frac{y_1}{x_1}+\log \frac{y_2}{y_2} \) which after exponentiating is equivalent to
the latter inequality follows from \(y_1\ge x_1\), \(y_2\ge x_2\).\(\square \)
Now in order to prove (51) it is enough to show that \( \left| \phi _\sigma ^\pm (X)-\phi _{\sigma '}^\pm (X)\right| \le d_1(\sigma _1,\sigma '_1)+ d_2(\sigma _2,\sigma '_2) \) which in turn via (48) is the same as
which in turn follow from the following:
Lemma 5.4
For any real numbers \(x_1,x_2,y_1,y_2\) we have:
Proof
If \(\mathrm{max}\{x_1,x_2\}=x_i\) and \(\mathrm{max}\{y_1,y_2\}=y_i\) for the same i, then the inequalities follow immediately. So let \(\mathrm{max}\{x_1,x_2\}=x_i\) \(\mathrm{max}\{y_1,y_2\}=y_j\), \(i\ne j\), e.g. let \(i=1\), \(j=2\). Then \(x_1\ge x_2\), \(y_1\le y_2\), and the lemma follows from:
\(\square \)
Thus, we have (50), (51) and they imply that (45) is homeomorphism for \(n=2\).
Let  ,
,  , \(i=1,2\) be the projections \(proj(Z, {\mathcal {P}})=Z\). Then the following diagram (the first row is the map (45) and the second row is the assignment \(Z\mapsto (Z\circ pr_1,Z\circ pr_2)\)) is commutative:
, \(i=1,2\) be the projections \(proj(Z, {\mathcal {P}})=Z\). Then the following diagram (the first row is the map (45) and the second row is the assignment \(Z\mapsto (Z\circ pr_1,Z\circ pr_2)\)) is commutative:

If we take any connected component \(\Sigma {\subset } \mathrm {Stab}({\mathcal {T}})\), then (since \(\varphi \) is homeomorphism) \(\varphi (\Sigma )=\Sigma _1 \times \Sigma _2\) is a connected component of \(\mathrm {Stab}({\mathcal {T}}_1)\times \mathrm {Stab}({\mathcal {T}}_2)\), resp. \(\Sigma _i\) are connected components of \(\mathrm {Stab}({\mathcal {T}}_i)\), and furthermore \(m=\dim _{\mathbb {C}}(\Sigma )=\dim _{\mathbb {C}}(\Sigma _1\times \Sigma _2)\). From the Bridgeland’s main theorem we know that proj restricts to local biholomorphisms between \(\Sigma \) and an m-dimensional vector subspace \(V{\subset } \mathrm {Hom}(K_0({\mathcal {T}}),{\mathbb {C}}) \) and \(proj_1\times proj_2\) restricts to local biholomorphisms between \(\Sigma _1\times \Sigma _2\) and an m-dimensional vector subspace \(V_1\times V_2 {\subset } \mathrm {Hom}(K_0({\mathcal {T}}_1),{\mathbb {C}}) \times \mathrm {Hom}(K_0({\mathcal {T}}_2),{\mathbb {C}}) \). It follows (using that \(\varphi '\) is a linear isomorphism and that each open subset in a vector subset contains a basis of the space) that \(\varphi '(V)=V_1\times V_2\). Thus, the diagram above restricts to a diagram with vertical arrows which are local biholomorphisms, the bottom arrow is biholomorphism, and the top arrow is a homeomorphism, it follows with standard arguments that the the top arrow must be biholomorphic. It follows that \(\varphi \) is biholomorphism and we proved the proposition. \(\square \)
From this proposition and Definition 4.3 it follows:
Corollary 5.5
Let \({\mathcal {T}} = {\mathcal {T}}_1 \oplus {\mathcal {T}}_2 \oplus \dots \oplus {\mathcal {T}}_n \) be an orthogonal decomposition (Definition 5.1) and let \({\mathrm{rank}}(K_0({\mathcal {T}}_i))<+\infty \) for \(i=1,\dots ,n\). Let \( \mathrm {Stab}({\mathcal {T}}) \rightarrow \mathrm {Stab}({\mathcal {T}}_1)\times \cdots \times \mathrm {Stab}({\mathcal {T}}_n), \sigma \mapsto \left( \sigma _1, \sigma _2,\dots ,\sigma _n \right) \) be the biholomorphism from Proposition 5.2a.
For any \(0<\varepsilon <1\) the following are equivalent: (a) \(\sigma \in \mathrm {Stab}_{\varepsilon }({\mathcal {T}})\); (b) \(\{ \sigma _i \in \mathrm {Stab}_{\varepsilon }({\mathcal {T}}_i) \}_{i=1}^n\) and there exists a closed \(\varepsilon \)-arc \(\gamma \) such that \(P_{\sigma _i}^{{\mathcal {T}}_i}\cap \gamma = \emptyset \) for each \(1\le i \le n\).
In particular \({\mathcal {T}}\) has a phase gap iff \({\mathcal {T}}_i\) has a phase gap for each \(1\le i \le n\).
Since the closure of \(A \cup B\) equals the union of closures of A and B and \(\mathrm {vol}(A)\le \mathrm {vol}(A\cup B)\le \mathrm {vol}(A)+\mathrm {vol}(B)\), from Corollary 5.5 it follows:
Corollary 5.6
Let \({\mathcal {T}} ={{\mathcal {T}}}_{1}\oplus {{\mathcal {T}}}_{2}\oplus \dots \oplus {{\mathcal {T}}}_{n}\) be an orthogonal decomposition with finite rank Grothendieck groups of the factors, and let \(0<\varepsilon <1\).
If \({\mathcal {T}}\) has a phase gap and \(\left\| {\mathcal {T}}_j\right\| _{\varepsilon }=0\) for some j, then \(\left\| {\mathcal {T}}\right\| _{\varepsilon } = \left\| \langle {{\mathcal {T}}}_{1},{{\mathcal {T}}}_{2},{{\mathcal {T}}}_{j-1}, {{\mathcal {T}}}_{j+1},\dots ,{{\mathcal {T}}}_{n}\rangle \right\| _{\varepsilon }\).
6 The inequality \(\left\| \langle {\mathcal {T}}_1,{\mathcal {T}}_2\rangle \right\| _{\varepsilon }\ge \max \{\left\| {\mathcal {T}}_1\right\| _{\varepsilon },\left\| {\mathcal {T}}_2\right\| _{\varepsilon } \}\)
Here we show conditions which ensure \(\left\| \langle {\mathcal {T}}_1,{\mathcal {T}}_2\rangle \right\| _{\varepsilon }\ge \max \{\left\| {\mathcal {T}}_1\right\| _{\varepsilon },\left\| {\mathcal {T}}_2\right\| _{\varepsilon } \}\) for any \(\varepsilon \in (0,1)\), where \( \langle {\mathcal {T}}_1, {\mathcal {T}}_2 \rangle \) is a semi-orthogonal decomposition (see Definition 5.1) of some \({\mathcal {T}}\).
Theorem 6.1
Let \({\mathcal {T}}\) be proper and let \(K_0({\mathcal {T}})\) has finite rank. Assume \(0<\varepsilon <1\). Let \({\mathcal {T}} = \langle {\mathcal {T}}_1, {\mathcal {T}}_2 \rangle \) be a semi-orthogonal decomposition. If \({\mathcal {T}}_1\), \({\mathcal {T}}_2\) are categories with phase gaps, then \({\mathcal {T}}\) is a category with phase gap and for any \(0<\varepsilon <1\) holds :
Proof
Take any \(0<\mu \). Let \(\sigma _i=(Z_i, {\mathcal {P}}_i)\in \mathrm {Stab}_\varepsilon ({\mathcal {T}}_i)\) be full stability conditions, s. t.
Due to (36) we can assume that \(\exp ({\mathrm {i}}\pi [0,\varepsilon ]) {\subset } {\mathbb {S}}^1{\setminus } P^{{\mathcal {T}}_i}_{\sigma _i}\). By the same arguments as in the last paragraph of the proof of Lemma 4.7 it follows that \({\mathcal {P}}_{\sigma _i}(0,1]\) are finite length abelian categories, therefore the simple objects in them are a basis of \(K_0({\mathcal {T}}_i)\) for \(i=1,2\), and these abelian categories are the extension closures of their simple objects. In particular the sets of simple objects are finite and it follows that for some \(j\in {\mathbb {Z}}\) holds
Recalling (29) we deduce that \(\mathrm {Hom}^{\le 1} ({\mathcal {P}}_{\sigma _1}(0,1],{\mathcal {P}}_{(-{\mathrm {i}}j \pi )\star \sigma _2}(0,0+1])=0\). By replacing \(\sigma _2\) with \((-{\mathrm {i}}j \pi )\star \sigma _2\) we obtain stability conditions \(\sigma _i\in \mathrm {Stab}_\varepsilon ({\mathcal {T}}_i)\) for \(i=1,2\) satisfying the following conditions:
In the listed properties of \(\sigma _i \in \mathrm {Stab}({\mathcal {T}}_i)\) with the given semi-orthogonal decomposition \({\mathcal {T}}=\langle {\mathcal {T}}_1, {\mathcal {T}}_2 \rangle \) are contained the conditions of [16, Proposition 3.5 (b)]. This proposition ensures a glued (see [16, Definition ]) locally finite stability condition \(\sigma =(Z,{\mathcal {P}})\in \mathrm {Stab}({\mathcal {T}})\). The glued stability condition satisfies the following (we use [16, Proposition 2.2 (3)] and write \({\mathcal {P}}_i\) instead of \({\mathcal {P}}_{\sigma _i}\))
We will show that
Indeed, let \(s_{11}, s_{12}, \dots , s_{1n}\) and \(s_{21}, s_{22}, \dots , s_{2m}\) be the simple objects of \({\mathcal {P}}_1(0,1]\) and \({\mathcal {P}}_2(0,1]\), respectively. Then \(\{s_{1 i}\}_{i=1}^n {\subset } \sigma ^{ss}_1\), \(\{s_{2 i}\}_{i=1}^m {\subset } \sigma ^{ss}_2\) and by (62), (65), and (17) we deduce that
and on the other hand by (63) it follows that Z(X) is a positive linear combination of \(\{ Z(s_{1 i}) \}_{i=1}^n\), \(\{ Z(s_{2 i}) \}_{i=1}^m\) for \(X\in {\mathcal {P}}(t){\setminus } \{0\}\), \(t\in (0,1]\), and therefore \(Z(X) \in {\mathbb {R}}_{>0} \exp ({\mathrm {i}}\pi (\varepsilon ,1))\) , hence (17) gives \(\phi _\sigma (X) \in (\varepsilon ,1) \) and (66) follows. This in turn implies \(\exp ({\mathrm {i}}\pi [0,\varepsilon ])\cap P_\sigma ^{{\mathcal {T}}} = \emptyset \) and then for obtaining \(\sigma \in \mathrm {Stab}_\varepsilon ({\mathcal {T}})\) (recall Definition 4.3) it remains to show that \(\sigma \) is a full stability condition. We will prove this by showing that \({\mathcal {P}}(0,1]\) is a finite length abelian category (then it follows that \({\mathbb {H}}^{{\mathcal {P}}(0,1]}\cong {\mathbb {H}}^{n+m}\) and \(\sigma \) is full, since \(\sigma \in {\mathbb {H}}^{{\mathcal {P}}(0,1]}\)). However [16, Proposition 3.5 (a)] claims that if 0 is an isolated point for \(\mathfrak {I}\left( Z_i({\mathcal {P}}_i(0,1]) \right) \) for \(i=1,2\) (which is satisfied due to (61) and (62)), then \({\mathcal {P}}(0,1)\) is a finite length category, and on the other hand due to (66) holds \({\mathcal {P}}(0,1]={\mathcal {P}}(0,1)\). Therefore indeed \({\mathcal {P}}(0,1]\) is finite length category and \(\sigma \) is a full stability condition.
Finally, from (64) it follows that \(P^{{\mathcal {T}}_i}_{\sigma _i}{\subset } P^{{\mathcal {T}}}_\sigma \), therefore \(\overline{P^{{\mathcal {T}}_i}_{\sigma _i} }{\subset } \overline{P^{{\mathcal {T}}}_\sigma }\), and hence \(\mathrm {vol}\left( \overline{P^{{\mathcal {T}}_i}_{\sigma _i} } \right) \le \mathrm {vol}\left( \overline{P^{{\mathcal {T}}}_\sigma } \right) \) for \(i=1,2\), recalling (59) we derive:
This ineqaullity holds for any \(\mu >0\) and from the very definition 4.11 we deduce (58). \(\square \)
Remark 6.2
Let \({\mathcal {T}}\), \({\mathcal {T}}_1\), \({\mathcal {T}}_2\) be as in Theorem 6.1 (in particular there is a SOD \({\mathcal {T}}=\langle {\mathcal {T}}_1, {\mathcal {T}}_2\rangle \)). From the proof of Theorem 6.1 we see that if for some \(i=1,2\) there exists a full \(\sigma \in \mathrm {Stab}({\mathcal {T}}_i)\) with infinite set of phases \(P_{\sigma _i}\), then there exists a full \(\sigma \in \mathrm {Stab}({\mathcal {T}}_i)\) with infinite \(P_{\sigma }\) as well.
Corollary 6.3
For any exceptional collection \((E_0,E_1,\dots ,E_n)\) in a proper triangulated category and for any \(0\le i\le n\) we have:
Proof
Due to Remark 4.10 the categories \(\left\langle E_0,E_1,\dots ,E_n\right\rangle \), \(\left\langle E_0,E_1,\dots ,E_i\right\rangle \), \(\left\langle E_{i+1},E_{i+2},\dots ,E_n\right\rangle \) have phase gaps. All the conditions of Theorem 6.1 are satisfied for the semi-orthogonal decomposition \(\left\langle E_0,\dots ,E_n\right\rangle =\left\langle \left\langle E_0,\dots ,E_i\right\rangle , \left\langle E_{i+1},\dots , E_n\right\rangle \right\rangle \), hence equality (58) gives rise to (69). \(\square \)
Corollary 6.4
Let X be a smooth algebraic variety and let Y be a smooth sub-variety so that \(K_0(D^b(X))\), \(K_0(D^b(Y))\) have finite rank and \(D^b(X)\), \(D^b(Y)\) have phase gaps. Denote by \(\widetilde{X}\) the smooth algebraic variety obtained by blowing up X along the center Y.
Then \(D^b(\widetilde{X})\) has phase gap and \(\left\| D^b(\widetilde{X})\right\| _{\varepsilon }\ge \max \left\{ \left\| D^b(X)\right\| _{\varepsilon }, \left\| D^b(Y)\right\| _{\varepsilon }\right\} \) for any \(\varepsilon \in (0,1)\).
Proof
[7, Theorem 4.2] ensures that there is a semi-orthogonal decomposition
\(D^b(\widetilde{X})=\langle {\mathcal {T}}_1, {\mathcal {T}}_2,\dots ,{\mathcal {T}}_k, D^b(X)\rangle \), where \({\mathcal {T}}_i\) is equivalent to \(D^b(Y)\) for \(i=1,2,\dots ,k\). Now Theorem 6.1 ensures that the inequality holds. \(\square \)
7 Norm of \(D^b(K(l))\)
7.1 The Helix in \(D^b(K(l))\) for \(l\ge 2\)
From now on we assume that \(l\ge 2\) and denote \({\mathcal {T}}_l = D^b(K(l))\). We write \(\underline{\dim }(X)=(n,m)\), \(\underline{\dim }_0(X)=n\), \(\underline{\dim }_1(X)=m\) for a representation:

Recall that \(Rep_{{\mathbb {K}}}(K(l))\) is hereditary category in which for any two \(X, Y \in Rep_{{\mathbb {K}}}(Q)\) with dimension vectors \(\underline{\dim }(X)=(n_x,m_x)\), \(\underline{\dim }(Y)=(n_y,m_y)\) holds the equality (the Euler Formula):
Let \(s_0, s_1 \in {\mathcal {T}}_l\) be so that \(s_0[1]\), \(s_1\) are the simple objects in \(Rep_{{\mathbb {K}}}(Q)\) with \(\underline{\dim }(s_0[1])=(1,0)\) and \(\underline{\dim }(s_1)=(0,1)\). Using (70) one easily computes \(\hom (s_0,s_1)=l\), \(\hom ^p(s_0,s_1)=0\) for \(p\ne 0\) and \(\hom ^*(s_1,s_0)=0\). With the terminology from Sect. 2 we say that \((s_0, s_1)\) is a full strong exceptional pair in \({\mathcal {T}}_l = D^b(K(l))\).
Remark 7.1
Recall that (see e.g. [9, p. 222]) for any exceptional pair (A, B) in any proper triangulated category \({\mathcal {T}}\) one defines objects \(L_A(B)\) (left mutation) and \(R_B(A)\) (right mutation) by the triangles

and \((L_A(B),A)\), \((B,R_B(A))\) are exceptional pairs as well, they are full if (A, B) is full.
It follows, that for any exceptional collection \({\mathcal {E}}=(E_0,E_1,\dots , E_n)\) in \({\mathcal {T}}\) and for any \(0\le i < n\) the sequences \(R_i({\mathcal {E}})=(E_0,E_1,\dots ,E_{i+1},R_{E_{i+1}}(E_i),\dots , E_n)\), \(L_i({\mathcal {E}})=(E_0,E_1,\dots ,L_{E_{i}}(E_{i+1}),E_{i},\dots , E_n)\) are exceptional and \(\left\langle R_i({\mathcal {E}})\right\rangle =\left\langle L_i({\mathcal {E}})\right\rangle = \left\langle {\mathcal {E}}\right\rangle \). The sequences \(L_i({\mathcal {E}})\) and \(R_i({\mathcal {E}})\) are called left and right mutations of \({\mathcal {E}}\).
From the exceptional pair \((s_0,s_1)\) we get objects \(L_{s_0}(s_1)\), \(R_{s_1}(s_0)\) via left and right mutation, denoted by \(s_{-1}\), \(s_2\), respectively, and each two adjacent elements in the sequence \(s_{-1}, s_{0} ,s_1,s_2\) form a full exceptional pair. Applying iteratively left/right mutations on the left/right standing exceptional pair generates a sequence (infinite in both directions) of exceptional objects \(\{s_i\}_{i\in {\mathbb {Z}}}\). This is the helix induced by the exceptional pair \((s_0,s_1)\), as defined in [9, p. 222]. In [19, Section 5 - see (25), (27) and Lemma 5.2] with the help of results for geometric helices in [9] and is proved that:
7.2 The set of phases
We prove first the following Proposition
Proposition 7.2
We have a disjoint union \(\mathrm {Stab}({\mathcal {T}}_l) = {\mathcal {Z}} \amalg \left( \amalg _{i\in {\mathbb {Z}}} {\mathcal {Z}}_i \right) \) and:
The subset \({\mathcal {Z}}\) is open and it is biholomorphic to the specified subset of \({\mathbb {C}}^2\) via the following map:
Furthermore, if \(\sigma \in {\mathcal {Z}}_i \) and \(\phi (s_{i+1})>\phi (s_i)+1\), then \(s_j\not \in \sigma ^{ss}\) for \(j\ne i, j \ne i+1\). If \(\sigma \in {\mathcal {Z}}_i \) and \(\phi (s_{i+1})=\phi (s_i)+1\), then \(s_j\in \sigma ^{ss}\) for each \(j\in {\mathbb {Z}}\).
Proof
The existence ot a disjoint union \(\mathrm {Stab}({\mathcal {T}}_l) = {\mathcal {Z}} \amalg \amalg _{i\in {\mathbb {Z}}} {\mathcal {Z}}_i\), with the properties (77), (78) and the biholomorphism (79) follow from [23, Proposition 6.1, formula (35), Lemma 6.2].
Assume now that \(\sigma \in {\mathcal {Z}}_i \) and \(\phi (s_{i+1})>\phi (s_i)+1\) for some i \(\phi (s_{i+1})>\phi (s_i)+1\). If \(s_j \in \sigma ^{ss}\) for some \(j>i+1\), then due to (75) \(\phi (s_j)\ge \phi (s_{i+1})\), and hence \(\phi (s_j)>\phi (s_i)+1\), \(\hom ^1(s_j,s_i)=0\), which contradicts (76). The arguments for the case \(j<i\) are similar.
Finally, assume that \(\sigma \in {\mathcal {Z}}_i \) and \(t=\phi (s_{i+1})=\phi (s_i)+1\). Recall that \(s_0[1]\) and \(s_1\) are the simple ojects in \(Rep_{{\mathbb {K}}}(K(l))\) (see after (70)). It follows that for each j we have that \(s_j[k]\) is in the extension closure of \(s_0[1]\) and \(s_1\) for some k. Using [23, Corollary 5.3] one deduces easily that for each j we have that \(s_j[k]\) is in the extension closure of \(s_i[1]\) and \(s_{i+1}\) for some k, and since \(s_i[1], s_{i+1} \in {\mathcal {P}}(t)\) it follows that \(s_j[k]\in {\mathcal {P}}(t)\), therefore \(s_j\in \sigma ^{ss}\). \(\square \)
We start by some comments on the root system of K(l). The root system of K(l) is \( \Delta _{l+}=\Delta _+(K(l)) = \Delta _{l+}^{re} \cup \Delta _{l+}^{im}, \) where \(\Delta _{l+}^{re }=\{(n,m)\in {\mathbb {N}}^2 : n^2 + m^2 - l m n = 1 \}\) and \(\Delta _{l+}^{im }=\{(n,m)\in {\mathbb {N}}^2 : n^2 + m^2 - l m n \le 0 \}{\setminus } \{(0,0)\}\). It is well known that the real roots \(\Delta _{l+}^{re}\) are exactly the dimension vectors of the exceptional representations in \(Rep_{{\mathbb {K}}}(K(l))\) and for the imaginary roots \(\Delta _{l+}^{im}\) we have formula (74) in [18]. From (72) and Lemma 7.3 we have the complete list \(\{s_{\le 0}[1], s_{\ge 1}\}\) of exceptional representations in \(Rep_{{\mathbb {K}}}(K(l))\). Let us denote the corresponding dimension vectors as follows:
Therefore we can write:
We will need later the following facts for the real roots \(\{(n_i,m_i): i\in {\mathbb {Z}}\}\):
Lemma 7.3
-
(a)
\((n_{-1},m_{-1})=(l,1)\), \((n_0,m_0)=(1,0)\), \((n_1,m_1)=(0,1)\), \((n_2,m_2)=(1,l)\)
-
(b)
\((m_{-i},n_{-i})=(n_{i+1},m_{i+1})\) for \(i\ge 0\).
-
(c)
\(n_{-i}>m_{-i}\) and \(n_{i+1}<m_{i+1}\) for \(i\ge 0\); \(n_{i+1}>0\) and \(m_{-i}>0\) for \(i\ge 1\).
-
(d)
\(\frac{n_i}{m_i} = \frac{l}{2}-\sqrt{\frac{l^2}{4}-1+\frac{1}{m_i^2}}\) and \(\frac{n_{-i}}{m_{-i}} = \frac{l}{2}+\sqrt{\frac{l^2}{4}-1+\frac{1}{m_{-i}^2}}\) for \(i\ge 1\).
-
(e)
\(\frac{n_{-1}}{m_{-1}}>\frac{n_{-2}}{m_{-2}}>\cdots >\frac{n_{-i}}{m_{-i}}\xrightarrow {{i\rightarrow \infty }} a_l\) and \(0=\frac{n_{1}}{m_{1}}<\frac{n_{2}}{m_{2}}<\cdots <\frac{n_{i}}{m_{i}}\xrightarrow {{i\rightarrow \infty }} a_l^{-1}\).
Proof
-
(a)
\((n_0,m_0)=(1,0)\), \((n_1,m_1)=(0,1)\) follow from the definition. The triangles (74) for \(i=1\), and \(i=0\) amount to short exact sequences:
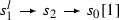 and
and 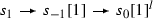 in \(Rep_{{\mathbb {K}}}(K(l))\), and it follows that \(\underline{\dim }(s_2)= (1,l)\), \(\underline{\dim }(s_{-1}[1])= (l,1)\)
in \(Rep_{{\mathbb {K}}}(K(l))\), and it follows that \(\underline{\dim }(s_2)= (1,l)\), \(\underline{\dim }(s_{-1}[1])= (l,1)\) -
(b)
The equality for \(0\le i \le 1\) follows from (a). We make the induction assumption that for some \(p\ge 1\) the equality holds for any \(0\le i\le p\), we will make the induction step, namely that the equality for \(i=p+1\) follows from this induction assumption. Indeed, for \(i\ge 1\) from (74) we obtain the following short exact sequences in \(Rep_{{\mathbb {K}}}(K(l))\):
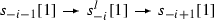 ,
, 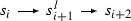 therefore for \(i\ge 1\) we obtain: $$\begin{aligned} n_{-i-1}= & {} l n_{-i} - n_{-i+1} \quad m_{-i-1}= l m_{-i} - m_{-i+1} \end{aligned}$$(83)$$\begin{aligned} n_{i+2}= & {} l n_{i+1} - n_{i} \quad m_{i+2}= l m_{i+1} - m_{i} \end{aligned}$$(84)
therefore for \(i\ge 1\) we obtain: $$\begin{aligned} n_{-i-1}= & {} l n_{-i} - n_{-i+1} \quad m_{-i-1}= l m_{-i} - m_{-i+1} \end{aligned}$$(83)$$\begin{aligned} n_{i+2}= & {} l n_{i+1} - n_{i} \quad m_{i+2}= l m_{i+1} - m_{i} \end{aligned}$$(84)having these recursive formulas one easily caries out the inductive step.
-
(c)
Due to (b) it is enough to show that \(n_{i+1}<m_{i+1}\). For \(i=0\) this is shown in (a). For \(i\ge 1\) we have \(\hom (s_{i+1}, s_{-i}[1])> 0\), \(\hom ^1(s_{i+1}, s_{-i}[1])=0 \) (recall Lemma 7.3), hence the Euler formula amounts to:
$$\begin{aligned}&\left\langle \underline{\dim }(s_{i+1}),\underline{\dim }(s_{-i}[1])\right\rangle = \hom (s_{i+1}, s_{-i}[1])-\hom ^1(s_{i+1}, s_{-i}[1])>0 \\&\quad \Rightarrow \left\langle (n_{i+1},m_{i+1}), (n_{-i},m_{-i})\right\rangle =n_{i+1} n_{-i} + m_{i+1} m_{-i} - l n_{i+1}m_{-i} >0. \end{aligned}$$Putting the equality from (b) in the last inequality we get \(n_{i+1} m_{i+1} + m_{i+1} n_{i+1} - l n_{i+1}n_{i+1} >0\). Therefore \(n_{i+1}(2 m_{i+1} - l n_{i+1}) >0\), hence \(n_{i+1}>0\), \( m_{i+1} >\frac{l}{2} n_{i+1}\ge n_{i+1}\) and (c) is proved.
-
(d)
Take any \(i\in {\mathbb {Z}}\), \(i\ne 0\). From (c) we know that \(m_i\ne 0\). From (81) we know that \(n_i^2 +m_i^2 - l n_i m_i =1 \), hence via the quadratic equation \(\left( \frac{n_i}{m_i} \right) ^2- l \frac{n_i}{m_i}+1 -\frac{1}{m_i^2} =0 \) we get \(\frac{n_i}{m_i}=\frac{1}{2}\left( l\pm \sqrt{l^2 - 4 + \frac{4}{m_i^2}} \right) \). One checks that \(\frac{1}{2}\left( l+ \sqrt{l^2 - 4 + \frac{4}{m_i^2}} \right) >1\), \(\frac{1}{2}\left( l- \sqrt{l^2 - 4 + \frac{4}{m_i^2}} \right) <1\) and then from (c) we deduce (d).
-
(e)
Using (83), (84), and induction one shows that \( m_{i}<m_{i+1}\), \(m_{-i-1}>m_{-i}\) for \(i\ge 0\) and then (e) follows from (d).
\(\square \)
We write for short \(P_\sigma ^l\) instead of \(P_\sigma ^{{\mathcal {T}}_l}\), and now we determine \(P_\sigma ^l\):
Proposition 7.4
. Let \(\mathrm {Stab}({\mathcal {T}}_l) = {\mathcal {Z}} \amalg \amalg _{i\in {\mathbb {Z}}} {\mathcal {Z}}_i\) be the decomposition from Proposition 7.2. Let \(\sigma \in \mathrm {Stab}(D^b(K(l)))\).
-
(a)
If \(\sigma \not \in {\mathcal {Z}}\), then the set of phases \(P_{\sigma }^l\) is finite (has up to 4 elements).
-
(b)
If \(\sigma \in {\mathcal {Z}}\), then for any \(j\in {\mathbb {Z}}\) we have the following formulas:
$$\begin{aligned}&0<\phi _\sigma (s_{j+1})-\phi _\sigma (s_{j})<1 \end{aligned}$$(85)$$\begin{aligned}&\exp ({\mathrm {i}}\pi (1-\phi _{\sigma }(s_j))) \cdot P_\sigma ^l = \{ \pm 1\} \cup \{\pm \exp \left( {\mathrm {i}}f\left( n_i/m_i \right) \right) :i\ne 0 \} \cup \nonumber \\&\quad \pm \exp \left( {\mathrm {i}}f\left( {\mathbb {Q}}\cap \left[ a_l^{-1}, a_l\right] \right) \right) , \end{aligned}$$(86)where x, y, and the function (strictly increasing smooth) \(f:[0,\infty )\rightarrow [\pi (\phi _\sigma (s_{j+1})-\phi _\sigma (s_{j})), \pi )\) are:
$$\begin{aligned}&f(t)=\arccos \left( \frac{ x y-t}{\sqrt{t^2 + x^2 - 2 t x y}} \right) \quad x =\frac{\left| Z(s_{j+1})\right| }{\left| Z(s_j)\right| } \quad \nonumber \\&y= \cos \left( \pi (\phi _\sigma (s_{j+1})-\phi _\sigma (s_{j})) \right) . \end{aligned}$$(87) -
(c)
For \(\sigma \in {\mathcal {Z}} \) holds the equality \(\{\pm \exp ({\mathrm {i}}\pi \phi _\sigma (s_i))\}_{i\in {\mathbb {Z}}}= P_\sigma ^l{\setminus } L(P_\sigma ^l)\) (recall that by \(L(P_\sigma ^l)\) we denote the set of limit points in the circle of \(P_\sigma ^l\)).
-
(d)
For any \(\sigma \in {\mathcal {Z}}\) and any \(j\in {\mathbb {Z}}\) hold:
$$\begin{aligned}&\lim _{k\rightarrow +\infty } \pi \phi _\sigma (s_{k}[-1]) = u_\sigma \le v_\sigma = \lim _{k\rightarrow -\infty } \pi \phi _\sigma (s_{k}) \end{aligned}$$(88)$$\begin{aligned}&\pi (\phi _\sigma (s_j)-1)<\pi \phi _\sigma (s_{j+1}[-1])<\pi \phi _\sigma (s_{j+2}[-1])<\cdots<u_\sigma \le \nonumber \\&\quad \le v_\sigma<\cdots<\pi \phi _\sigma (s_{j-2})< \pi \phi _\sigma (s_{j-1}) <\pi \phi _\sigma (s_j) \end{aligned}$$(89)$$\begin{aligned}&\overline{P_\sigma ^l} =\pm \exp \left( {\mathrm {i}}\{\pi \phi _\sigma (s_{j+k}[-1])\}_{k\ge 1} \cup {\mathrm {i}}[u_\sigma ,v_\sigma ]\cup {\mathrm {i}}\{\pi \phi _\sigma (s_{j-k})\}_{k\ge 0} \right) \end{aligned}$$(90)$$\begin{aligned}&\frac{v_\sigma - u_\sigma }{u_\sigma -\pi \phi _\sigma (s_{j+1}[-1])}=\frac{f(a_l)-f(a_{l}^{-1})}{f(a_{l}^{-1})-\arccos (y)} \quad \frac{v_\sigma - u_\sigma }{\pi \phi _\sigma (s_{j})-v_\sigma }\nonumber \\&\quad =\frac{f(a_l)-f(a_{l}^{-1})}{\pi -f(a_l)}, \end{aligned}$$(91)where f, x, y are as in (87) and \( u_\sigma =f(a_{l}^{-1})+\pi (1-\phi _{\sigma }(s_j))\), \( v_\sigma =f(a_{l})+\pi (1-\phi _{\sigma }(s_j))\).
-
(e)
Let \(\sigma \in {\mathcal {Z}} \) and \(0<\varepsilon <1\). Then \({{\mathbb {S}}}^1{\setminus } P_{\sigma }^l\) contains a closed \(\varepsilon \)-arc iff there exists \(i\in {\mathbb {Z}}\) such that \(\phi _\sigma (s_{i+1})-\phi _\sigma (s_{i})>\varepsilon \).
Before giving the proof of this proposition we make some preparatory steps.
For a pair of complex numbers \(v=(z_1,z_2)\) we discussed in [18] (see [18, Lemma 3.18] and the first row of the proof) the following subset of the circle
From [18, Remark 3.16] and (81) we deduce that:
Lemma 7.5
For any pair of complex numbers \(v=(z_1,z_2)\) of the form \( z_i= r_i \exp ({\mathrm {i}}\phi _i)\), \(r_i>0\), \(i=1,2\), \(0< \phi _2 < \phi _1 \le \pi \) holds:
where \(f:[0,\infty )\rightarrow [\phi _2, \phi _1){\subset } (0, \pi )\) is the strictly increasing smooth function:
Proof of Proposition 7.4
Let \(\sigma = (Z, {\mathcal {P}}) \in \mathrm {Stab}(D^b(K(l)))\). From Proposition 7.2 we have either \(\sigma \in {\mathcal {Z}}_j\) for some \(j\in {\mathbb {Z}}\) or \(\sigma \in {\mathcal {Z}}\).
-
(a)
Assume first that \(\sigma \in {\mathcal {Z}}_j\) for some \(j\in {\mathbb {Z}}\). Then by (78) we see that
$$\begin{aligned} s_j, s_{j+1} \in \sigma ^{ss} \quad \phi (s_j)+1\le \phi ( s_{j+1}). \end{aligned}$$(95)
We will show that in this case \(P_\sigma ^l=\{\pm \exp ({\mathrm {i}}\pi \phi _\sigma (s_j)), \pm \exp ({\mathrm {i}}\pi \phi _\sigma (s_{j+1}))\}\). Indeed, (95) implies that there exists \(k\ge 1\) such that \(\phi (s_j)\le \phi (s_{j+1}[-k])< \phi (s_j)+1\). From Lemma 7.3 it follows that \((s_j,s_{j+1}[-k])\) is a \(\sigma \)-exceptional pair (as defined in [22, Definition 3.17]). From [22, Corollary 3.18] (and its proof) it follows that the extension closure of \((s_j,s_{j+1}[-k])\) equals \({\mathcal {P}}(t,t+1]\) for some \(t\in {\mathbb {R}}\). Since \((s_j, s_{j+1}[-k])\) is an exceptional pair, each element Y in the extension closure of \((s_j, s_{j+1}[-k])\) can be put in a triangle of the form  for some \(a,b\in {\mathbb {N}}\). Take any \(X\in \sigma ^{ss}\), then for some \(i\in {\mathbb {Z}}\) we have \(\phi _\sigma (X[i]) \in (t,t+1]\) and therefore we have a triangle:
for some \(a,b\in {\mathbb {N}}\). Take any \(X\in \sigma ^{ss}\), then for some \(i\in {\mathbb {Z}}\) we have \(\phi _\sigma (X[i]) \in (t,t+1]\) and therefore we have a triangle:

\(\square \)
If \(a=0\) or \(b=0\), then \(X[i]\cong s_j^b \) or \(X[i]\cong s_{j+1}[-k]^a \) and hence \(\phi _\sigma (X[i])=\phi (s_j)\) or \(\phi _\sigma (X[i])=\phi (s_{j+1}[-k])\) and the \(\exp ({\mathrm {i}}\pi \phi _\sigma (X)) \in \{\pm \exp ({\mathrm {i}}\pi \phi _\sigma (s_j)), \pm \exp ({\mathrm {i}}\pi \phi _\sigma (s_{j+1}))\}\).
Next assume that \(a\ne 0\) and \(b\ne 0\). If \(\phi (s_{j})=\phi (s_{j+1}[-k])\), then we get \(\exp ({\mathrm {i}}\pi \phi _\sigma (X)) = \exp ({\mathrm {i}}\pi \phi _\sigma (s_j))\) using (96). Thus, we reduce to \(\phi (s_{j})<\phi (s_{j+1}[-k])\), which in turn by (96), \(X[i]\in \sigma ^{ss}\), and (18) implies that \(\alpha =0\) or \(\beta =0\). If \(\alpha =0\), then \(s_j^b \cong X[i] \oplus s_{j+1}[-k+1]^b\) and by [22, Lemma 3.7] it follows that \(\phi (s_j) = \phi (X[i])=\phi (s_{j+1}[-k+1])\); if \(\beta =0\), then \(s_{j+1}[-k]^a \cong X[i] \oplus s_{j}[-1]^b\) and by [22, Lemma 3.7] it follows that \(\phi (s_{j+1}[-k]) = \phi (X[i])=\phi (s_{j}[-1])\). Thus we see that (95) implies \(P_\sigma ^l=\{\pm \exp ({\mathrm {i}}\pi \phi _\sigma (s_j)), \pm \exp ({\mathrm {i}}\pi \phi _\sigma (s_{j+1}))\}\) and (a) is proved.
-
(b)
If \(\sigma \in {\mathcal {Z}}\), then (77) shows that for any \(j\in {\mathbb {Z}}\) holds \( s_j, s_{j+1} \in \sigma ^{ss} \), \( \phi _\sigma (s_j)< \phi _\sigma (s_{j+1}) < \phi _\sigma (s_j) +1 . \) Choosing one \(j\in {\mathbb {Z}}\), denoting \(\sigma '=(Z',{\mathcal {P}}')= (-\log \left| Z(s_j)\right| + {\mathrm {i}}\pi (1-\phi _{\sigma }(s_j)))\star \sigma \) and using (30), (31), we get:
$$\begin{aligned}&Z'(s_j)=-1, \ \ \left| Z'(s_{j+1})\right| =\frac{\left| Z(s_{j+1})\right| }{\left| Z(s_{j})\right| }, \nonumber \\&\phi _{\sigma '}(s_{j+1})=\phi _{\sigma }(s_{j+1})+1-\phi _{\sigma }(s_{j})\end{aligned}$$(97)$$\begin{aligned}&1=\phi _{\sigma '}(s_j)< \phi _{\sigma '}(s_{j+1})< \phi _{\sigma '}(s_j) +1=2 \nonumber \\&\qquad \ \Rightarrow \ 0< \phi _{\sigma '}(s_{j+1}[-1]) < \phi _{\sigma '}(s_j) =1 . \end{aligned}$$(98)Let \({\mathcal {A}}\) be the extension closure of \((s_j,s_{j+1}[-1])\). Utilizing Lemma 7.3 and recalling that \(\hom (s_j,s_{j+1})=l\ge 2\) (see for example the arguments before 74) we see that \((s_j,s_{j+1}[-1])\) is an l-Kronecker pair [21, Definition 3.20], and by (98) it is a \(\sigma '\)-exceptional pair as well. From [22, Corollary 3.18] (and its proof) we see that the extension closure \({\mathcal {A}}\) of \((s_j,s_{j+1}[-1])\) coincides with \({\mathcal {P}}'(0,1]\). Applying [21, Lemma 3.19] to \((s_j,s_{j+1}[-1])\) we see that \({\mathcal {A}}\) is the heart of a bounded t-structure of \({\mathcal {T}}_l\) and due to the equality \({\mathcal {A}}={\mathcal {P}}'(0,1]\) we have actually \(\sigma ' \in {\mathbb {H}}^{{\mathcal {A}}}\) (see [21, Definition 2.28]). Now all the conditions of [21, Corollary 3.21] with the exceptional pair \((s_j,s_{j+1}[-1])\) hold and we deduce that \(P_{\sigma '}^l=R_{v,\Delta _{l+}}\), where \(v=(Z'(s_j),Z'(s_{j+1}[-1]))\). On the other hand (35) shows that \(\exp ({\mathrm {i}}\pi (1-\phi _{\sigma }(s_j))) \cdot P_{\sigma }^l=R_{v,\Delta _l}\)
To determine the set \(R_{v,\Delta _l}\) we use Lemma 7.5 and observe that now (see 97) \(v=\left( -1,\frac{\left| Z(s_{j+1})\right| }{\left| Z(s_{j})\right| } \exp ({\mathrm {i}}\pi (\phi _{\sigma }(s_{j+1})-\phi _{\sigma }(s_{j})) \right) \), \(0< \pi (\phi _{\sigma }(s_{j+1})-\phi _{\sigma }(s_{j})) < \pi \), in particular the equality (93) yields (86) and the function (94) has the form (87).
-
(c)
Let \(\sigma \in {\mathcal {Z}}\). In (b) j was any integer, here we choose \(j=0\). Now formulas (97) and (98) give:
$$\begin{aligned}&Z'(s_0)=-1 \quad Z'(s_1[-1])=\left| Z'(s_1)\right| \exp ({\mathrm {i}}\pi \phi _{\sigma '}(s_1[-1])), \nonumber \\&0< \phi _{\sigma '}(s_{1}[-1]) < \phi _{\sigma '}(s_0)=1. \end{aligned}$$(99)Since \(s_0[1]\), \(s_1\) are the simple representations and since \(s_{\ge 1}, s_{\le 0}[1] \in Rep_{{\mathbb {K}}}(K(l))\) (Lemma 7.3), it follows that (see also 80) for any \(i\ge 1\) \(Z'(s_i)=n_i Z'(s_0[1]) + m_i Z'(s_1)\), and for any \(i\le 0\) \(Z'(s_i[1])=n_i Z'(s_0[1]) + m_i Z'(s_1)\), and now using [18, Remark 3.16] (in particular f is as in 87) we obtain :
$$\begin{aligned} \pm \frac{Z'(s_i)}{\left| Z'(s_i)\right| }= \left\{ \begin{array}{ll} \mp \frac{n_i Z'(s_0) + m_i Z'(s_1[-1])}{\left| n_i Z'(s_0) + m_i Z'(s_1[-1])\right| } = \mp \exp ({\mathrm {i}}f(n_i/m_i)) &{}\quad i\ge 1\\ \mp 1 &{}\quad i=0 \\ \pm \frac{n_i Z'(s_0) + m_i Z'(s_1[-1])}{\left| n_i Z'(s_0) + m_i Z'(s_1[-1])\right| } = \pm \exp ({\mathrm {i}}f(n_i/m_i)) &{}\quad i \le -1 \end{array} \right. .\nonumber \\ \end{aligned}$$(100)In (b) we showed that \(P_{\sigma '}^l\) equals the set on the RHS of (86). Due to Lemma 7.3 we get that \(L(P_{\sigma '}^l)=\pm \exp \left( {\mathrm {i}}f\left( \left[ a_l^{-1}, a_l\right] \right) \right) \), and therefore (100) and (17) imply that \(P_{\sigma '}^l{\setminus } L(P_{\sigma '}^l)=\{\pm \exp ({\mathrm {i}}\pi \phi _{\sigma '}(s_i))\}_{i\in {\mathbb {Z}}}\). Recalling that \(\sigma ' = \lambda \star \sigma \) for certain \(\lambda \in {\mathbb {C}}\) with the help of formulas (30) and (35) we deduce the desired \(P_{\sigma }^l{\setminus } L(P_{\sigma }^l)=\{\pm \exp ({\mathrm {i}}\pi \phi _{\sigma }(s_i))\}_{i\in {\mathbb {Z}}}\).
-
(d)
In (b) we showed that \(P_{\sigma '}^l\) for \(\sigma '=(Z',{\mathcal {P}}')= (-\log \left| Z(s_j)\right| + {\mathrm {i}}\pi (1-\phi _{\sigma }(s_j)))\star \sigma \) equals the RHS of (86) and taking into account Lemma 7.3 we deduce that \(P_{\sigma '}^l{\setminus } L(P_{\sigma '}^l)=\pm 1 \cup \{\pm \exp \left( {\mathrm {i}}f\left( n_i/m_i \right) \right) :i\ne 0 \}\), which combined with (c) yields:
$$\begin{aligned} \pm 1 \cup \{\pm \exp \left( {\mathrm {i}}f\left( n_i/m_i \right) \right) :i\ne 0 \} = \{\pm \exp ({\mathrm {i}}\pi \phi _{\sigma '}(s_i))\}_{i\in {\mathbb {Z}}}. \end{aligned}$$(101)Recalling that (85) holds for any \(j\in {\mathbb {Z}}\) and also (76), (98) we derive:
$$\begin{aligned}&0=\phi _{\sigma '}(s_j)-1< \phi _{\sigma '}(s_{j+1}[-1])<\phi _{\sigma '}(s_{j+2}[-1])<\cdots< \phi _{\sigma '} (s_{j-2}) \nonumber \\&\quad< \phi _{\sigma '} (s_{j-1}) < \phi _{\sigma '}(s_j) =1 \end{aligned}$$(102)We already know that (see (b) of the proposition and (e) in Lemma 7.3)
$$\begin{aligned} f(0)= & {} f(n_1/m_1)=\pi (\phi _{\sigma }(s_{j+1})-\phi _{\sigma }(s_{j}))\nonumber \\= & {} \pi \phi _{\sigma '}(s_{j+1}[-1])=\arccos (y). \end{aligned}$$(103)Furthermore from (e) in Lemma 7.3 we deduce:
$$\begin{aligned}&0<f\left( \frac{n_1}{m_1}\right)<f\left( \frac{n_2}{m_2}\right)<\cdots<f(a_l^{-1})\nonumber \\&\quad \le f(a_l)<\cdots<f\left( \frac{n_{-2}}{m_{-2}}\right)<f\left( \frac{n_{-1}}{m_{-1}}\right) <\pi . \end{aligned}$$(104)By induction the equalities (101), (102), (104) imply:
$$\begin{aligned} k\ge 1 \ \ \Rightarrow \ \ f\left( \frac{n_k}{m_k}\right) =\pi \phi _{\sigma '}(s_{j+k}[-1]) \quad f\left( \frac{n_{-k}}{m_{-k}}\right) =\pi \phi _{\sigma '}(s_{j-k}). \end{aligned}$$(105)Now recalling that (see (31))
$$\begin{aligned} \forall i \in {\mathbb {Z}}\ \ \ \phi _{\sigma '}(s_{i}) = \phi _{\sigma }(s_{i})+1-\phi _\sigma (s_{j}) \end{aligned}$$(106)we deduce (88), (89), (91) from (105), (103), and (102). The equality (90) in turn follows from (86), (105), (106).
-
(e)
Follows easily from the already proven (d).
7.3 Computing \(\left\| D^b(K(l))\right\| _\varepsilon \)
.
If we define the function:
then using Proposition 7.4 (a), Lemma 7.3 (e), and formulas (86), (87) one concludes that:
Proposition 7.6
Let \(\sigma = (Z, {\mathcal {P}})\in \mathrm {Stab}({\mathcal {T}}_l)\).
If \(\sigma \not \in {\mathcal {Z}}\), then \(\mathrm {vol}\left( \overline{P_\sigma ^l}\right) =0\). If \(\sigma \in {\mathcal {Z}}\), then for any \(j\in {\mathbb {Z}}\) holds:
One computes
and therefore:
which implies that for any \(x>0\), \(y\in (-1,+1)\) we have:
On the other hand one computes that for any \(y\in (-1,+1), t \in (0,+\infty )\) holds:
Therefore the numbers (115) depending on \(\varepsilon \in (0,1)\) and \(l\ge 2\) satisfy (116), (117), (118):
The inequality (111) and the derivative (113) imply that for \(\varepsilon \in (0,+1)\) and \( l\ge 2\) holds:
Note that \(\sup _{(x,y)\in (0,+\infty )\times (-1,1)}\left\{ F(x,y,a_l)- F(x,y,a_l^{-1})\right\} \) is always equal to \(\pi \) independently on \(l\ge 3\) as opposed to \(K_\varepsilon (l)\), which is strictly increasing on l.
Finally we note that for \(\varepsilon =1/2\) the expression (115) takes a simple form (recall that \(l=\frac{a_l^2+1}{a_l}\)):Footnote 6 \( K_{\frac{1}{2}}(l)=\arccos \left( \frac{2}{l}\right) . \) and from Proposition 7.7 follows (12).
Now we can compute \( \left\| D^b(K(l))\right\| _{\varepsilon }\).
Proposition 7.7
Let \(\varepsilon \in (0,1)\), \(l\ge 2\), and let \( K_{\varepsilon }(l)\) be as in (115). Then \( \left\| D^b(K(l))\right\| _{\varepsilon } = K_{\varepsilon }(l)\).
Proof
From Proposition 7.4 (a), (b), (e) we see that \(P_\sigma \) is not dense in \({\mathbb {S}}^1\) for all \(\sigma \), and (38) reduces to the following formula:
By using (108) and (120) we will show that for all \(j \in {\mathbb {Z}}\) holds:
and then the proposition follows. Recalling Proposition 7.2 we see that \(\sigma \in \mathcal {Z}\) and \(\phi _\sigma (s_{j+1})-\phi _\sigma (s_{j})>\varepsilon \) iff \(s_{j}, s_{j+1} \in \sigma ^{ss}\) and \(\varepsilon<\phi _\sigma (s_{j+1})-\phi _\sigma (s_{j})< 1\), furthermore restricting the map (79) to the set of stability conditions \(\sigma \) with \(s_{j}, s_{j+1} \in \sigma ^{ss}\) and \(\varepsilon<\phi _\sigma (s_{j+1})-\phi _\sigma (s_{j})< 1\) we see that the set of pairs \((x_j(\sigma )\), \(y_j(\sigma ))\) from (108) for these \(\sigma \) is:
Combining the latter equality with (108) and (120) leads to (121). \(\square \)
8 The inequality \(\left\| \left\langle E_1,E_2\right\rangle \right\| _{\varepsilon }\ge K_\varepsilon (\hom ^{min}(E_1,E_2))\)
In this section we dervie a formula, which will help us to compute other norms. To that end it is useful to extend the definition of \(K_\varepsilon (l)\) in (115) by postulating \(K_\varepsilon (0)=K_\varepsilon (1)=0\). Recall that the notation \(\hom ^{min}(E_1,E_2)\) is explained in (14): this is the dimension of \(\mathrm {Hom}^i(E_1,E_2)\) for the smallest i such that \(\mathrm {Hom}^i(E_1,E_2)\ne 0\), if there is no such i \(\hom ^{min}(E_1,E_2)\) is by definition 0.
Proposition 8.1
Let \({\mathcal {T}}\) be a proper category, and let \((E_1,E_2)\) be any exceptional pair in it. Then
Proof
We can assume that \(\hom ^{\le 0}(E_1,E_2)=0\) and \(l=\hom ^1(E_1,E_2)\ne 0\), and under these assumption we have to show that
Let \({\mathcal {D}}\) be the triangulated subcategory \(\left\langle E_1,E_2\right\rangle \). The assumptions on \((E_1,E_2)\) are the same as in the definition of an l-Kronecker pair, [21, Definition 3.20], and we can apply [21, Lemma 3.19, Corollary 3.21] to it. In particular the extension closure \({\mathcal {A}}\) of \((E_1,E_2)\) is a heart of a bounded t-structure in \({\mathcal {D}}\) with simple objects \(E_1,E_2\), and any stability condition \(\sigma = (Z, {\mathcal {P}}) \in {\mathbb {H}}^{{\mathcal {A}}}{\subset } \mathrm {Stab}({\mathcal {D}})\) with \(\arg (Z(E_1))>\arg (Z(E_2))\) satisfies \(P_\sigma ^{{\mathcal {D}}}=R_{v,\Delta _{l+}}\), where \(v=(Z(E_1),Z(E_2))\). The arguments in the beginning of the proof of Lemma 4.7 show that for each \(v\in {\mathbb {H}}^2\) there exists unique \(\sigma =(Z, {\mathcal {P}}) \in {\mathbb {H}}^{{\mathcal {A}}}\) with \(v=(Z(E_1),Z(E_2))\) and that \(\sigma \) is full. For any \(0<\mu \) such that \(\mu +\varepsilon <1\) choose the vector \((-1,\exp ({\mathrm {i}}\pi (\varepsilon +\mu )))=v_{\mu }\) and denote by \(\sigma _{\mu }\) the stability condition \(\sigma _{\mu }=({\mathcal {P}}_{\mu }, Z_{\mu }) \in {\mathbb {H}}^{{\mathcal {A}}}\) with \((Z_{\mu }(E_1), Z_{\mu }(E_2))=v_{\mu }\). The given arguments ensure that \(\sigma _{\mu }\) is full and \(P_{\sigma _{\mu }}^{{\mathcal {D}}}= R_{v_{\mu },\Delta _{l+}}\). Using the formula for \(R_{v_{\mu },\Delta _{l+}}\) in Lemma 7.5 for the given \(v_\mu \) one derives:
where \(K_{\varepsilon + \mu }(l) \) is in (115). Note that the arc \(\exp \left( {\mathrm {i}}\pi [\mu /2,\varepsilon +\mu /2]\right) \) is in the complement of \(P^{{\mathcal {D}}}_{\sigma _\mu }\) and therefore \(\sigma _\mu \in \mathrm {Stab}_{\varepsilon }({\mathcal {D}})\). Now from the very Definition 4.11 we see that \(\left\| {\mathcal {D}}\right\| _{\varepsilon }\ge K_{\varepsilon + \mu }(l)\) for any small enough positive \(\mu \), letting \(\mu \rightarrow 0\) we derive the desired \(\left\| {\mathcal {D}}\right\| _{\varepsilon }\ge K_{\varepsilon }(l)\). \(\square \)
Corollary 8.2
Let \({\mathcal {E}} = (E_0, E_1,\dots ,E_n)\) be an exceptional collection in a proper triangulated category \({\mathcal {T}}\). Then for any \(0\le i<j\le n\) we have \(\left\| \left\langle {\mathcal {E}}\right\rangle \right\| _{\varepsilon } \ge K_\varepsilon \left( \hom ^{min}(E_i,E_j) \right) \).
Proof
Take \(0\le i < j \le n\). By mutating the sequence \({\mathcal {E}}\) (see Remark 7.1) one can get a sequence \({\mathcal {E}}'\) of the form \({\mathcal {E}}'=(E_i,E_j,C_2,\dots ,C_n)\) such that \(\left\langle {\mathcal {E}}\right\rangle =\left\langle {\mathcal {E}}'\right\rangle \). Corollary 6.3 implies \(\left\| \left\langle {\mathcal {E}}\right\rangle \right\| _{\varepsilon }=\left\| \left\langle {\mathcal {E}}'\right\rangle \right\| _{\varepsilon }\ge \left\| \left\langle E_i,E_j\right\rangle \right\| _{\varepsilon }\), and due to Proposition 8.1 we get \(\left\| \left\langle E_i,E_j\right\rangle \right\| _{\varepsilon }\ge K_\varepsilon (\hom ^{min}(E_i,E_j))\). \(\square \)
Corollary 8.3
Let \({\mathcal {T}}\) be a proper triangulated category such that for each \(l\in {\mathbb {N}}\) there exists a full exceptional collection \((E_0,E_1,\dots , E_n)\) and integers \(0\le i<j\le n\) for which \(\hom ^{min}(E_i,E_j)\ge l\). Then \(\left\| {\mathcal {T}}\right\| _{\varepsilon }= \pi (1-\varepsilon )\) for any \(\varepsilon \in (0,1)\).
Proof
The given property of \({\mathcal {T}}\) combined with Corollary 8.2 amounts to \(\left\| {\mathcal {T}}\right\| _{\varepsilon }\ge K_{\varepsilon }(l)\) for each \(l\ge {\mathbb {N}}\) (Recall also 118). Now from (119) and Remark 4.14 we obtain \(\left\| {\mathcal {T}}\right\| _{\varepsilon }=\pi (1-\varepsilon )\). \(\square \)
Corollary 8.4
Let \({\mathcal {T}}\) be a proper category, and let \(0<\varepsilon <1\).
-
(a)
If \(\left\| {\mathcal {T}}\right\| _{\varepsilon }=0\), then for any full exceptional collection \({\mathcal {E}}=(E_0,E_1,\dots , E_n)\) and for any \(0\le i<j\le n\) we have \(\hom ^{min}(E_i,E_j)\le 2\).
-
(b)
If \(\left\| {\mathcal {T}}\right\| _{\varepsilon }\le K_\varepsilon (l)\), \(l\ge 2\), then for any full exceptional collection \({\mathcal {E}}=(E_0,E_1,\dots , E_n)\) and for any \(0\le i<j\le n\) we have \(\hom ^{min}(E_i,E_j)\le l\).
-
(c)
If \(\left\| {\mathcal {T}}\right\| _{\varepsilon }<\pi (1-\varepsilon )\), then there exists \(l\in {\mathbb {N}}\) such that for any full exceptional collection \({\mathcal {E}}=(E_0,E_1,\dots , E_n)\) and for any \(0\le i<j\le n\) we have \(\hom ^{min}(E_i,E_j)\le l\).
We will aply Corollary 8.3 to various examples. More precisely we will show that
Proposition 8.5
In the following examples of triangulated categories are satisfied the conditions of Corollary 8.3. In particular \(\left\| {\mathcal {T}}\right\| _{\varepsilon }=(1-\varepsilon ) \pi \) for any \({\mathcal {T}}\) in this list of examples.
-
(a)
\(D^b(Q)\), where Q is an acyclic quiver, s.t. there exists a subset \(A{\subset } V(Q)\) such that the quiver \(Q_A\) is affine and there exists a vertex \(v \in V(Q)\) such that v is a source or a sink in \(Q_{A\cup \{v\}}\) (see Definition 8.6 for the terminology)
-
(b)
\(D^b({\mathbb {P}}^n), n\ge 2\);
-
(c)
\(D^b({\mathbb {P}}^1\times {\mathbb {P}}^1)\);
-
(d)
Footnote 7 \(D^b({{\mathbb {F}}}_m), m\ge 0\)
-
(e)
\(D^b(X)\), where X is a smooth algebraic variety obtained from \({\mathbb {P}}^n\), \(n\ge 2\), or from \({\mathbb {P}}^1\times {\mathbb {P}}^1\), or from \({{\mathbb {F}}}_m, m\ge 0\) by a sequence of blow ups at finite number of points;
-
(f)
\(D^b(S)\), where S is any smooth complete rational surfaceFootnote 8
Definition 8.6
For any quiver Q and any subset \(A{\subset } V(Q)\) we denote by \(Q_A\) the quiver whose vertices are A and whose arrows are those arrows of Q whose initial and final vertex is in A. A vertex \(v \in V(Q)\) is called adjacent to A if there exists an arrow in Q starting at v and ending at a vertex of A or an arrow starting at a vertex of A and ending at a v.
Proof of Proposition 8.5 (a)
Let \(l\ge 3\). By [21, Corollary 3.36] for any \(l\ge 3\) there exists a an exceptional pair \((E_0,E_1)\) in \(D^b(Q)\) such that \(\hom ^{min}(E_0,E_1)\ge l\). In [17] is shown that \((E_0,E_1)\) can be extended to a full exceptional collection. Therefore we can apply Corollary 8.3 to \(D^b(Q)\). \(\square \)
Now we present one method (Lemma 8.8) to obtain l-Kronecker pairs with arbitrary big l as part of full exceptional collections, i.e. method to obtain the conditions of Corollary 8.3. This method relies on full exceptional collections in which a triple remains strong after certain mutations (see (c) in the statement of Lemma 8.8). In [9] a strong exceptional collection \({\mathcal {E}}\) which remains strong under all mutations is called non-degenerate. Furthermore in [9] are defined so called geometric exceptional collections and [9, Corollary 2.4] says that geometricity implies non-degeneracy. Furthermore, [9, Proposition 3.3] claims that a full exceptional collection of length m of coherent sheaves on a smooth projective variety X of dimension n is geometric if and only if \(m=n+1\). In particular it follows:
Remark 8.7
The full exceptional collection \({\mathcal {E}}=\{{\mathcal {O}}, {\mathcal {O}}(1),\dots , {\mathcal {O}}(n)\}\) in \(D^b({\mathbb {P}}^n)\) introduced by Beilinson [3] is geometric and therefore non-degenerate, whereas the well known (see [24, 38]) strong full exceptional collection of line bundles \(({\mathcal {O}}(0,0), {\mathcal {O}}(0,1), {\mathcal {O}}(1,0), {\mathcal {O}}(1,1))\) in \(D^b({\mathbb {P}}^1\times {\mathbb {P}}^1)\) is not geometric.
That’s why the method of Lemma 8.8 is readily applied to \(D^b({\mathbb {P}}^n)\), whereas applying it to \(D^b({\mathbb {P}}^1\times {\mathbb {P}}^1)\) requires some additional arguments to ensure (c) in Lemma 8.8.
Lemma 8.8
Let \({\mathcal {T}}\) be a proper triangulated category and \(\varepsilon \in (0,1)\). Let \({\mathcal {E}}=(F_0,F_1,F_2,E_3,\dots ,E_n)\) be a full exceptional collection with \(n\ge 3\). Let \(\{F_i\}_{i\in {\mathbb {N}}}\) be a sequence starting with \(F_0,F_1,F_2\) and \(F_{i+1}=R_{F_{i}}(F_{i-1})\) for \(i\ge 2\). If the following three properties hold:
-
(a)
\(\hom (F_0,F_1)<\hom (F_0,F_2)\);
-
(b)
\(l=\hom (F_1,F_2)\ge 2\);
-
(c)
\((F_0,F_i,F_{i+1})\) is strong for all \(i\ge 1\), then \({\mathcal {T}}\) satisfies the condition of Corollary 8.3 and \(\left\| {\mathcal {T}}\right\| _{\varepsilon }=\pi (1-\varepsilon )\).
Proof
Now (71) becomes

Since the property of being full is preserved under mutations, it follows that \((F_0,F_{i-1},F_i,E_3\dots ,E_n)\) is full for each \(i\ge 2\). We will show that (127) holds, and then our \({\mathcal {T}}\) satisfies the conditions of Corollary 8.3, hence \(\left\| {\mathcal {T}}\right\| _{\varepsilon }=\pi (1-\varepsilon )\).
To show (127) we first note that due to (c) we have \(\hom ^k(F_{i-1},F_i)=0\) for each \(k\ne 0\) and each \(i\ge 2\) and it follows that (see e.g. [9, Example 2.7]) \(l=\hom (F_{1},F_{2})=\hom (F_{i-1},F_{i})=\hom (F_{i},F_{i+1})\) for each \(i\ge 2\) and then (126) has the form:

In (a) we are given \(\hom (F_{0},F_{i-1})<\hom (F_{0},F_{i})\) for \(i=2\) and we will show (127) by induction. Indeed, since \((F_0,F_{i-1},F_i)\) is a strong exceptional collection for each \(i\ge 2\), applying \(\mathrm {Hom}(F_0,\_)\) to (128) yields short exact sequences between finite dimensional vector spaces:

The obtained exact sequences and \(l \ge 2\) imply:
hence for \(i\ge 2\) the inequality \(\hom (F_0,F_{i}) > \hom (F_0,F_{i-1})\) implies \(\hom (F_0,F_{i+1}) > \hom (F_0,F_{i})\). The lemma is proved. \(\square \)
Proof of Proposition 8.5 (b)
In Remark 8.7 is given a full strong exceptional collection \({\mathcal {E}}\) on \(D^b({\mathbb {P}}^n)\) which remains strong under all mutations. Using [9, Example 2.9] one computes \(\hom ({\mathcal {O}},{\mathcal {O}}(1))=\hom ({\mathcal {O}}(1),{\mathcal {O}}(2))=n+1<\hom ({\mathcal {O}},{\mathcal {O}}(2))=\frac{(n+1)(n+2)}{2}\). Therefore we can apply Lemma 8.8 and the corollary follows. \(\square \)
Proof of Proposition 8.5 (c)
Let us denote here \({\mathcal {T}}=D^b({\mathbb {P}}^1 \times {\mathbb {P}}^1)\). Exceptional collections in \({\mathcal {T}}\) have been studied in [38] and [24]. In particular the full strong exceptional collection \(({\mathcal {O}}(0,0), {\mathcal {O}}(0,1), {\mathcal {O}}(1,0), {\mathcal {O}}(1,1))\) mentioned in Remark 8.7 satisfies \(\hom ({\mathcal {O}}(0,0),{\mathcal {O}}(0,1))= \hom ({\mathcal {O}}(0,1),{\mathcal {O}}(1,1))=2\) and \(\hom ({\mathcal {O}}(0,0),{\mathcal {O}}(1,1))=4\) (see [35, p. 3] or [8, Example 6.5]). After one mutation we get a full exceptional collection \((F_0,F_1,F_2,E_3)\) in which \((F_0,F_1,F_2)\) is strong, \(\hom (F_0,F_1)<\hom (F_0,F_2)\), and \(\hom (F_1,F_2)=2\). Let \(\{F_i\}_{i\in {\mathbb {N}}}\) be a sequence starting with \(F_0,F_1,F_2\) and \(F_{i+1}=R_{F_{i}}(F_{i-1})\) for \(i\ge 2\). To apply Lemma 8.8 and deduce that \(\left\| {\mathcal {T}}\right\| _{\varepsilon }=\pi (1-\varepsilon )\) we need to show that \((F_0,F_i,F_{i+1})\) is strong for all \(i\ge 1\).
From [24, Proposition 5.3.1, Theorem 3.3.1.] it follows that:
From the way we defined \(\{F_i\}_{i\in {\mathbb {N}}}\) it follows (see e.g. [9, Example 2.7]) \(2=\hom (F_{1},F_{2})=\hom (F_{i-1},F_{i})=\hom (F_{i},F_{i+1})\) for all \(i\ge 2\), hence taking into account (131), to show that \((F_0,F_i,F_{i+1})\) is strong for all \(i\ge 1\) suffices to show that \(\hom (F_0,F_i)\ne 0\) for each \(i\ge 1\). Now (71) becomes distinguished triangle

We have \(0<\hom (F_0,F_1)<\hom (F_0,F_2)\). Assume that for some \(i\ge 2\) holds
we will show that this implies \(\hom (F_0,F_{i})<\hom (F_0,F_{i+1})\) and by induction the corollary follows. Applying \(\mathrm {Hom}(F_0,\_)\) to (132) and since \(\hom ^k(F_0,F_{i-1})=\hom ^k(F_0,F_{i})=0\) for \(k\ne 0\) one easily deduces that \(\hom ^k(F_0,F_{i+1})=0\) for \(k\not \in \{ -1, 0\}\). If \(\hom ^{-1}(F_0,F_{i+1})\ne 0\), then by (131) it follows that \(\hom (F_0,F_{i+1})=0\) and applying \(\mathrm {Hom}(F_0,\_)\) to (132) yields an exact sequence of vector spaces:

which contradicts (133). Therefore \(\hom ^{-1}(F_0,F_{i+1})=0\) and \(\hom ^k(F_0,F_{i+1})=0\) for \(k\ne 0\). Now we apply \(\mathrm {Hom}(F_0,\_)\) to (132) again and get a short exact sequence as in (128) which by the same computation as in (130) implies \( \hom (F_0,F_{i+1})> \hom (F_0,F_{i})\), thus we proved the corollary. \(\square \)
Lemma 8.9
Let X be a smooth algebraic variety s. t. \(D^b(X)\) satisfies the conditions of Corollary 8.3. Let \(\widetilde{X}\) be obtained from X by blowing up a point. Then \(D^b(\widetilde{X})\) satisfies the conditions of Corollary 8.3 as well.
Proof
[7, Theorem 4.2] ensures that there is a semi-orthogonal decomposition
\(D^b(\widetilde{X})=\langle {\mathcal {T}}_1, {\mathcal {T}}_2,\dots ,{\mathcal {T}}_k, D^b(X)\rangle \), where \({\mathcal {T}}_i\) is equivalent to \(D^b(point)\) for \(i=1,2,\dots ,k\), which implies that \({\mathcal {T}}_i\) is generated by an exceptional object for each i. Now it is clear that the full exceptional sequences of \(D^b(X)\) ensuring the conditions of Corollary 8.3 extend to full exceptional collections on \(D^b(\widetilde{X})\), so these conditions are satisfied in \(D^b(\widetilde{X})\) as well. \(\square \)
Proof of Proposition 8.5 (d), (e), and (f)
Since \({{\mathbb {F}}}_0={\mathbb {P}}^1\times {\mathbb {P}}^1\) and \({{\mathbb {F}}}_1\) is \({\mathbb {P}}^2\) blown up at a point, then the cases \(a=0,1\) are contained in Proposition 8.5 (a), (b), and Lemma 8.9. In [28] they construct families of full exceptional collections of invertible sheaves on \(D^b({{\mathbb {F}}}_a)\) for any a. To show that their exceptional collections furnish the conditions of Corollary 8.3 we just need to combine some results in [28]. First adopt here some notations and terminology from [28]: P, Q denotes basis of \(Pic({{\mathbb {F}}}_a)\) (see [28, Section 4, p.1224]) s.t.
Hille and Perling study certain sequences of Cartier divisors on a rational surfaces X which they call toric systems. Furthermore a toric system \(A_1,A_2,\dots , A_n\) is called strongly exceptional (see [28, Definition 3.6]), if they generate a sequence of invertible sheaves
which is strong exceptional. For such a toric system each divisor \(A_j\) is numerically left orthogonal [28, Definition 3.1 (a)], which means that \(\chi (-A_j)=0\). Indeed, we have
for each \(k\in {\mathbb {Z}}\), since the sequence is exceptional, and on the other hand
(see e.g. [28, the beginning of Section 3]), and hence \(\chi (-A_j)=0\). Note also that since the sequence is strong it follows that \(\chi (A_j)=\dim (H^0({\mathcal {O}}_X(A_j)))=\hom \left( O_X\left( \sum _{i=1}^{j-1}A_i\right) , O_X\left( \sum _{i=1}^{j}A_i\right) \right) \). On the other hand, having that \(A_j\) is numerically left orthogonal and using [28, Lemma 3.3 (i)] we derive:
[28, Proposition 5.2] proves that \(P, s P +Q, P, -(a+s)P+Q\) is a strongly exceptional toric system on \({{\mathbb {F}}}_a\) when \(s\ge -1\). If we denote by \(E_1^{s},E_2^{s},E_3^{s},E_4^{s}\) the corresponding strong exceptional collection, then using the formula (136) and the property of toric system, that \(\sum _{i=1}^n A_i = -K_X\) (see [28, p. 1233 down]), and also the equalities (135) we compute:
Thus we see that \(\hom (E_2^s,E_3^s)\) can be done arbitrary big. The sequence \(E_1^{s},E_2^{s},E_3^{s},E_4^{s}\) is already shown to be full (see [28, Theorem 5.8.], also [28, the beginning of the proof of Theorem 8.6.] or [29, Proposition 2.1]). Part (d) is proved. Part (e) follows by recursively applying Lemma 8.9 and the already proven cases. Part (f) reduces to part (e), since any smooth complete rational surface S can be constructed after applying a finite sequence of blow ups starting with \({\mathbb {P}}^2\) of \({\mathbb {F}}_a\), \(a\ge 0\) (see e.g. [28, the beginning of Section 4, p. 1243]). \(\square \)
9 The inequality \(\left\| {{\mathcal {T}}}_{l_1}\oplus \dots \oplus {{\mathcal {T}}}_{l_n}\right\| _{\varepsilon }<\pi (1-\varepsilon )\)
The goal of this seciton is to prove the following:
Proposition 9.1
Let \(n\ge 1\), let \(l_i\ge 1\), \(i=1,2,\dots ,n\) be a sequence of integers, and let \(0<\varepsilon <1\). Then for any orthogonal decomposition of the form \({\mathcal {T}} ={{\mathcal {T}}}_{l_1}\oplus {{\mathcal {T}}}_{l_2}\oplus \dots \oplus {{\mathcal {T}}}_{l_n}\), where \({\mathcal {T}}_{l_i} \cong D^b(K(l_i))\), holds \(\left\| {\mathcal {T}}\right\| _{\varepsilon }<\pi (1-\varepsilon )\). Furthermore \(\left\| {\mathcal {T}}\right\| _{\varepsilon }>0\) iff \(l_i\ge 3\) for some \(1\le i\le n\).
Before going to the proof of this proposition we prove some facts for the case \(l\ge 3\) and denote \({\mathcal {T}}_l=D^b(K(l))\). We will use notations and results from Sect. 7. The first step is:
Lemma 9.2
For \(\sigma \not \in {\mathcal {Z}}\) the set \(P_\sigma ^l=\overline{P_\sigma ^l}\) is finite. Otherwise, for \(\sigma \in {\mathcal {Z}}\), we use the description of the set \(\overline{P_\sigma ^l}\) as in Proposition 7.4 (88), (89), (90).
For any \(0<\varepsilon <1\) there exists \(M_{l,\varepsilon } >0\) such that for any \(\sigma \in {\mathcal {Z}}\) and for any \(j\in {\mathbb {Z}}\) :
Proof
The part of the lemma which is not contained in Proposition 7.4 are the inequalities (138). So, let us chose \(\sigma \in {\mathcal {Z}}\), \(j\in {\mathbb {Z}}\) and \(0<\varepsilon <1\) and assume that \(\phi _\sigma (s_{j+1})-\phi _\sigma (s_{j})>\varepsilon \). In terms of the function (107) we can rewrite (91) as follows:
where (recall that \(\sigma \in {\mathcal {Z}}\) implies \(\phi _\sigma (s_{j+1})-\phi _\sigma (s_{j})<1\)):
For any \(a\in (0,+\infty )\), \(b\in (-1,+1)\) the differentiable functions \((0,+\infty )\ni t \mapsto F(a,b,t)\) and \((0,+\infty )\ni t \mapsto F(t,b,a)\) can be extended uniquely to continuous functions in \([0,+\infty )\) having values \(\arccos (b)\) and \(\pi \) at 0, respectively, and therefore we can apply the mean value theorem to these functions. More precisely, if \(h:[0,+\infty )\rightarrow {\mathbb {R}}\) is a function obtained in such a way, then for any \(0\le \alpha< \beta < +\infty \) there exists \(\alpha< t < \beta \), such that \(h(\beta )-h(\alpha )=(\beta - \alpha ) h'(t)\). In particular, for any x, y as in (140) we can represent all the differences in (139) as follows (recall 109):
And now looking back at (139) we deduce:
Now since \(t'^2+x^2- 2 t' x \cos (\pi \varepsilon )\) gets minimal values for \( t'= x \cos (\pi \varepsilon )\) (with respect to the variable \(t'\)) and for \(x=t' \cos (\pi \varepsilon )\) (with respect to the variable x) we have \(t'^2+x^2- 2 t' x \cos (\pi \varepsilon )\ge x^2(1-\cos ^2(\pi \varepsilon ))= x^2\sin ^2(\pi \varepsilon )\) and \(t'^2+x^2- 2 t' x \cos (\pi \varepsilon )\ge t'^2 \sin ^2(\pi \varepsilon ) \ge a_l^{-2} \sin ^2(\pi \varepsilon ) \), therefore:
and (144), (145) can be continued (recall that \(0<t<a_l^{-1}\) in (142) and \(0<x'<x\) in (141)):
hence (138) follows. \(\square \)
Corollary 9.3
For any \(\sigma \in {\mathcal {Z}}\) there is closed \(\frac{\mathrm {vol}(\overline{P_\sigma ^l})}{2}\)-arc \(p_\sigma ^l{\subset } \overline{P_\sigma ^l}\) s.t. \( \overline{P_\sigma ^l}{\setminus } (p_\sigma ^l \cup - p_\sigma ^l) \) is countable.
Let \(0<\varepsilon <1\). For any closed \(\varepsilon \)-arc \(\gamma \) satisfying \(P_\sigma ^l \cap \gamma = \emptyset \) hold \((p_\sigma ^l\cup -p_\sigma ^l)\cap (\gamma \cup -\gamma )=\emptyset \) and any (of the four) connected component c of \({\mathbb {S}}^1{\setminus }\{p_\sigma ^l\cup -p_\sigma ^l\cup \gamma \cup -\gamma \}\) restricts \(\mathrm {vol}(\overline{P_\sigma ^l})\) as follows:
where \(M_{l,\varepsilon }\) is as in Lemma 9.2.
Proof
For \(\sigma \in {\mathcal {Z}}\), the set \(\overline{P_\sigma ^l}\) is as described in (88), (89), (90) and then we can choose \(p_\sigma ^l\) to be \(\exp ({\mathrm {i}}[u_\sigma ,v_\sigma ])\) and \({\mathbb {S}}^1\) can be divided as follows (for any \(j\in {\mathbb {Z}}\)):
Furthermore, let \(\gamma \) be a closed \(\varepsilon \)-arc with \(P_\sigma ^l\cap \gamma =\emptyset \), then using (89) one easily sees that \(\gamma {\subset } \exp ({\mathrm {i}}\pi (\phi _\sigma (s_j),\phi _\sigma (s_{j+1})))\) or \(-\gamma {\subset } \exp ({\mathrm {i}}\pi (\phi _\sigma (s_j),\phi _\sigma (s_{j+1})))\) for some \(j\in {\mathbb {Z}}\) and therefore \(\pi (\phi _\sigma (s_{j+1})-\phi _\sigma (s_{j}))>\mathrm {vol}(\gamma )=\pi \varepsilon \), hence by Lemma 9.2 follow the inequalities (138) and
Therefore, taking into account the disjoint union (148) we see that the four components of \({\mathbb {S}}^1{\setminus } \{ \gamma \cup -\gamma \cup p_\sigma ^l \cup -p_\sigma ^l \}\) can be ordered as \(c_1\), \(c_2\), \(-c_1\), \(-c_2\) so that: \(c_1 \supset {\mathrm{e}}^{{\mathrm {i}}[\pi \phi _\sigma (s_{j+1}[-1]), u_\sigma )}\), \(c_2\supset \mathrm{e}^{{\mathrm {i}}(v_\sigma ,\pi \phi _\sigma (s_{j}))}\), in particular:
and the corollary follows from (138). \(\square \)
Proof of Proposition 9.1
From Remark 4.15 and Sect. 7.3 we see that:
hence the proposition follows for \(n=1\). \(\square \)
Assume that we have already proved the proposition for \(1\le n \le N\). And assume that \({\mathcal {T}} ={{\mathcal {T}}}_{l_1}\oplus {{\mathcal {T}}}_{l_2}\oplus \dots \oplus {{\mathcal {T}}}_{l_N}\oplus {{\mathcal {T}}}_{l_{N+1}}\), where \({\mathcal {T}}_{l_i} \cong D^b(K(l_i))\) and denote by L the set \(L=\{l_1,l_2,\dots ,l_N,l_{N+1}\}\).
If \(1\le l_j\le 2\) for some j, then \(\left\| {\mathcal {T}}_{l_j}\right\| _\varepsilon =\left\| D^b(K(l_j))\right\| _\varepsilon =0\), and the statement follows from the induction assumption, Corollary 5.6, and \(\left\| {{\mathcal {T}}}_{l_j}\right\| _\varepsilon = 0\). Therefore we can assume that all integers in L are at least 3. From the induction assumption there exists \(\delta >0\) such that:
Note that due to Remark 4.2, Proposition 5.2 (d), and Corollary 5.5 for any sequence \(x_1,x_2,\dots ,x_j\) in L holds:
Assume now that \(\sigma _i \in \mathrm {Stab}(D^b(K(l_i)))\) for \(i=1,\dots ,N+1\) and that there exists a closed \(\varepsilon \)-arc \(\gamma \) satisfying \( \emptyset = P_{\sigma _i}^{l_i} \cap \gamma =\emptyset \) for \(i=1,\dots ,N+1\). In particular we can represent the circle \({\mathbb {S}}^1\):
where \(\alpha \in {\mathbb {R}}\) and \(\beta =\alpha +\pi (1-\varepsilon )\). If for some k the corresponding \(\sigma _k \not \in {\mathcal {Z}}_{l_k} {\subset } \mathrm {Stab}(D^b(K(l_k)))\), then by Lemma 9.2\(\overline{P_{\sigma _k}^{l_k}}\) is finite and taking into account (152), (153) we derive:
otherwise for all i we have \(\sigma _i \in {\mathcal {Z}}_{l_i}\), and then by Corollary 9.3 \( \frac{\mathrm {vol}\left( \bigcup _{i=1}^{N+1}\overline{P_{\sigma _i}^{l_i}}\right) }{2}= \mathrm {vol}\left( \bigcup _{i=1}^{N+1}p_{\sigma _i}^{l_i}\right) \), where \(p_{\sigma _i}^{l_i}\) is a closed arc as explained in Corollary 9.3 and we can assume that \(p_{\sigma _i}^{l_i}{\subset } \exp ({\mathrm {i}}(\alpha ,\beta ))\) for all i (see (154)). There exist \(\delta _->0\), \(\delta _+>0\) such that \(\bigcup _{i=1}^{N+1}p_{\sigma _i}^{l_i}{\subset } \exp ({\mathrm {i}}[\alpha +\delta _-,\beta -\delta _+])\), \(\exp ({\mathrm {i}}(\alpha +\delta _-), \exp ({\mathrm {i}}(\beta -\delta _+))\) \(\in \bigcup _{i=1}^{N+1}p_{\sigma _i}^{l_i}\). Let j, k be such that \(\exp ({\mathrm {i}}(\alpha +\delta _-) \in p_{\sigma _j}^{l_j}\) and \(\exp ({\mathrm {i}}(\beta -\delta _+) \in p_{\sigma _k}^{l_k}\) If we denote \(M={\mathrm{max}}\{ M_{l_i,\varepsilon }:1\le i \le N+1 \}\), then from Corollary 9.3 we obtain \(\mathrm {vol}(p_{\sigma _j}^{l_j})+\mathrm {vol}(p_{\sigma _k}^{l_k})\le M(\delta _++\delta _-)\). Since \(\bigcup _{i=1}^{N+1}p_{\sigma _i}^{l_i}{\subset } \exp ({\mathrm {i}}[\alpha +\delta _-,\beta -\delta _+])\) it follows that \(\delta _++\delta _- \le \pi (1-\varepsilon )- \mathrm {vol}\left( \bigcup _{i=1}^{N+1}p_{\sigma _i}^{l_i}\right) \), therefore we can write:
The obtained inequalities (155), (156), and the formula (153) with \(x_i = l_i\), for \(i=1,2,\dots ,N+1\) show that for a certain set Y and a real function G on Y we have:
Now recalling (152) we get \(G(y)\le M(\pi (1-\varepsilon )-G(y)) + \pi (1-\varepsilon )-\delta \) for any \(y\in Y\), which is the same as \(G(y)\le \pi (1-\varepsilon )-\frac{\delta }{M+1}\). Therefore the proof completes with the following inequality:
10 Discrete derived categories and their norms
There are categories, in which every heart of a bounded t-structure has finitely many indecomposable objects up to isomorphism. Due to the following lemma the norm of these categories vanishes:
Lemma 10.1
For any triangulated category \({\mathcal {T}}\) and any \(a \in {\mathbb {R}}\) we have:
Proof
From [18, Lemma 3.9] we know that
Furthermore, the properties that for any \(j\in {\mathbb {Z}}\) holds \(I\in \sigma ^{ss}\) iff \(I[j]\in \sigma ^{ss}\), and that \(\phi _\sigma (I[j])=\phi _\sigma (I)+j\) whenever \(I \in \sigma ^{ss}\) are axioms of Bridgeland , which together with (159) imply
From [22, Lemma 3.7] it follows that an object \(I\in {\mathcal {P}}(a,a+1]\) is \({\mathcal {T}}\)-indecomposable iff it is \({\mathcal {P}}(a,a+1]\)-indecomposable, hence the lemma follows. \(\square \)
Corollary 10.2
Let \({\mathcal {T}}\) be a category with phase gap, s.t. every heart of a bounded t-structure has finitely many indecomposable objects up to isomorphism. Then \(\left\| {\mathcal {T}}\right\| _\varepsilon = 0\) for every \(\varepsilon \in (0,1)\).
Proof
First recall that for each \(\sigma = (Z,{\mathcal {P}})\in \mathrm {Stab}({\mathcal {T}})\) and for any \(a\in {\mathbb {R}}\) the subcategory \({\mathcal {P}}(a,a+1]\) is a heart of a bounded t-structure. From the previous lemma \(P_\sigma ^{\mathsf T}\) is finite for each \(\sigma \in \mathrm {Stab}({\mathcal {T}})\). Therefore from Definition 39 it follows that \(\left\| {\mathcal {T}}\right\| _\varepsilon = 0\). \(\square \)
In representation theory was introduced a class of triangulated categories with a particularly discrete structure, called Discrete derived categories (Vossieck [42]), they were classified in [4] and thoroughly studied in [14], whereas the topology of the stability spaces on them were studied in [13, 37], in particular it was shown that these spaces are all contractible. This class contains the categories \(\{D^b(Q): Q \ \hbox {is Dynkin}\}\), and the discrete derived categories not contained in this list are of the form \(D^b(\Lambda (r,n,m))\) for \(n\ge r \ge 1\) and \(m\ge 0\), where \(\Lambda (r,n,m)\) is the path algebra of the quiver with relations shown on [37, Section 4.3, Figure 1].
Proposition 10.3
For any discrete derived category \({\mathcal {T}}\) (in the sense of [4, 42]) and any \(\varepsilon \in (0,1)\) holds \(\left\| {\mathcal {T}}\right\| _\varepsilon = 0\).
Proof
[14, Proposition 7.1] says that each heart of a bounded t-structure in \({\mathcal {T}}\) has finitely many indecomposable objects and is of finite length. In articular (see Lemma 4.7) \({\mathcal {T}}\) has a phase gap and it satisfies the conditions of Lemma 10.2, therefore \(\left\| {\mathcal {T}}\right\| _\varepsilon = 0\). \(\square \)
11 Topology on the class of proper triangulated categories with a phase gap
In this section we denote by \({\mathfrak {T}}'\) the set of all small triangulated categories within a certain universe (a universe which contains the derived categories of representations of algebras) and by \(\mathfrak {PG}'{\subset } {\mathfrak {T}}'\) we denote the subset of proper categories with finite rank Grothendieck group and with a phase gap. From Proposition 10.3 (see also its proof) it follows that each discrete category is in \(\mathfrak {PG}'\). Furthermore, from [14, Proposition 7.6] it follows that each discrete derived category has a full Exceptional collection. Thus if we denote by \(\mathfrak {DDK}'\) the subset in \(\mathfrak {T}'\) of discrete derived categories, and by \(\mathfrak {E}'\) the subset of proper categories with a full exceptional collection, then we have the inclusions: \( \mathfrak {DDK}' {\subset } \mathfrak {E}' {\subset } \mathfrak {PG}' {\subset } \mathfrak {T}'. \) When we write \({\mathcal {A}} \cong {\mathcal {B}}\) for \({\mathcal {A}}\), \({\mathcal {B}} \in {\mathfrak {T}}'\), we mean an equivalence between triangulated categories, and by \({\mathfrak {T}}={\mathfrak {T}}'/\cong \) , \(\mathfrak {PG}=\mathfrak {PG}'/\cong \), \(\mathfrak {DDK}=\mathfrak {DDK}'/\cong \) we denote the corresponding sets of equivalence classes and then we have inclusions:
We give first an example of a topology on the largest \( \mathfrak {T}\) and give evidence that this topology is too coarse.
Definition 11.1
For any \({\mathcal {T}}\in {\mathfrak {T}}'\) we denote a subset of \({\mathfrak {T}}'\) as follows :
By definition we have \(B({\mathcal {T}}_1)=B({\mathcal {T}}_2)\), if \({\mathcal {T}}_1 \cong {\mathcal {T}}_2\).
Lemma 11.2
Let \({\mathcal {T}}'\), \({\mathcal {T}}\) be triangulated categories. If \({\mathcal {T}}'\in B({\mathcal {T}})\), then \(B({\mathcal {T}}'){\subset } B({\mathcal {T}})\). In particular, the family of sets \(\{ B({\mathcal {T}}) \}_{{\mathcal {T}} \in {\mathfrak {T}}'}\) is a base of a topology on \({\mathfrak {T}}'\), and the family of sets \(\{ B({\mathcal {T}})/\cong \}_{{\mathcal {T}} \in {\mathfrak {T}}'}\) is a base of a topology on \({\mathfrak {T}}\).
Proof
Since \({\mathcal {T}}'\in B({\mathcal {T}})\), by definition there is a SOD \({\mathcal {T}}'=\langle {\mathcal {A}}, {\mathcal {B}} \rangle \) with \({\mathcal {A}} \cong {\mathcal {T}}\).
Let \({\mathcal {T}}_1 \in B({\mathcal {T}}')\), therefore there is a SOD \({\mathcal {T}}_1=\langle {\mathcal {C}}, {\mathcal {D}} \rangle \) with \({\mathcal {C}} \cong {\mathcal {T}}'\), now the SOD \({\mathcal {T}}'=\langle {\mathcal {A}}, {\mathcal {B}} \rangle \) implies a SOD \({\mathcal {C}} = \langle {\mathcal {A}}', {\mathcal {B}}' \rangle \), where \( {\mathcal {A}}' \cong {\mathcal {A}} \cong {\mathcal {T}}\). Therefore we obtain a SOD \({\mathcal {T}}_1=\langle \langle {\mathcal {A}}', {\mathcal {B}}' \rangle , {\mathcal {D}} \rangle =\langle {\mathcal {A}}', \langle {\mathcal {B}}', {\mathcal {D}} \rangle \rangle \) with \({\mathcal {A}}' \cong {\mathcal {T}}\). i.e. \({\mathcal {T}}_1 \in B({\mathcal {T}}) \). \(\square \)
Lemma 11.3
If \({\mathcal {T}}\) is indecomposable with respect to semi-orthogonal decompositions, then \([{\mathcal {T}}]\in {\mathfrak {T}}\) is a closed points w.r. to the topology introduced in Lemma 11.2. If there exists a SOD \({\mathcal {T}}=\langle {\mathcal {A}}, {\mathcal {B}} \rangle \), where \({\mathcal {T}} \not \cong {\mathcal {A}}\), then \([{\mathcal {T}}]\in {\mathfrak {T}}\) is not a closed point in this topology.
Proof
Let \({\mathcal {T}}\) be indecomposable and \({\mathcal {T}}' \not \cong {\mathcal {T}} \), then \({\mathcal {T}} \not \in B({\mathcal {T}}')\) by the definition 11.1, therefore \([{\mathcal {T}}]\) is a closed point indeed.
Assume that there exists a SOD \({\mathcal {T}}=\langle {\mathcal {A}}, {\mathcal {B}} \rangle \) and \({\mathcal {T}} \not \cong {\mathcal {A}}\), it follows that \([{\mathcal {T}}] \in B({\mathcal {A}})/\cong \) and \([{\mathcal {T}}]\not = [{\mathcal {A}}] \), therefore all open subsets containing \([{\mathcal {A}}]\), contain \([{\mathcal {T}}]\) as well. i.e. \([{\mathcal {A}}]\) is in the closure of \([{\mathcal {T}}]\), and it is different from \([{\mathcal {T}}]\), so \([{\mathcal {T}}]\) is not a closed point. \(\square \)
Corollary 11.4
The only closed point in \(\mathfrak {E}\) w.r. to the topology introduced in Lemma 11.2 (also with respect to the induced on \(\mathfrak {E}\) topology) is \([{\mathcal {T}}]=[D^b(point)]\).
Proof
It is well known that \(D^b(point)\) is indecomposable with respect to semi-orthogonal decomposition. Now the corollary follows from Lemma 11.3. \(\square \)
Now we define a refinement of the topology discussed so far, in which we have many closed points, furthermore we have many discrete subsets, in particular the set of discrete derived categories (up to equivalence) will be a discrete subset as well. However this new topology is defined only on \(\mathfrak {PG}'\), respectively \(\mathfrak {PG}\).
Definition 11.5
For any \(\varepsilon \in (0,1)\) and any \({\mathcal {T}}\in \mathfrak {PG}' \) we denote
For any \({\mathcal {T}}\in \mathfrak {PG}'\), any \(\delta >0\) we denote a subset of \(\mathfrak {PG}'\) as follows:
By definition we have \(B_\delta ^\varepsilon ({\mathcal {T}}_1)=B_\delta ^\varepsilon ({\mathcal {T}}_2)\), if \({\mathcal {T}}_1 \cong {\mathcal {T}}_2\). Furthermore from Theorem 6.1 it follows that for any \({\mathcal {T}}_1\), \({\mathcal {T}}_2 \in \mathfrak {PG}'\) and any SOD \({\mathcal {T}}=\langle {\mathcal {T}}_1, {\mathcal {T}}_2 \rangle \) holds:
From now on \(\varepsilon \) is a real number in (0, 1) and we will write just \(B_\delta ({\mathcal {T}})\) instead of \(B_\delta ^\varepsilon ({\mathcal {T}})\).
Lemma 11.6
If \({\mathcal {T}}, {\mathcal {T}}' \in \mathfrak {PG}'\), \(\delta >0\) and \({\mathcal {T}}'\in B_\delta ({\mathcal {T}})\), then \(B_{\delta '}({\mathcal {T}}'){\subset } B_\delta ({\mathcal {T}})\) for any \(\delta '>0\). In particular, the family of sets \(\{ B_\delta ({\mathcal {T}}) \}_{{\mathcal {T}} \in \mathfrak {PG}', \delta >0}\) is a base of a topology on \(\mathfrak {PG}'\), and the family of sets
\(\{ B_\delta ({\mathcal {T}})/\cong \}_{{\mathcal {T}} \in \mathfrak {PG}', \delta >0}\) is a base of a topology on \(\mathfrak {PG}\).
Proof
Since \({\mathcal {T}}'\in B_\delta ({\mathcal {T}})\), by definition \({\mathcal {T}}'=\langle {\mathcal {A}}, {\mathcal {B}} \rangle \) with \({\mathcal {A}} \cong {\mathcal {T}}\), \({\mathcal {B}} \in \mathfrak {PG}'\) and \(\left\| {\mathcal {B}}\right\| ^{\varepsilon }<\delta \).
Let \({\mathcal {T}}_1 \in B_{\delta '}({\mathcal {T}}')\), therefore \({\mathcal {T}}_1=\langle {\mathcal {C}}, {\mathcal {D}} \rangle \) with \({\mathcal {C}} \cong {\mathcal {T}}'\), \({\mathcal {D}} \in \mathfrak {PG}'\). As in the proof of Lemma 11.2 one dervies a SOD \({\mathcal {T}}_1= \langle {\mathcal {A}}', \langle {\mathcal {B}}', {\mathcal {D}} \rangle \rangle \) with \({\mathcal {A}}' \cong {\mathcal {T}}\), \( {\mathcal {B}}'\cong {\mathcal {B}}\). From (165) we deduce the inequality \(\left\| \langle {\mathcal {B}}', {\mathcal {D}} \rangle \right\| ^\varepsilon \le \left\| {\mathcal {B}}'\right\| ^\varepsilon < \delta \), which amounts to the required \({\mathcal {T}}_1 \in B_\delta ({\mathcal {T}})\). \(\square \)
Proposition 11.7
-
(a)
The function below is upper semi-continuous:
 (166)
(166) -
(b)
For any \(x> 0\) the subset \(\mathfrak {PG}_{\ge x}=\{y \in \mathfrak {PG} : \left\| y\right\| ^\varepsilon \ge x \}\) is a discrete subset of \(\mathfrak {PG}\) w. r. to the topology from Lemma 11.6.
Proof
-
(a)
follows from the following application of (165): for any \(\delta >0\), \({\mathcal {T}} \in \mathfrak {PG}'\) holds
$$\begin{aligned} \forall [{\mathcal {T}}'] \in (B_\delta ({\mathcal {T}}) / \cong ){\setminus } \{[{\mathcal {T}}]\} \quad 0\le \left\| {\mathcal {T}}'\right\| ^\varepsilon \le \min \{\left\| {\mathcal {T}}\right\| ^\varepsilon , \delta \}. \end{aligned}$$(167) -
(b)
follows from the same formula. Indeed, from this formula one checks that for any \([{\mathcal {T}}] \in \mathfrak {PG}_{\ge x}\) and any \(0<\delta <x\) we have \(\mathfrak {PG}_{\ge x}\cap (B_\delta ({\mathcal {T}})/\cong ) = \{[{\mathcal {T}}]\}\).
\(\square \)
Corollary 11.8
\(\mathfrak {DDK} \cup \{[D^b(Q)]: Q \ \hbox {is affine} \}\) is a discrete subset of \(\mathfrak {PG}\) with respect to the topology introduced in Lemma 11.6.
Proof
From Propositions 4.19 and 10.3 it follows that for any \([{\mathcal {T}}] \in \mathfrak {DDK} \cup \{[D^b(Q)]: Q \ \hbox {is affine} \} \) has \(\left\| {\mathcal {T}}\right\| ^{\varepsilon }=\pi (1-\varepsilon )\), hence (since the function 164 takes values in \((0,\pi (1-\varepsilon ))\)) we obtain:
On the other hand from Proposition 11.7(b) we know that \( \mathfrak {PG}_{\ge \pi (1-\varepsilon )}\) is a discrete subset and the corollary follows. \(\square \)
Examples of non-closed points are contained in Proposition 8.5. More precisely:
Proposition 11.9
The element \([D^b(point)]\in \mathfrak {PG}\) is in the closure of \([{\mathcal {T}}]\in \mathfrak {PG}\) for any \({\mathcal {T}} \in \mathfrak {PG}'\) which satisfies the conditions of Corollary 8.3 and such that \({\mathrm{rank}}(K_0({\mathcal {T}}))\ge 3\).
Proof
We will show that \([{\mathcal {T}}]\in B_\delta (D^b(point))/\cong \) for any \(\delta >0\). Indeed, take any \(\delta >0\). From (119) it follows that there exists N s.t. \(\pi (1-\varepsilon )-K_\varepsilon (l) < \delta \) for \(l\ge N\). Since \({\mathcal {T}}\) satisfies the conditions of Corollary 8.3 and \({\mathrm{rank}}(K_0({\mathcal {T}}))\ge 3\), therefere there is a full exceptional collection \(E_0,E_1,\dots ,E_{n-1},E_{n}\) with \(n\ge 2\), s. t. \(\hom ^{min}(E_i,E_j)>N\) for some \(i<j\). Since we can apply mutations, we can assume that \(\hom ^{min}(E_{n-1},E_{n})>N\). Now let us denote \({\mathcal {A}}=\langle E_0 \rangle \), \({\mathcal {B}} = \langle E_1,\dots , E_n \rangle \). Then we have a SOD \({\mathcal {T}} = \langle {\mathcal {A}}, {\mathcal {B}} \rangle \) with \({\mathcal {A}} \cong D^b(point)\), and \(\left\| {\mathcal {B}}\right\| ^{\varepsilon } \le \left\| \langle E_{n-1}, E_n \rangle \right\| ^{\varepsilon }\le \pi (1-\varepsilon ) - K_\varepsilon (\hom ^{min}(E_{n-1},E_{n}))<\delta \), where in the latter chain of inequalities we used (165), Proposition 8.1. Recalling the definition of \(B_\delta (D^b(point))\) ( Definition 11.5) we conclude that \({\mathcal {T}} \in B_\delta (D^b(point))\) and the proposition follows. \(\square \)
Corollary 11.10
For any smooth complete rational surface surface S holds \([D^b(point)] \in \mathrm{Cl}([D^b(S)])\).
12 Non-commutative curve-counting
12.1 Rescaling \(\left\| \right\| _{\frac{1}{2}}\) so that all natural numbers are values
Following Kontsevich–Rosenberg [32] we denote \(D^b(K(l+1))\) by \(N{\mathbb {P}}^l\) (non-commutative projective space) for \(l\ge 0\). Note that we include the case \(l=0\), and \(N{\mathbb {P}}^0\) is a non-trivial cateogry. We denote also \(N{\mathbb {P}}^{-1}= D^b(K(l+1))\), i.e. this is a category generated by an orthogonal exceptional pair. Then we define for a category with a phase gap \({\mathcal {T}}\):
and using (12), and table (9) we see that
Due to Theorem 6.1 and Remark 6.2 we have
whenever \({\mathcal {A}}\), \({\mathcal {B}}\) have phase gap and \(\langle {\mathcal {A}}, {\mathcal {B}} \rangle \) is a semi-orthogonal decomposition of a proper category. (170) ensures that whenever \({\mathcal {T}}\) has a finite \(\dim _{nc}({\mathcal {T}})<+\infty \) and \({\mathcal {A}} {\subset } {\mathcal {T}}\) is a good enough embedded subcategry, then \({\mathcal {A}}\) has also finite \(\dim _{nc}({\mathcal {A}})\le \dim _{nc}({\mathcal {T}})<+\infty \). We note also that
Remark 12.1
Proposition 4.19 and table (9) imply that for an acyclic quiver Q we have \(\dim _{nc}\left( D^b(Q) \right) = 0\) iff Q is Dynkin and \(\dim _{nc}\left( D^b(Q) \right) = 1\) iff Q is affine.
12.2 A question and a definition
We start with two remarks:
Remark 12.2
Recall that the homological dimension of \( N{\mathbb {P}}^l\), \(l\ge 0\) is one. Also due to table (10) we have \(\mathrm {Stab}(N {\mathbb {P}}^l)\cong {\mathbb {C}}\times {\mathbb {C}}\) for \(l=0,1\) and \(\mathrm {Stab}(N {\mathbb {P}}^l)\cong {\mathbb {C}}\times {\mathcal {H}}\) for \(l\ge 2\). Note also that, whereas the spirals in \(N {\mathbb {P}}^0\) are periodic (up to shifts there are only three exceptional objects), for \(l\ge 1\) the spirals in \(N {\mathbb {P}}^l\) consist of pairwise non-isomorphic objects.
In view of these notes, we find it convenient to view \( N{\mathbb {P}}^l\) as a non-commutative curve of genus l.
Note that \(N{\mathbb {P}}^{-1}\) has homological dimension 0 and one should not think of this as a curve. Nevertheless, in order that we include also \(N{\mathbb {P}}^{-1}\) in the terminology we refer to it as a “non-commutative curve of genus \(-1\)” (a kind of degenerate curve).
Remark 12.3
Let \(l\ge -1\) and \({\mathcal {T}}\) be any triangulated cateogry linear over \({\mathbb {K}}\), let  be any fully faithful \({\mathbb {K}}\)-linear exact functor,Footnote 9 and denote by \({\mathcal {A}}\) the isomorphism closure of the image of F in \({\mathcal {T}}\). Then \({\mathcal {A}}\) is a triangulated subcategory of \({\mathcal {T}}\) generated by two exceptional objects and it is equivalent to \(N{\mathbb {P}}^l\), hence due to [8, Theorem 3.2] the functor F has left and right adjoints and there are SOD \({\mathcal {T}}=\langle {\mathcal {A}}, {\mathcal {A}}^{\perp } \rangle \), \({\mathcal {T}}=\langle ^{\perp }{\mathcal {A}}, {\mathcal {A}} \rangle \), in particular \({\mathcal {T}} \in B(N {\mathbb {P}}^l)\) (see Definition 11.1).
be any fully faithful \({\mathbb {K}}\)-linear exact functor,Footnote 9 and denote by \({\mathcal {A}}\) the isomorphism closure of the image of F in \({\mathcal {T}}\). Then \({\mathcal {A}}\) is a triangulated subcategory of \({\mathcal {T}}\) generated by two exceptional objects and it is equivalent to \(N{\mathbb {P}}^l\), hence due to [8, Theorem 3.2] the functor F has left and right adjoints and there are SOD \({\mathcal {T}}=\langle {\mathcal {A}}, {\mathcal {A}}^{\perp } \rangle \), \({\mathcal {T}}=\langle ^{\perp }{\mathcal {A}}, {\mathcal {A}} \rangle \), in particular \({\mathcal {T}} \in B(N {\mathbb {P}}^l)\) (see Definition 11.1).
Due to (170) we see that whenever we have \({\mathcal {T}} \in B_\delta (N{\mathbb {P}}^l)\) for some real \(\delta >0\) (recall that by definition 11.5 this implies that there is a SOD of the form \({\mathcal {T}}=\langle N{\mathbb {P}}^l, {\mathcal {A}} \rangle \) where \({\mathcal {A}}\) has a phase gap) and some integer \(l\ge 0\), then \(\dim _{nc}({\mathcal {T}})\ge l\). In particular if \({\mathcal {T}} \in B_{\delta _l}(N{\mathbb {P}}^l)\) for arbitrary big l, then \(\dim _{nc}({\mathcal {T}})=+\infty \), and this was used in Sect. 8. Now we come to the question of this section:
Question 12.4
Incidences \({\mathcal {T}} \in B(N{\mathbb {P}}^l)\)Footnote 10 are embeddings of \(N{\mathbb {P}}^l\) into \({\mathcal {T}}\). Viewing such embeddings as non-commutative curves in the category \({\mathcal {T}}\) we ask how many are these curves in a given \({\mathcal {T}}\) ?
In this section we sketch the concept of non-commutative curve-counting and give several numbers which result from this counting. The proofs and further numbers are in [20] and in future works. The first step is the following definition (see [20, Sections 3,4] for details):
Definition 12.5
Let \({\mathcal {A}}\), \({\mathcal {T}}\) be any triangulated categories. And let \(\Gamma {\subset } {\mathrm{Aut}}({\mathcal {T}})\) be a subgroup of the group of auto-equivalences. We denote

Next we fix an equivalence relation in \(C'_{{\mathcal {A}} ,P}({\mathcal {T}})\), and we will be interested in the set of equivalence classes, in particular the size of this set.
where \( F \circ \alpha \cong \beta \circ F' \) means equivalence of exact functors between triangulated categories (this is so called graded equivalence).
12.3 First non-trivial examples with \({\mathcal {A}}=N{\mathbb {P}}^l\), \(l\ge -1\) and three different targets: two quivers, and \(D^b({\mathbb {P}}^2)\)
Here we specify \({\mathcal {A}} = N{\mathbb {P}}^l\) in Definition 12.5 and \({\mathcal {T}}\) is a \({\mathbb {K}}\)-linear category. We note first an example of a choice for the additional property P in Definition 12.5:
Remark 12.6
Let us choose the additional properties P from (171) as follows:
This paper contains examples of \({\mathcal {T}}\) and \(l\ge 0\), s. t. \(C_{N{\mathbb {P}}^l, P}^{\Gamma }({\mathcal {T}}) \ne \emptyset \). On the other hand from (170) follows:
In all the examples of categories \({\mathcal {T}}\) with \(\dim _{nc}({\mathcal {T}}) = \infty \) given in Sect. 8 one has \( C_{N{\mathbb {P}}^l, P}^{\Gamma }({\mathcal {T}}) \ne \emptyset \) for infinitely many l.
Next we note examples, where the additional restriction P from Remark 12.6 is equivalent to requiring only \({\mathbb {K}}\)-linearity:
Remark 12.7
When \({\mathcal {T}} = D^b({\mathbb {P}}^2)\) or \({\mathcal {T}} = D^b(Q)\) for an acyclic quiver Q, then for any fully faithful exact \({\mathbb {K}}\)-linear functor \(F:N{\mathbb {P}}^l \rightarrow {\mathcal {T}}\) the right and the left orthogonal to the image of F is generated by an exceptional collection, therefore any such functor automatically satisfies the additional property P in 173. This follows from the fact that every exceptional pair in \({\mathcal {T}}\) can be extended to a full exceptional collection in \({\mathcal {T}}\) (this is proved in [17] and [26]).
So, let us specify Definition 12.5 with this simpler P, that is (see [20, Section 5] for detailed exposition):
Definition 12.8
Let \(l\in {\mathbb {Z}}_{\ge -1}\) and let \({\mathcal {T}}\) be any \({\mathbb {K}}\)-linear triangulated category. And let \(\Gamma {\subset } {\mathrm{Aut}}_{{\mathbb {K}}}({\mathcal {T}})\) (where \( {\mathrm{Aut}}_{{\mathbb {K}}}({\mathcal {T}})\) is the group of \({\mathbb {K}}\)-linear auto-equivalences). Let the property P from Definition 12.5 be “F is \({\mathbb {K}}\)-linear”. We denote \(C_{N{\mathbb {P}}^l, P }'({\mathcal {T}})\) and \(C_{N{\mathbb {P}}^l, P }^\Gamma ({\mathcal {T}})\) by \(C_{l }'({\mathcal {T}})\) and \(C_{l}^{\Gamma }({\mathcal {T}})\), respectively and refer to the elements of \(C_{l}^{\Gamma }({\mathcal {T}})\) as to non-commutative curves of genus l in \({\mathcal {T}}\) modulo \(\Gamma \).
The invariants just defined are computed for two affine quivers in [20, Section 6], the result is:
Proposition 12.9
Let \({\mathcal {T}}_i=D^b(Q_i)\), \(i=1,2\), where: \(Q_1\), \(Q_2\)

Then the numbers \( \left| C_{l}^{\Gamma }({\mathcal {T}}_i) \right| \) for \(l\in \{-1,0,+1\}\), \(i=1,2\), \(\Gamma \in \{ \{{\text {Id}}\}, \langle S \rangle , {\mathrm{Aut}}_{{\mathbb {K}}}({\mathcal {T}}_i) \}\) are:

Proof
The vanishings follow from (8). The rest of the proof is in [20]. \(\square \)
In [20] we estimate the new invariants defined in Definition 12.8, the result is as follows:
Proposition 12.10
Let \({\mathbb {K}}={\mathbb {C}}\). Denote \({\mathcal {T}} = D^b({\mathbb {P}}^2)\). Let \(\langle S \rangle {\subset } {\mathrm{Aut}}_{{\mathbb {C}}}({\mathcal {T}})\) be the subgroup generated by the Serre functor. Then \(C_{-1}^{\{{\text {Id}}\}}({\mathcal {T}}) =\emptyset \) and \(\forall l\ge 0\) the set \(C_{l}^{\langle S \rangle }({\mathcal {T}})\) is finite. It is non-empty for:
Furthermore, for any Markov numberFootnote 11 m we have
where \(c_1(E)\), r(E) are the first Chern class (which we consider as an integer) and the rank of E.
Proof
See [20, Section 8]. \(\square \)
Corollary 12.11
Denote \({\mathcal {T}} = D^b({\mathbb {P}}^2)\). The first several non-trivial \(\left| C_{3m-1}^{\mathrm {Aut}_{{\mathbb {C}}}({\mathcal {T}})}({\mathcal {T}})\right| \) are (recall that m is a Markov number and on the first row are listed the first 9 Markov numbers):

Furthermore, the so called Tyurin’s conjecture, which is equivalent to the Markov’s conjecture (this equivalence is proved in [36, p. 100], see also [25, Section 7.2.3 ]) is equivalent to the following statement: for all Markov numbers \(m\ne 1, m\ne 2\) we have \(\left| C_{3 m -1}^{\mathrm {Aut}_{{\mathbb {C}}}({\mathcal {T}})}({\mathcal {T}})\right| =2\).
Proof
See [20, Section 8]. \(\square \)
12.4 Dependence on a stability condition: semistable, resp. stable. non-commutative curves
Definition 12.12
Let \(l\in {\mathbb {Z}}_{\ge -1}\) and let \({\mathcal {T}}\) be a triangulated category linear over \({\mathbb {K}}\) and s.t. \(\ \mathrm {Stab}({\mathcal {T}})\ne \emptyset \), let \(\Gamma \) and P be as in Definition 12.5. One approach to define, semi-stable w.r. to a stability condition non-commutative curves in \({\mathcal {T}}\) is as follows. Choose \(\sigma \in \mathrm {Stab}({\mathcal {T}})\). Now we apply the same Definition 12.5 with \({\mathcal {A}}=N{\mathbb {P}}^l\) and P is the one from Definition 12.8 twisted by an additional restriction depending on \(\sigma \). We give two options for this additional restriction. More precisely, let \(\{s_j\}_{j\in {\mathbb {Z}}}\) be a Helix in \(N{\mathbb {P}}^l\) (see [20, Section 7.2]), then let us denote:
where \(C'_{N{\mathbb {P}}^l,{\mathbb {K}}}\), is the set (171) (see also Definition 12.8) and \(\sigma ^{ss}\) is the set of \(\sigma \)-semistable objects. The formulas (172) give equivalence relations in \(C'_{l,\sigma }({\mathcal {T}})\) and in \(C'_{l,\sigma \sigma }({\mathcal {T}})\) and we define \(\sigma \)-semistable (resp. \(\sigma \)-stable) non-commutative curves of genus l in \({\mathcal {T}}\), and modulo \(\Gamma \):
Note that for \(l=0, l=-1\) we have always \( C_{l, \sigma }^{\Gamma }({\mathcal {T}})=\emptyset \).
We will give two examples. In both of them \(\Gamma =\{{\text {Id}}\}\). Here we proof only one of them. To that end we note first a lemma
Proposition 12.13
Let \(l\ge 1\). Then \(\left| C^{\{{\text {Id}}\}}_{k}(N{\mathbb {P}}^l)\right| =\delta _{k,l}\). Let \({\mathcal {Z}}{\subset } \mathrm {Stab}(N{\mathbb {P}}^l)\) be as in Proposition 7.2. Then we have \(\left| C^{\{{\text {Id}}\}}_{l,\sigma \sigma }(N{\mathbb {P}}^l)\right| =1\) for \(\sigma \in \mathrm{Cl}({\mathcal {Z}})\) and \(\left| C^{\{{\text {Id}}\}}_{l,\sigma }(N{\mathbb {P}}^l)\right| =0\) for \(\sigma \not \in \mathrm{Cl}({\mathcal {Z}})\).
Proof
From the Remark 12.3 it follows that, if for some integer \(j\ge -1\) there exists a fully faithful \({\mathbb {K}}\)-linear functor  , then \(l=j\) and F is equivalence (from [17] we know that any exceptional pair in \(N{\mathbb {P}}^l\) is full). It follows the equality \(\left| C^{\{{\text {Id}}\}}_{k}(N{\mathbb {P}}^l)\right| =\delta _{k,l}\). For the proof of the rest we note fist that for any j the subset in \(\mathrm {Stab}(N{\mathbb {P}}^l)\) where \(s_j\) is semi-stable is closed subset. From Proposition 7.2 we know that for \(\sigma \in {\mathcal {Z}}\) all alements in \(\{s_j\}_{j \in {\mathbb {Z}}}\) are semi-stable, therefore this holds also for \(\sigma \in ({\mathcal {Z}})\). Thus we see that \( \sigma \in \mathrm{Cl}({\mathcal {Z}}) \Rightarrow \left| C_{l,\sigma \sigma }(N{\mathbb {P}}^l)\right| =1\).
, then \(l=j\) and F is equivalence (from [17] we know that any exceptional pair in \(N{\mathbb {P}}^l\) is full). It follows the equality \(\left| C^{\{{\text {Id}}\}}_{k}(N{\mathbb {P}}^l)\right| =\delta _{k,l}\). For the proof of the rest we note fist that for any j the subset in \(\mathrm {Stab}(N{\mathbb {P}}^l)\) where \(s_j\) is semi-stable is closed subset. From Proposition 7.2 we know that for \(\sigma \in {\mathcal {Z}}\) all alements in \(\{s_j\}_{j \in {\mathbb {Z}}}\) are semi-stable, therefore this holds also for \(\sigma \in ({\mathcal {Z}})\). Thus we see that \( \sigma \in \mathrm{Cl}({\mathcal {Z}}) \Rightarrow \left| C_{l,\sigma \sigma }(N{\mathbb {P}}^l)\right| =1\).
Now let \(\sigma \not \in \mathrm{Cl}({\mathcal {Z}})\). We will show that \(\left| C_{l,\sigma }(N{\mathbb {P}}^l)\right| =0\) and the Proposition follows. Indeed recalling also that in Proposition 7.2 we have also disjoint union \(\mathrm {Stab}(N{\mathbb {P}}^l) = {\mathcal {Z}} \amalg \amalg _{i\in {\mathbb {Z}}} {\mathcal {Z}}_i\) and (78) we deduce that for some \(i\in {\mathbb {Z}}\) we have \(s_i,s_{i+1}\in \sigma ^{ss}\), \(1\le \phi (s_{i+1})-\phi (s_{i+1})\). Now if \(1 = \phi (s_{i+1})-\phi (s_{i+1})\), then using (79) this would imply that \(\sigma \in \mathrm{Cl}({\mathcal {Z}})\), therefore \(1 < \phi (s_{i+1})-\phi (s_{i+1})\). In this case the last statement in Proposition 7.2 ensures that only \(s_i, s_{i+1}\) are semi-stable, therefore \(\left| C_{l,\sigma }(N{\mathbb {P}}^l)\right| =0.\) \(\square \)
In the master thesis [6] is proved:
Proposition 12.14
Let \({\mathcal {T}} = D^b(Q_1)\) (\(Q_1\) is as in Proposition 12.9). As \(\sigma \) varies in \(\mathrm {Stab}({\mathcal {T}})\) the subset \(C_{1,\sigma }^{\{{\text {Id}}\}}({\mathcal {T}}){\subset } C^{\{{\text {Id}}\}}_{1}({\mathcal {T}})\) takes all possible subsets of \(C_{1}^{\{{\text {Id}}\}}({\mathcal {T}})\).
Remark 12.15
We expect that Porposition 12.14 holds for \(C_{1,\sigma \sigma }^{\{{\text {Id}}\}}({\mathcal {T}})\) as well.
12.5 Non-commutative Calabi–Yau curve-counting
Now we sketch a conjectural example of a finite \(C_{{\mathcal {A}},P}^{\Gamma }({\mathcal {T}})\) (defined in Definition 12.5) coming from categories appearing naturally on the A-side. Here the categories are \({\mathbb {C}}\)-linear and we fix the property P of the functor F in Definition 12.5 to be “F is \({\mathbb {C}}\)-linear” and we will write \(C_{{\mathcal {A}},{\mathbb {C}}}^{\Gamma }({\mathcal {T}})\) instead of \(C_{{\mathcal {A}},P}^{\Gamma }({\mathcal {T}})\). Now the domain category \({\mathcal {A}}\) is a modification of \(D^b(K(l))\), which is Calabi–Yau. We pass from \(D^b(K(l))\) to the new domain by changing

and this amounts to considering \({\mathcal {A}}=CY(l)\), instead of \({\mathcal {A}}=D^b(K(l))\). The definition is based on the quiver:

In the next conjectural example \(\Gamma =\mathrm {Aut}_{\mathbb {C}}({\mathcal {T}})\) is the group of \({\mathbb {C}}\)-linear auto-equivalences of \({\mathcal {T}}\):
Conjecture 12.16
Let \({\mathcal {T}}={\text {Fuk}}(E)\) with E an elliptic curve. In this case we have a correspondence:
It follows that: \(\left| C_{CY(l),C}^{\mathrm {Aut}_C({\mathcal {T}})}({\mathcal {T}})\right| =\#\{d | gcd(d,n) = 1, 1 \le d\le n \}.\)
We plan to work on Conjecture 12.16 in a future work.
Remark 12.17
For curves S of higher genus we expect that finding of the cardinality of \(C_{CY(n),{\mathbb {C}}}^{\mathrm {Aut}_{\mathbb {C}}({\mathcal {T}})}({\mathcal {T}})\) for \({\mathcal {T}} = {\mathrm{Fuk}}(S)\) is related to very recent insights on counting of geodesics—see [33].
13 A-side interpretation and holomorphic sheaves of categories
In this section we give a different point of view on the category of representations of the Kronecker quiver and introduce the notion of holomorphic families of Kronecker quivers.
We suggest a framework in which sequences of holomorphic families of categories are viewed as sequences of extensions of non-commutative manifolds by relating our norm to the notion of holomorphic family of categories introduces by Kontsevich. Several questions and conjectures are posed.
First we sketch how to interpret \(D^b(K(n))\) as a perverse sheaf of categories. Recall that LG model of \({\mathbb {P}}^2\) is \({{\mathbb {C}}^*}^2\), \(w=x+y+\frac{1}{xy}\)—see [1].

The category \(D^b(K(3))\) can be obtained by taking the part of the Landau Ginzburg model over a disc D which contains 2 singular fibers.
Surgeries on the manifold:

can be performed so that the Floer homology \({\text {HF}}(L_1, L_2)=3\) changes to \({\text {HF}}(L_1, L_2)=n\) and as a result we get \(D^b(K(n))\).
To interpret \(D^b(K(n))\) as a perverse sheaf of categories one considers a locally constant sheaf of categories over a graph \(\Gamma \) shown on the picture below, the picture encodes also the data about the sheaf:

The locally constant sheaf is denoted by \( {\mathcal {F}}\). The stalks over inner points of the edges of \(\Gamma \) are isomorphic to \({\mathrm{Fuk}}(E)\), the stalk over the vertex where three edges meet is \(D^b(A_2) \otimes {\mathrm{Fuk}}(E)\), the stalks over the two end points of \(\Gamma \) on the left is \(D^b(A_1)\) (these points correspond to the two singular points of the LG model). There are three functors from \(D^b(A_2) \otimes {\mathrm{Fuk}}(E)\) to \({\mathrm{Fuk}}(E)\) coming from three functors from \(D^b(A_2)\) to \(D^b(A_1)\). The letters \(p_1\), \(p_2\) from the figure above denote two spherical functors from \(D^b(A_1)\) to \({\mathrm{Fuk}}(E)\), thus this figure encodes a diagram of functors. One defines the category of global sections \(H^0(\Gamma , {\mathcal {F}})\) of the sheaf \({\mathcal {F}}\) as a category which is obtained by a limit of the described diagram of functors. For appropriately chosen spherical functors the category \(H^0(\Gamma , {\mathcal {F}})\) is the same as \(D^b(K(n)).\) The surgeries are recorded by the changes of the spherical functors \(p_1\), \(p_2\). What we explained about interpreting \(D^b(K(n))\) as a perverse sheaf of categories is only a sketch . More details are given in a subsequent work of the second author with Pandit and Spaide [31, Example 3.22]. In [31, page 41] are discussed also the surgeries.
The category \(D^b(K(4))\) can be interpreted also as part of the LG model of \({\mathbb {P}}^3\), \({{\mathbb {C}}^*}^3\), \(w=x+y+z+\frac{1}{xyz}\):


In this case surgeries on the fiber - a K3 surface:

can be performed so that the category changes from \(D^b(K(4))\) to \(D^b(K(n))\).
The Landau Ginzburg models with K3 surfaces in the fibers can be interpreted as perverse sheafs of categories, encoded in the following picture—see [27]:

Remark 13.1
The property of having a phase gap, which we require in this paper to define the norm, can also be interpret as existence of a CY form with certain properties.
Namely let Y be a LG model, \(\Omega \) is a CY form on Y. Let L be a Lagrangian s.t. \(\theta _ 1 \le arg \Omega |_ {L} \le \theta _2 \). Assume that there exits a form \(\beta \) on Y s.t. (1) \(\beta = d \alpha \), (\(\alpha \) is an \(n-1\) form), (2) \(Re \beta | _{L} > 0.\) (3) \(\alpha \rightarrow 0\) when \(\omega \rightarrow 0\).
Then there are no stable lagrangians L with \(\theta _ 1 \le arg \Omega |_ {L} \le \theta _2 \). In other words existence of such forms \(\Omega \) and \(\alpha \) lead to gaps in phases.
One more direction for future research is holomorphic families of categories, in particular holomorphic families of Kronecker quivers.
Holomorphic families of categories over X with fiber K(n) should be defined by homomorphisms \(\varphi _i: {\mathcal {O}}(U_i) \rightarrow {\text {HH}}^0(D^b(K(n)))\) in the zero-th Hochschild cohomology of \(D^b(K(n))\) where \(\{U_i\}\) is a covering of X by open sets. We use the following picture for such a holomorphic family of categories:

The holomorphic sheaves of categories are enhanced by perverse sheaves of stability conditions - see [30] for defining morphisms and the gluing between the categories on intersecting opens that defines the sheaf.
The case of holomorphic family of K(2) is the classical case of conic bundles:

The global sections \(H^0(X, {\mathcal {F}})\) are \({\text {D}}^{{\text {b}}}(Z)\). Similarly \(H^0(X, {\mathcal {F}})\) with K(n) for \(n\ge 3\) produces a new non-commutative variety.
Iterating the procedure described above results in a family of categories over a family of categories. Some questions addressing relations between the norms of the fibers and of the gobal sections follow:
Question 13.2
Under what condition \(||{\mathcal {C}}||_{\varepsilon } \geqslant ||H^0(X,{\mathcal {F}})||_{\varepsilon } ?\) (here \({\mathcal {C}}\) is the category in the fiber)

Question 13.3
Let us consider a tower of families of categories and each of the fiber categories \({\mathcal {C}}_i\) has non maximal \(\left\| \cdot \right\| _{\varepsilon }\)(recall the relation of \(\left\| \cdot \right\| ^{\varepsilon }\) and \(\left\| \cdot \right\| _{\varepsilon }\) in Definition 11.5). Is it true that if the Rouquier dimension [2] of the category in the combined fiber is one then the norm \(\left\| \cdot \right\| _{\varepsilon }\) of this category is non-maximal ?
We summarise the proposed analogy in the table bellow.

Question 13.4
Do we have a similar theory as the classical theory of conic bundles for sheaves of categories with fibers categories of representations of Kronecker quivers or any other quiver category with a Rouquier dimension [2] equal to one?
In a certain way our norm can be seen as analogue of height function defined in [15]. We expect that some higher analogues of this norm for higher Rouquier dimensions can be defined. In fact in this paper we only scratch the surface proposing a possible approach to “noncommutative Galois theory”—representing “noncommutative manifolds” (categories) as a sequence of perverse sheaves of categories and holomorphic families of categories.
It will be interesting to study categories which can be represented as a tower of holomorphic families of categories with nonmaximal norms \(\left\| \cdot \right\| _{\varepsilon }\). One example of such category is \(D^b({\mathbb {P}}^1 \times \cdots \times {\mathbb {P}}^1)\).
Question 13.5
Characterise projective varieties X whose derived categories \(D^b(X)\) can be represented as tower of holomorphic families of categories with non-maximal norms starting with \(D^b(Z)\), whehre Z is a rational variety.
-
(1)
Under what conditions are these projective varieties X rational? (It is rather clear that a nontrivial condition is needed since every hyperelliptic curve can be seen as such a tower).
-
(2)
We conjecture that for a unirational variety U there is a tower of families of categories
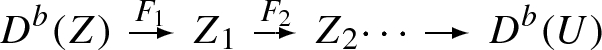
and each of the fiber categories has non-maximal norm: \(\left\| F_i\right\| _{\varepsilon }<\pi (1- \varepsilon )\) (see [5]), and Z is rational.
Notes
By proper we mean that \(\sum _{i\in {\mathbb {Z}}} \hom ^i(X,Y)<+\infty \) for any two objects X, Y in \({\mathcal {T}}\) (see also Sect. 2 dedicated to Notations).
The meaning of \(\hom ^{min}(A,B)\) can be seen in formula (14).
We recall what is a full stability condition in Sect. 4.1. The stability conditions on the third raw of (9) are full.
For a Lebesgue measurable subset \(X{\subset } {\mathbb {S}}^1\) we denote by \(\mathrm {vol}(X)\) its Lebesgue measure with \(\mathrm {vol}({\mathbb {S}}^1)=2 \pi \).
Neighborhood of \({\text {Id}}_{\mathbb {C}}\in GL^+(2,{\mathbb {R}})\).
One shows this using the equality \(\arccos (x)-\arccos \left( \sqrt{1-x^2}\right) =\arccos \left( 2 x \sqrt{1-x^2}\right) \), which holds for \(0\le x \le \frac{1}{\sqrt{2}}\).
Where \({\mathbb {F}}_m\) is the m-th Hirzebruch surface
In particular any smooth projective surface.
Recall that an exact functor is actually a a pair of a functor \(F'\) and a natural isomorphism between the functors \(F'\circ T_1\) and \(T_2\circ F_2\), where \(T_1\), \(T_2\) are the translation functors of the source and the target categories, respectively.
i.e. a SOD \(\langle N{\mathbb {P}}^l, {\mathcal {A}} \rangle \).
Recall that a Markov number x is a number \(x \in {\mathbb {N}}_{\ge 1}\) such that there exist integers y, z with \(x^2+y^2+z^2=3 x y z\).
References
Auroux, D., Katzarkov, L., Orlov, D.: Mirror symmetry for weighted projective planes and their noncommutative deformations. Ann. of Math. (2) 167(3), 867–943 (2008)
Ballard, M., Favero, D., Katzarkov, L.: Orlov spectrum: bounds and gaps. Invent. Math. 189(2), 359–430 (2012)
Beilinson, A.A.: Coherent sheaves on Pn and problems in linear algebra. Funkts. Anal. I Prilozhen 12(3), 68–69 (1978)
Bobiński, G., Geiß, C., Skowroński, A.: Classification of discrete derived categories. Cent. Eur. J. Math 2(1), 19–49 (2004). (electronic)
Bogomolov, T., (in preparation)
Bojko, A.: Stability conditions on quivers and semistable noncommutative curve counting, Master thesis, University of Vienna. Fakultät für Mathematik, Betreuer: L. Katzarkov and G. Dimitrov (2018)
Bondal, A.I., Orlov, D.: Derived categories of coherent sheaves. Proceedings of the International Congress of Mathematicians, vol. II 46–54. Beijing (2002)
Bondal, A.I.: Representation of associative algebras and coherent sheaves. Math. USSR-Izv. 34(1), 23–42 (1990)
Bondal, A.I., Polishchuk, A.E.: Homological properties of associative algebras: the method of helices. Russ. Acad. Sci. Izv. Math. 42(2), 219–260 (1994)
Bridgeland, T.: Stability conditions on triangulated categories. Ann. Math. 166(2), 317–345 (2007)
Bridgeland, T.: Stability conditions on K3 surfaces. Duke Math. J. 141(2), 241–291 (2008)
Bridgeland, T., Smith, I.: Quadratic differentials as stability conditions. Publ. mathématiques de l’IHÉS 121(1), 155–278 (2015)
Broomhead, N., Pauksztello, D., Ploog, D.: Discrete derived categories II: The silting pairs CW complex and the stability manifold (2014). arXiv:1407.5944
Broomhead, N., Pauksztello, D., Ploog, D.: Discrete derived categories I: homomorphisms, autoequivalences and t-structures. Math. Z. 285(1–2), 39–89 (2017)
Brosnan, P., Pearlstein, G.: Jumps in archimedian height (in preparation)
Collins, J., Polishchuck, A.: Gluing stability conditions. Adv. Theor. Math. Phys. 14(2), 563–608 (2010)
Crawley-Boevey, W.: Exceptional sequences of representations of quivers. In: Dlab, V., Lenzing, H. (eds.) Proceedings of the Representations of Ulgebras, Ottawa 1992. Canadian Mathematical Society Conference Proceedings vol. 14, pp. 117–124. American Mathematical Society (1993)
Dimitrov, G., Haiden, F., Katzarkov, L., Kontsevich, M.: Dynamical systems and categories. In: The Influence of Solomon Lefschetz in Geometry and Topology: 50 Years of Mathematics at CINVESTAV, Volume 621 of Conference of the Mathematics, pp. 133–170. American Mathematical Society (AMS), Providence, RI (2014)
Dimitrov, G., Katzarkov, L.: Bridgeland stability conditions on Wild Kronecker Quivers. arXiv:1602.09117v1
Dimitrov, G., Katzarkov, L.: Non-commutative curve-counting invariants. arXiv:1805.00294
Dimitrov, G.: Bridgeland stability conditions and exceptional collections. Dissertation, University of Vienna. Fakultät für Mathematik, Betreuer: Ludmil Katzarkov (2015)
Dimitrov, G., Katzarkov, L.: Non-semistable exceptional objects in hereditary categories. Int. Math. Res. Not. rnv336, 85 (2015)
Dimitrov, G., Katzarkov, L.: Bridgeland stability conditions on the acyclic triangular quiver. Adv. Math. 288, 825–886 (2016)
Gorodentsev, A.L.: Exceptional bundles on surfaces with a moving anticanonical class. Izv. Akad. Nauk SSSR Ser. Mat. 52(4), 740–757 (1988)
Gorodentsev, A.L., Kuleshov, S.A.: Helix theory. Mosc. Math. J. 4(2), 377–440 (2004)
Gorodentsev, A.L., Rudakov, A.N.: Exceptional vector bundles on projective spaces. Duke Math. J. 54, 115–130 (1987)
Harder, A., Katzarkov, L., Liu, Y.: Pervers sheaves of categories and rationality. Proceeding of Simons Proposal on Rationality
Hille, L., Perling, M.: Exceptional sequences of invertible sheaves on rational surfaces. Compos. Math. 147(4), 1230–1280 (2011)
Hille, L., Perling, M.: Tilting bundles on rational surfaces and quasi-hereditary algebras. Ann. Inst. Fourier Grenoble 6(2), 625–644 (2014)
Katzarkov, L., Kontsevich, M.: Holomorphic families of categories (in preparation)
Katzarkov, L., Pandit, P., Spaide, T.: Calabi-Yau structures, spherical functors, and shifted symplectic structures. arXiv: 1701.07789v2
Kontsevich, M., Rosenberg, A.: Noncommutative Smooth Spaces, The Gelfand MathematicalS Eminars, 1996–1999, 85–108. Birkhaäuser, Boston (2000)
Mirzakhani, M.: Growth of the number of simple closed geodesics on hyperbolic surfaces. Ann. Math. 168(1), 97–125 (2008)
Okada, S.: Stability manifold of \({\mathbb{P}}^1\). J. Algeb. Geom. 15(3), 487–505 (2006)
Perling, M.: Some quivers describing the derived category of the toric del Pezzos. Preprint (2003)
Рудаков, А.Н.: Числа Маркова и исключительные расслоения на Р2, Изв. АН СССР. Сер. матем., 1988, том 52, выпуск 1, 100–112 (1988)
Qiu, Y., Woolf, J.: Contractible stability spaces and faithful braid group actions. Geom. Topol. 22(6), 3701–3760 (2018)
Rudakov, A.N.: Exceptional vector bundles on a quadric. Izv. Akad. Nauk SSSR Ser. Mat. 52, 788–812 (1988). (English transl. in Math. USSR Izv. 33, 1989)
Rudin, W.: Real and complex analysis, Third edn. McGraw-Hill Book Company, New York (2006)
Seidel, P.: Fukaya Categories and Picard–Lefschetz Theory. Zurich Lecture Notes in Advance Mathematics. European Mathematical Society, Zürich (2008)
Vial, C.: Exceptional collections, and the Néron–Severi lattice for surfaces. arxiv: 1504.01776v3
Vossieck, D.: The algebras with discrete derived category. J. Algebra 243(1), 168–176 (2001)
Acknowledgements
Open access funding provided by University of Vienna. The authors wish to express their gratitude to Dhyan Aranha, Aleksej Bondal, Bogdan Georgiev and Maxim Kontsevich for their interest. The authors are very thankful to Denis Auroux for his help on the last Sect. 13. The first author was supported by FWF Projects P 29178-N35, P 27784. Parts of this work was carried out during the stay 01.07.15-30.06.16 of the first author at the Max-Planck-Institute für Mathematik Bonn and his stay 01.07.16-30.06.17 at International Centre for Theoretical Physics Trieste and G. Dimitrov gratefully acknowledges the support and the excellent conditions at these institutes. The second author was supported by Simons research Grant, NSF DMS 150908, ERC Gemis, DMS-1265230, DMS-1201475 OISE-1242272 PASI. Simons collaborative Grant-HMS. HSE-Grant, HMS and automorphic forms. The second author is partially supported by Laboratory of Mirror Symmetry NRU HSE, RF Government Grant, ag. No 14.641.31.0001. Connection with our preprint arXiv:1602.09117: Following advice by Auroux, Pantev, Kontsevich and one referee we split the paper arXiv:1602.09117 into two parts. The present paper is the second part.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.


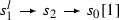 and
and 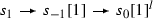 in
in 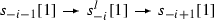 ,
, 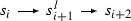 therefore for
therefore for