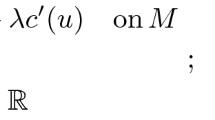Abstract
In this paper, by using variational methods we investigate the existence of solutions for the following system of elliptic equations
where (M, g) is a smooth closed Riemannian manifold of dimension \(n\ge 3, \Delta _{g}\) is the Laplace–Beltrami operator, a, b and c are functions Hölder continuous in M, f is a smooth function and \(\alpha>1, \beta >1\) are two real numbers such that \(\alpha + \beta = 2^*,\) where \( 2^{*}= 2n/(n-2)\) denotes the critical Sobolev exponent. We get these results by assuming sufficient conditions on the function \(h= \frac{\alpha }{2^{*}} a + \frac{2\sqrt{\alpha \beta }}{2^{*}}b + \frac{\beta }{2^{*}} c\) related to the linear geometric potential \(\frac{n-2}{4(n-1)}R_{g}\), where \(R_{g}\) is the scalar curvature associated to the metric g.
Similar content being viewed by others
Data Availibility
All data generated or analysed during this study are included in this published article.
References
Ablowitz, M.J., Prinari, B., Trubatch, A.D.: Discrete and Continuous Nonlinear Schrödinger Systems. Cambridge University Press, Cambridge (2004)
Alves, C.O., de Morais Filho, D.C., Souto, M.A.S.: On systems of equations involving subcritical or critical Sobolev exponents. Nonlinear Anal. 42, 771–787 (2000)
Aubin, T.: Equations différentielles non linéaires et problème de Yamabe concernant la courbure scalaire. J. Math. Pures Appl. 55, 269–296 (1976)
Aubin, T.: Some Nonlinear Problems in Riemannian Geometry. Springer, Berlin (1998)
Aubin, T., Hebey, E.: Courbure scalaire prescrite. Bull. Sci. Math. 115, 125–132 (1991)
Chabrowski, J., Yang, J.: On the Neumann problem for an elliptic system of equation involving the Sobolev expoent. Colloq. Math. 90, 1–35 (2001)
Deng, S., Yang, J.: Critical Neumann problem for nonlinear elliptic systems in exterior domains. Electron. J. Differ. Equ. 153, 1–13 (2008)
Druet, O.: Generalized scalar curvature type equations on compact Riemannian manifolds. Proc. R. Soc. Edinb. Sect. A 130, 767–788 (2000)
Druet, O.: Optimal Sobolev inequalities and extremal functions the three-dimensional case. Indiana Univ. Math. J. 51, 69–88 (2002)
Druet, O., Hebey, E.: Sharp asymptotics and compactness for local low energy solutions of critical elliptic systems in potential form. Calc. Var. Partial Differ. Equ. 31, 205–230 (2008)
Druet, O., Hebey, E., Vétois, J.: Bounded stability for strongly coupled critical elliptic systems below the geometric threshold of the conformal Laplacian. J. Funct. Anal. 258, 999–1059 (2010)
Dou, J., Qu, C.: Classification of positive solutions for an elliptic system with a higher-order fractional Laplacian. Pac. J. Math. 261, 311–334 (2013)
Escobar, J.F., Schoen, R.M.: Conformal metrics with prescribed scalar curvature. Invent. Math. 86, 243–254 (1986)
Gilbarg, D., Trudinger, N.: Elliptic Partial Differential Equations of Second Order. Springer, Berlin (1983)
Hebey, E.: Nonlinear Analysis on Manifolds: Sobolev Spaces and Inequalities. Courant Institute of Mathematical Sciences, New York (2000)
Hebey, E., Vaugon, M.: Courbure scalaire prescrite pour des variétés non conformément difféomorphes à la sphŕe. C.R. Acad. Sci. 316, 281 (1993)
Hebey, E., Vaugon, M.: Le problème de Yamabe équivariant. Bull. Sci. Math. 117, 241–286 (1993)
Hebey, E.: Critical elliptic systems in potential form. Adv. Differ. Equ. 11, 511–600 (2006)
Hebey, E., Vaugon, M.: Meilleures constantes dans le théorème d’inclusion de Sobolev. Ann. Inst. H. Poincaré. Anal. Non Linéaire 13, 57–93 (1996)
Hebey, E., Vétois, J.: Multiple solutions for critical elliptic systems in potential form. Commun. Pure. Appl. Anal. 7, 715–741 (2008)
Ishiwata, M.: Multiple solutions for semilinear elliptic systems involving critical Sobolev exponent. Differ. Integr. Equ. 20, 1237–1252 (2007)
Kavian, O.: Introduction à la Thèorie des Points Critiques: et Applications aux Problèmes Elliptiques. Springer, Berlin (1993)
Lee, J.M., Parker, T.H.: The Yamabe problem. Bull. Am. Math. Soc. New Ser. 17, 37–91 (1987)
Schoen, R.: Conformal deformation of a Riemannian metric to constant scalar curvature. J. Differ. Geom. 20, 479–495 (1984)
Schoen, R., Yau, S.-T.: Lectures on Differential Geometry. International Press, Cambridge (2010)
Trudinger, N.: Remarks concerning the conformal deformation of Riemannian structures on compact manifolds. An. Scuola Norm. Sup. Pisa 22, 265–274 (1968)
Vétois, J.: Multiple solutions for nonlinear elliptic equations on compact Riemannian manifolds. Int. J. Math. 9, 1071–1111 (2007)
Yamabe, H.: On a deformation of Riemannian structures on compact manifolds. Osaka J. Math. 12, 21–37 (1960)
Funding
This work were supported by Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), Grant 309998/2020-4, and by Paraíba State Research Foundation (FAPESQ), Grant 3034/2021.
Author information
Authors and Affiliations
Contributions
All authors have contributed equally to this work for writing, review and editing. All authors have read and agreed to the published version of the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
de Oliveira Sousa, N., de Souza, M. On Solutions for Strongly Coupled Critical Elliptic Systems on Compact Riemannian Manifolds. Results Math 78, 91 (2023). https://doi.org/10.1007/s00025-023-01866-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00025-023-01866-x