2D FDM Simulation of Seismic Waves and Tsunamis Based on Improved Coupling Equations Under Gravity

Abstract

To understand the characteristics of seismic waves and tsunamis recorded simultaneously by the ocean-bottom observation networks, the coupling between the solid Earth and the ocean has to be modeled in the presence of gravity. However, previous coupled simulations adopted approximate equations that did not fully incorporate the effects of gravity. In this study, we derived correctly linearized governing equations under gravity and compared them with those of previous studies. Numerical experiments were performed for a two-dimensional P-SV wavefield, using the finite difference method (FDM). To validate the accuracy of the calculated tsunamis, we computed the theoretical tsunami dispersion relation using a propagator matrix and compared it with our results and those of previous studies. We found that our proposed method provided more accurate results than those of previous studies, particularly in the short-period band. We also investigated the applicability of the proposed method to distant tsunamis by examining the difference between calculated and theoretical tsunami phase velocities in the long-period band. The proposed formulation provides accurate results that properly incorporate gravity into the simultaneous simulation of seismic waves and tsunamis.

1 Introduction

When an earthquake occurs beneath the seafloor, various waves, such as seismic waves, ocean acoustic waves, and tsunamis are excited, and permanent deformation remains around the source area. With recent developments in ocean-bottom observation networks, obtaining data where seismic waves, ocean acoustic waves, and tsunamis are superimposed near a wave source has become feasible (e.g., Kubota et al. 2021a, 2021b; Matsumoto et al. 2017; Nosov and Kolesov 2007). A unified modeling of these waves is important to better understand the rupture processes of earthquakes occurring in subduction zones (e.g., Fujii and Satake 2007, 2013; Gusman et al. 2015; Yokota et al. 2011), and to provide fast and accurate tsunami early warnings (e.g., Kozdon and Dunham 2014; Mizutani et al. 2020; Tsushima et al. 2009).

Several methods have been proposed to simulate seismic waves and tsunamis simultaneously in the vicinity of the source. Abrahams et al. (2023) reviewed coupled earthquake–tsunami modeling methods and classified them into four categories. The first is the instantaneous source method (e.g., Tanioka and Seno 2001), where the static displacement of the seafloor caused by the earthquake was used as the initial condition for tsunami propagation calculation. The second is the time-dependent source method (e.g., Kervella et al. 2007; Madden et al. 2021; Saito and Furumura 2009; Saito and Tsushima 2016), where the time-dependent velocity of the seafloor was used as a forcing term to generate tsunamis. The third is the superposition method (Saito et al. 2019); the seismic and ocean acoustic waves were first calculated in the absence of gravity. The recorded sea surface velocity was then used as a forcing term to calculate tsunamis. These three methods are two-step methods that do not calculate seismic waves and tsunamis simultaneously. Only the fully-coupled method (Lotto and Dunham 2015; Maeda and Furumura 2013) can achieve simultaneous calculations. Fully-coupled methods have been applied in many studies such as Krenz et al. (2021), Lotto et al. (2019), Ma (2022), Maeda et al. (2013), Wilson and Ma (2021).

On the other hand, the analysis of distant tsunami data has progressed over the past decade (see Watada 2023 for details). This has motivated the development of correctly coupled simulation schemes for seismic waves and tsunamis. The 2010 Chile Maule earthquake (Mw 8.8) and the 2011 Tohoku-Oki earthquake (Mw 9.0) were the first large earthquakes with trans-oceanic tsunamis since the Deep-ocean Assessment Reporting of Tsunamis (DART) system was installed in the Pacific Ocean. In the high-quality data from the DART system, phase velocity reductions were observed for long periods compared to those expected from conventional long-wave simulations. A new tsunami propagation theory was developed to explain the discrepancy between observations and simulations. This theory considers previously neglected effects, such as seawater compressibility, the elasticity of the seafloor, and gravitational potential perturbation due to the redistribution of Earth’s mass during tsunami propagation. Several tsunami calculation methods have been proposed based on this new theory (e.g., the phase correction method proposed by Watada et al. 2014 and the loading Green’s function convolution method proposed by Allgeyer and Cummins 2014). By contrast, the aforementioned fully-coupled methods (Lotto and Dunham 2015; Maeda and Furumura 2013) do not fully account for these effects described above. As will be discussed later, both methods use approximate equations that do not fully evaluate the effects of gravity. Therefore, the accuracies of these methods should be evaluated, for example, by comparing the phase velocities of the calculated tsunamis with the theoretical predictions without approximation.

In the following, we first derived the governing equations without approximation, focusing on the distinction between Lagrangian and Eulerian changes. Consequently, we obtained two equivalent equations (Lagrangian and Eulerian formulations, described later) and found that the former is close to the formulation in Maeda and Furumura (2013) and the latter is close to the formulation in Lotto and Dunham (2015). Based on the derived equations, numerical experiments were performed for a two-dimensional P-SV wavefield using the finite difference method (FDM). The accuracy of the calculated tsunamis was examined by comparing them with the theoretical tsunami dispersion relation obtained using the propagator matrix method. We then examined whether tsunami phase velocity reduction at longer periods is correctly calculated using the proposed method and the conventional methods. We also discussed the influence of the finite computational domain on the propagation of long-period tsunamis in FDM calculations. This provides important implications for the application of our method to distant tsunami modeling.

2 Governing Equations

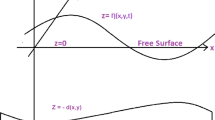
In this study, we treated the solid Earth and the ocean as a semi-infinite elastic medium and a fluid layer above it, respectively. We addressed two-dimensional P-SV problems in the xz-plane (we used Cartesian coordinates such that the z-axis is vertically downward).

When we consider small deformations of the solid and the fluid under gravity, it is essential to distinguish between the Lagrangian and Eulerian changes. For the convenience of the reader, we first review the concepts of the Lagrangian and Eulerian descriptions of continuum mechanics (experienced readers should begin reading at Sect. 2.3). The complete theory of Lagrangian and Eulerian equations for tsunamis in the deformable Earth (including the gravitational potential perturbation) can be found, for example, in Watada (2023).

2.1 Lagrangian and Eulerian Changes

We consider the Lagrangian and Eulerian changes in a certain physical quantity A. We write the value of A in the absence of medium deformation as $A_0$ (sometimes referred to as the “background” field), which is generally a function of the coordinates. There are two methods for describing the perturbation from $A_0$ when the medium is deformed. The first is the Lagrangian change, which is the perturbation measured in the coordinates moving with the parcel. We denote this change as $\delta A$. The second is the Eulerian change, which is the perturbation measured at a fixed point in space. We denote this change as $A'$.

In this study, we considered the infinitesimal deformation and took into account small quantities up to the first order of the displacement. Neglecting the higher-order terms, the relationship between $\delta A$ and $A'$ becomes

$$\begin{aligned} \delta A = A' + \textbf{u} \cdot \nabla A_0. \end{aligned}$$

(1)

Here $\textbf{u} = (u_x, u_z)$ represents the displacement, which follows the notations commonly used in seismology (velocity is represented as $\textbf{v} = (v_x, v_z)$). In the presence of gravity, it is natural to assume that the horizontal gradient of $A_0$ is small and negligible compared with the vertical gradient. In other words, we assume that the background field $A_0$ depends only on z. Then, Eq. (1) becomes

$$\begin{aligned} \delta A = A' + u_z \frac{d A_0}{dz}. \end{aligned}$$

(2)

Although these equations are for a scalar, they evidently hold when A is a vector or a tensor.

2.2 System of Equations

Next, we present a system of equations describing the motion of the solid and the fluid. The equation of continuity is written in the Lagrangian form as

$$\begin{aligned} \delta \rho = -\rho _0 \frac{\partial u_k}{\partial x_k}, \end{aligned}$$

(3)

and in the Eulerian form as

$$\begin{aligned} \rho ' = - \frac{\partial (\rho _0 u_k) }{\partial x_k}, \end{aligned}$$

(4)

where $\rho$ denotes the mass density and the Einstein summation convention is used.

In the Eulerian description, the equation of motion under gravity is given by

$$\begin{aligned} \rho \frac{D v_i}{Dt} = \frac{\partial \sigma _{ij}}{\partial x_j} + \rho g_i, \end{aligned}$$

(5)

where the subscripts i, j represent x, z, $D/Dt = \partial /\partial t + \textbf{v} \cdot \nabla$ denotes the material derivative, $\sigma _{ij}$ the stress tensor, $(g_i) = \textbf{g} = (0, g)$ the gravitational acceleration vector. We assume that the gravitational acceleration $g = 9.81 \, {\mathrm {m/s}}^{2}$ is a constant, and gravitational potential perturbations were not considered. Neglecting the higher-order terms of $\textbf{u}$ and $\textbf{v}$, we can write $Dv_i/Dt \simeq \partial v_i/\partial t$ and $v_i = Du_i/Dt \simeq \partial u_i / \partial t$. By substituting $\sigma _{ij} = \sigma _{0ij} + \sigma _{ij}'$ and $\rho = \rho _0 + \rho '$ into Eq. (5) and omitting the higher-order terms, we obtain

$$\begin{aligned} \rho _0 \frac{\partial ^2 u_i}{\partial t^2} = \frac{\partial }{\partial x_j} ( \sigma _{0ij} + \sigma _{ij}' ) + (\rho _0 + \rho ') g_i. \end{aligned}$$

(6)

Equation (6) contains two types of quantities of different orders of magnitude. One is the background field, the equation of which is

$$\begin{aligned} \sigma _{0ij} = - p_0 \delta _{ij}, \quad \frac{d p_0}{dz} = \rho _0 g, \end{aligned}$$

(7)

where $\delta _{ij}$ denotes the Kronecker delta and p denotes the pressure. The other is perturbation due to medium deformation, which is considerably smaller than the background quantities. Its equation is

$$\begin{aligned} \rho _s \frac{\partial ^2 u_i}{\partial t^2} = \frac{\partial \sigma _{ij}'}{\partial x_j} + \rho ' g_i \end{aligned}$$

(8)

for the solid, and

$$\begin{aligned} \rho _f \frac{\partial ^2 u_i}{\partial t^2} = - \frac{\partial p'}{\partial x_i} + \rho ' g_i \end{aligned}$$

(9)

for the fluid. Note that the background densities of the solid and the fluid are written simply as $\rho _s$ and $\rho _f$, omitting the subscript 0.

As the physical properties of the medium are unique to each parcel, the constitutive law is described using Lagrangian changes. Assuming that the solid Earth is an isotropic linear elastic body and the deformation is adiabatic, the constitutive law is given by

$$\begin{aligned} \delta \sigma _{ij} = \left( K-\frac{2}{3}\mu \right) \frac{\partial u_k}{\partial x_k} \delta _{ij} + \mu \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right) , \end{aligned}$$

(10)

where K is the bulk modulus and $\mu$ is the shear modulus. Note that the infinitesimal strain tensor $\varepsilon _{ij} = \frac{1}{2} \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right)$ has the same form in both Lagrangian and Eulerian descriptions, when we consider the terms up to the first order of $\textbf{u}$. For a fluid, using Eq. (3), the constitutive law is given by

$$\begin{aligned} \delta p = \frac{K}{\rho _f} \delta \rho = -K \frac{\partial u_k}{\partial x_k}. \end{aligned}$$

(11)

Figure 1

Geometry and coordinate system used in this study

Finally, we consider the boundary conditions. Because the boundary conditions require the forces to be balanced where the parcel exists after deformation, these are written using Lagrangian changes. Let the unperturbed free surface (sea surface) be at $z=0$ and the flat fluid–solid boundary (seafloor) be at $z=d$ (Fig. 1). We treated the air column as a vacuum, that is, there is no air pressure. Therefore, the boundary condition at the sea surface becomes

$$\begin{aligned} \delta p(x,0,t) = 0 \end{aligned}$$

(12)

(the arguments of the variables are explicitly written if necessary). At the seafloor, the vertical components of displacement ($u_z$) and velocity ($v_z$) must be continuous. In addition, the normal stress of the solid and the pressure of the fluid must have opposite signs and shear stress must vanish at the boundary.

$$\begin{aligned} \delta \sigma _{zz}(x,d,t) = -\delta p(x,d,t), \quad \delta \sigma _{xz}(x,d,t) = 0. \end{aligned}$$

(13)

2.3 The Lagrangian Formulation

Because the equations derived thus far involve both Lagrangian and Eulerian changes, it is convenient to write equations using only one of the these. First, we consider the case with only Lagrangian changes. This approach is hereafter referred to as the “Lagrangian formulation”, and it is similar to the formulation in Maeda and Furumura (2013).

Using Eqs. (2) and (7), we obtain

$$\begin{aligned} \sigma _{ij}' = \delta \sigma _{ij} + \rho _s g u_z \delta _{ij}, \; p' = \delta p - \rho _f g u_z. \end{aligned}$$

(14)

By writing $\rho '$ using Eq. (4), and noting that $\rho _s$ and $\rho _f$ depend only on z, we can write the equations of motion (Eqs. 8 and 9) using Lagrangian changes. For the solid, we have

$$\begin{aligned} \rho _s \frac{\partial ^2 u_x}{\partial t^2}&= \frac{\partial \delta \sigma _{xx}}{\partial x} + \frac{\partial \delta \sigma _{xz}}{\partial z} + \rho _s g \frac{\partial u_z}{\partial x}, \end{aligned}$$

(15)

$$\begin{aligned} \rho _s \frac{\partial ^2 u_z}{\partial t^2}&= \frac{\partial \delta \sigma _{xz}}{\partial x} + \frac{\partial \delta \sigma _{zz}}{\partial z} - \rho _s g \frac{\partial u_x}{\partial x}. \end{aligned}$$

(16)

For the fluid, we have

$$\begin{aligned} \rho _f \frac{\partial ^2 u_x}{\partial t^2}&= - \frac{\partial \delta p}{\partial x} + \rho _f g \frac{\partial u_z}{\partial x} , \end{aligned}$$

(17)

$$\begin{aligned} \rho _f \frac{\partial ^2 u_z}{\partial t^2}&= - \frac{\partial \delta p}{\partial z} - \rho _f g \frac{\partial u_x}{\partial x} . \end{aligned}$$

(18)

Equations (10)–(13), (15)–(18) constitute a complete system of equations in the Lagrangian formulation.

The right-hand sides of Eqs. (15)–(18) contain the displacement gradients. Therefore, the displacements must be used as independent variables in the FDM calculations. In this study, we employed a less commonly used displacement–velocity–stress (DVS) formulation for the FDM calculations. However, this formulation has several advantages. First, implementation of the boundary conditions is easier than that of the Eulerian formulation (see Sect. 2.4). Second, it is straightforward to compare the calculated values with the observation data recorded by the ocean-bottom pressure gauges. Because the ocean-bottom pressure gauges are fixed to the seafloor, they measure $\delta p(x,d,t)$.

2.4 The Eulerian Formulation

Next, we consider the case with only Eulerian changes. This approach is hereafter referred to as the “Eulerian formulation”, and it is similar to the formulation in Lotto and Dunham (2015).

Writing Eq. (8) separately for the x- and z-components, we have

$$\begin{aligned} \rho _s \frac{\partial ^2 u_x}{\partial t^2}&= \frac{\partial \sigma _{xx}'}{\partial x} + \frac{\partial \sigma _{xz}'}{\partial z}, \end{aligned}$$

(19)

$$\begin{aligned} \rho _s \frac{\partial ^2 u_z}{\partial t^2}&= \frac{\partial \sigma _{xz}'}{\partial x} + \frac{\partial \sigma _{zz}'}{\partial z} + \rho ' g. \end{aligned}$$

(20)

For Eq. (9), we have

$$\begin{aligned} \rho _f \frac{\partial ^2 u_x}{\partial t^2}&= - \frac{\partial p'}{\partial x}, \end{aligned}$$

(21)

$$\begin{aligned} \rho _f \frac{\partial ^2 u_z}{\partial t^2}&= - \frac{\partial p'}{\partial z} + \rho ' g. \end{aligned}$$

(22)

In this formulation, the perturbations $\sigma _{ij}'$ and $p'$ are calculated using Eq. (14) and the density perturbation $\rho '$ using Eq. (4). We now write these equations again.

$$\begin{aligned} \sigma _{ij}'&= \left( K-\frac{2}{3}\mu \right) \frac{\partial u_k}{\partial x_k} \delta _{ij} + \mu \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right) + \rho _s g u_z \delta _{ij}, \end{aligned}$$

(23)

$$\begin{aligned} p'&= -K \left( \frac{\partial u_x}{\partial x} + \frac{\partial u_z}{\partial z} \right) - \rho _f g u_z, \end{aligned}$$

(24)

$$\begin{aligned} \rho '&= - \rho _0 \left( \frac{\partial u_x}{\partial x} + \frac{\partial u_z}{\partial z} \right) - u_z \frac{d \rho _0}{dz} . \end{aligned}$$

(25)

Note that $\rho _0$ represents $\rho _s$ or $\rho _f$.

To clearly illustrate the boundary conditions, we introduce new variables. Let $\eta (x,t) = -u_z(x,0,t)$ and $b(x,t) = -u_z(x,d,t)$ be the vertical uplift at the sea surface and seafloor, respectively. Using Eqs. (12) and (14), the boundary condition at the sea surface becomes

$$\begin{aligned} p' (x,0,t) = \rho _f(0) g\eta (x,t). \end{aligned}$$

(26)

Similarly, using Eqs. (13) and (14), the boundary conditions at the seafloor become

$$\begin{aligned} \sigma _{zz}'(x,d,t) + p'(x,d,t) = -(\rho _s(d)-\rho _f(d)) g b(x,t), \quad \sigma _{xz}'(x,d,t) = 0. \end{aligned}$$

(27)

Equations (19)–(27) constitute a complete system of equations for the Eulerian formulation.

In the FDM simulations of seismic waves, the velocity–stress formulations are often used. The displacements can be removed by differentiating the above equations with respect to time. The time differentiation of Eqs. (23)–(25) yields

$$\begin{aligned} \frac{\partial \sigma _{ij}'}{\partial t}&= \left( K-\frac{2}{3}\mu \right) \frac{\partial v_k}{\partial x_k} \delta _{ij} + \mu \left( \frac{\partial v_i}{\partial x_j} + \frac{\partial v_j}{\partial x_i} \right) + \rho _s g v_z \delta _{ij}, \end{aligned}$$

(28)

$$\begin{aligned} \frac{\partial p'}{\partial t}&= -K \left( \frac{\partial v_x}{\partial x} + \frac{\partial v_z}{\partial z} \right) - \rho _f g v_z, \end{aligned}$$

(29)

$$\begin{aligned} \frac{\partial \rho '}{\partial t}&= - \rho _0 \left( \frac{\partial v_x}{\partial x} + \frac{\partial v_z}{\partial z} \right) - v_z \frac{d \rho _0}{dz}. \end{aligned}$$

(30)

The boundary conditions are the same as those in Eqs. (26) and (27), and we require the equations to update variables $\eta$ and b. By neglecting the higher-order terms, we obtain

$$\begin{aligned} \frac{\partial \eta }{\partial t} = -v_z(x,0,t), \quad \frac{\partial b}{\partial t} = -v_z(x,d,t). \end{aligned}$$

(31)

2.5 Equations used in Previous Fully-Coupled Calculations

Now that we obtain all the necessary equations, we review the equations used in the previous fully-coupled calculations. As previously noted, the formulation in Maeda and Furumura (2013) is similar to our Lagrangian formulation. In Maeda and Furumura (2013), the tsunami term $-\rho _f(0) g \partial \eta /\partial x$, which is proportional to the displacement gradient at the sea surface, was added to the x-component of their equation of motion. This tsunami term resembles the last terms in Eqs. (15) and (17), which represent the displacement gradient at each point. The presence of the tsunami term implies that information regarding the sea surface is instantaneously transmitted throughout the medium. Because the upper bound of the propagation speed of any perturbation is the sound speed (C), the tsunami term appears to assume $C \rightarrow \infty$, whereas C was set to a finite value for the calculation of the acoustic waves.

In contrast, the formulation in Lotto and Dunham (2015) is similar to our Eulerian formulation. They derived equations corresponding to Eqs. (21), (22), (29), (26), and (31), by linearizing the governing equations of the fluids using Eulerian changes. However, their method included approximations. First, in the derivation of equations, they assumed $\frac{1}{\rho _f} \frac{d\rho _f}{dz} = \frac{1}{K}\frac{dp_0}{dz}$, which means the fluid is adiabatically density stratified (see Sect. 4.1). In contrast, $\rho _f$ was set to a constant value in their numerical calculations. Next, they considered the gravity terms in the governing equations for a fluid ($\rho ' g$ in Eq. (22) and $-\rho _f g v_z$ in Eq. (29)) to be small, and neglected them in their numerical calculations. Furthermore, it is unclear whether the gravity is considered in their governing equations of solids. The continuity condition for the stress at the seafloor (corresponding to Eq. 27) also does not seem to include gravity.

This treatment corresponds to a surface gravity approximation (Segall 2010), that considers gravity only as a boundary condition at the free surface and does not include it directly in the governing equations. This is an effective approach for avoiding the gravitational instability that can occur when an appropriate density profile is not used (an alternative method is to use stratified density profiles. See Sect. 4.1). As Abrahams et al. (2023) and Lotto and Dunham (2015) noted, calculations based on this approximation may yield a dispersion relation that differs slightly from the exact relation. One of our objectives is to investigate the extent of this difference quantitatively.

3 Numerical Implementation

Next, we describe numerical experiments based on the following four formulations:

• Lagrangian formulation

• Eulerian formulation

• Maeda and Furumura’s (2013) formulation

• Lotto and Dunham’s (2015) formulation

Although the governing equations differ among these formulations, the basic FDM implementations described below are common, i.e., DVS formulation with a staggered grid system, interpolation for gravity terms, injection of sources, implementation of anelastic attenuation, special treatment of physical boundary conditions, and non-reflecting boundary condition.

3.1 Staggered-Grid FDM

Figure 2

Grid system used in this study. The symbol $\delta$ indicating Lagrangian changes and prime $(')$ indicating Eulerian changes are omitted for stresses and pressure

For the simulations of seismic waves, ocean acoustic waves, and tsunamis, we employed a staggered-grid FDM with a fourth-order accuracy in space and a second-order accuracy in time (e.g., Levander 1988; Moczo et al. 2007). The grid system is shown in Fig. 2.

As explained in Sect. 2.4, the Eulerian formulation can be implemented in velocity–stress equations, whereas the Lagrangian formulation requires displacement terms. For calculation and comparison under the same conditions, a displacement–velocity–stress (DVS) formulation of the FDM simulation was employed in this study. The calculation procedure based on the DVS formulation is shown in Algorithm 1.

From the similarities between the equations, Maeda and Furumura’s (2013) formulation can be calculated in a manner similar to the Lagrangian formulation, and Lotto and Dunham’s (2015) formulation can be calculated using the Eulerian formulation by setting $g=0$ except for the sea surface. Note that the constitutive laws presented by Lotto and Dunham (2015) and Maeda and Furumura (2013) are in a time-differentiated form, that is, the velocity–stress formulation. Therefore, results obtained using the DVS formulation may not be exactly identical to them.

Algorithm 1

Outline of time-integration scheme in DVS formulation. The subscripts i, j represent x or z, superscripts represent the time levels, RHS represents the right-hand side of the equations of motion (e.g., Equations 15–18 or 19–22), and dt denotes a time step. The symbol $\delta$ indicating Lagrangian changes and prime $(')$ indicating Eulerian changes are omitted for stresses and pressure.

When discretizing the equations including gravity on a staggered grid system, it must be noted that not all variables are calculated at the same grid point. To clarify this issue, we consider the x-component of the equation of motion in the Lagrangian formulation (Eq. 15). In this equation, the stress gradients are computed on the same grids as $u_x$, whereas the gravity term $\rho _s g \partial u_z / \partial x$ is computed on grids half a grid away from $u_x$ (see Fig. 2). Therefore, when updating $u_x$ in the FDM calculation, we must use the values on the neighboring grids. The same is true for Eqs. (16)–(18). In the Eulerian formulation, the issue also arises for the gravity term $\rho ' g$ in Eqs. (20) and (22), and the last term on the right-hand side of Eqs. (28) and (29). In our FDM calculations, these gravity terms were calculated by a linear interpolation between two neighboring values (if one of the two neighboring values was not present, linear extrapolation or substitution of one neighboring value was performed. See the codes for the detailed implementation). In this study, interpolated and extrapolated values are represented by a tilde.

To simplify the simulation results and compare them with theoretical solutions, the tsunami simulations in this study were performed using a point source. Actual tsunami calculations need to account for heterogeneous slip distribution on the fault plane (e.g., Adriano et al. 2017), which can be achieved by placing a large number of point sources along the fault plane, since our formulation is linear. Let $\left. A \right| _{i, j}$ or $(A)_{i, j}$ be the discretized value of quantity A defined at $(x,z)=(idx, jdz)$, where dx and dz denote the grid sizes in the x- and z-directions. Furthermore, let $(i_0, j_0$) be the grid location where the source acts, and $M_{pq}$ be the strength of the seismic moment tensor. The stresses were then updated as follows (Moczo et al. 2014):

$$\begin{aligned} \left. \sigma _{xx} \right| _{i_0, j_0}&= \left. \sigma _{xx} \right| _{i_0, j_0} - \frac{M_{xx} \, f(t)}{dx\cdot dz} \end{aligned}$$

(32)

$$\begin{aligned} \left. \sigma _{zz} \right| _{i_0, j_0}&= \left. \sigma _{zz} \right| _{i_0, j_0} - \frac{M_{zz} \, f(t)}{dx\cdot dz} \end{aligned}$$

(33)

$$\begin{aligned} \left. \sigma _{xz} \right| _{i_0-1/2, j_0-1/2}&= \left. \sigma _{xz} \right| _{i_0-1/2, j_0-1/2} - \frac{M_{xz} \, f(t)}{4dx\cdot dz} \end{aligned}$$

(34)

$$\begin{aligned} \left. \sigma _{xz} \right| _{i_0-1/2, j_0+1/2}&= \left. \sigma _{xz} \right| _{i_0-1/2, j_0+1/2} - \frac{M_{xz} \, f(t)}{4dx\cdot dz} \end{aligned}$$

(35)

$$\begin{aligned} \left. \sigma _{xz} \right| _{i_0+1/2, j_0-1/2}&= \left. \sigma _{xz} \right| _{i_0+1/2, j_0-1/2} - \frac{M_{xz} \, f(t)}{4dx\cdot dz} \end{aligned}$$

(36)

$$\begin{aligned} \left. \sigma _{xz} \right| _{i_0+1/2, j_0+1/2}&= \left. \sigma _{xz} \right| _{i_0+1/2, j_0+1/2} - \frac{M_{xz} \, f(t)}{4dx\cdot dz}. \end{aligned}$$

(37)

Note that the moment time function was used instead of the moment rate function because we used the DVS formulation. We adopted the Küpper wavelet (e.g., Mavroeidis and Papageorgiou 2003) as f(t); that is,

$$\begin{aligned} f(t) = \int _{0}^{t} \dot{f}(t') dt', \quad \dot{f}(t) = {\left\{ \begin{array}{ll} \frac{3\pi }{4T_{rise}} \sin ^3 \left( \frac{\pi t}{T_{rise}} \right) &{} 0 \le t \le T_{rise} \\ 0 &{} \text {else}, \end{array}\right. } \end{aligned}$$

(38)

where $T_{rise}$ is the characteristic source duration time.

Theoretically, the quality factor of a solid should be discriminated between the P- and S-waves. However, for simplicity, we did not distinguish between them here and incorporated them into the FDM calculation using Graves’ (1996) procedure. This was achieved by multiplying the factor $\exp (-\pi f_0 dt/Q)$ by the updated velocity and displacement values at each time step (Graves 1996), where $f_0$ denotes a reference frequency (we set $f_0 = 2 / T_{rise}$ in the calculations), and Q represents the quality factor. We write the quality factor of the solid and fluid as $Q_s$ or $Q_f$, respectively (note that the subscript s represents “solid”, not “shear waves”).

3.2 Physical Boundary Conditions

Here, we illustrate how to implement boundary conditions at the seafloor and the sea surface, following Okamoto and Takenaka (2005). We assumed that the seafloor is located at $j=j_{sf}$ and that the sea surface is located at $j=0$. First, we consider the seafloor (fluid–solid boundary) in the Lagrangian formulation.

The seafloor was placed on grids of shear stress $\sigma _{xz}$. Furthermore, when the derivatives near the boundary were calculated, we did not use the values of both sides of the boundary but used reduced-order finite differences. That is, only the values of the medium to which the evaluation point belongs were used. For example, $\partial u_z / \partial z$ just above the seafloor was evaluated using the second-order difference instead of the fourth-order difference as follows:

$$\begin{aligned} \left. \frac{\partial u_z}{\partial z}\right| _{i,j_{sf}-1/2} = \frac{ \left. u_z \right| _{i,j_{sf}} - \left. u_z \right| _{i,j_{sf}-1} }{dz}. \end{aligned}$$

(39)

Next, the method for updating the velocities near the boundary is explained. As $v_x$ is not defined at the boundary, they can be updated using the discretized form of Eqs. (15) and (17). By contrast, $v_z$ is defined at the boundary and we must be careful when discretize Eqs. (16) and (18) (note that the continuity of $v_z$ and $u_z$ holds because the fluid and the solid share the same grid). The equation updating $v_z$ at the boundary evaluates the z-derivatives of the stress and pressure as one-sided differences. Noting that $\delta \sigma _{xz}=0$ at the boundary, Eqs. (16) and (18) become

$$\begin{aligned} \left( \rho _s \frac{\partial v_z}{\partial t} \right) _{i, j_{sf}} = 0 + \frac{ \left. \delta \sigma _{zz} \right| _{i, j_{sf}+1/2} - \left. \delta \sigma _{zz} \right| _{i, j_{sf}} }{dz/2} - \left. \rho _s \right| _{j_{sf}} g \left. \widetilde{\frac{\partial u_x}{\partial x}} \right| _{i, j_{sf}}^{(s)} \end{aligned}$$

(40)

and

$$\begin{aligned} \left( \rho _f \frac{\partial v_z}{\partial t} \right) _{i, j_{sf}} = - \frac{ \left. \delta p \right| _{i, j_{sf}} - \left. \delta p \right| _{i, j_{sf}-1/2} }{dz/2} - \left. \rho _f \right| _{j_{sf}} g \left. \widetilde{\frac{\partial u_x}{\partial x}} \right| _{i, j_{sf}}^{(f)}, \end{aligned}$$

(41)

where the superscripts (s) and (f) represent the values interpolated from the solid and fluid values, respectively. By adding Eqs. (40) and (41) and considering $(\delta \sigma _{zz} + \delta p)_{i, j_{sf}} = 0$, we obtain the Lagrangian formula for updating $\left. v_z \right| _{i, j_{sf}}$:

$$\begin{aligned} \left( (\rho _f + \rho _s) \frac{\partial v_z}{\partial t} \right) _{i, j_{sf}}&= \frac{ \left. \delta p \right| _{i, j_{sf}-1/2} + \left. \delta \sigma _{zz} \right| _{i, j_{sf}+1/2} }{dz/2} \nonumber \\&\quad - g \left( \left. \rho _f \right| _{j_{sf}} \left. \widetilde{\frac{\partial u_x}{\partial x}} \right| _{i, j_{sf}}^{(f)} + \left. \rho _s \right| _{j_{sf}} \left. \widetilde{\frac{\partial u_x}{\partial x}} \right| _{i, j_{sf}}^{(s)} \right) . \end{aligned}$$

(42)

For the sea surface, considering $\left. \delta p \right| _{i, 0} = 0$ and $\partial u_x/\partial x = 0$ in the air column, we obtain

$$\begin{aligned} \left( (\rho _a + \rho _f) \frac{\partial v_z}{\partial t} \right) _{i, 0} = - \frac{ \left. \delta p \right| _{i, 1/2} - 0 }{dz/2} - \left. \rho _f \right| _0 g \left. \widetilde{\frac{\partial u_x}{\partial x}} \right| _{i, 0}. \end{aligned}$$

(43)

This procedure can be repeated for the Eulerian formulation. The only difference was that $(\sigma _{zz}' + p' )_{i, j_{sf}} = - (\rho _s-\rho _f)_{j_{sf}} g \left. b \right| _i$ and $\left. p' \right| _{i, 0} = \left. \rho _f \right| _0 g \left. \eta \right| _i$. The Eulerian formulas corresponding to Eqs. (42) and (43) are as follows:

$$\begin{aligned} \left( (\rho _f + \rho _s) \frac{\partial v_z}{\partial t} \right) _{i, j_{sf}}= & {} \frac{ \left. p' \right| _{i, j_{sf}-1/2} + \left. \sigma _{zz}' \right| _{i, j_{sf}+1/2} + (\rho _s-\rho _f)_{j_{sf}} g \left. b \right| _i }{dz/2} + \left( \left. \widetilde{\rho '} \right| _{i, j_{sf}}^{(f)} + \left. \widetilde{\rho '} \right| _{i, j_{sf}}^{(s)} \right) g, \end{aligned}$$

(44)

$$\begin{aligned} \left( (\rho _a + \rho _f) \frac{\partial v_z}{\partial t} \right) _{i, 0}= & {} - \frac{ \left. p' \right| _{i, 1/2} - \left. \rho _f \right| _0 g \left. \eta \right| _i }{dz/2} + \left. \widetilde{\rho '} \right| _{i, 0} ^{(f)} g. \end{aligned}$$

(45)

In our numerical experiments, the implementation of the boundary conditions in the Maeda and Furumura’s (2013) formulation was similar to that in the Lagrangian formulation, and that in the Lotto and Dunham’s (2015) formulation was similar to that in the Eulerian formulation.

3.3 Non-reflecting Boundary Condition

To prevent the artificial reflection of seismic and acoustic waves from the edges of the computational domain, a perfectly matched layer (PML) boundary condition was used. The auxiliary differential equation (ADE) of the complex-frequency shifted perfectly matched layer (CFS-PML) (Zhang and Shen 2010) was implemented in the DVS formulation. The damping profile used is the same as Zhang and Shen (2010), with PML layer of 20 grid points.

4 Results

4.1 Problem Setup

Table 1 Parameters used in the FDM calculations

Here, we present the results of the numerical experiments. The parameters used in the experiments are listed in Table 1. In the simulation, a fluid layer with a thickness of 4 km was placed on top of the solid. Ideally, a solid should be a semi-infinite medium; however, a finite depth was set for computational purposes. The influence of finite domain depth on tsunami propagation in the FDM calculations is discussed in Sect. 5.3. The seismic wave velocities $\alpha , \beta$ and sound speed C were assumed to be constant, whereas densities were not constant. To determine the vertical profile of the density, we introduce the concept of Brunt–Väisälä frequency (or buoyancy frequency) N. It is defined by

$$\begin{aligned} N^2 = g \left( \frac{1}{\rho _0}\frac{d \rho _0}{dz} - \frac{\rho _0 g}{K} \right) \end{aligned}$$

(46)

(note that we take the z-axis vertically downward). If the medium is uniform ($d \rho _0/dz=0$), then $N^2<0$, which indicates gravitational instability. In this case, when a small perturbation is added, it continues to increase with time. With a constant density profile, we confirmed that both the Lagrangian and Eulerian formulations yield this physical instability. One method to avoid instability is to adopt the surface gravity approximation. The other is to use a non-uniform density profile. To avoid both gravitational instability and buoyancy oscillations, we require $N^2=0$, which provide stratified density profiles. For the fluid, we have

$$\begin{aligned} \rho _f(z) = \rho _f(0) \exp \left( \frac{z}{H_f} \right) , \quad H_f = \frac{C^2}{g}, \end{aligned}$$

(47)

where $\rho _f(0) = 1.0 \, {\mathrm {g/cm}}^{3}$ denotes the density of the fluid at the sea surface. $H_f \simeq 2.3 \times 10^2$ km is a constant scale height of the fluid. For the solid, we have

$$\begin{aligned} \rho _s(z) = \rho _s(d) \exp \left( \frac{z-d}{H_s} \right) , \quad H_s = \frac{\alpha ^2-\frac{4}{3}\beta ^2}{g}, \end{aligned}$$

(48)

where $\rho _s(d) = 3.0 \, {\mathrm {g/cm}}^{3}$ is the density of the solid at the seafloor. $H_s \simeq 1.3 \times 10^3$ km is a constant scale height of the solid.

4.2 Simulation Results

Figure 3

Snapshots of the displacement field, calculated in the Lagrangian formulation. The width and depth of the computational domain were set to 200 km and 40 km, respectively. The amplitude of horizontal displacement $|u_x|$ is shown in red and that of vertical displacement $|u_z|$ in blue (each color is blended according to the ratio of $|u_x|$ and $|u_z|$). The origin of time was taken as the time when the earthquake occurred

Figure 4

Diagrams of the time variation of the vertical displacement calculated in the Lagrangian formulation, demonstrating the propagation of seismic waves, ocean acoustic waves and their multiple reflections, and tsunamis. The computational domain width and depth were same as in Fig. 3. Positive values correspond to uplift

Figure 3 shows the snapshots of the displacement wavefields calculated using the Lagrangian formulation. The snapshot at $t = 5$ s shows P- and S-waves propagating in the solid Earth. The snapshot at $t = 20$ s shows that permanent deformation existed near the epicenter after the seismic waves have passed through the solid. Snapshots at $t = 20$ s and 50 s show multiple reflections of ocean acoustic waves between the sea surface and seafloor. The snapshot at $t = 200$ s shows that the tsunami propagated to the left and right within the fluid layer. The spatiotemporal variation in the wavefields obtained by the simulation corresponds well with Figure 5 in Maeda and Furumura (2013).

Figure 4 shows the time variation of the vertical displacements containing the various types of waves described above, indicating a complex superposition of acoustic waves and tsunamis near the epicenter. The seafloor pressure waveforms obtained just above the epicenter indicate that the characteristic oscillations of seawater were reproduced well (see Supplementary File 1). The latter part of the waveform also shows that the calculated tsunamis are dispersive.

5 Discussion

5.1 Verification of Permanent Deformation

Figure 5

Comparison of the calculated seafloor displacements at $t = 5000$ s with the analytical solution (Singh and Garg 1985). The vertical displacement $u_z$ is flipped upside down so that the uplift corresponds to positive $u_z$. Note that the computational domain width was set to 2000 km, but only the center portion is shown in this figure for ease of viewing. The computational domain depth was set to 400 km

To verify the simulation results, the calculated permanent deformations are compared with the analytical solution. When the computational domain width was not sufficiently large (200 km), the PML boundary causes the shape of the permanent deformation to bend in non-physical directions at both ends of the computational domain. To avoid this problem, we set the computational domain width to 2000 km. The analytical solution for the surface displacement produced by a $45^\circ$-dipping fault in two-dimensional semi-infinite space without an ocean layer is given by Singh and Garg (1985). Figure 5 shows that the results for both the Lagrangian and Eulerian formulations differ slightly from the analytical solution. In particular, the calculated values of the vertical uplift were slightly larger than the analytical values. This discrepancy may have been due to a decrease in seawater loading as the water mass moved away from the elevated epicentral region.

5.2 Verification of Tsunami Phase Velocity

Figure 6

Simulated tsunami waveforms at two stations used to examine the frequency dependence of phase velocity. The symbol $\Delta$ in legend indicates epicentral distance

Figure 7

Comparison of the frequency dependence of tsunami phase velocity obtained by FDM simulation based on four formulations and the theoretical values based on the propagator matrix method. The phase velocity of the linear long wave ($c_\phi = \sqrt{gd}$) and the linear gravity wave ($c_\phi = \sqrt{\frac{g}{k} \tanh (kd)}$) are also included for comparison, where k is the wavenumber

To validate the propagation properties of the calculated tsunamis, we examine the frequency dependence of the tsunami phase velocity $c_\phi$. For this calculation, we used tsunami waveforms cut to appropriate lengths. The linear trends were removed and Tukey windows were applied to calculate the discrete Fourier transform. The phase velocity $c_\phi$ at each frequency was then calculated from the phase difference between the two distant points (see the Supplementary File 2 for more details).

In this experiment, the computational domain width was set to 2000 km to evaluate tsunami propagation over a long period ($\gtrsim 1000$ s). On the real Earth, however, the effects of the sphericity of the Earth and the gravitational potential perturbation cannot be neglected at this scale. It should be emphasized that this experiment was only intended to compare the tsunami phase velocities among the four formulations, rather than simulating the actual tsunami propagation on the Earth. The computational domain was deepened (400 km) to reduce the influence of the finite computational domain on long-wavelength tsunamis. The influence of the domain depth on tsunami propagation is discussed in detail in Sect. 5.3.

The waveforms used are shown in Fig. 6, and a comparison of the calculated tsunami phase velocity with a theoretical prediction obtained using the propagator matrix method (see Appendix A) are presented in Fig. 7. Note that the measured phase velocities for the longest periods may not be accurate because they are strongly affected by the preprocessing of the Fourier transform.

The results confirmed that the phase velocity curves of tsunamis obtained by both the Lagrangian and Eulerian formulations were almost identical to the theoretical ones. It was also confirmed that the phase velocity was slower than that of linear gravity waves for long periods, which is consistent with the slowdown of the measured phase velocity in real tsunami data (Watada et al. 2014). However, the dispersion curve obtained by the Maeda and Furumura’s (2013) formulation is slightly ($\sim 0.2 \, \%$) upshifted from the theoretical curve, whereas the curve in the Lotto and Dunham’s (2015) formulation is downshifted significantly ($\sim 1 \, \%$). Underestimating the phase velocity implies that the actual tsunami arrives earlier than the predicted arrival time. Therefore, one should be careful when applying Lotto and Dunham’s (2015) formulation to a precise estimate of the tsunami arrival time.

The underestimation in Lotto and Dunham’s (2015) formulation can be explained as follows: the gravitational energy of seawater resulting from the uplift of the seafloor $E_g$ is equal to the kinetic energy of the tsunami $E_k$ (we neglect the elastic strain energy of the seawater and solids, which is significantly small). Because Lotto and Dunham (2015) considered gravity only at the sea surface, they underestimated $E_g$ and therefore $E_k$, resulting in a slower phase velocity. However, the results in Maeda and Furumura (2013) are much closer to the theoretical values. This may be due to the inclusion of gravity in the entire medium, although gravity was not evaluated correctly in their formulation. These results discussed thus far suggest the importance of the correct implementation of gravity in coupled tsunami calculations.

5.3 Implications for Distant Tsunami Simulation

Figure 8

Same as in Fig. 7, but with different computational domain depth (calculated in the Lagrangian formulation)

Figure 9

Normalized tsunami eigenfunctions in the solid computed by the propagator matrix method ($T=4000$ s). Left: eigenfunctions of displacements normalized by the maximum amplitude of $\hat{u}_z$. Right: eigenfunctions of stresses normalized by the maximum amplitude of $\hat{\sigma }_{zz}$

Figure 8 shows a comparison of the tsunami phase velocities with different computational domain depths. When the depth was 100 km, the simulated tsunami phase velocity was significantly underestimated from the theoretical value in the long-period bands. However, the accuracy increased gradually with increasing domain depth. This is presumably because of the inability to correctly represent the large-scale deformation of the solid associated with long-period tsunami propagation when the computational domain depth was insufficient. Figure 9 shows that the tsunami eigenfunctions in the solid exhibit large amplitudes even at 100–200 km when the period is 4000 s. The eigenfunction decays rapidly with depth, but the amplitude decay rate is smaller for longer periods (e.g., Ward 1980), indicating that the deeper parts of the domain affected tsunami propagation. Therefore, it is necessary to take a sufficient domain depth to calculate long-period ($> 1000$ s) tsunamis correctly.

It should be noted that how the PML boundary condition imposed at the edge of the domain affects the large-scale deformation of the solid is not yet fully understood. Therefore, when the PML condition is used, care should be taken regarding the accuracy of the deformation at long scales, along with the finite depth issue of the computational domain.

5.4 Potential Applications of our Coupled Tsunami Simulation

Finally, we briefly discuss cases in which our method is more effective than conventional fully-coupled methods. In the equations for elastic or fluid bodies under gravity, the ratio of the gravity term to the elastic term is of the order of $g\lambda /c^2$ (where $\lambda$ is the wavelength of the wave considered, and c is the sound speed or seismic wave velocity). Therefore, if the gravity is large relative to the elastic force, that is, the ratio $g\lambda /c^2$ is not sufficiently small compared to 1, Lotto and Dunham (2015) and Maeda and Furumura’s (2013) formulations, which do not correctly implement the effects of gravity, will not produce the correct tsunami waveform. This is the case, for example, when there is a thick seafloor sedimentary layer with very low elastic wave velocities. In addition, if the seawater has large density jumps in the middle, for example in a two-layer system, the buoyancy due to the density difference will not be correctly evaluated. In such cases, the proposed formulation will provide more accurate results.

6 Conclusion

We derived the governing equations describing the deformation of a solid and fluid under gravity, considering the distinction between Lagrangian and Eulerian changes. The equations were then compared with those used in previous studies on coupled tsunami simulations. Based on the numerical experiments using FDM, the effectiveness of our new formulation was examined by comparing the tsunami phase velocity with theoretical values.

Since our numerical experiments were limited to 2D cases with a simple geometry, the computational cost is relatively low; for example, it takes 5–10 min to compute a 200 km × 40 km domain for 500 s with the Lagrangian Formulation (OpenMP thread parallel computation with 20 cores on 1 CPU). To apply it to a realistic tsunami simulation, one can simply replace the 2D equations with 3D ones. The computation time for a 3D simulation in a 200 km × 200 km × 40 km domain is estimated to be several thousand times longer than a 2D simulation due to the increase in variables and grid points to be solved, but this can be achieved by a multi-CPU parallel simulation using MPI.

We must add that our formulation does not include the sphericity of the Earth and the effect of the gravitational potential perturbation, which are necessary to simulate distant tsunamis. Addressing these problems will enable a more realistic coupled modeling of seismic waves and tsunamis.

Appendix A. Propagator Matrix Method to Obtain Tsunami Dispersion Relations

Here, we obtain the propagator matrix of a compressible fluid layer on a semi-infinite elastic body under gravity. This enabled us to calculate the theoretical dispersion relation and eigenfunctions of tsunamis, which can be used as a benchmark for the measured phase velocities. If the equations are written in the Lagrangian formulation, the boundary conditions are expressed without gravity terms and are easily implemented. Therefore, we use the Lagrangian formulation and omit the symbol $\delta$ indicating Lagrangian changes in this section.

We assume that the solid and the fluid are density stratified with constant scale heights $H_s$ and $H_f$, respectively. The seismic wave velocities in the solid $\alpha , \beta$ and the sound speed in the fluid C are assumed to be constant. The effects of anelastic attenuation are not considered.

1.1 A.1 Semi-Infinite Solid under Gravity

We first rewrite the system of equations for a density-stratified solids under gravity. To incorporate the stratified density profile, we introduce density-scaled variables (e.g., Watada 2013):

$$\begin{aligned} U_x&= \sqrt{\rho _s} u_x, \; U_z = \sqrt{\rho _s} u_z, \nonumber \\ \Sigma _{xx}&= \frac{\sigma _{xx}}{\sqrt{\rho _s}}, \; \Sigma _{xz} = \frac{\sigma _{xz}}{\sqrt{\rho _s}}, \; \Sigma _{zz} = \frac{\sigma _{zz}}{\sqrt{\rho _s}}. \end{aligned}$$

(A1)

Using $\frac{1}{H_s} = \frac{1}{\rho _s} \frac{d\rho _s}{dz}$, the equations of motion and constitutive laws become:

$$\begin{aligned} \frac{\partial ^2 U_x}{\partial t^2}&= \frac{\partial \Sigma _{xx}}{\partial x} + \left( \frac{\partial \Sigma _{xz}}{\partial z} + \frac{\Sigma _{xz}}{2H_s} \right) + g \frac{\partial U_z}{\partial x} \end{aligned}$$

(A2)

$$\begin{aligned} \frac{\partial ^2 U_z}{\partial t^2}&= \frac{\partial \Sigma _{xz}}{\partial x} + \left( \frac{\partial \Sigma _{zz}}{\partial z} + \frac{\Sigma _{zz}}{2H_s} \right) - g \frac{\partial U_x}{\partial x}, \end{aligned}$$

(A3)

$$\begin{aligned} \Sigma _{xx}&= \alpha ^2 \frac{\partial U_x}{\partial x} + \left( \alpha ^2 - 2\beta ^2 \right) \left( \frac{\partial U_z}{\partial z} - \frac{U_z}{2H_s} \right) \end{aligned}$$

(A4)

$$\begin{aligned} \Sigma _{xz}&= \beta ^2 \left( \frac{\partial U_x}{\partial z} - \frac{U_x}{2H_s} + \frac{\partial U_z}{\partial x} \right) \end{aligned}$$

(A5)

$$\begin{aligned} \Sigma _{zz}&= \alpha ^2 \left( \frac{\partial U_z}{\partial z} - \frac{U_z}{2H_s} \right) + \left( \alpha ^2 - 2\beta ^2 \right) \frac{\partial U_x}{\partial x} . \end{aligned}$$

(A6)

We seek a solution to the above equations in the form of a plane wave (e.g., Aki and Richards 2002):

$$\begin{aligned} \begin{pmatrix} U_x(x, z, t) \\ U_z(x, z, t) \\ \Sigma _{xx}(x, z, t) \\ \Sigma _{xz}(x, z, t) \\ \Sigma _{zz}(x, z, t) \end{pmatrix} = \begin{pmatrix} \hat{U}_x (z) \\ i\hat{U}_z (z) \\ i\hat{\Sigma }_{xx}(z) \\ \hat{\Sigma }_{xz}(z) \\ i\hat{\Sigma }_{zz}(z) \end{pmatrix} e^{i(kx-\omega t)}, \end{aligned}$$

(A7)

where k and $\omega$ denote the wavenumber and angular frequency, respectively. Eliminating $\hat{\Sigma }_{xx}$ yields the first-order differential equation for the motion–stress vector $\textbf{f}_{solid}= (\hat{U}_x, \hat{U}_z, \hat{\Sigma }_{xz}, \hat{\Sigma }_{zz})^T$, where the superscript T denotes the transpose.

$$\begin{aligned} \frac{d \textbf{f}_{solid}}{dz} = \textbf{A} \textbf{f}_{solid}, \quad \textbf{A} = \begin{pmatrix} \frac{1}{2H_s} &{} k &{} \frac{1}{\beta ^2} &{} 0 \\ -k \left( 1-\frac{2\beta ^2}{\alpha ^2} \right) &{} \frac{1}{2H_s} &{} 0 &{} \frac{1}{\alpha ^2} \\ -\omega ^2 + 4k^2\beta ^2 \left( 1-\frac{\beta ^2}{\alpha ^2} \right) &{} gk &{} -\frac{1}{2H_s} &{} k \left( 1-\frac{2\beta ^2}{\alpha ^2} \right) \\ gk &{} -\omega ^2 &{} -k &{} -\frac{1}{2H_s} \end{pmatrix}. \end{aligned}$$

(A8)

Let the four eigenvalues of $\textbf{A}$ be $\lambda _1< \lambda _2< \lambda _3 < \lambda _4$, the corresponding eigenvectors be $\textbf{v}_1, \textbf{v}_2, \textbf{v}_3, \textbf{v}_4$, and the solution matrix be

$$\begin{aligned} \textbf{F}(z) = \textbf{E} \mathbf {\Lambda }(z) = \begin{pmatrix} &{} &{} &{} \\ \textbf{v}_1 &{} \textbf{v}_2 &{} \textbf{v}_3 &{} \textbf{v}_4 \\ &{} &{} &{} \end{pmatrix} \begin{pmatrix} e^{\lambda _1 z} &{} &{} &{} \\ &{} e^{\lambda _2 z} &{} &{} \\ &{} &{} e^{\lambda _3 z} &{} \\ &{} &{} &{} e^{\lambda _4 z} \end{pmatrix}. \end{aligned}$$

(A9)

Then, the solution for Eq. (A8) is given by $\textbf{f}_{solid}(z) = \textbf{F}(z) \textbf{w}$, where $\textbf{w}$ denotes a weight vector.

1.2 A.2 Compressible Fluid Layer under Gravity

Next, we obtain the propagator matrix of a density-stratified compressible fluid layer under gravity. We again introduce variables scaled by density.

$$\begin{aligned} U_x = \sqrt{\rho _f} u_x, \; U_z = \sqrt{\rho _f} u_z, \; -P = \frac{-p}{\sqrt{\rho _f}}. \end{aligned}$$

(A10)

Using $\frac{1}{H_f} = \frac{1}{\rho _f} \frac{d\rho _f}{dz}$, we have

$$\begin{aligned} \frac{\partial ^2 U_x}{\partial t^2}&= \frac{\partial (-P)}{\partial x} + g \frac{\partial U_z}{\partial x} \end{aligned}$$

(A11)

$$\begin{aligned} \frac{\partial ^2 U_z}{\partial t^2}&= \left( \frac{\partial (-P)}{\partial z} + \frac{-P}{2H_f} \right) - g \frac{\partial U_x}{\partial x}, \end{aligned}$$

(A12)

$$\begin{aligned} -P&= {C}^2 \left( \frac{\partial U_x}{\partial x} + \frac{\partial U_z}{\partial z} - \frac{U_z}{2H_f} \right) . \end{aligned}$$

(A13)

Let us write

$$\begin{aligned} \begin{pmatrix} U_x(x, z, t) \\ U_z(x, z, t) \\ -P(x, z, t) \end{pmatrix} = \begin{pmatrix} \hat{U}_x(z) \\ i\hat{U}_z(z) \\ i(-\hat{P}(z)) \end{pmatrix} e^{i(kx-\omega t)}. \end{aligned}$$

(A14)

Eliminating $\hat{U}_x$ yields the following equation for the motion-stress vector $\textbf{f}_{fluid} = (\hat{U}_z, -\hat{P})^T$:

$$\begin{aligned} \frac{d \textbf{f}_{fluid}}{dz} = \textbf{B} \textbf{f}_{fluid}, \quad \textbf{B} = \begin{pmatrix} \frac{1}{2H_f} - \frac{gk^2}{\omega ^2} &{} \frac{1}{{C}^2} - \frac{k^2}{\omega ^2} \\ \frac{g^2k^2}{\omega ^2} - \omega ^2 &{} \frac{gk^2}{\omega ^2} - \frac{1}{2H_f} \\ \end{pmatrix}. \end{aligned}$$

(A15)

Let the two eigenvalues of the coefficient matrix $\textbf{B}$ be

$$\begin{aligned} \pm \kappa \equiv \pm \sqrt{ \left( \frac{gk^2}{\omega ^2} - \frac{1}{2H_f} \right) ^2 + \left( \frac{g^2k^2}{\omega ^2} - \omega ^2 \right) \left( \frac{1}{{C}^2} - \frac{k^2}{\omega ^2} \right) }. \end{aligned}$$

(A16)

Then, the relationship between $\textbf{f}_{fluid}(0)$ and $\textbf{f}_{fluid}(z)$ can be written as

$$\begin{aligned} \textbf{f}_{fluid}(z) = \textbf{Q}(z) \textbf{f}_{fluid}(0), \end{aligned}$$

(A17)

where

$$\begin{aligned} \textbf{Q}(z) \equiv \exp (z\textbf{B}) = \frac{\sinh (\kappa z)}{\kappa }\textbf{B} + \cosh (\kappa z) \textbf{I} \end{aligned}$$

(A18)

is a propagator matrix from the sea surface to z, and $\textbf{I}$ denotes a $2\times 2$ identity matrix.

Substituting $z=d$ into Eq. (A17) and considering $-\hat{P}(0) = 0$, we have

$$\begin{aligned} \hat{U}_z(d) = Q_{11}(d) \hat{U}_z(0), \quad -\hat{P}(d) = Q_{21}(d) \hat{U}_z(0), \end{aligned}$$

(A19)

and in non-scaled form

$$\begin{aligned} \hat{u}_z(d)&= Q_{11}(d) \sqrt{\frac{\rho _f(0)}{\rho _f(d)}} \hat{u}_z(0), \end{aligned}$$

(A20)

$$\begin{aligned} -\hat{p}(d)&= Q_{21}(d) \sqrt{\rho _f(d)\rho _f(0)}\hat{u}_z(0) , \end{aligned}$$

(A21)

where

$$\begin{aligned} Q_{11}(d) = \frac{\sinh (\kappa d)}{\kappa d} d \left( \frac{1}{2H_f} - \frac{gk^2}{\omega ^2} \right) + \cosh (\kappa d), \end{aligned}$$

(A22)

$$\begin{aligned} Q_{21}(d) = \frac{\sinh (\kappa d)}{\kappa d} d \left( \frac{g^2k^2}{\omega ^2} - \omega ^2 \right) . \end{aligned}$$

(A23)

The inverse of $Q_{11}(d) \sqrt{\rho _f(0)/\rho _f(d)}$ corresponds to the transfer function defined in Abrahams et al. (2023), which represents the response of the sea surface to seafloor uplift in the Fourier domain.

1.3 A.3 Methods for Obtaining Tsunami Dispersion Relations

1.3.1 A.3.1 The Case where the Seafloor is Rigid

First, we consider a case in which the fluid is separated by a rigid floor. In this case, the left-hand side of the Eq. (A20) becomes zero. This equation has a non-trivial solution if and only if $Q_{11}(d)=0$, which provides the dispersion relation in this case.

$$\begin{aligned} c_\phi = \frac{\omega }{k} = \sqrt{ \left( g - \frac{\omega ^2}{2k^2H_f} \right) d \cdot \frac{\tanh (\kappa d)}{\kappa d} }. \end{aligned}$$

(A24)

This is the same as the dispersion relation given by Equation 25 in Watada (2013). In the limit where $H_f$ is infinite (i.e., when the density of the fluid is constant), we have

$$\begin{aligned} c_\phi \rightarrow \sqrt{ gd \cdot \frac{\tanh (\kappa d)}{\kappa d} }, \; \kappa \rightarrow \sqrt{ k^2 + \frac{g^2k^2}{\omega ^2{C}^2} - \frac{\omega ^2}{{C}^2} }. \end{aligned}$$

(A25)

This provides the dispersion relation for acoustic gravity waves, the same as the Equation 26 in Watada (2013). By contrast, Lotto and Dunham (2015) and Wilson and Ma (2021) obtained a slightly different relations: $\omega ^2 = g\overline{k} \cdot \tanh (\overline{k}d), \overline{k} = \sqrt{ k^2 - \omega ^2/{C}^2 }$. This difference is probably due to use of the surface gravity approximation.

Furthermore, in the limit where C is also infinite (i.e., when the fluid is incompressible), it follows that $\kappa \rightarrow k$. This provides a dispersion relation for linear surface gravity waves in an incompressible uniform fluid layer.

1.3.2 A.3.2 The Case Where the Fluid Layer is on a Semi-Infinite Solid

Now, we consider the case in which a semi-infinite solid exists beneath the fluid layer. In the solid, using the radiation condition at $z \rightarrow \infty$, we obtain

$$\begin{aligned} \begin{pmatrix} w_1 \\ w_2 \\ 0 \\ 0 \\ \end{pmatrix} = \textbf{G} \begin{pmatrix} \hat{U}_x(d) \\ \hat{U}_z(d) \\ \hat{\Sigma }_{xz}(d) \\ \hat{\Sigma }_{zz}(d) \\ \end{pmatrix} = \textbf{G} \begin{pmatrix} \sqrt{\rho _s(d)} \hat{u}_x(d) \\ \sqrt{\rho _s(d)} \hat{u}_z(d) \\ \hat{\sigma }_{xz}(d)/\sqrt{\rho _s(d)} \\ \hat{\sigma }_{zz}(d)/\sqrt{\rho _s(d)} \\ \end{pmatrix}, \end{aligned}$$

(A26)

where $\textbf{G} = \textbf{F}^{-1}(d)$ (see Section 7.2 in Aki and Richards 2002 for more details).

Concerning $\hat{\sigma }_{xz}(d) = 0, \hat{\sigma }_{zz}(d) = -\hat{p}(d)$ and using Eqs. (A20) and (A21), we obtain

$$\begin{aligned} \begin{pmatrix} G_{31} &{} G_{32} Q_{11}(d) + G_{34} Q_{21}' \\ G_{41} &{} G_{42} Q_{11}(d) + G_{44} Q_{21}' \\ \end{pmatrix} \begin{pmatrix} \hat{u}_x(d) \\ \hat{u}_z'(0) \\ \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ \end{pmatrix}, \end{aligned}$$

(A27)

where $Q_{21}' = Q_{21}(d) \rho _f(d)/\rho _s(d), \; \hat{u}_z'(0) = \hat{u}_z(0) \sqrt{ \rho _f(0)/\rho _f(d)}$. Equation A27 has a non-trivial solution if and only if the determinant of the coefficient matrix is zero. Thus, we obtain

$$\begin{aligned} G_{31} (G_{42} Q_{11}(d) + G_{44} Q_{21}') - G_{41} ( G_{32} Q_{11}(d) + G_{34} Q_{21}') = 0. \end{aligned}$$

(A28)

Equation (A28) provides the required dispersion relation. Instead of writing the phase velocity as an explicit function of $\omega$ or k, we calculated it numerically. For a given $\omega$, there are numerous solutions $c_\phi (\omega )$ that satisfy Eq. (A28), and the fundamental mode among them corresponds to the tsunami. Such $c_\phi (\omega )$ was obtained using the bisection method, which is labeled “Propagator Matrix Method” in the Figs. 7 and 8. If a solution appeared to converge to the wrong solution, it was removed from the graph.

Notably, under the following assumptions:

• 1. Both $\rho _s$ and $\rho _f$ are constant.

• 2. Gravity is not acting on the solid (only on the fluid).

• 3. The wavelength of tsunamis is sufficiently long ($kd \ll 1$).

Equation (A28) yields

$$\begin{aligned} c_\phi \simeq \sqrt{gd} \left( 1 - \frac{gd}{6C^2} - \frac{(1-\sigma )\rho _f g}{2\mu k} \right) , \end{aligned}$$

(A29)

where $\sigma$ denotes the Poisson’s ratio in the solid (for details of the calculation, see the Supplementary File 3). The second term in the parentheses represents the effect of seawater compressibility (Okal 1982). The third term represents the effect of the seafloor elasticity (Tsai et al. 2013).