1 Introduction

The utilization of renewable energy increased by 13.7% (British Petroleum, 2020) in 2019. In particular, the proportion of geothermal energy consumption has continued to rise in many countries in recent years (International Energy Agency, 2020) because of its characteristics such as geographical distribution, base-load dispatchability without a separate energy source, modest use of land, low carbon emissions during operations, and possible sequestration of carbon dioxide (Tester et al., 2006). Since there are some limitations in the conventional geothermal energy extraction to exploit the subsurface hydrothermal circulation (Lund et al., 2008, for example), the enhanced geothermal system (abbreviated as EGS hereafter) was proposed so that heat could be extracted from artificially created reservoirs (Potter et al., 1974). In EGS, we may consider a two-step procedure in the securement of fluid circulation. The first step is hydraulic fracturing, for which pressurized fluid is injected through wells drilled down to high-temperature rock bodies in the subsurface to artificially create cracks in the rocks (Lu et al., 2018). The second step is the creation of fluid paths in the vicinity of the wells. With the careful design of the hydraulic fracturing procedure in the amount of fluid and pressure sequence, many cracks could be created in the high-temperature rocks and form a complex crack network. The network becomes fluid paths to carry the geothermal energy from the surrounding rocks to a power plant on the ground surface (Montgomery & Michael, 2010). Unlike conventional geothermal power generation methods, the high-temperature rocks in EGS may contain no hydrothermal steam or fluid, but the geothermal energy is carried by artificially injected fluid (Olasolo et al., 2016; Pruess, 2006). EGS opened a new path for geothermal development in an environment with poor hydrothermal circulation and for recovering the enormous amount of thermal energy stored in the earth beyond the conventional geothermal resources (Tester et al., 2006). For efficient heat production in EGS, creating a long and complicated crack network in the reservoir rock is crucial. Although hydraulic fracturing is a well-practiced technology (Fraser‐Harris et al., 2020; Zhao et al., 2020), fracturing parameters such as fracturing fluid properties, fracturing pressure, and procedure need to be carefully selected depending on the physical properties of the surrounding rocks (Kim & Moridis, 2015, for example). In particular, temperature effects on the hydraulic fracturing of granitic rocks are known as unignorable (Zhou et al., 2018; for example). Geothermal research is moving toward the region below the brittle-ductile transition zone in the ground (Reinsch et al., 2017), and the investigation of physical and mechanical properties of rocks at high-temperature beyond the brittle-ductile transition zone has to be conducted to better deal with hydraulic fracturing (Zhang et al., 2018).

Many factors influence the behavior of hydraulic fracturing in EGS, including state quantities such as confining pressure, temperature, mechanical properties of rock and injection fluid, and the coupling effect of these parameters. Due to the limitations of laboratory conditions, many researchers have studied the influence of a single factor on conventional rock specimens: the effects of high-temperature treatments of granite samples (Yang et al., 2017), the impact of thermal deterioration on the physical and mechanical properties of rocks after multiple cooling shocks (Shen et al., 2020), or an intragranular damage mechanism in the brittle-ductile transition in porous sandstone (Wang et al., 2008), for example. Although these studies have made elucidating discussion on the brittle-ductile transition under high confining pressure or the effect of high-temperature treatment, their results could provide no direct indication for the hydraulic fracturing process in EGS. It is presumed that the zones suitable for EGS located at a depth of 3–10 km underground (Lu & Wang, 2015) have low permeability and high temperature. The results of hydraulic fracturing in such an environment should be thoroughly investigated prior to implementation. Also, the severe pressure-temperature conditions of the brittle-ductile transition zones are close to or beyond the region where water becomes supercritical. Although laboratory experiments on hydraulic fracturing in the conditions near brittle-ductile transition were carried out (Watanabe et al., 2017), their experiments were conducted on the laboratory scale and may not easily be reproduced. Numerical simulation, therefore, is a feasible scheme to realize such severe conditions of the brittle-ductile transition zone for studying the behavior of hydraulic fracturing. It is essential to clarify qualitatively the influence of the physical quantities and mechanical properties mentioned above in the practice of EGS in the vicinity of brittle and ductile transition zones.

In this study, we employed the approach of the distinct element method (DEM; Cundall & Strack, 1979) for our numerical simulation because of its high applicability to reproduce intermittent behavior of rock failure and hydraulic fracturing (Nagaso et al., 2019, for example). In our approach, we tried to supplement the deficiencies in the current studies by introducing the following attempts. We considered the thermal volumetric changes of rock grains due to high temperature that could cause fracturing. The effects of initial thermal stress cracks on the mechanical response of reservoir rocks in hydraulic fracturing are included in our numerical simulation. Moreover, we avoided the two-step procedure, i.e., heating and cooling, to study the thermal response of rock specimens in the laboratory test to conduct our numerical experiments in environments much closer to the actual practice of EGS. Our numerical experiments would successfully simulate hydraulic fracturing in EGS under high-pressure and high-temperature conditions. A solid-liquid-thermal coupling model is proposed for studying the mechanical behavior of rock under such conditions using DEM. In this article, after the developed scheme has been validated by comparing laboratory results of the uniaxial and biaxial compression tests, we qualitatively study the influence of different factors through multiple sets of numerical experiments. Based on the hydraulic fracturing simulations with several combinations of temperature, confining pressure, and injection fluid, we try to find the role of environmental temperature and pressure and the viscosity of injection fluid in a complex crack network generation.

2 Methodology

In this section, we explain the details of DEM and our original strategy for reproducing the mechanical behavior of rock and injected fluid and their interaction. First, the conventional DEM theory is briefly reviewed. Then, our proposed scheme for incorporating the effects of temperature, confining pressure, and hydro-thermomechanical interactions into DEM is introduced. As a brief introduction to the hydro-thermal-mechanical interactions, fluid could flow through the gap between particles and accumulate in the domain surrounded by them, resulting in corresponding hydraulic stress. In fluid flow and accumulation, the particles will also be cooled by the surrounding fluid, i.e., heat exchange occurs. A similar heat exchange phenomenon occurs when two particles at different temperatures are in contact.

2.1 The Basic Theory of Distinct Element Method

The strength of an entire rock material is obtained by introducing a bond between particles in DEM (Potyondy & Cundall, 2004). In a two-dimensional case, an intact rock is modeled as a dense packing of small rigid circular particles. The macroscopic deformation and failure behavior of the rock is represented by the sliding, rotation, and fragmentation between undeformable particles. Neighboring particles are bonded together at their contact points with normal, shear, and rotational springs and interact with each other. Since thorough details of the fundamental algorithm can be found in the literature (e.g., Potyondy & Cundall, 2004), only a general summary is described as follows.

As for the bond behavior, the increment of the normal force \({df}_{nb}\), tangential force \({df}_{sb}\), and the moment \({dM}_{b}\) can be calculated based on the relative motion of the bonded particles and are given as:

$$\begin{array}{c}{df}_{\mathrm{nb} }= {K}_{\mathrm{nb}}({dn}_{\mathrm{j}} - {dn}_{\mathrm{i}}), \\ {df}_{\mathrm{sb}} = {K}_{\mathrm{sb}}({ds}_{\mathrm{j}} - {ds}_{\mathrm{i}}- \frac{L}{2} ({d\theta }_{\mathrm{i}} + {d\theta }_{\mathrm{j}})),\\ {dM}_{\mathrm{b}} = {K}_{\theta }({d\theta }_{\mathrm{j}} - {d\theta }_{\mathrm{i}}).\end{array}$$
(1)

Here, \({K}_{\mathrm{nb}}\), \({K}_{\mathrm{sb}}\), and \({K}_{\uptheta }\) are the normal, shear, and rotational stiffness of parallel bond, respectively; \(\mathrm{dn}\), \(\mathrm{ds}\), and \(\mathrm{d\theta }\) are normal, shear displacement and rotation of particles; L is the bond length. Subscripts i and j are indices of particles. The bond length L and diameter D could be given by

$$\begin{array}{c}L = {r}_{\mathrm{i}} + {r}_{\mathrm{j}},\\ D = \frac{4{r}_{\mathrm{i}}{r}_{\mathrm{j}}}{{r}_{\mathrm{i}} + {r}_{\mathrm{j}}}.\end{array}$$
(2)

Here, \({r}_{\mathrm{i}}\) and \({r}_{j}\) are the radii of the particles i and j, respectively. When the tensile stress exceeds the tensile strength \({\upsigma }_{\mathrm{c}}\) or the shear stress exceeds the shear strength \({\uptau }_{\mathrm{c}}\), the bond breaks, and it is removed from the model along with its accompanying force, moment, and stiffness.

In addition to the bond behavior, the linear contact behavior is active if two particles contact each other. The corresponding increment of the normal force \({df}_{n}\), tangential force \({df}_{s}\), and the moment \(dM\) can be calculated by:

$$\begin{array}{c}{df}_{n} = {K}_{n}({dn}_{\mathrm{j}} - {dn}_{\mathrm{i}}),\\ {df}_{s} = {K}_{s}({ds}_{\mathrm{j}} - {ds}_{\mathrm{i}}- ({r}_{\mathrm{i}}{d\theta }_{\mathrm{i}} + {r}_{\mathrm{j}}{d\theta }_{\mathrm{j}})),\\ dM = {r}_{\mathrm{i}}{df}_{s} .\end{array}$$
(3)

Here, \({K}_{\mathrm{n}}\) and \({K}_{\mathrm{s}}\) are the normal and shear stiffness of contact, respectively. Since the DEM is a fully dynamic formulation, some form of damping is necessary to dissipate kinetic energy; the damping force in normal and shear directions can correspondingly be computed by the following equations:

$$\begin{array}{c}{f}_{nd} = {C}_{n}\frac{({dn}_{\mathrm{j}} - {dn}_{\mathrm{i}})}{dt},\\ {f}_{sd} = {C}_{s}\frac{({ds}_{\mathrm{j}} - {ds}_{\mathrm{i}}- ({r}_{\mathrm{i}}{d\theta }_{\mathrm{i}} + {r}_{\mathrm{j}}{d\theta }_{\mathrm{j}}))}{dt}.\end{array}$$
(4)

Here, dt is the time step; the damping coefficients, \({C}_{\mathrm{n}}\) and \({C}_{\mathrm{s}}\), are calculated by the following equations (Cundall & Strack, 1979).

$$\begin{array}{c}{C}_{n} = 2\sqrt{{K}_{n}m ,}\\ {C}_{s} = 2\sqrt{{K}_{s}m }.\end{array}$$
(5)

where m is the contact mass. When two particles have contact with each other (for example, particle i and grain j, m is taken as \(\frac{{m}_{\mathrm{i} }{m}_{\mathrm{j}}}{{m}_{\mathrm{i}} + {m}_{\mathrm{j}}}\)). For the case of particle-wall contact, m is taken from the particle mass.

2.2 Numerical Algorithm Considering Thermal Expansion Behavior

In EGS, the target rock has a high temperature, usually > 300 °C. Under such a severe environment, the mechanical behaviors of rock change significantly compared with the normal temperature state. Based on the experimental results obtained by Yang et al. (2017), these differences are mainly caused by different thermal-expansion behaviors of various mineral grains such as quartz, feldspar, biotite, and many other silicate minerals. In addition, the mechanical properties of the mineral grains themselves will also accordingly change with the increase in temperature.

We propose a numerical model considering the thermally induced cracks to incorporate the effect of the above-mentioned thermal expansions and related mechanisms into the DEM simulation process. The inclusion of thermal expansion behavior is different from the bond damage determination algorithm in the conventional DEM. To specify the damage of bonds, a damage variable D is introduced. When D equals zero, the bond is intact (no damage). When D equals one, the bond is completely damaged. The exponential form is applied to calculate the damage variable D to ensure a smooth transition between the intact and broken bonds.

$$\begin{gathered} {\text{D}} = 1 - e^{{ - \left( {\frac{{\varepsilon _{{\text{n}}} - \varepsilon _{{\text{n}}}^{{\text{u}}} }}{{\varepsilon _{{\text{n}}}^{{\text{u}}} }} + \frac{{\varepsilon _{{\text{s}}} - \varepsilon _{{\text{s}}}^{{\text{u}}} }}{{\varepsilon _{{\text{s}}}^{{\text{u}}} }}} \right)}} ,\,\left( {\varepsilon _{{\text{n}}} \ge \varepsilon _{{\text{n}}}^{{\text{u}}} \,\,{\text{and}}\,\,\varepsilon _{{\text{s}}} \ge \varepsilon _{{\text{s}}}^{{\text{u}}} } \right) \hfill \\ {\text{D}} = 1 - e^{{ - \left( {\frac{{\varepsilon _{{\text{n}}} - \varepsilon _{{\text{n}}}^{{\text{u}}} }}{{\varepsilon _{{\text{n}}}^{{\text{u}}} }}} \right)}} ,\,\left( {\varepsilon _{{\text{n}}} \ge \varepsilon _{{\text{n}}}^{{\text{u}}} \,\,{\text{and}}\,\,\varepsilon _{{\text{s}}} \ge \varepsilon _{{\text{s}}}^{{\text{u}}} } \right) \hfill \\ {\text{D}} = 1 - e^{{ - \left( {\frac{{\varepsilon _{{\text{s}}} - \varepsilon _{{\text{s}}}^{{\text{u}}} }}{{\varepsilon _{{\text{s}}}^{{\text{u}}} }}} \right)}} ,\,\left( {\varepsilon _{{\text{n}}} \ge \varepsilon _{{\text{n}}}^{{\text{u}}} \,\,{\text{and}}\,\,\varepsilon _{{\text{s}}} \ge \varepsilon _{{\text{s}}}^{{\text{u}}} } \right) \hfill \\ {\text{D}} = 0,\,\left( {\varepsilon _{{\text{n}}} \ge \varepsilon _{{\text{n}}}^{{\text{u}}} \,\,{\text{and}}\,\,\varepsilon _{{\text{s}}} \ge \varepsilon _{{\text{s}}}^{{\text{u}}} } \right) \hfill \\ \end{gathered}$$
(6)

where \({\upvarepsilon }_{\mathrm{n}}\) and \({\upvarepsilon }_{\mathrm{n}}^{\mathrm{u}}\) are the total and elastic ultimate strains, respectively, in the direction normal to the contact face of the particles in contact. The other parameters, \({\upvarepsilon }_{\mathrm{s}}\) and \({\upvarepsilon }_{\mathrm{s}}^{\mathrm{u}}\), are the total and elastic ultimate strains, respectively, in the direction tangential to the contact face. The strains mentioned here are calculated based on the deformation of the bonds between the particles in contact. When the bond is subjected to tensile or shear stress, its length in the corresponding direction will change, and the ratio of this change to the corresponding original length is the strain.

The strength and stiffness of a bond are updated by multiplying the damage variable so that all the bonds in the DEM model are gradually damaged with the increase in strain shown as follows:

$$\begin{array}{c}\begin{array}{c}{\sigma }^{c} = {\sigma }^{c} (1- D),\\ {\tau }^{c} = {\tau }^{c} (1-D),\end{array}\\ {K}_{n} = {K}_{n} (1-D),\\ {K}_{s} = {K}_{s} (1-D).\end{array}$$
(7)

Considering the different thermal expansion behaviors of mineral grains in real rock, different thermal expansion coefficients \(\mathrm{\alpha }\) are assigned to DEM particles randomly so that the particle radius changes with the temperature by the following equation:

$${r}_{\mathrm{i}}^{T} = {r}_{\mathrm{i}}^{0} + {\alpha }_{\mathrm{i}} \Delta T {r}_{\mathrm{i}}^{0},$$
(8)

where \({r}_{\mathrm{i}}^{\mathrm{T}}\) and \({r}_{\mathrm{i}}^{0}\) are the radius of particle i when its temperature is T and room temperature (25 °C), respectively, \({\alpha }_{\mathrm{i}}\) is the thermal expansion coefficient of particle i; \(\Delta T\) is the temperature change. Thermal stress is also generated with the expansion or shrinkage of particles in the DEM model.

As the temperature rises, the strength of the bond will increase to simulate the increasing mutual attraction between mineral grains:

$$\begin{array}{c}{\sigma }_{T}^{c}={\sigma }^{c} \left(1 + {\upgamma }_{\mathrm{T}1}T\right),\\ {\tau }_{T}^{c} = {\tau }^{c} (1 + {\upgamma }_{\mathrm{T}1}T)\end{array}$$
(9)

Here, \({\upgamma }_{\mathrm{T}1}\) is a coefficient, which is set to be 0.0005. T is the temperature. \({\sigma }_{T}^{c}\) and \({\tau }_{T}^{c}\) are the bond strength at temperature T (°C). In these equations, when T is greater than the threshold temperature (300 °C in this paper), T takes 300 °C.

A coefficient \({\upgamma }_{\mathrm{T}2}\) is introduced to update the contact stiffness of the particles to consider the effect of high temperature on the mineral grains, such as chemical phase change or origination of transgranular cracks, for temperature higher than the threshold temperature. The coefficient does not apply to the stiffness of the bond because the thermal stress could lead to bond damage, i.e., the damage behavior of the bond has been considered with the non-zero value of D. Therefore, the updated normal and shear contact stiffness, \({K}_{n}^{T}\) and \({K}_{s}^{T}\), are expressed by the following function of temperature T and the coefficient \({\upgamma }_{\mathrm{T}2}\).

$$\begin{array}{c}{K}_{n}^{T}= {K}_{n} (1 - {\gamma }_{T2}(T-300))\\ {K}_{s}^{T} = {K}_{s} (1 - {\gamma }_{T2}(T-300))\end{array} ,$$
(10)

This study simplifies the relationship between thermal expansion coefficient and temperature as a linear relationship. When the temperature is lower than the threshold degree, the thermal expansion coefficient remains unchanged, while when the temperature is higher than the threshold degree, the thermal expansion coefficient increases linearly with temperature shown in the following:

$$\tilde{\alpha }_{{\text{i}}} = {\alpha }_{\mathrm{i}}+ {k}_{\mathrm{i}}^{t} \Delta \mathrm{T},$$
(11)

where \({k}_{\mathrm{i}}^{\mathrm{t}}\) is a coefficient, which is constantly selected to be 0.75 in this article.

In addition, considering the size of large pores and thermal stress cracks in the actual rock induced by thermal stress, an extra gap is added to completely broken bonds (damage variable D is > 0.999). The updated normal initial distance between two particles is given as follows:

$${G}_{\mathrm{ij}}^{T} = {G}_{\mathrm{ij}}^{0} + {K}_{\mathrm{gap}}\left({r}_{\mathrm{i}}+{r}_{\mathrm{j}}\right).$$
(12)

Here, \({\mathrm{G}}_{\mathrm{ij}}^{\mathrm{T}}\) and \({\mathrm{G}}_{\mathrm{ij}}^{0}\) are the gaps between particles i and j at temperature T and the room temperature, respectively; \({K}_{\mathrm{gap}}\) is the gap coefficient. The premise of the application of this formula is that the bond between particles i and j has completely broken.

For a micro-crack with the initial gap, the contact force between corresponding particles is zero until they move a distance toward each other greater than the initial gap.

2.3 Brittle-Ductile Transition Algorithm

As one of the common heat source rocks (Lu & Wang, 2015), granite exhibits typical brittleness under normal temperature and confining pressure. However, laboratory test results show that as the confining pressure increases, the mechanical behavior of granite gradually transits from brittle to ductile. In the practical implementation, it is necessary to consider the influence of the high confining pressure on the rock mechanical behavior since the rocks in EGS has buried depths of several kilometers.

The strength and stiffness gradually decrease as cracks develop for general rock specimens, a phenomenon called degradation. Laboratory results suggest that this degradation behavior changes significantly with confining pressure (Brady & Brown, 1992). Specifically, the strength and stiffness degrade sharply after the peak stress in the uniaxial compression case, which shows a typical brittle behavior. As confining pressure increases, the strength and stiffness degradation is suppressed, and the rock shows less brittle behavior. Finally, the rock becomes fully ductile under high confining pressure, and no degradation occurs. Fang and Harrison (2001) simplified this brittle-to-ductile transition behavior with a degradation index, as given by Eq. 13. Although the original work in Fang and Harrison (2001) was incorporated into a numerical method with a continuum approach (Fang & Harrison, 2002), we apply their idea to DEM calculation.

$${\gamma }_{d}= \frac{\delta \sigma }{\delta {\sigma }_{h}}.$$
(13)

Here, \(\mathrm{\delta \sigma }\) is the degradation of rock strength when subjected to a certain confining pressure; \(\updelta {\upsigma }_{\mathrm{h}}\) is the corresponding hypothetical degradation if the strength degradation behaves like a uniaxial case. This degradation index is closely related to the confining pressure, as summarized by Fang and Harrison (2001).

In this article, degradation behavior under different confining pressures is considered by updating the damage variable D:

$$\tilde{D }=D{\gamma }_{d},$$
(14)

where \(\tilde{D }\) is the updated damage variable. The degradation index is given by an exponential form to ensure a smooth transition from brittle to ductile as follows:

$${\upgamma }_{\mathrm{d}}= {\mathrm{e}}^{-{\mathrm{n}}_{\mathrm{d}}{\upsigma }_{3}}$$
(15)

Here, \({\upsigma }_{3}\) (unit: MPa) is the confining pressure, and \({\mathrm{n}}_{\mathrm{d}}\) is the degradation parameter that can be estimated from experimental data. As the confining pressure on the bond increases, \({\gamma }_{d}\) decreases from 1 to nearly 0, which indicates that the increment of the confining pressure suppresses the damage of bonds.

2.4 Fluid-Solid-Thermal Coupling Algorithm

Since the heat source rocks in the EGS system are at a high temperature, the mechanical response of the rock mass to the hydraulic pressure induced by the fracturing fluid and the heat exchange between the fracturing fluid and the rock mass need to be considered. In the following, we introduce algorithms for combining the effect of hydraulic and thermal effects on the calculation process in DEM.

2.4.1 Hydraulic Effect

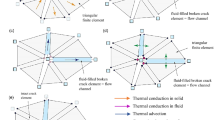
To reproduce fluid flow in the rock mass and its effect on the mechanical behavior of rock, the channel-domain model (Shimizu et al., 2011) is introduced into the proposed scheme, as illustrated in Fig. 1.

Fig. 1
figure 1

In the channel-domain model, domains are represented as areas enclosed by solid green lines. Yellow circles represent particles

Full size image

In the channel-domain model, the closed area enclosed by the particles is called a domain. The fluid-solid coupling is achieved through the mutual relationship between domains and particles. In a two-dimensional DEM, every three or more particles will form a domain. The following algorithm is proposed to define these domains for computation.

Step 1: Randomly select particle i, randomly select a particle j in contact with it, and then randomly select a particle k in contact with particle j (except for particle i). At this time, the vector from the particle i to the particle j and then to the particle k will be clockwise or counterclockwise; then select a particle with the same direction from the particles in contact with particle k;

Step 2: When there are multiple particles in contact with particle k that meet the above condition, select the particle that forms the smallest angle and then continue to select particles using the same principle;

Step 3: Repeat step 2 until a closed-loop (domain) is formed;

Step 4: Repeat the above steps until all particles are processed. The corresponding result is shown in Fig. 1.

Fluid flows among the formed domains through the aperture between the adjoining particles are called channels. The following equation gives the corresponding laminar flow rate based on the Poiseuille flow.

$${Q}_{f}= \frac{{\mathrm{w}}^{3}}{12\upmu }\frac{\Delta P}{{L}_{\mathrm{c}}},$$
(16)

where \({Q}_{f}\) is the flow rate, \(\Delta P\) is the change in pressure across a channel, \({L}_{\mathrm{c}}\) is the length of the channel, \(\upmu\) is the fluid’s viscosity, and w is the aperture of the channel. When two particles are not in contact, the aperture w is the normal distance between particles. To ensure the fluid can still pass through a channel with two particles in contact, an initial aperture \({\mathrm{w}}_{0}\) is introduced, so that the aperture of the closed channel could be obtained by (Al‐Busaidi et al., 2005):

$$w=\frac{{w}_{0}{F}_{0}}{F + {F}_{0}},$$
(17)

where F is the compressive normal force acting on the channel, and \({w}_{0}\) is the initial aperture, which is an input parameter.

When two particles are in contact, the compressive normal force F between them is 0. Therefore, w equals the initial aperture \({w}_{0}\).

As the two particles come in closer contact, F will gradually increase from 0\(.\) When F equals the parameter \({F}_{0}\), the channel aperture w decreases to \({w}_{0}\)/2. To reduce the number of input parameters, \({F}_{0}\) is taken as the product of the contact stiffness between the corresponding two particles and \({w}_{0}\)/2.

When the volume of fluid injected into the domain is greater than the volume of the pore (\({V}_{\mathrm{pore}}\)) between particles, the fluid pressure in the domain will start to rise from zero:

$$\mathrm{d}P = \frac{{K}_{\mathrm{f}}}{{V}_{\mathrm{r}}} \left( \sum {Q}_{f}\mathrm{d}t -\mathrm{ d}{V}_{\mathrm{r}} \right)$$
(18)

Here, \(\sum {Q}_{f}\) is the total flow rate for a one-time step from the surrounding channels, \({K}_{\mathrm{f}}\) is the fluid bulk modulus, \({V}_{\mathrm{r}}\) is the apparent volume of the domain (the polygonal area enclosed by the centerline of particles), and d\({V}_{\mathrm{r}}\) is the change of the volume in the domain. The following three steps are used for the pressure calculation in each domain. First, \(\sum {Q}_{f}\), \({V}_{\mathrm{r}}\), and d\({V}_{\mathrm{r}}\) corresponding to the domain are calculated. Second, the pressure change dP is obtained by Eq. 18. Third, the pressure in each domain is updated by adding the pressure change. This process is also applicable to the central borehole. The only difference is that the influence of the injected fluid should be considered to calculate \(\sum {Q}_{f}\).

Each domain accumulates the fluid pressure, and for a domain with a fluid pressure P, the total force \({f}_{d}\) that acts on the surrounding particles is given by the integral:

$${f}_{d} = \int P\mathrm{ cos}\theta r\mathrm{ d}\theta$$
(19)

In addition, when fluid flows through a channel, shear stress will be induced. The corresponding force that acts on the surface of two particles forms a channel that can be obtained by:

$${f}_{c} = \frac{w}{2} \Delta P$$
(20)

Since the assembly of simple circular particles expresses the DEM model, there will be many pores inside. For a densely packed two-dimensional model, the overall porosity is about 16% (Potyondy & Cundall, 2004), i.e., much larger than the actual rock. Therefore, it is difficult to reproduce an actual rock’s porosity accurately. For this reason, an assumed porosity is introduced into the numerical calculation (Shimizu et al., 2011). For a pore area surrounded by several particles (or called “domain”), instead of using its actual volume, its assumed volume is used, which is given by:

$${V}_{\mathrm{pore}}= \mathrm{\varphi }{V}_{\mathrm{r}}$$
(21)

Here, \(\mathrm{\varphi }\) is the assumed porosity. Considering the thermal expansion behavior of particles induced by the high-temperature treatment, a temperature correction term is introduced by:

$${\mathrm{\varphi }}_{\mathrm{T}}= \left(1.0 - {\upgamma }_{\mathrm{T}3}(\mathrm{T}-25)\right) {\mathrm{\varphi }}_{0}$$
(22)

Here, \({\upgamma }_{\mathrm{T}3}\) is a correction coefficient, which is set to be 0.00075, \({\mathrm{\varphi }}_{0}\) is the assumed porosity at room temperature (25 °C), and \({\mathrm{\varphi }}_{\mathrm{T}}\) is the assumed porosity at temperature T (°C).

2.4.2 Thermal Effect

In addition to the mechanical response of fluid-solid coupling, the heat exchanges of particle-particle, particle-domain, and domain-domain are introduced based on the formed particle-domain system.

For the heat exchange between particles, Fourier’s law of heat conduction is applied:

$$\frac{\Delta Q}{\mathrm{d}t} = -{k}_{\mathrm{t}} {\mathrm{A}}_{\mathrm{c}} \frac{\Delta T}{\Delta x} .$$
(23)

Here, \(\Delta T\) and \(\Delta x\) are the temperature difference and distance between two particles, Q is the amount of heat that flows through a cross-section between two particles during a time interval dt, \({k}_{\mathrm{t}}\) is the thermal conductivity coefficient (assumed independent of temperature and averaged over the surface, unit: \(\frac{W}{mK}\)), and the area \({A}_{\mathrm{c}}\) of the cross-section is given by the radius of particle:

$$\begin{array}{c}{A}_{\mathrm{c}} = \frac{4{r}_{\mathrm{i}}{r}_{\mathrm{j}}}{{r}_{\mathrm{i}} + {r}_{\mathrm{j}}} \left(\mathrm{bonded}\right)\\ {A}_{\mathrm{c}} = \frac{{r}_{\mathrm{i}}{r}_{\mathrm{j}}}{{r}_{\mathrm{i}} + {r}_{\mathrm{j}}} (\mathrm{Unbonded})\end{array}$$
(24)

For the heat exchange between particle and domain, based on Newton’s law of cooling, when there is a temperature difference between the surface of a particle and the surroundings, the heat lost from a unit area per unit time is proportional to the temperature difference expressed as follows:

$$\frac{\mathrm{d}Q}{\mathrm{d}t} = -h {A}_{\mathrm{c}}^{\mathrm{domain}} \left({T}_{\mathrm{t}}-{T}_{\mathrm{domain}}\right).$$
(25)

Here, \({T}_{\mathrm{t}}\) and \({T}_{\mathrm{domain}}\) are the temperature of the particle and surrounding domain (unit: K), respectively, h is the surface heat transfer coefficient (assumed independent of temperature and averaged over the surface, unit: \(\frac{W}{{m}^{2}K}\)), and \({A}_{\mathrm{c}}^{\mathrm{domain}}\) is the contact area between the domain and the particle.

Heat exchange occurs when the fluid flows between the particles of the channel wall and the fluid passing through the channel. When the fluid flows through the channel with an average temperature (called “environment temperature”) of \({T}_{\mathrm{env}}\), if \({T}_{\mathrm{env}}\) is a constant, the fluid temperature \({T}_{\mathrm{t}}\) has the following relationship with \({T}_{\mathrm{env}}\):

$$\frac{\mathrm{d}{T}_{\mathrm{t}}}{\mathrm{d}t} = -\frac{hA}{C} \left({T}_{\mathrm{t}}-{T}_{\mathrm{env}}\right),$$
(26)

where C is the heat capacitance (unit: \(\frac{\mathrm{J}}{\mathrm{Kg}\cdot \mathrm{K}}\)) and the solution of this differential equation is given by:

$${T}_{\mathrm{t}} = {T}_{\mathrm{env}}+ \left({T}_{0}-{T}_{\mathrm{env}}\right){\mathrm{e}}^{-\frac{\mathrm{dt}\cdot \mathrm{h}\cdot \mathrm{A}}{\mathrm{m}\cdot \mathrm{C}}}.$$
(27)

Here, \({T}_{\mathrm{env}}\), regarded as a constant during time interval \(\mathrm{d}t\), is the average temperature of particles that form the channel. We notice that after the time with \(\mathrm{d}t\), the fluid with an initial temperature \({T}_{0}\) will be heated to \({T}_{\mathrm{t}}\) under the environment temperature \({T}_{\mathrm{env}}\). When the surrounding fluid cools particles, the channel will shrink, and extra thermal stress will be induced correspondingly.

3 Calibration

Before DEM simulation starts, it is necessary to determine the micro-parameters (e.g., the strength of parallel bonds), which affect the macroscopic behavior of the numerical model. For the irregular arrangement of particles, theoretical relationships between micro-parameters and macroscopic behavior could not be expressed by mathematical equations because of the characteristics of DEM. Therefore, the micro-parameters are adjusted until the corresponding model behavior becomes similar to the actual experiment’s outputs. This approach is called calibration (Coetzee, 2017). The conversion between micro- and macro-parameters can be related to this process. Granite is a common rock type in EGS (Lu & Wang, 2015). Many DEM-based numerical simulations use the Lac du Bonnet granite as a calibration target (e.g., Potyondy & Cundall, 2004). The physical parameters such as strength and Young’s modulus are reasonable. In this study, the granite of Lac du Bonnet was also selected as the target of parameter calibration. Uniaxial compression, uniaxial tensile, and constant head permeability tests are performed to calibrate micro-parameters where the values of related model parameters are listed in Table 1. All parameters are calibrated at room temperature.

Table 1 Micro-parameters of the DEM model
Full size table

A loading wall is placed above the model and moved slowly down to apply compression stress during the uniaxial compression test simulation. The velocity of the wall is 0.05 m/s, which is very large in the actual experiment. However, since the time step is very small in the numerical simulation, the wall moving distance in each iteration is minimal, which is enough to ensure the accuracy of the numerical simulation. The crack width in this article is obtained by Eq. 28.

$$\upomega = \sqrt{{D}_{n}^{2}+{D}_{s}^{2} }.$$
(28)

Here, \(\upomega\) is the crack width; \({D}_{\mathrm{n}}\) and \({D}_{\mathrm{s}}\) are the distance between the two particles in the normal and the tangential directions, respectively. When two particles are in contact, i.e., the normal force between them is compressive stress, whether bonded or not, the value of \({D}_{\mathrm{n}}\) is taken as 0. When two particles are not in contact, i.e., the normal force between the two particles is not compressive stress, in the bonded case, the gap is calculated by Eq. 28, and in the unbonded case, the gap is equal to its normal distance \({D}_{\mathrm{n}}\).

Some particles on the model are used as sensors in the calibration process of Young’s modulus and Poisson’s ratio. Their displacements will be recorded and averaged respectively to measure the axial and lateral strains of the specimen.

Based on the uniaxial compression test simulation, the crack distribution pattern is shown in Fig. 2a, from which the model presents a typical failure mode of rocks.

Fig. 2
figure 2

Crack distribution patterns of uniaxial compression test (a) and uniaxial tension test (b)

Full size image

The lines in Fig. 2 show the distribution of cracks, and the color of the lines represents the normalized crack width.

The tensile strength of the model must be measured to verify the ratio of the uniaxial compressive strength (UCS) to the tensile strength (TS) (UCS/TS ratio). The uniaxial tensile test is chosen to characterize the tensile strength since the numerical implementation is straightforward and does not suffer from the difficulties encountered experimentally. The crack distribution pattern for the uniaxial tension test is shown in Fig. 2b.

Based on the numerical simulation, the macro-properties of the models are measured. The comparison between this numerical result and Lac du Bonnet granite is listed in Table 2. We find that the simulation results agree with the laboratory experimental results.

The constant head permeability test is conducted to calibrate the permeability of the model. First, the upper and lower ends of the numerical model are defined as fluid inlet and fluid outlet, respectively. The fluid flows through the fluid inlet and out through the fluid outlet. The other sides of the model are set to be impermeable. During the numerical simulation, the upper and lower ends of the model are given a fixed pressure difference. When the flow rates at the fluid injection and fluid outflow ends are equal, the permeability coefficient k of the model can be measured accordingly:

$$k= \frac{{Q}_{\mathrm{s}}}{A\mathrm{ i}} .$$
(29)

Here, \({Q}_{\mathrm{s}}\) is the flow rate when the model reaches stability, A is the cross-sectional area of the model through which the fluid flows, and i is the hydraulic gradient.

The calibrated permeability coefficient of the model is \(1.9 \times {10}^{-12}\) m/s, which is in the range of published data of Lac du Bonnet granite (\({10}^{-13}\)–\({10}^{-4}\) m/s, Miguel et al., 2009).

Table 2 Comparison between the simulation result and Lac du Bonnet granite
Full size table

Similarly, to calibrate the thermal conductivity coefficient of the model, the particles at the lower end of the model are given with a high initial temperature (100 °C; here it does not consider the thermal expansion caused by temperature) and remain unchanged. Then, due to the uneven temperature distribution of the model, heat will be conducted from the high-temperature particles to the low-temperature particles. In this process, based on Fourier’s law, the heat conductivity coefficient between a group of particles can be given by:

$${k}_{\mathrm{t}} = - \frac{\Delta Q \Delta x}{A\mathrm{d}t \Delta T} .$$
(30)

Corresponding parameters are the same as in Eq. (21).

Figure 3 shows the temperature distribution (°C) of the model at the initial state and after 300,000 iterations.

Fig. 3
figure 3

Changes in the temperature distribution of the numerical model. The color scale represents the temperature of every particle

Full size image

We can observe the heat conduction from the high-temperature particles to the low-temperature particles after the iteration. By measuring the thermal conductivity coefficient between multiple groups of particles and taking the average value, the thermal conductivity coefficient of the model can be obtained as 3.57 \(\frac{W}{mK}\), which is in the range of granite thermal conductivity coefficient (1.7–4.0 \(\frac{W}{mk}\), Vazifeshenas & Sajadi, 2010).

4 Validation of the Proposed Methods

Numerical simulations of uniaxial compression tests after different temperature treatments and biaxial compression tests under different confining pressures are carried out to verify the validity of the proposed algorithm. The comparison with the experimental results is illustrated as well. The thermal treatment algorithm of the numerical model can be briefly described as follows: First, the temperatures of numerical specimens are increased to their target temperature (200, 300, 400, 500, 600, 700, and 800 °C) at a slow rate of 0.45 °C/min to reduce the influence of the heating rate itself. In this process, the radius of the particles expands with the increase in temperature. After the model reaches a steady state, the specimens are cooled to room temperature (25 °C). Subsequently, as the temperature decreases, the particle radius will also shrink. The DEM particle can simulate the different thermal expansion and contraction behavior that leads to the thermal stress and then generate the thermally induced cracks through different thermal expansion coefficients. After different thermal treatments, numerical models with initial thermal stress cracks are used for uniaxial compression tests. The stress-strain curves obtained by the above procedure are shown in Fig. 4a.

Fig. 4
figure 4

Axial stress-strain curves of uniaxial compression tests under different temperatures (°C) that obtained by numerical simulation and experiments (Yang et al., 2017)

Full size image

Figure 4a shows that the results obtained based on the proposed algorithm have the following characteristics.

When the specimen temperature increases from the normal temperature to 300 °C, the uniaxial compressive strength increases to show typical brittle failure characteristics in the stress-strain curves. However, the uniaxial compressive strength and static elastic modulus of granite specimens decrease significantly, and a more ductile failure of granite appears when the temperature increases from 300 to 800 °C. The peak axial strain shows an increasing trend as the temperature rises. The stress-strain curve is non-linear at the beginning of loading. This non-linear phenomenon becomes more evident as the temperature rises, caused probably by the closure of thermal cracks.

These behaviors of granite specimens after different thermal treatments match very well compared with the experimental test shown in Fig. 4b (Yang et al., 2017). Since many scholars have carried out similar experiments, it is necessary to discuss the subtle differences briefly. Practically speaking, the differences between the experiments occur mainly in the mild temperature range (25–300 °C). On the other hand, all the above experiments show a tendency of transition from brittle to ductile failure mode due to the decreasing strength and increasing peak strain as the temperature rises to higher temperature. In the mild temperature range, some experiments showed that the strength of granite specimens increases with increasing temperature (Rossi et al., 2018; Yang et al., 2017), while some other experiments showed that the strength of the specimen decreases with the increase of temperature (Shen et al., 2020). The reasons for these differences are complex, including rock mineral composition, porosity, initial fluid content, and many other rock physical properties (Wong et al., 2020). Since the rock types of the EGS heat source rocks are not unique, and the environment is far more complex than the laboratory environment, this article used the threshold temperature mentioned in Eq. 9 to distinguish these two cases. In addition, because the difference between these two cases is mainly concentrated in the mild temperature range, and the temperature discussed in this article has exceeded this range, only the results considering the strength enhancement in the mild temperature range are shown. In contrast, the case where the strength and temperature are negatively correlated in the mild temperature range could be achieved by adjusting the threshold temperature in Eq. 9.

In addition, the failure mode of the rock gradually changes from brittle failure to ductile failure with increasing temperature. The corresponding crack patterns of the numerical model are shown in Fig. 5.

Fig. 5
figure 5

Numerical model (a–d) and experimental specimen (reference) (e–h) at different temperatures after uniaxial compression failure

Full size image

The granite at room temperature is a kind of typically brittle rock material, showing axial splitting tensile failure mode, which is visible as several axial tensile cracks. After the high-temperature treatment, thermally induced cracks affect the crack evolution process. Instead of axial tensile cracks, more shear failure along tensile cracks is observed because of thermal damage before the compression. The propagation and coalescence of thermal cracks lead to a complicated crack network, which is different from the process for specimens at lower temperatures. These phenomena are consistent with the experimental results obtained by Yang et al. (2017).

Next, we investigate the effect of the confining pressure using biaxial compression tests with different confining pressure.

The stress-strain curves of biaxial test simulations are shown in Fig. 6a. The numerical specimen’s ductility and peak strength gradually increase with the confining pressure. The difference between the peak strength and post-peak residual strength decreases with increasing the confining pressure. The trend described above has good agreement with the laboratory experiments, as shown in Fig. 6b. Corresponding crack patterns of the numerical specimen with different values of the confining pressure are shown in Fig. 7.

Fig. 6
figure 6

Axial stress-strain curves with different confining pressure obtained by numerical simulations (a) and experiments (b, Yuan & Harrison, 2005)

Full size image
Fig. 7
figure 7

Crack patterns in the numerical specimens of biaxial compression tests under different confining pressure

Full size image

Figure 7 illustrates the crack patterns of the numerical models under different confining pressures. In the uniaxial case, several axial splitting cracks are observed. The model shows axial splitting tensile failure mode, i.e., one of granite’s primary forms of brittle failure under room temperature. As confining pressure increases, the number of axial splitting cracks decreases, and the shear cracks gradually dominate. Finally, shear cracks spread over the entire specimen volume under high confining pressure. It is indicated that the numerical model fails under a more diffuse failure mode.

To characterize the proportion of tensile failure and shear failure of the specimen, this article uses the average ratio \({D}_{n}\)/\(\upomega\) of cracks to represent the proportion of tensile failure. The definition of \({D}_{n}\) and \(\upomega\) is given in Eq. 28. The average ratio \({D}_{n}\)/\(\upomega\) value under different confining pressures when the specimen reaches the peak stress is shown in Table 3.

Table 3 Average \({D}_{n}\)/\(\upomega\) under different confining pressures
Full size table

From Table 3, as the confining pressure increases, the average value of \({D}_{n}\)/\(\upomega\) gradually decreases, which means that the proportion of tensile failure decreases, which also verifies the transition of the specimen from a brittle failure mode to a more complex ductile failure mode.

5 Hydraulic Fracturing Simulation

The previous section confirmed that the proposed method could reproduce the mechanical behavior of rock under high temperature and high confining pressure. In this section, numerical simulations of hydraulic fracturing under various conditions are performed to study the combined effects of confining pressure, temperature, fluid injection rate, and viscosity of injection fluid on the results of hydraulic fracturing. The numerical specimens are heated to predetermined temperatures of 25, 400, and 600 °C and remain unchanged before injection, according to the thermal expansion algorithm described above. The isotropic confining pressures of 5 and 30 MPa are applied through four frictionless walls. The micro-parameters used in this simulation are shown in Table 4.

Table 4 Physical properties used in numerical experiments
Full size table

When the injection rate is 0.001 \({m}^{3}\)/s, several numerical simulations are conducted. Each of the figures in Figs. 8 and 9 includes the numerical results with two confining pressures of 5 MPa and 30 MPa and three temperatures of 25 °C, 400 °C, and 600 °C. When the injection fluid viscosity is 0.1 mPa.s, the crack patterns, fluid pressure distribution, and temperature distribution of DEM model after hydraulic fracturing at different temperatures are shown in Fig. 8. The domain color represents corresponding hydraulic pressure, while the particle color represents its temperature. All patterns are obtained after the borehole pressure is stabilized.

Fig. 8
figure 8

Crack and fluid pressure distribution patterns and corresponding temperature distribution (°C) when the fluid injection rate and injection fluid viscosity are 0.001 m3/s and 0.1 mPa.s, respectively

Full size image
Fig. 9
figure 9

Crack patterns, fluid pressure distribution patterns, and corresponding temperature distribution (°C) when the fluid injection rate and injection fluid viscosity are 0.001 m3/s and 100.0 mPa.s, respectively

Full size image

Figure 8 shows that hydraulic cracks and crack width decrease with increasing confining pressure. Compared with the room temperature, when the temperature is 400 °C and 600 °C, more hydraulic cracks appear, especially when the temperature is 600 °C. Moreover, many micro-cracks can be observed away from the central borehole. The distribution of saturated domains is consistent with the distribution of hydraulic cracks, and the borehole has the highest fluid pressure. The farther away from the central borehole, the lower the fluid pressure of the domain is. When the injection fluid has high viscosity (100.0 mPa.s), numerical results with different confining pressure and temperature are obtained, as illustrated in Fig. 9.

From Fig. 9, except for the phenomenon similar to Fig. 8, high-viscosity fluid induces more branches of hydraulic cracks than the low viscosity group. In addition, some of the domains connected to the central borehole are not saturated, which is caused by the weaker flowability of high-viscosity fluids. The development of borehole pressure during hydraulic fracturing is illustrated in Fig. 10.

Fig. 10
figure 10

The development of borehole pressure when the injection rate is 0.001 \({\mathrm{m}}^{3}\)/s (left: \(\upmu\) = 0.1 mPa.s; right: \(\upmu\) = 100.0 mPa.s)

Full size image

Figure 10 shows that the time variation of borehole pressure at 400 °C is not significantly different from that of the standard temperature case because 400 °C is close to the mild temperature range mentioned earlier. It is believed that in this temperature range, mutual attraction and bond strength between mineral grains increase (Yang et al., 2017) with thermal expansion. Therefore, thermal failure caused by thermal expansion is not significant. As the temperature increases beyond this range, thermal expansion-induced failure dominates, making it more prone to damage during hydraulic fracturing. This mechanism reflects the borehole pressure curve as a reduction in the breakdown pressure at 600 °C. Several numerical simulations are conducted for the injection rate is 0.01 \({\mathrm{m}}^{3}\)/s. Each of the following figures includes two confining pressures of 5 MPa and 30 MPa and three temperatures of 25 °C, 400 °C, and 600 °C. When the injection fluid viscosity is 0.1 mPa.s, numerical results with different confining pressure and temperature are obtained, as shown in Fig. 11.

Fig. 11
figure 11

Crack patterns, fluid pressure distribution patterns, and corresponding temperature distribution (°C) when the fluid injection rate and injection fluid viscosity are 0.01 m3/s and 0.1 mPa.s, respectively

Full size image

Figure 11 confirms that the effects of temperature and confining pressure are comparable, although the number and width of cracks increase compared to the group with a smaller injection volume of 0.001m3/s.

The development of hydraulic cracks is suppressed with increasing confining pressure that decreases the widths and the number of hydraulic cracks. Compared with room temperature, when the temperature is 400 °C and 600 °C, more cracks can be observed. The distribution of saturated domains is basically the same as that of hydraulic cracks. When the injection fluid has high viscosity (100.0 mPa.s), numerical results with different confining pressure and temperature are obtained, as shown in Fig. 12.

Fig. 12
figure 12

Crack patterns, fluid pressure distribution patterns, and corresponding temperature distribution (°C) when the fluid injection rate and injection fluid viscosity are 0.01 m3/s and 100.0 mPa.s, respectively

Full size image

Figure 12 shows that more hydraulic cracks induced by high-viscosity fluid could be observed, except for the phenomenon similar to Fig. 11. The fluid distribution pattern indicates that many branches of hydraulic cracks are not saturated because the high-viscosity fluid has more difficulty flowing between domains. The borehole pressure development with a high injection rate is shown in Fig. 13.

Fig. 13
figure 13

The development of borehole pressure when the injection rate is 0.01 \({\mathrm{m}}^{3}\)/s (left: \(\upmu\) = 0.1 mPa.s; right: \(\upmu\) = 100.0 mPa.s)

Full size image

When using a high fluid injection rate, borehole pressure increases more rapidly, and the model breaks earlier. The relationship between the average crack width and the confining pressure when the borehole pressure reaches stabilized pressure is summarized in Fig. 14.

Fig. 14
figure 14

Average crack width under different conditions

Full size image

Based on Fig. 14, as the confining pressure increases, the average crack width decreases in all simulation groups. For the simulation groups using a low injection rate (0.001 m3/s), the average crack width increases with increasing temperature. Especially when the temperature is 600 °C, the average crack width becomes much more expansive than that at room temperature or 400 °C. The hydraulic cracks induced by the high-viscosity fluid of 100.0 mPa.s will be broader, and the average crack width becomes broader than that with a low viscosity fluid.

For the simulation groups using a high injection rate (0.01 m3/s), when the temperature is 400 °C, a decrease in the average crack width could be observed in some simulation groups (compared with room temperature). When the temperature is 600 °C, the average crack width in all simulation groups is much larger than at room temperature or 400 °C. More hydraulic cracks induced by high-viscosity fluid of 100.0 mPa.s lead to an increase in average crack width than using low-viscosity fluid. In addition, the above numerical simulation results show that when other conditions are the same, the average crack width increases with the increase of the injection rate.

Considering the influence of thermal failure on the principal stress direction of hydraulic cracks, we set anisotropic stress conditions to the model. The normal stresses of 5 and 10 MPa are applied to the model in vertical and horizontal directions. When the injection rate is 0.001 \({\mathrm{m}}^{3}\)/s, numerical simulation results with anisotropic stress conditions are illustrated in Fig. 15.

Fig. 15
figure 15

Crack patterns and corresponding temperature distribution (°C) with the injection rate of 0.001 m3/s under anisotropic stress conditions

Full size image

Figure 15 shows that as the temperature rises, the crack pattern of the model becomes more complicated, manifested by the increase of branches of hydraulic cracks and remote micro-cracks. When high-viscosity fluid is used, more and broader hydraulic cracks appear. In addition, when the temperature and the injection fluid viscosity change, the crack morphology is slightly different. The main crack directions present a horizontal distribution consistent with the maximum principal stress direction. When the injection rate is 0.01 \({\mathrm{m}}^{3}\)/s, numerical simulation results with anisotropic stress conditions are shown as Fig. 16.

Fig. 16
figure 16

Crack patterns and corresponding temperature distribution (°C) with the injection rate of 0.01 m3/s under anisotropic stress conditions

Full size image

Figure 16 shows more hydraulic cracks and remote micro-cracks as the temperature increases. When high-viscosity fluid is used, more and broader hydraulic cracks appear. Under the condition of high injection rate, the color of the crack is darker than that of the low injection rate group under the same conditions. These phenomena are the same as the previous simulation with isotropic stress conditions. Similarly, the crack patterns obtained by most of the test groups also show that the direction of hydraulic crack is consistent with the direction of principal stress. Only the test group with a high injection rate (0.01 \({\mathrm{m}}^{3}\)/s), high-viscosity injection fluid (100.0 mPa.s), and temperature of 600 °C showed some cracks that are inconsistent with the principal stress direction, which should be caused by the combined effect of factors that can aggravate the development of cracks. The development of borehole pressure under anisotropic stress conditions during hydraulic fracturing is illustrated in Fig. 17.

Fig. 17
figure 17

The development of borehole pressure under anisotropic stress conditions (left: \(dv\) = 0.001 \({\mathrm{m}}^{3}\)/s; right: \(dv\) = 0.01 \({m}^{3}\)/s)

Full size image

The development of borehole pressure is similar to that of the isotropic stress cases. The breakdown pressure is reached earlier at high injection rates. The high fluid viscosity leads to an increase of the borehole pressure, and the high temperature treatment causes the breakdown pressure to decrease.

We also simulate hydraulic fracturing under real environmental conditions of EGS filed in Basel, Switzerland, for further research based on the above results. The following regional stress information at Basel is inferred based on borehole analysis (Valley & Evans, 2019):

$$\begin{gathered} {\text{Shmin }}\left[ {{\text{MPa}}} \right] \, = {\text{ 7z }}\left[ {{\text{km}}} \right] \, + { 42}, \hfill \\ {\text{SHmax }}\left[ {{\text{MPa}}} \right] \, = {\text{ 5z }}\left[ {{\text{km}}} \right] \, + { 9}0\,. \hfill \\ \end{gathered}$$
(31)

Here, Shmin and SHmax are the minimum and maximum horizontal principal stress, respectively; z is the depth below the ground surface. These linear trends are applicable for the depth range 2500–5000 m.

For the thermal history of the borehole, the measurement data vary with logging and time. To obtain a representative result, the data obtained by the temperature log on 10 December 2008, which are taken to be representative of the in-situ conditions without the drilling-induced temperature perturbation, are applied. Based on these data, a linear trend was proposed as follows (Valley & Evans, 2019):

$$T\,(^\circ {\text{C}}) \, = \, 27.6{\text{z }}[{\text{km}}] \, + \, 47$$
(32)

Here, T is the temperature. These linear trends are applicable for the depth range 2500–4600 m. Based on the above formulas, we take the depth of 4 km for numerical simulation, where the corresponding parameters, Shmin, SHmax, and T, are 70 MPa, 110 MPa, and 157.4 °C, respectively.

We performed numerical simulations of hydraulic fracturing under different injection fluid conditions based on these field conditions. The results are shown in Fig. 18.

Fig. 18
figure 18

Crack patterns with field stress and thermal conditions

Full size image

The above results show that when a high stress difference (40 MPa) is applied, the development of hydraulic cracks is significantly suppressed (Fig. 18a). This phenomenon is consistent with the conclusions of previous scholars (Hofmann et al., 2016). However, under the existence of the suppression from the high stress difference, more and wider cracks can still be generated by increasing the injection rate and the viscosity of the injection fluid (Fig. 18b–d). This result indicates that when the field stress conditions are not conducive to crack development, it is a possible solution to induce complex crack networks by increasing the injection rate and viscosity of the injection fluid.

Notably, even at the same depth, as the borehole orientation changes, the stress conditions around the borehole also change. In this section, the confining pressure applied in the two directions of the model is based on the field data of the minimum and maximum horizontal principal stress, which represents the maximum stress difference at the same depth. Changing borehole orientation could reduce the stress difference around the borehole. The results in the previous section under smaller stress differences would be applicable if surrounding stress conditions acting on a surface perpendicular to the borehole axis could be reduced.

6 Discussion

For EGS used for power generation, in addition to the factors mentioned above, different heating rates caused by different geothermal gradients are also significant factors that affect the mechanical properties of rock mass, which is worth discussing. Considering the difference in the magnitude of loading rate and strain rate in the DEM algorithm from experimental data, we know it is essential to discuss the influence of different heating rates on the mechanical properties of the rock rather than calibrating the precise thermodynamic rock responses.

In the numerical simulation process, the numerical model is first heated to the target temperature at different rates of 0.45, 0.9, and 1.35 °C/min and then cooled to room temperature at the same rate after the model reaches a stable state. After this thermal treatment process, the model is used for the uniaxial compression test. The numerical results of stress-strain curves are shown in Fig. 19.

Fig. 19
figure 19

Stress-strain curves after treatments at different heating rates and temperatures

Full size image

In Fig. 19, the dynamic compressive strength and dynamic elastic modulus decrease with the increasing heating rate, whereas the peak strain increases gradually. This trend is consistent with the experimental results (Shu et al., 2019). Thus, it is also expected that the rocks are more likely to be induced to fracture by the injection fluid under a high heating rate. Although the heating rate is an important influencing factor, the complicated heating mechanism and the stress history of thermal source rocks make it challenging to determine the corresponding heating rate in actual projects.

Research on the development of geothermal resources has attracted the interest of scholars for a long time. As mentioned before, many experiments on the thermodynamic response of rocks have been carried out (Rossi et al., 2018; Shu et al., 2019; Yang et al., 2017 for example), which were mainly distinguished from conventional mechanical experiments of rock by the thermal treatment of specimen. In the thermal treatment stage, specimens are heated to their target temperature through a high-temperature furnace, and they are then cooled naturally to room temperature (25 °C) in a confined space. After the thermal treatment, loading tests (mainly the uniaxial compression test) were conducted to analyze the thermodynamic response of the thermally treated rock specimen. Some theoretical research applied the effects of temperature on rock mechanical properties obtained from this type of experiment in numerical simulations (Ohtani et al., 2019a, 2019b, for example). It is noteworthy that the heating and cooling phases of the numerical model are separated to simulate more realistic conditions because the high-temperature geothermal reservoir rock does not have a cooling phase like the process before developing a laboratory sample. In the theoretical validation, the thermal treatment of the numerical model includes heating and cooling to keep it consistent with laboratory experiments; only the heating part is retained during the numerical simulation of hydraulic fracturing to be consistent with the state of the geothermal reservoir rocks. Since thermal stress and thermal stress cracks are also generated during the cooling stage, it is expected that our numerical model will have less initial damage than the model that does not distinguish between heating and cooling stages.

A more significant temperature difference between reservoir rock and injection fluid helps to induce more cracks and also theoretically proves the feasibility of using cryogenic liquid (such as liquid nitrogen and supercritical carbon dioxide) instead of water for fracturing. In recent years, waterless fracturing technology has become an alternative to traditional hydraulic methods (Huang et al., 2020). In particular, these technologies are usually closely related to supercritical fluids. Take liquid nitrogen (\({\mathrm{LN}}_{2}\)) as an example, the critical pressure and temperature of \({\mathrm{LN}}_{2}\) are 3.4 MPa and − 147 °C, respectively. During field application of \({\mathrm{LN}}_{2}\) fracturing, the injection pressure will exceed the critical pressure in most cases, and the injected \({\mathrm{LN}}_{2}\) goes into a supercritical state after being heated. In the supercritical state, distinct liquid and gas phases do not exist. The properties of the fluid will change significantly with temperature and pressure. Since the complex heat transfer phenomena in the supercritical state are still unclear, corresponding theoretical research is of great importance, i.e., one of our future research directions.

7 Conclusions

In the present study, we developed a new scheme to incorporate the effect of thermal stress cracks induced by thermal expansion or shrinkage into DEM for simulating the failure behavior of reservoir rocks in EGS. We conduct hydraulic fracturing simulations under various temperatures, confining pressure, stress, and injection fluid conditions. The numerical results show that high-temperature, high-injection rate, and high-viscosity injection fluid all tend to cause more complicated failure mode, resulting in more and broader hydraulic cracks. The propagation of hydraulic cracks shows a decreasing trend with increasing confining pressure caused by crack closure. In high-temperature cases, the thermal expansion of particles will cause the width of the hydraulic cracks to decrease. However, the initial thermal stress cracks caused by the thermal expansion of particles help form more hydraulic cracks. The influence of initial thermal stress cracks gradually dominates with the increase of temperature. In addition, when anisotropic stress condition is applied to the model, although the crack pattern will change due to changes in temperature and fluid injection conditions, the main crack direction is consistent with the principal stress direction. In addition, the fluid pressure distribution pattern shows that the saturation of domains is usually attributed to the development of hydraulic cracks. However, in the case of using high-viscosity fluids, the distribution of saturated domains lags behind hydraulic cracks because of the weaker fluidity of high-viscosity fluids. The network of the hydraulic cracks is affected by the combined effect of temperature, injection fluid condition, and the confining stress condition. In actual geothermal development, high-viscosity fluid or a high injection rate could be a feasible solution to induce more hydraulic cracks. In addition, since the temperature of rocks is often proportional to the buried depth, high temperature and high pressure usually appear together. Although the higher temperature of the thermal source rocks is conducive to generating more hydraulic cracks during the fracturing process, the confining pressure that increases with the temperature also suppresses the development of cracks more. Therefore, a more considerable temperature difference between reservoir rock and injection fluid is needed to overcome the inhibition of high confining pressure on the development of cracks and form a complex and extensive network of cracks.