Abstract
The decay of solutions to the Klein–Gordon equation is studied in two expanding cosmological spacetimes, namely
-
the de Sitter universe in flat Friedmann–Lemaître–Robertson–Walker (FLRW) form and
-
the cosmological region of the Reissner–Nordström–de Sitter (RNdS) model.
Using energy methods, for initial data with finite higher-order energies, decay rates for the solution are obtained. Also, a previously established decay rate of the time derivative of the solution to the wave equation, in an expanding de Sitter universe in flat FLRW form, is improved, proving Rendall’s conjecture. A similar improvement is also given for the wave equation in the cosmological region of the RNdS spacetime.
We’re sorry, something doesn't seem to be working properly.
Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.
Avoid common mistakes on your manuscript.
1 Introduction
The aim of this article is to obtain exact decay rates for solutions to the Klein–Gordon equation in a fixed background of some expanding cosmological spacetimes. The two spacetimes we will consider are the de Sitter universe in flat Friedmann–Lemaître–Robertson–Walker (FLRW) form and the cosmological region of the Reissner–Nordström–de Sitter (RNdS) model. The problem we consider is linear, in that the background is fixed. This constitutes a first step towards understanding the more complicated nonlinear coupled problem, where one also considers the effect of the energy–momentum tensor of the solution to the Klein–Gordon equation on the Einstein equation. This nonlinear coupled problem is much more complicated and usually requires, as a first step, a detailed understanding of our simpler linear problem.
There are several motivations behind the interest in this question. Firstly, one may consider the linear wave equations as a proxy for the Einstein equations, with the ultimate goal of understanding the qualitative behaviour of solutions to the Einstein equations. (The vacuum Einstein equations become wave-like equations in harmonic coordinates; see for example [18, §5.4, p. 110]). After this first step, one may then proceed to consider linearised Einstein equations (which can be reduced to tensor wave-like linear equations) and, finally, the full nonlinear Einstein equations. With the addition of a positive cosmological constant to the Einstein field equations, the expectation is that the resulting accelerated expansion has a dominating effect on the decay of solutions. Precise estimates on solutions may then prove useful in formulating and proving cosmic no-hair theorems (e.g. [3, 7]).
The wave equation \(\square _g \phi =0\) in expanding cosmological spacetimes (M, g) has been amply studied in the literature; see for example [5, 8, 10, 23] and the references therein. It is a natural question to also study the Klein–Gordon equation \(\square _g\phi -m^2\phi =0\), the degenerate version of which, when \(m^2=0\), is the wave equation. For example, in [23, §6], also the case of the Klein–Gordon equation in the Schwarzschild–de Sitter spacetime is considered. In [21], the asymptotic behaviour of the solutions to the Klein–Gordon equation near the Big Bang singularity is studied, while we investigate the asymptotics of the Klein–Gordon equation in the far future in the case of the de Sitter universe in flat FLRW form, and in the cosmological region of the Reissner–Nordström–de Sitter solution. Recently, in [11] (see also [26] and [22]), among other things, decay estimates for the solutions to the Klein–Gordon equation were obtained in de Sitter models (see in particular, Corollary 2.1 and the less obvious Proposition 3.1 of [11]). However, these results are proved via Fourier transformation (reminiscent of our mode calculation in Appendix A (Section 6)) and do not seem to be as sharp as our Theorem 3.1.
The wave equation in the de Sitter spacetime having flat three-dimensional spatial sections was considered in Rendall [20]. There, it was shown that the time derivative \(\partial _t \phi =:\dot{\phi }\) decays at least as \(e^{-Ht}=(a(t))^{-1}\), where \(H=\sqrt{\Lambda /3}\) is the Hubble constant and \(\Lambda >0\) is the cosmological constant. Moreover, it was conjectured that the decay is of the order \(e^{-2Ht}=(a(t))^{-2}\). The almost-exact conjectured decay rate of \(|\dot{\phi }|\lesssim (a(t))^{-2+\delta }\) (where \(\delta >0\) can be chosen arbitrarily at the outset) follows as a corollary of a result shown recently [8, Remark 1.1]. We improve this result, to obtain full conformity with Rendall’s conjecture, in our result Theorem 2.3.
Finally, from the pure mathematical perspective, analysis of linear wave equations on Lorentzian manifolds is a natural topic of study within the realm of hyperbolic partial differential equations and differential geometry; see for example [2, 25, §7, Chap. 2].
A naive heuristic indication of the effect of the accelerated expansion on the decay of the solution, based on physical energy considerations, can be obtained as follows. Considering an expanding FLRW model with flat n-dimensional spatial sections of radius a(t), we have on the one hand that the energy density of a solution \(\phi \) of the Klein–Gordon equation is of the order of \(m^2 \phi ^2\). On the other hand, if the wavelength of the particles associated with \(\phi \) follows the expansion, then it is proportional to a(t), and so the energy varies as \( E^2\sim m^2+p^2\sim A+\frac{B}{(a(t))^2}, \) where \(A,B>0\) are constants. Thus,
giving \( m^2 \phi ^2 \sim (a(t))^{-n} (A+\frac{B}{(a(t))^2} ). \) As \(\dot{a}\geqslant 0\) (expanding FLRW spacetime), the term \( A+\frac{B}{(a(t))^2} \) approaches a finite positive value, and so one may expect
We will find out that in fact things are much more complicated: this decay rate is valid only for \(|m|\geqslant \frac{n}{2}\). In order to obtain precise conjectures on the expected decay, we will consider Fourier modes for spatially periodic solutions to the Klein–Gordon equation or, equivalently, consider the expanding de Sitter universe in flat FLRW form with toroidal spatial sections. This exercise already demonstrates that the underlying decay mechanism is the cosmological expansion, as opposed to dispersion. The Fourier mode analysis, which is peripheral to the rest of the paper, is relegated to Appendix A (Section 6).
In the cosmological region of the Reissner–Nordström–de Sitter spacetimes, the expanding region is foliated by spacelike hypersurfaces of ‘constant r’. One expects the decay rate with respect to r, for the solution to the Klein–Gordon equation, in the cosmological region of the Reissner–Nordström–de Sitter spacetime, to be the same as the one for the de Sitter universe in flat FLRW form, when \(e^t\) is replaced by r. We show that this expectation is correct, and a suitable modification of the technique used in the case of the de Sitter universe in flat FLRW form does enable one to obtain the expected decay rates also for the case of the Reissner–Nordström–de Sitter spacetime.
Our main results are as follows:
-
Theorem 2.3 considers the \(m=0\) case (wave equation), and we obtain a decay estimate on \(\partial _t{\phi }\), improving a corollary of [8, Theorem 1], and proving the aforementioned Rendall’s conjecture.
-
Theorem 5.3 improves [8, Theorem 2], and we obtain a decay estimate on \(\partial _r \phi \), using a similar method to the one we use for proving Rendall’s conjecture.
-
Theorem 3.1 gives the decay rate of the solutions \(\phi \) to the Klein–Gordon equation in the de Sitter universe in flat FLRW form.
-
Theorem 4.2 gives the decay rate of the solutions \(\phi \) to the Klein–Gordon equation in the cosmological region of the RNdS model.
Theorems 2.3, 3.1, 4.2 and 5.3 are stated and proved in Sects. 2–5, respectively. The Fourier mode analysis for spatially-periodic solutions to the Klein–Gordon equation is given in Appendix A(Section 6), while Appendix B (Section 7) contains a technical lemma which is needed in the proof of Theorem 3.1. Finally, in Appendix C (Section 8), we establish the sharpness of the bound of the \(|m|=\frac{n}{2}\) case of Theorem 3.1.
1.1 Relation of Our Results to Previous Work
Our decay rates for the Klein–Gordon equation solutions in the case of the de Sitter universe can be retrieved from the article [26] by setting \(x=e^{-t}\), \(Y=\mathbb {R}^n\) therein. However, the methods used are entirely different: our proof in this case is more explicit and more elementary (relying on energy methods, rather than technical tools from microlocal analysis of partial differential operators).
In the article [13], the Klein–Gordon equation is studied in the Nariai spacetime using energy methods, and en route it is also established that solutions of the Klein–Gordon equation decay exponentially in the de Sitter case (with spherical spatial sections). However, the decay rates are not given explicitly.
The article [9] contains a general discussion of redshift estimates, which we use to prove our results in the context of the Reissner–Nordström–de Sitter spacetime. Similar estimates are used in the article [23] to study the wave equation in the Schwarzschild–de Sitter spacetime, of which the Reissner–Nordström–de Sitter spacetime is a perturbation for large radius. Nevertheless, we do not appeal to these results, and instead of extracting what we need from these sources, we give a less technical, self-contained derivation for the convenience of the reader in Sect. 4.5. Here, we follow [8] (where a similar derivation was given for the wave equation).
2 Decay in the de Sitter Universe in Flat FLRW Form; \(m=0\)
In [8, Theorem 1], the following result was shown:
Theorem 2.1
Suppose that
-
\(\delta >0\),
-
\(I\subset \mathbb {R}\) is an open interval of the form \((t_*,+\infty )\), \(t_0\in I\),
-
\(a(\cdot ) \in C^1(I)\) with \(\dot{a}(t)\geqslant 0\) for \(t\geqslant t_0\), and \(\epsilon >0\) is such that
$$\begin{aligned} \int _{t_0}^\infty \frac{1}{(a(t))^\epsilon } \mathrm{d}t <+\infty , \end{aligned}$$ -
\(n\geqslant 2\),
-
(M, g) is an expanding FLRW spacetime with flat n-dimensional sections, given by \(I\times \mathbb {R}^n\), with the metric
$$\begin{aligned} g=-dt^2 +(a(t))^2 \left( (dx^1)^2+\cdots +(dx^n)^2\right) , \end{aligned}$$(1) -
\(k>\frac{n}{2}+2\), \(\;\;\phi _0\in H^k(\mathbb {R}^n)\), \(\;\;\phi _1\in H^{k-1}(\mathbb {R}^n)\), and
-
\(\phi \) is a smooth solution to the Cauchy problem
$$\begin{aligned} \left\{ \begin{array}{rcll} \square _g \phi &{}=&{}0,&{} \;\;\;\;(t\geqslant t_0,\;\mathbf {x}\in \mathbb {R}^n), \\ \phi (t_0,\mathbf {x})&{}=&{} \phi _0(\mathbf {x}) &{}\;\;\;\;(\mathbf {x}\in \mathbb {R}^n),\\ \partial _t \phi (t_0,\mathbf {x})&{}=&{} \phi _1(\mathbf {x}) &{} \;\;\;\;(\mathbf {x}\in \mathbb {R}^n). \end{array}\right. \end{aligned}$$
Then
Here, the symbol \(\lesssim \) is used to mean that there exists a constant \(C(\delta )\), independent of \(\epsilon \), such that
We also use the standard notation \(H^k(\mathbb {R}^n)\) for the Sobolev space,
where \({\varvec{\alpha }}=(\alpha _1,\ldots ,\alpha _n)\in \mathbb {N}_0^n\), \(\mathbb {N}_0=\{0,1,2,3,\ldots \}\), \(|{\varvec{\alpha }}|:=\alpha _1+\cdots +\alpha _n\), and \(\partial _{\varvec{\alpha }}= (\partial _{x_1})^{\alpha _1}\cdots (\partial _{x_n})^{\alpha _n}\); see for example [27, p. 249] or [25, Chap. 4].
Remark 2.2
(Smoothness assumption on the solution \(\phi \)) In Theorem 2.1 (and later also in Theorems 2.3, 3.1, 4.2, 5.1, 5.3), we will assume, for the sake of simplicity of exposition, that the solution \(\phi \) to the wave/Klein–Gordon equation is smooth. However, these theorems are also true without this assumption. To see this, we note that for non-smooth solutions with initial data in \(H^k \times H^{k-1}\), we can approximate the initial data by smooth functions in \(H^k \times H^{k-1}\), prove the bounds for the \(H^k\) norms of the corresponding solutions, and then take limits. Since the solution of the problem with rough initial data is in \(C^0(I, H^k) \cap \;\!C^1(I, H^{k-1})\), these bounds will continue to be true in the limit, and we can then use the Sobolev embedding theorem. This enables one to drop the smoothness assumption.
In Theorem 2.1, in particular, if \( a(t)=e^{Ht}, \) where H is the Hubble constant, then since \(\epsilon >0\) can be taken to be arbitrarily small, we obtain
and this is in agreement with Rendall’s conjecture up to the small quantity \(\delta >0\). We will show below that in fact one gets the exact rate \((a(t))^{-2}\) when \(n>2\). There is no loss of generality in assuming that \(H=1\). Our result is the following.
Theorem 2.3
Suppose that
-
\(I\subset \mathbb {R}\) is an open interval of the form \((t_*,+\infty )\), \(t_0\in I\),
-
\(n> 2\),
-
(M, g) is the expanding de Sitter universe in flat FLRW form, with flat n-dimensional sections, given by \(I\times \mathbb {R}^n\), with the metric
$$\begin{aligned} g=-dt^2 +e^{2t} \left( (dx^1)^2+\cdots +(dx^n)^2\right) , \end{aligned}$$ -
\(k>\frac{n}{2}+2\), \(\;\;\phi _0\in H^k(\mathbb {R}^n)\), \(\;\;\phi _1\in H^{k-1}(\mathbb {R}^n)\), and
-
\(\phi \) is a smooth solution to the Cauchy problem
$$\begin{aligned} \left\{ \begin{array}{rcll} \square _g \phi &{}=&{} 0,&{}\;\; \;\;(t\geqslant t_0,\;\mathbf {x}\in \mathbb {R}^n), \\ \phi (t_0,\mathbf {x}) &{}=&{} \phi _0(\mathbf {x}) &{}\;\;\;\;(\mathbf {x}\in \mathbb {R}^n),\\ \partial _t \phi (t_0,\mathbf {x}) &{}=&{} \phi _1(\mathbf {x}) &{}\;\;\;\; (\mathbf {x}\in \mathbb {R}^n). \end{array}\right. \end{aligned}$$
Then
Proof
We proceed in several steps.
Step 1: Bound on \(\Delta \phi \).
We will follow the preliminary steps of the proof of [8, Theorem 1] in order to obtain a bound on \(\Delta \phi \), which will be needed in the proof of our Theorem 2.3. We repeat this preliminary step here from [8, §2.2] for the sake of completeness and for the convenience of the reader.
For a vector field \(X=X^\mu \partial _\mu \), it can be shown that
where \(g:=\det [g_{\mu \nu }]\) is the determinant of the matrix \([g_{\mu \nu }]\) describing the metric in the chart. Then, it follows that
Thus, \(\square _g \phi =0\) can be rewritten as \(\partial _\mu (\sqrt{-g} \;\!\partial ^\mu \phi )=0\). With the metric for the de Sitter universe in flat FLRW form given by
the wave equation can be rewritten as \( \partial _\mu (a^n \partial ^\mu \phi )=0, \) that is,
We recall (see e.g. [27, Appendix E]) that the energy–momentum tensor for the wave equation is
Then, it can be shown that \( \nabla _\mu T^{\mu \nu }=0. \) From (2), we have in particular that
Define the vector field
Then, X is future-pointing (\(g(X,\partial _t)<0\)) and causal (X is time-like since \(g(X,X)<0\)). We form the current J, given by
Then, (set \(m=0\) in [18, Ex.5.7(1), p. 116], but a justification is given below)
Here, \(X\cdot \phi \) is the application of X on \(\phi \). To see (\(\star \)), note that
It follows from (\(\star \)) that \(g(J,J)\leqslant 0\), so that J is causal. Also, J is past-pointing. To see this, we choose \(E_1,\ldots ,E_n\) orthogonal and spacelike such that \(\{X,E_1,\ldots , E_n\}\) forms an orthogonal basis in each tangent space. Then, expressing \( \text {grad } \phi =c^0X+c^1E_1+\cdots c^n E_n, \) we obtain
Set \( N=\frac{\partial }{\partial t}, \) the future unit normal vector field. We define the energy E by
We note that \([X,\partial _\mu ]=[a^{2-n}\partial _t,\partial _\mu ]\), and
so that \(dx^i[X,\partial _\mu ]=0\). The deformation tensor \(\Pi \) associated with the multiplier X is
Here, we used the facts \(\mathcal {L}_X (a^2)=a^{2-n} \frac{\partial }{\partial t}a^2=a^{2-n}2a\dot{a}\) and \(\mathcal {L}_X dx^i=0\) (since \(0=\mathcal {L}_X(dx^i(\partial _{\mu })) =(\mathcal {L}_X dx^i)_\mu +dx^i([X,\partial _{\mu }])=(\mathcal {L}_X dx^i)_\mu +0\)). We have \( 0=\mathcal {L}_X(dt(\partial _\mu ))=(\mathcal {L}_X dt)_\mu +dt[X,\partial _\mu ] \), and so from the above expression for \([X,\partial _\mu ]\), we obtain
Thus, \( \Pi = (n-2) \dot{a} a^{1-n} dt^2 +\dot{a} a^{3-n} \delta _{ij} dx^i dx^j. \)
It can be shown that \(\nabla _\mu J^\mu =T^{\mu \nu }\Pi _{\mu \nu }.\) Indeed, from the expression for the Lie derivative of the metric given in [18, Exercise 2, p. 93] and the expression for the divergence of \(T^{\mu \nu }X_\nu \) given in [18, §5.2], we have
So the ‘bulk term’ is
For each \(R>0\), define the set \( B_0:=\{(t_0,\mathbf {x})\in I\times \mathbb {R}^n: \langle \mathbf {x},\mathbf {x}\rangle _{\scriptscriptstyle \mathbb {R}^n} \leqslant R^2\}. \) The future domain of dependence of \(B_{0}\) is the set
(Here by a causal curve, we mean one whose tangent vector at each point is a causal vector. A curve \(c:(a,b)\rightarrow M\) which is smooth and future directedFootnote 1 is called past inextendible if \(\lim \limits _{t\rightarrow a}c(t)\) does not exist.)
Let \(t_1>t_0\). We will now apply the divergence theorem to the region
For preliminaries on the divergence theorem in the context of a time-oriented Lorentzian manifold, we refer the reader to [27, Appendix 7]. We have

where \(\partial \mathcal {R}\) denotes the boundary of \(\mathcal {R}\), \(\epsilon \) is the volume form on M induced by g, and  denotes contraction in the first index.
denotes contraction in the first index.

Since J is past-pointing, the boundary integral over the null portion C of the boundary \(\partial \mathcal {R}\) is nonpositive. Also, because \(\nabla _\mu J^\mu \) is nonnegative, we have that the volume integral over \(\mathcal {R}\) is nonnegative. This gives an inequality on the two boundary integrals, one over \(B_0\) and the other over \(B_1:=D^+(B_0) \cap \{t=t_1\}\), as follows:
Passing the limit \(R\rightarrow \infty \) yields \( E(t_0)\geqslant E(t_1). \) (We note that the radius of \(B_1\) also goes to infinity as \(R\rightarrow \infty \).) As the choice of \(t_1>t_0\) was arbitrary, we have that for all \( t\geqslant t_0\), \(E(t)\leqslant E(t_0)<\infty .\) The finiteness of \(E(t_0)\) follows from our assumption that \(\phi _0\in H^k(\mathbb {R}^n)\) and \(\phi _1\in H^{k-1}( \mathbb {R}^n)\) for a k satisfying \(k>\frac{n}{2}+2\geqslant 1\). From here, it follows that for all \(t \geqslant t_0\),
But since each partial derivative \(\partial _i \phi \) is also a solution of the wave equation, and as \(k\geqslant 2\), we obtain, by applying the above to the partial derivatives \(\partial _i \phi \), that also
In fact, since \(k>\frac{n}{2}+2\), we also obtain that for a \(k'>\frac{n}{2}\), \( \Vert \Delta \phi \Vert _{H^{k'} (\mathbb {R}^n)}\lesssim 1. \) Finally, by the Sobolev inequality (see e.g. [14, (7.30), p. 158]), we obtain
This completes Step 1 of the proof of Theorem 2.3. We note that this step loses two derivatives when we drop the smoothness assumption on \(\phi \).
Step 2: The wave equation in conformal coordinates.
The key point of departure from the earlier derivation of the estimates from [8] is the usage of ‘conformal coordinates’, which renders the wave equation in a form where it becomes possible to integrate, leaving essentially just the time derivative of \(\phi \) with other terms (e.g. \(\Delta \phi \)) for which we have a known bound. An application of the triangle inequality will then deliver the desired bound.
Define \(\displaystyle \tau =\int _{t_0}^t \frac{1}{a(s)} \mathrm{d}s. \) Then we obtain that \( \displaystyle \frac{\mathrm{d}\tau }{\mathrm{d}t}=\frac{1}{a(t)}\) and \( a(t) \displaystyle \frac{\mathrm{d}}{\mathrm{d}t}=\frac{\mathrm{d}}{\mathrm{d}\tau }. \)
With a slight abuse of notation, we write \(a(\tau ):=a(t(\tau ))\). Then, \(dt=a(\tau ) d\tau \). So \( g= -dt^2 +(a(t))^2 \left( (dx^1)^2+\cdots + (dx^n)^2\right) = (a(\tau ))^2 \big (-d\tau ^2 +\delta _{ij} dx^i dx^j\big ). \) The wave equation \(\square _g \phi =0\) can be rewritten as \(\partial _\mu (\sqrt{-g} \;\!\partial ^\mu \phi )=0\), and so we obtain \(\partial _\mu (a^{n+1} \partial ^\mu \phi )=0. \) Separating the partial derivative operators with respect to the \(\tau \) and \(\mathbf {x}\) coordinates, we obtain the wave equation in conformal coordinates \( \partial _\tau (a^{n-1} \partial _\tau \phi )=a^{n-1} \Delta \phi , \) where \(\Delta \) is the usual Laplacian on \(\mathbb {R}^n\). This completes Step 2 of the proof of Theorem 2.3.
Step 3: \(n>2\) and \(a(t)=e^t\). We have
and so \( a(\tau )=\displaystyle \frac{1}{e^{-t_0}-\tau }. \) We note that \(\tau \in [0,e^{-t_0})\). Also,
Integrating \( \partial _\tau (a^{n-1}\partial _\tau \phi )=a^{n-1}\Delta \phi \) from \(\tau =0\) to \(\tau \), we obtain
and so \(\displaystyle a^{n-1} a\partial _t \phi =a(t_0)^{n-1} a(t_0) \left. \partial _t\phi \right| _{t=t_0}+ \int _0^\tau \Delta \phi \frac{1}{(e^{-t_0}-\tau )^{n-1} }\mathrm{d}\tau , \) that is,
Hence, using the bound from (3), namely \(\Vert \Delta \phi (t,\cdot )\Vert _{L^\infty (\mathbb {R}^n)}\leqslant C\) for all \(t\geqslant t_0\),

Hence,
and so
This completes the proof of Theorem 2.3. \(\square \)
Remark 2.4
The case when \(n=2\) and \(a(t)=e^t\):
Integrating \(\partial _\tau (a\partial _\tau \phi )=a\Delta \phi \) from \(\tau =0\) to \(\tau \), we obtain
and so
Hence,
and so
This can be viewed as an improvement to [8, Theorem 1] in the special case when \(a(t)=e^t\) and \(n=2\), since
Remark 2.5
The case when \(a(t)=t^p\), \(p\geqslant 1\):
One can prove an analogue of Theorem 2.3 when \(a(t)=t^p\) as well. In this case, the \(\epsilon \) from Theorem 2.1 can be chosen to be any number satisfying
and so Theorem 2.1 gives the decay estimate
where \(\delta '>0\) can be chosen arbitrarily. We can improve this to the following:
The proof is the same, mutatis mutandis, as that of Theorem 2.3.
Remark 2.6
Using a similar method, one can also obtain an improvement to [8, Theorem 2]. But we will postpone this discussion until after Sect. 4, since we will need some preliminaries about the RNdS spacetime, which will be established in Sect. 4.
3 Decay in the de Sitter Universe in Flat FLRW Form
The Klein–Gordon equation is \( \square _g\phi -m^2\phi =0\), that is,
In the case of the de Sitter universe in flat FLRW form, we obtain
In this section, we will prove Theorem 3.1. We arrive at the guesses for the specific estimates given in Theorem 3.1, based on an analysis using Fourier modes, assuming spatially periodic solutions. This Fourier mode analysis is given in ‘Appendix 6’.
Theorem 3.1
Suppose that
-
\(I\subset \mathbb {R}\) is an open interval of the form \((t_*,+\infty )\), \(t_0\in I\),
-
\(m\in \mathbb {R}\),
-
\(n> 2\),
-
(M, g) is the expanding de Sitter universe in flat FLRW form, with flat n-dimensional sections, given by \(I\times \mathbb {R}^n\), with the metric
$$\begin{aligned} g=-dt^2 +e^{2t} \left( (dx^1)^2+\cdots +(dx^n)^2\right) , \end{aligned}$$ -
\(k>\frac{n}{2}+2\), \(\;\;\phi _0\in H^k(\mathbb {R}^n)\), \(\;\;\phi _1\in H^{k-1}(\mathbb {R}^n)\), and
-
\(\phi \) is a smooth solution to the Cauchy problem
$$\begin{aligned} \left\{ \begin{array}{rcll} \square _g \phi -m^2 \phi &{}=&{}0,&{} \quad (t\geqslant t_0,\;\mathbf {x}\in \mathbb {R}^n), \\ \phi (t_0,\mathbf {x})&{}=&{} \phi _0(\mathbf {x}) &{}\quad (\mathbf {x}\in \mathbb {R}^n),\\ \partial _t \phi (t_0,\mathbf {x})&{}=&{} \phi _1(\mathbf {x}) &{} \quad (\mathbf {x}\in \mathbb {R}^n). \end{array}\right. \end{aligned}$$
Then, for all \(t\geqslant t_0\), we have
Remark 3.2
We recall that the conformally invariant wave equation in \(n+1\) dimensions is
where \(R_g\) is the scalar curvature of the metric g; see for instance [27]. If g is a FLRW metric with flat n-dimensional spatial sections, having the form given by (1), then
Thus, in de Sitter space in flat FLRW form, the conformally invariant wave equation can be interpreted as a Klein–Gordon equation, with the mass parameter satisfying \(m^2 = \frac{n^2-1}{4}\). From [8, Appendix 7], we have
which follows from using the fact that the \(L^\infty \)-norm of \(\psi (\cdot , t)\), defined by \(\phi =a^{1-\frac{n+1}{2}}\psi \) (see [8, eq. (178)]), is uniformly bounded with respect to t. The estimate (6) is in complete agreement with the result of our Theorem 3.1, since the relation \(\frac{n^2}{4} - m^2 = \frac{1}{4}\) reduces our bound \(a^{-\frac{n}{2}+\sqrt{\frac{n^2}{4}-m^2}}\) precisely to \(a^{\frac{1-n}{2}}\).
3.1 Preliminary Energy Function and Estimates
Define the energy–momentum tensor T by
Then, \(\nabla _\mu T^{\mu \nu }=0\). Also, in particular,
Set \( X=a^{-n}\frac{\partial }{\partial t}. \) Then, X is time-like and hence causal, and X is future-pointing. Define J by \( J^\mu =T^{\mu \nu }X_\nu . \) Then, J is causal and past-pointing. Let \(N=\partial _t\). Define the energy E by
Define
As \( \mathcal {L}_X dt=-na^{-n-1}\dot{a} dt, \) we have
Hence,
For \(R>0\), define \( B_0:=\{(t_0,\mathbf {x})\in I\times \mathbb {R}^n: \langle \mathbf {x},\mathbf {x}\rangle _{\scriptscriptstyle \mathbb {R}^n} \leqslant R^2\}. \) The future domain of dependence of \(B_{0}\) is denoted by \(D^+(B_0)\). Let \(t_1>t_0\). We will apply the divergence theorem to the region \( \mathcal {R}:=D^+(B_{0})\;\!\cap \;\!\{(t,\mathbf {x})\in M: t\leqslant t_1\}. \) We have

Using
-
\(\nabla _\mu J^\mu \geqslant 0\), and
-
the fact that the boundary contribution on C, the null portion of \(\partial \mathcal {R}\), is nonpositive (since J is causal and past-pointing),
we obtain the inequality
Passing the limit \(R\rightarrow \infty \) yields \(E(t_1)\leqslant E(t_0)<+\infty \). As \(t_1>t_0\) was arbitrary, we obtain
From here, it follows that for all \(t \geqslant t_0\),
But since each partial derivative \((\partial _{x^1})^{i_1}\cdots (\partial _{x^n})^{i_n} \phi \) is also a solution of the Klein–Gordon equation, it follows from \(\phi _0 \in H^k(\mathbb {R}^n)\) and \(\phi _1 \in H^{k-1}(R^n)\) for a \(k > \frac{n}{2 }+ 2\), that also \(\phi (t,\cdot ) \in H^k(\mathbb {R}^n)\) and \(\partial _t \phi (t,\cdot ) \in H^{k-1}(\mathbb {R}^n)\), and moreover,
where \(k':=k-1\).
3.2 The Auxiliary Function \(\psi \) and Its PDE
Motivated by the decay rate we anticipate for \(\phi \), we define the auxiliary function \(\psi \) by \( \psi := a^{\kappa }\phi , \) where
Then, using (5), it can be shown that \(\psi \) satisfies the equation
3.3 The Case \(|m|>\frac{n}{2}\)
We have \(\kappa =\frac{n}{2}\), so that \(n-2\kappa =0\), while \( \kappa ^2-n\kappa +m^2=m^2-\frac{n^2}{4}, \) and thus (7) becomes
We note that if \(\phi \in H^\ell (\mathbb {R}^n)\) and \(\dot{\phi }\in H^{\ell -1}(\mathbb {R}^n)\) for some \(\ell \), then \(\psi \in H^\ell (\mathbb {R}^n)\) too, and also
Define the new energy \(\mathcal {E}\), associated with the \(\psi \)-evolution, by
Then, using the fact that \(a=e^t=\dot{a}>0\), and also Eq. (7), we obtain
For a fixed t, and for a ball \(B(\mathbf {0},r)\subset \mathbb {R}^n\), where \(r>0\), it follows from the divergence theorem (since \(\dot{\psi }\) and \(\nabla {\psi }\) are smooth) that
where \(d\sigma _r\) is the surface area measure on the sphere \(S_r=\partial B(\mathbf {0},r)\) and \(\mathbf {n}\) is the outward-pointing unit normal. The right-hand side surface integral tends to 0 as \(r\rightarrow +\infty \), by an application of Lemma 7.1, given in ‘Appendix 7’.
So for \(t\geqslant t_0\), we have \(\mathcal {E}'(t)\leqslant 0\), which yields \(\mathcal {E}(t)\leqslant \mathcal {E}(t_0)\). In particular, for all \(t\geqslant t_0\), \(\Vert \psi (t,\cdot )\Vert _{L^2(\mathbb {R}^n)}\lesssim C\), that is, \(\Vert a^{\frac{n}{2}}\phi (t,\cdot )\Vert _{L^2(\mathbb {R}^n)}\lesssim C\), and soFootnote 2
Then, with enough regularity on \(\phi _0,\phi _1\) at the outset, that is, if \(\phi _0\in H^k(\mathbb {R}^n)\) and \(\phi _1\in H^{k-1}(\mathbb {R}^n)\) for a \(k>\frac{n}{2}+2\), and by considering \((\partial _{x^1})^{i_1}\cdots (\partial _{x^n})^{i_{n}}\phi \) as a solution to the Klein–Gordon equation, we arrive atFootnote 3
where \(k':=k-2\). As \(k'=k-2>\frac{n}{2}\), we have, using the Sobolev inequality, that
This completes the proof of Theorem 3.1 in the case when \(|m|>\frac{n}{2}\).
3.4 The Case \(|m|<\frac{n}{2}\)
We have \( \kappa = \frac{n}{2}-\sqrt{\frac{n^2}{4}-m^2},\) \( n-2\kappa =2 \sqrt{\frac{n^2}{4}-m^2}\;>0, \) and \(\kappa ^2-n\kappa +m^2=0\). Equation (7) becomes
Defining \(\displaystyle \widetilde{\mathcal {E}}(t):=\frac{1}{2}\int _{\mathbb {R}^n} \Bigg (\dot{\psi }^2+\frac{1}{a^2}|\nabla \psi |^2 \Bigg ) d^n\mathbf {x}, \) we obtain
Using \(a=e^t=\dot{a}\), we obtain
where
So \(\widetilde{\mathcal {E}}'(t)+\theta \cdot \widetilde{\mathcal {E}}(t)\leqslant 0\). Multiplying throughout by \(e^{\theta t}>0\), we obtain
Integrating from \(t_0\) to t yields \( e^{\theta t}\cdot \widetilde{ \mathcal {E}}(t)\leqslant e^{\theta t_0}\cdot \widetilde{ \mathcal {E}}(t_0), \) that is, \(\widetilde{\mathcal {E}}(t)\lesssim e^{-\theta t}\). So
We have \(\displaystyle \psi (t,\mathbf {x})=\psi (t_0,\mathbf {x})+ \int _{t_0}^t (\partial _t \psi )(s,\mathbf {x}) \mathrm{d}s, \) and so
Thus, for all \(t\geqslant t_0\), we have
By considering \((\partial _{x^1})^{i_1}\cdots (\partial _{x^n})^{i_n}\phi \) and using the Sobolev inequality, we have
This completes the proof of Theorem 3.1 in the case when \(|m|<\frac{n}{2}\).
3.5 The Case \(|m|=\frac{n}{2}\)
We have \(\kappa = \frac{n}{2}\), and equation (7) becomes \( \displaystyle \ddot{\psi } -\frac{1}{a^2} \Delta \psi =0. \)
Defining the same energy as we used earlier in the case when \(|m|<\frac{n}{2}\),
we obtain
So \(\widetilde{\mathcal {E}}(t)\leqslant \widetilde{\mathcal {E}}(t_0)\) for \(t\geqslant t_0\). In particular, \(\Vert \dot{\psi }(t,\cdot )\Vert _{L^2(\mathbb {R}^n)}\lesssim B\) for \(t\geqslant t_0\). Again,
gives
Thus, for all \(t\geqslant t_0\), we have
Hence (by considering \((\partial _{x^1})^{i_1}\cdots (\partial _{x^n})^{i_n}\phi \) and using the Sobolev inequality),
(One can show that this bound is sharp; see Appendix C (Section 8).)
This completes the proof of Theorem 3.1.
4 Decay in the Cosmological Region of the \(\mathrm {RNdS}\) Spacetime
The Reissner–Nordström–de Sitter (RNdS) spacetime (M, g) is a solution to the Einstein–Maxwell equations with a positive cosmological constant, and it represents a pairFootnote 4 of antipodal charged black holes in a sphericalFootnote 5 universe which is undergoing accelerated expansion. The Reissner–Nordström–de Sitter metric in \(n+1\) dimensions is given by
where
and \(d\Omega ^2\) is the unit round metric on \(S^{n-1}\). The constants M and e are proportional to the mass and the charge, respectively, of the black holes, and the cosmological constant is chosen to be
by an appropriate choice of units.
Consider the polynomial
As \(p(0)=-e^2<0\) and as \(p(r){\mathop {\longrightarrow }\limits ^{r\rightarrow \infty }} \infty \), it follows that p will have a real root in \((0,+\infty )\), and the largest real root of p, which we denote by \(r_c\), must be positive. If \(r>r_c\), then clearly \(p(r)>0\), and so also \(V(r)>0\).
It can also be seen that p has at most three distinct positive roots. Suppose, on the contrary, that p has more than three distinct positive roots: \(r_1<r_2<r_3<r_4\). Applying Rolle’s theorem to p on \([r_i,r_{i+1}]\) (\(i=1,2,3\)), we conclude that \(p'\) must have three distinct roots \(r_i'\in (r_i,r_{i+1})\) (\(i=1,2,3\)). Applying Rolle’s theorem to \(p'\) on \([r_i',r_{i+1}']\) (\(i=1,2\)), we conclude that \(p''\) must have two distinct roots \(r_i''\in (r_i',r_{i+1}')\) (\(i=1,2\)). But
which has only one positive root, a contradiction.
The ‘subextremality’ assumption on the RNdS spacetime made in Theorem 3.1 refers to a nondegeneracy of the positive roots of p: we assume that there are exactly three positive roots, \(r_-, r_+\) and \(r_c\), and \( 0<r_-<r_+<r_c. \) These describe the event horizon \(r=r_+\), and the Cauchy ‘inner’ horizon \(\;r=r_-\). It can be seen that the subextremality condition then implies \(p'(r_c)>0\). (Indeed, \(p'(r_c)\) cannot be negative, as otherwise p would acquire a root larger than \(r_c\) since \(p(r){\mathop {\longrightarrow }\limits ^{r\rightarrow \infty }}\infty \). Also, if \(p'(r_c)=0\), then Rolle’s theorem implies again that \(p'\) would have three positive roots, ones in \((r_-,r_+)\) and \((r_+,r_c)\), and one at \(r_c\), which is impossible, as we had seen above.) \(p'(r_c)>0\) implies that \(V'(r_c)>0\). We will also assume that
(See [6, Appendix 6] for the range of parameters for which this is guaranteed.) Our assumptions have the following consequence, which will be used in our proof of Theorem 4.2.
Lemma 4.1
(Global redshift) \(V'(r)>0\) for all \(r\geqslant r_c\).
Proof
We have
As \(V'(r_c)>0\), we have \(q(r_c)>0\). Also, \(V''(r_c)>0\) and so \(V'\) is increasing near \(r_c\). But then \(q(r)=r^n V'(r)\) is also increasing near \(r_c\), and in particular, \(q'(r_c)\geqslant 0\). Let us suppose that there exists an \(r_*>r_c\) such that \(V'(r_*)=0\), and let \(r_*\) be the smallest such root. Then, \(q(r_*)=0\) too. We note that
and so \(q'\) can have only one nonnegative root, namely \( \left( \frac{(n-3)}{n+1}M\right) ^{\frac{1}{n}}\geqslant 0. \)
- \(1^\circ \):
-
\(r_*\) is a repeated root of q. Then, \(q'(r_*)=0\).
If in addition \(q'(r_c)=0\), then we arrive at a contradiction, since \(q'\) then has two positive roots (at \(r_c\) and at \(r_*\)), which is impossible.
If \(q'(r_c)>0\), then we arrive at a contradiction as follows. As q is increasing near \(r_c\), and since \(q(r_c)>0=q(r_*)\), it follows by the intermediate value theorem that there is some \(r_{c}' \in (r_c,r_*)\) such that \(q(r_{c}')=q(r_c)\). But by Rolle’s theorem applied to q on \([r_c,r_{c}']\), there must exist an \(r_*'\in (r_c, r_{c}')\) such that \(q'(r_*')=0\). Again, \(q'\) acquires two zeros (at \(r_*\) and at \(r_*'\)), which is impossible.
- \(2^\circ \):
-
\(r_*\) is a simple root of q. But as \(q(r){\mathop {\longrightarrow }\limits ^{r\rightarrow \infty }}\infty \), it follows that there must be at least one more root \(r_{**}>r_{*}\) of q. By Rolle’s theorem applied to q on \([r_*, r_{**}]\), it follows that \(q'(r_{**}')=0\) for some \(r_{**}' \in (r_*,r_{**})\).
If in addition \(q'(r_c)=0\), then we arrive at a contradiction, since \(q'\) then has two positive roots (at \(r_c\) and at \(r_{**}'\)), which is impossible.
If \(q'(r_c)>0\), then, as in the last paragraph of \(1^\circ \) above, there exists an \(r_{*}'\in (r_c,r_c')\subset (r_c,r_*)\) such that \(q'(r_*')=0\). Thus, \(q'\) again gets two positive roots (at \(r_*'\) and at \(r_{**}'\)), which is impossible.
This shows that our assumption that \(V'\) is zero beyond \(r_c\) is incorrect. \(\square \)
We will need the previous result in Sect. 4.5 in the analysis following (12) (where in particular \(V'\) appears in the denominator).
The hypersurfaces of constant r are spacelike cylinders with a future-pointing unit normal vector field \( N=V^{\frac{1}{2}} \frac{\partial }{\partial r}\) and volume element \( dV_n=V^{\frac{1}{2}} r^{n-1} \mathrm{d}t \mathrm{d}\Omega . \)
The global structure of a maximal spherically symmetric extension of this metric can be depicted by a conformal Penrose diagram shown below, repeated periodically; see for example [7].
We are interested in the behaviour of the solution to the Klein–Gordon equation in the cosmological region \(\mathcal {R}_5\) of this spacetime (see Figure 1), bounded by the cosmological horizon branches \(\mathcal {C}\mathcal {H}_1^+\), \(\mathcal {C}\mathcal {H}_2^+\), the future null infinity \({\mathscr {I}}^+\), and the point \(i^+\). In particular, we want to obtain estimates for the decay rate of \(\phi \) as \(r\rightarrow \infty \). We guess the decay rates simply by substituting r instead of \(e^t\) in the estimates we had obtained for the decay rate of \(\phi \) with respect to t in the case of the de Sitter universe in flat FLRW form from the previous Sect. 3.
We will prove the following result.
Theorem 4.2
Suppose that
-
\(\epsilon >0\),
-
\(m\in \mathbb {R}\),
-
\(M>0\),
-
\(e> 0\),
-
\(n> 2\),
-
(M, g) is the \((n+1)\)-dimensional subextremal Reissner–Nordström–de Sitter solution given by the metric
$$\begin{aligned} g=-\frac{1}{V} dr^2+Vdt^2 +r^2 d\Omega ^2, \end{aligned}$$where
$$\begin{aligned} V= r^2+\frac{2M}{r^{n-2}} -\frac{e^2}{r^{n-1}}-1, \end{aligned}$$and \(d\Omega ^2\) is the metric of the unit \((n-1)\)-dimensional sphere \(S^{n-1}\),
-
\(k>\frac{n}{2}+2\), and
-
\(\phi \) is a smooth solution to \(\square _g \phi -m^2 \phi =0\) such that
$$\begin{aligned} \Vert \phi \Vert _{H^{k}(\mathcal {C}\mathcal {H}_1^+)}<+\infty \;\;\;\;\text { and }\;\;\;\;\Vert \phi \Vert _{H^{k}(\mathcal {C}\mathcal {H}_2^+)}<+\infty , \end{aligned}$$where \(\mathcal {C}\mathcal {H}_1^+\simeq \mathcal {C}\mathcal {H}_2^+\simeq \mathbb {R}\times S^{n-1}\) are the two components of the future cosmological horizon, parameterised by the flow parameter of the global Killing vector field \(\frac{\partial }{\partial t}\). (For \(\mathcal {C}\mathcal {H}_1^+\) and \(\mathcal {C}\mathcal {H}_2^+\), we use the usual Sobolev norms for \(\mathbb {R}\times S^{n-1}\); see e.g. [4].)
Then, there exists a \(r_0\) large enough so that for all \(r\geqslant r_0\),
4.1 Preliminary Energy Function
For a \(\phi \) defined in the cosmological region \(\mathcal {R}_5\), we define
We will also use the following notation:

Suppose that \(\phi \) satisfies the Klein–Gordon equation \(\square _g\phi -m^2 \phi =0\). Recall that the energy–momentum tensor associated with \(\phi \) is given by
Thus,

Define \( X:=\frac{V^{\frac{1}{2}}}{r^{n-1}} N=\frac{V^{\frac{1}{2}}}{r^{n-1}} V^{\frac{1}{2}}\frac{\partial }{\partial r}=\frac{V}{r^{n-1}}\frac{\partial }{\partial r}. \) We define the energy

4.2 The Auxiliary Function \(\psi \) and Its PDE
The Klein–Gordon equation \(\square _g\phi -m^2\phi =0\) can be rewritten as:

This becomes

that is,

Define \( \psi :=r^{\kappa }\phi , \) where
Then, using the PDE for \(\phi \), it can be shown that

where \(\displaystyle \theta :=\frac{m^2}{V}+\frac{\kappa }{r}\Big (\frac{1}{r}-\frac{V'}{V}\Big )-\frac{\kappa }{r^2} (n-1-\kappa ). \)
4.3 The Case \(|m|>\frac{n}{2}\)
Then, \(\kappa =\frac{n}{2}\), and (10) becomes

where
We will use an energy function to obtain the required decay of \(\psi \) for large r, and in order to do so, we will need to keep careful track of the limiting behaviour of the various functions appearing in the expression for \(\theta \) and the coefficients of the PDE (11). We will do this step-by-step in a sequence of lemmas.
Lemma 4.3
Given any \(\epsilon >0\), there exists an \(r_0\) large enough so that for all \(r\geqslant r_0\),
Proof
This follows immediately from
\(\square \)
Lemma 4.4
There exists \(r_0\) large enough so that for \(r\geqslant r_0\), we have \(\theta >0\).
(We note that the proof uses the fact that \(|m|>\frac{n}{2}\), and so this result is specific to this subsection.)
Proof
As \(\displaystyle \lim _{r\rightarrow \infty }\frac{r^2}{V}\!=\!\lim _{r\rightarrow \infty }\frac{1}{1\!+\!\frac{2M}{r^n}\!-\!\frac{e^2}{r^{n+1}}\!-\!\frac{1}{r^2}}\!=\!1, \) there exists a \(r_0'\) such that
for \(r\geqslant r_0'\). Also, by the previous lemma, there exists a \(r_0>r_0'\) such that \( \frac{V'}{V}\leqslant \frac{2+\epsilon }{r} \) for all \(r\geqslant r_0\). Then, we have for \(r>r_0\) that
where \( \delta :=m^2-\frac{n^2}{4}>0. \)
Taking \(\epsilon \) at the outset small enough so as to satisfy \( 0<\epsilon <\frac{\delta }{\delta +\frac{n}{2}+\frac{n^2}{4}}, \) we see that \(\theta >0\) for \(r\geqslant r_0\). \(\square \)
Define the energy

(We assume for the moment that this is finite for a sufficiently large \(r_0\). Later on, in the subsection on redshift estimates, we will see how our initial finiteness of Sobolev norms of \(\phi \) on the two branches \(\mathcal {C}\mathcal {H}_1^+\), \(\mathcal {C}\mathcal {H}_2^+\) of the cosmological horizon guarantees this.)
We now proceed to find an expression for \(\mathcal {E}'(r)\), and to simplify it, we will use (11), and the divergence theorem, to get rid of the terms involving \(\ddot{\psi }\) and  , the spherical Laplacian of \(\psi \):
, the spherical Laplacian of \(\psi \):

We note that in the above, getting rid of the spherical Laplacian by using the divergence theorem is allowed because the compact sphere \(S^{n-1}\) has no boundary. For the second time derivative, however, there is a boundary at infinity (with two connected components), namely
which can be seen to be equal to 0, by Lemma 7.3 from ‘Appendix B’.
Thus,

Let \(\epsilon >0\) be given. Then, there exists an \(r_0\) large enough such that:
-
(a)
\(\displaystyle \frac{V'}{V}-\frac{1}{r}\geqslant \frac{2-\epsilon }{r}-\frac{1}{r}=\frac{1-\epsilon }{r}\),
-
(b)
\(\displaystyle \Big (\frac{1}{V^2}\Big )'=-2\frac{V'}{V}\frac{1}{V^2}\leqslant -2\frac{(2-\epsilon )}{r}\frac{1}{V^2}\),
-
(c)
\(\displaystyle \Big (\frac{1}{r^2V}\Big )'=-\frac{1}{r^2V}\Big (\frac{2}{r}+\frac{V'}{V}\Big )\leqslant -\frac{1}{r^2V}\Big (\frac{2}{r}+\frac{2-\epsilon }{r}\Big )=-\frac{1}{r^2 V} \frac{(4-\epsilon )}{r}\),
-
(d)
\(\displaystyle \frac{\theta '}{\theta }\! =\!\frac{1}{r} \Big ( \frac{ -\frac{n}{2}(\frac{n}{2}-1)(-2)\!-\frac{m^2V'}{r^3 V^2} \!-\frac{n}{2r^5}(\frac{1}{r}-\frac{V'}{V}) +\frac{n}{2r^4}(-\frac{1}{r^2}-\frac{V''V-V'^2}{V^2}) }{ -\frac{n}{2}(\frac{n}{2}-1)+\frac{m^2}{r^2 V} +\frac{n}{2r^3}(\frac{1}{r}-\frac{V'}{V}) } \Big )\)
\(\displaystyle \leqslant \frac{1}{r}(-2+\epsilon ).\)
Hence, using (a)–(d) above, we obtain

Using Grönwall’s inequality (see e.g. [12, Appendix 7(j)]), we obtain
Thus, \(\displaystyle \int _{\mathbb {R}\times S^{n-1}} \theta \psi ^2 \mathrm{d}t \mathrm{d}\Omega \;\leqslant \; 2\mathcal {E}(r) \;\lesssim \; r^{-2+2\epsilon }, \) and so
Hence, \( \Vert \psi (r,\cdot )\Vert _{L^2(\mathbb {R}\times S^{n-1})} \lesssim r^\epsilon . \) Consequently,
Recall that \(S^{n-1}\) admits \(\frac{n(n-1)}{2}\) independent Killing vectors, given by
for \(i<j\) (under the usual embedding \(S^{n-1}\subset \mathbb {R}^n\)). As \(\frac{\partial }{\partial t}\) and \(L_{ij}\) are Killing vector fields, it follows that \(\dot{\phi }\) and \(L_{ij}\cdot \phi \) are also solutions to \(\square _g \phi -m^2 \phi =0\). Commuting with the Killing vector fields \(\frac{\partial }{\partial t}\) and \(L_{ij}\), if we assume at the momentFootnote 6 that at \(r_0\) we have \( \Vert \phi (r_0,\cdot )\Vert _{H^k(\{r=r_0\})} <+\infty , \) then we also obtain for all \(r\geqslant r_0\) that \( \Vert \phi (r,\cdot )\Vert _{H^{k'}(\mathbb {R}\times S^{n-1})} \lesssim r^{-\frac{n}{2}+\epsilon }, \) where \(k'=k-2>\frac{n}{2}\). By the Sobolev inequality,Footnote 7\( \Vert \phi (r,\cdot )\Vert _{L^\infty (\mathbb {R}\times S^{n-1})} \lesssim r^{-\frac{n}{2}+\epsilon }. \)
This completes the proof of Theorem 4.2 in the case when \(|m|>\frac{n}{2}\) (provided we show the aforementioned finiteness of energy, which will be carried out in Sect. 4.5 on redshift estimates).
4.4 The Case \(|m|\leqslant \frac{n}{2}\)
Let \(\epsilon '>0\) be given. Define

We now proceed to find an expression for \(\widetilde{\mathcal {E}}'(r)\), and we will simplify it using (10) and the divergence theorem, in order to get rid of the terms involving \(\ddot{\psi }\) and the spherical Laplacian of \(\psi \):

Again, for getting rid of the spherical Laplacian, we use the divergence theorem, noting that the sphere \(S^{n-1}\) has no boundary. For handling the second time derivative, as before, we note that there is a boundary at infinity (with two connected components), which can be seen to be equal to 0, by Lemma 7.3 from Appendix B (Section 7). Thus,

Now, there exists an \(r_0\) large enough such that for all \(r\geqslant r_0\), we have:
-
(i)
 , using \(n\!-\!2\kappa \!\geqslant \!0\).
, using \(n\!-\!2\kappa \!\geqslant \!0\). -
(ii)
 .
. -
(iii)
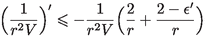 .
.
Using (i), (ii) and (iii), it can be seen that

Hence, \(\displaystyle \widetilde{\mathcal {E}}'(r)\leqslant -\frac{2(1-\epsilon ')}{r}\widetilde{\mathcal {E}}(r)+\Big ( \frac{\epsilon '}{r^2}-\theta \Big )\int _{\mathbb {R}\times S^{n-1}} \psi \psi ' \mathrm{d}t \mathrm{d}\Omega . \) We have
As \(\displaystyle \frac{V}{r^2}{\mathop {\longrightarrow }\limits ^{r\rightarrow \infty }} 1\) and \(\displaystyle \frac{V'}{V}r{\mathop {\longrightarrow }\limits ^{r\rightarrow \infty }} 2\), it follows that
Thus, given \(\epsilon '>0\), there exists an \(r_0\) large enough such that for \(r\geqslant r_0\), \(|r^2\theta |<\epsilon '\), that is, \( |\theta |<\frac{\epsilon '}{r^2}. \) So
The Cauchy–Schwarz inequality applied to the last integral gives
So we obtain
Application of Grönwall’s inequality yields
So
Thus, \(\displaystyle \Vert \psi (r,\cdot )\Vert _{L^2(\mathbb {R}\times S^{n-1})} \leqslant \sqrt{\frac{2\widetilde{\mathcal {E}}(r_0)}{\epsilon '}} \frac{1}{r_0^{-1+\epsilon '+2\sqrt{\epsilon '}}} r^{\epsilon '+2\sqrt{\epsilon '}}, \) and so
Given \(\epsilon >0\), arbitrarily small, we can choose \(\epsilon '=\epsilon '(\epsilon )>0\) small enough so that \(\epsilon '+2\sqrt{\epsilon '}<\epsilon \) at the outset, so that \( \Vert \phi (r,\cdot )\Vert _{L^2(\mathbb {R}\times S^{n-1})} \lesssim r^{-\kappa +\epsilon }. \) Again assuming at the moment that at \(r_0\) we have \( \Vert \phi (r_0,\cdot )\Vert _{H^k(\{r=r_0\})} <+\infty , \) and by commuting with the Killing vector fields \(\frac{\partial }{\partial t}\) and \(L_{ij}\), then we also obtain for all \(r\geqslant r_0\) that
where \(k'=k-2>\frac{n}{2}\). By the Sobolev inequality, this yields
This completes the proof of Theorem 4.2 in the case when \(|m|\leqslant \frac{n}{2}\) (provided we show the finiteness of energy, which will be carried out in the subsection on redshift estimates below).
4.5 Redshift Estimates
The last step is to use redshift estimates to transfer finiteness of the energies along the branches \(\mathcal {C}\mathcal {H}_1^+\) and \(\mathcal {C}\mathcal {H}_2^+\) of the cosmological horizon to finiteness at \(r=r_0\), justifying the finiteness of the energies \(\mathcal {E}(r_0)\) and \(\widetilde{\mathcal {E}}(r_0)\) assumed in the previous two subsections. Here, we do not include all the details of the computations, since they are analogous to the corresponding estimates given in [8, §3.6], and the interested reader can also find the details for our case spelt out in the arxiv version of our paper [19].
Define \(\displaystyle u:=t+\int _{r_*}^r \frac{1}{V} \mathrm{d}r, \) where \(r_*>r_c\) is arbitrary, but fixed. Then,
The Reissner–Nordström–de Sitter metric can be rewritten using the coordinates \((u,r,\ldots )\), instead of the old \((t,r,\ldots )\)-coordinates, as follows:
This new coordinate system \((u,r,\ldots )\) extends across the cosmological horizon \(r=r_c\) (where \(V=0\)). The hypersurfaces of constant u are null and transverse to the cosmological horizon. Thus, only one of the branches of the cosmological horizon, namely \(\mathcal {C}\mathcal {H}_1^+\), is covered by the \((u,r,\ldots )\)-coordinates. (In order to cover the other branch \(\mathcal {C}\mathcal {H}_2^+\), where \(u=-\infty \), we can introduce
and use the \((v,r,\ldots )\)-coordinate chart.) We will only consider \(\mathcal {C}\mathcal {H}_1^+\) in the remainder of this subsection, since \(\mathcal {C}\mathcal {H}_2^+\) can be treated analogously.

The Killing vector field \(K=\frac{\partial }{\partial u}=\frac{\partial }{\partial t} \) is well defined across \(\mathcal {C}\mathcal {H}_1^+\) and is null on the cosmological horizon \(\mathcal {C}\mathcal {H}_1^+\), even though the t-coordinate is not defined there. Consider the vector field in the \((u,r,\ldots )\)-coordinate chart, \( Y=( \frac{\partial }{\partial r})_{u}. \) The subscript u means that the integral curves of Y in the \((u,r,\ldots )\)-coordinate chart have a constant u-coordinate. Then, \(du(Y)=0\) and \(dr(Y)=1\). In the \((t,r,\ldots )\)-coordinate chart, Y can be expressed as \( Y=\frac{\partial }{\partial r}-\frac{1}{V}\frac{\partial }{\partial t}. \) Let the vector field X be defined by \( X=\frac{V^{\frac{1}{2}}}{r^{n-1}}N=\frac{V}{r^{n-1}}\frac{\partial }{\partial r} \) in the old \((t,r,\ldots )\)-coordinate chart. To find the expression for X in the \((u,r,\ldots )\)-coordinate chart induced basis vectors, we first find \( N=-\frac{\text {grad }r}{|\text {grad }r|} \) in the \((u,r,\ldots )\)-coordinate chart induced basis vectors. If \(\omega :=-\frac{1}{\sqrt{V}} dr\), then \( N=g^{\mu \nu } \omega _\nu = \frac{1}{\sqrt{V}} \Big ( \frac{\partial }{\partial u}+V\frac{\partial }{\partial r}\Big ). \) So \( X=\frac{\sqrt{V}}{r^{n-1}} N=\frac{1}{r^{n-1}}(\frac{\partial }{\partial u}+V\frac{\partial }{\partial r}). \) The energy

(since \(V(r_c)=0\)). So E(r) ‘loses control’ of the transverse and angular derivatives as \(r\rightarrow r_c\). To remedy this problem, we define a new energy \(\widetilde{E}\), by adding Y to X, obtaining
In \((t,r,\ldots )\)-coordinates, \(N=\sqrt{V}\;\!\partial _r\). So \( T(Y,N) =\frac{1}{\sqrt{V}}(T(N,N)-T(\partial _t,\partial _r)). \) We have \( T(\partial _t,\partial _r)=\dot{\phi }\;\!\phi '. \) So

We now have

so that using \(\widetilde{E}\) instead of E allows some control of the angular derivatives as \(r\rightarrow r_c\). Note that \(\widetilde{E}(r_c)\) is equivalent to \( \Vert \phi \Vert ^2_{H^1(\mathcal {C}\mathcal {H}_1^+)} +\Vert \phi \Vert ^2_{H^1(\mathcal {C}\mathcal {H}_2^+)}. \) We will now compute the deformation tensor \(\Xi \) corresponding to the multiplier Y. We have \([-\frac{1}{V} \partial _t,\partial _r]=-\frac{V'}{V} \partial _t\), \( \mathcal {L}_{\partial _r} g = \frac{V'}{V} dr^2 +V'dt^2+2rd\Omega ^2\), and \( \mathcal {L}_{-\frac{1}{V}\partial _t} g =2V dt \;(- \frac{V'}{V^2}) dr\). Hence, \(\Xi = \frac{1}{2} \mathcal {L}_Y g=\frac{1}{2} V' du^2 +r d\Omega ^2\). We have \( du=-g(Y,\cdot ). \) Also, we recall that \(T_{\mu \nu } = \partial _\mu \phi \partial _\nu \phi -\frac{g_{\mu \nu }}{2}(\partial _\alpha \phi \partial ^\alpha \phi +m^2\phi ^2) \),

We have  Combining (12) and the above, we obtain
Combining (12) and the above, we obtain

Now as \(V'(r)> 0\) for \(r\geqslant r_c\) (global redshift), it follows that the first summand in the last expression is nonnegative, and so we obtain the inequality

Now suppose that \(r_0\) is fixed. As \(r^2 V'(r)>0\) for all \(r\in [r_c,r_0]\), we have \( \min \limits _{r\in [r_c,r_0]}r^2 V'(r)>0. \) Thus, \( -\frac{(n-1)^2}{2r^2 V'}\geqslant -\frac{(n-1)^2}{\min \limits _{r\in [r_c,r_0]}r^2 V'(r)} =:-C_1(r_0). \) Similarly, for \(r\in [r_c,r_0]\), \(\displaystyle \frac{1}{r^3}\leqslant \frac{1}{r_c^3}\), and so \( -\frac{n-3}{2r^3} \geqslant -\frac{n-3}{2r_c^3} =:-\widetilde{C}_2(r_c). \) Also, for \(r\in [r_c,r_0]\), \( -\frac{(n-1)}{2r}m^2 \geqslant -\frac{(n-1)}{2r_c}m^2 =:-C_3(r_c). \) If we set \( \Pi :=\frac{1}{2}\mathcal {L}_X g, \) then from Step 1 of the proof of Theorem 5.3 (see in particular the inequality (17) on page 35), we have for \(r>r_c\) that

Set \(C_2(r_c):=\widetilde{C}_2(r_c)+\widetilde{\widetilde{C}}_2(r_c)\). We have

For \(r_1\in (r_c,r_0)\), and \(T>0\), define \( \mathcal {D}=\{r=r_1\}\;\!\cap \;\! \{-T\leqslant t\leqslant T\}. \) We now apply the divergence theorem, with the current J corresponding to the multiplier \(X+Y\), in the region \( \mathcal {T}=D^+(\mathcal {D})\;\! \cap \;\! \{r\leqslant r_0\}. \) Noticing that the flux across the future null boundaries is less than or equal to 0, we obtain, after passing the limit \(T\rightarrow \infty \), that

But

We have

Using the above three estimates, it follows from (14) that
where \( k(r_0,r_c):=C(r_0,r_c)( 2r_0^{n-1}+2r_0^2+\frac{2}{m^2}). \) Now suppose \(r_2\) is such that \( r_c<r_1<r_2<r_0. \) If we redo all of the above steps in order to obtain (15), but with \(r_2\) replacing \(r_0\), we obtain
where \( k(r_2,r_c)=C(r_2,r_c)( 2r_2^{n-1}+2r_2^2+\frac{2}{m^2}). \) But
As \( C_1(r_2)\!=\!\frac{(n-1)^2}{\min \limits _{r\in [r_c,r_2]}r^2 V'(r)} \!\leqslant \! \frac{(n-1)^2}{\min \limits _{r\in [r_c,r_0]}r^2 V'(r)}\!=\!C_1(r_0), \) \(k(r_2,r_c)\leqslant k(r_0,r_c)\). From (16), we get
Consequently, for all \(r_2\in [r_1,r_0)\), \(\displaystyle \widetilde{E}(r_2)\leqslant \widetilde{E}(r_1)+\int _{r_1}^{r_2} k(r_0,r_c) \widetilde{E}(r) \mathrm{d}r \). By the integral form of Grönwall’s inequality (see e.g. [24, Thm. 1.10]), we obtain for all \(r_2\in [r_1,r_0)\) that
As \(r_2\nearrow r_0\), we get \( \widetilde{E}(r_0) \leqslant \widetilde{E}(r_1)e^{ k(r_0,r_c)\cdot (r_0-r_1)}. \) This holds for all \(r_1\in (r_c, r_0)\). Passing the limit as \(r_1\searrow r_c\), we obtain \( \widetilde{E}(r_0)\leqslant \widetilde{E}(r_c)e^{ k(r_0,r_c)\cdot (r_0-r_c)}. \) So 
Commuting with the Killing vector fields \(\frac{\partial }{\partial t}\) and \(L_{ij}\), we see that the hypothesis from Theorem 4.2, namely \( \Vert \phi \Vert _{H^k(\mathcal {C}\mathcal {H}_1^+)}<+\infty \) and \(\Vert \phi \Vert _{H^k(\mathcal {C}\mathcal {H}_2^+)}<+\infty , \) for some \(k>\frac{n}{2}+2\), yields also \( \Vert \phi \Vert _{H^k(\{r=r_0\})}\lesssim \Vert \phi \Vert _{H^k(\mathcal {C}\mathcal {H}_1^+)}+\Vert \phi \Vert _{H^k(\mathcal {C}\mathcal {H}_2^+)}<+\infty . \) We now show that this justifies the assumption used in the previous two subsections. For simplicity, we only consider just one of the energies

(The proof of the finiteness of \(\widetilde{\mathcal {E}}(r_0)\) is entirely analogous.) As \(\psi =r^{\kappa } \phi \), we obtain finiteness of the last summand, namely
We have \( \displaystyle \int _{\mathbb {R}\times S^{n-1}} \left( \phi '(r_0,\cdot )\right) ^2 \mathrm{d}t \mathrm{d}\Omega \leqslant \frac{2E(r_0)}{(V(r_0))^2} <+\infty .\)
Since \(\psi '(r_0,\cdot )=\kappa r_0^{\kappa -1} \phi (r_0,\cdot )+r_0^\kappa \phi '(r_0,\cdot )\), and as \(\phi (r_0,\cdot )\in H^1(\{r=r_0\})\), we have \(\psi (r_0,\cdot )\in L^2(\mathbb {R}\times S^{n-1})\), that is, \( \displaystyle \int _{\mathbb {R}\times S^{n-1}} \left( \psi '(r_0,\cdot )\right) ^2 \mathrm{d}t\mathrm{d}\Omega <+\infty . \)
We also have
Finally,

Thus, each summand in the expression for \(\mathcal {E}(r_0)\) is finite. This completes the proof of Theorem 4.2.
5 Decay in \(\mathrm {RNdS}\) When \(m=0\), the Wave Equation
In [8, Theorem 2], the following result was shown:
Theorem 5.1
Suppose that
-
\(\delta >0\),
-
\(M>0\),
-
\(e\geqslant 0\),
-
\(n> 2\),
-
(M, g) is the \((n+1)\)-dimensional subextremal Reissner–Nordström–de Sitter solution given by the metric
$$\begin{aligned} g=-\frac{1}{V} dr^2+Vdt^2 +r^2 d\Omega ^2, \end{aligned}$$where
$$\begin{aligned} V= r^2+\frac{2M}{r^{n-2}} -\frac{e^2}{r^{n-1}}-1, \end{aligned}$$and \(d\Omega ^2\) is the metric of the unit \((n-1)\)-dimensional sphere \(S^{n-1}\),
-
\(k>\frac{n}{2}+2\), and
-
\(\phi \) is a smooth solution to \(\square _g \phi =0\) such that
$$\begin{aligned} \Vert \phi \Vert _{H^{k}(\mathcal {C}\mathcal {H}_1^+)}<+\infty \;\;\;\text { and }\;\;\;\Vert \phi \Vert _{H^{k}(\mathcal {C}\mathcal {H}_2^+)}<+\infty , \end{aligned}$$where \(\mathcal {C}\mathcal {H}_1^+\simeq \mathcal {C}\mathcal {H}_2^+\simeq \mathbb {R}\times S^{n-1}\) are the two components of the future cosmological horizon, parameterised by the flow parameter of the global Killing vector field \(\frac{\partial }{\partial t}\).
Then, there exists a \(r_0\) large enough so that for all \(r\geqslant r_0\),
Using a method similar to the one we used to show Rendall’s conjecture in Theorem 2.3, we can improve the almost-exact bound of \(r^{-3+\delta }\) to \(r^{-3}\).
Remark 5.2
As observed in [8, Remark 1.4], this decay rate bound of \(r^{-3}\) for \(\partial _r \phi \) is in fact the decay rate one would expect in the light of Rendall’s conjecture. Indeed, for freely falling observers in the cosmological region, one has
where \(\tau \) is the proper time, and \(a(\tau )\) is the radius of a comparable de Sitter universe in flat FLRW form, giving
Thus, our improved version of Theorem 5.1 is the following result.
Theorem 5.3
Suppose that
-
\(M>0\),
-
\(e\geqslant 0\),
-
\(n> 2\),
-
(M, g) is the \((n+1)\)-dimensional subextremal Reissner–Nordström–de Sitter solution given by the metric
$$\begin{aligned} g=-\frac{1}{V} dr^2+Vdt^2 +r^2 d\Omega ^2, \end{aligned}$$where
$$\begin{aligned} V= r^2+\frac{2M}{r^{n-2}} -\frac{e^2}{r^{n-1}}-1, \end{aligned}$$and \(d\Omega ^2\) is the metric of the unit \((n-1)\)-dimensional sphere \(S^{n-1}\),
-
\(k>\frac{n}{2}+2\), and
-
\(\phi \) is a smooth solution to \(\square _g \phi =0\) such that
$$\begin{aligned} \Vert \phi \Vert _{H^{k}(\mathcal {C}\mathcal {H}_1^+)}<+\infty \;\;\;\text { and }\;\;\;\Vert \phi \Vert _{H^{k}(\mathcal {C}\mathcal {H}_2^+)}<+\infty , \end{aligned}$$where \(\mathcal {C}\mathcal {H}_1^+\simeq \mathcal {C}\mathcal {H}_2^+\simeq \mathbb {R}\times S^{n-1}\) are the two components of the future cosmological horizon, parameterised by the flow parameter of the global Killing vector field \(\frac{\partial }{\partial t}\).
Then, there exists a \(r_0\) large enough so that for all \(r\geqslant r_0\),
Proof
Step 1: We will first establish the following estimates: there exists an \(r_0\) large enough such that for all \(r\geqslant r_0\),

We will follow [8, §3.2] in order to obtain the bounds above, which will be needed in Step 2 of our proof below. We repeat this preliminary step here from [8, §3.2] for the sake of completeness and for the convenience of the reader.
Suppose \(\phi \) satisfies the wave equation \(\square _g\phi =0\). The energy–momentum tensor associated with \(\phi \) is given by \( T_{\mu \nu }=\partial _\mu \phi \partial _\nu \phi -\frac{1}{2} g_{\mu \nu } \partial _\alpha \partial ^\alpha \phi . \) Thus,

Define \(\displaystyle X:=\frac{V^{\frac{1}{2}}}{r^{n-1}} N=\frac{V^{\frac{1}{2}}}{r^{n-1}} V^{\frac{1}{2}}\frac{\partial }{\partial r}=\frac{V}{r^{n-1}}\frac{\partial }{\partial r}. \)
The current J is given by \( J_\mu :=T_{\mu \nu } X^\nu . \) We define the energy

The deformation tensor \(\Pi \) associated with the multiplier X is given by
It can be shown that \(\displaystyle \mathcal {L}_X dr =\Big (\frac{V'}{r^{n-1}}-\frac{(n-1) V}{r^n} \Big )dr. \) Thus,
We have

Also,  Finally,
Finally,

Consequently, the full bulk term is

Using the expression for V, we compute
For \(r>r_c\), we have \(V(r)>0\), and so
Hence,

For each \(T<0\), define the set \( \mathcal {C}:=\{r=r_0\} \;\! \cap \;\! \{-T\leqslant t\leqslant T\}. \) Also, consider the region \( \mathcal {S}:=D^+(\mathcal {C})\;\!\cap \;\! \{r\leqslant r_1\}. \)

We will apply the divergence theorem to the current J on the region \(\mathcal {S}\). As the flux across the future null boundaries is nonpositive, we have

So  We have
We have

Since
there exists an \(r_0\) large enough such that for all \(r\geqslant r_0\), \(|\frac{2r^2}{V}-2|<1\), and in particular, \( (0<) \frac{2r^2}{V}<3. \) Hence,

Using Grönwall’s inequality (see for e.g. [24, Thm. 1.10]), we obtain
as was also noted in [8, Eq.(71)]. Thus, we have in particular that there exists an \(r_0\) large enough such that for all \(r\geqslant r_0\),

Commuting with the Killing vector fields \(\frac{\partial }{\partial t}\) and \(L_{ij}\), we obtain (after the transferral of the finiteness of the energies along the branches \(\mathcal {C}\mathcal {H}_1^+\) and \(\mathcal {C}\mathcal {H}_2^+\) of the cosmological horizon to finiteness at \(r=r_0\), and an application of Sobolev’s inequality) that for all \(r\geqslant r_0\),

Step 2: In this step, we will write the wave equation in new coordinates which ‘equalises’ the magnitude of the coefficient weights for the r and t coordinates in the matrix of the metric.
To this end, we define \(\displaystyle \rho = \int _{r_0}^r \frac{1}{V(r)} \mathrm{d}r. \) Then, \( \displaystyle \frac{\mathrm{d}\rho }{\mathrm{d}r}=\frac{1}{V(r)}\text { and } V(r) \displaystyle \frac{\mathrm{d}}{\mathrm{d}r}=\frac{\mathrm{d}}{\mathrm{d}\rho }. \)
With a slight abuse of notation, we write \( V(\rho ):=V(r(\rho )). \) We have
The wave equation \(\square _g \phi =0\) can be rewritten as \(\partial _\mu (\sqrt{-g} \;\!\partial ^\mu \phi )=0\), which becomes \( \partial _\mu (Vr^{n-1} \partial ^\mu \phi )=0. \) Separating the differential operators with respect to the \(\rho ,t,\ldots \) coordinates, we obtain

Integrating from \(\rho _0:=\rho (r_0)=0\) to \(\rho =\rho (r)\), we obtain

and so  i.e.,
i.e.,

Hence,

Using the fact that \(V\sim r^2\) for \(r\geqslant r_0\), with \(r_0\) large enough, and the estimates from Step 1 above, we obtain
Recalling that \(n>2\), we have
This completes the proof of Theorem 5.3. \(\square \)
Notes
That is, \(\dot{c}\) is future-pointing.
We note that to reach this conclusion, we used Lemma 7.1, for which we need \(\dot{\psi }(t,\cdot ), \nabla \psi (t,\cdot )\in H^1(\mathbb {R}^n)\), which means that the initial conditions for \(\phi \) must be such that \(\phi _0\in H^2(\mathbb {R}^n)\) and \(\phi _1 \in H^1(\mathbb {R}^n)\).
Note that in order to use the estimate (8), for \(D\phi :=(\partial _{x^1})^{i_1}\cdots (\partial _{x^n})^{i_{n}}\phi \) replacing \(\phi \), where \(|(i_1,\ldots ,i_n)|=:k'\), we must ensure that the initial conditions for \(D\phi \), namely \((D \phi (t_0,\cdot ),D\dot{\phi }(t_0,\cdot ))\), are in \( (H^2(\mathbb {R}^n), H^1(\mathbb {R}^n))\), which is guaranteed if the initial condition for \(\phi \), namely \((\phi _0,\phi _1)\), is in \( (H^k(\mathbb {R}^n), H^{k-1}(\mathbb {R}^n))\), with \(k-k'=2\).
We note that there is no solution analogous to RNdS but with only one black hole. This is analogous to (but much more complicated than, and still not fully understood) the fact that one cannot have a single electric charge on a spherical universe. (Gauss’s law requires that the total charge must be zero.) In fact, the fundamental solution of the Laplace equation on the sphere gives a unit positive charge at some point and a unit negative charge at the antipodal point. One can have more than two black holes, for instance the so-called Kastor–Traschen solution [17].
‘Spherical’ here means that the Cauchy hypersurface (that is, ‘space’) is an n-sphere.
This will be proved later in the subsection on redshift estimates.
References
Abramowitz, M., Stegun, I.: Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Volume 55 in the National Bureau of Standards Applied Mathematics Series, Superintendent of Documents, U.S. Government Printing Office (1964)
Alinhac, S.: Geometric Analysis of Hyperbolic Differential Equations: An Introduction. London Mathematical Society Lecture Note Series, vol. 374. Cambridge University Press, Cambridge (2010)
Andréasson, H., Ringström, H.: Proof of the cosmic no-hair conjecture in the \({\mathbb{T}}^3\)-Gowdy symmetric Einstein–Vlasov setting. J. Eur. Math. Soc. 18(7), 1565–1650 (2016)
Aubin, T.: Nonlinear Analysis on Manifolds. Monge-Ampère equations, vol. 252, Grundlehren der Mathematischen Wissenschaften. Springer (1982)
Bär, C., Ginoux, N., Pfäffle, F.: Wave Equations on Lorentzian Manifolds and Quantization. ESI Lectures in Mathematics and Physics. European Mathematical Society (2007)
Costa, J., Girão, P., Natário, J., Silva, J.: On the global uniqueness for the Einstein–Maxwell-Scalar field system with a cosmological constant: part 3. Mass inflation and extendibility of the solutions. Ann. PDE. Journal Dedicated to the Analysis of Problems from Physical Sciences, vol. 3, Paper No. 8, 55, no. 1 (2017)
Costa, J., Natário, J., Oliveira, P.: Cosmic no-hair in spherically symmetric black hole spacetimes. Ann. Henri Poincaré, Online first, July 2019. https://doi.org/10.1007/s00023-019-00825-z
Costa, J., Natário, J., Oliveira, P.: Decay of solutions of the wave equation in expanding cosmological spacetimes. J. Hyperbol. Differ. Equ. 16(1), 35–58 (2019)
Dafermos, M., Rodnianski, I.: Lectures on Black Holes and Linear Waves. In Evolution Equations, Clay Math. Proc. 17:97–205. American Mathematical Society (2013)
Dafermos, M., Rodnianski, I.: The wave equation on Schwarzschild–de Sitter spacetimes. arXiv:0709.2766
Ebert, M., Reissig, M.: Regularity theory and global existence of small data solutions to semi-linear de Sitter models with power non-linearity. arXiv:1703.09838
Evans, L.: Partial Differential Equations, vol. 19, Graduate Studies in Mathematics. American Mathematical Society (1998)
Gajic, D.: Linear waves on constant radius limits of cosmological black hole spacetimes. Adv. Theor. Math. Phys. 22(4), 919–1005 (2018)
Gilbarg, D., Trudinger, N.: Elliptic Partial Differential Equations of Second Order. Springer, Berlin (2001)
Grisvard, P.: Elliptic Problems in Nonsmooth Domains, vol. 24. Monographs and Studies in Mathematics. Pitman (1985)
Hebey, E.: Nonlinear Analysis on Manifolds: Sobolev Spaces and Inequalities, vol. 5. Courant Lecture Notes in Mathematics. American Mathematical Society (1999)
Kastor, D., Traschen, J.: Cosmological multi-black-hole solutions. Phys. Rev. D (3) 47(12), 5370–5375 (1993)
Natário, J.: An Introduction to Mathematical Relativity. Latin American Mathematics Series. Springer, Berlin (2021)
Natário, J., Sasane, A.: Decay of solutions to the Klein–Gordon equation on some expanding cosmological spacetimes. arxiv.org/abs/1909.01292
Rendall, A.: Asymptotics of solutions of the Einstein equations with positive cosmological constant. Ann. Henri Poincaré 5(6), 1041–1064 (2004)
Ringström, H.: A unified approach to the Klein–Gordon equation on Bianchi backgrounds. arXiv:1808.00786
Ringström, H.: Linear systems of wave equations on cosmological backgrounds with convergent asymptotics. arXiv:1707.02803
Schlue, V.: Global results for linear waves on expanding Kerr and Schwarzschild de Sitter cosmologies. Commun. Math. Phys. 3344(0), 977–1023 (2015)
Tao, T.: Nonlinear Dispersive Equations. Local and Global Analysis, vol. 106. CBMS Regional Conference Series in Mathematics. American Mathematical Society (2006)
Taylor, M.: Partial Differential Equations I. Basic Theory, vol. 115. Applied Mathematical Sciences. Springer (2011)
Vasy, A.: The wave equation on asymptotically de Sitter-like spaces. Adv. Math. 223, 49–97 (2010)
Wald, R.: General Relativity. University of Chicago Press, Chicago (1984)
Watson, G.: A Treatise on the Theory of Bessel Functions. Cambridge University Press, Cambridge (1944)
Acknowledgements
We thank Pedro Girão for suggesting the idea behind the proofs of Theorems 2.2 and 5.3. JN was partially supported by FCT/Portugal through UIDP/MAT/04459/2020, UID/MAT/04459/2013 and Grant (GPSEinstein) PTDC/MAT-ANA/1275/2014.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Mihalis Dafermos.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Fourier Modes (de Sitter in Flat FLRW Form)
In this appendix, we outline the Fourier modal analysis that motivates the specific estimates given in Theorem 3.1, starting with spatially periodic solutions to the Klein–Gordon equation. We only give highlights, since the computations are similar to the ones in [8], and moreover, the details can be found in the arxiv version of our paper [19].
Let \(\mathbb {T}^n=\mathbb {R}^n/(2\pi \mathbb {Z})^n\). Suppose that the ‘spatially periodic’ \(\phi :\mathbb {R}\times \mathbb {T}^n\rightarrow \mathbb {R}\) satisfies the Klein–Gordon equation (5). Writing
(5) yields \( \ddot{c}_{\mathbf {k}}+\frac{n\dot{a}}{a}\dot{c}_\mathbf {k}+\frac{k^2}{a^2} c_{\mathbf {k}}+m^2c_{\mathbf {k}}=0, \) where \( k^2:=\langle \mathbf {k},\mathbf {k}\rangle . \) So
Let \( \tau =\int \frac{1}{a(t)} \mathrm{d}t. \) Then, \( \frac{\mathrm{d}}{\mathrm{d}t}=\frac{1}{a} \frac{\mathrm{d}}{\mathrm{d}\tau }, \) and so (18) becomes (with \( \frac{\mathrm{d}}{\mathrm{d}\tau }=:^{\prime }\;\))
Defining \(d_\mathbf {k}\) by \( c_\mathbf {k}=: a^{-\frac{n-1}{2}} d_\mathbf {k}, \) we have
Now if \(a(t)=e^t\), then we may take \(\tau =-e^{-t}\), so that \(-t=\log (-\tau )\), that is, \(-\tau =e^{-t}\). We remark that relative to our earlier use of conformal coordinates in (4) on page 10, we are taking \(t_0=+\infty \) for simplicity. Then, (20) becomes
where \( \mu :=n-1+\frac{(n-1)(n-3)}{4}-m^2. \) The general solution to this equation isFootnote 8 given by
where \(\nu \) satisfies \( \nu ^2=\frac{1}{4}+\mu =\frac{n^2}{4}-m^2. \) Here, \(J_\nu \) denotes the Bessel function of the first kind,
and \(Y_\nu \) is the Bessel function of the second kind,
where the right-hand side is replaced by its limiting value if \(\nu \) is an integer. Without loss of generality, in the solution (22), we may only consider \(\nu \) such that \(\text {Re}(\nu )\geqslant 0\).
We note that as \(t\rightarrow \infty \), \(-\tau =e^{-t}\searrow 0\), and so \(\tau \nearrow 0\). We now use the asymptotic expansions of \(J_\nu (z)\) and \(Y_\nu (z)\) as \(z\nearrow 0\) (see e.g. [1, 9.1.7–9]):
- \(\underline{1}^\circ \):
-
If \(\nu \ne 0\) (that is, \(m\ne \pm \frac{n}{2}\)), then as \(\tau \nearrow 0\), we have
$$\begin{aligned} J_\nu (|k|\tau )= & {} C(-\tau )^\nu +O(|\tau |),\\ Y_\nu (|k|\tau )= & {} A (-\tau )^\nu +B(-\tau )^{-\nu }+C(-\tau )^{2-\nu }+O(|\tau |). \end{aligned}$$Using these, as \(\tau \nearrow 0\) or \(t\rightarrow \infty \), \( |c_\mathbf {k}|= C'e^{-\left( \frac{n}{2}-\text {Re}(\nu )\right) t}+O(e^{-\frac{n+1}{2}t}). \) Thus, we expect \(\phi \) to satisfy
$$\begin{aligned} \Vert \phi (t,\cdot )\Vert _{L^\infty (\mathbb {R}^n)}\lesssim \left\{ \begin{array}{ll} a^{-\frac{n}{2}} &{} \text {if } \;|m|> \frac{n}{2},\\ a^{-\frac{n}{2}+\sqrt{\frac{n^2}{4}-m^2}} &{}\text {if }\;|m|<\frac{n}{2}. \end{array}\right. \end{aligned}$$ - \(\underline{2}^\circ \):
-
If \(\nu =0\) (that is, \(m=\pm \frac{n}{2}\)), then as \(\tau \nearrow 0\), we have
$$\begin{aligned} J_\nu (|k|\tau )= & {} C + O(|\tau |),\\ Y_\nu (|k|\tau )= & {} C\log (-\tau )+O(|\tau |). \end{aligned}$$Using these, we get \( |c_\mathbf {k}|=(A+Bt)e^{-\frac{n}{2} t}+O(e^{-\frac{n+1}{2}t}) \) as \(t\rightarrow +\infty \). Thus, we expect \(\phi \) to satisfy
$$\begin{aligned} \Vert \phi (t,\cdot )\Vert _{L^\infty (\mathbb {R}^n)}\lesssim a^{-\frac{n}{2}}\log a \;\;\text { if } \; m=\pm \frac{n}{2}. \end{aligned}$$
Summarising, \(\phi \) is expected to have the decay
This motivates the decay estimates in Theorem 3.1.
Appendix B
In this section, we prove the technical result we had used in the proof of Theorem 3.1, in Sect. 3.
Lemma 7.1
If \(f,g\in H^1(\mathbb {R}^n)\), then \(\displaystyle \lim _{r\rightarrow +\infty }\int _{S_r} fg \mathrm{d}\sigma _r=0. \)
Proof
By the Cauchy–Schwarz inequality,
and so, it is enough to show that
Suppose this does not hold. Then, there exists an increasing sequence \((r_k)_{k}\) such that \(r_k{\mathop {\longrightarrow }\limits ^{k\rightarrow \infty }}\infty \), and there exists an \(\epsilon >0\) such that for each k,
(The plan is to use the trace theorem to fatten these \(S_{r_k}\)-slices to ‘annuli’ \(A_k\) and obtain \(\Vert f\Vert _{H^1(A_k)}^2>\widetilde{\epsilon }>0\) for all k, giving the contradiction that
So we will construct a subsequence \((r_{k_m})_m\) of \((r_k)_k\) and a sequence \((\delta _m)_m\) of positive numbers such that \(r_{k_1}<r_{k_1}+\delta _1<r_{k_2}<r_{k_2}+\delta _2<r_{k_3}<\cdots \), and such that for the ‘annuli’ \(A_m:=\{\mathbf {x}: r_{k_m}<|\mathbf {x}|<r_{k_m}+\delta _m\}\), we have \(\Vert f\Vert _{H^1(A_m)}^2>\widetilde{\epsilon }\). We will need to keep track of the constants in the trace theorems on our annuli \(A_m\), and we will use the following [15, p. 41].) \(\square \)
Theorem 7.2
Let \(\Omega \) be a bounded open subset of \(\mathbb {R}^n\) with a Lipschitz boundary \(\Gamma \). Then, for \(f\in H^1(\Omega )\) and for all \(\epsilon \in (0,1)\),
where \(\varvec{\mu }\in C^1(\overline{\Omega },\mathbb {R}^n)\) is such that \(\varvec{\mu }\cdot \mathbf {n}\geqslant \delta \) on \(\partial \Omega \), and \(\mathbf {n}\) is the outer normal vector.
If \(\Omega \) is an annulus \(A=\{\mathbf {x}:r<\Vert \mathbf {x}\Vert <R\}\) (which is clearly bounded, open, and also it has the Lipschitz boundaries which are the two spheres \(S_r\) and \(S_R\)), then with \(\varvec{\mu }(\mathbf {x})=\mathbf {x}\), we have
Also, if we take \(\epsilon =1/4\), then
As \(\displaystyle \Vert \varvec{\mu }\Vert _{C^1(\overline{A})} =\max \limits _{\overline{A}} \Vert \varvec{\mu }\Vert + \max \limits _{\overline{A}} |\nabla \cdot \varvec{\mu }|=R+n, \) we obtain
Now, we will construct \((r_{k_m})_{m}\) and \((\delta _m)_m\).
We choose \(k_1\) such that \(r_{k_1}>n\). Let \(\delta _1\) be such that \(0<\delta _1<r_{k_1}-n\). Then, for the annulus \( A_1:=\{ \mathbf {x}: r_{k_1}<\Vert \mathbf {x}\Vert <r_{k_1}+\delta _1\}, \) we have
Now suppose \(r_{k_1},\ldots , r_{k_m}, \delta _1,\ldots , \delta _m\) possessing the desired properties have been constructed. Choose \(k_{m+1}\) such that \(r_{k_{m+1}}>r_{k_m}+\delta _m\). Let \(\delta _{m+1}\) be such that \(0<\delta _{m+1}<r_{k_{m+1}} -n\).
Then, for the annulus \( A_{m+1}:=\{\mathbf {x}: r_{k_{m+1}}<\Vert \mathbf {x}\Vert <r_{k_{m+1}}+\delta _{m+1}\}, \) we have
This completes the induction step.
So we have arrived at the contradiction that
This shows that our original assumption was incorrect, and so
completing the proof of our lemma. \(\square \)
An analogous result also holds for the cylinder \(\mathbb {R}\times S^{n-1}\). This was used in the proof of our Theorem 4.2.
Lemma 7.3
If \(n\geqslant 3\) and \(f,g\in H^1(\mathbb {R}\times S^{n-1})\), then
Proof
(Sketch) The proof is based on the same idea as the above, but is somewhat simpler, since the radius of \(S^{n-1}\) does not change, and the constants one has in the trace theorem for a ‘cylindrical band’ of the form \((a,b) \times S^{n-1}\) already work, as opposed to having to keep careful track, via Theorem 7.2, of the constants in the earlier case when the radii of the \(S_{r}^{n-1}\) were changing. Proceeding in the same way as in the previous lemma, we assume that
and so there exists an \(\epsilon >0\) and a sequence \((t_k)_{k\in \mathbb {N}}\) such that \(\lim \limits _{k\rightarrow \infty }t_k=+\infty \), and
In order to fatten the ‘circle’ \(\{t_k\}\times S^{n-1}\) to a cylindrical band of the form \(I=(t_k,t_k+\delta )\times S^{n-1}\), while keeping the \(L^2\)-norm of f on the band uniformly (in k) bigger than a fixed positive quantity, one can use the inequality
This follows from [25, Prop. 4.5, p. 287], by taking \(\Omega =[t_k,t_k+\delta ] \times S^{n-1}\). The rest of the proof is along the same lines. \(\square \)
Appendix C: Sharpness of Bound When \(|m|=\frac{n}{2}\) in Theorem 3.1
In this appendix, we will show the sharpness of the bound from Theorem 3.1 we had obtained for the decay of the solution to the Klein–Gordon equation in the de Sitter universe in flat FLRW form, when \(|m|=\frac{n}{2}\). Let us recall this bound:
If \(|m|=\frac{n}{2}\), then with \(\psi :=a^{\frac{n}{2}}\phi \), we had seen that
We will now construct a solution \(\psi \) that satisfies
showing that
and so the bound
cannot be improved.
We want
Taking the Fourier transform with respect to only the (spatial) \(\mathbf {x}\)-variable, and denoting
(23) becomes
which is a family of ordinary differential equations in t, parameterised by \(\varvec{\xi }\in \mathbb {R}^n\). For a fixed \(\varvec{\xi }\in \mathbb {R}^n\), the general solution to the ODE (24) is given by
where
-
\(J_0\) is the Bessel function of first kind and of order 0, and
-
\(Y_0\) is the Bessel function of second kind and of order 0.
In order to construct our \(\psi \), we will make special choices of \(C_1\) and \(C_2\).
We recall [1, (9.1.7–8)] that
as \(z\searrow 0\) (\(z\in \mathbb {R}\)).
Now as \(t\rightarrow \infty \), \(e^{-t}\searrow 0\), and so from the above limiting behaviour of \(J_0\) and \(Y_0\), we obtain that as \(t\rightarrow \infty \),
By Plancherel’s identity (see e.g. [25, Prop. 3.2]),
Since we want the linear behaviour in t of \(\Vert \psi (t,\cdot )\Vert _{L^2(\mathbb {R}^n)}\), we keep \(C_2\) nonzero, but may take \(C_1\equiv 0\). Then, as \(t\rightarrow \infty \),
In order to have \(\widehat{\psi }(t,\cdot )\) (and so also \(\psi (t,\cdot )\)) in \(L^2(\mathbb {R}^n)\) for all t, we choose \(C_2\) to have a sufficiently fast decay.
We recall [1, §9.2.2] that
as \(z\rightarrow \infty \) (\(z\in \mathbb {R}\)). So we have
as \(\Vert \varvec{\xi }\Vert \rightarrow +\infty \) (and t is kept fixed). So to arrange \(\widehat{\psi }(t,\cdot )\in L^2(\mathbb {R}^n)\) for all t, we may take
(Also this choice makes
which will be needed below.)
Then, \(\widehat{\psi }(t,\cdot )\in L^2(\mathbb {R}^n)\) for all t. Also, as \(t\rightarrow \infty \),
and
for large t.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Natário, J., Sasane, A. Decay of Solutions to the Klein–Gordon Equation on Some Expanding Cosmological Spacetimes. Ann. Henri Poincaré 23, 2345–2389 (2022). https://doi.org/10.1007/s00023-022-01172-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00023-022-01172-2



 , using
, using  .
.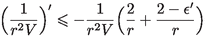 .
.