1 Introduction

Morning glory is a fascinating seasonal cloud formation, composed of a (train of) low roll cloud(s), stretching through horizon. This phenomenon is frequently observed in coastal regions, but is also occasionally occurring over the land and the sea (see Fig. 1). Even though one finds the most mentions of this phenomenon in Australia (in particular, in the Gulf of Carpentaria, [3, 6]), it has been also reported over the English Channel, Central USA, Germany, Eastern Russia, Canada, Mexico, Brazil and Uruguay. The morning glory is usually observed in the early morning and its appearance is connected to a particular thermal structure of the lower atmosphere over the land and the sea [10].

There is an extended amount of literature addressing the mechanism of this cloud formation. To align with observations scientists construct mathematical models that are able to capture main properties of this atmospheric flow. They mainly originate from analogies of the nonlinear shallow-water flows with stratification (see among others discussions in [3, 6, 11, 12, 21, 23]). One of the latest results in this direction is due to Constantin, Johnson who applied asymptotic analysis to the Navier–Stokes governing equations and equations of mass conservation in order to obtain a physically reliable and properties preserving model of the morning glory clouds [9, 10]. Derivatives from their model are boundary value problems (BVPs) modeling the bore- and breeze-like flows [5, 10]. The last ones fall under the focus of this paper.

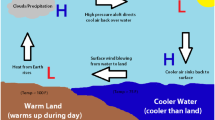
When talking about the breeze-like flows one should distinguish between the sea and the land breeze (Fig. 2).

Sea breeze is an atmospheric flow that develops due to a strong temperature contrast between the land and sea surfaces. This flow is caused by the heating of the boundary layer over land, that results in the movement of low-level air from the sea to land [22, 23, 25]. Land breeze, on the contrary, is a local wind system characterized by a flow from land to water and is often referred to as a return flow. It is typically shallower than the sea breeze since the cooling of the atmosphere over land is confined to a shallower layer at night than the heating of the air during the day [15, 26].

The layout of this paper is as follows. In Sect. 2 we present a mathematical model of the sea-breeze flow adapted to the Gulf of Carpentaria, and make a connection between the model and the corresponding Sturm–Liouville problem [1, 13]. The last one is the key for our solvability analysis, since knowing the spectrum of the eigenvalue problem answers the question of existence/uniqueness of solutions to the original inhomogeneous BVP (see [2, 4, 7, 18, 19]). These results are presented in Sect. 3 of the paper, and they complement and generalize contributions published in [10, 20]. And last but not least, in Sect. 4 we formulate our conclusions and give possible directions for future research on this topic.

Fig. 1
figure 1

The morning glory cloud formation formation, https://www.couriermail.com.au/news/queensland/warwick/morning-glory-clouds-go-viral-as-world-looks-to-our-skies/news-story/2d5950ae8e55c6ffa090cfb985396111

Full size image
Fig. 2
figure 2

The breeze flow formation, https://www.britannica.com/science/sea-breeze

Full size image

Note that the results we discuss in this paper are also relevant for the study of atmospheric undular bores (see the discussions in [8, 14, 16]).

2 Mathematical Model and the Associated Sturm–Liouville Problem

In this section we briefly introduce a mathematical model of the breeze-like flow, derived from the governing equations describing the ’morning glory’ phenomenon (see results of Constantin, Johnson in [10]), and give connection between the physical and the associated eigenvalue problems [10, 20].

2.1 Physical Problem

In [10] Constantin and Johnson derive a non-dimensional model of the breeze-like flow, expressed in terms of a horizontal velocity profile \(V_0(z, \Phi )\) as

$$\begin{aligned} \rho _0 \sigma S V_0+\frac{1}{R_e}\frac{\partial }{\partial z}\left( m(z)\frac{\partial V_0}{\partial z}\right) =-\left\{ \cos ^2(\alpha )+\frac{\sin ^2(\alpha )}{C}\right\} K(z, \Phi ), \end{aligned}$$
(1)

where

  • - z is the thickness of the flow;

  • - \(\rho _0(z)\) is the density function;

  • - S, \(\alpha \), C and \(\sigma =\frac{2(\sin ^2\alpha +C\cos ^2\alpha )}{(1-C)\sin \alpha \cos {\alpha }}\) are characteristics of the flow in a specific region;

  • - \(R_e\approx 10^5\) is the Reynolds number;

  • - m(z) is the viscosity function;

  • - \(\Phi \) is a parameter, corresponding to the direction of the flow propagation and

  • - \(K(z, \Phi )\) is the forcing term in the model.

In addition, authors specify physically relevant boundary conditions that read

$$\begin{aligned} V_0(0,\Phi )=0,\end{aligned}$$
(2)
$$\begin{aligned} V_0(z_0,\Phi )=0, \end{aligned}$$
(3)

with (2) standing for a no-slip condition at the surface of the Earth, and (3) indicating level of the temperature inversion.

By fixing parameter values S, \(\alpha \), C and \(\sigma \) one can focus on a particular zone, where the breeze is observed. One of those regions is the Gulf of Carpentaria that corresponds to

$$C\approx 0.97, \ \ S\approx -0.24, \ \ \sigma \approx 133\ \ \text{ and } \ \ \alpha =\frac{5\pi }{4},$$

which localize a flow propagating in the south-west direction. In this case BVP (1)–(3) can be rewritten as

$$\begin{aligned} \beta V_0-\frac{\partial }{\partial s}\left( \hat{m}(s)\frac{\partial V_0}{\partial s}\right) =k_0(s, \Phi ), \ \ 0<s<1, \end{aligned}$$
(4)
$$\begin{aligned} V_0(0)=V_0(1)=0, \end{aligned}$$
(5)

with

$$\begin{aligned} \beta =-\sigma S R_e>0, \ \ s=\frac{1}{\int _{0}^{z_0}\rho _0(\xi ) d\xi }\int _{0}^{z}\rho _0(\xi ) d\xi , \end{aligned}$$
$$\begin{aligned} \hat{m}(s)=\frac{\rho _0(z)m(z)}{\left( \int _{0}^{z_0}\rho _0(\xi ) d\xi \right) ^2} \end{aligned}$$
(6)

and

$$\begin{aligned} k_0(z, \Phi )=Re\left\{ \cos ^2(\alpha )+\frac{\sin ^2(\alpha )}{C}\right\} \frac{K(z, \Phi )}{\rho _0(z)}, \end{aligned}$$

where functions \(\rho _0(z)\) and \(K(z, \Phi )\) are assumed to be continuous (with \(\Phi \) being a parameter), while m(z) is continuously differentiable.

In order to derive existence results for the inhomogeneous problem (4), (5) we aim to use spectral theory, applied to the corresponding Sturm–Liouville problem [1, 2].

2.2 Eigenvalue Problem Arising in the Sea-Breeze Flow Model

Let us associate with the BVP (4), (5) an eigenvalue problem of the form:

$$\begin{aligned} \beta V_0-\frac{\partial }{\partial s}\left( \hat{m}(s)\frac{\partial V_0}{\partial s}\right) =\lambda V_0(s), \ \ 0<s<1, \end{aligned}$$
(7)
$$\begin{aligned} V_0(0)=V_0(1)=0, \end{aligned}$$
(5)

where function \(\hat{m}(s)\) is given by formula (6) and does not change its sign at [0, 1].

We seek for spectrum of the problem (7), (5) that will lead to existence and uniqueness of solutions to the original BVP (4), (5).

Some of the already known results in this direction were published by Constantin, Johnson and Marynets (see discussions in [10, 20]), where authors considered particular cases of the mass-density function \(\hat{m}(s)\) to derive an explicit Dirichlet spectrum of the Sturm–Liouville problem (7), (5). In particular, in [10] it was shown that if

$$\hat{m}(s)\equiv m_0,$$

one obtains a sequence of eigenvalues

$$\lambda _k=\beta +m_0\pi ^2k^2, \ \ k\ge 1$$

that for a particular value of \(\beta \) admits a zero value in the sequence \(\lambda _k\). This means that the original BVP (4), (5) has a unique solution, if its right hand-side \(k_0(s, \Phi )\) is orthogonal to the corresponding eigenfunction \(f_k(z)\). Later this result was extended to polynomial profiles of (6), such as

$$\hat{m}(t)=(at+b)^2$$

and

$$\hat{m}(t)=(1-t^2),$$

that in turn also enabled construction of the Dirichlet spectrum in an explicit form (see [20]).

In the next section we extend the aforementioned results by deriving general conditions on \(\hat{m}(s)\) that admit non-zero eigenvalues of the Sturm–Liouville problem (7), (5).

3 Main Results

Let us rewrite the eigenvalue problem (4), (5) as follows:

$$\begin{aligned} V_0''(s)+\mu (s)V_0'(s)+\gamma \nu (s) V_0(s)=0, \ \ 0<s<1, \end{aligned}$$
(8)
$$\begin{aligned} V_0(0)=V_0(1)=0, \end{aligned}$$
(5)

where \(\mu (s)=\frac{\hat{m}'(s)}{\hat{m}(s)}\), \(\nu (s)=\frac{1}{\hat{m}(s)}\) and \(\gamma =\lambda -\beta \).

By a change of variables

$$\begin{aligned} W(s)=\exp \left( \frac{1}{2}A(s)\right) V_0(s), \ \ \mu (s)=\frac{dA}{ds} \end{aligned}$$

we eliminate the first-order term from Eq. (8) and reduce the whole problem (8), (5) to the one below:

$$\begin{aligned} W''(s)+Q(s)W(s)=0, \ \ 0<s<1,\end{aligned}$$
(9)
$$\begin{aligned} W(0)=W(1)=0, \end{aligned}$$
(10)

with \(Q(s)=-\frac{1}{2}\frac{d\mu }{ds}-\frac{1}{4}\mu ^2(s)+\gamma \nu (s).\)

We prove the following existence/uniqueness results.

Theorem 1

For the BVP (4), (5) the following statements hold:

  1. 1.

    If the mass density function \(\hat{m}(s)\) in (4) satisfies a differential inequality

    $$\begin{aligned} \hat{m}''(s)\hat{m}(s)-\frac{1}{2}\hat{m}'^{2}\ge 0, \end{aligned}$$
    (11)

    then there exists a unique solution to the BVP (4), (5), for all \(s \in [0, 1]\).

  2. 2.

    If for the mass density profile \(\hat{m}(s)\) it holds that

    $$\begin{aligned} \hat{m}''(s)\hat{m}(s)-\frac{1}{2}\hat{m}'^{2}< 0, \end{aligned}$$
    (12)

    then the BVP (4), (5) has at least one solution. In addition, the inhomogeneous BVP(4), (5) admits a unique solution, if for the eigenfunction \(V_k(s)\), corresponding to a zero-eigenvalue \(\lambda _k\) of the Sturm–Liouville BVP (7), (5), the orthogonality property

    $$\begin{aligned} \int _0^1k_0(s, \Phi )V_k(s)ds=0 \end{aligned}$$

    holds.

Proof

Let us prove the first statement of the theorem. Multiplying (9) by W(s) and integrating its left hand-side by parts over the interval [0, 1] yields

$$\begin{aligned} -\int _0^1W'^2(s)ds=-\int _0^1Q(s)W^2(s)ds\le 0. \end{aligned}$$

For the inequality above to hold function Q(s) has to be nonnegative, that leads to a differential inequality:

$$\begin{aligned} -\frac{1}{2}\frac{d\mu }{ds}-\frac{1}{4}\mu ^2(s)+\gamma \nu (s)\ge 0. \end{aligned}$$

This relation, expressed in terms of the mass-density function, reads as follows:

$$\begin{aligned} \hat{m}''(s)\hat{m}(s)-\frac{1}{2}\hat{m}'^{2}-2\gamma \hat{m}(s)\le 0, \end{aligned}$$
(13)

wherefrom we deduce that

$$\begin{aligned} \gamma \ge \mathop {\sup }\limits _{s}\frac{\hat{m}''(s)\hat{m}(s)-\frac{1}{2}\hat{m}'^{2}}{\hat{m}(s)}, \end{aligned}$$
(14)

\(\square \)

which, recalling that \(\gamma =\lambda - \beta \), results in the following conclusions:

(i):

all eigenvalues of the Sturm–Liouville BVP (9), (10) are positive if

$$\begin{aligned} \hat{m}''(s)\hat{m}(s)-\frac{1}{2}\hat{m}'^{2}\ge 0; \end{aligned}$$
(15)
(ii):

there exists a zero eigenvalue to the Sturm–Liouville BVP (9), (10) if

$$\begin{aligned} \hat{m}''(s)\hat{m}(s)-\frac{1}{2}\hat{m}'^{2}< 0. \end{aligned}$$
(16)

Based on (14), (15), the Fredholm alternative insures existence of a unique solution to the BVP (4), (5). If, on the contrary, (1618) holds, then the BVP (4), (5) admits at least one solution, and it has a unique solution if the eigenfunction \(V_k(s)\), corresponding to a zero eigenvalue \(\lambda _k\), is orthogonal to the right hand-side \(k_0(s, \Phi )\) of the differential equation (4) (see [2]).

This completes the proof.\(\square \)

We can generalize the result above in the following theorem.

Theorem 2

Assume that \(V_k(s)\) is an eigenfunction, corresponding to the eigenvalue \(\lambda _k\) of the Sturm–Liouville problem (7), (5). The original BVP (4), (7) admits a unique solution if

$$\begin{aligned} \int _0^1k_0(s, \Phi )V_k(s)ds=0. \end{aligned}$$
(17)

Proof

Multiplying (7) by \(V_k(s)\) and introducing a notation \(\gamma _k=\beta -\lambda _k\) yields

$$\begin{aligned} V_k(s)\left[ \hat{m}(s)V_k'(s)\right] '=\gamma _n V_k^2(s), \end{aligned}$$
(18)

where \(V_k(0)=V_k(1)=0\).

Integrating (1618) by parts and taking into account the homogeneous boundary conditions (5) we get a relation between the eigenvalues \(\lambda _k\) of the problem (7), (5) and the corresponding eigenfunctions which reads:

$$\begin{aligned} \lambda _k=\beta -\frac{\int _0^1 \hat{m}(s)V_k'^{2}(s)ds}{\int _0^1 V_k^2(s)ds}. \end{aligned}$$
(19)

Since the expression \(\frac{\int _0^1 \hat{m}(s)V_n'^{2}(s)ds}{\int _0^1 V_n^2(s)ds}\) is positive and \(\beta \) is a given parameter (positive by assumption), we conclude that some mass density profiles and parameter values \(\beta \) might lead to a zero eigenvalue \(\lambda _k\) of the analyzed eigenvalue problem (7), (5). This means that by the Fredholm alternative the inhomogeneous problem (4), (5) admits a unique solution if the orthogonality condition (17) holds. This completes the proof. \(\square \)

Remark 1

Note, that all eigenvalues of the BVP (7), (5) can be ordered in a ascending sequence as \(\lambda _0<\lambda _1<\lambda _2<\cdots \), with the ground state eigenvalue

$$\lambda _0=\beta -\mathop {\min }_{V_0(s)}\frac{\int _0^1 \hat{m}(s)V_0^{2'}(s)ds}{\int _0^1 V_0^2(s)ds}.$$

For more details we refer the reader to [17, 18].

4 Conclusions and Future Developments

In this paper we used spectral analysis approach to prove existence and uniqueness of solutions to one inhomogeneous BVP modeling the sea-breeze flow of the Gulf of Carpentaria. These results contain sufficient conditions applied to the mass density function of a general form. As we have pointed out in Sect. 2.2 of the paper, one could also think of special cases of the mass density profile that enable construction of the Dirichlet spectrum in an explicit form [1]. For example, in [24] Rahbar analyzed periodic potentials that by a sequence of substitutions enabled identification of all eigenvalues of the given Sturm–Liouville problem. On the other hand, a different choice of parameters \(C, R, \sigma \) and \(\alpha \) in (1) would lead to a different region for the sea-breeze, where our model is still valid. One of such examples is taking \({C \approx 0.62, S\approx 0.77, \sigma \approx 8.5}\) and \(\alpha =\frac{\pi }{4}\) that correspond to the Calgary area.