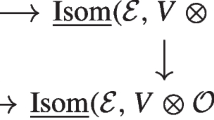1 Introduction

A continuous map \(f:X\rightarrow Y\) is called proper if \(f^{-1}(C)\) is compact for all compact subsets C of Y. A homotopy of proper maps is a homotopy \(F:[0,1]\times X\rightarrow Y\) such that F is a proper map. The assumption that a homotopy is a homotopy of proper maps is stronger than the assumption that the homotopy is homotopy through proper maps, i.e. the assumption that the maps \(F_t:X\rightarrow Y\) are proper for every \(t\in [0,1]\). A simple example of a homotopy through proper maps that is not a homotopy of proper maps is the map \(F:[0,1]\times \mathbb {R}\rightarrow \mathbb {R}\) defined by \(F(t,x)=t x^2+x\). To see this, note that the sequence \((\frac{1}{n},-n)\) is unbounded, but \(F(\frac{1}{n},-n)=0\). This example is closely related to the compactness issues discussed in [5].

We denote by [X, Y] the set of (unbased) homotopy classes of maps from X to Y and with \([X,Y]_{\mathrm {prop}}\) the set of (unbased) homotopy classes of proper maps. For the set of homotopy classes of based maps between pointed spaces we write \(\langle X,Y\rangle \).

In [1], we classified the homotopy classes of proper Fredholm maps of Hilbert manifolds into its model (real and separable) Hilbert space in terms of a suitable notion of framed cobordism. This classification uses an infinite dimensional and proper analogue of the Pontryagin–Thom collapse map, which is due to Elworthy and Tromba [3], see also the paper of Gęba [4]. The existence of the collapse map hinges on the fact that an infinite dimensional Hilbert space is diffeomorphic to the Hilbert space minus a point. This is of course not true for a finite dimensional vector space and the construction does not work in this setting. As we will discuss in Section 4, even though the framed cobordism class of a regular value is an invariant of the homotopy class of a proper map in the finite dimensional setting, the framed cobordism class is not able to distinguish all proper homotopy classes of proper maps into \({\mathbb {R}}^k\), nor do all framed submanifolds come from proper maps. Thus there does not exist a finite dimensional proper Pontryagin–Thom construction, which is why we are not able to compute \([E,\mathbb {R}^k]_{\mathrm {prop}}\) for all open finite dimensional manifolds E using a Pontryagin–Thom collapse map. In this paper, we are content with the classification of \([E,\mathbb {R}^k]_{\mathrm {prop}}\) where E is a real vector bundle over a compact Hausdorff space M. This classification does not use a Pontryagin–Thom collapse map.

Theorem 1.1

Let \(E\rightarrow M\) be a normed real vector bundle over a compact Hausdorff space M. Denote by \(S(E)\rightarrow M\) the associated sphere bundle of unit vectors. Then the set \([E,{\mathbb {R}}^k]_{\mathrm {prop}}\) is in bijective correspondence with \([S(E),S^{k-1}]\).

We have the following corollary of Theorem 1.1 by taking M to be a point and using the fact that based and unbased homotopy classes of maps from spaces to positive dimensional spheres coincide, cf. [6, Section 4A].

Corollary 1.2

\([\mathbb {R}^n,\mathbb {R}^k]_{\mathrm {prop}}\) is in bijective correspondence with \([S^{n-1},S^{k-1}]\). Thus if \(n>1\) and \(k>1\), we have that \([\mathbb {R}^n,\mathbb {R}^k]_{\mathrm {prop}}\) is in bijection with \(\pi _{n-1}(S^{k-1})\). The set \( [\mathbb {R}^n,\mathbb {R}]_{\mathrm {prop}}\) has two elements if \(n>1\) and four elements if \(n=1\).

A proper map between non-compact and locally compact Hausdorff spaces extends to a continuous map between the one point compactifications by sending infinity to infinity. Similarly a homotopy of proper maps induces a homotopy in the one point compactification.

The one point compactification of a real vector bundle \(E\rightarrow M\) over a compact Hausdorff space M equals the Thom space \({{\,\mathrm{Th}\,}}(E)\) of the vector bundle and the one point compactification of \(\mathbb {R}^k\) is homeomorphic to \(S^k\) by stereographic projection. Thus we obtain a map \(Q:[E,\mathbb {R}^k]_{\mathrm {prop}}\rightarrow \langle {{\,\mathrm{Th}\,}}(E),S^k\rangle \). In Section 3, we show that the map Q is bijective if k is sufficiently large. If \(E=\mathbb {R}^n\), the map Q is nothing but the suspension \(\pi _{n-1}(S^{k-1})\rightarrow \pi _n(S^k)\) under the identification of \([\mathbb {R}^n,\mathbb {R}^k]_{\mathrm {prop}}\) and \(\pi _{n-1}(S^{k-1})\) of Corollary 1.2.

For l sufficiently large, the sets \([E\oplus \mathbb {R}^l,\mathbb {R}^{k+l}]_{\mathrm {prop}}\) and \([E\oplus \mathbb {R}^{l+1},\mathbb {R}^{k+l+1}]_{\mathrm {prop}}\) are in bijection. Thus it makes sense to define the stable proper homotopy classes as

$$\begin{aligned}{}[E,\mathbb {R}^k]^S_{\mathrm {prop}}=\lim _{l\rightarrow \infty }[E\oplus \mathbb {R}^l,\mathbb {R}^{k+l}]_{\mathrm {prop}}, \end{aligned}$$

which are in bijection with the stable cohomotopy groups \(\pi ^k_S({{\,\mathrm{Th}\,}}(E))\), cf. Corollary 3.2. Using Atiyah duality, we obtain the following result.

Theorem 1.3

Let M be an m-dimensional compact manifold with boundary \(\partial M\). Let E be the normal bundle of M of some embedding of M into \(\mathbb {R}^{m+n}\). Then there is a bijection of \([E,\mathbb {R}^k]^S_{\mathrm {prop}}\) with \(\pi _{n+m-k}^S(M/\partial M)\).

In Section 4.4, we speculate on the classification problem in the case that E is an arbitrary open manifold.

2 The proof of Theorem 1.1

For the remainder of the paper, \(E\rightarrow M\) denotes a normed real vector bundle over a compact Hausdorff space M. The associated sphere and disk bundles of radius \(R>0\) are

$$\begin{aligned} S_R(E)=\{v\in E\,|\,\left| \left| v\right| \right| =R\}\, \quad \text {and}\quad B_R(E)=\{v\in E\,|\,\left| \left| v\right| \right| <R\}. \end{aligned}$$

We write S(E) for \(S_1(E)\) and B(E) for \(B_1(E)\).

Given a homotopy \(F:[0,1]\times S(E)\rightarrow S^{k-1}\), we define the homotopy \(PF:[0,1]\times E\rightarrow \mathbb {R}^k\) of proper maps by

$$\begin{aligned} PF(t,v)={\left\{ \begin{array}{ll} \left| \left| v\right| \right| F\left( t,\frac{v}{\left| \left| v\right| \right| }\right) ,\qquad &{}v\not =0,\\ 0,\qquad &{}v=0. \end{array}\right. } \end{aligned}$$

Compact subsets of E are characterized as follows: A subset \(K\subseteq E\) is compact if and only if it is closed and bounded. Here bounded means that \(K\subseteq B_R(E)\) for some \(R>0\). As \(PF(\cdot ,t)\) is norm preserving for all t, it follows that PF is proper.

The same construction assigns to a map \(f:S(E)\rightarrow S^{k-1}\) a proper map \(Pf:E\rightarrow \mathbb {R}^k\) and it therefore induces a map \(P:[S(E),S^{k-1}]\rightarrow [E,\mathbb {R}^k]_{\mathrm {prop}}\).

We will show that P is bijective. Let us start with the injectivity. We need to show that \(f_0\) and \(f_1\) are homotopic if \(g_0=Pf_0\) and \(g_1=Pf_1\) are homotopic as proper maps. Let \(G:[0,1]\times E\rightarrow \mathbb {R}^k\) be a homotopy of proper maps between \(g_0\) and \(g_1\). Then there exists an \(R>0\) such that \(G^{-1}(B(\mathbb {R}^k))\subseteq [0,1]\times B_R(E)\). It follows for any \(v\in E\) with \(\left| \left| v\right| \right| =R\) that \(G(t,v)\not =0\). The map \(F:[0,1]\times S(E)\rightarrow S^{k-1}\) given by

$$\begin{aligned} F(t,x)=\frac{G(t,Rx)}{\left| \left| G(t,Rx)\right| \right| } \end{aligned}$$

is a homotopy between \(f_0\) and \(f_1\), hence P is injective.

To show that P is surjective, we need to show that, given a proper map \(g:E\rightarrow \mathbb {R}^k\), there exists a homotopy of proper maps from g to Pf, where f is some map \(f:S(E)\rightarrow S^{k-1}\). As g is proper, there exists an \(R>0\) such that \(g^{-1}(B(\mathbb {R}^k))\subseteq B_R(E)\). The sphere bundle \(S_R(E)\) is compact, hence there exists an \(r\ge 1\) such that

$$\begin{aligned} 1\le \left| \left| g(v)\right| \right| \le r,\quad \text {for all}\quad v\in S_R(E). \end{aligned}$$

Consider the map \(h:\mathbb {R}^k\rightarrow \mathbb {R}^k\) defined by

$$\begin{aligned} h(x)={\left\{ \begin{array}{ll}x,\qquad &{}\left| \left| x\right| \right| \le 1,\\ \frac{x}{\left| \left| x\right| \right| },\qquad &{}1\le \left| \left| x\right| \right| \le r,\\ \frac{x}{r},\qquad &{}r\le \left| \left| x\right| \right| , \end{array}\right. } \end{aligned}$$

and define \(g_1:E\rightarrow \mathbb {R}^k\) by \(g_1(v)=h\circ g(Rv)\). As h is homotopic as proper map to the identity via \((t,x)\mapsto (1-t) h(x)+x\), it follows that the map \(g_1\) is proper homotopic to g. Note that if \(\left| \left| v\right| \right| <1 \), then \(\left| \left| Rv\right| \right| <R\) and therefore \(\left| \left| g(Rv)\right| \right| < 1\). We see that \(g_1(B(E))\subseteq B(\mathbb {R}^k)\) and similarly that \(g_1(S(E))\subseteq S^{k-1}\). Define \(G_1:[0,1]\times E\rightarrow E\) by

$$\begin{aligned} G_1(t,v)={\left\{ \begin{array}{ll}\frac{\left| \left| g_1(v)\right| \right| }{\left| \left| g_1\left( (1-t) v+\frac{t}{\left| \left| v\right| \right| }v\right) \right| \right| }g_1\left( (1-t)v+\frac{t}{\left| \left| v\right| \right| }v\right) , \qquad &{}\left| \left| v\right| \right| \ge 1,\\ g_1(v), \qquad &{}\left| \left| v\right| \right| \le 1. \end{array}\right. } \end{aligned}$$

The equation \(\left| \left| G_1(t,v)\right| \right| =\left| \left| g_1(v)\right| \right| \) implies that \(G_1^{-1}(B_s(\mathbb {R}^k))\subseteq [0,1]\times g_1^{-1}(B_s(\mathbb {R}^k))\) for all s and hence that \(G_1\) is proper if \(g_1\) is. Thus \(g_2:E\rightarrow \mathbb {R}^k\), given by \(g_2(x)=G_1(1,x)\), is a proper map that is proper homotopic to g. Let \(f:S(E)\rightarrow S^{k-1}\) be the map obtained by restriction of \(g_2\). Consider

$$\begin{aligned} G_2(t,v)=(1-t)g_2(v)+t Pf(v). \end{aligned}$$

We want to prove that \(G_2\) is proper. Note that \(G_2\) sends \(\overline{ [0,1]\times B(E)}\) to \(\overline{B(\mathbb {R}^k)}\) and \([0,1]\times (E\setminus B(E))\) to \(\mathbb {R}^k\setminus B(\mathbb {R}^k)\). The map \(G_2\bigr |_{\overline{[0,1]\times B(E)}}: \overline{[0,1]\times B(E)}\rightarrow \overline{B(\mathbb {R}^k)}\) is proper as the domain is compact. We conclude that \(G_2\) is proper if and only if

$$\begin{aligned} G_2\bigr |_{[0,1]\times (E\setminus B(E))}: [0,1]\times (E\setminus B(E))\rightarrow \mathbb {R}^k\setminus B(\mathbb {R}^k) \end{aligned}$$

is proper.

For this, it is sufficient to show that for all \(s>1\), there exists an \(S>1\) such that \(G_2^{-1}(B_s(\mathbb {R}^k)\setminus B(\mathbb {R}^k))\subseteq [0,1]\times (B_S(E)\setminus B(E))\). Note that for all \((t,v)\in [0,1]\times (E\setminus B(E))\), we have that

$$\begin{aligned} G_2(t,v)=\left( (1-t)\left| \left| g_1(v)\right| \right| +t \left| \left| v\right| \right| \right) f\left( \frac{v}{\left| \left| v\right| \right| }\right) . \end{aligned}$$

Consider all \((t,v)\in [0,1]\times (E\setminus B(E))\) such that \(\left| \left| G_2(t,v)\right| \right| \le s.\) As \(\left| \left| f(\frac{v}{\left| \left| v\right| \right| })\right| \right| =1\), this amounts to

$$\begin{aligned} (1-t)\left| \left| g_1(v)\right| \right| +t\left| \left| v\right| \right| \le s. \end{aligned}$$

Suppose the set of solutions of this equation is not contained in \([0,1]\times (B_S(E)\setminus B(E))\) for any S. Then we have a sequence \((t_n,v_n)\) of solutions such that \(\left| \left| v_n\right| \right| \ge n\). Without loss of generality we take a subsequence such that \(t_n\) converges to t by the compactness of [0, 1]. This subsequence will also satisfy \(\left| \left| v_n\right| \right| \ge n\). If \(t>0\), then there exists an N such that for all \(n\ge N\), we have \(t_n>\frac{t}{2}\) and

$$\begin{aligned} \left| \left| v_n\right| \right| \le \frac{1}{t_n}\left( (1-t_n)\left| \left| g_1(v_n)\right| \right| +t_n\left| \left| v_n\right| \right| \right) \le \frac{2s}{t}, \end{aligned}$$

which contradicts the unboundedness of \(v_n\). If \(t=0\), then there exists an N such that for all \(n\ge N \), the sequence satisfies \(t_n<\frac{1}{2}\) and

$$\begin{aligned} \left| \left| g_1(v_n)\right| \right| \le \frac{1}{(1-t_n)}\left( (1-t_n)\left| \left| g_1(v_n)\right| \right| +t_n\left| \left| v_n\right| \right| \right) \le 2s. \end{aligned}$$

The sequence \(g_1(v_n)\) is therefore bounded and as the map \(g_1\) is proper, it follows that the sequence \(v_n\) is also bounded. This contradicts the assumption that \(v_n\) is unbounded. This means that \(G_2\bigr |_{[0,1]\times (E\setminus B(E))}\) is proper. Thus Pf is proper homotopic to g and \(P:[S(E),S^{k-1}]\rightarrow [E,\mathbb {R}^k]_{\mathrm {prop}}\) is surjective. We have already shown that P is injective and Theorem 1.1 follows.

3 The one point compactification and stable (co)homotopy

Recall that the one point compactification of a non-compact, locally compact Hausdorff space X is the space \(X^*=X\cup \{\infty \}\) equipped with the following topology. All open sets U of X are declared open in \(X^*\) along with all sets of the form \((X\setminus C)\cup \{\infty \}\) for all compact sets C in X. Proper maps between non-compact, locally compact Hausdorff spaces induce continuous maps between the one point compactifications by imposing that \(\infty \) is mapped to \(\infty \). A homotopy of proper maps \(F:[0,1]\times X\rightarrow Y\) induces a continuous map \(F^*:([0,1]\times X)^*\rightarrow Y^*\). But \(([0,1]\times X)^*\cong ([0,1]\times X^*)/[0,1]\times \{\infty \}\). By the universal property of the quotient topology, we therefore also obtain a continuous map \(F^*:[0,1]\times X^*\rightarrow Y^*\) which sends every \((t,\infty )\) to \(\infty \). A homotopy of proper maps between unbased spaces is mapped to a based homotopy between the based spaces. The one point compactification of a vector bundle \(E\rightarrow M\) over a compact Hausdorff space M is called the Thom space of the bundle and we will write \({{\,\mathrm{Th}\,}}(E):=E^*\). Stereographic projection shows that \((\mathbb {R}^k)^*\cong S^k\) and in more generality, it holds that \({{\,\mathrm{Th}\,}}(E)\cong \overline{B(E)}/S(E)\). As was mentioned in the introduction, the map that forgets the basepoint induces a bijection between \(\langle {{\,\mathrm{Th}\,}}(E),S^k\rangle \) and \([{{\,\mathrm{Th}\,}}(E),S^k]\) if \(k\ge 1\). Thus from the one point compactification we obtain a map \(Q:[E,\mathbb {R}^k]_{\mathrm {prop}}\rightarrow [{{\,\mathrm{Th}\,}}(E),S^k]\).

In our setting there are three suspension maps, which we all denote by S. To a map \(g:S(E)\rightarrow S^{k-1}\) we associate the map \(S g:S(E\oplus \mathbb {R})\rightarrow S^k\) by

$$\begin{aligned} Sg(v,s)={\left\{ \begin{array}{ll} (\left| \left| v\right| \right| g\left( \frac{v}{\left| \left| v\right| \right| }\right) ,s),\qquad &{}v\not =0,\\ (0,s),&{}v=0, \end{array}\right. } \end{aligned}$$

where we have normed the vector bundle \(E\oplus \mathbb {R}\) via the formula \(\left| \left| (v,t)\right| \right| =\left| \left| v\right| \right| +\vert t \vert .\) To a map \(f:{{\,\mathrm{Th}\,}}(E)\rightarrow S^k\) we associate the map \(Sf:{{\,\mathrm{Th}\,}}(E\oplus \mathbb {R})\rightarrow S^{k+1}\) via the same formula and to a proper map \(f:E\rightarrow \mathbb {R}^k\) we associate the proper map \(Sf:E\oplus \mathbb {R}\rightarrow \mathbb {R}^{k+1}\) by \(Sf(x,s)=(f(x),s)\). The following diagram is commutative

(1)

In the proof of Theorem 1.1, we saw that the maps P are bijections. We now investigate when the other maps in the diagram are bijective.

Let us now assume that \(k\ge 2\), that M is a finite connected CW-complex of dimension m, and that E is a normed real vector bundle of rank n. Since \(k\ge 2\), based and unbased homotopy classes into \(S^{k-1}\) and \(S^k\) coincide, as well as based or unbased proper homotopy classes into \(\mathbb {R}^k\) and \(\mathbb {R}^{k+1}\). We denote by

$$\begin{aligned} \pi ^{k-1}(S(E)):=\langle S(E),S^{k-1}\rangle \end{aligned}$$

the \((k-1)\)-th cohomotopy set of S(E). We refer to [7, Chapter VII] for information on the cohomotopy sets we use below. The cohomotopy set \(\pi ^{k-1}(S(E))\) is not always a group, but it is if \(m+n\le 2k-3\). We investigate the long exact sequence of the pair \((\overline{B(E)},S(E))\) if \(m+n\le 2k-3\):

$$\begin{aligned} \pi ^{k-1}(\overline{B(E)})\rightarrow \pi ^{k-1}(S(E))\xrightarrow {\delta } \pi ^k(\overline{B(E)},S(E))\rightarrow \pi ^k(\overline{B(E)}). \end{aligned}$$
(2)

Since \(\overline{B(E)}\) deformation retracts to M and \(S^{k-1}\) is \((k-2)\)-connected, we see that if \(m\le k-2\), there are isomorphisms

$$\begin{aligned} \pi ^{k-1}(\overline{B(E)})\cong \pi ^{k-1}(M)\cong 0\quad \text { and}\quad \pi ^{k}(\overline{B(E)})\cong \pi ^{k}(M)\cong 0. \end{aligned}$$

Thus we conclude that for \(2k\ge m+3+\max (n,m+1)\), there is an isomorphism \(\pi ^{k-1}(S(E))\cong \pi ^k(\overline{B(E)},S(E))\). The relative cohomotopy set is the cohomotopy set of the quotient for nice spaces, thus \(\pi ^{k}(\overline{B(E)},S(E))=\pi ^k(\overline{B(E)}/S(E))=\pi ^k({{\,\mathrm{Th}\,}}(E))\). The coboundary map is an isomorphism \(\pi ^{k-1}(S(E))\cong \pi ^k({{\,\mathrm{Th}\,}}(E))\) in the dimension range. Let us consider the based version of Diagram (1)

(3)

The horizontal maps can be identified with the coboundary map \(\delta \) in (2) and therefore the horizontal maps are isomorphisms in the right dimension range. Freudenthal’s suspension theorem, cf. [8], states that if \(m+n\le 2k-2\), the suspension map \(\pi ^k({{\,\mathrm{Th}\,}}(E))\rightarrow \pi ^{k+1}(S{{\,\mathrm{Th}\,}}(E))\cong \pi ^{k+1}({{\,\mathrm{Th}\,}}(E\oplus \mathbb {R}))\) is an isomorphism. Combining all this information gives us the following theorem.

Theorem 3.1

Let M be a finite CW complex of dimension m and E a normed real vector bundle over M of rank n. Let \(k\ge 2\) and suppose that \(2k\ge m+3+\max (n,m+1)\). Then all maps in Diagram (1) are bijections.

This theorem expresses a stability phenomenon: For all l sufficiently large, the map Q induces bijections \([E\oplus \mathbb {R}^l,\mathbb {R}^{k+l}]_{\mathrm {prop}}\rightarrow [E\oplus \mathbb {R}^{l+1},\mathbb {R}^{k+l+1}]_{\mathrm {prop}}\). We define the stable homotopy classes of proper maps as

$$\begin{aligned}{}[E,\mathrm {\mathbb {R}^k}]^S_{\mathrm {prop}}=\lim _{l\rightarrow \infty }[E\oplus \mathbb {R}^l,\mathbb {R}^{k+l}]_{\mathrm {prop}}. \end{aligned}$$

Recall that the stable homotopy and cohomotopy groups of a space X are similarly defined

$$\begin{aligned} \pi _k^S(X)=\lim _{l\rightarrow \infty }\langle S^l S^k,S^l X\rangle \quad \text {and}\quad \pi _S^k(X)=\lim _{l\rightarrow \infty }\langle S^l X,S^l S^k\rangle . \end{aligned}$$

A direct corollary of Theorem 3.1 is then

Corollary 3.2

Let M be a finite CW complex of dimension m and E a normed real vector bundle of rank n. Then Q induces a bijection of \([E,\mathbb {R}^k]^S_{\mathrm {prop}}\) with \(\pi ^k_S({{\,\mathrm{Th}\,}}(E))\).

Stable homotopy and cohomotopy groups are related via Spanier–Whitehead duality, which we recall now. We refer to the original references [11, 12] for these statements. Let \(i:X\rightarrow S^N\) be a sufficiently nice embedding of a sufficiently nice space X into a sphere (e.g. a smooth embedding of a compact manifold, or the inclusion of a CW complex as a subcomplex). Then the space \(D_NX=S^N\setminus i(X)\) is a Spanier–Whitehead dual of X. The stable homotopy type of \(D_NX\) is well defined: It is independent of the dimension N and the choice of embedding. The fundamental result is that \(\lim _{l\rightarrow \infty }[S^lX,S^lY]\) is in bijection with \(\lim _{l\rightarrow \infty }[S^lD_NY,S^lD_NX]\). In particular, the stable cohomotopy groups of X are the stable homotopy groups of \(D_NX\) with a dimension shift. Now let us assume that M is a compact manifold with boundary \(\partial M\). There is a unique (up to isotopy) embedding of M into \(\mathbb {R}^{m+n}\) for n sufficiently large. Let E be the normal bundle of such an embedding, i.e. let E be the stable normal bundle of M. Atiyah [2, Proposition 3.2] showed that \(SD_{m+n}(M/\partial M)\simeq {{\,\mathrm{Th}\,}}(E)\). If the boundary \(\partial M\) is empty, we should interpret \(M/\partial M\) as M with a disjoint basepoint added. The Spanier–Whitehead dual of a sphere is \(D_{n+m} S^{n+m-k}=S^{k-1}\). We have

$$\begin{aligned} \pi _{n+m-k}^S(M/\partial M)&:=\lim _{l\rightarrow \infty }\langle S^lS^{n+m-k},S^l M/\partial M\rangle \\&=\lim _{l\rightarrow \infty }\langle S^l D_{n+m}(M/\partial M),S^l D_{n+m} S^{n+m-k}\rangle \\&=\lim _{l\rightarrow \infty }\langle S^{l-1}{{\,\mathrm{Th}\,}}(E),S^l S^{k-1}\rangle \\&=\lim _{l\rightarrow \infty }\langle S^l{{\,\mathrm{Th}\,}}(E),S^l S^k\rangle \\&=\pi ^k_S({{\,\mathrm{Th}\,}}(E)). \end{aligned}$$

Theorem 3.1 states that \(\pi ^k_S({{\,\mathrm{Th}\,}}(E))\) is in bijection with \([E,\mathbb {R}^k]^S_{\mathrm {prop}}\). We have proven Theorem 1.3.

4 Framed submanifolds and cobordisms

Pontryagin [10] showed that homotopy classes of maps \(M\rightarrow S^k\), where M is a closed manifold, are in one to one correspondence with framed cobordism classes of \((n-k)\)-dimensional manifolds in M. Framed cobordism classes are also invariants of homotopy classes of proper maps \(E\rightarrow \mathbb {R}^k\) but they are not complete, nor is every cobordism classed realized by some proper map. In this section, we discuss this.

4.1 Invariants of proper maps: framed submanifolds and cobordisms

Let M be a smooth m-dimensional manifold and N be a connected oriented smooth k-dimensional manifold. Every continuous proper map is homotopic as a proper map to a smooth proper map, hence we can consider only proper smooth maps in the proper homotopy classification of proper maps. Suppose that \(f:M\rightarrow N\) is a smooth map that is proper. Proper maps between manifolds are closed maps. The set of critical points is closed, hence the set of regular values of a proper map is open. By Sard/Brown’s theorem, regular values of f are residual, and by Baire’s category theorem, it follows that the regular values are dense. Thus the set of regular values of a proper map is open and dense. An example of a smooth function \(\mathbb {R}_{>0}\rightarrow \mathbb {R}\) whose set of regular values is not open is \(x\mapsto \frac{1}{x(2+\sin (x))}\), but of course this map fails to be proper and closed. The preimage of a regular value y is a closed submanifold \(X=f^{-1}(y)\) of dimension \(m-k\). Such a manifold can be framed: Let \(e_1,\ldots ,e_k\) be a basis of \(T_yN\) that is compatible with the orientation of N. Then for every \(x\in X\), the differential of f induces an isomorphism \(df_x:N_xX\rightarrow T_yN\) of the normal space \(N_xX\) to X at x with \(T_yN\). Then \((\nu _f)_x=((df_x)^{-1}(e_1),\ldots , (df_x)^{-1}(e_k))\) is an ordered basis of the normal space \(N_xX\) at x. Letting x vary, this patches together to a map \(\nu _f\) that trivializes the normal bundle of X. The map \(\nu _f\) is called the framing of X. We call \((X,\nu _f)\) a Pontryagin manifold of f and it depends on the choices we made.

Let \(F:[0,1]\times M\rightarrow N\) be a homotopy of proper maps between \(f_0=F(0,\cdot )\) and \(f_1=F_1(1,\cdot )\). By a reparametrization of the homotopy variable, we may assume that \(F(t,x)=f_0(x)\) and \(F(1-t,x)=f_1(x)\) for t small. If y is a regular value of the maps \(F,f_0\), and \(f_1\) simultaneously, then \((W=F^{-1}(y),\nu _F)\) is a framed compact submanifold with framed boundary \((X_0=f_0^{-1}(y),\nu _{f_0})\) and \((X_1=f_0^{-1}(y),\nu _{f_1})\). The framed manifold \((W,\nu _F)\) is a framed cobordism between the framed manifolds \((X_0,\nu _{f_0})\) and \((X_1,\nu _{f_1})\). Being framed cobordant, defines an equivalence relation on the set of framed submanifolds and the framed cobordism class of a Pontryagin manifold of a proper map \(f:M\rightarrow N\) does not depend on the choice of the regular value y and the choice of the oriented basis of \(T_yN\) and is an invariant of the proper homotopy class of f. We denote the set of framed \((m-k)\)-dimensional closed submanifolds of M up to framed cobordism by \(\Omega ^{\mathrm {fr}}_{m-k}(M)\).

4.2 The Pontryagin–Thom construction

The framed cobordism class of the preimage of a regular value is in some cases enough to recover the homotopy class of the map: Suppose M is closed and \((X,\nu )\) is a \((m-k)\)-dimensional framed submanifold. Out of this data we can construct a (proper) map \(f:M\rightarrow S^k\), for which \((X,\nu )\) is a Pontryagin manifold: We define f to map X to the northpole y of \(S^k\) and describe what happens in a tubular neighborhood of X. The framing \(\nu \) defines, for each point \(x\in X\), a diffeomorphism of the normal space around x to a neighborhood of y. We use this to extend the map to the tubular neighborhood of X in M. One can arrange this in such a way that if one approaches the boundary of the tubular neighborhood, the image under f converges to the south pole. The map f can now be extended to the whole of M by mapping everything outside the tubular neighborhood to the south pole. The northpole is a regular value for f and the Pontryagin manifold at the north pole is exactly the framed manifold \((X,\nu )\). This construction also works for framed cobordisms. This proves the following theorem.

Theorem 4.1

The Pontryagin–Thom construction gives a one to one correspondence between the set \(\Omega ^{\mathrm {fr}}_{m-k}(M)\) of framed cobordisms in M and the set \( [M,S^k]\) of homotopy classes of maps from M to \(S^k\).

For more details of the Pontryagin–Thom construction in this classical setting, we refer to Milnor [9] and Pontryagin [10].

4.3 How good of an invariant is the framed cobordism class of the Pontryagin manifold of a proper map?

A proper map \(f:\mathbb {R}^n\rightarrow \mathbb {R}^k\) is proper homotopic to a map Pg, where \(g:S^{n-1}\rightarrow S^{k-1}\) is a smooth map. The map Pg fails to be smooth at the origin, but can be smoothed without affecting the Pontryagin manifolds below. Let \(y\in S^{n-1}\) be a regular value of g, and \((X,\nu _g)\) be the Pontryagin manifold of g at y. The value \(y\in S^{k-1}\subseteq \mathbb {R}^k\) is also a regular value for the map Pg. The Pontryagin manifold of Pg at x is \((X,(\nu _{g},\mu ))\), where \(\mu \) is the last component of the framing which points radially outward from the sphere. So a framed submanifold cannot occur as a Pontryagin manifold if it is not framed cobordant to a framed submanifold that lies on a sphere where the last component of the framing is radially pointing outward.

Let us discuss an explicit example of a framed manifold that does not occur as the Pontryagin manifold of a map. Consider the submanifold \(X=\{-1,1\}\subseteq \mathbb {R}\) with framing \(\nu _{-1}=\nu _1=\frac{\partial }{\partial t}\). Then \((X,\nu )\) cannot occur as the preimage of a regular value of a proper map \(f:\mathbb {R}\rightarrow \mathbb {R}\). Suppose on the contrary that such a map exists with \(f(-1)=f(1)\). From the framing and the definition of the derivative, we see that there exists an \(\epsilon >0\) such that \(f(-1+\epsilon )>f(-1)\) and \(f(1-\epsilon )<f(1)\). The intermediate value theorem then gives the existence of another point \(-1+\epsilon<p<1-\epsilon \) such that \(f(p)=f(-1)=f(1)\). Hence \(f^{-1}(f(1))\not =X\) and we conclude that there does not exist a proper \(f:\mathbb {R}\rightarrow \mathbb {R}\) with \((X,\nu )\) as a Pontryagin manifold.

But there are also framed submanifolds which are framed cobordant to a framed submanifold which is contained in the unit sphere and has a framing with last component pointing radially outward which do not arise from proper maps. To see this, consider the manifold \(X=\{-2,-1,1,2\}\) with framing \(\nu (-2)=\nu (2)=\frac{\partial }{\partial t}\) and \(\nu (-1)=\nu (1)=-\frac{\partial }{\partial t}\). Then \((X,\nu )\) is framed cobordant to the empty set, however it cannot occur as the Pontryagin manifold of a proper map: If y is the regular value for which \((X,\nu )\) is hypothetically the Pontryagin manifold at y, there must be a point \(x \in (-1,1)\) such that \(f(x)=y\) by the same reasoning as above. The framed submanifold \((X,\nu )\) does not occur as the Pontryagin manifold of a proper map, but the empty set, which is framed cobordant to it, does.

Finally we discuss the fact that the invariant is not complete. The maps \(f,g:\mathbb {R}\rightarrow \mathbb {R}\) given by \(f(x)=x^2\) and \(g(x)=-x^2\) are not proper homotopic. However as the maps are not surjective the framed cobordism class of both maps is the empty manifold. Hence the framed cobordism class of a regular value cannot distinguish these maps. Here is a more complicated example: Let \(f,g:S^3\rightarrow S^2\) be the Hopf map and the Hopf map precomposed with a degree \(-1\) map of \(S^3\) respectively. These maps represent \(+1\) and \(-1\) in \(\pi _3(S^2)\cong \mathbb {Z}\) and are not homotopic. By Theorem 1.1, Pf and Pg are therefore not proper homotopic, however their Pontryagin manifolds are framed cobordant. To see this, note that QPf and QPg are the suspensions of f and g and the Pontryagin manifolds of QPf and QPg can be identified with those of Pf and Pg. The suspension map \(S:\pi _3(S^2)\cong \mathbb {Z}\rightarrow \pi _4(S^3)\cong \mathbb {Z}/2\mathbb {Z}\) is the reduction modulo 2. Therefore the maps QPf and QPg are homotopic, so their Pontryagin manifolds must be framed cobordant. But this implies that the Pontryagin manifolds of PF and PG are framed cobordant by general position.

4.4 Open manifolds and the Pontryagin–Thom construction

In Corollary 3.2, we have seen that the homotopy classes of proper maps out of vector bundles stabilize. We expect that if M is an arbitrary open manifold, the homotopy classes of proper maps \([M\times \mathbb {R}^l,\mathbb {R}^{k+l}]_{\mathrm {prop}}\) stabilize when \(l\rightarrow \infty \). This suggests that there is a stable Pontryagin–Thom construction for proper maps. A framed submanifold \((X,\nu )\in \Omega ^{\mathrm {fr}}_{m-k}(M)\) gives rise to a framed submanifold \(((X,0),\nu \oplus \mu )\in \Omega ^{\mathrm {fr}}_{m-k}(M\times \mathbb {R}^l)\) via stabilization. The framing \(\nu \oplus \mu \) extends the framing \(\nu \) with a fixed basis \(\mu \) of \(\mathbb {R}^l\). Since we expect that the homotopy classes of proper maps stabilize, we also expect that there is a well defined stable bijective Pontryagin–Thom construction \(\Omega ^{\mathrm {fr}}_{m-k}(M\times \mathbb {R}^l)\rightarrow [M\times \mathbb {R}^l,\mathbb {R}^{l+k}]_{\mathrm {prop}}\) for l sufficiently large.