On a statement of O. Frink about free pseudo-complemented meet-semilattices

Abstract

Orrin Frink in 1962 stated incorrectly, that there exist free pseudocomplemented meet-semilattices, which are not lattices. This is disproved in the present paper. We have shown that any free PCS is in fact a sectionally pseudocomplemented lattice.

1 Introduction

In this paper we are going to describe some elementary properties of pseudocomplemented meet-semilattices (shortly PCS’s). The concept of a PCS was first introduced and studied by Orrin Frink in 1962 (see [5]) by a natural generalization of pseudocomplemented lattices, without making any use of the join operation. There already exist well-developed theory of PCS’s and particularly of free PCS’s. Balbes and Jones have independently obtained similar results concerning the finitely generated free PCS’s: see [1, 9, 10]. Schmid [18] succeeded in presenting a characterization of all free PCS’s. Recently, the authors of this paper, obtained promising results concerning free PCS’s as well as a new description of any free PCS’s (see [15]). For the other early papers see Grätzer [7].

The main purpose of the present paper is to provide a new answer to the following short remark of Frink [5], p. 506: There exist also pseudo-complemented semi-lattices which are not lattices, examples being the free pseudo-complemented semi-lattice with two or more generators. Theorem 3.3 of Schmid [18] shows that every free PCS is a complemented lattice, we shall give an alternative proof of this result in Theorem 4.4 and Corollary 5.5.

In the first two sections we outline the basic theory of PCS. Section 3 deals exclusively with PCS’s that are lattices. In Section 4 we show that any free PCS is a lattice. In the last section we present some new results about complemented PCS’s.

2 Preliminaries

A PCS is an algebra $(S; \wedge , ^{*}, 0,1)$ of type (2,1,0,0), where $(S;\wedge , 0,1)$ is a bounded meet-semilattice and, for every $a\in S$, the element $a^{*}$ is a pseudocomplement of a, i.e. $x\le a^{*}$ if and only if $x\wedge a=0$. A PCS S is said to be nontrivial, whenever $|S|\ge 2$. An element $a\in S$ is called closed, if $a=a^{**}$. Let B(S) denote the set of all closed elements of S. It is known that

$$\begin{aligned} (B(S);\sqcup ,\wedge , ^{*},0,1) \end{aligned}$$

forms a Boolean algebra with join operation

$$\begin{aligned} a \sqcup b=(a^*\wedge b^*)^*, \end{aligned}$$

(see [5]–[7] or [2]). Moreover, we may form the Glivenko–Frink congruence relation $\Gamma (S)$ (or shortly $\Gamma$) on S as follows:

$$\begin{aligned} x\equiv y(\Gamma )\quad \textrm{iff}\quad x^*=y^* \quad \textrm{iff} \quad x^{**}=y^{**}. \end{aligned}$$

Each Glivenko–Frink congruence class $[c]\Gamma$ contains exactly one closed element $a=c^{**}$, which is the largest one of $[c]\Gamma$. We shall mostly write $S_c$ instead of $[c]\Gamma (S)$. Significant is the class $[1]\Gamma (S)=D(S)=\{\,d\in S:d^*=0\,\}$ which is a dual ideal (filter) of S and elements $d\in D(S)$ are called dense. Moreover, the map $\gamma :a\mapsto a^{**}$ from a PCS S to the Boolean algebra B(S) is a homomorphism of S onto B(S), preserving meets, pseudocomplements, the elements 0 and 1, and joins when they exist (see [5] and [6]), i.e. $\gamma$ is a PCS-epimorphism. Clearly, a PCS S is a Boolean algebra iff S satisfies the identity $x=x^{**}$.

An element p of a meet-semilattice S is said to be irreducible, if $x\wedge y=p$ in S implies $x=p$ or $y=p$. Moreover, $p\in S$ is called (weakly) prime, if $x\wedge y\le p$ (respectively, $0< x\wedge y\le p$) in S implies $x\le p$ or $y\le p$.

A PCS S is called sectionally pseudocomplemented, if for each $a\in S$, the section $[a)\subseteq S$ is pseudocomplemented. However, a sectionally pseudocomplemented semilattice need not to be distributive. This is shown by the example of the pentagon, which is a free PCS with one generator. (For more details see [15, Theorem 4.7].) We only need to define a binary operation ‘$\circ$’ on S such that

$$\begin{aligned} a\wedge x=a\wedge b \Leftrightarrow x\le a\circ b \end{aligned}$$

for any $a,b,x \in S$, and satisfying $a^*=(a\circ 0)$ for any $a\in S$. Generally, $a\circ b$ denotes the pseudocomplement of a in $[a\wedge b,1]$. If $p\in S$ is irreducible in S, then the section [p, 1] has only two pseudocomplements $\{p, 1\}$. It is easy to verify that

$$\begin{aligned} a\circ b=a\circ (a\wedge b). \end{aligned}$$

To avoid a confusion, we also recall a similar structure, namely the relative pseudocomplemented semilattice or Brouwerian semilattice, which is defined by

$$\begin{aligned} a\wedge x\le b \Leftrightarrow x\le a*b, \end{aligned}$$

and $a*b$ is called a relative pseudocomplement of a in b. A Brouwerian semilattice with 0 is called a Heyting semilattice. The Heyting semilattices are a special subclass of the sectionally pseudocomplemented PCS’s.

We now recall in a brief summary, the most important properties of free PCS’s. We start with some results of Jones [10]:

Lemma 2.1

Let $F=F[X]$ be a PCS freely generated by X. Then

• (i) B(F) is a Boolean algebra freely generated by $X^{**}=\{\,x^{**}\in F:x\in X\,\}$, i.e. $B(F)=FB[X^{**}]=[X^{**}]_{{{\,\textrm{Bool}\,}}}$, where for a set $Y\subseteq B(F)$, $[Y]_{{{\,\textrm{Bool}\,}}}$ here denotes the subuniverse of $(B(F);\sqcup ,\wedge , ^{*},0,1)$ generated by Y;

• (ii) $F[X]=F[Y]$ implies $X=Y$;

• (iii) $x\ne x^{**}$ for each $x\in X$;

• (iv) $x\le y$ for $x, y\in X$ implies $x=y$;

• (v) If $x_1, x_2\in X$ and $x_1\ne x_2$, then $x_1{^*}\ne x_2{^*}$ and $x_1^{**}\ne x_2^{**}$;

• (vi) The elements of X are weakly prime in F;

• (vii) The Glivenko–Frink congruence classes on F are finite.

As one can easily see, $X\subseteq F$ is an antichain of F (see (iii)-(vi) of Lemma 2.1). More precisely, the elements of X are weakly prime elements in F such that $B(F)\cap X=\emptyset$. Moreover, each element $x\in X$ is a member of the Glivenko–Frink congruence class $[x^{**}]\Gamma (F)$.

The first of next two lemmas is in [13, 15], second one is in [18] and [15].

Lemma 2.2

Let S be a PCS and let $X\subseteq S$ be arbitrary. Then S is generated by X, i.e. $S=[X]$, iff $[X^{**}]_{{{\,\textrm{Bool}\,}}}=B(S)$ and $S=[X\cup B(S)]_{{{\,\textrm{sem}\,}}}$, where for a set $Y\subseteq S$, $[Y]_{{{\,\textrm{sem}\,}}}$ is the subuniverse of $(S;\wedge )$ generated by Y, i.e. as a meet-semilattice. Moreover, S consists of all elements

$$\begin{aligned} u=a\wedge \bigwedge (\,x:x\in U\,) \end{aligned}$$

with $a\in B(S)$ and U ranging over all finite subsets of X.

It is possible to obtain the canonical ordering of elements from S. We shall use it here for free PCS’s. Elements $0\ne u\in F=F[X]$ have a unique canonical form

$$\begin{aligned} u=u^{**}\wedge \bigwedge (\,x:x\in U\,) \end{aligned}$$

where $u^{**} \in B(F)$ and $U\subseteq X$ is finite — for uniqueness see Lemma 2.3(v). Observe that $1=1\wedge \bigwedge (\,x:x\in \emptyset \,)$ and $0=0\wedge \bigwedge (\,x:x\in U\,)$ for all nonempty finite subsets U of X.

Lemma 2.3

Let $F=F[X]$ be a free PCS. Then for elements $u, v \in F$ in canonical form we have

• (i) $0< u=u^{**}$ iff $U=\emptyset$;

• (ii) $u=0$ in F iff $u^{**}=0$ in B(F) and U is arbitrary;

• (iii) $0<u\le v<1$ in F iff $0<u^{**}\le v^{**}$ in B(F) and $V\subseteq U$;

• (iv) if $x_1, x_2\in X$, then $x_1\ne x_2$ iff $x^*_1\ne x^*_2$ and $x_1^{**}\ne x_2^{**}$;

• (v) $u=v$ iff $u^{**}=v^{**}$ and $U=V$, for $u\ne 0\ne v$;

• (vi) $0<u^{**}\le v$ implies $v=v^{**}$ and

• (vii) The Glivenko–Frink congruence classes on F are finite Boolean lattices.

Remark 2.4

Part (vi) of Lemma 2.3 will be of considerable use in Sections 3 and 4. This result is essentially due to Jones [10]. We show in the next lemma that (vi) follows from Lemma 2.3, parts (i) and (iii).

Lemma 2.5

Let $F=F[X]$ be a free PCS. Then $0<u^{**}\le v$ implies $v=v^{**}$.

Proof

By (i) we get $U=\emptyset$ and by (iii) $V\subseteq U=\emptyset$. Hence, $v=v^{**}$. $\square$

The notation $FS_1[X]$ means the free meet-semilattice over X with unit 1. Similarly, $[X]_{{{\,\textrm{sem1}\,}}}$ denotes the meet-semilattice generated by X with unit 1.

The consequence of the next lemma is important. See [8] and [2, Ch.II.7].

Lemma 2.6

Let S be a meet-semilattice with unit 1 generated by the nonempty subset Y of all dual atoms of S. Then S is a free meet-semilattice over Y, and every member of Y is prime in S. In addition,

• (i) If $k=|Y|$, then S is a finite Boolean lattice with $|S|=2^k$ and

• (ii) S is a relatively complemented distributive lattice with unit 1 for infinite Y.

The following result from [15] will be useful:

Proposition 2.7

Let $F=F[X]$ be a freely generated PCS over X. Then

• (i) B(F) is a free Booelan algebra over $X^{**};$

• (ii) the map $\gamma _X :X\rightarrow X^{**}$ given by the rule $x\mapsto x^{**}$ is a bijection;

• (iii) both X and $X^{**}$ are antichains;

• (iv) the map $\gamma :[X]_{{{\,\textrm{sem1}\,}}}\rightarrow [X^{**}]_{{{\,\textrm{sem1}\,}}}$ defined by $\gamma :u\rightarrow u^{**}$ is a $\{\wedge ,1\}$-isomorphism between meet-semilattices;

• (v) $0\notin [X]_{{{\,\textrm{sem1}\,}}}$ and

• (vi) $FS_1[X]=[X]_{{{\,\textrm{sem1}\,}}}\cong [X^{**}]_{{{\,\textrm{sem1}\,}}}= FS_1[X^{**}]$.

Corollary 2.8

Let $F=F[X]$ be a free PCS over X. Then $FS_1[X]_{{{\,\textrm{sem}\,}}}$ is a free meet-semilattice with 1, such that

$$\begin{aligned} B(F)\cap [X]_{{{\,\textrm{sem1}\,}}}=\{1\}. \end{aligned}$$

Proof

Take an arbitrary element

$$\begin{aligned} 1\ne u=\bigwedge (\,x:x\in U\,) \end{aligned}$$

from $[X]_{{{\,\textrm{sem1}\,}}}$. Clearly, $U\ne \emptyset$. Suppose to the contrary that there exists $0<a$ in B(F) such that $a\le u$ in F. Therefore, by Lemmas 2.3 and 2.5 we see that $0<a\le u$ for any $u\in U\subseteq X$, which implies $U\subseteq B(F)$. But this is a contradiction, as $U\subseteq X$. Thus $X\cap B(F)=\emptyset$. We conclude $B(F)\cap [X]_{{{\,\textrm{sem1}\,}}}=\{1\}$. $\square$

Using ideas and auxiliary results of Jones [10] we present the following remarkable result.

Lemma 2.9

Let $F=F[X]$ be a PCS freely generated by X. Assume that $F_1=[1]\Gamma (F)$. Then $F_1=\{1\}$.

Proof

The statement is trivially true for $X=\emptyset$ and $|X|=1$, as $F[\emptyset ]={\textbf {2}}$, where ${\textbf {2}}$ is a two-element Boolean algebra and $F[\{x\}]=N_5$. Assume that $|X|\ge 2$. Suppose to the contrary that there exists an element $u\in F_1$ with $u<1$ in F. There is a canonical form of

$$\begin{aligned} u=u^{**}\wedge \bigwedge (\,x:x\in U\,) \end{aligned}$$

for some finite $\emptyset \ne U\subseteq X$ (see [15]). Since $u^{**}=1$, we get $u=\bigwedge (\,x:x\in U\,)$. It follows that $1=u^{**}=\bigwedge (\,x^{**}:x\in U\,)$ which implies that $x^{**}=1$ for any $x\in U$. This is impossible, as $X^{**}$ is an antichain in B(F) (Proposition 2.7). Thus $F_1=\{1 \}$. $\square$

3 Pseudocomplemented meet-semilattices which happen to be lattices

It is well known that any complete meet-semilattice is a lattice, hence this is also true for any finite bounded meet-semilattice and any finite PCS. For a more general result we need some definitions and preliminaries concerning the Axiom of Choice or Zorn’s lemma.

We start with a definition: A meet-semilattice $(S;\wedge ,1)$ (considered as a poset) is said to satisfy the Descending Chain Condition (DCC) iff all decreasing chains terminate; that is, if in S $x_{0}> x_{1}> \cdots> x_{i} > \cdots$, then for some m, we have $x_{m} = x_{m+1}= \cdots$. Dually, we get the Ascending Chain Condition (ACC). (See [7]).

The Axiom of Choice states that if $\{\,A_i: i\in I\,\}$ is a nonempty family of non-empty sets, then the Cartesian product $\prod (\,A_i: i\in I\,)\ne \emptyset$. It is known that the Axiom of Choice and Zorn’s lemma are equivalent. We shall prefer here the dual version of Zorn’s lemma (see [2] or [7]):

Lemma 3.1

If every chain in a nonempty poset $(P,\le )$ has a lower bound, then there exists a minimal element $z\in P$. $\Box$

Lemma 3.2

Let $S=(S;\wedge ,1)$ be a meet-semilattice satisfying $(\mathrm DCC)$. Then S is a lattice.

Proof

It is well known (see [7]) that a meet-semilattice $(S;\wedge ,1)$ is a lattice iff sup$\{x,y\}$ exists for all incomparable elements $x, y \in S$, or in other words, the lattice join $x\vee y$ exists in S for any $x, y\in S$, and finally, $\sup \{x,y\}=x\vee y$. Let $(S;\le )$ denote the poset of the semilattice $(S;\wedge ,1)$. Take arbitrary incomporable elements $x,y\in S$. Suppose that P is the set of all of upper bounds of $\{x,y\}$ in S. Since $1\in P$, we see that $P\ne \emptyset$, and $P=[x)\cap [y)$ is a filter in S. If P is finite then P is a principal filter with generator $x\vee y$. In the infinite case we apply Lemma 3.1. We have to verify that P satifies the hypothesis of Zorn’s lemma. The condition (DCC) guaranties that a nonempty chain in P has a least element, which is its lower bound. Indeed, let $C\subseteq P$ be a nonempty chain in P. If there is no least element in C, for $x_i\in C$ there is $x_{i+1}\in C$ with $x_i>x_{i+1}$, and using this we can construct an infinite decreasing chain $x_1>x_2>x_3>\cdots$ of elements of C which contradicts (DCC) for P. Therefore, by Zorn’s lemma, P has a minimal element, which is the least element of P, because if $z\in P$ is minimal, for any $u\in P$ which is incomparable with z we have $z>u\wedge z\in P$, which contradicts the mininality of z in P. The least element of P is the generator $x\vee y$ of P. Thus, $(S;\wedge ,1)$, is in fact a lattice. $\square$

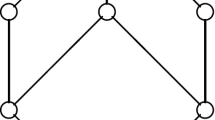
It is important to note that a PCS S (or a PCL) has two sorts of joins: the lattice join $\sup \{x,y\}=x\vee y$ for $x, y \in S$ and the Boolean join $\sup _{B(S)}\{a,b\}=a\sqcup b$ for $a, b \in B(S)$. (Even if S is a PCL, the lattice join in S need not be the same as the Boolean join; see Figure 1.) Moreover, let H denote the filter of all upper bounds of $\{a,b\}$ in S, and $a, b\in B(S)$. Consider the order relation $\le$ on S. Take a restriction of this relation $\le$ to B(S). It is easy to see that it is the natural semilattice ordering on B(S). More precisely, we get

$$\begin{aligned} H_B=H\cap B(S)\subseteq H \end{aligned}$$

Then $H_B$ is again a filter in B(S) of all upper bounds of $\{a,b\}$ with $a, b\in B(S)$. Hence, $H_B\subseteq H$ is the filter of all closed upper bounds of $\{a,b\}$ in B(S).

But, $H_B$ is a principal filter with generator $a\sqcup b$ in B(S) (see [5] or [7]). This is the Boolean join

$$\begin{aligned} {\sup }_{B(S)}\{a,b\}=a\sqcup b=(a^*\wedge b^*)^*. \end{aligned}$$

Consider the PCS (PCL) represented by Figure 1. The elements a and b are closed and $a\vee b=d<1$, but $a\sqcup b=1$. Notice that PCS in Figure 1 does not satisfy the condition (vi) of Lemmas 2.3 or 2.5.

Fig. 1

An example of a PCS in which the Boolean join is not the restriction of the lattice join

Fig. 2

An example of a PCS which is not PCL

Fig. 3

An example of free PCS, which is not free in the class of PCL’s

Our aim in this paper is to show, in which PCS S the lattice join $\sup \{x,y\}=x\vee y$ exists for any elements x and y of S. In other words, whether S is a lattice, or more precisely, if S is actually a PCL.

Proposition 3.3

Let S be a PCS such that each Glivenko–Frink congruence class of S satisfies $(\mathrm DCC)$. Then S is a pseudocomplemented lattice.

Proof

We have only to prove that there exists $\sup \{x,y\}=x\vee y$ in S for arbitrary $x, y\in S$, which are incomparable elements. Using Lemma 3.2, we see that the Glivenko–Frink congruence classes $S_a$, $a\in B(S)$, are lattices.

Now, we start with closed elements $a,b\in B(S)$. The Boolean join exists and $a\sqcup b\in B(S)$. Suppose that the filter $H\subseteq S$ is the subset of all upper bounds of $\{a,b\}$ in S. Since $a\sqcup b$ is the smallest closed element in H, we get $a\sqcup b \in H\cap S_{a\sqcup b}=H_{a\sqcup b}$. Clearly, $a\sqcup b$ is the largest element of $S_{a\sqcup b}$. We claim that $H_{a\sqcup b}$ is the filter of upper bounds of $\{a,b\}$ in $S_{a\sqcup b}$. Take an arbitrary element $q\in H$. We wish to show that $t=(a\sqcup b)\wedge q\in S_{a\sqcup b}$. Since $a\le q$, we get $a=a^{**}\le q^{**}$. Similarly, $b\le q^{**}$. Hence, $a\sqcup b\le q^{**}$ which implies that $t^{**}={a\sqcup b}$. Therefore,

$$\begin{aligned} t=(a\sqcup b)\wedge q \in H_{a\sqcup b}\subseteq S_{a\sqcup b}. \end{aligned}$$

By our (DCC) hypothesis $H_{a\sqcup b}$ is a principal filter of $S_{a\sqcup b}$. Thus, $a\vee b\le a\sqcup b$ (see Lemma 3.2 and Figure 1). Moreover, we have proved that $a\vee b$ exists in S, and

$$\begin{aligned} a\vee b\le (a\vee b)^{**}=a\sqcup b. \end{aligned}$$

Similarly we can proceed in a more general situation: $x, y\in S$ with

$$\begin{aligned} x \le x^{**}=a\ne b=y^{**}\ge y. \end{aligned}$$

It follows that $x,x^{**}\in S_a$ and $y,y^{**}\in S_b$, as the elements are congruent by the Glivenko–Frink congruence. Again suppose that $H\subseteq S$ is the subset of all upper bounds of $\{x,y\}$ in S. Now, $a\sqcup b \in H$ is the smallest closed element in H, and $a\sqcup b \in S_{a\sqcup b}$. Take $p\in H$ arbitrary. We have to show that

$$\begin{aligned} s=(a\sqcup b)\wedge p\in H_{a\sqcup b}\subseteq S_{a\sqcup b}. \end{aligned}$$

Clearly, $s\in H$. Similarly, as above, we have

$$\begin{aligned} s^{**}=(a\sqcup b)\wedge p^{**}=a\sqcup b \end{aligned}$$

which means that $s\in S_{a\sqcup b}$. Thus, $H_{a\sqcup b}$ is the filter of upper bounds of $\{x,y\}$ in $S_{a\sqcup b}$. Again, by our (DCC) hypothesis $H_{a\sqcup b}$ is a principal filter in $S_{a\sqcup b}$ (see Lemma 3.2). Hence $x\vee y$ exists in $S_{a\sqcup b}$, and $x\vee y\le a\sqcup b$. $\square$

The next corollary is an immediate consequence of Lemma 2.2 and Proposition 3.3.

Corollary 3.4

Every finitely generated PCS is a finite PCL.

Remark 3.5

Balbes [1] and Jones [9, 10] have independently shown that finitely generated free PCS’s are finite. It is well known that $F[\emptyset ]$ is a 2-element chain and F[1] is a 5-element non-modular lattice $N_5$ (pentagon). The last example of F[2] is known as a Hasse diagram of a free PCS with two free generators (see Balbes [1]). F[2] is a lattice (Corollary 3.4). See also [15].

Remark 3.6

We can present here a PCS S which is not a lattice (cf. [11]). Clearly, S will be infinite (Corollary 3.4). Let

$$\begin{aligned} S=\{\,0,a,b,1, x_1, x_2, \dots ,x_n, \dots \,\} \end{aligned}$$

Now, $a\wedge b=0$ and 1 is a unit of S. H is a chain

$$\begin{aligned} 1>x_1>x_2> \cdots>x_n> \cdots \end{aligned}$$

of all upper bounds of $\{a,b\}$ in S. H is a filter of S, but not principal. Thus S is a PCS and $\sup \{a,b\}$ does not exists in S (see Figure 2).

Remark 3.7

Nontrivial example of a semilattice with top element which satisfies (DCC) is

$$\begin{aligned} P_Z=\{\,x\subseteq Z:x \mathrm {\ is\ finite}\,\}\cup \{Z\} \end{aligned}$$

for an infinite set Z, ordering is a set inclusion.

Let B be a Boolean algebra, for $0\ne a\in B$ let $Z_a$ be an infinite set such that for $a\ne b\in B\setminus \{0\}$, $Z_a$ and $Z_b$ be disjoint ($Z_a$, $Z_b$ can have the same cardinality). The construction described in [16, Theorem 5.1, Corollary 5.3] allows us to construct a PCS S in which $B(S)\cong B$ and Glivenko–Frink congruence classes of S are $P_{Z_a}$ for $0\ne a\in B$ and Glivenko–Frink congruence class of 0 is $\{0\}$. Hence S is a nontrivial example of a semilattice which satisfies assumption of Proposition 3.3—Glivenko–Frink congruence classes $[a]\Gamma \cong P_{Z_a}$ satisfy (DCC) but are infinite for $0\ne a\in B$, $[0]\Gamma =\{0\}$ also satisfies (DCC).

4 Free PCS’s and the lattice join

We shall see that the class of free PCS’s (= the most general PCS’s) undergoes a good deal of simplification concerning the partial order. We recall that the order relation $\le$ on a PCS S is given by the condition $a\le b$ iff $a=a\wedge b$ for all $a, b \in S$. The subset B(S) of closed elements, the heart of S, contains the meet of any two of its elements and possess the pseudocomplement of each of its elements. The order on S partially orders B(S) and makes B(S) into a Boolean lattice. The Boolean join operation is given by the formula $a\sqcup b=(a^* \wedge b^*)^*$ (see [5] or [7]).

In [15] we introduced a definition of a plain PCS.

Definition 4.1

Let S be a PCS. Denote $\textrm{wPi}(S)$ the set of weekly prime elements p of S such that $p\ne 1$, put $P(S)= \textrm{wPi}(S)\cup B(S)$ and $Y(S)=\textrm{wPi}(S){\setminus } B(S)$. The PCS S is called plain if

• (i) $S=[Y(S)]=[P(S)]_{{{\,\textrm{sem}\,}}}$ and

• (ii) $0<a\le u$ in S implies $u\in B(S)$, whenever $a\in B(S)$.

It follows that every free PCS F is plain (see [15]), and satisfies the condition:

$$\begin{aligned} 0<u^{**}\le v \Rightarrow v=v^{**}. \end{aligned}$$

We now immediately deduce

Lemma 4.2

Every free PCS F is sectionally pseudocomplemented.

Proof

Apply [15, Theorem 4.7]. See also Corollary 3.4.$\square$

Lemma 4.3

Let $F=F[X]$ be a free PCS. Suppose that $a,b\in B(F)$ with $a\ne b$. Let $0<y<y^{**}=b$ in F. Then $\sup \{a,y\}$ in F exists and

$$\begin{aligned} a\vee y=\sup \{a,y^{**}\}={\sup }_{B(S)}\{a,b\}=a\sqcup b. \end{aligned}$$

In other words, the Boolean join $a\sqcup y^{**}$ is identical with the lattice join $a\vee y$.

Proof

Take $a\in B(F)$ such that $a>0$ and $0<y\le y^{**}=b$. Let H be the filter of all upper bounds of $\{a,y\}$ in F. By Lemma 2.3(vi) (or Lemma 2.5), we get that $H\subseteq B(F)$ because element a is closed. Hence, $H=H_B$. Since $H_B$ is a principal filter with generator $a\sqcup b$ in B(F), we see that H is also principal filter in F. Hence, the lattice join of $\{a,y\}$ in F exists. Thus, $a\vee y=a\sqcup y^{**}=a\sqcup b$. $\square$

Theorem 4.4

Every free PCS is a sectionally pseudocomplemented lattice.

Proof

The idea of our proof is similar to that of Proposition 3.3. Let $F=F[X]$ be a free PCS. We have to show that there exists the lattice join $x\vee y$ for any incomparable $x, y \in F$. Combining Lemma 2.3(vii) with Proposition 3.3 we know that this is true, the aim of this proof is to give more explicit description of $x\vee y$ in some cases.

If elements x and y are closed, then by Lemma 4.3 is $x\vee y=x\sqcup y$ in F.

Consider first the Glivenko–Frink congruence relation $\Gamma (F)$ on F. The congruence classes $[c]\Gamma (F)=F_c$ for $c\in B(F)$ form a partition of F. Let $x, y \in F_c$ for some $c\in B(F)$. The lattice join $x\vee y$ exists, because $F_c$ is a finite Boolean lattice (Lemma 2.3(vii)). Thus $x\vee y \in F_c$.

Now, suppose that $x, y \in F$ with

$$\begin{aligned} x\le x^{**}=a\ne b=y^{**}\ge y. \end{aligned}$$

Since generally the Boolean join $a\sqcup b$ exists in any nontrivial PCS (see [7]), then by Lemma 4.3 the lattice join $a\vee b$ really exists in F, and

$$\begin{aligned} a\sqcup b=c=a\vee b. \end{aligned}$$

Hence c is the largest element of $F_c$, and is also an upper bound of $\{x,y\}$ in F. Now, suppose that $z\in F$ is an upper bound of $\{x,y\}$ in $F_c$. We know that the Glivenko–Frink congruence classes in F are finite Boolean lattices (Lemma 2.3). Hence, $x\vee y$ exists in $F_c$.

In the case $x<x^{**}=a\ne b=y^{**}>y$, we can use the same argument as in the proof of Proposition 3.3.

It remains the last part: Take $a\in F_a$ and $y\in F_b$ for $a\ne b$, and $y< b$. Since $y^{**}=b$, the Boolean join $a\sqcup b$ exists in F. Again, by Lemma 4.3 we have

$$\begin{aligned} a\vee y=a\vee y^{**}=a\sqcup b \end{aligned}$$

in F. Concluding we use Lemma 4.2. $\square$

As we have already mentioned, the fact that a free PCS is a lattice was proved in [18, Theorem 3.3], value added by this proof is mainly in more specific information about joins in some cases.

Remark 4.5

Theorem 4.4 raises the question of whether the pseudocomplemented lattices, which are free PCS’s, possess the property, that they are free in the class of PCL’s? The answer is NO. This is shown by a simple counterexample (see Figure 3).

5 Complemented PCS’s

We start this section with some definitions: A complemented lattice is a bounded lattice in which every element has a complement (see [7]). In the case of a PCL, we require that the pseudocomplement $x^*$ is the complement of x for every element x (see [12].) More precisely, PCS S consists of two kinds of elements: closed elements from B(S), such as $x^*$ or $x^{**}$, and elements $x\in S{\setminus }B(S)$. There are lot of examples for complemented PCL’s: Boolean algebras or free PCS’s.

L. A. Lambrou in [17] shows that a pseudocomplemented lattice L is complemented if L is nontrivially pseudocomplemented. The nontriviallity assumption is defined by condition

$$\begin{aligned} x\ne 1 \Rightarrow x^*\ne 0. \end{aligned}$$

We show here that Lambrou’s result can be extended to PCS’s using elementary methods.

To prepare for this we prove:

Lemma 5.1

Let S be a PCS and $x\in S$. Then $x^*=0$ iff $x\in [1]\Gamma (S)=D(S)$.

Proof

We shall apply the Glivenko–Frink Theorem (cf. [7]). We recall that $\Gamma (S)$ is the Glivenko–Frink congruence relation. Every congruence class of $\Gamma (S)$ contains exactly one closed element $c^{**}$ of S, which is the largest one of $[c^{**}]\Gamma (S)$. The factor algebra $S/\Gamma (S)$ is a Boolean algebra, which is isomorphic to the Boolean algebra B(S) of all closed elements. Now, it is clear that $x^*=0$ iff $x\equiv 1(\Gamma )$. $\square$

Lemma 5.2

Let S be a PCS. Then the following conditions are equivalent:

• (i) $D(S)=\{1\}$ and

• (ii) $x\ne 1 \Rightarrow x^*\ne 0$.

Proof

The proof of (i) $\Rightarrow$ (ii) is routine (Lemma 5.1). For the converse, assume for the contrary that there exists $y\in D(S)$ such that $1\ne y$. Again by Lemma 5.1, we get $y^*=0$, which is a contradiction to (ii). Thus, $D(S)=\{1\}$.

$\square$

Theorem 5.3

Let S be a PCS. Then the following conditions are equivalent:

• (i) $D(S)=\{\,x\in S: x^*=0\,\}=\{1\}$ and

• (ii) S is complemented.

Proof

Let $D(S)=\{1\}$, and take $x\in S$ arbitrary. Assume that $z\ge x$ and $z\ge x^*$ in S, i.e. z is an upper bound of $\{x,x^*\}$. Therefore, $x^*\ge z^*$ and $x^{**}\ge z^*$, and this implies that $z^*\le x^*\wedge x^{**}=0$. It follows that $z\in D(S)$. By (i), we have $z=1$. Thus $x\vee x^*=1$, and $x^*$ is a complement of x in S, as $x\wedge x^*=0$ is true in any PCS.

Conversely, assume that $x\vee x^*=1$, and suppose $x^* =0$. Then $x^* \le x$ and $x\le x$, hence $x=1$. Hence, if S is complemented, then $D(S)=\{1\}$. $\square$

We now present some properties concerning the free PCS’s, which all are actually pseudocomplemented lattices (Theorem 4.4).

Theorem 5.4

Let $F=F[X]$ be a free PCS considered as a lattice. Then F satisfies the following identities

• (i) $x\vee x^*=1;$

• (ii) $x^*\vee x^{**}=1;$

• (iii) $x^*\vee y^*=(x\wedge y)^*$ and

• (iv) $(x\vee y)^*=x^*\wedge y^*$.

Proof

(i) Clearly, $(x\vee x^*)^*=0$, because (iv) is true for any PCL (see [5] or [7]). It follows that $x\vee x^* \in F_1=D(F)$. But, by Lemma 2.9, we have $F_1=\{1\}$, and consequently we obtain (i). Similarly, we can establish (ii). Applying Lemma 4.3 we can prove (iii). The condition (iv) is true in any PCL.

$\square$

Corollary 5.5

If F is a free PCS, then F is both a complemented and sectionally pseudocomplemented lattice. Moreover, the Boolean algebra of closed elements B(F) is a sublattice of F.

Proof

Apply Theorems 4.4, 5.4 and Lemmas 4.2, 4.3. $\square$

Definition 5.6

Let L be a p-algebra, that means L is a PCL. We say that L is a complemented p-algebra, if L satisfies the identity

$$\begin{aligned} x\vee x^*=1. \end{aligned}$$

Corollary 5.7

Let F be a free PCS considered as a lattice. Then F is a complemented p-algebra.

Proof

See Theorem 5.4(i).$\square$

Definition 5.8

Let L be a pseudocomplemented lattice. Then L is called a generalized Stone lattice, if it satisfies the conditions (ii) and (iii) of Theorem 5.4.

Corollary 5.9

Let F be a free PCS considered as a lattice. Then F is a generalized Stone lattice.

Proof

See Theorem 5.4(ii)–(iv). (Notice that F is not a distributive lattice.)$\square$