Numerical Solutions of High-Order Differential Equations with Polynomial Coefficients Using a Bernstein Polynomial Basis

Abstract

The paper presents a novel method that allows one to establish numerical solutions of linear and nonlinear ordinary differential equations—with polynomial coefficients—that contain any finite products of the unknown functions and/or their general derivatives. The presented algorithm provides numerical solutions of these differential equations subject to initial or boundary conditions. This algorithm proposes the desired solution in terms of B-polynomials (Bernstein polynomial basis) and then uses the orthonormal relation of B-polynomials with its weighted dual basis with respect to the Jacobi weight function to construct a linear/nonlinear system in the unknown expansion coefficients which can be solved using a suitable solver. The properties of B-polynomials provide greater flexibility in which to impose the initial or boundary conditions at the end points of the interval [0, R] and enable us to obtain exactly and explicitly some of the unknown expansion coefficients in the form of a suggested numerical solution. Consequently, the presented algorithm leads to a linear or nonlinear algebraic system in the unknown expansion coefficients that has a simpler form than that was obtained by the other algorithms. So that, this procedure is a powerful tool that we may utilize to overcome the difficulties associated with boundary and initial value problems with less computational effort than the other techniques. An accepted agreement is obtained between the exact and approximate solutions for the given examples. The error analysis was also studied, and the obtained numerical results clarified the validity of the theoretical results.

1 Introduction

A boundary-value problem for an ordinary differential equation (or system of equations) is obtained by requiring that the dependent variable (or variables) is satisfying subsidiary conditions at one or more distinct points. If these conditions are imposed at one or two points, the existence and uniqueness theory for initial/boundary-value problems can be expanded for many special classes of equations and systems of equations. Many approximate methods for obtaining numerical solutions for various classes of differential equations using orthogonal polynomials are available in the literature (see, for instance, [4,5,6, 50]).

A great interest to use B-polynomials

$$\begin{aligned} B_{n,i}(x)=\left( {\begin{array}{c}n\\ i\end{array}}\right) \frac{(b-x)^{n-i}(x-a)^{i}}{(b-a)^{n}}, \,\,\,i=0,1,...,n, \end{aligned}$$

for solving different classes of differential equations (see, for instance, [7,8,9, 12, 16, 35, 36, 42,43,44,45]) due to the perfect properties like the recursive relation, the appropriate properties, and making partition of unity (see, for instance, [17, 24,25,26, 28, 40]). These advantages make them the most known used basis in approximation theory and computer-aided geometric design (CAGD) (see, [23, 32, 37]). Farouki and GoodMan [26] show that there is no other nonnegative basis that provides systematically smaller condition numbers than B-polynomials, in the sense that they have optimal stability. Also, they declare that although B-polynomials are not uniquely optimal, no other basis in popular use provides this distinction, and it is uncertain whether other optimally stable bases would present the advantages and algorithms that we associate with the Bernstein form. Farouki and Rajan [29] had a head start in developing Bernstein formulations for all the procedures of basic polynomials required in geometric modeling algorithms, and they declared that these formulations were as simple as their customary power formulations.

In the current paper, a new numerical algorithm to find numerical solutions of higher order linear and nonlinear ordinary differential equations—with polynomial coefficients—that contain any finite products of the unknown functions and/or their derivatives subject to initial and boundary conditions will be discussed. Our interest in such models stems from the fact that they appear as models of many practical problems in mechanics and other areas of mathematical physics. For instance, the study of hydrodynamics, hydromagnetics, fluid dynamics, astrophysics, astronomy, beam and long wave theory, and applied physics. To be precise, for example, fifth-order boundary-value problems (BVPs) can be used to model viscoelastic flows (see, [19, 34]), sixth-order BVPs arise in the narrow convecting layers bounded by stable layers, which are believed to surround A-type stars [10, 14, 22, 48], the seventh-order BVPs generally arise in modeling induction motors with two rotor circuits [41] and ordinary convection and overstability yield a tenth-order and a twelfth-order BVPs, respectively.

The suggested numerical algorithm approximates the solution in the B-polynomials and it is based on the orthonormal relation of B-polynomials with its weighted dual basis with respect to the Jacobi weight function to construct a linear/nonlinear system in the unknown expansion coefficients which can be solved using a suitable solver. It will also be demonstrated that this algorithm provides excellent agreement between exact and approximate solutions, with the maximum pointwise error of no more than $O(10^{-20})$. In this paper, we discuss formulae related to B-polynomials, which are useful in many ways. These formulae enable us with great flexibility to impose boundary conditions at $x=0,\, R$ or initial conditions at $x=0$. Thus, the contribution of this paper can be summarized in the following items:

• A new explicit formula expressing the general-order derivative of B-polynomial in terms of the B-polynomials themselves is proved (see Lemma 2).

• A formula for the B-polynomial coefficients of the moments of one single or a general-order derivative of B-polynomial is given (see Theorem 1).

• An explicit formula, which expresses the B-polynomial coefficients of a general-order derivative of any polynomial in terms of its original B-polynomial coefficients, is also proved (see Theorem 2).

• Establishing an expression of the B-polynomial coefficients of the finite products of polynomials and/or their general-order derivatives in terms of its original B-polynomial coefficients is given (see Theorem 3 and Corollary 3).

• Establishing an expression of the B-polynomial coefficients of the moments of finite products of polynomials and/or their general-order derivatives in terms of its original B-polynomial coefficients is given (see Corollary 2).

• Designing an approach based on the orthonormal relation of B-polynomials with its weighted dual basis with respect to the Jacobi weight function to treat two types of high-order initial and initial-boundary problems.

• Investigating the error analysis of the B-polynomial expansion.

• Examining the accuracy of the proposed method via the presentation of some illustrative examples.

Up to now, and to the best of our Knowledge, it is worthy to state that the proven formulae in Theorems 1–3, two Corollaries 2 and 3 and Lemma 2 for those previously mentioned are new and traceless in the literature. These formulae lead to the systematic character and simplicity of the proposed algorithm, which allow it to be implemented in any computer algebra (here, the Mathematica 12) symbolic language used. Also, the proposed algorithm provide exactly and explicitly some of the unknown expansion coefficients (see Eqs. (54) and (61)) in the form of a suggested numerical solution. Consequently, the presented algorithm leads to a linear or nonlinear algebraic system with unknown expansion coefficients that has a simpler form than that obtained by the other algorithms. So that, this procedure is a powerful tool that we may utilize to overcome the difficulties associated with boundary and initial value problems with less computational effort than the other techniques.

The current paper is organized as follows: In Sect. 2, computational implementations which have useful uses in introducing the proposed algorithm are given. In Sects. 3 and 4, the details of the proposed numerical method to solve linear and nonlinear differential equations with polynomial coefficients are provided. The error analysis is presented in Sect. 5. Numerical examples are given in Sect. 6, and the obtained numerical results illustrate the validity of the theoretical results in Sect. 5.

2 Polynomial Basis

The general form of the B-polynomials of nth degree is defined by [12, pp.273–274]

$$\begin{aligned} B_{i,n}(x)=\left( {\begin{array}{c}n\\ i\end{array}}\right) \frac{x^{i}(R-x)^{n-i}}{R^{n}}, \,\,x \in [0,R],\,\,0\le i\le n, \end{aligned}$$

(1)

which constitute the entire basis of $(n+1)$ nth-degree polynomials. For convenience, we set $B_{i,n}(x)=0,$ if $i<0$ or $i>n$.

A recursive definition can also be used to generate the B-polynomials over this interval, allowing us to write the ith nth-degree B-polynomial in the form

$$\begin{aligned} B_{i,n}(x)=\frac{(R-x)}{R}B_{i,n-1}(x)+\frac{x}{R}B_{i-1,n-1}(x). \end{aligned}$$

(2)

The derivative of $B_{i,n}(x)$ is given by

$$\begin{aligned} DB_{i,n}(x)=\frac{n}{R}(B_{i-1,n-1}(x)-B_{i,n-1}(x)),\,\,\,D=\frac{d}{dx}. \end{aligned}$$

(3)

Each B-polynomial is positive and the sum of all the B-polynomials is unity for all $x \in [0,R]$, that is

$$\begin{aligned} \sum \limits _{i=0}^{n}B_{i,n}(x)=1. \end{aligned}$$

(4)

The set of functions which has these properties is called a partition of unity on the interval [0, R]. In addition, any given polynomial P(x) of degree n can be expanded as follows [27, p.3]:

$$\begin{aligned} P(x)=\sum \limits _{i=0}^{n}C_{i}\,B_{i,n}(x),\,\,n\ge 1. \end{aligned}$$

The dual basis to the Bernstein polynomials

$$\begin{aligned} b_{i,n}(u)=\left( {\begin{array}{c}n\\ i\end{array}}\right) u^{i}(1-u)^{n-i},\,\,0\le i\le n, \end{aligned}$$

(5)

with respect to the Jacobi weight function $w(x)=2^{\alpha +\beta }x^{\beta }(1-x)^{\beta },\,x\in [0,1]$ is characterized by the property [39, p.1587]

$$\begin{aligned} \int \limits _{0}^{1}w(x)\,b_{i,n}(u)\,d_{k,n}(u)du=\delta _{i,k} =\left\{ \begin{array}{l} 1,\,\,\,\,\,\,\,\,i=j, \\ 0,\,\,\,\,\,\,\,i\ne j, \end{array}\right. \end{aligned}$$

(6)

where the dual basis functions $d_{k,n}(u)$ have explicit representations

$$\begin{aligned} d_{j,n}(u)=\sum \limits _{k=0}^{n}c_{j,k}(n)\,b_{k,n}(u), \,\,\,0\le j\le n, \end{aligned}$$

(7)

and the coefficients $c_{j,k}(n)$ are defined by

$$\begin{aligned} c_{j,k}(n)= & {} \frac{(-1)^{j+k}}{2^{\alpha +\beta }\left( {\begin{array}{c}n\\ j\end{array}}\right) \left( {\begin{array}{c}n\\ k\end{array}}\right) } \sum \limits _{i=0}^{\min (j,k)}A_{i}\left( {\begin{array}{c}n+\beta +i+1\\ n-j\end{array}}\right) \left( {\begin{array}{c}n+\alpha -i\\ n+\alpha -j\end{array}}\right) \nonumber \\{} & {} \times \left( {\begin{array}{c}n+\beta +i+1\\ n-k\end{array}}\right) \left( {\begin{array}{c}n+\alpha -i\\ n+\alpha -k\end{array}}\right) , \end{aligned}$$

(8)

where $A_{i}=(2i+\beta +1)\left( {\begin{array}{c}n+\alpha +\beta +i+1\\ n+\beta +i+1\end{array}}\right) \left( {\begin{array}{c} n+\alpha -i\\ n-i\end{array}}\right) ^{-1}.$ Therefore, the dual basis, $D_{k,n}(x)=\frac{1}{R} d_{k,n}(x/R),$ to the Bernstein basis, $\,B_{i,n}(x)=$ $b_{i,n}(x/R),\,$can be characterized by the property

$$\begin{aligned} \int \limits _{0}^{R}\omega (x)\,B_{i,n}(x)\,D_{k,n}(x)\,dx=\,\delta _{i,k},\,\,\omega (x)=w(x/R)=(2/R)^{\alpha +\beta }x^{\beta } (R-x)^{\alpha }, \end{aligned}$$

(9)

and has the explicit representations

$$\begin{aligned} D_{j,n}(x)=\frac{1}{R}\,\sum \limits _{k=0}^{n}c_{j,k}(n) \,B_{k,n}(x),\,\,\,0 \le j\le n. \end{aligned}$$

(10)

Lemma 1

$$\begin{aligned} \int \limits _{0}^{R}\omega (x)\,D_{j,n}(x)\,\,dx=1. \end{aligned}$$

(11)

Proof

Using relation (4), we have

$$\begin{aligned} \int \limits _{0}^{R}\omega (x)\,D_{j,n}(x)\,\,dx=\sum \limits _{i=0}^{n}\int \limits _{0}^{R}\omega (x)\,B_{i,n}(x)\,D_{j,n}(x)\,\,dx; \end{aligned}$$

then using the orthogonality relation (9), one can see that (11) is valid, and the proof of Lemma 1 is complete. $\square$

Remark 1

Formula (11) is a generalization for the result of Jani et al. [33, p.7666]

$$\begin{aligned} \int \limits _{0}^{1}\,d_{i,n}(x)\,\,dx=1. \end{aligned}$$

Lemma 2

Let $B_{i,n}(x)$ be the ith nth-degree B-polynomial, and then, the pth-derivatives can be written in the form

$$\begin{aligned} D^{p}B_{i,n}(x)=\sum \limits _{k=0}^{p}\lambda _{k}^{(p,n)} B_{i-k,n-p}(x),\,\,0\le i,p\le n, \end{aligned}$$

(12)

where $\lambda _{k}^{(p,n)}=\dfrac{(-1)^{p+k}\,n!}{R^{p}(n-p)!}\genfrac(){0.0pt}0{p}{k}.$

Proof

To prove (12), we proceed by induction. In view of relation (3), we may write

$$\begin{aligned} D^{p}B_{i,n}(x)=\sum \limits _{k=0}^{1}\lambda _{k}^{(1,n)}B_{i-k,n-p}(x), \end{aligned}$$

and this in turn shows that (12) is true for $p=1.$ Proceeding by induction, assuming that (12) is valid for p,  we want to prove that

$$\begin{aligned} D^{p+1}B_{i,n}(x)=\sum \limits _{k=0}^{p+1} \lambda _{k}^{(p+1,n)}B_{i-k,n-p-1}(x). \end{aligned}$$

(13)

From (3) and assuming the validity for p,  we have

$$\begin{aligned} D^{p+1}B_{i,n}(x)=\sum \limits _{k=0}^{p} \lambda _{k}^{(p,n)}\frac{n-p}{R}[B_{i-k-1,n-p-1}(x)-B_{i-k,n-p-1}(x)]. \end{aligned}$$

Collecting similar terms and using the relations

$$\begin{aligned} \left( {\begin{array}{c}p+1\\ k\end{array}}\right) =\left( {\begin{array}{c}p\\ k-1\end{array}}\right) +\left( {\begin{array}{c}p\\ k\end{array}}\right) , \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\left( {\begin{array}{c}p\\ -1\end{array}}\right) =\left( {\begin{array}{c}p\\ p+1\end{array}}\right) =0, \end{aligned}$$

we get (13) and the proof of Lemma 2 is complete. $\square$

Note 1

Since $B_{i,n}(x)=0,$ if $i<0$ or $i>n$, then formula (12) takes the form

$$\begin{aligned} D^{p}B_{i,n}(x)=\sum \limits _{k=\max (0,i+p-n)}^{\min (p,i)} \lambda _{k}^{(p,n)}B_{i-k,n-p}(x),\,0\le i,\,p\le n. \end{aligned}$$

(14)

In particular, and for the special case $R=1$, this formula coincides formula (3.1) in [20].

Corollary 1

Let $B_{i,n}(x)$ be the ith nth-degree B-polynomial, then it is not difficult to show that

$$\begin{aligned} x^{m}B_{i,n}(x)=R^{m}\frac{(i+1)_{m}}{(n+1)_{m}}B_{i+m,n+m}(x),\,\,\,0\le i\le n, \end{aligned}$$

(15)

where $(a)_{n}=\Gamma (a+n)/\Gamma (a)$ is the pochhammer symbol.

Theorem 1

Let $B_{i,n}(x)$ be the ith nth degree B-polynomial, then

$$\begin{aligned} x^{m}D^{p}B_{i,n}(x)=\sum \limits _{k=0}^{n+m+r}\Theta _{k,\,i}^{(p)}(m,r)\,B_{k,n+m+r}(x),\,\,\,\,\,0\le i\le n,\,\,p\le n,\,r\ge 0, \end{aligned}$$

(16)

where

$$\begin{aligned} \Theta _{k,\,i}^{(p)}(m,r)= & {} \dfrac{R^{m-p}n!p!(p+r)!k!}{(n+m+r-k+1)_{k}}\nonumber \\{} & {} \quad \times \sum \limits _{j=\max (0,k-(m+r+i))}^{\min (p,k+p-m-i)} \dfrac{(-1)^{j}}{j!(n-i-j)!(i+j-p)!(p-j)!}\nonumber \\{} & {} \quad \times \dfrac{1}{(p+k-i-j-m)!(m+r+i+j-k)!}. \end{aligned}$$

(17)

Proof

Using Corollary 1 and Lemma 2, we obtain

$$\begin{aligned} x^{m}D^{p}B_{i,n}(x)=\sum \limits _{k=0}^{p}C_{k}^{(i)}(m,n,p) \,B_{i-k+m,n-p+m}(x),\,\,i\ge 0,\,p\le n, \end{aligned}$$

(18)

where

$$\begin{aligned} C_{k}^{(i)}(m,n,p)=\lambda _{k}^{(p,n)}R^{m} \dfrac{(i-k+1)_{m}}{(n-p+1)_{m}}. \end{aligned}$$

(19)

By $(n-k)$-fold degree elevation (see, [28]), we can express each Bernstein basis function of degree k in the Bernstein basis of degree n as

$$\begin{aligned} B_{i,k}(x)=\sum \limits _{j=0}^{s-k}d_{j}^{(i)}(k,s)\,B_{i+j,s} (x),\,k\le s, \end{aligned}$$

(20)

where

$$\begin{aligned} d_{j}^{(i)}(k,s)=\left( {\begin{array}{c}k\\ i\end{array}}\right) \left( {\begin{array}{c}s-k\\ j\end{array}}\right) \left( {\begin{array}{c}s\\ i+j\end{array}}\right) ^{-1}. \end{aligned}$$

(21)

Then, by the aid of (20), formula (18) can be written in the form

$$\begin{aligned} x^{m}D^{p}B_{i,n}(x)= & {} \sum \limits _{k=0}^{p}C_{k}^{(i)}(m,n,p)\nonumber \\{} & {} \times \sum \limits _{j=0}^{p+r}d_{j}^{(i-k+m)}(n-p+m,n+m+r) \,B_{i+j-k+m,n+m+r}(x),\,\,r\ge 0.\nonumber \\ \end{aligned}$$

(22)

Collecting similar terms and using $B_{i,n}(x)=0,$if $i<0$ or $i>n$, then formula (22) takes the form

$$\begin{aligned} x^{m}D^{p}B_{i,n}(x)= & {} \sum \limits _{k=p-m-i}^{n-i+p+r}\left[ {} \,\sum \limits _{j=\max (0,k-(p+r))}^{\min (p,k)} C_{p-j}^{(i)}(m,n,p)\right. \nonumber \\{} & {} \left. d_{k-j}^{(i+m-p+j)}(n-p+m,n+m+r) \,\,\right] B_{i+m+k-p,n+m+r}(x).\nonumber \\ \end{aligned}$$

(23)

Substitution of (19) and (21) into (23) gives (16), and this completes the proof of Theorem 1. $\square$

According to Theorem 1, we can state the following theorem which relates the B-polynomial basis coefficients of the moments of a general-order p-derivative of a polynomial f(x) in terms of its B-polynomial basis coefficients.

Theorem 2

Assume that a polynomial f(x) of degree N at most, and the moments of a general-order p-derivative of $f(x),\,x^{m}f^{(p)}(x),$ are formally expanded in a finite series of B-polynomial basis

$$\begin{aligned} f(x)=\sum \limits _{n=0}^{N}a_{n}\,B_{n,\,N}(x), \end{aligned}$$

(24)

and

$$\begin{aligned} x^{m}f^{(p)}(x)=\sum \limits _{n=0}^{N+m+r}a_{n}^{(p)}(m,r) \,B_{n,N+m+r}(x),\,\,\,\,r\ge 0, \end{aligned}$$

(25)

then

$$\begin{aligned} a_{n}^{(p)}(m,r)=\sum \limits _{k=0}^{N}\Theta _{n,\,k}^{(p)} (m,r)\,a_{k},\,n=0,1,...,N+m+r. \end{aligned}$$

(26)

Proof

Using relation (16) gives

$$\begin{aligned} x^{m}f^{(p)}(x)=\sum \limits _{n=0}^{N}a_{n}\,\,x^{m}\,D^{p}B_{n,\,N}(x) =\sum \limits _{n=0}^{N}a_{n}\,\,\sum \limits _{k=0}^{n+m+r} \Theta _{k,\,n}^{(p)}(m,r)\,B_{k,n+m+r}(x). \end{aligned}$$

Collecting similar terms, we get

$$\begin{aligned} x^{m}f^{(p)}(x)=\sum \limits _{n=0}^{N+m+r} \left[ \sum \limits _{k=0}^{N}\Theta _{n,\,k}^{(p)}(m,r)\,a_{k}\right] \,B_{k,n+m+r}(x), \end{aligned}$$

which completes the proof of Theorem 2. $\square$

Note 2

It is to be noted here that

$$\begin{aligned} \Theta _{n,\,k}^{(0)}(0,0)=\delta _{n,k},\,\,\,0\le k,n\le N, \end{aligned}$$

(27)

and then

$$\begin{aligned} a_{n}^{(0)}(0,0)=a_{n},\,\,\,\,0\le n\le N. \end{aligned}$$

(28)

Also, it is worth to note that

$$\begin{aligned} \Theta _{n,\,k}^{(p)}(m,r)=0\text { for }\,n<k+m-p\text { or }n>k+m+p+r. \end{aligned}$$

(29)

In particular, and for the special case $m=r=0$, and using relation (29)—and after some rather manipulation—formula (26) takes the form

$$\begin{aligned} a_{i}^{(p)}(0,0)=\sum \limits _{k=-p}^{p}\Theta _{i,\,i-k}^{(p)} (0,0)\,a_{i-k},\,i=0,1,...,N, \end{aligned}$$

(30)

where

$$\begin{aligned} \Theta _{i,\,i-k}^{(p)}(0,0)=R^{-p}\,p!\sum \limits _{j=0}^{p} (-1)^{j+p}\left( {\begin{array}{c}p\\ j\end{array}}\right) \left( {\begin{array}{c}i\\ j+k\end{array}}\right) \left( {\begin{array}{c}n-i\\ p-j-k\end{array}}\right) ,\,i=0,1,...,N. \end{aligned}$$

(31)

This shows that Theorem 3.3 in [20] is a direct consequence of Theorem 2 for $R=1$.

Farouki and Rajan[29, pp.13–14] show that if the two functions f(x) and g(x) have the form

$$\begin{aligned} f(x)=\sum \limits _{i=0}^{m}f_{i}^{m}\,B_{i,\,m}(x) \,\, and\,\, g(x)=\sum \limits _{i=0}^{n}g_{i}^{n}\,B_{i,\,n}(x), \end{aligned}$$

then the product f(x)g(x) may be expressed as

$$\begin{aligned} f(x)g(x)=\sum \limits _{i=0}^{m+n} \left( \sum \limits _{j=\max (0,i-n)}^{\min (m,i)} \frac{\left( {\begin{array}{c}m\\ j\end{array}}\right) \,\left( {\begin{array}{c}n\\ i-j\end{array}}\right) }{\left( {\begin{array}{c}m+n\\ i\end{array}}\right) } f_{j}^{m}g_{i-j}^{n}\right) B_{i,\,m+n}(x). \end{aligned}$$

(32)

In view of this result and Theorem 2, the following theorem can be proved.

Theorem 3

Assume that the polynomials $f_{\ell }(x)$ of degrees $N_{\ell }\,\,(\ell =1,2,\dots ,s)$ at most, respectively, are formally expanded in finite series of B-polynomial basis

$$\begin{aligned} f_{\ell }(x)=\sum \limits _{n_{\ell }=0}^{N_{\ell }}b_{n_{\ell }}^{(\ell )} \,B_{n_{\ell },\,N_{\ell }}(x),\,\,(\ell =1,2,\dots ,s), \end{aligned}$$

(33)

and let $M_{k}=\sum _{j=1}^{k}N_{j}$, then

$$\begin{aligned} \prod \limits _{\ell =1}^{s} f_{\ell }^{(p_{\ell })}(x) =\sum \limits _{j_{s}=0}^{M_{s}}C_{j_{s}}^{(p_{1},p_{2},\dots ,p_{s})} \,B_{j_{s},M_{s}}(x),\,\,p_{\ell }\le N_{\ell },\,s\ge 2, \end{aligned}$$

(34)

where

$$\begin{aligned} C_{j_{s}}^{(p_{1},p_{2},\dots ,p_{s})}= & {} \underset{(s-1)}{\sum } \underset{(s-2)}{\sum }\dots \underset{(1)}{\sum } \,\frac{\prod \limits _{k=1}^{s}\left( {\begin{array}{c}N_{k}\\ j_{k}-j_{k-1}\end{array}}\right) }{\left( {\begin{array}{c}M_{s}\\ j_{s}\end{array}}\right) } \nonumber \\{} & {} \prod \limits _{k=1}^{s}\,a_{j_{k} -j_{k-1}}^{(p_{k})}(0,0),\,j_{s}=0,1,\dots ,M_{s}, \,j_{0}=0, \end{aligned}$$

(35)

where

$$\begin{aligned} \underset{(k)}{\sum }\equiv \sum \limits _{j_{k} =\max {(0,j_{k+1}-N_{k+1})}}^{\min {(M_{k},j_{k+1})}},\,k=1,2,\dots ,s-1, \end{aligned}$$

and

$$\begin{aligned} a_{n}^{(p_{\ell })}(0,0)=\sum \limits _{k=0}^{N_{\ell }} \Theta _{n,\,k}^{(p_{\ell })}(0,0)\,b_{k}^{(\ell )}, \,n=0,1,...,N_{\ell },\,\ell =1,2,\dots ,s. \end{aligned}$$

Proof

In view of Theorem 2, we have

$$\begin{aligned} f_{\ell }^{(p_{\ell })}(x)=\sum \limits _{n_{\ell }=0}^{N_{\ell }} a_{n_{\ell }}^{(p_{\ell })}(0,0)\,B_{n_{\ell },N_{\ell }}(x), \,\,\,\ell =1,2,\dots ,s. \end{aligned}$$

(36)

By repeating the application of formula (32)—and after some rather manipulation—one can obtain (34). $\square$

Note 3

It is worthy to note that formula (34) for the case of $s=1$ can be written as

$$\begin{aligned} f_{1}^{(p_{1})}(x)=\sum \limits _{j_{1}=0}^{M_{1}}C_{j_{1}}^{(p_{1})} \,B_{j_{1},\,M_{1}}(x), \end{aligned}$$

where the coefficients $C_{j_{1}}^{(p_{1})}$ can be defined as

$$\begin{aligned} C_{j_{1}}^{(p_{1})}=a_{j_{1}}^{(p_{1})}(0,0),\,\,\,\,0 \le j_{1}\le M_{1}. \end{aligned}$$

(37)

In view of two Theorems 2 and 3, we obtain the following corollary.

Corollary 2

Under the assumptions of two Theorems 2 and 3, we get

$$\begin{aligned} x^{m}\,\prod \limits _{\ell =1}^{s} f_{\ell }^{(p_{\ell })} (x)=\sum \limits _{j_{s}=0}^{M_{s}+m+r}a_{j_{s}}^{(p_{1}, p_{2},\dots ,p_{s})}(m,r)\,B_{j_{s},M_{s}+m+r}(x),\,\, s \ge 1, \end{aligned}$$

(38)

where

$$\begin{aligned} a_{j_{s}}^{(p_{1},p_{2},\dots ,p_{s})}(m,r) =\sum \limits _{k=0}^{M_{s}}\Theta _{j_{s},\,k}^{(0)} (m,r)\,C_{k}^{(p_{1},p_{2},\dots ,p_{s})},\,j_{s}=0,1,\dots ,M_{s}+m+r, \end{aligned}$$

(39)

In view of Note 2, formula (32) can be generalized as a direct consequence of Corollary 2 as in the following corollary.

Corollary 3

Under the assumptions of Theorem 3, we get

$$\begin{aligned} \prod \limits _{\ell =1}^{s} f_{\ell }(x) =\sum \limits _{j_{s}=0}^{M_{s}}a_{j_{s}}^{(0,0,\dots ,0)} (0,0)\,B_{j_{s},M_{s}}(x),\,\, s \ge 2, \end{aligned}$$

(40)

where

$$\begin{aligned} a_{j_{s}}^{(0,0,\dots ,0)}(0,0)=\underset{(s-1)}{\sum } \underset{(s-2)}{\sum }\dots \underset{(1)}{\sum } \,\frac{\prod \limits _{k=1}^{s}\left( {\begin{array}{c}N_{k}\\ j_{k}-j_{k-1}\end{array}}\right) }{\left( {\begin{array}{c}M_{s}\\ j_{s}\end{array}}\right) } \prod \limits _{k=1}^{s}\,b_{j_{k} -j_{k-1}},\,j_{s}=0,1,\dots ,M_{s}. \end{aligned}$$

(41)

Corollary 4

Under the conditions of two Theorems 2 and 3, we get

$$\begin{aligned}{} & {} \int \limits _{0}^{R}\omega (x)\,x^{m} \,\prod \limits _{\ell =1}^{s} f_{\ell }^{(p_{\ell })}(x) \,D_{j,M_{s}+m+r}(x)\,dx=a_{j}^{(p_{1},p_{2}, \dots ,p_{s})}(m,r),\nonumber \\{} & {} \qquad 0\le j\le M_{s}+m+r, r\ge 0,\,s \ge 1. \end{aligned}$$

(42)

3 An Application for the Solution of High-Order Linear Differential Equations with Polynomial Coefficients

In this section, we aim to discuss an algorithm for approximating solutions to qth-order ordinary linear differential equations

$$\begin{aligned} Ly(x)=\sum \limits _{j=0}^{q}p_{j}(x)\,\,y^{(j)}(x)=f(x), \end{aligned}$$

(43)

subject to the boundary conditions

$$\begin{aligned} y^{(j)}(0)= & {} \alpha _{j},\,\,\,\,j=0,1,...,q_{1}, \nonumber \\ y^{(j)}(R)= & {} \beta _{j},\,\,\,\,\,\,\,j=0,1,...,q_{2}, \end{aligned}$$

(44)

where $q_{1}+q_{2}+2=q$, or the initial conditions

$$\begin{aligned} y^{(j)}(0)=\alpha _{j},\,\,\,\,j=0,1,...,q-1, \end{aligned}$$

(45)

where $p_{i}(x),i=0,1,...,q,$ are given polynomials. Without loss of any generality, we suppose that $p_{i}(x)=\gamma _{i}x^{m_{i}},i=0,1,...,q,$ where $m_{i}$ are positive integers and $\gamma _{i}$ are constants, f(x) is a given source function and $\alpha _{j}\,\,(j=0,1,...,q_{1}),\beta _{j}$ $(\,j=0,1,...,q_{2})$ are constants. An approximation to the solution of (43) may be written as

$$\begin{aligned} y_{N}(x)=\sum \limits _{i=0}^{N}a_{i}\,B_{i,N}(x),\,N\ge q. \end{aligned}$$

(46)

In the case of boundary-value problem (43) and (44):

We make $y_{N}(x)$ satisfies the following equations:

$$\begin{aligned}{} & {} \sum \limits _{j=0}^{q}\gamma _{j}\int \limits _{0}^{R}\omega (x)\,x^{m_{j}}\,\,y_{N}^{(j)}(x)D_{n,N+m}(x)\,dx\nonumber \\{} & {} \quad =\int \limits _{0}^{R}\omega (x)f(x)\,D_{n,N+m}(x)\,dx, \,\,\,m=\underset{0\le \,j\,\le q}{\max }m_{j}, \end{aligned}$$

(47)

for $n=q_{1}+1,...,N-q_{2}-1$, and

$$\begin{aligned} y_{N}^{(j)}(0)= & {} \alpha _{j},\,\,\,\,\,\,\,\, j=0,1,...,q_{1},\nonumber \\ y_{N}^{(j)}(R)= & {} \beta _{j},\,\,\,j=0,1,...,q_{2}. \end{aligned}$$

(48)

In this case, the coefficients $a_{0},...,a_{q_{1}},a_{N-q_{2}},...,a_{N}$ can be determined as follows: According to relation (12) and $B_{i,N}(0)=\delta _{i,0},\,B_{i,\,N}(R)=\delta _{i,n},$ we have for $j=1,...,N-1$

$$\begin{aligned}{} & {} D^{j}B_{i,N}(0)=\left\{ \begin{array}{l} \lambda _{i}^{(j,\,N)},\,\,0\le i\le j, \\ 0,\,\,\,\,\,\,\,\,\,\,\,\,j<i\le N, \end{array}\right. \,\,\,\,\text {and}\nonumber \\{} & {} D^{j}B_{i,N}(R)=\left\{ \begin{array}{l} 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0\le i<N-j, \\ \lambda _{i+j-N}^{(j,\,N)},\,\,\,\,N-j\le i\le N, \end{array}\right. \end{aligned}$$

(49)

then Eq. (49) takes the form

$$\begin{aligned} \sum \limits _{i=0}^{j}\lambda _{i}^{(j,\,N)}\,a_{i} =\alpha _{j},\,\,\,j=0,1,...,q_{1}, \end{aligned}$$

(50)

and

$$\begin{aligned} \sum \limits _{i=N-j}^{N}\lambda _{i-N+j}^{(j,\,N)}\,a_{i} =\beta _{j},\,\,\,j=0,1,...,q_{2}. \end{aligned}$$

(51)

Since (50) and (51) are two triangular systems, then we obtain [15, p.362]

$$\begin{aligned} a_{i}= & {} \left[ \alpha _{i}-\sum \limits _{k=0}^{i-1} \lambda _{k}^{(i,\,N)}\,a_{k}\right] /\,\lambda _{i}^{(i,\,N)} \,,\,i=1,...,q_{1}, \nonumber \\ a_{0}= & {} \alpha _{0,\,\,\,} \end{aligned}$$

(52)

and

$$\begin{aligned} \,a_{i}= & {} [\beta _{N-i}-\sum \limits _{k=0}^{N-i-1} \lambda _{N-i-k}^{(N-i,\,N)}\,a_{N-k}]\,/ \lambda _{0}^{(N-i,\,N)},\,i=N-1,...,N-q_{2}, \nonumber \\ a_{N}= & {} \beta _{0}. \end{aligned}$$

(53)

It is not difficult to show that

$$\begin{aligned} a_{i}=\left\{ \begin{array}{l} \dfrac{1}{N!}\sum \limits _{k=0}^{i}\left( {\begin{array}{c}i\\ k\end{array}}\right) (N-k)!\,R^{k} \,\,\alpha _{k},\,\,\,\,\,i=0,1,...,q_{1}, \\ \dfrac{1}{N!}\sum \limits _{k=0}^{N-i}\left( {\begin{array}{c}N-i\\ k\end{array}}\right) (N-k)! (-\,R)^{k}\,\,\beta _{k},\,\,\,\,\,i=N-q_{2},,...,N. \end{array}\right. \end{aligned}$$

(54)

Now, the coefficients $a_{q_{1}+1},...,a_{N-q_{2}-1}$ can be obtained as follows:

In view of Theorem 2, we obtain

$$\begin{aligned} x^{m_{j}}\,y_{{N}}^{(j)}(x)=\sum \limits _{n=0}^{N+m} a_{n}^{(j)}(m_{j},r_{j})\,B_{n,N+m}(x),\,\,\,\, \,j=0,1,...,q,\,\,r_{j}=m-m_{j}, \end{aligned}$$

(55)

then substituting (55) in (47) and using the formula (26) and the orthonormal relation

$$\begin{aligned} \int \limits _{0}^{R}\omega (x)\,B_{k,N+m}(x) \,D_{n,N+m}(x)=\delta _{n,k},\,n=q_{1}+1,...,N-q_{2}-1, \end{aligned}$$

(56)

lead to

$$\begin{aligned} \sum \limits _{k=0}^{N}\left( \sum \limits _{j=0}^{q} \gamma _{j}\,\Theta _{n,\,k}^{(q)}(m_{j},r_{j})\right) a_{k}=\sum \limits _{i=0}^{N+m}c_{n,i}(N+m)\,\,f_{i}, \,\,n=q_{1}+1,...,N-q_{2}-1, \end{aligned}$$

(57)

where $f_{i}=\dfrac{1}{R}\int \nolimits _{0}^{R}\omega (x)f(x)\,B_{i,N+m}(x)\,dx.$ Any appearance of $a_{0},...,a_{q_{1}},a_{N-q_{2}},...,a_{N}$ in (57) is moved to the right-hand side, then the system of equations (57) is equivalent to the following matrix equation:

$$\begin{aligned} {A}_{{N}}^{(q)}\,{a}_{{N}}^{(q)}{=B}_{{N}}^{(q)}, \end{aligned}$$

(58)

where ${a}_{{N}}^{(q)}=[a_{q_{1}+1},...,a_{N-q_{2}-1}]^{T}$, and the elements of ${A}_{{N}}^{(q)}=(a_{n+q_{1}, \,k+q_{1}}^{(q)})_{n,k=1}^{N-(q_{1}+q_{2}+1)}$ and ${B}_{{N} }^{(q)}=[b_{q_{1}+1},...,b_{N-q_{2}-1}]^{T}$ have the forms

$$\begin{aligned} a_{n,\,k}^{(q)}=\,\sum \limits _{j=0}^{q}\gamma _{j} \,\Theta _{n,\,k}^{(j)}\,(m_{j},r_{j}), \end{aligned}$$

(59)

and

$$\begin{aligned} b_{n}=\sum \limits _{i=0}^{N+m}c_{n,i}(N+m)\,\,f_{i} -\sum \limits _{k=0}^{q_{1}}a_{n,\,k}^{(q)}\,a_{k} -\sum \limits _{k=N-q_{2}}^{N}a_{n,\,k}^{(q)}\,a_{k}, \end{aligned}$$

(60)

respectively.

In the case of the initial value problem (43) and (45):

In similar way, it can be shown that the coefficients $a_{0},...,a_{q-1}$ have the form

$$\begin{aligned} a_{i}=\dfrac{1}{N!}\sum \limits _{k=0}^{i}\left( {\begin{array}{c}i\\ k\end{array}}\right) (N-k)!\,R^{k} \,\,\alpha _{k},\,\,\,\,\,i=0,1,...,q-1, \end{aligned}$$

(61)

and the coefficients $a_{q},...,a_{N}$ can be obtained by making $y_{N}(x)$ satisfies (47) for $n=q,...,N.$ Then, the obtained equations can be written in the matrix form (58) where ${a}_{{N}}^{(q)}=[a_{q},...,a_{N}]^{T}$, and the elements of ${A}_{{N}}^{(q)}=(a_{n+q,\,k+q}^{(q)})_{n,k=1}^{N-q}$ and ${B}_{{N}}^{(q)}=[b_{q},...,b_{N}]^{T}$ have the forms (59) and

$$\begin{aligned} b_{n}=\sum \limits _{i=0}^{N+m}c_{n,i}(N+m)\,\,f_{i} -\sum \limits _{k=0}^{q-1}a_{n,\,k}^{(q)}\,a_{k}, \end{aligned}$$

(62)

respectively.

Note 4

It is worthy to note that, if the polynomials $p_{j}(x)\, (j=0,1,\dots ,q)$ have the form $p_{j}(x)=\sum \nolimits _{i=0}^{m_{j}}\gamma _{i}^{(j)}x^{i}$, then the elements of ${A}_{{N}}^{(q)}$ have the form

$$\begin{aligned} a_{n,\,k}^{(q)}=\sum \limits _{j=0}^{q} \Big (\sum \limits _{i=0}^{m_{j}}\gamma _{i}^{(j)} \,\Theta _{n,\,k}^{(j)}\,(i,m-i)\Big ). \end{aligned}$$

4 An Application for the Solution of High-Order Nonlinear Differential Equations with Polynomial Coefficients

In this section, we are interested in solving numerically the nonlinear differential equation with polynomial coefficients

$$\begin{aligned} \sum \limits _{i=0}^{q}Q_{i}(x) \left( \prod \limits _{j=1}^{s_{i}} y^{(p_{i,j})}(x)\right) =f(x), \end{aligned}$$

(63)

subject to the boundary conditions (44) or the initial conditions (45), where $Q_{i}(x)=\sum \nolimits _{k=0}^{m_{i}}\gamma _{k}^{(i)}x^{k},\, i=0,1,\dots ,q.$ Assume the proposed approximated solution $y_{N}(x)$ as in (46).

In the case of boundary-value problem (63) and (44):

We make $y_{N}(x)$ satisfies the equations (48) and

$$\begin{aligned}{} & {} \sum \limits _{i=0}^{q}\int \limits _{0}^{R}\omega (x)\,Q_{i}(x) \prod \limits _{j=1}^{s_{i}} y^{(p_{i,j})}(x)\,D_{n,sN+m}(x)\,dx\nonumber \\{} & {} \quad =\int \limits _{0}^{R}\omega (x)f(x)\,D_{n,sN+m}(x)\,dx, \,n=q_{1}+1,...,N-q_{2}-1, \end{aligned}$$

(64)

where $s=\underset{0\le \,i\,\le q}{\max }s_{i}$ and $m=\underset{0\le \,i\,\le q}{\max }m_{i}$. Using Corollary 2 gives the expansions

$$\begin{aligned} Q_{i}(x)\,\prod \limits _{j=1}^{s_{i}} y^{(p_{i,j})}(x)= & {} \sum \limits _{k=0}^{m_{i}}\sum \limits _{j_{s}=0}^{sN+m} \gamma _{k}^{(i)}a_{j_{s}}^{(p_{i,1},p_{i,2}, \dots ,p_{i,s_{i}})}\nonumber \\{} & {} (k,m-k)\,B_{j_{s},sN+m}(x),\,\, i= 0, 1,\dots , q. \end{aligned}$$

(65)

Substituting (65) in (64) leads to the system of equations

$$\begin{aligned}{} & {} \sum \limits _{i=0}^{q}\sum \limits _{k=0}^{m_{i}} \gamma _{k}^{(i)}a_{n}^{(p_{i,1},p_{i,2},\dots , p_{i,s_{i}})}(k,m-k)\nonumber \\{} & {} \quad =\int \limits _{0}^{R}\omega (x) f(x)\,D_{n,sN+m}(x)\,dx,\, n=q_{1}+1,...,N-q_{2}-1. \end{aligned}$$

(66)

Now, the coefficients $a_{0},...,a_{q_{1}},a_{N-q_{2}},...,a_{N}$ have the form (54) and the coefficients $a_{q_{1}+1},...,a_{N-q_{2}-1}$ can be obtained by solving $(N-q+1)$ nonlinear equations (66) using an appropriate solver. Substituting the obtained coefficients, $a_{i}\, (i=0,1,\dots ,N)$, in the form (46) gives the approximated solution of (63).

In the case of initial value problem (63) and (45):

In similar way, the coefficients $a_{0},...,a_{q-1}$ have the form (61). While the coefficients $a_{q},...,a_{N}$ can be obtained by making $y_{N}(x)$ satisfy (64) for $n=q,...,N,$ which can be written in the form of nonlinear equations (66) for $n=q,...,N.$ Then, these nonlinear equations can be solved using an appropriate solver to obtain these coefficients.

5 Error Analysis

In this section, we provide the studying of error resulting from the presented numerical method. For a positive integer N,  consider the space $S_{N}$ defined by

$$\begin{aligned} S_{N}=\text {Span}\{B_{0,N},\,B_{1,N},...,B_{N,N}\,\}. \end{aligned}$$

Let $P_{N}$ denote the orthogonal projection of the $\omega$-weighted $L^{2}$ onto $S_{N}.$ This projection has the following approximation properties, whose proof is standard.

Proposition 1

There exists a constant C independent of N, such that for any $h\in H^{r}[a,b]=\{y:y^{(i)}\in L^{2},\,i=0,1,..,r\}$

$$\begin{aligned} \left\| h-P_{N}h\right\| _{\infty }\le CN^{\,1/2-r} \left\| h\right\| _{r}. \end{aligned}$$

(67)

Lemma 3

The approximated solutions $y_{N}(x),$ in the form (46), of the differential Eq. (43) with the boundary conditions (44) or the initial conditions (45) satisfy the inequality

$$\begin{aligned} \left\| y_{N}\right\| _{\infty }=\underset{0\le \,i\,\le N}{\max } \left| a_{i}\right| \,. \end{aligned}$$

(68)

Proof

We have

$$\begin{aligned} \left\| y_{N}\right\| _{\infty } =\underset{0\le \,x\le R}{\max } \left| \sum \limits _{i=0}^{N}a_{i}\,B_{i,N}(x) \right| \le \underset{0\le \,i\,\le N}{\max }\left| a_{i}\right| \, \underset{0\le \,x\le R}{\max } \left| \sum \limits _{i=0}^{N}\,B_{i,N}(x)\right| . \end{aligned}$$

Using $\sum \nolimits _{k=0}^{N}\,B_{k,N}(x)=1,$ we can see that

$$\begin{aligned} \left\| y_{N}\right\| _{\infty }\le \underset{0\le \,i\,\le N}{\max } \left| a_{i}\right| . \end{aligned}$$

(69)

Also, we have

$$\begin{aligned} a_{i}=\int \limits _{0}^{R}\omega (x)y_{N}(x)\,D_{i,n}(x)\,dx,i=0,1,...N, \end{aligned}$$

then

$$\begin{aligned} \underset{0\le \,i\,\le N}{\max }\left| a_{i}\right| \le \left\| y_{N}\right\| _{\infty }\int \limits _{0}^{R}\omega (x)\,D_{i,n}(x)\,dx. \end{aligned}$$

In view of relation (11), we get

$$\begin{aligned} \underset{0\le \,i\,\le N}{\max }\left| a_{i}\right| \le \left\| y_{N}\right\| _{\infty }. \end{aligned}$$

(70)

From (69) and (70), we obtain (68). $\square$

The following lemma proves the stability of the presented solution (As an analog of the results in [8]).

Lemma 4

The obtained approximated solutions $y_{N}(x)$ satisfy the following two inequalities:

$$\begin{aligned}{} & {} \left\| y_{N}\right\| _{\infty }\le \frac{5}{4}C\,N^{-1/2} +\left\| y\right\| _{\infty }, \end{aligned}$$

(71)

$$\begin{aligned}{} & {} \left\| y_{N}\right\| _{r}\le R^{\frac{1}{r}}h_{r}^{(\alpha ,\beta )} \left( \frac{5}{4}C\,N^{-1/2}+\left\| y\right\| _{\infty }\right) , \end{aligned}$$

(72)

where $\,h_{r}^{(\alpha ,\beta )}=\,\left( 2^{\alpha +\beta }\frac{\Gamma (\alpha +1)\Gamma (\beta +1)}{\Gamma (\alpha +\beta +2)}\right) ^{\frac{1}{r} }$ and C is a constant independent of N. Hence, for sufficient large N, we have

$$\begin{aligned}{} & {} \left\| y_{N}\right\| _{\infty } \le \left\| y\right\| _{\infty }, \end{aligned}$$

(73)

$$\begin{aligned}{} & {} \left\| y_{N}\right\| _{r}\le R^{\frac{1}{r}} \,h_{r}^{(\alpha ,\beta )}\left\| y\right\| _{\infty }.\,\,\,\, \end{aligned}$$

(74)

Proof

If f is a function defined on [0, 1],  then the Bernstein polynomial $B_{N}(f,x)$ of f is given by

$$\begin{aligned} B_{N}(f,x)=\sum \limits _{k=0}^{N}f(k/N)\,b_{k,N}(x), \,\,b_{k,N}(x)=\left( {\begin{array}{c}N\\ k\end{array}}\right) x^{k}(1-x)^{N-k},\,\,\, \end{aligned}$$

converges to f(x) uniformly on [0, 1] if f is continuous there [11, 18]. Regarding the rate of converges to f(x),  Popviciu [38] has shown that

$$\begin{aligned} \left| B_{n}(f,x)-f(x)\right| \le \frac{5}{4} \,\omega _{f}\,\,(N^{-1/2}), \end{aligned}$$

(75)

where $\,\omega _{f}\,\,$is the modulus of continuity of f in [0, 1],  which have the form $\,\omega _{f}\,\,(N^{-1/2})=C$ $N^{-1/2}$. Without loss of generality, we can consider $[0,R]=[0,1],$ then we obtain

$$\begin{aligned} y_{N}(x)\simeq B_{N}(y,x)=\sum \limits _{k=0}^{N}y(k/N)\,b_{k,N}(x), \end{aligned}$$

(76)

and

$$\begin{aligned} \left| B_{N}(y,x)-y_{N}(x)\right| \le \frac{5}{4}C\,N^{-1/2}. \end{aligned}$$

(77)

Now, using (77), one can obtain

$$\begin{aligned} \left| y_{N}(x)\right| \le \left| B_{N}(y,x)-y_{N}(x)\right| +\left| B_{N}(y,x)\right| \le \frac{5}{4}C\,N^{-1/2} +\left| B_{N}(y,x)\right| , \end{aligned}$$

(78)

then using (76) and (78) give

$$\begin{aligned} \left\| y_{N}\right\| _{\infty }\le & {} \frac{5}{4}C\,N^{-1/2} +\underset{0\le \,x\le R}{\max }\left| B_{N}(y,x)\right| \nonumber \\\le & {} \frac{5}{4} C\,N^{-1/2}+\underset{0\le \,x\le R}{\max } \sum \limits _{k=0}^{N}\left| y(k/N)\right| \,b_{k,N}(x), \end{aligned}$$

(79)

From (79) and using that $\sum \nolimits _{k=0}^{N}\,b_{k,N}(x)=1\$lead to

$$\begin{aligned} \left\| y_{N}\right\| _{\infty }\le \frac{5}{4}C\,N^{-1/2} +\left\| y\right\| _{\infty }, \end{aligned}$$

then relation (71) is proved, and this implies that for sufficient large N, we have

$$\begin{aligned} \left\| y_{N}\right\| _{\infty }\le \left\| y\right\| _{\infty } \,\,as\,\,\,N\rightarrow \infty , \end{aligned}$$

and this completes the proof of (73). Also, we have

$$\begin{aligned} \left\| y_{N}\right\| _{r}= & {} \left( \int \limits _{0}^{R}\omega (x) \left| \sum \limits _{i=0}^{N}a_{i}\,B_{i,N}(x)\right| ^{r} dx\right) ^{\frac{1}{r}}\nonumber \\\le & {} \underset{0\le \,i\,\le N}{\max } \left| a_{i}\right| \,\,\left( \int \limits _{0}^{R}\omega (x) \left| \sum \limits _{i=0}^{N}B_{i,N}(x)\right| ^{r} dx\right) ^{\frac{1}{r}}, \end{aligned}$$

(80)

then using that $\sum \nolimits _{k=0}^{N}\,B_{k,N}(x)=1$ leads to obtain

$$\begin{aligned} \left\| y_{N}\right\| _{r}\le R^{\frac{1}{r}}h_{r}^{(\alpha ,\beta )} \underset{0\le \,i\,\le N}{\max }\left| a_{i}\right| . \end{aligned}$$

(81)

From (81) and using two relations (68) and (71) enable one to get

$$\begin{aligned} \left\| y_{N}\right\| _{r}\le R^{\frac{1}{r}}h_{r}^{(\alpha ,\beta )} \left\| y_{N}\right\| _{\infty }\le R^{\frac{1}{r}}h_{r}^{(\alpha ,\beta )} \left( \frac{5}{4}C\,N^{-1/2}+\left\| y\right\| _{\infty }\right) , \end{aligned}$$

then (72) is proved, and hence, for sufficient large N, we have

$$\begin{aligned} \left\| y_{N}\right\| _{r}\le R^{\frac{1}{r}}h_{r}^{(\alpha ,\beta )} \left\| y\right\| _{\infty }, \end{aligned}$$

which completes the proof of (74) and the proof of Lemma 4 is complete. $\square$

Theorem 4

Let $y(x)\in H^{r}[0,R],$ for some integer $r\ge 2,$ and $y_{N}(x)$ be the obtained approximate solution, then we have

$$\begin{aligned} \left\| y-y_{N}\right\| _{\infty }\le \lambda \left( \left\| y\right\| _{r}+\left\| y_{N} \right\| _{r}\right) N^{1/2\,-r},\, \end{aligned}$$

(82)

where $\lambda$ is a constant independent of N. Hence, for sufficient large N, we have

$$\begin{aligned} \left\| y-y_{N}\right\| _{\infty }\le \lambda \,c_{r}\,\,N^{\,1/2-r},\,c_{r}=2\,R^{\frac{1}{r}} h_{r}^{(\alpha ,\beta )}\left\| y\right\| _{\infty },\, \end{aligned}$$

(83)

in addition to

$$\begin{aligned} \left\| y-y_{N}\right\| _{\infty }=O(\,N^{\,1/2-r}), \end{aligned}$$

(84)

and

$$\begin{aligned} \left\| y-y_{N}\right\| _{\infty }\rightarrow 0 \text { as }N\rightarrow \infty . \end{aligned}$$

(85)

Proof

Let $P_{N}$ denote an orthogonal projection of the $\omega$ -weighted $L^{2}$ onto $S_{N}.$ We can define it as follows:

$$\begin{aligned} P_{N}h=\frac{M}{\mu (N)}\sum \limits _{i=0}^{N} \,\langle h,D_{i,N} \rangle \,B_{i,N}(x), \end{aligned}$$

(86)

where $\mu (N)=\sum \nolimits _{i=0}^{N}\left\| D_{i,N}\right\| _{\infty }$ for $N\ge 1$ and $\,M<1.$ Then, we can deduce that $P_{N}$ is a bounded, such that $\left\| P_{N}h\right\| _{\infty }\le M\,\left\| h\right\| _{\infty }.$

We have

$$\begin{aligned} \left\| y-y_{N}\right\| _{\infty }=\left\| y-P_{N}y+P_{N}y-y_{N}\right\| _{\infty }\le \left\| y-P_{N}y\right\| _{\infty } +\left\| P_{N}y-y_{N}\right\| _{\infty }. \end{aligned}$$

In view of Proposition 1, we get

$$\begin{aligned} \left\| y-y_{N}\right\| _{\infty }\le C_{1}N^{\,1/2-r} \left\| y\right\| _{r}+\left\| P_{N}y-y_{N}\right\| _{\infty }. \end{aligned}$$

(87)

However

$$\begin{aligned}{} & {} \left\| P_{N}y-y_{N}\right\| _{\infty }\le \left\| P_{N}y-P_{N}y_{N}\right\| _{\infty }+\left\| P_{N}y_{N}-y_{N} \right\| _{\infty }\le M\left\| y-y_{N}\right\| _{\infty }\nonumber \\{} & {} \quad +C_{2}N^{\,1/2-r} \left\| y_{N}\right\| _{r}\,, \end{aligned}$$

(88)

then the two inequalities (87) and (88) lead to

$$\begin{aligned} \left\| y-y_{N}\right\| _{\infty }\le C_{1}N^{\,1/2-r} \left\| y\right\| _{r}+C_{2}N^{\,1/2-r}\left\| y_{N}\right\| _{r}+M \left\| y-y_{N}\right\| _{\infty }. \end{aligned}$$

(89)

The inequality (89) can be written as

$$\begin{aligned} \left\| y-y_{N}\right\| _{\infty }\le \lambda \left( \left\| y\right\| _{r}+\left\| y_{N}\right\| _{r}\right) N^{1/2\,-r},\, \end{aligned}$$

where $\lambda =\frac{\max (C_{1},C_{2})}{1-M}\,$is a constant independent of N, then (82) is proved. Hence, for sufficient large N, (74) and (82) give

$$\begin{aligned} \left\| y-y_{N}\right\| _{\infty }\le \lambda \left( \left\| y\right\| _{r}+R^{\frac{1}{r}}h_{r}^{(\alpha ,\beta )} \left\| y\right\| _{\infty }\right) N^{1/2\,-r}. \end{aligned}$$

(90)

However, we have

$$\begin{aligned} \left\| y\right\| _{r}=\,\left( \int \limits _{0}^{R}\,\omega (x) \left| y(x)\right| ^{r}\,dx\right) ^{\frac{1}{r}} \le \left\| y\right\| _{\infty } \,\left( \int \limits _{0}^{R}\omega (x) \,dx\right) ^{\frac{1}{r}}=R^{\frac{1}{r}} h_{r}^{(\alpha ,\beta )}\left\| y\right\| _{\infty }, \end{aligned}$$

(91)

then using (90) and (91) lead to (83). Then, (84) and (85) are obtained directly from (83) which completes the proof of this theorem. $\square$

The following two corollaries ensure that the stability of the solutions as N increases (see [1,2,3, 8]).

Corollary 5

Under the assumptions of Theorem 4, we have for sufficient large N,  and for minimum integer $r\ge 2$, such that (83) is valid, we have

$$\begin{aligned} \left\| y_{N+1}-y_{N}\right\| _{\infty }=O(N^{\,1/2-r}), \end{aligned}$$

(92)

and

$$\begin{aligned} \left\| y_{N+1}-y_{N}\right\| _{\infty }\rightarrow 0 \,\,\text { as } N\rightarrow \infty . \end{aligned}$$

(93)

Proof

We have

$$\begin{aligned} \left\| y_{N+1}-y_{N}\right\| _{\infty }=\left\| y_{N+1} -y+y-y_{N}\right\| _{\infty }\le \left\| y_{N+1}-y\right\| _{\infty } +\left\| y-y_{N}\right\| _{\infty }. \end{aligned}$$

In view of (83), we get (92). Then, (93) is a direct consequence of (92). $\square$

Corollary 6

Under the assumptions of Theorem 4, we have for sufficient large N,  and for minimum integer $r\ge 2$, such that (83) is valid, we have

$$\begin{aligned} \left\| y_{N+1}-y_{N}\right\| _{r}=O(N^{\,1/2-r}), \end{aligned}$$

(94)

and

$$\begin{aligned} \left\| y_{N+1}-y_{N}\right\| _{r}\rightarrow 0 \,\,\text {as } N\rightarrow \infty . \end{aligned}$$

(95)

Proof

We have

$$\begin{aligned} \left\| y_{N+1}-y_{N}\right\| _{r}= & {} \left( \int \limits _{0}^{R} \,\omega (x)\left| y_{N+1}-y_{N}\right| ^{r}\,dx\right) ^{\frac{1}{r}}\nonumber \\\le & {} \left\| y_{N+1}-y_{N}\right\| _{\infty } \,\left( \int \limits _{0}^{R}\omega (x)\,dx\right) ^{\frac{1}{r}}\nonumber \\= & {} R^{\frac{1}{r}}h_{r}^{(\alpha ,\beta )}\left\| y_{N+1}-y_{N} \right\| _{\infty }, \end{aligned}$$

(96)

In view of Corollary 5, we get (94). Then, (95) is a direct consequence of (94). $\square$

Table 1 $\left\| E_{N}\right\| _{\infty }$ for $N=6,10,14.$ and various values of $(\alpha ,\beta )$ for Example 1

Table 2 Comparison between different methods for Example 1

6 Numerical Results

In this section, we use the algorithms presented in Sects. 3 and 4 to solve several numerical examples. All computations presented were performed on a computer (Intel(R) Core(TM) i9-10850 CPU@ 3.60GHz, 3600 Mhz, 10 Core(s), 20 Logical Processor (s)) running Mathematica 12 . Comparisons between the maximum absolute errors

$$\begin{aligned} \left\| E_{N}\right\| _{\infty }=\left\| y-y_{N}\right\| _{\infty } =\underset{x\in [0,1]}{\max }\left| y(x)-y_{N}(x)\right| , \end{aligned}$$

(97)

obtained by the present method and other methods proposed in [20, 21, 31, 46, 47, 49] are made. In view of Theorem 4, we have

$$\begin{aligned} \left\| E_{N}\right\| _{\infty }<{UB}_{r}(N), \end{aligned}$$

where

$$\begin{aligned} {UB}_{r}(N)=2R^{1/r}h_{r}^{(\alpha ,\beta )}N^{1/2-r} \left\| y\right\| _{\infty },\,r=1,2,3,..., \end{aligned}$$

is the upper bound of absolute errors.

Example 1

Consider the following boundary-value problem to demonstrate that the B-polynomials are powerful to approximate the solution to desired accuracy:

$$\begin{aligned} Ly(x)= & {} [D^{4}-3]y(x)=f(x),\,\,\,\,\,f(x) =-2e^{x},\,\,\,\,0\le x\le 1, \nonumber \\ \,y^{(i)}(0)= & {} 1,\,y^{(i)}(1)=e,\,i=0,1, \end{aligned}$$

(98)

whose exact solution is $y(x)=e^{x}.$ Computational results for $\left\| E_{N}\right\| _{\infty }$, with various choices of $\alpha , \beta$ and N, are presented in Table 1 with displaying the computational time (CT(s)), in seconds, to get these results. In Table 2, a comparison between the error obtained using the presented method (using $\alpha =\beta =2$), the sinc-Galerkin, modified decomposition methods, BGM, and PBGM (see, [20, 21]) is displayed which shows improved performance in the presented method. Figure 1a shows that the obtained absolute errors $E_{12}(x)$ and $E_{13}(x)$ at $\alpha =2$ and $\beta =2$, to demonstrate the convergence of solutions. Additionally, Fig. 1b shows an excellent agreement between the exact and approximate solution $y_{14}(x)$ to the given problem (98).

Remark 2

In this example, we find that $\left\| y\right\| _{\infty }=e\approx 2.71828182845904524,$ and $\left\| y_{N}\right\| _{\infty } =2.7182817685212886,2.7182817685002005,2.7182817685001983,$ for $N=6,10,14,$ respectively, with $\alpha =\beta =2$. The computations of $\left\| y_{N}\right\| _{r}$ $(r=2,...,7)$ are presented in Table 3 which show that

$$\begin{aligned} \left\| y_{N}\right\| _{r}<h_{r}^{(2,2)}\left\| y\right\| _{\infty } =\,e\,\left( \dfrac{8}{15}\right) ^{1/r}. \end{aligned}$$

These results ensure the validity of results (71)–(74) for $N=6,10,14$. Also, the computations of $\left\| y_{N}\right\| _{r}$ and $\left\| y\right\| _{r},$ $r=2,3,...7,$ and using the numerical results of $\left\| E_{N}\right\| _{\infty }=\left\| y-y_{N}\right\| _{\infty }$ in Table 1 tell us that

$$\begin{aligned} \left\| y-y_{N}\right\| _{\infty }\le \,N^{\,1/2-r} \left( \left\| y\right\| _{r}+\left\| y_{N}\right\| _{r}\right) , \,\,r=2,3,...,7, \end{aligned}$$

which ensures the validation of (82) for $N=6,10,14$. Also, the computations of upper bound

$$\begin{aligned} {UB}_{r}(N)=2h_{r}^{(2,2)}N^{1/2-r}\left\| y\right\| _{\infty } =\,2e\,\left( \dfrac{8}{15}\right) ^{1/r}N^{1/2-r}, \end{aligned}$$

for $r=2,3,4,...,7$ and $N=6,10,14$, are presented in Table 4. In view of Tables 1 and 4, we can see that $\left\| y-y_{N}\right\| _{\infty }\le \,{UB}_{r}(N),$ for $r=2,3,4,5,6,7,$ and $N=6,10,14,$ which ensures the validation of (84). In fact, the computations show that the maximum values of r such that $\left\| y-y_{N}\right\| _{\infty }\le {UB}_{r}(N)$ for $N=6,10,14$ are $r=7,11,14,$ respectively. Hence, the obtained approximated solutions $y_{N}(x)$ converge to the exact solution y(x) with order 13.5 when r = 14. Additionally, the last row of Table 1 shows the upper bounds ${MUB}_{r}(N)$ which are the maximum values of the computed upper bounds ${UB}_{r}(N)$ at $(\alpha ,\beta )\in \{(2,2),(0,1),(-1/2,-1/2),(1/20,-1/20)$,

$(1/200,-1/200)\}$ using $r=7,10,14$ and $N=6,10,14$, respectively.

Fig. 1

Figures of obtained errors $E_{N}$ and approximate solution for Example 1

Table 3 Computations of $\left\| y\right\| _{r}$ and $\left\| y_{N}\right\| _{r}$ for Example 1

Table 4 Computations of ${UB}_{r}(N)$ using $\alpha =\beta =2$ for Example 1

Example 2

Consider the following seventh-order linear boundary-value problem:

$$\begin{aligned} Ly(x)= & {} [D^{7}-x]y(x)=f(x),\,\,\,\,\,f(x)=e^{x}(x^{2}-2x-6), \,\,\,\,0\le x\le 1, \nonumber \\ y(0)= & {} 1,\,y^{(1)}(0)=0,\,y^{(2)}(0)=-1,\,\,y^{(3)}(0)=-2, \nonumber \\ y(1)= & {} 0,\,y^{(1)}(1)=-e,\,y^{(2)}(1)=-2e, \end{aligned}$$

(99)

whose exact solution is given by $y(x)=(1-x)e^{x}$. Computational results for $\left\| E_{N}\right\| _{\infty }$-error norm with various choices of $\alpha ,\beta$ and N,  are presented in Table 5. A comparison between the absolute errors obtained by using the present method (using $N =17$, $\alpha =0$, and $\beta =0$) and the methods in [46, 47] at various values of x, is given in Table 6. This shows that the present method is more accurate. Figure 2a shows Log-errors for various N values, when $\alpha =0$ and $\beta =0$, to demonstrate the stability of solutions. Additionally, Fig. 2b shows an excellent agreement between the exact and approximate solution $y_{17}(x)$ to the given problem (99).

Table 5 $\left\| E_{N}\right\| _{\infty }$ for $N=10,14,17$ and various values of $(\alpha ,\beta )$ for Example 2

Table 6 Comparison between the absolute errors of numerical results for Example 2

Fig. 2

Graph of $Log_{10}(E_{N})$ and approximate solution for Example 2

Example 3

Consider the following linear initial value problem:

$$\begin{aligned} Ly(x)= & {} [D^{8}-1]y(x)=f(x),\,\,\,\,\,f(x)=-8e^{x}, \,\,\,\,0\le x\le 1, \nonumber \\ y(0)= & {} 1,\,y^{(1)}(0)=0,\,y^{(2)}(0)=-1,\,\,y^{(3)}(0)=-2, \nonumber \\ y^{(4)}(0)= & {} -3,\,y^{(5)}(0)=-4,\,y^{(6)}(0)=-5,\,y^{(7)}(0)=-6, \end{aligned}$$

(100)

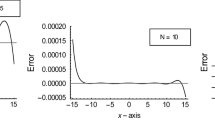
whose exact solution is given by $y(x)=(1-x)e^{x}$. Computational results for $\left\| E_{N}\right\| _{\infty }$-error norm with various choices of $\alpha ,\beta$ and N,  are presented in Table 7. A comparison between the absolute errors obtained by using the present method (using $N =20$, $\alpha =0$ and $\beta =1$) and the methods in [31, 49] at various values of x is given in Table 8. Figure 3a shows that the obtained absolute error $E_{20}(x)$ at $\alpha =0$ and $\beta =1$, to demonstrate the convergence of solutions. Additionally, Fig. 3b shows an excellent agreement between the exact and approximate solution $y_{20}(x)$ to the given problem (100).

Table 7 $\left\| E_{N}\right\| _{\infty }$ for $N=10,16,20$ and various values of $(\alpha ,\beta )$ for Example 3

Table 8 Comparison between the absolute errors of numerical results for Example 3

Fig. 3

Graph of $E_{N}$ and approximate solution for Example 3

Example 4

Consider the following initial value problem to demonstrate that the B-polynomials are powerful to approximate the solution to desired accuracy:

$$\begin{aligned}{} & {} y^{(5)}(x)+y(x)y^{(4)}(x)=f(x),\,\,0\le x\le 1,\nonumber \\{} & {} y^{(i)}(0)=0,\,i=0,1,\dots ,4, \end{aligned}$$

(101)

where f(x) is selected, such that exact solution is such that the exact solution is $y(x)=x^5\,cosx$. In Table 9, we list the obtained maximum absolute errors with different values of $\alpha , \beta$ at $N=9,13,17$. Table 10 compares the obtained absolute errors from the presented method (using $N =17$, $\alpha =-1/2$ and $\beta =-1/2$) to those of [13] at various values of x. Figure  4a shows that the obtained absolute errors $E_{16}(x)$ and $E_{17}(x)$ at $\alpha =1$ and $\beta =0$, to demonstrate the convergence of solutions. Additionally, Fig. 4b shows an excellent agreement between the exact and approximate solution $y_{9}(x)$ to the given problem (101).

Table 9 $\left\| E_{N}\right\| _{\infty }$ for $N=9,13,17$ and various values of $(\alpha ,\beta )$ for Example 4

Table 10 Comparison between the absolute errors of numerical results for Example 4

Fig. 4

Graph of $E_{N}$ and approximate solution for Example 4

Example 5

Consider the Abel equation of the second kind

$$\begin{aligned}{} & {} y(x)y^{(1)}(x)+x\,y(x)+y^{2}(x)+x^{2}y^{3}(x)=x \,e^{-x}+x^{2}\,e^{-3x},\nonumber \\{} & {} 0\le x\le 1, y(0)=1, \end{aligned}$$

(102)

where the exact solution is $y(x)=e^{-x}$. In Table 11, we list the obtained maximum absolute errors with different values of $\alpha , \beta$ at $N=5,10,20$. Table 12 compares the obtained absolute errors from the presented method (using $N=5$, $\alpha =0$ and $\beta =0$) to those of [30] at various values of x. Figure 5a shows Log-errors for various N values, when $\alpha =0$ and $\beta =1$, to demonstrate the stability of solutions. Additionally, Fig. 5b shows an excellent agreement between the exact and approximate solution $y_{6}(x)$ to the given problem (102).

Table 11 $\left\| E_{N}\right\| _{\infty }$ for $N=5,10,20$ and various values of $(\alpha ,\beta )$ for Example 5

Table 12 Comparison between the absolute errors of numerical results for Example 5

Fig. 5

Graph of $Log_{10}(E_{N})$ and approximate solutions for Example 5

Example 6

Consider the boundary value problem

$$\begin{aligned}{} & {} x\,y(x)y^{(2)}(x)+x^{2}\,y(x)+x\,y^{2}(x)+x^{3}y^{3}(x) =f(x),\,\,0\le x\le 1,\nonumber \\{} & {} y(0)=0,y(1)=\frac{1}{e}, \end{aligned}$$

(103)

where f(x) is selected, such that the exact solution is $y(x)=x^{1.5}\,e^{-x}$.

In Table 13, we list the obtained maximum absolute errors with different values of $\alpha , \beta$ at $N=10,15,20$. Figure 6a shows Log-errors for various N values, when $\alpha =1$ and $\beta =0$, to demonstrate the stability of solutions. Additionally, Fig. 6b shows an excellent agreement between the exact and approximate solution $y_{10}(x)$ to the given problem (103).

Remark 3

In Example 6, the proposed algorithm is applied to a nonlinear differential equation with a nonsmooth solution. Also, Table 13 shows that the obtained accuracy is less than that obtained in Examples 1–5 where the exact solutions are smooth. Therefore, the effectiveness of the proposed algorithm in the case of problems that have nonsmooth solutions is lower but still accepted.

Table 13 $\left\| E_{N}\right\| _{\infty }$ for $N=10,15,20$, and various values of $(\alpha ,\beta )$ for Example 6

Fig. 6

Graph of $Log_{10}(E_{N})$ and approximate solutions for Example 6

7 Conclusions

The proposed algorithm discussed some properties and formulae related to B-polynomials which are utilized with either the boundary conditions (44) or the initial conditions (45) to obtain explicitly the q unknown expansion coefficients (54) or (61), respectively. This algorithm leads to a linear algebraic system of $(N-q+1)$ equations in $(N-q+1)$ unknowns which has the matrix form (58) when the numerical solution of a linear differential equation with polynomial coefficients is discussed. While it leads to a nonlinear algebraic system of $(N-q+1)$ equations in $(N-q+1)$ unknowns when the numerical solution of a nonlinear differential equation with polynomial coefficients is discussed. In each case, a comparison between the absolute errors obtained by the presented method and other methods is given. Furthermore, in all of the numerical examples presented, agreements were reached for between $10^{-16}$ and $10^{-20}$. All computations presented were performed on a computer running Mathematica 12 [Intel(R) Core(TM) i9-10850 CPU@ 3.60 GHz, 3600 Mhz, 10 Core(s), 20 Logical Processor (s)]. We have shown that the presented B-polynomial method will return a valid solution for a differential equation and is a powerful tool that we may utilize to overcome the difficulties associated with boundary and initial value problems with less computational effort. We have also provided some theoretical results regarding the error resulting from the presented numerical method. These theoretical results have been validated through the presented numerical examples, and the corresponding explanations have been given.