Keywords

1 Introduction

Active magnetic bearings (AMBs) have the advantages of no friction, no lubrication or sealing requirements, long lifespan, low maintenance and active vibration control and have widely application in helium-turbine circle of the high temperature gas-cooled reactor and many other high-speed rotating machinery [1, 2]. In fact, the dynamic characteristics of AMBs mainly depend on the controller. A suitable controller is the core problem of AMBs design. As a matter of fact, the AMB-rotor system is open-loop unstable because of the high nonlinearity of electromagnetic bearing force. Besides, the AMBs-rotor system is always influenced by external disturbance, which makes it harder to design a suitable controller to achieve moderate rotor displacement response during normal operation.

In order to solve this problem, many researches have been carried out. The proportional-integral-differential (PID) controller is widely used in industrial applications because of its simplicity and robustness. Markus Hutterer designed PID controller through linear quadratic regulator method and validated the controller on a turbomolecular pump [3]. Tianhao Zhou proposed a robust PD control via eigenstructure assignment and evaluated the closed-loop sensitivity to change of the bias current [4]. Sun zhe applied a PID controller on a prototype of a 27000 rpm/150 kw blower and analyzed the nonlinearity of the system [5]. Chenzi Liu proposed a simple lead-lag controller, which parameters were determined through backprogation neural network [6].

Moreover, many advanced controllers have also been developed. Alexander presented a μ-synthesis-based controller to robustly minimize the difference between the tool reference and the estimated tool position in tooltip tracking spindle [7]. Syed Muhammad amrr proposed a robust control law based on high-order sliding mode control scheme, and carried out numerical analysis [8]. Xuan Yao proposed a dual-loop neural network sliding mode control to achieve large-motion rotor tracking, and validated its effectiveness through simulations [9].

These advanced controllers show better performance compared with PID controllers, but they have more complex structure and may have difficulties in parameter adjustment. Besides, they are model-based controller and may have deteriorated performance on an imprecise model.

Nowadays, linear active disturbance rejection controllers (LADRCs) have been attractive because it can achieve robust performance on an imprecise model and can simply realize parameter adjustment [10,11,12,13,14].

In this paper, a plant model of the decentralized controller is established based on the AMB-rigid rotor system model. This model adopts lumped uncertainty to describe nonlinear error and external load disturbance. Furthermore, a LADRC is designed, which can attenuating the impact of model nonlinear and external disturbance. The LADRC contains a proportional-differential controller and a three-order external state observer. The adjustable parameters of the LADRC can be selected according to pole assignment. In order to verify the effectiveness of the LADRC, levitation experiments, rotation experiments, and re-levitation experiments are carried out with traditional PID controller as comparison.

This paper is organized as follows. First, in Sect. 2, the plant model of the decentralized controller is established. Then, the LADRC is designed in Sect. 3. Experiments are developed in Sect. 4. Finally, Sect. 5 concludes this paper.

2 Description of the AMB-rotor System

2.1 The Rotor Model

Fig. 1.
figure 1

AMB-rotor system

Full size image

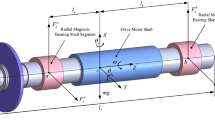
The structure of the AMB-rigid rotor system is shown in Fig. 1. \(x_{c} ,y_{c}\) denote the displacement of the centroid of rotor; \(\alpha ,\beta\) are the angular displacement of the rotor around x and y axes. \(l_{bA} ,l_{bB} ,l_{sA} ,l_{sB}\) show the distance between the A/B bearing/sensor and the centroid. In AMB-rigid rotor system, the coupling between the axial DOF and radial DOF is negligible. Thus, axial DOF is not mentioned in this model and merely radial 4 DOF and axial angle \(\gamma\) are considered. There are three popular coordinates to illustrate the motion of rotor, which are centroid coordinate \({\mathbf{y}}^{c} = \left[ {\begin{array}{*{20}c} {x_{c} } & \alpha & {y_{c} } & \beta \\ \end{array} } \right]^{T}\), sensor coordinate \({\mathbf{y}}^{s} = \left[ {\begin{array}{*{20}c} {y_{Ax}^{s} } & {y_{Ay}^{s} } & {y_{Bx}^{s} } & {y_{By}^{s} } \\ \end{array} } \right]^{T}\) and bearing coordinate \({\mathbf{y}}^{b} = \left[ {\begin{array}{*{20}c} {y_{Ax}^{b} } & {y_{Ay}^{b} } & {y_{Bx}^{b} } & {y_{By}^{b} } \\ \end{array} } \right]^{T}\). \({\mathbf{y}}^{c}\) describes the displacement of rotor centroid, \({\mathbf{y}}^{s}\) and \({\mathbf{y}}^{b}\) are rotor displacement at sensor/bearing. The relation between them can be expressed as \({\mathbf{y}}^{s} = {\mathbf{T}}_{s}^{sc} {\mathbf{y}}^{c} ,{\mathbf{y}}^{s} = {\mathbf{T}}_{b}^{cb} {\mathbf{y}}^{b}\), in which

$$ {\mathbf{T}}_{b}^{cb} = \left[ {\begin{array}{*{20}c} 1 & 0 & 1 & 0 \\ 0 & { - l_{bA} } & 0 & {l_{bB} } \\ 0 & 1 & 0 & 1 \\ {l_{bA} } & 0 & { - l_{bB} } & 0 \\ \end{array} } \right],{\mathbf{T}}_{s}^{sc} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & {l_{sA} } \\ 0 & { - l_{sA} } & 1 & 0 \\ 1 & 0 & 0 & { - l_{sB} } \\ 0 & {l_{sB} } & 1 & 0 \\ \end{array} } \right] $$

Define bearing force as \({\mathbf{f}}_{b}^{b} = \left[ {\begin{array}{*{20}c} {f_{bAx} } & {f_{bAy} } & {f_{bBx} } & {f_{bBy} } \\ \end{array} } \right]^{T}\) under bearing coordinate, and then define external disturbance as \({\mathbf{f}}_{g}^{c} = \left[ {\begin{array}{*{20}c} {f_{gx}^{c} } & {f_{g\alpha }^{c} } & {f_{gy}^{c} } & {f_{g\beta }^{c} } \\ \end{array} } \right]^{T}\) under rotor centroid coordinate. The equation of motion of the rotor can be written as:

$$ \left\{ \begin{gathered} m\ddot{x}_{c} = f_{bAx} + f_{bBx} + f_{gx}^{c} \\ J_{r} \ddot{\alpha } + J_{z} \dot{\gamma }\dot{\beta } = - l_{bA} f_{bAy} + l_{bB} f_{bBy} + f_{g\alpha }^{c} \\ m\ddot{y}_{c} = f_{bAy} + f_{bBy} + f_{gy}^{c} \\ J_{r} \ddot{\beta } + J_{z} \dot{\gamma }\dot{\beta } = l_{bA} f_{bAx} - l_{bB} f_{bBx} + f_{g\beta }^{c} \\ \end{gathered} \right. $$
(1)

Transform Eq. (1) to sensor coordinate, it gives:

$$ \left\{ \begin{gathered} \ddot{y}_{Ax}^{s} = - \frac{{J_{z} \Omega l_{sA} }}{{J_{r} \left( {l_{sA} + l_{sB} } \right)}}\left( {\dot{y}_{Ay}^{s} - \dot{y}_{By}^{s} } \right) + \left( {\frac{1}{m} + \frac{{l_{bA} l_{sA} }}{{J_{r} }}} \right)f_{bAx} \\ + \left( {\frac{1}{m} - \frac{{l_{sA} l_{bB} }}{{J_{r} }}} \right)f_{bBx} + f_{gAx}^{s} \\ \ddot{y}_{Ay}^{s} = - \frac{{J_{z} \Omega l_{sA} }}{{J_{r} \left( {l_{sA} + l_{sB} } \right)}}\left( {\dot{y}_{Bx}^{s} - \dot{y}_{Ax}^{s} } \right) + \left( {\frac{1}{m} + \frac{{l_{bA} l_{sA} }}{{J_{r} }}} \right)f_{bAy} \\ + \left( {\frac{1}{m} - \frac{{l_{sA} l_{bB} }}{{J_{r} }}} \right)f_{bBy} + f_{gAy}^{s} \\ \ddot{y}_{Bx}^{s} = - \frac{{J_{z} \Omega l_{sB} }}{{J_{r} \left( {l_{sA} + l_{sB} } \right)}}\left( {\dot{y}_{By}^{s} - \dot{y}_{Ay}^{s} } \right) + \left( {\frac{1}{m} - \frac{{l_{bA} l_{sB} }}{{J_{r} }}} \right)f_{bAx} \\ + \left( {\frac{1}{m} + \frac{{l_{bB} l_{sB} }}{{J_{r} }}} \right)f_{bBx} + f_{gBx}^{s} \\ \ddot{y}_{By}^{s} = - \frac{{J_{z} \Omega l_{sB} }}{{J_{r} \left( {l_{sA} + l_{sB} } \right)}}\left( {\dot{y}_{Ax}^{s} - \dot{y}_{Bx}^{s} } \right) + \left( {\frac{1}{m} - \frac{{l_{bA} l_{sB} }}{{J_{r} }}} \right)f_{bAy} \\ + \left( {\frac{1}{m} + \frac{{l_{bB} l_{sB} }}{{J_{r} }}} \right)f_{bBy} + f_{gBy}^{s} \\ \end{gathered} \right. $$
(2)

For slender rotor, the rotor shape usually satisfies \(\left| {\frac{1}{m} + \frac{{l_{bA} l_{sA} }}{{J_{r} }}} \right| \gg \left| {\frac{1}{m} - \frac{{l_{sA} l_{bB} }}{{J_{r} }}} \right|,\left| {\frac{1}{m} + \frac{{l_{bB} l_{sB} }}{{J_{r} }}} \right| \gg \left| {\frac{1}{m} - \frac{{l_{sB} l_{bA} }}{{J_{r} }}} \right|,\) and \(J_{r} \gg J_{z}\). Then, Eq. (2) can be simplified as

$$ \ddot{y}^{s} = k_{stru} f_{b} { + }f_{g}^{s} $$
(3)

where \(k_{stru} = \frac{1}{m} + \frac{{l_{bA} l_{sA} }}{{J_{r} }}\) in AMB A and \(k_{stru} = \frac{1}{m} + \frac{{l_{bB} l_{sB} }}{{J_{r} }}\) in AMB B.

2.2 The AMB Model

The AMB always works under differential-driven mode, shown in Fig. 2. There are two electromagnets placed in one direction, since each electromagnet can only achieve attractive force. The electromagnetic force generated by the single electromagnet can be expressed as

$$ f_{p} = k\frac{{i_{a}^{2} }}{{s^{2} }},k = \frac{{\mu_{0} AN^{2} }}{4}\cos \theta $$
(4)

where \(i_{a}\) is the current, s is the gap, \(\mu_{0}\) is the magnetic field constant in vacuum, N is the number of coils turns, A is the cross-section area of the pole and \(\theta\) is the angle of the electromagnet. Then, the net AMB force in one direction is the differential force of a pair of electromagnets. The net force can be linearized around the neighborhood of the operating point [1, 15], and can be expressed as

$$ f_{b} = k_{i} i_{c} + k_{s} y^{s} $$
(5)

where \(i_{c} = i_{a1} - i_{a2}\), \(k_{i}\) and \(k_{s}\) are the current-force factor (in N/A) and the displacement-force factor (in N/m) respectively.

Fig. 2.
figure 2

Differential-driven mode in AMBs. (a) AMB force of a radial magnet. (b) AMB force of a pair of magnets.

Full size image

2.3 The AMB-rotor Model

Substituting Eq. (5) into (3), the decentralized AMBs-rotor model can be written as:

$$ \ddot{y}^{s} = k_{stru} k_{i} i_{c} + k_{stru} k_{s} y^{s} { + }f_{g}^{s} $$
(6)

It is noticed that the precise position of the rotor centroid is hard to determine due to its complex shape and its heterogeneous material, which indicate \(k_{stru}\) has uncertainty. This parameter variation can be described as \(k_{stru} { = }\left( {1 + \lambda } \right)k_{stru,0}\). Then, Eq. (6) can be rewritten as

$$ \ddot{y}^{s} = k_{x0} \left( {1 + \lambda } \right)\left( {i_{c} + \frac{{k_{s} }}{{k_{i} }}y^{s} } \right){ + }f_{g}^{s} $$
(7)

where \(k_{x0} { = }k_{i} k_{stru,0} .\)

3 LADRC Design

Fig. 3.
figure 3

The structure of LADRC.

Full size image

The structure of LADRC is shown in Fig. 3. The LADRC contains a proportional-differential controller and a three-order external state observer. The transfer function of the proportional-differential (PD) controller and the linear extended state observer (LESO) in LADRC can be written as

$$ \begin{gathered} u_{PD} (s) = - k_{c} \frac{{\alpha s + \omega_{c} }}{{s + \omega_{c} }}y^{s} (s) \hfill \\ u_{ESO} (s) = \frac{{\omega_{0}^{3} s^{2} y_{r} (s) + k_{x0} i_{c} (s)}}{{(s + \omega_{0} )^{3} }} \hfill \\ \end{gathered} $$
(8)

where \(\omega_{0}\) is the bandwidth of the LESO, \(k_{c} ,\omega_{c} ,\alpha\) are parameters of the PD controller.

Thus, the transfer function of LADRC can be obtained as

$$ G_{c} (s) = \frac{{i_{c} \left( s \right)}}{{y^{s} \left( s \right)}} = - \frac{{k_{c} (\alpha s + \omega_{c} )(s + \omega_{0} )^{3} + \omega_{0}^{3} s^{2} (s + \omega_{c} )}}{{k_{x0} s(s + \omega_{c} )(s^{2} + 3\omega_{0} s + 3\omega_{0}^{2} )}}. $$
(9)

The transfer function of the closed-loop system can be written as

$$ G_{cl} \left( s \right) = \frac{{y^{s} \left( s \right)}}{{f_{g}^{s} \left( s \right)}} = \frac{{k_{i} }}{{k_{i} s^{2} - k_{x0} \left( {1 + \lambda } \right)\left[ {k_{i} G_{c} \left( s \right) - k_{s} } \right]}}. $$
(10)

Therefore, the closed-loop system can achieve robust stability through proper pole assignment. If designing \(\omega_{0} = 50,\omega_{c} = 500,\alpha = 3.25,k_{c} = 25\) with nominal parameter \(k_{x0} = 20\), the root locus of the closed-loop system with parameter variation can be calculated. Consider that the range of \(\lambda\) is \(\lambda \in \left[ {0.5,1.5} \right]\). The roots of the closed-loop system (10) is shown in Fig. 4. The designed LADRC shows good robustness. The mapping from \(f_{g}^{s} \left( s \right)\) to \(y^{s} \left( s \right)\) under the LADRC is shown in Fig. 5. This demonstrates the capability of the LADRC to suppress the disturbance \(f_{g}^{s} \left( s \right)\) under the plant with lumped uncertainty. In fact, \(f_{g}^{s} \left( s \right)\) mainly contains a static load and unbalanced force. Unbalanced force causes an auto-balance effect after rigid critical speed; thus, it does not require compensation within a high-frequency range. The peak is larger when \(\lambda\) is smaller.

Fig. 4.
figure 4

The root locus diagram of the closed-loop system under LADRC.

Full size image
Fig. 5.
figure 5

The mapping from \(f_{g}^{s}\) to \(y^{s}\) under LADRC.

Full size image

4 Experimental Results

This section contains two type of experiments, levitation experiments, and rotation experiments. In levitation experiments, the transient responses are analyzed. In rotation experiments, the analysis of rotor displacement responses within working speed range are given.

4.1 Description of the Experimental Platform

In order to verify the effectiveness of the LADRC, verification experiments are carried out on the AMBs-supported permanent magnet synchronous motor platform at Tsinghua University [16], pictured in Fig. 6. The rotor of the platform is 0.4866 m long with a total mass of 13.98 kg and is horizontally supported by two radial AMBs and one axial AMB. The radial clearance of the AMBs is 0.4 mm and the clearance of touchdown bearings (TDBs) is 0.2 mm. Radial and axial displacements of the rotor were measured by five inductive sensors. Ten pulse width modulated amplifiers power the magnet coils to generate the expected bearing force.

For comparison, a traditional PID controller, the most popular controller in industrial practice, is involved in this section. This PID controller is well-designed and performs well in various working conditions.

Fig. 6.
figure 6

The experimental platform.

Full size image

4.2 Levitation Experiments

The transient response at AMB A of levitation experiments are shown in Fig. 7 and Fig. 8 since AY channel has the worst results of the four. Sub-figure (a) gives the rotor trajectory. In this sub-figure, the transient response is divided into 3 phases. The first phase ends when the differential signal reaches its maximum. In this phase, the proportional signal plays the most important role. It starts at its maximum absolute value and its proportion in the total control signal gradually reduce. This phase is very short and the end position of the rotor during this phase mostly depends on the PD controller. The PID and LADRC nearly have similar displacement response in this phase. The second phase ends when the proportional signal line intersects with the compensation signal line (I in PID and ESO in LADRC) at the first time. During this phase, the compensation signal increase gradually and cannot be ignored. The displacement response of the rotor results from the combined influence of three signals and is more complex. Under PID, this phase is about 0.042 s and the rotor trajectory in Fig. 7(a) displays fluctuation. Under LADRC, this phase is 0.012 s and there is less fluctuation in rotor trajectory because ESO signal has faster response. The third phase ends when the displacement response remains within 5% of the radial clearance of the TDBs (0.2 mm). The compensation signal plays important role in this phase. Since ESO signal has faster response, this phase is shorter under LADRC controller. The total startup period is 0.14 s under PID and is 0.05 s under LADRC, which shows LADRC have better performance in transient response. This indicator is significant for AMB controllers.

Fig. 7.
figure 7

The transient response in levitation experiments under PID controller

Full size image

4.3 Rotation Experiments

Rotation experiments are of great significance not only due to being the most common working conditions but also because synchronous excitation caused by residual unbalance can help to analyze the frequency domain characteristics of the system and the control strategy.

Fig. 8.
figure 8

The transient response in levitation experiments under LADRC

Full size image
Fig. 9.
figure 9

The displacement response in rotation experiments under PID and LADRC controller

Full size image

The displacement response of rotation experiments from 0–200 Hz (up to 12000 r/min) under PID and LADRC are given in Fig. 9. During the rigid rotation speed range, both of the two controllers show good displacement response. The amplitude of vibration remains within half of the TDBs clearance. There are four peaks within the speed range, shown in Fig. 9 (a), which correspond to the four vibration modes of the system.

However, LADRC shows better performance at the four peaks and under 100 Hz. It seems that the proposed LADRC have better damping property. When it comes to low rotating speed range, it indicates that ESO signal shows better performance in isolation of low-frequency vibration. There is a feedback loop in ESO, so that ESO signal has a more specific frequency truncation characteristic than integral signal. In fact, integral signal shows obvious synchronous fluctuations until 60 Hz while it vanishes at 20 Hz in ESO signal. Besides, the integral signal always has phase lag, which further suppress the effect of differential signal and make the AMBs show less damping than designed.

5 Conclusions

In view of the high nonlinearity, parameter perturbation and external disturbance existing in AMB-rotor system, a LADRC is designed in this paper to suppress the rotor displacement response while attenuating the impact of uncertainties. A plant model of the decentralized controller is established with lump uncertainties including the model error of the AMB force, the external load, and related parametric perturbation. Then, a LADRC is designed. The LADRC contains a proportional-differential controller and a three-order external state observer. The adjustable parameters of the LADRC can be selected according to pole assignment. In order to verify the effectiveness of the LADRC, levitation experiments and rotation experiments are carried out with traditional PID controller as comparison.