Keywords

1 Introduction

Nuclear energy is a clean and efficient energy source that can also facilitate the reduction of carbon emissions for power generation in countries worldwide, thereby providing essential solutions toward sustainable human development. In 2002, the American Nuclear Society proposed six Generation IV advanced nuclear reactor types [1]. Compared with other fast reactors, the structure of lead-cooled fast reactors has been significantly simplified [2]. Moreover, many countries are trying to implement lead-cooled fast reactors as they have attracted considerable attention due to their good nuclear fuel transmutation capability, excellent economics, and inherent safety [3].

Lead-cooled fast reactors mostly use spacer wires for positioning to maintain the fuel rods at the same pitch. A reasonable thermal-hydraulic design inside the core enables the safe operation of fuel assemblies and other components in a reactor. Therefore, it is imperative to elucidate the flow characteristics of fuel assemblies with spacer wires. The thermal-hydraulic properties of heavy metals greatly differ from those of conventional media; thus, the radiation shielding of lead critically hampers experimental analysis, and the internal flow characteristics cannot be studied using devices such as X-rays [4]. Given this limitation, most previous studies have used numerical simulations to obtain the thermal-hydraulic parameters.

Ahmad performed numerical simulations of a 7-rod bundle assembly and found that the transverse gradient induced by spacer wires exhibited certain periodic pattern among the sub-channels [5]. Gajapathy performed numerical simulations of the flow field inside various rod bundle assemblies containing spacer wires and found that increasing the diameter of the spacer wires while decreasing the pitch increased the friction coefficient and Nussle number [6]. Hamman revealed a 10–15% error in pressure drop calculations compared to empirical formulations; this error was affected by the factors such as turbulence and geometric models [7]. Merzari performed numerical calculations using various RANS models for a 7-rod bundle assembly containing spacer wires and demonstrated that the k–ω SST model better simulated the velocity field near the spacer wires [8]. Zhao performed numerical calculations using OpenFOAM for a single-pitch model of a 7-rod bundle assembly of sodium-cooled and analyzed the distribution of transverse velocities in different gaps [9]. Overall, a significant corpus of previous studies about spacer wires was focused on full-size calculations based on coarser large-size grids. In this way, they determined the outcomes for larger-size models and calculations using commercial software for 7-rod bundle and 19-rod bundle assembly models.

Given the complexity of spacer wires, the effect of multi-pitch axial height, and the subsequent two-phase flow model development, this study investigated the flow characteristics of lead-bismuth coolant in a lead-based fast reactor within a fuel assembly containing spacer wires. Methodologically, we used the open-source OpenFOAM software to refine the calculation of multi-pitch wire-wrapped bundle assemblies in CiADS [10] and provide interface parameters for two-phase flow model development under accident conditions.

2 Models and Methods

2.1 Geometric Model

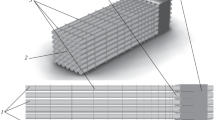
For advanced reactors with a conventional design of lead/lead-bismuth alloy as coolant, the fuel rods are usually arranged in a triangular fashion to form a hexagonal assembly, as shown in Fig. 1. The sub-channels of the assembly are divided into three types, namely internal, edge, and corner channels.

Fig. 1.
figure 1

Sub-channel division method of the fuel assembly

Full size image

In this study, we referred to the fuel assembly parameters in CiADS [11] for the simulations. The regular hexagonal fuel assembly contained 60 fuel rods and one stainless steel rod located in the center. The stainless-steel rod represented a locking device designed to prevent the assembly from floating in the liquid lead/lead-bismuth alloy. The simulation area was part of the active area of the fuel assembly. The spacer wires were placed in the clockwise direction. The geometric parameters of the fuel assemblies are summarized in Table 1.

Table 1. The geometry parameters of the fuel assembly
Full size table

The spacer wires and fuel rods were aligned tangentially to each other, thus signifying a line contact and forming sharp angles at the contact location where the points and lines affected the quality of the grids. The model simplification used in this study was based on the Natesan [12] approach, as shown in Fig. 2. To this end, the diameters of fuel rods and spacer wires were kept constant, and indent spacer wires were placed toward the center of fuel rods by 0.1 mm. To improve the quality of the generated grids, a 0.25 mm chamfering process was performed at the location where the spacer wires and fuel rods were in contact. Figure 3 shows the geometric model of the fuel assembly.

Fig. 2.
figure 2

Simplified model approach

Full size image
Fig. 3.
figure 3

61 wire-wrapped rod bundle assembly (a) top view (b) 3D view

Full size image

2.2 Grid Division

It is challenging to delineate the structured grids for complex geometric features, such as many large-curvature spacer wire surfaces in the fuel assembly. This simulation was used to delineate the polyhedral grids for spacer wires. The grid encryption process is described in Table 2, while the grid division in the Z-plane is shown in Fig. 4. The quality of grids was evaluated by the “checkMesh” method in OpenFOAM. The evaluation demonstrated that the grids satisfied the computational requirements.

Table 2. Method of grid encryption
Full size table
Fig. 4.
figure 4

Section of grid in Z direction

Full size image

2.3 Boundary Condition Setting

For numerical simulation problems, suitable boundary conditions must be provided for each boundary, according to the actual working conditions. Table 3 lists the established boundary conditions based on the CiADS [10, 11] method.

Table 3. Boundary conditions for the fuel assembly
Full size table
Fig. 5.
figure 5

Axial linear power density distribution of fuel rods

Full size image

2.4 Coolant Thermal Physical Parameters and Turbulence Model

Due to the special thermal properties of lead-bismuth, it will show different phenomena from the conventional coolant in the calculation process, and according to the recommendation of OECD/NEA [15], the expression of the thermal property parameter was selected as follows.

Density, kg/m3:

$$ \rho_{{{\text{LBE}}}} = {11096} - {1}{\text{.3236}}T $$
(1)

Constant pressure specific heat capacity, J/(\({\text{kg}} \cdot {\text{K}}\)):

$$ C_{{p{\text{,LBE}}}} = {159}{\text{.0}} - 0.0272T + {7}{\text{.12}} \times {10}^{ - 6} T^{2} $$
(2)

Power viscosity, \({\text{Pa}} \cdot {\text{s}}\):

$$ \mu_{{{\text{LBE}}}} = {0}{\text{.00456}} - {7}{\text{.03}} \times {10}^{ - 6} T + {3}{\text{.61}} \times {10}^{ - 9} T^{2} $$
(3)

Thermal conductivity, W/(\({\text{m}} \cdot {\text{K}}\)):

$$ \lambda_{{\text{ LBE}}} = {3}{\text{.61}} + 1.517 \times {10}^{ - 2} T - {1}{\text{.741}} \times {10}^{ - 6} T^{2} $$
(4)

The comparison with the LES calculation results of Merzari [8] shows that the k-ω SST model calculations agree better compared to the k-ε turbulence model, so the k-ω SST turbulence model was used in this calculation. The k-ω SST turbulence model can be described by the following five equations:

$$ \frac{{{\text{D}}(\rho \omega )}}{{{\text{D}}t}} = \frac{\partial }{{\partial x_{i} }}\left( {\left( {\mu + \sigma_{k} \mu_{t} } \right)\frac{\partial k}{{\partial x_{i} }}} \right) + G_{\omega } - \rho \beta^{*} \omega k $$
(5)
$$ \frac{{{\text{D}}(\rho \omega )}}{{{\text{D}}t}} = \frac{\partial }{{\partial x_{i} }}\left( {\left( {\mu + \sigma_{\omega } \mu_{t} } \right)\frac{\partial k}{{\partial x_{i} }}} \right) + G_{k} - \rho \beta \omega^{2} + 2\left( {1 - F_{1} } \right)\rho \sigma_{{\omega^{2} }} \frac{1}{\omega }\frac{\partial k}{{\partial x_{i} }}\frac{\partial \omega }{{\partial x_{i} }} $$
(6)
$$ G_{k} = \rho \gamma S^{2} - \frac{2}{3}\rho k\frac{{\partial U_{i} }}{{\partial x_{i} }} - \frac{2}{3}\mu_{t} \left( {\frac{{\partial U_{i} }}{{\partial x_{i} }}} \right)^{2} $$
(7)
$$ G_{\omega } = \rho \gamma \left( {{\text{S}}^{2} - \frac{2}{3}\left( {\frac{{\partial U_{i} }}{{\partial x_{i} }}} \right)^{2} - \frac{2}{3}\omega \frac{{\partial U_{i} }}{{\partial x_{i} }}} \right) $$
(8)
$$ F_{1} = \tanh \left( {\min \left( {\max \left( {\frac{\sqrt k }{{0.09\omega y}},\frac{500v}{{\omega y^{2} }}} \right),\frac{2k}{{y^{2} CD_{k\omega } }}} \right)^{4} } \right) $$
(9)

In these equations, ρ is the density (kg/m3). Gk is the generating term of turbulent kinetic energy k. Gω is the generating term of the specific dissipation rate ω. t is the time term (s). x is the Cartesian coordinate system direction. μ is the kinetic viscosity (\({\text{Pa}} \cdot {\text{s}}\)). μt = ρkT, and T is the turbulence time scale. The parameters σk, \(\sigma_{{\omega^{2} }}\), β*, β are solved by the mixing function. γ is the cross-mixing factor. S is the mode of the mean stress tensor of the fluid. U is the fluid velocity (m/s). y is the distance from the wall. ν is the fluid kinematic viscosity. CDkω is the term associated with the lateral diffusion term of the fluid.

2.5 Grid Independence Analysis

According to the 61-rod bundle assembly model, grids were classified into three groups with different degrees of sparseness. The grid-independence analysis was carried out by comparing the variation in temperature along the axial direction near the central rod bundle. The number of grids and the calculated y+ for the three cases are summarized in Table 4. As seen, all three cases yielded the average value of y+ less than 1. Figure 6 shows a comparison of the calculated results for the three temperature groups. As observed, the calculated results for the grid number of 16.9 million were very close to the calculated results for the grid number of 26.7 million. Furthermore, the accuracy of the calculation and the length of the calculation time were taken into account, and Case 2 was selected as the grid division scheme for the subsequent calculation.

Table 4. Grids for independence studies
Full size table
Fig. 6.
figure 6

Grid independence analysis

Full size image

2.6 Solver Validation

buoyantSimpleFoam is a finite-volume method-based solver for solving the N-S equation for a steady-state compressible Newtonian fluid in OpenFOAM. The SIMPLE/SIMPLEC algorithm was used in this study for the pressure-velocity coupling in this solver. The simulation was validated using the uniform heating of the coolant to evaluate the accuracy of this solver in the simulation of lead-based fast reactors. The calculated results were further compared with those of the experimentally calibrated SACOS-PB sub-channel program [16] under the same conditions. The model geometry parameters used to evaluate the accuracy of the solver were as follows: the fuel rod diameter was 8.2 mm. The pitch was 10.49 mm. The helical wire diameter was 2.2 mm. The helical pitch was 328 mm. A comparison of the calculated coolant temperature results for an axial height of 54.6 mm in the active zone is shown in Fig. 7.

Fig. 7.
figure 7

Coolant temperature distribution at the axial height of 54.6 mm in the active zone

Full size image

Figure 7 shows the differences in the coolant temperature within different sub.channels on the same cross.section. As seen, the inner channel coolant temperature was higher than the outer channel coolant temperature. The coolant temperature within different sub.channels on the same cross.section under the same calculation conditions for both programs matched well, with the maximum relative error of <1%. Therefore, the results of OpenFOAM were deemed to be accurate, based on which the additional 61.rod bundle assembly calculations were performed.

3 Results and Discussion

3.1 Pressure Distribution Characteristics

Besides the coolant flow in the sub-channels along the axial direction, a complex transverse flow is also present. The drivers behind the transverse flow can be divided into natural and forced mixing; these transverse effects strengthen the resistance pressure drop of the flow. The cross-sectional pressure distributions at the axial heights of 60, 90, 120, and 150 mm within the 61-rod bundle fuel assembly are shown in Fig. 8, with the arrow direction reflecting the spin-in direction of the spacer wires. The pressure cloud contours at different axial heights exhibited similar distributions, while a clear difference between the high-pressure zone, low-pressure zone, and both sides of the spacer wires was identified. The low-pressure zone was generally distributed upstream of the spacer wires in the spin-in direction and downstream of the high-pressure zone. When the spacer wires rotated past the nearby fuel rods, the pressure inside the gaps between the fuel rod and spacer wires was low. Moreover, a pressure difference between the two sides of the spacer wire was identified.

Fig. 8.
figure 8

Pressure distribution at different axial heights

Full size image

Spacer wires force the coolant to mix, thereby making the transverse pressure distribution uneven. In general, a high-pressure zone is an area with a strong cross-flow effect. The pressure cloud contours for different axial heights revealed that the axial pressure tended to decrease as the Z-axis coordinate increased. Figure 9 shows the pressure cloud contours for each 1/6H interval of the axial height within a pitch. As seen, for each 1/6H increase in the axial height, the direction of the pressure cloud contours was rotated 60° clockwise, and the value of the pressure distribution decreased along the axial fluctuation.

Fig. 9.
figure 9

Pressure distribution at 1/6H intervals within a pitch

Full size image

3.2 Velocity Distribution Characteristics

The velocity distributions at different axial heights are shown in Fig. 10. Given the effects of the spacer wires, the velocity in the cross-section exhibited heterogeneity. The cloud contours indicate that the high-speed zone was generally dispersed around the assembly box upstream of the spin-in direction of the spacer wires. The fundamental driver of the variable coolant flow rates in the different sub-channels was the variance in the sub-channel flow area. The flow area of the channel near the assembly box was large, while the frictional resistance was relatively small, thus suggesting that the peripheral channel could obtain a larger velocity distribution. The inner sub-channels exhibited a more uniform velocity distribution due to the mixing of the spacer wires.

Fig. 10.
figure 10

Velocity distribution at different axial heights

Full size image

The velocity cloud contours for each 1/6H interval of the axial height within the pitch are shown in Fig. 11. For every 1/6H increase in axial height, the direction of the velocity cloud contours rotated 60° clockwise, and the velocity distribution period was 1H. The position of the maximum velocity also rotated periodically, and within a pitch, the maximum velocity distribution seemingly rotated by 360°. The maximum velocity decreased at the higher axial heights along the flow direction. Moreover, as the axial height increased, the lateral mixing introduced by the spacer wires caused the coolant momentum exchange in different channel positions, thereby making the velocity distribution continuously uniform with the flow.

Fig. 11.
figure 11

Velocity distribution per 1/6H interval within a pitch

Full size image

3.3 Temperature Distribution Characteristics

The temperature cloud contours at different axial heights are shown in Fig. 12, where the high- and low-temperature zones are reflected in the cross-section. The high-temperature zone was identified at the same position and rotated continuously along the spin direction of the spacer wires. The temperature of the central sub-channel was higher than that of the peripheral sub-channel because of the difference in the velocity distribution between the inner and outer channels. The coolant flow rate near the assembly box was high and the coolant was not sufficiently heated. Due to the mixing effect of the spacer wires, the velocity distribution of the inner sub-channels was uniform, the flow rate was low, the coolant was fully heated, and the high-temperature zones emerged.

Fig. 12.
figure 12

Temperature distribution at different axial heights

Full size image

The temperature distribution in the cross-section was also not hexagonally symmetric, thereby yielding some bias according to the relative position of the spacer wires. The temperature of the sub-channels near the center stainless-steel rod was lower. Although the average velocity of the sub-channels in the presence of spacer wires exceeded the average velocity of the sub-channels without spacer wires, the overall mass flow rate was smaller, and the average temperature was higher. Figure 13 shows the average and maximum temperatures of the surfaces at the different axial heights. As seen, the average temperature exhibited a linear increase along the axial direction, while the maximum temperature varied along the axial direction. The maximum difference between the maximum and average temperatures in the axial direction was 16.86K. Moreover, the maximum temperature difference between the average temperatures of the two cross-sections of the inlet and outlet could reach 25K. Given the linear power density peaks at 0.09 m axial height, the temperature growth reached its highest levels here.

Fig. 13.
figure 13

Average and maximum temperature of cross.sections at different axial heights

Full size image

The temperature cloud contour of the fuel assembly with an axial height of 180 mm is shown in Fig. 14. As seen, the temperature of the inner sub-channels located in the central region was generally higher than that of the peripheral side sub-channels and corner sub-channels. The calculation demonstrated that the maximum temperature difference in the radial direction at Z = 180 mm could be up to 28.23K. Moreover, the spacer wires strongly affected the temperature distribution, thereby strengthening the heat transfer of coolant between sub-channels but also inducing local overheating. With the increase in axial height, the maximum temperature difference in the radial direction of the cross-section seemingly exhibited a gradual increase, and the flow field temperature near some fuel rods was excessively high. The uneven thermal expansion of the fuel rods near the flow field with a higher temperature was greater. Thus, the uneven thermal expansion of the fuel rods would result in the narrowing of the flow sub-channels, thus potentially causing a sub-channel block accident. Different helical pitches, pitch ratios, and winding methods of spacer wires can all affect the thermal-hydraulic behavior of the assembly. Future studies should elucidate the effects of the structural parameters of the fuel assembly on the flow heat transfer of the coolant within the fuel assemblies in CiADS.

Fig. 14.
figure 14

The temperature cloud contour of Z = 180 mm

Full size image

4 Conclusion

In this study, the flow characteristics of lead-bismuth coolant in a lead-based fast reactor within a fuel assembly containing spacer wires were elucidated using the open-source CFD software OpenFOAM and the buoyantSimpleFoam solver. To this end, the 61-rod bundle assembly was finely modeled, the polyhedral grids were delineated, and the physical parameters of the lead-bismuth coolant were implanted in OpenFOAM. The k–ω SST turbulence model was applied, the boundary conditions were set, and the solver was validated using a sub-channel procedure. The analysis of the physical field characteristics, such as pressure, velocity, and temperature inside the assembly demonstrated the following results:

  1. (1)

    A significant pressure difference on both sides of the spacer wires was identified, which forced the transverse mixing of the coolant inside the assembly. Given the mixing effect, the transverse pressure distribution in the module was not uniform, while prominent high-pressure and low-pressure zones were formed. The high-pressure zone was generally located downstream of the spin in the direction of the spacer wires. Within a pitch (H), for every 1/6H increase in axial height, the direction of the pressure cloud contours rotated 60° clockwise, thereby weakening the pressure distribution variability.

  2. (2)

    The velocity on the cross-section was not uniform. The inner sub-channels inside the assembly exhibited low-velocity zones, and the velocity distribution of the central sub-channels was more uniform due to the effect of mixing. The flow area of the sub-channels near the assembly box was large, while the friction resistance was relatively small, and the coolant flow rate in the peripheral channel was larger. For every 1/6H increase in axial height, the velocity cloud contours rotated 60° clockwise, and the velocity distribution period was 1H.

  3. (3)

    Under the action of spacer wires, the temperature distribution of the internal sub-channels of the fuel assembly was more uniform. Given the uniform velocity distribution and low flow rate of the inner channel, the coolant was fully heated, and a high-temperature zone appeared. Although the temperature distribution in the cross-section was not hexagonally symmetrical, some bias was revealed according to the relative position of the spacer wires. At the outlet, the temperature difference between the internal and side sub-channels near the assembly box was large. Moreover, the temperature of the flow field near some fuel rods was excessively high, thereby being conductive for the burning of the cladding under accident conditions.