Subcriticality

Abstract

For a subcritical reactor system driven by a periodically pulsed spallation neutron source in KUCA, the Feynman-α and the Rossi-α neutron correlation analyses are conducted to determine the prompt neutron decay constant and quantitatively to confirm a non-Poisson character of the neutron source. The decay constant determined from the present Feynman-α analysis well agrees with that from a previous analysis for the same subcritical system driven by an inherent source. Considering the effect of a higher mode excited, the disagreement can be successfully resolved. The power spectral analysis on frequency domain is also carried out. Not only the cross-power but also the auto-power spectral density have a considerable correlated component even at a deeply subcritical state, where no correlated component could be previously observed under a 14 MeV neutron source. The indicator of the non-Poisson character of the present spallation source can be obtained from the spectral analysis and is consistent with that from the Rossi-α analysis. An experimental technique based on an accelerator-beam trip or restart operation is proposed to determine the subcritical reactivity of ADS. Applying the least-squares inverse kinetics method to the data analysis, the subcriticality can be inferred from time-sequence neutron count data after these operations.

2.1 Feynman-α and Rossi-α Analyses

2.1.1 Experimental Settings

2.1.1.1 Core Configurations

The Feynman-α and the Rossi-α neutron correlation analyses considering a non-Poisson character of the spallation source [1] are carried out in the A-core that has two kinds of fuel assemblies: 1/8”P60EUEU and 1/8”P4EUEU. Figure 2.1 shows a side view of the fuel assembly referred to as 1/8”P60EUEU. Fuel and moderator plates of the assembly were set in a 1.5 mm-thick aluminum sheath and the cross section of these plates within the assembly was the square of 2” (50.8 mm). The fuel assembly consisted of 60 unit cells. The unit cell was composed of two (1/16” thick) uranium plates with Al cladding and one (1/8” thick) polyethylene plate. Each of the fuel assemblies had 120 sheets of the uranium plates. The active height of the core, namely 60 unit cells, was 15” (about 38 cm). Adjacent to both axial sides of the active region of each fuel assembly, about 22” (57 cm) upper and 24” (52 cm) lower polyethylene reflectors were attached, respectively. Another fuel assembly referred to as 1/8” P4EUEU consisted of 4 unit cells with upper and lower polyethylene reflectors. The core configuration employed in this study is shown in Fig. 2.2. The twenty-five 1/8”P60EUEU assemblies and one 1/8”P4EUEU assembly were loaded on a grid plate to constitute a critical reactor core. The core was surrounded with many polyethylene-reflector assemblies.

Fig. 2.1

Description of 1/8”P60EUEU fuel assembly (Ref. [2])

Fig. 2.2

Top view of core configuration and neutron detector location (Ref. [1])

The subcriticality for the present experiment was adjusted by changing the axial position of the central fuel loading [3], as well as the positions of safety and control rods. These subcritical and critical patterns employed in the present experiments are shown in Table 2.1, where these respective subcriticalities are calculated by the continuous-energy Monte Carlo code MVP version 3 (MVP3) [3, 4] with the nuclear data library JENDL-4.0 [5] are also included. The error of the subcriticality indicates statistical uncertainty ±1σ of the MVP calculation.

Table 2.1 Experimental patterns of control rods and central fuel loading (Ref. [1])

2.1.1.2 Experimental Conditions

Four BF₃ proportional neutron counters (LND-202101, 1” dia., 15.47” len.) were used for the present experiment. These BF3 counters on locations (Q, 12), (P, 8), (L, 7), and (E, 8) are referred to as B1, B2, B3, and B4, respectively. The axial center of effective length of these counters was located at the axial center position of active region of the fuel assembly. The present nuclear instrumentation system consisted of conventional detector bias-supply, pre-amplifier, spectroscopy amplifier, and discriminator modules. Finally, signal pulses from these BF₃ neutron counters were fed to a time-sequence data acquisition system, which registered the arriving time of the signal as digital data. The time length of the acquired data for each subcritical pattern was about 30 min.

The pulsed proton beams were supplied by a fixed-field alternating gradient (FFAG) accelerator. The proton beam intensity of the accelerator was set to 30 pA for any subcritical patterns except for pattern A. For only pattern A, we necessarily made the proton beam intensity fall to 12 pA, to reduce counting loss originated from the dead-time effect of neutron counter. Throughout the present accelerator operations, the pulsed repetition frequency and the beam width were set to 30 Hz and 100 ns, respectively.

2.1.2 Formulae for Data Analyses

2.1.2.1 Feynman-α Formula

Rana and Degweker [6] derived the Feynman-α and the Rossi-α formulae for a periodically pulsed non-Poisson source, where delayed neutron contribution was considered and each pulse was assumed to be a delta function. Since the pulse width of 100 ns of our accelerator is much shorter than the time scale of the present correlation analyses, the assumption is acceptable. First, we consider the zero-power transfer function G(s) as follows:

$$\frac{1}{G(s)}\, = \,s\,\left( {\varLambda \, + \,\mathop \sum \limits_{i = 1}^{7} \frac{{\beta_{i} }}{{\lambda_{i} \, + \,s}}} \right)\, - \,\rho ,$$

(2.1)

where the six group model of delayed neutrons is supposed. When the poles and the residues of the above transfer function are represented by s_i and A_i, respectively, a parameter Y_i of the Feynman-α analysis can be defined as [7].

$$Y_{i} \, = \,2\,\frac{{\overline{{\nu \,\left( {\nu \, - \,1} \right)}} }}{{\bar{\nu }^{2} }}\,\frac{{A_{i} \,G(\alpha_{i} )}}{{\alpha_{i} }},$$

(2.2)

where

$$\alpha_{i} \, = \, - \,s_{i} .$$

(2.3)

Then, the Feynman-α formula derived by Rana and Degweker [6] can be written as follows:

$$\begin{aligned} Y(T) = & \frac{{\bar{\nu }^{2} \lambda_{d} }}{{m_{1} }}\mathop \sum \limits_{i = 1}^{7} Y_{i} \left( {1 - \frac{{1 - e^{{ - \alpha_{i} T}} }}{{\alpha_{i} T}}} \right)\left\{ {m_{1} \lambda_{f} + \frac{{\left( {m_{2} - m_{1}^{2} } \right)\left( { - \rho } \right)}}{{\overline{{\nu \left( {\nu - 1} \right)}} \varLambda }}} \right\} \\ + & \frac{{\bar{\nu }^{2} \lambda_{d} m_{1} \left( { - \rho } \right)}}{{\overline{{\nu \left( {\nu - 1} \right)}} \varLambda }}\mathop \sum \limits_{i = 1}^{7} Y_{i} \left\{ {\frac{{e^{{ - \alpha_{i} \,\left( {T - \frac{{\left[ {fT} \right]}}{f}} \right)}} + e^{{ -\frac{{\alpha_{i} }}{f}}} e^{{\alpha_{i} \left( {T - \frac{{\left[ {fT} \right]}}{f}} \right)}} - 1 - e^{{ -\frac{{\alpha_{i} }}{f}}} }}{{T\,\alpha_{i} \,\left( {1\, - \,e^{{ -\frac{{\alpha_{i} }}{f}}} } \right)}}} \right\}, \\ + & \frac{{\lambda_{d} m_{1} \varLambda }}{{\left( { - \rho } \right)}}\left\{ {1 + 2\left[ {fT} \right] - \frac{{\left[ {fT} \right]}}{fT}\left( {\left[ {fT} \right] + 1} \right) - fT} \right\} \\ \end{aligned}$$

(2.4)

where f is pulse repetition frequency and [f T] represents largest integer less or equal to f T. The largest α₇ is a prompt-neutron decay constant to be determined and the other α_i is a decay constant of each delayed-neutron mode. Other notations are conventional except for m₁ and m₂, which are first and second factorial moment of source multiplicity distribution and are defined by the following equations [8], respectively:

$$m_{1} \, = \,\bar{N}\,\overline{{\nu_{\text{sp}} }} ,$$

(2.5)

$$m_{2} \, = \, \overline{{N\,\left( {N\, - \,1} \right)}} \, \overline{{\nu_{\text{sp}} }}^{2} \, + \, \bar{N}\,\overline{{\nu_{\text{sp}} \,\left( {\nu_{\text{sp}} \, - \,1} \right)}} ,$$

(2.6)

where N and ν_sp are number of protons in a pulsed bunch and number of neutrons produced by each spallation event, respectively. These definitions lead to the following expression:

$$m_{2} \, - \,m_{1}^{2} \, = \,\left( {\overline{{N^{2} }} - \bar{N} - \bar{N}^{2} } \right)\, \overline{{\nu_{\text{sp}} }}^{2} + \, \bar{N}\,\overline{{\nu_{\text{sp}} \,\left( {\nu_{\text{sp}} \, - \,1} \right)}} .$$

(2.7)

The above quantity gives an expression for non-Poisson character of a neutron source and is included in the first term of Eq. (2.4). When the proton number N follows the Poisson distribution, the first term of Eq. (2.7) disappears. The second term is expected to increase with an increase in proton energy but the present energy 100 MeV may lead to a small positive value.

Equation (2.4) is not available for least-squares fitting to the Y data because of a complexity of the delayed neutron terms and many unknown parameters included in the terms. Here, we reduce the rigorous equation to obtain a practical fitting formula. First, the gate-time T of the Feynman-α analysis is restricted within the following range:

$$T\, \ll \,\frac{1}{{\alpha_{i} }}\, i\, = \,1,\,2,\, \ldots,\,6.$$

(2.8)

In the above range, the following Maclaurin expansions can be done:

$$e^{{ - \,\alpha_{i} \,T}} \, \simeq \,1\, - \,\alpha_{i} \,T\, + \,\frac{{\left( { - \,\alpha_{i} \,T} \right)^{2} }}{2},$$

(2.9)

$$e^{{ \pm \,\alpha_{i} \left( {T\, - \,\frac{{\left[ {f\,T} \right]}}{f}} \right)}} \, \simeq \,1\, \pm \,\alpha_{i} \,\left( {T\, - \,\frac{{\left[ {f\,T} \right]}}{f}} \right)\, + \,\frac{1}{2}\,\alpha_{i}^{2} \,\left( {T\, - \,\frac{{\left[ {f\,T} \right]}}{f}} \right)^{2} ,$$

(2.10)

$$e^{{ -\frac{{\alpha_{i} }}{f}}} \, \simeq \,1\, -\frac{{\alpha_{i} }}{f}.$$

(2.11)

We substitute Eqs. (2.9), (2.10), and (2.11) into Eq. (2.4) to obtain the following final form:

$$\begin{aligned} Y(T) = & C_{1} \left( {1 - \frac{{1 - e^{ - \alpha \,T} }}{\alpha T}} \right) \\ + & C_{2} \left\{ {\frac{{e^{{ - \,\alpha \,\left( {T\, -\frac{{\left[ {fT} \right]}}{f}} \right)}} \, + \,e^{{ -\frac{\alpha }{f}}} e^{{\alpha \,\left( {T\, -\frac{{\left[ {fT} \right]}}{f}} \right)}} \, - \,1\, - \,e^{{ -\frac{\alpha }{f}/}} }}{{T\,\alpha_{p} \,\left( {1\, - \,e^{{ -\frac{\alpha }{f}}} } \right)}}} \right\}, \\ + & C_{3} \,\left\{ {1\, + \,2\,\left[ {f\,T} \right]\, - \frac{{\left[ {f\,T} \right]}}{f\,T}\,\left( {\left[ {fT} \right]\, + \,1} \right)\, - \,f\,T} \right\}\, + \,C_{4} T \\ \end{aligned}$$

(2.12)

where

$$C_{1} \, = \,\bar{\nu }^{2} \,\lambda_{d} \,Y_{7} \,\left\{ {\lambda_{f} \, + \,\frac{{\left( {m_{2} \, - \,m_{1}^{2} } \right)\,\left( { - \rho } \right)}}{{m_{1} \,\overline{{\nu \,\left( {\nu \, - \,1} \right)\,}} \varLambda }}} \right\},$$

(2.13)

$$C_{2} \, = \,\frac{{\bar{\nu }^{2} \,\lambda_{d} \,m_{1} \,\left( { - \rho } \right)}}{{\overline{{\nu \,\left( {\nu \, - \,1} \right)\,}} \varLambda }}\,Y_{7} ,$$

(2.14)

$$C_{3} \, = \,\frac{{\lambda_{d} \,m_{1} \,\varLambda }}{{\left( { - \rho } \right)}}\, - \frac{{\bar{\nu }^{2} \,\lambda_{d} \,m_{1} \,\left( { - \rho } \right)}}{{\overline{{\nu \,\left( {\nu \, - \,1} \right)\,}} \varLambda }}\,\mathop \sum \limits_{i\, = \,1}^{6} \,Y_{i} ,$$

(2.15)

$$C_{4} \, = \,\bar{\nu }^{2} \,\lambda_{d} \,\mathop \sum \limits_{i\, = \,1}^{6} \frac{{Y_{i} \,\alpha_{i} }}{2}\,\left\{ {\lambda_{f} \, + \,\frac{{\left( {m_{2} \, - \,m_{1}^{2} } \right)\,\left( { - \rho } \right)}}{{m_{1} \,\overline{{\nu \,\left( {\nu \, - \,1} \right)}} \,\varLambda }}} \right\},$$

(2.16)

$$\alpha \, = \,\alpha_{7} .$$

(2.17)

In this Feynman-α analysis, Eq. (2.12) is fitted to the Y data to obtain the prompt-neutron decay constant α and the four coefficients (C₁, C₂, C₃, C₄).

2.1.2.2 Rossi-α Formula

In the same manner as a derivation of the practical Feynman-α formula, the Rossi-α formula proposed by Rana and Degweker [6] can be reduced. Their formula can be written as follows:

$$\begin{aligned} p\,(\tau ) = & \frac{{\lambda_{d} \,\bar{\nu }^{2} }}{2}\,\mathop \sum \limits_{i\, = \,1}^{7} \,\alpha_{i} \,Y_{i} \,e^{{ - \,\alpha_{i} \,\tau }} \,\left\{ {\lambda_{f} \, + \,\frac{{\left( {m_{2} \, - \,m_{1}^{2} } \right)\,\left( { - \rho } \right)}}{{m_{1} \,\overline{{\nu \,\left( {\nu \, - \,1} \right)\,}} \varLambda }}} \right\} \\ + & \frac{{\lambda_{d} \,m_{1} \,\bar{\nu }^{2} \,\left( { - \rho } \right)}}{{2\,\overline{{\nu \,\left( {\nu \, - \,1} \right)\,}} \varLambda }}\,\mathop \sum \limits_{i\, = \,1}^{7} \,\alpha_{i} \,Y_{i} \,\left\{ {\frac{{e^{{ - \,\alpha_{i} \,\left( {\tau \, - \,\frac{{\left[ {f\,\tau } \right]}}{f}} \right)}} \, + \,e^{{ -\frac{{\alpha_{i} }}{f}}} \,e^{{\alpha_{i} \,\left( {\tau \, - \frac{{\left[ {f\,\tau } \right]}}{f}} \right)}} }}{{\left( {1\, - \,e^{{ -\frac{{\alpha_{i} }}{f}}} } \right)}}} \right\}. \\ \end{aligned}$$

(2.18)

The conditional counting probability p(τ)Δτ is a probability that, given a neutron count at a time, there is a subsequent count in Δτ around time τ later. First, the time interval τ of the Rossi-α analysis is restricted within the following range:

$$\tau \, \ll \,\frac{1}{{\alpha_{i} }}\, i\, = \,1,\,2, \ldots,\,6.$$

(2.19)

Under the above time-interval range, the following Maclaurin expansions can be done:

$$e^{{ - \alpha_{i} \,\tau }} \, \simeq \,1\, - \,\alpha_{i} \,\tau ,$$

(2.20)

$$e^{{ \pm \,\alpha_{i} \,\left( {\tau \, - \,\frac{{\left[ {f\tau } \right]}}{f}} \right)}} \, \simeq \,1\, \pm \,\alpha_{i} \,\left( {\tau \, - \,\frac{{\left[ {f\,\tau } \right]}}{f}} \right)\, + \,\frac{1}{2}\,\alpha_{i}^{2} \,\left( {\tau \, - \,\frac{{\left[ {f\,\tau } \right]}}{f}} \right)^{2} .$$

(2.21)

We substitute the above equations into Eq. (2.18) to obtain the final form:

$$p(\tau )\,\Delta \tau \, = \,C_{5} \,e^{ - \,\alpha \,\tau } \, + \,C_{6} \,\left\{ {\frac{{e^{{ - \,\alpha \,\left( {\tau \, - \,\frac{{\left[ {f\,\tau } \right]}}{f}} \right)}} \, + \,e^{{\alpha \,\left( {\tau \, - \,\frac{{\left[ {f\,\tau } \right]\, + \,1}}{f}} \right)}} }}{{\left( {1\, - \,e^{{ - \,\frac{\alpha }{f}}} } \right)}}} \right\}\, + \,C_{7} \, - \,C_{8} \,\tau ,$$

(2.22)

where

$$C_{5} \, = \,\frac{{\lambda_{d} \,\bar{\nu }^{2} }}{2}\,\alpha_{7} \,Y_{7} \,\left\{ {\lambda_{f} \, + \,\frac{{\left( {m_{2} \, - \,m_{1}^{2} } \right)\,\left( { - \rho } \right)}}{{m_{1} \,\overline{{\nu \,\left( {\nu \, - \,1} \right)\,}} \varLambda }}} \right\}\Delta \tau ,$$

(2.23)

$$C_{6} \, = \,\frac{{\lambda_{d} \,m_{1} \,\bar{\nu }^{2} \,\left( { - \rho } \right)}}{{2\,\overline{{\nu \,\left( {\nu \, - \,1} \right)\,}} \varLambda }}\,\alpha_{7} \,Y_{7} \,\Delta \tau ,$$

(2.24)

$$\begin{aligned} C_{7} = & \frac{{\lambda_{d} \,\bar{\nu }^{2} }}{2}\,\mathop \sum \limits_{i\, = \,1}^{6} \,\alpha_{i} \,Y_{i} \,\left\{ {\lambda_{f} \, + \,\frac{{\left( {m_{2} \, - \,m_{1}^{2} } \right)\,\left( { - \rho } \right)}}{{m_{1} \overline{{\,\nu \,\left( {\nu \, - \,1} \right)\,}} \varLambda }}} \right\}\Delta \tau \\ + & \frac{{f\,\lambda_{d} \,m_{1} \,\bar{\nu }^{2} \,\left( { - \rho } \right)}}{{\overline{{\nu \,\left( {\nu \, - \,1} \right)}} \,\varLambda }}\,\mathop \sum \limits_{i\, = \,1}^{6} \,Y_{i} \,\Delta \tau , \\ \end{aligned}$$

(2.25)

$$C_{8} \, = \,\frac{{\lambda_{d} \,\bar{\nu }^{2} }}{2}\,\mathop \sum \limits_{i\, = \,1}^{6} \,\alpha_{i}^{2} \,Y_{i} \,\left\{ {\lambda_{f} \, + \,\frac{{\left( {m_{2} \, - \,m_{1}^{2} } \right)\,\left( { - \rho } \right)}}{{m_{1} \,\overline{{\nu \,\left( {\nu \, - \,1} \right)}} \,\varLambda }}} \right\}\,\Delta \tau ,$$

(2.26)

$$\alpha \, = \,\alpha_{7} .$$

(2.27)

In this Rossi-α analysis, Eq. (2.22) is fitted to the p(τ)Δτ data to obtain the prompt-neutron decay constant α and the four coefficients (C₅, C₆, C₇, C₈).

2.1.3 Results and Discussion

2.1.3.1 Feynman-α Analyses

Time-sequence counts data within a time interval (gate time) of 1 ms were generated from the arriving time data registered, and then the count data within longer gate times were synthesized by the moving-bunching technique [9] to calculate a gate-time dependence of the Y defined as variance-to-mean ratio minus 1 of the count’s data. Figure 2.3 shows a gate-time T and a subcriticality dependence of the Y obtained by the Feynman-α analysis, where neutron counter is B1. The gate-time dependence of the Y is oscillatory due to the periodicity of the pulsed source. The Y of the slightly subcritical pattern B tends to increase with a lengthening in gate time, while that of the deeply subcritical patterns C, D, and E scarcely have the increasing trend and the difference of the amplitude among these patterns is small. At pattern F, whose Y is not drawn in Fig. 2.3, the Y scarcely has the increasing trend and the amplitude is slightly smaller than that at pattern E. The least-squares fits of Eq. (2.12) to the Y data are included in Fig. 2.3, where the fitted curves are in very good agreement with the Y data. The result obtained from counter B2 and B3 was similar to the above observation obtained from counter B1 but that from counter B4 was entirely different.

Fig. 2.3

Subcriticality dependence of Y value of counter B1 (Ref. [1])

Figure 2.4 shows a gate-time T and a subcriticality dependence of the Y obtained by the Feynman-α analysis, where neutron counter is B4. In a shorter gate-time range than about 0.03 s, a slight difference in the Y among subcritical patterns can be observed. In the longer range, however, the Y data of respective patterns are overlapped. This feature suggests that counter B4 hardly detects fission neutrons which have an information of the subcriticality and most of the neutron counts must be generated from the detection of source neutrons arriving from the target.

Fig. 2.4

Subcriticality dependence of Y value of counter B4 (Ref. [1])

In Fig. 2.5, the prompt-neutron decay constant α_p obtained from the present Feynman-α analysis under the pulsed spallation source is compared with the average decay constant done from the previous analysis under a stationary source inherent in nuclear fuels [2], where the previous three decay constants from three neutron counters (B1, B2, B3) are averaged to obtain the average and the standard deviation. The error of the present decay constant represents statistical uncertainty ±1σ derived from a nonlinear least-squares method. Since counter B4 was placed far from the core and consequently had very small detection efficiency, the previous analysis for the counter was unsuccessful.

Fig. 2.5

Comparison of respective prompt neutron decay constants obtained from Feynman-α analyses under pulsed spallation and stationary inherent source (Ref. [1])

The present decay constants of counters B1, B2, and B3 agree well with the previous average decay constant, while the decay constant of counter B4 is much larger than the previous one. As mentioned in Fig. 2.4, the counter B4 placed far from the fuel region and closely to the target must scarcely detect fission neutrons and consequently have little information about fission chain. Most of neutron counts of the counters B1, B2, and B3 located closely to the fuel region are expected to be generated from the detection of fission neutrons.

2.1.3.2 Rossi-α Analyses

Figure 2.6 shows a time-interval τ and subcritical-pattern dependences of the conditional counting probability p(τ)Δτ obtained by the Rossi-α analysis, where neutron counter is B1. The least-squares fits of Eq. (2.22) to the counting probability data are included in this figure, where the fitted curves seem to be in good agreement with the data but the fittings are unsuccessful. Figure 2.7 shows an enlarged view near the second peak in Fig. 2.6. A considerable difference between the counting probability data and Eq. (2.22) fitted to the data can be observed. The probability data have a smooth convex top at every integral multiple of pulse period, while the fitted curve of Eq. (2.22) has a sharp cusp arising from a delta-function-like shape of pulsed neutron. Since the pulse width of 100 ns of our accelerator is much shorter than the time scale of the present correlation analyses, the assumption that each pulse has a delta-function-like shape is acceptable. Here, we consider the reason why the Rossi-α data had the smooth convex top.

Fig. 2.6

Subcriticality dependence of P(τ)Δτ of counter B1 (Ref. [1])

Fig. 2.7

Enlarged view near a peak in Fig. 2.6 (Ref. [1])

In the previous pulsed-neutron-source experiments [10,11,12], a considerable delay in counter response to neutron generation has been observed. The delay has been considered to originate primarily from a slowing down and a thermalization time of high-energy source neutrons for moderation to thermal energy and from a diffusion time of the thermalized source neutrons for arrival at core. The delay could be also interpreted as a higher harmonics effect [13, 14].

In the previous pulsed-neutron-source experiments mentioned above, the decay data deviated from a single exponential curve were masked to determine the fundamental prompt-neutron decay constant from a least-squares fitting of a conventional formula based on the one-point kinetics model. We tried to apply this masking technique to the present Rossi-α analysis. As shown in Fig. 2.8, the data around each smooth convex top were masked for a least-squares fitting of the present Rossi-α formula. The cusps of these fitted curves appear sharper than those of Fig. 2.7. The correlation coefficient is an indication of a goodness of the least-squares fitting. In this study, we employed the mask width with the maximum coefficient. The optimal mask width for every counter and every subcritical pattern was determined.

Fig. 2.8

Masking data around peaks for least-squares fitting (Ref. [1])

In Fig. 2.9, the prompt-neutron decay constant α obtained from the present Rossi-α analysis under the pulsed spallation source is compared with the average decay constant done from the previous analysis under a stationary source inherent in nuclear fuels [2], where the masking technique is not applied to the present analysis. The present decay constant is in poor agreement with the previous one. This disagreement could be resolved by applying the masking technique, as shown in Fig. 2.10. Except for counter B4, the decay constant obtained from the present analysis with the masking technique is in good agreement with that done from the previous analysis. The counter B4 placed far from the fuel region and closely to the neutron source derives a large decay constant of source neutrons in reflector. As shown in Fig. 2.5, the decay constant obtained from the present Feynman-α analysis, except for counter B4, well agreed with the previous decay constant. We can have this fortunate agreement because the respective negative and positive sharp cusps of the uncorrelated second and third terms of Eq. (2.12) barely cancel out, as shown in Fig. 2.5. In contrast, the present Rossi-α formula has no cancelation mechanism and has sharp cups at every integral multiple of pulse period.

Fig. 2.9

Comparison of respective prompt-neutron decay constants obtained from Rossi-α analyses under pulsed spallation and inherent source (Ref. [1])

Fig. 2.10

Effect of masking data around peaks on prompt-neutron decay constant obtained from Rossi-α analysis under pulsed spallation source (Ref. [1])

2.1.3.3 Comparison of Correlation Amplitude Between Spallation and Poisson Sources

Many authors [6, 8, 15,16,17,18] theoretically showed that the non-Poisson spallation source enhanced the correlation amplitudes of various reactor noise analyses. Here, we compare the correlation amplitudes obtained from the Feynman-α and Rossi-α analyses under the present non-Poisson spallation source with those under the previous Poisson inherent source [2]. First, the respective prompt correlation amplitudes C₁ and C₅ of the present Feynman-α and Rossi-α formulae are rewritten in the familiar forms. The prompt quantity Y₇ included in the correlation amplitudes can be described as follows [6]:

$$Y_{7} \, = \,\frac{{\overline{{\nu \,\left( {\nu \, - \,1} \right)}} }}{{\bar{\nu }^{2} \,\alpha^{2} }}.$$

(2.28)

When the above equation is substituted for Eqs. (2.13) and (2.23), the following equations can be, respectively, obtained:

$$C_{1} \, = \,\lambda_{d} \,\frac{{\overline{{\nu \,\left( {\nu \, - \,1} \right)}} }}{{\alpha^{2} }}\,\left\{ {\lambda_{f} \, + \,\frac{{\left( {m_{2} \, - \,m_{1}^{2} } \right)\,\left( { - \rho } \right)}}{{m_{1} \,\overline{{\nu \,\left( {\nu \, - \,1} \right)\,}} \varLambda }}} \right\},$$

(2.29)

and

$$C_{5} \, = \,\frac{{\lambda_{d} \,\overline{{\nu \,\left( {\nu \, - \,1} \right)}} }}{2\,\alpha }\,\left\{ {\lambda_{f} \, + \,\frac{{\left( {m_{2} \, - \,m_{1}^{2} } \right)\,\left( { - \rho } \right)}}{{m_{1} \,\overline{{\nu \,\left( {\nu \, - \,1} \right)}} \,\varLambda }}} \right\}\,\Delta \tau .$$

(2.30)

The respective correlation amplitudes C_1P and C_5P of the conventional Feynman-α and Rossi-α formulae for a stationary Poisson source can be described as follows [7]:

$$C_{1P} \, = \,\lambda_{d} \,\lambda_{f} \,\frac{{\overline{{\nu \,\left( {\nu \, - \,1} \right)}} }}{{\alpha^{2} }},$$

(2.31)

and

$$C_{5P} \, = \,\frac{{\lambda_{d} \,\lambda_{f} \,\overline{{\nu \,\left( {\nu \, - \,1} \right)}} }}{{2\,\alpha \,X_{P} }}\,\Delta \tau ,$$

(2.32)

where

$$\lambda_{d} \, = \,\varepsilon \,\lambda_{f} .$$

(2.33)

Assuming that a detection efficiency ε has no difference between the non-Poisson spallation and the Poisson sources, the following relationships hold:

$$C_{1} \, = \,C_{1P} \, + \,\frac{{\lambda_{d} \,\left( {m_{2} \, - \,m_{1}^{2} } \right)\,\left( { - \rho } \right)}}{{m_{1} \,\alpha^{2} \,\varLambda }},$$

(2.34)

and

$$C_{5} \, = \,C_{5P} \, + \,\frac{{\lambda_{d} \,\left( {m_{2} \, - \,m_{1}^{2} } \right)\,\left( { - \rho } \right)}}{{2\,m_{1} \,\alpha \,\varLambda }}\,\Delta \tau .$$

(2.35)

The respective second terms of the right-hand sides of the above two equations express the enhancement by the non-Poisson character of the spallation source. The enhancement disappears at a critical state and increases with an increase in subcriticality.

Next, the subcriticality dependence of the enhancement is experimentally confirmed. Figure 2.11 shows a comparison of respective prompt correlation amplitudes obtained from the Feynman-α analyses under the present pulsed spallation and the stationary inherent sources. The latter is a stationary Poisson source since the inherent source neutrons are dominantly produced by (α, n) reaction and spontaneous fissions negligibly contribute to the source strength [2]. This figure indicates that the enhancement of the prompt correlation amplitude increases with an increase in subcriticality. The non-Poisson character of the spallation source enhances the amplitude clearly.

Fig. 2.11

Comparison of respective prompt-neutron correlation amplitudes obtained from Feynman-α analyses under pulsed spallation and stationary inherent sources (Ref. [1])

Figure 2.12 also shows another comparison of respective prompt correlation amplitudes obtained from the Rossi-α analyses under the present pulsed spallation and the stationary inherent sources. This also indicates that the non-Poisson character of the spallation source significantly enhances the amplitude. The above discussion is confined to the qualitative observation and some quantitative evaluation of the non-Poisson character must be difficult. This is because a detection efficiency ε has a considerable difference between the external spallation and the inherent sources and the efficiency must depend on the subcriticality. A spatially uniform inherent source in fuels hardly excites any higher modes, however, another spatially localized external source significantly excites a higher mode with an increase in subcriticality, as could be observed in a source multiplication measurement [2]. In next Sect. 2.1.3.4, we try to derive a quantitative indicator of the non-Poisson character.

Fig. 2.12

Comparison of respective prompt-neutron correlation amplitudes obtained from Rossi-α analyses under pulsed spallation and stationary inherent sources (Ref. [1])

2.1.3.4 Indicator of Non-poisson Character of Spallation Source

Dividing Eq. (2.23) by Eq. (2.24) of the present Rossi-α formula, the following equation can be obtained:

$$\frac{{C_{5} }}{{C_{6} }}\, = \,\frac{{\lambda_{f} \,\overline{{\nu \,\left( {\nu \, - \,1} \right)}} \,\varLambda }}{{m_{1} \,\left( { - \rho } \right)}}\, + \,\frac{{m_{2} \, - \,m_{1}^{2} }}{{m_{1}^{2} }}.$$

(2.36)

The above equation has no detection efficiency and asymptotically approaches the second term with an increase in the subcriticality. The second term quantitatively expresses a non-Poisson character of the spallation source and may be referred to as “the Degweker’s factor” of multiplicity distribution of neutrons in a pulse bunch. When the multiplicity follows the Poisson distribution, the factor becomes zero. Degweker et al. theoretically simulated the Rossi-α analysis changing parametrically the above factor to investigate an impact of non-Poisson source [8].

Generally, the ratio of the second factorial moment to the first factorial moment squared of a multiplicity distribution has been employed as an indication characterizing the distribution. As an example, Diven factor [19] is defined as the ratio of the second factorial moment to the first factorial moment squared of a multiplicity distribution of fission neutrons emitted from a fission event and is a useful indication characterizing the multiplicity distribution. Adding 1 to the Degweker’s factor, the result is the ratio of the second factorial moment to the first factorial moment squared of the multiplicity distribution of neutrons in a pulse bunch. Consequently, this factor is eligible to employ as the indication characterizing the multiplicity distribution and should be determined experimentally.

Figure 2.13 shows a subcriticality dependence of the ratio C_5/C₆ determined from the present Rossi-α analysis. At the more deeply subcritical system than pattern C, the ratio seems to be an asymptotic value. Seeing the ratio within the subcritical range from pattern C to F, no systematic dependence on the subcriticality can be observed. Averaging the ratios over the subcritical range and over four counters, we obtain the second term, i.e., the Degweker’s factor of 0.067 ± 0.011. The non-zero value convinces us that the present spallation source has the non-Poisson character. If the accelerator had higher energy proton beam than 100 MeV, the factor would be larger [20].

Fig. 2.13

Subcriticality dependence of coefficient ratio C_5/C₆ obtained from Rossi-α analysis (Ref. [1])

2.2 Power Spectral Analyses

2.2.1 Experimental Settings

The power spectral analysis on frequency domain is carried out in the same A-core as shown in Fig. 2.2 [21]. Figure 2.14 shows the present signal processing circuit, whose former stage consisted of conventional charge preamplifier (PA), detector bias-supply (HV), spectroscopy amplifier (SA), and single-channel analyzer (SCA) modules. A special count-rate meter (Oken S-1955) input logic pulse train from SCA to output analog signal proportional to instantaneous count rate. The rate meter could be well modeled by a primary delay element which had the time constant of 3.88 ms (break frequency 41.0 Hz). The time constant of the meter is so short that a large portion of reactor noise passes through the filtration. Finally, analog signals from the two count-rate meters were fed to a fast Fourier transform (FFT) analyzer (Ono DS-3200) to obtain auto- and cross-power spectral densities and to record the analog signals as digital data. This FFT analyzer has a highly resolvable analog-to-digital converter whose number of bits and dynamic range are 24 bits and above 110 dB, respectively. An analysis range in frequency from 1.25 to 1000 Hz was specified to obtain 800-point spectral data. Delayed neutrons are expected to contribute hardly to the power spectral density obtained from the FFT analyzer because the above minimum frequency of 1.25 Hz is larger than the 6th decay constant 3.01 s⁻¹ (0.48 Hz) of a delayed neutron data given by Keepin [22].

Fig. 2.14

Signal processing circuit for power spectral analysis (Ref. [21])

In each subcritical pattern, time-sequence signal data were acquired for about 10 min. A response function of the above count-rate meter was measured in advance and the auto-and cross-power spectral densities obtained were divided by the auto-power spectral density of the response of the count-rate meter, so as to compensate an influence of the meter. Throughout the present accelerator operations, the pulsed repetition frequency and the beam width were set to 30 Hz and 100 ns, respectively. The proton beam intensity of an accelerator was set to 30 pA.

2.2.2 Formula for Power Spectral Analyses

2.2.2.1 Degweker’s Formula

Degweker and Rana [8] formulated the auto- and cross-power spectral densities for a periodically pulsed non-Poisson source, where delayed neutron contribution was neglected and each pulse was assumed to be a delta function. The neglect of delayed neutron contribution is acceptable as mentioned in the above Sect. 2.2.1. Since the pulse width 100 ns of our accelerator is much shorter than the time scale of the present analysis, the assumption of the delta function is also acceptable. Here, their formulae are rewritten as a function of not angular frequency ω s⁻¹ but frequency f Hz. Then, their cross-power spectral density between neutron detector 1 and 2 can be described as follows:

$${{\varPhi }}_{12} (f)\, = \,\frac{{C_{1} (f)}}{{\left( {2\,\pi f} \right)^{2} \, + \,\alpha^{2} }}\, + \,C_{2} (f)\,\mathop \sum \limits_{n\, = \, - \infty }^{\infty } \,\frac{{\delta \,\left( {f\, - \,n\,f_{R} } \right)}}{{\left( {2\,\pi f} \right)^{2} \, + \,\alpha^{2} }},$$

(2.37)

where

$$C_{1} (f)\, = \,H(f)\,q^{2} \,f_{R} \,\lambda_{d1} \,\lambda_{d2} \,\left( {m_{2} \, - \,m_{1}^{2} \, + \,2m_{1} \,Y_{1} } \right),$$

(2.38)

$$C_{2} (f)\, = \,H(f)\,q^{2} \,f_{R}^{2} \,\lambda_{d1} \,\lambda_{d2} \,m_{1}^{2} ,$$

(2.39)

$$Y_{1} \, = \,\lambda_{f} \,\frac{{\overline{{\nu \,\left( {\nu \, - \,1} \right)}} }}{2\,\alpha }.$$

(2.40)

Their auto-power spectral density of neutron detector 1 can be also described as follows:

$${{\varPhi }}_{11} (f)\, = \,C_{3} (f)\, + \,\frac{{C_{4} (f)}}{{\left( {2\,\pi f} \right)^{2} \, + \,\alpha^{2} }}\, + \,C_{5} \left( f \right)\,\mathop \sum \limits_{n\, = \, - \infty }^{\infty } \,\frac{{\delta \left( {f\, - \,n\,f_{R} } \right)}}{{\left( {2\,\pi f} \right)^{2} \, + \,\alpha^{2} }},$$

(2.41)

where

$$C_{3} (f)\, = \,\frac{{H(f)\,q^{2} \,f_{R} \,\lambda_{d1} \,m_{1} }}{\alpha },$$

(2.42)

$$C_{4} (f)\, = \,H(f)\,q^{2} \,f_{R} \,\lambda_{d1}^{2} \,\left( {m_{2} \, - \,m_{1}^{2} \, + \,2\,m_{1} \,Y_{1} } \right),$$

(2.43)

$$C_{5} (f)\, = \,H(f)\,q^{2} \,f_{R}^{2} \,\lambda_{d1}^{2} \,m_{1}^{2} ,$$

(2.44)

where α and f_R represent prompt-neutron decay constant and pulse repetition frequency, respectively. H(f) is a power spectral density of an impulse response of detector and processing-circuit system.

2.2.2.2 Formula Applied to Present Analyses

The auto-power spectral density has a white chamber noise indicated by the first term of Eq. (2.41). The correlated component done by the second term is completely hidden by the chamber noise in a higher frequency range, and this feature suggests a difficulty in estimating the break frequency, i.e., the prompt-neutron decay constant [12, 23]. In previous reactor noise analysis for a stationary source, Nomura [24] proposed the use of two neutron detectors with independent electronic circuits to reduce this spurious white noise and demonstrated the usefulness of his proposal. His original improvement referred to as the two-detector method is identical with the cross-power spectral analysis familiar to signal processing field. Actually, Eq. (2.37) for the cross-power spectral density has no term of the white noise. In the present study, we analyze only the cross-power spectral density free from the white noise.

The two coefficients defined by Eqs. (2.38) and (2.39) include H(f) and depend on frequency f. When the frequency response of the count-rate meter is compensated as mentioned in Sect. 2.2.1, these coefficients are independent of the frequency. For the following expressions, each coefficient is described as a constant. Then, Eq. (2.37) can be rewritten as

$$\varPhi_{12} (f)\, = \,\frac{{C_{1} }}{{\left( {2\,\pi f} \right)^{2} \, + \,\alpha^{2} }}\, + \,C_{2} \,\mathop \sum \limits_{n\, = \, - \infty }^{\infty } \,\frac{{\delta \left( {f\, - \,n\,f_{R} } \right)}}{{\left( {2\,\pi f} \right)^{2} \, + \,\alpha^{2} }}.$$

(2.45)

The second term of the above equation gives an expression to the uncorrelated delta-function peaks at the multiple of pulse repetition frequency f_R. At frequency of the integral multiple, Eq. (2.45) can be reduced as follows:

$$\varPhi_{12} (n\,f_{R} ) = \frac{{C_{1} }}{{\left( {2\,\pi \,n\,f_{R} } \right)^{2} \, + \,\alpha^{2} }} + \frac{{C_{2} }}{{\left( {2\,\pi \,n\,f_{R} } \right)^{2} \, + \,\alpha^{2} }},\;n = 1,2,3 \ldots .$$

(2.46)

The second uncorrelated term of the above equation is larger than the first correlated term by over two orders of magnitude [12, 23]. Then, Eq. (2.46) can be simplified as

$$\varPhi_{12} (n\,f_{R} )\; \simeq \;\frac{{C_{1} }}{{\left( {2\,\pi \,n\,f_{R} } \right)^{2} \, + \,\alpha^{2} }},\;n = 1,2,3 \ldots .$$

(2.47)

From a least-squares fit of Eq. (2.47) to peak data at frequency of the integral multiple of f_R, the prompt-neutron decay constant α and coefficient C₂ can be determined.

Next, a well-known effect of a higher mode excited by the injection of pulsed neutrons [10,11,12] should be considered. Sakon et al. employed the following equation to consider the effect successfully [12, 23].

$$\varPhi_{12} (n\,f_{R} ) \simeq \frac{{C_{2} }}{{\left( {2\,\pi \,n\,f_{R} } \right)^{2} \, + \,\alpha^{2} }} + \frac{{C_{2H} }}{{\left( {2\,\pi \,n\,f_{R} } \right)^{2} \, + \,\alpha_{H}^{2} }},\;n = 1,2,3, \ldots .$$

(2.48)

When certain a higher prompt mode as well as a fundamental prompt mode are excited, such a higher term as the second term of the above equation can be added to the fundamental term of the power spectral density [25,26,27]. The prompt-neutron decay constant of the higher mode is represented by α_H. The coefficient C_2H includes the eigenfunction and the adjoint eigenfunction of the higher prompt mode. We try to apply Eq. (2.48) as well as Eq. (2.47) to derive the fundamental decay constant α from the uncorrelated peaks.

When the uncorrelated peaks of the cross-power spectral density are masked, Eq. (2.45) can be reduced to the following equation for the remaining data unmasked:

$$\varPhi_{12} (f)\, = \,\frac{{C_{1} }}{{\left( {2\,\pi f} \right)^{2} \, + \,\alpha^{2} }}.$$

(2.49)

From a least-squares fit of Eq. (2.49) to the unmasked data, the prompt neutron decay constant α and coefficient C₁ can be also determined. The above equation gives an expression to the correlated noise component and is identical to the familiar formula for a stationary neutron source.

2.2.3 Results and Discussion

2.2.3.1 Power Spectral Density

Figure 2.15a, b show measured auto-power spectral density of counter B1 and cross-power spectral density between neutron detector B1 and B2, respectively, where subcritical pattern is F. The auto-power spectral density is composed of a continuous correlated component, another constant chamber noise and many delta-function-like peaks at the integral multiple of the repetition frequency, as expected by Eq. (2.41). The correlated component tends to be hidden by the white chamber noise with an increase in frequency and this feature suggests a difficulty in estimating the break frequency, i.e., the prompt-neutron decay constant.

Fig. 2.15

Power spectral density measured at subcritical pattern F (Ref. [21])

On the other hand, the cross-power spectral density has no white chamber noise, expected by Eq. (2.37). The correlated component is larger than one decade (20 dB). This feature is significantly different from that of the auto-power spectral density as shown above. Obviously, the cross-power spectral density is favorable to estimating the decay constant.

For almost the same subcritical system driven a pulsed 14 MeV Poisson source, previously, a power spectral analysis was carried out [12]. Figure 2.16a, b show the cross-power spectral densities measured previously, where the respective pulse repetition frequencies are 20 and 500 Hz and the subcriticality 13.59 %Δk/k is almost same as that of the present pattern F. In these cross-power spectral densities, no correlated noise component could be observed, and we failed in determining the prompt-neutron decay constant from correlated component. Naturally, the auto-power spectral density also had no correlated component. In contrast to the previous analysis, the present analysis gives a considerable correlated component as shown in Fig. 2.15. The non-Poisson character of the spallation source must enhance the amplitude of the correlated component over a precision limit of the FFT analyzer.

Fig. 2.16

Cross-power spectral density measured previously at a subcritical KUCA system driven by a pulsed DT neutron source (Ref. [21])

2.2.3.2 Prompt Neutron Decay Constant

Figure 2.17 shows a least-squares fit of Eq. (2.49) to the correlated noise component of the cross-power spectral density measured at pattern F. In this fitting, 33 delta-function-like peaks were masked. No systematical deviation of the fitted curve from the data can be seen. Figure 2.18 shows a least-squares fit of Eqs. (2.47) and (2.48) to the peak points of the cross-power spectral density at pattern F. No systematical deviation of fitted Eq. (2.47) from the peak point can be seen in a lower frequency range than roughly 500 Hz, while above this frequency, a systematical deviation of the fitted curve from the peak points is significant. In contrast to Eq. (2.47), no deviation of fitted Eq. (2.48) from the peaks can be observed over the frequency range. At all subcritical patterns, the fittings of Eq. (2.48) were very successful.

Fig. 2.17

Least-squares fit to correlated component of cross-power spectral density (Ref. [21])

Fig. 2.18

Least-squares fit to uncorrelated peaks of cross-power spectral density (Ref. [21])

In Fig. 2.19, the prompt-neutron decay constant obtained from the present cross-power spectral analysis is compared with the average decay constant done from the previous Rossi-α analysis under the same spallation source [1]. When Eq. (2.47) is fitted to uncorrelated peaks, the present decay constant is in poor agreement with the previous one. Fortunately, the fitting of Eq. (2.48) completely resolves this disagreement. When Eq. (2.49) is fitted to continuous correlated data, the agreement with the previous decay constant is not too bad. The analysis for a much longer time than 10 min may be required to enhance the agreement.

Fig. 2.19

Comparison of respective prompt neutron decay constants obtained from present cross-power spectral and previous Rossi-α analyses (Ref. [21])

2.2.3.3 Indicator of Non-poisson Character of Spallation Source

Dividing Eq. (2.38) by Eq. (2.39) of the formula for cross-power spectral density, the following equation can be obtained:

$$f_{R} \,\frac{{C_{1} }}{{C_{2} }}\, = \,\frac{{\uplambda_{f} \,\overline{{\nu \,\left( {\nu \, - \,1} \right)}} }}{{m_{1} \,\alpha }}\, + \,\frac{{m_{2} \, - \,m_{1}^{2} }}{{m_{1}^{2} }}.$$

(2.50)

The above equation has no detection efficiency and asymptotically approaches to the second term with an increase in the subcriticality, i.e., the prompt-neutron decay constant α. The second term quantitatively expresses a non-Poisson character of the spallation source and may be referred to as “the Degweker’s factor” of multiplicity distribution of neutrons in a pulse bunch. When the multiplicity follows the Poisson distribution, the factor becomes zero. Degweker et al. theoretically simulated the Rossi-α analysis changing parametrically the above factor to investigate an impact of non-Poisson source [8]. The Degweker’s factor is a useful indication characterizing the multiplicity distribution of the spallation neutrons in a pulsed bunch.

Figure 2.20 shows a subcriticality dependence of the ratio f_R C₁/C₂ determined from the present cross-power spectral analysis. At the more deeply subcritical system than pattern C, the ratio seems to be an asymptotic value. Seeing the ratio within the subcritical range from pattern C to F, no systematic dependence on the subcriticality can be observed and these ratios are considered to be the asymptotic value, i.e., the Degweker’s factor. Averaging the ratios over the subcritical range from Pattern C to F, we obtained the second term, i.e., the Degweker’s factor of 0.082 ± 0.021. This value is consistent with 0.067 ± 0.011 determined from the previous Rossi-α analysis [1].

Fig. 2.20

Subcriticality dependence of f_R C₁/C₂ (Ref. [21])

2.3 Beam Trip and Restart Methods

2.3.1 Experimental Settings

2.3.1.1 Core Configurations

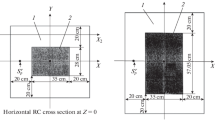
A series of accelerator-beam trip and restart experiments is carried out to determine the subcriticality of a reactor system driven by a pulsed 14 MeV neutron source [28]. This core configuration is shown in Fig. 2.21. The core was composed of 20 regular fuel assemblies and one partial fuel assembly, which were loaded on the grid plate. The fuel and moderator elements of each assembly were set in a 1.5-mm-thick aluminum sheath and the cross section of the elements within the assembly was the square of 2”. The regular fuel assembly was composed of 36 unit cells of one (1/16” thick) uranium plate with Al clad and two (1/8” and 1/4” thick) polyethylene plates, while the partial fuel assembly was composed of 12 unit cells of these plates. The partial fuel assembly was employed to adjust the excessive reactivity of the core. The active height of the core was about 40 cm, with additional about 60 cm upper and lower polyethylene reflectors. The configuration of these fuel assemblies was reported in detail by Pyeon et al. [29].

Fig. 2.21

Top view of core configuration and neutron detector location (Ref. [28])

A pulsed neutron generator was combined with the core, where 14 MeV pulsed DT neutrons were injected into the subcritical system through the polyethylene reflector. The generator consisted of a duoplasmatron-type ion source, a Cockcroft-Walton-type accelerator for deuteron (D⁺) beam, and tritium (T) target of gas-in-metal type. The pulsed neutrons are generated through the D-T reaction by the pulsed and accelerated D⁺ beam and T in the target metal. The target was placed outside the polyethylene reflector, as shown in Fig. 2.21. The pulse duration and repetition period of the D⁺ beam pulse can be remotely controlled by using an arc-pulser installed in the control room of KUCA. The current and acceleration voltage of the D⁺ beam pulse can also be controlled from the control room. In the present experiment, the major parameters of the accelerator drive were set to 160 keV in beam energy, 0.6–0.8 mA in beam current, 0.8 ms in pulse width, 1 ms in pulse repetition period, and 5.1–9.2 V in arc voltage of the ion source.

2.3.1.2 Experimental Procedures and Conditions

Four BF₃ proportional counters (1” dia.) were employed as experimental channels. As shown in Fig. 2.21, these BF₃ counters were placed on several positions around the core to measure the reactor response to beam trip and restart operations and to investigate the spatial dependence. The nuclear instrumentation system consisted of a detector bias supply, a preamplifier, a spectroscopy amplifier, and discriminator modules. Finally, signal pulses from four neutron counters were fed to a multichannel scaler to acquire time-sequence count data. The gate width of the scaler was set to 0.1 s. At a slightly subcritical state, the count rate of each neutron counter was expected to be so high that count losses would be induced by the dead-time effect of the neutron counter. Hence, the acquired count data were corrected for the losses on the basis of the non-paralysable model, where we used the dead time of 4 μs predetermined by an improved Feynman-α analysis [30].

First, an Am–Be neutron source for reactor startup was inserted. Then, the subcriticality for the experiment was adjusted by changing the axial positions of safety rods and control ones. The neutron source was taken out of the core and the injection of pulsed neutrons began. The control rod patterns employed in the experiment are shown in Table 2.2. The reference reactivity, included in this table, was evaluated from the reactivity worth of each rod, whose worth was predetermined by the positive period method and the rod drop one.

Table 2.2 Control rod patterns employed in the present experiment (Ref. [28])

In a beam trip experiment, a certain arc voltage of the ion source was suddenly dropped to turn off the D⁺ pulse beam. In the succeeding beam restart experiment, the voltage was rapidly returned to the original value to turn on the beam.

2.3.2 Data Analyses Method

2.3.2.1 Least-Squares Inverse Kinetics Method

First, the theory of the least-squares inverse kinetics method (LSIKM) [31,32,33] is briefly described. Assuming the zero-power and one-point kinetics model, the time-dependent neutron behavior of a subcritical reactor system driven by an external neutron source can be described as

$$\frac{dN(t)}{dt}\, = \,\frac{\rho \, - \,\beta }{\varLambda }\,N(t)\, + \,\mathop \sum \limits_{k\, = \,1}^{6} \,\lambda_{k} \,C_{k} (t)\, + \,S,$$

(2.51)

$$\frac{{dC_{k} (t)}}{dt}\, = \,\frac{{\beta_{k} }}{\varLambda }\,N(t)\, - \,\lambda_{k} \,C_{k} (t),$$

(2.52)

where N(t) is the neutron density, C_k(t) the concentration of k-th-group precursor, and S the neutron source strength. Other notations are conventional. As the above neutron density, usually, time-sequence count-rate data can be employed to determine the reactivity ρ. The differential term of Eq. (2.51) is usually neglected to simplify the analysis. The assumption is applicable to the KUCA system. Consequently, the discrete form of Eq. (2.51) on time domain is described as

$$N(t_{j} )\, = \,\frac{\varLambda }{\beta \, - \,\rho }\,Q\,(t_{j} )\, + \,\frac{\varLambda \,S}{\beta \, - \,\rho },$$

(2.53)

$$Q\,(t_{j} )\, = \,\mathop \sum \limits_{k\, = \,1}^{6} \,\lambda_{k} \,C_{k} (t_{j} ),$$

(2.54)

where t_j is the jth discrete time. As the time-dependent neutron density N(t_j), the time-sequence count data were employed. The time-dependent precursor density C_k(t_j) of delayed neutrons can be obtained by solving numerically Eq. (2.52). In this study, the implicit time-integration method was employed to obtain the precursor density. When the time-sequence data N(t_j) and Q(t_j) are plotted on the x-y coordinate, two unknown constants, i.e., the reactivity and the source strength, can be determined from the least-squares fitting of Eq. (2.53) to these data. By applying the LSIKM to beam trip data, Eq. (2.53) is reduced to

$$N(t_{j} ) = \frac{\varLambda }{\beta - \rho }Q\,(t_{j} ),$$

(2.55)

where the source strength is set to zero.

The delayed neutron data and prompt-neutron generation time of the present reactor system were generated using the SRAC code system [34], where a three-dimensional, 19-energy-group diffusion calculation was done with JENDL-3.2 nuclear library [35].

2.3.2.2 Integral Count Technique

The integral count technique has been frequently employed to determine the subcriticality from a source jerk experiment and a rod drop one [31, 36]. When a neutron source is rapidly taken out of a subcritical reactor core or a control rod is dropped into a critical core at t = 0, the reactivity of the core can be expressed as

$$\rho \, = \, - \,\mathop \sum \limits_{k\, = \,1}^{6} \,\frac{{\beta_{k} }}{{\lambda_{k} }}\,\frac{N(0)}{{\mathop \smallint \nolimits_{0}^{\infty } N(t)\,dt}}.$$

(2.56)

The above expression is a familiar formula for the integral count technique.

The technique is also applied to the present beam trip experiment. Prior to beam trip operation, the average count rate used as N(0) is measured using a conventional counting scaler. Then, the integral counts after the operation, which can be used as an integral appearing in the denominator of Eq. (2.56), are also measured using the scaler.

2.3.3 Results and Discussion

2.3.3.1 Time-Sequence Data

Figure 2.22 shows the time-sequence N(t) and Q(t) data obtained from counter B4 in a beam trip experiment, where the control rod pattern is A and the beam is turned off at zero time. The time-sequence N(t) data in this figure are indicated as instantaneous count rate at every 0.1 s. After the beam trip, N(t) and Q(t) promptly decrease and then asymptotically tend to zero. The statistical fluctuation of Q(t) defined using Eq. (2.54) is slight, compared with that of N(t). This is because the delayed-neutron emission rate Q(t) is an integral quantity of N(t) over a passing time. The least-squares approximation fits a model function with minimum error on the y-axis assuming no error on the x-axis. Therefore, the time-sequence Q(t) and N(t) data should be assigned to x- and y-axis variables, respectively, for successful least-squares fitting on the x-y coordinate.

Fig. 2.22

Time-sequence data N(t) and Q(t) in a beam trip experiment (Ref. [28])

Figure 2.23 shows the time-sequence N(t) and Q(t) data obtained from counter B4 in a beam restart experiment, where the control rod pattern is A and the beam is turned on at zero time. After the beam restart, N(t) and Q(t) promptly increase and then asymptotically tend to their individual constants.

Fig. 2.23

Time-sequence data N(t) and Q(t) in a beam restart experiment (Ref. [28])

2.3.3.2 Least-Squares Fitting

In Fig. 2.24, the above Q(t) and N(t) data are plotted on the x-y coordinate, where the fitted lines are drawn by a straight line. Equations (2.55) and (2.53) were fitted to the data sets of Fig. 2.24a, b, respectively. The fitting is successful and the subcritical reactivity can be determined from the slope of the fitted line.

Fig. 2.24

Plot of variables and fitted line on x-y coordinate (Ref. [28])

Table 2.3 summarizes the reactivities obtained from the beam trip and restart experiments. As the errors of these results of the LSIKM, the statistical uncertainties that originated from the least-squares fit were employed, while the uncertainty of delayed-neutron yield β was not taken into account. The errors of the integral count technique were estimated from counting statistics. For comparison, the results obtained by a pulsed neutron experiment [11] are also shown in Table 2.4, where the subcriticality obtained by a conventional analysis technique has a significant counter-position dependence. This dependence is originated from a higher mode excited by a pulsed neutron source. The mask analysis technique was employed to reduce the dependence.

Table 2.3 Reactivity obtained by beam trip and restart experiments [%Δk/k] (Ref. [28])

Table 2.4 Reactivity obtained by pulsed neutron experiments [%Δk/k] (Ref. [28])

It is obvious from Table 2.3 that counter B1 significantly overestimates the subcriticality. This feature is originated from a large amount of source neutrons traveling from the DT target. This is because the counter relatively close to the target counts much more the source neutrons during successive pulse injection, and then the source neutrons decay out with a larger decay constant after beam trip and more steeply increase after beam restart. The decay of fission neutrons contains information on the reactivity, while that of the source neutrons is free from such information. Generally, the decay constant of the source-neutron mode free from the neutron-production process is larger than that of the prompt mode of the fission neutron [11]. In Fig. 2.25, the decay data of counter B1 are compared with those of B4 in a beam trip experiment, where the control rod pattern is C and the data is normalized in such a way that the average counts before the beam trip become one. This figure shows a larger decay of B1 data just after the trip, as noted above. For an actual ADS, a neutron counter should be placed at a position far from a spallation target. Table 2.3 also shows that the results of the LSIKM for beam trip data are consistent with those of the integral count technique except for counter B1.

Fig. 2.25

Difference in decay data between counters B1 and B4 (Ref. [28])

As seen from Tables 2.3 and 2.4, the present subcriticality obtained using the counters other than B1 has a slight counter-position dependence compared with those obtained in a conventional pulsed neutron experiment and agrees with the result of the pulsed neutron experiment based on the mask analysis within experimental errors. Here, we note a further observation from this table, which is a larger error of the beam restart experiment than that of the beam trip one. From the least-squares fitting of Eq. (2.55) to beam trip data, only the reactivity is determined. From the fitting of Eq. (2.53) to beam restart data, however, not only is the reactivity but also the source strength is simultaneously determined. The additional unknown constant to be inferred is responsible for the larger error of the beam restart experiment. For the smaller error, the trip experiment is advantageous. Nevertheless, the restart experiment is useful for the simultaneous determination of both the reactivity and source strength.

2.4 Conclusion

We derived the Feynman-α and the Rossi-α formulae applicable to the respective correlation data analyses for a pulsed non-Poisson neutron source. These formulae were applied to the Feynman-α and the Rossi-α analyses for a subcritical system driven by a pulsed spallation source in KUCA. The prompt-neutron decay constant determined from the present Feynman-α analysis well agreed with that done from a previous analysis for the same subcritical system driven by an inherent neutron source. However, the decay constant determined from the present Rossi-α analysis was in poor agreement with that done from the above previous analysis. When the data around the convex top were masked for least-squares fitting of the present Rossi- When the data around the convex top of the counting probability distribution were masked for least-squares fitting of the present Rossi-α formula, the disagreement could be successfully resolved. formula, the disagreement could be successfully resolved. When the respective prompt-neutron correlation amplitudes determined from the present Feynman-α and Rossi-α analyses were compared with those done from the previous analyses under the Poisson inherent source, the non-Poisson spallation source definitely enhanced the respective correlation amplitudes. The Degweker’s factor (m₂ − m ²₁ )/m ²₁ of 0.067 ± 0.011, which is a quantitative indication of the non-Poisson character, could be determined from the present Rossi-α analysis.

The power spectral analysis on frequency domain was conducted in the same A-core as the above Feynman-α and Rossi-α analyses. Not only the cross-power but also the auto-power spectral density had a considerable correlated noise component even at a deeply subcritical state, where no correlated component could be observed under a pulsed DT(14 MeV) neutron source. The non-Poisson character of the spallation source must enhance the correlation amplitude of these power spectral densities. The Degweker’s factor of 0.082 ± 0.021 could be determined from the present analysis and was consistent with that obtained by the above Rossi-α analysis.

An experimental technique based on accelerator-beam trip and restart operation was proposed to determine the subcritical reactivity of ADS. A series of these experiments was performed in a subcritical thermal core of KUCA. The results demonstrated the applicability of the proposed technique to the thermal ADS of KUCA. We expect the proposed technique to be applied for an actual ADS in start-up or shut-down operation.