Skip to main content
SpringerLink
Log in

Transient Pressure Analysis in Partially Perforated Vertical Wells

  • Conference paper
  • First Online:
Proceedings of the International Field Exploration and Development Conference 2018 (IFEDC 2018)

Part of the book series: Springer Series in Geomechanics and Geoengineering ((SSGG))

Included in the following conference series:

Abstract

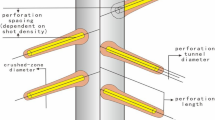
Due to engineering or geological reasons, oil and gas wells are frequently completed using a partially perforated method. Complicated spatial distribution of perforation tunnels is too difficult to be considered in the conventional analytic solution model, and there is still short of a well test model regarding the partially perforated well. Therefore, this paper develops a 3D numerical well test model for partially perforated wells, which not only accurately describe the perforation tunnels distribution near the wellbore, but also consider the characteristics of perforation compacted zone, formation damaged zone, and permeability anisotropy. The 3D finite element method is utilized to conduct numerical solutions to the model, and the pressure response curves and pressure fields are obtained for the first time. Characteristics of the pressure response curves and pressure fields are studied as well as the effects of other factors, such as perforated position, perforation compacted zone, and formation damaged zone on the pressure response curve. The results show that the pressure response of partially perforated well is characterized by both totally perforated well and partially penetrated well. It not only has an early locally radial flow characteristic around the perforation tunnels, but also has an ellipsoidal (spherical) flow characteristic. Compared with perforation at either top or bottom, the perforation in the middle weakens the inter-perforation interference. The effect of perforation compacted zone can be replaced by reducing the effective perforation radius. The increase of perforation length can largely reduce the effect of formation damaged zone on the pressure response curve and productivity of partially perforated well. Finally, the total skin computing formula of the partially perforated well is verified by means of calculation of cases with different perforation lengths and different perforated level coefficients.

Copyright 2018, Shaanxi Petroleum Society.

This paper was prepared for presentation at the 2018 International Field Exploration and Development Conference in Xi’an, China, 18–20 September, 2018.

This paper was selected for presentation by the IFEDC Committee following review of information contained in an abstract submitted by the author(s). Contents of the paper, as presented, have not been reviewed by the IFEDC Committee and are subject to correction by the author(s). The material does not necessarily reflect any position of the IFEDC Committee, its members. Papers presented at the Conference are subject to publication review by Professional Committee of Petroleum Engineering of Shaanxi Petroleum Society. Electronic reproduction, distribution, or storage of any part of this paper for commercial purposes without the written consent of Shaanxi Petroleum Society is prohibited. Permission to reproduce in print is restricted to an abstract of not more than 300 words; illustrations may not be copied. The abstract must contain conspicuous acknowledgment of IFEDC. Contact email: paper@ifedc.org.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 259.00
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 329.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info
Hardcover Book
USD 329.99
Price excludes VAT (USA)
  • Durable hardcover edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

Abbreviations

A j :

Area of grid cell surface of perforation inner boundary, m2

A jD :

Dimensionless area of inner boundary discrete unit surface

b :

Perforated ratio

B :

Volume ratio, m3/m3

C t :

Total compressibility, 1/MPa

C :

Wellbore storage coefficient, m3/MPa

C D :

Dimensionless wellbore storage coefficient

h :

Formation thickness, m

h D :

Dimensionless formation thickness

H p :

Perforated thickness of formation, m

K v :

Vertical permeability of initial reservoir, mD

K h :

Horizontal permeability of initial reservoir, mD

K Lh :

Regional horizontal permeability, mD

K Ph :

Horizontal permeability of perforation compacted zone, mD

K Fh :

Horizontal permeability of formation damaged zone, mD

K vD :

Dimensionless vertical permeability

K LD :

Dimensionless regional permeability

K PD :

Dimensionless permeability of perforation compacted zone

K FD :

Dimensionless permeability of formation damaged zone

L p :

Perforation length, m

L pD :

Dimensionless perforation length

N :

Number of discrete unit surfaces of inner boundary

p :

Reservoir pressure, MPa

p i :

Initial reservoir pressure, MPa

p w :

Bottom hole flowing pressure(BHFP), MPa

p D :

Dimensionless pressure

q :

Total flow rate, m3/d

r w :

Wellbore radius, m

r p :

Perforation radius, m

r pD :

Dimensionless perforation radius

r pd :

Radius of perforation compacted zone

t :

Time, h

t D :

Dimensionless time

T D :

Dimensionless effective time

ϕ :

Reservoir porosity

μ :

Viscosity of fluid in reservoir, \( {\text{mPa}} \cdot {\text{s}} \)

References

  1. Muskat M. The effect of casing perforations on well productivity[J]. Trans AIME. 1943;151:175–87.

    Article  Google Scholar 

  2. McDowell JM, Muskat M. The effect on well productivity of formation penetration beyond perforated casing[J]. Trans AIME. 1950;189:309–12.

    Google Scholar 

  3. Harris SD. The effect of perforating on well productivity[J]. JPT, (April);1966, pp. 518–528.

    Google Scholar 

  4. Klotz JA, Kruger RF, Pye DS. Effect of perforation damage on well productivity[J]. JPT. 1974;26(Nov):1303–14.

    Google Scholar 

  5. Locke S. An advanced method for predicting the productivity ratio of a perforated well[J]. J Petrol Technol. 1981;33(12):2481–8.

    Article  Google Scholar 

  6. Tariq SM. Evaluation of flow characteristics of perforations including nonlinear effects with the finite-element method[J]. SPE Prod Eng. 1987;2(2):104–12.

    Article  Google Scholar 

  7. Karakas M, Tariq SM. Semianalytical productivity models for perforated completions[J]. SPE Prod Eng. 1991;6(1):73–82.

    Article  Google Scholar 

  8. Yildiz T. Assessment of total skin factor in perforated wells[J]. SPE Reservoir Eval Eng. 2006;9(1):62–76.

    Article  Google Scholar 

  9. Hagoort J. An analytical model for predicting the productivity of perforated wells[J]. J Petrol Sci Eng. 2007;56(4):199–218.

    Article  Google Scholar 

  10. Atkinson C, Monmont F, Zazovsky A. Flow performance of perforated completions[J]. Transp Porous Media. 2009;80(2):305–28.

    Article  MathSciNet  Google Scholar 

  11. Jamiolahmady M, et al. A new method for productivity calculation of perforated wells in gas condensate reservoirs[J]. J Petrol Sci Eng. 2011;77(3–4):263–73.

    Article  Google Scholar 

  12. Aiyin S, Yueping F, Qi L, et al. Electric analog research on perforation completion[J]. Oil Drilling Prod Technol. 1988;6:99–107 (in Chinese).

    Google Scholar 

  13. Yula T, Yingde P. Evaluation of perforating completion by finite element method[J]. Acta Pertrolei Sinica. 1989;10(3):48–58 (in Chinese).

    Google Scholar 

  14. Yildiz T, Ozkan E. Pressure-transient analysis for perforated wells[J]. SPE J. 1999;4(2):167–76.

    Article  Google Scholar 

  15. Ozkan E, Yildiz T. Pressure-transient analysis of perforated slant and horizontal wells[R]. SPE 56421;1999.

    Google Scholar 

  16. Weiping O, Yuewu L. Effects of perforating parameters on well test type curves. Acta Petrolei Sinica. 2013;34(03):528–34.

    Google Scholar 

  17. Gringarten AC, Ramey JR, Henry J. An approximate infinite conductivity solution for a partially penetrating line-source well. SPE J. 1975;15(2):140–8.

    Google Scholar 

  18. Abbott WA, Collins T, Tippie DB. Practial application of spherical flow transient analysis. In: SPE annual fall technical conference and exhibition, Houston, Texas;1978-10-1-3.

    Google Scholar 

  19. Kuchuk FJ, Klrwan PA. New skin and wellbore storage type curves for partially penetrated wells. SPE Formation Eval. 1987;2(4):546–54.

    Article  Google Scholar 

  20. Yildiz T, Bassiouni Z. Transient pressure analysis in partially penetrating wells. In: SPE international technical meeting, Calgary, Alberta;1990-06-10-13.

    Google Scholar 

  21. Yildiz T, Cinar Y. Inflow performance and transient pressure behavior of selectively completed vertical wells. SPE Reservoir Eval Eng. 1998;5(1):467–75.

    Article  Google Scholar 

  22. Yildiz T. Assessment of total skin factor in perforated wells. SPE Reservoir Eval Eng. 2006;9(1):62–76.

    Article  Google Scholar 

  23. Houqing Z. An analytical solution of gas flow towards a partially penetrated well in double porous media. Acta Petrolei Sinica. 1982;3(2):51–62.

    Google Scholar 

  24. Ciqun L. Axisymmetrical two-dimensional steady and unsteady flow through porous media. Chin J Theor Appl Mech. 1983;15(2):103–10.

    MATH  Google Scholar 

  25. Ciqun L, Deli H. A study of characteristics of the pressure build-up curves of a partially penetrated well in multiple porosity media by a method of numerical inversion of laplace transforms. Petrol Explor Dev. 1983;10(1):49–54.

    Google Scholar 

  26. Ciqun L, Jie Y. The pressure behavior in imperfect well in bottom water limestone oil reservoir. Oil Drilling Prod Technol. 1989;11(1):47–52.

    Google Scholar 

  27. Jun Y, Minglu W. Streamline numerical well testing interpretation model and pressure response for partially perforated wells. Petrol Explor Dev. 2009;36(4):513–8.

    Article  Google Scholar 

  28. Weiping O, Yuewu L, Yizhao W. Effects of formation damage zone on bottom-hole pressure response of partially penetration-wells. Chin J Theoret Appl Mech. 2014;46(2):234–40.

    Google Scholar 

Download references

Acknowledgements

Thanks to Changqing Downhole Technology Company for allowing the publication of this paper.

Author information

Authors and Affiliations

  1. Changqing Downhole Technology Company, CNPC Chuanqing Drilling Engineering Company Limited, Xi’an, 710018, Shaanxi, China

    Weiping Ouyang & Deyong Yang

  2. National Engineering Laboratory for Exploration and Development of Low-Permeability Oil and Gas Fields, Xi’an, 710018, Shaanxi, China

    Weiping Ouyang & Deyong Yang

  3. Department of Gas Field Development, PetroChina Research Institute of Petroleum Exploration and Development, Langfang, 065007, Hebei, China

    Hedong Sun

Authors
  1. Weiping Ouyang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Deyong Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hedong Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Weiping Ouyang .

Editor information

Editors and Affiliations

  1. College of Petroleum Engineering, Xi’an Shiyou University, Xi’an, Shaanxi, China

    Jia'en Lin

Rights and permissions

Reprints and permissions

Copyright information

© 2020 Springer Nature Singapore Pte Ltd.

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Ouyang, W., Yang, D., Sun, H. (2020). Transient Pressure Analysis in Partially Perforated Vertical Wells. In: Lin, J. (eds) Proceedings of the International Field Exploration and Development Conference 2018. IFEDC 2018. Springer Series in Geomechanics and Geoengineering. Springer, Singapore. https://doi.org/10.1007/978-981-13-7127-1_81

Download citation

  • DOI: https://doi.org/10.1007/978-981-13-7127-1_81

  • Published:

  • Publisher Name: Springer, Singapore

  • Print ISBN: 978-981-13-7126-4

  • Online ISBN: 978-981-13-7127-1

  • eBook Packages: EngineeringEngineering (R0)

Publish with us

Policies and ethics

Search

Navigation