S-Conical CMC Surfaces. Towards a Unified Theory of Discrete Surfaces with Constant Mean Curvature

Abstract

We introduce a novel class of s-conical nets and, in particular, study s-conical nets with constant mean curvature. Moreover we give a unified description of nets of various types: circular, conical and s-isothermic. The later turn out to be interpolating between the circular net discretization and the s-conical one.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

A variety of approaches have been pursued to obtain a notion of discrete constant mean curvature (cmc) surfaces. Two different starting points arise from the interpretation of cmc surfaces as critical points of an area functional [9, 16], and on the other hand from an integrable systems point of view [4, 10]. One principal difference of the two approaches is that, in the first approach, the underlying combinatorial structure is naturally that of a simplicial surface, whereas the integrable systems approach demands a quadrilateral structure of the discrete surface, and one reads about discrete parametrized surfaces. Recently these two approaches were partially merged as soon as a curvature theory for general polyhedral surfaces based on the notions of parallel surfaces and mixed area was developed [5].

Restricting to quadrilateral meshes, and, in particular, to planar quadrilaterals (discrete conjugate nets), may at first sight appear to be a severe restriction. However, it turns out that every surface can be approximated by discrete nets with these properties [3, 6], reflecting the existence of the corresponding parametrizations in the smooth case. In fact these integrable discretizations are structure preserving, i.e. they preserve the key aspects of the geometry. A characteristic feature of surfaces described by integrable systems is the existence of special transformations of Bäcklung and Darboux type that preserve the class of surfaces. In the discrete setup these transformations lead to consistent multi-dimensional nets. The last property has established itself as the integrable structure in discrete differential geometry [6].

There exists a rather developed theory of discrete cmc surfaces from an integrable point of view, reflected in numerous publications. They include Q-nets (nets with planar quadrilaterals) [5], circular nets (nets with circular quadrilaterals) [4, 6, 8, 10, 11, 14, 18, 19], semi-discrete nets [15], s-isothermic nets [12]. The latter can be characterized geometrically [6] by having a sphere at every vertex of the net such that the intersection angles of the spheres along opposite edges in every quadrilateral are the same and the four spheres either have a common orthogonal circle, share a pair of points, or (as a limiting case) all meet in exactly one point.

The key observation of the present paper is that the last subclass of s-isothermic nets is in fact conical. Although the class of conical nets introduced in [13] is very important for applications and belongs to integrable discrete differential geometry [6, 17], investigation of discrete conical surfaces with constant curvature has just started [2]. In this paper we introduce a novel class of s-conical nets and, in particular, study s-conical nets that are cmc. The identification of s-conical surfaces with special s-isothermic surfaces mentioned above leads not only to a description of conical cmc nets but also to a unified description of discrete cmc nets. One can think of s-isothermic nets as “interpolating” between the circular net discretization and the s-conical one.

2 Conical Nets

Here we consider Q-nets, which are discrete surfaces with planar quadrilateral faces. Since we are mostly developing a local theory, for simplicity we consider surfaces with the combinatorics of the square grid $f:\mathbb Z^2\rightarrow \mathbb R^3$. Some parts of the theory can be generalized to a more general combinatorics $f:G\rightarrow \mathbb R^3$, where G is a quad-graph. The latter is a strongly regular cell decomposition of a two-dimensional manifold with all faces being quadrilaterals. Moreover in the developed theory of discrete CMC surfaces the quad-graph should be edge-bipartite, i.e. there is a black and white edge coloring such that for each quadrilateral opposite edges are of the same color.

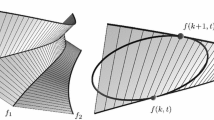
Through this paper we will use a notation that indicates shifts in the various directions by subscript. For a net $f:\mathbb Z^2\rightarrow \mathbb R^3$ we will denote a generic point f(k, l) simply by f. Then it is understood that $f_1 =f(k+1,l)$, $f_2 = f(k,l+1)$, $f_{12} = f(k+1,l+1)$, $f_{\bar{1}} = f(k-1,l)$ and so forth. This is of particular use in case of $\mathbb Z^n$ lattices but also as long as only one or two neighboring quadrilaterals of a quad-graph are concerned it is a useful shorthand. The following definition first appeared in [13].

Definition 2.1

A Q-net $f:\mathbb Z^2\rightarrow \mathbb R^3$ is said to be conical if for each vertex all incident faces touch a common sphere $\sigma$.

The touching spheres in the Definition 2.1 of conical nets are not unique. In general there is a 1-parameter family of spheres touching all incident faces for each vertex. These spheres are inscribed in a cone, and their centers lie on the cone axis. This furnishes a canonical normal direction (or line) in each vertex of f.

The normal lines of neighboring vertices are coplanar. Due to this fact conical nets have parallel nets in normal direction. The following theorem as well as all properties of conical nets mentioned in this section are due to [13] (see also [5, 6]).

Theorem 2.2

Let $f:\mathbb Z^2\rightarrow \mathbb R^3$ be a conical net. There is a 1-parameter family of conical nets $f^t:\mathbb Z^2\rightarrow \mathbb R^3$ such that $(f^t-f)$ lies in normal direction to f, f and $f^t$ have parallel edges, and the distance between corresponding faces is constant.

Proof

Given a conical net $f:\mathbb Z^2\rightarrow \mathbb R^3$ one chooses $f^t$ at a vertex f such that $f^t-f$ is in normal direction. Then there is a touching sphere $\sigma$ with center at $f^t$. Let r be its radius. Now one can find touching spheres $\sigma$ of radius r at all other vertices. Set $f^t$ to be their centers. Then $(ff^t)$ is in normal direction everywhere. Consider a quadrilateral $(f,f_1,f_{12},f_2)$. Since the edge $(ff_1)$ lies in the intersection of two common tangent planes of $\sigma _1$ and $\sigma$ it is parallel to the difference of their centers $f^t_1-f^t$ as well (the spheres are of equal radius). Thus the corresponding edges (and hence also the faces) of the quadrilaterals $(f,f_1,f_{12},f_2)$ and $(f^t,f^t_1,f^t_{12},f^t_2)$ are parallel. Moreover since all the spheres have the same radius r, the distance between the planes of these quadrilaterals is r. Since the faces of f and $f^t$ are parallel $f^t$ is conical as well.

Definition 2.3

Let $f:\mathbb Z^2\rightarrow \mathbb R^3$ be a conical net. $n:\mathbb Z^2\rightarrow \mathbb R^3$ is called a Gauss map of f if n points in normal direction and the parallel net $f^1 = f+ n$ has constant face offset 1, i.e. the distance between the planes of the corresponding faces of f and $f^1$ is equal to 1.

Proposition 2.4

Let $f:\mathbb Z^2\rightarrow \mathbb R^3$ be a conical net and $n:\mathbb Z^2\rightarrow \mathbb R^3$ its Gauss map. Then the edges of n are parallel to the edges of f and the faces of n touch the unit sphere $S^2$.

Proof

Since $f+n$ is parallel to f, n is parallel to f as well. Moreover since the distance between the faces of $f+n$ and f is equal to 1, the projection of n to the face normals N of f (and n) is 1. Thus the faces of n touch the unit sphere.

The parallel nets in Theorem 2.2 are then given by

$$\begin{aligned} f^t = f+tn. \end{aligned}$$

(1)

We will refer to these nets as (parallel) nets in constant distance.

We can use the notion of parallel nets to give yet another characterization for conical nets:

Proposition 2.5

A Q-net $f:\mathbb Z^2\rightarrow \mathbb R^3$ is a conical net if and only if f has parallel nets with constant face offset. If f is generic the constant face offset nets lie in normal direction.

Proof

Theorem 2.2 shows that conical nets have parallel nets with constant face offset. Now if f is a net with parallel net $\tilde{f}$ in constant face distance d, then $\hat{f} = \tilde{f} - f$ is parallel to f as well, and the faces of $\hat{f}$ touch a sphere of radius d. Thus $\hat{f}$ is conical. This also ensures conicality of all its parallel nets, in particular of f and $\tilde{f}$. Finally, $\hat{f} = \tilde{f} -f$ is the cone axes for $\hat{f}$ and therefore $(f\tilde{f})$ is the normal direction for $\tilde{f}$ and f as well.

The following angle characterization of conical nets was proven in [20].

Proposition 2.6

A Q-net $f:\mathbb Z^2\rightarrow \mathbb R^3$ is a conical net if and only if at each vertex the sums of the opposite angles (of quadrilaterals) are equal.

Example 2.7

Take any planar polygon $\gamma (k) = (\gamma ^1(k),\gamma ^2(k))$ with non vanishing edges and an angle $0<\phi <\pi$. Then the discrete rotational net

$$ f(k,l) = (\gamma ^1(k),\cos (l \phi ) \gamma ^2(k),\sin (l \phi )\gamma ^2(k)) $$

is a conical net.

3 Curvatures of Conical Nets via Steiner’s Formula

The classical Steiner formula couples the areas of a surface f and a parallel offset surface $f^t$ with the mean and Gauss curvature of f. If f is an infinitesimal surface patch and $f^t$ the parallel one in distance t in normal direction, then Steiner’s formula gives:

$$\begin{aligned} A(f^t) = A(f)(1 - 2 H t + K t^2), \end{aligned}$$

(2)

where A is the area, and H and K are the mean and the Gauss curvatures of f.

A discrete analogue of this formula was used in [5] to define curvatures for Q-nets with a given Gauss map (see also [18] where this formula first appeared for Q-nets with circular quadrilaterals). Let $Q = (q,q_1,q_{12},q_2)$ be a planar quadrilateral and N a unit normal of the plane of Q. Denoting its diagonals with $d_1 = q_{12} - q$ and $d_2= q_2-q_1$ the area A(Q) can be computed as

$$ A(Q) = \frac{1}{2} \det (d_1,d_2,N). $$

If P is another quadrilateral with edges parallel to the edges of Q and with diagonals $c_1$ and $c_2$ the area of $P+t Q$ is equal to

$$\begin{aligned} A(P+t Q) = A(P) +2 t \frac{1}{4}(\det (d_1,c_2,N)+ \det (c_1,d_2,N)) + t^2A(Q). \end{aligned}$$

(3)

The space of all planar quadrilaterals with edges parallel to a given one Q is a four dimensional vector space. Moding out the translations leaves a two dimensional one. On this space the area is a quadratic form A(P) and the mixed area is the corresponding symmetric form $A(P_1,P_2)$.

Since a conical mesh f and its Gauss map n have parallel edges, the area of the quadrilaterals of the offset net $f^t = f + t n$ is quadratic in the distance t. A discrete version of Steiner’s formula suggested in [5] (see also [6]) reads as follows.

Definition 3.1

Let $f:\mathbb Z^2\rightarrow \mathbb R^3$ be a conical net with the Gauss map $n:G\rightarrow \mathbb R^3$. Then the discrete Steiner formula

$$\begin{aligned} A(f+t n) = A(f) (1 - 2 H t + K t^2) \end{aligned}$$

(4)

defines a discrete mean curvature H and a discrete Gauss curvature K on the faces of the net f:

$$\begin{aligned} H = -\frac{A(f,n)}{A(f)}, \quad K= \frac{A(n)}{A(f)}. \end{aligned}$$

(5)

Here A(f) and A(n) are the areas of the quadrilaterals $(f,f_1,f_{12},f_2)$ and $(n,n_1,n_{12},n_2)$ respectively, and A(f, n) is their mixed area.

4 Dual Quadrilaterals and Koenigs Nets

As we mentioned already, the mixed area A(P, Q) is a symmetric bilinear form on a two-dimensional vector space of quadrilaterals with parallel edges. Quadrilaterals P and Q with $A(P,Q)=0$ are “orthogonal” with respect to this form. For any non-vanishing planar quadrilateral Q there is a P with $A(P,Q) = 0$ and P is unique up to scaling.

Definition 4.1

Two planar quadrilaterals P and Q with parallel edges are called dual to each other if their mixed area vanishes:

$$ A(P,Q) = 0. $$

Whenever scaling is unimportant we will simply talk about the dual quadrilateral $P^*$, satisfying $A(P,P^*)=0$.

Let $P = (p, p_1, p_{12}, p_2)$ and $Q = (q,q_1,q_{12},q_2)$ be two planar quadrilaterals with parallel edges and let N be their common normal then (3) implies the following formula for their mixed area

$$\begin{aligned} A(P,Q) = \frac{1}{4} \left( \det (p_{12}-p,q_2-q_1,N)+ \det (q_{12}-q,p_1-p_2,N)\right) . \end{aligned}$$

(6)

The duality can be described in terms of the diagonals [5, 6].

Proposition 4.2

The mixed area A(P, Q) of two planar quadrilaterals with parallel edges $P= (p, p_1, p_{12}, p_2)$ and $Q(q,q_1,q_{12},q_2)$ vanishes if and only if their non-corresponding diagonals are parallel, i.e. $p_{12}-p\parallel q_2-q_1$ and $q_{12}-q\parallel p_2-p_1$.

Let us present also useful explicit formulas for the dual quadrilateral. Let $o$ be the intersection point of the diagonals of a planar quadrilateral $P= (p,p_1,p_{12},p_2)$, $e_1 = \frac{p_{12}-p}{\Vert p_{12}-p\Vert },\ e_2 = \frac{p_{2}-p_1}{\Vert p_{2}-p_1\Vert }$ be the unit vectors of diagonals and define $\alpha ,\beta ,\gamma ,\delta$ as the oriented lengths of the connection intervals of the intersection point $o$ to the vertices: $p -o= \alpha e_1$, $p_{12} -o= \gamma e_1$, $p_1 -o= \beta e_2$, $p_2 -o= \delta e_2$. Then the quadrilateral $P^* = (p^*, p_1^*, p_{12}^*, p_2^*)$ determined by

$$\begin{aligned} p^*-o^* = -\frac{1}{\alpha } e_2,\ p_{12}^*-o^* = -\frac{1}{\gamma } e_2,\ p_1^*-o^* = \frac{1}{\beta } e_1,\ p_2^*-o^* = \frac{1}{\delta } e_1 \end{aligned}$$

(7)

with some $o^*$ is dual to P.

Every planar quadrilateral has a dual one. However generic Q-nets are not dualizable as a whole. Dualizable Q-nets were introduced in [7] (see also [6]).

Definition 4.3

A Q-net $f:\mathbb Z^2\rightarrow \mathbb R^3$ is called a Koenigs net if there is a Q-net $f^*:\mathbb Z^2\rightarrow \mathbb R^3$ such that the corresponding quadrilaterals of f and $f^*$ are dual to each other; $f^*$ is called (Christoffel) dual of f.

Koenigs nets can be characterized [6, 7] in terms of the intersection points of the diagonals.

Proposition 4.4

A Q-net $f:\mathbb Z^2\rightarrow \mathbb R^3$ in general position (each vertex and its neighbours are not co-planar) is a Koenigs net if and only if the intersection points of the diagonals of four quadrilaterals around each vertex are coplanar.

Since the planes of a planar quadrilateral and its dual are parallel, the conicality conditions for $f^*$ and f are satisfied simultaneously.

Proposition 4.5

If $f:\mathbb Z^2\rightarrow \mathbb R^3$ is conical and Koenigs, its Christoffel dual $f^*:\mathbb Z^2\rightarrow \mathbb R^3$ is conical as well.

5 Conical Nets with Constant Mean Curvature and S-Conical Nets

Definition 5.1

A conical net $f:\mathbb Z^2\rightarrow \mathbb R^3$ is called a net with constant mean curvature (cmc net) if its mean curvature H defined by (5) is constant. Conical nets with vanishing mean curvature are called minimal.

Fig. 1

To definition of s-conical nets. The cone touches all four neighboring quadrilaterals. The intersection points of the diagonals are circular, and the axis of the circle coincides with the axis of the cone

Theorem 5.2

A conical net $f:\mathbb Z^2\rightarrow \mathbb R^3$ is a cmc net with mean curvature $H\ne 0$ if and only if it is a Koenigs net with its Christoffel dual in constant distance $\frac{1}{H}$:

$$\begin{aligned} H=\mathrm{const} \Leftrightarrow f^*= f-\frac{1}{H} n. \end{aligned}$$

(8)

The dual net $f^*$ is a conical cmc net with mean curvature H as well.

Indeed, we have

$$ HA(f,f) = -A(f,n) \Leftrightarrow 0 = A(f,f-\frac{1}{H}n). $$

Thus $f^*$ exists and is given by (8).

There is a tight connection (see [6, 17]) of conical nets and circular nets, i.e. Q-nets with circular faces. Given a conical net one can choose a point on one of the face’s planes arbitrarily. Mirroring this point at the planes spanned by the face’s edges and their incident normals gives a circular net. Each vertex of this circular net corresponds to a face of the conical net and vice versa. This way each conical net gives rise to a 2-parameter family of circular nets. The circle centers of the circular net lie on the cone axes of the conical one.

On the other hand, given a circular net, we can choose an initial unit vertex normal arbitrarily. Mirroring that normal at the edge-bisecting planes gives rise to a consistent set of vertex normals such that neighboring normals intersect. Their orthogonal planes passing through the vertices of the circular net give rise to a conical net. This way each circular Q-net gives rise to a 2-parameter family of conical nets. We will call these conical and circular nets corresponding to each other.

We complete this section with an introduction of particular conical nets.

Definition 5.3

A discrete conical net $f:\mathbb Z^2\rightarrow \mathbb R^3$ is called s-conical if for every vertex the intersection points of the diagonals of the quadrilaterals sharing the vertex lie on a circle, and the axis of this circle is the vertex normal (the cone axis at the vertex).

It is easy to see that an s-conical net and its circular net formed by the intersection points of the diagonals are corresponding (see Fig. 1). Indeed two triangles on two neighboring faces sharing an edge built by this edge and the intersection points of the diagonals are congruent. Therefore they are symmetric with respect to the reflection in the symmetry plane of the planes of the neighboring faces.

Theorem 5.4

• (i) S-conical nets are Koenigs nets.

• (ii) The dual net of an s-conical net is also s-conical.

Proof

• (i) follows from Proposition 4.4 since the intersection points of the diagonals are circular.

• (ii) Consider two (congruent) triangles $\varDelta _1, \varDelta _2$ on two neighboring faces of f with a common edge built by this edge and the intersection points of the diagonals. As it was explained above they are symmetric with respect to the reflection in the symmetry plane P of the planes of the faces. The dualization formula (7) implies that the corresponding triangles $\varDelta ^*_1, \varDelta ^*_2$ of the dual net $f^*$ are also symmetric with respect to P. This implies that $f^*$ is s-conical.

In Sect. 7 we give an alternative definition of this class and investigate it.

6 S-Isothermic Nets

For an s-conical net the intersection points $o$ of the diagonals are circular with the circle centers lying on the corresponding cone axes. Let f be a vertex of an s-conical net and $o_{\bar{1}\bar{2}},o_{\bar{2}},o,o_{\bar{1}}$ the diagonal intersection points of the quadrilaterals incident to f. The points $o_{\bar{1}\bar{2}},o_{\bar{2}},o,o_{\bar{1}}$ lie on a sphere s with center f. This furnishes a map $s:\mathbb Z^2\rightarrow \{\text {spheres in }\; \mathbb R^3\}$ such that each sphere s is centered at the vertex f and in each diagonals intersection point $o$ four spheres $s,s_1,s_{12},s_2$ meet. Furthermore, opposite spheres s and $s_{12}$ as well as $s_1$ and $s_2$ touch at $o$.

In order to proceed further we recall some basic facts about s-isothermic nets and their Möbius geometric description (see [6] for details).

Let $\mathbb R^{4,1}$ be the five dimensional Minkowski space with the standard Lorenz inner product

$$\langle x,y\rangle = -x_0 y_0 + \sum _{k=1}^4 x_ky_k.$$

There is a bijection between oriented spheres and planes s in $\mathbb R^3$ and unit vectors $\hat{s}\in \mathbb R^{4,1}$ (here we consider planes as degenerate spheres), as well as points p in $\mathbb R^3\cup \infty$ and isotropic vectors $\hat{p}\in \mathbb {L}^{4} \subset \mathbb R^{4,1}$. For points p one sets

$$\begin{aligned} \hat{p} = (\frac{1+\Vert p\Vert ^2}{2},p,\frac{1-\Vert p\Vert ^2}{2}) \end{aligned}$$

(9)

with $\langle \hat{p},\hat{p}\rangle = 0$. The point at infinity $\infty$ is then given by $(1,0,0,0,-1)$. An oriented sphere s with center c and radius r in $\mathbb R^3$is represented as

$$\begin{aligned} \hat{s} = \frac{1}{r} \left( \frac{1+(\Vert c\Vert ^2 -r^2)}{2}, c, \frac{1-(\Vert c\Vert ^2 -r^2)}{2}\right) . \end{aligned}$$

(10)

A plane with the normal form $\langle v,n\rangle |_{\mathbb R^3} = d$, $\Vert n \Vert = 1$ is is given by

$$ \hat{s} = (d, n, -d).$$

In both cases $\langle \hat{s},\hat{s}\rangle = 1$. Changing the orientation of the sphere or plane corresponds to the transformation $\hat{s}\mapsto - \hat{s}$. A point p lies on a sphere s if and only if

$$\begin{aligned} p \in s \Leftrightarrow \langle \hat{p} , \hat{s}\rangle = 0. \end{aligned}$$

(11)

The intersection angle $\alpha$ between two spheres $s_1$ and $s_2$ can be calculated as

$$\begin{aligned} \cos \alpha = \langle \hat{s}_1, \hat{s}_2\rangle . \end{aligned}$$

(12)

In particular touching spheres satisfy

$$\langle \hat{s}_1, \hat{s}_2\rangle =-1.$$

From here on we will use the same notation p, s for points and spheres in $\mathbb R^3$ and their representatives (10) in $\mathbb R^{4,1}$. The meaning will be clear from the context.

Definition 6.1

A net $s:\mathbb Z^2\rightarrow \mathbb R^{4,1}$ of space-like unit vectors solving the discrete Moutard equation

$$\begin{aligned} s + s_{12} = \lambda (s_1 + s_2), \lambda \ne 0, \end{aligned}$$

(13)

is called s-isothermic.

Proposition 6.2

Let $s:\mathbb Z^2\rightarrow \mathbb R^{4,1}$ be an s-isothermic net. Then

$$\begin{aligned} \langle s_{12},s_1\rangle = \langle s_2,s\rangle \quad \text {and}\quad \langle s_{12},s_2\rangle = \langle s_1,s\rangle . \end{aligned}$$

(14)

Proof

The unit length condition implies

$$ 1 = \langle s_{12},s_{12}\rangle = \lambda ^2\langle s_1+s_2,s_1+s_2\rangle - 2 \lambda \langle s_1+s_2,s\rangle + 1, $$

and finally

$$\begin{aligned} \lambda \langle s_1+s_2,s_1+s_2\rangle - 2\langle s_1+s_2,s\rangle =0. \end{aligned}$$

(15)

If $\langle s_1+s_2,s_1+s_2\rangle =0$ (this is the touching spheres case $\langle s_1,s_2\rangle =-1$) we get from (15) $\langle s_1,s\rangle =-\langle s_2,s\rangle$. This implies $\langle s_{12},s_1\rangle = \langle \lambda (s_1+s_2) - s, s_1\rangle = -\langle s, s_1\rangle =\langle s, s_2\rangle$. In the non-touching case $\langle s_1+s_2,s_1+s_2\rangle \ne 0$ substituting $\lambda$ given by (15) into (13) we obtain (14).

S-isothermic nets have the following geometric properties formulated in terms of the centers c and the radii r of the corresponding spheres (10) (see [6, 7] for the proof).

Theorem 6.3

• (i) The centers $c\in \mathbb R^3$ of an s-isothermic net build Koenigs nets.

• (ii) Let s be an s-isothermic net of spheres with the centers $c:\mathbb Z^2\rightarrow \mathbb R^3$ and (signed) radii $r:\mathbb Z^2\rightarrow \mathbb R$. The spheres $s^*$ with the centers $c^*:\mathbb Z^2\rightarrow \mathbb R^3$ and the radii $r^*:\mathbb Z^2\rightarrow \mathbb R$ given by

  $$\begin{aligned} c_1^* - c^* = \frac{ c_1 - c}{r_1 r},\ c_2^* - c^* = -\frac{ c_2 - c}{r_2 r}, \ r^*=\frac{1}{r}, \end{aligned}$$

  (16)

  build an s-isothermic net (called Christoffel dual net).

S-isothermic nets belong to integrable structures of discrete differential geometry [6], i.e. they can be extended consistently to the $\mathbb Z^N$ lattice so that all two-dimensional coordinate subnets are s-isothermic. This property can be interpreted as a transformation of two-dimensional s-isothermic nets called Darboux transformation [12].

Fig. 2

A Darboux cube

Definition 6.4

Consider two s-isothermic nets $s:\mathbb Z^2\rightarrow \mathbb R^{4,1}$ and $\hat{s}:\mathbb Z^2\rightarrow \mathbb R^{4,1}$, and their spheres with the same indexes as corresponding. Thus, for example, the spheres $s,s_1,s_{12},s_2,\hat{s},\hat{s}_1,\hat{s}_{12},\hat{s}_2$ build a combinatorial cube shown in Fig. 2, and we treat the faces of s and $\hat{s}$ as bottom and top faces of the cube. The s-isothermic nets s and $\hat{s}$ are said to be Darboux transforms of each other if the spheres corresponding to the side faces of the cube also satisfy the discrete Moutard equations (with different signs corresponding to two different pairs of opposite faces):

$$\begin{aligned} \hat{s}_{1}+s=a(\hat{s}+s_1),\quad \hat{s}_{12}+s_2=a_2(\hat{s_2}+s_{12}),\\ \hat{s}_{2}-s=b(\hat{s}-s_2), \quad \hat{s}_{12}-s_1=b_1(\hat{s_1}-s_{12}). \end{aligned}$$

Remark 6.5

Given s its Darboux transform $\hat{s}$ is uniquely determined by one vertex of $\hat{s}$ which can be chosen arbitrary.

Remark 6.6

Note that the sides of a Darboux cube that correspond to the solutions of the Moutard equation with plus sign have embedded quadrilaterals while the ones with minus sign give rise to non-embedded quadrilaterals.

Remark 6.7

To pass to a multidimensional consistent picture mentioned above one should change the orientations of the spheres for every second line $s_{ij}\rightarrow (-1)^{i}s_{ij}$.

7 S-Conical Nets as S-Isothermic Nets

The Moutard equation implies that the four spheres of each quadrilateral are linearly dependent vectors in $\mathbb R^{4,1}$. Thus an s-isothermic net s is in particular a Q-net. We obtain three types of s-isothermic surfaces characterized by the fact that the four spheres $s,s_1,s_2,s_{12}$:

• share a common orthogonal circle (Type 1),

• intersect in a pair of points (Type 2),

• intersect in exactly one point (Type 3).

These three cases are distinguished by the signature of the Lorentz metric restricted to the subspace of the corresponding spheres $s,s_1,s_{12},s_2$ which span a 3-dimensional subspace $U\subset \mathbb R^{4,1}$. Denote its orthogonal complement by $U^\perp$. If the inner product on $U^\perp$ is positive definite the unit vectors therein form a 1-parameter family of spheres orthogonal to $s,s_1,s_{12}$, and $s_2$. This family shares a circle (given by the isotropic vectors of U) which thus is perpendicular to $s,s_1,s_{12}$, and $s_2$.

If the inner product on $U^\perp$ is indefinite and non degenerate then it contains two isotropic directions $\hat{p}_1$ and $\hat{p}_2$ which give rise to two points $p_1$ and $p_2$ that are contained in all four spheres.

Finally if the inner product is degenerate on $U^\perp$ the subspace touches the light-cone of $\mathbb R^{4,1}$ and that direction gives rise to one common point of $s,s_1,s_{12}$, and $s_2$.

The first type has a particularly nice special case when all the inner products are 1. In this case the four spheres for each quadrilateral touch cyclically [1, 6]. The orthogonal circle then must pass through the four touching points.

S-isothermic surfaces of type 3 are of particular interest for us. It is the case where the orthogonal circle (or the pair of common points) collapses into a point (Fig. 3).

Fig. 3

An s-conical quadrilateral as an s-isothermic net of type 3

Theorem 7.1

For a map $s:\mathbb Z^2\rightarrow \mathbb R^{4,1}$ with $\langle s,s\rangle =1$ the following statements are equivalent:

• (i) s is s-isothermic of type 3.

• (ii) s is a solution to the Moutard equation (13) and the intersection angles of the spheres are complimentary: $\langle s,s_1\rangle = -\langle s,s_2\rangle$ and $|\langle s,s_1\rangle |\le 1$.

• (iii) $s+s_{12}$ and $s_1+s_2$ are parallel isotropic vectors.

• (iv) The centers c of s form an s-conical net and the intersection points $o$ of the diagonals lie on the corresponding spheres $s,s_1,s_{12},s_2$.

Proof

 

$(i)\Rightarrow (ii)$.:

The centers of the spheres $s,s_1,s_{12},s_2$ are coplanar and the opposite spheres touch in a common point. Thus this must be the intersection point of the diagonals. The intersection angle of the diagonals $\alpha$ and its complimentary angle $\pi -\alpha$ are exactly the intersection angles of the corresponding neighboring spheres. Then the claim follows from (12).

$(ii)\Rightarrow (iii)$.:

For $\langle s,s_1\rangle = -\langle s,s_2\rangle$ Eq. (15) implies that $s_1+s_2$ is isotropic (note that $\lambda \ne 0$). Due to (13) $s_{12}+s$ is parallel and therefore isotropic as well.

$(iii)\Rightarrow (iv)$.:

The isotropy $\langle s_1+s_2,s_1+s_2\rangle =0$ implies the touching condition $\langle s_1,s_2\rangle =-1$. Moreover $s_1+s_2$ and $s+s_{12}$ are equivalent projective representations of the common touching point $o$. The centers c of the spheres form a planar quadrilateral for which the diagonals $(c_1,c_2)$ and $(c,c_{12})$ intersect at the touching points $o$. Since $o_{\bar{1}\bar{2}},o_{\bar{2}},o,o_{\bar{1}}$ are the points in which the spheres $s_{\bar{1}},s_{\bar{2}},s_1,s_2$ touch cyclically, $o_{\bar{1}\bar{2}},o_{\bar{2}},o,o_{\bar{1}}$ lie on a circle,¹ which we denote by C. This implies that the net c is a Koenigs net with a circular net of points $o$. It remains to show that it is conical as well.

Since the quadrilateral formed by say $c,o,c_2$, and $o_{\bar{1}}$ is a folded kite (two pairs of non-opposing edges are equal in length), the planes spanned by $c,o,c_2$ and $c,c_2,o_{\bar{1}}$ are symmetric with respect to the plane spanned by $c,c_2$, and the axis of the circle C. The same holds for the other edges and thus c is a conical net corresponding to the circular net o.

$(iv)\Rightarrow (i)$.:

Let s have a central net c that is s-conical. The intersection points $o,o_{\bar{1}},o_{\bar{1}\bar{2}},o_{\bar{2}}$ lie on the sphere s. Since the connection line through the centers $c,c_{12}$ passes through the common point $o$ of the spheres $s, s_{12}$, these must touch at $o$. The isotropic vector of $o$ is projectively equivalently represented by $s_{12}+s$ or $s_1+s_2$. This implies that these vectors are parallel, thus s solves the Moutard equation. Since the four spheres share a single point the solution is of the third type.

 

We have shown that s-conical nets and s-isothermic nets of type 3 can be canonically identified: the centers of the spheres of an s-isothermic net of type 3 are the vertices of the corresponding s-conical net, and their intersection (touching) points $o$ are the intersection points of the diagonals of the s-conical net.

Christoffel dualizations defined for both these classes also coincide. The following theorem follows from the dualization formulas (7) and (16).

Proposition 7.2

The Christoffel dual net of an s-isothermic net of type 3 is an s-isothermic net of type 3. Moreover the centers c and $c^*$ of the corresponding spheres build Christoffel dual s-conical nets in the sense of Theorem 5.4.

Finally a Darboux transform of s-isothermic surfaces preserves nets of type 3 and therefore is well defined for s-conical surfaces.

Theorem 7.3

Let $c:\mathbb Z^2\rightarrow \mathbb R^3$ be s-conical with the corresponding s-isothermic net $s:\mathbb Z^2\rightarrow \mathbb R^{4,1}$ and let $\hat{s}:\mathbb Z^2\rightarrow \mathbb R^{4,1}$ be a Darboux transform of s with central net $\hat{c}:\mathbb Z^2\rightarrow \mathbb R^3$. Then $\hat{c}$ is s-conical as well.

Moreover every Darboux cube possesses a (Ribaucour) sphere $R\in \mathbb R^{4,1}$ which is orthogonal to all spheres $s,s_1,\ldots ,\hat{s}_{12}$ of the Darboux cube,

$$ \langle R,s\rangle =\langle R,s_1\rangle =\ldots =\langle R,\hat{s}_{12}\rangle =0, $$

and passes through the intersection points $o, \hat{o}$ of diagonals of c and $\hat{c}$.

Proof

Let us use the characterization (ii) of s-isothermic nets of type 3 from Theorem 7.1 that is $\langle s,s_1\rangle = -\langle s,s_2\rangle$. Due to the Moutard equation the scalar products of the spheres at the opposite edges of any face of the Darboux cube are equal (see Proposition 6.2), for example, $\langle s,s_1\rangle =\langle s^*,s^*_1\rangle$. This implies $\langle s^*,s^*_1\rangle = -\langle s^*,s^*_2\rangle$.

To prove the second claim, consider the one-parameter family of the spheres touching the quadrilateral $(c,c_1,c_{12},c_2)$ at the point $o$. They all are orthogonal to $s,s_1,s_{12},s_2$. Take the sphere R from this family that is orthogonal to $\hat{s}$. Due to Moutard equations it is orthogonal to $\hat{s}_1,\hat{s}_2,\hat{s}_{12}$ as well. Thus it touches the quadrilateral $(\hat{c},\hat{c}_1,\hat{c}_2,\hat{c}_{12})$ at $\hat{o}$.

8 S-Conical Nets with Constant Mean Curvature

In this section we consider s-conical nets with constant mean curvature $H\ne 0$. S-conical minimal surfaces, $H=0$, build an interesting subclass of s-conical surfaces with a rich theory (associated family, Weierstrass representation, variational principle). This is a subject of a separate publication [2].

Lemma 8.1

Let $f, f^*:\mathbb Z^2\rightarrow \mathbb R^3$ be two s-conical nets. Then any two of the following conditions imply the third:

• (i) $f^*$ is a Christoffel dual of f.

• (ii) $f^*$ is a Darboux transform of f.

• (iii) $f^*$ and f are in constant face offset, and it is equal to the distance $\Vert o^* - o\Vert$ between the intersection points of diagonals of the corresponding faces of f and $f^*$.

Proof

$1.\; \text {and}\; 2. \Rightarrow 3.$:

Let s and $s^*$ be the s-isothermic nets corresponding to f and $f^*$ respectively. Consider the Darboux cube formed by the spheres $s,s_1,s_2,s_{12}$ and their dual $s^*, s_1^*, s_2^*, s_{12}^*$. In the following $f, f_1$ etc. will denote the sphere’s centers, which were previously denoted by $c,c_1$ etc. Since the quadrilaterals $(f,f_1,f_{12},f_2)$ and $(f^*, f_1^*, f_{12}^*, f_2^*)$ are dual they are parallel. Due to Theorem 7.3 they touch the Ribaucour sphere R at $o$ and $o^*$ respectively. This implies that the line trough $o$ and $o^*$ intersects these two quadrilaterals orthogonally (Fig. 4).

Next, consider two neighboring quadrilaterals $(f,f_1,f_{12},f_2)$ and $(f_1,f_{11},f_{112},f_{12})$ with their duals. The common edge $f_{12}f_{1}$ of the quadrilaterals is the axis of the circle $C=s_{1}\cap s_{12}$. Obviously $o,o_1\in C$. Moreover because of the orthogonality the lines $(oo^*)$ and $(o_1o^*_1)$ are tangents to C. The same argument implies that they are also tangent to the circle $C^*=s^*_{1}\cap s^*_{12}$.

The circles C and $C^*$ are co-planar and two co-planar circles have two sets of common tangents distinguished by whether they intersect the edge between the circle centers or not. Since the Darboux cubes are “flipped over” this happens for one of the lattice directions and not for the other (see Remark 6.6). Therefore $\Vert o^*-o\Vert = \Vert o_1- o_1^*\Vert$. Since those lines are orthogonal to the quads, the face distance for the nets is constant as well.

Fig. 4

A geometric cube in Lemma 8.1. The quadrilaterals $(ff_1f_{12}f_2)$, $(f^*f^*_1f^*_{12}f^*_2)$, $(ff_1f^*_1f^*)$ are embedded, the quadrilateral $(ff_2f^*_2f^*)$ is not. The diagonal intersection points $o, o^*,o',\tilde{o}$ lie on a common line orthogonal to the planes of the quadrilaterals $(ff_1f_{12}f_2)$ and $(f^*f^*_1f^*_{12}f^*_2)$

$2.\; \text {and}\; 3. \Rightarrow 1.$:

Again consider the Darboux cube. All sides are planar quadrilaterals and since f and $f^*$ are in constant face distance, they have parallel edges. Moreover all the diagonal intersection points for a Darboux cube are collinear. Let us assume that the quadrilateral $(f,f_1,f^*_1,f^*)$ is the one of the embedded sides of the Darboux cube (see Remark 6.6). Its diagonal intersection point $o'$ and the points $o, o^*$ are collinear. The triangles $(f,f_1,o')$ and $(f^*_1,f^*,o')$ are obviously similar. The triangles $(f,f_1,o)$ and $(f^*_1,f^*,o^*)$ are their orthogonal projections and are similar as well. Thus $f-o$ and $f^*_1-o^*$ are parallel, i.e. the diagonals for f and $f^*$ satisfy the duality criteria of Proposition 4.2.

$3.\; \text {and}\; 1. \Rightarrow 2.$:

Again, the planes of corresponding quadrilaterals for f and $f^*$ are parallel since $f^*$ is dual to f. Since $(f,f_{2},o)$ and $(f_{2}^*,f^*,o^*)$ are similar triangles, the arguments of the previous item in the proof imply that the intersection points of the diagonals of all side-quadrilaterals lie on the line connecting $o$ and $o^*$. In particular this is the case with the intersection point $\tilde{o}$ of the diagonals of the quadrilateral $(f,f_{2},f^*_{2},f^*)$. We will prove the claim in case that this quadrilateral is non-embedded, for embedded quadrilaterals the proof differs just by a minor change of signs ±.

We can assume that $\tilde{o}$ lies at the origin. The triangles $(\tilde{o},f^*,o^*)$ and $(\tilde{o},f_{2},o)$ are similar and $\Vert of_{2}\Vert =r_{2}$, $\Vert o^*f^*\Vert =r^*=\frac{1}{r}$. This implies for $f^*$ and similarly for $f^*_{2}$:

$$f^*=\frac{1}{r r_{2}}f_{2},\quad f^*_{2}=\frac{1}{r r_{2}}f.$$

Then the middle three coordinates (10) of the spheres $s,s_{2},s^*_{2}$ and $s^*$ are equal $\frac{f}{r},\frac{f_{2}}{r_{2}}$, $\frac{f_{2}^*}{r_{2}^*} =\frac{ f}{r}$, and $\frac{f^*}{r^*} = \frac{ f_{2}}{r_{2}}$ respectively. To prove the Moutard identity

$$ s - s^*_{2} =\mu (s^* - s_{2}), \quad \mu =-\frac{r_{2}}{r} $$

it remains to verify it for the terms of the form $\frac{1}{r}$ and $\frac{\Vert f\Vert ^2-r^2}{r}$ in (10). The identity

$$ \frac{1}{r}-\frac{1}{r^*_{2}}=\mu (\frac{1}{r^*}-\frac{1}{r_{2}}) $$

is obvious. For the terms of the form $\frac{\Vert f\Vert ^2-r^2}{r}$ the computation is slightly more involved. The claim finally follows from

$$ \Vert f\Vert ^2-r^2=\Vert f_{2}\Vert ^2-r^2_{2}=\Vert \tilde{o}-o\Vert ^2. $$

Thus the cube is Darboux.

Remark 8.2

Considering degenerated examples it is not difficult to convince yourself that the extra condition that the face distance equals the distance between the points $o$ and $o^*$ (or equivalently that the line $(oo^*)$ is perpendicular to the quadrilaterals) in Lemma 8.1 cannot be dropped.

Let us recall that a parallel net in constant distance in the sense of (1) to a conical net lies in a constant distance face offset. We formulate the obtained properties of s-conical cmc nets in the following

Theorem 8.3

• (i) An s-conical net f is cmc if and only if it has a Christoffel dual $f^*$ in constant distance. The lines $(oo^*)$ connecting the points of intersection of diagonals of the corresponding quadrilaterals of f and $f^*$ intersect the planes of these quadrilaterals at constant angle $\theta$. The distance $\Vert oo^*\Vert$ is constant for the whole net.

• (ii) An s-conical net f has a Darboux transform $f^D$ in constant distance if and only if f is cmc with $\theta =\pi /2$. Then the Darboux transform is Chistoffel dual $f^D=f^*$.

Proof

The first claim in (i) is Theorem 5.2. To prove the claim about the angles, note that the the points $o$ and $o^*$ corresponding to four quadrilaterals with a common vertex f lie on two circles with the common axis $(ff^*)$. Moreover the corresponding intervals $oo^*$ are symmetric with respect to the reflections in the symmetry planes that identify the planes of the faces. This implies that the distance $\Vert oo^*\Vert$ is constant for the whole net, and the lines $(oo^*)$ intersect the planes of the corresponding quadrilaterals at constant angle.

A Darboux transform $f^D$ in constant distance (thus in constant distance face offset) implies that the line through the touching points of the Ribaucour sphere $(oo_D)$ is orthogonal to the faces of the quadrilaterals, and the distance $\Vert oo_D\Vert$ is constant. Here we have denoted by $o^D$ the diagonal intersection points of $f^D$. Then the Darboux transform is Chistoffel dual due to Lemma 8.1, which implies that f is cmc. The reverse statement also follows from this Lemma. Indeed, if f is cmc and $f^*$ its dual with orthogonal $(oo^*)$ then $f^*$ is a Darboux transform of f.

Remark 8.4

Geometric characterizations of s-conical cmc surfaces turn out to be quite similar to the ones of circular cmc surfaces, that also can be characterized as possessing a Christoffel dual, which is simultaneously a Darboux transform, at constant distance [10].

9 Delaunay Nets

In this section we will construct s-conical Delaunay nets that are s-conical analogues of rotationally symmetric cmc surfaces.

A planar polygon $c:\mathbb Z\rightarrow \mathbb R^2$ with non-vanishing edges, gives rise to a discrete surface of revolution. Denoting the components of a vertex $c_k$ by $c_k = (x_k, y_k)$ and choosing an angle $\phi$ one can form

$$ f(k_,l) = (x_k, \cos (l\phi ) y_k, \sin (l\phi ) y_k). $$

Since all the polygons $f(\cdot , l_0)$ are planar we will not distinguish between the generating polygon c and its resulting rotational symmetric net f in what follows. This abuses the notation to some extend but it is understood that shifts in the first direction are along the polygon and whenever a shift in the second direction occurs it refers to the rotational direction of the net.

By symmetry c is s-isothermic. In order for it to be of type 1 with touching spheres ($\langle s_1,s\rangle = \langle s_2,s\rangle = 1$) the polygon must satisfy in addition

$$ \Vert c_1 - c\Vert = \sin \frac{\phi }{2}\; (y_1 +y). $$

Instead of the polygon c one can look at the midpoint connectors in axial direction. They form a planar polygon as well (see Fig. 5). Calling this polygon $p = (x,v)$ one finds that above condition translates to

$$ \Vert p_1 - p\Vert ^2 = 4 \tan ^2\frac{\phi }{2}\; v_1 v. $$

Fig. 5

Rotationally symmetric nets

Thus in order to allow for the net to be s-isothermic with touching spheres one needs

$$\begin{aligned} \frac{\Vert p_1 - p\Vert ^2}{v v_1} = const. \end{aligned}$$

(17)

This holds true in particular for a polygon p that arises when unrolling the billiard in an ellipse.

Fig. 6

Unrolling the billiard in an ellipse: consecutively place the edges of the billiard on the axis and mark the position of one of the foci. The second polygon is generated by the other focus and mirroring on the axis

The construction is as follows [11] (see also [5]): Starting with a polygon given by a billiard in an ellipse, unroll it by placing each edge on the axis consecutively and marking the location of one of its foci in this process. This gives rise to a new polygon p (see Fig. 6). The same can be done with the other focus and after mirroring that second polygon along the axis the two polygons p and $p^*$ are known to give rise to a pair of discrete cmc nets in the discrete isothermic sense. In particular pairs of edges $p_1 p$ and $p^*_1 p^*$ form trapezoids (see Fig. 7) with constant distances and diagonals $\Vert p^* - p\Vert = d = \Vert p^*_1 - p_1\Vert$ and $\Vert p^*-p_1 \Vert = l = \Vert p^*_1 - p\vert$. Corresponding quadrilaterals from the two nets are dual to each other.

To see that this polygon satisfies Eq. (17) one needs to know that $\tan \alpha \tan \beta$, with the angles $\alpha , \beta$ in Fig. 7, is an integral of motion for the billiard in an ellipse, i.e.

$$\begin{aligned} \tan \frac{\alpha }{2}\tan \frac{\beta }{2} = \tan \frac{\alpha _1}{2}\tan \frac{\beta _1}{2}. \end{aligned}$$

(18)

We have

$$ \begin{array}{rcl} \gamma &{}=&{} \pi - \alpha - \beta ,\\ \Vert p_1 -p\Vert &{}=&{} 2 \Vert p-o\Vert \sin \frac{\gamma }{2},\\ v &{}=&{} \Vert p-o\Vert \sin \alpha ,\\ v_1 &{}=&{} \Vert p-o \Vert \sin \beta . \end{array} $$

This implies

$$ \frac{\Vert p_1 - p\Vert ^2}{v_1 v} = \cot \frac{\alpha }{2}\cot \frac{\beta }{2} + \tan \frac{\alpha }{2}\tan \frac{\beta }{2} -2 = \mathrm{const}. $$

Fig. 7

The polygons from unrolling an ellipse

Summarizing, the billiard in an ellipse gives rise to a pair of polygons p and $p^*$ that generate a discrete isothermic cmc surface of revolution and its dual. The same polygons $p = (x,v)$, $p^* = (x^*,v^*)$ can be read as midpoint connectors in two rotational symmetric s-isothermic nets that are generated by polygons $c, c^*$ where

$$ c = (x,y) = (x, \frac{v}{\cos \frac{\phi }{2}}), \quad c^* = (x^*,y^*) = (x^*, \frac{v *}{\cos \frac{\phi }{2}}). $$

Note that the corresponding scaling $(x,y)\mapsto (x,y/\cos \frac{\phi }{2})$ is an affine mapping and thus preserves parallelity. Due to Proposition 4.2 the Christoffel duality can be formulated in terms of parallel edges and diagonals, therefore dual quadrilaterals stay dual after such scaling. So, the two resulting s-isothermic nets c and $c^*$ are dual to each other as well.

Recall that the s-isothermic nets of type 1 have an orthogonal circle for each quadrilateral of spheres and in the case of touching spheres the circle passes through the touching points. For the s-isothermic nets c and $c^*$ one can think of the edges $p_1 p$ as diameters in the inscribed circles and we will denote the touching points along the edges $c_1 c$ with $\tilde{p}$ (see Fig. 8).

Fig. 8

The net c and its dual $c^*$ with the inscribed circles

Since $p,p_1,p^*_1$, and $p^*$ form a symmetric trapezoid, the circles for the quadrilaterals $(c,c_1, c_{12},c_2)$ and its dual $(c^*,c^*_1, c^*_{12},c^*_2)$ are co-axial. Moreover, since the lines $(c_1c)$ and $(c^*_1c^*)$ are parallel and tangent (in $\tilde{p}$ and $\tilde{p}^*$) to co-axial circles, their distance is $\Vert \tilde{p}-\tilde{p}^*\Vert = l$. Likewise $(c_2 c)$ and $(c^*_2 c^*)$ are parallel and touch the circles in p and $p^*$ thus their distance is $\Vert p^* -p\Vert = d$. Together we see that the two dual s-isothermic nets are in constant edge distance (but with two different distances for the two lattice directions). This is a way to define s-isothermic cmc nets (see [12]).

Fig. 9

An s-conical Delaunay net

Now define a third pair of polygons

$$ q = (x,u) = (x,\frac{y}{\cos \frac{\phi }{2}}) = (x, \frac{v}{\cos ^2\frac{\phi }{2}}),\quad q^* = (x,u^*)= (x,\frac{y^*}{\cos \frac{\phi }{2}})= (x, \frac{v^*}{\cos ^2\frac{\phi }{2}}). $$

Rotating these polygons one gets nets for which one can think of c and $c^*$ as the polygons of midpoint connectors. The resulting faces for q and $q^*$ thus will have constant face offset. Moreover they will be dual by the same argument as above.

The sphere s centered at c contains $\tilde{p}$. Since (cq) and $(c \tilde{p})$ are orthogonal a sphere t centered at q that meets $\tilde{p}$ also contains $\tilde{p}_{\bar{1}}$. By symmetry the quadrilaterals formed by the $\tilde{p}$ are circular. Finally one finds that the points $\tilde{p}$ are the diagonal intersection points of the quadrilaterals of the net q. One can see this for example by noting that the radii for the s-isothermic spheres are $r = v \tan \frac{\phi }{2}$, so $\Vert \tilde{p}-c\Vert = r$ and half an edge in rotational direction is $g = \Vert c - q\Vert = y \tan \frac{\phi }{2}$. Thus $\frac{g}{r} = \frac{y}{v}$ which is constant by construction.

Fig. 10

Nested circular, s-isothermic, and s-conical Delaunay nets

We see that the third net formed by q is in fact an s-conical net with the dual net $q^*$ in constant face offset equal the distance between the corresponding diagonal intersection points. Due to Theorem 8.3 this an s-conical cmc net. Figure 9 shows an example of such an s-conical Delaunay net. It is worth mentioning that the three types of discrete Delaunay nets (discrete isothermic, s-isothermic in the touching case, and s-conical) can be arranged in such a way that the second touches the first and the third touches the second as shown in Fig. 10. This is a direct consequence of the construction.