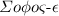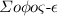Verifiable and Forward Secure Dynamic Searchable Symmetric Encryption with Storage Efficiency

Abstract

Searchable symmetric encryption (SSE) provides private searching over an encrypted database against an untrusted server. Though various SSE schemes have been studied, recently, it is shown that most of existing schemes are vulnerable to file injection attacks. At ACM CCS 2016, Bost proposed a forward secure SSE scheme to resist such attacks, called ${\varSigma }{o}{\phi }{o}{\varsigma }$. Besides the basic scheme (${\varSigma }{o}{\phi }{o}{\varsigma }$) secure against semi-honest servers, a verifiable scheme () secure against malicious servers is also introduced. In , each client keeps hash values of indexes of documents corresponding to each keyword. Thus, the client storage cost is higher than for ${\varSigma }{o}{\phi }{o}{\varsigma }$, and the hash table must be reconstructed when a new document is added. Also, since any security definition and proof of security against malicious servers are not provided, what guarantees against malicious server is unclear. In this paper, we propose a new verifiable and forward secure SSE scheme against malicious servers. An advantage of our scheme to is the client storage cost; that is, our scheme only needs the same storage cost as ${\varSigma }{o}{\phi }{o}{\varsigma }$. Our key idea is to bind each index and keyword with a tag generated by an algebraic pseudo-random function, and to store the tag to the server as well as the encrypted index on an update phase. The client can efficiently check validity of answers to search queries by verifying the combined tag thanks to closed form efficiency of the algebraic pseudo-random function; and thus, the client does not need to keep the hash table. Also, we formally prove security against malicious servers. Specifically, we show that our scheme satisfies the strong reliability definition.

1 Introduction

In our daily life, we use various cloud storage services, and our sensitive data are stored in an outside server. Because many leakage incidents of databases stored in cloud storage servers recently happen (e.g., “The Fappening” of Apple’s iCloud in 2014), these data must be encrypted. However, if we use ordinary symmetric encryption schemes like AES, it is difficult to search a document for clients. For this problem, Song et al. [1] introduced the notion of searchable symmetric encryption (SSE). The aim of SSE is to provide private search over the encrypted database store in an untrusted server. Specifically, the client wants to hide information of keywords in the search phase as well as information of documents. SSE schemes need to guarantee that small (or inevitable) information only leaks to the server.

The first strongly secure SSE scheme was proposed by Curtmola et al. [2]. Their scheme is static; that is, the encrypted database is stored in the server only in the setup phase, and if a new document is added, then the encrypted database must be reconstructed. Hence, static SSE schemes are not suitable for environments that data is frequently updated. Kamara et al. [3] proposed an efficient dynamic SSE scheme¹ that the client can add/delete a document corresponding to a set of keywords to/from the already stored encrypted database without reconstructing it. Thus, dynamic SSE schemes are more useful in cloud storage services than static SSE schemes. Various dynamic SSE schemes have been studied to improve efficiency and search flexibility. From the viewpoint of security, it is important to resist attacks by an untrusted server because some malicious insiders may operate cloud storage services. Especially, we must consider that the malicious server tries to respond a fake answer to a search query (i.e., The true answer for keyword w is document D, but the server returns another document $D'$). Kurosawa and Ohtaki [4] introduced the notion of verifiable SSE which guarantees that the client can verify if the answer is true or not, and they extended it to the dynamic SSE setting [5]. Kurosawa et al. [6] formally defined verifiability as strong reliability such that no malicious server can make the client accepted for any fake answer.

In the sense of adversary, Islam et al. [7] introduced a new type of attacks to SSE schemes, called leakage-abuse attacks. In this attack, if the server knows (almost) all the contents of the client’s documents, then it can determine the client’s queries from leakage of query pattern (i.e., when a query is repeated) and the file-access pattern (i.e., which files are returned in response to each query). Since such leakage is considered as practically small leakage, their attack clarifies that security of some existing SSE schemes are not enough in reality. Moreover, Cash et al. [8] extended the attack such that full plaintext of the encrypted database can be recovered by allowing larger leakage. For dynamic SSE setting, Zhang et al. [9] showed an attack to reveal the content of a past search query by injecting few new documents in the update phase, called file injection attacks. Their attack is very powerful because most of existing dynamic SSE schemes are not resistant to the attack (i.e., The server can learn that the new document matches a previous search query.).

Related to file injection attacks, Chang and Mitzenmacher [10] proposed an (inefficient) forward secure dynamic SSE scheme with linear search cost. The notion of forward security guarantees that no server can tell if a newly inserted document matches previous search queries. Thus, forward secure SSE schemes can resist to file injection attacks. Also, forward secure SSE schemes allow for an online build of the encrypted database because the update phase does not leak information. In most of non-forward secure SSE schemes, inverted indexes of the database are necessary in the setup phase; and thus, an indexing step may be an efficiency bottleneck of the system. Stefanov et al. [11] proposed a forward secure dynamic SSE scheme based on the oblivious RAM (ORAM). However, their scheme is not verifiable, and needs large bandwidth overhead on updates due to ORAM. Bost et al. [12] extended Stefanov et al.’s scheme to verifiable. Their scheme also need large bandwidth overhead on updates.

Recently, Bost [13] proposed an efficient forward secure dynamic SSE scheme (${\varSigma }{o}{\phi }{o}{\varsigma }$) without relying on ORAM. ${\varSigma }{o}{\phi }{o}{\varsigma }$ achieves optimal search and update complexity for both computation and communication for forward secure SSE. The key idea of ${\varSigma }{o}{\phi }{o}{\varsigma }$ is that the location of the newly added encrypted document and the search token are unlinkable by preventing the adversary to generate any new search token from old one, but the client can compute new one by using trapdoor permutations. Also, he shows an extension to verifiable scheme (). The idea of is that the client keeps each hash value of indexes of documents for each keyword. If the malicious server returns a fake answer, then the client can verify validity by comparing the hash value. However, needs the additional storage cost for clients than ${\varSigma }{o}{\phi }{o}{\varsigma }$ because of keeping the hash table. Specifically, whereas ${\varSigma }{o}{\phi }{o}{\varsigma }$ needs $O(W\log {D})$ storage, needs $O(W(\log {D}+\kappa ))$ storage, where W is the number of distinct keywords, D is the number of documents and $\kappa$ is the security parameter. For an implementation in [13], experimental parameters sizes are set as $D \le 2^{48}$, $W \le 2^{23}$ and $\kappa$ is 128 bit; and thus, the extra client storage cost of is about 128MB to the cost of ${\varSigma }{o}{\phi }{o}{\varsigma }$. Therefore, to achieve both of forward security against malicious servers and client storage efficiency is an important remaining problem. Also, any formal definition and proof of security against malicious servers is not shown in [13]. Hence, it is unclear that is actually secure against malicious servers.

1.1 Our Contribution

The contribution of this paper is twofold: one is to resolve the problem on the storage cost in , and the other is to show the formal security against malicious servers.

New Forward Secure Dynamic SSE. We propose a new forward secure dynamic SSE scheme which is secure against malicious servers. The storage cost of our scheme is asymptotically the same as ${\varSigma }{o}{\phi }{o}{\varsigma }$; that is, $O(W\log {D})$. We show a comparison among previous forward secure SSE schemes and our scheme in Table 1.

Table 1. Comparison among previous forward secure SSE schemes and our scheme

Our key idea is to change the way to verify the answer of the server. In , verifiability is achieved by using client’s hash table of indexes of documents for each keyword. Thus, an additional storage cost is necessary. In our scheme, verifiability is achieved by using the mechanism of message-authentication codes (MAC) based on a pseudo-random function (PRF). Specifically, each client generates a secret key for the PRF in the setup phase, and computes and sends a tag to bind the document index and the keyword with the PRF to the server in the update phase. The client can erase tags after the update phase. In the search phase, the client can check the validity of the search result by receiving and verifying indexes and tags. Since the secret key for the PRF is only known by the client, it is difficult to forge a tag by the server from the property of the PRF. Thus, the security against malicious servers without increasing the storage size can be achieved. However, in this approach, the communication cost and the computational cost for the client are large.

Hence, we use the other idea to resolve the problems on costs. We use an algebraic PRF (APRF) with closed form efficiency [14]. The APRF is a special type of PRF such that certain algebraic operations on these outputs can be computed more efficiently with the secret salt than computing separately. We generate tags for document indexes by using the APRF instead of the standard PRF. Then, in the search phase, the server composes these tags by using the algebraic property of APRF, and the client can efficiently check the validity with the secret salt. Hence, the communication and computation cost is comparable to without increasing the storage cost.

Formal Security Proof against Malicious Servers. We adapt strong reliability [6] as the definition of security against malicious servers. Strong reliability guarantees that no malicious server can make an client accept a fake answer or a fake tag to a search query. It is a suitable definition for schemes which uses tags to check the validity of the search result because tags are explicitly defined. Hence, we use strong reliability. The SSE scheme in [12] is also proved to be secure against malicious servers. Their security definition is called soundness which also guarantees that no adversary output a fake search result that is accepted by the client. However, in the soundness definition, since tags are not explicitly defined, the adversary is not regarded to win even if a tag is forged but the search result is valid. On the other hand, in the strong reliability definition, the adversary wins if a tag is forged but the search result is valid. Therefore, strong reliability is stronger than soundness. The detailed discussion about the difference between two types of definitions is shown in [6]. We formally prove that our scheme satisfies strong reliability by assuming the APRF. Specifically, we show a reduction to pseudo-randomness of the APRF from strong reliability.

Also, we prove that our scheme satisfies forward security by assuming the APRF and the one-way trapdoor permutation in the random oracle model. The definition of forward security is the same as in [13].

2 Preliminaries

Notations. Throughout this paper we use the following notations. We denote $\kappa$ as the security parameter, and $negl(\kappa )$ as the negligible function in $\kappa$. Hereafter, we omit the security parameter for inputs of algorithms except cases that we must explicitly state it. If $\mathsf {Set}$ is a set, then by $m \in _R \mathsf {Set}$ we denote that m is sampled uniformly from $\mathsf {Set}$. If $\mathcal {ALG}$ is an algorithm, then by $y \leftarrow \mathcal {ALG}(x;r)$ we denote that y is output by $\mathcal {ALG}$ on input x and randomness r (if $\mathcal {ALG}$ is deterministic, r is empty). When X is a bit-string, we denote |X| as the bit length, and when X is a set, we denote |X| as the number of elements.

2.1 Building Blocks

Pseudo-Random Function and Algebraic Pseudo-Random Function. Let $\mathsf {F}=\{F_\kappa : Salt_\kappa \times Dom_\kappa \rightarrow Rng_\kappa \}_{\kappa }$ be a function family with a family of domains $\{Dom_\kappa \}_{\kappa }$, a family of salt spaces $\{Salt_\kappa \}_{\kappa }$ and a family of ranges $\{Rng_\kappa \}_{\kappa }$.

Definition 1

(Pseudo-Random Function). We say that function family $\mathsf {F}=\{F_\kappa \}_{\kappa }$ is the pseudo-random function (PRF) family, if for any PPT distinguisher $\mathcal {D}$ and salt $s \in _R Salt_\kappa$, advantage $\mathsf {Adv}_{\mathcal {D}} = |\Pr [1 \leftarrow \mathcal {D}^{F_\kappa (s, \cdot )}]$ − $\Pr [1 \leftarrow \mathcal {D}^{\textit{RF}_\kappa (\cdot )}]| \le negl(\kappa )$, where $\textit{RF}_\kappa : Dom_\kappa \rightarrow Rng_\kappa$ is a truly random function.

Definition 2

(Algebraic Pseudo-Random Function [14]). We say that PRF function family $\mathsf {F}=\{F_\kappa \}_{\kappa }$ is the algebraic pseudo-random function (APRF) family if the following two properties are satisfied:

• Algebraic. The range Rng of PRF $F(\cdot )$ for every $\kappa$ and the salt s forms an Abelian multiplicative group. We require that the group operation on Rng be efficiently computable.

• Closed form Efficiency. Let N be the order of the range sets of F for security parameter $\kappa$. Let $z = (z_1, \dots , z_\ell ) \in \{\{0,1\}^m\}^\ell$, $k \in N$, and efficiently computable $h: \mathbb {Z}^k_N \rightarrow \mathbb {Z}^\ell _N$ with $h(x)=\langle h_1(x),\dots ,h_\ell (x)\rangle$. There exists an algorithm $\mathsf {CFEval}_{h,z}$ such that for every $x \in \mathbb {Z}^k_N$, $\mathsf {CFEval}_{h,z}(x,s) = \prod _{i=1}^\ell [F(s,z_i)]^{h_i(x)}$ and the running time of $\mathsf {CFEval}$ is polynomial in $\kappa , m, k$ but sublinear in $\ell$.

Hereafter, we omit $\kappa$ in $F_\kappa$ for simplicity.

2.2 Dynamic Searchable Symmetric Encryption

Syntax. In this paper, we focus on the single keyword search and inverted index schemes (i.e., The server returns index lists corresponding to each search query.). Let $\mathsf {D}=\{D_1, \dots ,$ $D_n\}$ be a set of documents, and $\mathsf {DB}:= (\mathsf {ind}_i, \mathsf {W}_i)_{i=1}^n$ be a database containing pairs of index $\mathsf {ind}_i$ corresponding to document $D_i$ and set of keywords $\mathsf {W}_i$ included in $D_i$, where $\mathsf {ind}_i \in \{0, 1\}^l$ for constant l and $\mathsf {W}_i \subseteq \{0, 1\}^*$. Also, let $\mathsf {W} := \cup _{i=1}^n \mathsf {W}_i$ be the set of keywords, $W:=|\mathsf {W}|$ be the number of distinct keywords, D be the number of documents, and $\mathsf {DB}(w)= \{\mathsf {ind}_i| w \in \mathsf {W}_i \}$ be the set of indexes of documents including keyword w. For example, if $\mathsf {DB}(w)=\{\mathsf {ind}_1, \mathsf {ind}_2, \mathsf {ind}_3\}$, then documents including keyword w are $D_1$, $D_2$ and $D_3$.

A dynamic SSE scheme consist of three phases $(\mathsf {Setup}, \mathsf {Search},\mathsf {Update})$.  

$\mathsf {Setup}(\mathsf {DB})$: :

On input $\mathsf {DB}$, the client outputs encrypted database $\mathsf {EDB}$, secret key K and state of the client $\sigma$, and stores $\mathsf {EDB}$ to the server.

$\mathsf {Search}(K, w, \sigma , \mathsf {EDB}) = (\mathsf {Search}_C(K,w,\sigma ), \mathsf {Search}_S(t(w),\mathsf {EDB}))$: :

On input secret key K, state $\sigma$ and keyword w for the client, and encrypted database $\mathsf {EDB}$ for the server, the client sends trapdoor t(w) to the server, and the server returns $\mathsf {DB}(w)$. The server returns verifier $\mathsf {Ver}=\{Ver_i | ind_i \in \mathsf {DB}(w)\}$ as well as $\mathsf {DB}(w)$, and the client verifies $\mathsf {Ver}$ for $\mathsf {DB}(w)$. If the verification holds, the client regards that $\mathsf {DB}(w)$ is the valid answer.

$\mathsf {Update}(K, \sigma , op, in, \mathsf {EDB}) = (\mathsf {Update}_C(K, \sigma , op, in),\ \mathsf {Update}_S(\mathsf {EDB}, u(in)))$: :

On input K, $\sigma$, operation $op \in \{add,del\}$ and a document/keyword pair $in = (\mathsf {ind},w)$ for index $\mathsf {ind}$ and keyword w for the client, and $\mathsf {EDB}$ for the server, the client sends update information u(in) corresponding to in to the server, and the server updates $\mathsf {EDB}$, where add/del means the addition/deletion of in.

 

It is required that an honest server always returns the true answer for any search query.

Definition 3

(Correctness). For any $\mathsf {DB}$ the following holds:

$$\begin{aligned}&\Pr [(\mathsf {EDB}, K, \sigma ) \leftarrow \mathsf {Setup}(\mathsf {DB}); \text {repetition of }\mathsf {Update}(K, \sigma , op, in, \mathsf {EDB}); \\&\quad t(w) \leftarrow \mathsf {Search}_C(K,w,\sigma ); x \leftarrow \mathsf {Search}_S(t(w),\mathsf {EDB}); x\not =\mathsf {DB}(w)] \le negl(\kappa ) \end{aligned}$$

Security Model. For SSE schemes, privacy against the server is required. It is ideal if there is no leaked information to the server. However, it is not realistic in the SSE setting. Hence, we define leakage function $\mathcal {L}= (\mathcal {L}^{Stp}, \mathcal {L}^{Srch}, \mathcal {L}^{Updt})$ to represent what a SSE scheme leaks to the adversary. $\mathcal {L}^{Stp}$/$\mathcal {L}^{Srch}$/$\mathcal {L}^{Updt}$ means the leakage function in the setup/search/update phase. The leakage function $\mathcal {L}$ keeps the query list Q as it state. Q contains entries (i, w) for a search query on keyword w, or entries (i, op, in) for an update query. i is incremented at each query. The search pattern sp(w) is defined as $sp(w) = \{j : (j,x) \in Q\}$. The history of keyword hist(w) contains the set of documents indexes matching w at the setup phase, and the set of updated documents indexes matching w at the update phase. As the security model of dynamic SSE schemes, we show definitions of confidentiality, forward security, and strong reliability.

Confidentiality. It is required that there is no leak from each phase except derivable information from leakage functions. Confidentiality is defined by the simulation paradigm (i.e., indistinguishability between the real world and the ideal world), and is parametrized by leakage functions.

Definition 4

(Confidentiality). The real world $SSE_{real}$ and the ideal world $SSE_{ideal}$ containing a simulator $\mathcal {S}$ are defined as follows:

• 1. An adversary $\mathcal {A}$ chooses database $\mathsf {DB}$.

• 2. $\mathcal {A}$ obtains $\mathsf {EDB}\leftarrow \mathsf {Setup}(\mathsf {DB})$ in $SSE_{real}$, or a simulated output $\mathsf {EDB}\leftarrow \mathcal {S}(\mathcal {L}^{Stp}(\mathsf {DB}))$ in $SSE_{ideal}$.

• 3. $\mathcal {A}$ can repeatedly pose search (resp. update) queries with input w (resp. (op, in)), and obtains $\mathsf {DB}(w) \leftarrow \mathsf {Search}(K, w, \sigma , \mathsf {EDB})$ (resp. $\mathsf {EDB}\leftarrow \mathsf {Update}(K,$ $\sigma , op, in, \mathsf {EDB})$) in $SSE_{real}$, or a simulated output $\mathsf {DB}(w) \leftarrow \mathcal {S}(\mathcal {L}^{Srch}(w))$ (resp. $\mathsf {EDB}\leftarrow \mathcal {S}(\mathcal {L}^{Updt}(op,in))$) in $SSE_{ideal}$.

• 4. $\mathcal {A}$ outputs a bit b.

We say that a SSE scheme is $\mathcal {L}$-adaptively secure if for any PPT $\mathcal {A}$ there exists $\mathcal {S}$ such that

$$\begin{aligned} |\Pr [1 \leftarrow \mathcal {A}\text {in} SSE_{real}] - \Pr [1 \leftarrow \mathcal {A}\text {in} SSE_{ideal}]| \le negl(\kappa ). \end{aligned}$$

Forward Security. It is required that the adversary cannot tell if an updated document is corresponding to keywords in previous search queries.

Definition 5

(Forward Security [13]). We say that a $\mathcal {L}'$-adaptively secure SSE scheme is forward secure if the update leakage function $\mathcal {L}^{Updt}$ is represented as follows:

$$\begin{aligned} \mathcal {L}^{Updt}(op, in) = \mathcal {L}'(op, ({\mathsf {ind}}_i, {\mu }_i)), \end{aligned}$$

where $({\mathsf {ind}}_i, {\mu }_i)$ is a set of modified documents paired with the number $\mu _i$ of modified keywords for the updated document $\mathsf {ind}_i$.

Strong Reliability. It is required that no malicious server can make a client accept a fake answer to a search query. Especially, strong reliability guarantees unforgeability of a verifier corresponding to a document.

Definition 6

(Strong Reliability [6]). We consider the following game between an honest client and an adversary $\mathcal {A}$.  

$\mathsf {Setup}$ phase :

$\mathcal {A}$ chooses $\mathsf {DB}$, and sends it to the client. The client generates secret key K and $\mathsf {EDB}$, and sends $\mathsf {EDB}$ to $\mathcal {A}$.

$\mathsf {Update}$ phase :

$\mathcal {A}$ chooses $(op_i,in_i)$, and sends it to the client. The client generates update information $u(in_i)$, and sends $(op_i, u(in_i))$ to $\mathcal {A}$.

$\mathsf {Search}$ phase :

$\mathcal {A}$ chooses keyword $w_i$, and sends it to the client. The client generates $t(w_i)$, and sends it to $\mathcal {A}$. $\mathcal {A}$ returns $(\mathsf {DB}(w)',\mathsf {Ver}')$ to the client.

We note that the $\mathsf {Update}$ phase and the $\mathsf {Search}$ phase can be adaptively repeated by $\mathcal {A}$. We define that the adversary $\mathcal {A}$ wins if for some $\mathsf {Search}$ phase the client accepts $(\mathsf {DB}(w)',\mathsf {Ver}')$ as a true answer, and $(\mathsf {DB}(w)',\mathsf {Ver}') \not = (\mathsf {DB}(w),\mathsf {Ver})$, where $(\mathsf {DB}(w),\mathsf {Ver}) \leftarrow \mathsf {Search}(K, w, \sigma , \mathsf {EDB})$. We say that a dynamic SSE scheme is strong reliable if for any PPT $\mathcal {A}$, $\Pr [\mathcal {A}\text {wins}] \le negl(\kappa )$.

3 , Revisited

In this section, we recall , a forward secure dynamic SSE scheme secure against malicious servers.

3.1 Overview of ${\varSigma }{o}{\phi }{o}{\varsigma }$ and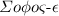

To guarantee forward security, ${\varSigma }{o}{\phi }{o}{\varsigma }$ introduces a search token update mechanism with a one-way trapdoor permutation (OWTP) $\pi$. Here, we roughly recall the design of ${\varSigma }{o}{\phi }{o}{\varsigma }$. In the $\mathsf {Setup}$ phase, the client generates secret key sk for OWTP. In the $\mathsf {Update}$ phase to add a new index $\mathsf {ind}$ corresponding to keyword w, for the first addition of keyword w the client randomly chooses the initial search token $ST_0^{(w)}$, sets counter $c^{(w)} := -1$, keeps $(ST_0^{(w)},c^{(w)})$ as the current search token, computes update token $UT_0^{(w)} = H_1(ST_0^{(w)})$ and the encrypted index $e^{(w)}_0=\mathsf {ind}\oplus H_2(ST_0^{(w)})$ with hash function $H_1$ and $H_2$ (modelled as random oracles (ROs)), and sends $(UT_0^{(w)},e^{(w)}_0)$ to the server. For previously added keyword w the client computes new search token $ST_{c+1}^{(w)} = \pi ^{-1}_{sk}(ST_c^{(w)})$, keeps $(ST_{c+1}^{(w)},c^{(w)}+1)$ as the current search token, computes update token $UT_{c+1}^{(w)} = H_1(ST_{c+1}^{(w)})$ and the encrypted index $e^{(w)}_{c+1}=\mathsf {ind}\oplus H_2(ST_{c+1}^{(w)})$, and sends $(UT_{c+1}^{(w)},e^{(w)}_{c+1})$ to the server. The server stores $(UT_{c+1}^{(w)},e^{(w)}_{c+1})$ to $\mathsf {EDB}$. We note that the malicious server cannot compute $ST_{c+1}^{(w)}$ even if $UT_{c+1}^{(w)}$ is given because RO $H_1$ is not invertible. Similarly, $\mathsf {ind}$ is hidden even if $e^{(w)}_{c+1}$ is given because RO $H_2$ is not invertible. In the $\mathsf {Search}$ phase for keyword w, the client sends the current search token $ST_{c}^{(w)}$ to the server. Since the server know public key pk, the server can derive ${ST_i^{(w)}}_{0 \le i \le c-1}$. Also, since $UT_i^{(w)}= H_1(ST_i^{(w)})$, then the server can find $\mathsf {DB}(w)$ by decrypting each $e^{(w)}_i$ for $0 \le i \le c-1$. We note that the malicious server cannot compute $ST_{c+1}$ even if $ST_{c}$ is given because secret key sk is only known to the client. Therefore, ${\varSigma }{o}{\phi }{o}{\varsigma }$ guarantees forward security.

is a verifiable version of ${\varSigma }{o}{\phi }{o}{\varsigma }$. In the $\mathsf {Update}$ phase, the client also keeps $H(\mathsf {DB}(w))$ for each keyword w as well as $(ST_{c+1}^{(w)},c^{(w)}+1)$ with a collision resistance hash function H. In the $\mathsf {Search}$ phase, the client verifies if $\mathsf {DB}(w)'$ sent from the server is valid by checking $H(\mathsf {DB}(w))\overset{?}{=}H(\mathsf {DB}(w)')$. From collision resistance of H, it is infeasible to find $\mathsf {DB}(w)'\not =DB(w)$ such that $H(\mathsf {DB}(w))=H(\mathsf {DB}(w)')$. Thus, is secure against malicious servers.

3.2 Complexity of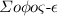

In the sense of the storage cost, each client must keep table $\mathbf {W}$ and $\mathbf {H}$. Table $\mathbf {W}$ contains $(i_w,c)$ for every keyword; and hence, the storage cost is $O(W \log {D})$. Table $\mathbf {H}$ contains $H_3(\mathsf {DB}(w))$ for every keyword; and hence, the storage cost is $O(W\kappa )$. Therefore, the total storage cost for a client is $O(W(\log {D}+\kappa ))$.

The computational cost is $O(a_w)$ in the $\mathsf {Search}$ phase and O(1) in the $\mathsf {Update}$ phase, where $a_w$ is the number of times that the queried keyword w was historically added to the database. Also, the communication cost is $O(n_w)$ in the $\mathsf {Search}$ phase and O(1) in the $\mathsf {Update}$ phase, where $n_w$ is the size of the search result set.

3.3 Naive Approach to Reduce Storage Cost

There are several naive approaches to reduce the extra $O(W\log {D})$ storage cost for . For example, the client encrypts $H_3(\mathsf {DB}(w))$ and stores it to the server instead of storing by him/her. Then, in the $\mathsf {Search}$ phase, the client receives the ciphertext of $H_3(\mathsf {DB}(w))$ and $\mathsf {DB}(w)$, decrypts the ciphertext, and can check the validity of $\mathsf {DB}(w)$. Thus, the storage cost can be the same as ${\varSigma }{o}{\phi }{o}{\varsigma }$. However, in the $\mathsf {Update}$ phase, an additional round is necessary to receive the ciphertext of $H_3(\mathsf {DB}(w))$ because the client does not memorize it and $H_3(\mathsf {DB}(w))$ must be updated. Therefore, this naive approach is not very good from the viewpoint of round complexity.

4 Our Scheme

In this section, we show the protocol of our scheme. It is based on ${\varSigma }{o}{\phi }{o}{\varsigma }$, but achieves verifiability by another way than .

4.1 Design Principle

In our scheme, we do not use any client-local verification table like table $\mathbf {H}$ in , but use a “tag” binding the keyword and the index as a verifier. Specifically, the client sends a verifier $Ver_{c+1}^{(w)}$ as well as $(UT_{c+1}^{(w)}, e_{c+1}^{(w)})$ to the server in the $\mathsf {Update}$ phase, and checks if $Ver_{c+1}^{(w)}$ is correctly bound with $\mathsf {DB}(w)$ in the $\mathsf {Search}$ phase. We note that the client do not have to keep $Ver_{c+1}^{(w)}$ after sending it, but the client receives the verifier corresponding to indexes. We use a PRF to generate the verifier, and unforgeability of the verifier is guaranteed from pseudo-randomness of the PRF.

However, if the client receives $Ver_{c+1}^{(w)}$ for $n_w$ indexes matching with w in each $\mathsf {Search}$ phase, the communication complexity increases by $n_w$ PRF values and the client needs to compute $n_w$ PRF values. Hence, we use a algebraic PRF (APRF) AF with closed form efficiency. APRF is a special type of PRF with a range that forms an Abelian group such that group operations are efficiently computable. In addition, certain algebraic operations on these outputs can be computed significantly more efficiently if one possesses the salt of the PRF that was used to generate them. As Definition 2, since $\prod _{i=1}^{n_w} [AF(s,z_i)]^{h_i(x)}$ can be efficiently computed by $\mathsf {CFEval}_{h,z}(x,s)$, the server can just compute and send $\prod _{i=1}^{n_w} [AF(s,z_i)]$ to the client, and the client can just compute $\mathsf {CFEval}_{h,z}(x,s)$ with a sublinear running time in $n_w$ to check the validity of the verifier, where $h(x)=\langle 1,\dots ,1 \rangle$. It saves the increase of the communication complexity only to one group element, and the computational cost for the client is bounded by sublinear in $n_w$. For example, we can use the APRF from the decisional Diffie-Hellman (DDH) assumption [15] or from the strong DDH assumption proposed [14].

4.2 Protocol Description

Let $\pi$ be a OWTP with the key generation algorithm $\mathsf {KeyGen}$, $F : \{0,1\}^\kappa \times \{0,1\}^* \rightarrow \{0,1\}^\kappa$ be a PRF, $AF : \{0,1\}^\kappa \times \{0,1\}^* \rightarrow G$ be an APRF (where G is an Abelian group and $h(x)=\langle 1,\dots ,1 \rangle$), and $H_1$ and $H_2$ are hash functions modelled as random oracles.

• $\mathsf {Setup}(\mathsf {DB})$:

  • 1. $K_S \in _R \{0,1\}^\kappa$

  • 2. $K_V \in _R \{0,1\}^\kappa$

  • 3. $(sk, pk) \leftarrow \mathsf {KeyGen}(1^\kappa )$

  • 4. $\mathbf {W}, \mathbf {T}\leftarrow$ empty tables

  • 5. store $\mathsf {DB}$ to $\mathbf {W}$ and $\mathbf {T}$ according to $\mathsf {Update}$ phase

  • 6. return $(K_S, K_V, sk)$ as secret key K and $\mathbf {W}$ as the state of the client $\sigma$

  • 7. return $\mathbf {T}$ as encrypted database $\mathsf {EDB}$

• $\mathsf {Update}(add, \mathbf {W}, (\mathsf {ind},w), \mathbf {T})$:

  • Client:

    • 1. $K_w \leftarrow F(K_S,w)$

    • 2. $(ST_c^{(w)}, c^{(w)})\leftarrow \mathbf {W}[w]$

    • 3. if $(ST_c^{(w)}, c^{(w)}) =$ $\perp \mathbf{{then}}$

    • 4. generate $ST_0^{(w)}$ by using the storage reducing technique [13]

    • 5. $c^{(w)} \leftarrow -1$

    • 6. else

    • 7. $ST_{c+1}^{(w)} \leftarrow \pi _{sk}^{-1}(ST_c^{(w)})$ by using the storage reducing technique [13]

    • 8. end if

    • 9. $\mathbf {W}[w] \leftarrow (i_w, c^{(w)}+1)$

    • 10. $Ver_{c+1}^{(w)} \leftarrow AF(K_V,(c^{(w)}+1,w, \mathsf {ind}))$

    • 11. $UT_{c+1}^{(w)} \leftarrow H_1(K_w, ST_{c+1}^{(w)})$

    • 12. $e_{c+1}^{(w)} \leftarrow \mathsf {ind}\oplus H_2(K_w,ST_{c+1}^{(w)})$

    • 13. send $(UT_{c+1}^{(w)}, e_{c+1}^{(w)},Ver_{c+1}^{(w)})$ to the server as update information $u(\mathsf {ind},w)$

  • Server:

    • 1. $\mathbf {T}[UT_{c+1}^{(w)}] \leftarrow (e_{c+1}^{(w)},Ver_{c+1}^{(w)})$

• $\mathsf {Search}$($w,\mathbf {W}, \mathbf {T}$):

  • Client:

    • 1. $K_w \leftarrow F(K_S,w)$

    • 2. $(ST_c^{(w)}, c^{(w)}) \leftarrow \mathbf {W}[w]$

    • 3. if $(ST_c^{(w)}, c^{(w)}) =$ $\perp$

    • 4. return $\emptyset$

    • 5. send $(K_w, ST_c^{(w)}, c^{(w)})$ to the server as trapdoor t(w)

  • Server:

    • 1. for $i = c$ to 0 do

    • 2. $UT_i^{(w)} \leftarrow H_1(K_w, ST_i^{(w)})$

    • 3. $(e_i^{(w)},Ver_i^{(w)}) \leftarrow \mathbf {T}[UT_i^{(w)}]$

    • 4. $\mathsf {ind}_i^{(w)} \leftarrow e_i^{(w)} \oplus H_2(K_w, ST_i^{(w)})$

    • 5. $ST_{i-1} \leftarrow \pi _{pk}(ST_i)$

    • 6. end for

    • 7. send $(\mathsf {DB}(w) = \{\mathsf {ind}_i^{(w)}\}_{0 \le i \le c},\mathsf {Ver}^{(w)}= \prod _{i=0}^{c} Ver_i^{(w)})$ to the client

  • Client:

    • 1. if $|\mathsf {DB}(w)| \ge c+1$ or $\mathsf {Ver}^{(w)} \not = \mathsf {CFEval}_{h,\{i,w,\mathsf {ind}_i^{(w)}\}_{0 \le i \le c}}(0,K_V)$

    • 2. return 0

Remark 1

The input of AF is $(c,w,\mathsf {ind})$. If the domain of APRF AF is also required to be a group, the input is hashed by some collision-resistance hash function which maps to the group.

4.3 Correctness

According to the protocol, for any search query, an honest server can return true answer $(\mathsf {DB}(w),\mathsf {Ver}^{(w)})$, and the client always accept the answer except the probability that some collision on UT occur. If a collision of UT for distinct inputs to $H_1$ occurs, the server cannot find the correct encrypted index and verifier. However, since $H_1$ is a RO, the collision probability is negligible in $\kappa$.

4.4 Deletion Support

Our scheme is easily extended to supporting deletions of indexes by duplicating the data structure as the extension of . Specifically, one instance of our scheme is used for insertions, and the other for deletions. In the $\mathsf {Search}$ phase, the server derives two $\mathsf {DB}(w)$ for two instances, and regards the difference of them as indexes to be returned. The verifier is also duplicated for each instance, and the client can check the validity of both instances respectively. If the verification of one of instances is rejected, then the client decides that the response is not valid. Therefore, strong reliability is also satisfied for this extension.

4.5 Complexity of Our Scheme

Each client must keep only table $\mathbf {W}$. It is not necessary to keep $ev_{c+1}^{(w)}$ sent in the $\mathsf {Update}$ phase because the client can check validity of verifier $Ver_{i}^{(w)}$ only with secret salt $K_V$, state $ST_c^{(w)}$ and received $\mathsf {ind}_i$. Table $\mathbf {W}$ contains $(i_w,c)$ for every keyword; and hence, the storage cost is $O(W \log {D})$. Therefore, the total storage cost for a client is $O(W\log {D})$. It is the same as ${\varSigma }{o}{\phi }{o}{\varsigma }$ whereas ${\varSigma }{o}{\phi }{o}{\varsigma }$ is not secure against malicious servers.

The computational cost and communication cost are asymptotically the same as . The exact additional communication cost is only one group element (i.e., 160-bit for 80-bit security) both in the $\mathsf {Update}$ phase and the $\mathsf {Search}$ phase. Also, the exact additional computational cost for the client is an APRF computation in the $\mathsf {Update}$ phase and a sublinear computation in $n_w$ in the $\mathsf {Search}$ phase. Therefore, our scheme is still efficient even in exact costs.

5 Security of Our Scheme

In this section, we prove that our scheme satisfies forward security and strong reliability. Especially, to prove strong reliability as verifiability is a distinguished point from because there is no formal security proof of verifiability of in [13].

5.1 Forward Security

Theorem 1

We assume that F is a PRF, AF is an APRF, and $\pi$ is a OWTP. Then, our scheme satisfies forward security for leakage functions $\mathcal {L}^{Stp}(\mathsf {DB})= \bot$, $\mathcal {L}^{Srch}(w)=(sp(w),hist(w))$ and $\mathcal {L}^{Updt}(add,(\mathsf {ind},w)) = \bot$ in the RO model, where sp(w) is the search pattern and hist(w) is the history of keyword w.

The proof of Theorem 1 is almost the same as [13, Theorem 1]. We use hybrid games that proceed from the real world game to the ideal world game. The difference from the previous proof is the treatment of verifier $\mathsf {Ver}$. We add a hybrid game to change the computation of $Ver_{c+1}^{(w)}$ in the $\mathsf {Update}$ phase and the $\mathsf {Search}$ phase to using a random function RF instead of using APRF AF. The proof is given in the full version.

5.2 Strong Reliability

Theorem 2

We assume that AF is an APRF. Then, our scheme satisfies strong reliability.

We can directly reduce the security of APRF to strong reliability. It means that, if there exists an adversary who breaks strong reliability, then a distinguisher for APRF can be constructed. The proof is given in the full version.