Classification of Hyperspectral Imagery Based on Dictionary Learning and Extended Multi-attribute Profiles

Abstract

In recent years, sparse representation has shown its competitiveness in the field of image processing, and attribute profiles have also demonstrated their reliable performance in utilizing spatial information in hyperspectral image classification. In order to fully integrate spatial information, we propose a novel framework which integrates the above-mentioned methods for hyperspectral image classification. Specifically, sparse representation is used to learn a posteriori probability with extended attribute profiles as input features. A classification error term is added to the sparse representation-based classifier model and is solved by the k-singular value decomposition algorithm. The spatial correlation of neighboring pixels is incorporated by a maximum a posteriori scheme to obtain the final classification results. Experimental results on two benchmark hyperspectral images suggest that the proposed approach outperforms the related sparsity-based methods and support vector machine-based classifiers.

1 Introduction

Hyperspectral imagery (HSI) has been widely used in the field of remote sensing for the past decade. Its capability to acquire hundreds of images with a wide range of wavelengths makes HSI a powerful tool in many areas, such as military surveillance, natural resources detection, land cover classification, etc. [1]. However, the unique properties of HSI have posed difficult image processing problems; for instance, it has been identified as a challenging task to analyze the spectral and spatial information simultaneously for HSI classification [2].

Many attempts have been made to solve this problem. In [3], the authors proposed a new sampling strategy to extract both spectral and spatial information. In addition, Markov Random Field (MRF) is considered to be a powerful method for integrating both spectral and spatial information [4]. However, its efficiency and effectiveness are questionable due to the high computational complexity and the uncertainty of the smoothing parameter to be chosen. Another category of approaches to deal with contextual information is based on attribute profiles (APs) which are constructed by a set of attribute filters (AFs). AFs operate only on the connected components based on a criterion that evaluates the attribute against a threshold. When multiple layers of HSI are considered, the stack of individually computed APs can be referred to as an extended attribute profile (EAP) [5]. Moreover, if different attributes are considered and multiple EAPs are stacked together, an extended multi-attribute profile (EMAP) can be constructed [6]. EMAP can effectively deal with both spectral and contextual information [7].

Sparse representation-based classifiers (SRCs) have been found to be efficient tools in many image processing areas in the last few years [8,9,10]. SRC assumes that each signal can be expressed as a linear combination of prototypes selected from a dictionary. The advantages of applying SRC as a classification method have been investigated [11,12,13]. SRC can achieve good performance on HSI classification because the pixels with highly correlated bands can be sparsely represented. Usually a SRC dictionary is directly constructed by training atoms, which limits the HSI classification accuracy due to the large number of training atoms. Hence it is sensible to construct a reliable dictionary for the classification problem.

Based on the aforementioned knowledge, a novel framework using both EMAP and SRC is developed and presented in this paper particularly for HSI classification, which we name it as extended SRC (ESRC) method. Apart from spectral information, EMAPs have been constructed to initialize the dictionary for SRC. Thus, both spectral and spatial context can be considered to maximize among class separability. Subsequently, we optimize the dictionary using an effective method known as k-singular value decomposition (K-SVD) [14]. Similar to Jiang [15], we add a classification error term to the SRC model, then the reconstruction error and the classification error can be modelled simultaneously. Finally, the class label can be derived via the MRF-based maximum a posteriori (MAP) method, where the spatial energy term is improved by a Gaussian framework in this paper. It should be noted that the spatial information is utilized via EMAPs and then regularized by the MRF-MAP method, therefore our ESRC can further improve the classification results.

The remainder of this paper is organized as follows. The proposed framework is described in Sect. 2. The effectiveness of the framework is demonstrated by the experiments in Sect. 3. Finally, we conclude and provide some remarks in Sect. 4.

2 Design of Framework

2.1 EMAP Feature Extraction

EAPs are built by concatenating many attribute profiles (APs), and each AP is generated for each feature in a scalar hyperspectral image. That is:

$$ EAP = \{ AP(f_{1} ),AP(f_{2} ), \ldots ,AP(f_{n} )\} $$

(1)

APs are a generalized form of morphological profiles, which can be obtained from an image by applying a criterion $T$. By using $n$ morphological thickening ($\varphi^{T}$) and $n$ thinning ($\emptyset^{T}$) operators, an AP can be constructed as:

$$ AP(f) = \{ \varphi_{n}^{T} (f),\varphi_{n - 1}^{T} (f), \ldots ,\varphi_{1}^{T} (f),f,\phi_{1}^{T} (f), \ldots ,\phi_{n - 1}^{T} (f),\phi_{n}^{T} (f)\} $$

(2)

Generally, there are some common criteria associated with the operators, such as area, volume, diagonal box, and standard deviation. According to the operators (thickening or thinning) used in the image processing, the image can be transformed to an extensive or anti-extensive one. In this paper, area, standard deviation, the moment of inertia, and length of the diagonal are used as the attributes to compute EMAP features for classification tasks. The stack of different EAPs leads to EMAPs, and the detailed information of EMAPs can be found in the report [7].

2.2 Dictionary Learning for SRC

Suppose $\left\{ {x_{i} } \right\}_{i = 1}^{N}$ represents $N$ training samples from a $L$-dimensional hyperspectral dataset, and $x$ belongs to $c$ labelled classes while $y_{i} \in \left\{ {1 \ldots .c} \right\}$ is the label of each observed pixel $x_{i}$. For each class $c$, there exists a matrix ${\text{D}}_{C} \in R^{{m \times n^{c} }} \left( {N = \sum\nolimits_{i = 1}^{c} {n_{c} } } \right)$ containing $n_{c}$ prototype atoms for columns. Each pixel with a $c$ -th label can be represented approximately as follows:

$$ x_{i} \approx {\text{D}}_{C} {\text{r}}_{i}^{c} ,\,\,\,\,\,\,\, \, \left\| {{\text{r}}_{i}^{c} } \right\| \le K,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\forall y_{i} = c $$

(3)

where ${\text{r}}^{c} \in R^{m}$ is the representation coefficient of signal $x$, $\left\| {\, \cdot \,} \right\|_{0}$ is a $l_{0}$ norm which counts the number of nonzero atoms in a coefficient vector, and $K$ is a predefined sparsity constraint. Assuming that the global dictionary ${\text{D}} = [{\text{D}}_{1} ,{\text{D}}_{2} \ldots {\text{D}}_{c} ]$ is known, the corresponding representation coefficients ${\text{r}} = [{\text{r}}^{1} ,{\text{r}}^{2} \ldots {\text{r}}^{c} ]$ can be computed by solving the following equation:

$$ r_{i}^{c} = \arg \mathop {\hbox{min} }\limits_{r} \left\| {x_{i} - Dr_{i}^{c} } \right\|_{2}^{2} \,\,\,\,\,\,\,s.t.\,\,\,\,\,\forall i, \left\| {{\text{r}}_{i} } \right\|_{0} \le K $$

(4)

There exist many algorithms to optimize this problem, for example, orthogonal matching pursuit (OMP) [16] is one of the most efficient methods. OMP is a greedy method which simply selects the dictionary prototypes in sequence. The pixels belong to the class which has the minimum class-wise reconstruction error ${\text{e}}_{\text{i}}^{\text{c}}$, where ${\text{e}}_{\text{i}}^{\text{c}} = {\text{x}}_{\text{i}}$ - ${\text{D}}_{\text{C}} {\text{r}}_{\text{i}}^{\text{c}}$:

$$ \hat{y}_{i} = \arg \mathop {\hbox{min} }\limits_{c} \left\| {e_{i}^{c} } \right\|_{2}^{2} $$

(5)

The main goal of this paper is to find a dictionary ${\text{D}}$ which can help maximize classification accuracy. In order to minimize the reconstruction error and the classification error simultaneously, a classification error term $\left\| {{\text{H}} - {\text{W}}^{\text{T}} {\text{r}}} \right\|_{2}^{2}$ which has the sparse code directly as a feature for classification, is included in the objective function. Following the solution by Jiang et al. [15], the objective function for learning optimal dictionary and sparse code can be redefined as follows:

$$ \begin{aligned} & < D,r,W > = \arg \mathop {\hbox{min} }\limits_{D,r,W} \left\| {X - Dr} \right\|_{2}^{2} + \alpha \left\| {H - W^{T} r} \right\|_{2}^{2} \\ & s.t.\forall i\,\,\,\,\,\,\,\left\| {r_{i} } \right\|_{0} \le K \\ \end{aligned} $$

(6)

where $H = [h_{1} ,h_{2} \ldots h_{N} ] \in R^{c \times N}$ represents the class labels of the training samples; $h_{i} = [0,0 \ldots 1 \ldots 0,0] \in R^{c}$, where the nonzero $c$ -th position represents the $c$ -th class that contains $x_{i}$; $Wr$ is a linear classification function that supports learning an optimal dictionary; and $\alpha$ is a scalar controlling corresponding terms.

In order to use ${\text{K}} - {\text{SVD}}$ as the efficient solution, Eq. (6) can be rewritten as the following:

$$ \begin{aligned} & < D,r,W > = \arg \mathop {\hbox{min} }\limits_{D,r,W} \left\| {\begin{array}{*{20}c} X \\ {\sqrt \alpha H} \\ \end{array} \begin{array}{*{20}c} {} & {\left( {\begin{array}{*{20}c} D \\ {\sqrt \alpha W^{T} } \\ \end{array} } \right)r} \\ \end{array} } \right\|_{2}^{2} \\ & s.t.\forall i\,\,\,\,\,\,\,\,\left\| {r_{i} } \right\|_{0} \le K \\ \end{aligned} $$

(7)

The initial dictionary is obtained by EMAPs; given the initialized ${\text{D}}$, the original ${\text{K}} \text{-} {\text{SVD}}$ is employed to obtain ${\text{r}}$, and ${\text{r}}$ can be used to compute the initial ${\text{W}}$ with linear support vector machine (SVM); both ${\text{D}}$ and ${\text{W}}$ are updated by the ${\text{K}} \text{-} {\text{SVD}}$ algorithm.

Let $X_{new} = (X^{T} ,\sqrt \alpha H^{T} )^{T}$, $D_{new} = (D^{T} ,\sqrt \alpha W^{{}} )^{T}$, then Eq. (7) can be rewritten as:

$$ \begin{aligned} & < D_{new} ,r > = \arg \mathop {\hbox{min} }\limits_{{D_{new} ,r}} \{ \left\| {X_{new} - D_{new} r} \right\|_{2}^{2} \} \\ & s.t.\forall i,\,\,\,\,\,\,\,\left\| {r_{i} } \right\|_{0} \le K \\ \end{aligned} $$

(8)

Then ${\text{K}} \text{-} {\text{SVD}}$ algorithm is employed to optimize this problem. Let ${\text{d}}_{\text{k}}$ and ${\text{r}}_{\text{k}}$ represent the ${\text{kth}}$ row in ${\text{D}}$ and its corresponding coefficients, respectively. The overall processing steps of ${\text{K}}\text{-}{\text{SVD}}$ is summarized in the report by Ahron et al. [14]. $D_{new}$ and ${\text{r}}$ are computed by ${\text{K}}\text{-}{\text{SVD}}$, and then $D = \{ d_{1} ,d_{2} \ldots d_{k} \}$ and $r = \{ r_{1} ,r_{2} \ldots r_{k} \}$ can be obtained from $D_{new}$. The representation error vector can be computed from $e_{ic} = x_{i} - D_{c} r_{i}^{c}$. Additionally, the posterior probability $\rho (y_{ic} /x_{i} )$ is inversely proportional to $e_{ic}$[17]:

$$ \rho (y_{ic} /x_{i} ) = \frac{1}{{\left\| {e_{ic} } \right\|_{2}^{2} \mu }} $$

(9)

where $y_{ic}$ refers to labelled class $c$ for the pixel $x_{i}$ and $\mu$ is a normalized constant.

2.3 Spatial Information Regularization

We have described the mechanism that is used to obtain the class probability in the previous section. In this section, we will show how to implement the spatial information characterization.

By utilizing the MAP theory, a pixel is likely to have the same label with its neighboring pixels. According to the Hammersley-Clifford theory [18], the MAP estimation of ${\text{y}}$ is represented as follows:

$$ \begin{aligned} & \hat{y} = \arg \mathop {\hbox{min} }\limits_{y} ( - \sum\limits_{i \in N(i)} {\log } \rho (y_{i} /x_{i} ) - \log \rho (y)) \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\rho (y) = e^{{\sigma \sum\limits_{i \in N(i)} {\delta (y_{i} - y_{j} )} }} \\ \end{aligned} $$

(10)

where the term $\rho (y_{i} /x_{i} )$ is the spectral energy function and can be estimated from previous Eq. (8). $\rho (y)$ is regularized by a unit impulse function $\delta (y_{i} - y_{j} )$, where $\delta (0) = 1$ and $\delta (y) = 0$ for $y \ne 0$; additionally, $\sigma$ is a smoothing parameter. This term attains the probability of one to equal neighboring labels and zero to the other way around. In this way, non-probability might result in a misclassification for some mixing regions. In this paper, we modify this term by a Gaussian radial basis network to make it a more efficient way, and the entire image is decomposed into local patches with a neighborhood size $N \times N$. For $j \in N(i)$, the function applied on the pixels constrained by the neighborhood size can be represented as:

$$ \delta (y_{i} - y_{j} ) = \left\{ {\begin{array}{*{20}c} {1,} & {\begin{array}{*{20}c} {if} & {y_{i} = y_{j} } \\ \end{array} } \\ {\exp ( - \left( {\frac{{u_{ij} }}{{s_{{u_{ij} }} }}} \right)^{2} - \left( {\frac{{v_{ij} }}{{s_{{v_{ij} }} }}} \right)^{2} )} & {\begin{array}{*{20}c} {if} & {y_{i} \ne y_{j} } \\ \end{array} } \\ \end{array} } \right. $$

(11)

We improve the unit impulse function by optimizing the weight of different class probability using a smoothing function. $\delta (y_{i} - y_{j} )$ is a function of standardized Euclidian distance between pixels ${\text{x}}_{\text{i}}$ and ${\text{x}}_{\text{j}}$, where ${\text{u}}_{\text{ij}}$ and ${\text{v}}_{\text{ij}}$ are the horizontal and vertical distances from ${\text{x}}_{\text{i}}$ and ${\text{x}}_{\text{j}}$, respectively. $s_{{u_{ij} }}$ and $s_{{v_{ij} }}$ represent the stand deviation in each direction. The range of Eq. (11) can meet the definition of probability constrained by (0,1]. Given the prior class information and spatial locations of pixels, this improvement can be trained quickly and efficiently.

The value 1 is assigned to $\rho (y_{i} = y_{j} )$ which indicates that the pixels tend to appear around those of the same class. Since homogenous areas are dominant, the improved function will yield a good approximation for the regions, especially for the edge area. As shown in Eq. (11), the spatial relationship is modelled directly by the spatial locations.

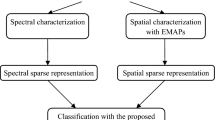
In this paper, we utilize the $\propto - {\text{expansion}}$ algorithm to optimize this combinatorial problem. To better understand the main procedures of presented framework, the flowchart is shown as in Fig. 1.

Fig. 1.

Flowchart of the proposed framework

3 Experiment Analysis

3.1 Experimental Setup

Two benchmark hyperspectral images are used to evaluate the proposed method. The attribute values used for EMAPs transformations are described as follows. Area of regions: 5000, length of the diagonal: 100, moment of inertia: 0.5, and standard deviation: 50. Smoothing parameter $\sigma$ is set as 0.2 in this paper.

The best parameters are chosen via cross-validation for classifiers in this paper, and the results are compared with those acquired by kernel SVM (KSVM), sparsity representation model using OMP (SRC), Kernel SVM with EMAP features (EKSVM), sparsity representation model using OMP with EMAP features (ERAP), SVM probability with EMAP features and original MRF (SVM_AP), and original MRF with probability obtained with ERAP (referred as ERAP_MRF).

All experiments are implemented with Matlab 2015b. Average accuracy (AA), Overall accuracy (OA), kappa coefficient ($k$) are calculated as the accuracy assessment, which are commonly used for classification tasks.

3.2 Experiments on Indian Pines Data Set

The Indian Pines data set was acquired by Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) in 1992. It covers 145 × 145 pixels with a spatial resolution of 20 m. After removing 20 water absorption bands, 200 spectral bands from 0.2 to 2.4 µm as the original features. There are 16 labelled classes, which are shown in Table 1, as well as the numbers of training and testing datasets.

Table 1. Class information for Indian Pines image

The average results of ten experiments repeatedly run on different randomly chosen training and testing datasets are shown in Table 2. The classification maps as well as the ground truth are shown in Fig. 2.

Table 2. Classification accuracies (%) for Indian Pines image

Fig. 2.

Classification maps of Indian Pines. (a) Ground truth. (b) SRC. (c) KSVM. (d) ERAP. (e) EKSVM. (f) SVM_AP (g) ERAP_MRF. (h) ESRC.

The listed results in Table 2 and Fig. 2 show that our framework outperforms most techniques and is especially better than KSVM which is known as a state-of-the-art method. The visual results also show that the spatial information involved techniques lead to a much smoother classification map than algorithms with only spectral information involved.

One can observe that EMAP with normal classifiers have already provided high classification accuracy, however, the transform of a probabilistic work and including a MAP segmentation work improve the classification accuracies as it can be particularly observed in the ERAP_MRF, SVM_AP and ESRC. This confirms the ability of the work in a probabilistic sense that MAP segmentation can indeed correct the results by regularizing the spatial information. It also should be noted that our proposed ESRC obtains the best result, which classifies most of regions accurately.

As for a SRC based method, the proposed ESRC exhibits the best performance especially in the edge areas, which can be observed from the classification maps. In addition, ESRC has also shown its potential effectiveness in dealing with the small training data sets, which is meaningful for practice applications. ESRC achieves the best result when compared to EKSVM and SVM_AP, which further confirms that our method can learn a discriminative dictionary and implement a more accurate spatial regularization. The results show that the proposed ESRC method is more accurate than original MRF-based spatial regularization methods. Particularly, ESRC performs well on the minority classes (e.g. Class 1 and Class 7).

The visual comparison of ERAP_MRF and SVM_AP also confirms the competitive efficiency of optimization model for SRC used in this paper. However, both of them fail to identify Class 9. This is due to the insufficient training samples for this class. The experiments also indicate that the improved method has a potential to obtain a more accurate result with a smaller training set.

For ERAP_MRF and ESRC, a window size 8 × 8 is applied. The former method over-smooths the oat-covered region and misclassifies Oats as Grass/Trees or Corn-min. This is because each oat pixel is dominated by Class 3 (Corn-min) and Class 6 (Grass/Trees). The improvement of spatial regularization gives a weight of pixels far away from the central pixel via spatial locations, which is helpful for the dominated regions.

The accuracy varies with different sparsity constraint factor $K$ and neighborhood size $N$. The effect of $K$ and $N$ on the classification accuracy is shown in Fig. 3. The sparsity constraint factor plays an important role in the experiment, which produces less sparse codes when set too small, and makes the dictionary no longer sparse and more time-consuming when set too large. The neighborhood size is also an important parameter in the spatial regularization network. As shown in Fig. 3, a too large $N$ may cause over-smoothing and produce noisy information, while a too small $N$ cannot preserve enough spatial features. $N$ is set as 8 × 8 throughout the experiment to achieve the best accuracy.

Fig. 3.

The effect of neighborhood size $N$ and sparsity constraint factor $K$

We apply SRC, ERAP, ERAP_MRF and ESRC with different sparsity level factor $K,$ ranging from ${\text{K}} = 5$ to ${\text{K}} = 80$, and the best accuracy is chosen for this experiment.

The parameter α which controls the contribution of the classification error is determined by cross validation experiments on training images. For Indian Pines data set, it is set to 0.001. This small value for α is due to the high dimension sparse vector of the training samples. The normalized large scale sparse vector results in small component values for the extracted features, therefore the weight of this controlling term is lower, compared to the sparse reconstruction errors.

3.3 Experiments on ROSIS Pavia University Data Set, Italy

The image was collected by the Reflective Optics Systems Imaging spectrometer (ROSIS), and the sensor generates 115 spectral bands covering from 0.43 to 0.86 µm with a spatial resolution of 1.3 m. In our experiments, 103 bands are used with 12 noisy bands removed from both data sets. It consists of 610 × 340 pixels with 9 labelled classes. As discussed above, the sparsity constraint factor $T$ is set to range from 5 to 80 for SRC, ERAP, ERAP_MRF and ESRC. $N$ is set as a 9 × 9 and α is set as 0.005 for this dataset. Table 3 shows the class information of this data set.

Table 3. Class information for Pavia University image

The classification accuracies and classification maps are summarized in Table 4 and Fig. 4. The classification results for this imagery are consistent with Indian Pines imagery. Our proposed method (i.e. ESRC) performs better than the other methods in most cases.

Table 4. Classification accuracies (%) for Pavia University image

Fig. 4.

Classification maps of Pavia University. (a) Ground truth. (b) SRC. (c) KSVM. (d) ERAP. (e) EKSVM. (f) SVM_AP (g) ERAP_MRF. (h) ESRC

4 Conclusion

In this paper, a novel framework is proposed for HSI classification. This framework is based on EMAP and SRC. HSI pixels are considered as sparse representation by the atoms in a selected dictionary. In the proposed algorithm, a classification error term is added to the SRC model and is solved by the K-SVD algorithm. To improve the classification accuracy, we also have taken into account the influence of neighboring pixels of the pixel of interest in the MAP spatial regularization model. Experiments conducted on two different hyperspectral images show that the proposed method yields high classification accuracy, which is especially better than the state-of-the-art SVM classifiers.