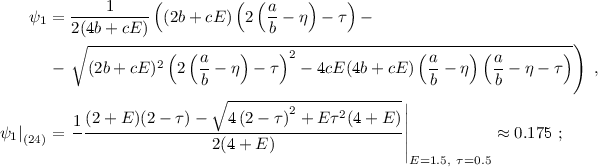Emerging Trade Patterns in a 3-Region Linear NEG Model: Three Examples

Abstract

This chapter draws attention to a specific feature of a NEG model that uses linear (and not iso-elastic) demand functions, namely its ability to account for zero trade. Thus, it represents a suitable framework to study how changes in parameters that are typical for NEG models, such as trade costs and regional market size, not only shape the regional distribution of economic activity, but at the same time determine the emergence of additional trade links between formerly autarkic regions. We survey some related papers and present a three-region framework that potentially nests many possible trade patterns. To focus the analysis, we study in more detail three specific trade patterns frequently found in the EU trade network. We start with three autarkic regions; then we introduce the possibility that two regions trade with each other; and, finally, we allow for one region trading with the other two, but the latter are still not trading with each other. We find a surprising plethora of long-run equilibria each involving a specific regional distribution of economic activity and a specific pattern of trade links. We show how a reduction in trade costs shapes simultaneously industry location and the configuration of the trade network.

1 Introduction

In this chapter, we address the questions of what determines the creation of trade links between regions, and their direction, and how the presence of a trade link may interfere with the distribution of the manufacturing activity across space. Indeed, it easy to infer that the presence of a trade link may affect the processes of agglomeration or dispersion of such activity and, in turn, the degree of spatial concentration of industry has a bearing on the formation of trade links by increasing/reducing the accessibility of a region for outside firms. As is well-known, the interplay between agglomeration and dispersion forces and how it shapes the spatial economic landscape is at the core of the new economic geography (NEG) literature.

The NEG approach, originating from Krugman (1991) and Fujita, Krugman and Venables (1999) (see Baldwin et al. (2003), for a review), aims to explain what determines the distribution of industrial activities across space. Its main building blocks are Dixit-Stiglitz monopolistic competition, increasing returns, CES preferences over industrial varieties and isoelastic demands, multiplicative/iceberg trade costs and a dynamic mechanism based on factor migration (for example, in Krugman’s seminal Core-Periphery model, this factor is undifferentiated labour; NEG model variants consider other factors such as physical capital or skilled workers/entrepreneurs). Mainly dealing with two-region economies, the predictions of NEG models depend on the balance between agglomeration and dispersion forces. Most NEG models involve two forces, related to market access and consumers’ prices, that have agglomeration effects; and a third force, related to local competition, that has a dispersion effect. Which of these forces dominate, depends on trade costs: in a standard NEG set-up, high trade costs favours dispersion and low trade costs agglomeration. At intermediate trade costs, long-term dispersion or agglomeration of the industry may prevail, depending on its initial distribution of this sector between the regions. In the analytic perspective, this translates into coexistence of dispersion and agglomeration equilibria. A slight change in the initial distribution of economic activities may induce a catastrophic change from dispersion to agglomeration, switching from an equilibrium to another with completely different properties. For the present question it is important to note that – given the specific model set-up – firms always export, except when trade costs are infinite. This implication is at odds with empirical observations, where finding zero trade is quite common.

Ottaviano et al. (2002) propose an alternative model in which firms may not export even when trade costs are finite. Their model set up involves quadratic preferences, implying a linear demand (elasticity depends on prices and market fundamentals), segmented markets and additive trade costs. In Ottaviano et al. (2002) the local competition effect is reinforced by a variable mark-up. In a two-region framework, they show the following results: high trade costs imply dispersion; low trade costs imply agglomeration; and after a specific threshold for trade costs the economy may experience an abrupt change from dispersion to agglomeration. However, there is no coexistence of dispersion and agglomeration stable equilibria. Notice that Ottaviano et al. (2002) assume that trade costs are always sufficiently low to allow for bilateral trade between the regions.

Within the same framework, Behrens (2004) examines the opposite case by assuming trade costs sufficiently high that interregional trade never occurs. This author shows that even when regions are fully autarkic, agglomeration is still possible. Depending on the size of the immobile demand (fixing the size of the demand that could shift),¹ dispersion, agglomeration or partial agglomeration are possible long-run outcomes. A large immobile local demand reinforces the dispersion forces and higher prices in autarky weakens the agglomeration ones, so that stable coexisting partial agglomeration equilibria are possible. Moreover, by reducing the size of immobile demand a smooth process from dispersion to agglomeration takes place. In a later paper, Behrens (2005) examines the case of intermediate trade costs, showing that, depending on the initial industry distribution across space and on trade costs, different trade patterns may emerge between two regions: autarky, unilateral or bilateral trade (alternatively, no trade, one-way trade or two-way trade). This author addresses also the interplay between patterns of trade and of regional distribution of economic activity. He shows that unilateral trade favours agglomeration forces over dispersion forces leading to the concentration of industry in the region that, in an initial stage, has the larger share of industry.²

Ago et al. (2006) consider an economy where three regions takes a specific hub-and-spoke configuration: they are aligned with the central region positioned at the same distance from the two peripheral ones. Dealing with the case of linear demand,³ the authors show that in an economy with an intermediate size of the manufacturing a reduction in trade costs intially leads to a reduction in the share of the mobile factor located in the central region; subsequently, it leads to an increase; finally, when trade costs are sufficiently low, the mobile factor is fully agglomerated in the central region. Instead, when the size of the manufacturing sector (shifting demand) is relatively large compared to the agricultural sector (immobile demand) by reducing trade costs the share of industry in the central region shrinks and the mobile factor moves to the peripheral ones (finally agglomerating in one of them). In the linear framework, the competition effect is more intense, thus, firms have a move to the peripheral regions to protect themselves from such competition.⁴ Moreover, confining their analysis to a neighbourhood of the symmetric equilibrium, Ago et al. (2006) shows what patterns of trade may emerge, following a reduction in trade costs, given the specific geography assumed.

Finally, Commendatore et al. (2017) consider a three-region developing economy with poor infrastructure. A specific geography is assumed: two regions are relatively close to each other, whereas the third one is remote and difficult to access. Two stages of development are considered: in the first stage trade costs are so high that none of the regions trade; in the second stage, the first two regions improve their integration by lowering trade costs. Depending on the degree of integration and on the distribution of the industrial activity across the regions, different trade patterns may emerge (no trade, one-way trade or two way trade), but they only involve the two more integrated regions.

In this chapter we extend and/or integrate these contributions. We represent a small trade network, formed by three regions, aiming to: (i) highlight how distance and trade costs may determine the existence of a trade link and its direction; (ii) examine the long-term consequences of trade integration on the emergence/disappearance of trade links and on the distribution of economic activities across space; (iii) explore how the spatial distribution of economic activities and the presence/absence of trade links are interrelated. Given the large number of possible trade structures, we only consider three examples, representing three frequently realized trade patterns in the EU trade network (see Basile et al. (2016)): three regions in autarky; two regions engaging in trade with each other, with a third region in autarky; a hub and spoke economy but with a different structure from that suggested by Ago et al. (2006).

We structure the paper as follows. In Sect. 2, we present the basic economic framework, introducing three examples modelling trade network structures frequently realized in real world economies. In Sect. 3, we presents the short-run equilibrium solutions for these models. In Sect. 4, we move on to the discussion of the properties of the long-run equilibria and their economic interpretation. Section 5 concludes.

2 The Model

2.1 Basic Set-Up

The economy is composed of three regions (labelled $r=1,2,3$) distributed asymmetrically across space; two sectors, Agriculture (A) and manufacturing (M). The first characterized by perfect competition, constant returns and production of a homogeneous good and the second by monopolistic competition, increasing returns and production of a differentiated good; two factors of production, unskilled labour or simply labour (L) and skilled labour or entrepreneurial activity (E). Regions have the same endowment of labour. Workers are immobile, whereas entrepreneurs are allowed to migrate across regions.

2.2 Production

In the A-sector one unit of labour gives one unit of output. In the M-sector production requires use of one entrepreneur as fixed component plus $\eta$ units of labour for each additional unit of output. The total cost of production (TC) corresponds to:

$$ TC=\pi _{i}+w\eta q_{i}, $$

where $\pi _{i}$ represents the operating profits and the remuneration of an entrepreneur, w the wage rate, $\eta$ the labour input requirement and $q_{i}$ the quantity produced of variety i.

Due to increasing returns and absence of economies of scope, each firm produces a single variety. Following the assumption that only one entrepreneur is required to activate production, the number of entrepreneurs (E) is equal to the number of firms and to the number of varieties (N). Denoting by $\varLambda _{r}$ the share of entrepreneurs located in region r, the number of varieties produced in that region is:

$$ N_{r}=\lambda _{r}N=\lambda _{r}E, $$

where $0\le \lambda _{r}\le 1$, $\sum \limits _{r=1}^{3}\lambda _{r}=1$ and $r=1,2,3$.

2.3 Utility

The representative consumer’s (unskilled or entrepreneur) preferences are quasi-linear (see Ottaviano et al. 2002), composed of a quadratic part defining the choice across the n varieties of the M-good and a linear component for the consumption of the A-good:

$$\begin{aligned} U=\alpha \sum _{i=1}^{n}c_{i}-\left( \frac{\beta -\delta }{2}\right) \sum _{i=1}^{N}c_{i}^{2}-\frac{\delta }{2}\left( \sum _{i=1}^{N}c_{i}\right) ^{2}+C_{A} \end{aligned}$$

(1)

where $c_{i}$ is the consumption of variety i and $C_{A}$ the consumption of the agricultural good. The parameters are interpreted as follows: $\alpha >0$ is the intensity of preference over the M-varieties, $\delta >0$ the degree of substitutability across those varieties and the difference $\beta -\delta$ measures the taste for variety; where $\alpha >0$ and $\beta>\delta >0$.

The budget constraint is

$$\begin{aligned} \sum _{i=1}^{n}p_{i}c_{i}+p_{A}C_{A}=y+p_{A}\overline{C_{A}} \end{aligned}$$

(2)

where $p_{i}$ is the price of variety i including trade costs, $p_{A}$ is the price of the agricultural good, y is the consumer’s income and $\overline{C_{A}}$ is her endowment of the agricultural good, sufficiently large to allow for positive consumption in equilibrium.

2.4 Trade Costs

The cost of trading varieties of the M-good from r to s (or in the opposite direction from s to r) is $T_{rs}$ ($=T_{sr}$); $T_{rs}>0$ for $r\ne s$ and $T_{rr}=0$, with $r=1,2,3$. Trade costs separate the regions. Different combinations are possible, we will consider here three examples and leave to future research more general cases:

• 1. In the first example, all regions are in autarky: we assume that trade cost are sufficiently high that no trade can occur between the regions, independently of other factors (esp. the distribution of the economic activity across the regions). In this example, we assume that the cost of trading the M-varieties is very large and, for the sake of simplicity, it is the same for all the regions: $T_{12}=T_{13}=T_{23}=T\gg 0$. The specific value that T should take will be detailed below.

• 2. In the second example, only regions 1 and 2 may trade with each other, while region 3 is still in autarky. In this example, we assume $T_{12}=T-\varepsilon$ and $T_{13}=T_{23}=T$, where $0<\varepsilon <T$ (this implies $T_{12}<T_{13}=T_{23}$). One-way trade from 1 to 2 or from 2 to 1 or two-way trade between 1 and 2 can occur for $\varepsilon$ sufficiently close to T.

• 3. In the third example, the three regions are positioned along a ‘Hub and spoke’ structure. Region 1 is the central and regions 2 and 3 are peripheral. In this example, we consider a special case: trade costs between region 1 and 2 and so small that these two regions are always engaged in bilateral trade independently of other factors (esp. the distribution of the economic activity across space); region 1 and 3 may trade as well; whereas no trade between 2 and 3 can occur. With respect to the other two examples, region 3 is getting closer to region 1 but is still too far from region 2. In this example, we assume $T_{12}=\tau$, $T_{13}=$ and $T_{23}=T$, where $0<\psi <T$ and where $\tau$ is sufficiently small to allow always for two-way trade between 1 and 2 (this implies $T_{12}=\tau \le T-\psi <T$). The specific value that $\tau$ should take will be detailed below. One-way trade from 1 to 3 or from 3 to 1 or two-way trade between 1 and 2 can occur for $\varepsilon$ sufficiently close to T.

3 Short-Run Equilibrium

In a short-run equilibrium, the distribution of entrepreneurs across space is given. All markets are in equilibrium. We choose the agricultural good as the numeraire. From perfect competition in the A-sector, it follows: $p_{A}=w=1$.

To determine the short-run equilibrium solutions related to the M-sector, we proceed as follows.

Maximizing the utility (1) subject to the constraint (2), we obtain the first order conditions for $i=1,...N$:

$$ \frac{\partial U}{\partial c_{i}}=\alpha -(\beta -\delta )c_{i}-\delta \sum \limits _{i=1}^{N}c_{i}-p_{i}=0 $$

from which

$$ p_{i}=\alpha -(\beta -\delta )c_{i}-\delta \sum \limits _{i=1}^{N}c_{i}\ . $$

Solving this system for $c_{i}$, we obtain the individual linear demand function for each variety i:

$$\begin{aligned} c_{i}=\max [0,a-(b+cN)p_{i}+cP] \end{aligned}$$

(3)

where $P=\sum \limits _{i=1}^{N}p_{i}$ is the price index and

$$ a=\frac{\alpha }{(N-1)\delta +\beta },\; \;b=\frac{1}{(N-1)\delta +\beta },\; \;c=\frac{\delta }{(\beta -\gamma )[(N-1)\delta +\beta ]}\ . $$

Moreover, $c_{i}>0$ for $p_{i}<\widetilde{p_{i}}=\frac{a+cP}{b+cN}$, $\widetilde{p_{i}}$ representing the cut-off price below which demand for variety i is positive.

The representative consumer’s indirect utility corresponds to

$$ V=S+y+\overline{C_{A}} $$

where S is the consumer’s surplus:

$$ S=U-\sum _{i=1}^{N}p_{i}c_{i}-C_{A}=\frac{a^{2}N}{2b}+\frac{b+cN}{2}\sum _{i=1}^{N}p_{i}^{2}-aP-\frac{c}{2}P^{2} $$

The consumer’s demand originating from region $s(=1,2,3)$ for a good produced in region $r(=1,2,3),$ dropping the subscript i because of symmetric firm behaviour, is:

$$ c_{rs}=\max \left[ 0,a-(b+cN)p_{rs}+cP_{s}\right] $$

where $p_{rs}$ is the price of a good produced in region r and consumed in region s; and

$$\begin{aligned} P_{s}=\sum _{k=1}^{3}N_{k}p_{ks}=\sum _{k=1}^{3}\lambda _{k}Ep_{ks} \end{aligned}$$

(4)

is the price index in region s($=1,2,3$). As before $c_{rs}>0$ if and only if $p_{rs}<\widetilde{p_{r}}=\frac{a+cP_{s}}{b+cN}$, where $\widetilde{p_{r}}$ is the cut-off price above which demand is positive ($r,s=1,2,3$).

Taking into account that $L_{1}=L_{2}=L_{3}=\frac{L}{3}$, with segmented markets, the operating profit of a firm located in r($=1,2,3$) is:

$$\begin{aligned} \pi _{r}=\sum _{s=1}^{3}(p_{rs}-\eta -T_{rs})q_{rs}\left( \frac{L}{3}+\lambda _{s}E\right) \end{aligned}$$

(5)

In a short-run equilibrium, demand is equal to supply in each segmented market s($=1,2,3$): $q_{rs}=c_{rs}$. From profit maximization, recalling that $N=E$ and that firms consider the price index as given, the first order conditions for $r,s=1,2,3$ follow:

$$ \frac{\partial \pi _{r}}{\partial p_{rs}}=\left[ a+(\eta +T_{rs})(b+cE)+cP_{s}-2p_{rs}(b+cE)\right] \left( \frac{L}{3}+\lambda _{s}E\right) =0 $$

Taking into account trade costs and letting $\widetilde{p_{r}}>\eta$ for $r=1,2,3$, to allow for positive production in the local market, profit maximizing prices correspond to:

$$\begin{aligned} p_{rr}=\frac{a+cP_{r}+\eta (b+cE)}{2(b+cE)}=\frac{1}{2}(\widetilde{p_{r}}+\eta ) \end{aligned}$$

(6)

which is the price that firms quote in the market where they are located; and to

$$\begin{aligned} p_{rs}=\left\{ \begin{array}{ccc} \frac{a+cP_{s}+(\eta +T_{rs})(b+cE)}{2(b+cE)}=\frac{1}{2}(\widetilde{p_{s}}+\eta +T_{rs}) &{} if &{} T_{rs}<\widetilde{p_{s}}-\eta \\ \widetilde{p_{s}} &{} if &{} T_{rs}\ge \widetilde{p_{s}}-\eta \end{array} \right. \end{aligned}$$

(7)

which is the price that a firm located in region r quotes in region s, with $r,s=1,2,3$ and $r\ne s$.

Using the demand and the price functions, we can write:

$$\begin{aligned} q_{rr}=(b+cE)(p_{rr}-\eta ) \end{aligned}$$

(8)

which is the quantity sold in the local market; and

$$\begin{aligned} q_{rs}=\left\{ \begin{array}{ccc} (b+cE)(p_{rs}-\eta -T_{rs}) &{} if &{} T_{rs}<\widetilde{p_{s}}-\eta \\ 0 &{} if &{} T_{rs}\ge \widetilde{p_{s}}-\eta \end{array} \right. \end{aligned}$$

(9)

which is the quantity that a firm located in region r sells in region s, with $r,s=1,2,3$ and $r\ne s$.

According to (7) and (9), if a firm located in r quotes in the market s a price larger than the reservation price consumers living in s are prepared to pay, the export from region r to region s is zero. The boundary conditions for trade, as reported in these expressions, are crucial in the following analysis to determine the patterns of trade between the regions.

The indirect utility for a r-entrepreneur is

$$ V_{r}=S_{r}+\pi _{r}+\overline{C_{A}} $$

where

$$ \pi _{r}=\sum _{s=1}^{3}(p_{rs}-\eta -T_{rs})q_{rs}\left( \frac{L}{3}+\lambda _{s}E\right) $$

is the equilibrium profit for a r-firm, and

$$\begin{aligned} S_{r}=\frac{a^{2}E}{2b}+\frac{b+cE}{2}\sum _{s=1}^{3}\lambda _{s}Ep_{sr}^{2}-aP_{r}-\frac{c}{2}P^{2} \end{aligned}$$

(10)

is the consumer’s surplus of the entrepreneur.

3.1 Short-Run Solutions

3.1.1 Model 1. All Autarkic Regions

In this set-up, we assume that the three regions are equidistant, with $T_{12}=T_{13}=T_{23}=T$ and sufficiently far away in terms of trade costs that trade cannot take place for any of the possible distributions of economic activity. When no region is trading, the condition $T_{rs}\ge \widetilde{p}_{s}-\eta$ holds for all r,s, with $r,s=1,2,3$ and $r\ne s$. It corresponds to:

$$ T_{rs}=T\ge \widetilde{p}_{s}-\eta =\frac{2(a-\eta b)}{2b+c\lambda _{s}E}. $$

This expression can be alternatively written as

$$ \lambda _{s}\ge \frac{2(a-\eta b-bT)}{cET}=\overline{\lambda }. $$

No trade occurs for any distribution of the economic activity across the regions when:

$$ T \ge \frac{a}{b}-\eta \; \; \textit{or}\; \; \overline{\lambda }\le 0, $$

which is what we assume in the first set-up.⁵

From (4)–(9), taking into account the linear demand non-negativity constraint, we derive the equilibrium short-run profit for a firm located in region r, which sells in the local market⁶:

$$ \pi _{r}=\pi _{r}^{no}=(p_{rr}^{no}-\eta )^{2}(b+cE)\left( \frac{L}{3} +\lambda _{r}E\right) =\pi _{rr}^{no} $$

Finally, taking also into account (10), we obtain the indirect utility of entrepreneur resident in r:

$$ V_{r}=V_{r}^{no}=S_{r}^{no}+\pi _{r}^{no}+\overline{C_{A}}=S_{r}^{no}+\pi _{rr}^{no}+\overline{C_{A}}. $$

3.1.2 Model 2. Allowing Trade only Between Regions 1 and 2

In the second set-up, trade costs between regions 1 and 2 are reduced, so that trade between these two regions can take place. We assume $T_{12}=T-\varepsilon$, where $0<\varepsilon \le T$,⁷ then trade may occur when $\varepsilon$ is sufficiently close to T. We also assume $T_{13}=T_{23}=T\ge \frac{a}{b}-\eta$ so that trade between regions 1 and 2 as well as 2 and 3 is still too costly leaving region 3 in autarky.

There are four different scenarios depending on the ‘trade distance’ between regions 1 and 2, that is on $\varepsilon$.

In the first scenario, regions 1 and 2 still do not trade with each other: from (4), (6), and (7), the condition of no trade $T_{rs}\ge \widetilde{p_{s}}-\eta$ for $r,s=1,2$ and $r\ne s$ corresponds to:

$$ T_{rs}=T-\varepsilon \ge \frac{2(a-\eta b)}{2b+c\lambda _{s}E} $$

This expression can alternatively be expressed as:

$$ \lambda _{r}\ge \widetilde{\lambda }\; \; \textit{for}\;r=1,2 $$

where $\widetilde{\lambda }=\frac{2(a-\eta b-bT+\varepsilon b)}{cE(T-\varepsilon )}$.

The same results as before apply, thus the equilibrium short-run profit for a firm located in region r is $\pi _{r}=$ $\pi _{r}^{no}$ and the indirect utility of an entrepreneur resident in r is $V_{r}=$ $V_{r}^{no}$.

In the second and third scenarios, unilateral or one-way trade occurs (from 1 to 2 in the second and from 2 to 1 in the third scenario). We consider these two scenarios together. We have that $T_{rs}<\widetilde{p_{s}}-\eta$ and $T_{rs}\ge \widetilde{p_{s}}-\eta$ holds for $r,s=1,2$ and $r\ne s$ (i.e. for $r=1$ and $s=2$ in the second and for $r=2$ and $s=1$ in the third scenario). From (4), (6), and (7), the conditions for unidirectional trade from r to s are obtained:

$$ T_{rs}=T-\varepsilon <\frac{2(a-\eta b)}{2b+c\lambda _{s}E}\; \; \; \textit{and}\; \; \; T_{rs}=T-\varepsilon \ge \frac{2(a-\eta b)}{2b+c\lambda _{r}E} $$

or, alternatively:

$$ \widetilde{\lambda }\ge \lambda _{r}\; \; \; \textit{and}\; \; \; \widetilde{\lambda }<\lambda _{s} $$

with $r=1$ and $s=2$ in the second and $r=2$ and $s=1$ in the third scenario.

Letting $r=1$ and $s=2$ for the second and $r=2$ and $s=1$ for the third scenario and $k=3$ in both, from (4)–(9), the equilibrium short-run profits for the case of one-way trade from r to s are:

$$\begin{aligned} \pi _{r}= & {} \pi _{r}^{out}=(b+cE)\left[ (p_{rr}^{no}-\eta )^{2}\left( \frac{L}{3}+ \lambda _{r}E\right) +(p_{rs}^{out}-\eta -T_{rs})^{2}\left( \frac{L}{3}+\lambda _{s}E\right) \right] \\= & {} \pi _{rr}^{no}+\pi _{rs}^{out} \end{aligned}$$

$$ \pi _{s}=\pi _{s}^{in}=(b+cE)(p_{ss}^{in}-\eta )^{2}\left( \frac{L}{3}+\lambda _{s}E\right) =\pi _{ss}^{in} $$

$$ \pi _{k}=\pi _{k}^{no} $$

where $\pi _{r}^{out}$ is the profit of a firm located in r which is composed of two parts: the first part $\pi _{rr}^{no}$ is obtained by selling in the local market, which is not affected by its exports to s due to market segmentation, and the second part $\pi _{rs}^{out}$ by selling in s; $\pi _{s}^{in}$ is the profit of a firm located in s obtained only by selling in the local market, which is affected by the competition from the firms located in r; and $\pi _{k}^{no}$ is the profit of a firm located in k obtained only by selling in the local market, which is not affected by competition from outside.

Finally, taking also into account (10), the indirect utilities for the case of one-way trade from r to s are:

$$\begin{aligned} V_{r}= & {} V_{r}^{out}=S_{r}^{out}+\pi _{rr}^{out}+\overline{C_{A}}=S_{r}^{no}+\pi _{rr}^{out}+\overline{C_{A}} \\ V_{s}= & {} V_{s}^{in}=S_{s}^{in}+\pi _{s}^{in}+\overline{C_{A}}=S_{s}^{in}+\pi _{ss}^{in}+\overline{C_{A}} \\ V_{k}= & {} V_{k}^{no} \end{aligned}$$

where $V_{r}^{out}$ is the indirect utility of an entrepreneur located in r, whose profits are higher compared to autarky; $V_{r}^{in}$ is the indirect utility of an entrepreneur located in s, whose profits are lower and the surplus, $S_{s}^{in}$, is higher compared to autarky; and $V_{k}^{no}$ is the indirect utility of an entrepreneur located in k, which is the same as in the previous model.

In the fourth scenario bilateral or two-way trade occurs. In this scenario $T_{rs}<\widetilde{p_{s}}-\eta$ for $r,s=1,2$ and $r\ne s.$ From (4), (6), and (7), the conditions for unilateral trade between r and s are:

$$ T_{rs}=T-\varepsilon <\frac{2(a-\eta b)}{2b+c\lambda _{s}E}\; \; \; \textit{for}\; \;r=1,2\; \; \; \textit{and} \; \; \;r\ne s, $$

or, alternatively,

$$ \lambda _{r}<\widetilde{\lambda }\; \; \; \textit{for}\; \; \;r=1,2 $$

From (4)–(9), the equilibrium profits for the case of bilateral trade between r and s are:

$$\begin{aligned} \pi _{r}= & {} \pi _{r}^{bil}=\pi _{rr}^{bil}+\pi _{rs}^{bil}\; \; \; \textit{for}\; \; \; r=1,2\; \; \; \textit{and}\; \; \;r\ne s \\ \pi _{k}= & {} \pi _{k}^{no} \textit{ for}\; \; \;k=3 \end{aligned}$$

where $\pi _{r}^{bil}$ is the profit of a firm located in r, which is composed of two parts: the first part $\pi _{rr}^{bil}$ is obtained by selling in the local market, which is not affected by its export towards s but is affected by competition from the firms located in s and the second part $\pi _{rs}^{bil}$ by selling in s, with $r=1,2$ and $r\ne s$; and $\pi _{k}^{no}$, with $k=3$, is the profit of a firm located in k, which has the same meaning as before.

Finally, taking also into account 10, the indirect utilities for the case of two-way trade between r and s are:

$$\begin{aligned} V_{r}= & {} V_{r}^{bil}=S_{r}^{bil}+\pi _{r}^{bil}+\overline{C_{A}} =S_{r}^{bil}+\pi _{rr}^{bil}+\pi _{rs}^{bil}+\overline{C_{A}}\; \; \;for\; \; \;r=1,2\; \; \;and\; \; \;r\ne s \\ V_{k}= & {} V_{k}^{no}\quad for\; \; \;k=3 \end{aligned}$$

where $V_{r}^{bil}$ is the indirect utility of an entrepreneur located in r. Even though her profits originated from the local market $\pi _{rr}^{bil}$ are lower due to competition from firms located in s, she is enjoying profits by selling in region s, $\pi _{rs}^{bil}$. Moreover, her surplus, $S_{r}^{bil}$, is higher compared to when only local goods are available for consumption, with $r=1,2$ and $r\ne s$. As before, the indirect utility of an entrepreneur located in k is not changed, with $k=3$.

3.1.3 Model 3. Hub and Spoke

In the third set-up, region 1 may trade with regions 2 and 3 but regions 2 and 3 do not trade with each other. We consider a special case of an ‘hub and spoke’ structure: that is, we assume that trade costs between regions 1 and 2 are sufficiently low that bilateral trade between these two regions always occur, that is, we set $T_{12}=\tau <\frac{2(a-\eta b)}{2b+cE}$. We also assume prohibitive trade costs between 2 and 3:

$$ T_{23}=T\ge \frac{a}{b}-\eta $$

Moreover, letting $T_{13}=T-\psi$ and considering that $T_{12}\le T_{13}\le T_{23}$, we have that $\tau \le T-\psi \le T$.

There are four possible scenarios, depending on $\psi$. In the first scenario, no trade between regions 1 and 3 occurs: $T_{rk}\ge \widetilde{p}_{k}-\eta$ for $r,k=1,3$ and $r\ne k$. From (4), (6), and (7), the condition corresponding to no trade between 1 and 3 corresponds to:

$$ T_{13}=T-\psi \ge \max \left( \frac{2(a-\eta b)+cE\lambda _{2}T_{12}}{2b+c(\lambda _{1}+\lambda _{2})E}, \frac{2(a-\eta b)}{2b+c\lambda _{3}E}\right) $$

or to

$$ \lambda _{1}\ge \overline{\lambda }-\frac{T_{13}-T_{12}}{T_{13}}\lambda _{2}\; \; \; \textit{and}\; \; \; \lambda _{2}\le 1-\overline{\lambda }-\lambda _{1} $$

where $\overline{\lambda }=\frac{2(a-\eta b-bT_{13})}{cET_{13}}=\frac{2(a-\eta b-bT+\psi b)}{cET_{13}}.$

The equilibrium profits and indirect utilities correspond to those in the fourth scenario of the second set-up. These are: $\pi _{r}=\pi _{r}^{bil}$, $\pi _{k}=\pi _{k}^{no}$, $V_{r}=V_{r}^{bil}$ and $V_{k}=V_{k}^{no}$ for $r=1,2$, $r\ne s$ and $k=3$.

In the second and third scenarios. Unilateral trade occurs involving region 1 and 3 (from 1 to 3 in the second and from 3 to 1 in the third scenario). We consider these two scenarios together. We have that $T_{rk}<\widetilde{p}_{k}-\eta$ and $T_{rk}\ge \widetilde{p}_{r}-\eta$ holds for $r,k=1,3$ and $r\ne k$ (i.e. for $r=1$ and $k=3$ in the second and for $r=3$ and $k=1$ in the third scenario).

From (4), (6), and (7), one-way trade from region 1 to region 3 occurs when:

$$ \frac{2(a-\eta b)+cE\lambda _{2}T_{12}}{2b+c(\lambda _{1}+\lambda _{2})E}\le T_{13}=T-\psi <\frac{2(a-\eta b)}{2b+c\lambda _{3}E} $$

or when

$$ \lambda _{1}\ge \overline{\lambda }-\frac{T_{13}-T_{12}}{T_{13}}\lambda _{2}\; \; \; \textit{and}\; \; \; \lambda _{2}>1-\overline{\lambda }-\lambda _{1} $$

The short-run equilibrium profits for the case of one-way trade from region 1 to region 3 are:⁸

$$\begin{aligned} \pi _{1}= & {} \pi _{1}^{bil,\ out}=(b+cE)\left[ (p_{11}^{bil}-\eta )^{2}\left( \frac{L}{3}+\lambda _{1}E\right) +(p_{12}^{bil}-\eta -T_{12})^{2}\left( \frac{L}{3}+\lambda _{2}E\right) + \right. \\+ & {} \left. (p_{13}^{out}-\eta -T_{13})^{2}\left( \frac{L}{3}+\lambda _{3}E\right) \right] =\pi _{1}^{bil}+\pi _{13}^{out} \\ \pi _{2}= & {} \pi _{2}^{bil,\;out}=(b+cE)\left[ (p_{21}^{bil}-\eta )^{2}\left( \frac{L}{3}+\lambda _{1}E\right) +(p_{22}^{bil}-\eta -T_{12})^{2}\left( \frac{L}{3}+\lambda _{2}E\right) \right] \\= & {} \pi _{2}^{bil} \\ \pi _{3}= & {} \pi _{3}^{bil,\ out}=(b+cE)(p_{33}^{bil,\ out}-\eta )^{2}\left( \frac{L}{3}+\lambda _{3}E\right) =\pi _{33}^{bil,\ out} \end{aligned}$$

where $\pi _{1}^{bil,\ out}$ is the profit of a firm located in 1 which is composed of two parts: the first part corresponds to the profit obtained in the absence of the trade link from 1 to 3 $\pi _{1}^{bil}$ – which is itself composed of two parts (see above) – and the second part $\pi _{13}^{out}$ is obtained by selling in 3, which is not affected by its exports to 3 due to market segmentation; $\pi _{2}^{bil,\;out}$ is the profit of a firm located in region 2 which is equal to that in the fourth scenario of the second set-up; and $\pi _{3}^{bil,\ out}$ is the profit of a firm located in 3 obtained only by selling in the local market, which is affected by the competition from the firms located in 1.

Finally, taking also into account (10), the indirect utilities for the case of one-way trade from region 1 to region 3 correspond to:

$$\begin{aligned} V_{1}= & {} V_{1}^{bil,\ out}=V_{1}^{bil}+\pi _{13}^{out} \\ V_{2}= & {} V_{2}^{bil,\ out}=V_{2}^{bil} \\ V_{3}= & {} V_{3}^{bil,\ out}=V_{3}^{in}=S_{3}^{in}+\pi _{33}^{in}+\overline{C_{A}} \end{aligned}$$

where $V_{1}^{bil,\ out}$ is the indirect utility of an entrepreneur located in 1, whose profits are higher compared to the case when there are no trade links between 1 and 3; $V_{2}^{bil,\ out}$ is the indirect utility of an entrepreneur located in 2, which the same that the one obtained in the fourth scenario of the second set-up; and $V_{3}^{bil,\ out}$ is the indirect utility of an entrepreneur located in 3, whose profits are lower and the surplus $S_{3}^{in}$ is higher compared to the case of no trade links between 1 and 3.

From (4), (6), and (7), one-way trade from region 3 to region 1 occurs when:

$$ \frac{2(a-\eta b)}{2b+c\lambda _{3}E}\le T_{13}=T-\psi <\frac{2(a-\eta b)+cE\lambda _{2}T_{12}}{2b+c(\lambda _{1}+\lambda _{2})E} $$

or when

$$ \lambda _{1}<\overline{\lambda }-\frac{T_{13}-T_{12}}{T_{13}}\lambda _{2}\; \; \; \textit{and}\; \; \; \lambda _{2}\le 1-\overline{\lambda }-\lambda _{1}. $$

The short-run equilibrium profits for the case of one-way trade from region 3 to region 1 are:

$$\begin{aligned} \pi _{1}= & {} \pi _{1}^{bil,\ in}=(b+cE)\left[ (p_{11}^{bil,\ in}-\eta )^{2}\left( \frac{L}{3}+\lambda _{1}E\right) +(p_{12}^{out}-\eta -T_{12})^{2}\left( \frac{L}{3}+\lambda _{2}E\right) \right] \\= & {} \pi _{11}^{bil,\ in}+\pi _{12}^{out} \\ \pi _{2}= & {} \pi _{2}^{bil,\;in}=(b+cE)\left[ (p_{21}^{bil,\ in}-\eta )^{2}\left( \frac{L}{3}+\lambda _{1}E\right) +(p_{22}^{out}-\eta -T_{12})^{2}\left( \frac{L}{3}+\lambda _{2}E\right) \right] \\= & {} \pi _{21}^{bil,\;in}+\pi _{22}^{out} \\ \pi _{3}= & {} \pi _{3}^{bil,\ in}=(b+cE)\left[ (p_{31}^{bil,\ in}-\eta )^{2}\left( \frac{L}{3}+\lambda _{1}E\right) +(p_{33}^{no}-\eta -T_{12})^{2}\left( \frac{L}{3}+\lambda _{3}E\right) \right] \\= & {} \pi _{31}^{bil,\;in}+\pi _{33}^{no} \end{aligned}$$

where $\pi _{1}^{bil,\ in}$ is the profit of a firm located in 1 which is composed of two parts: the first part $\pi _{11}^{bil,\ in}$ is obtained by selling in the local market, which is not affected by its exports towards 2 but is affected by the competition from the firms located both in 2 and in 3 and the second part $\pi _{12}^{out}$ by selling in 2; $\pi _{2}^{bil,\;in}$ is the profit of a firm located in region 2 which is composed of two parts: the first part $\pi _{21}^{bil,\;in}$ is obtained by selling in 1 which is affected by the competition in that market not only from the local firms but also from the firms located in 3 and the second part $\pi _{22}^{bil}$ obtained by selling in the local market, which is not affected by the exports towards 1 but it is affected by competition from the firms located in 1; and $\pi _{3}^{bil,\ in}$ is the profit of a firm located in 3 composed of two parts: the first part $\pi _{31}^{bil,\;in}$ is obtained by selling in 1, which is affected by the competition in that market not only from the local firms but also from the firms located in 2 and the second part $\pi _{33}^{no}$, which is not affected by the exports towards 1.

Taking also into account (10), the indirect utilities for the case of one-way trade from region 3 to region 1 corresponds to:

$$\begin{aligned} V_{1}= & {} V_{1}^{bil,\ in}=S_{1}^{bil,\ in}+\pi _{1}^{bil,\ in}+\overline{C_{A}} \\ V_{2}= & {} V_{2}^{bil,\ in}=S_{2}^{bil}+\pi _{2}^{bil,\;in}+\overline{C_{A}} \\ V_{3}= & {} V_{3}^{bil,\ in}=S_{3}^{no}+\pi _{31}^{bil,\;in}+\overline{C_{A}} \end{aligned}$$

where $V_{1}^{bil,\ in}$ is the indirect utility of an entrepreneur located in 1, whose profits are lower and surplus is higher compared to when there are no trade links between 1 and 3; $V_{2}^{bil,\ in}$ is the indirect utility of an entrepreneur located in 2, whose profits are lower compared to when there are no trade links between 1 and 3; and $V_{3}^{bil,\ in}$ is the indirect utility of an entrepreneur located in 3, whose profits are higher compared to the case of no trade links between 1 and 3.

Finally, in the fourth scenario bilateral trade between regions 1 and 3 occurs. We have that $T_{rk}<\widetilde{p}_{k}-\eta$ for $r,k=1,3$ and $r\ne k.$ From (4), (6), and (7), bilateral trade between regions 1 and 3 occurs when:

$$ T_{13}=T-\psi <\min \left( \frac{2(a-\eta b)+cE\lambda _{2}T_{12}}{2b+c(\lambda _{1}+\lambda _{2})E}, \frac{2(a-\eta b)}{2b+c\lambda _{3}E}\right) $$

or when

$$ \lambda _{1}<\overline{\lambda }-\frac{T_{13}-T_{12}}{T_{13}}\lambda _{2}\; \; \; \textit{and}\; \; \; \lambda _{2}>1-\overline{\lambda }-\lambda _{1}. $$

The short-run equilibrium profits for the case of bilateral trade between regions 1 and 3 are:

$$\begin{aligned} \pi _{1}= & {} \pi _{1}^{bil,\ bil}=(b+cE)\left[ (p_{11}^{bil,\ in}-\eta )^{2}\left( \frac{L}{3}+\lambda _{1}E\right) +(p_{12}^{out}-\eta -T_{12})^{2}\left( \frac{L}{3}+\lambda _{2}E\right) \right. \\+ & {} \left. (p_{13}^{out}-\eta -T_{13})^{2}\left( \frac{L}{3}+\lambda _{3}E\right) \right] =\pi _{1}^{bil,\ in}+\pi _{13}^{out} \\ \pi _{2}= & {} \pi _{2}^{bil,\;bil}=(b+cE)\left[ (p_{21}^{bil,\ in}-\eta )^{2}\left( \frac{L}{3}+\lambda _{1}E\right) +(p_{22}^{out}-\eta -T_{12})^{2}\left( \frac{L}{3}+\lambda _{2}E\right) \right] \\= & {} \pi _{2}^{bil,\ in} \\ \pi _{3}= & {} \pi _{3}^{bil,\ bil}=(b+cE)\left[ (p_{31}^{bil,\ in}-\eta )^{2}\left( \frac{L}{3}+\lambda _{1}E\right) \right. \\+ & {} \left. (p_{33}^{bil,\ out}-\eta -T_{12})^{2}\left( \frac{L}{3}+\lambda _{3}E\right) \right] =\pi _{31}^{bil,\;in}+\pi _{33}^{bil,\ out} \end{aligned}$$

where $\pi _{1}^{bil,\ bil}$ is the profit of a firm located in 1 which is composed of two parts: the first part $\pi _{1}^{bil,\ in}$ is what is obtained in the third scenario and the second part $\pi _{13}^{out}$ by selling in 3; $\pi _{2}^{bil,\;bil}$ is the profit of a firm located in region 2 which is the same as in the third scenario; and $\pi _{3}^{bil,\; bil}$ is the profit of a firm located in 3 composed of two parts: the first part $\pi _{31}^{bil,\;in}$ is obtained by selling in 1, which is affected by the competition in that market not only from the local firms but also from the firms located in 2 and the second part $\pi _{33}^{bil,\; out}$ is obtained by selling in the local market, which is affected by the competition from the firms located in 1.

Finally, taking also into account (10), the indirect utilities for the case of bilateral trade between 1 and 3 correspond to:

$$\begin{aligned} V_{1}= & {} V_{1}^{bil,\ bil}=V_{1}^{bil,\ in}+\pi _{13}^{out} \\ V_{2}= & {} V_{2}^{bil,\ bil}=V_{2}^{bil,\ in} \\ V_{3}= & {} V_{3}^{bil,\ bil}=V_{3}^{bil,\ out}+\pi _{31}^{bil,\;in} \end{aligned}$$

where $V_{1}^{bil,\ bil}$ is the indirect utility of an entrepreneur located in 1, which is equal to the indirect utility enjoyed in the third scenario plus the profits obtained by selling in 3; $V_{2}^{bil,\ bil}$ is the indirect utility of an entrepreneur located in 2, which is the same as in the third scenario; and $V_{3}^{bil,\ bil}$ is the indirect utility of an entrepreneur located in 3, which is equal to that enjoyed in the second scenario plus the profits obtained by selling in 1.

4 Definition of the Basic Dynamic Equations

The dynamics of the three NEG model variants presented above is described by a two-dimensional (2D) system of difference equations, or map, Z:

$$\begin{aligned} Z:\left( \begin{array}{c} \lambda _{1} \\ \lambda _{2} \end{array} \right) \mapsto \left( \begin{array}{c} Z_{1}(\lambda _{1},\lambda _{2}) \\ Z_{2}(\lambda _{1},\lambda _{2}) \end{array} \right) , \end{aligned}$$

(11)

where

$$ Z_{i}(\lambda _{1},\lambda _{2})=\left\{ \begin{array}{ccccc} 0 &{} \textit{if} &{} F_{i}\le 0, &{} &{} \\ F_{i} &{} \textit{if} &{} F_{i}>0, &{} F_{j}>0, &{} F_{i}+F_{j}<1, \\ \frac{F_{i}}{F_{i}\ +\ F_{j}} &{} \textit{if} &{} F_{i}>0, &{} F_{j}>0, &{} F_{i}+F_{j}\ge 1, \\ \frac{F_{i}}{1\ -\ F_{j}} &{} \textit{if} &{} F_{i}>0, &{} F_{j}\le 0, &{} F_{i}+F_{j}<1, \\ 1 &{} \textit{if} &{} F_{i}>0, &{} F_{j}\le 0, &{} F_{i}+F_{j}\ge 1, \end{array} \right. $$

$$ \textit{with }i=1,\ j=2\textit{ for }Z_{1}(\lambda _{1},\lambda _{2})\textit{ and } i=2,\ j=1\textit{ for }Z_{2}(\lambda _{1},\lambda _{2})\ , $$

$$ F_{r}(\lambda _{1},\lambda _{2})=\lambda _{r}(1+\gamma \varOmega _{r}(\lambda _{1},\lambda _{2})),\ r=1,2\ , $$

$$ \varOmega _{r}(\lambda _{1},\lambda _{2})=\frac{V_{r}(\lambda _{1},\lambda _{2}) }{\lambda _{1}V_{1}(\lambda _{1},\lambda _{2})+\lambda _{2}V_{2}(\lambda _{1},\lambda _{2})+(1-\lambda _{1}-\lambda _{2})V_{3}(\lambda _{1},\lambda _{2})}-1. $$

Due to the constraint on the regional shares of entrepreneurs, the map Z is piecewise smooth. In Z, the indirect utilities $V_{i}(\lambda _{1},\lambda _{2}),$ $i=1,2,3,$ of an entrepreneur in regions 1,  2 and 3, respectively, are defined according to the assumptions of the considered models.

Independently on the specification of the indirect utilities the following properties hold:

• All the relevant dynamics in the $(\lambda _{1},\lambda _{2})$-phase plane is trapped in a triangle denoted S,  whose borders:

  $$\begin{aligned} I_{b1}=\{(\lambda _{1},\lambda _{2}):\lambda _{2}=0\},\ I_{b2}=\{(\lambda _{1},\lambda _{2}):\lambda _{1}=0\},\ I_{b3}=\{(\lambda _{1},\lambda _{2}):\lambda _{2}=1-\lambda _{1}\} \end{aligned}$$

  (12)

  are invariant lines ⁹ of map Z.

• A fixed point of the map Z, which lies inside S, corresponds to a stationary long-run equilbrium of the economy; the vertices of S are Core-periphery (CP) fixed points/equilibria:

  $$\begin{aligned} CP_{0}:(\lambda _{1},\lambda _{2})=(0,0),\ CP_{1}:(\lambda _{1},\lambda _{2})=(1,0),\ CP_{2}:(\lambda _{1},\lambda _{2})=(0,1), \end{aligned}$$

  (13)

  characterised by full spatial agglomeration of the industrial activity, with all the entrepreneurs located in only one region.

• Any interior fixed point of Z,  if it exists, is given by intersection of the curves

  $$\begin{aligned} \varOmega _{1}=\{(\lambda _{1},\lambda _{2}):\varOmega _{1}(\lambda _{1},\lambda _{2})=0\} \ \textit{and}\ \ \varOmega _{2}=\{(\lambda _{1},\lambda _{2}):\varOmega _{2}(\lambda _{1},\lambda _{2})=0\}. \end{aligned}$$

  (14)

  An interior (symmetric or asymmetric) equilibrium is characterised by positive shares of entrepreneurs in all regions (which can be equal or different).

• Any border fixed point belonging to $I_{bi},$ $i=1,2,$ if it exists, is an intersection point of $\varOmega _{i}$ and $I_{bi},$ while any border fixed point belonging to $I_{b3}$ is an intersection point of $\varOmega _{1},$ $\varOmega _{2}$ and $I_{b3}$. A border (symmetric or asymmetric) equilibrium is characterised by positive shares of entrepreneurs in two regions and no entrepreneurs in the third one. In the regions where entrepreneurs are present they can be equally distributed (in a border symmetric equilibrium) or unevenly distributed (in a border asymmetric equilibrium).

5 Long-Run Equilibria Properties in Model 1

Under the assumptions associated with Model 1 (when all the regions are in autarky) the indirect utilities of an entrepreneur in regions 1,  2 and 3,  respectively, correspond to:

$$\begin{aligned} V_{r}(\lambda _{r})=V_{r}^{no}(\lambda _{r})\ ,\quad r=1,2\ , \end{aligned}$$

(15)

$$\begin{aligned} V_{3}(\lambda _{1},\lambda _{2})=V_{3}^{no}(\lambda _{1},\lambda _{2})\ . \end{aligned}$$

(16)

and are defined in Commendatore et al. (2017). This case generalizes the model studied in Behrens (2004), where two regions in full autarky are considered. We have examined in full detail the mathematical properties of the system (15)–(16) in Commendatore et al. (2017). In this paper, we will focus more on the economic meaning of some results.

First note that for Model 1 not only the borders of the trapping triangle S but also its medians:

$$ I_{m1}=\{(\lambda _{1},\lambda _{2}):\lambda _{2}=1-2\lambda _{1}\},\ \ I_{m2}=\{(\lambda _{1},\lambda _{2}):\lambda _{1}=1-2\lambda _{2}\},$$

$$\begin{aligned} I_{m3}=\{(\lambda _{1},\lambda _{2}):\lambda _{1}=\lambda _{2}\}, \end{aligned}$$

are invariant lines of map Z.

Besides the Core-periphery equilibria (see (13)), Model 1 can have also border symmetric/asymmetric equilibria, as well as interior symmetric/asymmetric equilibria.

In the first place, border symmetric (BS) equilibria always exist:

$$ BS_{1}:(\lambda _{1},\lambda _{2})=(1/2,0),\ BS_{2}:(\lambda _{1},\lambda _{2})=(0,1/2),\ BS_{3}:(\lambda _{1},\lambda _{2})=(1/2,1/2)\ . $$

Considering the border asymmetric (BA) equilibria

(17)

where

$$\begin{aligned} p=\frac{1}{2}-\frac{1}{6cE}\sqrt{(4b+cE)(36b+3cE-8cL)} \end{aligned}$$

(18)

we can state that the equilibria $BA_{i}$ and $BA_{i}^{\prime }$ exist for

$$\begin{aligned} BT_{CP}<L<PF_{BS}\ , \end{aligned}$$

(19)

where

$$\begin{aligned} BT_{CP}=\frac{6b(3b+cE)}{c(4b+cE)}\; \; \; and \; \; \;PF_{BS}=\frac{36b+3cE}{8c}. \end{aligned}$$

(20)

It is easy to check that $PF_{BS}-BT_{CP}>0,$ thus the range (19) is nonempty.

Concerning the interior asymmetric (IA) equilibria

(21)

where $k_{1}$ and $k_{2}$ are given by

$$\begin{aligned} k_{1,2}=\frac{1}{cE}\left( \frac{1}{6}Lc-b+\frac{1}{4}cE\mp \frac{1}{12}\sqrt{24b\left( 42b-10Lc+9cE\right) -c^{2}(9E(4L-E)-4L^{2})}\right) , \end{aligned}$$

(22)

we can state that the interior asymmetric equilibria $IA_{i},$ $i=1,2,3,$ exist for

$$ BT_{CP}<L<F_{IA} \ and \ \ E>E_{1}\ , $$

and the interior asymmetric equilibria $IA_{i}^{\prime }$ exist for

$$ BT_{BS}<L<F_{IA}\; \; if \; \;E>E_{1}\; \; or \; \;BT_{BS}<L<BT_{CP}\; \; if \ \;0<E<E_{1}\ , $$

where

$$\begin{aligned} F_{IA}=\frac{3}{2c}\left( 20b+3cE-2\sqrt{2}\left( 6b+cE\right) \right) ,\;BT_{BS}=\frac{6b(cE+6b)}{c(8b+cE)},\; E_{1}=\frac{2b(7-5\sqrt{2})}{c(2\sqrt{2}-3)}, \end{aligned}$$

(23)

and where $F_{IA}=BT_{CP}$ at $E=E_{1}$. Moreover, it is easy to check that $F_{IA}-BT_{CP}>0$ (for $E\ne E_{1}$), $F_{IA}-BT_{BS}>0,$ and $BT_{CP}-BT_{BS}>0,$ thus, the existence ranges of $IA_{i}$ and $IA_{i}^{\prime }$ are nonempty. In the (E, L)-parameter plane the curves defined by $L=F_{IA}$ and $L=BT_{CP}$ are tangent at $E=E_{1}$.

Finally, the interior symmetric (IS) equilibrium

$$ IS:(\lambda _{1},\lambda _{2})=(1/3,1/3) $$

always exists. Moreover, for a sufficiently small $\gamma$ (namely, for $\gamma \le 1+6b/cE$) it is stable for any $L>T_{IS}=\frac{18b+cE}{4c}$.

To illustrate the existence and stability properties of the long-run equilibria, we choose a,  b,  c,  $\eta$ and E parameter values similar to those used in Behrens (2004):

$$\begin{aligned} a=1/3,\ \ b=1/3,\ \ c=1/3,\ \ \eta =0,\ \ E=1.5\ . \end{aligned}$$

(24)

We fix also

$$\begin{aligned} \gamma =10,\ \ \ \overline{C_{A}}=1 \end{aligned}$$

(25)

and vary L as in Commendatore et al. (2017).

Fig. 1.

Bifurcation curves related to fixed points of map Z in the (E, L)-parameter plane for $a=1/3$, $b=1/3$, $c=1/3$.

Figure 1 summarizes the properties of the long-run equilibria. In this Figure we plotted the bifurcation curves $L=BT_{BS},$ $L=BT_{CP},$ $L=T_{IS},$ $L=F_{IA}$ and $L=PF_{BS}$ in the (E, L)-parameter plane for the values of the other parameters as in (24) and (25). Crossing these curves the properties of the equilibria change.

In Fig. 1, the blue region is related to the coexisting attracting equilibria IS and $IA_{i},$ $i=1,2,3,$ while for the parameter values belonging to the yellow region the attracting equilibrium IS coexists with the attracting equilibria $CP_{i}$. Note that the curve $F_{IA}$ is meaningful for $E>E_{1}$ and that the curve $BT_{CP}$ intersects the curve $T_{IS}$ at $E=\frac{2b}{c}=:E_{2}$.

We now study how the properties of the equilibria of the dynamic system Z changes for a fixed $E<E_{2},$ for example, for $E=1.5,$ by increasing L:¹⁰

Fig. 2.

Attracting fixed points of Z (Model 1) and their basins; curves $\varOmega _{1}$ and $\varOmega _{2}$ given in (14) are also shown. Here $L=4.8$ in (a), $L=4.9$ in (b), $L=4.92$ in (c), $L=5$ in (d), and the other parameters are fixed as in (24) and (25).

• For $1<L<BT_{BS}$ there are three coexisting attracting CP equilibria, and crossing $L=BT_{BS}$ (when a transverse ‘border transcritical bifurcation’ of $BS_{i},$ $i=1,2,3,$ occurs), the fixed points $BS_{i}$ become repelling and the saddle fixed points $IA_{i}^{\prime }$ are born. Figure 2a (where the curves $\varOmega _{1}$ and $\varOmega _{2}$ given in (14) are also shown) depicts the case that holds for $BT_{BS}<L<T_{IS}$. In this Figure the basins of coexisting attracting CP equilibria – representing the set of initial conditions leading to a long-run equilibrium – are coloured red, blue and green (for $CP_{0}$, $CP_{1}$ and $CP_{2}$, respectively). For the interval $1<L<T_{IS}$, the size of invariant local demand, represented by the number of immobile workers (L), is ‘small’, compared with the size of demand that potentially could shift, represented by the number of entrepreneurs (E). A small initial advantage of one region – i.e. an initial distribution of entrepreneurs in that region slightly larger than in the other two – leads to full agglomeration of the industrial activity in that region: the agglomeration forces overcome the dispersion forces.

• Crossing $L=T_{IS}$ (where a ‘transcritical bifurcation’ of IS occurs at which $IS=IA_{i}^{\prime }$) the fixed point IS becomes attracting, so that, for $T_{IS}<L<BT_{CP}$, there are four coexisting attracting fixed points, IS and $CP_{i}$ (see Fig. 2b, where the basin of attraction of IS is coloured in purple). For this interval, the increase in L is sufficient to make the interior equilibrium locally stable and attracting for initial distribution of the economic activity (i.e. for shares of entrepreneurs) not too unequal. This particular type of coexistence cannot occur in a two-region context and it represents a novel result with respect to Behrens (2004).

• Crossing $L=BT_{CP}$ (where a ‘border transcritical bifurcation’ occurs) the CP equilibria become repelling while attracting fixed points $IA_{i}$ and saddle fixed points $BA_{i},$ $BA_{i}^{\prime }$ appear (see Fig. 2c where the basins of attraction of $IA_{1}$, $IA_{2}$ and $IA_{3}$ are coloured in dark yellow, brown and light blue, respectively). Thus, for $BT_{CP}<L<F_{IA}$, four coexisting attracting equilibria exist: the interior symmetric (IS) equilibrium and three interior asymmetric equilibria ($IA_{1}$, $IA_{2}$, $IA_{3}$). In this interval, the size of immobile local demand is sufficiently large so that all regions can keep the industrial sector, the relative dimension of which depends on the initial condition: it could be large for one region (as in an asymmetric equilibrium) or of equal size for all three (as in the symmetric equilibrium).

• Crossing $L=F_{IA}$ (where a ‘fold bifurcation’ occurs and at which $IA_{i}=IA_{i}^{\prime }$) the fixed points $IA_{i}$ and $IA_{i}^{\prime }$ disappear and the only attractor of map Z is IS (see Fig. 2d). Finally, at $L=PF_{BS}$ a pitchfork bifurcation of $BS_{i}$ occurs (at which $BS_{i}=BA_{i}=BA_{i}^{\prime }$); after this bifurcation the fixed points $BS_{i}$ become saddles. Thus, for $L>F_{IA}$ the only stable equilbrium is the symmetric equilibrium. The size of the immobile demand is sufficiently large, compared to the potentially shifting demand, so that there is scope for firms to locate in each region. Any initial condition involving positive shares of entrepreneurs leads to the complete dispersion of the economic activity across the three regions as dispersion forces overcome agglomeration forces.¹¹

Note that this model does not involve trade between the regions and for this reason it represents a useful reference point to be compared with the other two models in order to isolate the effects of trade on the long-run distribution of the economic activity.

6 Long-Run Equilibria Properties in Model 2

Based on the results related to the full autarky case discussed in the previous section, we now reduce the trade costs between regions 1 and 2 allowing uni- and bilateral trade between these regions, but not with region 3. In such a case the indirect utilities $V_{i}(\lambda _{1},\lambda _{2})=:V_{i},$ $i=1,2,3,$ of an entrepreneur in regions 1, 2 and 3, respectively, are defined as follows:

(26)

where $V_{r}^{in}(\lambda _{1},\lambda _{2}),$ $V_{r}^{out}(\lambda _{1},\lambda _{2}),$ $V_{r}^{bil}(\lambda _{1},\lambda _{2})$ for $r=1,2$ are given in Commendatore et al. (2017), $V_{1}^{no}(\lambda _{1}),$ $V_{2}^{no}(\lambda _{2})$ and $V_{3}^{no}(\lambda _{1},\lambda _{2})$ are defined as in Model 1. The dynamic system (or map) Z is modified accordingly.

We have examined in full detail the mathematical properties of the system Z modified to take into account 26 in Commendatore et al. (2017). In this paper, as for the previous model, we will focus more on the economic meaning of some results.

In our simulations, for convenience, we set $T=\frac{a}{b}-\eta$, that is, at the minimum value of trade costs which ensures no trade for any distribution of entrepreneurs across the regions, it follows

$$\begin{aligned} \widetilde{\lambda }=\left. \frac{2b^{2}\varepsilon }{cE(a-b\eta -b\varepsilon )}\right| _{\eta =0,a=b=c}=\frac{2\varepsilon }{E(1-\varepsilon )}\ . \end{aligned}$$

(27)

Moreover, we fix the parameter values as in (24)–(25), and vary L and $\varepsilon$ in the ranges

$$ 2<L<9,\ \ \ \ 0<\varepsilon <T=\left. \frac{a}{b}-\eta \right| _{a=b,\ \eta =0}=1\ . $$

Similarly to Model 1, the borders $I_{bi}$, $i=1,2,3$ (see (12)) of the trapping triangle S are invariant lines of map Z, while among the medians of S only the main diagonal $I_{m3}=\{(\lambda _{1},\lambda _{2}):\lambda _{1}=\lambda _{2}\}$ is invariant.

The straight lines $\lambda _{1}=\widetilde{\lambda }$ and $\lambda _{2}=\widetilde{\lambda },$ where $\widetilde{\lambda }$ is given in (27), separate the trapping triangle S into at most four regions, each of them characterized by a different trade pattern (see Fig. 3a):

• the region $S_{0}=\{ \lambda _{1}>\widetilde{\lambda },$ $\lambda _{2}>\widetilde{\lambda },$ $\lambda _{1}+\lambda _{2}<1\}$ corresponds to no trade;

• the regions $S_{1}=\{ \lambda _{1}>\widetilde{\lambda },$ $0<\lambda _{2}<\widetilde{\lambda },$ $\lambda _{1}+\lambda _{2}<1\}$ and $S_{2}=\{ \lambda _{2}>\widetilde{\lambda },$ $0<\lambda _{1}<\widetilde{\lambda },$ $\lambda _{1}+\lambda _{2}<1\}$ are related to unilateral trade;

• the region $S_{3}=\{0<\lambda _{1}<\widetilde{\lambda },$ $0<\lambda _{2}<\widetilde{\lambda }\}$ is related to bilateral trade.

It is easy to see that in the trapping triangle S there are only regions $S_{1}$, $S_{2}$ and $S_{3}$ (and there is no ‘no trade’ region $S_{0}$) for

$$ \frac{1}{2}<\widetilde{\lambda }<1\; \; \; or \; \; \; \varepsilon _{2}<\varepsilon <\varepsilon _{3} $$

where

$$\begin{aligned} \varepsilon _{2}=\frac{cE(a-b\eta )}{b(cE+4b)}\ ,\ \ \varepsilon _{3}=\frac{cE(a-b\eta )}{b(cE+2b)}\ , \end{aligned}$$

(28)

and S coincides to $S_{3}$ for $\widetilde{\lambda }>1$ or $\varepsilon >\varepsilon _{3}$, that is, the trapping triangle S is associated only with bilateral trade between regions 1 and 2.¹²

Compared with that associated with Model 1, the map Z considered in the present section can have more fixed points/equilibria. As an example, in Fig. 3b black, gray and white circles indicate attracting, saddle and repelling equilibria, respectively. Below we list different kinds of the equilibria of Model 2. Recall that for the region $S_{0}$ the results obtained for the Model 1 are valid.

Fig. 3.

In (a): Partitioning of the trapping triangle S into the regions of no trade ($S_{0}$), unilateral trade ($S_{1}$ and $S_{2}$) and bilateral trade ($S_{3}$); In (b): Attracting, saddle and repelling fixed points of map Z are shown by black, gray and white circles, respectively; curves $\varOmega _{1}$ and $\varOmega _{2}$ are shown in red and blue, respectively. Here $a=b=c=1/3$, $\eta =0$, $E=5,$ $L=5.8,$ $\varepsilon =0.2$.

The map Z keeps always all CP equilibria (see (13)) and the border symmetric equilibrium $BS_{3}:(\lambda _{1},\lambda _{2})=(1/2,1/2)$. Instead, the interior symmetric equilibrium, $IS:(\lambda _{1},\lambda _{2})=(1/3,1/3)$ is a fixed point of Z as long as $IS\in S_{0},$ that is, if $\widetilde{\lambda }<1/3$. This condition corresponds to $\varepsilon <\varepsilon _{1}$, where

$$\begin{aligned} \varepsilon _{1}=\frac{cE(a-b\eta )}{b(cE+6b)}\ . \end{aligned}$$

(29)

As we shall see later, the equilibrium IS may disappear,¹³ or it could move to region $S_{3}.$ In the later case, we denote it as $IA_{3,b},$ where the index ‘b’ refers to the bilateral trade region.

On the borders $I_{b1}$ and $I_{b2}$, map Z can have also border asymmetric (BA) equilibria:

$$ BA_{1}:(\lambda _{1},\lambda _{2})=(p_{1},0),\ \ BA_{1}^{\prime \prime }:(\lambda _{1},\lambda _{2})=(p_{2},0),\ BA_{1}^{\prime }:(\lambda _{1},\lambda _{2})=(p_{3},0)\ , $$

$$ BA_{2}:(\lambda _{1},\lambda _{2})=(0,p_{1}),\ \ BA_{2}^{\prime \prime }:(\lambda _{1},\lambda _{2})=(0,p_{2}),\ BA_{2}^{\prime }:(\lambda _{1},\lambda _{2})=(0,p_{3})\ , $$

where $0<p_{1}<p_{2}<p_{3}<1$ are solved numerically (see Commendatore et al. (2017)). The map Z can have, besides the CP equilibria, at most three equilibria on each border $I_{bi},$ $i=1,2$. Note that for $\varepsilon =0$ it holds that $BA_{i}^{\prime \prime }=BS_{i}$ with $p_{2}=1/2$.

We notice that the border asymmetric equilibria $BA_{i},$ $i=1,2,$ appear by increasing L (via a ‘border transcritical bifurcation’ of the equilibrium $CP_{0}$) at

$$\begin{aligned} L=BT_{CP0}\ =\frac{6bE(a-b\eta )^{2}(3b+cE)}{cE\left( 4b+cE\right) \left( a-b\eta \right) ^{2}+\left( 2b+cE\right) ^{2}\left( b\varepsilon \right) ^{2}}, \end{aligned}$$

(30)

and the border asymmetric equilibria $BA_{i}^{\prime }$, $i=1,2,$ appear by increasing L (via a ‘border transcritical bifurcation’ of the fixed points $CP_{i}$) at

$$\begin{aligned} L=BT_{CP1,2}\ =\frac{6bE\left( a-b\eta \right) ^{2}(3b+cE)}{cE\left( 4b+cE\right) (a-b\eta )^{2}-4b^{2}\left( b\varepsilon \right) ^{2}}. \end{aligned}$$

(31)

Note finally that for $\varepsilon =0$ it holds $BT_{CP0}=BT_{CP1,2}=BT_{CP},$ where $BT_{CP}$ is defined in (20).

As we shall see below an important difference in the properties of the border asymmetric equilibria $BA_{i}$ and $BA_{i}^{\prime }$, $i=1,2$ compared to the previous model is that, depending on parameters, they become attracting.

On the border $I_{b3}$, besides the equilibrium $BS_{3}$, map Z can have four border asymmetric (BA) equilibria:

$$ BA_{3}:(\lambda _{1},\lambda _{2})=(p,1-p),\ BA_{3}^{\prime }:(\lambda _{1},\lambda _{2})=(1-p,p)\ , $$

$$ BA_{3,u}:(\lambda _{1},\lambda _{2})=(l,1-l),\ BA_{3,u}^{\prime }:(\lambda _{1},\lambda _{2})=(1-l,l)\ , $$

where p is given in (18), the index ‘u’ refers to the unilateral trade regions, and $\lambda =l$, $0<l<\widetilde{\lambda }$, is solved numerically (see Commendatore et al. (2017)).

Map Z can have also the following interior asymmetric (IA) equilibria (see Fig. 3b):

• $IA_{i},\ IA_{i}^{\prime },\ i=1,2,3,$ belonging to $S_{0}$ (see (21));

• $IA_{i,u},\ IA_{i,u}^{\prime },\ \ IA_{i,u}^{\prime \prime },$ belonging to the unilateral trade regions $S_{i}$, $i=1,2;$

• $IA_{3,b}^{\prime },$ $IA_{3,b}^{\prime \prime }$ belonging to the bilateral trade region $S_{3}$.

Concerning the properties of these equilibria, we start noticing that, by increasing L and for $\varepsilon <\varepsilon _{t}$, the three couples, $IA_{1}$-$IA_{2,u}^{\prime },$ $IA_{2}$-$IA_{1,u}^{\prime }$ and $IA_{3}$-$IA_{3,b}^{\prime },$ appear simultaneously (via a ‘fold border collision bifurcation’) at

$$\begin{aligned} L=BC_{IA}=\frac{3b^{2}\varepsilon \left( (4b-cE)(a-b\varepsilon -b\eta )+4b^{2}\varepsilon \right) -6b\left( cE+3b\right) (a-b\varepsilon -b\eta )^{2}}{c(a-b\varepsilon -b\eta )\left( 2b^{2}\varepsilon -(4b+cE)(a-b\varepsilon -b\eta )\right) }\ , \end{aligned}$$

(32)

where $\varepsilon _{t}$ corresponds to the point where the curves $L=BC_{IA}$ and $L=F_{IA}$ are tangent (see Fig. 4b).¹⁴

Moreover, the equilibria $IA_{i},$ $i=1,2,3,$ disappear merging with $IA_{i}^{\prime }$ (due to a ‘smooth fold bifurcation’) at $L=F_{IA}$ defined in (23). It can be shown that for the considered parameter values $F_{IA}-BC_{IA}<0,$ thus, the existence range of the fixed points $IA_{i}$ is not empty.

Note that for $\varepsilon _{t}<\varepsilon <\varepsilon _{1}$ the curve $L=BC_{IA}$ corresponds to the collision of the equilibria $IA_{i}^{\prime },$ $i=1,2,3,$ with the related borders. As $L=BC_{IA}$ is crossed by increasing L, their stability properties are preserved, but not their location as $IA_{1}^{\prime }$ moves to $S_{2}$, $IA_{2}^{\prime }$ to $S_{1}$ and $IA_{3}^{\prime }$ to $S_{3}$.¹⁵

It can be also shown that, by increasing L,  the interior fixed point $IA_{3,b}^{\prime \prime }$ (belonging to the median $I_{m3}$) appears at $L=BT_{CP0}$ given in (30) (due to a ‘border transcritical bifurcation’ of $CP_{0}$); the equilibrium $IA_{3}^{\prime }$ is born (due to a ‘border transcritical bifurcation’ of the border symmetric equilibrium $BS_{3}$ at $L=BT_{BS}$) for $\varepsilon <\varepsilon _{2}$. The other conditions related to the existence and/or stability of the equilibria mentioned above can be obtained numerically, as we discuss below.

To investigate the influence of decreasing trade cost $T_{12}$ on the dynamics of the map, we begin with $\varepsilon =0$, that corresponds to Model 1, and then we increase gradually the value of $\varepsilon$. Complexity of bifurcation sequences associated with equilibria in Model 2 is caused by multistability, when up to 8 attracting equilibria may coexist (as, e.g., in Fig. 3b), and each of them follows its own way to appear, disappear and interact with other equilibria.

Fig. 4.

(a) Bifurcation structure of the $(\varepsilon ,L)$-parameter plane for $0<\varepsilon <1$, $2<L<9$; (b) an enlargement of the window indicated in (a) with regions of different coexisting attracting fixed points. The other parameters are fixed as in (24) and (25).

In Fig. 4a, representing the $(\varepsilon ,L)$-parameter plane for $2<L<9,$ $0<\varepsilon <1$ and for the other parameters fixed as in (24), (25), we summarize the properties of the attracting equilibria. Figure 4b shows an enlargement of the rectangle indicated in Fig. 4a. In these figures the parameter regions associated with different coexisting attracting equilibria are colored differently, being separated by various bifurcation curves. In particular, we have drawn the bifurcation lines $L=F_{IA}$, $L=BT_{BS},$ $L=T_{IS}$ associated with Model 1, the curves $L=BT_{CP0},$ $L=BT_{CP1,2}$, $L=BC_{IA}$ defined in (30)–(32), and the straight vertical lines $\varepsilon =\varepsilon _{i},$ $i=1,2,3$, defined in (28), (29). The values $L=BT_{CP}$, $L=PF_{BS}$ valid for $\varepsilon =0$ are also marked on the vertical axis. Recall that the stability range $T_{IS}<L<Fl_{IS}$ of the equilibrium IS obtained for Model 1 is suitable for Model 2 for $\varepsilon <\varepsilon _{1}$; the curve $L=BT_{BS}$ is valid for $\varepsilon <\varepsilon _{2}$ and corresponds to the transverse border transcritical bifurcation of the equilibrium $BS_{3}$; the curve $L=F_{IA}$ (related to the ‘smooth fold bifurcation’ at which $IA_{i}=IA_{i}^{\prime },$ $i=1,2,3$) is valid for $0<\varepsilon <\varepsilon _{t}$, where $(\varepsilon ,L)=(\varepsilon _{t},F_{IA})$ correspond to the point where the curves $L=F_{IA}$ and $L=BC_{IA}$ are tangent.

In Fig. 4b the bifurcation curves separating the regions of qualitatively different dynamics, besides those mentioned above, are obtained numerically, in particular, the curve $L=F_{BA1,2}$ (related to a ‘fold bifurcation’ leading, by increasing L, to the disappearance of the couples of the border equilibria $BA_{i}$-$BA_{i}^{\prime \prime }$, $i=1,2$); and the curve $L=BT_{BA^{\prime }1,2}$ (associated to a so-called ‘transverse border transcritical bifurcation’ of the border equilibria $BA_{i}^{\prime },$ $i=1,2,$ leading, by increasing $\varepsilon$, to their stabilization and to the appearance of the saddle interior equilibrium $IA_{i,u}^{\prime }$). Accordingly, we have marked in the largest and more visible regions of Fig. 4b the associated attracting equilibria that coexist in those regions (for a description of the smaller regions of coexistence, as well as other bifurcation curves, we refer to Commendatore et al. (2017)).

Below, we present several examples for different values of L to illustrate the effects of lowering trade costs, determined by increasing $\varepsilon$, on the long-run properties of the equilibria and on the patterns of trade. Moreover, we also provide an economic interpretation of the results.

Fig. 5.

Attracting fixed points of map Z (Model 2) and their basins for $L=4.8$ and $\varepsilon =0.1$ in (a), $\varepsilon =0.14$ in (b), $\varepsilon =0.15$ in (c), $\varepsilon =0.3$ in (d) (see the black circles in Fig. 4b). The other parameters are fixed as in (24) and (25).

One of the simplest scenarios is illustrated in Fig. 5 where $L=4.8$ and $\varepsilon =0.1$ in (a), $\varepsilon =0.14$ in (b), $\varepsilon =0.15$ in (c) and $\varepsilon =0.3$ in (d) (the corresponding points in the parameters space are indicated in Fig. 4b by black circles). For $\varepsilon =0$ there are three coexisting attracting CP equilibria (see Fig. 2a). When it is close to 0, an increase of $\varepsilon$ does not change abruptly the qualitative properties of the system Z (see Fig. 5a).¹⁶ Its most relevant effects occur in the subregions of S related to unilateral trade, $S_{1}$ and $S_{2}$,¹⁷ the basin of attraction of the equilibrium $CP_{0}$ shrinks, whereas those of the equilibria $CP_{1}$ (in $S_{2}$) and $CP_{2}$ (in $S_{2}$) expand. This implies that when the initial distribution of entrepreneurs is sufficiently in favour of region 1 (in $S_{1}$) or 2 (in $S_{2}$), all the firms move in that region enjoying additional profits obtained by selling goods in the outside market (in region 2 or 1, respectively).

An abrupt change occurs when $\varepsilon$ crosses the curve $L=BT_{CP0}$ (associated to a ‘border transcritical bifurcation’ of the equilibrium $CP_{0}$) involving a loss of stability and the consequent disappearance of the basin of attraction of $CP_{0}$. This also leads to the appearance of the attracting border equilibria $BA_{i},$ $i=1,2$ and of the saddle interior equilibrium $IA_{3,b}^{\prime \prime }$ in the subregion of S related to bilateral trade, $S_{3}$, so that map Z has now four attractors, $CP_{1}$, $CP_{2}$, $BA_{1}$ and $BA_{2}$ (see Fig. 5b). Compared with the equilibrium $CP_{0}$, in the equilibria $BA_{i}$, $i=1,2$, trade costs are sufficiently low to allow for the location of some industry in region 1 (at $BA_{1}$) or in region 2 (at $BA_{2}$). Firms in region 1 (at $BA_{1}$) and 2 (at $BA_{2}$) are enjoying additional profits by selling goods in the outside market (in region 2 or 1, respectively). In region 3, the size of the local market is sufficiently large that a large share of firms still finds convenient to locate there. Finally, being on the borders, the equilibria $BA_{i}$, $i=1,2$ are obviously characterised by a unilateral trade pattern, even if along the transition path towards the equilibrium regions 1 and 2 may engage in bilateral trade for distributions of entrepreneurs positioned in $S_{3}$.¹⁸

Then, when the $\varepsilon$ crosses the curve $L=F_{BA1,2}$ (and a ‘fold bifurcation’ occurs at which $BA_{i}=BA_{i}^{\prime \prime }$) the equilibria $BA_{1}$ and $BA_{2}$ disappear, and the remaining attractors are the fixed point $CP_{1}$ and $CP_{2}$ (see Fig. 5c). Thus for $\varepsilon$ sufficiently large (for trade costs sufficiently low) all initial distributions lead to an equilibrium in which the industrial sector is agglomerated in region 1 (or 2). Bilateral trade between regions 1 and 2 is possible along the transition path, however, only unilateral trade occurs in the long-run.

For larger values of $\varepsilon$ the equilibria $CP_{1}$ and $CP_{2}$ continue to be the only attractors of map Z and the economic interpretation is the same (see Fig. 5d).¹⁹

Fig. 6.

Attracting fixed points of map Z (Model 2) and their basins for $L=4.9$ and $\varepsilon =0.1$ in (a), $\varepsilon =0.15$ in (b) (see the gray circles in Fig. 4b). The other parameters are fixed as in (24) and (25).

Let now set $L=4.9$ and consider the cases (a) $\varepsilon =0.1$ and (b) $\varepsilon =0.15$ (the corresponding points in the parameter space are indicated in Fig. 4b by grey circles). For $\varepsilon =0$ the attracting equilibrium IS coexists with three attracting CP equilibria (see Fig. 2b). Increasing $\varepsilon$ at first the curve $L=BT_{CP0}$ is crossed leading to the loss of stability of $CP_{0}$ and to the appearance of the attracting border equilibria $BA_{1}$ and $BA_{2}$. In Fig. 6a (where $\varepsilon =0.1$) these equilibria coexist with the attracting equilibria IS,  $CP_{1}$ and $CP_{2}$. In $S_{0}$ the results are qualitatively similar to those that apply when $\varepsilon =0$: IS is still characterised by full autarky. However, there are initial distributions located in $S_{1}$ and $S_{2}$ (corresponding to short-run equilibria), leading to this equilibrium, for which unilateral trade may occur.

By further increasing $\varepsilon$ the equilibria $BA_{1}$ and $BA_{2}$ disappear when the curve $L=F_{BA1,2}$ is crossed (due to a ‘fold bifurcation’). After, map Z has three attractors, IS,  $CP_{1}$ and $CP_{2}$ (see Fig. 6b where $\varepsilon =0.15$). Then, the equilibrium IS disappears when the curve $\varepsilon =\varepsilon _{1}$ is crossed (due to a ‘fold border collision bifurcation’),²⁰ so that the only attractors of map Z are the equilibria $CP_{1}$ and $CP_{2}$. When $CP_{1}$ and $CP_{2}$ are the only stable equilibria, the properties of the system and their economic interpretation are analogous to those corresponding to Fig. 5d.

Fig. 7.

Attracting fixed points of map Z (Model 2) and their basins for $L=4.92$ and $\varepsilon =0.025$ in (a), $\varepsilon =0.05$ in (b) (see the red circles in Fig. 4b). The other parameters are fixed as in (24) and (25). The insets show the related parts enlarged.

The change in the properties of the system observed when $L=4.92$ by increasing $\varepsilon$ is a bit more complicated. To illustrate this case, we consider the examples: (a) $\varepsilon =0.025$ and (b) $\varepsilon =0.05$ (the corresponding points in the parameter space are indicated in Fig. 4b by red circles). For $\varepsilon =0$ (see Fig. 2c) the coexisting attracting equilibria are IS and $IA_{i},$ $i=1,2,3.$ If $\varepsilon$ is increased, the equilibria $BA_{1}^{\prime }$ and $BA_{2}^{\prime }$ gain stability (due to a ‘transverse border transcritical bifurcation’) when the curve $L=BT_{BA^{\prime }1,2}$ is crossed. After this bifurcation, map Z has six attracting equilibria, IS, $IA_{i},$ $BA_{1}^{\prime }$ and $BA_{2}^{\prime }$ (see Fig. 7a where $\varepsilon =0.025$). Again, the most important changes occur in the regions related to unilateral trade $S_{1}$ and $S_{2}$, where the border equilibria $BA_{1}^{\prime }$ (in $S_{1}$) and $BA_{2}^{\prime }$ ($S_{2}$) are now attracting (the basins of attraction of $BA_{1}^{\prime }$ and $BA_{2}^{\prime }$ are colored in dark yellow and dark blue, respectively). Initial distributions that for $\varepsilon =0$ were in the basins of attraction of $IA_{2}$ and $IA_{1}$, for $\varepsilon =0.025$ belong to the basins of $BA_{1}^{\prime }$ and $BA_{2}^{\prime }$, respectively. Unilateral trade gives an incentive to entrepreneurs to locate in region 1 (for initial distributions in the basin of $BA_{1}^{\prime }$) or region 2 (for initial distributions in the basin of $BA_{2}^{\prime }$) because of the additional profits obtained by selling goods in the outside market in region 2 or region 1.

Then after a sequence of bifurcations (which includes a ‘fold border collision bifurcation’ of $IA_{i}$ occurring when the curve $L=BC_{IA}$ is crossed, and ‘transverse border transcritical bifurcations’ of $BA_{i}$ and $BA_{i}^{\prime \prime },$ $i=1,2$) the attracting equilibria are IS,  $BA_{i}^{\prime }$, $BA_{i}$ and $IA_{3,b}^{\prime \prime }$ (see Fig. 7b where $\varepsilon =0.05$). The most relevant effects of the increase in $\varepsilon$ is the appearance of the stable equilibrium $IA_{3,b}^{\prime \prime }$ in the region related to bilateral trade, $S_{3}$, and the disappearance of the interior asymmetric equilibria $IA_{i}$, $i=1,2,3$. Initial distributions that were leading previously to $IA_{1}$ or $IA_{2}$ are now attracted respectively by $BA_{2}^{\prime }$ or $BA_{1}^{\prime }$. Concerning trade patterns, it is interesting to notice that a large set of initial distributions characterised by full autarky may lead to a long-run equilibrium in which unilateral ($BA_{2}^{\prime }$ or $BA_{1}^{\prime }$) or bilateral ($IA_{3,b}^{\prime \prime }$) trade prevails. Moreover, transition paths characterised by a switch from a unilateral to a bilateral trade regime are also possible.²¹

Further increasing $\varepsilon$ leads to reverse pitchfork bifurcation of $IA_{3,b}^{\prime \prime }$ which loses stability merging with saddles $IS_{1,b}$ and $IS_{2,b}$, then the fixed points $CP_{1}$ and $CP_{2}$ are stabilized (due to a ‘border transcritical bifurcation’, when the curve $L=BT_{CP1,2}$ is crossed), and the properties of the system and their interpretation become qualitatively similar to those holding for the case shown in Fig. 6a.

Fig. 8.

Attracting fixed points of map Z (Model 2) and their basins for $L=5$ and $\varepsilon =0.1$ in (a), $\varepsilon =0.2$ in (b) (see the white circles in Fig. 4b). The other parameters are fixed as in (24) and (25).

Further examples are shown in Fig. 8 where $L=5$ and (a) $\varepsilon =0.1$ and (b) $\varepsilon =0.2$ (the corresponding points in the parameter space are indicated in Fig. 4b by white circles). For $\varepsilon =0$, IS is the only stable equilibrium (see Fig. 2d). By increasing $\varepsilon$ at first the curve $L=BT_{BA^{\prime }1,2}$ is crossed leading to the stabilization of the equilibria $BA_{1}^{\prime }$ and $BA_{2}^{\prime }$ (see Fig. 8a where $\varepsilon =0.1$). $BA_{1}^{\prime }$ and $BA_{2}^{\prime }$ belong to the regions of S related to unilateral trade, $S_{1}$ and $S_{2}$, respectively, and are characterised by a large share of firms located in region 1 or 2 obtaining additional profit by selling in the outside market in region 2 or 1 and by a small share of firms located in region 3, attracted by a sufficiently large local market.

For this example, it is interesting to notice that transition paths are possible starting from a bilateral trade regime in $S_{3}$ or from a unilateral trade regime in $S_{1}$ or $S_{2}$ ending to the equilibrium IS in $S_{0}$ in which full autarky prevails. This is favoured by a relative large proportion of immobile local demand sufficient to countervail the effect of trade liberalization.

Crossing the curve $L=BT_{CP1,2}$ leads to the disappearance of the equilibria $BA_{1}^{\prime }$ and $BA_{2}^{\prime }$ and the stabilization of the equilibria $CP_{1}$ and $CP_{2}$ (due to a ‘border transcritical bifurcation’). Then (due to a ‘border collision bifurcation’) at $\varepsilon =\varepsilon _{1}$ the fixed point IS disappears (see Fig. 8b where $\varepsilon =\varepsilon _{1}=0.2$) after which the only attractors of map Z are the fixed points $CP_{1}$ and $CP_{2}$ and the properties of the system and their interpretation become qualitatively similar to those holding for the case shown in Fig. 5d.

7 Long-Run Equilibria Properties in Model 3

The economy in Model 3 takes a specific ‘hub and spoke structure. Indeed, for the third set-up we assumed that trade costs between regions 1 and 2 are always sufficiently low to establish bilateral trade (for this we let $T_{12}<\frac{2(a-\eta b)}{2b+cE}$), while trade costs between regions 2 and 3 are always sufficiently high to impede trade (so that $T_{23}\ge \frac{a}{b}-\eta$ holds). We set $T_{12}=\tau$, $T_{13}=T-\psi$ and $T_{23}=T$, with $T=\frac{a}{b}-\eta$.

The related indirect utilities $V_{i}(\lambda _{1},\lambda _{2})=:V_{i},$ $i=1,2,3,$ of an entrepreneur in regions 1, 2 and 3, respectively, are defined as follows:

(33)

where

$$ \overline{\lambda }=\frac{2\left( a-\eta b-bT_{13}\right) }{cET_{13}}=\frac{2b\psi }{cE\left( \frac{a}{b}-\eta -\psi \right) }\ ,$$

$$ \overline{\varLambda }(\lambda _{2})=\overline{\lambda }-\lambda _{2}\frac{T_{13}-T_{12}}{T_{13}}= \overline{\lambda }-\lambda _{2}\frac{\frac{a}{b}-\eta -\psi -\tau }{\frac{a}{b}-\eta -\psi }\ , $$

and $V_{i}^{bil},$ $V_{i}^{bil,\; out},$ $V_{i}^{bil,\; in},$ $V_{i}^{bil,\; bil}$ for $i=1,2,3$ are defined in Commendatore et al. (2017).

In the simulations we fix $\tau =0.5<\left. \frac{2(a-\eta b)}{2b+cE}\right| _{(24)}=\frac{4}{7}\approx 0.571\ ,$ and vary the values of parameters L and $\psi$, where $0<\psi <\tau =0.5,$ keeping the other parameters fixed as in (24) and (25).

Let the straight lines $\lambda _{2}=1-\overline{\lambda }-\lambda _{1}$ and $\lambda _{1}=\overline{\varLambda }(\lambda _{2})$ separating the regions associated with different indirect utilities be denoted as $C^{1}$ and $C^{2},$ respectively. These lines can be written as

Note that the slope of $C^{2}$ in the $(\lambda _{1},\lambda _{2})$-phase plane is larger in modulus than the slope of $C^{1};$ the lines $C^{1}$ and $C^{2}$ intersect the trapping triangle S if $\psi <\left. \frac{a}{b}-\eta \right| _{(24)}=1\ \$(related to $\overline{\lambda }>0$) and $\psi <\left. \left( \frac{a}{b}-\eta \right) \frac{cE}{2b+cE}\right| _{(24)}=\frac{3}{7}\$ (related to $\overline{\lambda }<1$).

Fig. 9.

Partitioning of the trapping triangle S into the regions $S_{0}$ (no trade between regions 1 and 3), $S_{1}$ (one-way trade from region 3 to region 1), $S_{2}$ (one-way trade from region 1 to region 3) and $S_{3}$ (two-way trade between regions 1 and 3). Here $L=4.8,$ $\tau =0.5$ and $\psi =0.15$ in (a), $\psi =0.23$ in (b) and $\psi =0.3$ in (c). The other parameters are fixed as in (24) and (25).

Depending on the parameters the straight lines $C^{1}$ and $C^{2}$ may separate the trapping triangle S into at most four regions denoted $S_{i},$ $i=\overline{0,3},$ where region $S_{0}$ is related to no trade between regions 1 and 3, regions $S_{1},$ $S_{2}$ correspond to unilateral trade from region 3 to region 1, and from region 1 to region 3, respectively, and region $S_{3}$ is associated with bilateral trade between regions 1 and 3. In fact, there are five qualitatively different cases:

• (1) if $\overline{\lambda }=0,$ that holds for $\psi =0$, then $S=S_{0}$, i.e., the complete trapping triangle S is associated with no trade between the regions 1 and 3, that is, we are back to Model 2;

• (2) if $0<\overline{\lambda }\le 1-\lambda ^{*}$ where $\lambda ^{*}=\left. \frac{2b\psi }{cE\left( \frac{a}{b}-\eta -\psi -\tau \right) }\right| _{(24)}=\frac{2\psi }{E\left( 1-\psi -\tau \right) },$ then $S=\cup _{j=0}^{2}S_{j}$ (see Fig. 9a), that is, in S there are ‘no trade’ and ‘unilateral trade’ regions while bilateral trade is not possible; this holds for $0<\psi \le \psi _{1},$ where

  

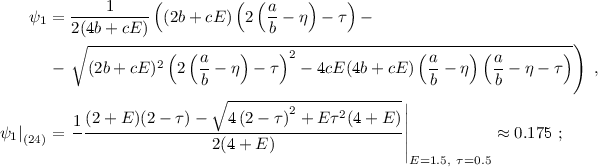
• (3) if $1-\lambda ^{*}<\overline{\lambda }<\frac{1}{2},$ then $S=\cup _{j=0}^{3}S_{j}$ (see Fig. 9b), that is, all four types of trade between regions 1 and 3 are possible; this occurs for $\psi _{1}<\psi <\psi _{2},$ where

  $$ \psi _{2}=\left. \frac{cE(a-b\eta )}{b(4b+cE)}\right| _{(24)}=\frac{3}{11}\approx 0.273\ ; $$

• (4) if $\frac{1}{2}\le \overline{\lambda }<1,$ then $S=\cup _{j=1}^{3}S_{j}$ (see Fig. 9c), that is, uni- and bilateral trade are possible, but there is no ‘no trade’ region; that holds for $\psi _{2}\le \psi <\psi _{3},$ where

  $$ \psi _{3}=\left. \frac{cE(a-b\eta )}{b(2b+cE)}\right| _{(24)}=\frac{3}{7}\approx 0.429\ ; $$

• (5) if $\overline{\lambda }\ge 1,$ that holds for $\psi _{3}\le \psi \le \tau ,$ then $S=S_{3}$.

Similar to Models 1 and 2, for Model 3 the borders $I_{bi}$, $i=1,2,3$ (see (12)) of the trapping triangle S are invariant lines of map Z.²² The border equilibria of Z are denoted $BA_{i}\in I_{bi},$ with additional upper index ‘$^{\prime }$’, or ‘$^{\prime \prime }$’ to distinguish between different equilibria belonging to the same border.

Besides the CP equilibria (see (13)) and BA equilibria, map Z can have also interior equilibria which we denote $IA_{i}\in S_{i}$.

Figure 10 summarizes the properties of the long-run equilibria. In Fig. 10a we present the bifurcation structure of the $(\psi ,L)$-parameter plane for $0<\psi <\tau =0.5,$ $2<L<9,$ and other parameters fixed as in (24) and (25). In this figure the regions of different coexisting attracting equilibria are separated by the curves $L=BT_{CP0}$, $L=BT_{CP1}$, $L=BT_{CP2}$ obtained numerically and related to border transcritical bifurcations of the equilibria $CP_{0},$ $CP_{1}$ and $CP_{2},$ respectively, as well as by the curve $L=F_{BA2}$ associated with a fold bifurcation of the border equilibria belonging to $I_{b2}$. Figure 10b shows an enlargement of Fig. 10a.

To study the influence of decreasing trade cost $T_{13}$, as a starting point we consider the bifurcation structure observed for $\psi =0,$ which is associated with Model 2 and corresponds to the cross-section at $\varepsilon =0.5$ of the $(\varepsilon ,L)$-parameter plane shown in Fig. 4a (recall that for Model 3 it holds that $T_{12}=\tau ,$ while for Model 2 $T_{12}=\frac{a}{b}-\eta -\varepsilon ,$ so $\varepsilon =\frac{a}{b}-\eta -\tau ;$ for the considered parameter values $\tau =0.5$ corresponds to $\varepsilon =0.5$). Below we comment several transformations of the basins of the attracting equilibria of map Z observed for fixed $L=4.8,$ $L=4.92,$ $L=5$ and increasing $\psi ,$ when various bifurcation curves are crossed.

Fig. 10.

(a) Bifurcation structure of the $(\psi ,L)$-parameter plane for $0<\psi <0.5$, $2<L<9,$ $\tau =0.5$; (b) an enlargement of the window indicated in (a) with regions of different coexisting attracting fixed points. The other parameters are fixed as in (24) and (25).

Let $L=4.8.$ For $\psi =0$ map Z has attracting equilibria $CP_{1}$ and $CP_{2}$ (see the parameter point $(\varepsilon ,L)=(0.5,4.8)$ in Fig. 4a, which belongs to the region denoted $CP_{1,2}$). For increasing $\psi$ these equilibria at first remain the only attractors of map Z: in Fig. 11a (where $\psi =0.15$) we show the basins of $CP_{1}$ and $CP_{2}$ separated by the closure of stable invariant sets of the saddle fixed points $IA_{0}\in S_{0}$ and $BA_{3}^{\prime \prime }\in I_{b3},$ and in Fig. 11b where $\psi =0.3$ the basins are separated by the closure of the stable invariant set of $BA_{3}^{\prime \prime }.$ What can be noticed from Figs. 11a and b is the progressive enlargement of the basin of attraction of $CP_{1}$, and the shrinking of that of $CP_{2}$, compared with the case $\psi =0$, as unilateral trade from 1 to 3 is allowed and firms in 1 could obtain additional profits by exporting goods in 3 exploiting their location. Indeed, in correspondence of $CP_{1}$ one-way trade from 1 to 2 and from 1 to 3 occurs; instead, in $CP_{2}$ only one way trade from 2 to 1 can take place. Interestingly, there are possible transition paths in which different trade patterns may occur, for example (looking at Fig. 11b) bilateral trade between 1 and 2 and 1 and 3 may occur for distributions of entrepreneurs in the partition $S_{3}$. However, at some point trade links are severed as all the industrial activity agglomerates in only one region.

Fig. 11.

Attracting fixed points of map Z (Model 3) and their basins for $L=4.8,$ $\tau =0.5$ and $\psi =0.15$ in (a), $\psi =0.3$ in (b), $\psi =0.47$ in (c), $\psi =0.5$ in (d). The other parameters are fixed as in (24) and (25).

A qualitative change is observed at $\psi \approx 0.469$ as the curve $L=F_{BA2}$ is crossed, see Fig. 10b (giving rise to a ‘fold bifurcation’) and a couple of border equilibria, attracting $BA_{2}$ and saddle $BA_{2}^{\prime \prime }$, appear. These are shown in Fig. 11c where basins of the attracting equilibria $CP_{1}$, $CP_{2}$ and $BA_{2}$ are plotted for $\psi =0.47$. Recall that for $\psi >\psi _{3}\approx 0.43$, it holds that $S=S_{3}$, that is, trade costs are sufficiently small that bilateral trade between 1 and 3 always occur for all distributions of entrepreneurs within S. The equilibrium $BA_{2}$ is quite interesting, since it is characterized by trade from 2 to 1 and from 3 to 1. Thus, initial distributions of entrepreneurs that largely favour region 3 lead to a long-run equilibrium where the hub region has no manufacturing sector and it is importing from the two spoke regions. By further increasing $\psi$ the curve $L=BT_{CP0}$ is crossed, and as a result the fixed point $BA_{2}$ disappears merging with the fixed point $CP_{0}$ that gains stability (due to a ‘border transcritical bifurcation’, see Fig. 11d where the basins of $CP_{1}$, $CP_{2}$ and $CP_{3}$ are shown for $\psi =0.5$). The economic interpretation is that when trade costs between 1 and 3 become close to that between 1 and 2, regions 2 and 3 become more symmetric and the basins of attraction of the CP equilibria $CP_{2}$ and $CP_{3}$ are similar: initial distributions of entrepreneurs that favour region 2 or region 3, that is one of the spoke regions, lead to $CP_{2}$ or $CP_{3}$, respectively. Notice also that the basin of attraction of $CP_{1}$ is much larger being region 1 the hub.

Fig. 12.

Attracting fixed points of map Z (Model 3) and their basins for $L=4.92,$ $\tau =0.5$ and $\psi =0.15$ in (a), $\psi =0.3$ in (b), $\psi =0.49$ in (c), $\psi =0.5$ in (d). The other parameters are fixed as in (24) and (25).

For $L=4.92$ the sequence of bifurcations at first is similar to the one described above: Starting from the attracting fixed points $CP_{1}$ and $CP_{2}$ coexisting for $\psi =0$ (the parameter point $(\varepsilon ,L)=(0.5,4.92)$ in Fig. 4a also belongs to the region $CP_{1,2},$ as in the previous example), by increasing $\psi$ these fixed points remain the only attractors (see Fig. 12a and b where $\psi =0.15$ and $\psi =0.3$, respectively). As before it is possible to observe a progressive change in the size of the basins of attraction of $CP_{1}$ (enlarging) and $CP_{2}$ (shrinking). By further increasing $\psi$ (after a ‘fold bifurcation’) a border attracting equilibrium $BA_{2}$ and a saddle equilibrium $BA_{2}^{\prime \prime }$ are born (see Fig. 12c where $\psi =0.49$). Comparing Figs. 11c and 12c, we see that, by increasing the immobile local demand L (intensifying the dispersion forces), $BA_{2}$ is characterised by a larger share of entrepreneurs located in region 2 (a smaller share located in region 3) and by a larger basin of attraction. Finally, by further increasing $\psi$ the fixed point $CP_{2}$ loses stability and the stable border equilibrium $BA_{2}^{\prime }$ is born (via a ‘border transcritical bifurcation’, see Fig. 12d where $\psi =0.5$). As before, by reducing trade costs between regions 1 and 3, regions 2 and 3 become more symmetric; differently from the previous case the larger immobile local demand allows for some entrepreneurs located in 2 (in $BA_{2}$) or in 3 ($BA_{2}^{\prime }$). Both $BA_{2}$ and $BA_{2}^{\prime }$ are characterised by one-way trade from the spokes to the hub.

When $L=5$, as for the previous cases, the attracting equilibria $CP_{1}$ and $CP_{2}$ coexist for $\psi =0$. By increasing $\psi$, after crossing the curve $L=BT_{CP2}$ (see Fig. 10b), the fixed point $CP_{2}$ loses stability and a border attracting equilibria $BA_{2}^{\prime }$ is born. Thus, as shown in Fig. 13a, where $\psi =0.48$, compared with the previous case (see Fig. 12b) the increase in L, allows for the location of some entrepreneurs in region 3 ($CP_{2}$ has lost stability in favour of $BA_{2}^{\prime }$). Further increasing $\psi$, leads (via a ‘fold bifurcation’) to a border attracting and a saddle equilibria $BA_{2}$ and $BA_{2}^{\prime \prime }$ (see Fig. 13b where $\psi =0.5$). Compared with the previous case, due to a larger L, this occurs for a lower value of $\psi$.

Fig. 13.

Attracting fixed points of map Z (Model 3) and their basins for $L=5,$ $\tau =0.5$ and $\psi =0.48$ in (a), $\psi =0.5$ in (b). The other parameters are fixed as in (24) and (25).

Fig. 14.

Attracting fixed points of map Z (Model 3) and their basins for $E=5,$ $L=4.8,$ $\tau =0.2$ and $\psi =0.4$ in (a), $\psi =0.55$ in (b), $\psi =0.62$ in (c), $\psi =0.75$ in (d), $\psi =0.779$ in (e), $\psi =0.8$ in (f). The other parameters are fixed as in (24) and (25).

To clarify better the importance of the size of immobile local demand (L) relative to the demand that could potentially shift (E), let us comment one more sequence of transformations of the basins observed for $E=5.$ We fix $\tau =0.2<\left. \frac{2(a-\eta b)}{2b+cE}\right| \approx 0.286,$ $L=4.8$ and will increase $\psi .$ As before, for $\psi =0$ map Z has two coexisting attracting equilibria $CP_{1}$ and $CP_{2}$. At first these equilibria remain the only attractors of Z (see Fig. 14a and 14b where $\psi =0.4$ and $\psi =0.55,$ respectively), the qualitative behaviour of the system and its economic interpretation are the same as before: compared with the case $\psi =0$, firms in region 1 (the hub) take advantage of the trade opening towards region 3 (one of the spokes), this leads to higher indirect utilities for the entrepreneurs located in 1 and to the progressive enlargement of the basin of attraction of $CP_{1}$ and the shrinking of that of $CP_{2}$. Then, by increasing $\psi$, an attracting and a saddle equilibria $BA_{1}$ and $BA_{1}^{\prime \prime }$ belonging to the border $I_{b1}$ appear (via a ‘fold bifurcation’, see Fig. 14c where $\psi =0.62$). The fixed point $BA_{1}$ is positioned in the partition $S_{1}$: the possibility of one-way trade from 3 to 1 allows for a long-run equilibrium where entrepreneurs are distributed between regions 1 and 3 and trade goes from 3 to 1 and from 1 to 2 (one-way trade to region 2 compensates for the stronger competition in the local market from firms located in 3, attracting some of the entrepreneurs to region 1).

If $\psi$ is further increased, this leads to the appearance of a border attracting equilibrium $BA_{3}\in I_{b3}$ (via a ‘border transcritical bifurcation’ of $CP_{2}$, see Fig. 14d where $\psi =0.75$), which mirrors $BA_{1}$. Indeed, reducing trade costs between 1 and 3 makes regions 2 and 3 more symmetric (while partition $S_{3}$ completely overlaps with S): In $BA_{3}$ (symmetrically with respect to $BA_{1}$) entrepreneurs are distributed between regions 1 and 2 and trade goes from 2 to 1 and from 1 to 3.

By further increasing $\psi$, at first the couple $BA_{1}$ - $BA_{1}^{\prime \prime }$ disappears (see Fig. 14e where $\psi =0.779$), and then the couple $BA_{3}$ - $BA_{3}^{\prime \prime }$ disappears (both via a ‘fold bifurcation). After these bifurcations the fixed point $CP_{1}$ is a unique attractor of Z (see Fig. 14f where $\psi =0.8$). Due to the relatively small ratio L / E the agglomeration forces are much stronger than in the previous examples, thus due to the central position, region 1 attracts all entrepreneurs, with the exception of the initial conditions in the basin of attraction of $BA_{3}$ in Fig. 14e or for all the initial conditions in the interior of S in Fig. 14f.

8 Final Remarks

In this paper we presented a basic analytic framework representing a small trade network whose main objectives were: (i) highlight how distance may affect the formation of trade links and their direction; (ii) examine the long-term consequences of trade integration on the emergence/disappearance of trade links and on the distribution of economic activities across space; (iii) explore how the spatial distribution of economic activities and the existence of trade links are interrelated. Given the large number of possible trade structures, we only considered three examples, representing three frequently realized patterns in the EU trade network (see Basile et al. (2016)) and we provided three respective models.

Some of our results are: For the first model, dealing with three autarkic regions, we found cases of coexistence of long-run equilibria which are absent in a two-region context (see Behrens (2004)); for the second model, when only region 1 and 2 trade with each other, we confirmed Behrens (2005) result that allowing for unilateral trade favours the region endowed with the higher initial distribution of entrepreneurs, however given the presence of a third region, not necessarily all entrepreneurs agglomerate in the region with the better initial endowment. Finally, for the third model, we found that, notwithstanding the different geography assumed, for some parameter combinations, the result of Ago et al. (2006) according to which centrality could translate into a locational disadvantage, is confirmed.

Appendix

For Model 3 the indirect utilities are defined as follows:

where

$$ \overline{\lambda }=\frac{2\left( a-\eta b-bT_{13}\right) }{cET_{13}}\ ,\ \overline{\varLambda }(\lambda _{2})=\overline{\lambda }-\frac{T_{13}-T_{12}}{ T_{13}}\lambda _{2}, $$

$$ V_{1}^{bil}=(\theta _{1}T_{12}+\psi _{1})T_{12}+\omega +\overline{C_{A}},\ \ \ V_{2}^{bil}=(\theta _{2}T_{12}+\psi _{2})T_{12}+\omega +\overline{C_{A}}, $$

$$\begin{aligned} \theta _{1}= & {} \frac{(b+cE)\left( 4\left[ c\lambda _{2}E(2b+c\lambda _{2}E)+2b^{2}\right] L+3\lambda _{2}E\varDelta _{1}\right) }{24\left[ 2b+cE(\lambda _{1}+\lambda _{2})\right] ^{2}},\ \\ \varDelta _{1}= & {} cE[cE(\lambda _{1}+\lambda _{2})(\lambda _{1}+2\lambda _{2})+4b(\lambda _{1}+3\lambda _{2})]+12b^{2}, \\ \psi _{1}= & {} -\frac{(a-\eta b)(b+cE)\left[ 3\lambda _{2}E(3b+2c\lambda _{2}E)+2bL\right] }{3\left[ 2b+cE(\lambda _{1}+\lambda _{2})\right] ^{2}},\ \\ \psi _{2}= & {} -\frac{(a-\eta b)(b+cE)\left[ 3\lambda _{1}E(3b+2c\lambda _{1}E)+2bL\right] }{3\left[ 2b+cE(\lambda _{1}+\lambda _{2})\right] ^{2}}, \\ \omega= & {} \frac{(a-\eta b)^{2}(b+cE)\left( 4bL+3E(\lambda _{1}+\lambda _{2})[3b+cE(\lambda _{1}+\lambda _{2})]\right) }{6b\left[ 2b+cE(\lambda _{1}+\lambda _{2})\right] ^{2}}, \\ \theta _{2}= & {} \frac{(b+cE)\left( 4\left[ c\lambda _{1}E(2b+c\lambda _{1}E)+2b^{2}\right] L+3\lambda _{1}E\varDelta _{2}\right) }{24\left[ 2b+cE(\lambda _{1}+\lambda _{2})\right] ^{2}},\ \\ \varDelta _{2}= & {} cE[cE(\lambda _{1}+\lambda _{2})(\lambda _{2}+2\lambda _{1})+4b(\lambda _{2}+3\lambda _{1})]+12b^{2}, \end{aligned}$$

$$ V_{3}^{bil}=V_{3}^{no}=\frac{(a-\eta )^{2}(b+cE)[3\lambda _{3}E(3b+c\lambda _{3}E)+2bL]}{6b(2b+c\lambda _{3}E)^{2}}+\overline{C_{A}}, $$

$$ V_{1}^{bil,\ out}=V_{1}^{bil}+\varPi _{13}^{out}, $$

$$ \varPi _{13}^{out}=(b+cE)\left[ \frac{a-\eta b-\left[ cE(1-\lambda _{1}-\lambda _{2})+2b\right] \frac{T_{13}}{2}}{2b+c(1-\lambda _{2})E}\right] ^{2}\left[ \frac{L}{3}+(1-\lambda _{1}-\lambda _{2})E\right] , $$

$$ V_{2}^{bil,\ out}=V_{2}^{bil}, $$

$$\begin{aligned} V_{3}^{bil,\ out}= & {} (f_{3}T_{13}+g_{3})T_{13}+h_{3}+\overline{C}_{A}, \\ f_{3}= & {} \frac{\lambda _{1}E(b+cE)\left( cE\left[ 12b(1-\lambda _{2})+2c\lambda _{1}L+3cE(1-\lambda _{1}-\lambda _{2})(1+2\lambda _{1}-\lambda _{2})\right] +12b^{2}\right) }{24\left[ 2b+cE(1-\lambda _{2}) \right] ^{2}}, \\ g_{3}= & {} \frac{3\lambda _{1}E(a-\eta b)(b+cE)(c\frac{L}{3}-b-c\lambda _{1}E) }{3\left[ 2b+cE(1-\lambda _{2})\right] ^{2}}, \\ h_{3}= & {} \frac{3(a-\eta b)^{2}(b+cE)\left( cE^{2}(1-\lambda _{2})^{2}+b[2 \frac{L}{3}+E(3-2\lambda _{1}-3\lambda _{2})]\right) }{6b\left[ 2b+cE(1-\lambda _{2})\right] ^{2}}, \end{aligned}$$

$$ V_{1}^{bil,\ in}=S_{1}^{bil,\ in}+\varPi _{11}^{bil,\ in}+\varPi _{12}^{bil,\ in}+ \overline{C_{A}}, $$

$$ S_{1}^{bil,\ in}=\frac{\lambda _{2}Q_{1}T_{12}+Q_{2}(1-\lambda _{1}-\lambda _{2})T_{13}+Q_{3}}{8(2b+cE)^{2}}(b+cE)E, $$

$$\begin{aligned} Q_{1}= & {} T_{12}\left( cE[cE(1-\lambda _{2})+4b]+4b^{2}\right) -8(b+cE)(a-\eta b)-2c^{2}E^{2}(1-\lambda _{1}-\lambda _{2})T_{13}, \\ Q_{2}= & {} [c^{2}E^{2}(\lambda _{1}+\lambda _{2})+4b(b+cE)]T_{13}-8(b+cE)(a-\eta b),\ Q_{3}=\frac{4(a-\eta b)^{2}(b+cE) }{b}, \end{aligned}$$

$$\begin{aligned} \varPi _{11}^{bil,\ in}= & {} (b+cE)\left[ \frac{a-\eta b+\left[ (1-\lambda _{1}-\lambda _{2})\frac{T_{13}}{2}+\frac{T_{12}}{2}\lambda _{2}\right] cE}{ 2b+cE}\right] ^{2}\left( \frac{L}{3}+\lambda _{1}E\right) , \\ \varPi _{12}^{bil,\ in}= & {} (b+cE)\left[ \frac{a-\eta b-\frac{T_{12}}{2} (2b+c\lambda _{2}E)}{2b+c(\lambda _{1}+\lambda _{2})E}\right] ^{2}\left( \frac{L}{3}+\lambda _{2}E\right) , \end{aligned}$$

$$ V_{2}^{bil,\ in}=S_{2}^{bil}+\varPi _{21}^{bil,\ in}+\varPi _{22}^{bil}+\overline{ C_{A}}, $$

$$ S_{2}^{bil}=\frac{\lambda _{1}\varOmega T_{12}+\varPsi }{8[2b+cE(\lambda _{1}+\lambda _{2})]^{2}}(b+cE)E, $$

$$\begin{aligned} \varOmega= & {} T_{12}\left\{ cE(\lambda _{1}+\lambda _{2})[cE\lambda _{2}+4b]+4b^{2}\right\} -8[b+cE(\lambda _{1}+\lambda _{2})](a-\eta b)\ , \\ \varPsi= & {} \frac{4(a-\eta b)^{2}(\lambda _{1}+\lambda _{2})[b+cE(\lambda _{1}+\lambda _{2})]}{b}, \end{aligned}$$

$$\begin{aligned} \varPi _{21}^{bil,\ in}= & {} (b+cE)\left[ \frac{a-\eta b+cE(1-\lambda _{1}-\lambda _{2})\frac{T_{13}}{2}-\frac{T_{12}}{2}[cE(1-\lambda _{2})+2b]}{ 2b+cE}\right] ^{2}\left( \frac{L}{3}+\lambda _{1}E\right) , \\ \varPi _{22}^{bil}= & {} (b+cE)\left[ \frac{a-\eta b+\frac{T_{12}}{2}c\lambda _{1}E }{2b+c(\lambda _{1}+\lambda _{2})E}\right] ^{2}\left( \frac{L}{3}+\lambda _{2}E\right) , \end{aligned}$$

$$ V_{3}^{bil,\ in}=V_{3}^{no}+\varPi _{31}^{bil,\ in}, $$

$$ \varPi _{31}^{bil,\ in}=(b+cE)\left[ \frac{a-\eta b+cE\lambda _{2}\frac{T_{12}}{ 2}-\frac{T_{13}}{2}[cE(\lambda _{1}+\lambda _{2})+2b]}{2b+cE}\right] ^{2}\left( \frac{L}{3}+\lambda _{1}E\right) , $$

$$ V_{1}^{bil,\ bil}=V_{1}^{bil,\ in}+\varPi _{13}^{out},\ \ V_{2}^{bil,\ bil}=V_{2}^{bil,\ in}\ ,\ \ V_{3}^{bil,\ bil}=V_{3}^{bil,\ out}+\varPi _{31}^{bil,\ in}. $$