1 Introduction

The capital budgeting problem is concerned with allocation of an organization’s capital to a suitable combination of projects (alternative projects) that can bring maximal profit to the organization [12]. In the literature we can find a variety of methods used in capital budgeting (see, e.g., [1, 2, 6, 22]). The main methods are: the net present value method (NPV), profitability index (PI), and internal rate of return (IRR). Based on the literature review we can state that the classical forms of these methods do not take into account the uncertainty and risk which may be inherent in the information used in them. This information includes future cash inflows, cash outflows and available investment capital, the required rate of return of the investment or cost of capital, and the duration of the project [21].

Traditionally, these investment parameters are assumed as a crisp value. As we know, the capital budgeting problem is accompanied by uncertainty and risk, which, in general, stem from the lack of access to certain data (imprecise data) [11, 21]. In practice, this involves, above all, the inability to predict the behavior of the market during the timeframe of the project’s execution, including weather conditions, the level of prices and costs, availability of resources, exchange rates, interest rates, behavior of competition, changes in the demand/supply level for a given product or service, and so on. Therefore several authors began to use fuzzy set theory to help solve the capital budgeting problem in a fuzzy environment. In the literature we can find another approach to capital budgeting, that is, fuzzy capital budgeting. Several authors studied fuzzy set theory and its application in capital budgeting [3, 5, 7, 11, 13, 14, 21]. Some authors indicated certain problems to solve the capital budgeting problem with fuzzy numbers [3, 5, 6, 21].

The notion of Ordered Fuzzy Numbers (OFN) was proposed by Kosiński, Prokopowicz and Ślȩżak, [20] to eliminate several drawbacks of classical convex fuzzy numbers (CFN) such as the loss of precision increasing with the number of performed operations and the fact that even linear equations cannot be solved in the set of fuzzy numbers. A new fuzzy number does not require any existence of a membership function and can be regarded as an extension of a parametric representation of a fuzzy number.

Ordered Fuzzy Numbers were first used as a tool for a decision- support system concerning financial project evaluation in the paper [18] and the research was continued in [8]. Their idea was based on the determination of the internal rate of return of an investment project in which all expenditures and income were imprecise and vague.

In this chapter we present a capital budgeting problem using OFNs. We continue the research started in the article by [9], which concerned the use of the net present value method to estimate the attractiveness of an investment opportunity. We now modify the method presented in the previous paper by transferring the defuzzification process to another stage of calculations and present the next discount methods- profitability index and internal rate of return-to make an evaluation of alternative investment projects more precise. We can see that the described methods dedicated to the investment project selection problem lay the foundations for a fuzzy decision-making system.

The chapter is organized as follows. In Sect. 8.2 we discuss the concept of fuzzy numbers and Ordered Fuzzy Numbers, which allow modeling using uncertain information. Section 8.3 is dedicated to the investment project’s estimation problem. It contains the main definitions of discounted values of cash flows, net present value method, profitability index, and internal rate of return. Section 8.4 presents the authors’ approach based on OFNs. In Sect. 8.5 we illustrate the issue on a computational example, demonstrating how the methods can be used for the capital budgeting problem. We utilize a MATLAB environment to demonstrate how the proposed methods can be applied to assess the profitability of an alternative investment project. Final remarks and conclusions are contained in Sect. 8.6.

2 Ordered Fuzzy Numbers

The introduction of the concepts of fuzzy sets and fuzzy numbers was propelled by the need to describe mathematically imprecise and ambiguous phenomena. The above concepts were described in the paper of Lotfi A. Zadeh [26] as a generalization of classical set theory. A fuzzy set A in a nonempty space X is a set of pairs \(A = \{(x,\mu _A(x));\;x\in X\},\) where \(\mu _A(x):X\rightarrow [0,1]\) is the membership function of a fuzzy set. This function assigns to each element \(x\in X\) its membership degree to a fuzzy set.

A fuzzy set, and hence its membership function, has two basic interpretations. It can be understood as a degree to which x possesses a certain feature, or as a probability with which a certain, and at this point not entirely known, value will assume a value x.

A triangular fuzzy number is denoted with three real numbers [a, b, c], where \(a< b < c\). Its membership function assumes the form:

$$\begin{aligned} \mu _A(x)= \left\{ \begin{array}{ll} 0 &{} \;\;\text{ if }\;\;\; x\le a;\\ \frac{x-a}{b-a} &{} \;\;\text{ if }\;\;\;\; a<x\le b;\\ \frac{c-x}{c-b} &{} \; \;\text{ if }\;\;\;b<x\le c;\\ 0 &{} \;\;\text{ if }\;\;\; x>c. \end{array}\right. \end{aligned}$$
(8.1)

If an expert generates a triangular fuzzy number as a result of assessing the distribution of possible values of a certain unknown quantity, it means that the expert deems the values below a, and above c, not possible; whereas the value b is possible with a degree of 1, and the remaining values are possible to a varying degree that decreases with their distance from b.

The notion of OFN, defined by Kosiński, Prokopowicz, and Ślȩzak, was introduced in order to eliminate postulated deficiencies of fuzzy numbers: the loss of precision increasing with the number of performed operations and the fact that even linear equations cannot be solved in the set of fuzzy numbers. The theorem formulated by Kosiński [17] concerning the universal approximation of any nonlinear and continuous defuzzification operator offers tools for the application of OFNs to fuzzy inference and modeling, including assessing the profitability of investment projects. Ordered Fuzzy Numbers give a precise and elegant framework for dealing with fuzzy objects (numbers) and many different methods of defuzzification.

Definition 1

An Ordered Fuzzy Number A is an ordered pair (f, g) of continuous functions \(f,g :[0,1]\rightarrow R\).

Graphically the curves of (f, g) and (g, f) do not differ. However, this pair of functions determines different OFNs; they vary in so-called orientation, which is denoted on diagrams by an arrow.

Let \(A = (f_A, g_A)\), \(B = (f_B, g_B)\), and \(C = (f_C, g_C)\) be OFNs. Sum \(C = A + B\), product \(C = A \cdot B\), and division \(C = A \div B\) are defined in the set of OFNs as follows.

$$\begin{aligned} f_C(x)=f_A(x) \star f_B(x) \;\; \text{ and } \;\; g_C(x)=g_A(x) \star g_B(x), \end{aligned}$$
(8.2)

where “\(\star \)”   denotes “\(+\)”, “\(\cdot \)”, and “\(\div \)”, respectively. Moreover, \(A\div B\) is only defined when \(f_B(x), g_B(x)\ne 0\) for each \( x\in [0,1].\) In the set of OFN, subtraction, exponentiation, and taking a root can also be defined in the usual fashion, for example:

$$\begin{aligned} (f,g)^n=(f^n,g^n). \end{aligned}$$
(8.3)

When considering the set of OFNs and the associated operations of addition and multiplication, we obtain a commutative ring with unity. By augmenting this with scalar multiplication, we obtain a linear space, that is, an algebra over real numbers. Moreover, this set constitutes a commutative Banach algebra with unity in the supremum norm in each of the factors \(C[0,1]\times C[0,1]\) that are the Banach space. By introducing an appropriate relation of partial order, we also obtain a lattice [8]. We say that an OFN \(A =(f, g)\) is

$$\begin{aligned} \text{ nonnegative } \text{ if } \;\; f(x)\ge 0 \text{ and } g(x)\ge 0 \text{ for } \text{ all } x \in [0,1]; \end{aligned}$$
(8.4)
$$\begin{aligned} \text{ positive } \text{ if } \;\; f(x)> 0 \text{ and } g(x)> 0 \text{ for } \text{ all } x \in [0,1]. \end{aligned}$$
(8.5)

Negative OFNs are defined in a similar way.

It is worthwhile to point out that the set of pairs of continuous functions, where one function is increasing and the other is decreasing, and, simultaneously, the increasing function always assumes values lower than the second function, is a subset of the set of OFNs, which represents the class of all convex fuzzy numbers with continuous membership functions [4, 10, 16, 23, 25].

Defuzzification is a process that converts a fuzzy set or a fuzzy number into a crisp value. Functionals, which map a fuzzy number to a real number, play a vital role in OFN applications.

Definition 2

Let A be an OFN and \(c\in R\). A mapping \(\phi \) from the space of all OFNs to the set of real numbers is called a defuzzification functional if it satisfies the following properties,

  1. 1.

    \(\phi (c,c) = c\, ,\)

  2. 2.

    \( \phi (A + (c,c)) = \phi (A) + c\, ,\)

  3. 3.

    \(\phi (c A) = c \phi (A)\, ,\)

  4. 4.

    \(\phi (A)\ge 0,\;\) if \(\;A\) is nonnegative (8.4)

where (c, c) is a pair of constant functions on the interval [0, 1] representing the constant c.

Therefore, a defuzzification functional must be homogeneous of order 1, as well as being restrictive, additive, and normalized. The model of constructing defuzzification functionals presented in [19] allows us to obtain a number of defuzzification functionals, whether linear or nonlinear. In this chapter we applied the nonlinear center of gravity defuzzification functional, defined by the following equations.

$$\begin{aligned} \phi _{COG}(f,g) =\left\{ \begin{array}{ll} \frac{\int \limits _{0}^{1}(f(s)+g(s))(f(s)-g(s)) ds}{2\int \limits _{0}^{1}(f(s)-g(s)) ds},&{}\text{ when } \;\int \limits _{0}^{1}(f(s)-g(s)) ds \ne 0\\ \frac{\int \limits _{0}^{1}f(s)ds}{\int \limits _{0}^{1}ds}\, ,&{}\text{ when } \;\int \limits _{0}^{1}(f(s)-g(s)) ds =0. \end{array} \right. \end{aligned}$$
(8.6)

3 Classic Capital Budgeting Methods

In economic practice, net present value is the most commonly used discount method. In essence, this method consists in assessing the present value of an investment project based on the forecasted streams of net cash flows, which are the measure of an investor’s future benefits. NPV is defined as a sum of net cash flows (NCFs) discounted separately for each year and executed over the entire calculation period, with a constant level of interest (discount) rate. This value expresses the updated (on the day of the assessment) value of benefits, which the undertaking in question can yield in the future. The general form of NPV can be expressed as:

$$\begin{aligned} NPV=\sum _{i=0}^n\frac{CF_i}{(1+r)^i}, \end{aligned}$$
(8.7)

where n is the number of years,

r is the market capitalization rate,

and \(CF_i\) is the cash flow in the ith year of investment.

NPV allows making an investment decision having analyzed cash flows, reduced by a specific outlay, and discounted by a weighted average cost of capital. Therefore, NPV allows the assessment of the economic value of an undertaking. The employment of a given method requires forecasting future cash flows, which involves forecasting several uncertain variables such as interest rate, prices of resources and services, and exchange rate. It affects the reliability and quality of forecasting future effects and outlay. NPV allows taking the time factor into account. If the net present value of an investment project is positive, the project will contribute to an increase in the value of the company and as a result the wealth of its owners. It is assumed that a given investment is profitable if the value of discounted cash flows during the completion of the investment is positive.

The profitability index (PI), also known as the profit investment ratio (PIR) or value investment ratio (VIR), is the ratio of payoff to investment of a proposed project. It is a useful tool for ranking projects because it allows us to quantify the amount of value created per unit of investment. The profitability index is a ratio of discounted cash inflows to the discounted cash outflows:

$$\begin{aligned} PI=\frac{\sum \limits _{i=0}^n\frac{CF_i^+}{(1+r)^i}}{\sum \limits _{i=0}^n\frac{CF_i^-}{(1+r)^i}}, \end{aligned}$$
(8.8)

where n is the number of years, r is the market capitalization rate, \(CF_i^+\) is the cash inflow in the ith year of investment, and \(CF_i^-\) is the cash outflow in the ith year of investment.

The PI helps in ranking investments and deciding the best investment that should be made. A PI greater than one indicates that the present value of future cash inflows from the investment is higher than the initial investment, thereby indicating that it will earn profits. A PI of less than one indicates loss from the investment, and a PI equal to one means that there are no profits. NPV and PI techniques in capital investment decisions are closely related to each other. The PI will be greater than 1 only when the NPV is positive. However, in the case of mutually exclusive proposals having different scales of investment, that is, where the initial investment in the alternative projects is not the same, a conflict in NPV and PI may occur.

Another capital budgeting method is the IRR. This method is described as the discount rate r that equates the present value of the expected future net cash inflows with its initial outlay so we have \(NPV = 0\). The IRR shows directly the rate of return on the examined projects. The project is cost-effective if its IRR is higher than the limit rate, which is the lowest rate of return acceptable to the investor. Generally, the higher the internal rate of return the investment project has the more profitable the project is [15]. Because of the general problem of finding the roots of the equation \(NPV = 0\), there are many numerical methods that can be used to estimate the IRR.

We use the method [24] consisting of several stages. First, we determine the value of the cash flows in subsequent years of an investment. Then, by successive approximations, we select two rates of return \(r_1\) and \(r_2\) satisfying the conditions:

  1. 1.

    \(NPV_1\) calculated for the rate \(r_1\) is close to zero and positive.

  2. 2.

    \(NPV_2\) calculated on the basis of the rate \(r_2\) is close to zero but negative.

On the basis of these values we calculate the IRR of the considered project. We apply the following formula for this purpose.

$$\begin{aligned} IRR=r_1+\frac{NPV_1(r_2-r_1)}{NPV_1-NPV_2}. \end{aligned}$$
(8.9)

In the presented method of calculating the IRR, the difference between \(r_1\) and \(r_2\) is particularly important. With the increase in difference between \(r_1\) and \(r_2\), calculation results become less and less accurate as compared to the actual IRR. In practice this difference should be less than one percentage point. In this case, the mistake in calculations of the IRR can be considered to be irrelevant.

4 Fuzzy Approach to the Discount Methods

The classic forms of NPV, PI, and IRR do not take uncertain data into account. When considering the fuzzy environment of an investment project, modifying discount methods to take into account uncertain data becomes necessary. This allows us to take into consideration information uncertainty and decreases the risk of making a mistake in assessing the profitability of an investment project.

For the problem of defining a generalization of the above-mentioned discount methods to OFNs, we assume that the capitalization rate R, cash flows CF, cash inflows \(CF^+_i\), and cash outflows \(CF^-_i\) are Ordered Fuzzy Numbers. The discounted cash flows in the ith year of investment are calculated as follows,

$$\begin{aligned} \frac{CF_i}{((1,1)+R)^i}, \end{aligned}$$
(8.10)

where (1, 1) stands for a pair of constant functions that assume a value of one, and \(+\) and \(\div \) signify addition and division in a set of OFNs defined through the Eq. 8.2. Exponentiation is performed according to the formula 8.3. Therefore, we have the formula for ordered fuzzy net present value:

$$\begin{aligned} OFNPV=\sum _{i=0}^n\frac{CF_i}{((1,1)+R)^i}. \end{aligned}$$
(8.11)

And for modified profitability index:

$$\begin{aligned} OFPI=\frac{\sum \limits _{i=0}^n\frac{CF_i^+}{((1,1)+R)^i}}{\sum \limits _{i=0}^n\frac{CF_i^-}{((1,1)+R)^i}}. \end{aligned}$$
(8.12)

Our modified method of calculating the internal rate of return requires selection of two ordered fuzzy rates of return \(R_1\) and \(R_2\) satisfying the following conditions.

  1. 1.

    \(OFNPV_1\) calculated for the rate \(R_1\) is close to ordered fuzzy zero (which means the pair of constant functions (0, 0)) and positive (see (8.5)).

  2. 2.

    \(OFNPV_2\) calculated for the rate \(R_2\) is close to ordered fuzzy zero and negative.

On the basis of these values we calculate the ordered fuzzy internal rate of return of the considered project. We use the following formula for this aim,

$$\begin{aligned} OFIRR=R_1+\frac{OFNPV_1(R_2-R_1)}{OFNPV_1-OFNPV_2}. \end{aligned}$$
(8.13)

Before presenting the results of the project evaluation to the investor, the selected defuzzification method should be applied in order to obtain real values:

$$ NPV=\phi _{COG}(OFNPV),\;\;\;\;\;\; PI=\phi _{COG}(OFPI) $$
$$ \text{ and }\;\;\; IRR=\phi _{COG}(OFIRR). $$

5 Computational Example of the Investment Project

In this section we present an example of a capital budgeting problem using three methods based on OFNs. These methods are: ordered fuzzy net present value method (OFNPV), ordered fuzzy profitability index (OFPI), and ordered fuzzy internal rate of return (OFIRR). We consider an example of potential alternatives of investment project execution: project one \(P_1\) and project two \(P_2\). Investment decisions are made under the conditions of uncertainty and risk, inasmuch as it is impossible to prepare an accurate description of economic and financial conditions for the functioning of the considered projects in the future. The use of OFNs allows us to limit the effects of uncertainty and risk. In order to define the fuzzy conditions of the execution of the investment project, the decision-making process involves an expert who has appropriate knowledge and experience in planning and executing similar projects.

A major problem related to the use of OFNs was the requirement for the experts to give an opinion on individual elements of these alternatives of investment projects in the form of OFNs, that is, pairs of functions. We propose that the expert describe project parameters by means of triangular fuzzy numbers, which will be subsequently converted into OFNs.

We assume that the considered projects are planned for the periods of 7 and 5 years, respectively. The remaining project parameters remain uncertain, therefore they are determined by the expert in the form of triangular fuzzy numbers. The triangular fuzzy capitalization rate assumes the form of \(R = [0.04;0.06;0.07]\). This means that according to the expert the capitalization rate of below \(4\% \) and above \(7\% \) is not possible, whereas the value of \(6\% \) is the most probable one, and other values are probable to a different degree: the higher they are, the closer they are to \(6\% \). In a similar way, the expert determines the fuzzy values of cash inflows and outflows in subsequent years for project \(P_1\) and project \(P_2\), respectively, in Tables 8.1 and 8.4. In order to simplify the analysis, the data are expressed in thousands of arbitrary monetary units (a.m.u.).

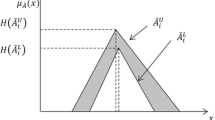
To a triangular fuzzy number \(A = [a,b,c]\) has a corresponding OFN:

$$\begin{aligned} A_{OFN}=((b-a)x+a,(b-c)x+c), \end{aligned}$$
(8.14)

which is the ordered pair of linear functions (Fig. 8.1).

By applying the formula 8.14 we define OFNs corresponding to the values determined by the expert. For instance, the capitalization rate expressed by OFNs assumes the form: \(R_{OFN} = (0.02x + 0.04;-0.01x + 0.07)\). Then we discount cash inflows and outflows using the formula 8.10. Obviously, discounted cash flows in the ith year of investment are obtained by adding discounted cash inflows and outflows in the ith year of an investment.

Subsequently, based on the formulas presented in the previous point we calculate the indexes OFNPV, OFPI, and OFIRR. Finally, these values undergo defuzzification using the functional 8.6. Thus we obtain crisp values, which can be presented to the investor. Calculations for the considered investment projects were performed using the MATLAB computer program.

Let us consider the alternative investment project \(P_1\). Table 8.1 presents the cash inflows and outflows of the project using triangular fuzzy numbers defined by the expert engaged in the decision process.

Table 8.1 Input data for the investment \(P_1\) using triangular fuzzy numbers
Full size table
Table 8.2 Cash inflows and discounted cash inflows for \(P_1\) with the use of OFNs
Full size table
Table 8.3 Selected rates of return for the project \(P_1\)
Full size table
Table 8.4 Input data for the investment project 2 using triangular fuzzy numbers
Full size table
Fig. 8.1
figure 1

The pair of linear functions corresponding to the triangular fuzzy number \(A = [a,b,c]\). The arrow denotes the order of functions, the so-called OFN orientation

Full size image

Table 8.2 presents the cash inflows for the first project expressed in OFNs. The cash outflows for this project and the cash inflows and outflows for the second project were calculated in an analogous way.

First we calculated the value of OFNPV and OFPI of the project. After defuzzification, the net present value for project \(P_1\) is equal to 47536 a.m.u., which means that the projected earnings generated by the proposed investment exceed the anticipated costs. The profitability index is equal to 1.0962, which further confirms the positive evaluation of the project.

In order to calculate OFIRR for the first project we selected by successive approximations of two rates of return \(R_1\) and \(R_2\) for which ordered fuzzy net present values are close to ordered fuzzy zero and positive (\(R_1\)) or negative (\(R_2\)), respectively (Table 8.3). The internal rate of return for this project is equal to \(8.21\%\).

Let us consider the alternative investment project \(P_2\). Table 8.4 presents the cash inflows and outflows of the project using triangular fuzzy numbers.

The NPV for the project \(P_2\) is equal to 44397 a.m.u. so the project would be estimated to be a valuable venture. The PI is equal to 1.0987, which further validates the positive evaluation of the project. The internal rate of return for the second project calculated on the data presented in Table 8.5 is equal to \(9.78\%\).

Table 8.5 Selected rates of return for the project \(P_2\)
Full size table

In Table 8.6 we present the results of calculation of the modified discount methods for considered projects \(P_1\) and \(P_2\). We compared the obtained values of the proposed new methods to aid the decision maker in choosing the best investment project. First we determined the NPV for each project; then we established the profitability index for each investment project, and finally the internal rates of return. According to the NPV analysis alone, project \(P_1\) is the most appropriate choice for the decision maker. The profitability indexes for project \(P_1\) and project \(P_2\) vary slightly and they are greater than 1, which confirms the profitability of both projects. According to the IRR analysis alone, project \(P_2\) is the most appropriate choice for the decision maker. The NPV and IRR analysis for these two projects give us conflicting results. This is due to the timing of the cash flows for each project as well as the size difference between the two projects. By the NPV rule the decision maker should choose project P1, so it can be executed. The convention is to use the NPV rule when the two methods are inconsistent. It better reflects the primary goal: to improve the financial wealth of the company.

Table 8.6 Summarized results of proposed discount methods for the projects
Full size table

6 Summary

The capital budgeting problem with Ordered Fuzzy Numbers corresponds to the project selection problem. We modified the method presented in our previous paper by transferring the defuzzification process to another stage of calculations and we presented the next discount methods, the profitability index and internal rate of return, to make an evaluation of alternative investment projects more precise. Tools of that kind can be perceived as a decision-support system based on OFNs. We presented the example of alternative investment project selection using new discount methods. The presented methods may be used to represent imprecise information, among others about cash flows and capitalization rate. They offer a clear simultaneous representation of several pieces of information. In addition, well-defined arithmetic operations on OFNs make it easy to perform even complex calculations connected, for example, with a long period of investment. Moreover, owing to the elimination of issues related to using classical fuzzy numbers such as increasing fuzziness over subsequent operations, impossibility to solve equations, or high computational complexity, the OFN model may prove to be good tool for economic analysis. It allows modeling the uncertainty associated with financial data and constructing a full decision-support system in the future.