Skip to main content
SpringerLink
Log in

Geometric Measures of Quantum Correlations with Bures and Hellinger Distances

  • Chapter
  • First Online:
Lectures on General Quantum Correlations and their Applications

Part of the book series: Quantum Science and Technology ((QST))

Abstract

This chapter contains a survey of the geometric approach to quantum correlations. We focus mainly on the geometric measures of quantum correlations based on the Bures and quantum Hellinger distances.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 119.00
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 159.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info
Hardcover Book
USD 159.99
Price excludes VAT (USA)
  • Durable hardcover edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Notes

  1. 1.

    We recall that \(\chi ( \{ \rho _{B|i} , \eta _i\})\) gives an upper bound on the classical mutual information between \( \{ \eta _i\}\) and the outcome probabilities when performing a measurement to discriminate the states \(\rho _{B|i}\).

  2. 2.

    By using the concavity of the entropy S, one can show that the maximum is achieved for projectors \( \Pi _{i}^{A}\) of rank one.

  3. 3.

    Let us recall that a POVM associated to a (generalized) measurement is a family \(\{ M_i\}\) of operators \(M_i \ge 0\) such that \(\sum _i M_i = 1\). The probability of outcome i is \(\eta _i = {\text {tr}}\,M_i \rho \) and the corresponding post-measurement conditional state is \(\eta _i^{-1} A_i \rho A_i^\dagger \), where the Kraus operators \(A_i\) satisfy \(A_i^\dagger A_{i} = M_i\).

  4. 4.

    This can be justified by using the identity (5) and a theorem due to Petz, which gives a necessary and sufficient condition on \(\rho \) such that \(I_{A: B} ( \rho )= I_{A: B} ( \mathcal{M}_{A} \otimes 1 ( \rho ) )\) for a fixed quantum operation \(\mathcal{M}_{A}\) on \(A\) (saturation of the data processing inequality) [39, 71]. We refer the reader to [81] for more detail. Note that the proof originally given in Ref. [66] is not correct.

  5. 5.

    A linear map \(\mathcal{M}: \mathcal{B}( \mathcal{H}) \rightarrow \mathcal{B}( \mathcal{H}' )\) is positive if it transforms a non-negative operator \(\rho \ge 0\) into a non-negative operator \(\mathcal{M}( \rho ) \ge 0\). It is CP if the map

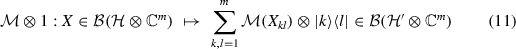
    figure a

    is positive for any integer \(m \ge 1\).

  6. 6.

    Recall that an entanglement monotone E on pure states is a function which does not increase under Local Operations and Classical Communication (LOCC), i.e., \(E ( | \Phi \rangle ) \le E ( | \Psi \rangle )\) whenever \(| \Psi \rangle \) can be transformed into \(| \Phi \rangle \) by a LOCC operation [44, 64].

  7. 7.

    Actually, \(D_A^{\,\mathrm ent}\) obeys axiom (i) by definition. Axiom (ii) follows from the unitary invariance of the entropy S. Axiom (iv) is a consequence of (7) and the entanglement monotonicity of the entanglement of formation. The proof of axiom (iii) is given e.g. in [81].

  8. 8.

    This follows from the facts that a function \(D_A\) on \(\mathcal{E}( \mathcal{H}_{AB})\) satisfying (iii) is maximal on pure states if \(n_A\le n_B\) [88] and that any pure state can be obtained from a maximally entangled pure state via a LOCC.

  9. 9.

    Furthermore, \(E^\mathrm{G}_{AB}\) is convex if d is the Bures or the Hellinger distance since then \(d^2\) is jointly convex, see Sect. 4.3. Convexity is sometimes considered as another axiom for entanglement measures, apart from entanglement monotonicity and vanishing for separable states and only for those states.

  10. 10.

    Actually, \(D_A^\mathrm{G}\) clearly obeys axiom (i), irrespective of the choice of the distance. It satisfies axiom (ii) for any unitary-invariant distance, thus in particular for contractive distances. One shows that it fulfills axiom (iii) by using the contractivity of d and the fact that the set of \(A\)-classical states \(\mathcal{C}_A\) is invariant under quantum operations acting on \(B\), as is evident from (9).

  11. 11.

    This identity follows from the relations \(I_{A: B} (\rho )= S( \rho || \rho _A\otimes \rho _B)\) and \(S( \rho || \sigma _A\otimes \sigma _B)- S( \rho || \rho _A\otimes \rho _B) = S( \rho _A|| \sigma _A) +S( \rho _B|| \sigma _B) \ge 0\). It means in particular that the “closest” product state to \(\rho \) for the relative entropy is the product \(\rho _A\otimes \rho _B\) of the marginals of \(\rho \) [59].

  12. 12.

    As we shall see below, \(\rho \) may have an infinite family of closest \(A\)-classical states.

  13. 13.

    See [76] for a discussion on the choice of the non-degenerate spectrum \(e^{\mathrm{{i}}\Lambda }\).

  14. 14.

    The word “local” refers here to the geometry on \(\mathcal{E}( \mathcal{H}_{AB})\) and should not be confused with the usual notion of locality in quantum mechanics.

  15. 15.

    This is a consequence of the following observations [36]: (a) any \(H \in \mathcal{B}( {\mathbb {C}}^2)_\mathrm{sa}\) with spectrum \(\{ \lambda _-, \lambda _+\}\) has the form \((\lambda _+-\lambda _-) \sigma _{\vec {u}}/2+ (\lambda _++\lambda -)/2\), where \(\sigma _{\vec {u}}= \sum _{m=1}^3 u_m \sigma _m\), \({\vec {u}}\) is a unit vector in \({\mathbb {R}}^3\), and \(\sigma _1\), \(\sigma _2\), and \(\sigma _3\) are the three Pauli matrices; (b) as noted in the proof of Proposition 4, the limit in the r.h.s. of (32) is equal to \(g_\rho (- \mathrm{{i}}[ H_A \otimes 1 , \rho ], -\mathrm{{i}}[ H_A \otimes 1, \rho ])\) where \(g_\rho \) is a scalar product. Hence changing the spectrum \(\Lambda \) from \(\{ 0, \pi \}\) to \(\{ \lambda _-, \lambda _+\}\) amounts to multiply \(D_A^\mathrm{SR}\) by the constant factor \([( \lambda _{+} - \lambda _-)/\pi ]^2\).

  16. 16.

    The justification by Lieb and Ruskai [52] of the strong subadditivity of the von Neumann entropy is based on this important theorem.

  17. 17.

    More precisely, the error \(\Delta t = \langle (t_\mathrm{est} - t )^2\rangle ^{1/2}\) in the parameter estimation is always larger or equal to \((\Delta t)_\mathrm{{best}}\) and equality is reached asymptotically as \(N \rightarrow \infty \) by using the maximum-likelihood estimator and an optimal measurement.

  18. 18.

    Actually, if a Riemannian distance d with metric g is such that \(d^2(\rho ,\sigma )\) is jointly convex, then \(g_\rho ( \sum _i p_i O_i, \sum _i p_i O_i ) \le \sum _i p_i g_{\rho _i} ( O_i, O_i)\) for any \(O_i \in \mathcal{{B}} (\mathcal{{H}} )_\mathrm{s.a.}^{0} \) and any \(\rho = \sum p_i \rho _i\). In view of their expressions (61) and (63) in terms of \(g_\mathrm{Bu}\) and \(g_\mathrm{He}\), this implies that the Fisher and skew informations are convex in \(\rho \).

  19. 19.

    This follows from (59) and, for the last bound, from (64) and the concavity of \(\rho \mapsto \langle ( \Delta H )^2 \rangle _\rho \).

  20. 20.

    Here, the contractivity of the classical metrics refers to Markov mappings \( \mathbf{{p}}\mapsto \mathcal{M}^\mathrm{clas}\mathbf{{p}}\) on \(\mathcal{E}_\mathrm{clas}\), with stochastic matrices \(\mathcal{M}^\mathrm{clas}\) having non-negative elements \(\mathcal{M}^\mathrm{clas}_{ij}\) such that \(\sum _i \mathcal{M}^\mathrm{clas}_{ij} =1\) for any \(j=1,\ldots , n\).

  21. 21.

    The first equality is a consequence of (71) and the identity \(S(\rho + t \dot{\rho } ) = S ( \rho ) - S ( \rho + t \dot{\rho } || \rho )- t {\text {tr}}( \dot{\rho } \ln \rho )\), and the second expression follows from \(\ln ( \rho + t \dot{\rho }) = \ln \rho + t \int _0^\infty \mathrm{{d}}u \, ( \rho + u)^{-1} \dot{\rho } ( \rho + u)^{-1} + \mathcal{O}( t^2)\).

  22. 22.

    This follows from the contractivity of \(S_{\alpha ,z} ( \rho || \sigma )\) applied to a measurement with rank-one projectors \(\{ | k \rangle \langle k | \}\) and the fact that \(S_\alpha ^\mathrm{clas} ( \mathbf{{p}}|| \mathbf{{q}}) \ge 0\) with equality if and only if \( \mathbf{{p}}= \mathbf{{q}}\). The property is actually true for any \(\alpha =z >0\) (see e.g. [81]) and, probably, for other values of \((\alpha ,z)\).

  23. 23.

    This family forms a \((n^2+n-2)\) real-parameter submanifold of \(\mathcal{E}( \mathcal{H}_{AB})\).

  24. 24.

    This measurement bears several other names: it is referred to as the “pretty good measurement” in [38] and is sometimes also called “square-root measurement” [29]. For a pure state ensemble \(\{ | \psi _i \rangle , \eta _i\}\), it is given by \(\{ M_i^\mathrm{lsm} = | \widetilde{\mu }_i \rangle \langle \widetilde{\mu }_i | \}\) and the vectors \(| \widetilde{\mu }_i \rangle = \sqrt{\eta _i} (\sum _j \eta _j | \psi _j \rangle \langle \psi _j |)^{-\frac{1}{2}} | \psi _i \rangle \) are such that they minimize the sum of the square norms \(\Vert | \widetilde{\mu }_i \rangle - \sqrt{\eta _i} | \psi _i \rangle \Vert ^2\) under the constraint that \(\{ M_i^\mathrm{lsm}\}\) is a POVM, i.e., \(\sum _i | \widetilde{\mu }_i \rangle \langle \widetilde{\mu }_i | = 1\) [43].

  25. 25.

    Note that the entropic discord can also be interpreted in terms of state distinguishability, but for states of subsystem \(B\). Actually, the measure of classical correlations \(J_{B|A}(\rho )\) is the maximum over all orthonormal bases \(\{ | \alpha _i \rangle \}\) of the Holevo quantity \(\chi (\{ \rho _{B| i}, \eta _i\} )\) (see (4) and the footnote after this equation). The latter is related to the problem of decoding a message encoded in the post-measurement states \(\rho _{{AB}| i}\) when one has access to subsystem \(B\) only.

  26. 26.

    In particular, if the states \(\rho _i = U^{i-1} \rho _1 (U^{i-1})^\dagger \) are related between themselves through conjugations by powers of a single unitary operator U satisfying \(U^m=\pm 1\), one can show that the least square measurement is optimal [9, 10, 23, 29].

  27. 27.

    We remark that by exploiting (81) and (110), this second bound is equivalent precisely to the lower bound in (127).

  28. 28.

    This inequality follows from the definitions of \(D_\mathrm{He}^\mathrm{R}\) and \(D_\mathrm{Bu}^\mathrm{R}\) and from the trace inequality \(F ( \rho , U_A\otimes 1 \,\rho \,U_A^\dagger \otimes 1) = \Vert \sqrt{\rho }\, U_A\otimes 1 \,\sqrt{\rho }\Vert _1^2 \le {\text {tr}}( \sqrt{\rho } \, U_A\otimes 1 \,\sqrt{\rho }\, U_A^\dagger \otimes 1 )\). It is saturated for pure states (see [78] for more detail).

References

  1. B. Aaronson, R.L. Franco, G. Adesso, Comparative investigation of the freezing phenomena for quantum correlations under nondissipative decoherence. Phys. Rev. A 88, 012120 (2013)

    Article  ADS  Google Scholar 

  2. T. Abad, V. Karimipour, L. Memarzadeh, Power of quantum channels for creating quantum correlations. Phys. Rev. A 86, 062316 (2012)

    Article  ADS  Google Scholar 

  3. M. Ali, A.R.P. Rau, G. Alber, Quantum discord for two-qubit \(X\) states. Phys. Rev. A 81, 042105 (2010)

    Article  ADS  Google Scholar 

  4. H. Araki, A remark on Bures distance function for normal states. Publ. RIMS Kyoto Univ. 6, 477–482 (1970)

    Article  MathSciNet  MATH  Google Scholar 

  5. K.M.R. Audenaert, N. Datta, \(\alpha \)-\(z\)-relative Rényi entropies. J. Math. Phys. 56, 022202 (2015)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  6. K.M.R. Audenaert, J. Calsamiglia, R. Muñoz-Tapia, E. Bagan, L.I. Masanes, A. Acin, F. Verstraete, Discriminating States: The Quantum Chernoff Bound. Phys. Rev. Lett. 98, 160501 (2007)

    Article  ADS  Google Scholar 

  7. R. Balian, The entropy-based quantum metric. Entropy 2014 16(7), 3878–3888 (2014)

    MathSciNet  MATH  Google Scholar 

  8. R. Balian, Y. Alhassid, H. Reinhardt, Dissipation in many-body systems: a geometric approach based on information theory. Phys. Rep. 131, 1 (1986)

    Article  ADS  MathSciNet  Google Scholar 

  9. M. Ban, K. Kurokawa, R. Momose, O. Hirota, Optimum measurements for discrimination among symmetric quantum states and parameter estimation. Int. J. Theor. Phys. 36, 1269–1288 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  10. S.M. Barnett, Minimum error discrimination between multiply symmetric states. Phys. Rev. A 64, 030303 (2001)

    Article  ADS  Google Scholar 

  11. H. Barnum, E. Knill, Reversing quantum dynamics with near-optimal quantum and classical fidelity. J. Math. Phys. 43, 2097–2106 (2002)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  12. C.H. Bennett, H.J. Bernstein, S. Popescu, B. Schumacher, Concentrating partial entanglement by local operations. Phys. Rev. A 53, 2046 (1996)

    Article  ADS  Google Scholar 

  13. C.H. Bennett, D.P. DiVincenzo, J.A. Smolin, W.K. Wootters, Mixed-state entanglement and quantum error correction. Phys. Rev. A 54, 3824 (1996)

    Article  ADS  MathSciNet  Google Scholar 

  14. T. Benoist, V. Jaks̆ić, Y. Pautrat, C.-A. Pillet, On entropy production of repeated quantum measurements I. General theory, arXiv:1607.00162 [math-ph]

  15. J.A. Bergou, U. Herzog, M. Hillery, Discrimination of quantum states, in Quantum State Estimation, vol. 649, Lecture Notes in Physics, ed. by M. Paris, J. Rehacek (Springer, Berlin, 2004), pp. 417–465

    Chapter  Google Scholar 

  16. R. Bhatia, Matrix Analysis (Springer, Berlin, 1991)

    MATH  Google Scholar 

  17. S.L. Braunstein, C.M. Caves, Statistical distance and the geometry of quantum states. Phys. Rev. Lett 72, 3439–3443 (1994)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  18. T.R. Bromley, M. Cianciaruso, R. Lo Franco, G. Adesso, Unifying approach to the quantification of bipartite correlations by Bures distance. J. Phys. A: Math. Theor. 47, 405302 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  19. D. Bures, An extension of Kakutani’s theorem on infinite product measures to the tensor product of semifinite \( w^{\ast } \)-algebras. Trans. Am. Math. Soc. 135, 199–212 (1969)

    MathSciNet  MATH  Google Scholar 

  20. D. Cavalcanti, L. Aolita, S. Boixo, K. Modi, M. Piani, A. Winter, Operational interpretations of quantum discord. Phys. Rev. A 83, 032324 (2011)

    Article  ADS  MATH  Google Scholar 

  21. N.N. Cencov, Statistical Decision Rules and Optimal Interferences, vol. 53, Translations of Mathematical Monographs (American Mathematical Society, Providence, 1982)

    Google Scholar 

  22. L. Chang, S. Luo, Remedying the local ancilla problem with geometric discord. Phys. Rev. A 87, 062303 (2013)

    Article  ADS  Google Scholar 

  23. C.-L. Chou, L.Y. Hsu, Minimal-error discrimination between symmetric mixed quantum states. Phys. Rev. A 68, 042305 (2003)

    Article  ADS  Google Scholar 

  24. F. Ciccarello, T. Tufarelli, V. Giovannetti, Towards computability of trace distance discord. New J. Phys. 16, 013038 (2014)

    Article  ADS  Google Scholar 

  25. B. Dakić, V. Vedral, C. Brukner, Necessary and sufficient condition for nonzero quantum discord. Phys. Rev. Lett. 105, 190502 (2010)

    Article  ADS  MATH  Google Scholar 

  26. A. Datta, S.T. Flammia, C.M. Caves, Entanglement and the power of one qubit. Phys. Rev. A 72, 042316 (2005)

    Article  ADS  Google Scholar 

  27. A. Datta, A. Shaji, C.M. Caves, Quantum discord and the power of one qubit. Phys. Rev. Lett. 100, 050502 (2008)

    Article  ADS  Google Scholar 

  28. Y.C. Eldar, von Neumann measurement is optimal for detecting linearly independent mixed quantum states. Phys. Rev. A 68, 052303 (2003)

    Article  ADS  MathSciNet  Google Scholar 

  29. Y.C. Eldar, G.D. Forney Jr., On quantum detection and the square-root measurement. IEEE Trans. Inf. Theory 47, 858–872 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  30. B.M. Escher, R.L. de Matos Filho, L. Davidovish, General framework for estimating the ultimate precision limit in noisy quantum-enhanced metrology. Nat. Phys. 7, 406–411 (2011)

    Google Scholar 

  31. R.L. Frank, E.H. Lieb, Monotonicity of a relative Rényi entropy. J. Math. Phys. 54, 122201 (2013)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  32. S. Gharibian, Quantifying nonclassicality with local unitary operations. Phys. Rev. A 86, 042106 (2012)

    Article  ADS  Google Scholar 

  33. S.M. Giampaolo, F. Illuminati, Characterization of separability and entanglement in (\(2 \times D\))- and (\(3\times D\))-dimensional systems by single-qubit and single-qutrit unitary transformations. Phys. Rev. A 76, 042301 (2007)

    Article  ADS  Google Scholar 

  34. S.M. Giampaolo, A. Streltsov, W. Roga, D. Bruß, F. Illuminati, Quantifying nonclassicality: global impact of local unitary evolutions. Phys. Rev. A 87, 012313 (2013)

    Article  ADS  Google Scholar 

  35. D. Girolami, G. Adesso, Quantum discord for general two-qubit states: analytical progress. Phys. Rev. A 83, 052108 (2011)

    Article  ADS  Google Scholar 

  36. D. Girolami, T. Tufarelli, G. Adesso, Characterizing nonclassical correlations via local quantum uncertainty. Phys. Rev. Lett. 110, 240402 (2013)

    Article  ADS  Google Scholar 

  37. D. Girolami, A.M. Souza, V. Giovannetti, T. Tufarelli, J.G. Filgueiras, R.S. Sarthour, D.O. Soares-Pinto, I.S. Oliveira, G. Adesso, Quantum discord determines the interferometric power of quantum states. Phys. Rev. Lett. 112, 210401 (2014)

    Article  ADS  Google Scholar 

  38. P. Hausladen, W.K. Wootters, A “pretty good” measurement for distinguishing quantum states. J. Mod. Opt. 41, 2385–2390 (1994)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  39. P. Hayden, R. Jozsa, D. Petz, A. Winter, Structure of states which satisfy strong subadditivity of quantum entropy with equality. Commun. Math. Phys. 246, 359–374 (2004)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  40. C.W. Helstrom, Quantum Detection and Estimation Theory (Academic Press, New York, 1976)

    MATH  Google Scholar 

  41. L. Henderson, V. Vedral, Classical, quantum and total correlations. J. Phys. A: Math. Gen. 34, 6899–6905 (2001)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  42. A.S. Holevo, On quasiequivalence of locally normal states. Theor. Math. Phys. 13(2), 1071–1082 (1972)

    Article  MathSciNet  MATH  Google Scholar 

  43. A.S. Holevo, On asymptotically optimal hypothesis testing in quantum statistics. Theory Probab. Appl. 23, 411–415 (1979)

    Article  MATH  Google Scholar 

  44. R. Horodecki, P. Horodecki, M. Horodecki, K. Horodecki, Quantum entanglement. Rev. Mod. Phys. 81, 865–942 (2009)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  45. Y. Huang, Quantum discord for two-qubit \(X\) states: analytical formula with very small worst-case error. Phys. Rev. A 88, 014302 (2013)

    Article  ADS  Google Scholar 

  46. Y. Huang, Computing quantum discord is NP-complete. New J. Phys. 16, 033027 (2014)

    Article  ADS  MathSciNet  Google Scholar 

  47. M. Hübner, Explicit computation of the Bures distance for density matrices. Phys. Lett. A 163, 239–242 (1992)

    Article  ADS  MathSciNet  Google Scholar 

  48. P. Hyllus, W. Laskowski, R. Krischek, C. Schwemmer, W. Wieczorek, H. Weinfurter, L. Pezzé, A. Smerzi, Fisher information and multiparticle entanglement. Phys. Rev. A 85, 022321 (2012)

    Article  ADS  Google Scholar 

  49. V. Jaks̆ić, C.-A. Pillet, Entropic Functionals in Quantum Statistical Mechanics, in Proceedings of XVIIth International Congress of Mathematical Physics (Aalborg 2012) (World Scientific, Singapore, 2013), 336–343

    Google Scholar 

  50. R. Jozsa, Fidelity for mixed quantum states. J. Mod. Opt. 41, 2315–2323 (1994)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  51. E.H. Lieb, Convex trace functions and the Wigner-Yanase-Dyson conjecture. Adv. Math. 11, 267–288 (1973)

    Article  MathSciNet  MATH  Google Scholar 

  52. E.H. Lieb, M.B. Ruskai, Proof of the strong subadditivity of quantum-mechanical entropy. J. Math. Phys. 14, 1938–1941 (1973)

    Article  ADS  MathSciNet  Google Scholar 

  53. S. Luo, Wigner-Yanase skew information and uncertainty relations. Phys. Rev. Lett. 91, 180403 (2003)

    Article  ADS  Google Scholar 

  54. S. Luo, Quantum discord for two-qubit systems. Phys. Rev. A 77, 042303 (2008)

    Article  ADS  Google Scholar 

  55. S. Luo, S. Fu, Geometric measure of quantum discord. Phys. Rev. A 82, 034302 (2010)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  56. V. Madhok, A. Datta, Interpreting quantum discord through quantum state merging. Phys. Rev. A 83, 032323 (2011)

    Article  ADS  Google Scholar 

  57. P. Marian, T.A. Marian, Hellinger distance as a measure of gaussian discord. J. Phys. A: Math. Theor. 48, 115301 (2015)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  58. J.A. Miszczak, Z. Puchala, P. Horodecki, A. Uhlmann, K. \(\dot{\rm Z}\)yczkowski, Sub- and super-fidelity as bounds for quantum fidelity. Quantum Inf. Comput. 9(1–2), 0103–0130 (2009)

    Google Scholar 

  59. K. Modi, T. Parerek, W. Son, V. Vedral, M. Williamson, Unified view of quantum and classical correlations. Phys. Rev. Lett. 104, 080501 (2010)

    Article  ADS  MathSciNet  Google Scholar 

  60. K. Modi, A. Brodutch, H. Cable, T. Paterek, V. Vedral, The classical-quantum boundary for correlations: discord and related measures. Rev. Mod. Phys. 84, 1655–1707 (2012)

    Article  ADS  Google Scholar 

  61. A. Monras, G. Adesso, S.M. Giampaolo, G. Gualdi, G.B. Davies, F. Illuminati, Entanglement quantification by local unitary operations. Phys. Rev. A 84, 012301 (2011)

    Article  ADS  Google Scholar 

  62. M. Müller-Lennert, F. Dupuis, O. Szehr, S. Fehr, M. Tomamichel, On quantum Rényi entropies: a new generalization and some properties. J. Math. Phys. 54, 122203 (2013)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  63. T. Nakano, M. Piani, G. Adesso, Negativity of quantumness and its interpretations. Phys. Rev. A 88, 012117 (2013)

    Article  ADS  Google Scholar 

  64. N.A. Nielsen, I.L. Chuang, Quantum Computation and Information (Cambridge University Press, Cambridge, 2000)

    MATH  Google Scholar 

  65. M. Nussbaum, A. Szkola, The Chernoff lower bound for symmetric quantum hypothesis testing, vol. 37, The Annals of Statistics (Institute of Mathematical Statistics, 2009), pp. 1040–1057

    Google Scholar 

  66. H. Ollivier, W.H. Zurek, Quantum discord: a measure of the quantumness of correlations. Phys. Rev. Lett. 88, 017901 (2001)

    Article  ADS  MATH  Google Scholar 

  67. M. Ozawa, Entanglement measures and the Hilbert-Schmidt distance. Phys. Lett. A 268, 158–160 (2000)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  68. F.M. Paula, T.R. de Oliveira, M.S. Sarandy, Geometric quantum discord through the Schatten 1-norm. Phys. Rev. A 87, 064101 (2013)

    Article  ADS  Google Scholar 

  69. D. Pérez-Garcia, M.M. Wolf, D. Petz, M.B. Ruskai, Contractivity of positive and trace-preserving maps under \(L^p\)-norms. J. Math. Phys. 47, 083506 (2006)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  70. D. Petz, Monotone metrics on matrix spaces. Lin. Alg. Appl. 244, 81–96 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  71. D. Petz, Monotonicity of quantum relative entropy revisited. Rev. Math. Phys. 15, 79–91 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  72. L. Pezzé, A. Smerzi, Entanglement, nonlinear dynamics, and the Heisenberg limit. Phys. Rev. Lett. 102, 100401 (2009)

    Google Scholar 

  73. M. Piani, Problem with geometric discord. Phys. Rev. A 86, 034101 (2012)

    Article  ADS  Google Scholar 

  74. M. Piani, S. Gharibian, G. Adesso, J. Calsamiglia, P. Horodecki, A. Winter, All nonclassical correlations can be activated into distillable entanglement. Phys. Rev. Lett. 106, 220403 (2011)

    Article  ADS  Google Scholar 

  75. M. Piani, V. Narasimhachar, J. Calsamiglia, Quantumness of correlations, quantumness of ensembles and quantum data hiding. New J. Phys. 16, 113001 (2014)

    Article  ADS  Google Scholar 

  76. W. Roga, S.M. Giampaolo, F. Illuminati, Discord of response. J. Phys A: Math. Theor. 47, 365301 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  77. W. Roga, D. Buono, F. Illuminati, Device-independent quantum reading and noise-assisted quantum transmitters. New J. Phys. 17, 013031 (2015)

    Article  ADS  Google Scholar 

  78. W. Roga, D. Spehner, F. Illuminati, Geometric measures of quantum correlations: characterization, quantification, and comparison by distances and operations. J. Phys. A: Math. Theor. 49, 235301 (2016)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  79. M.B. Ruskai, Beyond strong subadditivity: improved bounds on the contraction of the generalized relative entropy. Rev. Math. Phys. 6(5a), 1147–1161 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  80. H.-J. Sommers, K. \(\dot{\rm Z}\)yczkowski, Bures volume of the set of mixed quantum states. J. Phys. A: Math. Gen. 36, 10083–10100 (2003)

    Google Scholar 

  81. D. Spehner, Quantum correlations and distinguishability of quantum states. J. Math. Phys. 55, 075211 (2014)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  82. D. Spehner, M. Orszag, Geometric quantum discord with Bures distance. New J. Phys. 15, 103001 (2013)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  83. D. Spehner, M. Orszag, Geometric quantum discord with Bures distance: the qubit case. J. Phys. A: Math. Theor. 47, 035302 (2014)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  84. W.F. Stinespring, Positive functions on \( C^*\)-algebras. Proc. Am. Soc. 6, 211–216 (1955)

    MathSciNet  MATH  Google Scholar 

  85. A. Streltsov, H. Kampermann, D. Bruß, Linking a distance measure of entanglement to its convex roof. New J. Phys. 12, 123004 (2010)

    Article  ADS  Google Scholar 

  86. A. Streltsov, H. Kampermann, D. Bruß, Linking quantum discord to entanglement in a measurement. Phys. Rev. Lett. 106, 160401 (2011)

    Article  ADS  Google Scholar 

  87. A. Streltsov, H. Kampermann, D. Bruß, Behavior of quantum correlations under local noise. Phys. Rev. Lett. 107, 170502 (2011)

    Article  ADS  Google Scholar 

  88. A. Streltsov, G. Adesso, M. Piani, D. Bruß, Are general quantum correlations monogamous? Phys. Rev. Lett. 109, 050503 (2012)

    Article  ADS  Google Scholar 

  89. G. Toth, Multipartite entanglement and high-precision metrology. Phys. Rev. A 85, 022322 (2012)

    Article  ADS  Google Scholar 

  90. G. Tóth, D. Petz, Extremal properties of the variance and the quantum Fisher information. Phys. Rev. A 87, 032324 (2013)

    Article  ADS  Google Scholar 

  91. A. Uhlmann, Endlich-dimensionale Dichtematrizen II. Wiss. Z. Karl-Marx-Univ. Leipzig, Math.-Nat R. 22, 139–177 (1973)

    Google Scholar 

  92. A. Uhlmann, The “transition probability” in the state space of a \(\ast \)-algebra. Rep. Math. Phys. 9, 273–279 (1976)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  93. A. Uhlmann, Parallel transport and “quantum holonomy” along density operators. Rep. Math. Phys. 24, 229–240 (1986)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  94. V. Vedral, M.B. Plenio, Entanglement measures and purifications procedures. Phys. Rev. A 57, 1619–1633 (1998)

    Article  ADS  Google Scholar 

  95. V. Vedral, M.B. Plenio, M.A. Rippin, P.L. Knight, Quantifying entanglement. Phys. Rev. Lett. 78, 2275–2279 (1997)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  96. T.C. Wei, P.M. Goldbart, Geometric measure of entanglement and applications to bipartite and multipartite quantum states. Phys. Rev. A 68, 042307 (2003)

    Article  ADS  Google Scholar 

  97. E.P. Wigner, M.M. Yanase, Information contents of distributions. Proc. Natl. Acad. Sci. U.S.A. 49, 910–918 (1963)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  98. M.M. Wilde, A. Winter, D. Yang, Strong converse for the classical capacity of entanglement-breaking and Hadamard channels via a sandwiched Renyi relative entropy. Commun. Math. Phys. 331, 593–622 (2014)

    Article  ADS  MATH  Google Scholar 

  99. M.M. Wolf, Quantum Channels and Operations Guided Tour (2002). http://www-m5.ma.tum.de/foswiki/pub/M5/Allgemeines/MichaelWolf/QChannelLecture.pdf

Download references

Acknowledgements

We acknowledge support from the French ANR project No. ANR-13-JS01-0005-01, the EU FP7 Cooperation STREP Projects iQIT No. 270843 and EQuaM No. 323714, the Italian Minister of Scientific Research (MIUR) national PRIN programme, and the Chilean Fondecyt project No. 1140994.

Author information

Authors and Affiliations

  1. Université Grenoble Alpes, Institut Fourier, 38000, Grenoble, France

    D. Spehner

  2. CNRS, Laboratoire de Physique et Modélisation des Milieux Condensés, 38000, Grenoble, France

    D. Spehner

  3. Dipartimento di Ingegneria Industriale, Università degli Studi di Salerno, Via Giovanni Paolo II 132, 84084, Fisciano (SA), Italy

    F. Illuminati

  4. INFN, Sezione di Napoli, Gruppo collegato di Salerno, 84084, Fisciano (SA), Italy

    F. Illuminati

  5. Pontificia Universidad Católica, Instituto de Física, Casilla 306, Santiago 22, Chile

    M. Orszag

  6. Department of Physics, University of Strathclydeb, John Anderson Building, 107 Rottenrow, Glasgow, G4 0NG, UK

    W. Roga

Authors
  1. D. Spehner
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. F. Illuminati
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. Orszag
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. W. Roga
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to D. Spehner .

Editor information

Editors and Affiliations

  1. São Paulo State University, São Paulo, Brazil

    Felipe Fernandes Fanchini

  2. São Carlos Institute of Physics, University of São Paulo, São Paulo, Brazil

    Diogo de Oliveira Soares Pinto

  3. School of Mathematical Sciences, University of Nottingham, Nottingham, United Kingdom

    Gerardo Adesso

Rights and permissions

Reprints and permissions

Copyright information

© 2017 Springer International Publishing AG

About this chapter

Cite this chapter

Spehner, D., Illuminati, F., Orszag, M., Roga, W. (2017). Geometric Measures of Quantum Correlations with Bures and Hellinger Distances. In: Fanchini, F., Soares Pinto, D., Adesso, G. (eds) Lectures on General Quantum Correlations and their Applications. Quantum Science and Technology. Springer, Cham. https://doi.org/10.1007/978-3-319-53412-1_6

Download citation

Publish with us

Policies and ethics

Search

Navigation