The Impact of Cointegration on Commodity Spread Options

Abstract

In this work we explore the implications of cointegration in a system of commodity prices on the premiums of options written on various spreads on the futures prices of these commodities. We employ a parsimonious, yet comprehensive model for cointegration in a system of commodity prices. The model has an exponential affine structure and is flexible enough to allow for an arbitrary number of cointegration relationships. We conduct an extensive simulation study on pricing spread options. We argue that cointegration creates an upward sloping term structure of correlation, that in turn lowers the volatility of spreads and consequently the price of options on them.

1 Introduction

A distinctive feature of commodity markets is the existence of long-run equilibrium relationships that exist between the levels of various commodity prices, such as the one between the price of crude oil and the price of heating oil. These long-run equilibrium relations can be captured in economic models by so-called cointegration relations.

In this work we employ the continuous time model of cointegrated commodity prices developed by the authors in Farkas et al. [6] in order to conduct a simulation study for assessing the impact of cointegration on spread options. In our model, commodity prices are non-stationary and several cointegration relations are allowed amongst them, capturing long-run equilibrium relationships. Cointegration (Engle and Granger [5]) is the property of two or more non-stationary time series of having at least one linear combination that is stationary.

There is a vast literature on modeling the price of a single commodity as a non-stationary process (see Back and Prokopczuk [1] for a comprehensive recent review). For example, Schwartz and Smith [13] assume the log price of a commodity to be the sum of two latent factors: the long-term equilibrium level, modeled as a geometric Brownian motion, and a short-term deviation from the equilibrium, modeled as a zero mean Ornstein–Uhlenbeck (OU) process. More recently, Paschke and Prokopczuk [11] propose to model these deviations as a more general CARMA process and Cortazar and Naranjo [3] generalize the Schwartz and Smith [13] model in a multi-factor framework.

However, the literature on modeling a system of commodity prices is still quite scarce. Two fairly recent models are proposed in Cortazar et al. [4] and Paschke and Prokopczuk [10], both of which account for cointegration by incorporating common and commodity-specific factors into their modeling framework. Amongst the common factors, only one is assumed non-stationary. Although they explicitly take into account cointegration between prices, the cointegrated systems generated by these two models are not covering the whole range of possible number of cointegration relations, but allow for none or for exactly $n-1$ relations to exist between the n prices. In Farkas et al. [6] we propose an easy-to-use, yet comprehensive, model for a system of cointegrated commodity prices that retains the exponential affine structure of previous approaches and allows, in the same time, for an arbitrary number of cointegration relationships.

The rest of the work is organized as follows. In Sect. 2 we briefly describe the model proposed in Farkas et al. [6] and point out some qualitative aspects regarding the dynamics of the system. Section 3 is devoted to an extensive simulation study focused on computing spread options prices and on assessing the impact of cointegration on pricing spread options. Section 4 is reserved for concluding remarks.

2 Outline of the Model

Before proceeding to the simulation study, in this section we present for the sake of completeness, a short description of the model developed in Farkas et al. [6].

Consider n commodities with spot prices $\mathbf {S}(t)=(S_1(t),\ldots ,S_n(t))^\top$.

First it is assumed that the spot log-prices $\mathbf {X}(t) = \log \mathbf {S}(t)$ can be decomposed into three components:

$$\begin{aligned} \mathbf {X}(t)=\mathbf {Y}(t)+\mathbf {\varepsilon }(t)+\mathbf {\phi }(t), \end{aligned}$$

(1)

where $\mathbf {Y}$(t) signifies the long-run levels, $\mathbf {\varepsilon }(t)$ is an n-dimensional stationary process capturing short-term deviations, and $\mathbf {\phi }(t)=\mathbf {\chi }_1\cos (2\pi t)+\mathbf {\chi }_2\sin (2\pi t)$ controls for seasonal effects with $\mathbf {\chi }_1$ and $\mathbf {\chi }_2$ being n-dimensional vectors of constants.

The notion of cointegration (Engle and Granger [5], Johansen [7], Phillips [12]) refers to the property of two or more non-stationary time series of having a linear combination that is stationary. For example, if $X_1(t)$ and $X_2(t)$ are two non-stationary processes, one says that they are cointegrated if there is a linear combination of them, $X_1(t)-\alpha X_2(t)$, that is stationary for some positive real $\alpha$. Intuitively, cointegration occurs when two or more non-stationary variables are linked in a long-run equilibrium relationship from which they might depart only temporarily.

Regarding cointegration in the model, we stress that n cointegration relationships are implicitly assumed by (1): the n seasonally adjusted spot log-prices $\mathbf {X}(t)-\mathbf {\phi }(t)$ are cointegrated with their corresponding long-run levels, $\mathbf {Y}(t)$, since the linear combination $\mathbf {X}(t)-\mathbf {\phi }(t) - \mathbf {Y}(t)$ is stationary.

Secondly, cointegration is allowed to exist between the variables in $\mathbf {Y}(t)$ as well. We denote the number of cointegration relationships between them by h, where $h\ge 0$ and $h<n$. The corresponding cointegration matrix is symbolized by $\varTheta$, an $n \times n$ matrix with the last $n-h$ rows equal to zero vectors. Each of the h non-zero rows of $\varTheta$ encodes a stationary (i.e., cointegrating) combination of the variables in $\mathbf {Y}(t)$, normalized such that $\varTheta _{ii} = 1, \ i \le h$. The total $n+h$ cointegration relationships between the variables in the vector $\mathbf {Z}(t):=(\mathbf {X}(t)-\mathbf {\phi }(t),\mathbf {Y}(t))^\top$ can be characterized by the $(2n\times 2n)$-matrix $\begin{bmatrix} \mathbf {I}_n&-\mathbf {I}_n \\ \mathbf{O }_n&\varTheta \end{bmatrix}$ where $\mathbf{O }_n$ denotes the zero-matrix with dimension $n\times n$.

The dynamics of $\mathbf {X}(t)$ and $\mathbf {Y}(t)$ under the real-world probability measure is assumed to be given by:

$$\begin{aligned} d \begin{bmatrix} \mathbf {X}(t)-\phi (t) \\ \mathbf {Y}(t) \end{bmatrix}&= \begin{bmatrix} \mathbf {0}_n \\ \mu _y \end{bmatrix} dt + \begin{bmatrix} -K_x&\mathbf{O }_n \\ \mathbf{O }_n&-K_y \end{bmatrix} \begin{bmatrix} \mathbf {I}_n&-\mathbf {I}_n \\ \mathbf{O }_n&\varTheta \end{bmatrix} \begin{bmatrix} \mathbf {X}(t)-\phi (t) \\ \mathbf {Y}(t) \end{bmatrix} dt \nonumber \\&\quad {}+ \begin{bmatrix} \varSigma _x^{\frac{1}{2}}&\mathbf{O }_n \\ \varSigma _{xy}^{\frac{1}{2}}&\varSigma _y^{\frac{1}{2}} \end{bmatrix} d \begin{bmatrix} \mathbf {W}_x(t) \\ \mathbf {W}_y(t) \end{bmatrix}, \end{aligned}$$

(2)

where $\mathbf {0}_n$ is an n-dimensional vector of zeros, and $\mathbf {W}:=(\mathbf {W}_x,\mathbf {W}_y)^\top$ is a 2n-dimensional standard Brownian motion. Furthermore, the matrix $\begin{bmatrix} -K_x&\mathbf{O }_n \\ \mathbf{O }_n&-K_y \end{bmatrix}$ measures the speed by which $\mathbf {Z}(t)$ reverts to its long-run (cointegration) equilibrium level. More specifically, $K_x$ quantifies the speed of mean reversion of the elements in $\mathbf {X}$ around the long term levels in $\mathbf {Y}$. The matrix $K_y$ is an $n \times n$ matrix with the last $n-h$ columns equal to zero vector, such that $K_y \varTheta$ is an $n \times n$ matrix of rank h. Each of the h non-zero columns in $K_y$ quantifies the speed of adjustment of each element in $\mathbf {Y}$ to the corresponding cointegration relation. The dynamics given by Eq. (2) is “error-correcting” in that a deviation from a given cointegration relation induces an appropriate change in variables in the direction of correcting the deviation.

In order to assess qualitatively the role of the cointegration matrix $\varTheta$ on the properties of the dynamics of the system, Fig. 1 depicts the results of a simulation of a system of three variables for various choices of the $\varTheta$ matrix.

Fig. 1

Simulated price paths for various choices of the $\varTheta$ matrix. Top panel prices are non-stationary and there is one cointegration relation. Middle panel prices are non-stationary and there is no cointegration. Bottom panel prices are stationary

In the top panel of Fig. 1 we assume that there is a cointegration relation and the first line of the $\varTheta$ matrix is $\begin{bmatrix} 1&1&-1\end{bmatrix}$ and, therefore, the residual of the cointegration relation, $Y_1(t)+Y_2(t)-Y_3(t)$, is stationary. On the other hand, in the middle panel, depicts the case when $\varTheta$ is the null matrix and, therefore, the prices are non-stationary and not cointegrated. For example, the residual of the cointegration relation from the previous case, $Y_1(t)+Y_2(t)-Y_3(t)$, is no longer stationary. In fact, there is no stationary linear combination of the long run levels in this case. Moreover, as depicted in the bottom panel, the model also allows for stationary prices, if the $\varTheta$ matrix is of full rank.

The characteristic functions of $\mathbf {X}$ and $\mathbf {Y}$ can be readily computed analytically given they are normally distributed since the dynamics of $\mathbf {Z}(t)=(\mathbf {X}(t)-\mathbf {\phi }(t),\mathbf {Y}(t))^\top$ is in fact given by a multivariate Ornstein–Uhlenbeck (OU) process:

$$\begin{aligned} d\mathbf {Z}(t)&=\left[ \mathbf {\mu }-K\mathbf {Z}(t)\right] dt+\varSigma ^{\frac{1}{2}}d\mathbf {W}(t), \end{aligned}$$

(3)

with $\mathbf {\mu }:= \begin{bmatrix} \mathbf {0}_n \\ \mathbf {\mu }_y \end{bmatrix}, \ K:= \begin{bmatrix} K_x&-K_x \\ \mathbf{O }_n&K_y\varTheta \end{bmatrix}, \ \varSigma ^{\frac{1}{2}}:= \begin{bmatrix} \varSigma _x^{\frac{1}{2}}&\mathbf{O }_n \\ \varSigma _{xy}^{\frac{1}{2}}&\varSigma _y^{\frac{1}{2}} \end{bmatrix}, \ \mathbf {W}(t):= \begin{bmatrix} \mathbf {W}_x(t) \\ \mathbf {W}_y(t) \end{bmatrix}.$

At the same time, the vector of spot prices $\mathbf {S}(T)$ can be written as an exponential function of $\mathbf {X}(t)$ and $\mathbf {Y}(t)$:

$$\begin{aligned} \mathbf {S}(T)&=\exp \bigg \{e^{-K_x(T-t)}\mathbf {X}(t)+\psi (T-t)\mathbf {Y}(t)+\left[ \phi (T)-e^{-K_x(T-t)}\phi (t)\right] \nonumber \\&\qquad \qquad +\left[ \int _t^T\psi (T-u)du\right] \mu _y+\int _t^T\left[ e^{-K_x(T-u)}\varSigma _x^{\frac{1}{2}}+\psi (T-u)\varSigma _{xy}^{\frac{1}{2}}\right] d\mathbf {W}_x(u)\nonumber \\&\qquad \qquad +\int _t^T\psi (T-u)\varSigma _y^{\frac{1}{2}}d\mathbf {W}_y(u)\bigg \}. \end{aligned}$$

(4)

where

$$\psi (\tau ):=K_x\left[ \int _0^\tau e^{-K_x(\tau -u)}e^{-K_y\varTheta u}du\right] .$$

Given the affine structure of the model, futures prices can also be obtained in closed form. Under the simplifying assumption of constant market prices of risk, one has that $d \begin{bmatrix} \mathbf {W}_x^*(t) \\ \mathbf {W}_y^*(t) \end{bmatrix} = d \begin{bmatrix} \mathbf {W}_x(t) \\ \mathbf {W}_y(t) \end{bmatrix} + \begin{bmatrix} \mathbf {\lambda }_x \\ \mathbf {\lambda }_y \end{bmatrix}dt$ where $\mathbf {W}^*_x(t)$ and $\mathbf {W}^*_y(t)$ are standard Brownian motions under the risk-neutral measure, and $\mathbf {\lambda }_x$, $\mathbf {\lambda }_y$ are the market prices of $\mathbf {W}_x(t)$ and $\mathbf {W}_y(t)$ risks, respectively.

Under these circumstances it can be shown that at time t the vector of futures prices for the contracts with maturity T is given by

$$\begin{aligned} \mathbf {F}(t,T)=\exp \left\{ \alpha (t,T)+\beta (T-t)\mathbf {X}(t)+\psi (T-t)\mathbf {Y}(t)\right\} , \end{aligned}$$

(5)

with $\beta (\tau ):=e^{-K_x\tau }$ and with $\alpha (t,T)$ defined by

$$\begin{aligned} \alpha (t,t+\tau )&:=\left[ \phi (t+\tau )-e^{-K_x\tau }\phi (t)\right] -\left( \mathbf {I}_n-e^{-K_x\tau }\right) K_x^{-1}\mathbf {\mu }_x^*+\left( \int _0^\tau \psi (\tau -u)du\right) \mathbf {\mu }_y^*\nonumber \\&\quad {}+\mathrm {diag}\bigg \{\frac{1}{2} \begin{bmatrix} \mathbf {I}_n&\mathbf{O }_n \end{bmatrix} \left[ e^{-K\tau }\left( \int _0^\tau e^{Ku}\varSigma e^{Ku}du\right) e^{-K\tau }\right] \begin{bmatrix} \mathbf {I}_n \\ \mathbf{O }_n \end{bmatrix} \bigg \}, \end{aligned}$$

(6)

where $\mathrm {diag}(A)$ returns the vector with diagonal elements of A, and where

$$\mathbf {\mu }^*= \begin{bmatrix} \mathbf {\mu }^*_x \\ \mathbf {\mu }^*_y \end{bmatrix}=\mathbf {\mu }+\varSigma ^{\frac{1}{2}}\begin{bmatrix} \mathbf {\lambda }_x \\ \mathbf {\lambda }_y \end{bmatrix}.$$

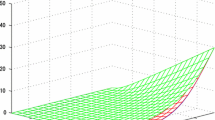
To better assess qualitatively the impact of the two factors, $\mathbf {X}(t)$ and $\mathbf {Y}(t)$, on the term structure of futures prices, we depict in Fig. 2 the relative contribution of the corresponding two terms in Eq. (5) to the logarithm of the futures prices on one of the commodities in a cointegrated system.

Fig. 2

The relative contribution of various components to log futures prices

The contribution of the $\mathbf {X}(t)$ component decreases exponentially as a function of time to maturity. On the other hand, the $\mathbf {Y}(t)$ component contributes significantly for higher maturities. Therefore, the two factors capture the short-end and, respectively, the long-end of the term-structure of futures prices.

By Itô’s lemma, the risk-neutral dynamics of $\mathbf {F}(t,T)$ is given by

$$\begin{aligned} \frac{d\mathbf {F}(t,T)}{\mathbf {F}(t,T)}&=\left[ e^{-K_x(T-t)}\varSigma _x^{\frac{1}{2}}+\psi (T-t)\varSigma _{xy}^{\frac{1}{2}}\right] d\mathbf {W}^*_x(t)+\psi (T-t)\varSigma _y^{\frac{1}{2}}d\mathbf {W}^*_y(t), \end{aligned}$$

(7)

and it follows immediately that the variance–covariance matrix of returns on futures prices is given by:

$$\begin{aligned} \varXi (\tau )&=e^{-K_x\tau }\varSigma _xe^{-K_x^\top \tau }+\psi (\tau )\varSigma _{xy}^{\frac{1}{2}}(\varSigma _x^{\frac{1}{2}})^\top e^{-K_x^\top \tau }+e^{-K_x\tau }\varSigma _x^{\frac{1}{2}}(\varSigma _{xy}^{\frac{1}{2}})^\top \psi ^\top (\tau )\nonumber \\&\quad {}+\psi (\tau )\varSigma _{xy}\psi ^\top (\tau )+\psi (\tau )\varSigma _y\psi ^\top (\tau ) \end{aligned}$$

(8)

where $\tau = T - t$.

Since the term structure of correlation of futures prices returns plays an important role in the results of the simulations performed in the following section, it is worthwhile to point out some qualitative results about this term structure.

First, Eq. (8) shows that unless $K_x=\mathbf{O }_n$, the variance–covariance matrix $\varXi (\tau )$ depends on $\tau$.

Second, let us consider the case that there is no instantaneous correlation between the shocks driving the dynamics, meaning that $\varSigma _x$ and $\varSigma _y$ are diagonal matrices and $\varSigma _{xy}$ is the null matrix. Moreover, let us assume that $K_x$ is diagonal, meaning that the spot price of a commodity reacts only to its deviation from the long run level and not to deviations of the other commodities. It follows that the first term in Eq. (8) is a diagonal matrix and the next three terms are null matrices. If, in addition, there is no cointegration in the system, meaning that $\varTheta$ is the null matrix, then the last term in Eq. (8) is a diagonal matrix since $\psi (\tau )$ is also a diagonal matrix. So, in this case, the variance–covariance matrix $\varXi (\tau )$ is diagonal and, therefore, there is no correlation at any maturity. However, if there is at least one cointegration relation in the system, then the last term in Eq. (8) is no longer a diagonal matrix since $\psi (\tau )$ is not diagonal. Therefore, cointegration induces correlation at various maturities although it was assumed there is no instantaneous correlation between the Brownian motions in the model.

3 Spread Option Prices

In this section, we focus on futures prices and prices of European-style options written on the spread between two or more commodities, such as the difference between the price of electric power and the cost of the natural gas needed to produce it, or the price difference between crude oil and a basket of various refined products, known as the crack spread. The crack spread is in fact related to the profit margin that an oil refiner realizes when “cracking” crude oil while simultaneously selling the refined products in the wholesale market. The oil refiner can hedge the risk of losing profits by buying an appropriate number of futures contract on the crack spread or, alternatively, by buying call options of the crack spread. Since spread options have become regularly and widely used instruments in financial markets for hedging purposes, there is a growing need for a better understanding of the effects of cointegration on their prices.

There is extensive literature on approximation methods for spread and basket options on two (e.g. Kirk [8]) or more than two commodities, with recent contributions from Li et al. [9] and Caldana and Fusai [2]. However, mostly for simplicity, we relay in this chapter on the Monte-Carlo simulation method for pricing spread options written on two or more than two commodities.

From Eq. (7), it follows that $\mathbf {F}(t,T)$ (conditional on information available up to time $s\le t\le T$) is distributed as follows:

$$\begin{aligned} \mathbf {F}(t,T)\sim \log \mathscr {N}\left( \log \mathbf {F}(s,T)-\frac{1}{2}\int _s^t\text {diag}(\varXi (T-u))du,\int _s^t\varXi (T-u)du\right) , \end{aligned}$$

(9)

where $\text {diag}(X)$ denotes the vector containing the diagonal elements of the matrix X. Note that $\mathbf {F}(s,T)$ can be either computed from (5) or observed from data.

The fact that the distribution function of $\mathbf {F}(t,T)$ is known in an easy-to-use and analytic form is one of the key features of the model we employ. It allows us to simulate futures price curves at any time t in the future based on today’s curves (time s) almost effortlessly. Hence, the price of a call option on the time-T value of a certain spread can be simply obtained by carrying out the following steps:

• (i) compute or observe today’s futures price curves $\mathbf {F}(s,T)$;

• (ii) compute M realizations $\mathbf {F}^{(m)}$ $(m=1,\ldots ,M)$ of $\mathbf {F}(T,T)$ by sampling from (9) as follows:

  $$\mathbf {F}^{(m)}=\mathbf {F}(s,T)\exp \left\{ \mathbf {\varepsilon }^{(m)}\right\} ,$$

  where $\mathbf {\varepsilon }^{(m)}$ is generated from a multivariate normal distribution with mean $-\frac{1}{2}\int _s^T\text {diag}(\varXi (T-u))du$ and variance–covariance matrix $\int _s^T\varXi (T-u)du$ ¹;

• (iii) compute the Monte-Carlo estimate of a call with strike k on the spread

  $$\sum _{n=1}^N\omega _nS_n(T)\qquad \left( =\sum _{n=1}^N\omega _nF_n(T,T)\right) ,$$

  with $\omega _n$, $n=1,\ldots ,N$ the weights of each component in the spread, as follows:

  $$\begin{aligned} \frac{1}{M}\sum _{m=1}^M\max \left\{ \left[ \sum _{n=1}^N\omega _nF^{(m)}_n\right] -k,0\right\} . \end{aligned}$$

  (10)

For the sake of clarity we have set the risk-free rate curve equal to zero. We note that the random variables $\mathbf {\varepsilon }^{(m)}$ can be simply re-used for pricing spread options with different maturity dates.

In the following we consider a system of three commodities² characterized by one cointegration relation with $\varTheta = \begin{bmatrix} 1&-0.4&-0.6 \\ 0&0&0 \\ 0&0&0 \end{bmatrix}$. The rest of the parameters describing the dynamics are $K_x = \begin{bmatrix} 1.5&0&0 \\ 0&1&0 \\ 0&0&0.5 \end{bmatrix}$, $\varSigma _x = \begin{bmatrix} 0.0625&0.0562&0.0437 \\ 0.0562&0.0900&0.0262 \\ 0.0437&0.0262&0.1225 \end{bmatrix}$, $\mu _y = \begin{bmatrix} 0.025\\ 0.025\\ 0.025 \end{bmatrix}$, $K_y = \begin{bmatrix} 1.5&0&0 \\ 0&0&0 \\ 0&0&0 \end{bmatrix}$, $\varSigma _y = \begin{bmatrix} 0.0225&0&0 \\ 0&0.0225&0 \\ 0&0&0.0225 \end{bmatrix}$, $\varSigma _{xy}=\mathbf{O }_3$. Since $K_x$ is diagonal, each spot price is error-corrected only with respect to deviations from its own long-run level. Moreover, given the specific form of the $K_y$ matrix, deviations from the cointegration relationships between the long-run levels influence only the dynamics of the first spot price. In this respect, the second and third commodities are “exogenous” in that their dynamics is not influenced by the variables characterizing the other commodities. Regarding instantaneous dependence, the shocks driving the dynamics of the long-run factors are not correlated, whereas we imposed positive correlations between the shocks driving the dynamics of the $\mathbf {X}(t)$. More specifically, the instantaneous variance–covariance matrix $\varSigma _y$ for long-run shocks corresponds to an annual volatility of 0.15 for all three commodities. At the same time, the instantaneous variance–covariance matrix $\varSigma _x$ for short-run shocks corresponds to an annual volatility of 0.25 for the first commodity, of 0.30 for the second and of 0.35 for the third and to a correlation coefficient of 0.75 between the first and the second commodities, of 0.50 between the first and the last and of 0.25 between the second and the third. For simplicity, we also assume there is no correlation between the two categories of shocks. Since we focus on the impact of cointegration on spread options, in the following simulations we have set, for illustration purposes, the vector of risk premiums $\mathbf {\lambda }_x$ and $\mathbf {\lambda }_y$ and the risk-free rate curve equal to zero.³

Fig. 3

Term structure of correlation, over a period of 5 years, between the futures log-returns of three commodities (from top to bottom: between 1 and 2, between 1 and 3, between 2 and 3)

Fig. 4

Relative ATM call spread option prices with up to 5 years to maturity, and relative standard deviations of the spread distribution at maturities up to 5 years. Top panel for the spread $S_1(t) - S_2(t)$. Bottom panel for the spread $S_1(t) - 0.5 (S_2(t) + S_3(t))$

Figure 3 depicts the term structure of correlation, over a period of 5 years, between the returns of futures prices of the three commodities in the system in two cases: the one when the cointegration relation is taken into account and, respectively, the one where the cointegration relation is abstracted from (i.e. $\varTheta =\mathbf{O }_3$).

One can observe that, regarding the correlation term structure between commodities 2 and 3, the two curves are identical (Fig. 3, bottom panel). This is not surprising since these two commodities are “exogenous” as explained above and their dynamics is not influenced by the cointegration relation. However, cointegration induces additional correlation when it comes to the commodities 1 and 2 and commodities 1 and 3, as also pointed out at the end of the previous section. In the absence of cointegration, the correlation vanishes after 2–3 years, whereas when the cointegration relation is taken into account the correlation exists also in the long run.

Next, we consider three spreads on two commodities, respectively $S_1(t) - S_2(t)$, $S_1(t) - S_3(t)$, $S_2(t) - S_3(t)$, and one spread on all the three commodities in the system $S_1(t) - 0.5 (S_2(t) + S_3(t))$. We assume that at time 0, the two factors are such that $\mathbf {X}(0) =\mathbf {Y}(0) = \begin{bmatrix} 2 \\ 2 \\ 2 \end{bmatrix}$ and, therefore, the current spot prices of all four spreads equal 0. We focus on studying the prices of the at-the-money (ATM) European-style call spread options with up to 5 years to maturity. Figure 4 shows the term structure of prices in the case with cointegration relative to the prices in the case the cointegration is not accounted for.⁴

Cointegration has a significant impact on spread option prices, with the price for the call with 5 years to maturity on the $S_1(t) - S_2(t)$ spread being almost 30 % lower in the case with cointegration and for the call on the $S_1(t) - 0.5 (S_2(t) + S_3(t))$ spread being almost 60 % lower. This can be explained by the fact that cointegration induces additional correlation that acts to lower the standard deviation of the distribution of the spread at maturity. To give a better grasp of this fact, Fig. 5 depicts the distribution of the spread at maturity in the two cases. We omitted from the figures the other two spreads, because the results for the $S_1(t) - S_3(t)$ spread are similar to those for the $S_1(t) - S_2(t)$ spread, and for the $S_2(t) - S_3(t)$ spread there is, as expected given the “exogenous” nature of these two prices, no difference between the cases with and without cointegration.

Fig. 5

The distribution of the spread at maturity (5 years). Top panel for the spread $S_1(t) - S_2(t)$. Bottom panel for the spread $S_1(t) - 0.5 (S_2(t) + S_3(t))$

If one were to add another cointegration relation to the system, linking the second and the third commodities in a long-run relationship, then the new cointegration relation would affect the prices of the options written on the $S_2(t) - S_3(t)$ spread. Moreover, the new cointegration relation might also affect the option prices written on the other three spreads, the magnitude of this influence depending on the structure of the $K_y$ matrix that captures the strength of responses in various spot prices to deviations in the new long-run relationship.

To have a better grasp of the influence of cointegration, next we run a series of sensitivity analyses concerning the existence of a second cointegration relationship in the system. To account for the new cointegration relation, we assume a new structure for $\varTheta = \begin{bmatrix} 1&-0.4&-0.6 \\ -\theta&1&-0.8 \\ 0&0&0 \end{bmatrix}$ and $K_y = \begin{bmatrix} 1.5&k_1&0 \\ 0&k_2&0 \\ 0&-k_3&0 \end{bmatrix}$, where $\theta , k_1, k_2, k_3 > 0$. The other parameters have the same values as before. We first focus on the impact of the parameters $k_2$ and $k_3$ on the $S_2(t) - S_3(t)$ spread. These two parameters quantify the strength that the second and, respectively, the third commodity reacts to deviations in the newly added cointegration relation. In the extreme case when both $k_2$ and $k_3$ are zero, we are in the same situation as before since the two commodities do not react to deviations. However, with the increase of these parameters the new cointegration relation will start to matter for the dynamics of the two commodities, and will have an impact on the distribution of the spread at maturity. Figure 6 presents the results of the sensitivity analysis when $k_2$ and $k_3$ are varied between 0 and 0.5, with the other parameters kept fixed at a level $\theta = 0.2$ and $k_1 = 0$.

Fig. 6

The impact of $k_2$ and $k_3$ on the distribution of the spread $S_2(t) - S_3(t)$ at maturity (5 years). Top left panel correlation between the futures log-returns of the two commodities in the basket. Top right panel relative standard deviations of the spread distribution (the values are normalized by division with the standard deviation in the case $k_2 = k_3 = 0$). Bottom panel the distribution for the two extreme cases in the analysis

A higher value for the two reaction parameters produces a higher extra correlation induced by the second cointegration relation, which, in turn, is reflected in a lower standard deviation of the distribution of the spread at maturity. Over a 5-years horizon, the standard deviation for the case $k_2 = k_3 = 0.5$ is 32 % lower than in the case the two parameters are equal to zero, and the ATM call price is 35 % lower.

Next, we focus on the impact of $\theta$ and $k_1$ on the $S_1(t) - 0.5 (S_2(t) + S_3(t))$ spread. The parameter $\theta$ is a free variable that determines the second cointegration relationship and the parameter $k_1$ measures the magnitude of the response of the first commodity to deviations from the second cointegration relation. Figure 7 presents the results of the sensitivity analysis when $k_1$ and $\theta$ are varied between 0 and 1 and, respectively, between 0.1 and 0.3, with the other parameters kept fixed at a level $k_2 = 0.25$ and $k_3 = 0.25$. An increase of $k_1$ generates a reduction in the correlation between the components of the spread, showing that the second cointegration relationship has the effect of pulling the components of the spread away from each other. This effect is marginally stronger for the smaller $\theta$. The result of the reduction in correlation is a higher standard deviation of the distribution of the spread at maturity.

Fig. 7

The impact of $k_1$ and $\theta$ on the distribution of the spread $S_1(t) - 0.5 (S_2(t) + S_3(t))$ at maturity (5 years). Top left panel correlation between the futures log-returns of the first commodity and the sum of the other two. Top right panel relative standard deviations of the spread distribution (the values are normalized by division with the standard deviation in the case $k_1 =0, \theta = 0.2$). Bottom panel the distribution for two specific cases in the analysis

For a maturity of 5 years, the standard deviation for the case $k_1 = 1$ is around 33 % higher than in the case the parameter equals zero, and the ATM call price is about 40 % higher. Therefore, the two cointegration relations influence the distribution of the $S_1(t) - 0.5 (S_2(t) + S_3(t))$ spread in different directions, the first one generating a reduction, and the second one an increase in the standard deviation. The overall impact depends on the magnitude of the parameters quantifying the responses of the commodities to deviations in the two cointegration relations.

4 Concluding Remarks

In this work, we explored the implications of cointegration between commodity prices on the premiums of options written on various spreads between these commodities. We employed the continuous time model of cointegrated commodity prices developed in Farkas et al. [6] and conducted a simulation study for a cointegrated system of three commodities. We calculated the prices of several spread options and found that cointegration significantly influences these prices. Furthermore, we pointed out that cointegration leads to an upward sloping correlation term-structure which lowers the volatility of spreads and therefore it also lowers the value of options on spreads. Although we restricted in this chapter to a simulation study, it is worthwhile to mention that the model can also be estimated using futures prices on various commodities, as shown in Farkas et al. [6].