Encoding Specific 3D Polyhedral Complexes Using 3D Binary Images

Abstract

We build upon the work developed in [4] in which we presented a method to “locally repair” the cubical complex Q(I) associated to a 3D binary image I, to obtain a “well-composed” polyhedral complex P(I), homotopy equivalent to Q(I). There, we developed a new codification system for P(I), called ExtendedCubeMap (ECM) representation, that encodes: (1) the (geometric) information of the cells of P(I) (i.e., which cells are presented and where), under the form of a 3D grayscale image $g_P$; (2) the boundary face relations between the cells of P(I), under the form of a set $B_P$ of structuring elements.

In this paper, we simplify ECM representations, proving that geometric and topological information of cells can be encoded using just a 3D binary image, without the need of using colors or sets of structuring elements. We also outline a possible application in which well-composed polyhedral complexes can be useful.

Authors partially supported by IMUS, Junta de Andalucia under grant FQM-369, Spanish Ministry under grants MTM2012-32706 and MTM2015-67072-P, and ACAT ESF Research Networking Programme.

1 Introduction

Consider $\mathbb {Z}^3$ as the set of points with integer coordinates. in 3D space $\mathbb {R}^3$. A 3D binary digital image is a set $I=(\mathbb {Z}^3,26,6,B)$ (or $I=(\mathbb {Z}^3,B)$, for short), where $B\subset \mathbb {Z}^3$ is the foreground, $B^c=\mathbb {Z}^3 {\backslash } B$ the background, and (26, 6) is the adjacency relation for the foreground and background, respectively. A 3D binary image I is well-composed [9] if the boundary surface of its continuous analog is a 2D manifold. 3D well-composed images enjoy important topological and geometrical properties in such a way that several algorithms used in computer vision, computer graphics and image processing are simpler. Unfortunately natural and synthetic images are not a priori well-composed. There are several “repairing” methods for turning them into well-composed images (see, for example, [8, 10, 12, 13]).

In [11], the authors extended the notion of “digital well-composedness” to nD sets. In [1], they proved that the digital well-composedness implies the equivalence of connectivities of the level set components in nD. They proposed and proved a self-dual discrete (non-local) interpolation method, based on a sub-part of a quasi-linear algorithm that computes the morphological tree of shapes, whose result is always a digitally well-composed function. Besides, it is proven in [2] that the only local self-dual well-composed interpolation of a 2D image is obtained by the median operator.

In this paper, we first recall, in Sect. 2, a method to “locally repair” the cubical complex Q(I) associated to a 3D binary image I, obtaining a “well-composed” polyhedral complex P(I), homotopy equivalent to Q(I), encoded using an ExtendedCubeMap (ECM) representation. A possible application of ECM representations is also sketched. In Sect. 3, we prove that the coordinates of the points in an ECM representation that encode the cells of Q(I) contain all the information of the cells. This result is extended to P(I) in Sect. 4. Therefore there is no need of using colors or sets of structuring elements to encode P(I). The paper ends up with a section of conclusions and future work.

2 ECM Representations

The notion of well-composedness is extended in [4, 14] to 3D complete polyhedral complexes K embedded in $\mathbb {R}^3$. This way, K is well-composed if the boundary surface of K is a 2D manifold.

In [4], we presented a method to “locally repair” the 3D complete cubical complex Q(I) (embedded in $\mathbb {R}^3$) associated to a voxel-based representation of a given image I, to obtain a well-composed polyhedral complex P(I) homotopy equivalent to Q(I). Our main motivation was that of (co)homology computations on the cell complex representing a 3D binary image I [3, 6]. We could take advantage of a well-composed-like representation since such computations could be performed only on the boundary surface of P(I). A new codification system called ExtendedCubeMap (ECM) representation, for P(I) were also developed in [4], encoding: (1) the (geometric) information of the cells of P(I), under the form of a 3D grayscale image $g_P$; and (2) the boundary face relations between the cells of P(I), under the form of a set $B_P$ of structuring elements that can be stored as indexes in a look-up table. A naive demo implemented in Matlab for computing ECM representations can be downloaded in [5].

In this paper, we improve such codification system, showing that the geometric and topological information of the cells of P(I) can be encoded using just a 3D binary image $J=(\mathbb {Z}^3,B)$. Geometric information of each cell $\sigma$ can be obtained by examining the coordinates of the point p in B that encodes $\sigma$ (no color is needed). Faces of such cell $\sigma$ can be computed by examining the points in a neighborhood of p in B (no look-up table is needed). As far as we know, this is the first time that a family of polyhedral complexes more general than cubical ones are stored using binary images.

2.1 Towards Applications: 3D Printing

3D CAD modeling and recent 3D printing deal mainly with 3D meshes. Typically, the physical objects are modeled in standard STL format where the objects are discretized as finite meshes (encoded as a 3D polyhedral complexes). The interplay between abstract representations and the physical objects natural raise a question about the meshes that can be practically constructed (i.e. printed). Possible obstacles are complexes which boundary surfaces are not combinatorial manifolds. Example of such a configuration are two cubes touching in a vertex or in an edge. Tools that detect, and fix such configurations are a first step towards an automatic tool to check if an abstract representation is realizable as a physical object and/or to change it so that the physical object is more robust (taking into account that non-manifold parts will break immediately).

Although most of the meshes for 3D printing are simplicial, others are cubical¹. This way, a “manifoldization technique” could be as follows: (1) Start with any cubical mesh (i.e., cubical complex) modeling a physical object. (2) Make a “manifold version” of it by computing a well-composed polyhedral complex P(I) homotopy equivalent to Q(I), to obtain a more robust version of the physical object. (3) Encode P(I) in a valid format for the 3D printing. The codification of P(I) in a 3D binary format presented in this paper, could help in this last step.

3 3D Cubical Complexes

3D digital images are usually represented by unit closed cubes in $\mathbb {R}^3$ with square faces parallel to the coordinate planes, centered at points in $\mathbb {Z}^3$ (also called voxels). In this paper, voxels are rescaled with factor 4, so we consider size$-4$ cubes centered at points $4\mathbb {Z}^3$.

A set of voxels together with all their faces (cells) constitute a combinatorial structure called cubical complex, denoted by Q. The $0{-}$ faces of a given voxel c are its 8 corners (vertices), its $1{-}$faces are its 12 edges, its $2{-}$faces are its 6 square faces and, finally, its $3{-}$face is the voxel itself.

Let Q be a cubical complex composed by a set of voxels (size$-4$ cubes) together with all their faces. Let $J=(\mathbb {Z}^3,B)$ be a 3D binary image. We say that J encodes Q if: (1) For any $\sigma$ in Q, $r_{\sigma }$ (the barycenter of $\sigma$) is in B. And (2), for any $p\in B$, p is the barycenter of a cell $\sigma$ in Q. Then, a point $p\in 2\mathbb {Z}^3$ encodes:

• A vertex iff $p \in \mathcal{E}_0=\{(4i+2,4j+2,4k+2)\}_{i,j,k\in \mathbb {Z}}$.

• An edge iff $p\in \mathcal{E}_1=\{(4i+2,4j+2,4k), (4i,4j+2,4k+2), (4i+2,4j,4k+2)\}_{i,j,k\in \mathbb {Z}}$.

• A square face iff $p\in \mathcal{E}_2=\{(4i+2,4j,4k)$,$(4i,4j+2,4k)$, $(4i,4j,4k+2)\}_{i,j,k\in \mathbb {Z}}$.

• A voxel iff $p\in \mathcal{E}_3=4\mathbb {Z}^3$.

Now, given a point $p\in B$ encoding a cell $\sigma \in Q$, our aim is to find the points in B encoding the faces of $\sigma$. First, recall that: $N_6^\ell =\{(\pm \ell ,0,0),(0,\pm \ell ,0)$, $(0,0,\pm \ell )\}$; $N_{12}^\ell = \{(0,\pm \ell ,\pm \ell ),(\pm \ell ,0,\pm \ell ),(\pm \ell ,\pm \ell ,0)\}$; $N_{8}^{\ell }=\{(\pm \ell ,\pm \ell ,\pm \ell )\}$; and for any $N\subseteq \mathbb {R}^3$ and $p\in \mathbb {R}^3$, N(p) denotes the set $\{p+q,$ $q\in N\}$.

Proposition 1

Let $\sigma$ be an $\ell {-}$cell of Q encoded by $p=r_{\sigma }$. Then, the set of $k{-}$faces of $\sigma$, for $0\le k< \ell$, is: (1) $N_6^2(p)\cap \mathcal{E}_{k}$ if $k=\ell -1$; (2) $N_{12}^2(p)\cap \mathcal{E}_{k}$ if $k=\ell -2$; (3) $N_{8}^2(p)\cap \mathcal{E}_{k}$ if $k=\ell -3$.

Proof. Let $\ell =2$. First, $p=r_{\sigma }\in \mathcal{E}_2$ so, assume that $r_{\sigma }=(4i+2,4j,4k)$ for some $i,j,k\in \mathbb {Z}^3$. Then, the barycenters of the $1{-}$faces of $\sigma$ are $\{(4i+2,4j\pm 2,4k),(4i+2,4j,4k\pm 2)\}$. Second, $N_6^2(p)= \{(4i,4j,4k),(4i+4,4j,4k),(4i+2,4j\pm 2,4k),(4i+2,4j,4k\pm 2)\}$. Finally, $N_6^2(p)\cap \mathcal{E}_{1}= \{(4i+2,4j\pm 2,4k),(4i+2,4j,4k\pm 2)\}$. The other cases can be proven in a similar way.    $\square$

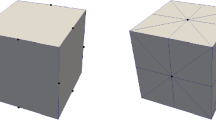
See Fig. 1 in which a voxel c (on the right) is encoded by a set of points (on the left). Colors are used to distinguish dimension of cells encoded but, it follows from Proposition 1 that J can be stored as a binary image.

Fig. 1.

(a) A voxel c. (b) Set of points encoding c. Color illustrates the type of coordinate of the point, which provides the dimension of the encoded cell: blue for $0{-}$cells (i.e. points in $\mathcal{E}_0$), red for $1{-}$cells (i.e. points in $\mathcal{E}_1$), green for $2{-}$cells (i.e. points in $\mathcal{E}_2$) and black for $3{-}$cells (i.e. points in $\mathcal{E}_3$) (Color figure online).

Remark 1

From now on, a cell in a 3D cubical complex (later, in the 3D polyhedral complex) will be sometimes identified with the point in $\mathbb {Z}^3$ encoding such cell.

4 Encoding Specific Polyhedral Complexes Using Binary Images

A 3D polyhedral complex K [7] is a combinatorial structure by which a space is decomposed into vertices ($0{-}$cells), edges ($1{-}$cells), polygons ($2{-}$cells) and polyhedra ($3{-}$cells) that are glued together by their boundaries (faces) such that the non-empty intersection of any two cells of K is also a cell of K. An $\ell {-}$cell $\sigma \in K$ is a face of an $\ell '{-}$cell $\sigma '\in K$ if $\sigma$ lies in the boundary of $\sigma '$ and $\ell \le \ell '$. A cell $\mu$ is maximal if it is not a face of any other cell $\sigma \in K$. A 3D polyhedral complex is complete if all its maximal cells have dimension 3. It is well-composed if its boundary surface is a 2D manifold. In [4] we developed a procedure to get as output a 3D complete well-composed polyhedral complex that is homotopy equivalent to the standard cubical complex representing an input 3D binary image. This type of 3D polyhedral complex will be called well-composed polyhedral complex over a picture and denoted by P. Besides, we say that a 3D binary image $J=(B,\mathbb {Z}^3)$ encodes P if B is the union of all the points encoding the polyhedra of P (together with all their faces). In this section, we show how to compute J and prove that J contains all the geometric and topological information of P.

We recall below the set S of 27 types of polyhedra used in [4] to construct P. For $v,w\in \mathcal {E}_0$, the edge with endpoints v and w (denoted by e(v, w)) is a size$-4$ edge. The size$-2$ cube centered at v with faces parallel to the coordinate planes is denoted by c(v) being s(v) a square face of c(v). Finally, k(v, w) will denote the pyramid with apex w and base the square face s(v) whose barycenter lies on e(v, w). Finally, t(v, w) denotes a triangle face of k(v, w).

Fig. 2.

List of 20 out of 22 types of hexahedra described in Definition 1e.

Definition 1

The set S consists of:

• (a) The voxel c centered at a point in $4\mathbb {Z}^3$. See Fig. 1a.

• (b) The size$-2$ cube c(v) centered at a point $v\in 2\mathbb {Z}^3$. See Table 1b.1

• (c) The pyramid k(v, w), where $v,w\in \mathcal{E}_0$. See Table 1c.1

• (d) The polyhedra $\{p_{\ell }(v, v_1,v_2,v_3)\}_{\ell =1,2,3,4}$, where $v, v_1,v_2,v_3 \in \mathcal{E}_0$ are distinct points forming a size$-4$ square s, being v adjacent to $v_1$ and $v_2$:

  • $p_1(v, v_1,v_2,v_3)$ is determined by the the edges $e(v_1,v_3)$, $e(v_2,v_3)$, and the triangles $t(v,v_1)$, $t(v,v_2)$, whose barycenters lie inside s. See Table 1d.1

  • $p_2(v, v_1,v_2,v_3)$ is determined by the edge $e(v_2,v_3)$, the triangles $t(v,v_2)$, $t(v_1,v_3)$, and the square face $s(\frac{v+v_1}{2})$, whose barycenters lie inside the square s. See Table 1e.1

  • $p_3(v, v_1,v_2,v_3)$ is determined by the four triangles $t(v,v_1)$, $t(v,v_2)$, $t(v_3,$ $v_1)$ and $t(v_3,v_2)$ whose barycenters lie inside s. See Table 1f.1

  • $p_4(v, v_1,v_2,v_3)$ is determined by the square faces $s(\frac{v+v_1}{2})$, $s(\frac{v_1+v_3}{2})$, and the triangles $t(v,v_2)$, $t(v_2,v_3)$, whose barycenters lie inside s. See Table 1g.1

• (e) The 22 hexahedra $\{h_{\ell }(v_1,\ldots v_8)\}_{\ell =1,\ldots ,22}$, where $\{v_1,\dots ,v_8\}\subset \mathcal{E}_0$ are the vertices of a voxel c, are determined by a set of vertices $\{x_1,\ldots x_8\}$. Each vertex $x_i$ is either $v_i$ or the vertex $w_i$ of $c(v_i)$, that lies inside c. Observe that $h_1(v_1,\ldots v_8)$ (when $x_{\ell }=v_{\ell }$ for $\ell =1,\dots ,8$) is the voxel c itself. Similarly, $h_{22}(v_1,\ldots v_8)$ (when $x_{\ell }=w_{\ell }$ for $\ell =1,\dots ,8$) is the size$-2$ cube $c(\frac{v_1+\cdots +v_8}{8})$ being $\frac{v_1+\cdots +v_8}{8}\in 4\mathbb {Z}^3$. All the other possible vertex combinations lead to the 20 hexahedra showed in Fig. 2

Although some of the $2{-}$faces of the polyhedra $\{p_{\ell }(v, v_1,v_2,v_3)\}_{\ell =1,2,3,4}$, are not planar (hence they are not polygons), P is always a CW-complex.

Notice that all the coordinates used in the representation of a cubical complex were even coordinates. Now, odd coordinates will also be needed. We denote:

• $\mathcal{O}_0=\{(2i+1,2j+1,2k+1)\}_{i,j,k\in \mathbb {Z}}$

• $\mathcal{O}_1=\{(2i,2j+1,2k+1), (2i+1,2j,2k+1), (2i+1,2j+1,2k)\}_{i,j,k\in \mathbb {Z}}$

• $\mathcal{O}_2=\{(2i,2j,2k+1), (2i,2j+1,2k), (2i+1,2j,2k)\}_{i,j,k\in \mathbb {Z}}$.

Now, from the ECM representation, (in fact, from the image $g_P$), we induce the coordinates of the points that codify the dimension, position and type of cell of any of the 27 different types of polyhedra in S and all their faces.

Proposition 2

Given a 3D binary image $J=(B,\mathbb {Z}^3)$ encoding a well-composed polyhedral complex over a picture P, for a point $p\in B$ we have that:

• If $p\in \mathcal{E}_0$ then p is a vertex if $N_6^1(p)\cap B= \emptyset$; otherwise, it is the cube described in Definition 1b.

• If $p\in \mathcal{E}_1$ then p is an edge if $N_6^1(p)\cap B= \emptyset$; otherwise, it is either the pyramid described in Definition 1c or the cube described in Definition 1b.

• If $p\in \mathcal{E}_2$ then p is a square face if $N_6^1(p)\cap B= \emptyset$; otherwise, it is one of the polyhedra described in Definition 1d.

• If $p\in \mathcal{E}_3$ then p is one of the 22 hexahedra listed in Definition 1e.

• If $p \in \mathcal{O}_{\ell }$, $\ell =0,1,2$ then p is an $\ell {-}$cell.

Proof. Any vertex $v\in P$ (i.e., $v\in B$) satisfies that either $v\in \mathcal{E}_0$ or $v\in \mathcal{O}_0$. See the blue voxels in Fig. 1, second column of Table 1 and Fig. 3.

• (a) A voxel c and its faces are encoded by their baricenters. This way, $c\in \mathcal{E}_3$ has square faces in $\mathcal{E}_2$, edges in $\mathcal{E}_1$ and vertices in $\mathcal{E}_0$. See Fig. 1b and Table 1a.1.

• (b) A size$-2$ cube c(v) centered at a point $v\in \mathcal{E}_0$ and its faces are encoded by their baricenters. This way, $c(v)\in \mathcal{E}_0$ has square faces in $\mathcal{O}_1$, edges in $\mathcal{O}_1$ and vertices in $\mathcal{O}_0$. See Table 1b.2.

• (c) The $3{-}$cell k(v, w) is encoded by $p=r_{(e(v,w))}\in \mathcal{E}_1$. Without loss of generality, suppose that $p=(4i,4j+2,4k+2)$ for some $i,j,k\in \mathbb {Z}$. Then, the four triangle faces of k(v, w) are $\{(4i,4j+2\pm 1,4k+2), (4i,4j+2,4k+2\pm 1)\}\subset \mathcal{O}_2$ (see green voxels in Table 1c.2). The four edges of k(v, w) incident to w are $\{(4i,4j+2\pm 1,4k+2\pm 1)\}\subset \mathcal{O}_1$.

• (d) The $3{-}$cell $p_{\ell }(v, v_1,v_2,v_3)$, $\ell =1,2,3,4$, where $v, v_1,v_2,v_3\in \mathcal{E}_0$, form a size$-4$ square face s, being v adjacent to $v_1$, $v_2$. Without loss of generality, suppose that $v=(i-2,j-2,k+2)$, $v_1=(i+2,j-2,k+2)$, $v_2=(i-2,j+2,k+2)$, and $v_3=(i+2,j+2,k+2)$. This way, $p_{\ell }(v, v_1,v_2,v_3)$ is encoded by $r_s=(4i,4j,4k+2)\in \mathcal{E}_2$. the two quadrangles of $p_{\ell }(v, v_1,v_2,v_3)$, $\ell =1,2,3,4$, are $\{(4i,4j,4k+2\pm 1)\}\subset \mathcal{O}_2$;

  • The two triangle faces of $p_1(v, v_1,v_2,v_3)$ are $\{(4i-1,4j,4k+2),(4i,4j-1,4k+2)\}\subset \mathcal{O}_2$; the non-(size-4) edges incident to $v_2$ are $\{(4i-1,4j,4k+2\pm 1)\}$ and the ones incident to $v_3$ are $\{(4i,4j-1,4k+2\pm 1)\}\subset \mathcal{O}_1$. See Table 1d.2.

  • The two triangle faces of $p_2(v, v_1,v_2,v_3)$ are $\{(4i\pm 1,4j,4k+2)\}\subset \mathcal{O}_2$; the non-(size-4) edges incident to $v_2$ or $v_3$ are $\{(4i\pm 1,4j,4k+2\pm 1)\}\subset \mathcal{O}_1$. See Table 1e.2.

  • The four triangles of $p_3(v, v_1,v_2,v_3)$ are $\{(4i\pm 1,4j,4k+2),(4i,4j\pm 1,4k+2)\}\subset \mathcal{O}_2$; the eight edges incident to $v_1$ or $v_2$ are $\{(4i\pm 1,4j,4k+2\pm 1),(4i,4j\pm 1,4k+2\pm 1)\}\subset \mathcal{O}_1$. See Table 1f.2.

  • The two triangles of $p_4(v, v_1,v_2,v_3)$ are $\{(4i-1,4j,4k+2),(4i,4j+1,4k+2)\}\subset \mathcal{O}_2$; the four edges incident to $v_2$ are $\{(4i-1,4j,4k+2\pm 1),(4i,4j+1,4k+2\pm 1)\}\subset \mathcal{O}_1$. See Table 1g.2.

• (e) The $3{-}$cell $h_{\ell }(v_1,\ldots v_8)$, $\ell =1,\ldots ,22$, where vertices $v_1,\ldots v_8 \in \mathcal{E}_0$ form a voxel c, is encoded by $p=\frac{v_1+\cdots +v_8}{2}\in \mathcal{E}_3$, (i.e., the barycenter of c). Let $p=(4i,4j,4k)$ for some $i,j,k\in \mathbb {Z}^3$. Then, the vertices $v_{\ell }$, $\ell =1,\dots ,8$, are $\{(4i\pm 2,4j\pm 2,4k\pm 2)\}$; and the vertices $w_{\ell }$, $\ell =1,\dots ,8$, are $\{(4i\pm 1,4j\pm 1,4k\pm 1)\}$, such that, for example, if $v_{\ell }=(4i+2,4j-2,4k+2)$ then $w_{\ell }=(4i+1,4j-1,4k+1)$. The non-square quadrangle $\{x_{\ell _1},x_{\ell _2},x_{\ell _3},x_{\ell _4}\}$ of $h_{\ell }(v_1,\ldots v_8)$, is encoded by the barycenter of the square face $\{w_{\ell _1},w_{\ell _2},w_{\ell _3},w_{\ell _4}\}$, which is in $\mathcal{O}_2$. Finally, a triangle $t(v_{\ell _i},v_{\ell _j})$ is encoded by $r_{e(w_{\ell _i},w_{\ell _j})}\in \mathcal{O}_1$.    $\square$

Table 1. First column: 7 out of 27 polyhedra used in the paper. Second column: their ECM representation. Third column: the proposed codification, where J is the 3D binary image encoding a polyhedral complex P.

Fig. 3.

Digital images encoding the 20 hexahedra showed in Fig. 2.

Now, given a cell $b\in B$, our aim is to directly compute the boundary faces of b without making use of any of the structuring elements listed in [4]. In that paper, boundary relations were obtained by running over a fixed set of 121 structuring elements (see Fig. 4) and looking for the ones that fitted around the point.

Fig. 4.

Set of structuring elements (modulo reflections and 90 degree rotations) for computing boundary face relations used in [4]: 3 structuring elements for the boundary of a $1{-}$cell (first row); 5 structuring elements for the boundary of a $2{-}$cell (second row); 8 structuring elements for the boundary of a $3{-}$cell (third and fourth rows).

Proposition 3

Let $p\in B$ be an $\ell {-}$cell of P, $\ell =1,\ldots , 3$. Then the $(\ell -1){-}$faces of p can be obtained by the following process. For each $q\in N_6^1(p)$:

• (1) if $q\in B\cap \mathcal{O}_{\ell -1}$, then q is an $(\ell -1){-}$face of p.

• (2) if $q\notin B$, then

  • (2.1) if $q'=p+2(q-p)\in B\cap \mathcal{E}_{\ell -1}$, then $q'$ is an $(\ell -1){-}$face of p;

  • (2.2) else, if there exists $q''\in B\cap N_8^1(q)\cap \mathcal{E}_{\ell -1}$ or $q''\in B\cap N_{12}^1(q)\cap \mathcal{E}_{\ell -1}$, then $q''$ is an $(\ell -1){-}$face of p.

Proof. The cell $p\in B$ corresponds to a specific polyhedron or face of a polyhedron described in Definition 1, depending on the type of coordinates of p and on whether or not there are points of B around p (Proposition 2). For each of them, one of the structuring elements of Fig. 4 (modulo reflection and 90 degree rotation) provides its boundary faces. Hence, the proof consists in a case verification to set the equivalence between the known structuring element and the points satisfying either (1) and/or (2.1) and/or (2.2).

Fig. 5.

On top, a naive example of a 3D polyhedral complex $P_{ex}$ over a picture (where vertex $v_0$ has coordinates (2, 2, 2)) and its codification J (proposed in this paper) on the right. Color illustrates the dimension of the cell. Matrices on bottom: the binary image J seen as a set of binary matrices.

• For $p\in \mathcal{E}_{\ell }$.

  • If $N_6^1(p)\cap B= \emptyset$, then one of the structuring elements in Fig. 4(a,d,i) fits around p [4] and the points in $N^2_6(p)\cap \mathcal{E}_{\ell -1}$ are the $(\ell -1){-}$faces of p. These points are obtained by applying (2.1).

  • Else,

    • $*$ If $p\in \mathcal{E}_0$, p is a size$-2$ cube, and hence, structuring element in Fig. 4j fits around p, whose points are obtained by step (1).

    • $*$ If $p\in \mathcal{E}_1$, then p is either a size$-2$ cube or a pyramid k(v, w), so one of the structuring elements in Fig. 4(j,n) fits around p, whose points are obtained by applying (1).

    • $*$ If $p\in \mathcal{E}_2$, then $p=p_{\ell }(v, v_1,v_2,v_3)$, $\ell =1,2,3,4$, or p is a size-2 cube, so one of the structuring elements in Fig. 4(j,o,p) fits around p, whose points are obtained by applying (1).

    • $*$ If $p\in \mathcal{E}_3$, then p is one of $\{h_{\ell }(v_1,\ldots v_8)\}_{\ell =2,\ldots ,22}$ and hence, one of the structuring elements in Fig. 4(j,k,l,m) fits around p, whose points are obtained by applying (1) and (2.1).

• For $p\in \mathcal{O}_\ell$:

  • If $p\in \mathcal{O}_0$, then p is a vertex of P and the proposition does not apply.

  • If $p\in \mathcal{O}_1$, then p is an edge of either a cube c(v) or a pyramid k(v, w). In the first case, the structuring element in Fig. 4b applies, that is obtained by (1). In the second case, the structuring element in Fig. 4c fits around p. Then, step (1) in the proposition provides one of the $1{-}$faces and step (2.2) provides (unambiguously) the other one.

  • If $p\in \mathcal{O}_2$, then p is one of the $2{-}$cells on the boundary of the polyhedra in Definition 1(b,c,d):

    Table 2. Boundary-face representation of $P_{ex}$ (see Fig. 5): E can be seen as a binary $22\times 54$ matrix, F as a binary $54\times 48$ matrix and C as a binary $48\times 15$ matrix.

    • $*$ If $p\in \{(2i+1,4j+2,4k+2),\,(4i+2,2j+1,4k+2),\,(4i+2,4j+2,2k+1)\}$, then p is a square face of a size$-2$ cube and, structuring element in Fig. 4e fits around p, whose points are obtained by applying (1).

    • $*$ If $p\in \{(4i+2,4j,2k+1), (4i,4j+2,2k+1),(2i+1,4j+2,4k),(2i+1,4j,4k+2),(4i+2,2j+1,4k),(4i,2j+1,4k+2)\}_{i,j,k\in \mathbb {Z}}$, then p is either a triangular face of a pyramid k(v, w) or a square face of a size$-2$ cube. In the first case, structuring element in Fig. 4f fits around p and in the second case, the one in Fig. 4e. Both cases are obtained by applying (1).

    • $*$ If $p\in \{(4i,4j,2k+1), (2i+1,4j,4k), (4i,2j+1,4k)\}_{i,j,k\in \mathbb {Z}}$, then p is a quadrangular face of some polyhedron from Definition 1d. The structuring elements that provide the faces in the different cases are those in Fig. 4(e,g,h). For the one in Fig. 4e, step (1) applies; in the other two cases, step (1) and (2.2) apply.

For each case, there are no other points $q\in \mathcal{O}_{\ell -1}$ or $q', q''\in \mathcal{E}_{\ell -1}$ that could be returned by the proposed steps. This can be deduced from the type of coordinates of p and its neighbors.    $\square$

In Fig. 5, a small example of a well-composed polyhedral complex over a picture is shown together with its codification under the form of a 3D binary digital image J. In fact, J can be given as a 3D binary matrix of size $9\times 9\times 9$, which are the nine 2D binary matrices shown on the bottom of Fig. 5. To give a naive comparison with our codification, we show in Table 2 the boundary-face representation of P. We can see that in our codification we just need to store a $9\times 9\times 9$ binary matrix plus the coordinates of vertex $v_0$. On the other hand, to store the boundary-face representation of P, we need to store the coordinates of all the vertices of P (list V) plus the three incidence matrices E, F and G of size $22\times 54$, $54\times 48$, $48\times 15$, respectively.

5 Conclusions

Given a well-composed polyhedral complex P over a picture (see Sect. 4), we have proved that geometric and topological information of the cells of P can be encoded by just using a 3D binary image. This way, the type of 3D coordinates codifying each cell, together with the information encoded at some neighbor points provide both the geometry and the boundary faces of each cell without the need of using a set of structuring elements. More specifically, this means a more efficient treatment of the ECM representation developed in [4] to codify well-composed polyhedral complexes that are homotopy equivalent to the standard cubical complex representing a (non-necessarily well-composed) 3D binary image.