Wave-Particle Dualism in Action

Abstract

The wave-particle dualism, that is the wave nature of particles and the particle nature of light together with the uncertainty relation of Werner Heisenberg and the principle of complementarity formulated by Niels Bohr represent pillars of quantum theory. We provide an introduction into these fascinating yet strange aspects of the microscopic world and summarize key experiments confirming these concepts so alien to our daily life.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The wave-particle dualism, that is the wave nature of particles and the particle nature of light together with the uncertainty relation of Werner Heisenberg and the principle of complementarity formulated by Niels Bohr represent pillars of quantum theory. We provide an introduction into these fascinating yet strange aspects of the microscopic world and summarize key experiments confirming these concepts so alien to our daily life.

“It looks strange and it looks strange and it looks very strange; and then suddenly it doesn’t look strange at all and you can’t understand what made it look strange in the first place.”

Gertrude Stein

The opening quote refers to modern art but might as well refer to the light quantum, that is the photon. Indeed, in his lecture entitled “Delayed choice experiment and the Bohr-Einstein-Dialogue” on June 5, 1980 in a joint session of the American Philosophical Society and the Royal Society John Archibald Wheeler notes:

“The quantum, the most revolutionary principle in all of science and the strangest continues today to unfold its wonders and raise every deeper questions about the relation between man and the universe.”

The year of the light constitutes an excellent opportunity to review the progress in our understanding of the light quantum and its idiosyncrasies made possible only recently thanks to novel experimental techniques of addressing and manipulating single particles.

1.1 The Strange Photon

Although we have learned a lot we still lack the full picture. In particular, there is still no unique answer to the long-standing question: “What is a photon?”

In the present essay we of course do not answer this deep question either but illuminate one important aspect of the photon that on first sight looks very strange that is the wave-particle dualism. Indeed, according to the quantum theory of radiation the photon is a wave and a particle at the same time and their respective distinct features manifest themselves in countless phenomena. The double-slit experiment with individual photons is one of them.

The ultimate goal of our article is to discuss a rather special double-slit experiment based on two entangled photons which seems to show simultaneously the wave and the particle nature of light. Such a behavior which is strictly forbidden by quantum theory and, in particular, by the principle of complementarity makes the photon even stranger. However, a closer look at the details of the light generation reveals that there is no violation of quantum mechanics, and in the words of G. Stein: “…suddenly it doesn’t look strange at all.”

1.2 Overview

In order to lay the foundations for our study we first recall important concepts of quantum mechanics such as the wave nature of matter, the uncertainty principle, complementarity, and the quantum eraser. We then focus on a brief description and an elementary analysis of this experiment.

Our article is organized as follows: In Sect. 19.2 we focus on the trademark of quantum mechanics, that is, discrete events and yes/no answers arising from measurements of single particles. Closely associated with this notion is the wave nature of particles discussed in more detail in Sect. 19.3. Here we consider not only matter waves but also light waves.

We then dedicate Sect. 19.4 to a historical overview starting with the Heisenberg uncertainty principle and arriving via the formulation of the principle of complementarity at the delayed-choice experiment and the game of twenty questions in its surprise version. In Sect. 19.5 we turn to the Bohr–Einstein dialogue on the recoiling double-slit and the quantum eraser.

Finally, Sect. 19.6 is devoted to the discussion of the double-slit experiment using two entangled photons suggesting “which-path” information while observing at the same time interference. We explain these rather counter-intuitive results by considering an elementary model. In particular, we demonstrate that the mutually exclusive scattering arrangements involve different atoms. Therefore, there is no contradiction to the principle of complementarity. We conclude in Sect. 19.7 by summarizing our results and by providing ideas for further research.

2 From the Macro- to the Microcosmos

The transition from the macroscopic to the microscopic world, that is from our daily life to that of an electron orbiting a nucleus, is not as smooth as the limit of classical mechanics of a particle moving with a large velocity to that with a small velocity, or vice versa. In the present section we provide an elementary introduction into some peculiarities of the quantum world, in particular the importance of single events. This fact which emerges from an elementary gedanken experiment suggests that trajectories of particles do not exist in the microscopic world.

2.1 Atommechanik

Newtonian mechanics is extremely successful and describes correctly the motion of macroscopic bodies, such as cars, trains, planes, and even planets. Indeed, the description of the motion of the earth around the sun on a Kepler orbit has been a great triumph of classical mechanics.

Of course there are deviations from Newtonian mechanics, for example, due to special relativity when the velocity of the moving object approaches the speed c of light, or due to general relativity, when the curvature of spacetime is no more negligible. An example for the latter is the perihelion shift of mercury.

Why not apply the Newtonian concept of planetary motion which has worked so beautifully for the macro-cosmos to problems of the microscopic world, such as a hydrogen atom. In complete analogy to the earth–sun system we now consider the motion of a single electron around the proton. The resulting Rutherford model of hydrogen supplemented by the appropriate quantization conditions of the actions as proposed by Niels Bohr, Arnold Sommerfeld, and William Wilson gives us a first glimpse of the inner workings of the atom.

However, the early success of “Atommechanik” as this field was called quickly faded. There were too many features of the atom this theory could not explain. Only quantum mechanics developed by W. Heisenberg, Erwin Schrödinger, and Paul Adrien Maurice Dirac could provide a complete and consistent picture.

What is the crucial element not included in Atommechanik? What is the unique feature distinguishing the macro- from the micro-world? Where is the borderline between them, as asked in Fig. 19.1?

Fig. 19.1

The interface of the classical and the quantum world depicted as the border between two countries with either well-defined structures such as the right part of the guard house, or fuzzy ones represented, for example, by the Schrödinger cat sitting alive in the tree and laying dead in the grass. [Taken from Zurek WH (1991) Decoherence and the transition from quantum to classical. Physics Today 44:36–44]

2.2 Single Events and Probabilities

In order to provide at least some partial answers to these questions we now consider gedanken experiments which are extremely popular and very helpful in quantum theory. Gedanken experiments whose outcome is predicted by quantum mechanics are constructed to emphasize certain alien aspects of the underlying theory and can be performed in our brain without ever really going to a laboratory.

We illustrate the concept of a gedanken experiment using a specific example. How to determine the motion of an electron in an atom around the nucleus?

Since the electron has an average separation from the nucleus which is of the order of a few Bohr radii we cannot just simply take a camera and take pictures of the electron, or look at it with a microscope. The only way to gain more information is to send a probe into the atom.

In the discussion of what defines the borderline between the microscopic and the macroscopic world one quantity stands out most clearly and allows us to make such a decisive cut: it is Planck’s constant $\hslash$. For a given object we can compare its angular momentum J to $\hslash$. When J is of the order of $\hslash$ we certainly deal with a problem from the microscopic world.

In classical mechanics, that is in the mechanics of macroscopic bodies we observe trajectories. At every instance of time we can determine uniquely the position of the body. The positions at different times form a world line in spacetime.

However, there are no continuous trajectories for a quantum particle. This feature originates from the discreteness of the particles and reflects the fact that we are trying to learn something about the properties of the microscopic world. Since we do not have a microscope with a resolving power large enough to observe the electron in the atom we have to send a probe from the outside into the atom. By measuring the change of that probe induced by the interaction with the electron we learn something about the electron.

When we use a single particle as a probe we get one bit of information from the detection of the scattered probe. In order to obtain more information we have to repeat this experiment many times. In this way these scattering events, each obtained from single quantum probes, provide us with information about the inside of the atom.

This analysis brings out most clearly that we do not see the electron in the atom move around the nucleus as suggested by the Bohr–Sommerfeld–Wilson atom model, but rather find probabilities that the electron had been at a certain position. Obviously, the scattering events do not tell us with certainty the locations where the electron was at a given time.

2.3 Single Clicks Reconstruct the Microcosmos

In summary, the microscopic world is only accessible through probes which have to be of the same size as the elements of the microscopic world that we want to investigate. Hence, we probe quantum objects by single microscopic particles.

From every scattering event we gain one bit of information and complete our picture of the microscopic world by recording a multitude of single events, that is, single clicks. Once more we are reminded of a quote by J. A. Wheeler who summarized this situation in his poetic style:

“Do we not do better to recognize that what we call existence consists of countably many iron posts of observations between which we fill in by an elaborate papier-mâché construction of imagination and theory?”

3 Double-Slit Experiments with Light and Matter

Wave-like aspects of light have already been observed around 1660. For example, Francesco Grimaldi noticed that when light passes a narrow slit in a wall the edges of the narrow band of brightness are slightly blurred suggesting that light diffracts.

However, it was only in the beginning of the twentieth century that a similar revolution took place for matter. Up to that moment electrons, atoms, or molecules were considered particles. However, the experiments of Clinton Joseph Davisson and Lester Halbert Germer in 1926 who scattered electrons from a nickel crystal brought out most clearly that also matter displays wave features as proposed earlier by Louis-Victor Pierre Raymond de Broglie.

In the present section we first recall the transition from the corpuscular theory of light due to Isaac Newton to the wave interpretation of Thomas Young. We then briefly review various double-slit experiments with matter waves and conclude by emphasizing subtleties associated with this arrangement.

3.1 Light: Corpuscle Versus Wave

More than 200 years ago, Th. Young demonstrated the wave nature of light. However, he did not use slits in an opaque screen as widely believed but rather pinholes. Despite this fact this famous experiment carries the name double-slit experiment.

Before his impressive demonstration the dominance of the corpuscular theory of light proposed by I. Newton had suppressed any wave theory. The following quote from Th. Young’s article may illustrate this strong influence of I. Newton even almost 100 years later:

“In making some experiments on the fringes of colors accompanying shadows, I have found so simple and so demonstrative a proof of the general law of the interference of two portions of light, which I have already endeavored to establish, that I think it right to lay before the Royal Society, a short statement of the facts which appear to me so decisive. The proposition on which I mean to insist at the present, is simply this, that fringes of colors are produced by the interference of two portions of light; and I think it will not be denied by the most prejudiced, that the assertion is proved by the experiments I am about to relate, which may be repeated with great ease, whenever the sun shines, and without any other apparatus than is at hand to every one.”

He continues his critique of the corpuscular theory by stating:

“Those who are attached to the Newton theory of light, or to hypotheses of modern opticians, founded on views still less enlarged, would do well to endeavor to imagine anything like an explanation of these experiments, derived from their own doctrines; and, if they fail in the attempt, to refrain at least from idle declamation against a system which is founded on the accuracy of its application to all these facts, and to a thousand others of a similar nature.”

It is amusing that the quantum theory of radiation brings back the particle aspect of light in the form of the photon, that is, the quantized excitation of a mode of the radiation field. In this way I. Newton and his corpuscular theory were vindicated after all.

3.2 Matter: Particle Versus Wave

Next we turn to the wave nature of matter which under appropriate conditions can also manifest itself in interference fringes in the far field of a double-slit. Here we discuss “slits in space” as well as “slits in time.”

3.2.1 Slits in Space

In Fig. 19.2 we show the essential ingredients of a double-slit experiment for matter waves consisting of a particle source, an opaque screen with two slits, and a detector in the far field. We assume that the source emits one particle at a time and there is a long delay between two successive emissions. In this case there is only a single particle between the source and the detector at a time.

Fig. 19.2

Elementary building blocks of a double-slit experiment for particles involving a source of particles (left), a screen with two slits (middle), and a detector in the far field (right). The particles to be scattered could be electrons, neutrons, atoms, or rather large molecules. We observe an oscillatory count rate ( far right) as the detector moves along an axis parallel to the screen demonstrating the existence of matter waves

Each particle can only go either through the upper or the lower slit. After many particles have passed the slits, we should observe a double-hump distribution where the two maxima correspond to the two slits. However, numerous experiments clearly show that under appropriate conditions this by classical notions motivated picture is incorrect.

Figure 19.3 depicts the intensity pattern of neutrons in the far field of a mechanical double-slit which displays interference fringes. This effect is quite remarkable when we recognize the count rates on the vertical axis. At a maximum of the fringe we find approximately 4000 counts per 125 min. This rate corresponds to two neutrons going through the apparatus per second. Since the velocity of the neutrons was 200 m/sec there was never more than one neutron in the apparatus.

Similar experiments have been performed earlier by Claus Jönsson in the group of Gottfried Möllenstedt at the Universität Tübingen with electrons. Figure 19.4 shows the count rate of a double-slit experiment with electrons and the interference fringes are clearly visible.

It is interesting to note that in September 2002 the journal Physics World reported a poll concerning the top ten most beautiful experiments in physics. The Jönsson experiment was the number one.

This phenomenon of matter–wave interference is not limited to neutrons or electrons. Even bigger objects such as the fullerene molecule C₆₀ exhibit an interference pattern, as shown in Fig. 19.5.

Fig. 19.3

Interference pattern of a double-slit experiment with cold neutrons. [Taken from Zeilinger A et al. (1988) Single and double-slit diffraction of neutrons. Rev Mod Phys 60:1067–1073]

Fig. 19.4

Distribution of electrons scattered from two slits in a screen. [Taken from Jönsson C (1961) Elektroneninterferenzen an mehreren künstlich hergestellten Feinspalten. Z f Phys 161:454–474, for an English translation see: Jönsson C (1974) Electron Diffraction at Multiple Slits. Am J Phys 42(1), 4–11]

Fig. 19.5

Double-slit interference pattern (right) of fullerene molecules (left) which are regular structures of 60 carbon atoms in the shape of a soccer ball. For this reason the fullerene molecule is sometimes jokingly referred to as soccerballium. When individual molecules are sent one at a time through a double-slit the pattern found on a screen in the far field shows clear interference fringes. [Taken from Arndt M et al. (1999) Wave particle duality of C₆₀ molecules. Nature 401:680–682]

3.2.2 Slits in Time

A rather intriguing version of a double-slit experiment with electrons was carried out by the group of the late Herbert Walther using ultra-short laser pulses. Here the interference appears in the time rather than the space domain.

Light pulses in the femto-second regime consist of a few optical cycles and can ionize single electrons in atoms, as shown in Fig. 19.6. However, this process only occurs when the associated electric field is above a threshold. Since the pulses are short the intensity necessary for ionization exists only during one or two time periods with an extension of an atto-second. By shifting the envelope of the pulse relative to the oscillation we can control the time window of ionization and create in this way a single- or a double-slit type of excitation of the atom.

Fig. 19.6

Double-slit experiment in time. A sub-cycle laser pulse ionizes an electron in an atom (top). Depending on the phase of the oscillation relative to the envelope (middle) we either have two maxima (left) or a single dominant maximum (right) that can ionize the electron. In case of two maxima we cannot identify which one ionized the electron. As a result, the ionization current (bottom) displays oscillations (left) as a function of energy due to the indistinguishable excitation paths. In contrast, no interference arises for a single intensity maximum (right). [After Lindner F et al. (2005) Attosecond double-slit experiment. Phys Rev Lett 95:040401]

Indeed, the double-slit situation appears when the sub-cycle pulse contains two narrow time windows in which the atom can be ionized. Therefore, the electron which reaches the detector with a well-defined momentum results from field ionization either in the first, or in the second time window. As long as we cannot decide in principle in which one the electron was born the two ionization paths in time must interfere. Since only a single electron is ionized in each event the interference takes place on the level of individual particles. Moreover, it manifests itself in the energy spectrum of the electron shown in the bottom of Fig. 19.6. If there is only one time window for ionization representing a single-slit situation there is no interference.

3.3 The Mystery of the Double-Slit Experiment

The physics of the double-slit experiment has occupied physicists since the early days of quantum mechanics. The rather paradoxical phenomenon of an interference pattern for particles can be expressed most vividly by the following situation borrowed from a wild-west movie.

Imagine a person shooting bullets towards a screen with two slits. Due to the wave nature of the bullets the interference pattern in the far field of the slits enjoys positions where no bullet will ever hit. Hence, a person standing behind the screen at one of these zeros of the fringes is safe. However, if one of the holes gets closed the interference and, hence, the zeros cease to exist. As a consequence, the next bullet might kill the person.

This discussion of the double-slit experiment also brings out most clearly the importance of the single event emphasized already in Sect. 19.2.3 as a building block of our conception of the microscopic world. Indeed, we send individual particles through the apparatus, one at a time. Each particle is detected after it has passed the slits and will either hit the screen at this position or at another position. After we have sent many such particles through the apparatus we have a histogram, that is, a number of counts at every position on the screen which will not be uniform but will show oscillations. From individual counts we have built up a continuous distribution.

4 Complementary Views of an Uncertain World

In the present section we lay the ground work for the discussion of the two-photon double-slit experiment presented in Sect. 19.6 by briefly summarizing pioneering articles related to the principle of complementarity. We admit that this selection is rather biased and mainly motivated by our own considerations. We start from the seminal paper by W. Heisenberg introducing the uncertainty principle and then turn to N. Bohr’s introduction of complementarity culminating in the concept of a delayed-choice experiment and the game of twenty questions in its surprise version.

4.1 The Uncertainty Principle

It was during a stay at Copenhagen in the institute of N. Bohr in 1927 that W. Heisenberg concluded that the discreteness of quantum mechanics and, in particular, the non-existence of a continuous trajectory of a particle make it impossible to determine simultaneously with arbitrary accuracy its position and its momentum. We quote from his seminal paper in which he considers the use of the Compton effect, that is, the scattering of a photon from an electron to determine its position and momentum:

“At the instant at which the position of the electron is known, its momentum therefore can be known up to magnitudes which correspond to that discontinuous change. Thus, the more precisely the position is determined the less precisely the momentum is known, and conversely. In this circumstance we see a direct physical interpretation of the equation $\mathbf{p}\mathbf{q}-\mathbf{q}\mathbf{p}=-i\hslash$. Let q ₁ be the precision with which the value q is known (q ₁ is, say, the mean error of q), therefore here the wavelength of the light. Let p ₁ be the precision with which the value p is determinable: that is here the discontinuous change of p in the Compton effect. Then, according to the elementary laws of the Compton effect p ₁ and q ₁ stand in the relation

$$ {p}_1{q}_1\sim h. $$

(19.1)

That this relation (19.1) is a straight-forward mathematical consequence of the rule $pq-qp=-i\hslash$ will be shown below.¹”

It is interesting to note that in this article W. Heisenberg does not use the notation Δ q and Δ p for the uncertainties but rather q ₁ and p ₁. Moreover, it is also amusing that he applies Schrödinger wave functions rather than matrices to illustrate the consequences of the uncertainty principle. The only remnants of matrix mechanics are the non-commuting operators q and p.

Heisenberg submitted his manuscript during a skiing vacation of N. Bohr who upon his return pointed out various mistakes and brought to light a deeper concept. As a result, W. Heisenberg felt obliged to include the following note added in proof:

“After the conclusion of the foregoing paper, more recent investigations of Bohr have led to a point of view which permits an essential deepening and sharpening of the analysis of quantum-mechanical correlations attempted in this work. In this connection Bohr has brought to my attention that I have overlooked essential points in the course of several discussions in this paper. Above all, the uncertainty in our observation does not arise exclusively from the occurrence of discontinuities, but is tied directly to the demand that we ascribe equal validity to the quite different experiments which show up in the corpuscular theory on one hand, and in the wave theory on the other hand.²”

According to N. Bohr the uncertainty principle does not arise from the discontinuities but from the choice of the wave versus particle description demanded by the specific experimental setup. Hence, he supports the idea of an uncertainty relation but identifies a different origin of it.

4.2 The Birth of Complementarity

The article by N. Bohr summarizing his point of view appeared a year later, that is in 1928, with the title “The quantum postulate and the recent development of atomic theory.” It was based on a lecture he gave on September 16, 1927 in Como at the International Congress of Physics in commemoration of the centenary of the death of Alessandro Volta. The reason for this delay originated from an unusual twist of events associated with his original manuscript on complementarity, his passport, and his train to Como.³

In his typical style N. Bohr draws attention to the fundamental difference between the classical and the quantum world when he states:

“The very nature of the quantum theory thus forces us to regard the space-time coordination and the claim of causality, the union of which characterises the classical theories, as complementary but exclusive features of the description, symbolising the idealisation of observation and definition respectively.”

Here the words “complementary” and “exclusive” enter the stage of physics for the first time.

Moreover, N. Bohr has a clear picture how the observer changes the microscopic world by the intrusion necessary for his measurement. Indeed, he writes:

“…the measurement of the positional coordinates of a particle is accompanied not only by a finite change in the dynamical variables, but also the fixation of its position means a complete rupture in the causal description of its dynamical behaviour, while the determination of its momentum always implies a gap in the knowledge of its spatial propagation. Just this situation brings out most strikingly the complementary character of the description of atomic phenomena which appears as an inevitable consequence of the contrast between the quantum postulate and the distinction between object and agency of measurement, inherent in our very idea of observation.”

Obviously N. Bohr associates with the act of the measurement physical effects on the system to be measured. We shall return to this aspect in Sect. 19.5.

4.3 A Mechanical Model of Complementarity?

In 1939 at the world exhibition in New York the University of Copenhagen presented a mechanical model illustrating the principle of complementarity. Figure 19.7 shows a sketch of this device originating from J. A. Wheeler.

Fig. 19.7

Mechanical model of the principle of complementarity designed by the University of Copenhagen. Reading the numbers on the top faces of the dice stored in the two different compartments of a drawer in a filing cabinet corresponds to measuring two conjugate variables such as position and momentum, or path and interference. Unfortunately, this mechanical model misses the central lesson of quantum mechanics: There is no number on the dice until we make an observation. [Taken from Wheeler JA (1994) At Home in the Universe. AIP Press]

An unusual filing cabinet contains a drawer which can be pulled out in the front as well as in the back and which is divided into two compartments each of which contains a die. The task is to read the number shown on the top of both dice.

However, there is a slight problem. We cannot observe both dice simultaneously. When we pull the drawer to the front we can see only the die in the front compartment. When we push the drawer through to the back we can observe only the one in the back.

Of course, we could first copy down the number on the top of the first die and then pull the drawer out on the other side to have a look at the other die. However, a devilish device hidden underneath the floor of the drawer, such as a little hammer, is set into action as the drawer slides through the cabinet. Due to the kick imparted onto the floor the die whose number has just been recorded gets knocked over.

Although we can now record the number shown on the die confined to the back compartment it does not even make sense to do so. In our attempt to obtain information about the back die we have lost the information about the front one.

Unfortunately, we face the same dilemma if we start from the back die and move the drawer forward. Again the hammer is set in action and makes the knowledge we have just obtained redundant.

Obviously, the top faces of the dice play the role of two complementary quantities, such as position and momentum, and on first sight this model seems to illustrate in an impressive way the principle of complementarity. However, it lacks the fundamental ingredient of quantum mechanics summarized by J. A. Wheeler in the pregnant phrase:

“No elementary quantum phenomenon is a phenomenon until it is a recorded phenomenon, brought to a close by an irreversible act of amplification.”

According to quantum mechanics it is not a meaningful question to ask: What would the numbers on the dice have been, if we measured them. They do not exist until they are observed.

4.4 No Existence Without Measurement

The unusual property of quantum mechanical observables such as position or momentum, or components of angular momentum to take on a definite value only after observation comes out most clearly in the delayed-choice experiment. When we inject a single particle, one at a time, into the upper entrance of the Mach–Zehnder interferometer shown in Fig. 19.8 we expect the particle to either go on the upper or the lower road. When we leave out the beam splitter at the lower right corner we can detect the path of the particle, because only one of the two detectors will respond.

Fig. 19.8

Mach–Zehnder interferometer in a delayed-choice mode. A particle entering the interferometer in one of the two ports at the upper left beam splitter BS₁ either takes the high or the low road. When the beam splitter BS₂ at the lower right corner is inserted the two paths interfere at the two detectors D₁ and D₂. However, when we remove BS₂ we obtain “which-path” information. We can delay our decision concerning BS₂ till the particle hits it. Loosely speaking, at the moment of our decision we force the particle to retrace its tracks and change its history. Indeed, when BS₂ is part of the interferometer as the particle passes BS₁ and we remove BS₂ later we force the particle to alter its nature. Before our decision it was supposed to display interference properties, but afterwards it needs to provide us with path information. In this arrangement the particle was supposed to move along a single path rather than on both paths. This paradoxical situation can only be resolved by the assumption that the particle does not have any path whatsoever until we observe it, nor can it display any interference fringes until we measure them. In the language of J. A. Wheeler: “The particle is a great smoky dragon that is only sharp where it enters the interferometer and where it leaves the interferometer biting the detector”

However, when we do insert the beam splitter and have many particles, one at a time, pass through the interferometer we will find all particles in one of the exit ports provided we adjust the arm length appropriately. This behavior is a consequence of the wave nature of matter. Indeed, due to destructive interference no particles are in the other port.

So far we have only discussed another manifestation of the complementarity principle. However, we can now go one step further, and use our knowledge of the time at which the particle entered the interferometer. Moreover, if we know the initial velocity of the particle we can predict the time at which it will impinge on the second beam splitter. Within the period defined by the entrance of the particle into and its exit from the Mach–Zehnder interferometer we can now decide if we want to insert the second beam splitter or not. In this way we make a delayed choice between our ultimate observation of interference or “which-path.”

We start from a situation where the second beam splitter is present when the particle enters the interferometer. In the language of the macroscopic world the particle has to display its interference nature and has to move on both paths.

This interpretation runs into problems when in the last moment before the particle hits the second beam splitter, we take it out. Now, we are asking for path information and the particle had to go on one path only. However, by that time the particle has almost reached the beam splitter. It can therefore not go back and retrace its tracks. Our procrastination in making a decision, that is, the delayed choice of interference versus “which-path” highlights the idea that in the microscopic world the properties of particles are not well-defined until they are observed.

We emphasize that many delayed-choice experiments with light and matter waves have been performed. They clearly show that the delay has no influence on the observation. We observe the features that we choose to observe. As J. A. Wheeler puts it:

“The past has no existence, except as it is recorded in the presence.”

4.5 Our Questions Create the Microscopic World

The delayed-choice experiment demonstrates in a striking way that observables of a quantum system have no existence until we observe them. Hence, our measurement has an enormous influence on how we view the microscopic world. In order to emphasize this aspect J. A. Wheeler has coined the phrase “participatory universe,” whose meaning stands out most clearly in the game of twenty questions in its surprise version.

A group of friends sends one victim out of the room while his/her remaining colleagues agree on a word to be guessed. After the person has returned he/she is allowed to ask twenty questions. The answers must be given truthfully with “yes” or “no” and after this question-answer-period the person is confronted with the challenge to produce the word.

However, when once the turn came to J. A. Wheeler to be the victim he found upon reentering the room his friends with a grin on their faces. He knew something was up.

He started by asking: “Is it a cloud?” A quick response came: “No!” The second question: “Is it a car?” Now the answer took a little bit longer. His friends had to think about it and finally they answered: “No!” The more questions he asked the longer it took them to answer.

This hard work on their part was difficult to understand because a word had been agreed on and all that had to be done was to see if his guess was correct. Nevertheless, it took even longer as they approached the final trial answers.

Finally J. A. Wheeler had to make a decision. Challenging one of his opponents he put forward one final question: “Is it a bear?”

Again the challenged had to think for a long time before he eventually admitted: “Yes, you are right!” – Laughter broke out in the room.

How come his friends had to think at least as hard as he? The answer to this question originates from the fact that when he had left the room they had decided not to agree on a word at all. However, their individual answers would have to be consistent with each other and he would only win if his guess was consistent with the chain of their answers.

As a result of these new rules the game was as difficult for them as it was for him. No word existed in the room until it was challenged by the observer who became the “creator” of the word.

This game of twenty questions in its surprise version encapsulates the crucial point of quantum mechanics: The microscopic world does not exist until we observe it.

5 Physical Disturbance Versus Correlations

In our discussion of the principle of complementarity in Sect. 19.4.2 the second quote of N. Bohr shows that he associated with a measurement of the microscopic world a physical disturbance. His point of view stands out most clearly in the Bohr–Einstein discussion of the recoiling double-slit designed by Albert Einstein to obtain “which-path” information together with interference fringes. This dialogue started at the Solvay meeting of 1927 and continued for almost 30 years.

We dedicate this section to a brief introduction of this gedanken experiment which later has been analyzed by William Wootters and Wojciech Hubert Zurek using the formalism of modern quantum mechanics and, in particular, of joint measurements. We conclude by highlighting the key ingredients of the quantum eraser developed in various forms by Marlan Orvil Scully and coworkers.

5.1 Recoiling Double-Slit

With his friend the philosopher Harald Høffding, N. Bohr frequently discussed the double-slit experiment and Høffding asked: “Where can the particle be said to be?” Bohr answered in the familiar Hamlet way: “To be? To be? What does it mean ‘to be’?”

What does it mean to talk about a particle going through the upper or lower slit, or through both slits if we do not make a measurement to prove our claim? But how can we make such a measurement?

The proposal of A. Einstein for such a measurement of “which-path” information and interference involves a movable rather than a fixed screen. By measuring the momentum transfer of the scattering particle on the slit, and the interference fringes in the far field A. Einstein argued that in principle we can observe simultaneously position and momentum with arbitrary accuracy. However, N. Bohr showed that this claim is not correct since the momentum transfer of the scattering particle wipes out the fringes. Measurements of this type are still limited by the uncertainty principle.

In 1979 W. Wootters and W. H. Zurek revisited this arrangement of a recoiling double-slit and demonstrated that the interference pattern is surprisingly sharp even when the trajectories have been determined with a fairly high accuracy. In their analysis the entanglement between the center-of-mass motions of the scattering particle and the slit plays a crucial role.

5.2 Quantum Eraser

We emphasize that the mechanism for the destruction of the interference fringes discussed in the preceding subsection relies heavily on random phase disturbances. Indeed, the key argument is always the physical transfer of momentum which leads to an uncontrollable phase disturbance and wipes out the fringes. We now analyze two situations which show that this notion is not correct.

5.2.1 Double-Slit with Two Atoms

A new era in the analysis of the double-slit experiment started in 1982 with the proposal of the quantum eraser illustrated in Fig. 19.9. Here the two mechanical slits are replaced by two identical atoms excited by the incident radiation. Each atom decays with the emission of a photon which is detected in the far field. When the radiation is so weak that only one of the two atoms gets excited at a time the paths of excitation can either interfere giving rise to fringes in the far field, or leave “which-path” information in the atom creating a smooth intensity pattern.

Fig. 19.9

Realization of a double-slit experiment based on the scattering of light from two atoms (top) and the concept of the quantum eraser (bottom). In this arrangement we replace the two slits in the screen by two atoms in the absence of any screen and scatter one light quantum from both atoms which are initially in the ground state. After the scattering event both atoms are again in their respective ground states provided we deal with two-level atoms. Since in this case it is impossible to tell which atom scattered the quantum we observe interference in the far field (top-left). For two three-level atoms one will always remain in the long-living intermediate state which provides us with “which-path” information and no interference occurs (top right). However, the fringes reemerge when instead we use two four-level atoms (bottom) together with a joint measurement between the two emitted quanta γ and ϕ. In this case we have erased the “which-path” information of the scattering since both atoms have again returned to their ground states. It is this process of erasing the “which-path” information which recreates the interference fringes

This decisive difference is dictated by the internal structure of the atoms. In order to bring this fact out most clearly we first consider two two-level atoms which are initially in their ground states. After the excitation by and subsequent emission of the photon both atoms are again in their ground states. As a result, we cannot tell from the final arrangement which atom has scattered the light and interference fringes occur.

However, when we use two three-level atoms with a long-living intermediate state the scattering path can be reconstructed from the final internal state. Indeed, the atom that has been excited and has reemitted the photon will be left in the middle state, whereas the atom that did not participate in the scattering process is still in the ground state. Due to the availability of “which-path” information no fringes appear in this situation.

We finally consider a four-level atom. After the emission of the photon γ and the decay to the intermediate state we pump into the fourth level which decays rapidly to the ground state by emitting a second photon ϕ. The intensity pattern of γ-photons measured in the far field now conditioned on the detection of ϕ-photons displays oscillations since we have erased the information about the path of the excitation.

The quantum eraser brings out clearly that the disappearance of the interference fringes is not related to uncontrollable disturbances of the phases of the atoms, or the field, but rather originates from the correlations established between the internal states of the atom and the field.

5.2.2 Double-Slit with Two Cavities

This shift of paradigm is also emphasized by the gedanken experiment shown in Fig. 19.10 combining the wave nature of matter, that is, atom optics with cavity quantum electrodynamics. Here a single two-level atom whose transverse center-of-mass motion is in a superposition of two locations, prepared, for example, by a double-slit, passes two high Q-cavities whose mode maxima are aligned with these slits. The atom is initially in the excited state and the experimental parameters are chosen such that the atom must deposit its internal excitation in one of the two cavities. Hence, the manifestation of interference in the transverse center-of-mass motion depends on the initial state of the cavities.

Fig. 19.10

“Which-path” information encoded in the quantum states of two cavity fields. A single two-level atom initially in its excited state and with a center-of-mass motion in a coherent superposition of passing the upper and the lower cavities interacts with the single-mode fields indicated here by their lowest modes in such a way as to deposit with certainty its internal excitation. When both fields are in a number state $\left|n\right\rangle$ one of them must change by one quantum, that is go from $\left|n\right\rangle$ to $\left|n+1\right\rangle$ and in this way create “which-path” information. As a consequence, no interference occurs in the center-of-mass motion in the far field of the second double-slit. However, when both fields are in a coherent state $\left|\alpha \right\rangle$ of large amplitude one quantum does not make a difference. In this case the path of the atom cannot be reconstructed and fringes emerge

Indeed, when both are in a number state $\left|n\right\rangle$ the photon placed by the atom in one of the cavities increases the corresponding photon number n by one unit. We can reconstruct by this change the path the atom has taken, and since number states corresponding to different photon numbers such as $\left|n\right\rangle$ and $\left|n+1\right\rangle$ are orthogonal no interference fringes occur.

However, for a coherent state $\left|\alpha \right\rangle$ of large average number $\overline{n}$ of photons, that is $1\ll \overline{n}\equiv \left|\alpha \right|{}^2$, this change by one photon is negligible and the two coherent states corresponding to $\overline{n}$ and $\overline{n}+1$ are not orthogonal. As a consequence, in this case the path is unknown to us and interference fringes emerge.

Orthogonality of field states instead of uncontrollable phase changes as the eraser of interferences—this statement serves as the one-sentence-summary of this version of “which-path” detectors. It is interesting to note that this insight has led to a lively controversy. Indeed, the group of the late Daniel F. Walls has repeatedly emphasized that there is still room for an interpretation in terms of phase disturbances. However, the seminal experiment based on atom interferometry by the group of Gerhard Rempe has tilted the scale towards the notion of orthogonality.

6 A Two-Photon Double-Slit Experiment

We now briefly highlight the key features of a recent experiment on wave-particle dualism using entangled photons performed in the group of Ralf Menzel. On first sight their results seem to indicate a break-down of the principle of complementarity. However, a closer analysis of the groups of atoms creating the registered photons leading to “which-path” information and interference reveals that they are different in the two arrangements. As a consequence, this experiment constitutes another impressive verification of this corner stone of quantum theory.

6.1 A Violation of the Principle of Complementarity?

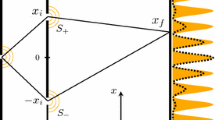
Figure 19.11 highlights the essential components of the experiment by Menzel et al. Here, a laser in a mode which displays two distinct maxima pumps a crystal and two entangled photons are born. The resulting two pairs consisting of signal and idler photons at the exit of the crystal are imaged with the help of a polarizing beam splitter onto the two slits of a double-slit and onto a single-photon counting detector D₁. Since the distances from the beam splitter to D₁ and to the double-slit are identical, the two spots of the signal photon in the two slits correspond to the two spots of the idler photon on D₁. Moreover, the low intensity of the pump beam ensures that only one photon pair is created at a time.

Fig. 19.11

Essential ingredients of the Menzel et al. experiment aimed at observing interference while obtaining “which-path” information in a double-slit arrangement. We pump a nonlinear crystal (gray area) with a light beam of transverse mode function u = u( y) with two distinct intensity maxima and a node between them. The correlated photon pair consisting of the signal and the idler photon and emerging from the crystal in two distinct spots is divided by a polarizing beam splitter. The signal photon passes a double-slit and is detected on detector D₂ which is either in the near field, or the far field. The widths and separation of the two slits are adjusted to match the two intensity spots on the end of the crystal. The idler photon is measured on the detector D₁ which is arranged in a way as to ensure that the distances from the beam splitter to D₁ are identical to the ones to the two slits. In this way the idler photon which is entangled with the signal photon allows us to obtain “which-path” information about the latter without ever touching it. Indeed, D₁ can be positioned on the left or right spot as indicated in the figure. We always perform measurements on the signal photon in coincidence with the idler photon

When we now observe on D₁ the idler photon in the left (right) intensity spot the signal photon is measured by the detector D₂ behind the upper (lower) slit. In this way we employ the entanglement between the signal and the idler photon to obtain “which-path” information about the signal photon without ever touching it.

However, we can also observe interference fringes while at the same time we gain “which-path” information when we scan D₂ in the far-field region of the double-slit along the vertical direction and measure in coincidence with the idler photons detected on D₁ in the left spot. In this case we still find interference fringes.

The appearance of fringes in coincidence is surprising since the idler photon provides us with “which-path”-information about the signal photon which still displays interference. In contrast, the principle of complementarity seems to suggest no interference.

6.2 Different Atoms Yield “Which-Path” or Interference

We now discuss these rather counter-intuitive results of the Menzel et al. experiment using the model summarized in Fig. 19.12. In particular, we explain the appearance of an interference pattern in the far field in coincidence with the “which-path” information contained in the correlations of the near field. However, we emphasize that there is no violation of the principle of complementarity.

In order to understand the origin of the observed near-field coincidence measurements, and in particular, the perfect correlations between the signal and the idler photon created by the subsequent emissions from a three-level atom we assume for the sake of simplicity that both detectors are in the plane parallel to the screen and consider a vanishing time delay between the clicks on D₁ and D₂. Hence, the atoms emitting the two photons must be in the plane located between the two detectors. When both detectors are in the same intensity maximum of the double-hump structure this plane is at the center of the maximum as well. As a result, we find simultaneous clicks in the two detectors.

Fig. 19.12

Elementary model to explain the correlations observed in the Menzel et al. experiment. We consider a frozen gas of three-level atoms which are excited by a single photon in a mode consisting of a coherent superposition of two light pencils. When the two detectors are both located at the end of the cell (near field) two clicks at the same time registering the signal and idler photon can only result from atoms that are on the symmetry line half-way between the two pencils (top). Due to the special mode function these atoms are not excited and the probability for this event to occur vanishes. However, when one detector is in the near field and the other in the far field (bottom) the idler photon triggers the detector in the near field. Due to the double-hump structure of the mode function, this click could have come from any atom excited by the two pencils with identical separations from the detector (dashed line). As a result, we observe interference fringes in the far field, in complete accordance with the scattering situation of two-level atoms discussed in Fig. 19.9

However, when they are in different maxima the only atoms satisfying the coincidence condition are half-in-between the detectors, that is, at the node of the mode as indicated in the top of Fig. 19.12. Therefore, the only atoms that could cause the appropriate clicks are not excited. From these perfect correlations between idler and signal photon on the left detector-upper slit or right detector-lower slit we deduce our “which-path” information. We get this knowledge about the signal photon from the idler photon.

Next we consider the measurements which involve the detector D₁ in the near field and D₂ in the far field. Here the idler photon which triggers D₁ was emitted by one atom anywhere in the light pencils. However, we cannot distinguish between two atoms with identical separations from D₁ as indicated by the bottom of Fig. 19.12. As a result, we find the interference of the signal photon emitted from two indistinguishable atoms very much in the spirit of Fig. 19.9.

6.3 No Contradiction But Confirmation

We are now in a position to summarize our main results. Three features were crucial for obtaining the on first-sight surprising results of the Menzel et al. experiment: (1) A special mode function of the electromagnetic field consisting of a coherent superposition of two maxima, (2) the entanglement between two photons, and (3) a joint measurement of both of them.

When both detectors are in the near field there are no counts at the same time since the only atoms that could have caused such a result sit at a node of the field and cannot be excited. When one detector is in the near field and one in the far field two indistinguishable atoms lead to an interference signal in the joint count statistics. Since the two experiments correspond to two different arrangements and different atoms are involved there is no contradiction to the principle of complementarity.

7 More Questions than Ever

At the center of our essay was the double-slit experiment symbolizing the wave-particle dualism of quantum theory. We have provided a historical perspective and at the end have addressed a rather counter-intuitive experiment. Although there exists a straight-forward explanation many questions associated with this outcome and avenues for further research offer themselves. Here we only allude to one.

Is it possible to perform the Menzel et al. experiment with atoms and would we find the same result? On first sight the answer is “yes” since we can create entangled atoms in complete analogy to photons. But is the measurement process the same?

This question is closely related to the discomfort of W. E. Lamb with the concept of the photon. Whereas in the case of the atoms a description based on single-particle quantum mechanics suffices the photon experiment requires quantum field theory. In the latter the measurement does not reduce the mode function but annihilates the quantum in the mode and leaves the mode intact. However, in the case of the atom the measurement leads to a localization of the particle due to the reduction of the wave packet.

We have started our article by a quote from J. A. Wheeler. Therefore, it is appropriate to close it with the following summary from the same lecture which emphasizes again the influence of the measurement and the role of the observer:

“Are billions upon billions of acts of observer—participancy the foundations of everything? We are about as far as we can be today from knowing enough about the deeper machinery of the universe to answer this question. Increasing knowledge about detail has brought an increasing ignorance about plan. The very fact that we can ask such a strange question shows how uncertain we are about the deeper foundations of the quantum and its ultimate implications.”

Although we have made impressive progress in our understanding of the photon since Wheeler’s lecture we are still far away from being able to say that we have discovered “‘the plan” or with the words of G. Stein that we “can’t understand what made it look strange in the first place.”