A Note on the Numerical Evaluation of the Hartman–Watson Density and Distribution Function

Abstract

The Hartman–Watson distribution is an infinitely divisible probability law on the positive half-axis whose density is difficult to evaluate near zero. We compare three different methods to evaluate this density and show that the straightforward implementation along Yor’s explicit formula can be improved significantly by resorting to dedicated Laplace inversion algorithms. In particular, the best method seems to be an approach that is specifically designed for distributions from the Bondesson class, to which the Hartman–Watson distribution belongs. The latter approach can furthermore be extended to yield an efficient Laplace inversion algorithm for evaluating the distribution function of the Hartman–Watson law.

1 Introduction

In the process of studying the probability distribution of the integral over a geometric Brownian motion, [14] introduced the function

$$\begin{aligned} \theta (r,x):=\frac{r\,e^{\frac{\pi ^2}{2\,x}}}{\sqrt{2\,\pi ^3\,x}}\,\int \limits _{0}^{\infty }e^{-\frac{y^2}{2\,x}-r\,\cosh (y)}\,\sinh (y)\,\sin \Big ( \frac{\pi \,y}{x}\Big )\,\mathrm {d}y, \end{aligned}$$

(1)

for $r,x>0$. Denoting by

$$\begin{aligned} I_{\nu }(z):=\sum _{m=0}^{\infty }\frac{1}{m!\,\Gamma (m+\nu +1)}\,\Big ( \frac{z}{2}\Big )^{2\,m+\nu } \end{aligned}$$

(2)

the modified Bessel function of the first kind, the function $f_r(x):= \theta (r,x)/I_0(r)$, $x >0,\,r>0$, is the density of a one-parametric probability law, say $\mu _r$, on the positive half-axis, called the Hartman–Watson law. The Hartman–Watson law arises as the first hitting time of certain diffusion processes, see [10], and is of paramount interest in mathematical finance in the context of Asian option pricing, see [2, 6, 14]. It was shown in [7] that this law is infinitely divisible with Laplace transform given by $\varphi _r(u):= I_{\sqrt{2\,u}}(r)/I_0(r)$, $u \ge 0$. Moreover, it follows from a result in [10] that $\mu _r$ is not only infinitely divisible, but even within the so-called Bondesson class, which is a large subfamily of infinitely divisible laws that is introduced in and named after [5]. Notice in particular that it follows from this fact together with ([13, Theorem 6.2, p. 49]) that the function $\varPsi _r(u):=-\log \big ( I_{\sqrt{2\,u}}(r)/I_0(r) \big )$, $u \ge 0$, is a so-called complete Bernstein function, which allows for a holomorphic extension to the sliced complex plane $\mathbb {C} \setminus (-\infty ,0)$. We will make use of this observation in Sect. 5.

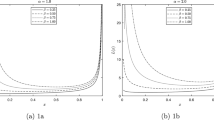
It is well-known that the numerical evaluation of the density of the Hartman–Watson law near zero is a challenging task because the integrand in the formula for $\theta (r,x)$ is highly oscillating. The following sections discuss several methods to evaluate the function $\theta (r,x)$ accurately. Figure 1 visualizes the function $\theta (r,x)$ for three different parameters $r$ and values $x \in (0.15,4)$, where all numerical computation routines discussed in the present note yield exactly the same result.

Fig. 1

Left The function $\theta (r,x)$ for three different parameters $r$ and values $x \in (0.15,4)$. Right The distribution function $F_r(x)$ for three different parameters $r$ and values $x \in (0.15,10)$

When looking at Fig. 1, mathematical intuition suggests that the approximation $\theta (0.5,x) \approx 0$ for $x<0.15$ might be a pragmatic—and numerically efficient—implementation close to zero. Nevertheless, [9] considers the numerical evaluation close to zero and obtains significant errors, see Sect. 3. Moreover, [6] studies the asymptotic behavior of $f_r(x)$ as $x \downarrow 0$ and [2] study the behavior of the distribution function $F_{r}$ of $\mu _r$ as the argument tends to zero. We like to mention that the right tail of the Hartman–Watson distribution $\mu _{r}$ becomes extremely heavy as $r \downarrow 0$. For instance, the distribution function $F_r(x)=\int _{0}^{x}f_r(t)\,\mathrm{d}t$ is still significantly smaller than $1$ for $x=10$ and different $r$, see Fig. 1.

The remaining article is organized as follows. Section 2 illustrates the occurrence of the Hartman–Watson distribution, in particular, in mathematical finance. Section 3 discusses the direct implementation of Formula (1). Section 4 proposes the use of the Gaver–Stehfest Laplace inversion technique. Section 5 proposes a complex Laplace inversion algorithm to numerically evaluate $f_r$ and $F_r$. Finally, Sect. 6 concludes.

2 Occurrence of the Hartman–Watson Law

The most prominent occurrence of the Hartman–Watson distribution is probably in directional statistics (see [8]): if $\mathbf W _t$ denotes a two-dimensional Brownian motion on the unit circle and $\tau \sim \mu _r$ is independent thereof, then $\mathbf W _{\tau }$ has the same law as $(\cos (X),\sin (X))$, where $X$ follows the so-called von Mises distribution with parameter $r$, which has density given by

$$\begin{aligned} f_X(x)=\frac{1}{2\,\pi \,I_0(r)}\,e^{r\,\cos (x)},\quad -\pi <x<\pi . \end{aligned}$$

The von Mises distribution is the most prominent law for an angle in the field of directional statistics, because it constitutes a tractable approximation to the “wrapped normal distribution” (i.e., the law of $Y$ mod $2\,\pi$ when $Y$ is normal), which is difficult to work with.

The importance of the Hartman–Watson distribution in the context of mathematical finance originates from the fact that

$$\begin{aligned} \frac{e^{-\frac{x^2}{2\,t}}}{\sqrt{2\,\pi \,t}}\,\mathbb {P}(A_t \in \mathrm {d}u\,|\,W_t = x) = \frac{1}{u}\,e^{-\frac{1+e^{2\,x}}{2\,u}}\,\theta \Big ( \frac{e^x}{u},t\Big ), \end{aligned}$$

where $W_t$ denotes standard Brownian motion and $A_t=\int _{0}^{t}e^{2\,W_s}\,\mathrm{ds}$ an associated integrated geometric Brownian motion, see [14]. The process $A_t$, and hence the Hartman–Watson distribution, naturally enters the scene when Asian stock derivatives, i.e., derivatives with “averaging periods,” are considered in the Black–Scholes world, see, e.g., [2, 9]. Another example, which is mathematically based on the exactly same reasoning, has recently been given in [3]: when the Black–Scholes model is enhanced by the introduction of stochastic repo margins, this leads to a convexity adjustment for all kinds of stock derivatives which involves the density of the Hartman–Watson distribution.

Let us furthermore briefly sketch a potential third application, which uses a stochastic representation for the Hartman–Watson law. Consider a diffusion process $\{X_t\}_{t \ge 0}$ satisfying the SDE

$$\begin{aligned} \mathrm {d}X_t = X_t\,\Big ( \Big ( \frac{1}{2}+X_t\,\frac{I_1(X_t)}{I_0(X_t)}\Big )\,\mathrm {d}t+\mathrm {d}W_t\Big ),\quad X_0=r>0. \end{aligned}$$

This explodes with probability one, as can be seen from Feller‘s test for explosion (the drift increases rapidly), i.e., there exists a stopping time $\tau \in (0,\infty )$ such that paths of $\{X_t\}$ are well defined on $[0,\tau )$ and $\lim _{t \uparrow \tau }X_t = \infty$ almost surely. Such explosive diffusions are used to model fatigue failures in solid materials. $X_t$ describes the evolution of the length of the longest crack and $\tau$ is the time point of ultimate damage. Kent [10] shows that $\tau \sim \mu _r$. We may rewrite $\tau$ as the first hitting time of zero of the stochastic process $Y_t:=1/X_t$, starting at $Y_0=1/r>0$. Observing the stock price $S_0>0$ of a highly distressed company facing bankruptcy, it might now make sense to model the evolution of this company‘s stock price until default as $S_t:=Y_t$ setting $r:=1/S_0$. The time of bankruptcy is defined as the first time the stock price hits zero, which has a Hartman–Watson law. A similar model, assuming $S_t$ to follow a CEV process that is allowed to diffuse to zero, is applied in [1].

3 Straightforward Implementation Based on Formula (1)

Regarding the exact numerical evaluation of the Hartman–Watson density, the article [9] shows that a straightforward numerical implementation of the Formula (1) for $r=0.5$ and $x \in [0.125,0.15]$ yields significant numerical errors. In particular, Fig. 2 in [9] shows that one ends up with negative density values. We come to the same conclusion, see Fig. 2.

Fig. 2

Evaluation of Formula (1) for $r=0.5$ and $x \in [0.125,0.15]$ in MATLAB applying the built-in adaptive quadrature routine quadgk, which can handle infinite integration domains

4 Evaluation via Gaver–Stehfest Laplace Inversion

We apply the Gaver–Stehfest algorithm in order to obtain $\theta (r,\cdot )$ from its Laplace transform $I_{\sqrt{2\,\cdot }}(r)$ via Laplace inversion for fixed values of $r$. For a rigorous proof and a good explanation of this method, see [11]. In particular, it is not difficult to observe from Yor‘s expression (1) that ([11] Theorem 1(iii)) applies, which justifies the approximation

$$\begin{aligned} \theta (r,x) \approx \frac{\log (2)}{x}\,\sum _{k=1}^{2\,n}a_{k}(n)\,I_{\sqrt{2\,k\,\log (2)/x}}(r), \end{aligned}$$

(3)

for $n \in \mathbb {N}$ large enough, where for $j=1,\ldots ,2n$ we have

$$\begin{aligned} a_k(n) = \frac{(-1)^{k+n}}{n!}\,\sum _{j=\lfloor (k+1)/2\rfloor }^{\min \{k,n\}}j^{n+1}\,\left( {\begin{array}{c}n\\ j\end{array}}\right) \,\left( {\begin{array}{c}2\,j\\ j\end{array}}\right) \,\,\left( {\begin{array}{c}j\\ k-j\end{array}}\right) . \end{aligned}$$

The Gaver–Stehfest algorithm has the nice feature that only evaluations of the Laplace transform on the positive half-axis are required. In particular, the required modified Bessel function $I_{\sqrt{2\,u}}(r)$ is efficient and easy to compute for $u>0$. In MATLAB, it is available as the built-in function besseli. The drawback of the Gaver–Stehfest algorithm is that it requires high-precision arithmetic because the involved constants $a_k(n)$ are alternating and become huge and difficult to evaluate. For practical implementations, this prevents the use of large $n$, which would theoretically be desirable due to the convergence result of [11]. Nevertheless, our empirical investigation shows that $n=10$ is still feasible on a standard PC without further precision arithmetic considerations and yields reasonable results for the considered parameterization. However, for larger values of $r$, the algorithm is less stable as can be seen at the end of Sect. 5.

The obtained values of $\theta (r,x)$ are visualized in Fig. 3. Comparing them to the brute force implementation in Fig. 2, the error for small $x$ becomes significantly smaller.

Fig. 3

Evaluation of $\theta (r,x)$ for $r=0.5$ and $x \in [0.125,0.15]$ in MATLAB applying the Gaver–Stehfest approximation (3) with $n=10$. Left The y-axis is precisely the same as in Fig. 2 for comparability. Right The y-axis is made finer to visualize smaller errors (scale $10^{-6}$)

5 Evaluation via a Complex Laplace Inversion Method for the Bondesson Class

As already mentioned in the introduction, the Hartman–Watson law is in the Bondesson class which allows to apply a Laplace inversion algorithm specifically derived for such distributions in [4]. Furthermore, this method has the advantage that it immediately implies as a corollary a similar formula for the distribution function $F_r$. To be precise, we have the formula

$$\begin{aligned} \theta (r,x) = \frac{M\,e^{x\,a}}{\pi }\,\int \limits _{0}^{1}\text{ Im }\Big ( \bar{e}^{x\,M\,\log (v)\,(b\,i-a)}\,I_{\sqrt{2\,(a-M\,\log (v)\,(b\,i-a))}}(r)\,(b\,i-a) \Big )\,\frac{\mathrm {d}v}{v} \end{aligned}$$

(4)

with arbitrary parameters $a,b>0$ and $M>2/(a\,x)$, and this integral is a proper Riemannian integral, since the integrand vanishes for $v \downarrow 0$, see [4]. Regarding the choice of the parameters, [4] have shown that $a=1/x, \, M=3$ is usually a good choice and we will use these parameters. Concerning the remaining parameter $b$, we choose $b=a$. For the evaluation of the distribution function $F_r$, it is also shown in [4] that

$$\begin{aligned} F_{r}(x) = \frac{M\,e^{x\,a}}{\pi }\,\int \limits _{0}^{1}\text{ Im }\Big ( \bar{e}^{x\,M\,\log (v)\,(b\,i-a)}\,\frac{\varphi _r\big (a-M\,\log (v)\,(b\,i-a)\big )}{a-M\,\log (v)\,(b\,i-a)}\,(b\,i-a) \Big )\,\frac{\mathrm {d}v}{v} \end{aligned}$$

with the same parameter restrictions as above. One particular challenge with this method is that the modified Bessel function $I_{\nu }$ needs to be evaluated for complex $\nu$. A straightforward implementation sufficient for our needs is achieved by using the partial sums related to the representation in Eq. (2). It has the advantage that error bounds can be computed, as for $r>0$ and $S_{n}^{\nu }(r):=\sum _{m=0}^{n}\frac{1}{m!\,\Gamma (m\,+\,\nu \,+\,1)}\,( \frac{r}{2})^{2\,m\,+\,\nu }$, one can compute

$$\begin{aligned} \left| S_{n}^{\nu }(r)- I_{\nu }(r)\right| \le \left( \frac{r}{2}\right) ^{\mathrm{Re }(\nu )}\sum _{m=n+1}^{\infty }\frac{1}{m!\,\vert \Gamma (m+\nu +1)\vert }\,\left( \frac{r}{2}\right) ^{2\,m}. \end{aligned}$$

Using the Gamma functional equation $\Gamma (z+1)=\Gamma (z)\,z$, it is easy to see that $\vert \Gamma (z+1) \vert \ge \vert \Gamma (z) \vert$ for $\vert z \vert \ge 1$. Thus, for $n\ge -\mathrm{Re }(\nu )-1$, the sequence $\{\vert \Gamma (m+\nu +1)\vert \}_{m=n+1,n+2,\ldots }$ is increasing, yielding

$$\begin{aligned} \left| S_{n}^{\nu }(r)- I_{\nu }(r)\right| \le \frac{\left( \frac{r}{2}\right) ^{\mathrm{Re }(\nu )}}{\vert \Gamma (n+\nu +2)\vert }\sum _{m=n+1}^{\infty }\frac{1}{m!}\,\left( \frac{r^{2}}{4}\right) ^{m}, \end{aligned}$$

where the series term is the residual of the Taylor expansion of $\exp (-r^{2}/4)$, which allows for a closed-form estimate. Consequently, one is able to choose $n$ such that the modified Bessel function is approximated up to a given accuracy. Using the Gamma functional equation, one has to compute the complex Gamma function only once which further increases efficiency. The complex Gamma function is computed using the Lanczos approximation, see [12].¹

Figure 4 shows the resulting values of $\theta (r,x)$, where the modified Bessel function is approximated with accuracy $10^{-6}$. Formula (4) is evaluated in MATLAB applying the built-in adaptive quadrature routine quadgk. Comparing the results to the Gaver–Stehfest inversion, the error for small $x$ is again significantly reduced and the results can be even improved by further increasing the accuracy of the modified Bessel function.

A second comparison of the presented methods is included for a larger value of $r$. The Laplace inversion method for the Bondesson class represents the most stable and accurate algorithm as can be seen in Fig. 5, which visualizes the values of $\theta (r,x)$ for small $x$ and $r=3$. Whereas the straightforward implementation based on Formula (1) fails due to numerical problems and the choice $n=10$ is not ideal for the Gaver–Stehfest Laplace inversion, the Bondesson method yields stable results.

Fig. 4

Evaluation of $\theta (r,x)$ for $r=0.5$ and $x \in [0.125,0.15]$ in MATLAB applying the Laplace inversion formula (4) with $a=b=1/x$ and $M=3$. The modified Bessel function is implemented with accuracy $10^{-6}$. Left The y-axis is precisely the same as in Fig. 2 for comparability. Right The y-axis is made finer to visualize smaller errors (scale $10^{-8}$)

Fig. 5

Evaluation of $\theta (r,x)$ for $r=3$ and $x \in [0.125,0.15]$ using the three presented methods with the same specifications as before, i.e., the Gaver–Stehfest approximation (3) with $n=10$ and the Laplace inversion formula (4) with $a=b=1/x$ and $M=3$

6 Conclusion

We compared three different methods to numerically evaluate the density of the Hartman–Watson law. We found that Laplace inversion algorithms significantly outperform direct implementation of Yor‘s formula (1). Moreover, a dedicated algorithm for distributions of the Bondesson class was proposed to numerically evaluate the distribution function of the Hartman–Watson law efficiently.