Keywords

1 Introduction

Geothermal energy is an energy resource which has its reserves in the depths of the earth, where heat is extracted and used to generate electricity in various applications [1]. The existing systems for its extraction are divided into two types: Conventional geothermal system (Hydrothermal) and enhanced geothermal system also known as Hot Dry Rock (HDR) [2]. The latter can be implemented in regions with lower geothermal potential than the conventional system and not necessarily near thermal water sources [2]. Three types of technologies can be used in HDR systems, Engineered Geothermal System (EGS), Downhole Heat Exchanger (DHE) and Super-Long Geothermal Heat Pipe (SLGHP) [3], this last one using heat pipe technology.

Heat pipes, or two-phase thermosyphons, are highly efficient heat transfer devices that operate in a closed cycle of evaporation and condensation [3], making them ideal for use in the geothermal industry. However, the main challenges are related to the difficulty and risk of working with thermosyphons up to 100 m without first corroborating with laboratory-scale studies that reliably represent the main physical phenomena associated with thermosiphon length. Several authors ([4,5,6,7,8,9]) mention the existence of an L/D (length-to-inner diameter) ratio as a key factor in the design of these large devices.

Lin et al. [4] carried out an experimental study of extra-long two-phase thermosyphons for geothermal applications. These authors concluded that one of the most problematic operational constraints in these devices is the flooding limit for L/D ratios greater than 1200. Seo et al. [5] and [6] developed a correlation to determine the flooding limit from the L/D ratio in extra-long heat pipes. They also suggest the development of further empirical studies to relate the flooding limit to the thermal performance of these devices. Cen et al. [7] studied the performance of a two-phase thermosyphon with an L/D ratio of about 1700. The experimental results obtained by the authors indicate that thermosyphons with extremely large L/D ratios can operate with similar performance to conventional thermosyphons.

Chen et al. [8] made a study on two-phase thermosyphons with high L/D ratio (>5000), where different multiphase flow regimes and their relationship with the device performance were observed. Based on the results, these authors showed that the Geyser Boiling regime is most likely in high L/D ratio thermosyphons.

The research presented above mention the L/D ratio as an alternative to analyze the performance and operational limits of super long two-phase thermosyphons. However, there is no research in literature presenting a study keeping the L/D ratio constant as a scaling alternative for this type of devices. In this context, the objective of this work is to experimentally study two thermosiphons with constant L/D ratio equal to 110, to compare the thermal performance of these devices and verify if it is possible to scale thermosiphons using only the geometric L/D ratio, aiming geothermal applications.

2 Experimental Setup

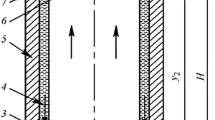
Two copper two-phase thermosyphons (Fig. 1 a) were fabricated with different internal diameters and lengths, keeping the L/D ratio constant at 110 [9]. The working fluid used was deionized water with a filling factor of 100%, i.e., with a fluid volume equal to the evaporator volume. Thermosyphon 1 has an internal diameter of D1 = 13.9 mm was manufactured with a total length of L1 = 1532 mm and a ratio between the dimensions of its sections, evaporator (le), adiabatic section (la) and condenser (lc) of le:la:lc = 1:3:1 [9]. Thermosyphon 2 was manufactured with an internal diameter of D2 = 10.8 mm, an overall length of L2 = 1191 mm and a ratio of le:la:lc = 1:1.13:1. The differences between the section sizes of the thermosyphons (evaporator, adiabatic and condenser) were chosen in order to keep the heat transfer areas equal in both devices.

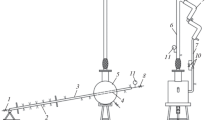
Figure 1 b, shows the experimental bench used in this work, consisting of: two-phase thermosyphon (1); heat supply system formed by a wire electrical resistance (2) of 28 Ω and 24.5 Ω for Thermosyphons 1 and 2 respectively, connected to a power supply (3) of the ISO-TECH brand, model IPS303DD; data acquisition system (4) of the Agilent brand, model 34970a; a cooling system consisting of a copper coil heat exchanger (5) with an external diameter of 6 mm, a total effective length of 500 mm and a pitch of 35 and 28 mm for Thermosyphons 1 and 2 respectively; a hydraulic bench (6) pumping water to the heat exchanger, instrumented by a rotameter (7) with a measuring range of 4 to 18 g/s and a maximum error of ±0.2 g/s.

Fig. 1.
figure 1

a) Geometrical relationship of two-phase thermosyphons b) Simplified scheme of the experimental bench

Full size image

The thermosyphons were instrumented with 8 K type thermocouples, with a maximum error of ±c, distributed as follows 3 in the evaporator, 2 in the adiabatic section and 3 in the condenser. In addition, two K-type thermocouples were connected at the inlet and outlet of the heat exchanger to monitor the temperature of the refrigerant throughout the operation of the unit. Finally, the thermosyphons were thermally insulated with glass wool with a thermal conductivity of 0.04 W/m2K.

Seven heat transfer rates were studied, applied in the following order: 25, 50, 75, 60, 40, 20 and 10 W. In each case, steady state was reached when the variation in the average temperature of each section after 10 min was less than \(0.5\,^\circ {\text{C}}\). It is important to note that the heat transfer rate was measured experimentally from Joule’s law, i.e., the product of the current and the voltage supplied by the power source.

3 Results

Figure 2a and 2b show the behaviors of the average temperatures of the evaporator, adiabatic section and condenser as a function of time for each of the heat transfer rates applied to the thermosyphons. It can be observed that both thermosyphons show large temperature oscillations when the heat transfer rate was lower than 25 W. These oscillations can be attributed to the Geyser Boiling phenomenon, which is characterized by symmetrical oscillations of the evaporator and condenser temperatures [10], i.e., when the evaporator temperature increases abruptly, the temperatures of the adiabatic zone and the condenser decrease abruptly and instantaneously. Similarly, when the evaporator temperature decreases abruptly, the temperatures of the other sections increase instantaneously, demonstrating the release cycle and the formation of vapor bubbles during the Geyser Boiling regime [11].

Fig. 2.
figure 2

Behavior of the temperatures of thermosyphon as a function of time a) Thermosyphon 1. b) Thermosyphon 2

Full size image

Furthermore, it is observed that Thermosyphon 2 (Fig. 2b), regardless of the analyzed heat transfer rate, always reached steady state at significantly lower temperatures than those recorded for Thermosyphon 1 (Fig. 2a), which could lead to a wrong interpretation regarding the performance of the devices, i.e., interpreting that thermosiphon 2 operated with a better performance than thermosiphon 1. For example, there is a difference of approximately 3 ℃ for the heat transfer rate of 10 W and approximately 20 ℃ for the heat transfer rate of 75 W.

Figure 3a shows the performance of the two-phase thermosyphons based on the comparison of thermal resistances as a function of heat transfer rate. The thermal resistance was defined as the quotient of the temperature difference between the evaporator and condenser and the heat transfer rate. It was observed that for heat transfer rates less than 20 W, the resistances of Thermosyphon 1 were 6% lower than Thermosyphon 2. For heat transfer rates greater than 20 W, Thermosyphon 1 showed 50% lower thermal resistances than Thermosyphon 2, suggesting that Thermosyphon 1 has better thermal performance according to this criterion, differing to what was analyzed in Fig. 2. However, it is shown that the constant L/D ratio is not sufficient to reach the two-phase thermosyphon scale.

Figure 3b shows a graph between the thermal resistances of the two thermosyphons as a function of the heat transfer rate per unit length characteristic of the two-phase thermosyphon, which was defined as the quotient of the square of the inner diameter and the length of the device, in order to present a new option of scaling extra-long two-phase thermosyphons.

Fig. 3.
figure 3

Thermosyphon thermal resistance. a) as a function of heat transfer rate. b) as a function of heat transfer rate per unit length characteristic.

Full size image

The results obtained from Fig. 3b show that the difference between the thermal resistances of the two thermosyphons was always less than 30%, which is significantly less than that obtained from Fig. 3a, but still large enough to conclude that only the use of this characteristic length is sufficient for scaling extra-long two-phase thermosyphons. These discrepancies may be related to the observed differences in the vapor temperatures of the two thermosyphons (Fig. 2), which cause significant changes in the thermophysical properties of the working fluid, mainly in density and viscosity, the properties associated with the interaction between the condensed liquid and vapor [12].

4 Conclusions

Two thermosyphons of different dimensions were studied, keeping the L/D ratio constant, equal to 110. It was found that Thermosyphon 1 operated at vapor temperatures up to 20 ℃ higher than Thermosyphon 2 and thermal resistances up to 50% lower than Thermosyphon 2. The above mentioned shows that the geometrical L/D ratio is not sufficient for the design of extra-long two-phase thermosyphons. A characteristic length has been proposed to reduce the differences between the thermal resistances of both thermosyphons, achieving differences of less than 30%. However, further experiments with two-phase thermosyphons of different dimensions and constant characteristic length are suggested. Furthermore, it is suggested that the scaling analysis of extra-long two-phase thermosyphons should include thermophysical properties of the working fluid such as density and viscosity.