Abstract
Existing dynamic partial order reduction (DPOR) algorithms scale poorly on concurrent data structure benchmarks because they visit a huge number of blocked executions due to spinloops.
In response, we develop Awamoche, a sound, complete, and strongly optimal DPOR algorithm that avoids exploring any useless blocked executions in programs with await and confirmation-CAS loops. Consequently, it outperforms the state-of-the-art, often by an exponential factor.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others


1 Introduction
Dynamic partial order reduction (DPOR) [13] has been promoted as an effective verification technique for concurrent programs: starting from a single execution of the program under test, DPOR repeatedly reverses the order of conflicting accesses in order to generate all (meaningfully) different program executions.
Applying DPOR in practice, however, reveals a major performance and scalability bottleneck: it explores a huge number of blocked executions, often outnumbering the complete program executions by an exponential factor. Blocked executions most commonly occur in programs with spinloops, i.e., loops that do not make progress unless some condition holds. Such loops are usually transformed into assume statements [14, 18], effectively requiring that the loop exits at its first iteration (and blocking otherwise).
We distinguish three classes of such blocked executions.
The first class occurs in programs with non-terminating spinloops, such as a program awaiting for \(x>42\) in a context where \(x=0\). For this program, modeled as the statement
 , DPOR obviously explores a blocked execution as the only existing value for x violates the assume condition. Such blocked executions should be explored because they indicate program errors.
, DPOR obviously explores a blocked execution as the only existing value for x violates the assume condition. Such blocked executions should be explored because they indicate program errors.
The second class occurs in programs with await loops. To see how such loops lead to blocked executions, consider the following program under sequential consistency (SC) [23] (initially \(x\,{=}\,y\,{=}\,0\)),

where each
 models an await loop, e.g.,
models an await loop, e.g.,
 for the
for the
 of the first thread. Suppose that DPOR executes this program in a left-to-right manner, thereby generating the interleaving
of the first thread. Suppose that DPOR executes this program in a left-to-right manner, thereby generating the interleaving
 . At this point,
. At this point,
 cannot be executed, since x would read 2. Yet, DPOR cannot simply abort the exploration. To generate the interleaving where the first thread reads \(y = 1\), DPOR must consider the case where the read of x is executed before the
cannot be executed, since x would read 2. Yet, DPOR cannot simply abort the exploration. To generate the interleaving where the first thread reads \(y = 1\), DPOR must consider the case where the read of x is executed before the
 assignment. In other words, DPOR has to explore blocked executions in order to generate non-blocked ones.
assignment. In other words, DPOR has to explore blocked executions in order to generate non-blocked ones.
The third class occurs in programs with confirmation-CAS loops such as:

Consider a program comprising two threads running the code above, with a and b being local variables. Suppose that DPOR first obtains the (blocked) trace where both threads concurrently try to perform their CAS:
 ,
,
 ,
,
 ,
,
 . Trying to satisfy the blocked assume of thread 2 by reversing the CAS instructions is fruitless because then thread 1 will be blocked.
. Trying to satisfy the blocked assume of thread 2 by reversing the CAS instructions is fruitless because then thread 1 will be blocked.
In this paper, we show that exploring blocked executions of the second and third classes is unnecessary.
We develop Awamoche, a sound, complete, and optimal DPOR algorithm that avoids generating any blocked executions for programs with await and confirmation-CAS loops. Our algorithm is strongly optimal in that no exploration is wasted: it either yields a complete execution or a termination violation. Awamoche extends
 [15], an optimal DPOR algorithm that supports weak memory models and has polynomial space requirements, with three new ideas:
[15], an optimal DPOR algorithm that supports weak memory models and has polynomial space requirements, with three new ideas:
-
1.
Awamoche identifies certain reads as stale, meaning that they will never be affected by a race reversal due to TruSt ’s maximality condition on reversals, and avoids exploring any executions that block on stale-read values.
-
2.
To deal with await loops, since it cannot completely avoid generating executions with blocking reads, Awamoche revisits such executions in place if a same-location write is later encountered. If no such write is found, then the blocked execution witnesses a program termination bug [21, 25].
-
3.
To effectively deal with confirmation-CAS loops, Awamoche only considers executions where the confirmation succeeds, by reversing not only races between conflicting instructions, but also speculatively revisiting traces with two reads reading from the same write event to enable a later in-place revisit.
As we shall see in Sect. 5, supporting these DPOR modifications is by no means trivial when it comes to proving correctness and (strong) optimality. Indeed, TruSt ’s correctness proof proceeds in a backward manner, assuming a way to determine the last event that was added to a given trace. The presence of in-place and speculative revisits, however, makes this impossible.
We therefore develop a completely different proof that works in a forward manner: from each configuration that is a prefix of a complete trace, we construct a sequence of steps that will lead to a larger configuration that is also a prefix of the trace. Our proof assumes that same-location writes are causally ordered, which invariably holds in correct data structure benchmarks, but is otherwise more general than TruSt ’s assuming less about the underlying memory model.
Our contributions can be summarized as follows:
-
Section 2 We describe how and why DPOR encounters blocked executions.
-
Section 3 We intuitively present Awamoche ’s three novel key ideas: stale reads, in-place revisits, and speculative revisits.
-
Section 4 We describe our algorithm in detail in a memory-model-agnostic framework.
-
Section 5 We generalize TruSt ’s proof and prove Awamoche sound, complete, and strongly optimal.
-
Section 6 We evaluate Awamoche, and demonstrate that it outperforms the state-of-the-art, often by an exponential factor.
2 DPOR and Blocked Executions
Before presenting Awamoche, we recall the fundamentals of DPOR (Sect. 2.1), and explain why spinloops lead to blocked explorations (Sect. 2.2).
2.1 Dynamic Partial Order Reduction
DPOR algorithms verify a concurrent program by enumerating a representative subset of its interleavings. Specifically, they partition the interleavings into equivalence classes (two interleavings are equivalent if one can be obtained from the other by reordering independent instructions), and strive to explore one interleaving per equivalence class. Optimal algorithms [2, 15] achieve this goal.
DPOR algorithms explore interleavings dynamically. After running the program and obtaining an initial interleaving, they detect racy instructions (i.e., instructions accessing the same variable with at least one of them being a write), and proceed to explore an interleaving where the race is reversed.
Let us clarify the exploration procedure with the following example, where both variables x and y are initialized to zero.

The RW+WW program has 5 interleavings that can be partitioned into 3 equivalence classes. Intuitively, the
 is irrelevant because the program contains no other access to y; all that matters is the ordering among the x accesses.
is irrelevant because the program contains no other access to y; all that matters is the ordering among the x accesses.
The exploration steps for RW+WW can be seen in Fig. 1Footnote 1. DPOR obtains a full trace of the program, while also recording the transitions that it took at each step at the respective transition’s
 set (traces
set (traces
 to
to
 ). After obtaining a full trace, it initiates a
). After obtaining a full trace, it initiates a
 -detection phase. During this phase, DPOR detects the races between \(r_x\) and the two writes \(w_1\) and \(w_2\). (While \(w_1\) and \(w_2\) also write the same variable, they do not constitute a race, as they are causally related.) For the first race, DPOR adds \(w_1\) in the backtrack set of the first transition, so that it can subsequently execute \(w_1\) instead of \(r_x\). For the second one, while \(w_2\) is not in the backtrack set of the first transition, \(w_2\) cannot be directly executed as the first transition without its causal predecessors (i.e., \(w_1\)) having already executed. Since \(w_1\) is already in the backtrack set of the first transition, DPOR cannot do anything else, and the race-detection phase is over.
-detection phase. During this phase, DPOR detects the races between \(r_x\) and the two writes \(w_1\) and \(w_2\). (While \(w_1\) and \(w_2\) also write the same variable, they do not constitute a race, as they are causally related.) For the first race, DPOR adds \(w_1\) in the backtrack set of the first transition, so that it can subsequently execute \(w_1\) instead of \(r_x\). For the second one, while \(w_2\) is not in the backtrack set of the first transition, \(w_2\) cannot be directly executed as the first transition without its causal predecessors (i.e., \(w_1\)) having already executed. Since \(w_1\) is already in the backtrack set of the first transition, DPOR cannot do anything else, and the race-detection phase is over.
After the race-detection phase is complete, the exploration proceeds in an analogous manner: DPOR backtracks to the first transition, fires \(w_1\) instead of \(r_x\) (trace
 ), re-runs the program to obtain a full trace (trace
), re-runs the program to obtain a full trace (trace
 ), and initiates another race-detection phase. During the latter, a race between \(r_x\) and \(w_2\) is detected, and \(w_2\) is inserted in the backtrack set of the second transition.
), and initiates another race-detection phase. During the latter, a race between \(r_x\) and \(w_2\) is detected, and \(w_2\) is inserted in the backtrack set of the second transition.
Finally, DPOR backtracks to the second transition, executes \(w_2\) instead of \(r_x\) (trace
 ), and eventually obtains the full trace
), and eventually obtains the full trace
 . During the last race-detection phase of the exploration, DPOR detects the races between \(r_x\) and the two writes \(w_1\) and \(w_2\). As \(r_x\) is already in the backtrack set of the first two transitions, DPOR has nothing else to do, and thus concludes the exploration.
. During the last race-detection phase of the exploration, DPOR detects the races between \(r_x\) and the two writes \(w_1\) and \(w_2\). As \(r_x\) is already in the backtrack set of the first two transitions, DPOR has nothing else to do, and thus concludes the exploration.
Observe that DPOR explored one representative trace from each equivalence class (traces
 ,
,
 , and
, and
 ). To avoid generating multiple equivalent interleavings, optimal DPOR algorithms extend the description above by restricting when a race reversal is considered. In particular, the TruSt algorithm [15] imposes a maximality condition on the part of the trace that is affected by the reversal.
). To avoid generating multiple equivalent interleavings, optimal DPOR algorithms extend the description above by restricting when a race reversal is considered. In particular, the TruSt algorithm [15] imposes a maximality condition on the part of the trace that is affected by the reversal.
2.2 Assume Statements and DPOR
To see how
 statements arise in concurrent programs, suppose that we replace the \(\texttt {if}\)-statement of RW+WW with an await loop (Fig. 2). Although the change does not really affect the possible outcomes for x, it makes DPOR diverge: DPOR examines executions where the loop terminates in 1, 2, 3, ... steps. Since, however, the loop has no side-effects, we can actually transform it into an
statements arise in concurrent programs, suppose that we replace the \(\texttt {if}\)-statement of RW+WW with an await loop (Fig. 2). Although the change does not really affect the possible outcomes for x, it makes DPOR diverge: DPOR examines executions where the loop terminates in 1, 2, 3, ... steps. Since, however, the loop has no side-effects, we can actually transform it into an
 statement, effectively modeling a loop bound of one.
statement, effectively modeling a loop bound of one.
Doing so guarantees DPOR’s termination but not its good performance. The reason is ascribed to the very nature of DPOR. Indeed, suppose that DPOR executes the first instruction of the left thread and then blocks due to
 statement. At this point, DPOR cannot simply stop the exploration due to the
statement. At this point, DPOR cannot simply stop the exploration due to the
 statement not being satisfied; it has to explore the rest of the program, so that the race reversals make the
statement not being satisfied; it has to explore the rest of the program, so that the race reversals make the
 succeed. All in all, DPOR explores 2 complete and 1 blocked traces for RW+WW-A.
succeed. All in all, DPOR explores 2 complete and 1 blocked traces for RW+WW-A.
In general, DPOR cannot know whether some future reversal will ever make an
 succeed. Worse yet, it might be the case that there is an exponential number of traces to be explored (due to the other program threads), until DPOR is certain that the
succeed. Worse yet, it might be the case that there is an exponential number of traces to be explored (due to the other program threads), until DPOR is certain that the
 statement cannot be unblocked.
statement cannot be unblocked.
To see this, consider the following program where runs in parallel with some threads accessing z:

For the trace of RW+WW-A where the
 fails, DPOR fruitlessly explores \(2^N\) traces in the hope that an access to x is found that will unblock the
fails, DPOR fruitlessly explores \(2^N\) traces in the hope that an access to x is found that will unblock the
 statement.
statement.
Given that executing an
 statement that fails leads to blocked executions, one might be tempted to consider a solution where
statement that fails leads to blocked executions, one might be tempted to consider a solution where
 statements are only scheduled if they succeed. Even though such a solution would eliminate blocking for RW+WW-A, it is not a panacea. To see why, consider a variation of RW+WW-A where the first thread executes
statements are only scheduled if they succeed. Even though such a solution would eliminate blocking for RW+WW-A, it is not a panacea. To see why, consider a variation of RW+WW-A where the first thread executes
 instead of
instead of
 . In such a case, the
. In such a case, the
 can be scheduled first (as it succeeds), but reversing the races among the x accesses will lead to blocked executions. It becomes evident that a more sophisticated solution is required.
can be scheduled first (as it succeeds), but reversing the races among the x accesses will lead to blocked executions. It becomes evident that a more sophisticated solution is required.
3 Key Ideas
Awamoche, our optimal DPOR algorithm, extends
 [15] with three novel key ideas: stale-read annotations (Sect. 3.1), in-place revisits (Sect. 3.2) and speculative revisits (Sect. 3.3). As we will shortly see, these ideas guarantee that Awamoche is strongly optimal: it never initiates fruitless explorations, and all explorations lead to executions that are either complete or denote termination violations. In the rest of the paper, we call such executions useful.
[15] with three novel key ideas: stale-read annotations (Sect. 3.1), in-place revisits (Sect. 3.2) and speculative revisits (Sect. 3.3). As we will shortly see, these ideas guarantee that Awamoche is strongly optimal: it never initiates fruitless explorations, and all explorations lead to executions that are either complete or denote termination violations. In the rest of the paper, we call such executions useful.
3.1 Avoiding Blocking Due to Stale Reads
Race reversals are at the heart of any DPOR algorithm. TruSt distinguishes two categories of race reversals: (1) write-read and write-write reversals, (2) read-write reversals. While the former category can be performed by modifying the trace directly in place (called a “forward revisit”), the latter may require removing events from the trace (called a “backward revisit”). To ensure optimality for backward revisits, TruSt checks a certain maximality condition for the events affected by them, namely the read, which will be reading from a different write, and all events to be deleted.
An immediate consequence is that any read events not satisfying TruSt ’s maximality condition, which we call stale reads, will never be affected by a subsequent revisit. As an example, consider the following program with a read that blocks if it reads 0:

After obtaining the trace
 , TruSt forward-revisits the read in-place, and makes it read 0. At this point, we know that (1) the assume will fail, and (2) that both the read and the events added before it cannot be backward-revisited, due to the read reading non-maximally (which violates TruSt ’s maximality condition). As such, no useful execution is ever going to be reached, and there is no point in continuing the exploration.
, TruSt forward-revisits the read in-place, and makes it read 0. At this point, we know that (1) the assume will fail, and (2) that both the read and the events added before it cannot be backward-revisited, due to the read reading non-maximally (which violates TruSt ’s maximality condition). As such, no useful execution is ever going to be reached, and there is no point in continuing the exploration.
Leveraging the above insight, we make Awamoche immediately drop traces where some assume is not satisfied due to a stale read. To do this, Awamoche automatically annotates reads followed by assume statements with the condition required to satisfy the assume, and discards all forward revisits that do not satisfy the annotation.
Even though stale-read annotations are greatly beneficial in reducing blocking, they are merely a remedy, not a cure. As already mentioned, they are only leveraged in write-read reversals, and are thus sensitive to DPOR’s exploration order. To completely eliminate blocking, Awamoche performs in-place and speculative revisits, described in the next sections.
3.2 Handling Await Loops with In-Place Revisits
Awamoche ’s solution to eliminate blocking is to not blindly reverse all races whenever a trace is blocked, but rather to only try and reverse those that might unblock the exploration.
As an example, consider Rw+ww-A-PAR (Fig. 3). After Awamoche obtains the first full trace, it detects the races among the z accesses, as well as the \({\langle {r_x,w_1}\rangle }\) race. (Recall that Awamoche is based on TruSt and therefore does not consider the \({\langle {r_x,w_2}\rangle }\) race in this trace.) At this point, a standard DPOR would start reversing the races among the z accesses. Doing so, however, is wasteful, since reversing races after the blockage will lead to the exploration of more blocked executions.
Instead, Awamoche chooses to reverse the \({\langle {r_x, w_1}\rangle }\) race (as this might make the
 succeed), and completely drops the races among the z accesses. We call this procedure in-place revisiting (denoted by
succeed), and completely drops the races among the z accesses. We call this procedure in-place revisiting (denoted by
 in Fig. 3). Intuitively, ignoring the z races is safe to do as they will have the chance to manifest in the trace where the \({\langle {r_x, w_1}\rangle }\) race has been reversed.
in Fig. 3). Intuitively, ignoring the z races is safe to do as they will have the chance to manifest in the trace where the \({\langle {r_x, w_1}\rangle }\) race has been reversed.
Indeed, reversing the \({\langle {r_x,w_1}\rangle }\) does make the
 succeed, at which point the exploration proceeds in the standard DPOR way. Awamoche explores \(2^N\) traces where the read of x reads 1, and another \(2^N\) where it reads 2. Note that, even though in this example Awamoche explores 2/3 of the traces that standard DPOR explores, as we show in Sect. 6 the difference can be exponential.
succeed, at which point the exploration proceeds in the standard DPOR way. Awamoche explores \(2^N\) traces where the read of x reads 1, and another \(2^N\) where it reads 2. Note that, even though in this example Awamoche explores 2/3 of the traces that standard DPOR explores, as we show in Sect. 6 the difference can be exponential.
Suppose now that we change the
 in Rw+ww-A-PAR to
in Rw+ww-A-PAR to
 so that there is no trace where the assume is satisfied. The key steps of Awamoche ’s exploration can be seen in Fig. 4. Upon obtaining a full trace, all races to z are ignored and Awamoche revisits \(r_x\) in place. Subsequently, as the assume is still not satisfied, Awamoche again revisits \(r_x\) in place (trace
so that there is no trace where the assume is satisfied. The key steps of Awamoche ’s exploration can be seen in Fig. 4. Upon obtaining a full trace, all races to z are ignored and Awamoche revisits \(r_x\) in place. Subsequently, as the assume is still not satisfied, Awamoche again revisits \(r_x\) in place (trace
 ). At this point, since there are no other races on x it can reverse, Awamoche reverses all the races on z, and finishes the exploration.
). At this point, since there are no other races on x it can reverse, Awamoche reverses all the races on z, and finishes the exploration.
In total, Awamoche explores \(2^N\) blocked executions for the updated example, which are all useful. As \(r_x\) is reading from the latest write to x in all these executions and the assume statement (corresponding to an await loop) still blocks, each of these executions constitutes a distinct liveness violation.
3.3 Handling Confirmation CASes with Speculative Revisits
In-place revisiting alone suffices to eliminate useless blocking in programs whose assume statements arise only due to await loops. It does not, however, eliminate blocking in confirmation-CAS loops. Confirmation-CAS loops consist of a speculative read of some shared variable, followed by a (possibly empty) sequence of local accesses and other reads, and a confirmation CAS that only succeeds if it reads from the same write as the speculative read.
As an example, consider the confirmation-CAS example from Sect. 1 and a trace where both reads read the initial value, the CAS of the first thread succeeds, and the CAS of the second thread reads the result of the CAS of the first. Although this trace is blocked and explored by DPOR (since the CAS read of the second thread is reading from the latest, same-location write), it does not constitute an actual liveness violation. In fact, even though the CAS read that blocks does read from the latest, same-location write, the
 read in the same loop iteration does not. In order for a blocked trace (involving a loop) to be an actual liveness violation, all reads corresponding to a given iteration need to be reading the latest value, and not just one.
read in the same loop iteration does not. In order for a blocked trace (involving a loop) to be an actual liveness violation, all reads corresponding to a given iteration need to be reading the latest value, and not just one.
To avoid exploring blocked traces altogether for cases likes this, we equip Awamoche with some builtin knowledge about confirmation-CAS loops and treat them specially when reversing races. To see how this is done, we present a run of Awamoche on the confirmation-CAS example of Sect. 1 (see Fig. 5).
While building the first full trace (trace
 ), another big difference between Awamoche and standard DPOR algorithms is visible: Awamoche does not maintain backtrack sets for confirmation CASes. Indeed, there is no point in reversing a race involving a confirmation CAS, as such a reversal will make the CAS read from a different write than the speculative read, and hence lead to an
), another big difference between Awamoche and standard DPOR algorithms is visible: Awamoche does not maintain backtrack sets for confirmation CASes. Indeed, there is no point in reversing a race involving a confirmation CAS, as such a reversal will make the CAS read from a different write than the speculative read, and hence lead to an
 failure.
failure.
After obtaining the first full trace (trace
 ), Awamoche initiates a race-detection phase. At this point, the final big difference between Awamoche and previous DPOR s is revealed. Awamoche will not reverse races between reads and CASes, but rather between speculative reads. (While speculative reads are not technically conflicting events, they conflict with the later confirmation-CASes.) As can be seen in trace
), Awamoche initiates a race-detection phase. At this point, the final big difference between Awamoche and previous DPOR s is revealed. Awamoche will not reverse races between reads and CASes, but rather between speculative reads. (While speculative reads are not technically conflicting events, they conflict with the later confirmation-CASes.) As can be seen in trace
 , Awamoche schedules the speculative read of the second thread before that of the first thread so that it explores the scenario where the confirmation of the second thread succeeds before the one of the first.
, Awamoche schedules the speculative read of the second thread before that of the first thread so that it explores the scenario where the confirmation of the second thread succeeds before the one of the first.
Finally, simply by adding the remaining events of the second thread before the ones of the first thread, Awamoche explores the second and final trace of the example (trace
 ), while avoiding having blocked traces altogether.
), while avoiding having blocked traces altogether.
4 Await-Aware Model Checking Algorithm
Awamoche is based on
 [15], a state-of-the-art stateless model checking algorithm that explores execution graphs [9], and thus seamlessly supports weak memory models. In what follows, we formally define execution graphs (Sect. 4.1), and then present Awamoche (Sect. 4.2).
[15], a state-of-the-art stateless model checking algorithm that explores execution graphs [9], and thus seamlessly supports weak memory models. In what follows, we formally define execution graphs (Sect. 4.1), and then present Awamoche (Sect. 4.2).
4.1 Execution Graphs
An execution graph G consists of a set of events (nodes), representing instructions of the program, and a few relations of these events (edges), representing interactions among the instructions.
Definition 1
An event,
 , is either the initialization event
, is either the initialization event
 , or a thread event
, or a thread event
 where
where
 is a thread identifier,
is a thread identifier,
 is a serial number inside each thread, and
is a serial number inside each thread, and
 is a label that takes one of the following forms:
is a label that takes one of the following forms:
-
Block label:
 representing the blockage of a thread (e.g., due to the condition of an “
representing the blockage of a thread (e.g., due to the condition of an “
 ” statement failing).
” statement failing). -
Error label:
 representing the violation of some program assertion.
representing the violation of some program assertion. -
Write label:
 where
where
 denotes special attributes the write may have (i.e., exclusive),
denotes special attributes the write may have (i.e., exclusive),
 is the location accessed, and
is the location accessed, and
 the value written.
the value written. -
Read label:
 where
where
 denotes special attributes the read may have (i.e., await, speculative, exclusive), and
denotes special attributes the read may have (i.e., await, speculative, exclusive), and
 is the location accessed. We note that if a read has the \(\textsf{awt} \) or the \(\textsf{spec} \) attribute, then it cannot have any other attribute.
is the location accessed. We note that if a read has the \(\textsf{awt} \) or the \(\textsf{spec} \) attribute, then it cannot have any other attribute.
We omit the \(\emptyset \) for read/write labels with no attributes. The functions
 ,
,
 ,
,
 , and
, and
 , respectively return the thread identifier, serial number, location, and value of an event, when applicable. We use
, respectively return the thread identifier, serial number, location, and value of an event, when applicable. We use
 ,
,
 ,
,
 , and
, and
 to denote the set of all read, write, block, and error events, respectively, and assume that
to denote the set of all read, write, block, and error events, respectively, and assume that
 . We use superscript and subscripts to further restrict those sets (e.g.,
. We use superscript and subscripts to further restrict those sets (e.g.,
 ).
).
In the definition above, read and write events come with various attributes. Specifically, we encode successful CAS operations and other similar atomic operations, such as fetch-and-add, as two events: an exclusive read followed by an exclusive write (both denoted by the \(\textsf{excl}\) attribute). Moreover, we have a \(\textsf{spec}\) attribute for speculative reads, and write
 for the corresponding confirmation reads (i.e., the first exclusive, same-location read that is
for the corresponding confirmation reads (i.e., the first exclusive, same-location read that is
 -after a given
-after a given
 ). Finally, we have the \(\textsf{awt}\) attribute for reads the outcome of which is tied with an
). Finally, we have the \(\textsf{awt}\) attribute for reads the outcome of which is tied with an
 statement, and write
statement, and write
 for the subset of
for the subset of
 that are reading a value that makes the assume fail (see below).
that are reading a value that makes the assume fail (see below).
Definition 2
An execution graph G consists of:
-
1.
a set
 of events that includes
of events that includes
 and does not contain multiple events with the same thread identifier and serial number.
and does not contain multiple events with the same thread identifier and serial number. -
2.
a total order \(\le _G\) on
 , representing the order in which events were incrementally added to the graph,
, representing the order in which events were incrementally added to the graph, -
3.
a function
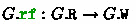 , called the reads-from function, that maps each read event to a same-location write from where it gets its value, and
, called the reads-from function, that maps each read event to a same-location write from where it gets its value, and -
4.
a strict partial order
 , called the coherence order, which is total on
, called the coherence order, which is total on
 for every location
for every location
 .
.
We write
 for the set
for the set
 and similarly for other sets. Given two events
and similarly for other sets. Given two events
 , we write
, we write
 if \(e_1 \le _G e_2\) and \(e_1 \ne e_2\). We write
if \(e_1 \le _G e_2\) and \(e_1 \ne e_2\). We write
 for the restriction of an execution graph G to a set of events E, and \(G\setminus E\) for the graph obtained by removing a set of events E.
for the restriction of an execution graph G to a set of events E, and \(G\setminus E\) for the graph obtained by removing a set of events E.
Based on the above graph representation, we define
 , which orders events in the same thread according to their
, which orders events in the same thread according to their
 component, and
component, and
 , which is the causal order among the graph events, as follows:
, which is the causal order among the graph events, as follows:

The semantics of a program
 under a memory model \(\textsf {m} \) is the set of execution graphs corresponding to the program that satisfy the consistency predicate of \(\textsf {m} \). Consistency predicates generally constrain the possible choices of
under a memory model \(\textsf {m} \) is the set of execution graphs corresponding to the program that satisfy the consistency predicate of \(\textsf {m} \). Consistency predicates generally constrain the possible choices of
 and
and
 , thereby indirectly constraining the possible final values of memory locations and the values that reads can return.
, thereby indirectly constraining the possible final values of memory locations and the values that reads can return.
TruSt (and by extension, Awamoche), assumes some properties on the memory model [15]:
 acyclicity,
acyclicity,
 -prefix-closedness,
-prefix-closedness,
 -maximal-extensibility. Intuitively, extensibility captures the idea that executing a program should never get stuck if a thread has more statements to execute.
-maximal-extensibility. Intuitively, extensibility captures the idea that executing a program should never get stuck if a thread has more statements to execute.
4.2 Awamoche
Similarly to TruSt, Awamoche verifies a concurrent program P by enumerating all of its consistent execution graphs (see Algorithm 1). In contrast to TruSt, however, Awamoche is strongly optimal: it never explores an execution G where there exists some blocked read
 that is reading from a non-
that is reading from a non-
 -maximal write. In other words, Awamoche only visits graphs that lead to useful executionsFootnote 2. In order to be able to do so, Awamoche makes stronger assumptions on the underlying memory model \(\textsf {m} \), namely that there are no write-write races, and that \(\textsf {m} \) does not allow
-maximal write. In other words, Awamoche only visits graphs that lead to useful executionsFootnote 2. In order to be able to do so, Awamoche makes stronger assumptions on the underlying memory model \(\textsf {m} \), namely that there are no write-write races, and that \(\textsf {m} \) does not allow
 to contradict
to contradict
 (i.e., that
(i.e., that
 ).
).

Next, we first describe how TruSt works, and then proceed with Awamoche ’s
 .
.
Given a program \(\textit{P} \), \(\textsc {Verify}\) visits all consistent execution graphs of \(\textit{P} \) by calling \(\textsc {Visit}\) on the execution graph
 containing only the initialization event.
containing only the initialization event.
At each step (Line 4), as long as the current graph remains consistent under the specified memory model \(\textsf {m} \), \(\textsc {Visit}\) obtains a new event a via \(\textsf{next}_{\textit{P}}({G}) \) (Line 5), and extends the current graph G with a (Line 6). We assume that
 adds a to
adds a to
 , and also to
, and also to
 , in case a is a write. (Recall that
, in case a is a write. (Recall that
 and so a’s
and so a’s
 -placing is unique.)
-placing is unique.)
If there are no more events to add to the graph, then G is complete, and \(\textsc {Visit}\) returns (Line 7). If a denotes an error, then it is reported to the user and verification terminates (Line 9).
If a is a read, \(\textsc {Visit}\) needs to examine all possible places where a could read from. To that end, for each same-location write w in G (Line 15), \(\textsc {Visit}\) recursively explores the possibility that a reads from w (Line 19). Formally, \(\textsf{SetRF}({G,r,w})\) returns a graph \(G'\) that is identical to G except for its
 component:
component:

If a is a write, \(\textsc {Visit}\) examines both the case when a is simply added to G (Line 22) and the “backward-revisit” cases for each existing same-location read in G that could read from a (Line 5). When a backward-revisits a read r, the resulting graph \(G'\) only contains the events that were added before r, or are
 -before a, and updates r to read from a. Since, however, there might be many backward revisits that lead to the exact same graph \(G'\), to ensure optimality, \(G'\) is visited only when the current graph G forms a maximal extension of \(G'\). We do not provide TruSt ’s definition of maximal extensions here, as Awamoche modifies it to achieve strong optimality.
-before a, and updates r to read from a. Since, however, there might be many backward revisits that lead to the exact same graph \(G'\), to ensure optimality, \(G'\) is visited only when the current graph G forms a maximal extension of \(G'\). We do not provide TruSt ’s definition of maximal extensions here, as Awamoche modifies it to achieve strong optimality.
Let us now move to the parts of Algorithm 1 that are Awamoche-specific.
First, Awamoche discards all graphs where some blocked read is reading non-maximally (Line 4). As explained in Sect. 3.2, such reads cannot be revisited and will thus only lead to blocked executions. In addition, to guarantee correctness, Awamoche raises an error if it detects unordered writes (Line 21).
Second, whenever a write event a is added, Awamoche revisits all same-location blocked reads in place making them read from a (Line 22) and excluding them from the normal backward-revisit procedure (Line 5). Formally, we define \(\textsf{IPR}(G, a)\) to return a graph \(G'\) that is identical to G apart from its
 component:
component:

Third, whenever a confirmation read a is added (Line 11), i.e., an exclusive read that succeeds an unmatched speculative read e, Awamoche only explores the execution where a reads from the same write as e (Line 13): any other write would make the confirmation CAS fail.
Fourth, whenever a speculative read a is added to read from a candidate write w and there is another speculative read b reading from the same write w (Line 16), Awamoche backward-revisits b to read from a. Note that, due to the atomicity of the confirming CASes, there can be at most one other speculative read b reading from w, and so Awamoche revisits it to read from a, making it blocked, so that it get revisited in place when the confirming CAS of a is added to the graph. (To ensure graph well-formedness, we assume that \(\textsf{IPR}(G,b)\) does not modify G when called with a read argument b, and that \(\textsf{SetRF}({G,b,\_})\) makes b read from \(\bot \), which \(\textsf{IPR}\) also considers.)

Finally, similarly to TruSt, Awamoche only performs a backward revisit if G forms a maximal extension, though Awamoche employs a slightly different definition of maximal extensions. Awamoche ’s backward-revisit algorithm can be seen in Algorithm 2.
Roughly, Awamoche performs a backward revisit from a to r that leads to a graph \(\textsf{IPR}(G_r, a)\) if, starting from \(G_r\) without r and a, and adding r and all the deleted events in a
 -maximal way (and performing in-place revisits along the way), leads to G. Formally, we write \(G_1 \overset{e}{\rightsquigarrow } G_2\) if there exists \(G_1'\) such that \(G_2 = \textsf{IPR}(G_1',e)\), \(G_1' = G_1 \mathbin {{+}\!{+}}e\) and:
-maximal way (and performing in-place revisits along the way), leads to G. Formally, we write \(G_1 \overset{e}{\rightsquigarrow } G_2\) if there exists \(G_1'\) such that \(G_2 = \textsf{IPR}(G_1',e)\), \(G_1' = G_1 \mathbin {{+}\!{+}}e\) and:

We note that, for the special case where
 and there is
and there is
 such that \(e'\) is not followed by the matching confirmation CAS, we consider \(\bot \) as the
such that \(e'\) is not followed by the matching confirmation CAS, we consider \(\bot \) as the
 . As a final remark, note that, Awamoche modifies \(\textsf{next}_{\textit{P}}({G}) \) so that (a) after scheduling a speculative read, it keeps scheduling events in the same threads until the respective confirming CAS is added, and (b) it does not schedule events from a thread whose last (speculative) read reads \(\bot \). These modifications ensure that the confirmation patterns are added one at a time, and that in-place revisits take place among confirming CASes and speculative reads.
. As a final remark, note that, Awamoche modifies \(\textsf{next}_{\textit{P}}({G}) \) so that (a) after scheduling a speculative read, it keeps scheduling events in the same threads until the respective confirming CAS is added, and (b) it does not schedule events from a thread whose last (speculative) read reads \(\bot \). These modifications ensure that the confirmation patterns are added one at a time, and that in-place revisits take place among confirming CASes and speculative reads.
5 Correctness and Optimality
Proving Awamoche correct is non-trivial, as we had to develop a novel proof strategy. In what follows, we first review TruSt ’s proof argument, show why it is inapplicable for Awamoche. Then, we explain our proof strategy (Sect. 5.1) and state our completeness and optimality results (Sect. 5.2).
5.1 Approaches to Correctness
TruSt. The proof of TruSt proceeds in a backward manner. Specifically, TruSt ’s proof is based on a procedure \(\textsc {Prev}{}\) that, given an execution G, recovers the unique “previous” execution \(G_p\) that the algorithm must reach in order to visit G. To do so, assuming a left-to-right addition order of events, \(\textsc {Prev}(G)\) finds the rightmost
 -maximal event e of G, and decides whether e was added in a non-revisit step, or e is a read that was just revisited by a write event located to its right. If e was added in a non-revisit step, then \(G_p\) is simply G without e. Otherwise, \(\textsc {Prev}{}\) obtains \(G_p\) from G in the following way: it removes e along with the write w that e reads from, and then iteratively adds the leftmost available event to G in a
-maximal event e of G, and decides whether e was added in a non-revisit step, or e is a read that was just revisited by a write event located to its right. If e was added in a non-revisit step, then \(G_p\) is simply G without e. Otherwise, \(\textsc {Prev}{}\) obtains \(G_p\) from G in the following way: it removes e along with the write w that e reads from, and then iteratively adds the leftmost available event to G in a
 -maximal way, until w is about to be added.
-maximal way, until w is about to be added.
TruSt ’s completeness and optimality are proved using \(\textsc {Prev}{}\). For the former, one can show that each consistent final execution can reach the initial empty execution through a series of \(\textsc {Prev}{}\) steps, and each of these steps is matched by a forward step of TruSt. For the latter, one can show that each step of TruSt is matched by the (unique) \(\textsc {Prev}{}\) step.
To see why we cannot follow a similar approach for Awamoche, consider the program of Fig. 6, along with one of its executions. We will show that in-place revisits make it impossible to trace the algorithm’s last step merely by inspecting the execution. Assuming a left-to-right addition order, Awamoche will reach this execution as follows: it first adds
 ,
,
 and
and
 (notice that at this point the first read is blocked), then in-place revisit
(notice that at this point the first read is blocked), then in-place revisit
 , and finally add
, and finally add
 and backward-revisit
and backward-revisit
 . This last revisit, however, creates a problem: TruSt ’s proof assumes that a backward revisit
. This last revisit, however, creates a problem: TruSt ’s proof assumes that a backward revisit
 implies that w is located at the right of r, which is clearly not the case here. The fact that in Awamoche backward revisits can happen in both directions, makes it impossible to trace the algorithm’s last step simply by inspecting an execution.
implies that w is located at the right of r, which is clearly not the case here. The fact that in Awamoche backward revisits can happen in both directions, makes it impossible to trace the algorithm’s last step simply by inspecting an execution.
Awamoche. In contrast to TruSt, Awamoche ’s proof proceeds in a forward fashion. For each consistent final execution \(G_f\) we show 1. which steps are taken by the algorithm in order to reach \(G_f\), and 2. that these are the only possible ones that lead to \(G_f\). To do so, we first define a notion of a prefix: we say that an execution G is a prefix of \(G'\) (written \(G \sqsubseteq G'\)), if \(G'\) can be reached from G with a series of operational steps. In turn, we define an operational step to be a step that the algorithm may take in the non-revisit case (without demanding it is the one actually taken by the algorithm), that may perform in-place revisits as well.
Using this notion of prefixes, our proof defines a procedure \(\textsc {Succs}\) that, given a consistent execution \(G_f\) and an execution G produced by the algorithm such that \(G \sqsubseteq G_f\), \(\textsc {Succs}\) returns the minimal sequence of algorithm steps that reach some execution \(G'\) for which it is \(G \sqsubseteq G' \sqsubseteq G_f\). Concretely, if \(\textsf{next}_{\textit{P}}({G}) \) can be added to G such that the resulting execution \(G'\) is a prefix of \(G_f\), \(\textsc {Succs}\) returns this addition step. Otherwise, \(\textsf{next}_{\textit{P}}({G}) \) is a read event r that must be first revisited by an event e in order to reach an execution that is a prefix of \(G_f\). \(\textsc {Succs}\) then returns the sequence of algorithm steps that reach the execution resulting from extending G with the
 -prefix of e and setting r to read from e (or from \(\bot \), if e is a speculative read). Both completeness and optimality follow from \(\textsc {Succs}\)’s properties, as well as from the observation that every consistent final execution can be reached by a series of operational steps.
-prefix of e and setting r to read from e (or from \(\bot \), if e is a speculative read). Both completeness and optimality follow from \(\textsc {Succs}\)’s properties, as well as from the observation that every consistent final execution can be reached by a series of operational steps.
5.2 Awamoche: Completeness, Optimality, and Strong Optimality
Before stating our results, we first formally define useful executions. Recall that these are executions where all blocking reads corresponding to await loops are reading maximally (such executions denote liveness violations), and no confirmation CAS fails.
Definition 3
A consistent execution G is useful if every read in
 reads from a
reads from a
 -maximal write and no confirmation CAS fails.
-maximal write and no confirmation CAS fails.
Next, we define the class of input programs that satisfy our assumptions.
Definition 4
A program \(\textit{P} \) is well-formed if every speculative read is followed by a confirmation CAS with no write in-between, and all writes to locations accessed by speculative reads write distinct values.
Completeness and Optimality. Completeness guarantees that every useful final execution is explored. Awamoche is complete for well-formed programs that do not exhibit write-write races.
Theorem 1 (Completeness)
Given a well-formed program \(\textit{P} \), \(\textsc {Verify}(\textit{P})\) either detects a write-write race and exits, or visits every useful final execution of \(\textit{P} \).
Optimality states that (1) no equivalent final executions are explored, (2) there are no fruitless explorations that never lead to a consistent final execution.
Definition 5
We call an execution G visited by Awamoche fruitless if it does not recursively lead to any \(\textsc {Visit}(\textit{P},G_f)\) call, for any consistent final execution \(G_f\).
Awamoche is optimal for well-formed programs.
Theorem 2 (Optimality)
Given a well-formed program \(\textit{P} \) (1) \(\textsc {Verify}(\textit{P})\) never visits two equivalent final executions, and (2) if \(\textsc {Visit}(\textit{P}, G)\) directly leads to a call to \(\textsc {Visit}(\textit{P}, G')\) with G being fruitless, then \(\textsc {Visit}(\textit{P}, G')\) will not initiate any other \(\textsc {Visit}\) calls.
Observe that in the optimality theorem above, fruitless exploration can lead to an extra \(\textsc {Visit}\) step. The reason for that is the treatment of CASes: the read part of a CAS c can be added so that it reads from the same write as a different (successful) CAS. In such a case, there is no way to consistently add the pending write of c without revisiting, which in turn may not be able to happen due to Awamoche ’s maximality condition.
Strong Optimality. Strong optimality states that, apart from being optimal, only useful executions are visited. Awamoche is strongly-optimal for well-formed programs.
Theorem 3 (Strong Optimality)
Given a well-formed program \(\textit{P} \), \(\textsc {Verify}(\textit{P}, G)\) only visits useful executions.
6 Evaluation
We implemented Awamoche as a tool that verifies C/C++ programs under the RC11 memory model [22]. Similarly to other stateless model checkers, Awamoche works at the level of the LLVM Intermediate Representation (LLVM-IR).
In what follows, we evaluate the effectiveness of Awamoche ’s key ideas (namely, stale-read annotations, in-place revisiting and speculative revisiting) both individually, and as a whole. To that end, we evaluate Awamoche on a set of benchmarks that both amplify the weaknesses of standard DPOR, as well as demonstrate the applicability of our approach in realistic workloads. In all our tests, we compare Awamoche against a vanilla version of TruSt, a version of TruSt that employs stale-read annotations (TruSt \(_{\textsc {stale}}\)), and a version of TruSt that employs both stale-read annotation and in-place revisiting (TruSt \(_{\textsc {IPR}}\)).
Even though there are other stateless model checking tools that can be used to verify C/C++ programs (namely, GenMC [19] and Nidhugg [1]), we do not compare against them here, as we care about Awamoche ’s performance compared to TruSt. We only mention in passing that we expect GenMC’s performance to be similar to that of TruSt \(_{\textsc {stale}}\) (as its implementation incorporates various optimizations for
 statements), and Nidhugg’s similar to TruSt \(_{\textsc {IPR}}\) (as it employs an optimization with a similar effect to in-place revisiting [14]). We also note that comparing with Nidhugg is difficult since it operates under a different memory model, and does not transform the same types of loops to
statements), and Nidhugg’s similar to TruSt \(_{\textsc {IPR}}\) (as it employs an optimization with a similar effect to in-place revisiting [14]). We also note that comparing with Nidhugg is difficult since it operates under a different memory model, and does not transform the same types of loops to
 statements as Awamoche (also see Sect. 7).
statements as Awamoche (also see Sect. 7).
We draw two major conclusions from our evaluation. First, Awamoche ’s optimization yields exponential performance benefits compared to standard DPOR approaches. Second, these benefits do not only apply to small synthetic benchmarks, but also extend to realistic concurrent data structures.
Experimental Setup. We conducted all experiments on a Dell PowerEdge M620 blade system, running a custom Debian-based distribution, with two Intel Xeon E5-2667 v2 CPU (8 cores @ 3.3 GHz), and 256 GB of RAM. We used LLVM 11.0.1 for Awamoche. Unless explicitly noted otherwise, all reported times are in seconds. We set a timeout limit of 30 min.
6.1 Results
Let us first focus on some benchmarks that help us better understand where each of Awamoche ’s components can be applied (Table 1). Starting with orch-run, we see that even though blocked executions greatly outnumber complete executions, stale-reads annotations alone suffice to bring the number of blocked executions down to zero. This, however, is partly due to luck: in orch-run, main() spawns a number of workers that do not execute until they are signaled by main() using a special variable. In turn, because TruSt \(_{\textsc {stale}}\) follows a left-to-right scheduling, when DPOR encounters the worker threads, the scenario where they are not signaled is not considered, since it implies reading a stale value.
By contrast, in wait-workers and nr+nw, stale-reads annotations are insufficient to eliminate blocking. In these benchmarks, some designated threads wait for the rest of the workers to perform some tasks before proceeding. However, it is not guaranteed that these designated threads are going to be always processed after the rest of the threads by DPOR, and thus stale-reads annotations have little to no effect. Employing in-place revisiting, on the other hand, leads to a dramatic performance improvement: the number of blocked executions is effectively eliminated (the single blocked execution in nr+nw is a liveness violation).
Analogously to wait-workers and nr+nw, conf-loop demonstrates why in-place revisiting is insufficient when the success of an
 does not depend on a single load, but rather on a sequence of actions (as is the case in confirmation loops). As it can be seen, TruSt \(_{\textsc {IPR}}\) still explores blocked executions, which Awamoche manages to eliminate thanks to speculative revisits.
does not depend on a single load, but rather on a sequence of actions (as is the case in confirmation loops). As it can be seen, TruSt \(_{\textsc {IPR}}\) still explores blocked executions, which Awamoche manages to eliminate thanks to speculative revisits.
Moving to the final part of our evaluation, Table 2 demonstrates that the benefits of Awamoche extend to realistic workloads as well. As can be seen from Table 1, none of Awamoche ’s optimizations is redundant, as they are often all required to eliminate the exploration of blocked executions. Observe, however, that our benchmarks only exercise push or enqueue operations. This is because the respective pop or dequeue operations contain
 statements in their confirmation-CAS loops, and therefore cannot be optimized by Awamoche.
statements in their confirmation-CAS loops, and therefore cannot be optimized by Awamoche.
7 Related Work
The seminal work of Flanagan and Godefroid [13] has spawned a number of papers on DPOR. Among these, Optimal-DPOR [2] and
 [15] stand out, as they provide the first optimal DPOR algorithm, and the first optimal DPOR algorithm with polynomial memory consumption, respectively. TruSt is based on [17] and thus has the extra advantage of being parametric in the choice of the underlying weak memory model.
[15] stand out, as they provide the first optimal DPOR algorithm, and the first optimal DPOR algorithm with polynomial memory consumption, respectively. TruSt is based on [17] and thus has the extra advantage of being parametric in the choice of the underlying weak memory model.
A lot of works improve on DPOR one way or another. Many techniques introduce coarser equivalence partitionings to combat the state-space explosion problem (e.g., [3, 6,7,8, 10,11,12]). Other works focus on extending it to weak memory models [1, 4, 5, 17, 20, 24], while others try to leverage particular programming patterns [14, 16, 18]. Kokologiannakis, Ren, and Vafeiadis [18] in particular, deal with transforming spinloops into
 statements, the handling of which we optimize in this paper.
statements, the handling of which we optimize in this paper.
Among those, the work that is closest to ours is Godot [14]. Godot is an extension to DPOR that has a similar effect to in-place revisiting in the sense that it only explores executions that are either complete, or denote program termination errors. That said, Godot only works under SC, and cannot handle stale-read annotations or confirmation loops (which are instrumental in scaling the verification of concurrent data structures, as we saw in Sect. 6). In addition, Godot’s loop transformation is static (in contrast to Awamoche ’s, which is dynamic), making it easy to construct examples where Godot’s transformation does not work. Finally, even though Godot does not impose a “no write-write race” restriction on the input programs, this restriction is trivially satisfied for models like SC or TSO [26]: in such models, it is sound to transform writes to atomic exchange statements that write the value they read, thereby ordering all writes to each location.
8 Conclusion
We presented Awamoche, the first memory-model-agnostic DPOR algorithm that is sound, complete, and strongly optimal for programs with await and confirmation-CAS loops. Awamoche avoids blocked executions that arise due to await loops by revisiting blocking reads in-place, and deals with confirmation-CAS loops by also considering revisits whenever two speculative reads read from the same write.
As our theoretical and experimental results demonstrate, Awamoche yields exponential benefits over the current state-of-the-art. Yet, it does not support certain more advanced patterns commonly appearing in concurrent programs, the handling of which we leave as future work. Examples of such patterns include confirmation-CAS loops with
 statements between the speculative and the confirmation reads (such statements may arise due to
statements between the speculative and the confirmation reads (such statements may arise due to
 instructions), elimination backoff data structures, and await loops that use CASes instead of plain reads. We also believe that our key ideas for achieving strong optimality in these cases should be applicable in other scenarios as well, such as in programs with mutual exclusion locks or transactions.
instructions), elimination backoff data structures, and await loops that use CASes instead of plain reads. We also believe that our key ideas for achieving strong optimality in these cases should be applicable in other scenarios as well, such as in programs with mutual exclusion locks or transactions.
References
Abdulla, P.A., Aronis, S., Atig, M.F., Jonsson, B., Leonardsson, C., Sagonas, K.: Stateless model checking for TSO and PSO. In: Baier, C., Tinelli, C. (eds.) TACAS 2015. LNCS, vol. 9035, pp. 353–367. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46681-0_28
Abdulla, P.A., Aronis, S., Jonsson, B., Sagonas, K.: Optimal dynamic partial order reduction. In: POPL 2014, pp. 373–384. ACM, New York (2014). https://doi.org/10.1145/2535838.2535845
Abdulla, P.A., Atig, M.F., Jonsson, B., Låang, M., Ngo, T.P., Sagonas, K.: Optimal stateless model checking for reads-from equivalence under sequential consistency. Proc. ACM Program. Lang. 3, 150:1–150:29 (2019). https://doi.org/10.1145/3360576
Abdulla, P.A., Atig, M.F., Jonsson, B., Leonardsson, C.: Stateless model checking for POWER. In: Chaudhuri, S., Farzan, A. (eds.) CAV 2016. LNCS, vol. 9780, pp. 134–156. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-41540-6_8
Abdulla, P.A., Atig, M.F., Jonsson, B., Ngo, T.P.: Optimal stateless model checking under the release-acquire semantics. Proc. ACM Program. Lang. 2(OOPSLA), 135:1–135:29 (2018). https://doi.org/10.1145/3276505
Agarwal, P., Chatterjee, K., Pathak, S., Pavlogiannis, A., Toman, V.: Stateless model checking under a reads-value-from equivalence. In: Silva, A., Leino, K.R.M. (eds.) CAV 2021. LNCS, vol. 12759, pp. 341–366. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-81685-8_16
Albert, E., Arenas, P., de la Banda, M.G., Gómez-Zamalloa, M., Stuckey, P.J.: Context-sensitive dynamic partial order reduction. In: Majumdar, R., Kunčak, V. (eds.) CAV 2017. LNCS, vol. 10426, pp. 526–543. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63387-9_26
Albert, E., Gómez-Zamalloa, M., Isabel, M., Rubio, A.: Constrained dynamic partial order reduction. In: Chockler, H., Weissenbacher, G. (eds.) CAV 2018. LNCS, vol. 10982, pp. 392–410. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96142-2_24
Alglave, J., Maranget, L., Tautschnig, M.: Herding cats: modelling, simulation, testing, and data mining for weak memory. ACM Trans. Program. Lang. Syst. 36(2), 7:1–7:74 (2014). https://doi.org/10.1145/2627752
Aronis, S., Jonsson, B., Lång, M., Sagonas, K.: Optimal dynamic partial order reduction with observers. In: Beyer, D., Huisman, M. (eds.) TACAS 2018. LNCS, vol. 10806, pp. 229–248. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-89963-3_14
Chalupa, M., Chatterjee, K., Pavlogiannis, A., Sinha, N., Vaidya, K.: Datacentric dynamic partial order reduction. Proc. ACM Program. Lang. 2(POPL), 31:1–31:30 (2017). https://doi.org/10.1145/3158119
Chatterjee, K., Pavlogiannis, A., Toman, V.: Value-centric dynamic partial order reduction. Proc. ACM Program. Lang. 3(OOPSLA) (2019). https://doi.org/10.1145/3360550
Flanagan, C., Godefroid, P.: Dynamic partial-order reduction for model checking software. In: POPL 2005, pp. 110–121. ACM, New York (2005). https://doi.org/10.1145/1040305.1040315
Jonsson, B., Lång, M., Sagonas, K.: Awaiting for Godot: stateless model checking that avoids executions where nothing happens. In: FMCAD 2022, pp. 163–172. TU Wien Academic Press (2022). https://doi.org/10.34727/2022/isbn.978-3-85448-053-2_35
Kokologiannakis, M., Marmanis, I., Gladstein, V., Vafeiadis, V.: Truly stateless, optimal dynamic partial order reduction. Proc. ACM Program. Lang. 6(POPL) (2022). https://doi.org/10.1145/3498711
Kokologiannakis, M., Raad, A., Vafeiadis, V.: Effective lock handling in stateless model checking. Proc. ACM Program. Lang. 3(OOPSLA) (2019). https://doi.org/10.1145/3360599
Kokologiannakis, M., Raad, A., Vafeiadis, V.: Model checking for weakly consistent libraries. In: PLDI 2019. ACM, New York (2019). https://doi.org/10.1145/3314221.3314609
Kokologiannakis, M., Ren, X., Vafeiadis, V.: Dynamic partial order reductions for spinloops. In: FMCAD 2021, pp. 163–172. IEEE (2021). https://doi.org/10.34727/2021/isbn.978-3-85448-046-4_25
Kokologiannakis, M., Vafeiadis, V.: GenMC: a model checker for weak memory models. In: Silva, A., Leino, K.R.M. (eds.) CAV 2021. LNCS, vol. 12759, pp. 427–440. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-81685-8_20
Kokologiannakis, M., Vafeiadis, V.: HMC: model checking for hardware memory models. In: ASPLOS 2020, pp. 1157–1171. ACM, Lausanne, Switzerland (2020). https://doi.org/10.1145/3373376.3378480
Lahav, O., Namakonov, E., Oberhauser, J., Podkopaev, A., Vafeiadis, V.: Making weak memory models fair. Proc. ACM Program. Lang. 5(OOPSLA) (2021). https://doi.org/10.1145/3485475
Lahav, O., Vafeiadis, V., Kang, J., Hur, C.-K., Dreyer, D.: Repairing sequential consistency in C/C++11. In: PLDI 2017, pp. 618–632. ACM, Barcelona, Spain (2017). https://doi.org/10.1145/3062341.3062352
Lamport, L.: How to make a multiprocessor computer that correctly executes multiprocess programs. IEEE Trans. Comput. 28(9), 690–691 (1979). https://doi.org/10.1109/TC.1979.1675439
Norris, B., Demsky, B.: CDSChecker: checking concurrent data structures written with C/C++ atomics. In: OOPSLA 2013, pp. 131–150. ACM (2013). https://doi.org/10.1145/2509136.2509514
Oberhauser, J., et al.: VSync: push-button verification and optimization for synchronization primitives on weak memory models. In: ASPLOS 2021 - Virtual, pp. 530–545. ACM, USA (2021). https://doi.org/10.1145/3445814.3446748
Owens, S., Sarkar, S., Sewell, P.: A better x86 memory model: x86-TSO. In: Berghofer, S., Nipkow, T., Urban, C., Wenzel, M. (eds.) TPHOLs 2009. LNCS, vol. 5674, pp. 391–407. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03359-9_27
Acknowledgments
We thank the anonymous reviewers for their feedback. This work has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 101003349).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this paper
Cite this paper
Kokologiannakis, M., Marmanis, I., Vafeiadis, V. (2023). Unblocking Dynamic Partial Order Reduction. In: Enea, C., Lal, A. (eds) Computer Aided Verification. CAV 2023. Lecture Notes in Computer Science, vol 13964. Springer, Cham. https://doi.org/10.1007/978-3-031-37706-8_12
Download citation
DOI: https://doi.org/10.1007/978-3-031-37706-8_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-37705-1
Online ISBN: 978-3-031-37706-8
eBook Packages: Computer ScienceComputer Science (R0)










 representing the blockage of a thread (e.g., due to the condition of an “
representing the blockage of a thread (e.g., due to the condition of an “
 ” statement failing).
” statement failing). representing the violation of some program assertion.
representing the violation of some program assertion. where
where
 denotes special attributes the write may have (i.e., exclusive),
denotes special attributes the write may have (i.e., exclusive),
 is the location accessed, and
is the location accessed, and
 the value written.
the value written. where
where
 denotes special attributes the read may have (i.e., await, speculative, exclusive), and
denotes special attributes the read may have (i.e., await, speculative, exclusive), and
 is the location accessed. We note that if a read has the
is the location accessed. We note that if a read has the  of events that includes
of events that includes
 and does not contain multiple events with the same thread identifier and serial number.
and does not contain multiple events with the same thread identifier and serial number. , representing the order in which events were incrementally added to the graph,
, representing the order in which events were incrementally added to the graph,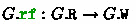 , called the reads-from function, that maps each read event to a same-location write from where it gets its value, and
, called the reads-from function, that maps each read event to a same-location write from where it gets its value, and , called the coherence order, which is total on
, called the coherence order, which is total on
 for every location
for every location
 .
.