Keywords

1 Introduction

Today’s predominant memory technology is based on the storage of electrical charge. In these devices relatively high energy barriers are required to prevent the loss of its memory state through electron tunneling currents. Due to approximately 1000 times larger mass of atoms compared to electrons, the tunneling of atoms to neighboring states is negligible. In contrast, memristive devices are based on the principle of resistive switching, whereby information is stored in the device resistance. These memory devices are based on the change of the atomic arrangement. Therefore, they do not require high energy barriers and could replace currently used memory concepts, especially with respect to scalability and energy efficiency.

The first memristive devices were introduced as early as the 1960s [1,2,3]. In 1976, specifically the emergence of Ag filaments as a possibility for resistive switching was recognized [4]. In the 1970s, Leon O. Chua further presented a theory of memristive systems [5, 6]. However, especially due to the rapid progress of silicon-based, integrated circuit technology, interest in memristive devices decreased from the end of the 1970s until new computer architectures were considered in the 1990s. In 2008, Strukov et al. demonstrated resistive switching in the context of the theory of memristive systems presented by Chua [7]. Due to their versatile usability, for example as artificial synapses in neural networks for new types beyond von Neumann computer architectures or as future, non-volatile storage elements, research on memristive devices is steadily increasing to this day [8,9,10].

Memristive devices are often used in pulsed mode operation. However, direct current operation and its related current-voltage (IV) characteristics provide important insights into the physical behavior of individual devices. For instance, on the basis of the IV characteristics a distinction can generally be made between unipolar and bipolar devices. In the case of bipolar switching devices, the voltage polarity in the set and reset process differs, whereas for unipolar devices it is the same. In addition to this very general classification, memristive devices can also be differentiated based on their physical behavior. For example there are memristive devices based on magnetic effects (such as magnetic tunnel devices [11]), on electrostatic effects (such as the trapping effect of electrons [12]). The memristive devices particularly considered in this work are based on a change in the atomic configuration. Even within this type of memristive systems, the exact physical mechanisms of resistive switching can be very different and range from diffusion and migration of ions [13] through chemical reactions to thermal effects [14] caused by Joule heating [15]. The exact switching behavior is often not understood and thus prevents a reliable integration of these devices in electronic circuits. As a theoretical approach, this chapter is henceforth dedicated to the modeling and simulation of electrochemical metallization (ECM) cells that exhibit filamentary switching behavior.

2 Electrochemical Metallization Cells

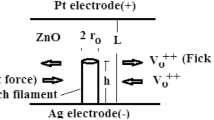
Typically, ECM cells consist of a solid electrolyte with poor electrical conductivity, embedded between a chemically active and an inert electrode. The active electrode usually consists of Ag, Cu, or Ni. In addition, resistive switching has already been demonstrated with active electrodes made of alloys containing Ag, Au, Cu, or Ni, like Au/Ag alloys [16]. In addition to the chemical inactivity, another requirement for the inert electrode is the poor miscibility with atoms of the active electrode. These requirements are met by materials like Pt, Ir, and W. A wide variety of materials have been demonstrated as possible electrolyte materials, such as TiO\(_2\), SiO\(_2\), Ge\(_x\)S\(_y\) [17].

Fig. 1
figure 1

Reprinted from [14], with the permission of AIP Publishing

Scheme of the ECM cell with incipient filament growth and illustration of the processes implemented in the simulation: (I) oxidation, (II) surface diffusion on the Pt electrode, (III) diffusion in the TiO\(_x\) , (IV) reduction on Ag, (V) reduction on a step, (VI) nucleation.

Full size image

In this work, the ECM devices based on the Ag/TiO\(_x\)/Pt materials system is investigated with the help of simulations [18]. Its general functionality is schematically presented in Fig. 1. Assume that the ECM cell is in the high-resistance state (HRS) initially. In the set process, the chemically active Ag electrode is subject to a positive voltage (with respect to the opposing grounded electrode). This leads to oxidation of the Ag electrode following the reaction,

$$\begin{aligned} \text {Ag} \rightarrow \text {Ag}^+ + \text {e}^- \end{aligned}$$
(1)

with monovalent Ag\(^+\) ions [see Fig. 1 (I)] resulting in a partial dissolution of the active Ag electrode. Along with a related transfer of charge through the electrode, the Ag\(^+\) ions are subject to the electric field in the solid electrolyte.

Due to this electric field, the Ag\(^+\) ions move through the TiO\(_x\) toward the Pt electrode [see Fig. 1 (III)]. When the Ag\(^+\) ions reach the Pt/TiO\(_x\) interface, they can undergo different processes. Since Ag and Pt are almost immiscible at room temperature (see phase diagram Ag-Pt), surface diffusion of the Ag\(^+\) ions occurs at the Pt/TiO\(_x\) interface [see Fig. 1 (II)]. In addition, Ag\(^+\) ions may form stable nuclei at the Pt electrode after reduction [19]. At these nuclei, additional Ag\(^+\) ions may be reduced based on the following reaction [see Fig. 1 (IV)–(V)]:

$$\begin{aligned} \text {Ag}^+ + \text {e}^- \rightarrow \text {Ag} \end{aligned}$$
(2)

This reaction leads to the growth of Ag filaments from the Pt electrode through the TiO\(_x\) electrolyte towards the Ag electrode. The two-step process of (i) formation of small Ag clusters and (ii) the reduction of Ag\(^+\) ions on these clusters by electron transfer has been proven experimentally in 1999 [20].

If the distance between the filament and the Ag electrode decreases, the Ohmic resistance also decreases (increases the probability of electron tunneling). This leads to an increase in the current through the device, which is often intentionally limited to a maximum value. This value of maximum current signifies whether there is a gap between the filament and the electrode, or the filament has formed up to the Ag electrode and begun to develop a galvanic contact. In this state, the device is in the low-resistance state (LRS). To reset the device to the HRS, the voltage polarity must be reversed. Depending on the current through the filament, it partially dissolves due to the electric field, supported by an increased temperature by Joule heating and by electromigration. The distance between the source and the sink of ions is determined by the thickness of the solid electrolyte and may therefore be very small. That may lead to desired properties like fast switching times and a very good scaling potential (<10 nm). In addition, only small voltages are required for device operation due to the small electrolyte thickness and the correspondingly very large electric field strengths. A very small energy consumption (< pJ) results. Despite these advantages and the technical feasibility of these devices, the randomness of the inherent physical processes remains an issue.

To gain a reliable understanding of the resistive switching of ECM cells, simulations on the atomic scale are indispensable. The multitude of different simulation models proposed so far range from concentrated models to molecular dynamics models. This also includes continuous models and kinetic Monte Carlo (kMC) models in 1D and 2D [21,22,23,24,25,26]. These models aim to describe resistive switching on various time scales. Since filament growth is a three-dimensional phenomenon, however, a 3D kMC simulation model is proposed as part of this work. The following central questions should be addressed: (i) How does filament growth proceed in ECM cells, (ii) what are the central influences that lead to the reset of ECM cells, and (iii) how does the distribution of atoms affect the resistance of the ECM cells?

3 Simulation Scenario and Simulation Methods

To simulate the characteristics of a real ECM cell, only a representative section of the device is considered in the model. The simulation box consists of a square base with an area of 40 nm \(\times \) 40 nm, a 10 nm thick TiO\(_x\) solid electrolyte and a 3 nm thick section of an active Ag electrode. The Ag electrode consists of 38,400 individual atoms, whereas the opposite inert Pt electrode was modeled as a boundary for Ag\(^+\) ion motion to compensate for the poor miscibility of Ag and Pt. At all other interfaces (i.e., the sides), periodic periodic boundary conditions were used for ion motion. Occupiable, stable ion positions were represented by a cubic primitive lattice with a lattice constant of 5 Å. The periodic lattice is reasoned by the corresponding short range order, which exists also in amorphous materials.

In titanium oxide, silver is preferably present as a monovalent ion at interstitial sites. It can diffuse through the bulk TiO\(_x\) under the influence of electric fields [27, 28]. The processes presented in Fig. 1 were taken into account also in the simulation, as these are identified as the primarily important processes. The rate of diffusion of Ag\(^+\) ions through TiO\(_x\) is given by

$$\begin{aligned} k_\text {diff}= \nu _0 \exp {\left( \frac{E_\text {a,diff}+0.5 z_i e (\phi _j-\phi _i)}{k_\text {b} T(\textbf{r},t)}\right) }. \end{aligned}$$
(3)

Here, \(\nu _0\) is the phonon frequency, \(E_\text {a,diff}\) is the activation energy for diffusion of Ag\(^+\) ions through TiO\(_x\), \(\phi _i\) and \(\phi _j\) are the potential at positions indicated by i and j, \(z_i\) is the charge number, e is the elementary charge, T is the local temperature, and \(k_\text {b}\) is the Boltzmann constant. Since diffusion at the material interfaces usually proceeds at higher velocities than in the volume, a smaller activation energy \(E_\text {a,surf}\) is used for surface diffusion compared to volume diffusion. All relevant simulation parameters are summarized in Table 1.

Table 1 Parameters for the simulation of ECM cells
Full size table

The rates for reduction and oxidation can be derived from the Butler-Volmer equation [24]. One finds

$$\begin{aligned} k_\text {red}&= \nu _0 \exp {\left( -\frac{E_\text {a,red}-\alpha _0 z_i e \Delta \phi }{k_\text {b} T(\textbf{r},t)}\right) }\end{aligned}$$
(4)
$$\begin{aligned} k_\text {ox}&= \nu _0 \exp {\left( -\frac{E_\text {a,ox}-(1-\alpha _0) z_i e \Delta \phi }{k_\text {b} T(\textbf{r},t)}\right) } \end{aligned}$$
(5)

with the charge transfer coefficient \(\alpha _0 = 0.5\) and the activation energies \(E_\text {a,red}\) and \(E_\text {a,ox}\) for reduction and oxidation.

The potential difference \(\Delta \phi \) at the electrode/TiO\(_x\) and filament/TiO\(_x\) interface is given as \(\Delta \phi =\phi _{\text {TiO}_x}-\phi _\text {electrode}\) and \(\Delta \phi =\phi _{\text {TiO}_x}-\phi _\text {filament}\), respectively. The process of heterogeneous nucleation depends on its environment. Thus, the time constant for nucleation can be given as a function of the Ag concentration. Here, the nucleation of Ag\(^+\) ions is modeled analogously to [26] as a one-particle process where the nucleation process is independent of the material concentration. This ensures a reduction in simulation time for the very time-consuming 3D simulations. The fact that a critical Ag concentration must first be reached so that nucleation becomes probable and the resulting slowing down of the process is represented here by an increased activation energy. In these simulations the following nucleation rate was used:

$$\begin{aligned} k_\text {nuc}= \nu _0 \exp {\left( -\frac{E_\text {a,nuc}-\alpha _0 z_i e \Delta \phi }{k_\text {b}T(\textbf{r},t)}\right) } \end{aligned}$$
(6)

with the activation energy \(E_\text {a,nuc}\) for nucleation. The correctness of this modeling approach may be confirmed experimentally afterwards from the activation energy for nucleation. The time it takes to set a filament (\(t_\text {set}\)) decreases exponentially for high voltages with the applied voltage. This is reflected in the equations of the process rates in Arrhenius form. \(t_\text {set}\) becomes infinite for small voltages [36]. Therefore, for every oxidation step additionally the voltage-dependent condition

$$\begin{aligned} \zeta < -\log \left[ \cos (\xi V_\text {appl})\right] \end{aligned}$$
(7)

must be satisfied, with the uniformly distributed random number \(\zeta \in [0,1]\), the fitting parameter \(\xi \), and the applied voltage \(V_\text {appl}\).

As an aside, it is well known that in TiO\(_x\), vacancies move in the electrical field and can form conductive filaments. Depending on the kinetics of silver ion migration and vacancy migration, the latter may have an effect on the electric field distribution and hence on the formation of silver filaments. However, this mechanism is neglected in this work.

All mentioned processes depend on the electric field. It can be calculated based on the continuity equation \(\nabla \cdot \textbf{j}=0\). Here, the displacement current has been neglected. With the help of a simple scale analysis, it can be shown that this assumption is justified. It turns out that the displacement current scales with \(\mu \epsilon L^2 / c^2 T^2\). Therein, L and T are the typical length and time scale of the system, respectively. With \(L\propto \) 1 nm and \(T\propto \) 1 s one finds that \(\mu \epsilon L^2 / c^2 T^2 \ll 1\).

Electron transport through the device is dominated by Ohmic conduction. In the literature, the tunneling current between the filament and the electrode is often reported as the dominant transport mechanism [19]. To show that electron transport is not dominated by tunneling electrons here, the Ohmic current is compared to the tunneling current at the smallest possible distance resolved in the simulation of 0.5 nm. This distance is chosen because the tunneling current scales exponentially with the thickness of the tunnel barrier, but the Ohmic current only linearly. Thus, for the minimum possible distance, the largest ratio between tunneling current and Ohmic current \(I_\text {tun}/I_\text {ohm}\) is expected. The tunneling current density may be calculated using the Simmons equation [37]. The height of the tunnel barrier was chosen to be \(\Phi _\text {TB}=\Phi _{\text {TiO}_x/\text {Ag}}=0.36\) eV [38]. The effective mass of electrons was chosen to be \(m^*_e = 9m_e\) [39].

The Ohmic current density was calculated from \(j=\sigma E\) with \(\sigma =\sigma _{\text {TiO}_x}= 100\) S/m. Due to the high conductivity of the TiO\(_x\) matrix, the Ohmic current density is significantly larger than the tunneling current density even in the case of the smallest possible distance between filament and electrode (see Fig. 2).

Fig. 2
figure 2

Comparison between tunneling current and Ohmic current density for a distance between electrode and filament of 0.5 nm [40]

Full size image

Consequently, a generalized Ohm’s law,

$$\begin{aligned} \textbf{j} = \sigma (\textbf{r})\textbf{E}(\textbf{r}), \end{aligned}$$
(8)

with the local conductivity \(\sigma (\textbf{r})\) of the respective material and the local electric field \(\textbf{E}(\textbf{r})\) is used to describe the electron current density. Since the dynamics of the system is quasi-stationary, the electric field can be written as \(\textbf{E}=-\nabla \Phi \). The differential equation for the electrostatic potential is thus given by

$$\begin{aligned} \nabla \cdot \left( \sigma (\textbf{r})\nabla \Phi \right) = 0 \end{aligned}$$
(9)

To solve this differential equation, Dirichlet boundary conditions are applied to the upper and lower interfaces. Periodic boundary conditions are applied to all other interfaces. The differential equation is solved numerically using the successive over-relaxation method on a structured grid. The current I through the device is calculated using the integral

$$\begin{aligned} I=\int _A \sigma (\textbf{r})\textbf{E}(\textbf{r})\cdot \textbf{n} dA. \end{aligned}$$
(10)

This can be evaluated at any vertical position, since the continuity equation is implicitly satisfied everywhere.

All rates for the chemical and physical processes in the ECM cell are exponentially dependent on the local temperature. The temperature is therefore a decisive parameter for the memristive behavior of ECM cells. Due to the fact that in the LRS a metallic filament forms through the high resistance electrolyte matrix and connects the top and bottom electrodes, the current flow through the ECM cell is concentrated to the filament. This leads to a significant current density through the filament and thus potentially to a large temperature due to Joule heating. Consequently, the assumption of a constant temperature may not be justified and therefore the temperature in the device is calculated. The material dependent parameters of the heat conduction equation are also listed in Table 1. To investigate the effect of temperature on the memristive behavior, the temperature in two different materials, Ag and TiO\(_x\), is calculated. The time constants of temperature evolution in these materials can be estimated based on a scale analysis to \(\tau _\text {Ag} \propto 5.7\times 10^{-15}\) s and \(\tau _\text {Ag} \propto 4.2 \times 10^{-13}\) s with a typical length scale of the system of 1 nm. The typical time scale of ion movement accordingly results from the largest jump rate \(k_{ij}\) of the ions of the respective iteration,

$$\begin{aligned} \tau _\text {hop}=\frac{\ln \zeta }{k_{ij}}= \ln \zeta \, \nu _0^{-1}\exp \left( \frac{E_\text {a}}{k_\text {b} T}\right) \approx 10^{-2}\text {s}, \end{aligned}$$
(11)

with the uniformly distributed random number \(\zeta \in ]0,1]\). The timescale of memristive behavior is thus significantly larger than the time constant of the temperature development. Therefore, the steady-state heat equation,

$$\begin{aligned} -\nabla \cdot (\lambda \nabla T) = \textbf{j} \cdot \textbf{E}, \end{aligned}$$
(12)

is solved to calculate the temperature. \(\lambda (\textbf{r})\) is the material-dependent thermal conductivity, whereas the right hand side represents the Joule heating source term. The upper and lower boundary surfaces are set to room temperature throughout the simulation. Periodic boundary conditions are again used at all other interfaces. This differential equation is solved numerically on the grid, which was also used for the potential. To account for the influence of temperature on the ion motion, the calculated temperature is inserted into the rate equations of the chemical and physical process rates.

4 Results and Discussion

The simulation model was used to calculate the IV characteristics of the Ag/TiO\(_x\)/Pt ECM cell as well as the atomic state and switching kinetics. An ideal voltage source was applied to the Ag electrode, whereas the inert Pt electrode was set to the constant potential of 0 V. The source voltage and the voltage applied to the device, as well as the calculated IV characteristic are shown in Fig. 3. The calculated IV characteristics is in excellent agreement with experimental measurements as reported by Yang [41]. Five instances of time characteristic of the applied voltage are indicated by the numbers (1)–(5) and six different instances of time characteristic of the reset process are indicated by the letters (a)–(f).

Fig. 3
figure 3

Reprinted from [14], with the permission of AIP Publishing

Input/output behavior of the ECM cell. Top: Ramped source voltage (red) and voltage applied to the simulation region (blue) as a function of time. Bottom: IV characteristics plotted versus source voltage. Five important instances of time during the voltage ramp (green dots) and six important instances of time during the reset process (red dots) are marked.

Full size image

The voltage ramp is applied as follows: The voltage source initially applies a voltage ramp with the slope 0.5 V/s to the device. To prevent an electrical breakdown, the current is limited to a maximum value of \(I_\text {CC} = 50 \,\upmu \)A. If the current through the device exceeds this value, the voltage source is replaced by an ideal current source which provides exactly \(I_\text {CC}\). Here, the linear relationship between current and voltage through the device can be exploited. Using a test voltage and a corresponding test current, the resistance of the device, \(R_\text {ECM}\), can be obtained. From this resistance and the current \(I_\text {CC}\) it is possible to calculate \(V_\text {CC}=R_\text {ECM} I_\text {CC}\), i.e., the actual voltage applied to the device. This applied voltage differs from the source voltage.

When the (original) source voltage reaches 0.5 V (this value was chosen to ensure resistive switching), the slope of the voltage ramp is inverted to a value of −0.5 V/s. If as a result the current drops below \(I_\text {CC}\), the current source is again replaced by a voltage source. When the voltage reaches −0.25 V, the slope of the voltage ramp is reversed to 0.5 V/s until the voltage returns to 0 V.

Fig. 4
figure 4

Reprinted from [14], with the permission of AIP Publishing

Status of ECM cell shown for the five marked instances of time from Fig. 3. Left: Status of filament growth. Right: Corresponding temperature distribution.

Full size image

The calculated temperature distribution (right) and the corresponding atomic state (left) for the five selected instances of time (1)–(5) from Fig. 3 are depicted in Fig. 4. In the original state, where the applied voltage is 0 V, no current flows through the device. All Ag atoms are within the electrode [time (1)]. Since no current flows through the device, the temperature in the device is at room temperature everywhere. When a positive voltage is applied to the Ag electrode, the oxidation process starts at the electrode due to the electric field induced by the externally applied voltage. The oxidized, positive Ag\(^+\) ions move through the solid-state electrolyte, forming a stable nucleus at the Pt electrode. They reduce at this nucleus and form a conductive filament through the solid-state electrolyte. Once the conductive filament connects the two electrodes, a significant current flow through the filament is observed [time (2)].

At this point it is important to mention that resistive switching does not necessarily require a connection between the two opposing electrodes. In addition to a connection, it is also possible for a gap to remain between the filament and the Ag electrode. Either a tunneling current flows across this gap, if the resistance of the solid electrolyte is correspondingly high, or an Ohmic current, as presented here. In both cases, the current through the device is significantly smaller than in the case of a connection through the filament, which leads to a lower temperature inside the device for the same applied voltage [42]. Therefore, the retention of a gap can only be guaranteed by a correspondingly small current limit.

Fig. 5
figure 5

Reprinted from [14], with the permission of AIP Publishing

Calculated current density distribution through the simulation area at time (2) from Fig. 3 immediately after electroforming of the conductive filament.

Full size image

Figure 5 shows the current density shortly after the filament has connected the upper and the lower electrode [time (2)]. This current density is used as a source term for the temperature calculation. As expected, the current mainly flows through the conductive filament and leads to a local heating of the device. The temperature of the device increases to a maximum value of 320.9 K due to Joule heating. When the current reaches the limiting current \(I_\text {CC}\), the voltage applied to the device decreases due to the reduced resistance (blue line on the right side of Fig. 3). Due to this reduced voltage during current limiting, further growth of the filament is significantly slowed down.

If the voltage polarity is reversed, the current increases again [time (3)]. Therefore, the temperature in the device also rises again and reaches values around 305 K. As soon as the filament breaks and thus the connection between the two opposing electrodes is dissolved [time (4)], the temperature drops again to room temperature. Due to the electric field within the solid state electrolyte, the filament is degraded [time (5)].

Fig. 6
figure 6

Reprinted from [14], with the permission of AIP Publishing

Calculated magnitude of the electric field in the simulation area at time point \(t = 0.66\) s directly before electroforming of the conductive filament.

Full size image

Since no nucleation seed was set in this simulation, nucleation occurs at random positions of the Pt electrode. At these nucleation sites, reduction occurs preferentially and stable clusters are formed. Figure 6 shows the magnitude of the electric field at time \(t = 0.66\) s. At the positions of the clusters, the electric field is increased due to sharp edges and because of a reduced distance between cluster and Ag electrode. Therefore, the growth of the filament is strongly accelerated at these positions. Due to the influence of the inhomogeneous electric field within the solid electrolyte, large clusters grow faster than small ones and eventually form a conductive filament.

Due to the periodic boundary conditions, a copy of the simulation box can be imagined attached to the simulation box in x and y direction for the electric field calculation. The electric field in these copies of the simulation box influences the electric field in the simulation box. This is correct in so far, since the real device extends much further in x and y direction than the simulation box. Since the surface roughness caused by the inhomogeneous distribution of the Ag in the simulation box is randomly distributed, periodic boundary conditions are a good assumption. It limits the interpretability to distinguish single or multi filament behavior, however, as coupling may occur.

Due to the fact that filament growth strongly depends on the electric field, the set time varies with the applied voltage. To investigate the switching kinetics of the ECM cell, different constant voltages were applied to the device and the time until electroforming of a filament was calculated. Figure 7 shows the result of these calculations. With set times in the range of 0.1 ms to 10 s depending on the applied voltage, the calculated switching kinetics of the device are comparable to corresponding experimental measurements of ECM cells [43].

Another aspect of particular interest in the context of the presented simulations are the kinetics of the reset process. At the time of maximum negative current, the maximum temperature is 304.6 K. Even though higher temperatures are expected for higher power densities within the device, this simulation result means that a critical temperature rise is not an issue for the typical use of ECM cells in integrated circuits [44]. Thus, it is clear that the dissolution and filament reset process is predominantly caused by the electric field.

Fig. 7
figure 7

Reprinted from [14], with the permission of AIP Publishing

Switching kinetics of the ECM cell. Calculated time to form of the conductive filament for different filament for different applied voltages.

Full size image

Unlike the set process, which is relatively abrupt, the reset process is often gradual. In addition, the reset process is stochastic and varies from cycle to cycle [45]. Figure 8 shows the atomic state of the conductive filament for the six instances of time of the reset process (a)–(f) selected in Fig. 3. This figure is instructive to explain the reset process in detail. At time (a), the filament is completely established and the reset process has not yet started. Due to the electric field, Ag atoms of the filament oxidize at random positions depending on the potential drop between filament and solid electrolyte and move away from the filament.

Fig. 8
figure 8

Reprinted from [14], with the permission of AIP Publishing

Atomic configuration of the conductive filament at the six times marked in Fig. 3. Marked instances of time of the reset process.

Full size image
Fig. 9
figure 9

Reprinted from [14], with the permission of AIP Publishing

Potential distribution at time \(t = 2.2\) s directly before electroforming of the conductive filament in a section through the simulation area at the position of the filament.

Full size image

Figure 9 shows the distribution of the electrostatic potential over a cross-section of the ECM cell at time \(t = 2.2\) s, shortly before the conductive filament breaks. Due to the connection through the conductive filament, the potential is nearly linear from the top to the bottom electrode. A slight variation is observed as the magnitude of the electric field increases at constrictions of the filament. The filament is subject to the electric field approximately uniformly in position and provides oxidation processes. The resulting thinning of the filament leads to several weak connections between the upper and lower electrode [time (b)], shown by red circles in Fig. 8. In consequence, the resistance of the device grows successively, subject to the random dissolution and ion motion. This leads to the stochastic behavior of the reset process. At these weak connection spots, both the temperature and the electric field increase, due to the enhanced current density and resistance. The breakup of the conductive filament occurs preferentially at these narrow spots [time (c)]. After the filament has split. It can nevertheless reconnect [time (d)], which again leads to a drop in resistance and thus to an increase in current. The final breakup of the conductive filament is shown at time (e). As the filament recedes, isolated islands are formed. Additionally, it can be observed that the growth of the filament also starts at the active Ag electrode. This growth mode can also be shown in other simulations [21] as well as in experiments [46].

At this point, two more important points should be discussed. First, it is important to note that the presented simulation model is only valid if the conductivity of the electrolyte matrix is such that Ohmic current dominates over tunneling currents and ionic current conduction. If this is not the case, these conduction mechanisms would have to be accounted for in the continuity equation.

Second, it should be pointed out that this model focuses especially on the influence of temperature and electric field on the reset process. Another mechanism of electromigration was considered in this model only indirectly, through the process of re-oxidation. In the literature, this mechanism is hardly discussed in the context of the reset process of ECM cells [47, 48]. Considering electric fields in a good electrical conductor, the force on an ion can be expressed as a function of an effective charge number. For silver, the effective charge number is −26 [49]. Thus, the force of the electron flow dominates over the force of the electric field on Ag in the filament. It becomes particularly large (but disappears in quantum point contacts) at the narrow spots of the filament. Electromigration can thus facilitate movement of Ag out of the filament. Once they dissolve from the filament, they have a monovalent charge and are no longer affected by electromigration, but by the electric field, since the electron current is confined to the filament according to Fig. 5. Consequently, electromigration may be a crucial mechanism for the initial breakup of the filament. Especially due to the magnitude of the force on Ag in the filament, this mechanism should be considered in future extensions of this model.

5 Conclusions and remarks

In this chapter, the memristive behavior of ECM cells was investigated using a typical Ag/TiO\(_x\)/Pt ECM cell as an example. The focus was on the phenomenon of resistive switching, the physical processes of filament growth, and the driving forces of the reset process. A simulation model was developed to address these aspects. The ion motion was described using the kMC method. The continuity equation assuming purely Ohmic behavior was solved to calculate the current density and the electric field. Additionally, the steady-state heat equation was solved to calculate the temperature within the device, subject to Joule heating. First, it was shown that the tunnelling currents are negligible compared to Ohmic currents in the devices at all times. The formation and dissolution of a conductive Ag filament could be identified as the main cause of resistive switching. In addition, the main chemical and physical processes leading to the filament growth could be described, such as oxidation, diffusion, reduction, and nucleation. It was shown that the main driving force for filament growth is the electric field. A large electric field results when the distance between filament and electrode becomes very small. Therefore, growth occurs predominantly at the tip of pre-formed (incomplete) filaments. Furthermore, it was argued that the calculated IV characteristics of the device is in very good agreement with measurements.

To investigate the different physical mechanisms that lead to the reset process, the distribution of the current density in the device and the resulting increase in temperature were calculated. Accordingly, the maximum current density is about \(8\times 10^{13}\) A/m2 and, as expected, flows mainly through the conductive filament. The maximum calculated increase in temperature during the reset process is approximately 5 K. Accordingly, it was concluded that the main driving force of the reset process is the electric field, not the temperature. In addition, it was discussed that the force due to electromigration on Ag in the closed filament may not be negligible. Up to now, this process has only been indirectly included in the simulation by the process of re-oxidation from the filament. Finally, the reset process of the atomic scale was described in detail.