Thermal Modeling Challenges of High-Speed Motorized Spindles

Abstract

This paper investigates the thermal modeling challenges of high-speed motorized spindles up to 40,000 rpm. The thermal expansion and deflection of motorized spindles are critical determinants for the resulting tool center point displacement and the achievable machining accuracy of machine tools. In order to compensate, finite element and reduced physical models (digital twins) therefore require an accurate understanding of the thermal boundary conditions. In motorized spindles, heat sources are of great significance to the resulting temperature field. However, it is very difficult to accurately quantify the heat sources in motorized spindles. This is a particular challenge for high-speed applications exceeding 20,000 rpm, where commonly used boundary conditions are not validated. While the power loss of the electric motor could be quantified with reasonable accuracy, the calculation approaches for air and bearing friction proved to be inadequate. This paper introduces approaches to quantify the air and bearing friction of motorized spindles with improved accuracy for applications up to 40,000 rpm. The method was verified based on a coupled thermal/fluid-mechanical spindle simulation model. The mean absolute temperature difference between the model and the test bench was 1.5 K.

1 Introduction

The precision of metal-cutting machine tools is reduced by non-reproducible displacements of the tool center point. This displacement has geometrical, static, dynamic and thermal causes [1]. The thermal shift accounts for up to 75% [2] of the total displacement and is therefore the center of many recent research actives.

The reproducibility of the thermal displacement is challenging because of the complexity of the underlying thermo-mechanical problem. As outlined in our previous article [3], the investigated compensation approaches can be divided into data-based and physical model-based approaches. Data-based approaches are problematic due to extensive calibration measurements. Physical model-based compensation strategies are challenging because the boundary conditions often lack the required accuracy. This is especially true for high-speed applications, where many of the earlier published quantification approaches for the boundary conditions are not validated.

Depending on the application, motorized spindles are regularly operated in speed ranges up to 60,000 rpm [4]. Spindles for internal grinding or drilling printed circuit boards operate even beyond 100,000 rpm. However, most of the previously published models are not considering high-speed applications. Figure 1 visualizes available models and their speed. Most publications [5,6,7,8,9,10,11,12,13,14,15,16,17,18] do not consider motorized spindles with more than 18,000 rpm. The recent addition of Denkana [19] showed modeling efforts for a spindle with 20,000 rpm. Denkana used manufacturer data for the problematic bearing friction loss and ignored air friction. That approach might lead to reasonable results in this speed range, but due to the nonlinear increase of air friction, it quickly becomes unsustainable beyond 20,000 rpm. Bossmanns [20] analyzed a motorized spindle with 25,000 rpm, including both bearing friction and air friction [22]. He derived an empirically-based bearing friction model through a curve fitting approach, circumventing the inaccuracy of the currently available bearing friction models. Furthermore, he recognizes the increasing issue of air friction, yet only quantifies the air friction directly in the air gap between stator and rotor. Gebert [21] simulated a motorized spindle with 36,000 rpm, modeling air and bearing friction. Solely Gebert sophistically analyzed the air friction issue of the entire rotating shaft. However, he acknowledged the issue of the incalculability of air and bearing friction, suggesting an alternative empirically-based approach.

Fig. 1.

Speed range of motor spindle models with the observed friction phenomena.

Unfortunately, Bossmanns’ and Gebert’s approaches to quantify the bearing friction cannot be transferred to different spindles without extensive measuring effort. This paper presents a newly developed set of boundary conditions for high-speed motorized spindles, which was validated at 40,000 rpm. As outlined by the authors cited above, the greatest modeling challenge is an accurate quantification of the heat sources at high speeds. We suggest an improved analytical calculation of air friction with a more comprehensive set of friction coefficients, including the effects of Taylor vortices. The calculation of bearing friction at high speed remains problematic and requires further research. However, the total bearing friction can be estimated with reasonable accuracy based on energy conversion observations of the spindle. Unlike the previous high-speed modeling approaches, the presented modeling guideline should be transferable to other high-speed motor spindles with minimal measuring effort.

2 General Approach

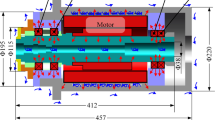
The development of a reasonable set of boundary conditions for high-speed motor spindles was established through extensive empirical observations of a synchronous motor driven spindle with 40,000 rpm and 10 kW (Fig. 2, left). The spindle had a total length of 585 mm and an outer rotor diameter of 66 mm. The test bench was equipped with temperature sensors, which were attached to the surface and in boreholes of the spindle (see Sect. 4.2). The simulation model (Fig. 2, right) was a Finite-Element-Model (FEM) with an additionally coupled Computational-Fluid-Dynamics (CFD) simulation for the fluid cooling systems inside the spindle housing.

Fig. 2.

Spindle test bench and simulation model.

The first version of the spindle simulation model was based on a set of boundary conditions published in our previous works on a spindle with 18,000 rpm [3, 18]. However, the empirical observation showed that this set of boundary conditions could not be conveyed to the test specimen of the analysis with 40,000 rpm. The comprehensive empirical observation allowed us to scrutinize the different boundary conditions separately. Temperature deviations were traced back to inaccuracies of individual boundary conditions, allowing additional research on each specific physical problem. The boundary conditions of the simulation model were refined until the temperature deviation was reduced to 1.5 K in thermal equilibrium at 40,000 rpm.

3 Boundary Conditions for High-Speed Motorized Spindles

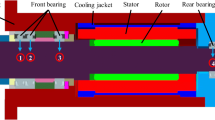
The boundary conditions required to reach that goal are visualized in Table 1 and the corresponding Fig. 3 below. The table visualizes the required heat transfer, heat sink and heat sources with recommended quantification approaches. The following Sects. 3.1–3.4 will discuss each quantification approach separately.

Table 1. Quantification approaches for thermal boundary conditions of high-speed motorized spindle models up to 40,000 rpm.

Fig. 3.

Visualization of the boundary conditions of the observed motor spindle.

3.1 Heat Transfer

The bearings of the spindle (Fig. 3) need to be described as heat sources and heat transfer systems. The heat transfer through a roller bearing is mostly limited by the contacts between rolling element and ball raceway. There are different approaches available in literature, but most of them are based on the Hertzian contact theory. For our investigations, the approach of Weidermann [23] gave accurate results.

We know from the observations of Gebert [21] that the heat transfer between the rotating shaft and the stationary housing is highly relevant for the generated temperature field of high-speed motorized spindles. The approach of Tachibana [24] worked for the geometrical dimensions and spindle speed relevant to our observation. If the spindle specimen does not meet the limitations of Tachibana, the review article of Fénot [25] is recommended. Fénot gives an overview of the available Nusselt correlations for concentric rotating cylinders with different dimensions and speeds.

The gap conductance of solid body contacts is quantified based on the works of Jovanovich [26, 27]. However, the suggested equations are often times not solvable, as they require specific knowledge of the contact parameters like pressure, roughness and air properties.

This is especially problematic for the bushings inside of the spindle. The floating bearings of motorized spindles are often times mounted in bushings (see Fig. 3) which allow an axial displacement to prevent thermally induced stresses. The parameters of these loose contacts are not quantifiable. However, the work of Negus and Yovanovich [28] gives tabular data for different load cases.

3.2 Heat Sinks

The most significant heat sink of motorized spindles is usually the fluid cooling. The fluid cooling primarily cools the electric motor, but often times the bearings are cooled through additional cooling rings. The coolant heats up over the course of the fluid flow, creating an asymmetric temperature field in the solid bodies of the spindle [3, 29]. In order to simulate accurate temperature fields and thermal deformations, this effect has to be considered. Therefore, the fluid cooling system has to be realized via a coupled CFD-simulation. The mesh of the fluid system should be created with boundary layer refinement to meet the Y+ value requirement.

Motorized spindles generally have a cylindrical shape. Accordingly, the free convection of a spindle toward the ambient air can be modeled based on the findings of Churchill [30].

Free convection generally leads to much lower heat transfer coefficients than forced convection. Forced convection only appears on the rotating shaft of the spindle, usually near the tool. The parts of the shaft, which can be modeled as a rotating cylinder, can be quantified based on the work of Dropkin [31]. The remaining parts of the shaft are usually modeled as a rotating plate [32].

The connection of the spindle toward the machine or test bench can be modeled as a solid body contact based on the work of Jovanovich [26,27,28]. As explained in Sect. 3.1, an accurate quantification of these heat transfer coefficients is difficult. In order to apply the heat transfer coefficient to a surface, the temperature of the opposite surface (test bench or machine part) must be considered. This temperature is not quantifiable without measurements. One alternative approach to circumvent that problem is modeling parts of the machine structure with their free convection boundary conditions. As displayed in Sect. 4.1, this boundary condition is not necessarily required for motorized spindles with fluid cooling.

The thermal influence of the drill hole systems, which are generally ignored by other authors, was also reviewed. Motorized spindles have a set of drill hole systems as exemplarily visualized in Fig. 3. These drill hole systems are required for the bearing lubrication, vacuum return, leakage, air sealing etc. They can be described by heat transfer coefficients based on tube flow observations. Often times the flow inside the boreholes is in transition between laminar and turbulent flow. The heat transfer coefficients can then be quantified based on Gnielinski [33]. Nusselt correlations for other flow conditions in tubes are discussed by Stephan [34]. However, the temperature of the flow inside of the boreholes rises quickly in some parts of the spindle, implying that the quantification based on fixed heat transfer coefficient and fluid temperature is not a sufficient method. If a drill hole system really is of significance for the spindle temperature, it should be modeled as separate CFD simulations, just as the fluid cooling system itself.

3.3 Heat Sources

Heat sources form the most significant boundary conditions for the resulting temperature field of motorized spindles. At the same time, they are the most difficult boundary conditions to quantify. Unlike the purely analytical approach on heat transfer systems (Sect. 3.1) and heat sinks (Sect. 3.2), the accurate quantification of the heat sources requires additional empirical observation of the input power of the spindle.

The electric motor is usually the most significant heat source in motorized spindles. The use of an asynchronous motor can be thermally quantified based on Richter [35]. Richter quantifies copper losses, iron losses and additional losses separately. Alternatively, asynchronous motors can be quantified based on motor slip [36], requiring less input parameters than Richter’s approach [35] but the aforementioned measurement of the input power.

The thermal description of a synchronous motor can be established based on the works of Rothenbücher [37] and Gieras [38]. While the results of an analytical copper loss quantification are usually accurate, it is more difficult to quantify the iron loss accurately. This is due to influences of the processing procedure, alternating the parameters of the metal sheets through shape and stress variations. For this reason, the analytically quantified iron loss value is multiplied by an empirical factor. In any case, it is advisable to directly contact the motor manufacturer. Only the manufacturers themselves know the empirical data of their motors.

Air Friction

Air friction becomes increasingly relevant with higher speed. It raises to nearly the power of three of the rotational speed. An accurate understanding of the problem is indispensable for a spindle with 40,000 rpm. However, the published approaches on air friction in motorized spindles [20, 21] were not suitable for quantifying the air friction accurately. The measurements suggest higher air friction losses than determined, especially in spindle areas with large cavities between shaft and housing.

Therefore, a new set of quantification approaches was developed and validated. The analytical determination of air friction is not a trivial problem, especially for high-speed applications. While exact solutions based on the Navier-Stockes equations are available for problems with low rotational speed and laminar flow, solving the equation is usually impossible for problems with high speed and turbulent flow [21]. The friction between two concentric cylinders can be expressed as the air’s shear stress $\tau$ [45]:

$$ \tau = \rho \left( {{\upnu } + \varepsilon_{M} } \right) \cdot r\frac{\partial }{\partial r} \cdot \left( \frac{u}{r} \right) $$

(1)

where $\rho$ is the air density, ${\upnu }$ is the kinematic viscosity, $\varepsilon_{M}$ is the eddy diffusivity of momentum, $r$ is the radius and $u$ is the tangential fluid velocity ($u = r \cdot \omega )$. Equation (1) is not solvable, as the eddy diffusivity and the velocity distribution are not determinable for turbulent flows. Therefore, a dimensionless friction coefficient $C_{f}$ is used instead for these problems, which is defined for rotating parts as follows:

$$ C_{f} = \frac{{\tau_{r} }}{{\frac{1}{2} \cdot \rho \cdot u_{r}^{2} }} $$

(2)

$\tau_{r}$ is the shear stress on the surface $A$ of the rotating body and $u_{r}$ is the tangential velocity on the rotor’s surface. Based on the shear stress $\tau_{r}$ (Eq. (2)) the resisting force $F$ can be quantified with Eq. (3). The air friction torque $M_{air}$ in Eq. (4) is then quantified by multiplying with the rotor’s radius $r_{r}$.

$$ F = \tau_{r} \cdot A $$

(3)

$$ M_{air} = F \cdot r_{r} = C_{f} \cdot \frac{1}{2} \cdot \rho \cdot u_{r}^{2} \cdot A \cdot r_{r} = C_{f} \cdot \frac{1}{2} \cdot \rho \cdot r_{r}^{3} \cdot \omega^{2} \cdot A $$

(4)

Equation (4) is generally valid. The shaft of motorized spindles is geometrically complex. In order to make the air friction of the shaft quantifiable, it has to be observed as a number of rotating cylinders and disks. The air friction torque of rotating cylinders in Eq. (5) is determined with its lateral surface. Where $l$ is the length of the observed cylinder. The frictional torque of the disks in Eq. (6) is quantified through observing the disk surface as annulus with outer and inner radii ($r_{o}$, $r_{i}$).

$$ M_{air, cylinder} = C_{f} \cdot \rho \cdot r_{r}^{4} \cdot \omega^{2} \cdot \pi \cdot l $$

(5)

$$ M_{air, disk} = C_{f} \cdot \frac{1}{2} \cdot \rho \cdot \omega^{2} \cdot \left( {r_{o}^{5} - r_{i}^{5} } \right) $$

(6)

The remaining unknown $C_{f}$ is then described as the empirically determined function of Reynolds number Re. There is a large number of foundational research on the empirical quantification of these functions. Table 2 visualizes our set of quantification approaches for $C_{f}$ which was developed for high-speed applications based on the empirical observation (Sect. 2). The calculation of the friction coefficients in Table 2 requires the tip Reynolds number ${\text{Re}}_{r}$ (Eq. (7)), the Couette Reynolds number ${\text{Re}}_{\delta }$ (Eq. (8)) and the axial Reynolds number ${\text{Re}}_{a}$ for observations with an additional axial flow (Eq. (9)).

$$ {\text{Re}}_{r} = \frac{{\rho \cdot u_{o} \cdot r_{o} }}{\mu } $$

(7)

$$ {\text{Re}}_{\delta } = \frac{{\rho \cdot u_{o} \cdot \delta }}{\mu } $$

(8)

$$ {\text{Re}}_{a} = \frac{{\rho \cdot v_{m} \cdot 2\delta }}{\mu } $$

(9)

where $u_{o}$ is the peripheral speed of the rotor, $\delta$ the air gap in radial direction, $\mu$ the dynamic viscosity of the fluid and $v_{m}$ the mean axial fluid velocity, which is calculated based on the axial flow rate and the cross section of the air gap. Table 2 is explained based on the corresponding Fig. 4, which displays a part of the spindle with all relevant physical phenomena. The parts of the shaft, which can be observed as disks rotating in free space ((1) in Fig. 4 and Table 2), are quantified based on the approaches of Kreith [39].

Fig. 4.

Exemplary observation of the air friction phenomena in high-speed motorized spindles.

Parts of cylindrical shape rotating in free air ((2) in Fig. 4 and Table 2) are described with Theodorson’s [40] approaches. A motorized spindle commonly features at least one air sealing. These sealings work through an additional axial airflow (3). The flow in the air gap between shaft and housing thus has tangential and axial components. In this case, the friction coefficient can be calculated based on the works of Yamada [41]. Radial surfaces in the enclosure of the housing (4) are quantified based on Schulz-Grunow’s work [42]. There is no known quantification approach for radial disks with an additional radial flow for areas with an air sealing. Therefore, they have to be described with Schulz-Grunow’s approach, which gave fitting results for these areas.

Table 2. Quantification approaches of air friction coefficients for high-speed motorized spindle models up to 40,000 rpm.

Parts of the shaft, which represent a cylinder rotating in an enclosure (5), are most difficult to quantify for high-speed motorized spindles. The results obtained from the previously suggested approach from Stuart [43] proposed by Gebert [21] were too low. The reason for this deviation is probably the occurrence of Taylor vortices, even though the rotational speed and Reynolds number are very high. This problem should be clarified based on Fig. 5. In order to make the graphs comparable, the Taylor number definition given by Saari [45] is applied to both illustrations. Figure 5 a) shows the conventional understanding of airflows in concentric cylinders. Up to a certain Taylor number (1.7 $\bullet$10³ [46]) the flow between the rotating shaft and the housing is laminar. The flow then changes into Taylor vortices, which are circular velocity fluctuations (see Fig. 4 and [43]).

Fig. 5.

Contradicting understandings of the flow regimes in concentric cylinders. The strictly separated regimes in (a) are conventionally used to describe the flow in motorized spindles or electric motors while the regimes outlined in (b), featuring an additional axial flow, are a better fit for our measurements.

After the second threshold in Fig. 5 a), the flow changes to an entirely turbulent flow. This regime is of greatest significance for high-speed applications, as the high speed should lead to a consistently turbulent flow. Comparing the results of an accordingly configured simulation model and the temperatures recorded in our experiments (see Sect. 4.2), we concluded that this understanding derived from idealized experimental assemblies of concentric cylinders, cannot be transferred to high-speed motorized spindles. Assuming an additional axial flow, leading to Taylor vortices, which increase the air friction, results in higher, more realistic temperatures with minor deviations.

According to Dorfman [47] (Fig. 5 b)), an additional axial flow leads to four instead of three flow regimes. The thresholds change with increasing axial Reynolds number. Interestingly, the Taylor vortices do not disappear with increasing rotational speed. These effects are not modeled in Stuart’s equations [43]. The approaches of Saari [45] (Eq. (19) and (20) in Table 2) based on the work of Bilgen [44] incorporate them. Previously, the measurements deviated most significantly in areas with large cavities between rotor and stator. The simulation results with the equations considering the occurrence of Taylor vortices [44, 45] are two to four times higher in these areas and the resulting temperatures are comparable to the measurements. The additional axial flow itself could be caused by two different reasons:

• The air sealings create an axial flow in motorized spindles. However, it appears to be unlikely that these additional devices have a significant impact on the airflow inside of the spindle housing.

• Motorized spindle shafts are geometries with varying radii. Different diameters lead to different tangential fluid velocities, creating pressure deviations in axial direction of the air gap, which might lead to an axial flow. This effect was actually observed by Daily [48] based on observations of rotating disks. Disks within an enclosure work like a centrifugal pump (visualized in Fig. 4). The air flows outwards near the rotating disk (4), than axially through the cavity and radially inward on the opposing static wall. The rotational direction of Taylor vortices next to each other is opposed. This phenomena together with the centrifugal pump issue, creates different opposed fluid flows, potentially causing the observed increase in air friction. This issue is only present with enough clearance between rotor and housing [48], directly explaining our previous measurement deviations in areas with large cavities. When the gap decreases, the boundary layers of the shaft and the wall merge. Under these circumstances, the axial flow component disappears, leading to a solely tangential flow.

In general, we strongly advice to make as few geometrical simplifications as possible for the calculation of air friction. Averaging radii quickly leads to significantly lower results as the air friction increases with the fourth or even fifth power of the radius (see Eq. (5) and (6)).

Bearing Friction

While the quantification of air friction appears to be possible with a more sophisticated understanding of the issue, the accurate analytical determination of bearing friction is not possible for high-speed applications. Although there is still research on the topic, the underlying issue of the empirical basis is not addressed. Instead of novel quantification strategies, the published approaches build on each other:

• Palmgren [49] quantifies the bearing friction moment $M_{b,1}$ based on separate determinations of a load-independent (viscous) moment $M_{0}$ and load-dependent moment $M_{1}$ (Eq. (21)). These quantification approaches are based on empirical observations carried out in the 1940s and 1950s.

  $$ M_{b, 1} = M_{0} + M_{1} $$

  (21)

• Harris [50] quantifies the load-independent $M_{0}$ and load-dependent moments $M_{1}$ based on Palmgren and adds an additional gyroscopic or spinning moment $M_{Spin}$ (Eq. (22)).

  $$ M_{b,2} = M_{0} + M_{1} + M_{Spin} $$

  (22)

• Kosmol [51] incorporates these works and adds additional friction torques due to rolling movement $M_{T\left( r \right)}$ and sliding movement $M_{T\left( s \right)}$ (Eq. (23)).

  $$ M_{b,3} = M_{0} + M_{1} + M_{Spin} + M_{T\left( r \right)} + M_{T\left( s \right)} $$

  (23)

  According to the comparison with our experiments (Sect. 4.2), the calculation of the viscous load-independent moment $M_{0}$ and load-dependent moment $M_{1}$ is highly inaccurate for high-speed applications of hybrid bearings in motorized spindles. Abele reported the same issue [4]. The calculated friction torque $M_{b,1}$ from Eq. (21) is already too high by two to five times in the examined speed range, making the more recently formulated additional terms of Harris [50] and Kosmol [51] ineffectual. The calculation is furthermore problematic, as the kinematic viscosity of the lubricant is highly temperature dependent. The lubricant temperature is not determinable without additional temperature sensors inside of the bearings. However, even conservatively estimated temperatures generate too high results. Therefore, the empirical basis itself [49] appears to be unsuitable for high-speed applications. Until the very basis of these quantification approaches is reworked, an analytical calculation of bearing friction probably stays impossible.

Our study on a motorized spindle with 18,000 rpm [3] already pointed toward a practical alternative solution for this problem. Instead of calculating bearing heat analytically, it can be quantified based on the energy conversion of the spindle. In idle mode, the input power $P_{in}$ is equal to the power loss of the spindle. The input power $P_{in}$ can be measured and the power loss can be split into motor $P_{motor}$, air $P_{air}$ and total bearing friction $P_{b,tot}$. Using the aforementioned approaches to quantify motor and air friction, they can be subtracted from the input power $P_{in}$ to determine the total bearing heat $P_{b,tot}$ (Eq. (24)).

$$ P_{b,tot} = P_{in} - P_{motor} - P_{air} $$

(24)

The total bearing heat can then be distributed to each bearing based on the aforementioned quantification approaches [49, 50]. While the absolute values of the results of these equations are unusable, their relation to each other appears to be reasonable.

3.4 Solid Motion Effects

The aim of the thermal modeling of machine tool components is usually a better understanding of the thermo-mechanical cause-effect relationships. This is achieved through an accurate representation of the temperature fields, which is primarily accomplished through an accurate set of thermal boundary conditions. However, our thermo-mechanical research pointed toward a kinematic problem, which has to be considered during the thermal modeling phase already. This issue is ignored by other thermal modeling approaches on motorized spindles, nevertheless appears to be essential if the temperature field and thermo-mechanical displacement should be quantified accurately.

The rotation of the shaft has a significant influence on its temperature field, which is explained based on Fig. 6. Usually the temperature field is determined without considering the shaft’s rotation. As displayed in Fig. 6 a), the temperature distribution looks in this case similar to the asymmetric [3] housings temperature field. Spindles only have these temperature fields if the shaft is not rotating. A temperature distribution as displayed in Fig. 6 b) is much more common. The shaft’s rotation leads to a homogenization in tangential direction. This difference is also relevant for the thermo-mechanical displacement. While the shaft’s temperature field in Fig. 6 a) leads to an axial and radial displacement at the tool center point, the shaft’s displacement with the temperature field in Fig. 6 b) is purely axial. The radial displacement of the shaft of a temperature field as displayed in Fig. 6 a) is often times counteractive to the radial tool center point displacement induced by the housing. This creates misleading results, making the consideration of the problem essential for accurate simulation results. The thermo-mechanical cause-effect relationships are explained in greater detail in Sect. 3.2 of our previous article [3].

Fig. 6.

Qualitative observation of the solid motion effect on the temperature field of motorized spindles. The shaft’s rotation leads to a homogenization of its temperature field.

Modern simulation programs have suitable boundary conditions to implement this homogenization-phenomenon. We suggest to realize it with a solid motion effect [52], which has to be applied to the rotating body parts. The thermal solver then calculates the problem in a number of rotational steps. Subsequently, the solver averages the thermal boundary conditions of the shaft, creating a tangentially homogenous temperature field as displayed in Fig. 6 b).

4 Spindle Model and Validation

In the next step, the boundary conditions given in the previous chapter are transferred to the test specimen with 40,000 rpm. The way the boundary conditions are applied to the coupled simulation model is outlined in Sect. 4.1. Finally, the validation of the model is presented in Sect. 4.2.

4.1 Boundary Condition Application to the Simulation Model

All heat transfer systems shown in Table 1 are applied to the spindle simulation model in Fig. 8. The three bearing geometry’s heat transition coefficients are applied to the housing’s and the shaft’s contact surfaces of each respective bearing. Tachibana’s approach [24] was used to quantify the heat transfer coefficients between the shaft and housing. The coefficients are separately calculated and applied to each respective combination of shaft and housing diameters. The spindle housing consisted of several solid bodies. Based on [28], the contacts in-between were modelled with a heat transfer coefficient of 3000 W/m²K. The contacts between the bushings and the housing are even harder to quantify, as the respective contact situation is not known (see Sect. 3.1). Based on [28] and our empirical observation we suggest a heat transfer coefficient of 1,500 W/m²K for the radial bushing contacts.

The fluid cooling is realized as heat sink through the definition of its inlet and outlet surface. The inlet surface’s flow rate is 10 l/min. The fluid domain’s material is water with 43% ethylene glycol. The heat transfer coefficients to the ambient air are applied to each respective surface of the housing (free convection) and the shaft (forced convection). Based on temperature measurements on the rig and additional thermal test bench simulation models, we concluded that the total heat transferred to the test rig is only about 40 W at 40,000 rpm. The nearby fluid cooling transfers about 1423 W out of the spindle, easily replacing the heat transfer to the test bench. Our validation suggests that this boundary condition, which always requires additional measurements, is not necessarily required for fluid cooled motorized spindle models. This perception greatly increases the transferability of the presented modeling approach. Therefore, the model iteration presented for the validation in Fig. 9 does intentionally not include this boundary condition, depicting the validity of the simplification. The drill hole systems were also modelled in earlier iterations of the model. Modeling them with constant heat transfer coefficients and fluid temperatures, increases the model accuracy locally, but decreases it at other positions. This is due to the continuous fluid temperature increase in reality, which cannot be modelled without CFD simulations. In order to get the mean absolute temperature deviation below 1.5 K (Fig. 9) such additional CFD simulations were not necessary. Nonetheless, the borehole systems are geometrically still part of the final model iteration (see Fig. 8).

The power loss of the synchronous motor was assigned to the stator and the rotor geometry. Each bearing’s heat generation is applied to its contact surfaces towards the housing and the shaft. In order to quantify the air friction, the spindle’s shaft shown in Fig. 3 was divided in 43 combinations of shaft and housing geometries to get accurate results with the approaches given in Table 2. Following the required mathematical simplification introduced with Eq. (2), the air friction is usually [45] applied solely to the surface of the shaft. Our validation (see Sect. 4.2) showed that this approach might be problematic, as the shaft becomes up to 7 K too warm, while the housing stays too cold. The mean absolute difference of the model (shaft and housing) than deviates by 3.12 K. While the physically accurate Eq. (1) quantifies the (entire) air’s sheer stress between shaft and housing, Eq. (2) reduces this issue to a surface layer problem of the shaft. The simplification issue can be visualized based on a quantification of the air’s velocity inside of a spindle cavity. Air speed directly determines the present air friction (see Eq. (1)). The velocity field can be quantified with a mechanical/fluid-mechanical model of the spindle, which is visualized in Fig. 7.

Fig. 7.

Coupled mechanical/fluid-mechanical observation of a cavity inside of the spindle. The air’s velocity at the housing is still about half of the velocity near the shaft, suggesting a different application method for the air friction boundary condition.

The spindle model in Fig. 7 is reduced to the area with the largest cavity on the right side of Fig. 3. In the first step (Fig. 7), the air’s domain is added to the model as geometry. The model (second step) is than reduced to the air domain and the solid shaft. As boundary conditions an opening and a fixed support is necessary. Furthermore, the model has a flow surface boundary condition, which is required to assign the spindle’s speed of 40,000 rpm to the shaft. The resulting velocity field is visualized in the third step of Fig. 7. The air speed near the shaft is about 35 m/s. Interestingly, the air speed near the housing’s wall is still about 17.5 m/s.

With the knowledge of the velocity distribution, applying the air friction to both the shaft and the housing seems more reasonable. The exact distribution is not quantifiable. The shaft’s surface area is about half of the opposing housing’s surface area. However, the air velocity near the shaft is about twice the velocity near the housing. Based on that, we suggest that the heat generation of each of the 43 air friction subranges is halved and equally assigned to both the shaft and the housing. This approach significantly increases the model’s accuracy, lowering the shaft temperature (see Fig. 9) and increasing the housing temperature. Therefore, the mean absolute temperature difference was reduced to 1.48 K, which is derived in the following chapter. Alternatively, the air domain geometry itself could be added to the thermal/fluid-mechanical model. The air friction could then be directly assigned to its origin. This idea should be further researched with additional simulation models in the future.

Finally, the rotation boundary condition is applied to the shaft of the spindle’s simulation model visualized in Fig. 8. The figure also visualizes the in- and outlet surfaces of the fluid domain. It also shows the individual geometries of the housing and the bushings, allowing the application of the contact boundary conditions.

Fig. 8.

Coupled thermal/fluid-mechanical simulation model of the motorized spindle.

4.2 Test Bench and Model Validation

The test bench visualized on the left of Fig. 9 measures input power, fluid flow rate and the temperature. Measuring the input power allows the calculation of the bearing friction (Sect. 3.3). The measurement of the flow rate and fluid’s in- and output temperature is required to monitor the cooling rate.

The temperature measurement in Fig. 9 and the developed validation method should be outlined in detail. The housing’s temperature is measured with 21 Pt100 sensors. The spindle was observed in different speed stages, the most challenging stage at 40,000 rpm is visualized in Fig. 9. The test bench temperatures are given after four hours at 40,000 rpm, which is directly comparable to the thermal equilibrium observation of the simulation model. In order to increase the reliability of the validation, the empirical observation was repeated five times. The sensor values shown in Fig. 9 are based on arithmetic averages of these measurements.

Fig. 9.

The spindle test bench (left) and the results of the simulation model (right) at 40,000 rpm. The model temperatures are picked at the same spots as the test bench’s temperatures. The temperatures are averaged at each spot and the difference between the test bench and the model is calculated. Finally, the mean absolute temperature differences are calculated for the validation.

The individual sensors were mainly applied to the housing’s surface on five different locations (h₁, h₂, h₃, h₄ and h₅). Based on the complexity of each location’s temperature field, a different number of sensors was attached to each position along the circumference. For example, h₁ required only two sensors, of which one is visible and the other arranged in an 180° angle. The sensor values of each position were averaged. The averaged values are visualized in the table in the figure (left column). The simulation model’s temperatures are taken at the same positions (see Fig. 9, right) and averaged in the same way (right column), creating comparable values.

Additionally, one sensor was positioned inside of the spindle. This sensor at h_b is located in a borehole near the rear bearing of the spindle, visualized based on the simulation model to the right. Furthermore, the shaft’s temperature was measured on five different locations, which are depicted based on the simulation model (s₁, s₂, s₃, s₄ and s₅) in Fig. 9. The shaft’s temperature field is symmetrical (Sect. 3.4), making the angular position of the shaft irrelevant for the measurement. However, while the housing temperature can be measured while the spindle is running, the rotating shaft’s temperature could only be measured after the spindle was stopped. This issue makes these values less reliable, but the additional information regarding the shaft’s temperature should nonetheless increase the validity.

The difference between the temperatures of the test bench and the simulation model is displayed in the center column of Fig. 9. Larger temperature differences can be observed at s₃, h₄ and in the frontal area at h₅ and s₅. The deviation at s₃ could be due to the geometrical complexity of the housing behind the electric motor (see Fig. 3), making an accurate calculation of the heat transfer coefficient based on correlation equations impossible. The difference at h₄ could be due to the missing CFD-simulation of the borehole systems (see Sect. 4.1) which are numerous in this area. The inaccuracies at h₅ and s₅ probably have the same reason: There is currently no model available to consider the transition between the forced convection on the shaft to the free convection on the surrounding spindle housing. The heat transfer coefficient to the ambient air abruptly drops from 312.37 W/m²K (shaft) to 4.87 W/m²K (housing), creating too high temperatures in the housing.

Finally, the mean absolute differences of the temperatures are calculated below the center column in Fig. 9. We generally suggest using absolute values for thermal validation procedures. As outlined above, the mean absolute difference of the housing’s temperatures (1.41 K) is the more reliable value. However, the mean absolute difference of the housing’s and the shaft’s temperatures (1.48 K) includes more information. Apart from the described outliers, the simulation model seems to represent the reality accurately with temperature differences of 1 K or less.

5 Spindle Power Loss Observation

This paper concludes with an observation of the spindle’s power loss in idle mode, depicting the loss distribution in different operating points (Fig. 10). The input power in the graphs (159 W, 412 W, 807 W and 1,507 W) are measured values from the test bench (Sect. 4.2), while the output values are calculated based on the approaches given in Sect. 3.3.

Fig. 10.

Observation of the motor spindle’s energy conversion in idle mode at 10,000 rpm (a), 20,000 rpm (b), 30,000 rpm (c) and 40,000 rpm (d).

Figure 10 a) displays the power loss at 10,000 rpm. The motor loss is clearly most significant at that point, while the bearing friction is much smaller. The air friction plays an insignificant role in this speed range. However, at 20,000 rpm the torque due to bearing and air friction is substantially larger (Fig. 10 b). Above 20,000 rpm, the electric motor’s field-weakening sets in. Even in the relative observation in Fig. 10 c), the air friction becomes more significant at 30,000 rpm. Interestingly, the relative share of the bearings stays almost identical at that point. At 40,000 rpm (Fig. 10 d)) more than one third of the frictional loss is caused by air friction. The percentage will increase even further above 40,000 rpm, underlining the increasing importance of air friction observations for high-speed applications.

6 Conclusion and Outlook

The thermally induced displacement of the tool center point most significantly decreases the manufacturing precision of metal cutting machine tools. In order to compensate the displacement, the cause-effect relationship has to be reproduced through thermal and mechanical modeling. Section 1 outlines that thermal modeling is especially challenging for high-speed motorized spindles, as over 20,000 rpm only two modeling attempts exist (25,000 rpm [20] and 36,000 rpm [21]), which rely on extensive empirical observations.

This paper introduces for the first time a thermal modelling approach for motorized spindles at 40,000 rpm with minimal measuring effort. The declared objective of the parallel simulative and empirical observation was the identification of inaccuracies of individual boundary conditions, allowing further research for additional or alternative quantification approaches. The investigated boundary conditions are subsequently presented in Sect. 3. They are split into heat transfer systems, heat sinks and heat sources. While quantification approaches for the heat transfer through the bearings and the gap between shaft and housing generated reliable results, the quantification of solid body contacts proved to be more challenging. Apart from the ambient air and the machine interface, the heat sinks should preferably be quantified as additional coupled CFD-simulations. The heat sources have the greatest influence on the resulting temperature field of motorized spindles. While the electric motor can be quantified with reasonable accuracy, the precise calculation of air and bearing friction is really challenging for high-speed applications. In Table 2 of this paper, a new set of quantification approaches for air friction coefficients in motorized spindles is introduced. This set incorporates for the first time the appearance of Taylor vortices in the air gap, significantly increasing the air friction torque. While such development was possible for the air friction, a comparable improvement could not be found for the bearing friction torque. All existing quantification approaches are based on the work of Palmgren [49], whose empirically determined equations are not compatible with high-speed applications of modern hybrid bearings. Instead, we suggest the calculation of the bearing friction torque based on a measurement of the input power. Additionally, a solid motion effect is introduced for the first time in thermal models of motorized spindles to consider the temperature homogenization-effect of rotation.

In order to show the validity of the introduced set of boundary conditions, they are applied to a motorized spindle with 40,000 rpm in Sect. 4. The conceptualized set of boundary conditions is applied to the developed thermal/fluid-mechanical simulation model. Further research on the distribution of air friction with an additional mechanical/fluid-mechanical simulation model allowed us to reduce the mean absolute difference between the thermal/fluid-mechanical simulation model and measurement to 1.5 K.

Conclusively, Sect. 5 shows the spindle’s energy conversion at 10,000 rpm, 20,000 rpm, 30,000 and 40,000 rpm in idle mode. The analysis shows that air friction becomes more significant with higher rotational speed. At 40,000 rpm the air friction causes already one third of the frictional losses, underlining the increasing importance of its accurate estimation for high-speed applications.

In the next steps, the inaccuracies of the current model iteration should be addressed further. The application of the air friction inside the spindle is still problematic, as it does not accurately represent the physical nature of the problem. Air friction occurs in the entire three dimensional air gap of the spindle. Therefore, its simplified application to the surrounding solid body surfaces (shaft, housing) is problematic. The problem could possibly be solved by adding the air inside the spindle as an additional geometric element. The air friction could then be assigned to the air element itself. The heat would then flow to the surrounding elements according to the second law of thermodynamics, representing the physical nature of the problem more accurately. Furthermore, the inaccuracy at the tip of the spindle near the tool (Fig. 9) should be investigated. Currently, there is no model for the transition area between the forced convection on the shaft and the free convection on the housing. A new boundary condition based on interpolation would further increase the validity of the presented modeling approach.