Simulating the Effects of Inertia and Frequency Response Services on Transient Propagation in a Networked Grid

Abstract

As part of climate change mitigation efforts, there has been acceleration in the deployment of distributed renewable generation replacing conventional thermal power plants in grids across the world. As a result, there has been a change in the aggregate and regional inertial capacity, with consequences for the stability of these networks and their ability to withstand large variations in frequency. Building on previous work that successfully simulated frequency events on the GB grid using a single bus model, this paper describes a networked grid model using an algebraic differential system of equations. This is used to simulate the effects of localized variation in inertia and frequency response services on the propagation of transients across a network. Using this model, the effects of varying responses to transients can be investigated, and grids of varying scales and topologies can be compared to determine differences in their response to outages. The propagation of disturbances across domains within the network that have different frequency response characteristics can be examined with a view to drawing conclusions about the optimal deployment of frequency response services, and their relative cost-effectiveness in delivering a stable supply as the proportion of renewable generation in the energy mix grows.

8.1 Introduction

The reduction in cost of renewable energy and the advent of the energy crisis has accelerated the migration from conventional large-scale thermal electricity generation to distributed wind and solar resources. This has contributed to the reduction in aggregate and regional inertia of power grids, and consequently a reduced ability of these networks to withstand large variations in frequency. Sudden surges or dips in frequency are therefore more likely to result in cascading outages affecting the entire grid.

Renewable generation plants are generally smaller in scale and greater in number than conventional generators, and are more widely distributed across the network. As each of these are expected to contribute to the stability of supply in the event of outages, this adds complexity to the planning for the provision of adequate frequency response resources.

In addition, the possibility of regional variation in resources arises, where inadequate frequency response to a localised outage can lead to a variation in local frequency disproportionate to the grid average, causing regional instability and possible islanding. This local reduction in moderating the effects of outages can also serve to amplify their effects, with consequences for the reliability of the grid as a whole.

This greater complexity in planning for sufficient frequency response to mitigate reduced aggregate and regional inertia is a consequence of this trend towards smaller, more distributed renewable energy generation. It suggests the necessity of developing analyses that take these factors into account so that their effects, and the measures that can be taken to alleviate adverse outcomes that may result, can be investigated.

This paper outlines the results from a mathematical model that simulates sudden variations in frequency on a national grid with local variation in inertia and frequency response (FR) services. The model is adapted from that by Pagnier [1] which modelled the effects of inertia and damping on a grid network. The system is initialised to reflect the relevant conditions on standard network topologies of various scales and characteristics.

The simulation outputs show the effect these outages have on local and aggregate frequency, and the ability of each grid configuration to withstand large frequency deviations beyond stipulated operating bounds and its ability to recover and remain within stable limits in a reasonable timeframe.

After confirming the operation of a generically configured network, local variations in inertia and frequency response can be set up to analyse the behaviour of frequency in response to outages and surges both locally and overall. The effects of the anticipated reduction in inertia can thereby be projected, and possible remedial solutions tested that can minimise the risk of uncontrolled variations in a cost-effective manner.

8.2 Methodology

In previous work [2] it has been demonstrated that the principal factors counterbalancing a power imbalance on an electric grid are system inertia $H_{SYS}$, Primary Frequency Response (PFR), Secondary Frequency Response (SFR), damping effects and Demand Response (DR). Inertia is the conversion of the mechanical energy stored in rotating turbines coupled to the grid to and from electrical energy in opposition to a change in the power level of the system. PFR and SFR are services provided by operators on the grid in agreement with the Transmission System Operator (National Grid ESO in the case of the GB grid) to make available resources that counter the deviation of frequency levels from safe operating levels. DR is the mechanical effect of the change in demand from load devices coupled to the grid in response to a change in frequency, where a drop in frequency will give rise to a proportional reduction in demand.

It was demonstrated [2] that it was sufficient to represent these effects in aggregate, without differentiating types of PFR, SFR or DR, in order to achieve a reasonable approximation of the frequency trace of an event. It was also shown that other network characteristics such as turbine response and deadbands have a limited additional influence on the trajectory of the frequency curve in the event of an outage or a surge. Whereas this work assumed that these effects were centralised, so that the disturbance and mitigation were acting on a single bus, in reality these services and network characteristics are distributed unevenly across a network, with consequent local variations in effects, and the incidents on the grid have a significant influence on its local and overall impact.

Using the example of [4] this single bus model is extended so as to examine the effects of this distribution in inertia, FR and disturbances. The one bus is separated into a number of buses with a single function, generation, transmission or load. Generation buses are responsible for FR, both PFR and SFR. They are also made the sources of system inertia, with each being assigned an inertia constant $m_{i}$. Demand inertia, from synchronous motors connected to the grid, is aggregated into the generator inertia profile. The distribution of grid load across the load buses is assumed to be on the basis of population density [1, 3] and load buses are the source of all DR on the network.

Disturbances are assumed to occur at one or more generator buses, so as to enable the simulation of cascading outages such as occurred on August 9, 2019 on the GB grid [4]. Whereas FR is expected to be active at these buses, there is assumed to be no inertia present. The frequency at each bus is assumed to change in response to the net imbalance in power at that bus. The propagation of the disturbance across the network is driven by the relative change in phase angles that are the result of this change in frequency, with greater phase angles between adjacent buses leading to a greater power flow between them, mediated by the susceptance of the line that connects them. These changes in frequency are resisted by FR at the generator buses and DR at the load buses. This flow of power across the network is responsible for the fluctuation in local frequency as well as the variation of aggregate frequency for the immediate area and the network as a whole.

By varying the conditions of the network at the time of a disturbance—the location of outages and surges, the distribution of inertia—as well as the magnitude of the mitigating measures—PFR, SFR, damping effects and DR—it is possible to compare the impact of similar incidents in a variety of configurations and the relative effectiveness of different counteracting network services in alternate configurations.

8.3 Models/Theory

The foundation of the model is the single-bus 3-dimensional system of differential equations set out in [2] (Table 8.1). The model was validated against frequency events on the GB grid during the period 2018–2019.

$$2H_{SYS} \dot{u} = p_{PFR} + p_{SFR} + p_{DR} - {\Delta }p$$

(8.1)

Table 8.1 Single-bus 3-dimensional differential equation system for simulating frequency during an imbalance

This model is adapted to the networked system described in [4] while preserving the FR characteristics of the single-bus system. The resulting model is an algebraic-differential system of equations representing an interconnected network of buses. In keeping with Pagnier the per-unit system is adapted to be in units of MW. Constants are modified accordingly and adopt a subscript, e.g. $i$, to indicate that these can be individual to the particular bus.

Central to the networked model is the flow of power between buses. Each bus has a relative voltage, and phase angle, and is connected to lossless transmission lines to adjacent buses. The power extracted at bus i at time t, $P_{i}^{e}$, is determined by the aggregate difference in phase angle ${\uptheta }_{{\text{i}}}$ at adjacent buses, for which the susceptance, $B_{ij}$, is non-zero. A larger variation in angle results in a greater flow of power between buses.

$$P_{i}^{e} = \mathop \sum \limits_{j \in \nu } B_{ij} V_{i} V_{j} \sin \left( {\theta_{i} - \theta_{j} } \right)\quad \quad \quad \mathop \theta \limits^{ \cdot }_{i} = \omega_{i}$$

(8.2)

The propagation of these changes in power affects the calculation of the local frequency at each bus.

Generator buses have inertia and provide PFR and SFR. PFR at bus i is determined by the differential equation

$$\tau_{p} \dot{P}_{PFR,i} + P_{PFR,i} = P_{i}^{e} - P_{i}^{\left( 0 \right)} + {\Delta }P_{i}$$

(8.3)

where ${\Delta }P_{i}$ is non-zero at buses where a disturbance occurs, while SFR is given by the equation

$$\dot{P}_{SFR,i} = - K_{i,i} \omega_{i}$$

(8.4)

where $K_{i,i}$ is a constant proportional to $K_{i}$.

The change in angular frequency at bus $i$, $\omega_{i}$, is determined by the classic swing bus equation, depending on the amplitude of the imbalance between the initial power $P_{i}^{\left( 0 \right)}$ and the current power $P_{i}^{e}$, and mitigated by inertia and the actions of the FR services.

$$m_{i} \mathop {\omega_{i} }\limits^{ \cdot } + d_{i} \omega_{i} = P_{i}^{\left( 0 \right)} - P_{i}^{e} + P_{PFR,i} + P_{SFR,i}$$

(8.5)

for $m_{i}$ and $d_{i}$ are the inertia and damping coefficients.

The bus (or buses) at which a disturbance occurs are assumed to be inertialess generator buses. The outage bus frequency is therefore determined by the imbalance resulting from net change in power at the bus, mitigated by Primary and Secondary Frequency Response

$$d_{b} \omega_{b} = P_{b}^{\left( 0 \right)} - {\Delta }P_{b} - P_{b}^{e} + P_{PFR,b} + P_{SFR,b}$$

(8.6)

The change in frequency at load buses is a result of the net power imbalance, moderated by DR.

$$\omega_{i} = P_{i}^{\left( 0 \right)} - P_{i}^{e} + P_{DR,i}$$

(8.7)

where DR is given by the equation

$$P_{DR,i} = - \,\alpha_{i} \omega_{i}$$

(8.8)

where $\alpha_{i}$ is a constant proportional to $\alpha$.

The configuration of initial conditions and values is obtained for the relevant testcase from the OATS simulation tool [3] has a total number of buses ${\upnu }$. A Runge–Kutta algorithm has been implemented to solve this algebraic differential system. It was found by experiment to converge to a solution with a precision of five decimal places using a step size of $h = 0.0003\;s$.

8.4 Results and Discussion

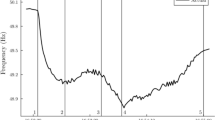
The model is demonstrated using the OATS 9 Bus testcase [3]. This consists of 3 generator buses and three load buses with three intermediate hub buses (Fig. 8.1). All generator buses are configured with the same coefficients for inertia, PFR and SFR. Load buses have the same coefficients for DR. A drop in power generation at bus Generator 2 with a magnitude of $100 \,{\text{MW}}$ is simulated at time $t = 0$. The resulting frequency simulation is shown in Fig. 8.2. The simulation shows a rapid drop in frequency at the loss bus, with more moderate drops at increasingly delayed intervals at the other buses. Focussing on the non-loss buses in Fig. 8.3 shows that the nearest adjacent bus to the loss bus, Hub 8, has the greatest fall in frequency, followed by the next nearest buses, Load 7 and Load 9. In addition to the magnitude of the drop in frequency, the trajectories of the frequency traces vary with distance from the loss bus, with the nadir of nearer buses occurring earlier than those further away. The overall system response, as demonstrated by the aggregate frequency trace, is moderated in its initial fall by the relative stability of buses more distant from the loss bus, which is situated at the edge of the network. The recovery of the aggregate frequency is limited by the propagation of the disturbance to these buses, resulting in a further fall after an initial recovery.

Fig. 8.1

Frequency response of generator, hub and load buses in response to transient on Generator 2 at time t = 0

Fig. 8.2

Layout for OATS 9 bus system

Fig. 8.3

Non-loss generators, hub and load buses, and aggregate non-loss bus frequency response to transient

8.5 Conclusion

The model demonstrated shows an effective simulation for frequency change across a network of generator, hub and load buses in response to a transient that propagates across the grid. The system is configurable to simulate varied topologies and scales, with configurable inertia, frequency and demand response at each bus. The model could facilitate the investigation of these factors to ascertain optimal strategies to minimise the impact of network incidents on the system frequency. This will be the subject of further work [5].