Logics for Extensional, Locally Complete Analysis via Domain Refinements

Abstract

Abstract interpretation is a framework to design sound static analyses by over-approximating the set of program behaviours. While over-approximations can prove correctness, they cannot witness incorrectness because false alarms may arise. An ideal, but uncommon, situation is completeness of the abstraction that can ensure no false alarm is introduced by the abstract interpreter. Local Completeness Logic is a proof system that can decide both correctness and incorrectness of a program: any provable triple $\vdash _{A}[P]~\textsf{c}~[Q]$ in the logic implies completeness of an intensional abstraction of program $\textsf{c}$ on input P and is such that Q can be used to decide (in)correctness. However, completeness itself is an extensional property of the function computed by the program, while the above intensional analysis depends on the way the program is written and therefore not all valid triples can be derived in the proof system. Our main contribution is the study of new inference rules which allow one to perform part of the intensional analysis in a more precise abstract domain, and then to transfer the result back to the coarser domain. With these new rules, all (extensionally) valid triples can be derived in the proof system, thus untying the set of provable properties from the way the program is written.

Research supported by MIUR PRIN Project 201784YSZ5 ASPRA–Analysis of Program Analyses.

1 Introduction

Static program analysis has been widely used to help developers produce valid software. Among static analysis techniques, abstract interpretation [6, 7] is a general formalism to define sound-by-construction over-approximations that has been successfully applied in many fields, such as model checking, security and optimization [8]. Static analyses are often defined as over-approximations, that is the analysis computes a superset of the behaviors. This leads to no false negatives, that is all issues of the software are identified by the analysis, but it can cause false alarms: an incorrect behavior may be an artifact of the analysis, added by the over-approximation. While the absence of false negatives allowed a wide applicability of abstract interpretation techniques, it also make tools less reliable to identify bugs. In fact, in many industrial applications any false alarm reported by the analysis to the developers diminishes its credibility, making it less effective in practice. This argument has recently led to the development of a logic of under-approximations, called incorrectness logic [16, 17].

The Problem. In abstract interpretation, an ideal situation is completeness. Given an expressible specification, that is, one represented exactly in the abstract domain, a complete abstraction reports no false alarms. In its most widespread formulation [7], completeness is a global property: a program $\textsf{c}$ is complete in the abstraction A if a condition holds for all possible inputs. Let C be the concrete domain and $\llbracket \textsf{c}\rrbracket : C \rightarrow C$ be the (collecting) denotational semantics of $\textsf{c}$. Given an abstract domain A, a concretization function $\gamma : A \rightarrow C$ and an abstraction function $\alpha : C \rightarrow A$, an abstract interpreter $\llbracket \textsf{c}\rrbracket ^{\sharp }_A: A \rightarrow A$ is complete in A if for all possible inputs P we have $\llbracket \textsf{c}\rrbracket ^{\sharp }_A \alpha (P) = \alpha (\llbracket \textsf{c}\rrbracket P)$. Unfortunately, because of universal quantification over the possible inputs, this condition is difficult to meet in practice. Moreover, in most cases completeness is checked on an intensional abstraction of $\llbracket \textsf{c}\rrbracket$ computed inductively on the syntax, through inductive reasoning by an abstract interpreter $\llbracket \textsf{c}\rrbracket ^{\sharp }_{A}$ making completeness an intensional property dependent on the program syntax [10]. However, in principle completeness is an extensional property, that only depends on the best correct abstraction $\llbracket \textsf{c}\rrbracket ^{A}$ of $\llbracket \textsf{c}\rrbracket$ in A, defined by $\llbracket \textsf{c}\rrbracket ^{A} \triangleq \alpha \llbracket \textsf{c}\rrbracket \gamma$. We sum up what we may call intensional (on the left) and extensional (on the right) completeness in the following equations:

$$\begin{aligned} \llbracket \textsf{c}\rrbracket ^{\sharp }_{A} \alpha = \alpha \llbracket \textsf{c}\rrbracket&\quad&\llbracket \textsf{c}\rrbracket ^{A} \alpha = \alpha \llbracket \textsf{c}\rrbracket \gamma \alpha = \alpha \llbracket \textsf{c}\rrbracket \end{aligned}$$

(1)

We show the difference between $\llbracket \textsf{c}\rrbracket ^{A}$ and $\llbracket \textsf{c}\rrbracket ^{\sharp }_{A}$ in the following example.

Example 1 (Extensional and intensional properties)

Consider the concrete domain of sets of integers and the abstract domain of signs:

The meaning of the abstract elements of $\textsf{Sign}$ is to represent concrete values that satisfy the respective property. So for instance, denoting with the function $\gamma$ the “meaning” of an abstract element, we have $\gamma (\mathbb {Z}_{< 0}) = \{ n \in \mathbb {Z}\,\vert \,n < 0 \}$. Conversely, $\alpha$ “abstracts” a concrete set of values to the least abstract property describing it, for instance $\alpha ( \{ 0; 1; 100 \}) = \mathbb {Z}_{\ge 0}$.

Consider the simple program fragment $\textsf{c}\triangleq \texttt {x := x + 1; x := x - 1}$. Its denotational semantics $\llbracket \textsf{c}\rrbracket$ is the identity function $\text {id}_{\mathbb {Z}}$, so its best correct abstraction is the abstract identity $\text {id}_{\textsf{Sign}} = \alpha ~\text {id}_{\mathbb {Z}}~\gamma$. This is an extensional property of the program because it only depends on the function it computes, i.e., its denotational semantics. However, an analyzer does not know the semantics of $\textsf{c}$, so it has to analyze the program syntactically, breaking it down in elementary pieces and gluing the results together. So for instance, starting from the concrete point $P = \{ 1 \}$ the analysis first abstracts it to the property $\alpha (P) = \mathbb {Z}_{> 0}$, then it computes

$$\begin{aligned} \llbracket \textsf{c}\rrbracket ^{\sharp }_{\textsf{Sign}} (\mathbb {Z}_{> 0})&= \llbracket \texttt {x := x - 1}\rrbracket ^{\sharp }_{\textsf{Sign}} \llbracket \texttt {x := x + 1}\rrbracket ^{\sharp }_{\textsf{Sign}} (\mathbb {Z}_{> 0}) \\&= \llbracket \texttt {x := x - 1}\rrbracket ^{\sharp }_{\textsf{Sign}} (\mathbb {Z}_{> 0}) = \mathbb {Z}_{\ge 0} . \end{aligned}$$

Analogous calculations for all properties in $\textsf{Sign}$ yields the abstraction

that, albeit sound, is less precise than $\text {id}_{\textsf{Sign}}$ (we highlight with a gray background all inputs on which $\llbracket \textsf{c}\rrbracket ^{\sharp }_{\textsf{Sign}}$ loses accuracy). If instead the program were written as $\textsf{c}' \triangleq \texttt {skip}$, the analysis in $\textsf{Sign}$ would yield the best correct abstraction $\llbracket \textsf{c}'\rrbracket ^{\sharp }_{\textsf{Sign}} = \text {id}_{\textsf{Sign}}$. Therefore, the abstraction depends on how the program is written and not only on its semantics: it is what it is called an intensional property (see e.g. [1] for more about intensional and extensional abstract properties).    $\square$

To overcome the former limitation of “global” completeness, the concept of local completeness [2] has been recently proposed that is related to some specific input. While this condition is much more common in practice, it is also much more complex to prove. In order to do so, the authors of [2] introduce a Local Completeness Logic parametric with respect to an abstraction A ($\text {LCL}_A$ for short), that is able to prove triples $\vdash _{A}[P]~\textsf{c}~[Q]$ with the following meaning

• 1. Q is an under-approximation of the concrete semantics $\llbracket \textsf{c}\rrbracket P$,

• 2. Q and $\llbracket \textsf{c}\rrbracket P$ have the same over-approximation in A,

• 3. A is locally complete for the intensional abstraction $\llbracket \textsf{c}\rrbracket ^{\sharp }_{A}$ on input P.

The important consequence of the previous points is the fact that a triple in $\text {LCL}_A$ is able to prove both correctness and incorrectness of a program with respect to a specification $\textit{Spec}$ expressible in A. By point (2), if the abstract analysis reports no errors in Q then there are none because of the over-approximation. However, if the analysis does report an issue, this must be present in the abstraction of $\llbracket \textsf{c}\rrbracket P$ as well, that is the same as the abstraction of Q: this means that Q contains a witness of the violation of $\textit{Spec}$, and this witness must be in $\llbracket \textsf{c}\rrbracket P$ because of the under-approximation ensured by point (1). While local completeness of point (3) is a key property to prove point (1-2), it would be enough to guarantee that (3) holds for the extensional best correct approximation $\llbracket \textsf{c}\rrbracket ^{A}$ of $\llbracket \textsf{c}\rrbracket$ rather than for the intensional abstract interpreter $\llbracket \textsf{c}\rrbracket ^{\sharp }_{A}$: this suggests that it is possible to weaken the hypothesis (3) in order to make the proof system able to derive more valid triples.

Main Contributions. Building on the proof system of $\text {LCL}_A$, we add new rules to relax point (3) to local completeness of the extensional abstraction $\llbracket \textsf{c}\rrbracket ^{A}$. This way, while the proof system itself remains intensional as it deduces program properties by working inductively on the syntax, the information it produces is more precise. Specifically, since the property associated with triples is extensional no precision is lost because of the intensional abstract interpreter, and in the end allows us to prove more triples. In order to achieve this goal, we introduce new rules to dynamically refine the abstract domain during the analysis. While in general an analysis in a more concrete domain is more precise, $\text {LCL}_A$ requires local completeness, which is not necessarily preserved by domain refinement [11]. For instance, a common way to combine two different abstract domains is their reduced product [7], but it is not always the case that the analysis in the reduced product is (locally) complete, even when it is such in the two domains.

To preserve local completeness, we introduce several rules for domain refinement in $\text {LCL}_A$ and compare their expressiveness and usability. All of them provide extensional guarantees, in the sense that point (3) is replaced with local completeness of the best correct abstraction $\llbracket \textsf{c}\rrbracket ^{A}$ on input P. The first one is called $(\mathsf {refine\hbox {-}ext})$. $\text {LCL}_A$ extended with $(\mathsf {refine\hbox {-}ext})$ turns out to be logically complete: any triple satisfying the above conditions (1–3) can be proved in our proof system. This is a theoretical improvement with respect to $\text {LCL}_A$, that instead was intrinsically incomplete as a logic, i.e., for all abstractions A there exists a sound triple that cannot be proved. While $(\mathsf {refine\hbox {-}ext})$ is theoretically interesting, one of its hypothesis is unfeasible to check in practice. To improve applicability, we propose two derived rules, $(\mathsf {refine\hbox {-}int})$ and $(\mathsf {refine\hbox {-}pre})$, whose premises can be checked effectively and imply the hypotheses of the more general $(\mathsf {refine\hbox {-}ext})$. Surprisingly, it turns out that $(\mathsf {refine\hbox {-}int})$ enjoys a logical completeness result too, while $(\mathsf {refine\hbox {-}pre})$ is strictly weaker (in terms of strength of the logic, see Example 6). Despite this, the latter is much simpler and preferable to use in practice whenever possible (see Example 5), while the former can be used in more situations and is at times the best choice.

Fig. 1.

Relations between the new proof systems

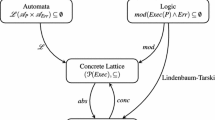
We present a pictorial comparison among the expressiveness of the various proof systems in Fig. 1. Each node represent the proof system $\text {LCL}_A$ extended with one rule (the bottom one being plain $\text {LCL}_A$). An arrow in the picture means a more powerful proof system, i.e., a proof system that can prove more triples, with its label pointing out the result justifying the claim. The two arrows between the two topmost nodes are because the two proof systems are logically equivalent, i.e., they can prove the same triples.

Structure of the paper. In Section 2 we explain the notation used in the paper and recall the basics of abstract interpretation. In Section 3 we present $\text {LCL}_A$, mostly summarizing the content of [2], with a focus on what is used in the following sections. In Section 4 we present and compare our new rules to refine the abstract domain, namely $(\mathsf {refine\hbox {-}ext})$ and the two derived rules $(\mathsf {refine\hbox {-}int})$ and $(\mathsf {refine\hbox {-}pre})$. We conclude in Section 5. Some proofs and technical examples are in Appendix A.

2 Background

Notation. We write $\mathcal {P}(S)$ for the powerset of S and $\text {id}_S: S \rightarrow S$ for the identity function on a set S, with subscripts omitted when obvious from the context. If $f : S \rightarrow T$ is a function, we overload the symbol f to denote also its lifting $f: \mathcal {P}(S) \rightarrow \mathcal {P}(T)$ defined as $f(X) = \{ f(x) \,\vert \,x \in X \}$ for any $X \subseteq S$. Given two functions $f: S \rightarrow T$ and $g: T \rightarrow V$ we denote their composition as $g \circ f$ or simply gf. For a function $f : S \rightarrow S$, we denote $f^n: S \rightarrow S$ the composition of f with itself n times, i.e. $f^{0} = \text {id}_S$ and $f^{n+1} = f \circ f^{n}$.

In ordered structures, such as posets and lattices, with carrier set C, we denote the ordering with $\le _C$, least upper bounds (lubs) with $\sqcup _C$, greatest lower bounds (glbs) with $\sqcap _C$, least element with $\bot _C$ and greatest element with $\top _C$. For all these, we omit the subscript when evident from the context. Any powerset is a complete lattice ordered by set inclusion. In this case, we use standard symbols $\subseteq$, $\cup$, etc. Given a poset T and two functions $f, g: S \rightarrow T$, the notation $f \le g$ means that, for all $s \in S$, $f(s) \le _T g(s)$. A function f between complete lattices is additive (resp. co-additive) if it preserves arbitrary lubs (resp. glbs).

2.1 Abstract Interpretation

Abstract interpretation [5,6,7] is a general framework to define static analyses that are sound by construction. The main idea is to approximate the program semantics on some abstract domain A instead of working on the concrete domain C. The main tool used to study abstract interpretations are Galois connections. Given two complete lattices C and A, a pair of monotone functions $\alpha : C \rightarrow A$ and $\gamma : A \rightarrow C$ define a Galois connection (GC) when

$$ \forall c \in C, a \in A.\quad \alpha (c) \le _A a \iff c \le _C \gamma (a) . $$

We call C and A the concrete and the abstract domain respectively, $\alpha$ the abstraction function and $\gamma$ the concretization function. The functions $\alpha$ and $\gamma$ are also called adjoints. For any GC, it holds $\text {id}_C \le \gamma \alpha$, $\alpha \gamma \le \text {id}_A$, $\gamma$ is co-additive and $\alpha$ is additive. A concrete value $c \in C$ is called expressible in A if $\gamma \alpha (c) = c$. We only consider GCs in which $\alpha \gamma = \text {id}_A$, called Galois insertions (GIs). In a GI $\alpha$ is onto and $\gamma$ is injective. A GI is said to be trivial if A is isomorphic to the concrete domain or if it is the singleton $\{ \top _A \}$.

We overload the symbol A to denote also the function $\gamma \alpha : C \rightarrow C$: this is always a closure operator, that is a monotone, increasing (i.e. $c \le A(c)$ for all c) and idempotent function. In the following, we use closure operators as much as possible to simplify the notation. Particularly, they are useful to denote domain refinements, as exemplified in the next paragraph. Note that they are still very expressive because $\gamma$ is injective: for instance $A(c) = A(c')$ if and only if $\alpha (c) = \alpha (c')$. Nonetheless, the use of closure operators is only a matter of notation and it is always possible to rewrite them using the adjoints.

We use $\text { Abs}(C)$ to denote the set of abstract domains over C, and we write $A_{\alpha , \gamma } \in \text { Abs}(C)$ when we need to make the two maps $\alpha$ and $\gamma$ explicit (we omit them when not needed). Given two abstract domains $A_{\alpha , \gamma }, A'_{\alpha ', \gamma '} \in \text { Abs}(C)$ over C, we say $A'$ is a refinement of A, written $A' \preceq A$, when $\gamma (A) \subseteq \gamma '(A')$. When this happens, the abstract domain $A'$ is more expressive than A, and in particular for all concrete elements $c \in C$ the inequality $A'(c) \le _C A(c)$ holds.

Abstracting Functions. Given a monotone function $f : C \rightarrow C$ and an abstract domain $A_{\alpha , \gamma } \in \text { Abs}(C)$, a function $f^{\sharp } : A \rightarrow A$ is a sound approximation (or abstraction) of f if $\alpha f \le f^{\sharp } \alpha$. Its best correct approximation (bca) is $f^{A} = \alpha f \gamma$, and it is the most precise of all the sound approximations of f: a function $f^{\sharp }$ is a sound approximation of f if and only if $f^{A} \le f^{\sharp }$.

A sound abstraction $f^{\sharp }$ of f is complete if $\alpha f = f^{\sharp } \alpha$. It turns out that there exists a complete abstraction $f^{\sharp }$ if and only if the bca $f^{A}$ is complete. If this is the case, we say that the abstract domain A is complete for f and denote it with $\mathbb {C}^{A}_{}(f)$. Intuitively, completeness means that the abstract function $f^{\sharp }$ is as precise as possible in the given abstract domain A, and in program analysis this allows to have greater confidence in the alarms raised. We remark that A is complete for f if and only if $\alpha f = f^{A} \alpha = \alpha f \gamma \alpha$. Since $\gamma$ is injective, this is true if and only if $\gamma \alpha f = \gamma \alpha f \gamma \alpha$, so that we define the (global) completeness property $\mathbb {C}^{A}_{}(f)$ as follows:

$$ \mathbb {C}^{A}_{}(f) \iff A f = A f A . $$

2.2 Regular Commands.

Following [2] (see also [16]) we consider a language of regular commands:

$$\begin{aligned} \textsf{Reg}\ni \textsf{r}::= \; \textsf{e}\mid \textsf{r};\textsf{r}\mid \textsf{r}\oplus \textsf{r}\mid \textsf{r}^*\end{aligned}$$

This is a general language and can be instantiated differently changing the set $\textsf{Exp}$ of basic transfer expressions $\textsf{e}$. These determines the kind of operations allowed in the language, and in our examples we assume to have deterministic assignments and boolean guards. Using standard definitions for arithmetic and boolean expressions $\texttt {a} \in \text {AExp}$ and $\texttt {b} \in \text {BExp}$, we consider

$$\begin{aligned} \textsf{Exp}\ni \textsf{e}::= \; \texttt {skip} \mid \texttt {x := a} \mid \texttt {b?} \end{aligned}$$

skip does nothing, x := a is a standard deterministic assignment. The semantics of b? is that of an “assume” statement: if its input satisfies b it does nothing, otherwise it diverges. The term $\textsf{r}; \textsf{r}$ represent the usual sequential composition, and $\textsf{r}\oplus \textsf{r}$ is nondeterministic choice. The Kleene star $\textsf{r}^*$ denote a nondeterministic iteration, where $\textsf{r}$ can be executed any number of time (possibly 0) before exiting. It can be thought as the solution of the recursive equation $\textsf{r}^*\equiv \texttt {skip} \oplus (\textsf{r}; \textsf{r}^{*})$. We write $\textsf{r}^n$ to denote sequential composition of $\textsf{r}$ with itself n times, analogously to how we use $f^n$ for function composition.

This formulation can accommodate for a standard imperative programming language [18] defining if and while statements as

Concrete semantics. We assume the semantics of basic transfer expressions on a complete lattice C to be additive. We believe this assumption not to be restrictive, and is always satisfied in collecting semantics. For our instantiation of $\textsf{Exp}$, we consider a finite set of variables $\text {Var}$, then the set of stores $\varSigma = \text {Var}\rightarrow \mathbb {Z}$ that are (total) functions $\sigma$ from $\text {Var}$ to integers. The complete lattice C is then defined simply as $\mathcal {P}(\varSigma )$ with the usual poset structure given by set inclusion. Given a store $\sigma \in \varSigma$, store update $\sigma [ x \mapsto v ]$ is defined as usual for $x \in \text {Var}$ and $v \in \mathbb {Z}$. We consider standard, inductively defined semantics for arithmetic and boolean expressions. The concrete semantics of regular commands $\llbracket \cdot \rrbracket : \textsf{Reg}\rightarrow C \rightarrow C$ is defined inductively as in Fig. 2a, where the semantics of basic transfer expressions $\textsf{e}\in \textsf{Exp}$ is defined as follows:

Fig. 2.

Concrete and abstract semantics of regular commands, side by side

Abstract Semantics. The (compositional) abstract semantics of regular commands $\llbracket \cdot \rrbracket ^{\sharp }_{A}: \textsf{Reg}\rightarrow A \rightarrow A$ on an abstract domain $A \in \text { Abs}(C)$ is defined inductively as in Fig. 2b. As common for abstract interpreters, we assume the analyser knows the best correct abstraction of expression and thus is able to compute $\llbracket \textsf{e}\rrbracket ^{A}$. A straightforward proof by structural induction shows that the abstract semantics is sound w.r.t. $\llbracket \textsf{r}\rrbracket$ (i.e., $\alpha \llbracket \textsf{r}\rrbracket \le \llbracket \textsf{r}\rrbracket ^{\sharp }_{A} \alpha$) and monotone. However, in general it is less precise than the bca, i.e., $\llbracket \textsf{r}\rrbracket ^{\sharp }_{A} \ne \llbracket \textsf{r}\rrbracket ^{A} = \alpha \llbracket \textsf{r}\rrbracket \gamma$.

Shorthands. Throughout the paper, we present some simple examples of program analysis. The programs discussed in the examples contain just one or two variables (usually x and y), so we denote their sets of stores just as $\varSigma = \mathbb {Z}$ or $\varSigma = \mathbb {Z}^2$. In these cases, the convention is that an element of $\mathbb {Z}$ is the value of the single variable in $\text {Var}$, and a pair $(n, m) \in \mathbb {Z}^2$ denote the store $\sigma (\texttt {x}) = n$, $\sigma (\texttt {y}) = m$. We also lift these conventions to sets of values in $\mathbb {Z}$ or $\mathbb {Z}^2$. At times, to improve readability, we use logical formulas such as $(y \in \{ 1; 2; 99 \} \wedge x = y)$ possibly using intervals, like in $x\in [0 ; 5]$, to describe set of stores.

3 Local Completeness Logic

In this section we present the notion of local completeness and introduce the proof system $\text {LCL}_A$ (Local Completeness Logic on A) as was defined in [2].

For a generic program and abstract domain, global completeness is a too strong requirement: for conditionals to be complete the abstract domain should basically contain a complete sublattice of the concrete domain. For this reason, the weaker notion of local completeness can be more convenient in many cases.

Definition 1

(Local completeness, cf. [2]). Let $f: C \rightarrow C$ be a concrete function, $c \in C$ a concrete point and $A \in \text { Abs}(C)$ and abstract domain for C. Then A is locally complete for f on c, written $\mathbb {C}^{A}_{c}(f)$, iff

$$ Af(c) = AfA(c) . $$

A remarkable difference between global and local completeness is that, while the former can be proved compositionally irrespective of the input [10], the latter needs it. Consequently, to carry on a compositional proof of local completeness, information on the input to each subpart of the program is also required, i.e., all traversed states are important. However, local completeness enjoys an “abstract convexity” property, that is, local completeness on a concrete point c implies local completeness on any concrete point d between c and its abstraction A(c). This observation has been exploited in the design of the proof system $\text {LCL}_A$. The system is able to prove triples $\vdash _{A}[P]~\textsf{r}~[Q]$ ensuring that:

• 1. Q is an under-approximation of the concrete semantics $\llbracket \textsf{r}\rrbracket P$,

• 2. Q and $\llbracket \textsf{r}\rrbracket P$ have the same over-approximation in A,

• 3. A is locally complete for $\llbracket \textsf{r}\rrbracket$ on input P.

The second point means that, given a specification Spec expressible in A, any provable triple $\vdash _{A}[P]~\textsf{r}~[Q]$ either proves correctness of $\textsf{r}$ with respect to Spec or expose some alerts in $Q \setminus \textit{Spec}$. These in turns correspond to true ones because of the first point, as spelled out by Corollary 1 below.

Fig. 3.

The proof system $\text {LCL}_A$.

The proof system is defined in Fig. 3. The crux of the proof system is to constrain the under-approximation Q to have the same abstraction of the concrete semantics $\llbracket \textsf{r}\rrbracket P$, as for instance explicitly required in rule $(\textsf{relax})$. This, by the abstract convexity property mentioned above, means that local completeness of $\llbracket \textsf{r}\rrbracket$ on the under-approximation P of the concrete store is enough to prove local completeness.

The three key properties (1–3) listed above are formalized by the following (intensional) soundness result:

Theorem 1

(Soundness, cf. [2]). Let $A_{\alpha , \gamma } \in \text { Abs}(C)$. If $\vdash _{A}[P]~\textsf{r}~[Q]$ then:

• 1. $Q \le \llbracket \textsf{r}\rrbracket P$,

• 2. $\alpha (\llbracket \textsf{r}\rrbracket P) = \alpha (Q)$,

• 3. $\llbracket \textsf{r}\rrbracket ^{\sharp }_{A} \alpha (P) = \alpha (Q)$.

As a consequence of this theorem, given a specification expressible in the abstract domain A, a provable triple $\vdash _{A}[P]~\textsf{r}~[Q]$ can determine both correctness and incorrectness of the program $\textsf{r}$:

Corollary 1

(Proofs of Verification, cf. [2]). Let $A_{\alpha , \gamma } \in \text { Abs}(C)$ and $a \in A$. If $\vdash _{A}[P]~\textsf{r}~[Q]$ then

$$ \llbracket \textsf{r}\rrbracket P \le \gamma (a) \iff Q \le \gamma (a) . $$

The corollary is useful in program analysis and verification because, given a specification a expressible in A and a provable triple $\vdash _{A}[P]~\textsf{r}~[Q]$, it allows to distinguish two cases.

• If $Q \subseteq \gamma (a)$, then we have also $\llbracket \textsf{r}\rrbracket P \subseteq \gamma (a)$, so that the program is correct with respect to the specification.

• If $Q \nsubseteq \gamma (a)$, then also $\llbracket \textsf{r}\rrbracket P \nsubseteq \gamma (a)$, that means $\llbracket \textsf{r}\rrbracket P \setminus \gamma (a)$ is not empty and thus contains a true alert of the program. Moreover, since $Q \subseteq \llbracket \textsf{r}\rrbracket P$ we have that $Q \setminus \gamma (a) \subseteq \llbracket \textsf{r}\rrbracket P \setminus \gamma (a)$, so that already Q pinpoints some issues.

To better show how this work, we briefly introduce the following example (discussed also in [2] where it is possible to find all details of the derivation).

Example 2

Consider the concrete domain $C = \mathcal {P}(\mathbb {Z})$, the abstract domain $\textsf{Int}$ of intervals, the precondition $P = \{ 1; 999 \}$ and the command $\textsf{r}\triangleq (\textsf{r}_1 \oplus \textsf{r}_2)^{*}$, where

In $\text {LCL}_A$ it is possible to prove the triple $\vdash _{\textsf{Int}}[P]~\textsf{r}~[Q]$, whose postcondition is $Q = \{ 0; 2; 1000 \}$. Consider the two specification $\textit{Spec}= (x \le 1000)$ and $\textit{Spec}' = (x \ge 100)$. The triple is then able to prove correctness of $\textit{Spec}$ and incorrectness of $\textit{Spec}'$. For the former, observe that $Q \subseteq \textit{Spec}$. By Corollary 1 we then know $\llbracket \textsf{r}\rrbracket P \subseteq \textit{Spec}$, that is correctness. For the latter, Q exhibits two witnesses to the violation of $\textit{Spec}'$, that are $0, 2 \in Q \setminus \textit{Spec}'$. By point (1) of soundness we then know that $0, 2 \in Q \subseteq \llbracket \textsf{r}\rrbracket P$ are true alerts.    $\square$

Strictly speaking, the proof of Corollary 1 only relies on points (1-2) of Theorem 1. Point (3) is in turn needed to ensure the first two, but extensional completeness would suffice to this aim. This means that we can weaken the soundness theorem (logically speaking, that is we prove a stronger conclusion, so the theorem as an implication is weaker) while still preserving the validity of Corollary 1. To this end, we propose a new soundness result involving extensional completeness: the important difference is that in point (3) we use the best correct abstraction $\llbracket \textsf{r}\rrbracket ^A$ in place of the inductively defined $\llbracket \textsf{r}\rrbracket ^{\sharp }_A$. Since Theorem 1 involves $\llbracket \textsf{r}\rrbracket ^{\sharp }_A$, an intensional property of the program $\textsf{r}$ that depends on how the program is written (see Example 1 or Example 1 in Section 5 of [13]), while the new statement we propose relies only on $\llbracket \textsf{r}\rrbracket ^A$, an extensional property of the computed function $\llbracket \textsf{r}\rrbracket$ and not of $\textsf{r}$ itself, for the rest of the paper we use the name intensional soundness for Theorem 1, and extensional soundness for the following Theorem 2.

Theorem 2 (Extensional soundness)

Let $A_{\alpha , \gamma } \in \text { Abs}(C)$. If $\vdash _{A}[P]~\textsf{r}~[Q]$ then:

• 1. $Q \le \llbracket \textsf{r}\rrbracket P$,

• 2. $\alpha (\llbracket \textsf{r}\rrbracket P) = \alpha (Q)$,

• 3. $\llbracket r\rrbracket ^A \alpha (P) = \alpha (Q)$.

Lastly, we remark that the original $\text {LCL}_A$ is intrinsically logically incomplete ([2], cf. Theorem 5.12): for every non trivial abstraction A there exists a triple that is intensionally sound (satisfies points (1-3) of Theorem 1) but cannot be proved in $\text {LCL}_A$. We will discuss logical (in)completeness for our extensional framework in Section 4.1.

4 Refining Abstract Domain

$\text {LCL}_A$ can prove a triple $[P]~\textsf{r}~[Q]$ for some Q only when $\llbracket \textsf{r}\rrbracket ^{\sharp }_{A}$ is locally complete, that is $\llbracket \textsf{r}\rrbracket ^{\sharp }_{A} \alpha (P) = \alpha (\llbracket \textsf{r}\rrbracket P)$ (see Theorem 1). Since $\llbracket \textsf{r}\rrbracket ^{\sharp }_{A}$ is computed in a compositional way, the above condition strictly depends on how $\textsf{r}$ is written: to prove the local completeness of $\llbracket \textsf{r}\rrbracket ^{\sharp }_{A}$, we need to prove that all its syntactic components are locally complete, that is an intensional property. However, the goal of the analysis is to study the behaviour of the function $\llbracket \textsf{r}\rrbracket$, not how it is encoded by $\textsf{r}$. Hence, our aim is to enhance the original proof system in order to be able to handle triples where the extensional abstraction $\llbracket \textsf{r}\rrbracket ^{A}$ is proved to be locally complete w.r.t. the given input, that is $\llbracket \textsf{r}\rrbracket ^{A} \alpha (P) = \alpha (\llbracket \textsf{r}\rrbracket P)$. To this end, we extend the proof system with a new inference rule, that is shown in Fig. 4. It is named after “refine” because it allows to refine abstract domains A to some $A' \preceq A$ and “ext” since it involves the extensional bca $\llbracket \textsf{r}\rrbracket ^{A'}$ of $\llbracket \textsf{r}\rrbracket$ in $A'$ (to distinguish it from the rules we will introduce in Section 4.2).

Fig. 4.

Rule refine for $\text {LCL}_A$.

Using $(\mathsf {refine\hbox {-}ext})$ it is possible to construct a derivation that proves local completeness of portions of the whole program in a more precise abstract domain $A'$ and then carries the result over to the global analysis in a coarser domain A. The only requirement for the application of the rule is that domain $A'$ is chosen in such a way that $A \llbracket \textsf{r}\rrbracket ^{A'} A(P) = A(Q)$ is satisfied.

Formally, given the two abstract domains $A_{\alpha , \gamma }, A'_{\alpha ', \gamma '} \in \text { Abs}(C)$, this last premise of rule $(\mathsf {refine\hbox {-}ext})$ should be written as $\alpha \gamma ' \llbracket \textsf{r}\rrbracket ^{A'} \alpha ' A(P) = \alpha (Q)$ to match function domains and codomains. However we prefer the more concise, albeit a little imprecise, notation used in Fig. 4. That writing is justified by the following intuitive argument: since $A' \preceq A$ we can consider with a slight abuse of notation (seeing abstract domains as closures) $A \subseteq A' \subseteq C$, so that for any element $a \in A \subseteq C$ we have $\gamma (a) = \gamma '(a) = a$ and for any $c \in C$ we have $\alpha ' A(c) = A(c)$. With these, it follows that

$$ \alpha \gamma ' \llbracket \textsf{r}\rrbracket ^{A'} \alpha ' A(P) = \alpha \llbracket \textsf{r}\rrbracket ^{A'} A(P) = A \llbracket \textsf{r}\rrbracket ^{A'} A(P) . $$

With rule $(\mathsf {refine\hbox {-}ext})$ we cannot prove intensional soundness (Theorem 1): since this rule allows to perform part of the analysis in a more concrete domain $A'$, we do not get any information on $\llbracket \textsf{r}\rrbracket ^{\sharp }_A$. However, we can prove extensional soundness (Theorem 2) and get all the benefits of Corollary 1.

Theorem 3

(Extensional soundness of $(\mathsf {refine\hbox {-}ext})$). The proof system in Fig. 3 with the addition of rule $(\mathsf {refine\hbox {-}ext})$ (see Fig. 4) is extensionally sound (cf. Theorem 2).

We also remark that a rule like $(\mathsf {refine\hbox {-}ext})$, that allows to carry on part of the proof in a different abstract domain, cannot come unconstrained. We present an example showing that a similar inference rule only requiring the triple $[P]~\textsf{r}~[Q]$ to be provable in an abstract domain $A' \preceq A$ without any other constraint would be unsound.

Example 3

Consider the concrete domain $C = \mathcal {P}(\mathbb {Z})$ of integers, the point $P = \{ -5; -1 \}$, the abstract domain $\textsf{Sign}$ of Example 1 and the program

$$ \textsf{r}\triangleq \texttt {x := x + 10} . $$

Then $C \preceq \textsf{Sign}$ and we can prove $\vdash _{C}[P]~\textsf{r}~[\{ 5; 9 \}]$ applying $(\textsf{transfer})$ since all assignments are locally complete in the concrete domain. However, if , it is not the case that $\mathbb {C}^{\textsf{Sign}}_{P}(f)$: indeed

$$\begin{aligned} \textsf{Sign}(f (\textsf{Sign}(P)))&= \textsf{Sign}(f(\mathbb {Z}_{< 0})) = \textsf{Sign}(\{ n \in \mathbb {Z}\,\vert \,n < 10 \}) = \top \end{aligned}$$

while

$$\begin{aligned} \textsf{Sign}(f(P))&= \textsf{Sign}(\{ 5, 9 \}) = \mathbb {Z}_{> 0}. \end{aligned}$$

This means that a rule without any additional condition can prove a triple which is not locally complete, hence it is unsound.    $\square$

4.1 Logical Completeness

Among all the possible conditions that can be added to a rule like $(\mathsf {refine\hbox {-}ext})$, we believe ours to be very general since, differently than the original $\text {LCL}_A$ proof system (see Section 5.2 of [2]), the introduction of $(\mathsf {refine\hbox {-}ext})$ allows us to derive a logical completeness result, i.e. the ability to prove any triple satisfying the soundness properties guaranteed by the proof system.

However, to prove such a result, our extension need an additional rule to handle loops, just like the original $\text {LCL}_A$ and Incorrectness Logic [16]. The necessary infinitary rule, called $(\textsf{limit})$, allows the proof system to handle Kleene star, and is the same as $\text {LCL}_A$:

Theorem 4

(Logical completeness of $(\mathsf {refine\hbox {-}ext})$). Consider the proof system of Fig. 3 with the addition of rules $(\mathsf {refine\hbox {-}ext})$ and $(\textsf{limit})$. If $Q \le \llbracket \textsf{r}\rrbracket P$ and $\llbracket \textsf{r}\rrbracket ^A \alpha (P) = \alpha (Q)$ then $\vdash _{A}[P]~\textsf{r}~[Q]$.

The previous theorem proves the logical completeness of our proof system with respect to the property of extensional soundness. Indeed, if $Q \le \llbracket \textsf{r}\rrbracket P$ and $\llbracket \textsf{r}\rrbracket ^A \alpha (P) = \alpha (Q)$ we also have:

$$\begin{aligned} \alpha (Q) \le \alpha (\llbracket \textsf{r}\rrbracket P) \le \llbracket \textsf{r}\rrbracket ^{A} \alpha (P) = \alpha (Q) , \end{aligned}$$

hence all three conditions of Theorem 2 are satisfied.

An interesting consequence of this result is the existence of a refinement $A'$ in which it is possible to carry out the proof. In principle such a refinement could be the concrete domain C (as shown in the proof in Appendix A), that is not computable. However, it is worth nothing that for a sequential fragment (a portion of code without loops) the concrete domain can be actually used (for instance via first-order logic). This opens up the possibility, for instance, to infer a loop invariant on the body using C, and then prove it using an abstract domain. In Section 4.3 we discuss this issue further.

4.2 Derived Refinement Rules

The hypothesis $A \llbracket \textsf{r}\rrbracket ^{A'} A(P) = A(Q)$ is added to rule $(\mathsf {refine\hbox {-}ext})$ in order to guarantee soundness: in general, the ability to prove a triple such as $[P]~\textsf{r}~[Q]$ in a refined domain $A'$ only gives information on $A \llbracket \textsf{r}\rrbracket ^{A'} A'(P)$ but not on $A \llbracket \textsf{r}\rrbracket ^{A'} A(P)$. In fact, the Example 4 shows that $A \llbracket \textsf{r}\rrbracket ^{A'} A'(P)$ and $A \llbracket \textsf{r}\rrbracket ^{A'} A(P)$ can be different.

Example 4

Consider the concrete domain $\mathcal {P}(\mathbb {Z})$, the abstract domain of signs $\textsf{Sign}_{\alpha , \gamma } \in \text { Abs}(\mathcal {P}(\mathbb {Z}))$ (introduced in Example 1) and its refinement $\textsf{Sign}_{1}$ below

For the command $\textsf{r}\triangleq \texttt {x := x - 1}$ and the concrete point $P = \{ 1 \}$ we have

$$ \textsf{Sign}\llbracket \textsf{r}\rrbracket ^{\textsf{Sign}_{1}} \textsf{Sign}_1(P) = \textsf{Sign}\llbracket \textsf{r}\rrbracket ^{\textsf{Sign}_{1}} (\mathbb {Z}_{= 1}) = \mathbb {Z}_{= 0} $$

but

$$ \textsf{Sign}\llbracket \textsf{r}\rrbracket ^{\textsf{Sign}_1} \textsf{Sign}(P) = \textsf{Sign}\llbracket \textsf{r}\rrbracket ^{\textsf{Sign}_1} (\mathbb {Z}_{> 0}) = \mathbb {Z}_{\ge 0} . $$

   $\square$

Despite being necessary, the hypothesis of rule $(\mathsf {refine\hbox {-}ext})$ cannot be checked in practice because the bca $\llbracket \textsf{r}\rrbracket ^{A'}$ of a composite command $\textsf{r}$ is not known by the analyser. To mitigate this issue, we present two derived rules whose premises imply the premises of Rule $(\mathsf {refine\hbox {-}ext})$, hence ensuring extensional soundness by means of Theorem 3.

The first rule we present replaces the requirement on the extensional bca $\llbracket \textsf{r}\rrbracket ^{A'}$ with requirements on the intensional compositional abstraction $\llbracket \textsf{r}\rrbracket ^{\sharp }_{A'}$ computed in $A'$. For this reason, we call this rule $(\mathsf {refine\hbox {-}int})$.

Proposition 1

The following rule $(\mathsf {refine\hbox {-}int})$ is extensionally sound:

It is worth noting that now the condition on the compositional abstraction $\llbracket \textsf{r}\rrbracket ^{\sharp }_{A'}$ can easily be checked by the analyser, possibly alongside the analysis of $\textsf{r}$ with LCL or using a stand-alone abstract interpreter. Moreover, this rule is as powerful as the original $(\mathsf {refine\hbox {-}ext})$ because it allows to prove a logical completeness result akin to Theorem 4.

Theorem 5

(Logical completeness of $(\mathsf {refine\hbox {-}int})$). Consider the proof system of Fig. 3 with the addition of rules $(\mathsf {refine\hbox {-}int})$ and $(\textsf{limit})$. If $Q \le \llbracket \textsf{r}\rrbracket P$ and $\llbracket \textsf{r}\rrbracket ^A \alpha (P) = \alpha (Q)$ then $\vdash _{A}[P]~\textsf{r}~[Q]$.

Just like logical completeness for $(\mathsf {refine\hbox {-}ext})$, this result implies the existence of a refinement $A'$ in which it is possible to carry out the proof (possibly the concrete domain C). The discussion about how to find one is sketched in Section 4.3.

The second derived rule we propose is simpler than $(\mathsf {refine\hbox {-}ext})$, as it just checks the abstractions A(P) and $A'(P)$, with no reference to the regular command $\textsf{r}$ nor to the postcondition Q. Since the premise is only on the precondition P, we call this rule $(\mathsf {refine\hbox {-}pre})$.

Proposition 2

The following rule $(\mathsf {refine\hbox {-}pre})$ is extensionally sound:

Rule $(\mathsf {refine\hbox {-}pre})$ only requires a simple check at the application site instead of an expensive analysis of the program $\textsf{r}$, so it can be preferred in practice.

We present an example to highlight the advantages of this rule (as well as $(\mathsf {refine\hbox {-}int})$), which allows us to use different domains in the proof derivation of different parts of the program.

Example 5

(The use of $(\mathsf {refine\hbox {-}pre})$).

and the program $\textsf{r}\triangleq \textsf{r}_1; \textsf{r}_2$. Here abs is a function to compute the absolute value, and we assume, for the sake of simplicity, that the analyser knows its best abstraction. Consider the concrete domain $\mathcal {P}(\mathbb {Z}^2)$ where a pair (n, m) denote a state $\texttt {x} = n$, $\texttt {y} = m$, and the initial state $P = (\texttt {y} \in [-100; 100])$, a logical description of the concrete $\{ (n, m) \,\vert \,m \in [-100; 100] \} \in \mathcal {P}(\mathbb {Z}^2)$. The bca $\llbracket \textsf{r}\rrbracket ^{\textsf{Int}}$ in the abstract domain of intervals is locally complete on P (since P is expressible in $\textsf{Int}$), but the compositional abstraction $\llbracket \textsf{r}\rrbracket ^{\sharp }_{\textsf{Int}}$ is not:

$$\begin{aligned} \llbracket \textsf{r}\rrbracket ^{\textsf{Int}} \alpha (P)&= \textsf{Int}(\llbracket \textsf{r}_2\rrbracket \llbracket \textsf{r}_1\rrbracket (\{ (n, m) \,\vert \,m \in [-100; 100] \})) \\&= \textsf{Int}(\llbracket \textsf{r}_2\rrbracket (\{ (n, m) \,\vert \,m \in [1; 100] \})) \\&= \textsf{Int}(\{ (1, 1) \}) \\&= ([1; 1] \times [1; 1]) , \end{aligned}$$

while

$$\begin{aligned} \llbracket \textsf{r}\rrbracket ^{\sharp }_{\textsf{Int}} \alpha (P)&= \llbracket \textsf{r}_2\rrbracket ^{\sharp }_{\textsf{Int}} \llbracket \textsf{r}_1\rrbracket ^{\sharp }_{\textsf{Int}} ([-\infty ; +\infty ] \times [-100; 100]) \\&= \llbracket \textsf{r}_2\rrbracket ^{\sharp }_{\textsf{Int}} \llbracket \texttt {y := abs(y)}\rrbracket ^{\textsf{Int}} ([-\infty ; +\infty ] \times [-100; 100]) \\&= \llbracket \textsf{r}_2\rrbracket ^{\sharp }_{\textsf{Int}} ([-\infty ; +\infty ] \times [0; 100]) \\&= ([1; 1] \times [0; 100]) \ne ([1; 1] \times [1; 1]) . \end{aligned}$$

The issues are twofold. First, the analysis of $\textsf{r}_1$ in $\textsf{Int}$ is incomplete, so we need a more concrete domain. For instance $\textsf{Int}_{\ne 0}$, the Moore closure of $\textsf{Int}$ with the addition of the element $\mathbb {Z}_{\ne 0}$ representing the property of being nonzero would work. Intuitively, $\textsf{Int}_{\ne 0}$ contains all intervals, possibly having a “hole” in 0. Formally

$$ \textsf{Int}_{\ne 0} = \textsf{Int}\cup \{ I_{\ne 0} \,\vert \,I \in \textsf{Int}\} $$

with $\gamma '(I_{\ne 0 }) = \gamma (I) \setminus \{ 0 \}$. However, note that there is no need for a relational domain to analyze $\textsf{r}_1$ since variable x is never mentioned in it. On the contrary, the analysis of $\textsf{r}_2$ requires a relational domain to track the information that the value of variable x is equal to the value of variable y. This suggests, for instance, to use the octagons domain $\textsf{Oct}$ [15] to analyze $\textsf{r}_2$. It is worth noting that the domain of octagons $\textsf{Oct}$ would not be able to perform a locally complete analysis of $\textsf{r}_1$ for the same reasons that the domain $\textsf{Int}$ could not.

However, rule $(\mathsf {refine\hbox {-}pre})$ allows us to combine these different proof derivations. Since the program state between $\textsf{r}_1$ and $\textsf{r}_2$ can be precisely represented in $\textsf{Int}$, we use this domain as a baseline and refine it in $\textsf{Int}_{\ne 0}$ and $\textsf{Oct}$ for the two parts respectively.

Fig. 5.

Derivation of $\vdash _{\textsf{Int}_{\ne 0}}[P]~\textsf{r}_1~[R]$ for Example 5.

Let $R = (\texttt {y} \in \{ 1; 2; 100 \})$ that is an under-approximation of the concrete state in between $\textsf{r}_1$ and $\textsf{r}_2$ with the same abstraction in $\textsf{Int}$, so we can prove the triple $\vdash _{\textsf{Int}}[P]~\textsf{r}_1~[R]$. Note that the concrete point 2 was added to R in order to have local completeness for (x> 1)? in $\textsf{r}_2$. However, this triple cannot be proved in $\textsf{Int}$ because $\llbracket \textsf{r}_1\rrbracket ^{\sharp }_{\textsf{Int}}$ is not locally complete on P, so we resort to $(\mathsf {refine\hbox {-}pre})$ to change the domain to $\textsf{Int}_{\ne 0}$. The full derivation in $\textsf{Int}_{\ne 0}$ is shown in Fig. 5, where $R_1 = (\texttt {y} \in [-100; 100] \wedge \texttt {y} \ne 0)$ and we omitted for simplicity the additional hypothesis of $(\textsf{relax})$.

Again $\llbracket \textsf{r}_2\rrbracket$ is locally complete on R in $\textsf{Int}$, but the compositional analysis $\llbracket \textsf{r}_2\rrbracket ^{\sharp }_{\textsf{Int}}$ is not. Hence to perform the derivation we resort to $(\mathsf {refine\hbox {-}pre})$ to introduce relational information in the abstract domain, using $\textsf{Oct}$ instead of $\textsf{Int}$. Let $Q = (\texttt {x} = 1 \wedge \texttt {y} = 1)$, that is the concrete output of the program, so that we can prove $\vdash _{\textsf{Int}}[R]~\textsf{r}_2~[Q]$. The derivation of this triple is only in Appendix A, Fig. 6. However, the proof is just a straightforward application of rules $(\textsf{seq})$, $(\textsf{iterate})$ and $(\textsf{transfer})$.

With those two derivation, the proof of the triple $\vdash _{\textsf{Int}}[P]~\textsf{r}~[Q]$ is straightforward using $(\mathsf {refine\hbox {-}pre})$:

For the derivation to fit the page, we write here the additional hypotheses of the rules. For the first application, $\textsf{Int}_{\ne 0} \preceq \textsf{Int}$ and $\textsf{Int}_{\ne 0}(P) = P = \textsf{Int}(P)$. For the second, $\textsf{Oct}\preceq \textsf{Int}$ and $\textsf{Int}(R) = (\texttt {y} \in [1; 100]) = \textsf{Oct}(R)$.

It is worth noting that, in this example, all applications of $(\mathsf {refine\hbox {-}pre})$ can be replaced by $(\mathsf {refine\hbox {-}int})$. This means that also the latter is able to exploit $\textsf{Int}_{\ne 0}$ and $\textsf{Oct}$ to prove the triple in the very same way, but its application requires more expensive abstract analyses than the simple checks of $(\mathsf {refine\hbox {-}pre})$.    $\square$

While $(\mathsf {refine\hbox {-}pre})$ is simpler than $(\mathsf {refine\hbox {-}ext})$ and $(\mathsf {refine\hbox {-}int})$, it is also weaker in both a theoretical and practical sense. On the one hand, $\text {LCL}_A$ extended with this rule does not admit a logical completeness result; on the other hand, there are situations in which, even though $(\mathsf {refine\hbox {-}pre})$ allows a derivation, the other rules are more effective. We show these two points by examples. For the first, we propose a sound triple that $\text {LCL}_A$ extended with $(\mathsf {refine\hbox {-}pre})$ cannot prove. Since the example is quite technical, here we only sketch the idea, and leave the details only in Appendix A, Example 8.

Example 6

(Logical incompleteness of $(\mathsf {refine\hbox {-}pre})$). Consider the concrete domain $C = \mathcal {P}(\mathbb {Z})$ of integers, the abstract domain $\textsf{Int}$ of intervals, the concrete point $P = \{ -1, 1 \}$ and commands $\textsf{r}_1 \triangleq$ x != 0?, $\textsf{r}_2 \triangleq$ x>= 0? and $\textsf{r}\triangleq \textsf{r}_1; \textsf{r}_2$. Then the triple $\vdash _{\textsf{Int}}[P]~\textsf{r}_1; \textsf{r}_2~[\{ 1 \}]$ is sound but cannot be proved in $\text {LCL}_A$ extended with $(\mathsf {refine\hbox {-}pre})$.

The key observations for this example are two. First, all strict subset $P' \subset P$ are such that $\textsf{Int}(P') \subset \textsf{Int}(P)$. Moreover, for all refinements $A' \preceq \textsf{Int}$ such that $A'(P) = \textsf{Int}(P)$ we have the same condition, namely if $P' \subset P$ then $A'(P') \subset A'(P)$. This is because for all $P' \subset P$ we have $A'(P') \subseteq \textsf{Int}(P') \subset \textsf{Int}(P) = A'(P)$. Second, $\llbracket \textsf{r}_1\rrbracket P = P$. This means that all triples appearing in the derivation tree of $\vdash _{\textsf{Int}}[P]~\textsf{r}_1; \textsf{r}_2~[\{ 1 \}]$ have the same precondition P. Since $(\mathsf {refine\hbox {-}pre})$ requires $A'(P) = \textsf{Int}(P)$, all possible applications of this rule change the abstract domain to some $A'$ satisfying the condition above. Since $\text {LCL}_A$ computes under-approximations with the same abstraction of the strongest postcondition, these two observations make it impossible to under-approximate P further, both with $(\textsf{relax})$ and $(\mathsf {refine\hbox {-}pre})$. This in turn make the triple not provable because $\llbracket \textsf{r}_2\rrbracket$ is not locally complete on P in $\textsf{Int}$ or in any refinement satisfying $A'(P) = \textsf{Int}(P)$:

$$\begin{aligned} A' \llbracket \textsf{r}_2\rrbracket (P)&= A'(\{ 1 \}) \subseteq \textsf{Int}(\{ 1 \}) = \{ 1 \} \\ A' \llbracket \textsf{r}_2\rrbracket A'(P)&\supseteq \llbracket \textsf{r}_2\rrbracket A'(P) = \llbracket \textsf{r}_2\rrbracket (\textsf{Int}(P)) = \{ 0, 1 \} . \end{aligned}$$

Example 8 in Appendix A exhibits the formal argument showing that this triple cannot be proved.    $\square$

As a corollary, this example (and more in general logical incompleteness) shows that is not always possible to find a refinement $A'$ to carry out the proof using $(\mathsf {refine\hbox {-}pre})$. Another consequence of this incompleteness result is the fact that, even when a command is locally complete in an abstract domain A, we may need to reason about properties that are not expressible in A in order to prove it, as $(\mathsf {refine\hbox {-}pre})$ may not be sufficient.

Second, we present an example to illustrate that there are situations in which $(\mathsf {refine\hbox {-}int})$ is more practical than $(\mathsf {refine\hbox {-}pre})$, even though they are both able to prove the same triple.

Example 7

Consider the two program fragments

$$\begin{aligned} \textsf{r}_1&\triangleq \texttt {(y != 0)?; x := y; y := abs(y)} \\ \textsf{r}_2&\triangleq \texttt {x := y; while (x > 1) \{ y := y - 1; x := x - 1 \}} \end{aligned}$$

and the program $\textsf{r}\triangleq \textsf{r}_1; \textsf{r}_2$. Consider also the initial state $P = \texttt {y} \in [-100; 100]$.

This example is a variation of Example 5: the difference is the introduction of the relational dependency x := y in $\textsf{r}_1$, that is partially stored in the postcondition R of $\textsf{r}_1$. Because of this, $\textsf{Oct}(R)$ and $\textsf{Int}(R)$ are different, so we cannot apply $(\mathsf {refine\hbox {-}pre})$ to prove $[R]~\textsf{r}_2~[Q]$ for some Q.

Following Example 5, the domain $\textsf{Int}_{\ne 0}$ is able to infer on $\textsf{r}_1$ a subset R of the strongest postcondition $\texttt {y} \in [1; 100] \wedge \texttt {y} = \text {abs}(\texttt {x})$ with the same abstraction $\textsf{Int}_{\ne 0}(R) = [-100; 100]_{\ne 0} \times [1; 100]$. However, for any such R we cannot use $(\mathsf {refine\hbox {-}pre})$ to prove the triple $\vdash _{\textsf{Int}}[R]~\textsf{r}_2~[\texttt {x} = 1 \wedge \texttt {y} = 1]$ via $\textsf{Oct}$ because $\textsf{Int}(R) = \texttt {x} \in [-100; 100] \wedge \texttt {y} \in [1; 100]$ while $\textsf{Oct}(R) = 1 \le \texttt {y} \le 100 \wedge -\texttt {y} \le \texttt {x} \le \texttt {y}$. More in general, any subset of the strongest postcondition contains the relational information $\texttt {y} = \text {abs}(\texttt {x})$, so relational domains like octagons and polyhedra [9] do not have the same abstraction as the non-relational $\textsf{Int}$, preventing the use of $(\mathsf {refine\hbox {-}pre})$. However, we can apply $(\mathsf {refine\hbox {-}int})$: considering $R = (\texttt {y} \in \{1; 2; 100\} \wedge \texttt {y} = \text {abs}(\texttt {x}) )$, $Q = (\texttt {x} = 1 \wedge \texttt {y} = 1)$ and $\textsf{r}_w \triangleq \texttt {while (x > 1) \{ y := y - 1; x := x - 1 \}}$, we have

$$\begin{aligned} \textsf{Int}\llbracket \textsf{r}_2\rrbracket ^{\sharp }_{\textsf{Oct}} \textsf{Int}(R)&= \textsf{Int}\llbracket \textsf{r}_2\rrbracket ^{\sharp }_{\textsf{Oct}} (\texttt {x} \in [-100; 100] \wedge \texttt {y} \in [1; 100])\\&= \textsf{Int}\llbracket \textsf{r}_w\rrbracket ^{\sharp }_{\textsf{Oct}} \llbracket \texttt {x := y}\rrbracket ^{\sharp }_{\textsf{Oct}} (\texttt {x} \in [-100; 100] \wedge \texttt {y} \in [1; 100]) \\&= \textsf{Int}\llbracket \textsf{r}_w\rrbracket ^{\sharp }_{\textsf{Oct}} (1 \le \texttt {y} \le 100, \texttt {y} = \texttt {x}) \\&= \textsf{Int}(\texttt {x} = 1 \wedge \texttt {y} = 1) \\&= \textsf{Int}(Q) . \end{aligned}$$

In this example, rule $(\mathsf {refine\hbox {-}pre})$ can be applied to prove the triple, but it requires to have relational information from the assignment x := y in $\textsf{r}_1$, hence forcing the use of a relational domain (eg. the reduced product [7] of $\textsf{Oct}$ and $\textsf{Int}_{\ne 0}$) for the whole $\textsf{r}$, making the analysis more expensive.    $\square$

4.3 Choosing The Refinement

All three new rules allow to combine different domains in the same derivation, but do not define an algorithm because of the choice of the right refinement to use is nondeterministic. A crucial point to their applicability is a strategy to select the refined abstract domain. While we have not addressed this problem yet, we believe there are some interesting starting points in the literature.

As already anticipated in previous sections, we settled the question from a theoretical point of view. Logical completeness results for $(\mathsf {refine\hbox {-}ext})$ (Theorem 4) and $(\mathsf {refine\hbox {-}int})$ (Theorem 5) implies the existence of a domain in which it is possible to complete the proof (if this were not the case, then the proof could not be completed in any domain, against the logical completeness). However, the proofs of those theorems exhibit the concrete domain C as an example, which is unfeasible in general. Dually, as $(\mathsf {refine\hbox {-}pre})$ is logically incomplete (Example 6), there are triples that cannot be proved in any domain with it.

As more practical alternatives, we envisage some possibilities. First, we are studying relationships with counterexample-guided abstraction refinement (CEGAR) [4], which is a technique that exploits refinement in the context of abstract model checking. However, CEGAR and our approach seem complementary. On the one hand, our refinement rules allow a dynamic change of domain, during the analysis and only for a part of it, while CEGAR performs a static refinement and then a new analysis of the whole transition system in the new, more precise domain. On the other hand, our rules lack an instantiation technique, while for CEGAR there are effective algorithms available to pick a suitable refinement.

Second, local completeness shell [3] were proposed as an analogous of completeness shell [11] for local completeness. In the article, the authors proposed to use local completeness shells to perform abstract interpretation repair, a technique to refine the abstract domain depending on the program to analyse, just like CEGAR does for abstract model checking. Abstract interpretation repair works well with $\text {LCL}_A$, and could be a way to decide the best refinement for one of our rules in presence of a failed local completeness proof obligation. The advantage of combining repair with our new rules is given by the possibility of discarding the refined domain just after its use in a subderivation instead of using it to carry out the whole derivation. Investigations in this direction is ongoing.

Another related approach, which shares some common ground with CEGAR, is Lazy (Predicate) Abstraction [12, 14]. Both ours and this approach exploits different abstract domains for different parts of the proof, refining it as needed. The key difference is that Lazy Abstraction unwinds the control flow graph (CFG) of the program (with techniques to handle loops) while we work inductively on the syntax. This means that, when Lazy Abstraction refines a domain, it must use it from that point onward (unless it finds a loop invariant). On the other hand, our method can change abstract domain even for different parts of sequential code. However, the technique used in Lazy Abstraction (basically to trace a counterexample back with a theorem prover until it is either found to be spurious or proved to be true) could be applicable to $\text {LCL}_A$: a failed local completeness proof obligation in $(\textsf{transfer})$ can be traced back with a theorem prover and the failed proof can be used to understand how to refine the abstract domain.

5 Conclusions

In this paper, we have proposed a logical framework to prove both correctness and incorrectness of a program exploiting locally complete abstractions. Indeed, from any provable triple $[P]~\textsf{r}~[Q]$ we can either prove that $\textsf{r}$ meets an expressible specification $\text {Spec}$ or find a concrete counterexample in Q. Differently from the original $\text {LCL}_A$ [2], that was proved to be intensionally sound, our framework is extensionally sound, meaning that is able to prove more properties about programs. To achieve this, our inference rules are based on the best correct abstraction of a program behaviour instead of a generic abstract interpreter. The key feature of our proof systems is the ability to exploit different abstract domains to analyse different portions of the whole program. In particular, the domains are selected among the refinements of a chosen abstract domain from which the analysis begins. The main advantage of our extensional approach is the possibility of proving many triples that could not be proved in $\text {LCL}_A$ because of the way the program is written. More in details, we presented three new rules to refine the abstract domain, each of which can be added independently to the proof system with different complexity-precision trade-off.

Table 1. Comparison of the proof systems

Table 1 summarizes the properties $\text {LCL}_A$ enjoys when extended with different rules, and Figure 1 from the Introduction graphically compare the logical strength of these proof systems. $(\mathsf {refine\hbox {-}ext})$ is the most general rule, from which the other two $(\mathsf {refine\hbox {-}int})$ and $(\mathsf {refine\hbox {-}pre})$ are derived. The former turns out to be as strong as $(\mathsf {refine\hbox {-}ext})$, since they are both logically complete, while the latter is simpler to use, although weaker.

Future work. In principle completeness could be achieved either refining or simplifying the abstract domain [11]. In this article we have only focused on refinement rules for local completeness, but we are investigating some simplification rules as well as their relation to the ones presented in this paper. To date, domain simplification seems theoretically weaker, but apparently it can accommodate for techniques useful in practice that are beyond the reach of refinement rules.

While the new rules we introduced are relevant from both a theoretical and practical point of view, they do not define an algorithm because of their nondeterminism: we need techniques to determine when a change of abstract domain is needed and how to choose the most convenient new domain. We believe these two issues are actually related. For instance, if the analysis is unable to satisfy a local completeness proof obligation to apply $(\textsf{transfer})$, an heuristics may determine both what additional information is needed to make it true (i.e., how to refine the abstract domain) and where that additional information came from (i.e., when to refine). We briefly discussed in Section 4.3 some possibilities to perform this choice. Ideally, one would systematically select an off-the- shelf abstract domain best suited to deal with each code fragment and the heuristic would inspect the proof obligations, and exploit some sort of catalog that can track suitable abstract domains that are locally complete for the code and input at hand or derive on-the-fly some convenient domain refinement as done, e.g., by partition refinement. To this aim, we intend to investigate a mutual exchange of ideas between CEGAR and our approach, and to integrate abstract interpretation repair into our framework.

Appendix A Proofs and Supplementary Material

1.1 A.1 Extensional Soundness (Theorem 2)

Proof

(Proof of Theorem 2). First we remark that points (1) and (3) implies point (2):

$$\begin{aligned} \alpha (Q)&\le \alpha (\llbracket \textsf{r}\rrbracket P)&[\text {(1) and monotonocity of }\alpha ] \\&\le \llbracket \textsf{r}\rrbracket ^{A} \alpha (P)&[\text {soundness of }\llbracket \textsf{r}\rrbracket ^{A}] \\&= \alpha (Q)&[\text {(3)}] \end{aligned}$$

So all the lines are equal, in particular $\alpha (Q) = \alpha (\llbracket \textsf{r}\rrbracket P)$. The proof is then by induction on the derivation tree of $\vdash _{A}[P]~\textsf{r}~[Q]$, but we only have to prove (1) and (3) because of the observation above. We only include one inductive case as an example, others are standard.

$(\textsf{seq})$: (1) $Q \le \llbracket \textsf{r}_2\rrbracket R \le \llbracket \textsf{r}_2\rrbracket (\llbracket \textsf{r}_1\rrbracket P) = \llbracket \textsf{r}1; \textsf{r}_2\rrbracket P$, where the inequalities follow from inductive hypotheses and monotonicity of $\llbracket \textsf{r}_2\rrbracket$.

(3) We recall that $\llbracket \textsf{r}_1; \textsf{r}_2\rrbracket ^{A} \le \llbracket \textsf{r}_2\rrbracket ^{A} \llbracket \textsf{r}_1\rrbracket ^{A}$.

$$\begin{aligned} \alpha (Q)&\le \alpha (\llbracket \textsf{r}_1; \textsf{r}_2\rrbracket P)&[\text {(1) and monotonicity of }\alpha ] \\&\le \llbracket \textsf{r}_1; \textsf{r}_2\rrbracket ^{A} \alpha (P)&[\text {soundness of }\llbracket \textsf{r}\rrbracket ^{A}] \\&\le \llbracket \textsf{r}_2\rrbracket ^{A} \llbracket \textsf{r}_1\rrbracket ^{A} \alpha (P)&[\text {recalled above}] \\&= \llbracket \textsf{r}_2\rrbracket ^{A} \alpha (R)&[\text {inductive hp}] \\&= \alpha (Q)&[\text {inductive hp}] \end{aligned}$$

So all the lines are equal, in particular $\llbracket \textsf{r}_1; \textsf{r}_2\rrbracket ^{A} \alpha (P) = \alpha (Q)$.

   $\square$

1.2 A.2 Soundness and Completeness of $(\mathsf {refine\hbox {-}ext})$

This technical lemma is used in the following proofs.

Lemma 1

If $A' \preceq A$ then $A = A A' = A' A$

Proof

Fix a concrete element $c \in C$. Since $A' \preceq A$ we have $c \le A'(c) \le A(c)$. Applying A, by monotonicity we get $A(c) \le AA'(c) \le AA(c) = A(c)$, where the last equality is idempotency of A. This means $A = AA'$. Now consider $A' A(c)$. Since A is a closure operator $A' A(c) \le A (A' A(c))$. But we just showed $A A' (A(c)) = A (A(c)) = A(c)$. Lastly, since $A'$ is a closure operator too, $A(c) \le A' A(c)$. Hence $A(c) \le A' A(c) \le A(c)$, so $A(c) = A' A(c)$.

We point out that, by injectivity of $\gamma$, this also means $\alpha \gamma ' \alpha ' = \alpha$.

Proof

(Proof of Theorem 3). We recall that the intuitive premise $A \llbracket \textsf{r}\rrbracket ^{A'} A(P) = A(Q)$ of the rule formally is $\alpha \gamma ' \llbracket \textsf{r}\rrbracket ^{A'} \alpha ' A(P) = \alpha (Q)$. Since the proof of Theorem 2 is by induction, we can extend it just proving the inductive case for $(\mathsf {refine\hbox {-}ext})$.

(1) It’s the same as point (1) of extensional soundness (Theorem 2) applied to $\vdash _{A'}[P]~\textsf{r}~[Q]$, since this conclusion does not depend on the abstract domain.

(2-3)

$$\begin{aligned} \alpha (Q)&\le \alpha (\llbracket \textsf{r}\rrbracket P)&[\text {(1) and monotonicity of }\alpha ] \\&\le \llbracket \textsf{r}\rrbracket ^{A} \alpha (P)&[\text {soundness of } \llbracket \textsf{r}\rrbracket ^{A}] \\&= \alpha \llbracket \textsf{r}\rrbracket \gamma \alpha (P)&[\text {definition}] \\&= \alpha \gamma ' \alpha ' \llbracket \textsf{r}\rrbracket \gamma ' \alpha ' \gamma \alpha (P)&[\text {Lemma}~1] \\&= \alpha \gamma ' \llbracket \textsf{r}\rrbracket ^{A'} \alpha ' A(P)&[\text {definition}] \\&= \alpha (Q)&[\text {hypothesis of the rule}] \end{aligned}$$

Hence all the lines are equal; in particular $\alpha (\llbracket r\rrbracket P) =\alpha (Q)$ and $\llbracket r\rrbracket ^{A} \alpha (P) = \alpha (Q)$.    $\square$

Proof

(Proof of Theorem 4). First, the hypotheses of the theorem implies $\mathbb {C}^{A}_{P}(\llbracket \textsf{r}\rrbracket )$:

$$\begin{aligned} \llbracket \textsf{r}\rrbracket ^A \alpha (P)&= \alpha (Q)&[\text {hp of the theorem}]\\&\le \alpha (\llbracket \textsf{r}\rrbracket P)&[\text {monotonicity of } \alpha \text { and hp of the theorem } Q \le \llbracket \textsf{r}\rrbracket P]\\&\le \llbracket \textsf{r}\rrbracket ^A \alpha (P)&[\text {soundness of } \llbracket \textsf{r}\rrbracket ^{A}] \end{aligned}$$

Hence $\alpha (\llbracket \textsf{r}\rrbracket P) = \llbracket \textsf{r}\rrbracket ^A \alpha (P) = \alpha \llbracket \textsf{r}\rrbracket \gamma \alpha (P)$, that is local completeness. Moreover $\alpha (Q) = \alpha (\llbracket \textsf{r}\rrbracket P)$.

Now consider a triple $P, \textsf{r}, Q$ satisfying the hypotheses. If $Q < \llbracket \textsf{r}\rrbracket P$, using $(\textsf{relax})$ we get

But the first condition is trivial, and the third one is made of $Q \le \llbracket r\rrbracket P$ (the hypothesis) and $\llbracket r\rrbracket P \le A(Q)$, that follows because $\alpha (\llbracket r\rrbracket P) = \alpha (Q)$ (shown above) and in a GC this implies $\llbracket r\rrbracket P \le \gamma \alpha (Q) = A(Q)$. Hence without loss of generality we can assume $Q = \llbracket \textsf{r}\rrbracket P$.

Now we want to apply $(\mathsf {refine\hbox {-}ext})$ to move to the concrete domain C. Clearly $C \preceq A$. The last hypothesis of the rule can be readily verified recalling that $\llbracket r\rrbracket ^{C} = \llbracket r\rrbracket$ and $\alpha ' = \gamma ' = \text {id}_C$:

$$\begin{aligned} \alpha \llbracket r\rrbracket ^{C} A(P)&= \alpha \llbracket r\rrbracket A(P) \\&= \llbracket r\rrbracket ^{A} \alpha (P) \\&= \alpha (\llbracket \textsf{r}\rrbracket P) \end{aligned}$$

so if we can show $\vdash _{C}[P]~\textsf{r}~[\llbracket \textsf{r}\rrbracket P]$ we can apply $(\mathsf {refine\hbox {-}ext})$ to prove the triple $\vdash _{A}[P]~\textsf{r}~[\llbracket \textsf{r}\rrbracket P]$:

Lastly, we resort to logical completeness of $\text {LCL}_A$ (cf. [2], Th 5.11) to say that the triple $\vdash _{C}[P]~\textsf{r}~[\llbracket \textsf{r}\rrbracket P]$ is provable. The hypothesis of that theorem are satisfied: all expressions are globally complete in the concrete domain C, $\llbracket r\rrbracket P \le \llbracket r\rrbracket P$ and $\llbracket r\rrbracket ^{\sharp }_C \text {id}_C(P) = \llbracket \textsf{r}\rrbracket P = \text {id}_C(\llbracket r\rrbracket P)$, where we used $\alpha ' = \text {id}_C$ and $\llbracket r\rrbracket ^{\sharp }_C = \llbracket r\rrbracket$.    $\square$

1.3 A.3 Derived Refinement Rules

Proof

(Proof of Proposition 1). We show that the hypotheses of $(\mathsf {refine\hbox {-}int})$ implies those of $(\mathsf {refine\hbox {-}ext})$. This means than whenever we can apply the former we could also apply the latter, that in turn means Theorem 3 ensures extensional soundness.

The first two hypotheses $\vdash _{A'}[P]~\textsf{r}~[Q]$ and $A' \preceq A$ are shared among the two rules, so we only have to show $\alpha \gamma ' \llbracket \textsf{r}\rrbracket ^{A'} \alpha ' A(P) = \alpha (Q)$. We recall that $\vdash _{A'}[P]~\textsf{r}~[Q]$ implies $Q \le \llbracket \textsf{r}\rrbracket P$ by extensional soundness.

$$\begin{aligned} \alpha (Q)&\le \alpha (\llbracket \textsf{r}\rrbracket P )&[Q \le \llbracket \textsf{r}\rrbracket P \text { and monotonicity of }\alpha ] \\&\le \llbracket \textsf{r}\rrbracket ^{A} \alpha (P)&[\text {soundness of }\llbracket \textsf{r}\rrbracket ^{A}] \\&= \alpha \llbracket \textsf{r}\rrbracket A(P)&[\text {definition}] \\&= \alpha \gamma ' \alpha ' \llbracket \textsf{r}\rrbracket A' A(P)&[\text {Lemma}~1] \\&= \alpha \gamma ' \llbracket \textsf{r}\rrbracket ^{A'} \alpha ' A(P)&[\text {definition}] \\&\le \alpha \gamma ' \llbracket \textsf{r}\rrbracket ^{\sharp }_{A'} \alpha ' A(P)&[\llbracket \textsf{r}\rrbracket ^{A'} \le \llbracket \textsf{r}\rrbracket ^{\sharp }_{A'}] \\&= \alpha (Q)&[\text {Last hypothesis of the rule}] \end{aligned}$$

Hence all the lines are equal, and in particular $\alpha \gamma ' \llbracket \textsf{r}\rrbracket ^{A'} \alpha ' A(P) = \alpha (Q)$.    $\square$

Proof

(Proof of Theorem 5). The proof is the same as that of Theorem 4, the only difference being that to apply $(\mathsf {refine\hbox {-}int})$ we need to show $A \llbracket \textsf{r}\rrbracket ^{\sharp }_{C} A(P) = A(\llbracket \textsf{r}\rrbracket P)$ instead of $A \llbracket \textsf{r}\rrbracket ^{C} A(P) = A(\llbracket \textsf{r}\rrbracket P)$. However, since in the concrete domain $\llbracket \textsf{r}\rrbracket ^{\sharp }_{C} = \llbracket \textsf{r}\rrbracket ^{C} = \llbracket \textsf{r}\rrbracket$ the proof still holds.    $\square$

Proof

(Proof of Proposition 2). As in the proof or Proposition 1 above, we show that the hypotheses of $(\mathsf {refine\hbox {-}pre})$ implies those of $(\mathsf {refine\hbox {-}ext})$.

The first two hypotheses $\vdash _{A'}[P]~\textsf{r}~[Q]$ and $A' \preceq A$ are shared among the two rules, so we only have to show $\alpha \gamma ' \llbracket \textsf{r}\rrbracket ^{A'} \alpha ' A(P) = \alpha (Q)$. We recall that $\vdash _{A'}[P]~\textsf{r}~[Q]$ implies by extensional soundness (1) $Q \le \llbracket \textsf{r}\rrbracket P$ and (3) $\llbracket \textsf{r}\rrbracket ^{A'} \alpha '(P) = \alpha '(Q)$.

$$\begin{aligned} \alpha (Q)&\le \alpha (\llbracket \textsf{r}\rrbracket P )&[Q \le \llbracket \textsf{r}\rrbracket P \text { and monotonicity of }\alpha ] \\&\le \llbracket \textsf{r}\rrbracket ^{A} \alpha (P)&[\text {soundness of }\llbracket \textsf{r}\rrbracket ^{A}] \\&= \alpha \llbracket \textsf{r}\rrbracket A(P)&[\text {definition}] \\&= \alpha \llbracket \textsf{r}\rrbracket A'(P)&[\text {hp of the rule}] \\&= \alpha \gamma ' \alpha ' \llbracket \textsf{r}\rrbracket A'(P)&[\text {Lemma}~1] \\&= \alpha \gamma ' \llbracket \textsf{r}\rrbracket ^{A'} \alpha '(P)&[\text {definition}] \\&= \alpha \gamma ' \alpha '(Q)&[\text {extensional soundness (3)}] \\&= \alpha (Q)&[\text {Lemma}~1] \end{aligned}$$

Hence all the lines are equal, and in particular $\alpha \gamma ' \llbracket \textsf{r}\rrbracket ^{A'} \alpha ' A(P) = \alpha (Q)$.    $\square$

Fig. 6.

Derivation of $\vdash _{\textsf{Oct}}[R]~\textsf{r}_2~[Q]$ for Example 5.

Details about Example  5. The full derivation of the triple $\vdash _{\textsf{Oct}}[R]~\textsf{r}_2~[Q]$ for Example 5 is shown in Fig. 6, rotated and split to fit the page. The command $\textsf{r}_i = \texttt {(x > 1)?; y := y - 1; x := x - 1}$ is iterated with the Kleene star and we let $R_2 = (\texttt {y} \in \{1; 2; 100\} \wedge \texttt {x} = \texttt {y})$. We also used the logical implication $R_2 \implies (\texttt {y} \in \{1; 99\} \wedge \texttt {x} = \texttt {y})$, both explicitly and implicitly in the equivalence $R_2 \vee (\texttt {y} \in \{1; 99\} \wedge \texttt {x} = \texttt {y}) = R_2$.

Example 8

(Supplement to Example 6). Consider the concrete domain $C = \mathcal {P}(\mathbb {Z})$ of integers, the abstract domain $\textsf{Int}$ of intervals, the concrete points $P = \{ -1, 1 \}$ and $Q = \{ 1 \}$, commands $\textsf{r}_1 \triangleq$ x != 0?, $\textsf{r}_2 \triangleq$ x>= 0? and $\textsf{r}\triangleq \textsf{r}_1; \textsf{r}_2$. Let $f_1 = \llbracket \textsf{r}_1\rrbracket$, $f_2 = \llbracket \textsf{r}_2\rrbracket$ and $f = \llbracket \textsf{r}\rrbracket = f_2 \circ f_1$. Observe that in the concrete semantics $f_1(P) = P$ and $f(P) = f_2(P) = \{ 1 \}$. Consider $\text {LCL}_A$ extended with $(\mathsf {refine\hbox {-}pre})$, and let us show that we cannot prove $\vdash _{\textsf{Int}}[P]~\textsf{r}~[Q]$. Inspecting the logic, we can only apply three rules to prove this triple: $(\textsf{relax})$, $(\mathsf {refine\hbox {-}pre})$ or $(\textsf{seq})$. To apply rule $(\textsf{relax})$ we would need either an under-approximation $P'$ of P with the same abstraction, that does not exist, or an over-approximation of Q, that would be unsound since $Q = f(P)$. Hence we cannot apply $(\textsf{relax})$. Suppose to apply $(\mathsf {refine\hbox {-}pre})$: any $A'$ used in the rule should satisfy $A' \preceq \textsf{Int}$ and $A'(P) = \textsf{Int}(P)$; as we remarked in Example 6 this means that $P' \subset P$ implies $A'(P') \subset A'(P)$. Again this means we cannot apply $(\textsf{relax})$ even after the domain refinement. The only rule that can be applied is then $(\textsf{seq})$: to do that, we must prove two triples $\vdash _{A'}[P]~\textsf{r}_1~[R]$ and $\vdash _{A'}[R]~\textsf{r}_2~[Q]$. Irrespective of how we prove the first triple, by soundness (Theorem 2) we have $R \subseteq f_1(P) = P$ and $A'(R) = A'(f_1(P)) = A'(P)$, so again $R = P$. Now we should prove a triple $\vdash _{A'}[P]~\textsf{r}_2~[Q]$, but this is impossible since by soundness this would imply local completeness of $\llbracket \textsf{r}_2\rrbracket = f_2$ on P in $A'$, that does not hold:

$$\begin{aligned} A' f_2(P)&= A'(\{ 1 \}) \subseteq \textsf{Int}(\{ 1 \}) = \{ 1 \} \\ A' f_2 A'(P)&\supseteq f_2 A'(P) = f_2(\textsf{Int}(P)) = \{ 0, 1 \} \end{aligned}$$

Fig. 7.

Derivation of $\vdash _{\textsf{Int}}[P]~\textsf{r}~[Q]$ for Example 8.

Observe that, if we add $(\mathsf {refine\hbox {-}int})$ to the proof system, we can use it to change the domain to one where we can express P (for instance, the concrete domain $\mathcal {P}(\mathbb {Z})$ or the refinement $\textsf{Int}\cup \{ P \}$) to prove the triple applying $(\textsf{seq})$ and then $(\textsf{transfer})$ on both subtrees, as shown in Fig. 7.    $\square$