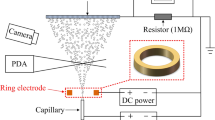
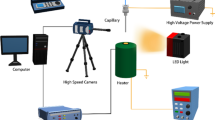
Abstract
When liquid desiccant systems are employed to dehumidify air electrospraying technique helps to increase the surface area of the liquid. Multiplexing of the jets by introducing several emitters for increased efficiency is commendable but, there is a tendency of the jets to cross talk with each other due to electrical shielding. Cross talking of jets will result in the failure of the jets to break properly into droplets for effective dehumidification. This piece of work analyzed the conditions for electrical shielding among jets which results in efficient electrospray. To evaluate how cross talking affects multiple emitter nozzles, the mathematical model was built by superimposing the electric potentials of one emitter in an array of emitters. A Computational Fluid Dynamics simulation model was developed to investigate the conditions for electrical shielding among jets during electrospray process with glycerol as the working substance. In flow modelling, Ansys Fluent with Volume of Fluid and the Taylor Dielectric model were involved. The flow rate that guarantees stability in the electrospray was determined together with the optimum voltage resulting in a spray current which reduces electrical shielding. An analysis on the electrical conductivity of the liquid to ensure stability and efficiency in electrospray was done. The pressure contours of the nozzle were determined together with velocity of the desiccant against density. Emitter spacing, applied voltage, flow rate and the electrical conductivity plays a pivotal role on the prevention of cross talking of jets during the electrospraying process.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
If air is to be conditioned, control is given to sensible load as well as latent load. The use of vapour compression based refrigeration systems to condition air has been condemned of their significant reliance on electricity [1]. This is so because the sensible and latent heat load are controlled by cooling air below due point which at times may require reheating to achieve required temperature which is an energy intensive effort, [2, 3] Evaporative cooling is an energy efficient technology which can be used in place of conventional vapour compression systems [4,5,6].
Nevertheless, in humid climates the use of evaporative cooling based air conditioning systems is ineffective due to high levels of humidity in the unprocessed air. The use of desiccant dehumidification in handling the latent load in such air is commendable, [7,8,9,10]. Both solid and liquid desiccants can be employed, however, the use of liquid desiccants is advantageous over that of solid desiccants, [11]. When using liquid desiccant to dehumidify, water removal rate is mainly determined by the size of the contact surface [3]. In order to ensure an increased surface contact between the desiccant and the air to be processed, droplet diameter reduction is fundamental. Reducing the diameter of the droplet drastically increases the efficiency of the dehumidification process [12].
Among other droplet reducing mechanism, research shows that the electrospray process is a capable, energy efficient process which produces a fine spray, [3, 12,13,14,15,16]. The meniscus is exposed to a heavy electric field so that the liquid desiccant is converted into a cone-jet by the electrostatic force, [17]. When there is a balance between the external electric forces and the surface tension forces, the electrically charged droplet becomes unstable resulting in the emission of a liquid jet, [18]. The process allows blending of electrical, rheological and geometric properties of the liquid jet as it flows from the electrically-charged orifice, [14]. This process is studied in a discipline called electro-hydrodynamics, (EHD [19].
The electrospraying method has found use in various areas for the creation of monodisperse sprays of very fine drops in industry [20, 21]. It is possible to use a single emitter or to have a number of emitters during the process, [17]. In the event that a jet is produced by a single emitter, the solo emitter offers advantages of elimination of cross talking of jets, nonetheless, the solo emitter have low flow rates thus its use compromises the electrospray process and the resultant dehumidification, [3, 12, 21].
If multiplexing is allowed by running several emitters simultaneously at high operating voltages, there will be an increase in dehumidification process efficiency because of the increased surface area, [12, 17]. Nevertheless, space charge becomes significant attributable to the cloud of charged droplets in the multiplexed emitters, [21]. Electrical shielding will then occur causing cross talking of jets which is basically the obstruction of the electric field neighboring the surface of some conical menisci hindering proper formation of the required Taylor cone, [22]. This electrical shielding results in reduced stability and effectiveness of the overall electrospray process, [23]. Cross talking of jets will result in the failure of the jets to break properly into droplets for effective dehumidification. The interaction problem between the jets in multiplexed spray presents a need to analyze this shielding effect in liquid desiccant dehumidification process, [14, 18].
2 Theory
The configuration of emitters in a multi-electrospray set up can be as presented in Fig. 1 where there is a representation of a mono-hole system whose tip can be levelled or pointed, a double and a triple-hole emitter, [12].
Emitter configuration in multi-electrospray[12]
Several researches have been done to analyse the interaction problem in multiplexed jets during electrospray, [13, 21]. It has been found that the factors that affect jet behavior include the operating voltage, flow rate and emitter spacing in an array of emitter [12]. If one emitter is in operation and the distance between the emitters is reduced, more potential is needed to produce cone jet which is stable because of shielding effect [13]. The required potential decreases at a very close spacing. When an electrical potential exists, the forming of a cone-jet which can decompose into equally-sized droplets is fundamental [12]. Several configurations like coaxial and parallel flows can be produced from the electrospray.
Flow rate is an important aspect to guarantee stability and efficiency of the electrospray. When the flow rate is approximately 6 mL/min or more, 2D, rotating 2D, and 3D spray forms will be observed. At low flow rates of ~ 6 mL/min or lower, there is no change in the discharge current with respect to flow rate across the liquids [21]. Flow rate in stable electrospray systems is always small. The applied voltage does influence the magnitude of the flow rate through the jet of the electrospray due to the variation in cone surface area with applied voltage [18].
Electrical forces mainly controls the velocity of droplets in wide range of dispersed liquid conductivity [14]. The diameter of the liquid is also determined by the electrical conductivity, the higher the liquid electrical conductivity the smaller the diameter [22]. More so, applied voltages strongly affects the diameter of droplet, and droplet diameter decreases with an increase in applied voltage which is of very high electric fields of several kilovolts, up to 30 kV. In a multiplex set up, spacing of emitters has a pivotal part in jet formation as there tends to be interference.
3 Mathematical Model
Figure 2 shows progression of equipotential lines where there is single and multiple jetting.
a) Central emitter jetting and (b) Three emitters jetting [21].
Therefore, the potential at point A of the ith emitter, Vi, can be obtained as follows by using Eq. (1) and superposingthe electric potential values from every emitter:
where \(A_{J}\) is a fraction of the electric potential contributed by \(jth \) emitter,
\(V_{ij}\) is the potential at A of the \(ith \) emitter.
The maximum electric field can be represented as:
where
Then the final equation for the operating voltage becomes
From these equations we can obtain the quantitative result for onset voltage using the required local electric field strength, E0, but this solution is only valid when dij is larger than 2rc to avoid overlapping of capillaries.
4 Simulation Model
The CFD simulations in this piece of work were done with the commercially available software package, ANSYS Fluent v16. The liquid spray is taken as laminar flow with the solid capillary subjected to huge electric potential. Glycerol (C3H8O3) was used as the jetting liquid, with density = 1.261gcm−3, viscosity = 1.412 cP (at 25◦C), surface tension = 63.4 mN/m, electrical conductivity = 0.05 µS/cm, [3].
An axis-symmetric multi-hole nozzle geometry was created using Design modeler of Ansys Fluent. Designer modeler is a built in geometry and grid creation system with CAD functions to create and manipulate whole geometries with a subsequent meshing. For better accuracy and better visualization of flow behavior of the desiccant falling film during numerical modeling, grid points after meshing were fine near the nozzles since there will be larger electric potential gradients and be coarse for areas afar. This will ensure accuracy with minimal computational effort since coarseness decreases accuracy whilst fineness increases time. A Cartesian mesh was applied to achieve this.
After setting up the geometry, the solver settings were chosen in Ansys Fluent the EHD was combined with other modules to allow simultaneous simulation of different physical domains at the same time. A pressure based solver based on transient time and an absolute velocity formulation was used. The Eulerain approach of the two phases of volume of fluid were used in the multiphase model. The Eulerian method was adopted instead of the Lagrangian because it works well for flow in a continuous phase. The primary phase was set to air, while the secondary phases were set to glycerol. The material properties of all phases were set to values that have been established in literature. An implicit velocity fraction parameters with an enhanced near wall treatment was adopted. The standard and non-equilibrium wall functions of near wall treatment work with a coarse mesh and they don’t provide details about velocity whilst the enhanced wall treatment needs a fine mesh giving a velocity profile which is more accurate and well predicted even in the viscous and buffer layers.
Boundary conditions were then defined so as to solve equations discussed in previous sections. The inlet was considered as having a constant velocity back flow fraction of glycerine whilst outlets had glycerine jets produced. A velocity specification method was used which is normal to the boundary and after passing the zero-voltage plane at constant velocity. To ensure a no-slip shear condition, a stationary wall was assumed [15].
For the flow solution, the equations were then solved numerically giving a full representation of the flow using a PISO solver. A transient formulation was employed with hybridization to improve accuracy was used together with compressive volume fraction for fluid flow and free surface, [12, 14, 18]. Standard initialization was used with a variable time step method and a reference frame relative to the cell zone.
5 Results and Discussions
5.1 Mesh Sensitivity Test
Outcome of convergence study is as in Fig. 3 having jet radius as a function of minimum cell size, [15]. The size of the mesh was of 2 × 10–7 m. It can be deduced from Fig. 3 that the jet radius is independent of grid size when its size is less than 0.24μm in the center line and it is related to the 761462 total mesh numbers.
5.2 Electrostatic Atomization
The presence of an electric body force allowed the liquid to produce a conical shape termed as Taylor cone and a thin jet was produced from its apex. Formation of a stable Taylor cone is possible with flow rate in the range of 3–10 ml/hr. And a constant electrical conductivity of 0.04 K(S/cm). For a single emitter, the tapered emitter design resulted in an effective Taylor cone which promotes stable electrospray process whilst maintaining constant fluid velocity charge density jet radius and electric field, Fig. 4
From the simulations, it can be seen that the kinetic energy was increasing as the Taylor cone was generated. Increasing flow rate at a constant voltage resulted in an increase in Taylor cone size. An attempt to further increase voltage results in a decrease in droplet size, however, very high voltage could not enable jet formation as the jets became too thin, breaking up leading to the loss of stability and this is in agreement with the literature. From the simulation results, it showed that a thicker jet will be produced due to the larger cone.
Apart from the operating voltage and liquid flow rates, jet formation was seen to be affected by the distance between the nozzles. Repulsive forces were experienced when emitters are close to each other (that is 60 µm apart), this will result in the jets exerting a force that will separate the jets. The results from these simulations agree with the experimental results reported in literature [3].
Designing a wide range of emitters which are spaced help in preventing cross talking whilst maintaining electrospray efficiency. The dehumidification section must be working continuously without changing the frequency to ensure improved efficiency with it knowing when to start and stop.
6 Conclusions
Ansys fluent has aided to successfully model the electrical shielding effect among jets using 3 emitters to allow multiplexing. The emitter spacing, voltage, flowrate and liquid conductivity plays a pivotal role on the prevention of cross talking of jets during the electrospraying process. The model is essential in atomization of liquid desiccant for moisture removal in air for air conditioning purposes using evaporative cooling technology. Future work needs to look at the possibility of spray blockages at the menisci due to electrical shielding in multiplexed jets in electrospray and allow the dehumidification section must be working continuously without changing the frequency to ensure improved efficiency with it knowing when to start and stop.
References
Mariotti, M., Moro, L.: Indirect evaporative cooling combined with dehumidification in a MVHR system for radiant cooling. Energy Procedia 101(September), 448–455 (2016)
Rafique, M.M., Gandhidasan, P., Bahaidarah, H.M.S.: Liquid desiccant materials and dehumidi fi ers – A review. Renew. Sustain. Energy Rev. 56, 179–195 (2016)
Salazar, M.G., Jiménez, R.Z., Loscertales, I.G., Reyes, A.H.: Electrospray technique to produce fine sprays of desiccant liquids. Application to moisture removal from air. Energy Build. 162, 187–197 (2018)
Cao, G., Storås, M.C.A., Aganovic, A., Stenstad, L.I., Skogås, J.G.: Do surgeons and surgical facilities disturb the clean air distribution close to a surgical patient in an orthopedic operating room with laminar airflow? Am. J. Infect. Control 46(10), 1115–1122 (2018)
Tao, W., Yimo, L., Lin, L.: A novel 3D simulation model for investigating liquid desiccant dehumidi fi cation performance based on CFD technology. Appl. Energy 240, 486–498 (2019)
Pomianowski, M., Andersen, C.H., Heiselberg, P.: Technical potential of evaporative cooling in Danish and European condition. Energy Procedia 78, 2421–2426 (2015)
Arandara, K.P., Attalage, R.A., Jayasinghe, M.T.R.: Thermal comfort with evaporative cooling. Int. Conf. Sustain. Built Environ. Kandy (2014)
Dai, Y.J., Wang, R.Z., Zhang, H.F., Yu, J.D.: Use of liquid desiccant cooling to improve the performance of vapor compression air conditioning. Appl. Therm. Eng. 21(12), 1185–1202 (2001)
Jain, S., Dhar, P.L., Kaushik, S.C.: Evaluation of liquid dessicant based evaporative cooling cycles for typical hot and humid climates. Heat Recovery Syst. CHP 14(6), 621–632 (1994)
Fakhrabadi, F., Kowsary, F.: Optimal design of a hybrid liquid desiccant-regenerative evaporative air conditioner. Energy Build. 133, 141–154 (2016)
Rafique, M.M., Gandhidasan, P., Rehman, S., Al-Hadhrami, L.M.: A review on desiccant based evaporative cooling systems. Renew. Sustain. Energy Rev. 45, 145–159 (2015)
Wu, X., Oleschuk, R.D., Cann, N.M.: Characterization of microstructured fibre emitters : in pursuit of improved nano electrospray ionization performance. Analyst 137(18), 4150–4161 (2012)
Jaworek, A., Sobczyk, A., Krupa, A., Lackowski, M., Czech, T.: Electrostatic deposition of nanothin films on metal substrate. Bull. Polish Acad. Sci.: Tech. Sci. 57(1), 63–70 (2009)
Najjaran, A., Ebrahimi, R., Rahmanpoor, M., Najjaran, A.: Numerical simulation of electrohydrodynamic(EHD) atomization in the cone-jet mode. Appl. Mech. Mater. 327(June), 180–185 (2013)
Rahmanpour, M., Ebrahimi, R., Pourrajabian, A.: Numerical simulation of two-phase electrohydrodynamic of stable Taylor cone–jet using a volume-of-fluid approach. J. Braz. Soc. Mech. Sci. Eng. 39(11), 4443–4453 (2017). https://doi.org/10.1007/s40430-017-0832-7
Borra, J.: Review on water electro-sprays and applications of charged drops with focus on the corona-assisted cone-jet mode for High Efficiency Air Filtration by wet electro-scrubbing of aerosols To cite this version : HAL Id : hal-02415646 (2019)
Parhizkar, M., et al.: Performance of novel high throughput multi electrospray systems for forming of polymeric micro/nanoparticles. Mater. Des. 126(April), 73–84 (2017)
Rahmanpour, M., Ebrahimi, R.: numerical simulation of electrohydrodynamic spray with stable Taylor cone-jet. Heat Mass Transf. 52(8), 1595–1603 (2015)
Pozniak, B.P., Cole, R.B.: Perspective on electrospray ionization and its relation to electrochemistry. J. Am. Soc. Mass Spectr. 26(3), 369–385 (2015)
Thompson, J.W., Eschelbach, J.W., Wilburn, R.T., Jorgenson, J. W.: Investigation of Electrospray Ionization Using a Three-Dimensional Electrospray (2005)
Quang, B., Si, T., Byun, D., Lee, S.: “Experimental and theoretical study of a cone-jet for an electrospray microthruster considering the interference effect in an array of nozzles. J. Aerosol Sci. 38(9), 924–934 (2007)
Bocanegra, R., Galán, D., Márquez, M., Loscertales, I.G., Barrero, A.: Multiple electrosprays emitted from an array of holes. J. Aerosol Sci. 36(12), 1387–1399 (2005)
Wang, J., Jansen, J.A., Yang, F.: Electrospraying : possibilities and challenges of engineering carriers for biomedical applications — a mini review. Front. Chem. 7, 1–9 (2019)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this paper
Cite this paper
Mutenhabundo, W., Mushiri, T., Gutu, T., Zvandasara, P. (2023). Liquid Desiccant Dehumidification Systems: Jet Cross-Talking Effect in Multi-electrosprays. In: Kohl, H., Seliger, G., Dietrich, F. (eds) Manufacturing Driving Circular Economy. GCSM 2022. Lecture Notes in Mechanical Engineering. Springer, Cham. https://doi.org/10.1007/978-3-031-28839-5_29
Download citation
DOI: https://doi.org/10.1007/978-3-031-28839-5_29
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-28838-8
Online ISBN: 978-3-031-28839-5
eBook Packages: EngineeringEngineering (R0)