Analysis of Chamber Data

Abstract

In this chapter, we focus on aspects of analysis of typical simulation chamber experiments and recommend best practices in term of data analysis of simulation chamber results relevant for both gas phase and particulate phase atmospheric chemistry. The first two sections look at common gas-phase measurements of relative rates and product yields. The simple yield expressions are extended to account for product removal. In the next two sections, we examine aspects of particulate phase chemistry looking firstly at secondary organic aerosol (SOA) yields including correction for wall losses, and secondly at new particle formation using a variety of methods. Simulations of VOC oxidation processes are important components of chamber work and one wants to present methods that lead to fundamental chemistry and not to specific aspects of the chamber that the experiment was carried out in. We investigate how one can analyse the results of a simulation experiment on a well-characterized chemical system (ethene oxidation) to determine the chamber-specific corrections. Finally, we look at methods of analysing photocatalysis experiments, some with a particular focus on NO_x reduction by TiO₂-doped surfaces. In such systems, overall reactivity is controlled by both chemical processes and transport. Chambers can provide useful practical information, but care needs to be taken in extrapolating results to other conditions. The wider impact of surfaces on photosmog formation is also considered.

7.1 Introduction

Previous chapters have examined various aspects of chamber characterization, preparation, details on how to introduce reagents (stable species, radicals, particulates) and carry out some concentration measurements. In this chapter, we focus on aspects of analysis of typical experiments.

Sections 7.2 and 7.3 focus on the simplest kinds of gas-phase measurements looking at how one conducts a relative rate experiment to determine rate coefficients (Sect. 7.2) and on making gas-phase yield measurements (Sect. 7.3). Yield measurements can be complex if the target product also reacts on a similar timescale as discussed in Sect. 7.3.3.

Sections 7.4 and 7.5 examine aspects of particulate phase chemistry. Section 7.4 focuses on secondary organic aerosol (SOA) yields including correction for wall loss for both SMPS and AMS measurements. Section 7.5 examines new particle formation using a variety of methods.

Simulations of VOC oxidation processes are an important component of chamber work and one wants to present results that reflect the fundamental chemistry and not specific aspects of the chamber that the experiment was carried out in. Section 7.6 addresses how one can analyse the results of a simulation experiment on a well-characterized chemical system (ethene oxidation) to determine the chamber-specific corrections.

Finally, in Sect. 7.7, we examine some studies on photocatalysis. Section 7.7.2 presents protocols for studying photocatalysis, with a particular focus on NO_x reduction by TiO₂-doped surfaces, which could be applied to most chambers and additionally considers some more applied applications that benefit from the accessibility of large chambers such as EUPHORE. The wider impact of surfaces on photosmog formation is considered in Sect. 7.7.3 where a discussion on how to incorporate additional reactions into studies on ethene and propene photo-oxidation is presented.

7.2 Relative Rate Measurements in a Chamber

7.2.1 Introduction

Relative Rate (RR) determinations of rate coefficients are a frequent activity in chambers. The measurements may be made to determine a novel rate coefficient or as a check on the radicals or oxidants present in a chamber. For example, in ozonolysis studies, radical scavengers (Malkin et al. 2010) are often introduced to remove OH; plotting the decay of two alkenes and checking that the ratio of alkene removal is consistent with the literature ratio of rate coefficients is a good test that radical scavenging is effective and that the system is behaving as it should.

The RR method is based on the following analysis of the decays of the test substrate, SH and a reference compound, RH, with a known rate coefficient, where X represents the reactive species, e.g. OH, Cl, NO₃ or O₃.

$$\begin{gathered} {\text{X}}\, + \,{\text{RH}}\, \to \,{\text{HX}}\, + \,{\text{R}} \hfill \\ {\text{X}}\, + \,{\text{SH}}\, \to \,{\text{HX}}\, + \,{\text{S}} \hfill \\ ln\left( {\frac{{\left[ {{\text{SH}}} \right]_{0} }}{{\left[ {{\text{SH}}} \right]_{t} }}} \right) = \frac{{k_{SH} }}{{k_{RH} }}ln\left( {\frac{{\left[ {{\text{RH}}} \right]_{0} }}{{\left[ {{\text{RH}}} \right]_{t} }}} \right) \hfill \\ \end{gathered}$$

(E7.2.1.1)

Therefore, a plot of $ln\left(\frac{{[{\text{SH}}]}_{0}}{{[{\text{SH}}]}_{t}}\right)$ versus $ln\left(\frac{{[\mathrm{RH}]}_{0}}{{[\mathrm{RH}]}_{t}}\right)$ should yield a straight line plot with gradient $\frac{{k}_{SH}}{{k}_{RH}}$ as shown in Fig. 7.1. Because the analysis involves a ratio of concentrations, we do not actually need the absolute concentrations, but rather something that is proportional to concentration such as GC area or FTIR peak height.

Fig. 7.1

Example of a relative rate plot for the reaction of OH with glycolaldehyde using diethyl ether as a reference compound (Hutchinson, M. MSc University of Leeds 2022)

RR measurements are subject to errors, as discussed below, but usefully these errors are different from those involved in a real-time flash photolysis or discharge flow experiment (Seakins 2007) and therefore one can have confidence in the accuracy of a rate coefficient if there is good agreement between RR and real-time measurements.

7.2.2 Procedures

• (1) Choice of Reference Compounds—The reference compound should have a similar rate coefficient to that predicted (e.g. via structure–activity relationships), (Atkinson 1987) otherwise the ratio measurements will be imprecise if one reagent has hardly reacted while the other has almost disappeared. The reference rate coefficient should be well defined and ideally have been reviewed in an evaluation (e.g. IUPAC Kinetics Evaluation). Databases such as EUROCHAMP and NIST are other sources of reference information if evaluated data are not available. Avoid using rate coefficients that are themselves derived from relative rate measurements. A major source of error in RR measurements is if a reagent is removed by another species, so in a study of OH reacting with a saturated species, where OH is generated from CH₃ONO photolysis (Atkinson et al. 1981; Jenkin et al. 1988) there is a potential for O₃ formation, so using an alkene as the reference compound (hence removal by OH and O₃) would not be a good choice. Use a photolysis database (e.g. Mainz Photolysis Database) to ensure that neither the reference nor substrate is predicted to be lost by photolysis (this should always be checked too). It is good practice to use more than one reference compound.

• (2) Experimental method

  • Introduce RH and SH into the chamber to test for wall-loss rates (Chap. 4). Leave for a reasonable period of time, (certainly much longer than the mixing time) sufficient to ensure an accurate estimate of the wall loss. Checks on wall-loss rates should be done on a regular basis as the conditions of the walls may change and wall-loss rates can vary with temperature and pressure. Turn on the lights to check for substrate photolysis, n.b. this could be due to generation of radicals from the walls. This can be checked by having a substrate that cannot be photolysed, but would be lost by radical chemistry. Turn off the lights.

  • Introduce the radical precursor to the mix (Chap. 4) to check for any reactions between RH and SH and the substrate. Obviously, this step is not possible for O₃ reactions.

  • Turn on the lights to generate the radical species. Make sufficient measurements to ensure a precise relative rate plot. A typical experiment might involve measurements over one half-life, but the exact time will depend on your measurement method. Measurements with significant reagent consumption will be less accurate because one is measuring small concentrations and there may be a higher potential for secondary chemistry. Further additions of radical precursors may be required. Once the lamps have been turned off, it is often useful to check the wall-loss rate again and use the average value determined from pre- and post-photolysis measurements.

  • Correct the reagent concentrations for wall-loss rate (or photolysis loss if applicable).

• (3) Data Analysis—plotting your data according to equation (E7.2.1.1) should lead to a straight line of the form y = mx. Check that the line does indeed pass through the origin. A non-zero intercept could suggest measurement problems and curvature of the plot could be due to the production of additional radical species or that measurements are being compromised (e.g. the reagent FTIR absorption overlaps with a product peak). Measurements using a range of methods (could simply be using several absorptions in an FTIR spectrum to having completely different techniques, e.g. FTIR and PTR-MS) and different reference compounds can identify problems.

When determining the gradient and intercept of the line it is important to weigh the data correctly, i.e. to use a regression analysis that includes errors in both x and y (Brauers and Finlayson-Pitts 1997).

• (D) Reporting Rate Coefficients—always ensure that you report the ratio $\frac{{k}_{SH}}{{k}_{RH}}$, this is your experimental measurements and needs to be available in the literature so that k_SH can be re-calculated if there is a revised recommendation or determination of k_RH. The reported error in the gradient is primarily going to be statistical from the regression analysis, but the reported error in the absolute measurement must include error in the reference compound.

7.3 Product Yield Measurements

7.3.1 Introduction

Product yields are a common target in simulation chamber measurements. The product yield is defined as

$$\frac{\text{amount of product, P, produced}}{\text{amount of reagent, R, consumed}}=\frac{\Delta P}{\left|\Delta R\right|}=Y$$

(E7.3.1.1)

Yields can give specific information about one step in a process or the overall yield of a particular product in a process. An example of the first process can be found in the reaction of OH with n-butanol:

$${\text{OH}}\, + \,{\text{CH}}_{{3}} {\text{CH}}_{{2}} {\text{CH}}_{{2}} {\text{CH}}_{{2}} {\text{OH}}\, \to \,{\text{H}}_{{2}} {\text{O}}\, + \,{\text{products}}$$

The abstraction could take place at the α, β, γ, δ or OH sites. Abstraction at the α site leads to the formation of CH₃CH₂CH₂CHOH which reacts with O₂ to give n-butanal. This is the only route to n-butanal formation and therefore n-butanal yield gives the branching ratio (Seakins 2007) for abstraction at the α position. As mentioned, overall yields are also important, for example, while most primary hydrocarbon emissions cannot be detected by satellite measurements, the oxidation products formaldehyde and glyoxal can be detected in the UV. As the yields of formaldehyde and glyoxal are different for different categories of VOC, satellite measurements of the ratio of glyoxal to formaldehyde, RGF, can give information on the primary VOC if the individual RGF is known (Wittrock et al. 2006).

The principles of yield measurements are therefore straightforward, a plot of the concentration (or something proportional to concentration) of product (Δ[P]) versus concentration of reagent removed ([R]₀ – [R]_t) should be a straight line with gradient, Y as shown in Fig. 7.2. A good example from Cl-initiated oxidation of n-butanol can be found in Hurley et al. (2009).

Fig. 7.2

Typical yield plot (formation of products is noted Δ[P] and concentration of reagent removed ([R]₀ – [R]_t)

However, despite this apparent simplicity, operators should be aware of a number of issues that can affect yield measurements:

• What is the fraction of reagent consumption that occurs via the target channel?

• Accurate measurement of [reagent] and/or [product].

• Consumption of product.

These issues are addressed in the protocol below.

7.3.2 Procedure

• (1) Identification of target production pathway—an example system might be looking at yields from a photolysis process. The reagent may be lost via wall uptake/dilution or via radical loss processes. To deal with wall loss, carry out measurements with just the reagent present and no lights to quantify this non-reactive reagent removal process. The overall concentration of removal will need to be corrected for this process. To avoid complications from removal via radical reactions, then a suitable radical scavenger needs to be present.

If the target process is a radical removal, then carry out tests for photolysis as described in the relative rate protocol. If more than one radical is generated, then it may be difficult to selectively remove radicals, however, it may be that radical concentrations can be measured (or calculated) and if the rate coefficients are known, then the fraction of reagent removed by the target radical can be determined.

• (B) Once background checks have been completed the relevant experiment can begin. As with other chamber experiments, selective and specific measurement is required to generate accurate results. As the reaction proceeds, a range of products will be produced and these can interfere (e.g. peak overlap in FTIR or GC measurements, isobaric peaks for MS measurements). Care should be taken to ensure that the calculated yields are independent of the method of measurement. If you are limited to a single method of analysis, make sure that appropriate checks are carried out to test for interference (e.g. for FTIR, measure at several characteristic absorption frequencies, for GC, vary the column conditions to check for underlying peaks).

Complexities in analysis will be minimized at low reagent conversions. Indeed, some yield plots normalize the x- and y-axes measurements, so that the amount of product is determined as a function of the degree of reagent consumption, with the most accurate values being obtained at low conversion, where secondary reactions are minimized, but sufficient reaction needs to occur so that accurate measurements of product production and reagent consumption can be made.

However, depending on the measurement technique used, it is not always possible to make sufficient measurements at low reagent conversion or indeed the target product for the yield measurement is not a primary, but rather a secondary or tertiary product of the reaction and hence may only be produced after significant reagent conversion.

7.3.3 Analysis with Product Consumption

If the target product is consumed by the radical species, then yield plots will tend to curve downwards (red points in Fig. 7.3) as a function of time and can even turnover. Alternatively, if the target product is produced during secondary reactions, then the yield plot (blue points) may curve upwards.

Fig. 7.3

a Examples of upward (blue points) and downward (red points) curvature in yield plots at higher reagent consumption. Upward curvature is associated with secondary production, downward curvature occurs with more reactive products. b Detailed plot of extensive curvature, so example more reactive iso-butanal produced in the oxidation of iso-butanol, see reaction (R7.3.3.1)

In the study of iso-butanol oxidation, the iso-butanal concentration is determined primarily by the following reactions:

$${\text{Cl}}\, + \,\left( {{\text{CH}}_{{3}} } \right)_{{2}} {\text{CHCH}}_{{2}} {\text{OH}}\, \to \,{\text{HCl}}\, + \,\left( {{\text{CH}}_{{3}} } \right)_{{2}} {\text{CHCHOH}}$$

(R7.3.3.1a)

$${\text{Cl}}\, + \,\left( {{\text{CH}}_{{3}} } \right)_{{2}} {\text{CHCH}}_{{2}} {\text{OH}}\, \to \,{\text{HCl}}\, + \,{\text{products}}$$

(R7.3.3.1)

$${\text{Cl}}\, + \,{\text{iso-butanal}}\, \to \,{\text{HCl}}\, + \,{\text{products}}$$

(R7.3.3.2)

Abstraction at the α position (R7.3.3.1a) gives the (CH₃)₂CHCHOH radical which in the presence of sufficient oxygen will react rapidly to give iso-butanal and HO₂, i.e. the rate-determining step in butanal formation is (R7.3.3.1). Under these conditions, it can be shown that

$$\frac{{[{\text{iso-butanal}}]}_{t}}{{[{\text{iso-butanol}}]}_{0}}=\frac{\alpha }{1-\frac{{k}_{7.3.3-2}}{{k}_{7.3.3-1}}}\left(1-x\right){[(1-x)}^{{k}_{7.3.3-2}/{k}_{7.3.3-1}}-1]$$

(E7.3.3.1)

where

$$x=1-\frac{{[{\text{iso-butanol}}]}_{t}}{{[{\text{iso-butanol}}]}_{0}}$$

(E7.3.3.2)

and

$$\alpha =\frac{{k}_{7.3.3-1a}}{{k}_{7.3.3-1}}$$

(E7.3.3.3)

In this case, α is essentially the yield of the reaction. Full details on the derivation can be found in the appendix of Meagher et al. (1997) and the yield plot will look similar to that shown in Fig. 7.3.

For more complex situations, it may be necessary to perform a numerical simulation to determine branching ratios or yields in a key reaction. In all circumstances, it is important to measure as many reagents and intermediates as possible as this will reduce the statistical errors in the returned parameters and reduces the chances of systematic errors influencing the results. An example is the study on the branching ratio in the reaction of acetyl peroxy radicals with HO₂ (Winiberg et al. 2016):

$${\text{CH}}_{{3}} {\text{C}}({\text{O}}){\text{O}}_{{2}} \, + \,{\text{HO}}_{{2}} \, \to \,{\text{CH}}_{{3}} {\text{C}}({\text{O}}){\text{OH}}\, + \,{\text{O}}_{{3}}$$

$${\text{CH}}_{{3}} {\text{C}}({\text{O}}){\text{O}}_{{2}} \, + \,{\text{HO}}_{{2}} \, \to \,{\text{CH}}_{{3}} {\text{C}}({\text{O}}){\text{OOH}}\, + \,{\text{O}}_{2}$$

$${\text{CH}}_{{3}} {\text{C}}({\text{O}}){\text{O}}_{{2}} \, + \,{\text{HO}}_{{2}} \, \to \,{\text{CH}}_{{3}} \, + \,{\text{CO}}_{{2}} \, + \,{\text{OH}}$$

where numerical modelling was used to extract the primary OH yield from the target reaction. A variety of numerical integration packages (e.g. AtChem (see Sect. 7.6.2) or Kintecus) can be used for the numerical fitting.

7.4 Estimating Secondary Organic Aerosol Yields

7.4.1 Introduction

Chemical transport models (CTMs) usually rely on fits to experimentally determine secondary organic aerosol (SOA) yields to model SOA formation in the atmosphere. The SOA mass yield, Y, is defined as the fraction of a volatile organic compound (VOC) that is converted to SOA:

$$Y=\frac{{C}_{SOA}}{\Delta VOC}$$

(E7.4.1.1)

where ${C}_{SOA}$ is the SOA mass concentration produced and ΔVOC is the amount of VOC reacted, both in μg m⁻³.

There are two approaches for calculating these yields. The first relies on the concentrations measured in the end of the experiment and the corresponding yield is characterized as “final”. This approach results in one measurement per experiment, but it has the advantage that it avoids issues related to the dynamics of the system (e.g. delays in the formation of SOA) given that the system has enough time to equilibrate. The second approach estimates the corresponding yield as a function of time by dividing the corresponding concentrations at a given point. This “dynamic” yield approach provides a range of yield measurement from a single experiment, but may be quite sensitive to the dynamics of the system. For example, the SOA concentration may keep increasing after all the initial VOC has reacted resulting in multiple yield values for the same ΔVOC. Comparison of the results of the two approaches can help ensure that the estimated dynamic yields are not influenced by time delays in the SOA formation processes. If this is the case in the system, then one should rely only on the final yields for the required SOA yield parameterizations.

The measurement of ΔVOC is straightforward in all cases in which the VOC concentration can be accurately measured. As a result, the accuracy of the measured yield mainly depends on the accuracy of the measurement for total formed SOA mass concentrations. However, the SOA mass concentrations in a Teflon chamber are influenced significantly by particle wall losses and corrections are needed. In experiments in which the measured SOA concentrations have not been corrected for wall losses, the corresponding SOA yields have been underestimated. The rest of this section focuses on methods that can be applied to correct SOA chamber experiments for particle wall-losses.

7.4.2 Particle Wall-Loss Correction Procedure

The procedure outlined below corrects for particle wall losses using data collected in a chamber using both a scanning mobility particle sizer (SMPS) and an aerosol mass spectrometer (AMS). This procedure assumes that a coagulation-corrected particle wall-loss constant as a function of particle size has already been calculated according to the method described in Sect. 2.5. However, in order to correct an experiment for particle wall-losses, the particle wall-loss profile must be applicable to the specific experiment (i.e. the profile was measured before/after the experiment, not changing with time during the experiment, etc.). It is recommended that for every SOA yield experiment, a new particle wall-loss profile is generated to account for small perturbations that can occur from daily chamber maintenance (Wang et al. 2018).

Correction of SMPS measurements for particle wall-losses

The correction process includes the following steps:

• (1) Acquisition of the coagulation-corrected particle wall-loss profile as a function of particle size.

• (2) Correction of the number distribution and of the total number concentration at each time. The corrected particle number concentration at size bin i and time t, ${N}_{i}^{tot}(t)$, can be calculated by

  $${N}_{i}^{tot}\left(t\right)={N}_{i}^{sus}\left(t\right)+{k}_{i}\int\limits_{0}^{t}{N}_{i}^{sus}(t)\mathrm{d}t$$

  (E7.4.2.2)

  where ${N}_{i}^{sus}(t)$ is the suspended aerosol number concentration (m⁻³) of size bin i and time t as measured by the SMPS and ${k}_{i}$ is the coagulation-corrected particle wall-loss constant for size bin i. ${N}_{i}^{sus}(t)$ includes SOA and seed (if applicable) particles. Once ${N}_{i}^{tot}(t)$ is known, the total number concentration at time t, ${N}^{tot}\left(t\right)$, can be calculated by summing the number concentrations at all size bins:

  $${N}^{tot}\left(t\right)=\sum_{i}{N}_{i}^{tot}\left(t\right)$$

  (E7.4.2.3)

• (3) Calculation of the corrected volume distribution and total volume concentration at each time. The corrected volume concentration at the same size bin and time, ${V}_{i}^{tot}(t)$, assuming spherical particles, can be determined by

  $${V}_{i}^{tot}\left(t\right)=\frac{\pi {D}_{p,i}^{3}}{6}{N}_{i}^{tot}(t)$$

  (E7.4.2.4)

  where ${D}_{p,i}$ is the particle diameter (m) in size bin i. Similar to the total number concentration, the corrected total volume concentration at time t, ${V}^{tot}\left(t\right)$, can be calculated by

  $${V}^{tot}\left(t\right)=\sum_{i}{V}_{i}^{tot}\left(t\right)$$

  (E7.4.2.5)

• (4) Calculation of the corrected total mass concentration at each time. If there are no seeds, the mass (μg m⁻³):

$${C}_{SOA}\left(t\right)={V}^{tot}\left(t\right){\rho }_{SOA}$$

(E7.4.2.6)

where ${\rho }_{SOA}$ is the density of the SOA (in μg m⁻³). If there are seeds, the corrected SOA mass concentration can be calculated by

$${C}_{SOA}\left(t\right)=\left({V}^{tot}\left(t\right)-{V}_{s}\right){\rho }_{SOA}$$

(E7.4.2.7)

where ${V}_{s}$ is the corrected seed volume concentration right before SOA formation. In seeded SOA experiments, ${V}_{s}$ should be constant after correction for particle wall-losses (Figs. 7.4 and 7.5).

Fig. 7.4

The SMPS derived coagulation-corrected particle wall-loss constants as a function of mobility diameter (black circles, left axis) and an average number distribution measured by the SMPS after 1 h of reaction without being corrected for particle wall losses (red, right axis). The error bars represent the uncertainty of the measured wall-loss constants. The black line is the fit to the measured wall-loss constants extended to encompass the whole diameter range of the SMPS

Fig. 7.5

The raw (black circles) and particle wall-loss corrected (red circles) a total number and b total mass concentrations measured by the SMPS over the course of this experiment. The mass concentrations were determined with a calculated density of 1.23 g cm⁻³

Correction of AMS measurements for particle wall-losses

The correction of the AMS measurements has similarities but also some important differences from the SMPS corrections. More specifically:

• (1) Conversion of the vacuum aerodynamic diameter measured by the AMS to a mobility diameter. Since the coagulation-corrected particle wall-loss rate constants were measured with an SMPS, the corresponding particle size distribution is based on the electrical mobility diameter, ${D}_{{p}_{m}}$. However, the AMS measures particle mass distributions based on the vacuum aerodynamic diameter, ${D}_{{p}_{va}}$. Therefore, assuming spherical particles, the vacuum aerodynamic diameters from the AMS can be converted to their equivalent mobility diameters using the density of the particles, ${\rho }_{p}$:

  $${D}_{{p}_{m}}=\frac{{D}_{{p}_{va}}}{{\rho }_{p}}$$

  (E7.4.2.8)

The density can be calculated using the AMS size-resolved composition and the corresponding densities.

• (B) Calculation of the AMS-specific wall-loss rate constants combining the values measured as a function of the electrical mobility diameter and then converting these values to the corresponding vacuum aerodynamic diameters using Eq. (E7.4.2.8).

• (C) Correction of AMS results. The AMS size distributions are split into n size bins. Using the wall-loss constants as a function of the AMS mobility diameters, and the collection efficiency (CE)-corrected AMS mass distributions, the particle wall-loss corrected mass distributions at size bin i and time t, ${OA}_{i}^{tot}\left(t\right)$, can be calculated by

$${OA}_{i}^{tot}\left(t\right)={OA}_{i}^{m}\left(t\right)+{k}_{i}\int\limits_{0}^{t}{OA}_{i}^{m}(t)\mathrm{d}t$$

(E7.4.2.9)

where ${OA}_{i}^{m}\left(t\right)$ is the measured mass concentration at each AMS size bin i and time t after correction for the CE and ${k}_{i}$ is the coagulation-corrected particle wall-loss constant for size bin i. Once ${OA}_{i}^{tot}(t)$ is known, the corrected total mass concentration at time t, ${OA}^{tot}\left(t\right)$, can be calculated by summing the mass concentrations at all size bins:

$${OA}^{tot}\left(t\right)=\sum_{i}{OA}_{i}^{tot}\left(t\right)$$

(E7.4.2.10)

If there are seeds, the corrected SOA mass concentration at time t, $SOA(t)$, can be calculated by

$$SOA\left(t\right)={OA}^{tot}\left(t\right)-{M}_{s}$$

(E7.4.2.11)

where ${M}_{s}$ is the corrected total seed mass concentration right before SOA formation. Again, after correction,${M}_{s}$ should be a constant. If there are no seeds, Eq. (E7.4.2.11) provides the corrected SOA mass concentration.

The above process can be simplified if the determined wall-loss rate constant is approximately constant in the range covered by the AMS mass size distribution. In this case, an average wall-loss constant, $k$, can be chosen and the corrected total SOA mass concentration at time t, $SOA\left(t\right)$, can be calculated using the expression from (Pathak et al. 2007):

$$SOA\left(t\right)={OA}^{m}\left(t\right)+k\int\limits_{0}^{t}{OA}^{m}\left(t\right)\mathrm{d}t-{M}_{s}$$

(E7.4.2.12)

where ${OA}^{m}\left(t\right)$ is the measured AMS organic aerosol (OA) mass concentration after correction for the CE and ${M}_{s}$ is the corrected total seed mass concentration right before SOA formation (Figs. 7.6 and 7.7).

Fig. 7.6

The SMPS derived coagulation-corrected particle wall-loss constants as a function of mobility diameter (black circles, left axis) and an average mass distribution measured by the AMS after 1 h of reaction without being corrected for particle wall losses (red, right axis). The AMS vacuum aerodynamic diameters have been converted to mobility diameters with a calculated density of 1.23 g cm⁻³ and the distribution has been corrected with a calculated CE of 0.55

Fig. 7.7

The raw (black circles) and particle wall-loss corrected (red circles) total mass concentration measured by the AMS over the course of this experiment. The measurements have been corrected with a calculated CE of 0.55

7.5 New Particle Formation

New particle formation is a secondary particle formation process by which low volatility vapours cluster and form particles under suitable conditions in the absence of any seed particles. In order to define the intensity of the new particle formation process, the rate at which particles are formed per volume per time can be derived by accounting for the change in particle concentration as a function of time while considering the particle losses, namely, the formation rate. Another measure of the strength of a specific new particle formation event or happening, the growth rate is calculated, which is a measure of how fast particles grow per unit time. In the next section, we provide methods on how to derive the particle formation and growth rates from new particle formation.

In the following sections, we explain in detail how to calculate the variables characterizing the new particle formation (NPF) process, i.e. the particle formation rate (J) at a certain size (dp) and the particle growth rate (GR), further details can be found in Dada et al. (2020). We start by describing different methods how to determine the particle growth (Sect. 7.5.1) and formation rates (Sect. 7.5.2), followed by the relevant processes for chamber experiments, which are needed to determine particle formation rates (Sect. 7.5.2) and finally how to estimate the error in the calculations (Sect. 7.5.5).

7.5.1 Determination of Particle Growth Rates (GR)

The particle growth rate (GR) is defined as the change of the diameter, d_p, as a function of time representing the growing mode:

$$GR=\frac{d{d}_{p}}{dt}$$

(E7.5.1.1)

Different methods are used to determine the particle growth rate during a particle formation event. These include the maximum concentration method (Lehtinen and Kulmala 2003), the appearance time method (Lehtipalo et al. 2014) and different general dynamics equation (GDE)-based methods (Kuang et al. 2012; Pichelstorfer et al. 2018). Other methods reported in literature, such as the log-normal distribution function method (Kulmala et al. 2012), are found to be incompatible for chamber experiments, due to the absence of distinct particle modes. The choice of the GR method depends on the characteristics of the experiment and the available size distribution data. In general, GRs can usually be determined more accurately from chamber experiments than from atmospheric measurements due to less fluctuation in the data as well as more accurate particle size distribution measurements. However, several studies compared the different growth rate methods using measurement and simulation data, and found a reasonable agreement within the error bars (Pichelstorfer et al. 2018; Yli-Juuti et al. 2011; Leppa et al. 2011; Li and McMurry 2018). Estimating uncertainties in GRs is explained in Sect. 7.5. It is worth mentioning here that GR is usually size dependent, and therefore it is useful to calculate the GR for several different size ranges rather than one growth rate for the individual particle formation event.

Maximum concentration method

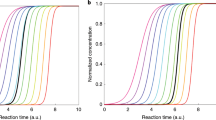
Determine the times, t_max,i, when the concentration in each size bin, i, of mean diameters of the size bins, d_p,mean,i, reaches the maximum. See Fig. 7.8 for an example of applying this method to chamber experiment data. To obtain the GR using the maximum concentration method:

Fig. 7.8

Calculating growth rates from chamber experiments using the maximum concentration method and the appearance time method. In Panel A, the concentration in a size bin is normalized by dividing with the maximum concentration reached during the experiment and then fitted using a Gaussian fit. The same is repeated for all size bins for which a growth rate is calculated. The time corresponding to maximum concentration is then plotted as diameter versus time (tmax) as shown in magenta in Panel C. X-axis uncertainty is the  ±1σ fit uncertainty from the Monte Carlo simulations of 10 000 runs, and Y-axis uncertainty is estimated instrumental sizing uncertainty. GR is obtained as the slope of the linear fit to dp versus tmax data; GR = 1.9 nm/h  ±  0.4. The GR uncertainty is ± 1σ from the Monte Carlo simulations. In Panel B, the concentration in a size bin is normalized by dividing with the maximum concentration reached during the experiment and then fitted using a sigmoidal fit. The same is repeated for all size bins for which a growth rate is calculated. The midpoint of the fits is then plotted as diameter versus time (tapp50) as shown in blue in Panel C. GR is obtained as the slope of the linear fit to dp versus tapp50, GR = 2.0 nm/h ± 0.3. Note that the maximum concentration method gives the GR at a later time during the experiment, so particle size distribution and gas concentrations in the chamber might have changed. Adapted with permission from Springer Nature: Nature Protocols, Dada et al. copyright 2020. All Rights Reserved

• Fit a Gaussian function to the time series of size classified particle concentration to obtain t_max,i as the time of maximum concentration per size bin of mean diameter (d_{p, mean, i}).

• Plot the mean diameters, d_p,mean,i, as a function of the maximum times t_max,i.

• Apply a linear fit to the size range at which the GR is determined.

• Obtain GR as a slope of the linear fit (Fig. 7.8).

Appearance time method

For the 50% appearance time method, determine the times, t_app50, _i, when the concentration in each size bin i reaches 50% of the maximum concentration (Leppa et al. 2011; Lehtipalo et al. 2014; Dal Maso et al. 2016). An example of t_app50,i determined from the size bin data is shown in Fig. 7.8. To obtain the GR using the 50% appearance time method:

• Fit a sigmoidal function to the time series of size classified particle concentration to obtain t_app50,i as the time when 50% of maximum concentration per size bin of mean diameter (d_p,mean,i) is reached.

• Plot the mean diameters of the size bins, d_p,mean,i, as a function of the appearance times t_app50,i or t_app,i.

• Apply a linear fit to the size range at which the GR is determined.

• Obtain GR as a slope of the linear fit (Fig. 7.8).

Note that the GR might change with size, especially during the beginning of the growth process (Tröstl et al. 2016), in this case, using a linear fit is a good assumption only in a narrow size range. It is also possible to determine t_app50,i and t_app,i from the total concentration measured with a CPC (Riccobono et al. 2012), instead of using the concentration in a certain size bin. Lehtipalo et al. (2014) compared different methods to determine appearance times and concluded that the most robust method is to either determine t_app50,i from size bin data or t_app,i from total concentration data. Instead of determining the appearance time at 50% of the maximum concentration t_app50,i, the appearance time at the onset of the maximum concentration can be determined by, for example, determining the 5% appearance time t_app5,i.

General Dynamic Equation methods

The time-evolution of the aerosol number distribution $n\left(v,t\right)$ is described by the so-called general dynamic equation (GDE), which in its continuous form can be written as.

$$\begin{aligned} \frac{\partial n\left(v,t\right)}{\partial t} 7& =\frac{1}{2}\underset{0}{\overset{v}{\int }}K\left(v-q,q\right)n\left(v-q,t\right)n\left(q,t\right)dq- n\left(v,t\right)\underset{0}{\overset{\infty }{\int }}K\left(v,q\right)n\left(q,t\right)dq \\ &\quad -\,\frac{\partial }{\partial v}\left(I\left(v\right)n\left(v,t\right)\right)+Q\left(v,t\right)-S\left(v,t\right). \end{aligned}$$

(E7.5.1.2)

Here K(v,q) is the coagulation kernel between particles of volume v and q, I(v) is the particle volume growth rate at volume v, and Q(v,t) and S(v,t) are the source and sink terms for particle with volume v. In a typical chamber experiment, the only source of particles is nucleation and the sink term arises from wall deposition. The time evolutions of n(v,t) and K(v,q) are known from the measurements.

Find the growth rate I(v,t) and source rate Q(v,t) corresponding to the optimal match between the measured data and the solution to the GDE. This can be done by using different approaches, e.g. (Lehtinen et al. 2004; Verheggen et al. 2006) and (Kuang et al. 2012). In practical applications to measurement data, the parts of the GDE needed are always turned into a discrete form, in addition, particle diameter is used instead of particle volume as a primary variable. Indeed, Pichelstorfer et al. (2018) developed a hybrid method in which GR(d_p,t) was estimated by fitting the evolution of regions of the size distribution to measured data, combined with solving the other microphysical processes from the GDE using process rates from theory. None of these methods, however, are suitable to estimate the error in GR (or Q) rigorously.

7.5.2 Particle Formation Rate

The rate of new particle formation, J_dp, is associated with the net flux of particles across the lower detection limit (d_p) of the particle counter. The rate of formation of particles (dN/dt) is obtained by integrating the GDE from the instrument detection limit up to infinity:

$$\frac{dN}{dt}={J}_{dp}-{S}_{dil}-{S}_{\text{wall}}-{S}_{coag}$$

(E7.5.2.1)

Equation (E7.5.2.1) accounts for the loss processes of particles once they have crossed the threshold for detection. dN/dt (preferably measured close to 1.5 nm) can readily be calculated from the total particle number concentration measured with a PSM or other CPC. The detection threshold d_p will be instrument dependent and depends on the cut-off size of the instrument, which is assumed to be a step function. A simple rearrangement leads to Kulmala et al. (2012).

$${J}_{dp}=\frac{dN}{dt}+{S}_{dil}+{S}_{\text{wall}}+{S}_{coag}{ [cm}^{-3}{ s}^{-1}]$$

(E7.5.2.2)

where dN/dt is the time-derivative of the total particle concentration and ${S}_{dil}, {S}_{\text{wall}}\,\,\text{and}\,\,{S}_{coag}$ are the loss rate of particles, described in detail in Sect. 7.5.3.

Figure 7.9 shows data from a typical chamber experiment. J_dp is variable, particularly at the beginning and end of the experiments as conditions (e.g. lamp fluxes, precursor concentrations) are changing rapidly. Representative values should be taken from the region of constant conditions and experiments should be adjusted so that these conditions, demonstrated by “steady” in Fig. 7.9, are maintained for as long as possible.

Fig. 7.9

Anticipated results from an NPF experiment performed in a chamber. Panel A shows the simulated time-evolution of particle size distribution during the experiment. Panel B shows the particle formation rate (J1.5) and its different components. Shaded areas correspond to ±1σ uncertainty obtained from the Monte Carlo simulations of 10 000 runs. The time between the dashed lines shows the time with the stable formation rate of particles (steady state), for which the average particle formation rate should be calculated. The magnitude of the components and time scales varies depending on the chamber specifications, experimental plan (gas concentrations, etc.) and particle formation and growth rates (affecting the particle size distribution). Adapted with permission from Springer Nature: Nature Protocols, Dada et al. copyright 2020. All Rights Reserved

7.5.3 Determination of Loss Processes

Determination of dilution losses

Dilution losses are to be accounted for in case the chamber is operated in continuous mode during which synthetic clean air is continuously flowing into the chamber and the instruments are continuously sampling from the chamber. This operation mode causes an artificially lower particle concentration in the chamber due to dilution which needs to be corrected, S_dil, in Eqs. (E7.5.3.1) and (E7.5.3.2). The dilution loss rate is determined as follows:

$${S}_{dil}={N}_{>dp}\cdot {k}_{dil} {[cm}^{-3} {s}^{-1}]$$

(E7.5.3.1)

$${\text{with }}{k}_{dil }\left[{s}^{-1}\right]=\frac{Flo{w}_{\text{synthetic air}}}{{V}_{\text{chamber}}}$$

(E7.5.3.2)

where N_>dp is the total particle concentration above the size for which you want to calculate particle formation rate, k_dil is the dilution rate, Flow_{synthetic air} is the flow rate of clean air and ${V}_{\text{chamber}}$ is the volume of the chamber.

Determination of wall losses

Diffusional losses of particles to the chamber walls (S_wall) are chamber specific (e.g. geometry and materials) and have been discussed earlier (Chap. 2). The rate coefficient for loss is inversely proportional to the mobility diameter in a size range below 100 nm where diffusional losses are the most critical (Seinfeld and Pandis 2012). This means that corrections can be made across the particle size range, see also Schwantes et al. (2017) and references therein. Equation (E7.5.3.3) defines wall-loss rates k:

$${S}_{{\text{wall}}}\left(T\right)=\sum_{i}{N}_{dpi-dpi+1}\cdot {k}_{\text{wall}}\left({d}_{p},T\right) \left[{\mathrm{cm}}^{-3} {\mathrm{s}}^{-1}\right]$$

(E7.5.3.3)

Here N(d_p) describes the number concentration of particles with a mobility diameter (d_p) while k_wall is a factor determined experimentally dependent on chamber mixing, chamber conditions and dark decay of the reference species in the absence of particles. The wall-loss rate coefficient can also be calculated (Lehtipalo et al. 2018; Wagner et al. 2017) theoretically, from the temperature dependence of diffusion coefficient, as D ~ (T/T_ref)^1.75 (Poling et al. 2001) and the wall-loss dependence on diffusion coefficient, k_wall ~ (D)^0.5. For a particle size less than ~ 100 nm on average (McMurry and Rader 1985), k_wall is given by

$${k}_{\text{wall}}\left({d}_{p},T\right)=\mathrm{F}\cdot {\left(\frac{T}{{T}_{\text{ref}}}\right)}^{0.875}\cdot \left(\frac{{d}_{\text{p,ref}}}{{d}_{p}}\right) {[\mathrm{s}}^{-1}].$$

(E7.5.3.4)

where F is a factor determined experimentally based on chamber mixing and other conditions in the chamber as well as dark decay of the reference species in the absence of particles. The mobility diameter of the reference species, the reference temperature at which the experimental loss rate was determined and the studied chamber temperature are given by d_p,ref,T_ref and T, respectively.

Determine the coagulation sink

The loss rate of formed particles to the background particles available in the chamber is known as the coagulation sink (S_coag). The pre-existing particles can either be introduced into the chamber for the purpose of studying polluted environments or can result from the growth of particles formed via nucleation processes. In the latter case, the coagulation sink is often negligible early in the experiment but increases gradually as the particles grow to larger sizes while more particles are formed in the chamber (Fig. 7.8). The coagulation sink is calculated as follows:

$${S}_{coag}\left({d}_{p}\right)=\int {k}_{coag}\left({d}_{p},{d}_{p}^{\mathrm{^{\prime}}}\right)n\left({d}_{p}^{\mathrm{^{\prime}}}\right)d{d}_{p}^{\mathrm{^{\prime}}}\cong \sum_{{d}_{p}^{\mathrm{^{\prime}}} =\, {d}_{p}}^{{d}_{p}^{{{\prime}}} =\, max} {k}_{coag}\left({d}_{p}, {d}_{p}^{\mathrm{^{\prime}}}\right){N}_{{d}_{p}^{\mathrm{^{\prime}}}} {[\mathrm{cm}}^{-3}{\mathrm{ s}}^{-1}]$$

(E7.5.3.5)

where $k_{{{\text{coag}}}} (d_{p} ,d^{\prime}_{p} )$ is the Brownian coagulation coefficient for particles sizes d_p and $d^{\prime}_{p}$. It is usually calculated using the Fuchs interpolation between continuum and free-molecule regimes (Seinfeld and Pandis 2016).

7.5.4 Ion Formation Rate

The ion size distributions can be used to calculate the ion formation rates (Kulmala et al. 2012), which allows for studying the importance of charging in the NPF process. When determining the formation rate of charged particles, additional terms need to be added to Eq. (E7.5.3.3) to account for the loss of ions due to their neutralization via ion–ion recombination (S_rec) and the production of ions by charging of neutral particles (S_att) (Manninen et al. 2009). Since the calculation of recombination and charging between all size bins is rather complicated, it is suggested that the charged formation rates are calculated from a size bin between diameters dp and upper diameter du. The loss of ions out of the studied size bin due to their growth (S_growth) needs to be determined. Dada et al. (2020) describe other methods of evaluating ion formation rates and calculate the charged formation rate for positive and negative ions (superscript + and –, respectively) as

$${J}_{dp}^{\pm }=\frac{d{N}_{dp-du}^{\pm }}{dt}+{S}_{dil}+{S}_{\text{wall}}+{S}_{growth }+{S}_{coag}+{S}_{rec} {-{S}_{att} [\mathrm{cm}}^{-3}{\mathrm{ s}}^{-1}]$$

(E7.5.4.1)

Here $\frac{d{N}_{dp-du}^{\pm }}{dt}$ is the time-derivative of the ion concentration in a defined size bin. The loss terms of ions due to dilution (S_dil), deposition on chamber walls (S_wall) and coagulation (S_coag) are calculated as given in Eqs. (E7.5.3.1)–(E7.5.3.5) for ions in a size bin between d_p and d_u instead of calculating them for all the particles larger than a certain threshold size.

Determine the growth out-of-the-bin losses

$${S}_{growth }=\frac{N}{({d}_{u}-{d}_{p})} \times GR$$

(E7.5.4.2)

where the growth rate of ions out of the size bin is given by GR, and is determined from the ion size distribution.

Determine ion–ion recombination losses

$${S}_{rec}= \alpha {N}_{dp-du }^{\pm }{N}_{<dp}^{\mp }$$

(E7.5.4.3)

where the ion–ion recombination coefficient (α) is usually assumed to be constant at 1.6 × 10 ⁻⁶ cm³ s^{– 1} (Bates 1985) although the recombination coefficient can depend on the size of the ions and their chemical composition as well as the temperature and relative humidity in the chamber (Franchin et al. 2015).

Determine the production rate of ions

$${S}_{att} = \chi {N}_{dp-du }{N}_{<dp}^{\pm }$$

(E7.5.4.4)

Here χ is the ion–aerosol attachment coefficient, which, similar to recombination coefficient, may depend on particle size and environmental conditions. χ is usually assumed to be equal 0.01 × 10⁻⁶ cm³ s ^–1 (Hoppel and Frick 1986).

7.5.5 Estimation of Errors

Determination of the error in the growth rate

Uncertainties on the growth rate when using the appearance time and maximum concentration methods are the result of uncertainty in the particle diameter measured by the particle counter and the uncertainty in the fits used for determining the appearance or maximum concentration times.

• In the case that one of either uncertainty is substantially larger than the other, a weighted least square fit on the variable with smaller error as an explanatory variable can be applied. The growth rate and error estimate can then be directly calculated based on the fit.

• In the case that both variables contain a similar magnitude of uncertainty, a fitting method allowing for error on both variables can be used, e.g. total least squares or geometric mean regression. In this case, the error on the GR can be determined using a numerical method, e.g. Monte Carlo simulation. Here, the statistical error on the growth rates using the Monte Carlo method can be estimated by reproducing the measurement data 10,000 times with the estimated uncertainties. The GR can be reproduced for all data sets by assuming normally distributed errors including random and systematic errors.

• The GR can be reported as the median value and the uncertainty as ± one standard deviation.

Determine the error in the formation rate

As with the growth rates, the Monte Carlo method for the error estimation can be applied on the formation rate as set out below:

• First, given that the instrumental cut-off diameter affects the detected particle number concentration above a given cut-off diameter, the relation between the cut-off diameter and detected particle concentration can be estimated.

• Assume independent uncertainties for the various parameters: cut-off diameter, N, k_dil, k_wall and k_coag. Assume that these uncertainties are normally distributed and should include random and systematic error.

• The uncertainty on k_dil can be estimated from the dilution flow rate on k_wall from a decay experiment to which the decay rate can be fitted, and on k_coag by assuming 10% error on the size distribution.

• Monte Carlo runs can be constructed so that the first cut-off diameter is selected from the cut-off distribution, which determines N, for which the uncertainty is normally distributed and randomly selected.

• Reproduce the formation rate 10,000 times at the plateau value (see Sect. 7.5.2 and Fig. 7.9), from which formation rate is usually determined. The J_dp can be reported as the median value with uncertainty as ± one standard deviation.

7.6 Analysis of Experiments and Application of Chamber-Specific Corrections

7.6.1 Introduction

When running complex experiment in simulation, chamber-specific box modelling can be an important tool for providing detailed chemical insight into chamber experiments.

This type of activities can be modelling exercises to design optimum conditions before specific chamber experiments. It often includes the exploration [oxidant]/[VOC] ratios or the [VOC]/[NO_x] ratios sensitivities or simulating précursors reactivity with respect to timescales of experimental systems as well as the formation and loss of target products or intermediates.

Modelling is also extremely valuable to aid interpretation of chamber experiments. It often proceeds by comparisons between temporal profiles of modelled and measured concentrations of not only O₃, NO_x and the precursor VOC, but also of a wide range of intermediates and products. These comparison request efficient chamber-specific auxiliary mechanisms and in-turn the use of modelling to interpret data provides meaningful interpretation and evaluation of the auxiliary mechanism.

Finally, chamber evaluation is key to the development and optimization of chemical mechanisms. It is indeed a central process in the knowledge transfer of our chemical understanding with real atmosphere models, linking fundamental laboratory and theoretical chemical understanding through to the chemical mechanisms used in science and policy models.

State-of-science detailed “benchmark” mechanisms are needed for fundamental chemical understanding and the development and optimization of reduced mechanisms, underpinning a range of atmospheric modelling activities. Mechanisms for individual VOCs in benchmark mechanisms are often tested using data from highly instrumented smog chambers. These experiments have not only been used to evaluate the mechanisms, but also to develop them further and to indicate, where necessary, the need for additional experimental measurements. Evaluation studies help to identify gaps and uncertainties in the mechanism where some revision or updating is necessary and to test new experimental data and theory.

A number of mechanisms, used widely in policy models, have been and continue to be developed and optimized on the basis of chamber data (e.g. SAPRC (Carter 2010)), and it is important that the benchmark chemical mechanism is evaluated alongside these, often “reduced” mechanisms, both in relation to the chamber and for atmospheric conditions. An example of such a detailed state-of-science benchmark mechanism is the Master Chemical Mechanism.

The Master Chemical Mechanism (MCM) is a near-explicit chemical mechanism that describes the detailed gas-phase degradation of a series of primary emitted VOCs. It is extensively employed by the atmospheric science community in a wide variety of science and policy applications where chemical detail is required to assess issues related to air quality and climate. The current version, MCMv3.3.1, treats the degradation of 143 emitted VOCs and currently contains about 17,500 elementary reactions of 6,900 closed-shell and radical species, constructed manually based on the mechanism development protocols (Jenkin et al. 1997; Saunders et al. 2003; Jenkin et al. 2015). The MCM is available to all, along with a series of interactive tools to facilitate its usage at the following websites: http://mcm.york.ac.uk, http://mcm.leeds.ac.uk/MCM/ and http://mcm.york.ac.uk.

The MCM has been extensively evaluated, optimized and developed using a wide range of smog chamber experiments. Examples include

• Development of MCMv3.1 aromatic chemistry was evaluated and optimized using an extensive range of photo-oxidation chamber experiments carried out at the highly instrumented EUPHORE chamber (Bloss et al. 2005).

• Chamber-specific box models have been used in the evaluation of the MCMv3.1 1,3,5-trimethylbenzene mechanism, and to investigate potential gas-phase precursors to the secondary organic aerosol (SOA) formed in photo-oxidation experiments carried out at the PSI aerosol chamber (Rickard et al. 2010).

• The performance of the MCMv3.2 β-caryophyllene mechanism, and its ability to form SOA in coupled gas-to-aerosol partitioning model was evaluated using a series of ozonolysis and β-caryophyllene/NO_x chamber experiments carried out at the University of Manchester aerosol chamber (Jenkin et al. 2012).

The following section describes how an MCM chamber-specific box model is constructed and run, how chamber-specific parameters are applied and how they can be used in the analysis of chamber experimental data.

7.6.2 General Approach

At the core of a zero-dimensional box model is the chemical mechanism, which describes the chemical system that is being modelled. At a mathematical level, the chemical mechanism is a system of coupled ordinary differential equations (ODE) which can be solved versus time using an appropriate numerical integrator. A number of open sources, free to use modelling toolkits designed to be used with the MCM are available, include the following:

• AtChem Online (Sommariva et al. 2020)—https://atchem.leeds.ac.uk/webapp/.

• AtChem2 (Sommariva et al. 2020)—https://github.com/AtChem/AtChem2.

• DSMACC (Emmerson and Evans 2009)—http://wiki.seas.harvard.edu/geos-chem/index.php/DSMACC_chemical_box_model.

• Kintecus—http://www.kintecus.com/.

• Chemistry with Aerosol Microphysics in Python (PyCHAM) box model (O’Meara et al. 2021)—https://github.com/simonom/PyCHAM.

The AtChem online website contains tutorial material and a number of examples. Any chemical mechanism can be integrated by these tools, as long as they are in an appropriate format.

In general, the following parameters need to be defined to run a basic chemical box model:

• model variables and constraints and solver parameters;

• environmental variables and constraints;

• photolysis rates;

• initial concentrations of chemical species and lists of output variables.

No two chambers are the same and they exhibit unique and evolving chemical characteristics. As such, chamber-specific “auxiliary mechanisms” are needed in chamber models in order to take into account the background reactivity of the chamber. This allows separation of the chamber-specific chemical processes from the underlying processes that are being studied in experiments. These auxiliary mechanisms are essential to make results from experiments carried out in different chambers comparable and transferable to the atmosphere.

Chamber auxiliary mechanisms mainly take into account chemical processes occurring at the chamber walls, which depend on the specific experimental conditions and recent chemical history (Rickard et al. 2010). Important chemical factors that need to be considered include the following:

• Rapid cycling of reactive NO_x−y species (especially with respect to HONO formation) to/from the chamber walls.

• Chamber wall sources of reactive species, which can significantly contribute to the radical budget throughout the experiment.

• Losses of reactive gas/aerosol species to the chamber walls.

• Chamber dilution effects via leaks and/or gas removal by instruments.

• Characterization and ageing of different types of UV lamp systems used to simulate photochemically important areas of the solar actinic spectrum.

Chamber auxiliary mechanisms can be evaluated and optimized in a range of chamber experiments using well-defined and simple photochemical systems (e.g. ethene or propene photo-oxidation (Chap. 2)).

7.6.3 Building a Chamber Box Model

Examples of how to build a chamber box model are given in the MCM/AtChem tutorial available via the MCM website (http://mcm.york.ac.uk/atchem/tutorial_intro.htt).

The modelling tool chosen to run the chamber model was AtChem Online (Sommariva et al. 2020). The complete MCM v3.3.1 ethene mechanism, along with the appropriate inorganic reaction scheme, was extracted from the MCM website using the “subset mechanism extractor” (http://mcm.york.ac.uk/extract.htt). The model was initiated using the values listed in Examples of how to build a chamber box model are given in the MCM/AtChem tutorial available via the MCM website (http://mcm.york.ac.uk/atchem/tutorial_intro.htt). Below, we will look at an example of building a chamber box model for a simple “high NOx” ethene photo-oxidation experiment carried out at the EUPHORE outdoor environmental chamber in Valencia, Spain on the 01/10/2001 (Zádor et al. 2005). Table 7.1 shows the initial conditions and other important parameters needed to initialisze the model.

Table 7.1 “Clear sky” photolysis rates were calculated according to a set of empirical parameterizations (http://mcm.york.ac.uk/parameters/photolysis_param.htt), defined for each photolysis reaction as described in Jenkin et al. (1997) and Saunders et al. (2003). The model was started at the time the chamber was opened and output every 5 min until the end of the experiment.

Table 7.1 Initial concentrations and other parameters needed for initialization of the chamber box model for the 01/10/2001 EUPHORE ethene “high NO_x” experiment

Base Model Run

Figure 7.10 shows the model-measurement comparison of the temporal evolution of C₂H₄ (ethene), NO₂, O₃ and HCHO. The pink lines show the base model run results, i.e. not constrained to dilution or the chamber auxiliary chemistry. The decay of ethene is substantially under-predicted, while all the product concentration profiles are over-predicted. The ozone peak is over-predicted by about 30% and has probably not yet peaked in the simulation.

Fig. 7.10

Model-measurement comparisons of the temporal evolution of C₂H₄, NO₂, O₃ and HCHO in the 01/10/2001 EUPHORE ethene “high-NO_x” photo-oxidation experiment. Four model scenarios are shown: red lines = base model run; blue lines = dilution effect included; green lines = dilution + tuned chamber auxiliary chemistry included; magenta lines = dilution + auxiliary chemistry + constrained to measured j(NO₂)–JFAC scaling–included. The black circles are the measured data

Chamber Dilution Effects

The blue lines in Fig. 7.10 show the model run results when dilution of species has been taken into account. Chamber dilution at EUPHORE is characterized by injecting SF₆ and measuring its concentration throughout the experiment by FTIR. The measured first-order dilution rate is given in Examples of how to build a chamber box model are given in the MCM/AtChem tutorial available via the MCM website (http://mcm.york.ac.uk/atchem/tutorial_intro.htt). Below, we will look at an example of building a chamber box model for a simple “high NO_x” ethene photo-oxidation experiment carried out at the EUPHORE outdoor environmental chamber in Valencia, Spain on the 01/10/2001 (Zádor et al. 2005). Table 7.1 shows the initial conditions and other important parameters needed to initialisze the model.

Table 7.1 as 1.64 × 10^–5 s⁻¹. Unsurprisingly, including dilution in the model significantly improves the profiles of all species.

Effects of Chamber Auxiliary Chemistry

A base case auxiliary mechanism was constructed from EUPHORE characterization experiments and literature data adapted to EUPHORE conditions (Zádor et al. 2005; Bloss et al. 2005). Discrepancies between the modelled and measured data and a detailed sensitivity analysis were used to derive a tuned auxiliary mechanism which is listed in Table 7.2.

Table 7.2 Parameters from the tuned auxiliary mechanism used to assess the impact of chamber-related processes on the ethene experiments (Bloss et al. 2005)

The green lines in Fig. 7.10 show the model run results when dilution and the above chamber-specific auxiliary chemistry are added to the model. The model now gives an excellent prediction of the ethene decay, with the temporal profiles of all modelled species coming more into line with the measurements. Peak ozone is now only over-predicted by 10%.

Radiation Effects

Radiation effects have been discussed in Chap. 2. All the calculated photolysis processes apply chamber-specific scaling factors (F_x) in order to take into account radiation effects of transmission through the chamber walls, backscatter from the aluminium chamber floor and cloud cover (Bloss et al. 2005; Sommariva et al. 2020). In addition, the photolysis rate of nitrogen dioxide, j(NO₂), is routinely measured in chamber A at EUPHORE and these data are available for the experiment above. Variations in actinic flux from day to day and during the experiment resulting from short temporal-scale variations in cloud cover are accounted for by considering the difference between the measured and clear sky calculated j(NO₂) at any given time during the experiment. This variable scaling factor, JFAC, is applied to all calculated photolysis rates along with F_x.

Figure 7.11 shows the temporal profile of the measured j(NO₂) for the 01/10/2001 EUPHORE ethene photo-oxidation experiment, along with the clear sky model calculated parameterized j(NO₂) and the calculated JFAC values (JFAC = j(NO₂)_measured/ j(NO₂)_calculated). The magenta lines in Fig. 7.10 show the model run results when dilution, chamber–specific auxiliary chemistry and constraints to the photolysis rate scaling factor JFAC have been added to the model. The timing of most of the profiles has improved further. However, owing to the measured j(NO₂) being generally higher than the calculated j(NO₂), the profiles are all slightly increased (with increased ethene decay) owing to the slight increase in the photo-reactivity of the system.

Fig. 7.11

Measured (5-min averages) and calculated j(NO₂) values from the 01/10/2001 EUPHORE ethene “high-NO_x” photo-oxidation experiment. JFAC scaling factor = j(NO₂) measured/j(NO₂) calculated. Red circles = 5-min average j(NO₂) measured values; blue line = calculated “clear sky” j(NO₂) values using the MCM parameterization (Saunders et al. 2003); Black dotted line = JFAC scaling factor (j(NO₂) measured/j(NO₂) calculated)

7.7 Use Simulation Chambers for the Assessment of Photocatalytic Material for Air Treatment

7.7.1 Introduction

Despite considerable progress in the past decades, ambient air pollution and, more specifically, fine particles, nitrogen dioxide and ozone, cause around 400.000 premature deaths each year in the EU (EEA Report 2019).

Photocatalysis has been shown to be a potential process for reducing atmospheric pollutants (Ângelo et al. 2013; Schneider et al. 2014; Boyjoo et al. 2017). Photocatalysis may be used for reducing pollutant levels in outdoors as well as indoors and has been applied mainly for reducing NO₂ concentrations outdoors. More specifically, one of the proposed measures is the photocatalytic degradation of NO_x on titanium oxide (TiO₂) containing surfaces, leading to the formation of adsorbed nitric acid (HNO₃) or nitrate (NO₃⁻), which is washed off by rain (Laufs et al. 2010). While photocatalytic nitrate formation has been critically reviewed, photocatalysis could help to improve urban air quality due to a variety beyond the simple reduction in NO_x. Firstly, the removal of NO_x reduces direct O₃ production as NO₂ photolysis is reduced and any photocatalytic VOC removal will indirectly reduce O₃ and smog formation. Secondly, while photocatalysis does not reduce the total amount of HNO₃ formation, nitric acid is formed and retained on the surface until washed off and hence will not damage plants or cause respiratory damage. Finally, total nitrate in the rain wash-off can be reduced if treated in wastewater plants.

However, poorly designed photocatalysts can have some negative effects such as the formation of nitrous acid, HONO, photolysis of which can accelerate photochemical smog formation (Laufs et al. 2010; Monge et al. 2010a; Gandolfo et al. 2015) or the production of HCHO or other oxygenated VOCs (Mothes et al. 2016; Toro et al. 2016; Gandolfo et al. 2018). In addition, nitrates need to be regularly removed to maintain efficiency and to prevent photocatalysis of the adsorbed nitrate (Monge et al. 2010a, b). Photocatalytic surfaces at best will only contribute to NO_x reduction; they are not the sole solution and should be considered as part of a wider range of solutions to the issue of poor air quality (Gallus et al. 2015; Kleffmann 2015).

TiO₂ can be found on the market in different formats for environmental purposes, for example, as paints, concrete, pavement stones, granules for asphalt surfaces, roof tiles, window glass, etc. Its effectiveness depends not only on the support (paints, textiles, etc.) but also on the impregnation method (layer, embedded, etc.). Nevertheless, a science-based approach is needed to assess the performance of this process before it is promoted as an effective solution and enters the market.

Atmospheric simulation chambers are well equipped to study the reduction potential of selected photocatalytic surfaces under well-defined atmospheric conditions. Simulation chamber studies can provide investigators and companies with large-scale assays helping them in developing efficient products and in reducing potentially problematic behaviour as well as providing a basis to encourage local authorities and stakeholders to adopt a more integrated approach to urban air quality management. While atmospheric simulation chambers have many advantages, initial studies can also be carried out in smaller photo-reactors that can characterize the uptake and are useful for screening before considering larger scale measurements (Ifang et al. 2014). These reactors are also the only way to determine the uptake kinetic parameter, i.e. uptake coefficients (γ) for fast photocatalytic reactions (see below). In contrast, in larger smog chambers, fast uptake will be limited by the transport to the active surfaces. However, in smaller flow reactors, secondary chemistry and the impact of photocatalysis on the complex chemistry of the atmosphere, e.g. on summer smog formation, cannot be investigated. Here larger simulation chambers are necessary.

The present section describes experimental approaches using atmospheric simulation chambers for the testing of different photocatalytic materials. Section 7.7.2 presents a protocol for the study of enhanced uptake, exemplified by looking at the removal of NO_x by TiO₂-doped surfaces, along with a number of examples. In Sect. 7.7.3, we look at how surface chemistry can be incorporated into more complex photosmog simulations and finally Sect. 7.7.4 provides recommendations for rigorously using simulation chambers in order to study the photocatalytic activity of material and the effect of their deployment on atmospheric composition.

7.7.2 Photocatalytic Activity Determination Using a Simulation Chamber

Introduction

Simulation chambers can be very useful tools to determine the photocatalytic activity of potential depolluting materials. The principle for the photocatalytic activity measurement can include both NO_x reduction and the production of intermediates such as HONO or oxygenated VOC. One of the assets of this approach, in contrast to more compact testbeds, is the ability to have more realistic conditions and to consider the production of a wider range of compounds. It must nevertheless be kept in mind that atmospheric chambers are not suitable to measure the uptake kinetic parameter for fast photocatalytic processes. Indeed, in a chamber, even if fans are used for efficient mixing, transport to the surface is most of the time the limiting parameter for active samples, at least with γ > 10^–4. This indicative value for γ will depend on mixing efficiency, available reactive surfaces and the volume of the chamber.

In the following sub-sections, we outline an experimental protocol using examples from studies at CNRS-Orléans, considering experimental procedures and data analysis. Finally, we briefly discuss these results highlighting considerations relevant for other studies.

Experimental protocol with an example of glass surfaces

• (1) Sample Preparation

For the present example study, a photoactive glass was compared to an equivalent area of normal glass. The tested glass consisted of two sets of pieces with different surfaces. Both types of glass are commercially available; the non-treated glass was standard windows glass, while the treated glass was Pilkington™ Activ™ self-cleaning glass. Each test piece consisted of panels of a surface area of 0.39 m² (0.88 m × 0.44 m). The preparation of the test samples prior to the experiment consisted of washing with deionized water, and then placing it into the chamber to be flushed with purified air for at least 1 h. In order to ensure the absence of contamination emissions from the materials, air samples were taken prior to the introduction of NO and NO₂. For the present study, both indoor and outdoor atmospheric simulation chambers have been used.

• (B) Chamber descriptions

• (a) Indoor chamber

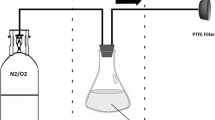
The indoor chamber setup consisted of a 275 L Teflon cube that was used as a static stirred reactor. The experiments were performed at room temperature (25 ± 3 °C) and 760 Torr in dry air (RH < 5%). In the present example, dry conditions were chosen for mechanism investigation purposes. It must be noted that dry conditions are not so relevant for the atmosphere and that photocatalysis is highly dependent on the availability of water molecules adsorbed on the material, which is a function of the relative humidity. It is generally recommended in standard procedures (e.g. ISO 22197-1 2007) to work at 50% RH. The UV exposure unit consisted of an ULTRA-VITALUX 300 W (® OSRAM) lamp used to simulate solar radiation. The test piece was laid flat on the middle of the floor of chamber to be exposed to pollutants. The desired amounts of nitrogen oxide (NO) and nitrogen dioxide (NO₂) were introduced into the chamber via a 20 L min⁻¹ air stream. The mixing ratios were measured periodically at regular intervals using a NO_x monitor. During the entire duration of the experiments, a slight airstream 100 mL min⁻¹ was added into the chamber in order to compensate the loss from the sampling volume and to maintain a slight overpressure to prevent the outside air from entering the setup.

• (b) Outdoor chamber

The outdoor chamber was a cube of 1.5 m edge with a volume of 3.4 m³ made of a 200 µm PTFE film. In addition to the NO_x and O₃ monitors, it was equipped with pressure, temperature and relative humidity sensors. The solar intensity was measured using a J(NO₂) radiometer. A fan positioned inside the chamber gave homogeneous mixing within the chamber in <2 min. The chamber could be covered by a black and opaque cloth that could be rapidly removed. As with the indoor chamber, NO and NO₂, were introduced via a 20 L/min air stream and their mixing ratios were measured continuously and a dilution flow was used to maintain a slight overpressure.

• (C) Experimental procedure

NO and NO₂ can be introduced into the environmental chambers (indoor and outdoor) in the desired concentration (e.g. to simulate “high” or “low” NO_x conditions) with initial concentrations in the range 43.3–170 and 11.45–50 ppbv, respectively, in this particular example. The system was allowed to stabilize for at least 1 h and the chamber was then exposed to radiation for 4 h. The NO_x concentration–time profiles were measured continuously.

Photocatalytic Efficiency Determination

The photocatalytic activity is studied here exemplarily by measurement of the NO_x loss. However, this loss can be due to combinations of

• (i) wall loss and dilution,

• (ii) adsorption on the surface of the sample,

• (iii) photolysis by UV light (for NO₂),

• (iv) photocatalysis by TiO₂ in the presence of UV light.

Therefore, the measurement of the concentration–time profiles of NO and NO₂ can give information on the TiO₂-material activity providing that the above side effects (i–iii) are considered. Hence, before performing the photocatalytic experiments, blank tests (chamber without material and in the presence of a material without TiO₂) were carried out in order to estimate the loss of NO_x.

The estimation of the catalytic activity of the materials is often represented through various parameters that are all arising from different approaches of various levels of scientific robustness.

• (i) the percentage of NO_x photo-removed (%NO_{x(photo-removed)}),

• (ii) the photocatalytic/oxidation rate (PR, μg m⁻² s⁻¹),

• (iii) the photocatalytic deposition velocity (ν_photo),

• (iv) the uptake coefficient (γ).

The percentage of NO_x photocatalytically removed is calculated by the following equation:

$$\% {\text{NO}}_{{{{x}}\;{\text{photo-removed}}}} = \, \left( {\frac{{\left[ {{\text{NO}}_{{\text{x}}} } \right]_{{{\text{UV}}}} - \left[ {{\text{NO}}_{{\text{x}}} } \right]_{{{\text{blank}}}} }}{{\left[ {{\text{NO}}_{{\text{x}}} } \right]_{{{\text{UV}}}} }} \times { 100}} \right)$$

(E7.7.2.1)

where [NO_x]_UV and [NO_x]_blank represent the amount of NO_x (ppb) removed, respectively, during the irradiation of TiO₂ containing sample and that removed during the blank experiment due to side effects.

While sometimes used to compare different material activities under similar conditions and time horizon, using a percentage of reduction is not compatible with kinetic theory. Here zero-order kinetic is applied to a typical first-order photocatalytic reaction at atmospheric relevant pollutant levels. The result is a parameter that can be time dependent in a smog chamber and that is not linearly correlated to the photocatalytic activity (see Ifang et al. 2014).

The photocatalytic/oxidation rate (PR, μg m⁻² s⁻¹) is calculated, taking the sample surface, the chamber volume and the duration of the experiment into consideration. Thus, it provides a more precise estimation of the cleansing capacity of a material than the percentage of photo-removal. However, the PR is directly proportional to the pollutant concentration investigated and can be only applied to the atmosphere, if the PR is normalized to atmospheric conditions. In addition, in this simplified formalism, zero-order conditions are again assumed, for typical first-order photocatalytic reactions. While often used by the industry to advertise the efficiency of depolluting products, this measure is not scientifically robust. Except when the experiments are performed under realistic concentration conditions, it can even be misleading. Indeed, as the experiments are often conducted at much higher NO_x condition than in the real atmosphere (e.g. at 1 ppm NO level recommended by ISO 22197-1 2007), the photolytic oxidation rates are derived often leading to unrealistically high values. It is not recommended to use this formalism unless the NO_x level of the experiment is systematically provided together with the PR values.

The photooxidation rate (PR) is given by the following equation:

$${\text{PR}} = \left( {\frac{{{\text{V}} \cdot \left[ {{\text{NOx}}} \right]_{{{\text{TiO}}_{{2}} {\text{UV}}}} }}{{{\text{A}} \cdot {\text{t}}}}} \right)$$

(E7.7.2.2)

where $\left[ {{\text{NOx}}} \right]_{{{\text{TiO}}_{{2}} {\text{UV}}}}$ is the concentration of NO_x photocatalytically removed due to the TiO₂ effect (µg m⁻³), A is the sample surface (m²), t is the irradiation time (s), and V (m³) = the volume of the experimental chamber (V = 3.4 or 0.275 m³).

The deposition velocity was also calculated in order to describe the photocatalytic activity independently, avoiding the influence of the pollution concentration. The photocatalytic velocity (PV) can be approximated by the following equation:

$${\text{PV}} = \left( {\frac{{{\text{PR}}}}{{\frac{{\left[ {{\text{NOx}}} \right]_{{{\text{in}}}} + \left[ {{\text{NOx}}} \right]_{{{\text{UV}}}} }}{{2}}}}} \right)$$

(E7.7.2.3)

where PR is the photocatalytic rate (µg m⁻² s⁻¹), [NO_x]_in is the initial amount of NO_x (µg m⁻³) before irradiation and [NO_x]_UV is the amount of NO_x (µg m⁻³) removed during the irradiation of the TiO₂ containing sample. Here again the main issue lies in the kinetic representation of the studied phenomenon. PV expresses itself as first-order kinetic parameter applied to a first-order process but calculated from a zero-order parameter (PR) and this mixed approach cannot be recommended.

The most robust approach is certainly to remain under the first-order kinetic assumption all along the data analysis process as recommended by Ifang et al. (2014). A first-order rate coefficient (k_rxn) can be obtained from experimental data only if either (a) there is an absence of secondary chemistry which may be achieved in a fast flow system, or (b) if a rigorous approach is taken to modelling secondary chemistry (e.g. NO₂ photolysis) or processes such as wall loss. In the absence of secondary processes:

$${k}_{\mathrm{rxn}}=\frac{\mathrm{ln}\frac{{\left[{\mathrm{NO}}_{\mathrm{x}}\right]}_{\mathrm{t}}}{{\left[{\mathrm{NO}}_{\mathrm{x}}\right]}_{0}}}{t}$$

(E7.7.2.4)

As a first-order rate coefficient, k_rxn will be independent of the NO_x concentration and it is recommended to repeat experiments at a range of concentrations to verify this. Of course, k_rxn depends on the geometry of the sample and reactor and will scale with the S_active/V ratio where S_active is the surface area (m²) of the photocatalytic sample and V is the gas-phase volume (m³) over the sample. This dependence on reactor configuration means that values of k_rxn cannot be directly compared; the dimensionless reactive uptake coefficient (γ) (Finlayson-Pitts and Pitts 2000) however can be compared. (γ) is defined as the ratio of the number of collisions that lead to reaction over all collisions of the gas-phase reactant with a reactive surface and is calculated from Eq. (E7.7.2.5).

$$\upgamma =\frac{4 \cdot {\mathrm{k}}_{\mathrm{rxn}} \cdot \mathrm{ V}}{\overline{\upnu } \cdot {\mathrm{S} }_{\mathrm{active}}},$$

(E7.7.2.5)

where $\overline{\nu }$ is the mean molecular velocity of the reactant (m s⁻¹) defined by kinetic theory:

$$\overline{\upnu }=\sqrt{\frac{8\cdot \mathrm{R}\cdot {T}}{\uppi \cdot {M}},}$$

(E7.7.2.6)

in which R is the ideal gas constant (R = 8.314 J mol⁻¹ K⁻¹), T is the absolute temperature (K) and M is the molecular mass of the reactant (kg mol⁻¹). When the uptake coefficient is known this can be easily converted into the photocatalytic deposition velocity (v_surf in m s⁻¹):

$$\nu_{\text{surf}} \, = \,\frac{{\gamma \cdot \overline{\nu}}}{4}.$$

(E7.7.2.7)

It has to be highlighted that the photocatalytic deposition velocity is not similar to the deposition velocity, typically used in flux modelling. It represents only the inverse of the surface resistance (r_C) in flux approaches. However, when the resistances for turbulent transport (r_A) and diffusion (r_B) are known, deposition velocities can be easily calculated, from which flux densities (molec. m⁻² s⁻¹) can be derived in atmospheric models by multiplying with the concentration (molec. m⁻³).

Examples of Photocatalytic Efficiency Results

• (a) Degradation on self-cleaning window glass

Typical concentration–time profiles of NO and NO₂ during the experiment conducted in the outdoor chamber are presented in Fig. 7.12.

Fig. 7.12

NO and NO₂ mixing ratios under natural irradiation at high NO_x concentration in the absence of any surface (left), in the presence of a non-treated glass surface (middle) and finally in the presence of a TiO₂-treated glass surface (right)

In high NO_x concentration (186–200) ppbV experiments, the loss in 4 h in the presence of a non-treated material under irradiation was (69–75) ppbV and was very similar to that of the loss in the absence of any material (60 ppbV) showing a negligible impact of the non-treated glass surface. The loss with low NO_x in the presence of a non-treated glass surface was found to be 13 ppbV, while that in the presence of TiO₂-based material was in the range 41–50 ppbV.

The decay of NO in the absence of any surface was 29% of the initial concentration over 4 h. In the presence of non-treated surface, it was equal to 28–39% showing that the non-treated material had an insignificant effect on the NO_x removal. Therefore, the removal was considered negligible and the experiments in the presence of a non-treated glass material were taken as reference to deduce the TiO₂ activity. In all the experiments, the presence of TiO₂ showed a significant role in the removal of NO_x. In Fig. 7.12, we observe a slight increase in the NO₂ which confirms the photocatalytic process of oxidation of NO_x according to the sequence: NO → NO₂ → HNO₃ (Laufs et al. 2010).

While being a quite illustrative example in a simulation chamber, such complex experiments can only be evaluated by using model description considering gas-phase photolysis of NO₂ (J(NO₂)), wall loss, dilution, in addition to the considered photocatalytic chemical mechanism. Through adjustment of the model with the experiment will lead to the first-order rate coefficients (k_rxn) for the NO and NO₂ reactions on the photocatalytic material, which may be converted into γ (see Eq. E7.7.2.5) by using the S/V ratios of the chambers.

• (b) Test of TiO₂ impregnated fabrics in the EUPHORE chamber

The large volume of the EUPHORE chamber (~200 m³) allows for the easy installation of a range of bulky samples as illustrated in Fig. 7.13. For example, 24 m² of a TiO₂ impregnated fabric was installed in a vertical position and 13 m² on the floor, with an S/V ratio of 0.185 m⁻¹. These studies could be carried out over extended time periods (e.g. 36 h), thus allowing a range of solar conditions to be sampled. If necessary, NO_x levels in the chamber could be controlled to simulate a typical diurnal profile with morning and evening rush-hour peaks. As with other chambers, relative humidity can be controlled, but obviously there is less control over temperature and solar radiation.

Fig. 7.13

Photocatalytic materials in the EUPHORE chamber. Left: textiles on structures and on the ground. Right: outdoor furniture

As an example of studying the effectiveness of pollution reduction by photocatalytic outdoor furniture, a surface of 4.4 m² of the photocatalytic material functionalized as furniture was installed, with a surface-to-volume ratio (S_active/V) of 0.022 m⁻¹. At such conditions, 50 ppb of NO and 60 ppb of NO₂ were introduced into the EUPHORE chamber. Figure 7.14 shows results of the NO_x evolution when both the photocatalytic and the non-photocatalytic materials (blank experiment) were exposed to the solar radiation.

Fig. 7.14

NO_x temporal evolution with non-photocatalytic (pink squares) and photocatalytic material (blue triangles)

At 120 ppb of NO_x under comparable condition, an initial NO_x reduction of 23.6% in 1 h was found with the photocatalytic materials, while only 7.4% h⁻¹ was derived with the non-photocatalytic materials. The quantification of NO₂ is more complicated due to secondary reactions by exposing both types of materials to the sunlight. Here NO degradation forms NO₂ and NO₂ photolyse back to NO in the gas phase.

Aware of the limitation of the percentage approach (see above), calculation of the uptake coefficient for NO_x was performed using the region where a first-order kinetic decay could be fitted. This resulted in a γ value of (5.3 ± 0.3) × 10^–5. As a reference, Gandolfo et al. (2015) reported uptake coefficient values of the order of 1.6 × 10^–5, which is lower than the photocatalytic material used here.

• (c) HONO formation on self-cleaning window glass in the CESAM chamber

The next example considers experiments in the CESAM chamber, where again the NO_x uptake on TiO₂-doped glass surfaces was examined, but with an additional focus on nitrous acid (HONO) detection via FTIR measurements. Samples were prepared and the experiments were carried out using a similar protocol (see Experimental protocol with an example of glass surfaces), which included experiments with uncoated glass with the same surface area. The initial NO concentration ranged from 20 to 100 ppb and the relative humidity was varied from 0 to 40% RH. Additional experiments were also carried out in an outdoor Teflon chamber.

Figure 7.15 shows experimental results for the treated and untreated surfaces. After introduction of synthetic air and NO into the CESAM chamber, the concentrations of NO, NO₂, HONO and O₃ were monitored in the dark for 1 h. Then the artificial illumination was turned on and the chemical system was again monitored for 90 min.

Fig. 7.15

NO, NO₂, HONO and O₃ profiles recorded in the presence of a: a TiO₂-coated glass and b: a standard glass in the CESAM chamber. The vertical line indicates the moment when the light was turned on

In agreement with previous studies, NO uptake on the TiO₂-coated glass was enhanced under irradiation, decreasing with time in both experiments. The NO₂ concentration profile exhibited a maximum under illumination, suggesting that it is formed from NO photocatalytic oxidation and then converted into HNO₃ on the surface. At the same time, a significant accumulation of ozone was observed. In agreement with previous studies, HONO production was enhanced under irradiation in the presence of TiO₂. In contrast, when a standard glass was analysed no ozone formation was detected. The NO₂ and NO concentration profiles were similar for the standard glass and the empty outdoor chamber with no evidence of additional photochemical effect. These results indicate that O₃ formation cannot be explained by the gas-phase chemistry (NO₂ photolysis) occurring in the chambers. The differences between the O₃ profiles obtained for the blank experiments and the coated glass suggested that TiO₂ should be involved in the reaction mechanism leading to O₃ formation via heterogeneous reaction. Using a complementary experimental approach (flow tube), a chemical mechanism explaining the formation of ozone has been suggested, see Monge et al. (2010a, b).

7.7.3 Photosmog Studies in the Presence of TiO₂-doped Surfaces

In contrast to the studies described above on the photocatalysis of pure NO_x, TiO₂-doped materials operating in the real world will be exposed also to VOCs in addition to NO_x and therefore photosmog-type experiments are required to examine the real-world performance.

As discussed in depth in Sect. 7.6, development of a chamber-specific auxiliary mechanism is the first step in a photosmog experiment. The experiments described in Sect. 7.7.2 allow for the adjustment of a dedicated auxiliary mechanism (Table 7.3) aimed at describing the effect of photocatalytic materials on the NO_x air chemical system.

Table 7.3 Chemical reactions involved a simplified NO_x chemistry in the presence of TiO₂ containing glass and used for the box modelling described below. Pseudo-first-order rate constants are given for standard glass and TiO₂-doped glass and are only relevant for the CESAM chamber and the available surface of active material used in these experiments

Experiments were performed in the CESAM chamber with the propene–NO_x–air system which was then irradiated for 3 h under dry conditions (RH < 1%) following an initial equilibration period of approximately 45 min in the dark. The simulated data were obtained using the standard glass model described in the previous section, combining MCM propene chemistry and the CESAM and standard-glass modules determined for the NO_x–air–light system. All kinetic parameters pertaining to NO_x heterogeneous chemistry were kept unchanged.

In spite of a very good ability of the initial model to capture the concentration of NO, NO₂, HONO and ozone, the propene loss remained constantly underestimated as shown in Fig. 7.16. This means that propene undergoes some degree of heterogeneous photocatalytic decomposition in the presence of TiO₂, probably triggered by the presence of hydroxyl groups formed from adsorbed water vapour molecules following photocatalytic site activation at the interface. As the formaldehyde and acetaldehyde buildup was also significantly underestimated, a simplified surface conversion reaction was added to the TiO₂-glass module accordingly:

$${\text{C}}_{{3}} {\text{H}}_{{6}} \, + \,{\text{hv}}\, \to \,{\text{CH}}_{{3}} {\text{CHO}}\, + \,{\text{HCHO}}$$

Fig. 7.16

Pseudo-first-order propene loss under similar conditions during photo-oxidation propene/NO_x/light experiments in the presence of various surfaces

The kinetics rate constant for this photocatalytic process was found to lead to the best fits when set to (8.7 ± 0.3) × 10^–5 s⁻¹ under dry condition and to (1.9 ± 0.7) × 10^–4 s⁻¹ at 45% relative humidity.

The comparison of Figs. 7.17 and 7.18 shows both the enhancement of propene removal in the presence of TiO₂-doped surfaces and the good agreement with the modified models. Such photosmog experiments are useful in assessing real-world performance and the studies have shown a significant reduction in propene loss with relative humidity.

Fig. 7.17

Concentration–time profiles for monitored species during an experiment with standard glass/propene/NO_x/light under dry conditions. Lights were switched on at t = 1800 s and switched off at t = 10300 s

Fig. 7.18

Concentration–time profiles for monitored species during an experiment TiO₂-glass/propene/NO_x/light under dry conditions. Lights were switched on at t = 1800 s and switched off at t=10300 s

7.7.4 Recommendations for the Use of Simulation Chambers in Photocatalysis

Before application in the real world, the overall efficiency of photocatalytic surfaces to improve the urban air quality has to be critically tested in the laboratory. Here not only the primary uptake should be studied, but also the potential formation of harmful intermediates, like nitrous acid (HONO) (Gustafsson et al. 2006; Ndour et al. 2008; Beaumont et al. 2009; Laufs et al. 2010; Monge et al. 2010a; Gandolfo et al. 2015) or oxygenated VOCs, like, for example, formaldehyde (HCHO) (Salthammer and Fuhrmann 2007; Auvinen and Wirtanen 2008; Geiss et al. 2012; Mothes et al. 2016; Toro et al. 2016; Gandolfo et al. 2018).

If only primary uptake is the major focus of study, consecutive product formation and pure material emissions should be studied, small-scale fast flow reactors (e.g. ISO 22197-1 2007) or smaller continuous stirred tank reactors (CSTR, see, e.g. Minero et al. 2013) are efficient tools, if properly applied (for details of the shortcomings of standard flow reactors/methods, see Ifang et al. 2014). Here fast uptake kinetics (e.g. uptake coefficients of several times 10^–4) and small product yields in the sub-percent range can be determined for atmospheric conditions when using sensitive analytical instrumentation.

However, when slower heterogenous chemistry, more complex secondary chemistry or the impact of heterogeneous photocatalysis on the complex gas-phase chemistry of the atmosphere (see summer smog) is the focus of study, simulation chambers are recommended. Here small flow reactors with reaction times from <1 s (see ISO 22197-1 2007) to some minutes (see CSTR reactors) are not suitable, for example, to study the impact of photocatalytic surfaces on the O₃-formation during summer smog.

The use of simulation chambers for photocatalysis studies can be undertaken with two different approaches: (a) static reactor approach and (b) continuous stirred tank reactor (CSTR) approach. While for both methods efficient mixing of the chamber air has to be obtained by the use of fans (see below), in a static reactor, the air exchange rate is small and mainly controlled by the leak rate of the chamber and the flow rates of the attached instruments. Here typically the concentration time profiles are recorded, from which uptake coefficients can be determined (see below). In contrast, if a simulation chamber is used as a CSTR reactor (see, e.g. Toro et al. 2016) much higher air exchange rates are applied and the photocatalysis is studied under steady-state conditions, which are typically reached after at least three times of chamber air exchange. Here the data evaluation is completely different and is based on the steady-state approach (Minero et al. 2013; Toro et al. 2016). Since the simulation chambers during the EUROCHAMP projects were used as static reactors, the CSTR concept will not be further considered here. For larger chambers, like, for example, EUPHORE, the CSTR concept is practically not possible, due to either the extremely high air exchange rates necessary or the long duration of experiments, for which stable conditions (e.g. photon flux) are not available.

If a simulation chamber is used in photocatalysis to quantify the initial uptake, there is a kinetic limitation caused by the transport of the reactants to the active surfaces. Here, in heterogeneous chemistry, a high surface-to-volume (S_active/V) ratio is recommended, for which unwanted side reactions in the gas phase (e.g. NO₂ photolysis) are minimized. In contrast, for simulation chambers, which are originally aimed to study gas-phase reactions, a small S/V is practical, leading to smaller wall-loss rates compared to the rates of gas-phase reactions. To overcome this mismatch, strong fans have to be used in simulation chambers to ensure an efficient mixing of the air and to minimize the transport limitation to the surfaces under investigation. However, typically, this mixing is not strong enough to study fast uptake kinetics (γ  > 10^–5) and the kinetic transport limit has to be determined individually in each chamber. Here instead of the photocatalytic surface, a perfect surface sink for a gas tracer has to be used. As an example, potassium-iodide-coated surfaces and the heterogeneous uptake of ozone can be used, for which close to unity uptake coefficients can be assumed. If the measured first-order uptake rate coefficient for this O₃ uptake (see Eq. E7.7.2.4) in the chamber, corrected for wall losses and the leak rate is converted into an uptake coefficient (see Eq. E7.7.2.5), this represents the upper limit transport coefficient γ_transport. If now the photocatalytic uptake is studied, the measured uptake coefficients (γ_measured) will approach this transport limit for fast true uptake kinetics (γ_true). Here the measured uptake can be described by the resistance approach:

$$\frac{1}{{\gamma }_{\text{measured}}}=\frac{1}{{\gamma }_{\text{transport}}+{\gamma }_{\text{true}}},$$

(E7.7.4.1)

for which the measured uptake is converging to γ_transport for very active photocatalytic surfaces. From the fixed γ_transport and the measured uptake, the true photocatalytic uptake can be calculated, if γ_true is not much higher than γ_transport. The upper limit for this method to determine high values of γ_true depends on the precision of both the measurements of γ_measured and γ_transport. If, for example, γ_transport is 10^–5 and the combined precision error in the smog chamber is 10%, the limit of γ_true will be 9 × 10^–5, which can be calculated by Eq. (E7.7.4.1) from a measured uptake coefficient of 9 × 10^–6 (only 10% lower than the transport limit). Since the error of γ_true will reach 100% at this limit, it is not recommended to study uptake kinetics more than five times faster than the individual transport limit in the chamber. If γ_true is higher, only a lower limit value should be specified and additional measurements in fast flow reactors are recommended.

If a more complex reaction system is studied in a smog chamber, simple analytical evaluation using Eq. (E7.7.2.4) is not possible and the use of a chemical box model is strongly recommended. Here all photocatalytic reactions involved should be implemented. The use of a chemical model for the interpretation of a simulation chamber experiment is especially necessary, if the impact of photocatalysis on the complex chemistry of the atmosphere, e.g. O₃ formation during summer smog, is to be investigated. Here the heterogeneous photochemical reactions have to be implemented as first-order rate coefficients into the existing model tools (e.g. MCM) after parameterization considering the S_active/V ratio inside the chamber. Only the use of such modified models can help to understand the observations inside the chamber.

As the simplest example, here the photocatalysis of pure NO₂ mixtures inside a simulation chamber is presented. While in a fast flow reactor, the uptake kinetics of NO₂ can be simply described in Eq. (E7.7.2.4) and only the formation of the side product HONO in the gas phase has to be considered besides the main reaction product of adsorbed HNO₃ (nitrate), the situation is much more complex in a simulation chamber.

Here the following simplified major processes will impact the concentration time profiles (for details regarding the main photocatalytic reactions, see Laufs et al. 2010; minor reactions are still missing below, e.g. wall loss of NO or HNO₃ photolysis):

Photocatalysis of NO2	NO2 + TiO2 + hν → nitrate
Photocatalytic formation of HONO by NO2	NO2 + TiO2 + hν → HONO
Wall loss of NO2	NO2 + wall → products
Heterogeneous formation of HONO on the chamber walls	NO2 + wall → HONO
Gas-phase photolysis of NO2 (Leighton)	NO2 + hν → NO + O(3P)
	O(3P) + O2 → O3
	O3 + NO → NO2 + O2
Photocatalysis of NO	NO + TiO2 + hν → NO2
Photocatalysis of O3	O3 + TiO2 + hν → products
Wall loss of O3	O3 + wall → products
Photocatalytic formation of O3	nitrate + TiO2 + hν → O3
Photocatalytic formation of HONO by NO	NO + TiO2 + hν → HONO
Photocatalysis of HONO	HONO + TiO2 + hν → products
Wall loss of HONO	HONO + wall → products
Adsorption of HONO to the catalyst	HONO + TiO2 → nitrite
Gas-phase photolysis of HONO	HONO + hν → NO + OH
Gas-phase oxidation of NO	NO + OH → HONO
Gas-phase oxidation of NO2	NO2 + OH → HNO3
Wall loss of HNO3	HNO3 + wall → products
Adsorption of HNO3 to the catalyst	HNO3 + TiO2 → nitrate
And dilution of all gas-phase species given by the air exchange rate

Although this is the simplest example of a photocatalytic experiment inside a simulation chamber, it is obvious that such a complex system can only be solved by numerical simulation in a box model and additional blank experiments, e.g. by measurements of the chamber wall-loss rates or the dark adsorption rates on the TiO₂. In contrast, any simple analytical evaluation will lead to a misinterpretation of the results, for example, to an overestimation of the photocatalytic uptake of NO₂ by the simultaneous gas-phase photolysis.

In the following, some final recommendations to the general conditions and the experimental requirements are given for photocatalytic simulation chamber experiments.

First, besides the analytical instrumentation necessary to detect all important species in the gas phase (in the above example: NO, NO₂, HONO, HNO₃, O₃), also the measurement of adsorbed species on the photocatalytic surfaces (in the above example: nitrite and nitrate) is helpful for the interpretation of the experimental results. For this purpose, extraction of smaller photocatalytic test surfaces by a suitable solvent and offline analysis is recommended (e.g. extraction by pure water and ion chromatography analysis, see Laufs et al. 2010).

Second, while the measurements of the spectral actinic fluxes is necessary to account for photochemical reactions in the gas phase, the spectral irradiance at the photocatalytic surface of interest is also necessary to evaluate photoactivation of the active material. The irradiance is critically depending on the orientation of the surfaces inside the chamber and on the solar zenith angle (SZA). If no analytical device for measuring the irradiance is available, at least the irradiance should be calculated by available models (see, e.g. TUV) This is only applicable if horizontal photocatalytic surfaces are used. The modelled irradiance should then be scaled inside the chamber by the ratio of measured/modelled actinic fluxes (or J(NO₂)).

Third, the photocatalytic surfaces should be washed by ultra-pure water and irradiated in clean synthetic air before the experiments, to remove adsorbed impurities and to obtain more reproducible results. In contrast, if, for example, nitrate has accumulated on the surface, the uptake kinetics of NO_x will slow down.

Fourth, if the pure photocatalytic effect should be studied, reference experiments with inactive similar surfaces should be performed under similar experimental conditions (“blank”). Here, for example, photocatalytic glass can be compared with normal glass (see Sect. 7.7.2) or photocatalytic active paints can be compared with similar normal paints (see Laufs et al. 2010).

Finally, the following experimental conditions are recommended for photocatalytic simulation chamber experiments (see also Ifang et al. 2014):

• Pollutants: When the photocatalysis of nitrogen oxides is studied, typically only NO is investigated. Here we recommend in addition to use the environmentally (and legislatively) more important NO₂. We also recommend investigating the different VOC classes, i.e. aromatics (e.g. toluene), unsaturated VOCs (e.g. propene) and biogenic VOCs (e.g. isoprene).

• Concentration: Since the assumed first-order kinetics of photocatalytic reactions are observed only at low reactant concentrations, atmospherically relevant pollution level should be used. Here experiments from typical urban background conditions (e.g. NO_x: 20 ppb, defined here as low) to heavily polluted kerbside conditions (e.g. NO_x: 100–200 ppb, defined here as high) should be investigated. However, conditions as typically recommended in available standard procedures (e.g. 1 ppm of NO in ISO 22197-1 2007) should not be used, since often the kinetics changes to zero order at such high pollution level.

• Humidity: Since photocatalysis is strongly dependent on the humidity (Laufs et al. 2010) no dry experiments are recommended, but the use of a medium humidity. Here in most standards on photocatalysis (e.g. ISO 22197-1 2007) a relative humidity of 50% is used, which is also recommended here.

• Irradiance: Since typically TiO₂ is used in photocatalysis, only the irradiance at ca. <400 nm has to be considered. This energy is necessary to activate the photocatalyst TiO₂: TiO₂ + hν → e_cb + h⁺_vb (see Laufs et al. 2010).

• In a smog chamber, often the light source is the sun, for which the UVA irradiance is varying between ca. 10 and 70 W m² depending mainly on the SZA and orientation of the sample inside the chamber. In contrast, in indoor chambers, artificial UV light sources are applied, for which a typical UVA irradiance of 10–20 W m⁻² is recommended in most standard procedures (average of typical ambient values). Care has to be taken, when the uptake kinetics of indoor experiments is compared to outdoor simulation chamber experiments, with often much higher irradiance used.