Abstract
We propose a novel algorithm to decide the language inclusion between (nondeterministic) Büchi automata, a PSpace-complete problem. Our approach, like others before, leverage a notion of quasiorder to prune the search for a counterexample by discarding candidates which are subsumed by others for the quasiorder. Discarded candidates are guaranteed to not compromise the completeness of the algorithm. The novelty of our work lies in the quasiorder used to discard candidates. We introduce FORQs (family of right quasiorders) that we obtain by adapting the notion of family of right congruences put forward by Maler and Staiger in 1993. We define a FORQ-based inclusion algorithm which we prove correct and instantiate it for a specific FORQ, called the structural FORQ, induced by the Büchi automaton to the right of the inclusion sign. The resulting implementation, called Forklift, scales up better than the state-of-the-art on a variety of benchmarks including benchmarks from program verification and theorem proving for word combinatorics. Artifact: https://doi.org/10.5281/zenodo.6552870
This work was partially funded by the ESF Investing in your future, the Madrid regional project S2018/TCS-4339 BLOQUES, the Spanish project PGC2018-102210-B-I00 BOSCO, the Ramón y Cajal fellowship RYC-2016-20281, and the ERC grant PR1001ERC02.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords

1 Introduction
In verification [19, 20] and theorem proving [31], Büchi automata have been used as the underlying formal model. In these settings, Büchi automata respectively encode 1) the behaviors of a system as well as properties about it; and 2) the set of valuations satisfying a predicate. Questions like asking whether a system complies with a specification naturally reduce to a language inclusion problem and so does proving a theorem of the form \(\forall x\, \exists y,\, P(x) \Rightarrow Q(y)\).
In this paper we propose a new algorithm for the inclusion problem between \(\omega \)-regular languages given by Büchi automata. The problem is PSpace-complete [23] and significant effort has been devoted to the discovery of algorithms for inclusion that behave well in practice [8, 10, 14, 18, 22, 25]. Each proposed algorithm is characterized by a set of techniques (e.g. Ramsey-based, rank-based) and heuristics (e.g. antichains, simulation relations). The algorithm we propose falls into the category of Ramsey-based algorithms and uses the antichain [11] heuristics: the search for counterexamples is pruned using quasiorders. Intuitively when two candidate counterexamples are comparable with respect to some considered quasiorder, the “higher” of the two can be discarded without compromising completeness of the search. In our setting, counterexamples to inclusion are ultimately periodic words, i.e., words of the form \(u^{}v^{\omega }\), where \(u\) and \(v\) are called a stem and a period, respectively. Therefore pruning is done by comparing stems and periods of candidate counterexamples during the search.
In the work of Abdulla et al. [7, 8] which was further refined by Clemente et al. [10] they use a single quasiorder to compare both stems and periods. Their effort has been focused on refining that single quasiorder by enhancing it with simulation relations. Others including some authors of this paper, followed an orthogonal line [13, 22] that investigates the use of two quasiorders: one for the stems and another one, independent, for the periods. The flexibility of using different quasiorders yields more pruning when searching for a counterexample. In this paper, we push the envelope further by using an unbounded number of quasiorders: one for the stems and a family of quasiorders for the periods each of them depending on a distinct stem. We use the acronym FORQ, which stands for family of right quasiorders, to refer to these quasiorders. Using FORQs leads to significant algorithmic differences compared to the two quasiorders approaches. More precisely, the algorithms with two quasiorders [13, 22] compute exactly two fixpoints (one for the stems and one for the periods) independently whereas the FORQ-based algorithm that we present computes two fixpoints for the stems and unboundedly many fixpoints for the periods (depending on the number of stems that belong to the first two fixpoints). Even though we lose the stem/period independence and we compute more fixpoints, in practice, the use of FORQs scales up better than the approaches based on one or two quasiorders.
We formalize the notion of FORQ by relaxing and generalizing the notion of family of right congruences introduced by Maler and Staiger [30] to advance the theory of recognizability of \(\omega \)-regular languages and, in particular, questions related to minimal-state automata. Recently, families of right congruences have been used in other contexts like the learning of \(\omega \)-regular languages (see [9] and references therein) and Büchi automata complementation [26].
Below, we describe how our contributions are organized:
-
We define the notion of FORQs and leverage them to identify key finite sets of stems and periods that are sound and complete to decide the inclusion problem (Sect. 3).
-
We introduce a FORQ called the structural FORQ which relies on the structure of a given Büchi automaton (Sect. 4).
-
We formulate a FORQ-based inclusion algorithm that computes such key sets as fixpoints, and then use these key stems and periods to search for a counterexample to inclusion via membership queries (Sect. 5).
-
We study the algorithmic complexity of the FORQ-based inclusion algorithm instantiated with structural FORQs (Sect. 6).
-
We implement the inclusion algorithm with structural FORQs in a prototype called Forklift and we conduct an empirical evaluation on a set of 674 benchmarks (Sect. 7).
2 Preliminaries
Languages. Let \(\varSigma \) be a finite and non-empty alphabet. We write \(\varSigma ^*\) to refer to the set of finite words over \(\varSigma \) and we write \(\varepsilon \) to denote the empty word. Given \(u \in \varSigma ^*\), we denote by \(|u|\) the length of \(u\). In particular \(|\varepsilon | = 0\). We also define \(\varSigma ^+ \triangleq \varSigma ^* \setminus \{ \varepsilon \}\), and \(\varSigma ^{\nabla n} \triangleq \{ u\in \varSigma ^* \mid |u|\mathrel {\nabla } n\}\) with \(\nabla \in \{\le ,\ge \}\), hence \(\varSigma ^* = \varSigma ^{\ge 0}, \varSigma ^+=\varSigma ^{\ge 1}\). We write \(\varSigma ^{\omega }\) to refer to the set of infinite words over \(\varSigma \). An infinite word \(\mu \in \varSigma ^{\omega }\) is said to be ultimately periodic if it admits a decomposition \(\mu =u^{}v^{\omega }\) with \(u\in \varSigma ^*\) (called a stem) and \(v\in \varSigma ^+\) (called a period). We fix an alphabet \(\varSigma \) throughout the paper.
Order Theory. Let \(E\) be a set of elements and \(\mathord {\ltimes }\) be a binary relation over \(E\). The relation \(\mathord {\ltimes }\) is said to be a quasiorder when it is reflexive and transitive. Given a subset \(X\) of \(E\), we define its upward closure with respect to the quasiorder \(\mathord {\ltimes }\) by  . Given two subsets \(X, Y\subseteq E\) the set \(Y\) is said to be a basis for \(X\) with respect to \(\mathord {\ltimes }\), denoted \({\mathfrak {B}_{\ltimes }(Y, X)}\), whenever \(Y\subseteq X\) and
. Given two subsets \(X, Y\subseteq E\) the set \(Y\) is said to be a basis for \(X\) with respect to \(\mathord {\ltimes }\), denoted \({\mathfrak {B}_{\ltimes }(Y, X)}\), whenever \(Y\subseteq X\) and  . The quasiorder \(\mathord {\ltimes }\) is a well-quasiorder iff for each set \(X\subseteq E\) there exists a finite set \(Y\subseteq E\) such that \(\mathfrak {B}_{\ltimes }(Y, X) \). This property on bases is also known as the finite basis property. Other equivalent definitions of well-quasiorders can be found in the literature [27], we will use the followings:
. The quasiorder \(\mathord {\ltimes }\) is a well-quasiorder iff for each set \(X\subseteq E\) there exists a finite set \(Y\subseteq E\) such that \(\mathfrak {B}_{\ltimes }(Y, X) \). This property on bases is also known as the finite basis property. Other equivalent definitions of well-quasiorders can be found in the literature [27], we will use the followings:
-
1.
For every \(\{e_i\}_{i\in \mathbb {N}}\in E^\mathbb {N}\) there exists \(i,j\in \mathbb {N}\) with \(i<j\) such that \(e_i \ltimes e_j\).
-
2.
No sequence \(\{X_i\}_{i\in \mathbb {N}}\in \wp (E)^\mathbb {N}\) is such that
 holds.Footnote 1
holds.Footnote 1
Automata. A (nondeterministic) Büchi automaton \(\mathcal {B}\) (BA for short) is a tuple \((Q, q_I, \varDelta , F)\) where Q is a finite set of states including \(q_I\), the initial state, \(\varDelta \subseteq Q \times \varSigma \times Q\) is the transition relation, and, \(F \subseteq Q\) is the set of accepting states. We lift \(\varDelta \) to finite words as expected. We prefer to write  instead of \((q_1, u, q_2) \in \varDelta \). In addition, we write
instead of \((q_1, u, q_2) \in \varDelta \). In addition, we write  when there exists a state \(q_F\in F\) and two words \(u_1, u_2\) such that
when there exists a state \(q_F\in F\) and two words \(u_1, u_2\) such that  .
.
A run \(\pi \) of \(\mathcal {B}\) over \(\mu = a_0 a_1 \cdots \in \varSigma ^\omega \) is a function \(\pi :\mathbb {N}\rightarrow Q\) such that \(\pi (0) = q_I\) and for all position \(i \in \mathbb {N}\), we have that  . A run is said to be accepting if \(\pi (i) \in F\) for infinitely many values of \(i\in \mathbb {N}\). The language \(L(\mathcal {B})\) of words recognized by \(\mathcal {B}\) is the set of \(\omega \)-words for which \(\mathcal {B}\) admits an accepting run. A language \(L\) is \(\omega \)-regular if it is recognized by some BA.
. A run is said to be accepting if \(\pi (i) \in F\) for infinitely many values of \(i\in \mathbb {N}\). The language \(L(\mathcal {B})\) of words recognized by \(\mathcal {B}\) is the set of \(\omega \)-words for which \(\mathcal {B}\) admits an accepting run. A language \(L\) is \(\omega \)-regular if it is recognized by some BA.
3 Foundations of Our Approach
Let \(\mathcal {A} \triangleq (P, p_I, \varDelta _{\mathcal {A}}, F_{\mathcal {A}})\) be a Büchi automaton and \(M\) be an \(\omega \)-regular language. The main idea behind our approach is to compute a finite subset \(T_\mathcal {A} \) of ultimately periodic words of \(L(\mathcal {A})\) such that:
Then \(L(\mathcal {A}) \subseteq M\) holds iff each of the finitely many words of \(T_\mathcal {A} \) belongs to \(M\) which is tested via membership queries.
First we observe that such a subset always exists: if the inclusion holds take \(T_\mathcal {A} \) to be any finite subset of \(L(\mathcal {A})\) (empty set included); else take \(T_\mathcal {A} \) to contain some ultimately periodic word that is a counterexample to inclusion. In what follows, we will show that a finite subset \(T_\mathcal {A} \) satisfying (\(\dagger \)) can be computed by using an ordering to prune the ultimately periodic words of \(L(\mathcal {A})\). We will obtain such an ordering using a family of right quasiorders, a notion introduced below.
Definition 1
(FORQ). A family of right quasiorders is a pair  where
where  is a right-monotonicFootnote 2 quasiorder as well as every
is a right-monotonicFootnote 2 quasiorder as well as every  where \(u \in \varSigma ^*\). Additionally, for all \(u, u' \in \varSigma ^*\), we require
where \(u \in \varSigma ^*\). Additionally, for all \(u, u' \in \varSigma ^*\), we require  called the FORQ constraint.
called the FORQ constraint.
First, we observe that the above definition uses separate orderings for stems and periods. The definition goes even further, the ordering used for periods is depending on stems so that a period may or may not be discarded depending on the stem under consideration. The FORQ constraint tells us that if the periods \(v\) and \(w\) compare for a stem \(u'\), that is  , then they also compare for every stem \(u\) subsuming \(u'\), that is
, then they also compare for every stem \(u\) subsuming \(u'\), that is  if
if  .
.
Expectedly, a FORQ needs to satisfy certain properties for \(T_\mathcal {A} \) to be finite, computable and for (\(\dagger \)) to hold (in particular the left to right direction). The property of right-monotonicity of FORQs is needed so that we can iteratively compute \(T_\mathcal {A} \) via a fixpoint computation (see Sect. 5).
Definition 2
(Suitable FORQ). A FORQ  is said to be finite (resp. decidable) when
is said to be finite (resp. decidable) when  , its converse
, its converse  , and
, and  for all \(u \in \varSigma ^*\) are all well-quasiorders (resp. computable). Given \(L\subseteq \varSigma ^\omega \), \(\mathcal {F} \) is said to preserve \(L\) when for all \(u,\hat{u}\in \varSigma ^*\) and all \(v, \hat{v} \in \varSigma ^+\) if \(u^{}v^{\omega }\in L\),
for all \(u \in \varSigma ^*\) are all well-quasiorders (resp. computable). Given \(L\subseteq \varSigma ^\omega \), \(\mathcal {F} \) is said to preserve \(L\) when for all \(u,\hat{u}\in \varSigma ^*\) and all \(v, \hat{v} \in \varSigma ^+\) if \(u^{}v^{\omega }\in L\),  ,
,  and
and  then \(\hat{u}^{}\hat{v}^{\omega }\in L\). Finally, \(\mathcal {F} \) is said to be \(L\)-suitable (for inclusion) if it is finite, decidable and preserves \(L\).
then \(\hat{u}^{}\hat{v}^{\omega }\in L\). Finally, \(\mathcal {F} \) is said to be \(L\)-suitable (for inclusion) if it is finite, decidable and preserves \(L\).
Intuitively, the “well” property on the quasiorders ensures finiteness of \(T_\mathcal {A} \). The preservation property ensures completeness: a counterexample to \(L(\mathcal {A})\subseteq M\) can only be discarded (that is, not included in \(T_\mathcal {A} \)) if it is subsumed by another ultimately periodic word in \(T_\mathcal {A} \) that is also a counterexample to inclusion.
Before defining \(T_\mathcal {A} \) we introduce for each state \(p\in P\) the sets of words

The set \(\mathtt {Stem} _p\) is the set of stems of \(L(\mathcal {A})\) that reach state \(p\) in \(\mathcal {A} \) while the set \(\mathtt {Per} _p\) is the set of periods read by a cycle of \(\mathcal {A} \) on state \(p\).
Given a \(M\)-suitable FORQ  , we let
, we let

where for all \(p\in P\), the set \(U_p\) is a basis of \(\mathtt {Stem} _p\) with respect to  , that is
, that is  holds. Moreover
holds. Moreover  holds and
holds and  holds for all \(w\in W_p\). Note that the quasiorder
holds for all \(w\in W_p\). Note that the quasiorder  used to prune the periods of \(\mathtt {Per} _p\) depends on a maximal w.r.t.
used to prune the periods of \(\mathtt {Per} _p\) depends on a maximal w.r.t.  stem \(w\) of \(\mathtt {Stem} _p\) since \(w\) belongs to the basis \(W_p\) for
stem \(w\) of \(\mathtt {Stem} _p\) since \(w\) belongs to the basis \(W_p\) for  . The correctness argument for choosing
. The correctness argument for choosing  essentially relies on the FORQ constraint as the proof of (\(\dagger \)) given below shows. In Sect. 8 we will show, that when \(w\) is not “maximal” the quasiorder
essentially relies on the FORQ constraint as the proof of (\(\dagger \)) given below shows. In Sect. 8 we will show, that when \(w\) is not “maximal” the quasiorder  yields a set \(T_\mathcal {A} \) for which (\(\dagger \)) does not hold.
yields a set \(T_\mathcal {A} \) for which (\(\dagger \)) does not hold.
Furthermore, we conclude from the finite basis property of the quasiorders of \(\mathcal {F} \) that \(U_p\), \(W_p\) and \(\{V_p^w\}_{w\in \varSigma ^*}\) are finite for all \(p\in P\), hence \(T_\mathcal {A} \) is a finite subset of ultimately periodic words of \(L(\mathcal {A})\). Next we prove the equivalence (\(\dagger \)). The proof crucially relies on the preservation property of \(\mathcal {F} \) which allows discarding candidate counterexamples without loosing completeness, that is, if inclusion does not hold a counterexample will be returned.
Proof
(of (\(\dagger \))). Consider  . It is easy to show that \(\texttt {Ultim}_\mathcal {A} = \{u^{}v^{\omega } \mid \exists s\in F_{\mathcal {A}}:u\in \mathtt {Stem} _s, v\in \mathtt {Per} _s\}\) (same definition as \(\texttt {Ultim}_\mathcal {A} \) but without the constraint
. It is easy to show that \(\texttt {Ultim}_\mathcal {A} = \{u^{}v^{\omega } \mid \exists s\in F_{\mathcal {A}}:u\in \mathtt {Stem} _s, v\in \mathtt {Per} _s\}\) (same definition as \(\texttt {Ultim}_\mathcal {A} \) but without the constraint  ) by reasoning on properties of well-quasi orders.Footnote 3 It is well-known that \(\omega \)-regular language inclusion holds if and only if it holds for ultimately periodic words. Formally \(L(\mathcal {A}) \subseteq M\) holds if and only if \(\texttt {Ultim}_\mathcal {A} \subseteq M\) holds. Therefore, to prove (\(\dagger \)), we show that \(T_\mathcal {A} \subseteq M \Leftrightarrow \texttt {Ultim}_\mathcal {A} \subseteq M\).
) by reasoning on properties of well-quasi orders.Footnote 3 It is well-known that \(\omega \)-regular language inclusion holds if and only if it holds for ultimately periodic words. Formally \(L(\mathcal {A}) \subseteq M\) holds if and only if \(\texttt {Ultim}_\mathcal {A} \subseteq M\) holds. Therefore, to prove (\(\dagger \)), we show that \(T_\mathcal {A} \subseteq M \Leftrightarrow \texttt {Ultim}_\mathcal {A} \subseteq M\).
To prove the implication \(\texttt {Ultim}_\mathcal {A} \subseteq M \Rightarrow T_\mathcal {A} \subseteq M\) we start by taking a word \(u^{}v^{\omega } \in T_\mathcal {A} \) such that, by definition (\(\ddagger \)), \(u \in U_s\) and \(v\in V_s^w\) for some \(s\in F_\mathcal {A} \) and \(w\in W_s\). We conclude from  and
and  that \(u\in U_s \subseteq \mathtt {Stem} _s\) and \(v\in V_s^w \subseteq \mathtt {Per} _s\). Thus, we find that \( u^{}v^{\omega }\in \texttt {Ultim}_\mathcal {A} \) hence the assumption \(\texttt {Ultim}_\mathcal {A} \subseteq M\) shows that \(u^{}v^{\omega } \in M\) which proves the implication.
that \(u\in U_s \subseteq \mathtt {Stem} _s\) and \(v\in V_s^w \subseteq \mathtt {Per} _s\). Thus, we find that \( u^{}v^{\omega }\in \texttt {Ultim}_\mathcal {A} \) hence the assumption \(\texttt {Ultim}_\mathcal {A} \subseteq M\) shows that \(u^{}v^{\omega } \in M\) which proves the implication.
Next, we prove that \(T_\mathcal {A} \subseteq M \Rightarrow \texttt {Ultim}_\mathcal {A} \subseteq M\) holds as well. Let \(u^{}v^{\omega } \in \texttt {Ultim}_\mathcal {A} \), i.e., such that there exists \(s\in F_\mathcal {A} \) for which \(u \in \mathtt {Stem} _s\) and \(v \in \mathtt {Per} _s\), satisfying  . Since \(u \in \mathtt {Stem} _s\) and \(v \in \mathtt {Per} _s\), there exist \(u_0\in U_s\), \(w_0 \in W_s\) and \(v_0\in V_s^{w_0}\) such that
. Since \(u \in \mathtt {Stem} _s\) and \(v \in \mathtt {Per} _s\), there exist \(u_0\in U_s\), \(w_0 \in W_s\) and \(v_0\in V_s^{w_0}\) such that  and
and  thanks to the finite basis property. By definition we have \(u_0^{}v_0^{\omega } \in T_\mathcal {A} \) and thus we find that \(u_0^{}v_0^{\omega } \in M\) since \(T_\mathcal {A} \subseteq M\). Next since
thanks to the finite basis property. By definition we have \(u_0^{}v_0^{\omega } \in T_\mathcal {A} \) and thus we find that \(u_0^{}v_0^{\omega } \in M\) since \(T_\mathcal {A} \subseteq M\). Next since  , the FORQ constraint shows that
, the FORQ constraint shows that  which, in turn, implies that
which, in turn, implies that  holds. Finally, we deduce from \(u_0^{}v_0^{\omega } \in M\),
holds. Finally, we deduce from \(u_0^{}v_0^{\omega } \in M\),  ,
,  ,
,  and the preservation of \(M\) by the FORQ \(\mathcal {F} \) that \(u^{}v^{\omega }\in M\). We thus obtain that \(\texttt {Ultim}_\mathcal {A} \subseteq M\) and we are done. \(\square \)
and the preservation of \(M\) by the FORQ \(\mathcal {F} \) that \(u^{}v^{\omega }\in M\). We thus obtain that \(\texttt {Ultim}_\mathcal {A} \subseteq M\) and we are done. \(\square \)
Example 3
To gain more insights about our approach consider the BAs of Fig. 1 for which we want to check whether \(L(\mathcal {A})\subseteq L(\mathcal {B})\) holds. From the description of \(\mathcal {A} \) it is routine to check that \(\mathtt {Stem} _{p_I} = \varSigma ^* \) and \(\mathtt {Per} _{p_I} = \varSigma ^+\). Let us assume the existenceFootnote 4 of  (hence
(hence  ),
),  and
and  such that
such that  holds and so does
holds and so does  ,
,  and
and  . In addition, we set \(U_{p_I}=\{\varepsilon ,a\}\) since
. In addition, we set \(U_{p_I}=\{\varepsilon ,a\}\) since  and \(W_{p_I}=\{\varepsilon ,aa\}\) since
and \(W_{p_I}=\{\varepsilon ,aa\}\) since  . Moreover \(V_{p_I}^\varepsilon =\{b\}\) since
. Moreover \(V_{p_I}^\varepsilon =\{b\}\) since  , and \(V_{p_I}^{aa}=\{a\}\) since
, and \(V_{p_I}^{aa}=\{a\}\) since  . Next by definition (\(\ddagger \)) of \(T_\mathcal {A} \) and from
. Next by definition (\(\ddagger \)) of \(T_\mathcal {A} \) and from  we deduce that \(T_\mathcal {A} = \{ \varepsilon ^{}(b)^{\omega }, a^{}(a)^{\omega } \}\). Finally, we conclude from (\(\dagger \)) and \( a^\omega \in T_\mathcal {A} \) that \(a^\omega \in L(\mathcal {A})\) (since \(T_\mathcal {A} \subseteq L(\mathcal {A})\)) hence that \(L(\mathcal {A}) \nsubseteq L(\mathcal {B})\) because \(a^\omega \notin L(\mathcal {B})\). By checking membership of the two ultimately periodic words of \(T_\mathcal {A} \) into \(L(\mathcal {B})\) we thus have shown that \(L(\mathcal {A}) \subseteq L(\mathcal {B})\) does not hold.
we deduce that \(T_\mathcal {A} = \{ \varepsilon ^{}(b)^{\omega }, a^{}(a)^{\omega } \}\). Finally, we conclude from (\(\dagger \)) and \( a^\omega \in T_\mathcal {A} \) that \(a^\omega \in L(\mathcal {A})\) (since \(T_\mathcal {A} \subseteq L(\mathcal {A})\)) hence that \(L(\mathcal {A}) \nsubseteq L(\mathcal {B})\) because \(a^\omega \notin L(\mathcal {B})\). By checking membership of the two ultimately periodic words of \(T_\mathcal {A} \) into \(L(\mathcal {B})\) we thus have shown that \(L(\mathcal {A}) \subseteq L(\mathcal {B})\) does not hold.
In the example above we did not detail how the FORQ was obtained let alone how to compute the finite bases. We fill that gap in the next two sections: we define FORQs based on the underlying structure of a given BA in Sect. 4 and show they are suitable; and we give an effective computation of the bases hence our FORQ-based inclusion algorithm in Sect. 5.
4 Defining FORQs from the Structure of an Automaton
In this section we introduce a type of FORQs called structural FORQs such that given a BA \(\mathcal {B} \) the structural FORQ induced by \(\mathcal {B} \) is \(L(\mathcal {B})\)-suitable.
Definition 4
Let \(\mathcal {B} \triangleq (Q, q_I, \varDelta _\mathcal {B}, F_\mathcal {B})\) be a BA. The structural FORQ of \(\mathcal {B}\) is the pair  where the quasiorders are defined by:
where the quasiorders are defined by:

with \(\mathtt {Tgt} _\mathcal {B} :\wp (Q) \times \varSigma ^* \rightarrow \wp (Q)\) and \(\mathtt {Cxt} _\mathcal {B} :\wp (Q) \times \varSigma ^* \rightarrow \wp (Q^2 \times \{\bot , \top \})\)

Given \(u \in \varSigma ^*\), the set  contains states that \(u\) can “target” from the initial state \(q_I\). A “context” \((q, q', k)\) returned by \(\mathtt {Cxt} _\mathcal {B} \), consists in a source state \(q \in Q\), a sink state \(q' \in Q\) and a boolean \(k \in \{\top , \bot \}\) that keeps track whether an accepting state is visited. Note that, having \(\bot \) as last component of a context does not mean that no accepting state is visited. When it is clear from the context, we often omit the subscript \(\mathcal {B} \) from \(\mathtt {Tgt} _\mathcal {B} \) and \(\mathtt {Cxt} _\mathcal {B} \). Analogously, we omit the BA from the structural FORQ quasiorders when there is no ambiguity.
contains states that \(u\) can “target” from the initial state \(q_I\). A “context” \((q, q', k)\) returned by \(\mathtt {Cxt} _\mathcal {B} \), consists in a source state \(q \in Q\), a sink state \(q' \in Q\) and a boolean \(k \in \{\top , \bot \}\) that keeps track whether an accepting state is visited. Note that, having \(\bot \) as last component of a context does not mean that no accepting state is visited. When it is clear from the context, we often omit the subscript \(\mathcal {B} \) from \(\mathtt {Tgt} _\mathcal {B} \) and \(\mathtt {Cxt} _\mathcal {B} \). Analogously, we omit the BA from the structural FORQ quasiorders when there is no ambiguity.
Lemma 5
Given a BA \(\mathcal {B} \), the pair  of Definition 4 is a FORQ.
of Definition 4 is a FORQ.
Proof
Let \(\mathcal {B} \triangleq (Q, q_I, \varDelta _\mathcal {B}, F_\mathcal {B})\) be a BA, we start by proving that the FORQ constraint holds:  . First, we observe that, for all \(Y \subseteq X \subseteq Q\) and all \(v, v' \in \varSigma ^*\), we have that
. First, we observe that, for all \(Y \subseteq X \subseteq Q\) and all \(v, v' \in \varSigma ^*\), we have that  . Consider \(u, u' \in \varSigma ^*\) such that
. Consider \(u, u' \in \varSigma ^*\) such that  and \(v, v' \in \varSigma ^*\) such that
and \(v, v' \in \varSigma ^*\) such that  . Let
. Let  and
and  , we have that \(X\subseteq X'\) following
, we have that \(X\subseteq X'\) following  . Next, we conclude from
. Next, we conclude from  that
that  , hence that
, hence that  by the above reasoning using \(X\subseteq X'\), and finally that
by the above reasoning using \(X\subseteq X'\), and finally that  .
.
For the right monotonicity, Definition 4 shows that if  , hence we have
, hence we have  implies
implies  for all \(a\in \varSigma \). The reasoning with the other quasiorders and \(\mathtt {Cxt}\) proceeds analogously. \(\square \)
for all \(a\in \varSigma \). The reasoning with the other quasiorders and \(\mathtt {Cxt}\) proceeds analogously. \(\square \)
Example 6
Consider the BA \(\mathcal {B}\) of Fig. 1 and let  be its structural FORQ. More precisely, we have
be its structural FORQ. More precisely, we have  ; and
; and  for all \(u \in \varSigma ^{\ge 2}\). In particular we conclude from
for all \(u \in \varSigma ^{\ge 2}\). In particular we conclude from  that
that  ,
,  and
and  ; \(\varepsilon \) and \(a\) are incomparable; and so are \(\varepsilon \) and \(aa\). Since \(\mathtt {Tgt}\) has only three distinct outputs, the set
; \(\varepsilon \) and \(a\) are incomparable; and so are \(\varepsilon \) and \(aa\). Since \(\mathtt {Tgt}\) has only three distinct outputs, the set  contains three distinct quasiorders.
contains three distinct quasiorders.
-
1.
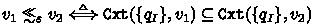 where
where -
-
2.
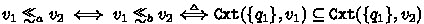 where
where-
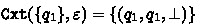
-
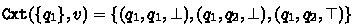 for all \(v\in \varSigma ^+\)
for all \(v\in \varSigma ^+\)
-
-
3.
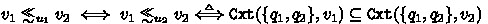 for all \(u_1,u_2\in \varSigma ^{{}\ge 2}\) where
for all \(u_1,u_2\in \varSigma ^{{}\ge 2}\) where-
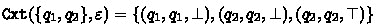
-
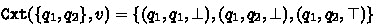 for all \( v \in {\varSigma }^{+} \{b\}^{+} \)
for all \( v \in {\varSigma }^{+} \{b\}^{+} \) -
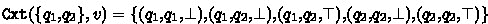 for all \( v \in \{b\}^{+} \)
for all \( v \in \{b\}^{+} \)
-
With the above definitions the reader is invited to check the following predicates  ,
,  ,
,  ,
,  ,
,  and
and  . Also observe that none of the above finite bases contains comparable words for the ordering thereof. We also encourage the reader to revisit Example 3.
. Also observe that none of the above finite bases contains comparable words for the ordering thereof. We also encourage the reader to revisit Example 3.
As prescribed in Sect. 3, we show that for every BA \(\mathcal {B} \) its structural FORQ is \(L(\mathcal {B})\)-suitable, namely it is finite, decidable and preserves \(L(\mathcal {B})\).
Proposition 7
Given a BA \(\mathcal {B}\), its structural FORQ is \(L(\mathcal {B})\)-suitable.
Proof
Let \(\mathcal {B} \triangleq (Q, q_I, \varDelta _\mathcal {B}, F_\mathcal {B})\) be a BA and  be its structural FORQ. The finiteness proof of \(\mathcal {F} \) is trivial since \(Q\) is finite and so is the proof of decidability by Definition 4. For the preservation, given \( u_0^{}v_0^{\omega } \in L(\mathcal {B})\), we show that for all \(u \in \varSigma ^*\) and all \(v \in \varSigma ^+\) such that
be its structural FORQ. The finiteness proof of \(\mathcal {F} \) is trivial since \(Q\) is finite and so is the proof of decidability by Definition 4. For the preservation, given \( u_0^{}v_0^{\omega } \in L(\mathcal {B})\), we show that for all \(u \in \varSigma ^*\) and all \(v \in \varSigma ^+\) such that  and
and  and
and  then \(u^{}v^{\omega } \in L(\mathcal {B})\) holds. Let a run
then \(u^{}v^{\omega } \in L(\mathcal {B})\) holds. Let a run  of \(\mathcal {B}\) over \(u_0^{}v_0^{\omega }\) which is accepting. Stated equivalently, we have
of \(\mathcal {B}\) over \(u_0^{}v_0^{\omega }\) which is accepting. Stated equivalently, we have  and
and  for every \(i\in \mathbb {N}\) with the additional constraint that \(x_i = \top \) holds infinitely often.
for every \(i\in \mathbb {N}\) with the additional constraint that \(x_i = \top \) holds infinitely often.
We will show that \(\mathcal {B}\) has an accepting run over \(u^{}v^{\omega }\) by showing that  holds;
holds;  holds for every \(i\in \mathbb {N}\); and \(x_i = \top \) holds infinitely often. Since
holds for every \(i\in \mathbb {N}\); and \(x_i = \top \) holds infinitely often. Since  and
and  we find that
we find that  by definition of
by definition of  . Next we show the remaining constraints by induction. The induction hypothesis states that for all \(0\le n\) we have
. Next we show the remaining constraints by induction. The induction hypothesis states that for all \(0\le n\) we have  . For the base case (\(n=0\)) we have to show that
. For the base case (\(n=0\)) we have to show that  . We conclude from
. We conclude from  ,
,  and the definition of
and the definition of  that
that  and finally that
and finally that  . For the inductive case, assume
. For the inductive case, assume  . The definition of context shows that
. The definition of context shows that  . It takes an easy an induction to show that
. It takes an easy an induction to show that  for all \(n\) using
for all \(n\) using  and right-monotonicity of
and right-monotonicity of  . We conclude from
. We conclude from  , the definition of
, the definition of  and \(q_{n+1} \in \mathtt {Tgt} (uv^{n+1})\) that
and \(q_{n+1} \in \mathtt {Tgt} (uv^{n+1})\) that  also holds, hence that
also holds, hence that  following the definition of contexts and that of \(\pi _0\). Next, we find that
following the definition of contexts and that of \(\pi _0\). Next, we find that  following a reasoning analogous to the base case, this time starting with
following a reasoning analogous to the base case, this time starting with  . Finally,
. Finally,  implies that
implies that  . We have thus shown that
. We have thus shown that  and
and  for every \(i\in \mathbb {N}\) with the additional constraint that \(x_i = \top \) holds infinitely often and we are done. \(\square \)
for every \(i\in \mathbb {N}\) with the additional constraint that \(x_i = \top \) holds infinitely often and we are done. \(\square \)
5 A FORQ-Based Inclusion Algorithm
As announced at the end of Sect. 3 it remains, in order to formulate our FORQ-based algorithm deciding whether \(L(\mathcal {A}) \subseteq M\) holds, to give an effective computation for the bases defining \(T_\mathcal {A} \). We start with a fixpoint characterization of the stems and periods of BAs using the function \(\mathtt {Rcat} _\mathcal {A} :\wp (\varSigma ^*)^{|P|} \rightarrow \wp (\varSigma ^*)^{|P|}\):

where \(\vec {S}.{p}\) denotes the \(p\)-th element of the vector \(\vec {S} \in \wp (\varSigma ^*)^{|P|}\). In Fig. 2, the repeat/until loops at lines 4 and 5 compute iteratively subsets of the stems of \(\mathcal {A}\), while the loop at line 10 computes iteratively subsets of the periods of \(\mathcal {A}\). The following lemma formalizes the above intuition.
Lemma 8
Consider \(\vec {U}_0\) and \(\vec {V}_1^s\) (with \(s\in F_\mathcal {A} \)) in the FORQ-based algorithm. The following holds for all \(n \in \mathbb {N}\):

Prior to proving the correctness of the algorithm of Fig. 2 we need the following result which is key for establishing the correctness of the repeat/until loop conditions of lines 4, 5, and 10.
Lemma 9
Let \(\mathord {\ltimes }\) be a right-monotonic quasiorder over \(\varSigma ^*\). Given \(\mathcal {A} \triangleq (P, p_I, \varDelta _\mathcal {A}, F_\mathcal {A})\) and \(\vec {S}, \vec {S'} \in \wp (\varSigma ^*)^{|P|}\), if \(\mathfrak {B}_{\mathord {\ltimes }}(\vec {S'}.{p}, \vec {S}.{p}) \) holds for all \(p \in P\) then \(\mathfrak {B}_{\mathord {\ltimes }}(\mathtt {Rcat} _\mathcal {A} ^{}(\vec {S'}).{p}, \mathtt {Rcat} _\mathcal {A} ^{}(\vec {S}).{p}) \) holds for all \(p \in P\).
Proof
Consider \(w\in \mathtt {Rcat} _\mathcal {A} ^{}(\vec {S}).{p}\) where \(p\in P\), we show that there exists \(w'\in \mathtt {Rcat} _\mathcal {A} ^{}(\vec {S}').{p}\) such that \(w' \ltimes w\). Assume that \(\mathfrak {B}_{\mathord {\ltimes }}(\vec {S}'.{p}, \vec {S}.{p}) \) holds for all \(p\in P\). In particular, for all \(w_1 \in \vec {S}.{p}\), there exists \(w'_1 \in \vec {S}'.{p}\) such that \(w'_1 \ltimes w_1\). In the case where \(w_1 \in \mathtt {Rcat} _\mathcal {A} ^{}(\vec {S}).{p} \setminus \vec {S}.{p}\), by definition of \(\mathtt {Rcat} _\mathcal {A} \) \(w_1\) is of the form \(w_2a\) for some \(a\in \varSigma \) and some \(w_2\in \vec {S}.{\hat{p}}\) such that  . Since \(\mathfrak {B}_{\mathord {\ltimes }}(\vec {S}'.{\hat{p}}, \vec {S}.{\hat{p}}) \) and \(w_2\in \vec {S}.{\hat{p}}\), there exists \(w_3\in \vec {S}'.{\hat{p}}\) such that \(w_3 \ltimes w_2\). We deduce that \(w_3 a \ltimes w_2a\) holds, hence \(w_3 a \ltimes w_1\) holds as well from the right-monotonicity of \(\mathord {\ltimes }\). Furthermore \(w_3a \in \mathtt {Rcat} _\mathcal {A} ^{}(\vec {S}').{p}\) by definition of \(\mathtt {Rcat} _\mathcal {A} \) and since
. Since \(\mathfrak {B}_{\mathord {\ltimes }}(\vec {S}'.{\hat{p}}, \vec {S}.{\hat{p}}) \) and \(w_2\in \vec {S}.{\hat{p}}\), there exists \(w_3\in \vec {S}'.{\hat{p}}\) such that \(w_3 \ltimes w_2\). We deduce that \(w_3 a \ltimes w_2a\) holds, hence \(w_3 a \ltimes w_1\) holds as well from the right-monotonicity of \(\mathord {\ltimes }\). Furthermore \(w_3a \in \mathtt {Rcat} _\mathcal {A} ^{}(\vec {S}').{p}\) by definition of \(\mathtt {Rcat} _\mathcal {A} \) and since  . Finally, we conclude that \(\mathfrak {B}_{\mathord {\ltimes }}(\mathtt {Rcat} _\mathcal {A} ^{}(\vec {S'}), \mathtt {Rcat} _\mathcal {A} ^{}(\vec {S})) \) holds. \(\square \)
. Finally, we conclude that \(\mathfrak {B}_{\mathord {\ltimes }}(\mathtt {Rcat} _\mathcal {A} ^{}(\vec {S'}), \mathtt {Rcat} _\mathcal {A} ^{}(\vec {S})) \) holds. \(\square \)
Theorem 10
The FORQ-based algorithm decides the inclusion of BAs.
Proof
We first show that every loop of the algorithm eventually terminates. First, we conclude from the definition of \(\mathtt {Rcat} _\mathcal {A} \) and the initializations (lines 3 and 9) of each repeat/until loop (lines 4, 5, and 10) that each component of each vector holds a finite set of words. Observe that the halting conditions of the repeat/until loops are effectively computable since every quasiorder of \(\mathcal {F} \) is decidable and because, in order to decide \(\mathfrak {B}_{\mathord {\ltimes }}(Y, X) \) where \(X,Y\) are finite sets and \(\mathord {\ltimes }\) is decidable, it suffices to check that \(Y\subseteq X\) and that for every \(x\in X\) there exists \(y\in Y\) such that \(y \ltimes x\). Next, we conclude from the fact that all the quasiorders of \(\mathcal {F} \) used in the repeat/until loops are all well-quasiorders that there is no infinite sequence \(\{X_i\}_{i\in \mathbb {N}}\) such that  Since \(\mathfrak {B}_{\mathord {\ltimes }}(Y, X) \) is equivalent to
Since \(\mathfrak {B}_{\mathord {\ltimes }}(Y, X) \) is equivalent to  and since each time \(\mathtt {Rcat} _\mathcal {A} \) updates a component its upward closure after the update includes the one before, we find that every repeat/until loop must terminate after finitely many iterations.
and since each time \(\mathtt {Rcat} _\mathcal {A} \) updates a component its upward closure after the update includes the one before, we find that every repeat/until loop must terminate after finitely many iterations.
Next, we show that when the repeat/until loop of line 5 halts,  holds for all \(p\in P\). It takes an easy induction on \(n\) together with Lemma 9 to show that if
holds for all \(p\in P\). It takes an easy induction on \(n\) together with Lemma 9 to show that if  holds for all \(p\in P\) then
holds for all \(p\in P\) then  holds for all \(m>n\). Hence Lemma 8 shows that
holds for all \(m>n\). Hence Lemma 8 shows that  holds for all \(p\in P\) where \(k\) is the number of iterations of the repeat/until loop implying
holds for all \(p\in P\) where \(k\) is the number of iterations of the repeat/until loop implying  holds when the loop of line 5 halts.
holds when the loop of line 5 halts.
An analogue reasoning shows that  holds for all \(p\in P\), as well as
holds for all \(p\in P\), as well as  holds for all \(w\in \vec {W}.{s}\) and all \(s\in F_\mathcal {A} \) upon termination of the loops of lines 4 and 10.
holds for all \(w\in \vec {W}.{s}\) and all \(s\in F_\mathcal {A} \) upon termination of the loops of lines 4 and 10.
To conclude, we observe that each time a membership query is performed at line 13, the ultimately periodic word \(u^{}v^{\omega }\) belongs to \(T_\mathcal {A} \) defined by (\(\ddagger \)). This is ensured since  ,
,  ,
,  for some \(s \in F_\mathcal {A} \) and, thanks to the test at line 12, the comparison
for some \(s \in F_\mathcal {A} \) and, thanks to the test at line 12, the comparison  holds. \(\square \)
holds. \(\square \)
Remark 11
The correctness of the FORQ-based algorithm still holds when, after every “\({:}{=}\)” assignment (at lines 3, 4, 5, 9 and 10), we remove from the variable content zero or more subsumed words for the corresponding ordering. The effect of removing zero or more subsumed words from a variable can be achieved by replacing assignments like, for instance, \(\vec {U} {:}{=}\mathtt {Rcat} _\mathcal {A} ^{}(\vec {U})\) at line 5 with \(\vec {U} {:}{=}\mathtt {Rcat} _\mathcal {A} ^{}(\vec {U}); \vec {U}{:}{=}\vec {U}_r\) where \(\vec {U}_r\) satisfies  for all \(p\in P\). The correctness of the previous modification follows from Lemma 9. Therefore, the sets obtained by discarding subsumed words during computations still satisfy the basis predicates of \(T_\mathcal {A} \) given at (\(\ddagger \)).
for all \(p\in P\). The correctness of the previous modification follows from Lemma 9. Therefore, the sets obtained by discarding subsumed words during computations still satisfy the basis predicates of \(T_\mathcal {A} \) given at (\(\ddagger \)).
It is worth pointing out that the correctness arguments developed above, do not depend on the specifics of the structural FORQs. The FORQ-based algorithm is sound as long as we provide a suitable FORQ. Next we study the algorithmic complexity of the algorithm of Fig. 2.
6 Complexity of the Structural FORQ-Based Algorithm
In this Section, we establish an upper bound on the runtime of the algorithm of Fig. 2 when the input FORQ is the structural FORQ induced by a BA \(\mathcal {B} \). Let \(n_\mathcal {A} \) and \(n_\mathcal {B} \) be respectively the number of states in the BA \(\mathcal {A} \) and \(\mathcal {B} \). We start by bounding the number of iterations in the repeat/until loops. In each repeat/until loop, each component of the vector holds a finite set of words the upward closure of which grows (for \(\subseteq \)) over time and when all the upward closures stabilize the loop terminates. In the worst case, an iteration of the repeat/until loop adds exactly one word to some component of the vector which keeps the halting condition falsified (the upward closure strictly increases). Therefore a component of the vector cannot be updated more than \(2^{n_\mathcal {B}}\) times for otherwise its upward closure has stabilized. We thus find that the total number of iterations is bounded from above by \(n_\mathcal {A} \cdot 2^{n_\mathcal {B}}\) for the loops computing \(\vec {U}\) and \(\vec {W}\). Using an analogous reasoning we conclude that each component of the \(\vec {V}\) vector has no more than \(2^{(2 {n_\mathcal {B}}^2)}\) elements and the total number of iterations is upper-bounded by \( n_\mathcal {A} \cdot 2^{(2 {n_\mathcal {B}}^2)}\). To infer an upper bound on the runtime of each repeat/until loop we also need to multiply the above expressions by a factor \(|\varSigma |\) since the number of concatenations in \(\mathtt {Rcat}\) depends on the size of the alphabet.
Next, we derive an upper bound on the number of membership queries performed at line 13. The number of iterations of the loops of lines 6, 8, 10, 11 and 12 is \(n_\mathcal {A} \), \(2^{n_\mathcal {B}}\), \( n_\mathcal {A} \cdot 2^{(2 {n_\mathcal {B}}^2)}\), \( 2^{(2 {n_\mathcal {B}}^2)}\) and \(2^{n_\mathcal {B}}\), respectively. Since all loops are nested, we multiply these bounds to end up with \(n_\mathcal {A} ^2 \cdot 2^{\mathcal {O}(n_\mathcal {B} ^2)}\) as an upper bound on the number of membership queries. The runtime for each ultimately periodic word membership query (with a stem, a period and \(\mathcal {B} \) as input) is upper bounded by an expression polynomial in the size \(n_\mathcal {B} \) of \(\mathcal {B} \), \(2^{n_\mathcal {B}}\) for the length of the stem and \(2^{(2 {n_\mathcal {B}}^2)}\) for the length of the period.
We conclude from the above that the runtime of the algorithm of Fig. 2 is at most \(|\varSigma | \cdot n_\mathcal {A} ^2 \cdot 2^{\mathcal {O}(n_\mathcal {B} ^2)}\).
7 Implementation and Experiments
We implemented the FORQ-based algorithm of Fig. 2 instantiated by the structural FORQ in a tool called Forklift [2]. In this section, we provide algorithmic details about Forklift and then analyze how it behaves in practice (Sect. 7.1).
Data Structures. Comparing two words given a structural FORQ requires to compute the corresponding sets of target for stems (\(\mathtt {Tgt}\)), and sets of context for periods (\(\mathtt {Cxt}\)). A naïve implementation would be to compute \(\mathtt {Tgt}\) and \(\mathtt {Cxt}\) every time a comparison is needed. We avoid to compute this information over and over again by storing each stem together with its \(\mathtt {Tgt}\) set and each period together with its \(\mathtt {Cxt}\) set.
Moreover, the function \(\mathtt {Rcat}\) inserts new words in the input vector by concatenating a letter on the right to some words already in the vector. In our implementation, we do not recompute the associated set of targets nor context for the newly computed word from scratch. For all stem \(u \in \varSigma ^*\) and all letter \(a \in \varSigma \), the set of states  can be computed from
can be computed from  thanks to the following equality essentially stating that
thanks to the following equality essentially stating that  can be computed inductively:
can be computed inductively:

Analogously, for all period \(v \in \varSigma ^+\), all \(X \subseteq Q\) and all \(a \in \varSigma \), the set of contexts  can be computed from
can be computed from  thanks to the following equality:
thanks to the following equality:

Intuitively \(\mathtt {Cxt}\) can be computed inductively as we did for \(\mathtt {Tgt}\). The first part of the condition defines how new context are obtained by appending a transition to the right of an existing context while the second part defines the bit of information keeping record of whether an accepting state was visited.
Bases, Frontier and Membership Test. We stated in Remark 11 that the correctness of the FORQ-based algorithm is preserved when removing, from the computed sets, zero or more subsumed words for the corresponding ordering. In Forklift, we remove all the subsumed words from all the sets we compute which, intuitively, means each computed set is a basis that contains as few words as possible. To remove subsumed words we leverage the target or context sets kept along with the words. It is worth pointing out that the least fixpoint computations at lines 4, 5, and 10 are implemented using a frontier. Finally, the ultimately periodic word membership procedure is implemented as a classical depth-first search as described in textbooks [17, Chapter 13.1.1].
Technical Details. Forklift, a naïve prototype implemented by a single person over several weeks, implements the algorithm of Fig. 2 with the structural FORQ in less than 1 000 lines of Java code. One of the design goals of our tool was to have simple code that could be easily integrated in other tools. Therefore, our implementation relies solely on a few standard packages from the Java SE Platform (notably collections such as HashSet or HashMap).
7.1 Experimental Evaluation
Benchmarks. Our evaluation uses benchmarks stemming from various application domains including benchmarks from theorem proving, software verification, and from previous work on the \(\omega \)-regular language inclusion problem. In this section, a benchmark means an ordered pair of BAs such that the “left”/“right” BAs refer, resp., to the automata on the left/right of the inclusion sign. The BAs of the Pecan [31] benchmarks encode sets of solutions of predicates, hence a logical implication between predicates reduces to a language inclusion problem between BAs. The benchmarks correspond to theorems of type \(\forall x, \exists y,\, P(x) \implies Q(y)\) about Sturmian words [21]. We collected 60 benchmarks from Pecan for which inclusion holds, where the BAs have alphabets of up to 256 symbols and have up to 21 395 states.
The second collection of benchmarks stems from software verification. The Ultimate Automizer (UA) [19, 20] benchmarks encode termination problems for programs where the left BA models a program and the right BA its termination proof. Overall, we collected 600 benchmarks from UA for which inclusion holds for all but one benchmark. The BAs have alphabets of up to 13 173 symbols and are as large as 6 972 states.
The RABIT benchmarks are BAs modeling mutual exclusion algorithms [8], where in each benchmark one BA is the result of translating a set of guarded commands defining the protocol while the other BA translates a modified set of guarded commands, typically obtained by randomly weakening or strengthening one guard. The resulting BAs are on a binary alphabet and are as large as 7 963 states. Inclusion holds for 9 out of the 14 benchmarks.
All the benchmarks are publicly available on GitHub [12]. We used all the benchmarks we collected, that is, we discarded no benchmarks.
Tools. We compared Forklift with the following tools: SPOT 2.10.3, GOAL (20200822), RABIT 2.5.0, ROLL 1.0, and BAIT 0.1.
-
SPOT [15, 16] decides inclusion problems by complementing the “right” BA via determinization to parity automata with some additional optimizations including simulation-based optimizations. It is invoked through the command line tool autfilt with the option –included-in. It is worth pointing out that SPOT works with symbolic alphabets where symbols are encoded using Boolean propositions, and sets of symbols are represented and processed using OBDDs. SPOT is written in C++ and its code is publicly available [6].
-
GOAL [34] contains several language inclusion checkers available with multiple options. We used the Piterman algorithm using the options containment -m piterman with and without the additional options -sim -pre. In our plots \(\text {GOAL}\) is the invocation with the additional options -sim -pre which compute and use simulation relations to further improve performance while \(\text {GOAL}^{-}\) is the one without the additional options. Inclusion is checked by constructing on-the-fly the intersection of the “left” BA and the complement of the “right” BA which is itself built on-the-fly by the Piterman construction [32]. The Piterman check was deemed the “best effort” (cf. [10, Section 9.1] and [33]) among the inclusion checkers provided in GOAL. GOAL is written in Java and the source code of the release we used is not publicly available [3].
-
RABIT [10] performs the following operations to check inclusion: (1) Removing dead states and minimizing the automata with simulation-based techniques, thus yielding a smaller instance; (2) Witnessing inclusion by simulation already during the minimization phase; (3) Using a Ramsey-based method with antichain heuristics to witness inclusion or non-inclusion. The antichain heuristics of Step (3) uses a unique quasiorder leveraging simulation relations to discard candidate counterexamples. In our experiments we ran RABIT with options -fast -jf which RABIT states as providing the “best performance”. RABIT is written in Java and is publicly available [4].
-
ROLL [24, 25] contains an inclusion checker that does a preprocessing analogous to that of RABIT and then relies on automata learning and word sampling techniques to decide inclusion. ROLL is written in Java and is publicly available [5].
-
BAIT [13] which shares authors with the authors of the present paper, implements a Ramsey-based algorithm with the antichain heuristics where two quasiorders (one for the stems and the other for the periods) are used to discard candidate counterexamples as described in Sect. 1. BAIT is written in Java and is publicly available [1].
As far as we can tell all the above implementations, including Forklift, are sequential except for RABIT which, using the -jf option, performs some computations in a separate thread.
Experimental Setup. We ran our experiments on a server with \(24\,\text {GB}\) of RAM, 2 Xeon E5640 \(2.6~\text {GHz}\) CPUs and Debian Stretch \(64\)-bit. We used openJDK 11.0.12 2021-07-20 when compiling Java code and ran the JVM with default options. For RABIT, BAIT and Forklift the execution time is computed using timers internal to their implementations. For ROLL, GOAL and SPOT the execution time is given by the “real” value of the time(1) command. We preprocessed the benchmarks passed to Forklift and BAIT with a reduction of the set of final states of the “left” BA that does not alter the language it recognizes. This preprocessing aims to minimize the number of iterations of the loop at line 6 of Fig. 2 over the set of final states. It is carried out by GOAL using the acc -min command. Internally, GOAL uses a polynomial time algorithm that relies on computing strongly connected components. The time taken by this preprocessing is negligible.
Plots. We use survival plots for displaying our experimental results in Fig. 3. Let us recall how to obtain them for a family of benchmarks \(\{p_i\}_{i=1}^n\): (1) run the tool on each benchmark \(p_i\) and store its runtime \(t_i\); (2) sort the \(t_i\)’s in increasing order and discard pairs corresponding to abnormal program termination like time out or memory out; (3) plot the points \((t_1,1), (t_1+t_2,2)\),..., and in general \((\sum _{i=1}^k t_i,k)\); (4) repeat for each tool under evaluation.
Survival plots are effective at comparing how tools scale up on benchmarks: the further right and the flatter a plot goes, the better the tool thereof scales up. Also the closer to the \(x\)-axis a plot is, the less time the tool needs to solve the benchmarks.
Survival plot with a logarithmic \(y\) axis and linear \(x\) axis. Each benchmark has a timeout value of 12 h. Parts of the plots left out for clarity. A point is plotted for abscissa value \(x\) and tool \(r\) iff \(r\) returns with an answer for \(x\) benchmarks. All the failures of BAIT and the one of Forklift are memory out.
Analysis. It is clear from Fig. 3a and 3b that Forklift scales up best on both the Pecan and UA benchmarks. Forklift ’s scalability is particularly evident on the PECAN benchmarks of Fig. 3a where its curve is the flattest and no other tool finishes on all benchmarks. Note that, in Fig. 3b, the plot for SPOT is missing because we did not succeed into translating the UA benchmarks in the input format of SPOT. On the UA benchmarks, Forklift, BAIT and GOAL scale up well and we expect SPOT to scale up at least equally well. On the other hand, RABIT and ROLL scaled up poorly on these benchmarks.
On the RABIT benchmarks at Fig. 3c both Forklift and SPOT terminate 13 out of 14 times; BAIT terminates 9 out of 14 times; and GOAL, ROLL and RABIT terminate all the times. We claim that the RABIT benchmarks can all be solved efficiently by leveraging simulation relations which Forklift does not use let alone compute. Next, we justify this claim. First observe at Fig. 3c how GOAL is doing noticeably better than GOAL\(^{-}\) while we have the opposite situation for the Pecan benchmarks Fig. 3a and no noticeable difference for the UA benchmarks Fig. 3b. Furthermore observe how ROLL and RABIT, which both leverage simulation relations in one way or another, scale up well on the RABIT benchmarks but scale up poorly on the PECAN and UA benchmarks.
The reduced RABIT benchmarks at Fig. 3d are obtained by pre-processing every BA of every RABIT benchmark with the simulation-based reduction operation of SPOT given by autfilt –high –ba. This preprocessing reduces the state space of the BAs by more than 90% in some cases. The reduction significantly improves how Forklift scales up (it now terminates on all benchmarks) while it has less impact on RABIT, ROLL and SPOT which, as we said above, already leverage simulation relation internally. It is also worth noting that GOAL has a regression (from 14/14 before the reduction to 13/14).
Overall Forklift, even though it is a prototype implementation, is the tool that returns most often (673/674). Its unique failure disappears after a preprocessing using simulation relations of the two BAs. The Forklift curve for the Pecan benchmarks shows Forklift scales up best.
Our conclusion from the empirical evaluation is that, in practice Forklift is competitive compared to the state-of-the-art in terms of scalability. Moreover the behavior of the FORQ-based algorithm in practice is far from its worst case exponential runtime.
8 Discussions
This section provides information that we consider of interest although not essential for the correctness of our algorithm or its evaluation.
Origin of FORQs. Our definition of FORQ and their suitability property (in particular the language preservation) are directly inspired from the definitions related to families of right congruences introduced by Maler and Staiger in 1993 [28] (revised in 2008 [30]). We now explain how our definition of FORQs generalizes and relaxes previous definitions [30, Definitions 5 and 6].
First we explain why the FORQ constraint does not appear in the setting of families of right congruences. In the context of congruences, relations are symmetric and thus, the FORQ constraint reduces to  . Therefore the FORQ constraint trivially holds if the set
. Therefore the FORQ constraint trivially holds if the set  is quotiented by the congruence relation
is quotiented by the congruence relation  , which is the case in the definition [29, Definition 5].
, which is the case in the definition [29, Definition 5].
Second, we point that the condition  which appears in the definition for right families of congruences [30, Definition 5] is not needed in our setting. Nevertheless, this condition enables an improvement of the FORQ-based algorithm that we describe next.
which appears in the definition for right families of congruences [30, Definition 5] is not needed in our setting. Nevertheless, this condition enables an improvement of the FORQ-based algorithm that we describe next.
Less Membership Queries. We put forward a property of structural FORQs allowing us to reduce the number of membership queries performed by Forklift. Hereafter, we refer to the picky constraint as the property of a FORQ stating  where \(u, v, v' \in \varSigma ^*\). We first show how thanks to the picky constraint we can reduce the number of candidate counterexamples in the FORQ-based algorithm and then, we show that every structural FORQ satisfies the picky constraint.
where \(u, v, v' \in \varSigma ^*\). We first show how thanks to the picky constraint we can reduce the number of candidate counterexamples in the FORQ-based algorithm and then, we show that every structural FORQ satisfies the picky constraint.
In the algorithm of Fig. 2, periods are taken in a basis for the ordering  where \(w \in \varSigma ^*\) belongs to a finite basis for the ordering
where \(w \in \varSigma ^*\) belongs to a finite basis for the ordering  . The only restriction on \(w\) is that of being comparable to the stem \(u\), as ensured by the test at line 10. The following lemma formalizes the fact that we could consider a stronger restriction.
. The only restriction on \(w\) is that of being comparable to the stem \(u\), as ensured by the test at line 10. The following lemma formalizes the fact that we could consider a stronger restriction.
Lemma 12
Let  be a quasiorder over \(\varSigma ^*\) such that
be a quasiorder over \(\varSigma ^*\) such that  is a right-monotonic well-quasiorder. Let \(S, S' \subseteq \varSigma ^*\) be such that
is a right-monotonic well-quasiorder. Let \(S, S' \subseteq \varSigma ^*\) be such that  and \(S'\) contains no two distinct comparable words. For all \(u\in \varSigma ^*\) and \(v\in \varSigma ^+\) such that \(u\in S\) and \(\{wv \mid w\in S\} \subseteq S\), there exists \(\mathring{w}\in S'\) such that
and \(S'\) contains no two distinct comparable words. For all \(u\in \varSigma ^*\) and \(v\in \varSigma ^+\) such that \(u\in S\) and \(\{wv \mid w\in S\} \subseteq S\), there exists \(\mathring{w}\in S'\) such that  and
and  for some \(i, j \in \mathbb {N}\setminus \{0\}\).
for some \(i, j \in \mathbb {N}\setminus \{0\}\).
As in Sect. 3, we show that the equivalence (\(\dagger \)) holds but this time for an alternative definition of \(T_\mathcal {A} \) we provide next. Given a \(M\)-suitable FORQ  , let
, let

where for all \(p\in P\) the sets \(U_p\), \(W_p\) and \(\{V_p^w\}_{w\in \varSigma ^*}\) such that  ,
,  and
and  for all \(w \in \varSigma ^*\). Since \(\hat{T}_\mathcal {A} \subseteq T_\mathcal {A} \) by definition, it suffices to prove the implication \(\hat{T}_\mathcal {A} \subseteq M \Rightarrow \texttt {Ultim}_\mathcal {A} \subseteq M\). Let \(u^{}v^{\omega } \in \texttt {Ultim}_\mathcal {A} \), i.e., such that there exists \(s\in F_\mathcal {A} \) for which \(u \in \mathtt {Stem} _s\) and \(v \in \mathtt {Per} _s\), satisfying
for all \(w \in \varSigma ^*\). Since \(\hat{T}_\mathcal {A} \subseteq T_\mathcal {A} \) by definition, it suffices to prove the implication \(\hat{T}_\mathcal {A} \subseteq M \Rightarrow \texttt {Ultim}_\mathcal {A} \subseteq M\). Let \(u^{}v^{\omega } \in \texttt {Ultim}_\mathcal {A} \), i.e., such that there exists \(s\in F_\mathcal {A} \) for which \(u \in \mathtt {Stem} _s\) and \(v \in \mathtt {Per} _s\), satisfying  . In the context of Lemma 12, taking \(S \triangleq \mathtt {Stem} _s\) and \(S'\triangleq W_s\) fulfills the requirements \(u \in S\) and \(\{wv \mid w \in S\} \subseteq S\). We can thus apply the lemma and ensure the existence of some \(w_0 \in W_s\) satisfying
. In the context of Lemma 12, taking \(S \triangleq \mathtt {Stem} _s\) and \(S'\triangleq W_s\) fulfills the requirements \(u \in S\) and \(\{wv \mid w \in S\} \subseteq S\). We can thus apply the lemma and ensure the existence of some \(w_0 \in W_s\) satisfying  and
and  for some \(i, j \in \mathbb {N}\setminus \{0\}\). Since \(uv^i \in \mathtt {Stem} _s\) and \(v^j \in \mathtt {Per} _s\) we find that there exist \(u_0\in U_s\) and \(v_0\in V_s^{w_0}\) such that
for some \(i, j \in \mathbb {N}\setminus \{0\}\). Since \(uv^i \in \mathtt {Stem} _s\) and \(v^j \in \mathtt {Per} _s\) we find that there exist \(u_0\in U_s\) and \(v_0\in V_s^{w_0}\) such that  and
and  thanks to the finite basis property. We conclude from above that
thanks to the finite basis property. We conclude from above that  , hence that
, hence that  by the picky condition, and finally that
by the picky condition, and finally that  by Lemma 12 and transitivity. By definition \(u_0^{}v_0^{\omega } \in \hat{T}_\mathcal {A} \) and the proof continues as the one in Sect. 3 for \(T_\mathcal {A} \).
by Lemma 12 and transitivity. By definition \(u_0^{}v_0^{\omega } \in \hat{T}_\mathcal {A} \) and the proof continues as the one in Sect. 3 for \(T_\mathcal {A} \).
To summarize, if the considered FORQ fulfills the picky constraint then the algorithm of Fig. 2 remains correct when discarding the periods \(v\) at line 11 such that  . Observe that discarding one period \(v\) possibly means skipping several membership queries (\(u_1^{}v^{\omega }, u_2^{}v^{\omega },\ldots \)). As proved below, the picky constraint holds for all structural FORQs.
. Observe that discarding one period \(v\) possibly means skipping several membership queries (\(u_1^{}v^{\omega }, u_2^{}v^{\omega },\ldots \)). As proved below, the picky constraint holds for all structural FORQs.
Lemma 13
Let \(\mathcal {B} \triangleq (Q, q_I, \varDelta _\mathcal {B}, F_\mathcal {B})\) be a BA and  its structural FORQ. For all \(u \in \varSigma ^*\) and all \(v, v' \in \varSigma ^+\) if
its structural FORQ. For all \(u \in \varSigma ^*\) and all \(v, v' \in \varSigma ^+\) if  then
then  .
.
Proof
For all  , there exists \(q \in Q\) such that
, there exists \(q \in Q\) such that  . Hence
. Hence  . In fact
. In fact  holds as well since
holds as well since  . We deduce from the definition of \(\mathtt {Cxt}\) that
. We deduce from the definition of \(\mathtt {Cxt}\) that  which implies
which implies  . Thus
. Thus  , i.e.,
, i.e.,  . \(\square \)
. \(\square \)
We emphasize that this reduction of the number of membership queries was not included in our experimental evaluation since (1) the proof of correctness is simpler and (2) Forklift already scales up well without this optimization. We leave for future work the precise effect of such optimization.
Why a Basis for  is Computed? Taking periods in a basis for the ordering
is Computed? Taking periods in a basis for the ordering  where \(w \in \varSigma ^*\) is picked in a basis for the ordering
where \(w \in \varSigma ^*\) is picked in a basis for the ordering  may seem unnatural. In fact, the language preservation property of FORQs even suggests that an algorithm without computing a basis for
may seem unnatural. In fact, the language preservation property of FORQs even suggests that an algorithm without computing a basis for  may exist. Here, we show that taking periods in a basis for the ordering
may exist. Here, we show that taking periods in a basis for the ordering  where \(u \in \varSigma ^*\) is picked in a basis for the ordering
where \(u \in \varSigma ^*\) is picked in a basis for the ordering  is not correct. More precisely, redefining \(T_\mathcal {A} \) as
is not correct. More precisely, redefining \(T_\mathcal {A} \) as
where for all \(p\in P\) we have that  and
and  for all \(w \in \varSigma ^*\), leads to an incorrect algorithm because the equivalence (\(\dagger \)) given by \(\tilde{T}_\mathcal {A} \subseteq M \iff L(\mathcal {A}) \subseteq M\) no longer holds as shown below in Example 14.
for all \(w \in \varSigma ^*\), leads to an incorrect algorithm because the equivalence (\(\dagger \)) given by \(\tilde{T}_\mathcal {A} \subseteq M \iff L(\mathcal {A}) \subseteq M\) no longer holds as shown below in Example 14.
Example 14
Consider the BAs given by Fig. 1. We have that \(L(\mathcal {A}) \nsubseteq L(\mathcal {B})\) and, in Example 3, we have argued that \(T_\mathcal {A} = \{\varepsilon ^{}(b)^{\omega }, a^{}(a)^{\omega } \}\) contains the ultimately periodic \(a^\omega \) which is a counterexample to inclusion. Recall from Example 3 and 6 that we can set \(U_{p_I}=\{\varepsilon ,a\}\) since  , and \(V_{p_I}^{a}=V_{p_I}^{\varepsilon }=\{b\}\) since
, and \(V_{p_I}^{a}=V_{p_I}^{\varepsilon }=\{b\}\) since  and
and  . We conclude from the above definition that \(\tilde{T}_\mathcal {A} = \{ \varepsilon ^{}(b)^{\omega }, a^{}(b)^{\omega } \}\), hence that \(\tilde{T}_\mathcal {A} \subseteq L(\mathcal {B})\) which contradicts (\(\dagger \)) since \(L(\mathcal {A})\nsubseteq L(\mathcal {B})\).
. We conclude from the above definition that \(\tilde{T}_\mathcal {A} = \{ \varepsilon ^{}(b)^{\omega }, a^{}(b)^{\omega } \}\), hence that \(\tilde{T}_\mathcal {A} \subseteq L(\mathcal {B})\) which contradicts (\(\dagger \)) since \(L(\mathcal {A})\nsubseteq L(\mathcal {B})\).
9 Conclusion and Future Work
We presented a novel approach to tackle in practice the language inclusion problem between Büchi automata. Our antichain heuristics is driven by the notion of FORQs that extends the notion of family of right congruences introduced in the nineties by Maler and Staiger [29]. We expect the notion of FORQs to have impact beyond the inclusion problem, e.g. in learning [9] and complementation [26]. A significant difference of our inclusion algorithm compared to other algorithms which rely on antichain heuristics, is the increased number of fixpoint computations that, counterintuitively, yield better scalability. Indeed our prototype Forklift, which implements the FORQ-based algorithm, scales up well on benchmarks taken from real applications in verification and theorem proving.
In the future we want to increase further the search pruning capabilities of FORQs by enhancing them with simulation relations. We also plan to study whether FORQs can be extended to other settings like \(\omega \)-visibly pushdown languages.
Notes
- 1.
The notation \(\wp (E)\) denotes the set of all subsets of \(E\).
- 2.
A quasiorder \(\mathord {\ltimes }\) on \(\varSigma ^*\) is right-monotonic when \(u \ltimes v\) implies \( u\, w \ltimes v\, w\) for all \(w\in \varSigma ^*\).
- 3.
The case \(\mathord {\subseteq }\) is trivial. For the case \(\mathord {\supseteq }\), let \(u^{}v^{\omega }\) with \(u\in \mathtt {Stem} _s\) and \(v\in \mathtt {Per} _s\). If
 then we are done for otherwise consider the sequence \(\{uv^i\}_{i \in \mathbb {N}}\). Since
then we are done for otherwise consider the sequence \(\{uv^i\}_{i \in \mathbb {N}}\). Since 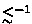 is a well-quasiorder, there exists \(x, y \in \mathbb {N}\) such that \(x < y\) and
is a well-quasiorder, there exists \(x, y \in \mathbb {N}\) such that \(x < y\) and 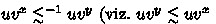 ). Therefore we have \((uv^x)^{}(v^{y-x})^{\omega } = u^{}v^{\omega }\), \((uv^x)\in \mathtt {Stem} _s\), \((v^{y-x})\in \mathtt {Per} _s\), and
). Therefore we have \((uv^x)^{}(v^{y-x})^{\omega } = u^{}v^{\omega }\), \((uv^x)\in \mathtt {Stem} _s\), \((v^{y-x})\in \mathtt {Per} _s\), and  .
. - 4.
The definition of the orderings, needed to compute the bases, are given in Example 6.
References
BAIT: an \(\omega \)-regular language inclusion checker. https://github.com/parof/bait. Accessed 17 Jan 2022
FORKLIFT: FORQ-based language inclusion formal testing. https://github.com/Mazzocchi/FORKLIFT. Accessed 7 Jun 2022
GOAL: graphical tool for omega-automata and logics. http://goal.im.ntu.edu.tw/wiki/doku.php. Accessed 17 Jan 2022
RABIT/Reduce: tools for language inclusion testing and reduction of nondeterministic Büchi automata and NFA. http://www.languageinclusion.org/doku.php?id=tools. Accessed 17 Jan 2022
ROLL library: Regular Omega Language Learning library. https://github.com/ISCAS-PMC/roll-library. Accessed 17 Jan 2022
Spot: a platform for LTL and \(\omega \)-automata manipulation. https://spot.lrde.epita.fr/. Accessed 17 Jan 2022
Abdulla, P.A.: Simulation subsumption in Ramsey-based Büchi automata universality and inclusion testing. In: Touili, T., Cook, B., Jackson, P. (eds.) CAV 2010. LNCS, vol. 6174, pp. 132–147. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14295-6_14
Abdulla, P.A.: Advanced Ramsey-based Büchi automata inclusion testing. In: Katoen, J.-P., König, B. (eds.) CONCUR 2011. LNCS, vol. 6901, pp. 187–202. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-23217-6_13
Angluin, D., Boker, U., Fisman, D.: Families of DFAs as acceptors of \(\omega \)-regular languages. Log. Meth. Comput. Sci. 14 (2018). https://doi.org/10.23638/LMCS-14(1:15)2018
Clemente, L., Mayr, R.: Efficient reduction of nondeterministic automata with application to language inclusion testing. Log. Meth. Comput. Sci. 15(1) (2019). https://doi.org/10.23638/LMCS-15(1:12)2019
De Wulf, M., Doyen, L., Henzinger, T.A., Raskin, J.-F.: Antichains: a new algorithm for checking universality of finite automata. In: Ball, T., Jones, R.B. (eds.) CAV 2006. LNCS, vol. 4144, pp. 17–30. Springer, Heidelberg (2006). https://doi.org/10.1007/11817963_5
Doveri, K., Ganty, P., Parolini, F., Ranzato, F.: Büchi automata benchmarks for language inclusion (2021). https://github.com/parof/buchi-automata-benchmark
Doveri, K., Ganty, P., Parolini, F., Ranzato, F.: Inclusion testing of Büchi automata based on well-quasiorders. In: 32nd International Conference on Concurrency Theory (CONCUR). LIPIcs (2021). https://doi.org/10.4230/LIPIcs.CONCUR.2021.3
Doyen, L., Raskin, J.F.: Antichains for the automata-based approach to model-checking. Log. Meth. Comput. Sci. 5(1) (2009). https://doi.org/10.2168/lmcs-5(1:5)2009
Duret-Lutz, A., Lewkowicz, A., Fauchille, A., Michaud, T., Renault, É., Xu, L.: Spot 2.0—a framework for LTL and \(\omega \)-automata manipulation. In: Artho, C., Legay, A., Peled, D. (eds.) ATVA 2016. LNCS, vol. 9938, pp. 122–129. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-46520-3_8
Duret-Lutz, A., et al.: From spot 2.0 to spot 2.10: what’s new? In: Shoham, S., Vizel, Y. (eds.) CAV 2022. LNCS, vol. 13372, pp. xx–yy (2022). https://doi.org/10.1007/978-3-031-13188-2_18
Esparza, J.: Automata Theory - An Algorithmic Approach. Lecture Notes (2017). https://www7.in.tum.de/~esparza/autoskript.pdf
Fogarty, S., Vardi, M.Y.: Efficient Büchi universality checking. In: Esparza, J., Majumdar, R. (eds.) TACAS 2010. LNCS, vol. 6015, pp. 205–220. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-12002-2_17
Heizmann, M.: Ultimate automizer and the search for perfect interpolants. In: Beyer, D., Huisman, M. (eds.) TACAS 2018. LNCS, vol. 10806, pp. 447–451. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-89963-3_30
Heizmann, M., Hoenicke, J., Podelski, A.: Software model checking for people who love automata. In: Sharygina, N., Veith, H. (eds.) CAV 2013. LNCS, vol. 8044, pp. 36–52. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39799-8_2
Hieronymi, P., Ma, D., Oei, R., Schaeffer, L., Schulz, C., Shallit, J.: Decidability for Sturmian words. In: 30th EACSL Annual Conference on Computer Science Logic (CSL). LIPIcs (2022). https://doi.org/10.4230/LIPIcs.CSL.2022.24
Kuperberg, D., Pinault, L., Pous, D.: Coinductive algorithms for Büchi automata. Fundam. Informaticae 180(4) (2021). https://doi.org/10.3233/FI-2021-2046
Kupferman, O., Vardi, M.Y.: Verification of fair transition systems. In: Alur, R., Henzinger, T.A. (eds.) CAV 1996. LNCS, vol. 1102, pp. 372–382. Springer, Heidelberg (1996). https://doi.org/10.1007/3-540-61474-5_84
Li, Y., Chen, Y.F., Zhang, L., Liu, D.: A novel learning algorithm for Büchi automata based on family of DFAs and classification trees. Inf. Comput. 281, 104678 (2020). https://doi.org/10.1016/j.ic.2020.104678
Li, Y., Sun, X., Turrini, A., Chen, Y.-F., Xu, J.: ROLL 1.0: \(\omega \)-regular language learning library. In: Vojnar, T., Zhang, L. (eds.) TACAS 2019. LNCS, vol. 11427, pp. 365–371. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17462-0_23
Li, Y., Tsay, Y.-K., Turrini, A., Vardi, M.Y., Zhang, L.: Congruence relations for büchi automata. In: Huisman, M., Păsăreanu, C., Zhan, N. (eds.) FM 2021. LNCS, vol. 13047, pp. 465–482. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-90870-6_25
de Luca, A., Varricchio, S.: Well quasi-orders and regular languages. Acta Informatica 31(6) (1994). https://doi.org/10.1007/BF01213206
Maler, O., Staiger, L.: On syntactic congruences for ω—languages. In: Enjalbert, P., Finkel, A., Wagner, K.W. (eds.) STACS 1993. LNCS, vol. 665, pp. 586–594. Springer, Heidelberg (1993). https://doi.org/10.1007/3-540-56503-5_58
Maler, O., Staiger, L.: On syntactic congruences for \(\omega \)-languages. Theor. Comput. Sci. 183(1) (1997). https://doi.org/10.1016/S0304-3975(96)00312-X
Maler, O., Staiger, L.: On syntactic congruences for \(\omega \)-languages. Technical report, Verimag, France (2008). http://www-verimag.imag.fr/~maler/Papers/congr.pdf
Oei, R., Ma, D., Schulz, C., Hieronymi, P.: Pecan: an automated theorem prover for automatic sequences using Büchi automata. CoRR abs/2102.01727 (2021). https://arxiv.org/abs/2102.01727
Piterman, N.: From nondeterministic Büchi and Streett automata to deterministic parity automata. Log. Meth. Comput. Sci. 3(3) (2007). https://doi.org/10.2168/lmcs-3(3:5)2007
Tsai, M., Fogarty, S., Vardi, M.Y., Tsay, Y.: State of Büchi complementation. Log. Meth. Comput. Sci. 10(4) (2014). https://doi.org/10.2168/LMCS-10(4:13)2014
Tsai, M.-H., Tsay, Y.-K., Hwang, Y.-S.: GOAL for games, omega-automata, and logics. In: Sharygina, N., Veith, H. (eds.) CAV 2013. LNCS, vol. 8044, pp. 883–889. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39799-8_62
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2022 The Author(s)
About this paper
Cite this paper
Doveri, K., Ganty, P., Mazzocchi, N. (2022). FORQ-Based Language Inclusion Formal Testing. In: Shoham, S., Vizel, Y. (eds) Computer Aided Verification. CAV 2022. Lecture Notes in Computer Science, vol 13372. Springer, Cham. https://doi.org/10.1007/978-3-031-13188-2_6
Download citation
DOI: https://doi.org/10.1007/978-3-031-13188-2_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-13187-5
Online ISBN: 978-3-031-13188-2
eBook Packages: Computer ScienceComputer Science (R0)





 holds.
holds.
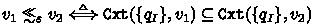 where
where


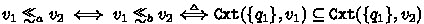 where
where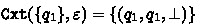
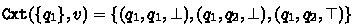 for all
for all 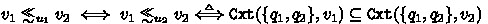 for all
for all 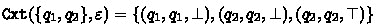
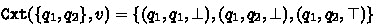 for all
for all 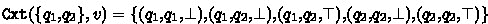 for all
for all 

 then we are done for otherwise consider the sequence
then we are done for otherwise consider the sequence  is a well-quasiorder, there exists
is a well-quasiorder, there exists  ). Therefore we have
). Therefore we have  .
.