1 Introduction

One of the key elements in the current technology development of rocket propulsion systems typical for cryogenic upper stage rocket engines like, e.g., the Vinci engine of Ariane 6, for cryogenic reaction and control system thrusters or for orbital and manoeuvring system engines is the substitution of toxic propellants like hydrazine by green propellants as well as the introduction of advanced ignition technologies like laser ignition [17]. These kind of rocket engines are all operating at high-altitude conditions. Hence, the used propellants are injected into a low-pressure atmosphere within the combustion chamber prior to ignition due to the vacuum of space. This means that the ambient pressure \(p_\infty \) is below the saturation pressure \(p_{sat}(T_{inj})\) at the corresponding injection temperature \(T_{inj}\) of the injected liquid fuel. During this sudden pressure drop the liquid gets into a metastable thermodynamic state called superheated. As a consequence of the superheated state, the liquid jet evaporates eruptively and expands fastly, which is called flash boiling. The evaporation chills down the two-phase flow and raises the pressure inside the combustor until the equilibrium or the desired operation pressure immediately before ignition is reached. An effective determination of ignition parameters for a secure operation of the rocket engine without any destructive pressure peaks requires to know the actual conditions of the propellants in the combustion chamber in terms of phase, temperature distribution, atomisation behaviour and species.

1.1 Flash Boiling

The injection temperature \(T_{inj}\) and the chamber or back pressure \(p_{ch}\) are the dominating injection parameters for flash boiling in a given liquid. The degree of superheat of a superheated liquid can be defined by those two parameters as the pressure ratio

$$\begin{aligned} R_{p} = \frac{p_{sat}(T_{inj})}{p_{ch}} \end{aligned}$$
(1)

or as the ratio of the temperature differences

$$\begin{aligned} \Delta T^*= \frac{\Delta T}{\Delta T_{sat}}= \frac{T_{inj}-T_{sat}(p_{ch})}{T_{sat}(p_{inj})-T_{sat}(p_{ch})} \end{aligned}$$
(2)

with the saturation temperatures \(T_{sat}(p_{ch})\) and \(T_{sat}(p_{inj})\) at the chamber pressure \(p_{ch}\) and at the injection pressure \(p_{inj}\), respectively, according to Fig. 1. For high degrees of superheat the injected jet is atomising close to or already in the injector which leads to the generation of a fine and wide-opened spray consisting of small droplets. According to reference [40] aerodynamical effects on the jet break-up can be neglected in flash boiling sprays. A new equilibrium state is reached after the chill-down of the two-phase system to the saturation state at \(T_{sat}(p_{ch})\) due to evaporation and expansion. Some authors even observed solidification of storable propellants during high-altitude injection due to strong chill-downs below the triple point [34]. Due to the complex nature of these non-equilibrium processes during the transient start-up phase of cryogenic rocket engines at high-altitude conditions, detailed experimental data is required.

Fig. 1
figure 1

p-T phase diagram of a superheated liquid injected into a low-pressure atmosphere with adiabatic depressurization

Full size image

1.2 State of Research

Liquid jet atomisation by the process of flash boiling is known since the beginning of the 20th century [18, 36]. Within the automotive industry, flash boiling of storable fluids like gasoline, diesel or similar substitute fuels were investigated in the last three decades [1,2,3, 10, 29, 30]. An increase of engine efficiency and a reduction of the exhaust emissions was reached by a stronger atomisation of the fuel due to an artificial superheated state by its pre-heating. [30]. Flash boiling due to nucleation within the liquid jet was observed as the predominant fuel atomisation mechanism while cavitation in the injector can be neglected [1]. Two different kinds of nucleation processes can occur which depend on the degree of superheat, the initial fuel temperature, the ambient pressure, the fuel’s critical temperature and the geometry [19, 31, 35]. The two types differ from each other by their mechanism and place of origin: The so-called homogeneous nucleation takes place within the bulk liquid itself, whereas the heterogeneous nucleation process needs a foreign phase like, e.g., at the interface between the nozzle wall and the liquid. The atomisation of a fuel can be enhanced by forced flash boiling after mixing the fuel with low boiling liquids of low concentrations [10]. Araneo and Dondè studied the injection of hydrocarbon sprays generated by a multi-hole injector [2]. They found a relation between the spray angle and the injection conditions by the analysis of backlight shadowgraphy images. Phase Doppler Anemometry (PDA) measurements in hydrocarbon sprays were performed by the same authors to show a similar break-up behavior of jets with dissolved air compared to superheated jets [3]. Several models were developed for the determination of the average spray droplet diameters in superheated water sprays [32], to predict nucleation rates and droplet sizes in flash boiling hydrocarbon sprays [29] or for the prediction of superheat within water sprays during a depressurization transient [7]. In the context of process safety in other industrial sectors like nuclear, chemical or process technology, studies about flash boiling of the storable liquids water, refrigerants like R-134A, ethanol or further hydrocarbons were published [4, 7, 28, 33, 39]. It was found that the injection conditions like the injection pressure and the diameter of the injector orifice influence the intensity of flash boiling besides the degree of superheat [39]. By shadowgraph imaging the region of the actual axial and radial jet break-up was identified as remaining liquid core within the flash boiling spray close to the injector orifice [28, 33]. Three characteristic break-up modes of flash boiling water sprays were found and differentiated into an aerodynamical break-up region, a fully flashing region and a transition region between both. These regions were empirically quantified by the usage of the dimensionless Weber and Jakob numbers derived from the injection conditions [4, 37]. The resulting correlations were found to be valid also for the superheated fluids acetone, ethanol and iso-octane within study [13]. In the same study an onset criterion basing on the classical nucleation theory for the inception of flash boiling as well as a model for the prediction of the spray angle close to the injector orifice depending on the degree of superheat and the dimensionless surface tension were developed. The difficult operating conditions due to the cryogenic as well as the high-altitude environments are the reason for only few experimental studies concerning cryogenic sprays atomised by flash boiling compared to storable fluids. In one of those few studies liquid nitrogen (LN2) sprays with about 10 s injection duration and varying injection conditions were visualised by means of high-speed shadowgraphy [16]. Besides maximum spray angles of about 140\(^{\circ }\), the study revealed that the influence of the injection geometry and the injection pressure on the spray angle evolution is negligible and that the LN2 sprays are cooling down below the triple point why solidification occurs at temperature measurement sensors which were positioned along the spray’s central axis. An experimental study about laser ignition of a coaxially with gaseous hydrogen injected superheated liquid oxygen (LOX) jet was performed at test bench M3.1 at DLR Lampoldshausen within a model rocket combustion chamber under high-altitude conditions [5]. However, the co-flow of the gaseous hydrogen suppressed the spray widening and significantly narrower spray angles were observed compared to flash boiling sprays of mono-component jets. During the first two funding periods of the SFB TRR75 project the influence of two different injection configurations on the flash boiling process of LOX jets was investigated at the same test bench facility. A comparison of the results with the data of storable fluids in study [12] revealed similar spray morphologies despite the strongly varying physical properties of the used fluids. However, the injection system of test bench M3.1 is limited in terms of controlling and adjusting the desired injection temperature since only the two different temperature levels \(T_\text {inj}={94}\,\text {K}\) and \(T_\text {inj}={113}\,\text {K}\) were achieved. Furthermore, these temperatures were measured about 200 mm away from the actual injector and they were very sensitive to ambient conditions because the injection system was not thermally insulated from the atmosphere around the test bench.

In this chapter we provide a summary about the behaviour of flash boiling LN2 sprays in respect of their degrees of superheat and their injection conditions. With the experimental data of these sprays we generate a comprehensive data base for further numerical investigations about cryogenic flash boiling, like e.g. in the studies [8, 9].

2 Experimental Set-Up

Since the adjustment and control of the injection temperature \(T_{inj}\), especially, was partly limited in the few experimental studies about cryogenic flash boiling and this temperature is the dominating parameter for the flash boiling process besides the back pressure \(p_{ch}\), these two parameters have to be adjustable, controllable during the injection period and reproducible for a systematic experimental investigation. Hence, we are operating the newly built test bench M3.3 at DLR Lampoldshausen [22, 25].

2.1 Cryogenic Test Bench M3.3

This test bench which is depicted in Fig. 2, can be divided into its three subsystems media supply and pressurization system, a cryogenic temperature adjustment and injection system (CTAIS) and a vacuum system. The first one serves as an interface between the gas infrastructure of DLR Lampoldshausen and the test bench to distribute and pressurize all gases (nitrogen, helium, oxygen) needed for the operation of the CTAIS, the second subsystem of the test bench. Basically, this system consists of an inner pressure tank with the actual test fluid LN2 or LOX within an outer one filled with the cooling agent liquid and gaseous nitrogen (GN2). The double-walled and vacuum-insulated casing of the outer pressure tank can be seen in Fig. 2 on the left and right. The temperature of the cooling agent within this thank is controlled by evacuating or pressurizing the GN2 phase depending on whether the fluid has to be cooled down or heated up, respectively: To reach a new saturation state after evacuation, LN2 vaporizes and the latent heat of vaporization necessary for this phase change causes a loss of heat of the two-phase nitrogen system and consequently to a decrease of its temperature. In the case of pressurization the new saturation state is achieved by condensation of the gaseous nitrogen phase which releases its latent heat of condensation and heats up the two-phased nitrogen. The inner pressure tank, also called run-tank, with a volume of 0.5 L is much smaller and quickly reaches the temperature of the surrounding cooling fluid. Apart from the run-tank, the injector unit with a pneumatic run valve and an injector nozzle, a coriolis mass flowmeter and piping in-between complete the test fluid feed and injection system, as can be seen in the middle of Fig. 2. Hence, the whole feed and injection system is surrounded by the cooling agent LN2/GN2 which ensures a homogeneous temperature distribution from the run-tank to the injector nozzle. For the secure operation of the CTAIS, for its temperature control and adjustment as well as to know the injection parameters of the test fluid, the CTAIS is equipped with various temperature and pressure sensors. Especially close to the injector a Pt100 temperature sensor as well as a dynamic pressure sensor of the type 601A by Kistler are installed not further than about 30 mm upstream of the injector nozzle exit. For safety reasons the cable ducts of the sensor cables inside the outer pressure tank are pressurized by gaseous helium which is also used as working fluid for the pneumatically triggered axial run valve of the type Axius by Stöhr Armaturen. The supply pipes for helium, for the test fluid and for the cooling agent as well as the sensor cables are connected to the media supply and pressurization system by a hand hole positioned at the top of the outer pressure tank. The third sub-system, i.e. the vacuum system, consists of a cylindrical chamber with an outer diameter of 360 mm, an inner diameter of 300 mm and a height of 225 mm from the injector nozzle exit to the bottom of the chamber. Four windows, installed at an angle of 90\({}^\circ \) to each other, with a diameter of 100 mm each provide an optical access to the interior of the vacuum chamber for spray visualisation and optical measurement techniques. Because of the cryogenic operation conditions the humidity of the ambient atmosphere condensates and freezes on the test bench’s surfaces. This is why we are operating a window heating with warm GN2 to prevent icing of the optical accesses. The copper pipes of the heating system can be seen on the right-hand side of Fig. 2 below and besides the cylindrical window. The near-vacuum atmosphere within the vacuum chamber for the high-altitude requirement is generated by a vacuum pump with a pumping speed of 87.5 \(\text {m}^{3}/h\) attached to the chamber. To get rid of the humidity within the CTAIS, all its pipes, tanks and vessels have to be evacuated before starting the chill-down process with LN2. The latter takes, e.g., about 90 minutes until a target test fluid temperature of 90 K is reached [24]. During the chill-down the gaseous test fluid nitrogen is filled into the run-tank and gets liquefied in the meantime. In our study [24] we show that the CTAIS allows a constant injection temperature \(T_{inj}\) during the whole injection time of about 2 s without significantly being affected by ambient conditions surrounding the test facility. In contrast to the former injection system at test bench M3.1, the CTAIS of test bench M3.3 enables the adjustment of the injection temperature within the range of \({77}\, \text {K} \le T_{inj} \le {96}\,\text {K}\) with a reproducibility of \(\pm {0.6}\,\text {K}\) for each test run and a homogeneous temperature distribution in the whole feed line systems [21, 22, 25].

Fig. 2
figure 2

Main sub-systems of DLR test bench M3.3: media supply and pressurization system, opened CTAIS, vacuum system (left); opened CTAIS with test fluid feed and injection system, i.e. run-tank, injector unit and sensors in-between (middle); chilled-down test bench during operation (right) [23]

Full size image

2.2 Injection Conditions

In our first measurement campaign we generate about 120 superheated LN2 sprays with varying injection parameters and visualise these sprays with the help of high-speed shadowgraph imaging. The respective temperature and pressure values are listed in Table 1. The injector with a sharp edge, a length-to-diameter ratio of \(\nicefrac {L}{D} = {2.9}\) and a diameter of \(D_{inj} = {1}\, \text {mm}\) is used during the whole measurement campaign. Further details about the injector can be found in references [23, 26]. From the total amount of the generated sprays we are analysing 22 of them more closely. Their injection conditions and \(R_\text {p}\)-values are listed in Table 2. Other parameters of those sprays like their degrees of superheat \(\Delta T\) and \(\Delta T^*\) or their dimensionless numbers like the Weber numbers \(We_\text {g,l} = \nicefrac {\rho _\text {g,l} u_\text {inj}^2 D_\text {inj}}{\sigma }\) for the gaseous and liquid phase, the Reynolds number \(Re = \nicefrac {\rho _\text {l} u_\text {inj} D_\text {inj}}{\eta }\), the Ohnesorge number \(Oh = \nicefrac {\sqrt{We}}{Re}\) and the Jakob number \(Ja = \nicefrac {\rho _\text {l} c_\text {p,l} \Delta T}{\rho _\text {g} \Delta h_\text {vap}}\) can be found in our study [26]. For their evaluation we are using the density \(\rho _\text {g}\) and \(\rho _\text {l}\) of the gaseous and liquid phase, respectively, the velocity of the liquid within the injector \(u_\text {inj}\), its diameter \(D_\text {inj}\), the liquid’s surface tension \(\sigma \), heat capacity \(c_\text {p,l}\), heat of vaporization \(h_\text {vap}\) and dynamic viscosity \(\eta \). The investigated 22 LN2 sprays are generated within the ranges of \({4}< We_\text {g} < {856}\) for the gaseous Weber number, \(1.73\cdot 10^{4}< We_\text {l} < {8.30\cdot 10^{4}}\) for the liquid Weber number, \({3}< Ja < {2001}\) for the Jakob number, \({8.19\cdot 10^{4}}< Re < {1.82\cdot 10^{5}}\) for the Reynolds number and \({1.45\cdot 10^{-3}}< Oh < {1.74\cdot 10^{-3}}\) for the Ohnesorge number.

Table 1 Range of the injection parameters of the generated LN2 sprays for high-speed shadowgraphy; republished with permission of Begell House Inc., from reference [26], permission conveyed through Copyright Clearance Center, Inc
Full size table
Table 2 Injection parameters of the 22 LN2 sprays for the high-speed shadowgraphy campaign
Full size table

In a second measurement campaign we generate LN2 sprays with a high degree of superheat of \(R_\text {p} \approx {60}\) to determine their droplet behaviour. Since the laser-based PDA measurement technique is a point measuring method instead of a global one, we set constant injection parameters for all of the sprays and the same injector as in the first measurement campaign is used. The respective parameter values are listed in Table 3. For comparison reasons we are using the definition of the degree of superheat \(R_{p}\) according to Eq. (1) despite its obviously big tolerance range in our analysed sprays. The huge range can be explained by deviations of the back pressure \(p_{ch}\) which strongly affects the degree of superheat.

Table 3 Injection conditions of the used LN2 sprays for PDA
Full size table

2.3 High-Speed Shadowgraphy

A high-speed shadowgraphy set-up with backlight illumination is used to visualise the flash boiling LN2 sprays [25,26,27]. According to the scheme in Fig. 3, we illuminate the generated sprays from one side of the chamber. The light of a xenon light source is bundled and directed by a parabolic mirror to one of the chamber windows in front of which we are using a translucent frosted glass for a homogeneous spray background. On the opposite side of the chamber we set-up the high-speed camera with its focus on the central plane of the injector. The camera Photron Fastcam SA-X is set to a frame rate of 10000 fps, a pixel resolution of \(1024 \times 1024\) pixels and a spatial resolution of 0.02 mm/pixel. For further details about this optical set-up as well as for the post-processing of the raw images we refer to our work [26]. In that study, we also show that steady-state spray conditions are reached after a period of about \({100}\,\textrm{ms}<t_\text {inj}<{120}\,\textrm{ms}\) after triggering the start of the injection process. Hence, we choose \(t_\text {inj}={120}\,\textrm{ms}\) as steady-state evaluation time and all of the investigated sprays are analysed at this time, except spray #8 which is optically too dense at \(t_\text {inj}={120}\,\textrm{ms}\) and is analysed at \(t_\text {inj}={100}\,\textrm{ms}\) instead.

Fig. 3
figure 3

High-speed backlight shadowgraphy set-up at test bench M3.3; republished with permission of Begell House Inc., from reference [26], permission conveyed through Copyright Clearance Center

Full size image

2.4 Phase Doppler System

We set-up the PDA system by the manufacturer Dantec Dynamics in a so-called 2D fibre configuration which allows the simultaneous measurement of the vertical and horizontal components of the droplet velocity and the droplet diameter distributions, which is depicted in Figs. 4 and 5 (left). By moving the optical components, namely the transmitter and the receiver probes, with the help of the 2D-traverse system various measurement positions in axial and radial directions within the sprays can be set. The geometrical alignment of the transmitter and the receiver probe to each other is depicted on the left of Fig. 4. The given geometry of the vacuum chamber in terms of its optical accesses allows a maximum intensity of scattering light by the dominant first order refraction for an off-axis angle of \(\varphi = {12}^{\circ }\) between both PDA probes. Tilting not only the receiver but also the transmitter with \(\varphi _\text {reci} = {5}^{\circ }\) and \(\varphi _\text {trans} = {7}^{\circ }\), respectively, expands the maximum field of view which is limited by the diameter and frame structures of the optical accesses. Basing on this field of view we can specify the measurement position matrix according to the right-hand side of Fig. 5. For each position of this matrix we generate at least one single wide flashing LN2 spray and record the data for a time of 12 s. Hence, we can not exclude small shot-to-shot variations between each test run at a certain measurement position. The data recording is synchronized with the trigger signal for the start of the injection process. As mentioned in Sect. 2.3, the steady-state of the injection process starts at \(t_\text {inj}={120}\,\textrm{ms}\) and, according to our study [24], ends after \(t_\text {inj}={220}\,\textrm{ms}\). Consequently, the detected Doppler signals are evaluated within this duration by the calculation of their arithmetical mean values. Two diode pumped solid state (DPSS) lasers with a wavelength of 488 nm and 514 nm, respectively, are used within the PDA system. We are operating both lasers at a power of approximately \({9}\,\text {mW}\), each measured at the position of the measurement volume prior to the first test run. The receiver probe is equipped with a spatial filter in terms of a 100 \(\upmu \text {m}\) slit. We can quantify a systematical measurement error of \(\pm {26}\,{\%}\) for the diameter determination as well as the maximum statistical errors \(\Delta U = \pm {6.1}\,{\text {m}}/{\text {s}}\), \(\Delta V = \pm {8.0}\,{\text {m}}/{\text {s}}\) and \(\Delta D = \pm {3.3}\,\upmu \text {m}\). For further details about the set-up, calibration and adjustment procedures as well as error estimation we refer to our work [23].

Fig. 4
figure 4

Optical alignment of the 2D Fibre PDA system at test bench M3.3 (left) and used aperture of the receiver probe (right) [23]

Full size image
Fig. 5
figure 5

2D Fibre PDA system at test bench M3.3 (left) and position matrix of measurement points in wide flashing LN2 sprays (right) [23]

Full size image

3 Results and Discussion

3.1 Shadowgraph Images Analysis

The shadowgraph images of a test series containing the 16 sprays #1 to #16 with varying degrees of superheat from \( {3.0} \le R_\text {p} \le {52.3}\) but at a constant injection temperature of \(T_\text {inj} = {82.5\pm 0.6}\,\text {K}\) are depicted in Fig. 6. The first two rows of shadowgraph images with the sprays #1 to #8 show the influence of a growing degree of superheat \(R_\text {p}\) on the spray morphology by a gradual reduction of the back pressure \(p_\text {ch}\) from 60 to 3.6 kPa. Their injection pressure is kept constant at \(p_\text {inj} = {800\pm 30}\,\text {kPa}\). Lowly superheated sprays with \(R_\text {p} \approx {3}\) still show aerodynamical break-up patterns like large liquid ligaments. An example of the latter is highlighted on the left-hand side of Fig. 7. Here, the relative motion of the surrounding chamber atmosphere with the surface of the liquid jet is still a dominant factor for the break-up of the jet. With growing degrees of superheat the jet collapse gets more and more eruptive and produces sprays with wider opening angles due to the decreasing influence of the chamber atmosphere and the simultaneous increase of internal energy in the liquid jet. This energy dissipates by enhanced vaporization. A further increase of superheat by back pressure reduction culminates in the heavily flash boiling sprays #7 and #8 with a bell-shaped spray pattern and opening angles of almost 180\(^{\circ }\). Especially in the highly superheated spray #8 with a degree of superheat of \(R_\text {p} = {28.4}\), the liquid jet breaks up already at the injector outlet around a liquid core in axial and radial direction. Such a liquid core is exemplarily shown on the right-hand side of Fig. 7. A detailed analysis and model about the relation between these remaining liquid cores and the degree of superheat is discussed in our publication [27]. Apart from these liquid cores, no other liquid structures with a magnitude of one millimetre or more remain in that highly superheated sprays. As discussed in our publication [26] the heterogeneous nucleation is the predominant process of nucleation compared to the homogeneous one for the sprays #1-#22 due to lower injection temperatures than the minimum necessary temperature for the inception of homogeneous nucleation according to references [6, 15, 19, 20].

Fig. 6
figure 6

Shadowgraph images of LN2 sprays #1-16 with varying degrees of superheat from \( {3.0} \le R_\text {p} \le {52.3}\) at \(T_\text {inj} = {82.5}\,\text {K}\)

Full size image
Fig. 7
figure 7

Shadowgraph images of LN2 spray #1 with highlighted liquid ligament (left) and of spray #8 with highlighted remaining liquid core (right)

Full size image

The third and fourth rows of shadowgraph images in Fig. 6 with the sprays #9 to #16 show the effect of the injection pressure \(p_\text {inj}\) on the spray pattern of flash boiling LN2 sprays. Here, the pressure is reduced by half to a value of \(p_\text {inj} = 400\pm 20\,\text {kPa}\). The other injection parameters like the temperature \(T_\text {inj}\) as well as the gradual reduction of the back pressure \(p_\text {ch}\) are the same as in the case of the sprays #1 to #8. Obviously, the general trend of the spray evolution with increasing degrees of superheat does not change significantly compared to the sprays #1 to #8, i.e. a decline of larger liquid structures due to enhanced evaporation and a widening of the spray. However, at low degrees of superheat the sprays #9 to #12 with the lower injection pressure are wider than the sprays #1 to #4. The lower injection pressure leads to weaker flow-dynamic effects of the chamber atmosphere on the surface of the LN2 jet because of a lower flow velocity \(u_\text {inj}\) in the injector and therefore a less pronounced relative motion between the two phases [26]. Furthermore, the residence time of the LN2 within the injector is higher, and therefore also the nucleation rate, as a consequence of the lower injection pressure. Hence, the ratio between flash boiling and aerodynamical break-up is shifted towards the more dominant flash boiling process already at low degrees of superheat. For higher degrees of superheat of \(R_\text {p} \ge {12}\) the jet break-up is solely driven by flash boiling why the influence of the different relative flow dynamics in the chamber nearly disappears and the spray patterns look very similar to the ones at the higher injection pressure.

Fig. 8
figure 8

Experimental data of superheated acetone and ethanol by the study of Lamanna et al. [13] as well as data of several LN2 sprays with respect to the break-up regime correlations from studies [4, 37]; republished with permission of Begell House Inc., from reference [26], permission conveyed through Copyright Clearance Center

Full size image

In Fig. 8 the dimensionless numbers \(We_\text {g}\) and Ja of superheated acetone and ethanol sprays from reference [13] are depicted with respect to the three different break-up regimes aerodynamical break-up, transition and fully-flashing according to the studies [4, 37]. Taking into account our data about superheated LN2 like the sprays #16 to #21 as well as some more LN2 sprays with varying injection temperatures of \({81}\,\text {K}< T_\text {inj} < {93}\,\text {K}\) demonstrates that our LN2 measurement campaign extends the validity range of the break-up regime correlations by two orders of magnitude towards higher Weber numbers. The LN2 sprays #22, #10 and #7 are depicted exemplarily in Fig. 9a–c to demonstrate the validity of the three break-up regimes aerodynamical break-up, transition regime and fully-flashing regime, originally derived for storable fluids, also for the cryogenic fluid LN2. Further details can be found in our work [26].

Determining the spray angles at the axial distance \(\nicefrac {L}{D} = {1}\) from the injector orifice by analysis of the shadowgraph images reveals spray angles of \(\theta > {170}^{\circ }\) for LN2 sprays with very high degrees of superheat in the range of \({18} \le R_\text {p} \le {192}\) like the sprays #8 and #16 to #21. In our work [26] we show that above a threshold angle of \(\theta _\text {thresh} \approx {160}^{\circ }\) the spray patterns look the same as, e.g., the one of spray #16 and do not significantly change any more despite increasing degrees of superheat. We call the break-up mechanism of these wide-opened and very highly superheated sprays wide flashing with the corresponding analytical correlation in terms of the Weber and the Jakob number

$$\begin{aligned} Ja \, \Phi = 330 \, We_\text {g}^{-\frac{1}{7}} \end{aligned}$$
(3)

with the Jakobs number Ja, the Weber number of the gaseous phase \(We_\text {g}\) and the factor

$$\begin{aligned} \Phi = 1 - \exp {\left[ -2300\frac{\rho _\text {g}}{\rho _\text {l}}\right] }. \end{aligned}$$
(4)

This curve is depicted as pink line in Fig. 8 and represents the transition from the fully flashing regime according to reference [4] into the newly introduced wide flashing regime [26]. A respective wide flashing LN2 spray is shown exemplarily in Fig. 9d).

Fig. 9
figure 9

Four exemplary superheated LN2 sprays (#22, #10, #7 and #16) to demonstrate the classic break-up regimes a aerodynamical break-up, b transition regime and c fully flashing regime according to study [4] and the new d wide flashing regime [26]

Full size image

3.2 PDA Results

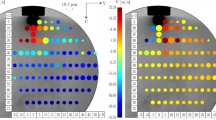
As listed in Table 3 in Sect. 2.2, the used wide flashing LN2 sprays for the PDA measurement campaign are highly superheated with an injection temperature of \(T_\text {inj}={89.7}\,\text {K}\) and a resulting degree of superheat of \(R_\text {p}={60}\). Their injection pressure is held constant at \(p_\text {inj}=4.4\cdot 10^5\,\text {Pa}\). The spatial distributions of the two mean velocity components vertical velocity U (left) and horizontal velocity V (right) as well as the droplet mean diameter \(D_\text {10}\) in these LN2 sprays are depicted in Fig. 10. Here, each data circle represents one single injection event and includes a colour code for the velocity value while the circle size represents the mean diameter of the droplet set at this position. The respective scales can be found in the figure. In the near-injector region with \({-10} \le \nicefrac {x}{D} \le {10}\) and \({10} \le \nicefrac {y}{D} \le {20}\) the highest vertical droplet velocities with values of \(U={50}-{70}\,{\text {m}}/{\text {s}}\) are measured. Since these droplets are moving at significantly higher vertical velocities than the flow velocity within the injector with a value of \(u_\text {inj}={18.1}\,{\text {m}}/{\text {s}}\), the explosive acceleration of the droplets due to evaporation and their subsequent expansion due to the flash boiling process is demonstrated. With growing radial direction the vertical droplet velocities are decreasing strongly because of the dominant radial momentum in the spray expansion from positions with \(\nicefrac {x}{D} \ge {15}\). The pronounced change of the velocity magnitude between the spray’s central axis and its periphery is the result of a complex interaction between non-equilibrium fluid transition effects and gas dynamics: Due to the high degree of superheat the liquid nitrogen nucleates within the injector and bubbles are generated already inside of it. As a consequence, the flow within the injector becomes choked and the speed of sound of the two-phased LN2 flow is reduced significantly. This leads to an under-expanded two-phase jet behaviour with a Prandtl-Mayer expansion flow at the exit of the injector [8, 11, 13]. Multiple characteristic expansion waves around the spray axis lead to the strong acceleration in this region while towards the spray edges only a few of them contribute to a significantly lower acceleration of the flow. After a vertical distance of \(\nicefrac {y}{D} \ge {30}\) from the injector exit after which the Mach disc is passed, the measured vertical velocities U are getting considerably smaller and the deviation to the vertical droplet velocities at the spray’s radial edges nearly disappears. This is due to a flattening of the vertical velocity profile as a consequence of the normal shock uniformly decelerating the flow in the radial direction. The right-hand side of Fig. 10 with the spatial profiles of the mean horizontal velocities V is consistent with these considerations since the measured horizontal droplet velocities at positions \(\nicefrac {y}{D} > {40}\) become more and more uniform and homogeneous because of the Prandtl-Mayer expansion system with the decelerating normal shock [23]. The spatial distributions of both velocity components reveal that the near-injector region is the zone with the highest droplet velocities. Here, the transformation of the internal energy within the LN2 jet into kinetic one takes place. [23].

Fig. 10
figure 10

Spatial distributions of the mean vertical velocity U (left), the mean horizontal velocity V (right) and of the droplet mean diameter \(D_\text {10}\) in wide flashing LN2 sprays [23]

Full size image

Concerning the droplet mean diameters \(D_\text {10}\), this near-injector region reveals small droplets with diameters as small as \(D_\text {10} = {6.5}\,{\upmu \text {m}}\) with no clear trend especially at the position \(\nicefrac {y}{D}={5}\) according to Fig. 10. However, the limitations of optical diagnostic techniques like PDA in these optically dense regions is repeatedly observed in literature [4, 14, 38]. Especially, the extensive presence of non-spherical particles and ligaments leads to low validation rates and biases the determination of the droplet diameters. Downstream in the region \({10} \le \nicefrac {y}{D} \le {30}\) the biggest mean diameters with values between 14 \({\upmu \text {m}}\) and 18.5 \({\upmu \text {m}}\) are measured within the centre of the spray. Laterally, the droplets are getting smaller with measured mean diameters of \(D_\text {10} \le {10}\,{\upmu \text {m}}\). In line with the velocity measurements, the droplet size distribution gets more and more uniform with mean diameters of \(D_\text {10} = {8}-{10}\,{\upmu \text {m}}\) at positions \(\nicefrac {y}{D} > {40}\). Reaching this monodisperse-like droplet diameter distribution shows that the upstream existing non-spherical liquid particles disintegrate by further evaporation and expansion during the flash boiling process. However, at the edges of the spray at positions of \(\nicefrac {x}{D} > {30}\) we observe an unsteady distribution with even increasing droplet diameters. As can be seen in Fig. 11, at these spray positions flow interactions between the LN2 spray and the window margins of the vacuum chamber occur which affects the diameter measurement and leads to an increase in diameter. These effects including recirculation flows are discussed in detail in our publication [23].

Fig. 11
figure 11

Flow interactions between a highly superheated LN2 spray and the window margins of the vacuum chamber

Full size image

The analysis of the PDA measurement data reveals two separate droplet populations at certain measurement positions within the LN2 sprays. The major distinctive factor of the two populations is a high mean vertical velocity of about \(U = {40}\,{\text {m}}/{\text {s}}\) for the so-called upper, or Hi-population while the one of the lower Lo-population is much lower with values even below zero. This is exemplarily shown on the left of Fig. 12 for the spray position \(\nicefrac {x}{D} = {0}\) and \(\nicefrac {y}{D} = {30}\). In contrast, however, the measurement data of the horizontal velocity does not show any distinguishable droplet populations. According to our data, we empirically choose a threshold value of \(U_\text {thresh}={5}\,{\text {m}}/{\text {s}}\) for the separation of the Hi-population with vertical mean velocity values of \(U>U_\text {thresh}={5}\,{\text {m}}/{\text {s}}\) from the Lo-population with velocities below the threshold. Besides the quite low vertical velocity range of \({-25}\,{\text {m}}/{\text {s}}< U_\text {Lo} < {5}\,{\text {m}}/{\text {s}}\) of the Lo-population, its droplet diameters are slightly smaller than the ones of the Hi-population. As shown in detail in our work [23], the range of the Hi-population with \({10}\,{\text {m}}/{\text {s}}< U_\text {Lo} < {70}\,{\text {m}}/{\text {s}}\) is much higher and strongly depends on the axial distance from the injector. The measurement position matrix of Fig. 5 from Sect. 2.4 is depicted on the right of Fig. 12 to show the local occurrence of the two droplet populations: At every blue coloured measurement position both populations are clearly distinguishable from each other. Furthermore, these positions coincide with flow recirculation zones caused by the shock systems mentioned above and observed in our studies [23, 26]. That allows us to conclude that the upstream direction of motion of the droplets in the Lo-population is due to these recirculation zones and the droplets’ capability to follow the gas flow of the wide flashing LN2 sprays. The bigger droplets of the Hi-population, however, do not seem to be affected by those zones of high-dynamic gas flows. Instead, their higher inertia ensures that they flow along the initial flow trajectories which are characterized by the injection conditions prior and during the injection.

Fig. 12
figure 12

Two droplet populations at the spray position \(\nicefrac {x}{D} = 0\) and \(\nicefrac {y}{D} = 30\) with their measured vertical velocities U as functions of the time t and of the measured droplet diameter \(D_\textrm{dro}\) (left) [22]; measurement position matrix in wide flashing LN2 sprays with local occurrence of Hi- and Lo-populations (right) [23]

Full size image

4 Conclusions

With the analysis of more than 200 superheated flash boiling liquid nitrogen (LN2) sprays by the optical measurement techniques high-speed shadowgraphy and laser-based Phase-Doppler droplet diagnostics (PDA) we generated a comprehensive data base about flash boiling LN2 sprays at high-altitude conditions which facilitates further numerical modelling. The closer examination of 22 of those LN2 sprays revealed an illustrative evolution of lowly superheated sprays with a narrow and turbulent shape to highly superheated ones with big opening angles and fine droplets depending on the injection conditions. Small changes like halving the injection pressure, e.g., did primarily affect only lowly superheated sprays in terms of wider spray cones due to enhanced nucleation within the injector compared to the ones with a higher injection pressure. With increasing degrees of superheat, these influences got negligible due to the growing dominance of flash boiling. We successfully applied correlations about break-up regimes derived for storable fluids on our test fluid LN2, extended the validity range of these correlations by about two orders of magnitude and introduced a new break-up regime called wide flashing regime for highly superheated jets. The droplet velocity and diameter measurements in wide flashing LN2 sprays by PDA revealed maximum vertical and horizontal mean velocities in the highly energetic near-injector region. Here, the transformation of the liquid’s internal energy into kinetic one takes place and the spray expands as a consequence of the evaporation processes. Due to the common known limitation of the PDA technique in the near-injector region the measured droplet diameters in this region are statistically not very reliable. However, the data rate increases drastically with growing axial distance to the injector and an almost monodisperse spray pattern develops with a homogeneous droplet distribution. Furthermore, at certain spray positions we observed the existence of two separate droplet populations which are distinguishable from each other mainly by the velocity magnitude, the direction of motion and also slightly by the diameters of their respective droplets. The separation is caused by recirculation zones due to the typical shock systems in flash boiling sprays and due to spray interaction with the structure of the vacuum chamber.